Расчет эквивалентного сопротивления цепи — Dudom

Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением R_экв, и вся схема представляется в виде схемы на рис. 1.3, где R=R_экв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.

Электрическая цепь с последовательным соединением элементов

Рис. 1.4

Рис. 1.5

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).

На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков.

Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R_экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

,

и по вышеприведенным формулам рассчитывают падение напряжений U₁, U₂, U₃ на соответствующих участках электрической цепи (рис. 1.4).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I₁ + I₂ + I₃, т.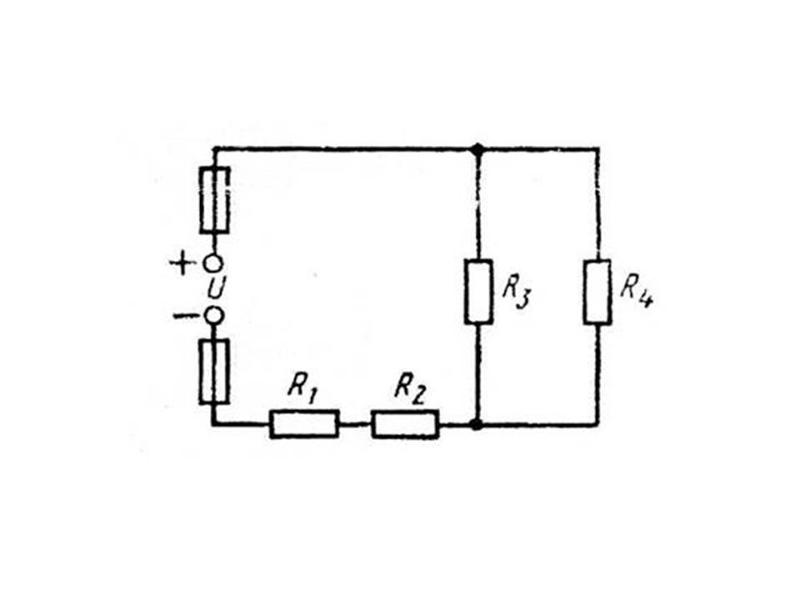 е.

,

откуда следует, что

.

В том случае, когда параллельно включены два сопротивления R₁ и R₂, они заменяются одним эквивалентным сопротивлением

.

Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление R_экв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

Отсюда следует, что

,

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R₁=R₂=R₃=R₄=R₅=R. Сопротивления R₄ и R₅ включены параллельно, тогда сопротивление участка цепи cd равно:

.

В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

На схеме (рис. 1.8) сопротивление R₃ и R_cd соединены последовательно, и тогда сопротивление участка цепи ad равно:

.

Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

На схеме (рис. 1.9) сопротивление R₂ и R_ad соединены параллельно, тогда сопротивление участка цепи аb равно

.

Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R₁ и R_ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

.

Рис. 1.10

Рис. 1.11

В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R_экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

Соединение элементов электрической цепи по схемам «звезда» и «треугольник»

В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R₁₂, R₁₃, R₂₄, R₃₄ включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.

Рис. 1.12

Рис. 1.13

В мостовой схеме сопротивления R₁₃, R₁₂, R₂₃ и R₂₄, R₃₄, R₂₃ соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R₂₄ R₃₄ R₂₃ звездой R₂ R₃ R₄ (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:

; ; .

Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:

; ; .

После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)

.

Любое последовательное соединение можно преобразовать к последовательному соединению одного эквивалентного резистора и одного источника ЭДС. Причем, сопротивление эквивалентного резистора равно сумме всех сопротивлений входящих в соединение, а ЭДС эквивалентного источника равна алгебраической сумме ЭДС источников входящих в соединение.

Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.

9. СОЕДИНЕНИЕ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ

Схему еоедииения трех ветвей, образующих замкнутый контур с тремя узлами называют треугольником.

взаимные замены треугольника и звезды сопротивлений должны быть эквивалентными, т.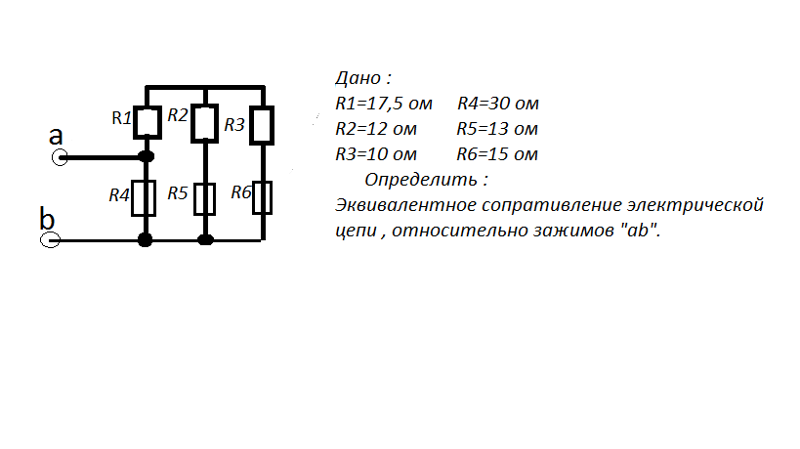

е. при соответственно равных напряжениях между вершинами А, Б и В треугольника и звезды токи I_A, I_Б, 1_В в подводящих проводах, соединяющих эти вершины с остальной частью цепи, должны остаться без изменений. Равенство токов должно выполняться при любых изменениях и переключениях в остальной части цепи и, в частности, при обрывах некоторых ее ветвей.

Рис 2.8 Соединение резисторов треугольником (а) и звездой (б)

Сопротивления эквивалентной звезды r_а, r_б, r_в находятся в определенных соотношениях с сопротивлениями треугольника r

аб, r_бв, r_ва. Для выяснения этой зависимости допустим сначала, что в вершине А произошел обрыв подводящего провода и, следовательно, ток I_а=0. Сопротивления между двумя оставшимися присоединенными вершинами Б и В для обеих схем должны быть одинаковы, чтобы были соответственно равны токи I_Б и I_в в обеих схемах.

Чтобы преобразовать треугольник в звезду при заданных сопротивлениях сторон треугольника r_аб,r_бв, r_ва, требуется определить сопротивления лучей эквивалентной звезды r_а, r_б, r_в .

Для этого составим полусумму левых и правых частей уравнений (2.15) и (2.16):

и вычтем из полученного выражения уменьшенные вдвое левую и правую части (2.14). В результате получим

(2.17)

(2.18)

сли сопротивления треугольника равны друг другу: r_аб = r_бв=r_ва=r_Δ, то будут равны друг другу и сопротив

ления звезды, т. е. r_а = r_б=r_в=r _λ, причем из формул (2.17)—(2.19) получается простое соотношение

(2.20)

При обратном преобразовании звезды в эквивалентный треугольник, т. е. при заданных сопротивленияхr_а, r_б, r_в, надо решить три уравнения (2.17)—(2 19) относительно сопротивлений r_аб, r_бв:

Таким образом, сопротивление стороны эквивалентного треугольника равно сумме сопротивлений двух лучей звезды, присоединенных к тем же вершинам, что и сторона треугольника, и их произведения, деленного на сопротивление третьего луча звезды.

11. Режимы работы электрической цепи

· Режим короткого замыкания ( КЗ )

В режиме короткого замыкания источник питания замкнут накоротко. Режим является аварийным. Ток короткого замыкания КЗ во много раз превышает значение номинального тока.

· Режим холостого хода ( ХХ )

В режиме холостого хода источник питания отсоединен от нагрузки и работает вхолостую. Сопротивление внешнего участка цепи и ток равен 0. R_н = ∞

· Режим согласованной нагрузки

Свойства электрической цепи – наибольшая мощность нагрузки развивается источником, когда сопротивление нагрузки ровно внутреннему сопротивлению источника.

Из графика видно с ростом сопротивления нагрузки растёт мощность на нагрузке при R_н = I₀ мощность нагрузки наибольшая при дальнейшем росте Rн – P_Rн уменьшается.

К выполнению контрольной работы

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Пример методики решения задачи №1. «Расчет цепей постоянного тока»

Для схемы, приведенной на рисунке 1.1, заданы сопротивления резисторов и ток I₄ в резисторе R₄. Определить:

1.эквивалентное сопротивление цепи R_AB,

2. токи в каждом резисторе,

3. напряжение U_AB, приложенное к цепи.

Решение. Задача относится к теме «Электрические цепи постоянного тока» После усвоения условия задачи приводим поэтапное решение, предварительно обозначив стрелкой направление тока в каждом резисторе. Индекс тока должен соответствовать номеру резистора, по которому он проходит.

1.1. Определяем общее сопротивление разветвления R₂, R₃. Резисторы соединены

= Ом

Теперь схема принимает вид, показанный на рисунке 1.2

1.2 Резисторы R_2,3 и R₅ соединены последовательно, их общее сопротивление

Соответствующая схема приведена на рисунке 1. 3

1.2. Резисторы R_2,3,5 и R₄ соединены параллельно, их общее сопротивление

Ом

Теперь схема цепи имеет вид, приведенный на рисунке 1.4

1.3. Находим эквивалентное сопротивление всей цепи:

2.Определение токов в резисторах

2.1.Зная силу тока I₄, находим напряжение на резисторе R₄:

Это же напряжение приложено к резисторам R_2,3 +R₅ (рисунок 1.2.). Поэтому ток в

2.2 Находим падение напряжения на резисторе R₅:

Поэтому напряжение на резисторах R₂ и R₃:

2.3 Определяем токи в резисторах R₂ и R₃ :

Применяя закономерности параллельного соединения резисторов, находим ток в резисторе R₁:

2.4. Вычисляем падение напряжения на резисторе R₁:

3. Находим напряжение U_AB, приложенное ко всей цепи:

Задача 1 (Варианты 01 – 30)

Цепь постоянного тока содержит шесть резисторов, соединенных смешанно.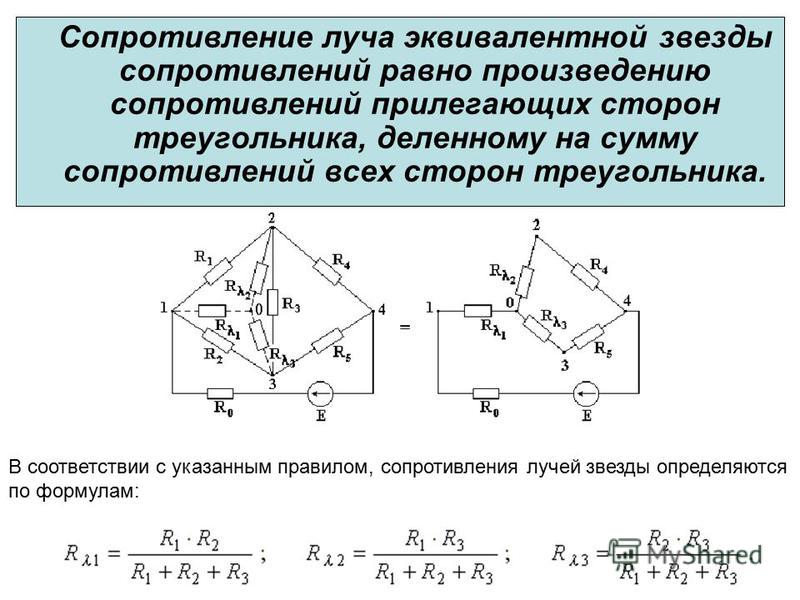 Схема цепи и значения резисторов указаны на соответствующем рисунке. Номер рисунка и величина одного из заданных токов или напряжений приведена в таблице 3. Индекс тока или напряжения совпадает с индексом резистора, по которому проходит этот ток или на котором действует указанное напряжение. Например, через резистор R₅ проходит ток I₅ и на нем действует напряжение U₅. Определить:

1) эквивалентное сопротивление цепи относительно вводов АВ;

2) ток в каждом резисторе;

3) напряжение на каждом резисторе;

4) расход электрической энергии цепью за 10 часов.

Эквивалентное сопротивление резисторов определить эквивалентное

Расчет реальной электрической цепи в идеальном виде невозможен по причине отсутствия математических методик учета индивидуальных параметров каждого составляющего элемента. Это естественно, так как любая деталь имеет свои паразитные характеристики, которые нереально учесть при расчетах. Для устранения этой проблемы было введено понятие эквивалентной замены. При этом в расчет принимается только одна определяющая характеристика элемента. Так, например, эквивалентное сопротивление резисторов в электрической схеме, отображает только величину сопротивления без влияния на него сторонних факторов.

В электротехнике существует два основных варианта включения деталей в электрической цепи – это последовательное и параллельное соединение. Объединяющей для них является смешанная схема, которая по сути может быть разбита на участки с вышеприведенными характеристиками.

Рассмотрим эквивалентное соединение резисторов в каждом отдельном случае.

Эквивалентное сопротивление при последовательно соединенных резисторов

При данном типе размещения резисторов в цепи условная схема будет соответствовать рис. 1.

Рисунок 1

Для того чтобы определить эквивалентное сопротивление резисторов необходимо вспомнить закон Ома. Для последовательного соединения он гласит что общее, а в нашем случае эквивалентное сопротивление, соответствует следующему уравнению:

R_экв= R₁+R₂+R₃+R_N-1+R_N

Рассмотрим пример последовательного соединения трех резисторов, сопротивление которых равно 10, 20 и 30 Ом, соответственно. Согласно выше приведенной формуле общее сопротивление всех этих резисторов на данном участке цепи будет равно 60 Ом. Таким образом, при расчетах параметров электрической схемы нет надобности использовать индивидуальные характеристики отдельных элементов. Их можно просто заменить одним значением эквивалентным их сумме.

Кроме теории, данное суммирование значений сопротивлений элементов, имеет и практическое применение – в случае необходимости всегда можно заменить несколько резисторов одним. Также имеет место и обратное утверждение – при отсутствии деталей с требуемой характеристикой ее можно заменить на несколько других, эквивалентное сопротивление которых будет соответствовать требуемому значению.  Все это справедливо и для параллельного соединения резисторов, только с некоторыми особенности.

Эквивалентное сопротивление при параллельном соединении резисторов

Общая схема при данном включении резисторов в цепь соответствует рис. 2.

Рисунок 2

Определить эквивалентное сопротивление параллельно соединенных резисторов позволяет закон Ома согласно которому, в данном варианте, справедливо равенство:

1/R _экв =1/R₁+1/R₂+1/R₃+1/R _N-1+1/R_N

Возвращаясь к нашему примеру с резисторами 10, 20 и 30 Ом. Можно определить эквивалентное сопротивление для данного случая, преобразуя уравнение и получаем следующую формулу:

R _экв = R₁ х R₂ х R₃ / (R₁ x R₂) + (R₁ x R₃) + (R₂ x R₃) = 5,45 Ом

Важный момент: При параллельном включении резисторов в цепь эквивалентное сопротивление будет всегда меньше наименьшего значения отдельного элемента. При последовательном соединении R _экв обязательно больше самого большого параметра.

Эквивалентное сопротивление при смешанном соединении резисторов

Определение эквивалентного сопротивления при смешанном соединении резисторов не представляет особых сложностей. Для этого достаточно разбить существующую цепочку на логические составляющие – блоки. Т.е. максимально упростить схему, приведя ее в соответствие с характеристиками свойственных тому или иному типу соединения. На рис. 3 приведена типичная схема упрощения, которая получила название метод свертывания цепи.

Рисунок 3

Данная схема позволяет наглядно понять, как можно определить эквивалентное сопротивление резисторов при смешанном соединении. Обращаем внимание, что начинать процесс упрощения можно в произвольном порядке. Так, например, объединение резисторов R₁ и R₂ не обязательно должно быть первым шагом. Можно совершенно смело на первом этапе найти R _экв сумме сопротивлений последовательно включенных в цепь резисторов R₄ и R₅.  Определение эквивалентного сопротивления для резисторов необходимо осуществлять в зависимости от типа соединения.

В заключение вернемся к самому понятию эквивалентной замены резисторов. В рассмотренных нами случаях речь шла об идеальном варианте. То есть в расчет принимается только величина сопротивления при нулевых значениях остальных характеристик. Также обращаем внимание, что при составлении эквивалентной схемы любых элементов электрической цепи, не только резисторов, можно вводить дополнительные переменные, которые будут влиять на конечные итоги.

Добавить отзыв

| Определить эквивалентное сопротивление цепи

Задача 3.12.

Определить эквивалентное сопротивление цепи, в которой XL=XC=R=10 Ом.

Задача 3.13.

Чему равно эквивалентное сопротивление цепи?

Задача 3.14.

При каком соотношении величин ток I на входе цепи опережает по фазе напряжение U?

3.6. Цепь синусоидального тока при смешанном соединении элементов.

Для цепей синусоидального тока справедливы все формулы расчета цепей постоянного тока, но в комплексной форме. Поэтому методика расчета цепей при смешанном соединении элементовсводится к постепенному упрощению схемы путем замены отдельных участков эквивалентными сопротивлениями, в результате чего определяется эквивалентное сопротивление всей цепи.

Решить задачи:

Задача 3.15.

Для электрической цепи, представленной на рисунке, найти полное сопротивление Z всей цепи при ХL=5 Ом, R=XC=10 Ом.

Задачи 3.16.

Найти комплексное сопротивление Z всей цепи при ХL=10 Ом, R=20 Ом, XC=5 Ом.

Задача 3.17.

Определить характер нагрузки цепи, если ХL=R=XC.

3.7. Мощность цепи синусоидального тока.

3.7.1. Мгновенная мощность – произведение мгновенных значений напряжения и тока, т. е. p=u*i.

Распишем её для отдельных элементов цепи, приняв начальную фазу для напряжения φu=0:

— цепь с резистивным (активным) элементом (см. рис. 3.5,а):

Рис. 3.10

Мгновенная мощность имеет две составляющие: постоянную и переменную , изменяющуюся по косинусоидальномузакону с удвоенной частотой.

В этой цепи мгновенная мощность всегда положительная, и энергия в цепи передается в одном направлении от источника к приемнику, где она полностью (необратимо) преобразуется в другие виды энергии (рис. 3.10).

— цепь с индуктивным элементом (см. рис. 3.6a )

Мгновенная мощность – переменная, изменяется по синусоидальному закону с удвоенной частотой. При возрастании тока i по абсолютной величине мгновенное значение мощности p>0, в это время происходит накопление энергии в магнитном поле индуктивности. При уменьшении тока i по абсолютной величине p<0 и в это время индуктивность становится источником электроэнергии (рис 3.11).

Рис 3.11

— цепь с емкостным элементом(см. рис. 3.7,а)

Мгновенная мощность – переменная, изменяющаяся по синусоидальному закону с удвоенной частотой.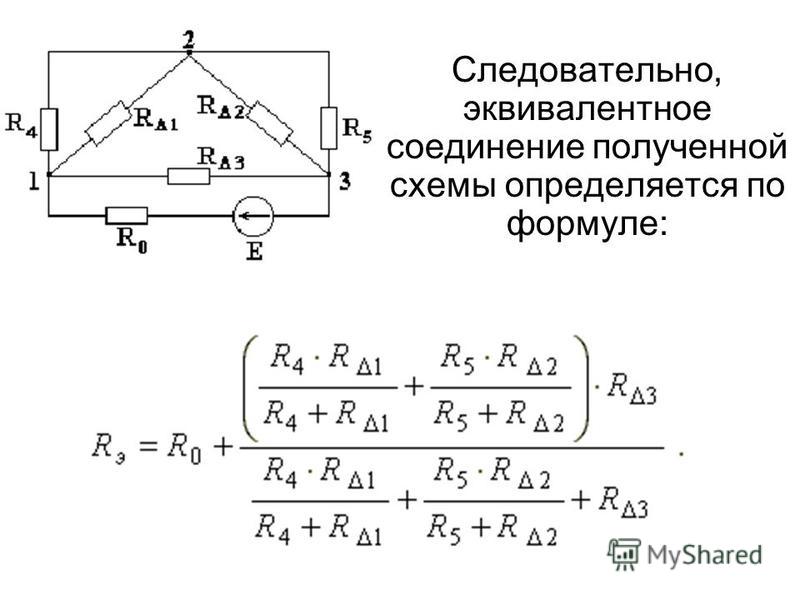 При возрастании тока по абсолютной величине мгновенное значение мощности p<0, в это время емкость становится источником электроэнергии. При уменьшении тока по абсолютной величине p>0, в это время происходит накопление энергии в электрическом поле емкости (рис 3.12).

Рис 3.12

3.7.2. Активная мощность – мощность необратимых преобразований электрической энергии на участке цепи за период:

Из формулы следует, что средняя за период мощность не равна нулю, если участок цепи имеет активное сопротивление.

3.7.3. Реактивная мощность – мощность реактивных элементов полейpP=pL+pC в среднем за период равна нулю, но в течение четверти периода она положительна, что означает накопление энергии в магнитном поле катушки или электрическом поле конденсатора, а в течение следующей четверти периода – отрицательная, что соответствует обратному процессу.

Таким образом, имеет место процесс колебания энергии, но необратимых преобразований энергии (при отсутствии активной мощности) нет.

3.7.4. Полная мощность. Под полной мощностью участка цепи понимается максимально возможная мощность при заданных значениях тока I и напряжения U.

Необходимость введения понятия мощности заключается в том, что при конструировании любых электрических устройств их рассчитывают на определенное номинальное напряжение Uном и на определенный номинальный ток Iном, а их произведение Sном=UномIном дает максимально возможную мощность данного устройства (именно она указывается в паспорте большинства электрических устройств переменного тока).

Связь между различными мощностями:

Для облегчения запоминания этих формул можно обратить к так называемому треугольнику мощности (рис 3.13).

Рис 3.13

3.7.5. Коэффициент мощности.

Коэффициент мощности показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии, в том числе используется для выполнения полезной работы.

Для повышения коэффициента мощности применяются меры, которые сводятся или к уменьшению реактивной мощности QL или к ее компенсации мощностью QC.

Решить задачу.

Задача 3.18.

Выбрать схему, которая является рациональной для увеличения cosφ, где Ском – компенсирующая емкость, Rпр, Lпр – активное и индуктивное сопротивление приемника соответственно.

Что такое эквивалентная схема и как она используется?

При анализе электрических цепей, в том числе для асинхронных двигателей переменного тока и двигателей постоянного тока, если цепь содержит два или более одинаковых пассивных элемента (например, резисторы) и соединена исключительно последовательно или исключительно параллельно, цепь может быть нарисована с более простым представлением, которое содержит источник напряжения и один эквивалентный пассивный элемент. Эта упрощенная версия сохраняет электрические характеристики исходной схемы и называется 9.0003 эквивалентная схема .

---

Пассивные элементы — это элементы, которые рассеивают, хранят или выделяют энергию в форме напряжения или тока. Примерами пассивных элементов являются резисторы , конденсаторы и катушки (иначе катушки индуктивности).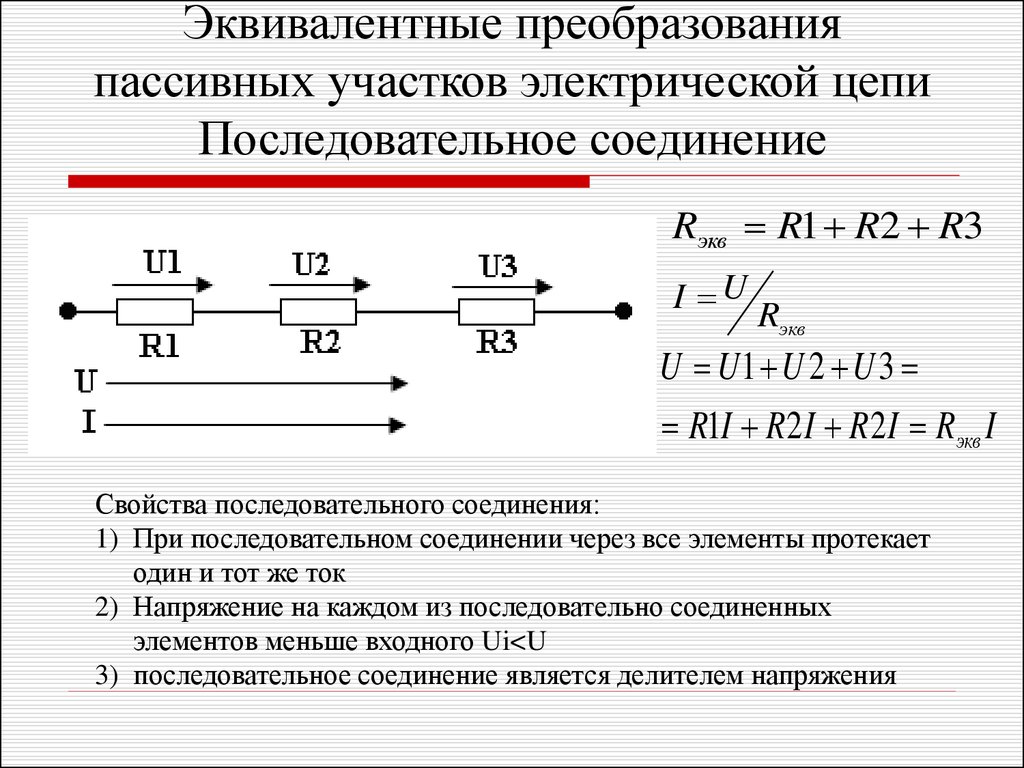

Активные элементы передают или производят энергию в форме напряжения или тока. Они включают полупроводниковые компоненты, такие как диоды, транзисторы (полевые транзисторы или полевые транзисторы и полевые транзисторы металл-оксид-полупроводник или полевые МОП-транзисторы).

---

Правила объединения резисторов для создания эквивалентной цепи основаны на законе Ома вместе с законами Кирхгофа.

Первый из законов Кирхгофа, известный как Текущий закон Кирхгофа (KCL), утверждает, что количество тока, протекающего в любой узел (соединение) в замкнутой цепи, равно количеству тока, протекающего из этого узла , тем самым обеспечивая сохранение заряда в замкнутом контуре.

Второй закон Кирхгофа, обозначаемый как Закон напряжения Кирхгофа (KVL) гласит, что для замкнутой цепи алгебраическая сумма всех напряжений вокруг цепи равна нулю. Закон напряжения Кирхгофа обеспечивает сохранение энергии в замкнутой цепи.

---

Нахождение эквивалентного сопротивления для последовательных цепей

Для последовательно соединенных цепей закон напряжения Кирхгофа, KVL, говорит нам, что напряжение вокруг цепи будет равно нулю. Это означает, что сумма падений напряжения на каждом резисторе будет равна напряжению питания. Для последовательной цепи с тремя резисторами напряжение питания, В _s , равно сумме напряжений на трех резисторах (V _R1 , V _R2 и V _R3 ):

любой узел равен заряду, вытекающему из этого узла. Последовательные цепи имеют только один узел (соединение), поэтому ток одинаков во всех точках цепи. Это означает, что через каждый резистор протекает один и тот же ток. Используя закон Ома, V = IR, чтобы выразить напряжение на каждом резисторе, мы можем переписать приведенное выше уравнение:

Теперь мы можем видеть, что эквивалентное сопротивление — это просто сумма всех сопротивлений в последовательной цепи.

Теперь напряжение можно выразить эквивалентным сопротивлением.

В приведенном ниже примере показана последовательная цепь с тремя резисторами.

Для этой схемы эквивалентное сопротивление:0036 экв. ).

Мы можем проверить нашу эквивалентную схему, рассчитав напряжение на эквивалентном резисторе и убедившись, что оно равно напряжению питания: каждая петля как отдельная цепь, соединенная последовательно. Закон напряжения Кирхгофа, KVL, говорит нам, что в каждой отдельной петле (последовательной цепи) падение напряжения на резисторе равно напряжению питания. Для параллельной цепи с тремя резисторами падение напряжения на каждом резисторе равно напряжению питания.

Согласно токовому закону Кирхгофа, KCL, ток делится в каждом узле или переходе так, что: закон:

Переставляя по напряжению, получаем:

Теперь эквивалентное сопротивление можно определить как:

находится путем сложения обратных величин отдельных значений сопротивления, а затем взятия обратной суммы.

В этой параллельной цепи с тремя резисторами эквивалентное сопротивление равно:

Опять же, мы можем проверить нашу эквивалентную схему, убедившись, что напряжение на эквивалентном резисторе равно напряжению питания:

5

---

Законы Кирхгофа, применяемые к последовательным цепям:  Для цепи, соединенной последовательно, напряжение, протекающее по цепи, делится между пассивными элементами, но ток через каждый пассивный элемент одинаков.

Законы Кирхгофа о цепях, применяемые к параллельным цепям: Для цепи, соединенной параллельно, напряжение, протекающее по цепи, одинаково на каждом пассивном элементе, но ток делится между пассивными элементами.

---

 

Эквивалент Thévenin’s And Norton

---

Эквивалент Тевенина и Нортона

 

---

  Пример 1: Найдите эквивалент Тевенина схемы

Решение: Шаг 1: Расчет цепи холостого хода           Шаг 2: Ток короткого замыкания Шаг 2: Другой способ найти Отключить источники напряжения, произвести короткое замыкание Отключить источники тока, разомкнуть цепь Затем рассчитать  из схемы Окончательное сопротивление равно

 

---

Эквивалентная схема Нортона :

Эквивалентная схема Нортона представляет собой общую схему с независимым источником тока, включенным параллельно с эквивалентным сопротивлением Нортона. Источник тока Norton ( ) эквивалентен току короткого замыкания на клеммах a и b Сопротивление Norton такое же, как сопротивление Thévenin. Для предыдущего примера Исходное преобразование От эквивалентной схемы Тевенина до Нортона От эквивалентной схемы Norton до Thévenin Может применяться к цепям общего назначения

---

Примеры:

Пример 1: Найдите представления эквивалентной схемы Тевенина и Нортона для следующей схемы

Раствор 2 источника тока и 2 параллельных сопротивления Преобразование источника тока 2 серийных резистора

 

---

Пример 2 : Найдите эквивалентную схему Тевенина для следующей схемы

Метод 1 Шаг 1. Найдите напряжение холостого хода, которое будет равно . Шаг 2: Отключите источник напряжения и замкните соединение источника Метод 2:  Использовать исходное преобразование Трансформация источника напряжения 2 параллельных сопротивления Преобразование источника тока 2 серийных резистора

 

---

Пример 3: Найдите эквивалент Тевенена и Нортона относительно терминалов a и b.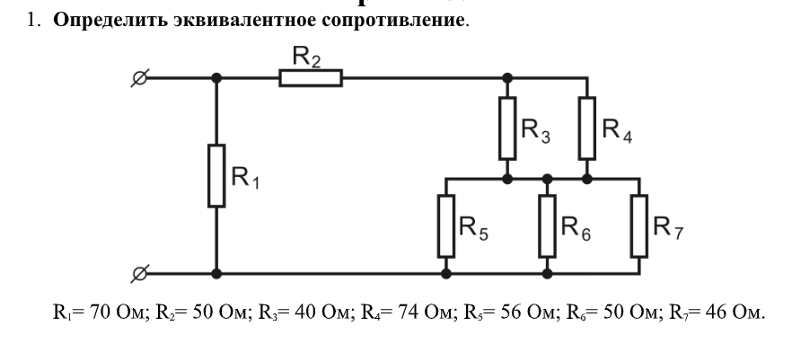

Использование метода 2 Преобразование источника напряжения 2 параллельных источника тока и 2 параллельных сопротивления Преобразование источника тока 2 резистора серии Преобразование источника напряжения 2 параллельных сопротивления

 

---

Практические задачи :

(Щелкните изображение, чтобы просмотреть решение)

Задача 1: Найдите эквивалент Тевенена и Нортона относительно терминалов a и b

Просмотр решения

---

Проблема 2: .

Посмотреть решение

Найдите такое значение RL, чтобы передаваемая мощность была максимальной. Каково максимальное значение Силы, передаваемой в RL? Подсказка: теорема Тевенина

---

Проблема 3:

Посмотреть решение

---

Проблема 4:

Посмотреть решение

---

Задача 5 :

Просмотр решения

---

Упражнения:

4

4

4

---

Опрос:

---

« Назад

---

19.3 Параллельные схемы | Техасский шлюз

Цели обученияПараллельное соединение резисторовУпражнения на резисторах, включенные параллельно и последовательноУпражнения на проверку знаний

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Интерпретировать принципиальные схемы с параллельными резисторами
• Расчет эквивалентного сопротивления комбинаций резисторов, содержащих последовательные и параллельные резисторы

Ключевые термины раздела

параллельно

Параллельные резисторы

В предыдущем разделе мы узнали, что последовательно соединенные резисторы — это резисторы, соединенные один за другим.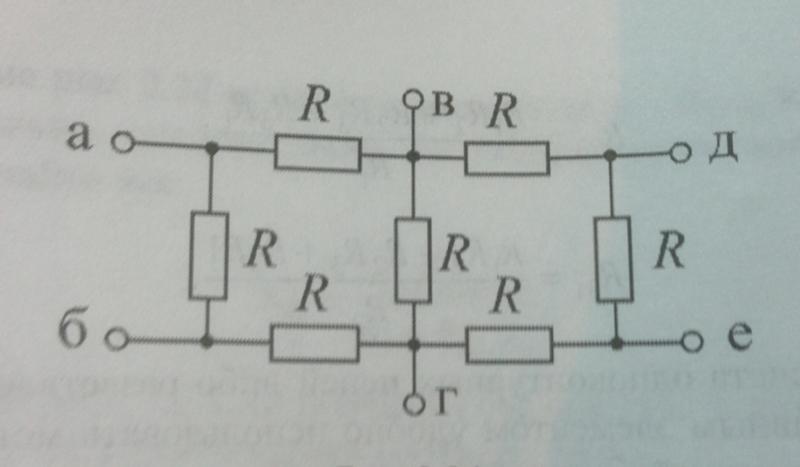 Если вместо этого мы объединим резисторы, соединив их рядом друг с другом, как показано на рисунке 19..19, то говорят, что резисторы соединены параллельно . Резисторы параллельны, когда оба конца каждого резистора соединены напрямую друг с другом.

Обратите внимание, что все вершины резисторов подключены к одному и тому же проводу, поэтому напряжение на вершине каждого резистора одинаково. Точно так же все основания резисторов подключены к одному и тому же проводу, поэтому напряжение внизу каждого резистора одинаково. Это означает, что падение напряжения на каждом резисторе одинаково. В этом случае падение напряжения равно номинальному напряжению В аккумулятора, потому что верхний и нижний провода подключаются к положительному и отрицательному полюсам аккумулятора соответственно.

Хотя падение напряжения на каждом резисторе одинаково, мы не можем сказать то же самое о токе, протекающем через каждый резистор.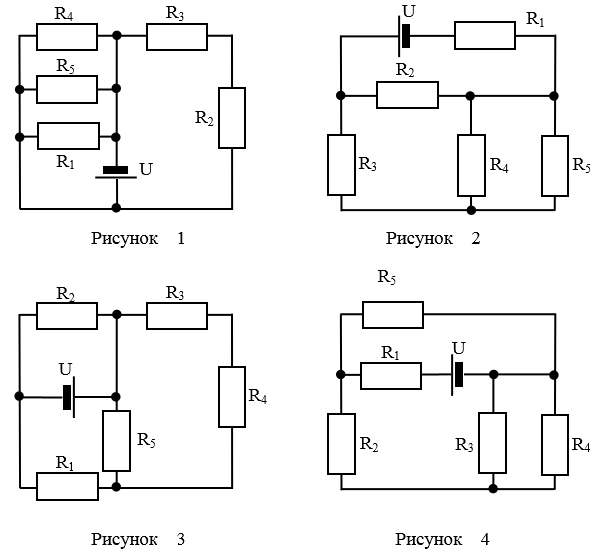 Таким образом, I1, I2, и I3I1, I2, и I3 не обязательно одинаковы, поскольку резисторы R1, R2, и R3R1, R2, и R3 не обязательно имеют одинаковое сопротивление.

Обратите внимание, что три резистора на рис. 19.19 обеспечивают три различных пути, по которым может течь ток. Это означает, что эквивалентное сопротивление этих трех резисторов должно быть меньше наименьшего из трех резисторов. Чтобы понять это, представьте, что наименьший резистор — это единственный путь, по которому может протекать ток. Теперь добавьте альтернативные пути, подключив другие резисторы параллельно. Поскольку у тока больше путей, общее сопротивление (т. Е. Эквивалентное сопротивление) уменьшится. Следовательно, эквивалентное сопротивление должно быть меньше наименьшего сопротивления параллельных резисторов.

Рис. 19.19 На левой принципиальной схеме показано параллельное подключение трех резисторов. Напряжение В батареи приложено ко всем трем резисторам. Токи, протекающие через каждую ветвь, не обязательно равны.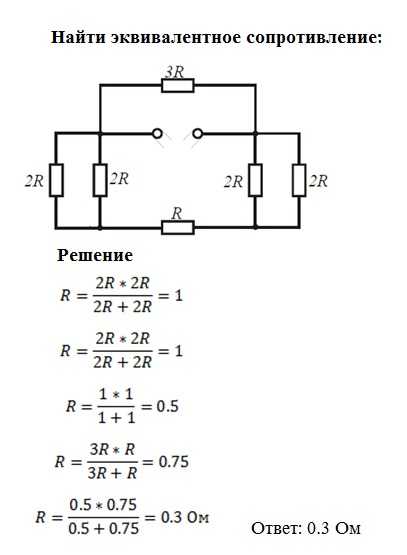 На правой принципиальной схеме показано эквивалентное сопротивление, которое заменяет три параллельных резистора.

Чтобы найти эквивалентное сопротивление RequivRequiv трех резисторов R1, R2, и R3R1, R2, и R3, применим закон Ома к каждому резистору. Так как падение напряжения на каждом резисторе равно В , получаем

19.21V=I1R1, V=I2R2, V=I3R3V=I1R1, V=I2R2, V=I3R3

или

19.22I1=VR1, I2=VR2, I3=VR3.I1=VR1, I2=VR2, I3=VR3.

Мы также знаем из закона сохранения заряда, что три тока I1, I2, и I3I1, I2, и I3 должны складываться, чтобы получить ток I , проходящий через батарею. Если бы это было не так, ток должен был бы таинственным образом создаваться или уничтожаться где-то в цепи, что физически невозможно. Таким образом, мы имеем

19.23I=I1+I2+I3.I=I1+I2+I3.

Подстановка выражений для I1, I2, и I3I1, I2, и I3 в это уравнение дает

19.24I=VR1+VR2+VR3=V(1R1+1R2+1R3)I=VR1+VR2+VR3=V(1R1+1R2+1R3)

или

19,25 В=I(11/R1+1/R2+1/R3).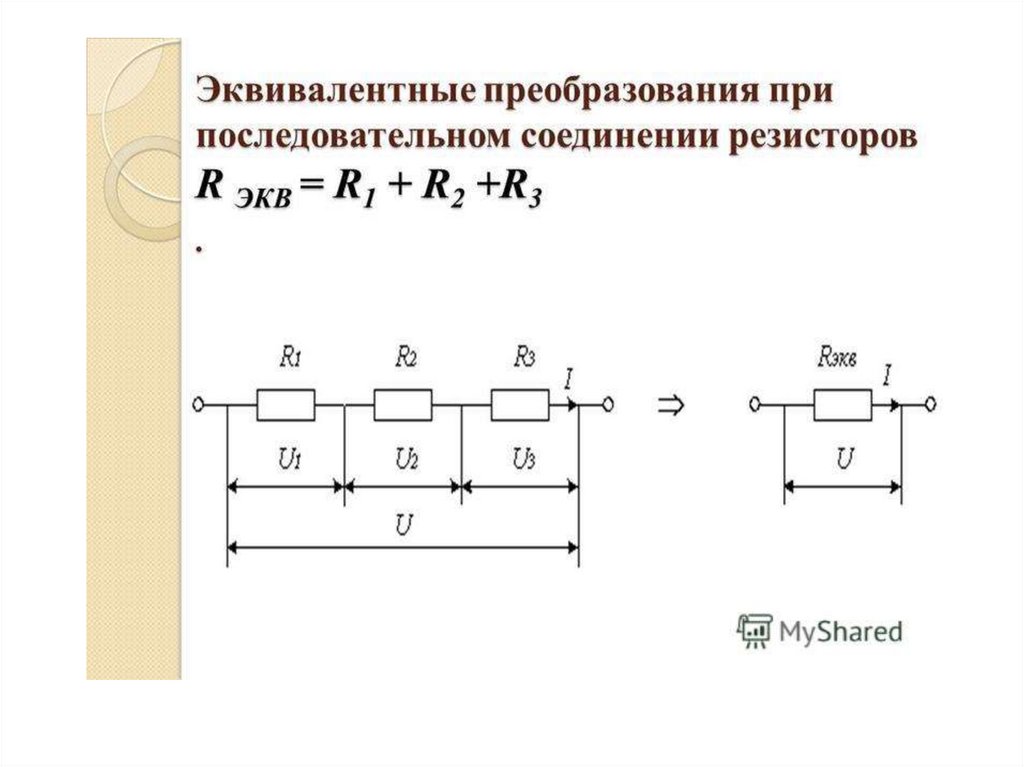 V=I(11/R1+1/R2+1/R3).

Эта формула представляет собой просто закон Ома, где множитель в скобках означает эквивалентное сопротивление.

19,26 В=I(11/R1+1/R2+1/R3)=IRэкв. V=I(11/R1+1/R2+1/R3)=IRэкв.

Таким образом, эквивалентное сопротивление трех резисторов, включенных параллельно, равно

19.27Requiv=11/R1+1/R2+1/R3.Requiv=11/R1+1/R2+1/R3.

Та же логика работает для любого количества параллельно соединенных резисторов, поэтому общая форма уравнения, которая дает эквивалентное сопротивление N резисторов, соединенных параллельно, равна

.

19.28 Requiv=11/R1+1/R2+⋯+1/RN.Requiv=11/R1+1/R2+⋯+1/RN.

Рабочий пример

Определение тока через параллельные резисторы

Три приведенные ниже схемы эквивалентны. Если номинальное напряжение батареи Vbattery=3 VVbattery=3 V, каково эквивалентное сопротивление цепи и какой ток протекает через цепь?

СТРАТЕГИЯ

Три резистора соединены параллельно, и падение напряжения на них составляет В _{аккумулятор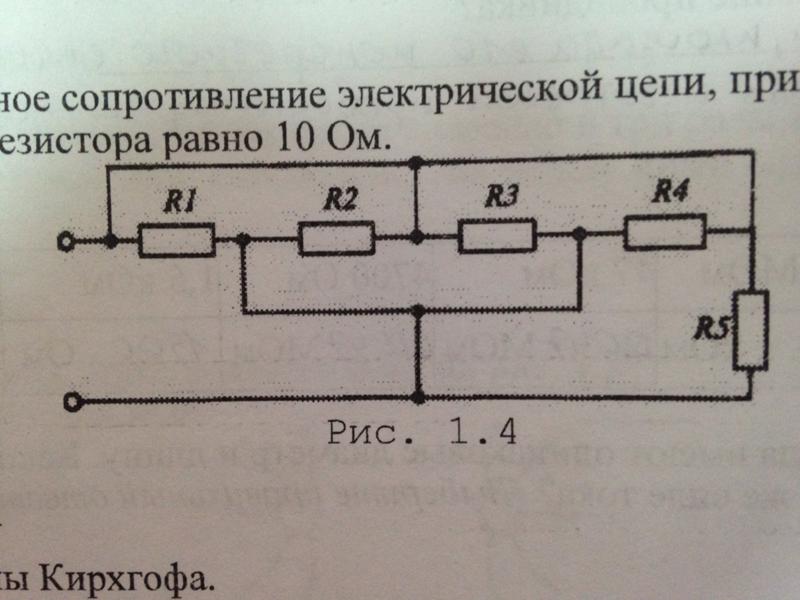} . Таким образом, мы можем применить уравнение для эквивалентного сопротивления параллельных резисторов, которое принимает вид

19,29Requiv=11/R1+1/R2+1/R3.Requiv=11/R1+1/R2+1/R3. .

Схема с эквивалентным сопротивлением показана ниже. Зная эквивалентное сопротивление, мы можем использовать закон Ома, чтобы найти ток в цепи.

Решение

Подставляя заданные значения сопротивления в уравнение для эквивалентного сопротивления, получаем 4,84 Ом. Requiv=11/R1+1/R2+1/R3=11/10 Ом+1/25 Ом+1/15 Ом=4,84 Ом.

Таким образом, ток в цепи равен

19,31 В=IRI=VR=3 V4,84 Ω=0,62 A.V=IRI=VR=3 V4,84 Ω=0,62 A. всей цепи, обратите внимание, что этот ток не протекает через каждый резистор. Однако, поскольку в цепи должен сохраняться электрический заряд, сумма токов, проходящих через каждую ветвь цепи, должна в сумме равняться току, проходящему через батарею. Другими словами, мы не можем волшебным образом создать заряд где-то в цепи и добавить этот новый заряд к току.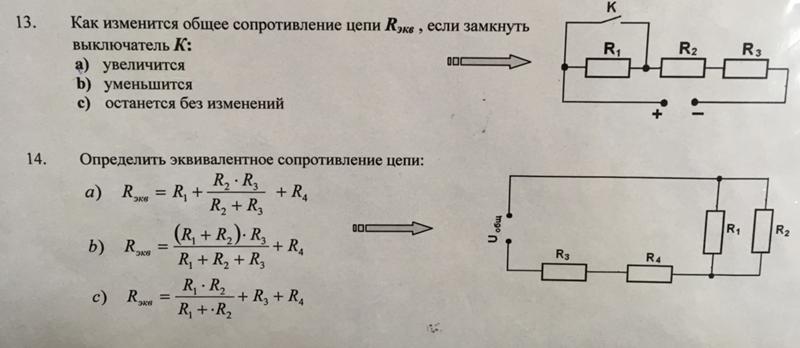 Давайте проверим это рассуждение, используя закон Ома, чтобы найти ток через каждый резистор.

19.32I1=VR1=3 V10 Ω=0,30 AI2=VR2=3 V25 Ω=0,12 AI3=VR3=3 V15 Ω=0,20 AI1=VR1=3 V10 Ω=0,30 AIV2=VR2=3 3 1 VR3=3 V15 Ω=0,20 A

Как и ожидалось, эти токи в сумме дают 0,62 A, что является общим найденным током, проходящим через эквивалентный резистор. Также обратите внимание, что через самый маленький резистор протекает наибольший ток, и наоборот.

Рабочий пример

Рассуждения с параллельными резисторами

Каково эквивалентное сопротивление трех одинаковых резисторов без каких-либо вычислений R параллельно?

СТРАТЕГИЯ

Три одинаковых резистора R , соединенные параллельно, создают три одинаковых пути, по которым может протекать ток. Таким образом, току через эти резисторы протекать в три раза легче, чем через один из них.

Раствор

Если протекать через три одинаковых резистора R в три раза легче, чем через один из них, то эквивалентное сопротивление должно быть в три раза меньше: Р /3.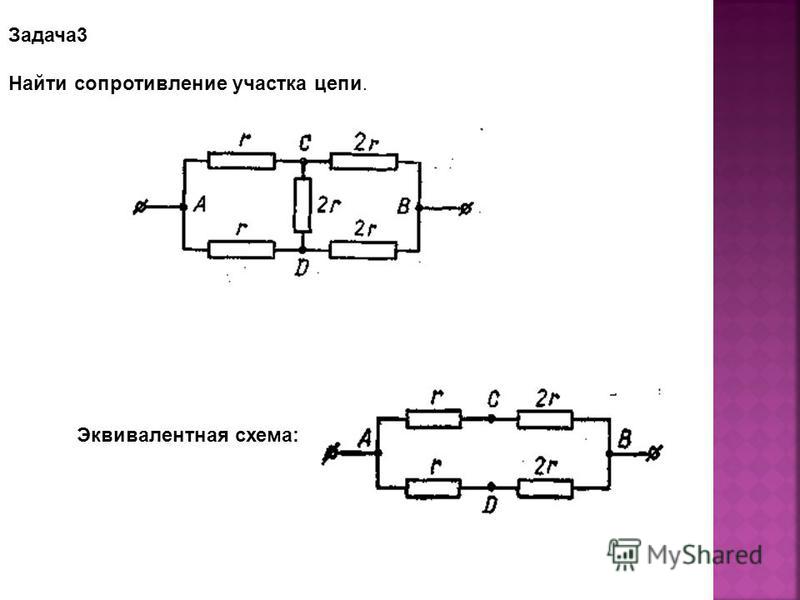

Обсуждение

Проверим наши рассуждения, рассчитав эквивалентное сопротивление трех одинаковых резисторов R , включенных параллельно. Уравнение для эквивалентного сопротивления параллельных резисторов дает

19,33Requiv=11/R+1/R+1/R=13/R=R3.Requiv=11/R+1/R+1/R=13/ Р=Р3.

Таким образом, наши рассуждения были верны. В общем, когда доступно больше путей, по которым может протекать ток, эквивалентное сопротивление уменьшается. Например, если у нас есть одинаковые резисторы R параллельно, эквивалентное сопротивление будет R /10.

Практические задачи

Три резистора, 10, 20 и 30 Ом, соединены параллельно. Чему равно сопротивление?

1. Эквивалентное сопротивление 5,5 Ом
2. Эквивалентное сопротивление 60 Ом
3. Эквивалентное сопротивление 6 × 103 Ом
4. Эквивалентное сопротивление 6 × 104 Ом

Если на R1 происходит падение напряжения 5 В, а R1 подключен параллельно R2, каково падение напряжения на R2?

1. Падение напряжения 0В.
2. Падение напряжения на 2,5В.
3. Падение напряжения на 5В.
4. Падение напряжения на 10В.

Резисторы параллельно и последовательно

Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Комбинации последовательных и параллельных резисторов можно свести к одному эквивалентному сопротивлению, используя метод, показанный на рисунке 19..20. Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее сокращаются до тех пор, пока не останется единственное сопротивление. Процесс скорее трудоемкий, чем сложный.

Рисунок 19.20 Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единое эквивалентное сопротивление.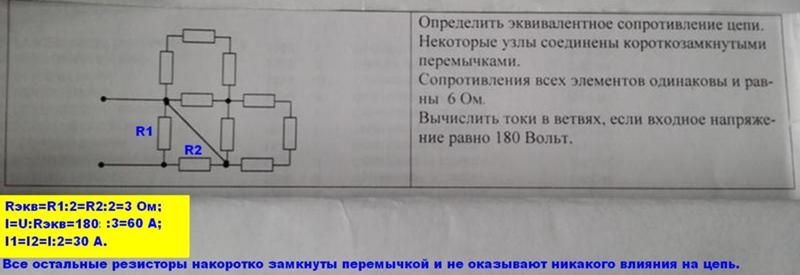

Давайте выполним четыре шага, показанные на рис. 19.20, чтобы уменьшить количество семи резисторов до одного эквивалентного резистора. Чтобы не отвлекаться на алгебру, мы будем считать, что сопротивление каждого резистора равно 10 Ом. На шаге 1 мы уменьшаем два набора параллельных резисторов, обведенных синей пунктирной петлей. Верхний набор имеет три параллельных резистора и будет уменьшен до одного эквивалентного резистора RP1RP1. Нижний набор имеет два параллельных резистора и будет уменьшен до одного эквивалентного резистора RP2RP2. Используя уравнение для эквивалентного сопротивления параллельно включенных резисторов, получаем

19.34RP1=11/R2+1/R3+1/R4=11/10 Ом+1/10 Ом+1/10 Ом=103 ОмRP2=11/R5+1/R6=11/10 Ом+1/10 Ом=5 Ом.RP1=11/R2+1/R3+1/R4=11/10 Ом+1/10 Ом+1/10 Ом=103 ОмRP2=11/R5+1/R6=11/10 Ом+ 1/10 Ом=5 Ом.

Эти два эквивалентных сопротивления обведены красной пунктирной петлей после шага 1. Они соединены последовательно, поэтому мы можем использовать уравнение для эквивалентного сопротивления последовательно соединенных резисторов, чтобы свести их к одному эквивалентному сопротивлению RS1RS1. Это делается на шаге 2, в результате чего получается

.

19.35RS1=RP1+RP2=103 Ом+5 Ом=253 Ом. RS1=RP1+RP2=103 Ом+5 Ом=253 Ом.

Эквивалентный резистор RS1RS1 появляется в зеленой пунктирной петле после шага 2. Этот резистор включен параллельно резистору R7R7, поэтому пара может быть заменена эквивалентным резистором RP3RP3, который определяется как

.

19.36RP3=11/RS1+1/R7=13/25 Ом+1/10 Ом=5011 Ом.RP3=11/RS1+1/R7=13/25 Ом+1/10 Ом=5011 Ом.

Это делается на шаге 3. Резистор RP3RP3 включен последовательно с резистором R1R1, как показано фиолетовым пунктиром после шага 3. Эти два резистора объединяются на последнем шаге, чтобы сформировать окончательный эквивалентный резистор RequivRequiv, который равен

19,37Requiv=R1+RP3=10 Ω+5011 Ω=16011 Ω.Requiv=R1+RP3=10 Ω+5011 Ω=16011 Ω.

Таким образом, всю комбинацию из семи резисторов можно заменить одним резистором с сопротивлением около 14,5 Ом.

Это было много работы, и вы можете спросить, почему мы это делаем. Нам важно знать эквивалентное сопротивление всей цепи, чтобы мы могли рассчитать ток, протекающий по цепи. Закон Ома говорит нам, что ток, протекающий по цепи, зависит от сопротивления цепи и напряжения в цепи. Но чтобы узнать ток, надо сначала узнать эквивалентное сопротивление.

Вот общий подход к поиску эквивалентного резистора для любой произвольной комбинации резисторов:

1. Определите группу резисторов, которые включены только параллельно или только последовательно.
2. Для резисторов, соединенных последовательно, используйте уравнение для эквивалентного сопротивления последовательно соединенных резисторов, чтобы привести их к одному эквивалентному сопротивлению. Для параллельных резисторов используйте уравнение для эквивалентного сопротивления параллельных резисторов, чтобы привести их к одному эквивалентному сопротивлению.
3. Нарисуйте новую принципиальную схему, заменив резисторы из шага 1 эквивалентными им резисторами.
4. Если в цепи осталось более одного резистора, вернитесь к шагу 1 и повторите. В противном случае вам конец.

Веселье в физике

Робот

Роботы захватывают наше коллективное воображение уже более века. Теперь эта мечта о создании умных машин для выполнения нашей грязной работы, а иногда и просто для того, чтобы составить нам компанию, становится реальностью. Робототехника стал огромной областью исследований и разработок, при этом некоторые технологии уже коммерциализированы. Вспомните, например, маленькие автономные пылесосы.

На рис. 19.21 показаны лишь некоторые из множества различных форм, которые могут принимать роботы. Самые продвинутые человекоподобные роботы умеют ходить, разливать напитки, даже танцевать (хотя и не очень грациозно). Другие роботы созданы на основе биологии, например собачий робот , показанный на средней фотографии рис. 19.21. Этот робот может перевозить сотни фунтов груза по пересеченной местности. Фотография справа на рисунке 19.21 показано внутреннее устройство М-блока , , разработанного Массачусетским технологическим институтом. Эти простые на вид блоки содержат инерционные колеса и электромагниты, которые позволяют им вращаться и подбрасываться в воздух, а также соединяться в различные формы. Общаясь по беспроводной связи между собой, они самособираются в различные формы, такие как столы, стулья, а когда-нибудь, возможно, даже здания.

Все роботы включают в себя огромное количество физики и техники. Роботы освоили простое действие по наливанию напитка лишь недавно, после более чем 30 лет исследований и разработок! Баланс и время, которые мы, люди, считаем само собой разумеющимися, на самом деле являются очень сложными действиями, требующими отличного баланса, ловкости и обратной связи. Чтобы справиться с этим, требуются датчики для определения баланса, вычислительная мощность для анализа данных и передачи соответствующих компенсационных действий, а также соединения и приводы для выполнения необходимых действий.

Помимо определения гравитации или ускорения, роботы могут иметь несколько различных датчиков для обнаружения света, звука, температуры, запаха, вкуса и т. д. Все эти устройства основаны на физических принципах, которые вы изучаете в этом тексте. Например, оптика, используемая для роботизированного зрения, аналогична той, что используется в ваших цифровых камерах: пиксельные полупроводниковые детекторы, в которых свет преобразуется в электрические сигналы. Для определения температуры можно использовать простые термисторы, представляющие собой резисторы, сопротивление которых изменяется в зависимости от температуры.

Создание робота сегодня намного проще, чем несколько лет назад. Сейчас многие компании предлагают комплекты для сборки роботов. По сложности они варьируются от подходящих для детей начальной школы до задач, которые могут бросить вызов лучшим профессиональным инженерам. Если интересно, вы можете легко найти их в Интернете и начать делать своего собственного робота уже сегодня.

Рис. 19.21 Роботы бывают разных форм и размеров, от классического гуманоида типа до роботов-собак в маленькие кубики, которые самостоятельно собираются для выполнения различных задач.

Watch Physics

Параллельные резисторы

В этом видео лектор обсуждает простую схему с батареей и парой резисторов, соединенных параллельно. Он подчеркивает, что электроны движутся в направлении, противоположном направлению положительного тока, а также использует тот факт, что напряжение одинаково во всех точках идеального провода. Вывод очень похож на то, что сделано в этом тексте, но лектор хорошо его проходит, объясняя каждый шаг.

Щелкните, чтобы просмотреть содержание

Проверка захвата

Верно или неверно — на принципиальной схеме мы можем предположить, что напряжение одинаково в каждой точке данного провода.

1. ложный
2. правда

Watch Physics

Резисторы, соединенные последовательно и параллельно

В этом видеоролике показано, как рассчитать эквивалентное сопротивление цепи, содержащей резисторы, соединенные параллельно и последовательно. Лектор использует тот же подход, что и изложенный выше, для нахождения эквивалентного сопротивления.

Щелкните, чтобы просмотреть содержание

Проверка захвата

Представьте, что N одинаковых резисторов соединены параллельно. Каждый резистор имеет сопротивление Р. Каково эквивалентное сопротивление этой группы параллельных резисторов?

1. Эквивалентное сопротивление ( R ) ^Н .
2. Эквивалентное сопротивление NR.
3. Эквивалентное сопротивление РН.РН.
4. Эквивалентное сопротивление NR.NR.

Рабочий пример

Найдите ток в цепи комплексного резистора

Батарея в схеме ниже имеет номинальное напряжение 10 В. Какой ток течет по цепи и в каком направлении?

СТРАТЕГИЯ

Примените стратегию нахождения эквивалентного сопротивления, заменив все резисторы одним эквивалентным сопротивлением, затем используйте закон Ома, чтобы найти ток через эквивалентный резистор.

Решение

Комбинация резисторов R4R4 и R5R5 может быть уменьшена до эквивалентного сопротивления 9 Ом.0005

19,38RP1=11/R4+1/R5=11/45 Ω+1/60 Ω=25,71 ΩR.RP1=11/R4+1/R5=11/45 Ω+1/60 Ω=25,71 ΩR.

Замена R4R4 и R5R5 этим эквивалентным сопротивлением дает следующую схему.

Теперь заменим два верхних резистора R2R2 и R3R3 эквивалентным резистором RS1RS1, а два нижних резистора RP1RP1 и R6R6 эквивалентным резистором RS2RS2. Эти резисторы включены последовательно, поэтому мы складываем их вместе, чтобы найти эквивалентное сопротивление.

19,39RS1=R2+R3=50 Ом+30 Ом=80 ОмRS2=RP1+R6=25,71 Ом+20 Ом=45,71 ОмRS1=R2+R3=50 Ом+30 Ом=80 ОмRS2=RP1+R6=25,71 Ом +20 Ом=45,71 Ом

Замена соответствующих резисторов эквивалентными им резисторами дает следующую схему.

Теперь замените два резистора RS1 и RS2RS1 и RS2, включенных параллельно, на эквивалентный им резистор RP2RP2. Сопротивление RP2RP2 составляет

19,40RP2=11/RS1+1/RS2=11/80 Ом+1/45,71 Ом=29,09 Ом. RP2=11/RS1+1/RS2=11/80 Ом+1/45,71 Ом =29,09 Ом.

Обновление электрической схемы путем замены RS1 и RS2RS1 и RS2 этим эквивалентным сопротивлением дает приведенную ниже схему.

Наконец, мы соединяем резисторы R1 и RP2R1 и RP2, которые включены последовательно. Эквивалентное сопротивление: RS3=R1+RP2=75 Ом+29,09 Ом=104,09 Ом. RS3=R1+RP2=75 Ом+29,09 Ом=104,09 Ом. Окончательная схема показана ниже.

Теперь воспользуемся законом Ома, чтобы найти силу тока в цепи.

19,41 В=IRS3I=VRS3=10 V104,09 Ом=0,096 AV=IRS3I=VRS3=10 V104,09 Ом=0,096 A поэтому в этой цепи он течет по часовой стрелке.

Обсуждение

Этот расчет может показаться довольно длинным, но немного потренировавшись, вы сможете комбинировать некоторые шаги. Обратите также внимание на то, что в расчетах учитывались дополнительные значащие цифры. Только в конце окончательный результат округлялся до двух значащих цифр.

Рабочий пример

Странно выглядящие принципиальные схемы

Иногда вы можете столкнуться с не очень аккуратно нарисованными принципиальными схемами, такими как схема, показанная ниже.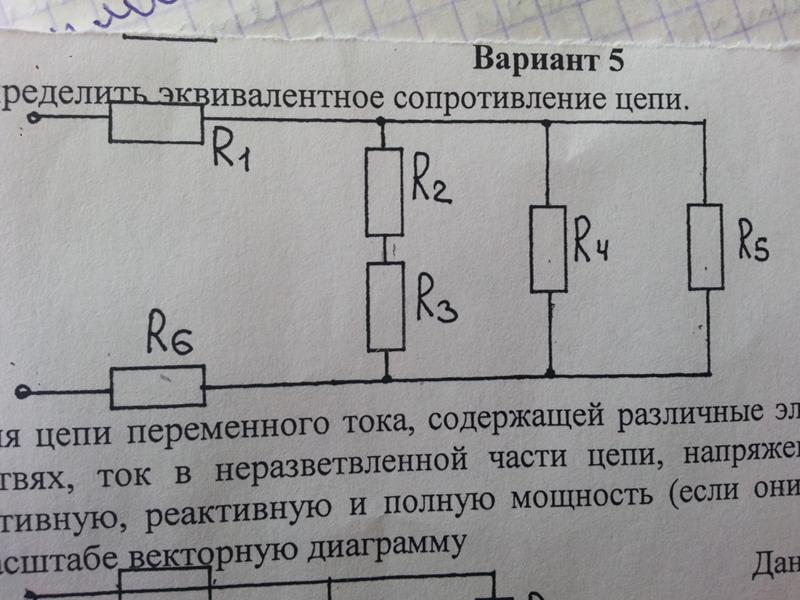 Эта принципиальная схема больше похожа на то, как реальная схема может выглядеть на лабораторном столе. Каково эквивалентное сопротивление резисторов на этой диаграмме, если предположить, что сопротивление каждого резистора равно 10 Ом, а номинальное напряжение батареи равно 12 В?

СТРАТЕГИЯ

Давайте перерисуем эту принципиальную схему, чтобы сделать ее более понятной. Затем мы применим описанную выше стратегию для расчета эквивалентного сопротивления.

Решение

Чтобы перерисовать диаграмму, рассмотрите рисунок ниже. В верхней схеме синие резисторы образуют путь от положительной клеммы батареи к отрицательной клемме. Параллельно этой цепи расположены красные резисторы, которые образуют еще один путь от положительного к отрицательному выводу батареи. Синие и красные пути показаны более четко на нижней принципиальной схеме. Обратите внимание, что как на верхней, так и на нижней принципиальных схемах синяя и красная дорожки соединяют положительную клемму батареи с отрицательной клеммой батареи.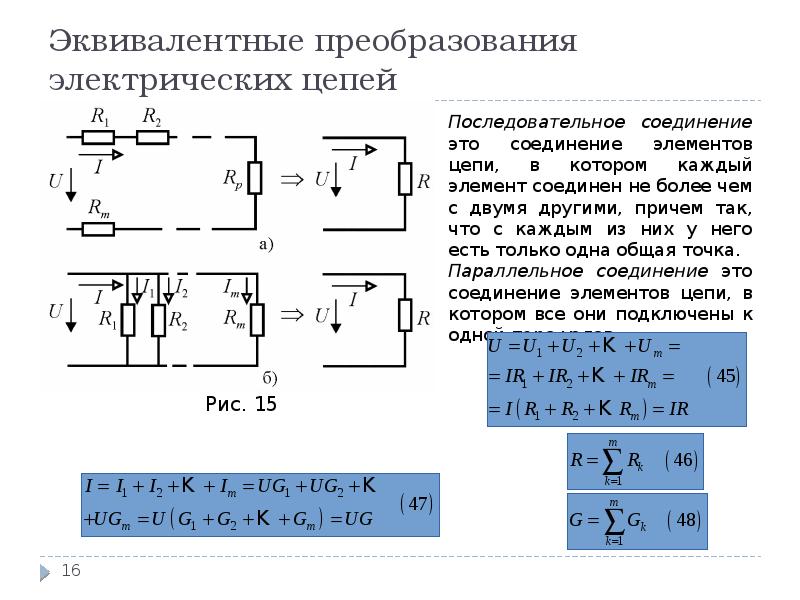

Теперь легче увидеть, что R1 и R2R1 и R2 параллельны, а параллельная комбинация последовательно с R4R4. Эта комбинация, в свою очередь, параллельна последовательной комбинации R3 и R5R3 и R5. Сначала мы вычисляем синюю ветвь, которая содержит R1, R2 и R4, R1, R2 и R4. Эквивалентное сопротивление

19,42Rсиний=11/R1+1/R2+R4=11/10 Ом+1/10 Ом+10 Ом=15 Ом.Rсиний=11/R1+1/R2+R4=11/10 Ом+1/10 Ом+10 Ом=15 Ом.

, где мы показываем вклад от параллельной комбинации резисторов и от последовательной комбинации резисторов. Теперь рассчитаем эквивалентное сопротивление красной ветви, которое равно

19,43Rкрасный=R3+R5=10 Ом+10 Ом=20 Ом.Rкрасный=R3+R5=10 Ом+10 Ом=20 Ом.

Вставка этих эквивалентных резисторов в цепь дает следующую схему.

Эти два резистора включены параллельно, поэтому их можно заменить одним эквивалентным резистором с сопротивлением

11/Rсиний+1/Rкрасный=11/15 Ом+1/20 Ом=8,6 Ом.

Окончательная эквивалентная схема показана ниже.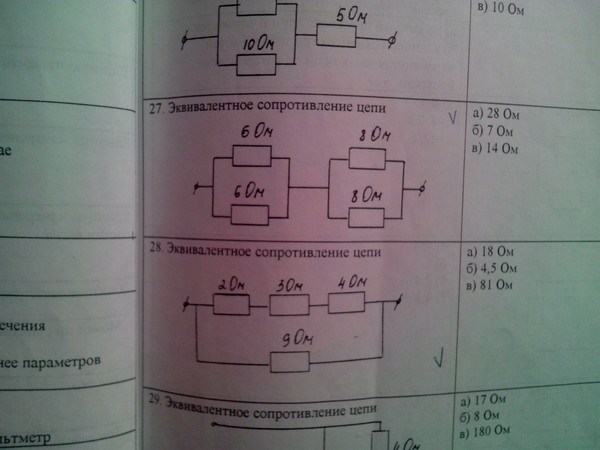

Обсуждение

Найти эквивалентное сопротивление было проще, если была понятная принципиальная схема. Вот почему мы пытаемся сделать четкие принципиальные схемы, где параллельно подключенные резисторы выстроены параллельно друг другу и в одном и том же горизонтальном положении на схеме.

Теперь мы можем использовать закон Ома, чтобы найти ток, проходящий через каждую ветвь этой цепи. Рассмотрим принципиальную схему с RblueRblue и RredRred. Напряжение на каждой из этих ветвей составляет 12 В (т. е. номинальное напряжение батареи). Ток в синей ветви

19,45Iblue=VRblue=12 V15 Ω=0,80 A.Iblue=VRblue=12 V15 Ω=0,80 A

Ток в красной ветви

19,46Ired=VRVred=12 Ω=0,60 A.Ired=VRred=12 V20 Ω=0,60 A.

Ток, проходящий через батарею, должен быть суммой этих двух токов (понимаете, почему?), или 1,4 A.

Практические задачи

Какова формула эквивалентного сопротивления двух параллельных резисторов с сопротивлением Ом ₁ и Ом ₂ ?

1. Эквивалентное сопротивление двух параллельных резисторов Reqv=R1+R2Reqv=R1+R2
2. Эквивалентное сопротивление двух параллельных резисторов Reqv=R1×R2Reqv=R1×R2
3. Эквивалентное сопротивление двух параллельных резисторов Reqv=R1-R2Reqv=R1-R2
4. Эквивалентное сопротивление двух параллельных резисторов Reqv=11/R1+1/R2Reqv=11/R1+1/R2

Рисунок 19. 22

Каково эквивалентное сопротивление двух показанных ниже резисторов?

1. Эквивалентное сопротивление 20 Ом
2. Эквивалентное сопротивление 21 Ом
3. Эквивалентное сопротивление 90 Ом
4. Эквивалентное сопротивление 1925 Ом

Проверьте свое понимание

Упражнение 6

Падение напряжения на параллельных резисторах ________.

1. одинаковы для всех резисторов
2. больше для больших резисторов
3. меньше для больших резисторов
4. больше для меньших резисторов

Упражнение 7

Рассмотрим цепь из параллельных резисторов. Минимальный резистор 25 Ом. Каков верхний предел эквивалентного сопротивления?

1. Верхний предел эквивалентного сопротивления составляет 2,5 Ом.
2. Верхний предел эквивалентного сопротивления составляет 25 Ом.
3. Верхний предел эквивалентного сопротивления составляет 100 Ом.