-

-

-

В книжной версии
Том 20. Москва, 2012, стр. 707-708
-

Скопировать библиографическую ссылку:
Авторы: Л. С. Ляхович
МОМЕ́НТ СОПРОТИВЛЕ́НИЯ, геометрич. характеристика поперечного сечения бруса, определяющая зависимость наибольших нормальных (при изгибе) или касательных (при кручении) напряжений в сечении от величины изгибающего или крутящего моментов. Различают М. с. осевой (при изгибе) и полярный (при кручении).
Осевым М. с. называется отношение момента инерции относительно данной центральной оси к расстоянию от этой оси до наиболее удалённой точки поперечного сечения: $W_x=\frac{I_x}{Y_{\text {макс}}}, W_y=\frac{I_y}{X_{\text {макс}}}$.
Полярным М. с. называется отношение полярного момента инерции к расстоянию от полюса, расположенного в центре тяжести поперечного сечения, до наиболее удалённой точки сечения: $W_{\text p}=\frac{I_{\text p}}{\rho_{\text {макс}}}$. Размерность М. с. – м

При расчёте на прочность бруса макс. нормальные (при изгибе) и касательные (при кручении) напряжения вычисляются по формулам: $\sigma_{\text {макс}}=\frac{M_{\text {изг}}}{W_x}, \tau_{\text {макс}}=\frac{M_{\text {кр}}}{W_р}$. Для круглого сечения радиуса $R$ имеем $W_x=\frac{\pi R^3}{4}$ и $W_{\text p}=\frac{\pi R^3}{2}$; для прямоугольного сечения со сторонами $b$ (параллельной гл. оси) и $h$ (перпендикулярной ей) – $W_x=\frac{bh^2}{6}$. Если поперечное сечение бруса не симметрично относительно оси изгиба, а материал имеет разные пределы прочности на растяжение и сжатие, то необходимо определять напряжения по обоим краям бруса и соответственно вычислять два момента сопротивления. Напр., для бруса треугольного сечения (рис.) момент инерции $I_x=\frac{bh^3}{36}$. М. с. относительно нижних волокон $W_{x \text н}=\frac {I_x}{\frac{h}{3}}=\frac{bh^2}{12}$, верхних – $W_{x \text в}=\frac {I_x}{\frac{2h}{3}}=\frac{bh^2}{24}$.
- МОМЕНТ СОПРОТИВЛЕНИЯ
геом. хар-ка поперечного сечения стержня (балки, вала), определяющая его сопротивляемость в рассматриваемом сечении изгибу или кручению и равная осевому (или полярному) моменту инерции, делённому на расстояние от оси (или центра тяжести) до наиболее удалённой точки сечения. М. с. применяют в ф-лах сопротивления материалов и строит. механики.
Большой энциклопедический политехнический словарь. 2004.
- МОМЕНТ СИЛЫ
- МОНАЦИТ
Смотреть что такое «МОМЕНТ СОПРОТИВЛЕНИЯ» в других словарях:
Момент сопротивления — – отношение момента инерции относительно определенной оси сечения к расстоянию от центра тяжести сечения до точки на линии, перпендикулярной оси (проходящей через центр тяжести), максимально удаленной от центра тяжести сечения. [Полякова, Т … Энциклопедия терминов, определений и пояснений строительных материалов
момент сопротивления — atsparumo momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Konstrukcijos elemento skerspjūvio geometrinė charakteristika, rodanti elemento atsparumą lenkimui arba sukimui. atitikmenys: angl. moment of resistance vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
момент сопротивления — atsparumo momentas statusas T sritis fizika atitikmenys: angl. moment of resistance vok. Widerstandsmoment, n rus. момент сопротивления, m pranc. moment résistant, m … Fizikos terminų žodynas
МОМЕНТ СОПРОТИВЛЕНИЯ — геометрическая характеристика поперечного сечения стержня, показывающая сопротивляемость стержня в рассматриваемом сечении изгибу или кручению (Болгарский язык; Български) съпротивителен момент (Чешский язык; Čeština) průřezový modul; modul… … Строительный словарь
МОМЕНТ СОПРОТИВЛЕНИЯ ПЛАСТИЧЕСКИЙ — момент сопротивления в поперечном сечении изгибаемого стержня, определяемый из условия образования в сечении пластического шарнира (Болгарский язык; Български) пластичен съпротивителен момент (Чешский язык; Čeština) plastický průřezový modul… … Строительный словарь
момент сопротивления (тормозной) вращающегося электродвигателя — 3.9 момент сопротивления (тормозной) вращающегося электродвигателя : Вращающий момент на валу электродвигателя, действующий так, чтобы снизить частоту вращения двигателя. Источник: СТО 70238424.29.160.30.002 2009: Электродвигатели. Организация… … Словарь-справочник терминов нормативно-технической документации
момент сопротивления сечения — ašinis ploto atsparumo momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus antrajam ploto momentui, padalytam iš atstumo nuo ašies iki toliausiai nuo jos esančio ploto taško. atitikmenys: angl. section modulus vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
момент сопротивления сечения — ašinis ploto atsparumo momentas statusas T sritis fizika atitikmenys: angl. section modulus vok. Widerstandsmoment gegen Biegung, n rus. момент сопротивления сечения, m pranc. module résistant, m … Fizikos terminų žodynas
Момент сопротивления качению колеса — 72. Момент сопротивления качению колеса Mf Источник: ГОСТ 17697 72: Автомобили. Качение колеса. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
момент сопротивления сечения — [section modulus] геометрическая характеристика поперечного сечения тела, равная отношению момента инерции к расстоянию от оси наиболее удаленной точки сечения. Смотри также: Момент момент прокатки момент количества движения момент инерции … Энциклопедический словарь по металлургии
Книги
- Заметки по метапсихологии агрессивности, С. Ф. Сироткин. Почему вновь и вновь возникает необходимость возвращения к теме агрессии? Потому что ее регуляция в социуме, несмотря на многие достижения цивилизации, остается крайне затруднительной? Потому… Подробнее Купить за 619 руб
- Моделирование при реконструкции механизма столкновения автомобиля с преградой, М. Н. Березуев, С. М. Соловьев, Н. П. Кузнецов, Р. А. Юртиков. Снижение аварийности на дорогах России в первую очередь связано с выявлением действительных причин дорожно-транспортных происшествий (ДТП), что напрямую зависит от объективности проведения… Подробнее Купить за 612 руб
- Принципы рандори. Путь непринужденного лидерства, Дэвид Баум, Джим Хассингер. Рандори (термин японского боевого искусства айкидо) означает способность применить нужную технику в нужном месте в нужный момент времени и с нужной силой. С помощью почти шестидесяти… Подробнее Купить за 390 руб
| ПОЛЕЗНЫЕ ССЫЛКИ: БОНУСЫ ИНЖЕНЕРАМ!: МЫ В СОЦ.СЕТЯХ: | Навигация по справочнику TehTab.ru:  главная страница / / Техническая информация главная страница / / Техническая информация
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Материалы / / Сопротивление материалов. Сопромат. Таблицы строительных конструкций. / / Таблица. Кручение. Геометрические характеристики жесткости и прочности для ходовых сечений при кручении прямого бруса. Осевые моменты инерции сечений (статические моменты сечений), осевые моменты сопротивления при кручении. Точка наибольшего напряжения. Поделиться:
| ||||||||||||
Статическим моментом Sx сечения (фигуры) относительно какой-либо оси х называется сумма произведений элементарных площадок dA на их расстояние y до данной оси, численно равная интегралу:
| $$S_x=\int_{A} y dA$$ | (1) |
и относительно оси у:
| $$S_y=\int_{A} x dA$$ | (2) |
Основные свойства статических моментов инерции
- Размерность статического момента — единица длины в третьей степени, обычно [см3] или [м3] .
- Статический момент может быть положительным, отрицательным и равным нулю.
- Ось, относительно которой статический момент равен нулю, называется центральной .
- Точка пересечения центральных осей назвается центром тяжести сечения.
- Статический момент составного сечения равен сумме статических моментов элементов этого сечения. Это вытекает со свойств определенного интеграла.
Определение положения центра тяжести
Из формулы (1) и (2) вытекает:
$$S_x=y_c\cdot A $$
$$S_y=x_c\cdot A $$
где A — площадь всей фигуры;
уc — расстояние от центра тяжести фигуры до оси х.
xc — расстояние от центра тяжести фигуры до оси y.
Тогда положение центра тяжести фигуры вычисляется по формулах:
$$x_c= { S_y \over A } = {{{\sum_{i=1}^{n}x_i \cdot A_i}\over {\sum_{i=1}^{n}A_i}}}$$
$$y_c= { S_x \over A } = {{{\sum_{i=1}^{n}y_i\cdot A_i}\over {\sum_{i=1}^{n}A_i}}}$$
где [math]A_i, y_i, x_i [/math] – площадь єлементов, на которые разбито сечение и координаты центра тяжести элементов, а n – количество таких элементов.
Если сечение имеет ось симметрии, то она всегда проходит через центр тяжести, а потому статический момент относительно оси симметрии всегда равен нулю.
Связанные статьи
метки: момент инерции
- момент сопротивления вращению
- момент среза
Смотреть что такое «момент сопротивления сечения» в других словарях:
момент сопротивления сечения — ašinis ploto atsparumo momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus antrajam ploto momentui, padalytam iš atstumo nuo ašies iki toliausiai nuo jos esančio ploto taško. atitikmenys: angl. section modulus vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
момент сопротивления сечения — ašinis ploto atsparumo momentas statusas T sritis fizika atitikmenys: angl. section modulus vok. Widerstandsmoment gegen Biegung, n rus. момент сопротивления сечения, m pranc. module résistant, m … Fizikos terminų žodynas
момент сопротивления сечения — [section modulus] геометрическая характеристика поперечного сечения тела, равная отношению момента инерции к расстоянию от оси наиболее удаленной точки сечения. Смотри также: Момент момент прокатки момент количества движения момент инерции … Энциклопедический словарь по металлургии
Момент сопротивления — – отношение момента инерции относительно определенной оси сечения к расстоянию от центра тяжести сечения до точки на линии, перпендикулярной оси (проходящей через центр тяжести), максимально удаленной от центра тяжести сечения. [Полякова, Т … Энциклопедия терминов, определений и пояснений строительных материалов
МОМЕНТ СОПРОТИВЛЕНИЯ — геом. хар ка поперечного сечения стержня (балки, вала), определяющая его сопротивляемость в рассматриваемом сечении изгибу или кручению и равная осевому (или полярному) моменту инерции, делённому на расстояние от оси (или центра тяжести) до… … Большой энциклопедический политехнический словарь
МОМЕНТ СОПРОТИВЛЕНИЯ — геометрическая характеристика поперечного сечения стержня, показывающая сопротивляемость стержня в рассматриваемом сечении изгибу или кручению (Болгарский язык; Български) съпротивителен момент (Чешский язык; Čeština) průřezový modul; modul… … Строительный словарь
полярный момент сопротивления — Геометрическая характеристика прочности бруса круглого поперечного сечения при кручении. [http://www.isopromat.ru/sopromat/terms] Тематики строительная механика, сопротивление материалов EN polar section modulus … Справочник технического переводчика
Момент инерции — Размерность L2M Единицы измерения СИ кг·м² СГС … Википедия
момент количества движения — [moment of momentum] кинетический момент, одна из мер механического движения материальной точки или системы. Особенно важную роль момент количества движения играет при изучении вращательного движения. Как и для момента силы, различают момент… … Энциклопедический словарь по металлургии
момент прокатки — [rolling torque] крутящий момент на рабочих валках, затрачиваемый на деформацию металла; определяет мощность двигателя прокатного стана и размеры его основных узлов. Моменты прокатки обычно рассчитаны из усилия прокатки или условия постоянства… … Энциклопедический словарь по металлургии
момент силы — [moment of force] величина, характеризизующая вращательный эффект силы при действии ее на твердое тело. Момент силы, Н • м, рассчитывается относительно центра (точки) вращения. Смотри также: Момент момент сопротивления сечения момент прокатки … Энциклопедический словарь по металлургии
6.1. Статический момент площади сечения
6.1. СТАТИЧЕСКИЙ МОМЕНТ ПЛОЩАДИ СЕЧЕНИЯ
Статический момент площади – распространенная на всю площадь сумма произведений элементарных площадок dA на расстояние от них до этой оси Это понятие аналогично моменту силы относительно оси. Если предположить, что А – вес пластины, имеющей форму нашего сечения, то статический момент Sz – это момент силы тяжести пластины относительно оси z. Размерность: единицы длины в третьей степени (см3; м3). Знаки: плюс, ноль и минус. Ось центральная – ось, относительно которой статический момент площади равен нулю. Центр тяжести сечения – точка пересечения центральных осей. Если фигура имеет ось симметрии, то эта ось является центральной. Статический момент составного сечения равен сумме статических моментов элементов этого сечения. Это следует из свойства определенного интеграла, который можно вычислять по частям – свойство аддитивности (от англ. add – прибавлять, присоединять, складывать). При известных статических Рис. 6.2. Связь знака статического момента площади с его положением в координатной системе моментах частей сечения можно найти координаты центра тяжести состав- ной фигуры: Пример 6.1. Определить положение центральных осей, параллельных основанию и высоте фигуры. Решение Разбиваем сложную фигуру на две простые, в конкретном примере – на два прямоугольника. Их центры тяжести расположены посредине высоты и посредине ширины. Координаты центров тяжести и площади простых фигур Статические моменты площадей простых фигур Координаты центра тяжести составной фигуры Через найденную точку проводим центральные оси zC и yC, параллельные основанию фигуры и ее высоте. Примечание. Центр тяжести фигуры, составленной из двух частей, лежит на линии, соединяющей центры тяжести простых фигур ее составляющих, причем расстояния до них обратно пропорциональны площадям простых фигур. Если сложная фигура составлена из нескольких простых, то общий центр тяжести находится внутри многоугольника, вершинами которого являются центры тяжести простых фигур.
Массовый момент инерции
Массовый момент инерции (Момент инерции) — I — это мера сопротивления объекта изменению направления вращения. Момент инерции имеет такое же отношение к угловому ускорению, как масса к линейному ускорению.
- Момент инерции тела зависит от распределения массы в теле относительно оси вращения
Для точечной массы Момент инерции — это масса, умноженная на квадрат перпендикулярного расстояния до вращения ось отсчета и может быть выражена как
I = mr 2 (1)
, где
I = момент инерции ( кг м 2 , слаг фут 2 , фунты f фтс 2 )
м = масса (кг, слизни)
r = расстояние между осью и массой вращения (м, футы)
Пример. Момент инерции одной массы.
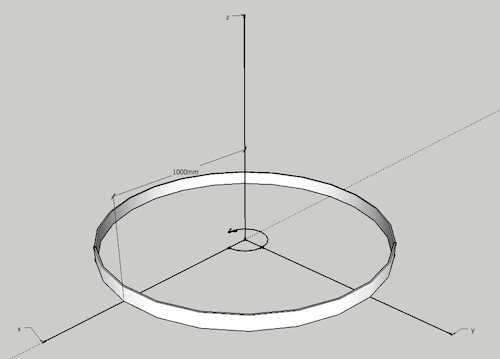
создают трехмерные модели с помощью бесплатного набора инструментов для создания эскизов ToolBox
Момент инерции. h относительно вращения вокруг оси z одиночной массы 1 кг , распределенной в виде тонкого кольца, как указано на рисунке выше, можно рассчитать как
I z = (1 кг) ((1000 мм ) (0.001 м / мм)) 2
= 1 кг м 2
Момент инерции — распределенные массы
Точечная масса является основой для всех других моментов инерции, поскольку любой объект может быть «построен» «из коллекции точечных масс.
I = 37 i м i r i 2 = m 1 r 1 2 + m 2 r 2 2 + ….. + m n r n 2 (2)
Для твердых тел с непрерывным распределением соседних частиц формула лучше выражается в виде интеграла
I = ∫ r 2 дм (2b)
, где
дм = масса бесконечно малой части тела
Преобразование между единицами за момент инерции
| до | ||||||||
| кг м 2 | г см 2 | фунт м фут 2 | фунт 2 9000 180038 в м Слизняк футов 2 | слизняк в 2 | ||||
| кг м 2 | 1 | 1 10 7 | 2.37 10 1 | 3,42 10 3 | 7,38 10 -1 | 1,06 10 2 | ||
| г см 2 | 1 10 -7 | 1 9 | 2,37 10 -6 | 3,42 10 -4 | 7,38 10 -8 | 1,06 10 5 | ||
| фунт м футов 2 | 4,21 10,201 2 | 4.21 10 5 | 1 | 1,44 10 2 | 3,11 10 -2 | 4,48 | ||
| фунт м в 2 | 2,93 10 901 5518 2,93 10 3 | 6,94 10 -3 | 1 | 2,16 10 -4 | 3,11 10 -2 | |||
| слаг, фут 2 | 136 | 136 | 1,36 | 1,3636 10 7 | 3,22 10 1 | 4,63 10 3 | 1 | 1,44 10 2 |
| слизняк в 2 | 9,418 10 9,43 10 9003 9,42 10 4 | 2,23 10 -1 | 3,22 10 1 | 6,94 10 -3 | 1 | |||
Момент инерции — общая формула
Обобщенное выражение в выражении уравнение равно
I = кмр 2 (2c)
, где
k = инерционная постоянная — в зависимости от формы тела
Радиус гирации (в механике )
Радиус инерции — это расстояние от оси вращения, где сосредоточенная точечная масса равна Моменту инерции t он фактическое тело.Радиус инерции для тела может быть выражен как
r г = (I / m) 1/2 (2d)
, где
r г = радиус инерции ( м, футы)
I = момент инерции тела ( кг, м 2 , слизняк фута 2 )
м = масса тела (кг, пули)
Некоторые типичные тела и их моменты инерции
Цилиндр
Тонкостенный полый цилиндр
Моменты инерции для тонкостенного полого цилиндра сопоставимы с точечной массой (1) и могут быть выражены как :
I = mr 2 (3a)
, где
м = масса пустоты (кг, слизняки)
r = расстояние между ось n и полость с тонкими стенками (м, футы)
r o = расстояние между осью и внешней полостью (м, футы)
полый цилиндр
I = 1/2 м (r i 2 + r o 2 ) (3b)
, где
м = масса пустоты (кг, слизняки)
r i = расстояние между осью и внутренняя полость (м, футы)
r o = расстояние между осью и внешней полостью (м, футы)
сплошной цилиндр
I = 1/2 mr 2 (3c)
, где
м = масса цилиндра (кг, пробки)
r = расстояние между осью и внешним цилиндром (м, футы)
Круглый диск
90 002 I = 1/2 mr 2 (3d), где
м = масса диска (кг, пробки)
r = расстояние между осью и внешним диском (м, футы)
Сфера
Тонкостенная полая сфера
I = 2/3 mr 2 (4а)
, где
м = масса полого шара (кг, слизняки)
r = расстояние между осью и полостью (м, футы)
Сплошная сфера
I = 2/5 mr 2 (4b)
, где
м = масса сферы (кг, слага)
r = радиус в сфере (м, футы)
Прямоугольная плоскость
Моменты инерции для прямоугольной плоскости с ось, проходящая через центр, может быть выражена как
I = 1/12 м (a 2 + b 2 ) (5)
, где
a, b = короткие и длинные стороны
Моменты инерции для прямоугольной плоскости с осью вдоль края могут быть выражены как
I = 1/3 мА 2 (5b)
Удлинительный стержень
Моменты инерции для тонкого стержня с осью сквозной центр может быть выражен как
I = 1/12 м L 2 (6)
, где
L = длина стержня
Моменты инерции для тонкого стержня с осью сквозной конец может быть выражен как
,Момент инерцииI = 1/3 м L 2 (6b)
— типичные поперечные сечения I
Момент инерции области или Момент инерции для области — , также известный как Второй момент зоны — I , является свойством формы, которая используется прогнозировать прогиб, изгиб и напряжение в балках.
Площадь Момент Инерции — Имперские единицы
Площадь Момент Инерции — Метрические единицы
Преобразование между Единицами
- 1 см 4 = 10 -8 м 4 = 10 4 мм 4
- 1 в 4 = 4.16×10 5 мм 4 = 41,6 см 4
Пример — преобразование между моментами инерции области
9240 см 4 можно преобразовать в мм 4 путем умножения с 10 4
(9240 см 4 ) 10 4 = 9.24 10 7 мм 4
Площадь Момент инерции (Момент инерции для области или второй момент площади)
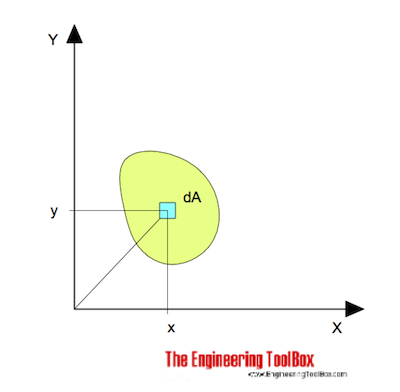
для изгиба вокруг оси x можно выразить как
I x = ∫ y 2 дА (1)
, где
I x = площадь Момент инерции, связанный с осью х ( м 4 , мм 4 , дюйм 4 )
y = перпендикулярный дис расстояние от оси x до элемента dA (м, мм, дюймов )
dA = элементная площадь ( м 2 , мм 2 , дюймов 2 )
Момент инерции для изгиба вокруг оси y можно выразить как
I y = ∫ x 2 dA (2)
, где
I x = Площадь Момент инерции относительно оси y ( м 4 , мм 4 , дюйм 4 )
x = перпендикулярное расстояние от оси y к элементу dA (м, мм, , дюймов, , ) , , , ,
,Площадь Момент инерции для типичных поперечных сечений I
Поперечное сечение сплошного квадрата
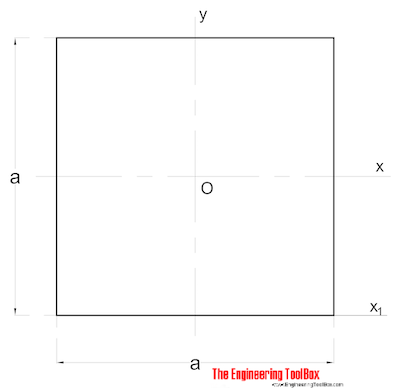
Момент инерции площади для сплошного квадратного сечения можно рассчитать как
I x = a 4 /12 (2)
, где
a = сторона (мм, м , в..)
I y = a 4 /12 (2b)
Сплошное прямоугольное поперечное сечение
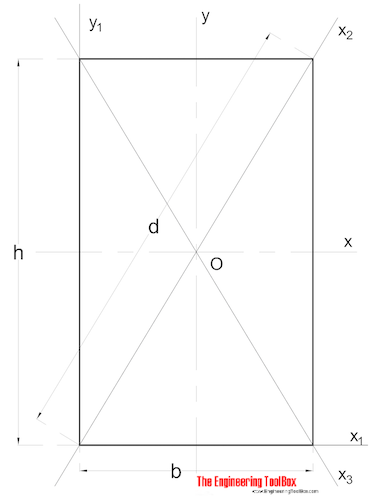
Площадь Момента Иния для прямоугольного сечения может быть рассчитана как
I x = bh 3 /12 (3)
, где
b = ширина
h = высота
I y = b 3 ч / 12 (3b)
сплошное круглое сечение
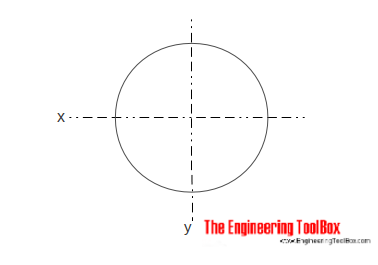
Площадь момента инерции для сплошного цилиндрического сечения можно рассчитать как
I x = π r 4 /4
= π д 4 /64 (4)
где 90 011
r = радиус
d = диаметр
I y = № 9009 4 /4
= № 4 /64 (4b)
Полое цилиндрическое сечение
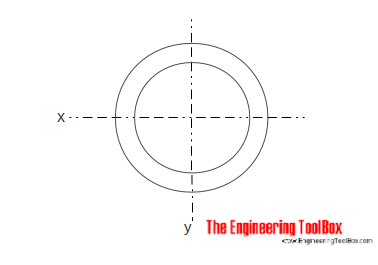
Площадь момента инерции для полого цилиндрического сечения можно рассчитать как
I x = π (d o 4 — d i 4 ) / 64 (5)
, где
d o = наружный диаметр цилиндра
d i = внутренний диаметр цилиндра
I y = π (d o 4 — d i 4 ) / 64 (5b)
квадратного сечения — диагональные моменты 9005 3 
Диагональные моменты площади инерции для квадратного сечения можно рассчитать как
I x = I y = 4 /12 (6)
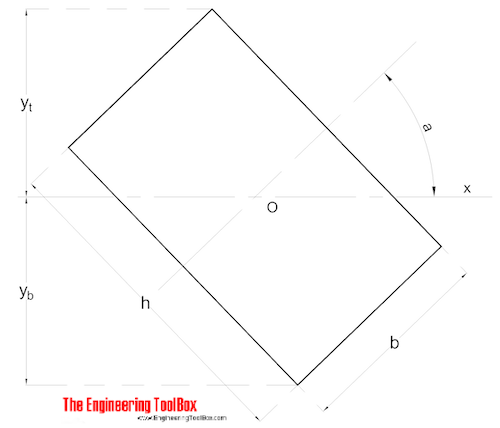
Прямоугольный разрез — Площадь моментов на любая линия, проходящая через Центр тяжести

Прямоугольное сечение и Площадь момента на линии, проходящей через Центр тяжести, можно рассчитать как
I x = (чч / 12) (ч 2 cos 2 a + b 2 sin 2 a) (7)
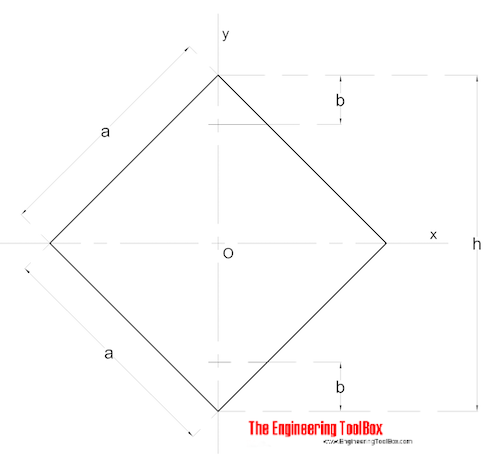
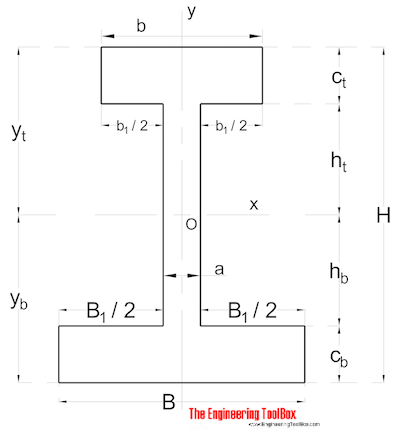
Симметричная форма

Площадь Момент инерции для сечения симметричной формы можно рассчитать как
I x = (ах 3 / 12) + (b / 12) (H 3 — h 3 ) (8)
I y = ( 3 ч / 12) + (b 3 /12) (Ч — ч) (8b)
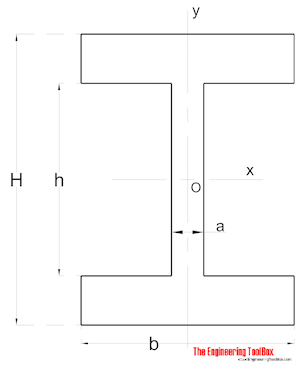
Несимметричная форма

Площадь Момент инерции для сечения несимметричной формы можно рассчитать как
I x = (1/3) (B y b 3 — B 1 ч b 3 + на т 3 — b1 ч т 3 ) (9)
Площадь Момент инерции иПолярный момент инерции против момента инерции
- «Момент инерции зоны» — это свойство формы, которое используется для прогнозирования прогиба, изгиба и напряжения в балках
- «Полярный момент инерции» как мера способности луча противостоять скручиванию — которое требуется для расчета скручивания балки, подвергнутой крутящему моменту
- «Момент инерции» является мерой сопротивления объекта изменению направления вращения.
Модуль сечения
- «Модуль сечения» определяется как W = I / y , где I — это момент момента инерции, а y — расстояние от нейтральной оси до любого заданного волокна
. Момент (физика) — Простая английская Википедия, бесплатная энциклопедия 
В физике момент силы (часто просто момент ) является мерой его склонности заставлять тело вращаться вокруг определенной точки или оси.
В этой концепции моментное плечо , расстояние от оси вращения, играет важную роль. Рычаг, шкив, редуктор и большинство других простых машин создают механическое преимущество, меняя моментный рычаг. Единица СИ для момента — это ньютон-метр (кгм² / с²).
Формула на момент:
момент
знак равно
сила
×
Перпендикулярное расстояние
{\ displaystyle {\ text {Moment}} = {\ text {Force}} \ times {\ text {Перпендикулярное расстояние}}}
Принцип Момента гласит, что когда система находится в равновесии, сумма ее ЧАСОВ ВРЕМЕНИ равняется сумме ее ПРОТИВ ЧАСОВЫХ МОМЕНТОВ.
Некоторые примеры, где применяются моменты (эффект поворота), включают рычаги, такие как качели, открывающиеся и закрывающиеся двери, щелкунчики, открывалки и ломы.
Рычаг — это простая машина, в которой одна сила, называемая усилием, используется для преодоления другой силы, называемой нагрузкой.
В физике момент — это комбинация физической величины и расстояния.
Принцип моментов вытекает из открытия Архимедом принципа действия рычага. В рычаге человек прикладывает силу, в свое время чаще всего человеческую мышцу, к руке , какой-то луч. Архимед отметил, что величина силы, приложенной к объекту, момент силы , определяется как M = rF , где F — приложенная сила, а r — расстояние от приложенной силы до объекта. ,
, Основы СИ: базовые и производные единицы

Для
простота понимания и удобство, было дано 22 производных единицы СИ
специальные имена и символы, как показано в таблице 3.
Таблица 3. Производные единицы СИ со специальными именами и символами
СИ производная единица
Производное количество Имя Символ Выражение
в терминах
других единиц СИ выражение
в терминах
базовых единиц СИ угол наклона радиан (а) рад — м · м -1 = 1 (b) телесный угол стерадиан (а) ср (с) — м 2 м -2 = 1 (b) Частота герц Гц — с -1 сила ньютон N — м · кг · с -2 давление, напряжение паскаля Па н / м 2 м -1 · кг · с -2 энергии, работа, количество тепла Джоуля J Н · м м 2 · кг · с -2 Мощность, поток излучения Вт Вт Дж / с м 2 · кг · с -3 электрический заряд, количество электричества кулона C — с · A разность электрических потенциалов,
электродвижущая сила вольт В W / A м 2 · кг · с -3 · A -1 Емкость фарад F C / V м -2 · кг -1 · с 4 · A 2 электрическое сопротивление Ом 
V / A м 2 · кг · с -3 · A -2 электрическая проводимость симен S A / V м -2 · кг -1 · с 3 · A 2 магнитный поток Вебер Wb В · с м 2 · кг · с -2 · A -1 плотность магнитного потока тесла Т Вт / м 2 кг · с -2 · A -1 Индуктивность Генри H Wb / A м 2 · кг · с -2 · A -2 по Цельсию температура градусов по Цельсию ° C — К световой поток люмен лм кд · ср (с) м 2 м -2 кд = кд освещенности люкс лк лм / м 2 м 2 м -4 кд = м -2 кд активность (радионуклидов) беккерель Бк — с -1 поглощенная доза, удельная энергия (переданная), керма серый Гр Дж / кг м 2 · с -2 эквивалентной дозы (д) Зиверт Зв Дж / кг м 2 · с -2 каталитическая активность катал кат с -1 · моль (а) Радиан
и стерадиан может быть выгодно использован в выражениях для производных
единицы, чтобы различать количества другой природы, но
того же измерения; некоторые примеры приведены в таблице 4.
(b) На практике символы rad и sr используются там, где
целесообразно, но производная единица «1» обычно опускается.
(с) В фотометрии название единицы стерадиан и единица измерения
Символ sr обычно сохраняется в выражениях для производных единиц.
(d) Другие величины, выраженные в зивертах, являются объемными
эквивалент дозы, эквивалент направленной дозы, эквивалент индивидуальной дозы,
и эквивалентная доза органа.
Примечание о градусах Цельсия. Производная единица в таблице 3 со специальным названием градус Цельсия и
Специальный символ ° C заслуживает комментария. Из-за температуры пути
весы, которые должны быть определены, остается обычной практикой для выражения термодинамики
температура, символ Т , с точки зрения ее отличия от эталона
температура Т 0 = 273.15 К, ледяная точка. Эта температура
Разница называется температурой Цельсия, символ т , и составляет
определяется уравнением количества
т = Т — Т 0 .
Единица измерения температуры в градусах Цельсия — градус Цельсия, символ ° C.
числовое значение по Цельсию температура т , выраженное в градусах
Цельсия дано
т / ° С = т / К — 273.15.
Из определения т следует, что градус Цельсия равен
по величине к Кельвину, что в свою очередь означает, что числовой
значение данной разности температур или температурного интервала которого
значение выражается в градусах Цельсия (° C), равных
числовое значение той же разницы или интервала, когда его значение
выражается в единицах кельвина (K). Таким образом, перепады температур или температуры
интервалы могут быть выражены в градусах Цельсия или Кельвина
используя то же числовое значение.Например, температура по Цельсию
разница  т и термодинамическая разница температур
т и термодинамическая разница температур  Т между температурой плавления галлия и тройной точки воды может
записывается как
Т между температурой плавления галлия и тройной точки воды может
записывается как  т = 29,7546 ° C =
т = 29,7546 ° C =  T = 29,7546 К.
T = 29,7546 К.
Специальные имена и символы из 22 производных единиц СИ со специальными именами и символами
приведенные в таблице 3, сами могут быть включены в названия и символы
другие производные единицы СИ, как показано в таблице 4.
Таблица 4. Примеры производных единиц СИ, чьи имена и символы
включает производные единицы СИ со специальными именами и символами
СИ производная единица
Производное количество Имя Символ Динамическая вязкость паскаль второй Па · с момент силы ньютон-метр Н · м поверхностное натяжение ньютона на метр Н / м угловая скорость радиан в секунду рад / с угловое ускорение радиан в секунду в квадрате рад / с 2 плотность теплового потока, освещенность Вт на квадратный метр Вт / м 2 теплоемкость, энтропия джоуля за кельвин J / K удельная теплоемкость, удельная энтропия джоуля на килограмм кельвина Дж / (кг · К) удельная энергия джоуля за килограмм Дж / кг теплопроводность Вт на метр Кельвина Вт / (м · К) плотность энергии Дж на кубический метр Дж / м 3 Напряжение электрического поля вольт на метр В / м плотность электрического заряда кулона за кубометр ц / м 3 плотность электрического потока кулона за квадратный метр ц / м 2 диэлектрическая проницаемость фарад на метр ф / м Проницаемость Генри за метр ч / м молярная энергия джоуля на моль Дж / моль молярная энтропия, молярная теплоемкость джоуля на моль кельвина Дж / (моль · К) экспозиции (х и  лучи)
лучи) кулона за килограмм ц / кг Мощность поглощенной дозы серых в секунду Гр / с интенсивность излучения Вт на стерадиан Вт / ср сияние Вт на квадратный метр стерадиан Вт / (м 2 · ср) каталитическая (активность) концентрация каталя на кубический метр кат / м 3
Продолжить
до префиксов СИ
.
В физике момент силы (часто просто момент ) является мерой его склонности заставлять тело вращаться вокруг определенной точки или оси.
В этой концепции моментное плечо , расстояние от оси вращения, играет важную роль. Рычаг, шкив, редуктор и большинство других простых машин создают механическое преимущество, меняя моментный рычаг. Единица СИ для момента — это ньютон-метр (кгм² / с²).
Формула на момент:
момент знак равно сила × Перпендикулярное расстояние {\ displaystyle {\ text {Moment}} = {\ text {Force}} \ times {\ text {Перпендикулярное расстояние}}}
Принцип Момента гласит, что когда система находится в равновесии, сумма ее ЧАСОВ ВРЕМЕНИ равняется сумме ее ПРОТИВ ЧАСОВЫХ МОМЕНТОВ.
Некоторые примеры, где применяются моменты (эффект поворота), включают рычаги, такие как качели, открывающиеся и закрывающиеся двери, щелкунчики, открывалки и ломы.
Рычаг — это простая машина, в которой одна сила, называемая усилием, используется для преодоления другой силы, называемой нагрузкой.
В физике момент — это комбинация физической величины и расстояния.
Принцип моментов вытекает из открытия Архимедом принципа действия рычага. В рычаге человек прикладывает силу, в свое время чаще всего человеческую мышцу, к руке , какой-то луч. Архимед отметил, что величина силы, приложенной к объекту, момент силы , определяется как M = rF , где F — приложенная сила, а r — расстояние от приложенной силы до объекта. ,
,  | Для
простота понимания и удобство, было дано 22 производных единицы СИ
специальные имена и символы, как показано в таблице 3.
Примечание о градусах Цельсия. Производная единица в таблице 3 со специальным названием градус Цельсия и Специальный символ ° C заслуживает комментария. Из-за температуры пути весы, которые должны быть определены, остается обычной практикой для выражения термодинамики температура, символ Т , с точки зрения ее отличия от эталона температура Т 0 = 273.15 К, ледяная точка. Эта температура Разница называется температурой Цельсия, символ т , и составляет определяется уравнением количества т = Т — Т 0 . Единица измерения температуры в градусах Цельсия — градус Цельсия, символ ° C. числовое значение по Цельсию температура т , выраженное в градусах Цельсия дано т / ° С = т / К — 273.15. Из определения т следует, что градус Цельсия равен
по величине к Кельвину, что в свою очередь означает, что числовой
значение данной разности температур или температурного интервала которого
значение выражается в градусах Цельсия (° C), равных
числовое значение той же разницы или интервала, когда его значение
выражается в единицах кельвина (K). Таким образом, перепады температур или температуры
интервалы могут быть выражены в градусах Цельсия или Кельвина
используя то же числовое значение.Например, температура по Цельсию
разница Специальные имена и символы из 22 производных единиц СИ со специальными именами и символами приведенные в таблице 3, сами могут быть включены в названия и символы другие производные единицы СИ, как показано в таблице 4.
Продолжить до префиксов СИ | |||


.gif)
1.gif)
1.gif)
1.gif)
1.gif)
.gif)
2.gif)
2.gif)
2.gif)
2.gif)
.gif)
3.gif)
3.gif)
.gif)
4.gif)
4.gif)
.gif)
5.gif)
5.gif)
.gif)
6.gif)
6.gif)
.gif)
7.gif)
7.gif)
7.gif)
.gif)
8.gif)
8.gif)
8.gif)
.gif)
9.gif)
9.gif)
.gif)
10.gif)
10.gif)

 т и термодинамическая разница температур
т и термодинамическая разница температур  лучи)
лучи)