Двоичный код и десятичный код: Перевод чисел из десятичной системы в двоичную — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Полупроводниковая схемотехника

Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство. Пер. с нем. М.: Мир, 1982. — 512 с.

В книге специалистов из ФРГ приведены параметры и описана структура современных полупроводниковых приборов и интегральных микросхем с различной степенью интеграции. Изложены принципы построения и методы расчета основных схем автоматики, радиоэлектроники и вычислительной техники.

Для специалистов в области электронной и вычислительной техники, студентов соответствующих специальностей вузов и радиолюбителей.

Пассивные RC- и LRC- цепи
2.1. ФИЛЬТР НИЖНИХ ЧАСТОТ
2.1.3. ДЛИТЕЛЬНОСТЬ ФРОНТА ИМПУЛЬСА И ЧАСТОТА СРЕЗА ФИЛЬТРА
2.2. ФИЛЬТР ВЕРХНИХ ЧАСТОТ
2.3. КОМПЕНСИРОВАННЫЙ ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ
2.4. ПАССИВНЫЙ ПОЛОСОВОЙ RC-ФИЛЬТР
2.5. МОСТ ВИНА-РОБИНСОНА
2.6. ДВОЙНОЙ Т-ОБРАЗНЫЙ ФИЛЬТР
2.7. КОЛЕБАТЕЛЬНЫЙ КОНТУР
3. Диоды
3.2. СТАБИЛИТРОНЫ
3.3. ВАРИКАПЫ
4. Транзистор и схемы на его основе
4.2. СХЕМА С ОБЩИМ ЭМИТТЕРОМ
4.2.2. НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ
4.2.3. СХЕМА С ОБЩИМ ЭМИТТЕРОМ И ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ ПО ТОКУ
4.2.4. ОТРИЦАТЕЛЬНАЯ ОБРАТНАЯ СВЯЗЬ ПО НАПРЯЖЕНИЮ
4.2.5. УСТАНОВКА РАБОЧЕЙ ТОЧКИ
4.3. СХЕМА С ОБЩЕЙ БАЗОЙ
4.4. СХЕМА С ОБЩИМ КОЛЛЕКТОРОМ, ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ

4.5. ТРАНЗИСТОР КАК ИСТОЧНИК СТАБИЛЬНОГО ТОКА
4.5.2. БИПОЛЯРНЫЙ ИСТОЧНИК ПИТАНИЯ
4.5.3. СХЕМА «ТОКОВОГО ЗЕРКАЛА»
4.6. СХЕМА ДАРЛИНГТОНА
4.7. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛИ
4.7.2. РЕЖИМ БОЛЬШОГО СИГНАЛА
4.7.3. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ ПО ТОКУ
4.

7.4. НАПРЯЖЕНИЕ РАЗБАЛАНСА
4.8. ИЗМЕРЕНИЕ НЕКОТОРЫХ ПАРАМЕТРОВ ПРИ МАЛОМ СИГНАЛЕ
4.9. ШУМЫ ТРАНЗИСТОРА
4.10. ПРЕДЕЛЬНЫЕ ПАРАМЕТРЫ
5. Полевые транзисторы
5.2. ХАРАКТЕРИСТИКИ И ПАРАМЕТРЫ МАЛЫХ СИГНАЛОВ
5.3. ПРЕДЕЛЬНЫЕ ЭЛЕКТРИЧЕСКИЕ ПАРАМЕТРЫ
5.4. ОСНОВНЫЕ СХЕМЫ ВКЛЮЧЕНИЯ
5.4.1. СХЕМА С ОБЩИМ ИСТОКОМ
5.4.2. СХЕМА С ОБЩИМ ЗАТВОРОМ
5.4.3. СХЕМА С ОБЩИМ СТОКОМ, ИСТОКОВЫЙ ПОВТОРИТЕЛЬ
5.5. ПОЛЕВОЙ ТРАНЗИСТОР КАК СТАБИЛИЗАТОР ТОКА
5.6. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
5.7. ПОЛЕВОЙ ТРАНЗИСТОР В КАЧЕСТВЕ УПРАВЛЯЕМОГО СОПРОТИВЛЕНИЯ
6. Операционный усилитель
6.1. СВОЙСТВА ОПЕРАЦИОННОГО УСИЛИТЕЛЯ
6.2. ПРИНЦИП ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗИ
6.3. НЕИНВЕРТИРУЮЩИЙ УСИЛИТЕЛЬ
6.4. ИНВЕРТИРУЮЩИЙ УСИЛИТЕЛЬ
7. Внутренняя структура операционных усилителей
7.2. ПРОСТЕЙШИЕ СХЕМЫ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
7.3. СТАНДАРТНАЯ СХЕМА ИНТЕГРАЛЬНОГО ОПЕРАЦИОННОГО УСИЛИТЕЛЯ
7.4. КОРРЕКЦИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
7.4.

2. ПОЛНАЯ ЧАСТОТНАЯ КОРРЕКЦИЯ
7.4.3. ПОДСТРАИВАЕМАЯ ЧАСТОТНАЯ КОРРЕКЦИЯ
7.4.4. СКОРОСТЬ НАРАСТАНИЯ
7.4.5. КОМПЕНСАЦИЯ ЕМКОСТНОЙ НАГРУЗКИ
7.5. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
8. Простейшие переключающие схемы
8.1. ТРАНЗИСТОРНЫЙ КЛЮЧ
8.2. БИСТАБИЛЬНЫЕ РЕЛАКСАЦИОННЫЕ СХЕМЫ
8.2.2. ТРИГГЕР ШМИТТА
8.3. МОНОСТАБИЛЬНАЯ РЕЛАКСАЦИОННАЯ СХЕМА
8.4. НЕСТАБИЛЬНАЯ РЕЛАКСАЦИОННАЯ СХЕМА
9. Базовые логические схемы
9.1. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ
9.2. СОСТАВЛЕНИЕ ЛОГИЧЕСКИХ ФУНКЦИЙ
9.2.1. ТАБЛИЦА КАРНО
9.3. ПРОИЗВОДНЫЕ ОСНОВНЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ
9.4. СХЕМОТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ ОСНОВНЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ
9.4.1. РЕЗИСТИВНО-ТРАНЗИСТОРНАЯ ЛОГИКА (РТЛ)
9.4.2. ДИОДНО-ТРАНЗИСТОРНАЯ ЛОГИКА (ДТЛ)
9.4.3. ТРАНЗИСТОРНО-ТРАНЗИСТОРНАЯ ЛОГИКА (ТТЛ)
9.4.4. ИНТЕГРАЛЬНАЯ ИНЖЕКЦИОННАЯ ЛОГИКА
9.4.5. ЭМИТТЕРНО-СВЯЗАННАЯ ЛОГИКА (ЭСЛ)
9.4.6. n-КАНАЛЬНАЯ МОП-ЛОГИКА
9.4.7. КОМПЛЕМЕНТАРНАЯ МОП-ЛОГИКА (КМОП)
9.4.8. ОБЗОР
9.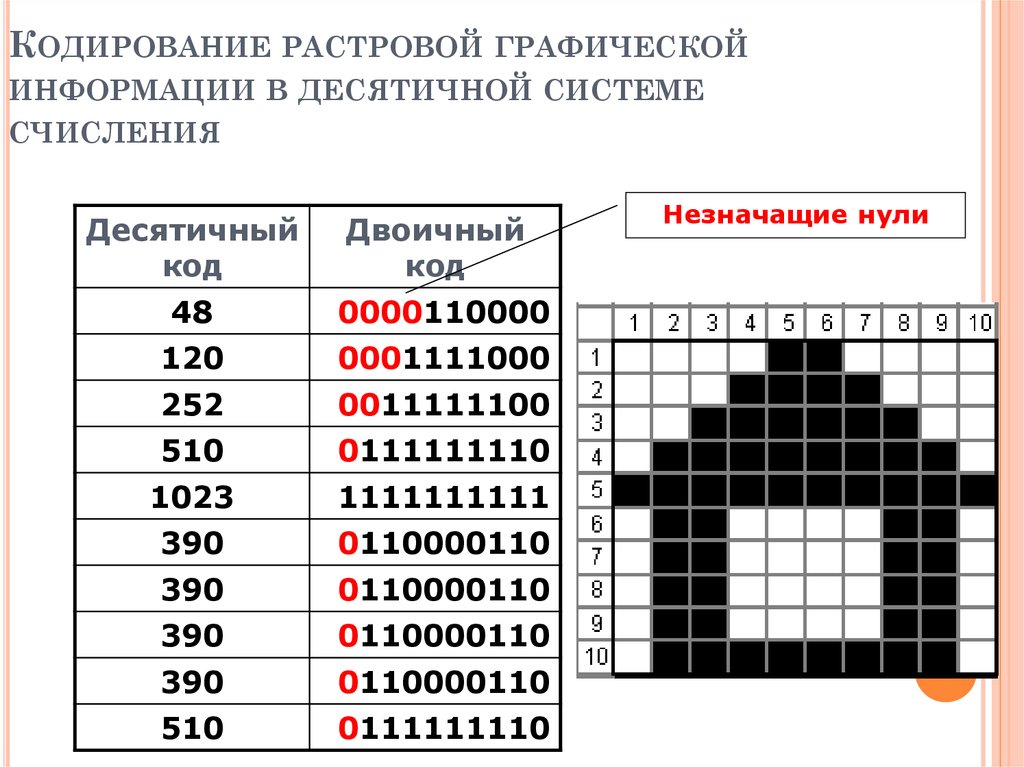

4.9. СПЕЦИАЛЬНЫЕ СХЕМЫ ВЫХОДНЫХ КАСКАДОВ
9.5. ИНТЕГРАЛЬНЫЕ ТРИГГЕРЫ
9.5.2. ТРИГГЕРЫ ТИПА M-S (MASTER-SLAVE)
9.5.3. ДИНАМИЧЕСКИЙ ТРИГГЕР
9.6. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
9.6.2. ПОСТОЯННЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА (ПЗУ)
9.6.3. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ (ПЛМ)
10. Оптоэлектронные приборы
10.1. ОСНОВНЫЕ ПОНЯТИЯ ФОТОМЕТРИИ
10.2. ФОТОРЕЗИСТОР
10.3. ФОТОДИОДЫ
10.4. ФОТОТРАНЗИСТОРЫ
10.5. СВЕТОДИОДЫ
10.6. ОПТРОНЫ
Часть II. Применения
11. Линейные и нелинейные аналоговые вычислительные схемы
11.1. СХЕМА СУММИРОВАНИЯ
11.2. СХЕМЫ ВЫЧИТАНИЯ
11.2.2. СХЕМА ВЫЧИТАНИЯ НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
11.3. БИПОЛЯРНОЕ УСИЛИТЕЛЬНОЕ ЗВЕНО
11.4. СХЕМЫ ИНТЕГРИРОВАНИЯ
11.4.1. ИНВЕРТИРУЮЩИЙ ИНТЕГРАТОР
11.4.2. ЗАДАНИЕ НАЧАЛЬНЫХ УСЛОВИЙ
11.4.3. СУММИРУЮЩИЙ ИНТЕГРАТОР
11.4.4. НЕИНВЕРТИРУЮЩИЙ ИНТЕГРАТОР
11.5. СХЕМЫ ДИФФЕРЕНЦИРОВАНИЯ
11.5.3. СХЕМА ДИФФЕРЕНЦИРОВАНИЯ С ВЫСОКИМ ВХОДНЫМ СОПРОТИВЛЕНИЕМ

11.

6. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
11.7. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
11.7.2. ЭКСПОНЕНТА
11.7.3. ВЫЧИСЛЕНИЕ СТЕПЕННЫХ ФУНКЦИЙ С ПОМОЩЬЮ ЛОГАРИФМОВ
11.7.4. ФУНКЦИИ SIN X И COS X
11.7.5. ПЕРЕСТРАИВАЕМЫЕ ФУНКЦИОНАЛЬНЫЕ СХЕМЫ
11.8. АНАЛОГОВЫЕ СХЕМЫ УМНОЖЕНИЯ
11.8.2. УМНОЖЕНИЕ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ ФУНКЦИОНАЛЬНЫХ ГЕНЕРАТОРОВ
11.8.3. СХЕМА УМНОЖЕНИЯ, ИСПОЛЬЗУЮЩАЯ ИЗМЕНЕНИЕ КРУТИЗНЫ ХАРАКТЕРИСТИКИ ТРАНЗИСТОРОВ
11.8.4. СХЕМА УМНОЖЕНИЯ С ИЗОЛИРОВАННЫМИ ЗВЕНЬЯМИ
11.8.5. БАЛАНСИРОВКА СХЕМ УМНОЖЕНИЯ
11.8.6. СХЕМЫ ЧЕТЫРЕХКВАДРАНТНОГО УМНОЖЕНИЯ
11.8.7. ПРИМЕНЕНИЕ СХЕМЫ УМНОЖЕНИЯ ДЛЯ ДЕЛЕНИЯ И ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ
11.9. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
11.9.2. ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ КООРДИНАТ В ПОЛЯРНЫЕ
12. Управляемые источники и схемы преобразования полного сопротивления
12.1. ИСТОЧНИКИ НАПРЯЖЕНИЯ, УПРАВЛЯЕМЫЕ НАПРЯЖЕНИЕМ
12.2. ИСТОЧНИКИ НАПРЯЖЕНИЯ, УПРАВЛЯЕМЫЕ ТОКОМ
12.3. ИСТОЧНИКИ ТОКА, УПРАВЛЯЕМЫЕ НАПРЯЖЕНИЕМ
12.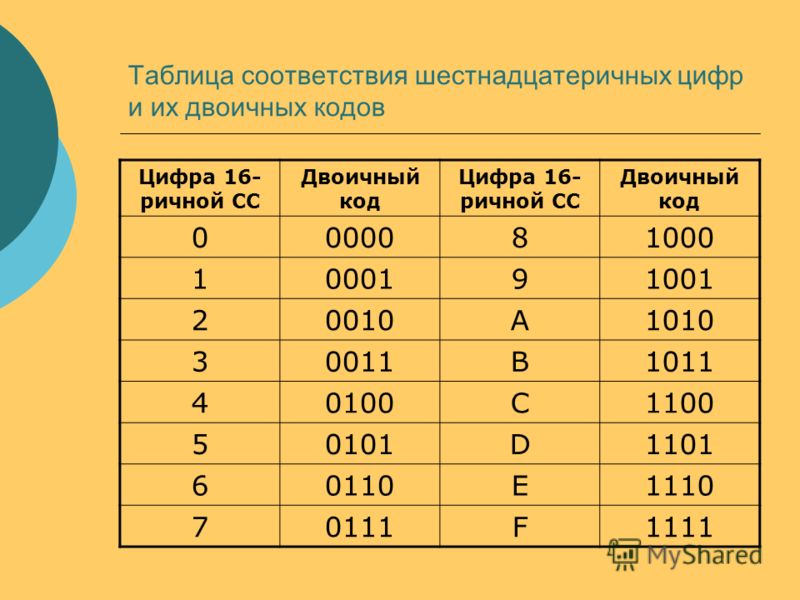

3.2. ИСТОЧНИКИ ТОКА С ЗАЗЕМЛЕННОЙ НАГРУЗКОЙ
12.3.3. ЭТАЛОННЫЕ ИСТОЧНИКИ ТОКА НА ТРАНЗИСТОРАХ
12.3.4. ПЛАВАЮЩИЕ ИСТОЧНИКИ ТОКА
12.4. ИСТОЧНИКИ ТОКА, УПРАВЛЯЕМЫЕ ТОКОМ
12.5. ПРЕОБРАЗОВАТЕЛЬ ОТРИЦАТЕЛЬНОГО СОПРОТИВЛЕНИЯ (NIC)
12.6. ГИРАТОР
12.7. ЦИРКУЛЯТОР
13. Активные фильтры
13.1. ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ
13.1.1. ФИЛЬТР БАТТЕРВОРТА
13.1.2. ФИЛЬТР ЧЕБЫШЕВА
13.1.3. ФИЛЬТРЫ БЕССЕЛЯ
13.1.4. ОБОБЩЕННОЕ ОПИСАНИЕ ФИЛЬТРОВ
13.2. ПРЕОБРАЗОВАНИЕ НИЖНИХ ЧАСТОТ В ВЕРХНИЕ
13.3. РЕАЛИЗАЦИЯ ФИЛЬТРОВ НИЖНИХ И ВЕРХНИХ ЧАСТОТ ПЕРВОГО ПОРЯДКА
13.4. РЕАЛИЗАЦИЯ ФИЛЬТРОВ НИЖНИХ И ВЕРХНИХ ЧАСТОТ ВТОРОГО ПОРЯДКА
13.4.2. ФИЛЬТР СО СЛОЖНОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
13.4.3. ФИЛЬТР С ПОЛОЖИТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
13.4.4. ФИЛЬТР НИЖНИХ ЧАСТОТ С ОМИЧЕСКОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
13.5. РЕАЛИЗАЦИЯ ФИЛЬТРОВ ВЕРХНИХ И НИЖНИХ ЧАСТОТ БОЛЕЕ ВЫСОКОГО ПОРЯДКА
13.6. ПРЕОБРАЗОВАНИЕ ФИЛЬТРА НИЖНИХ ЧАСТОТ В ПОЛОСОВОЙ ФИЛЬТР
13.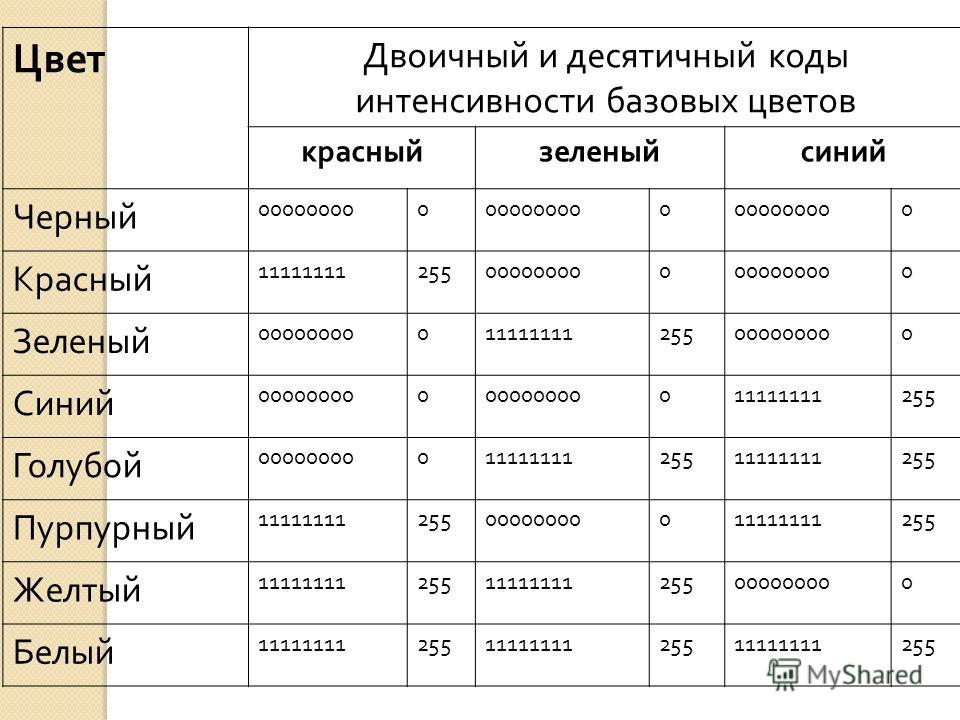

6.1. ПОЛОСОВОЙ ФИЛЬТР ВТОРОГО ПОРЯДКА
13.6.2. ПОЛОСОВОЙ ФИЛЬТР ЧЕТВЕРТОГО ПОРЯДКА
13.7. РЕАЛИЗАЦИЯ ПОЛОСОВЫХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
13.7.2. ПОЛОСОВОЙ ФИЛЬТР СО СЛОЖНОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
13.7.3. ПОЛОСОВОЙ ФИЛЬТР С ПОЛОЖИТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
13.7.4. ПОЛОСОВОЙ ФИЛЬТР С ОМИЧЕСКОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
13.8. ПРЕОБРАЗОВАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ В ЗАГРАЖДАЮЩИЕ ПОЛОСОВЫЕ ФИЛЬТРЫ
13.9. РЕАЛИЗАЦИЯ ЗАГРАЖДАЮЩИХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
13.9.1. ЗАГРАЖДАЮЩИЙ LRC-ФИЛЬТР
13.9.2. АКТИВНЫЙ ЗАГРАЖДАЮЩИЙ ФИЛЬТР С ДВОЙНЫМ Т-ОБРАЗНЫМ МОСТОМ
13.9.3. АКТИВНЫЙ ЗАГРАЖДАЮЩИЙ ФИЛЬТР С МОСТОМ ВИНА-РОБИНСОНА
13.10. ФАЗОВЫЙ ФИЛЬТР
13.10.2. РЕАЛИЗАЦИЯ ФАЗОВОГО ФИЛЬТРА ПЕРВОГО ПОРЯДКА
13.10.3. РЕАЛИЗАЦИЯ ФАЗОВОГО ФИЛЬТРА ВТОРОГО ПОРЯДКА
13.11. ПЕРЕСТРАИВАЕМЫЙ УНИВЕРСАЛЬНЫЙ ФИЛЬТР
14. Широкополосные усилители
14.1. ЗАВИСИМОСТЬ КОЭФФИЦИЕНТА УСИЛЕНИЯ ПО ТОКУ ОТ ЧАСТОТЫ
14.2. ВЛИЯНИЕ ВНУТРЕННИХ ЕМКОСТЕЙ ТРАНЗИСТОРА И ЕМКОСТЕЙ МОНТАЖА
14.

3. КАСКОДНАЯ СХЕМА

14.4. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ КАК ШИРОКОПОЛОСНЫЙ УСИЛИТЕЛЬ
14.5. СИММЕТРИЧНЫЙ ШИРОКОПОЛОСНЫЙ УСИЛИТЕЛЬ
14.5.2. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С ИНВЕРТОРОМ
14.5.3. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С КОМПЛЕМЕНТАРНОЙ КАСКОДНОЙ СХЕМОЙ
14.5.4. ДВУХТАКТНЫЙ ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ
14.6. ШИРОКОПОЛОСНЫЙ ПОВТОРИТЕЛЬ НАПРЯЖЕНИЯ
14.6.2. ДВУХТАКТНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ
14.7. ШИРОКОПОЛОСНЫЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ
15. Усилители мощности
15.1. ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ КАК УСИЛИТЕЛЬ МОЩНОСТИ
15.2. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ
15.2.2. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ В РЕЖИМЕ AB
15.2.3. СПОСОБЫ ЗАДАНИЯ НАПРЯЖЕНИЯ СМЕЩЕНИЯ
15.3. СХЕМЫ ОГРАНИЧЕНИЯ ТОКА
15.4. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ ПО СХЕМЕ ДАРЛИНГТОНА
15.5. РАСЧЕТ МОЩНОГО ОКОНЕЧНОГО КАСКАДА
15.6. СХЕМЫ ПРЕДВАРИТЕЛЬНЫХ УСИЛИТЕЛЕЙ НАПРЯЖЕНИЯ
15.7. ПОВЫШЕНИЕ НАГРУЗОЧНОЙ СПОСОБНОСТИ ИНТЕГРАЛЬНЫХ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
16. Источники питания
16.

1. СВОЙСТВА СЕТЕВЫХ ТРАНСФОРМАТОРОВ
16.2. ВЫПРЯМИТЕЛИ
16.2.1. ОДНОПОЛУПЕРИОДНЫЙ ВЫПРЯМИТЕЛЬ
16.2.2. МОСТОВОЙ ВЫПРЯМИТЕЛЬ
16.2.3. МОСТОВОЙ ВЫПРЯМИТЕЛЬ ДЛЯ ДВУХ СИММЕТРИЧНЫХ ОТНОСИТЕЛЬНО ЗЕМЛИ ВЫХОДНЫХ НАПРЯЖЕНИЙ
16.3. ПОСЛЕДОВАТЕЛЬНАЯ СТАБИЛИЗАЦИЯ НАПРЯЖЕНИЯ
16.3.2. СХЕМА С РЕГУЛИРУЮЩИМ УСИЛИТЕЛЕМ
16.3.3. ИНТЕГРАЛЬНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ
16.3.4. СТАБИЛИЗАТОР С МАЛЫМ НАПРЯЖЕНИЕМ ПОТЕРЬ
16.3.5. СТАБИЛИЗАЦИЯ НАПРЯЖЕНИЙ, СИММЕТРИЧНЫХ ОТНОСИТЕЛЬНО ЗЕМЛИ
16.3.6. СТАБИЛИЗАТОР НАПРЯЖЕНИЯ С ИЗМЕРИТЕЛЬНЫМИ ВЫВОДАМИ
16.3.7. ЛАБОРАТОРНЫЕ ИСТОЧНИКИ ПИТАНИЯ
16.3.8. ОКОНЕЧНЫЙ КАСКАД ЛАБОРАТОРНОГО ИСТОЧНИКА ПИТАНИЯ С БОЛЬШОЙ ВЫХОДНОЙ МОЩНОСТЬЮ
16.4. ПОЛУЧЕНИЕ ОПОРНОГО НАПРЯЖЕНИЯ
16.4.2. ПОЛУЧЕНИЕ МАЛЫХ ОПОРНЫХ НАПРЯЖЕНИЙ
16.5. ИМПУЛЬСНЫЕ РЕГУЛЯТОРЫ НАПРЯЖЕНИЯ
16.5.2. ПЕРВИЧНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ
17. Аналоговые коммутаторы и компараторы
17.2. ЭЛЕКТРОННЫЕ КОММУТАТОРЫ
17.2.2. ДИОДНЫЙ КОММУТАТОР
17.2.3. КОММУТАТОР НА БИПОЛЯРНЫХ ТРАНЗИСТОРАХ
17.

3. АНАЛОГОВЫЕ КОММУТАТОРЫ НА БАЗЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
17.3.2. КОММУТАТОР НА ПОЛЕВОМ ТРАНЗИСТОРЕ С ПЕРЕМЕНОЙ ЗНАКА ВЫХОДНОГО НАПРЯЖЕНИЯ
17.3.3. КОММУТАТОР НА БАЗЕ ДИФФЕРЕНЦИАЛЬНОГО УСИЛИТЕЛЯ
17.4. АНАЛОГОВЫЕ КОММУТАТОРЫ С ПАМЯТЬЮ
17.5. КОМПАРАТОРЫ
17.5.2. КОМПАРАТОР С ПРЕЦИЗИОННЫМ ВЫХОДНЫМ НАПРЯЖЕНИЕМ
17.5.3. ДВУХПОРОГОВЫЙ КОМПАРАТОР
17.6. ТРИГГЕР ШМИТТА
17.6.1. ИНВЕРТИРУЮЩИЙ ТРИГГЕР ШМИТТА
17.6.2. НЕИНВЕРТИРУЮЩИЙ ТРИГГЕР ШМИТТА
17.6.3. ПРЕЦИЗИОННЫЙ ТРИГГЕР ШМИТТА
18. Генераторы сигналов
18.1. LC-ГЕНЕРАТОРЫ
18.1.2. ГЕНЕРАТОР С ТРАНСФОРМАТОРНОЙ СВЯЗЬЮ (СХЕМА МАЙССНЕРА)
18.1.3. ТРЕХТОЧЕЧНАЯ СХЕМА С ИНДУKТИВНОЙ ОБРАТНОЙ СВЯЗЬЮ (СХЕМА ХАРТЛИ)
18.1.4. ТРЕХТОЧЕЧНАЯ СХЕМА С ЕМКОСТНОЙ ОБРАТНОЙ СВЯЗЬЮ (СХЕМА КОЛПИТЦА)
18.1.5. LC-ГЕНЕРАТОР С ЭМИТТЕРНОЙ СВЯЗЬЮ
18.1.6. ДВУХТАКТНЫЕ ГЕНЕРАТОРЫ
18.2. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ
18.2.1. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА КВАРЦЕВОГО РЕЗОНАТОРА
18.2.2. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ С LC-КОЛЕБАТЕЛЬНЫМ КОНТУРОМ
18.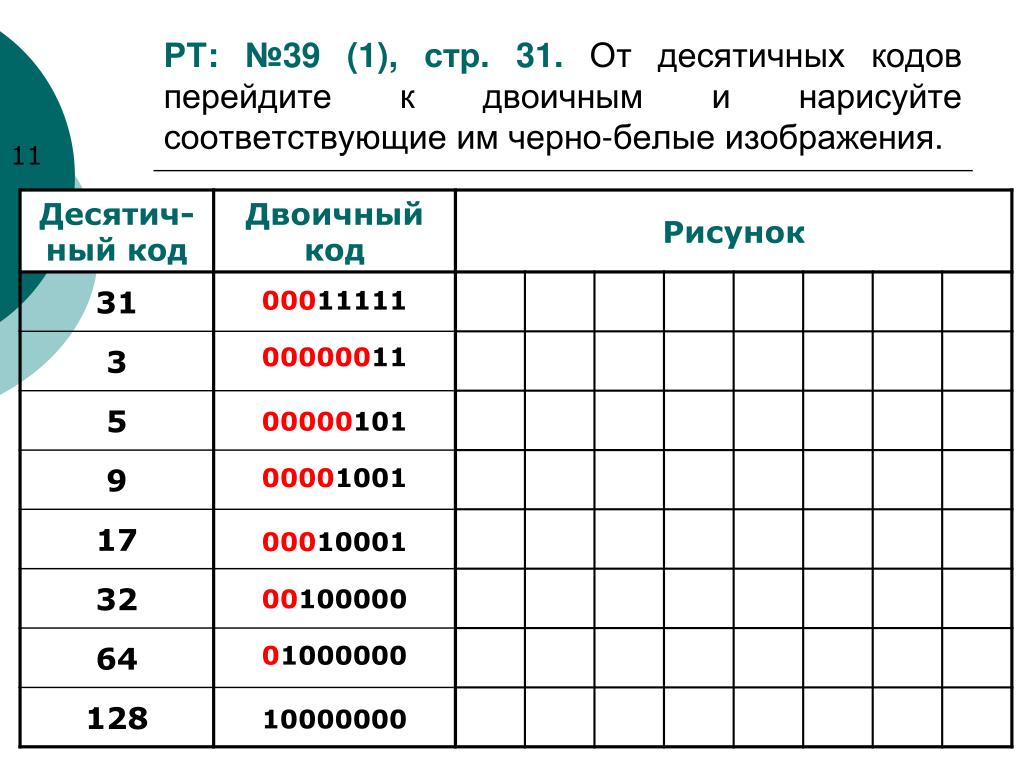

2.3. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ БЕЗ LC-КОНТУРА
18.3. СИНУСОИДАЛЬНЫЕ RC-ГЕНЕРАТОРЫ
18.3.2. МОДЕЛИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
18.4. ГЕНЕРАТОРЫ СИГНАЛОВ СПЕЦИАЛЬНОЙ ФОРМЫ (ФУНКЦИОНАЛЬНЫЕ ГЕНЕРАТОРЫ)
18.4.2. ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР С УПРАВЛЯЕМОЙ ЧАСТОТОЙ ВЫХОДНОГО СИГНАЛА
18.4.3. ВЫСОКОЧАСТОТНЫЙ ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР
18.5. МУЛЬТИВИБРАТОРЫ
18.5.1. НИЗКОЧАСТОТНЫЕ МУЛЬТИВИБРАТОРЫ
18.5.2. ВЫСОКОЧАСТОТНЫЕ МУЛЬТИВИБРАТОРЫ
19. Комбинационные логические схемы
19.1. ПРЕОБРАЗОВАТЕЛИ КОДОВ
19.1.2. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
19.1.3. КОД ГРЕЯ
19.2. МУЛЬТИПЛЕКСОР И ДЕМУЛЬТИПЛЕКСОР
19.3. КОМБИНАЦИОННОЕ УСТРОЙСТВО СДВИГА
19.4. КОМПАРАТОРЫ
19.5. СУММАТОРЫ
19.5.1. ПОЛУСУММАТОР
19.5.2. ПОЛНЫЙ СУММАТОР
19.5.3. СУММАТОРЫ С ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ
19.5.4. СЛОЖЕНИЕ ДВОИЧНО-ДЕСЯТИЧНЫХ ЧИСЕЛ
19.5.5. ВЫЧИТАНИЕ
19.5.6. СЛОЖЕНИЕ ЧИСЕЛ С ЛЮБЫМИ ЗНАКАМИ
19.6. УМНОЖИТЕЛИ
19.7. ЦИФРОВЫЕ ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
20.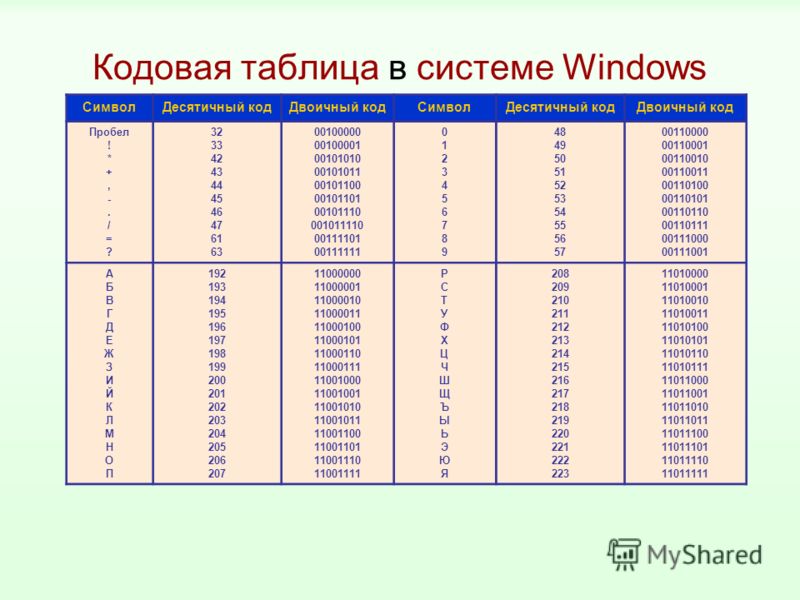

Интегральные схемы со структурами последовательностного типа
20.1. ДВОИЧНЫЕ СЧЕТЧИКИ
20.1.1. АСИНХРОННЫЙ (ПОСЛЕДОВАТЕЛЬНЫЙ) СЧЕТЧИК
20.1.2. СИНХРОННЫЙ (ПАРАЛЛЕЛЬНЫЙ) СЧЕТЧИК
20.2. ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК В КОДЕ 8421
20.2.1. АСИНХРОННЫЙ ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК
20.2.2. СИНХРОННЫЙ ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК
20.3. СЧЕТЧИК С ПРЕДВАРИТЕЛЬНОЙ УСТАНОВКОЙ
20.4. РЕГИСТРЫ СДВИГА
20.4.2. КОЛЬЦЕВОЙ РЕГИСТР
20.4.3. РЕГИСТР СДВИГА С ПАРАЛЛЕЛЬНЫМ ВВОДОМ
20.4.4. РЕГИСТР СДВИГА С ПЕРЕКЛЮЧАЕМЫМ НАПРАВЛЕНИЕМ СДВИГА
20.5. ПОЛУЧЕНИЕ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
20.6. ПЕРВОНАЧАЛЬНАЯ ОБРАБОТКА АСИНХРОННОГО СИГНАЛА
20.6.2. СИНХРОНИЗАЦИЯ ИМПУЛЬСОВ
20.6.3. СИНХРОННЫЙ ОДНОВИБРАТОР
20.6.4. СИНХРОННЫЙ ДЕТЕКТОР ИЗМЕНЕНИЙ
20.6.5. СИНХРОННЫЙ ТАКТОВЫЙ ПЕРЕКЛЮЧАТЕЛЬ
20.7. СИСТЕМАТИЧЕСКИЙ СИНТЕЗ ПОСЛЕДОВАТЕЛЬНОСТНЫХ СХЕМ
20.7.2. ПРИМЕР СИНТЕЗА ПЕРЕКЛЮЧАЕМОГО СЧЕТЧИКА
20.7.3. СОКРАЩЕНИЕ ЕМКОСТИ ПАМЯТИ
21. Микро-ЭВМ
21.1. ОСНОВНАЯ СТРУКТУРА МИКРО-ЭВМ
21.

2. ПРИНЦИП ДЕЙСТВИЯ МИКРОПРОЦЕССОРА
21.3. НАБОР КОМАНД
21.4. ОТЛАДОЧНЫЕ СРЕДСТВА
21.5. ОБЗОР МИКРОПРОЦЕССОРОВ РАЗЛИЧНОГО ТИПА
21.6. МОДУЛЬНОЕ ПОСТРОЕНИЕ МИКРО-ЭВМ
21.7. ПЕРИФЕРИЙНЫЕ УСТРОЙСТВА
21.7.1. ПАРАЛЛЕЛЬНЫЙ ИНТЕРФЕЙС
21.7.2. ПОСЛЕДОВАТЕЛЬНЫЙ ИНТЕРФЕЙС
21.7.3. ИНТЕРФЕЙС МАГИСТРАЛИ «ОБЩАЯ ШИНА»
21.7.4. ПРОГРАММИРУЕМЫЙ СЧЕТЧИК
21.7.5. ПОДКЛЮЧЕНИЕ ПЕРИФЕРИЙНЫХ МОДУЛЕЙ СЕМЕЙСТВА 8080 К МАГИСТРАЛЯМ СЕМЕЙСТВА 6800
21.7.6. ОБЗОР ПЕРИФЕРИЙНЫХ УСТРОЙСТВ
21.8. МИНИМАЛЬНЫЕ СИСТЕМЫ
21.8.2. ОДНОКРИСТАЛЬНАЯ МИКРО-ЭВМ
22. Цифровые фильтры
22.1. ТЕОРЕМА О ДИСКРЕТИЗАЦИИ (ТЕОРЕМА О ВЫБОРКАХ)
22.1.2. ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
22.2. ЦИФРОВАЯ ФУНКЦИЯ ПЕРЕДАЧИ ФИЛЬТРА
22.3. БИЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ
22.4. РЕАЛИЗАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ
22.4.2. СТРУКТУРА ЦИФРОВЫХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
22.4.3. ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
23. Передача данных и индикация
23.1. СОЕДИНИТЕЛЬНЫЕ ЛИНИИ
23.2. ЗАЩИТА ДАННЫХ
23.2.2. КОД ХЕММИНГА
23.

3. СТАТИЧЕСКИЕ ЦИФРОВЫЕ ИНДИКАТОРЫ
23.3.1. ДВОИЧНЫЕ ИНДИКАТОРЫ НА СВЕТОДИОДАХ
23.3.2. ДЕКАДНЫЕ ИНДИКАТОРЫ
23.3.3. ИНДИКАЦИЯ В ШЕСТНАДЦАТЕРИЧНОМ КОДЕ
23.4. МУЛЬТИПЛЕКСНЫЕ ИНДИКАТОРЫ
23.4.1. МНОГОРАЗРЯДНЫЕ 7-СЕГМЕНТНЫЕ ИНДИКАТОРЫ
23.4.2. МАТРИЦА ТОЧЕК
24. Цифро-аналоговые и аналого-цифровые преобразователи
24.1. СХЕМОТЕХНИЧЕСКИЕ ПРИНЦИПЫ ЦА-ПРЕОБРАЗОВАТЕЛЕЙ
24.1.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ С ПЕРЕКИДНЫМИ КЛЮЧАМИ
24.1.3. РЕЗИСТИВНАЯ МАТРИЦА ПОСТОЯННОГО ИМПЕДАНСА (МАТРИЦА ТИПА R-2R)
24.1.4. РЕЗИСТИВНАЯ МАТРИЦА ДЛЯ ДЕКАДНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
24.2. ПОСТРОЕНИЕ ЦА-ПРЕОБРАЗОВАТЕЛЕЙ С ЭЛЕКТРОННЫМИ КЛЮЧАМИ
24.2.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ С ТОКОВЫМИ КЛЮЧАМИ
24.3. ЦА-ПРЕОБРАЮВАТЕЛИ ДЛЯ СПЕЦИАЛЬНЫХ ПРИМЕНЕНИЙ
24.3.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ДЕЛЕНИЯ
24.3.3. ЦА-ПРЕОБРАЗОВАТЕЛЬ КАК ГЕНЕРАТОР ФУНКЦИЙ
24.4. ОСНОВНЫЕ ПРИНЦИПЫ АЦ-ПРЕОБРАЗОВАНИЯ
24.5. ТОЧНОСТЬ АЦ-ПРЕОБРАЗОВАТЕЛЕЙ
24.6. ПОСТРОЕНИЕ АЦ-ПРЕОБРАЗОВАТЕЛЕЙ
25. Измерительные схемы
25.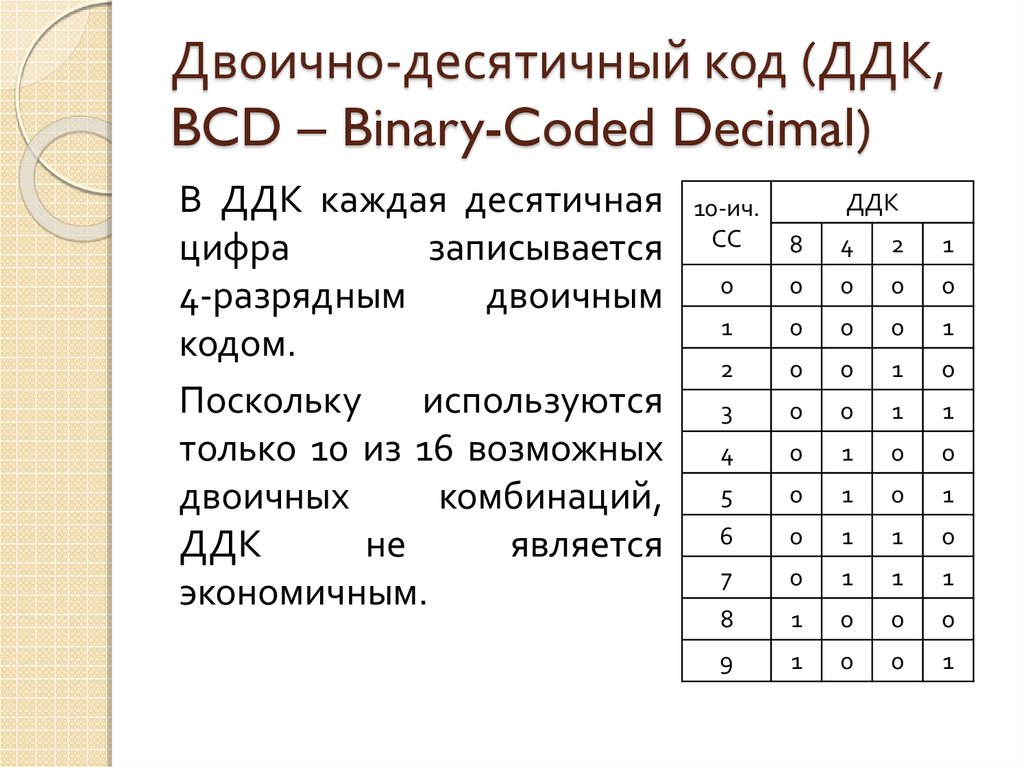

1. ИЗМЕРЕНИЕ НАПРЯЖЕНИЙ
25.1.2. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ
25.1.3. ИЗОЛИРОВАННЫЙ УСИЛИТЕЛЬ
25.2. ИЗМЕРЕНИЕ ТОКА
25.2.1. ИЗОЛИРОВАННЫЕ ОТ ЗЕМЛИ АМПЕРМЕТРЫ С МАЛЫМ ПАДЕНИЕМ НАПРЯЖЕНИЯ
25.2.2. ИЗМЕРЕНИЕ ТОКА ПРИ ВЫСОКОМ ПОТЕНЦИАЛЕ
25.3. ИЗМЕРИТЕЛЬНЫЙ ВЫПРЯМИТЕЛЬ
25.3.2. ИЗМЕРЕНИЕ ЭФФЕКТИВНОГО ЗНАЧЕНИЯ
25.3.3. ИЗМЕРЕНИЕ АМПЛИТУДНЫХ ЗНАЧЕНИЙ
25.3.4. СИНХРОННЫЙ ДЕТЕКТОР
26. Электронные регуляторы
26.2. ТИПЫ РЕГУЛЯТОРОВ
26.2.1. П-РЕГУЛЯТОР
26.2.2. ПИ-РЕГУЛЯТОР
26.2.3. ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫЙ РЕГУЛЯТОР
26.2.4. НАСТРАИВАЕМЫЕ ПИД-РЕГУЛЯТОРЫ
26.3. УПРАВЛЕНИЕ НЕЛИНЕЙНЫМИ ОБЪЕКТАМИ
26.4. ОТСЛЕЖИВАЮЩАЯ СИНХРОНИЗАЦИЯ (АВТОПОДСТРОЙКА)
26.4.1. ЭЛЕМЕНТЫ ВЫБОРКИ-ХРАНЕНИЯ В КАЧЕСТВЕ ФАЗОВОГО ДЕТЕКТОРА
26.4.2. СИНХРОННЫЙ ВЫПРЯМИТЕЛЬ В КАЧЕСТВЕ ФАЗОВОГО ДЕТЕКТОРА
26.4.3. ЧАСТОТНО-ЧУВСТВИТЕЛЬНЫЙ ФАЗОВЫЙ ДЕТЕКТОР
26.4.4. ФАЗОВЫЙ ДЕТЕКТОР С ПРОИЗВОЛЬНО УВЕЛИЧИВАЕМЫМ ДИАПАЗОНОМ ИЗМЕРЕНИЙ
26.4.5. ФАЗОРЕГУЛЯТОР В КАЧЕСТВЕ ПЕРЕМНОЖИТЕЛЯ ЧАСТОТ

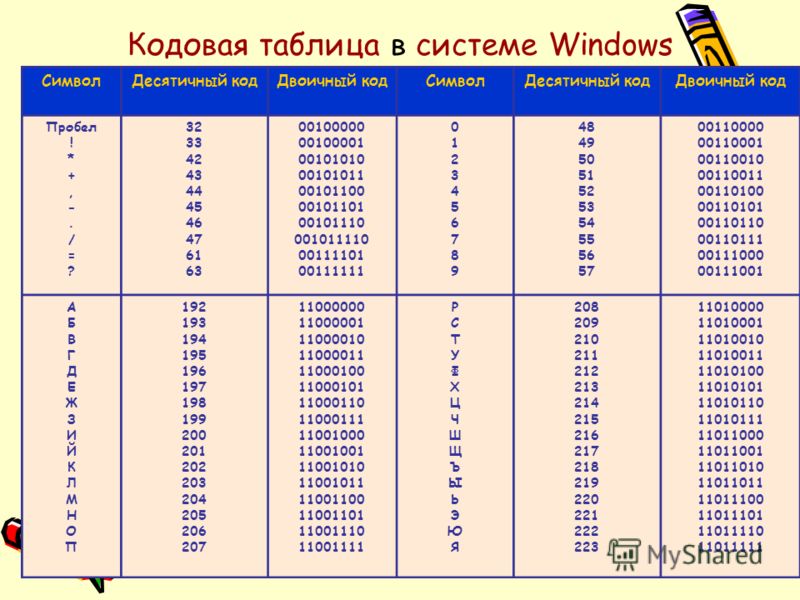
Системы счисления.

Двоично-десятичные коды (часть 5.0)

Похожие презентации:

Пиксельная картинка

Информационная безопасность. Методы защиты информации

Электронная цифровая подпись (ЭЦП)

Этапы доказательной медицины в работе с Pico. Первый этап

История развития компьютерной техники

От печатной книги до интернет-книги

Краткая инструкция по CIS – 10 шагов

Информационные технологии в медицине

Информационные войны

Моя будущая профессия. Программист

1. Системы счисления (часть 5.0)

Подготовил : Ганбаров Анар
Группа: ИТ11
АГУ
г. Астрахань 2016

2. Двоично-десятичные коды

Двоично-десятичный код — форма записи
чисел, когда каждый десятичный разряд
числа записывается в виде его
четырёхбитного двоичного кода (0…9).
Пример:
Записать число
584610 в двоично-десятичном коде.
0101
1000
0100
0110
5
8
4
6
Ответ : 0101100001000110

3.

Двоично-десятичные кодыКод 4221
Код 8421
Код 2421

4. Код 8421

Обычный перевод каждой цифры
десятичного числа в четырёхбитный
(четырёхзначный) двоичный код.
Пример:
Записать число
584610 в двоично-десятичном коде 8421 .
0101
1000
0100
0110
5
8
4
6
Ответ : 0101100001000110

5. Таблица 8421

Десятичный код
Двоично-десятичный 8421
0
0000
1
0001
2
0010
3
0011
4
0100
5
0101
6
0110
7
0111
8
1000
9
1001

6. Код 2421

Двоичный код 010 − 410 похож на код
8421,
двоичный код 510 − 910 содержат избыток
«+6»
Пример:
Записать число
584610 в двоично-десятичном коде 2421 .
1011
1110
0100
1100
5
8
4
6
Ответ : 1011111001001100

7. Таблица 2421

Десятичный код
Двоичнодесятичный 8421
Двоично-десятичный 2421
С 0-4 похож на 8421, с 5-9
прибавляем «+6»
0
0000
0000
1
0001
0001
2
0010
0010
3
0011
0011
4
0100
0100
5
0101
0101+0110=1011
6
0110
0110+0110=1100
7
0111
0111+0110=1101
8
1000
1000+0110=1110
9
1001
1001+0110=1111

8.

Код 4221Чтобы получить код 4221 числа 0-9, надо
к двоичному коду 8421 прибавить «+3».
Пример:
Записать число
584610 в двоично-десятичном коде 4221 .
1000
1011
0111
1001
5
8
4
6
Ответ : 1000101101111001

9. Таблица 4221

Десятичный код
Двоичнодесятичный 8421
Двоично-десятичный 4221
Код 8421+ «+3»
0
0000
0000+0011=0011
1
0001
0001+0011=0100
2
0010
0010+0011=0101
3
0011
0011+0011=0110
4
0100
0100+0011=0111
5
0101
0101+0011=1000
6
0110
0110+0011=1001
7
0111
0111+0011=1010
8
1000
1000+0011=1011
9
1001
1001+0011=1100

English Русский Правила

BCD или двоично-десятичный код

Улучшить статью

Сохранить статью

Уровень сложности: Базовый
Последнее обновление: 23 июн, 2022

Читать

Обсудить

Улучшить статью

Сохранить статью

Binary Coded Decimal или BCD — это еще один процесс преобразования десятичных чисел в их двоичные эквиваленты.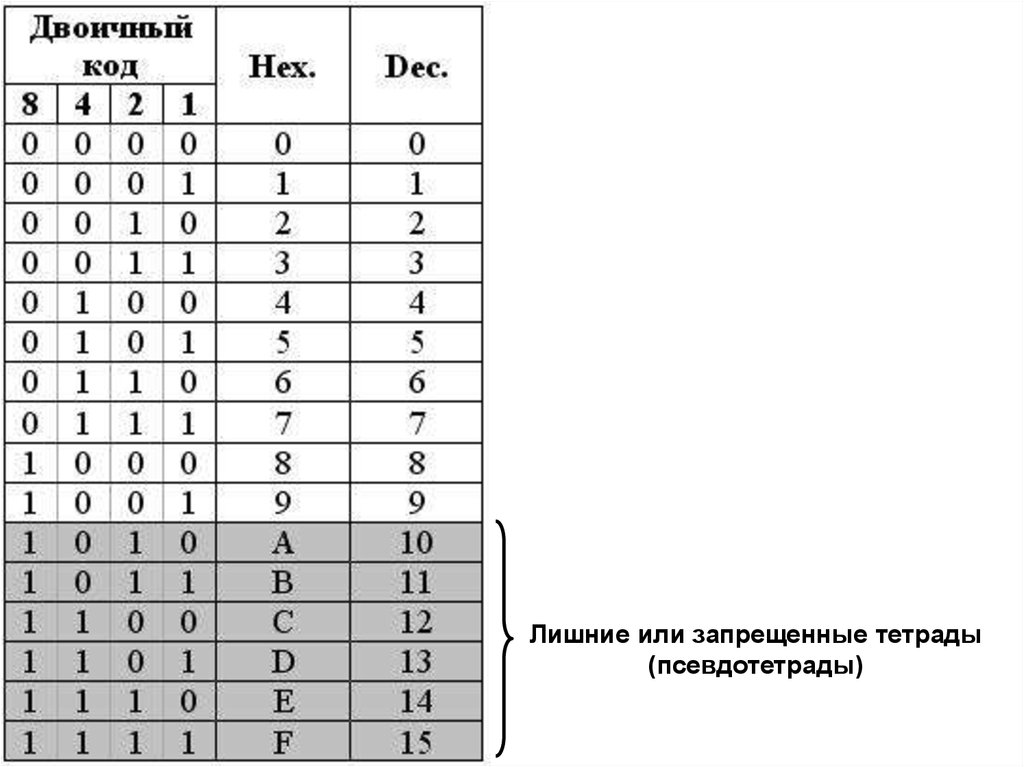

Это форма двоичного кодирования, в которой каждая цифра десятичного числа представлена в виде битов.
Это кодирование может быть 4-битным или 8-битным (обычно 4-битное предпочтительнее).
Это быстрая и эффективная система, которая преобразует десятичные числа в двоичные числа по сравнению с существующей двоичной системой.
Они обычно используются в цифровых дисплеях, где манипулирование данными является сложной задачей.
Таким образом, двоично-десятичный код играет здесь важную роль, поскольку манипуляция выполняется с учетом каждой цифры как отдельной отдельной подсхемы.

BCD-эквивалент десятичного числа записывается путем замены каждой десятичной цифры в целой и дробной частях ее четырехбитным двоичным эквивалентом. представляющие веса различных битов в четырехбитных группах, начиная с MSB и продвигаясь к LSB. Эта особенность делает его взвешенным кодом, что означает, что каждый бит в четырехбитной группе, представляющей данную десятичную цифру, имеет назначенный вес.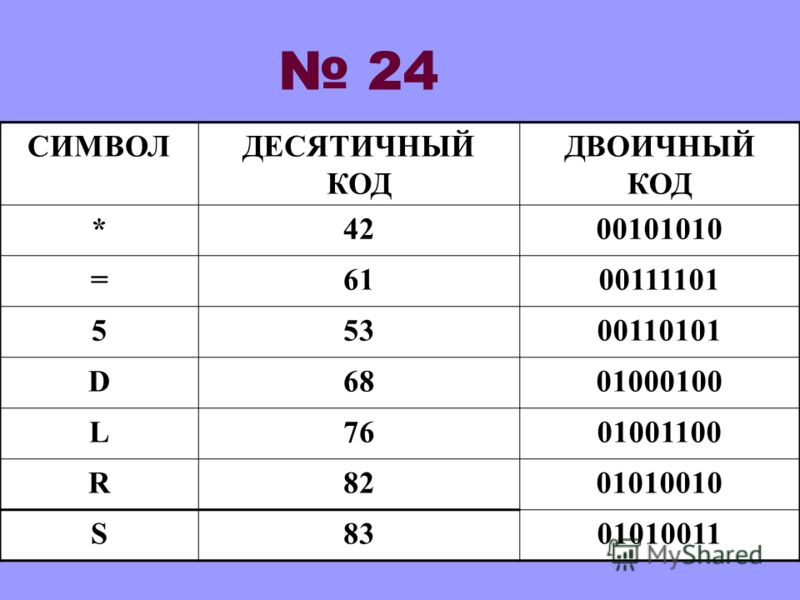
Многие десятичные значения имеют бесконечное представление разрядного значения в двоичном формате, но имеют конечное разрядное значение в двоично-десятичном коде. Например, 0,2 в двоичном формате — это 0,001100…, а в двоично-десятичном формате — 0,0010. Он позволяет избежать дробных ошибок, а также используется в огромных финансовых расчетах.

Рассмотрим следующую таблицу истинности и сосредоточимся на том, как они представлены.

Таблица истинности для двоично-десятичной системы счисления0055 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001

В системе нумерации BCD заданное десятичное число разделяется на части по четыре бита для каждой десятичной цифры в числе. Каждая десятичная цифра преобразуется в ее прямую двоичную форму (обычно представленную в 4 битах).

Например:

1. Преобразование (123)10 в BCD
Из приведенной выше таблицы истинности
1 -> 0001
2 -> 0010 ->
3 становится таким образом 0001 0010 0011

2. Преобразование (324) 10 в BCD
(324) 10 -> 0011 0010 0100 (BCD)
Снова из таблицы истины выше,
3 -> 0011
2 -> 0010
4 -> 0100
, таким образом, двоично-десятичный код становится -> 0011 0010 0100

Вот как десятичные числа преобразуются в эквивалентные им двоично-десятичные числа.

Примечательно, что BCD представляет собой не что иное, как двоичное представление каждой цифры десятичного числа.
Нельзя игнорировать тот факт, что двоично-десятичное представление данного десятичного числа использует дополнительные биты, что делает его тяжеловесным.

Related articles:

Program to Convert BCD number into Decimal number
BCD Adder in Digital Logic
BCD to 7 Segment Decoder

Next

Программа для преобразования числа BCD в десятичное число

Статьи по теме

Что нового

Мы используем файлы cookie, чтобы обеспечить вам максимальное удобство при просмотре нашего веб-сайта. Используя наш сайт, вы подтверждаете, что вы прочитали и поняли наши Политика использования файлов cookie & Политика конфиденциальности

Двоично-десятичное число — BCD

Двоично-десятичное число

Двоично-десятичное число представляет собой 4-битное двоичное число, закодированное специально для представления десятичного числа. «Закодированный» относится к процессу присвоения определенного или уникального двоичного кода конкретному десятичному числу. В двоично-десятичном коде или сокращенно BCD , десятичные числа от «0» до «9» закодированы в двоичном формате. Двоичный код, представляющий каждое десятичное число, называется двоично-десятичным кодом. Двоично-десятичные числа используются в цифровых системах, главным образом, для отображения десятичных значений.

Десятичные числа используют систему счисления с основанием 10 , и, таким образом, имеется в общей сложности десять (10) десятичных чисел от «0» до «9» . Точно так же двоичные числа используют систему нумерации с основанием 2 . Чтобы закодировать от «0» до «9” десятичные числа в двоичном формате, требуется десять (10) уникальных комбинаций двоичных чисел, каждая из которых представляет одно десятичное число. Количество комбинаций, которые могут быть получены из двоичных цифр или битов (n), равно 2 ⁿ . Для представления десяти (10) десятичных чисел требуется двоичный код, содержащий не менее четырех (4) двоичных цифр или битов.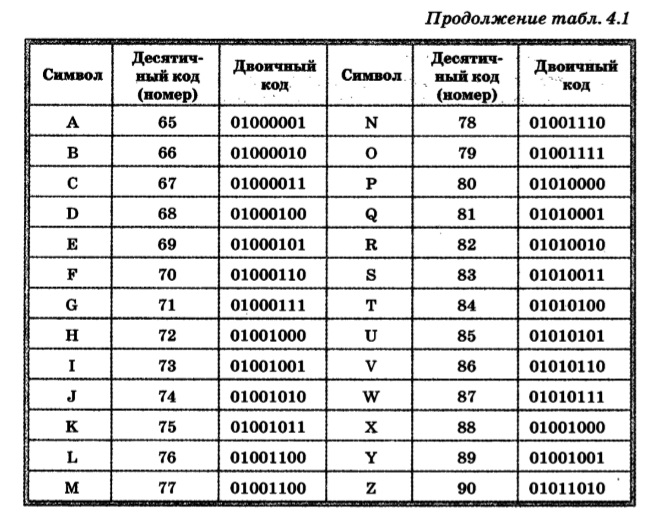 В двоично-десятичном коде для представления десятичных чисел используется минималистская опция «четыре (4) бита».

Знаменитая Шестнадцатеричная система счисления также использует четыре (4) бита для представления эквивалентных двоичных чисел. В шестнадцатеричном числе используется система нумерации с основанием 16 , и всего имеется шестнадцать (16) шестнадцатеричных чисел. Двоично-десятичные числа аналогичны шестнадцатеричным числам. Однако двоично-десятичное кодирование (BCD) использует только числа от «0» до «9», а остальные числа, то есть от «A» до «F» или от «10» до «15», не требуются. Шестнадцатеричные числа от «0» до «9» аналогичны двоично-десятичным числам от «0» до «9».», соответственно.

Использование двоично-десятичных чисел для представления десятичных чисел имеет много преимуществ в цифровых системах, среди которых основное преимущество заключается в простоте преобразования десятичных знаков и обратно. Однако существует потеря шести (6) номеров от «A» до «F» , как обсуждалось выше. В двоично-десятичном коде каждая десятичная цифра представлена четырехбитным двоичным числом (BCD), а каждая десятичная цифра может быть представлена взвешенной суммой двоичных значений. Из предыдущих статей известно, что вес десятичной цифры справа налево увеличивается в 10 раз, тогда как двоичной цифры (бита) в 2 раза. В четырехбитном двоично-десятичном коде первая, вторая, третья и четвертая цифры имеют вес 2·9.0216 0 = 1, 2 ¹ = 2, 2 ² = 4 и 2 ³ = 8 соответственно. В следующей таблице показана двоичная мощность или вес каждого бита BCD.

Используя приведенную выше таблицу, взвешенная сумма битов от «0000» до «1001» двоичных чисел равняется десятичным числам от «0» до «9» соответственно. Четыре бита BCD, начиная справа, имеют вес 8, 4, 2 и 1 соответственно. Веса (8, 4, 2 и 1) BCD в сумме составляют десятичное число. По этой причине BCD также называют 9.0023 8421 код , поскольку он представляет соответствующее десятичное число в 4-битном формате .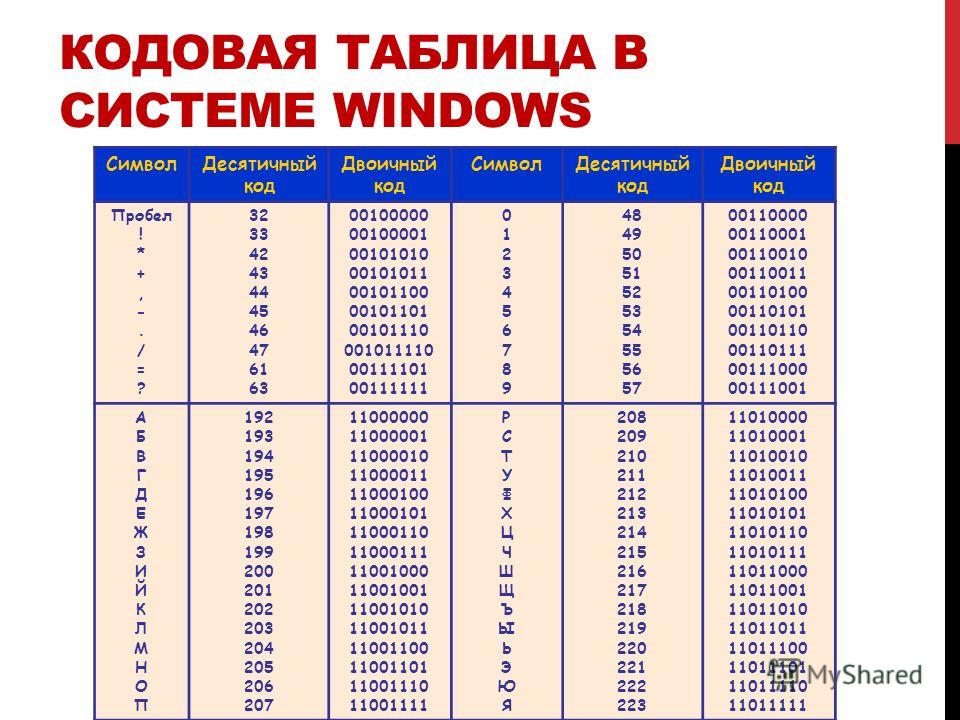

Преобразование десятичного числа, состоящего из нескольких десятичных цифр, требует получения эквивалентного двоично-десятичного числа для каждой десятичной цифры. Например, рассмотрим десятичное число 915 _10, , имеющее три десятичных знака, то есть «9», «1» и «5». Эти десятичные цифры «9», «1» и «5» имеют эквивалентные двоично-десятичные числа «1001», «0001» и «0101» соответственно. Комбинация этих двоично-десятичных знаков эквивалентна 9.15 ₁₀ в BCD, как указано ниже.

В следующей таблице каждое десятичное число приведено в сравнении с соответствующим двоично-десятичным числом (BCD). Код BCD или 8421 уникален для цифр от «0» до «9» и для чисел больше «9», таких как «10», «11» и «12» и т. д. Каждой десятичной цифре присваивается соответствующий уникальный код 8421. , раздельно. Например, «10» будет составлять код 8421 «0001 0000», где «0001» и «0000» — уникальные коды 8421 «1» и «0» соответственно.

Преобразование десятичного числа в двоично-десятичное

Существует несколько способов получения двоично-десятичного кода или кода 8421 десятичного числа. Каждый метод требует обработки каждой десятичной цифры отдельно, а не всего десятичного числа. Первый и самый простой способ — запомнить эти десять (10) кодов BCD или просмотреть таблицу истинности BCD для каждой десятичной цифры и найти соответствующий код BCD/8421. Второй метод потребует применения десятичного преобразования в двоичное для каждой (одной) десятичной цифры, т.е. повторного деления на 2. Третий метод состоит в том, чтобы разбить каждую десятичную цифру на веса битов, суммируясь с желаемой десятичной цифрой. Взвешенные двоичные цифры образуют эквивалентный код BCD/8421. Ниже приведены несколько примеров преобразования десятичных чисел в эквивалентные двоично-десятичные.

Примеры преобразования десятичных чисел в двоично-десятичные

Десятичные числа: 63 ₁₀ , 869 ₁₀ и 4728 ₁₀ преобразуются в эквивалентные им двоично-десятичные числа с использованием приведенной выше таблицы истинности двоично-десятичных чисел.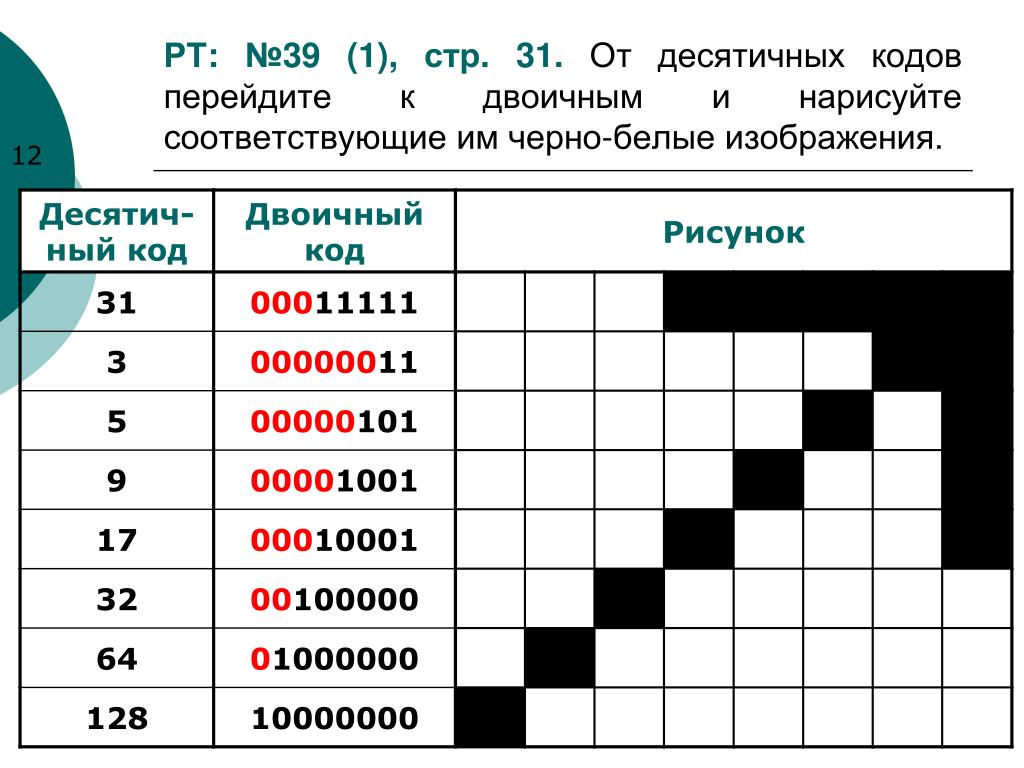

Преобразование двоично-десятичных чисел в десятичные числа

Поскольку каждая десятичная цифра представлена 4-битным двоично-десятичным числом , и, следовательно, необходимо разделить данное двоичное число на группы по 4-бит. 4-битные группы формируются от наименее значащей стороны (крайняя правая) к старшей значащей стороне (крайняя левая). В конце концов, это приводит к формированию последней 4-битной группы, которая может потребовать дополнительных значащих нулей для завершения 4-битной группы. Каждая 4-битная группа представляет соответствующий код BCD или 8421 этой десятичной цифры. Используя приведенную выше таблицу истинности BCD, получают эквивалентные десятичные цифры для соответствующих кодов BCD/8421. Комбинация десятичных цифр в конечном итоге дает представление желаемого десятичного числа. В следующих примерах преобразование BCD в десятичное выполняется для объяснения процесса преобразования.

BCD в десятичное преобразование Примеры

Бинарные номера: 1000 ₂, 10011 ₂, и 10010110010101 ₂ из них сходились в свои эквивалентные 40254 2 из 4024 40024 из 4025 40024 из 4024 из 40024 из 4025 из 40024 (B-exavilent upivalting по 40254 2 из 40024.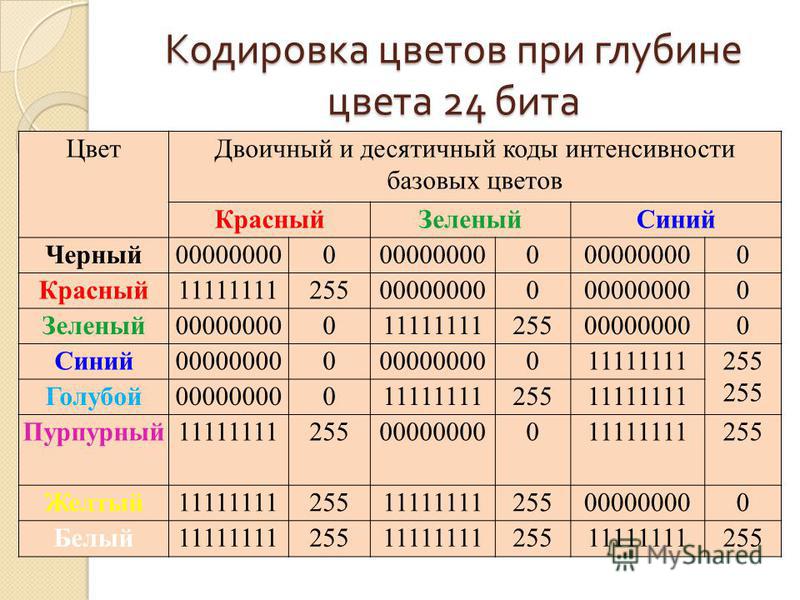 ) кодов, а затем найти эквивалентные десятичные числа против соответствующих кодов 8421 (BCD), используя приведенную выше таблицу истинности BCD.

Двоично-десятичное число представляет собой простое представление одной десятичной цифры, а десятичное число, представленное кодировкой BCD, не является фактическим двоичным эквивалентом этого десятичного числа. Например, двоично-десятичный эквивалент 63 ₁₀ — это 01100011 ₂, , тогда как чистый двоичный эквивалент 63 ₁₀ равен 00111111 ₂. Представление десятичных чисел в двоично-десятичном формате полезно для отображения десятичных значений и т. д., но не является эффективным способом хранения данных и выполнения арифметических операций. Для хранения с использованием двоично-десятичного кодирования потребуются дополнительные биты по сравнению с его эквивалентным истинным двоичным числом. Это связано с отбрасыванием шести (6) двоичных чисел из шестнадцати (16), как описано выше. Например, для представления трехзначного десятичного числа требуется 12 бит в двоично-десятичном коде и, наоборот, 9-битное число.0023 10-битное двоичное число может содержать десятичное число до «1024». Кроме того, двоично-десятичные числа не подходят для арифметических операций. Рассмотрим простой пример сложения двух двоично-десятичных двоичных чисел, который генерирует бит переноса. Добавление этого бита переноса к двоично-десятичному числу «1001» или «9» приведет к недопустимому двоично-десятичному коду «1010». Решение требует преобразования из двоичного в десятичное, т. е. 10 ₁₀, а затем возврата к эквиваленту BCD, т. е. «0001 0000». Однако удобнее и удобнее преобразовывать числа в двоично-десятичном коде в чистые двоичные числа перед выполнением каких-либо арифметических операций.

ИС двоично-десятичного декодера

Использование двоично-десятичного кода полезно в приложениях, требующих отображения информации в десятичных дробях. Цифровые или электронные системы отображают эту информацию на ЖК-дисплее или 7-сегментном светодиодном дисплее . Для отображения десятичных чисел двоичные числа преобразуются в эквивалентные двоично-десятичные числа, и для отображения десятичных чисел на этих дисплеях используется декодер BCD IC. В широко используемом 7-сегментном дисплее для отображения двоично-десятичных чисел используется ИС декодера BCD в 7-сегментный. 7-сегментные индикаторы выпускаются в двух вариантах в зависимости от конфигурации светодиодов с напряжением питания, то есть с общим анодом и общим катодом. Вариант с общим анодом 7-сегментного требует логического «НИЗКИЙ» на одном из входов его сегмента, чтобы включить его «ВКЛ». Принимая во внимание, что 7-сегментный катод с общим катодом требует логического «ВЫСОКОГО», чтобы зажечь сегмент. Коммерчески доступные микросхемы BCD для 7-сегментного декодера: 74LS47 и 74LS48 . 74LS47 выдает активный низкий уровень на выходе и поэтому подходит для 7-сегментного дисплея с общим анодом .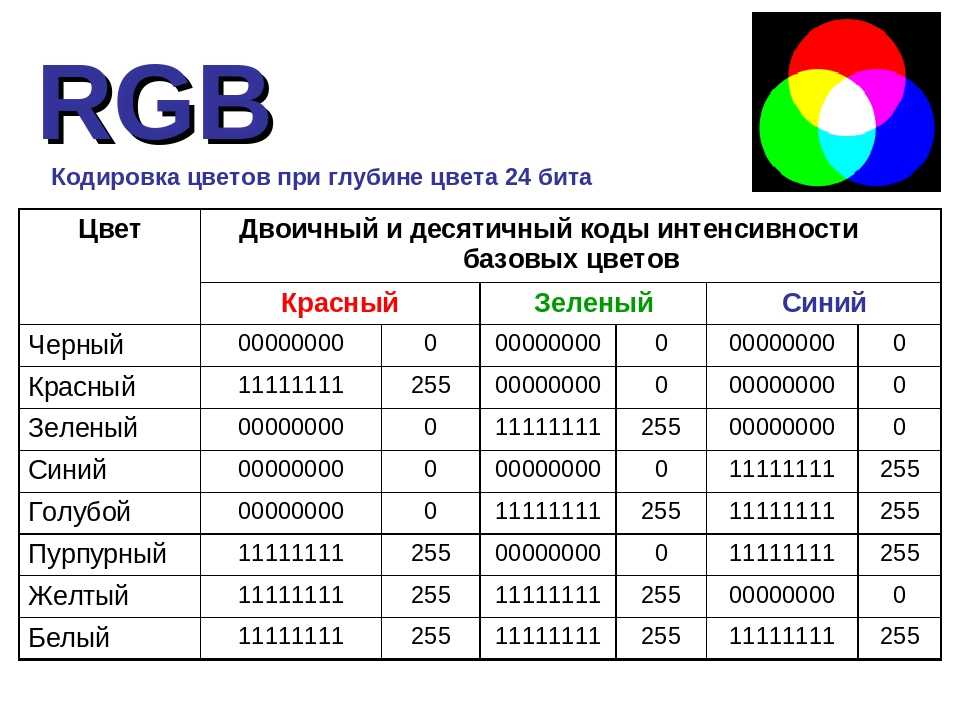 С другой стороны, для 7-сегментного дисплея с общим катодом требуется микросхема двоично-десятичного декодера с активным высоким выходным сигналом для 7-сегментного декодера, например 74LS48. На следующем рисунке показана микросхема декодера 74LS48 (активно-высокий выход) с 7-сегментным дисплеем с общим катодом.

Рисунок 1: 7-сегментный индикатор с общим катодом на микросхеме 74LS48

Вывод

Двоично-десятичный код (BCD) — это 4-битный двоичный код, предназначенный для представления десятичного числа. Двоично-десятичный код имеет десять (10) уникальных двоичных кодов, каждый из которых представляет десятичное число от «0» до «9».
Двоично-десятичный код также известен как код 8421, где 8, 4, 2 и 1 представляют вес 4 ^th , 3 ^rd , 2 ^nd и 1 ^st бит соответственно.
Двоично-десятичное число похоже на шестнадцатеричное число, но использует только от 0 до 9.», а остальные числа от «А» до «F» тратятся впустую.