Двоичный код что это: Что такое двоичный код и почему компьютеры используют его — RC74 — интернет-магазин радиоуправляемых моделей

Decimal	BCD
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001

Decimal	BCD	XS Code (+0011)
0	0000	0011
1	0001	0100
2	0010	0101
3	0011	0110
4	0100	0111
5	0101	1000
6	0110	1001
7	0111	1010
8	1000	1011
9	1001	1100

Decimal	BCD	Gray Code
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
0111
6	0110	0101
7	0111	0100
8	1000	1100
9	1001	1111

Содержание

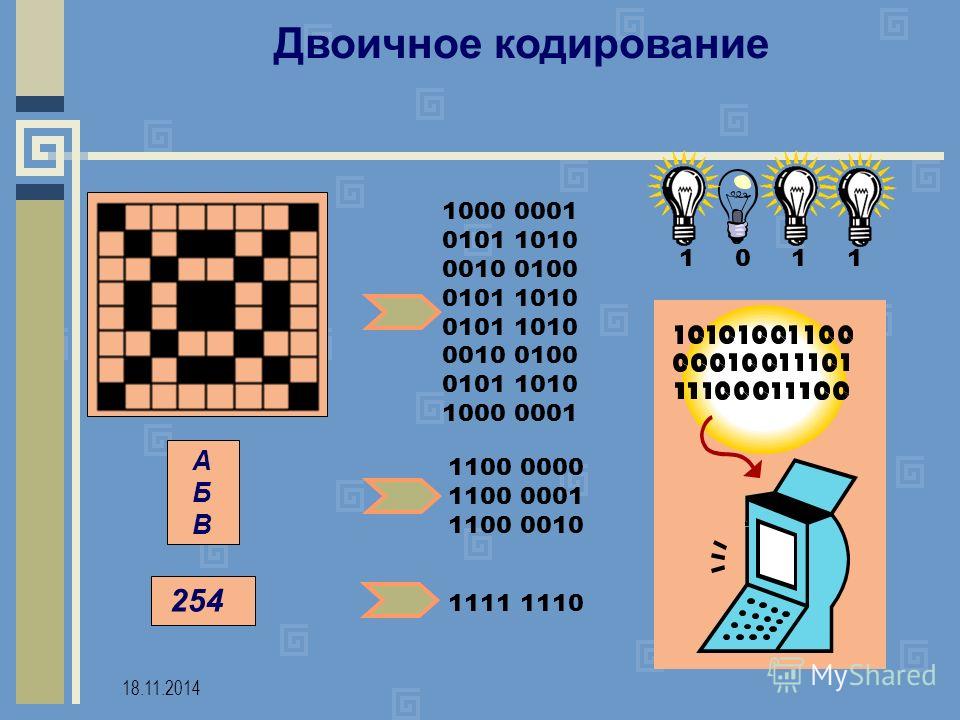
Виды двоичных кодов

В микропроцессорах двоичные коды используются для представления любой обрабатываемой информации. При этом разрядность обрабатываемых чисел может превышать разрядность самого процессора и используемой в нЈм памяти. В этом случае длинное число может занимать несколько ячеек памяти и обрабатываться несколькими командами процессора. При обработке все ячейки памяти, выделенные под многобайтное число, рассматриваются как одно число.

Для представления числовой информации могут использоваться знаковые и беззнаковые коды. Для определЈнности примем длину слова процессора равной восьми битам.

Беззнаковые двоичные коды.

Первый вид двоичных кодов, который мы рассмотрим — это целые беззнаковые коды. В этих кодах каждый двоичный разряд представляет собой степень цифры 2:

При этом минимально возможное число, которое можно записать таким двоичным кодом, равно 0. Максимально возможное число, которое можно записать таким двоичным кодом, можно определить как:

Этими двумя числами полностью можно определить диапазон, чисел которые можно представить таким двоичным кодом. В случае двоичного восьмиразрядного беззнакового целого числа диапазон будет: диапазон чисел, которые можно записать таким кодом: 0 .. 255. Для шестнадцатиразрядного кода этот 0 .. 65535. В восьмиразрядном процессоре для хранения такого числа используется две ячейки памяти, расположенные в соседних адресах. Для работы с такими числами используются специальные команды.

Второй вид двоичных кодов, который мы рассмотрим — это прямые целые знаковые коды. В этих кодах старший разряд в слове используется для представления знака числа. В прямом знаковом коде нулем обозначается знак ‘+’, а единицей — знак ‘-‘. В результате введения знакового разряда диапазон чисел смещается в сторону отрицательных чисел:

В случае двоичного восьмиразрядного знакового целого числа диапазон чисел, которые можно записать таким кодом: -127 .. +127. Для шестнадцатиразрядного кода этот диапазон будет: -32767 .. +32767. В восьмиразрядном процессоре для хранения такого числа тоже используется две ячейки памяти, расположенные в соседних адресах.

Недостатком такого кода является то, что знаковый разряд и цифровые разряды приходится обрабатывать раздельно. Алгоритм программ, работающий с такими кодами получается сложный. Для выделения и изменения знакового разряда приходится применять механизм маскирования разрядов, что резко увеличивает размер программы и уменьшает ее быстродействие. Для того, чтобы алгоритм обработки знакового и цифровых разрядов не различался, были введены обратные двоичные коды.

Знаковые обратные двоичные коды.

Обратные двоичные коды отличаются от прямых только тем, что отрицательные числа в них получаются инвертированием всех разрядов числа. При этом знаковый и цифровые разряды не различаются. Алгоритм работы с такими кодами резко упрощается.

Тем не менее при работе с обратными кодами требуется специальный алгоритм распознавания знака, вычисления абсолютного значения числа, восстановления знака результата числа. Кроме того, в прямом и обратном коде числа для запоминания числа 0 используется два кода, тогда как известно, что число 0 положительное и отрицательным не может быть никогда.

Знаковые дополнительные двоичные коды.

От перечисленных недостатков свободны дополнительные коды. Эти коды позволяют непосредственно суммировать положительные и отрицательные числа не анализируя знаковый разряд и при этом получать правильный результат. Все это становится возможным благодаря тому, что дополнительные числа являются естественным кольцом чисел, а не исскуственным образованием как прямые и обратные коды. Кроме того немаловажным является то, что вычислять дополнение в двоичном коде чрезвычайно легко. Для этого достаточно к обратному коду добавить 1:

Диапазон чисел, которые можно записать таким кодом: -128 .. +127. Для шестнадцатиразрядного кода этот диапазон будет: -32768 .. +32767. В восьмиразрядном процессоре для хранения такого числа используется две ячейки памяти, расположенные в соседних адресах.

В обратных и дополнительных кодах наблюдается интересный эффект, который называется эффект распространения знака. Он заключается в том, что при преобразовании однобайтного числа в двухбайтное достаточно всем битам старшего байта присвоить значение знакового бита младшего байта.

То есть для хранения знака числа можно использовать сколько угодно старших бит. При этом значение кода совершенно не изменяется.

Использование для представления знака числа двух бит предоставляет интересную возможность контролировать переполнения при выполнении арифметических операций. Рассмотрим несколько примеров.

1) Просуммируем числа 12 и 5

В этом примере видно, что в результате суммирования получается правильный результат. Это можно проконтролировать по флагу переноса C, который совпадает со знаком результата (действует эффект распространения знака).

2) Просуммируем два отрицательных числа -12 и -5

В этом примере флаг переноса C тоже совпадает со знаком результата, то есть переполнения не произошло и в этом случае

3) Просуммируем положительное и отрицательное число -12 и +5

В этом примере при суммировании положительного и отрицательного числа автоматически получается правильный знак результата. В данном случае знак результата отрицательный.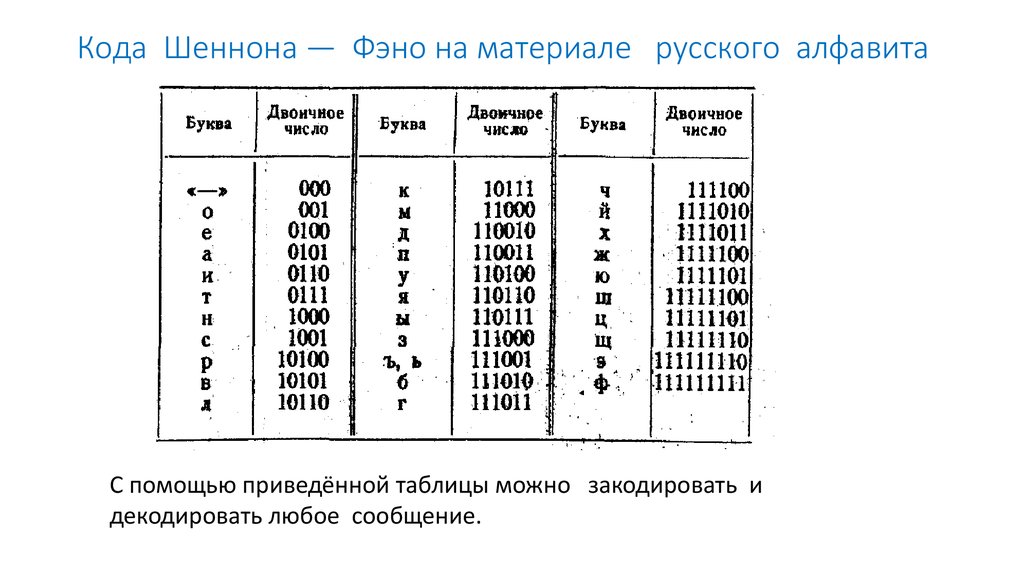 Флаг переноса совпадает со знаком результата, поэтому переполнения не было (мы можем убедиться в этом непосредственными вычислениями на бумаге или на калькуляторе).

4) Просуммируем положительное и отрицательное число +12 и -5

В данном примере знак результата положительный. Флаг переноса совпадает со знаком результата, поэтому переполнения не было и в этом случае.

5)Просуммируем числа 100 и 31

В этом примере видно, что в результате суммирования произошло переполнение восьмибитовой переменной, т.к. в результате операции над положительными числами получился отрицательный результат. Однако если рассмотреть флаг переноса, то он не совпадает со знаком результата. Эта ситуации является признаком переполнения результата и легко обнаруживается при помощи операции «исключающее ИЛИ» над старшим битом результата и флагом переноса C. Большинство процессоров осуществляют эту операцию аппаратно и помещают результат во флаг переполнения OV.

В этом примере результате операции над отрицательными числами в результате суммирования произошло переполнение восьмибитовой переменной, т.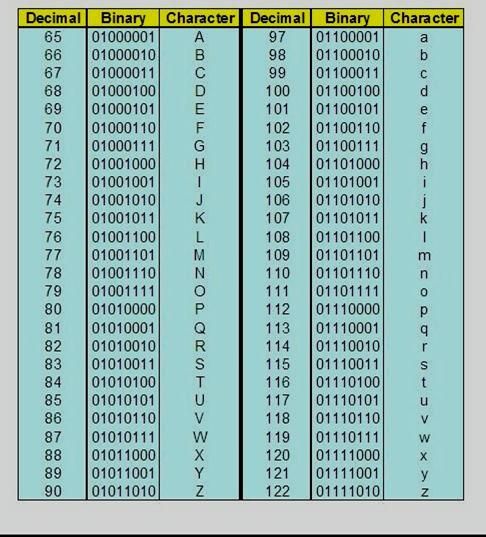 к. получился положительный результат. И в этом случае если рассмотреть флаг переноса C, то он не совпадает со знаком результата. Отличие от предыдущего случая только в комбинации этих бит. В примере 5 говорят о переполнении результата (комбинация 01), а в примере 6 об антипереполнении результата (комбинация 10).

Представление дробных чисел в двоичном коде с фиксированной запятой.

Кроме целых чисел часто требуется работать с дробными числами. Следующий вид двоичных кодов, который мы рассмотрим — это дробные коды. Как и в случае целых чисел, дробные числа могут быть беззнаковые и знаковые. Для записи знаковых чисел могут быть использованы прямые, обратные и дополнительные коды. Принцип их построения точно такой же, как и в случае целых чисел.

Рассмотрим, как можно записать дробное число. До сих пор мы предполагали, что двоичная запятая находится правее самого младшего разряда. Но кто сказал, что она должна всегда находиться в этом месте? Мы можем договориться, что запятая находится слева от самого старшего разряда, и тогда в такой переменной можно будет записывать только дробные числа:

Или договоримся, что она находится точно посередине переменной, и тогда мы сможем записывать смешанные числа:

Остальные случаи рассматривать не будем. Они строятся точно так же как и для целых чисел.

Представление чисел в двоичном коде с плавающей запятой.

Часто приходится обрабатывать очень большие числа (например, расстояние между звЈздами) или наоборот очень маленькие числа (например, размеры атомов или электронов). При таких вычислениях пришлось бы использовать числа с очень большой разрядностью. В то же время нам не нужно знать расстояние между звЈздами с точностью до миллиметра. Для вычислений с такими величинами числа с фиксированной запятой неэффективны.

В десятичной арифметике для записи таких чисел используется алгебраическая форма. При этом число записывается в виде мантиссы, умноженной на 10 в степени, отображающей порядок числа, Например:

0,2*105; 0,16*10-38

Для записи двоичных чисел тоже используется такая форма записи. Эта форма записи называется запись числа с плавающей точкой. Напомним, что мантисса не может быть больше единицы и после запятой в мантиссе не может записываться ноль.

А теперь рассмотрим промышленные стандарты, используемые для представления чисел в компьютерах. Существует стандарт IEEE 754 для представления чисел с одинарной точностью (float) и с двойной точностью (double). Для записи числа в формате с плавающей запятой одинарной точности требуется тридцатидвухбитовое слово. Для записи чисел с двойной точностью требуется шестидесятичетырЈхбитовое слово. Чаще всего числа хранятся в нескольких соседних ячейках памяти процессора. Форматы числа в формате с плавающей запятой одинарной точности и числа в формате с плавающей запятой удвоенной точности приведены на рисунке

На рисунке буквой S обозначен знак числа, 0 — это положительное число, 1 — отрицательное число. e обозначает смещЈнный порядок числа. Смещение требуется, чтобы не вводить в число еще один знак. СмещЈнный порядок всегда положительное число. Для одинарной точности для порядка выделено восемь бит. Для смещЈнного порядка двойной точности отводится 11 бит. Для одинарной точности смещение принято 127, а для двойной точности — 1023. В десятичной мантиссе после запятой могут присутствовать цифры 1:9, а в двоичной — только 1. Поэтому для хранения единицы после двоичной запятой не выделяется отдельный бит в числе с плавающей запятой. Единица подразумевается, как и двоичная запятая. Кроме того, в формате чисел с плавающей запятой принято, что мантисса всегда больше 1. То есть диапазон значений мантиссы лежит в диапазоне от 1 до 2.

Рассмотрим несколько примеров:

1) Определить число с плавающей запятой, лежащее в четырЈх соседних байтах:

11000001 01001000 00000000 00000000

— Знаковый бит, равный 1 показывает, что число отрицательное.

— Экспонента 10000010 в десятичном виде соответствует числу 130. Вычтя число 127 из 130, получим число 3.

— Теперь запишем мантиссу: 1,100 1000 0000 0000 0000 0000

— И, наконец, определим десятичное число: 1100,1b = 12,5d

2) Определить число с плавающей запятой, лежащее в четырЈх соседних байтах:

11000011 00110100 00000000 00000000

— Знаковый бит, равный 1 показывает, что число отрицательное.

— Экспонента 10000110 в десятичном виде соответствует числу 134. Вычтя число 127 из 134, получим число 7.

— Теперь запишем мантиссу: 1,011 0100 0000 0000 0000 0000

— И, наконец, определим десятичное число: 10110100b=180d

Для того чтобы записать ноль, достаточно записать в смещенный порядок число 00000000b. Значение мантиссы при этом не имеет значения. Число, в котором все байты равны 0, тоже попадает в этот диапазон значений.

Бесконечность соответствует смещенному порядку 11111111b и мантиссе, равной 1,0. При этом существует минус бесконечность и плюс бесконечность (переполнение и антипереполнение), которые часто отображаются на экран монитора как +INF и -INF.

Все остальные комбинации битов (в том числе и все единицы) воспринимаются как не числа и отображаются на экран: NaN.

Запись десятичных чисел.

Иногда бывает удобно хранить числа в памяти процессора в десятичном виде (Например, для вывода на экран дисплея). Для записи таких чисел используются двоично-десятичные коды. Для записи одного десятичного разряда используется четыре двоичных бита. Эти четыре бита называются тетрадой. Иногда встречается название, пришедшее из англоязычной литературы: нибл. При помощи четырех бит можно закодировать шестнадцать цифр. Лишние комбинации в двоично-десятичном коде являются запрещенными. Таблица соответствия двоично-десятичного кода и десятичных цифр приведена ниже:

Остальные комбинации двоичного кода в тетраде являются запрещенными. Запишем пример двоично-десятичного кода:

1258 = 0001 0010 0101 1000

589 = 0000 0101 1000 1001

Достаточно часто в памяти процессора для хранения одной десятичной цифры выделяется одна ячейка памяти (восьми, шестнадцати или тридцатидвухразрядная). Это делается для повышения скорости работы программы. Для того, чтобы отличить такой способ записи двоично-десятичного числа от стандартного, способ записи десятичного числа, как это показано в примере, называется упакованной формой двоично-десятичного числа.

Суммирование двоично-десятичных чисел.

Суммирование двоично-десяичных чисел можно производить по правилам обычной двоичной арифметики, а затем производить двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в проверке каждой тетрады на допустимые коды. Если в какой либо тетраде обнаруживается запрещенная комбинация , то это говорит о переполнении. В этом случае необходимо произвести двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в дополнительном суммировании числа шесть (число запрещенных комбинаций) с тетрадой, в которой произошло переполнение или произошЈл перенос в старшую тетраду. ПриведЈм два примера:

Запись текстов в памяти процессора.

Все символы и буквы могут быть закодированы при помощи восьми двоичных символов. Наиболее распространенными таблицами являются таблицы ASCII с национальными расширениями, применяющиеся в DOS (и которые можно использовать для записи текстов в микропроцессорах), и таблицы ANSI, применяющиеся в WINDOWS. В таблицах ASCII и ANSI первые 128 символов совпадают. В этой части таблицы содержатся символы цифр, знаков препинания, латинские буквы верхнего и нижнего регистров и управляющие символы. Национальные расширения символьных таблиц и символы псевдографики содержатся в последних 128 кодах этих таблиц, поэтому русские тексты в операционных системах DOS и WINDOWS не совпадают.

[Назад] [Содержание] [Вперёд]

Двоичный код это в информатике

Двои́чный код — это способ представления данных в виде кода, в котором каждый разряд принимает одно из двух возможных значений, обычно обозначаемых цифрами 0 и 1. Разряд в этом случае называется двоичным разрядом.

В случае обозначения цифрами «0» и «1», возможные состояния двоичного разряда наделяются качественным соотношением «1» > «0» и количественными значениями чисел «0» и «1».

Двоичный код может быть непозиционным и позиционным. Позиционный двоичный код лежит в основе двоичной системы счисления, широко распространенной в современной цифровой технике. > , где

Используя два двоичных разряда можно закодировать четыре различные комбинации: 00 01 10 11, три двоичных разряда — восемь: 000 001 010 011 100 101 110 111, и так далее.
При увеличении разрядности позиционного двоичного кода на 1, количество различных комбинаций в позиционном двоичном коде удваивается.

Двоичные коды являются комбинациями двух элементов и не являются двоичной системой счисления, но используются в ней как основа. Двоичный код также может использоваться для кодирования чисел в системах счисления с любым другим основанием. Пример: в двоично-десятичном кодировании (BCD) используется двоичный код для кодирования чисел в десятичной системе счисления.
При кодировании алфавитноцифровых символов (знаков) двоичному коду не приписываются весовые коэффициенты, как это делается в системах счисления, в которых двоичный код используется для представления чисел, а используется только порядковый номер кода из множества размещений с повторениями.

В системах счисления k-разрядный двоичный код, (k-1)-разрядный двоичный код, (k-2)-разрядный двоичный код и т. д. могут отображать одно и то же число. Например, 0001, 001, 01, 1 — одно и то же число — «1» в двоичных кодах с разным числом разрядов — k.

Примеры двоичных чисел [ править | править код ]

В таблице показаны первые 16 двоичных чисел и их соответствие десятичным и шестнадцатиричным числам.

Десятичное число	Шестнадцатеричное число	Двоичное число
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Пример «доисторического» использования кодов [ править | править код ]

Инки имели свою счётную систему кипу, которая физически представляла собой верёвочные сплетения и узелки. Генри Эртан обнаружил, что в узелках заложен некий код, более всего похожий на двоичную систему счисления [1] .

Задача сегодняшней публикации – разобраться в том, что такое двоичный код, для каких целей и где используется двоичный код и зачем вообще он нужен.

Двоичный код – это система обозначений из двух элементов, различные комбинации которых служат для представления (кодировки) информации.

В качестве элементов системы наиболее часто выступают цифры «0» и «1». Но в действительности обозначения могут быть произвольными, исходя из характера сведений, которые требуется кодировать.

Главное – чтобы соответствующие элементы обозначали взаимоисключающие либо противоположные по значению данные.

Великолепным примером двоичного кода могут служить любые пары антонимов, к примеру, «да/нет», «белое/черное», «включено/выключено» и т.д.

Для описания двоичного кода используется понятие разряда (более точно – двоичного разряда), объединяющего целочисленную группу элементов двоичного кода.

Например, в системе, использующей базовые элементы 0 и 1, два двоичных разряда могут быть представлены следующими четырьмя комбинациями: 00, 01, 10 и 11.

Три двоичных разряда могут иметь следующий вид: 000, 001, 010, 011, 100, 101, 110 и 111.

Число двоичных разрядов может быть сколь угодно большим в зависимости от характера решаемых задач и объема кодируемой информации.

Форма представления данных с помощью двоичных разрядов характерна для позиционного двоичного кода, лежащего в основе двоичной системы счисления, применяемой сплошь и рядом во всех типах вычислительной техники.

Увеличение разрядности на единицу приведет к удвоению числа комбинаций в позиционном двоичном коде.

При двух символах (смотри примеры выше) мы имеем 4 комбинации, при трех – 8 комбинаций, при четырех – 16 комбинаций, при n символах – 2 n комбинаций.

С помощью двух символов можно закодировать практически любую информацию. Доказательством тому служат современные компьютеры, работа которых невозможна без такой кодировки.

Характерная особенность систем счисления, использующих разрядный двоичный код, заключается в возможности обозначения одного и того же числа различной комбинацией символов, отличающихся между собой по разрядности.

Например, в двоичной системе счисления единицу можно представить по-разному: 1, 01, 001, 0001 и т.д.

Нумерация двоичных разрядов осуществляется справа налево.

Если взять двоичный код 01011, то первый разряд будет иметь значение 1, второй разряд – 1, третий разряд – 0, четвертый – 1 и пятый разряд – 0:

Примеры двоичного кода

С помощью трех двоичных разрядов можно обозначить восемь десятичных чисел от 0 до 7:

0 = 000
1 = 001
2 = 010
3 = 011
4 = 100
5 = 101
6 = 110
7 = 111

Эта таблица отражает перевод десятичных чисел в двоичный код.

Фото 1. Выключатели — прекрасный пример двоичного кода

Поскольку число двоичных разрядов ничем не ограничено, с помощью такой кодировки можно зашифровать любое привычное нам десятичное число.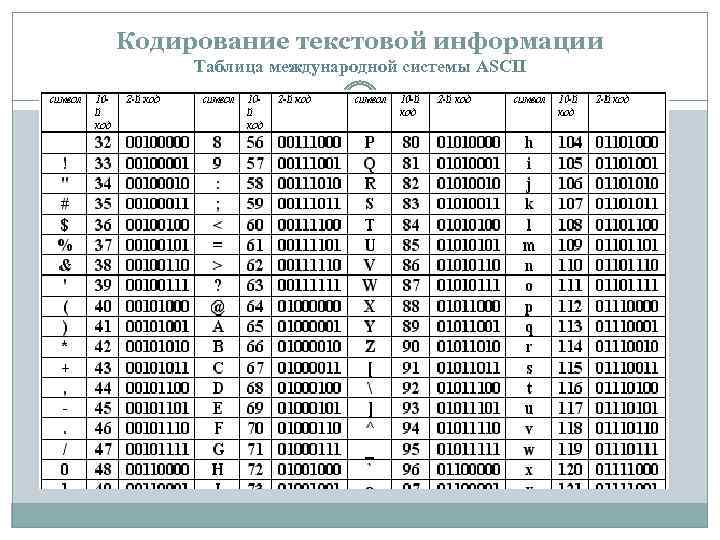

Чтобы перевести двоичный код обратно в десятичный, нужно 1-ый разряд двоичного кода умножить на 1 (или на 2 0 ), 2-ой разряд – на 2 (или на 2 1 ), третий разряд – на 4 (или на 2 2 ), n-ый разряд — на 2 n-1 , а затем сложить полученные значения.

111 → 1 * 2 2 + 1 * 2 1 + 1 * 2 0 = 4 + 2 + 1 = 7

101 → 1 * 2 2 + 0 * 2 1 + 1 * 2 0 = 4 + 0 + 1 = 5

Зачем нужен двоичный код

Основное назначение двоичного кода – шифрование и кодирование информации.

Его главные преимущества – минимальное число символов, используемых для кодирования информации, и удобство – с машинной точки зрения – оперирования зашифрованными с их помощью данными.

Допустим, нам необходимо закодировать фразу «ХОЛОДНОЕ ЛЕТО».

Установим произвольные соответствия букв двоичному коду: Х – 000, О – 001, Л – 010, Д – 011, Н – 100, Е – 101, Т – 111.

Фото 2. Двоичный код лежит в основе двоичной системы счисления

Тогда закодированная фраза примет следующий вид: 000001010001011100001101010101111001 (36 символов).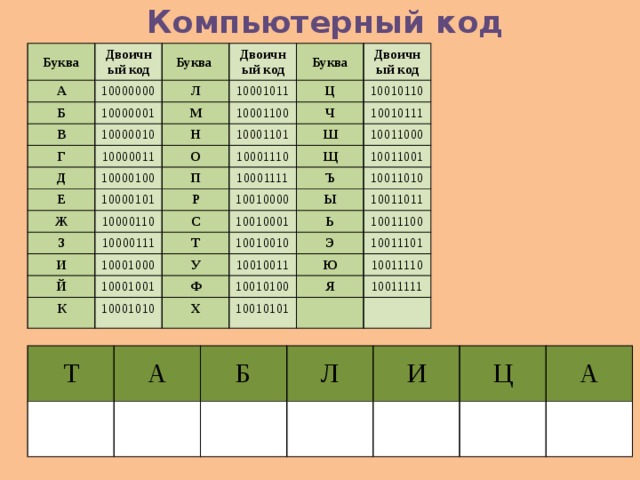

Если получатель зашифрованного кода знает, что в основе кодировки каждой буквы лежат три двоичных разряда, то расшифровать фразу ему не составит никакого труда.

В данном случае мы имеем дело с однозначно декодируемым кодом (то есть код может быть расшифрован одним единственным способом).

Для сокращения длины кода может применяться неравномерный двоичный код.

Тогда кодировщик сознательно отступает от принципа разрядности, присваивая буквам произвольное число разрядов.

Например, если Х будет иметь обозначение 01, О – 00, Л – 100, Д – 101, Н – 110, Е – 111, Т – 1111, то фразе «ХОЛОДНОЕ ЛЕТО» будет соответствовать строка 01001000010111000111100111111100 (32 символа).

В данной фразе будет однозначно декодироваться фрагмент «ХОЛОДНО», после чего дешифровщику придется ломать голову над выбором приемлемой трактовки кода: «Е ЛЕТО», «Е ЛЕЕЛ», «Е ЛТЕО», «ТОЕЕЛ» и т.д.

Данный пример указывает на проблемы с использованием непродуманных комбинаций двоичного кода.

При правильном же подборе кодов неравномерный двоичный код позволяет не только сократить объем передаваемого сообщения, но и начать его дешифровку после поступления уже первых нескольких символов, не дожидаясь пока сообщение будет получено в полном объеме.

Виды двоичных кодов

Представление в памяти компьютера целочисленных значений производится с помощью беззнакового двоичного кода, основанного на представлении двоичных разрядов степенями двойки.

При этом значение минимального числа в n-разрядном двоичном коде будет равно 0, а максимального вычисляться по формуле 2 n -1.

К примеру, для шестнадцатиразрядного кода допустимыми будут значения чисел от 0 до 65535.

На практике приходится решать задачи посложнее.

Фото 3. С помощью двоичного кода можно закодировать все что угодно

Машине или компьютеру достаточно трудно объяснить разницу между положительными и отрицательными числами. Отдельного представления требуют и числа с плавающей запятой, дробные или трансцендентные числа.

Инженеры придумали способ, как обходить эти проблемы, не выходя за пределы использования двоичного кода. Для решения озвученных проблем используется знаковый двоичный код.

В частности, для определения знака числа используется старший разряд в слове.

Если слово начинается с символа «0», значит число положительное (имеет знак «+»), если с символа «1», значит оно – отрицательное (имеет знак «-»).

При использовании шестнадцатиразрядного кода в таком случае мы сможем зашифровать числа в диапазоне от -32767 до +32767.

Недостаток знакового двоичного кода кроется в необходимости раздельной обработки цифрового и знакового разрядов, что заставляет разработчиков программного обеспечения прибегать к усложненным алгоритмам обработки данных.

Как следствие, программный код увеличивается в объеме, а скорость его работы замедляется.

Видео о двоичном коде:

На данном уроке будет рассмотрена тема «Кодирование информации.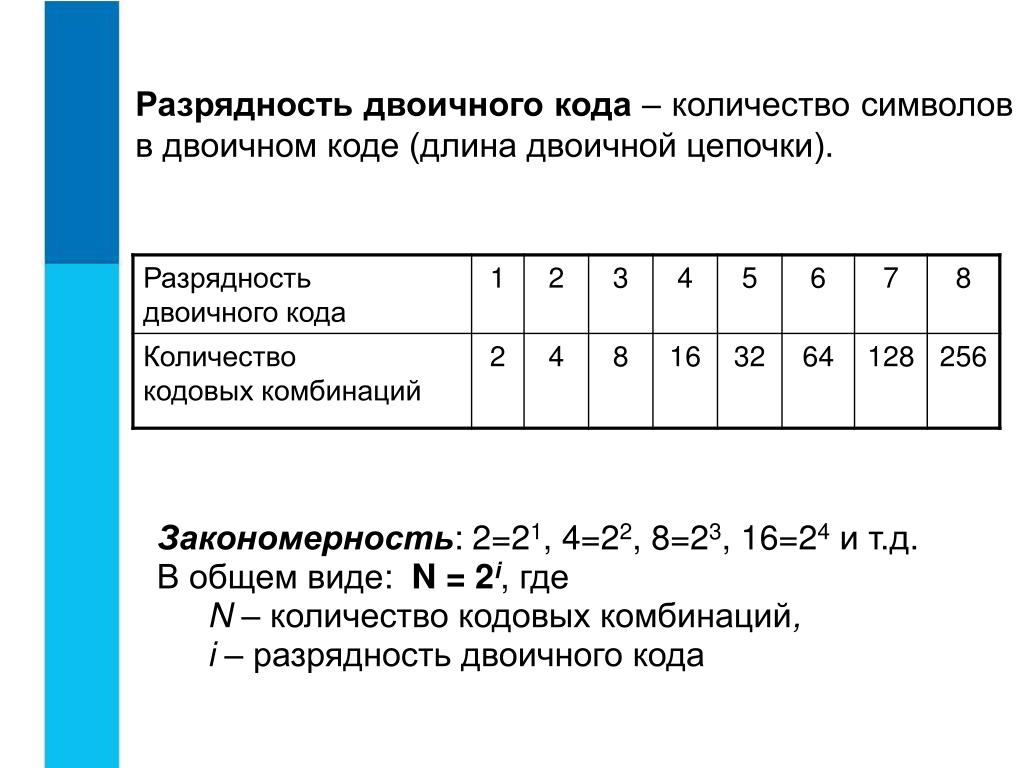 Двоичное кодирование. Единицы измерения информации». В ходе него пользователи смогут получить представление о кодировании информации, способах восприятия информации компьютеров, единицах ее измерения и двоичном кодировании.

Тема: Информация вокруг нас

Урок: Кодирование информации. Двоичное кодирование. Единицы измерения информации

1. Введение

На данном уроке будут рассмотрены следующие вопросы:

1. Кодирование как изменение формы представления информации.

2. Как компьютер распознает информацию?

3. Как измерить информацию?

4. Единицы измерения информации.

В мире кодов

Зачем люди кодируют информацию?

1. Скрыть ее от других (зеркальная тайнопись Леонардо да Винчи, военные шифровки).

2. Записать информацию короче (стенография, аббревиатура, дорожные знаки).

3. Для более легкой обработки и передачи (азбука Морзе, перевод в электрические сигналы — машинные коды).

Кодирование — это представление информации с помощью некоторого кода.

Код — это система условных знаков для представления информации.

Способы кодирования информации

1. Графический (см. Рис. 1) (с помощью рисунков и знаков).

Рис. 1. Система сигнальных флагов (Источник)

2. Числовой (с помощью чисел).

Например: 11001111 11100101.

3. Символьный (с помощью символов алфавита).

Например: НКМБМ ЧГЁУ.

Декодирование — это действие по восстановлению первоначальной формы представления информации. Для декодирования необходимо знать код и правила кодирования.

Средством кодирования и декодирования служит кодовая таблица соответствия. Например, соответствие в различных системах счисления — 24 — XXIV, соответствие алфавита каким-либо символам (Рис. 2).

Рис. 2. Пример шифра (Источник)

Примеры кодирования информации

Примером кодирования информации является азбука Морзе (см. Рис. 3).

Рис. 3. Азбука Морзе (Источник)

В азбуке Морзе используется всего 2 символа — точка и тире (короткий и длинный звук).

Еще одним примером кодирования информации является флажковая азбука (см. Рис. 4).

Рис. 4. Флажковая азбука (Источник)

Также примером является азбука флагов (см. Рис. 5).

Рис. 5. Азбука флагов (Источник)

Всем известный пример кодирования — нотная азбука (см. Рис. 6).

Рис. 6. Нотная азбука (Источник)

Рассмотрим следующую задачу:

Используя таблицу флажковой азбуки (см. Рис. 7), необходимо решить следующую задачу:

Старший помощник Лом сдает экзамен капитану Врунгелю. Помогите ему прочитать следующий текст (см. Рис. 8):

Представление информации происходит в различных формах в процессе восприятия окружающей среды живыми организмами и человеком, в процессах обмена информацией между человеком и человеком, человеком и компьютером, компьютером и компьютером.

Кодирование — это операция преобразования знаков или групп знаков одной знаковой системы в знаки или группы знаков другой знаковой системы.

Примером может служить язык жестов (см. Рис. 9).

Рис. 9. Азбука жестов (Источник)

Вокруг нас существуют преимущественно два сигнала, например:

— Светофор: красный — зеленый;

— Лампа: горит — не горит;

Всё это сигналы, обозначающие количество информации в 1 бит.

1 бит — это такое количество информации, которое позволяет нам выбрать один вариант из двух возможных.

Компьютер — это электрическая машина, работающая на электронных схемах. Чтобы компьютер распознал и понял вводимую информацию, ее надо перевести на компьютерный (машинный) язык.

Алгоритм, предназначенный для исполнителя, должен быть записан, то есть закодирован, на языке, понятном компьютеру.

Это электрические сигналы: проходит ток или не проходит ток.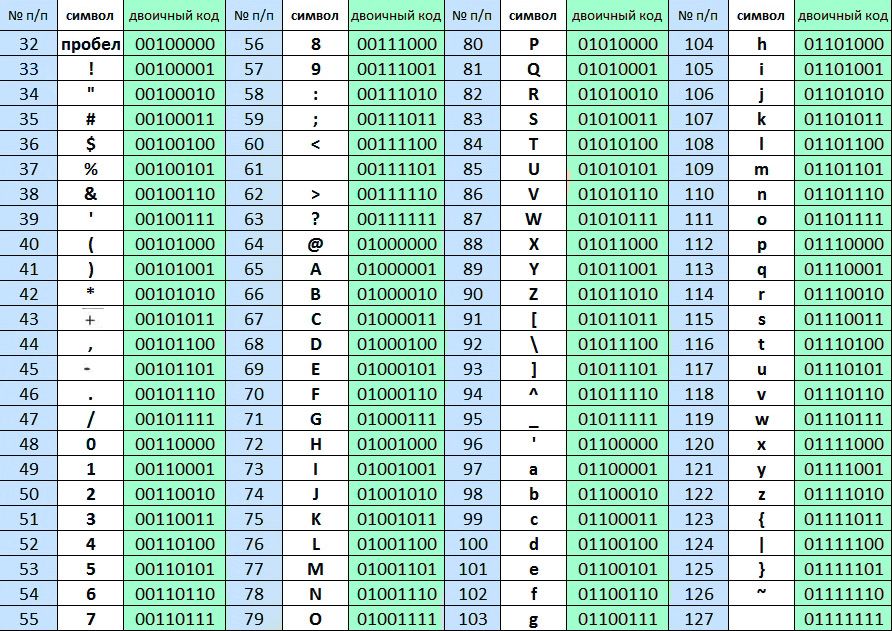

Машинный двоичный язык — последовательность «0» и «1». Каждое двоичное число может принимать значение 0 или 1.

Каждая цифра машинного двоичного кода несет количество информации, равное 1 бит.

Проводят электрический ток

Не проводят электрический ток

Участок поверхности магнитного носителя (жесткий диск, дискета)

Участок поверхности лазерного диска

Не отражает луч

5. Бит и байт

Двоичное число, которое представляет наименьшую единицу информации, называется бит. Бит может принимать значение либо 0, либо 1. Наличие магнитного или электронного сигнала в компьютере означает 1, отсутствие 0.

Строка из 8 битов называется байт. Эту строку компьютер обрабатывает как отдельный символ (число, букву).

Рассмотрим пример. Слово ALICE состоит из 5 букв, каждая из которых на языке компьютера представлена одним байтом (см. Рис. 10). Стало быть, Alice можно измерить как 5 байт.

Рис. 10. Двоичный код (Источник)

Кроме бита и байта, существуют и другие единицы измерения информации.

Двоичные коды — CoderLessons.com

В кодировании, когда числа, буквы или слова представлены определенной группой символов, говорят, что число, буква или слово кодируются. Группа символов называется кодом. Цифровые данные представляются, хранятся и передаются в виде группы двоичных битов. Эта группа также называется двоичным кодом . Двоичный код представлен числом, а также буквенно-цифровой буквой.

Преимущества двоичного кода

Ниже приведен список преимуществ, которые предлагает двоичный код.

Двоичные коды подходят для компьютерных приложений.
Двоичные коды подходят для цифровой связи.
Двоичные коды делают анализ и проектирование цифровых схем, если мы используем двоичные коды.
Поскольку используются только 0 и 1, реализация становится легкой.

Двоичные коды подходят для компьютерных приложений.

Двоичные коды подходят для цифровой связи.

Двоичные коды делают анализ и проектирование цифровых схем, если мы используем двоичные коды.

Поскольку используются только 0 и 1, реализация становится легкой.

Классификация двоичных кодов

Коды широко подразделяются на следующие четыре категории.

Взвешенные коды
Невзвешенные коды
Двоичный код десятичного кода
Буквенно-цифровые коды
Коды обнаружения ошибок
Коды, исправляющие ошибки

Взвешенные коды

Взвешенные двоичные коды – это те двоичные коды, которые подчиняются принципу позиционного веса. Каждая позиция числа представляет определенный вес. Несколько систем кодов используются для выражения десятичных цифр от 0 до 9. В этих кодах каждая десятичная цифра представлена группой из четырех битов.

Невзвешенные коды

В этом типе двоичных кодов позиционные веса не назначаются.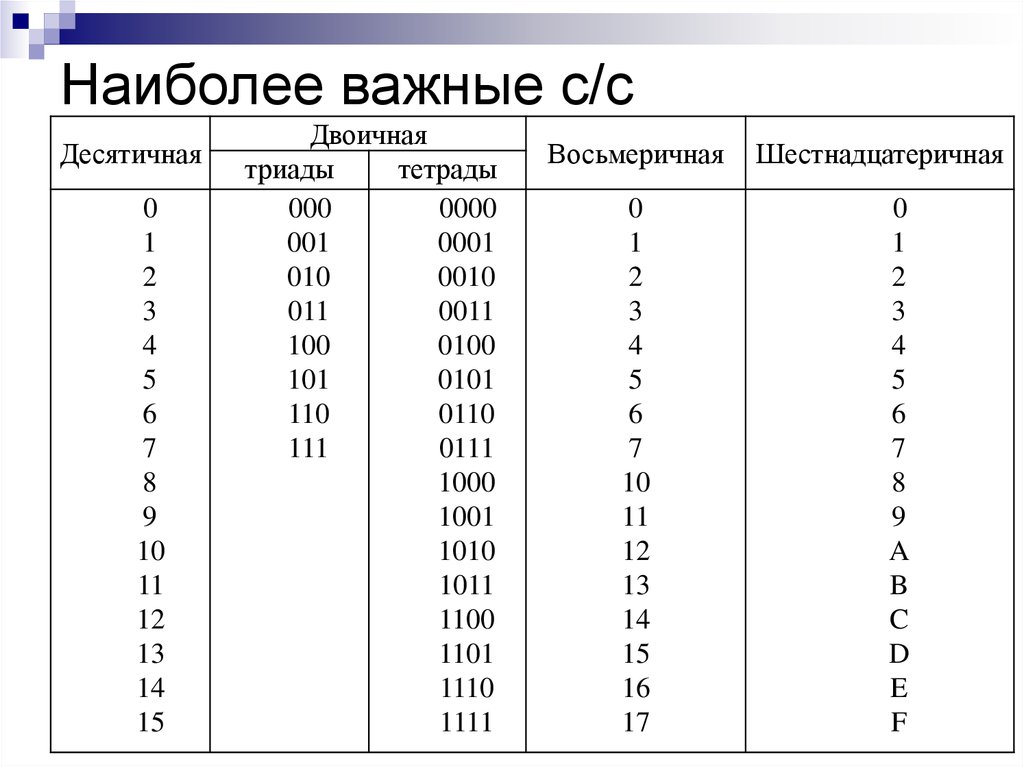 Примерами невзвешенных кодов являются код Excess-3 и код Грея.

Код избытка-3

Код Excess-3 также называется кодом XS-3. Это невзвешенный код, используемый для выражения десятичных чисел. Кодовые слова Excess-3 получаются из кодовых слов BCD 8421, добавляющих (0011) 2 или (3) 10 к каждому кодовому слову в 8421. Коды избыточного 3 получают следующим образом:

пример

Серый код

Это невзвешенный код и это не арифметические коды. Это означает, что для битовой позиции нет конкретных весов. У него есть особая особенность, что при каждом увеличении десятичного числа будет изменяться только один бит, как показано на рис. Поскольку за один раз изменяется только один бит, серый код называется единичным кодом расстояния. Серый код – это циклический код. Код Грея нельзя использовать для арифметической операции.

Применение кода Грея

Серый код широко используется в датчиках положения вала.

Датчик положения вала создает кодовое слово, которое представляет угловое положение вала.

Двоичный код (BCD)

В этом коде каждая десятичная цифра представлена 4-битным двоичным числом. BCD – это способ выразить каждую десятичную цифру двоичным кодом. В BCD с четырьмя битами мы можем представить шестнадцать чисел (от 0000 до 1111). Но в коде BCD используются только первые десять из них (от 0000 до 1001). Остальные шесть кодовых комбинаций, то есть 1010–1111, недопустимы в BCD.

Преимущества кодов BCD

Это очень похоже на десятичную систему.
Нам нужно запомнить двоичный эквивалент десятичных чисел только от 0 до 9.

Недостатки кодов BCD

Сложение и вычитание BCD имеют разные правила.
Арифметика BCD немного сложнее.
BCD требуется большее количество бит, чем двоичное, чтобы представить десятичное число. Так что BCD менее эффективен, чем двоичный.

Сложение и вычитание BCD имеют разные правила.

Арифметика BCD немного сложнее.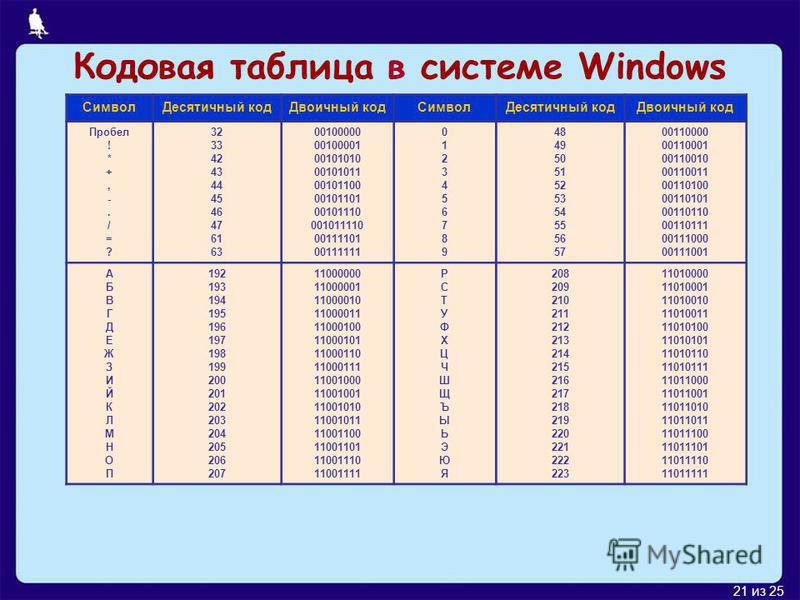

BCD требуется большее количество бит, чем двоичное, чтобы представить десятичное число. Так что BCD менее эффективен, чем двоичный.

Буквенно-цифровые коды

Бинарная цифра или бит может представлять только два символа, поскольку имеет только два состояния: «0» или «1». Но этого недостаточно для связи между двумя компьютерами, потому что там нам нужно гораздо больше символов для связи. Эти символы должны представлять 26 алфавитов с заглавными и строчными буквами, числами от 0 до 9, знаками препинания и другими символами.

Буквенно-цифровые коды представляют собой коды, которые представляют цифры и буквенные символы. В основном такие коды также представляют другие символы, такие как символы и различные инструкции, необходимые для передачи информации. Буквенно-цифровой код должен содержать не менее 10 цифр и 26 букв алфавита, т.е. всего 36 знаков. Следующие три буквенно-цифровых кода очень часто используются для представления данных.

Американский стандартный код для обмена информацией (ASCII).
Расширенный двоичный код десятичного кода обмена (EBCDIC).
Пяти битный код Бодо.

Код ASCII – это 7-битный код, тогда как EBCDIC – это 8-битный код. Код ASCII чаще используется во всем мире, в то время как EBCDIC используется в основном на больших компьютерах IBM.

Коды ошибок

Существуют методы двоичного кода, позволяющие обнаруживать и исправлять данные во время передачи данных.

Обнаружение и исправление ошибок

Разновидности и длина двоичного кода. Алгоритм считывания двоичного кода

Двоичный код представляет собой форму записи информации в виде единиц и нулей. Такая система исчисления является позиционной с основанием 2. На сегодняшний день двоичный код (таблица, представленная немного ниже, содержит некоторые примеры записи чисел) используется во всех без исключения цифровых устройствах. Его популярность объясняется высокой надежность и простотой данной формы записи. Двоичная арифметика весьма проста, соответственно, ее легко реализовать и на аппаратном уровне.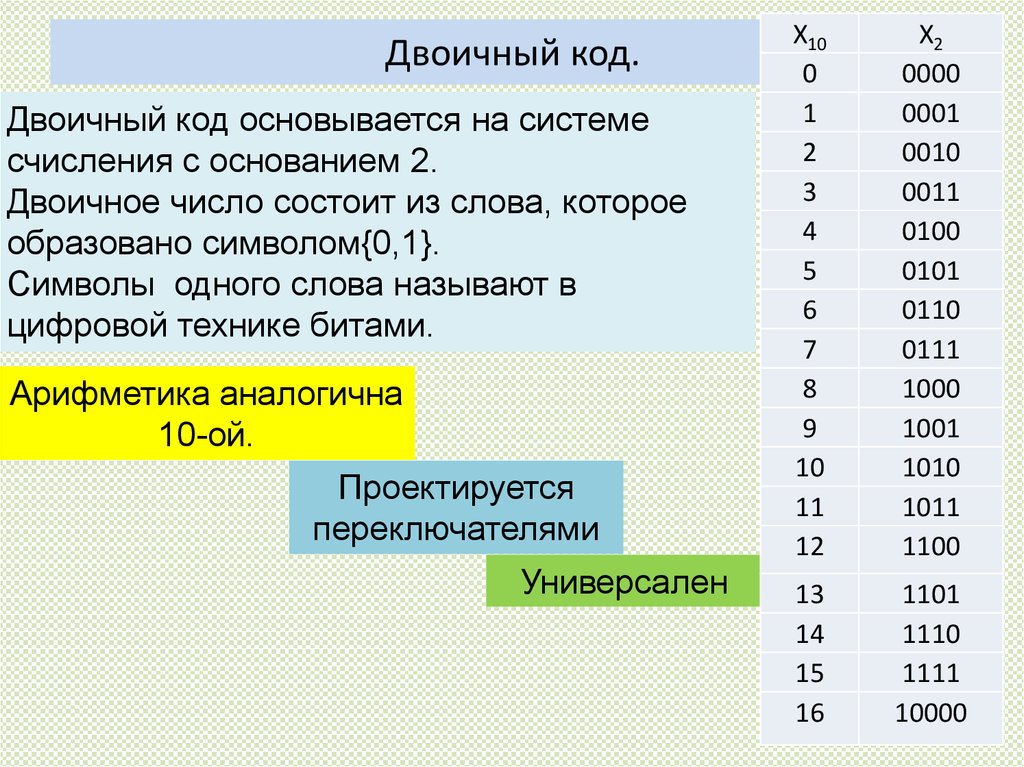 Цифровые электронные компоненты (или как их еще называют – логические) весьма надежны, так как они оперируют в работе всего двумя состояниями: логической единицы (есть ток) и логического нуля (нет тока). Тем самым они выгодно отличаются от аналоговых компонентов, работа которых основана на переходных процессах.

Как составляется двоичная форма записи?

Давайте разберемся, каким образом формируется такой ключ. Один разряд двоичного кода может содержать всего два состояния: ноль и единицу (0 и 1). При использовании двух разрядов появляется возможность записать четыре значения: 00, 01, 10, 11. Трехразрядная запись содержит восемь состояний: 000, 001 … 110, 111. В результате получаем, что длина двоичного кода зависит от числа разрядов. Это выражение можно записать с помощью следующей формулы: N =2m, где: m – это количество разрядов, а N – число комбинаций.

Виды двоичных кодов

В микропроцессорах такие ключи применяются для записи разнообразной обрабатываемой информации.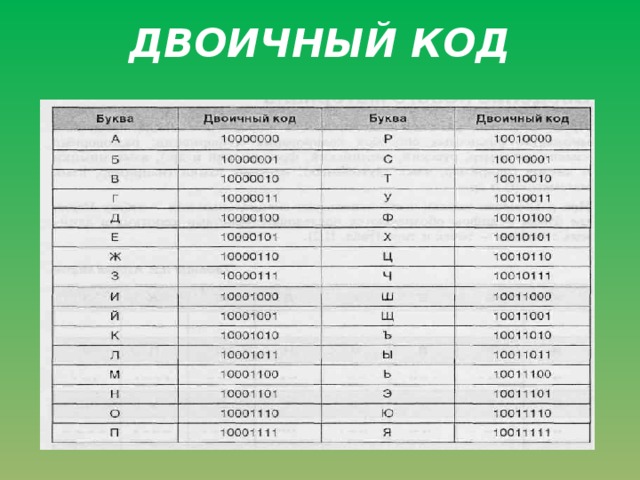 Разрядность двоичного кода может существенно превышать разрядность процессора и его встроенной памяти. В таких случаях длинные числа занимают несколько ячеек запоминающего устройства и обрабатываются с помощью нескольких команд. При этом все сектора памяти, которые выделены под многобайтный двоичный код, рассматриваются в качестве одного числа. В зависимости от необходимости предоставления той или иной информации, различают следующие виды ключей:

беззнаковые;
прямые целыезнаковые коды;
знаковые обратные;
знаковые дополнительные;
код Грея;
код Грея-Экспресс.;
дробные коды.

Рассмотрим более детально каждый из них.

Беззнаковый двоичный код

Давайте разберемся, что же представляет собой такой вид записи. В целых беззнаковых кодах каждый разряд (двоичный) представляет степень цифры два. При этом наименьшее число, которое можно записать в такой форме, равно нулю, а максимальное можно представить следующей формулой: М=2^п-1.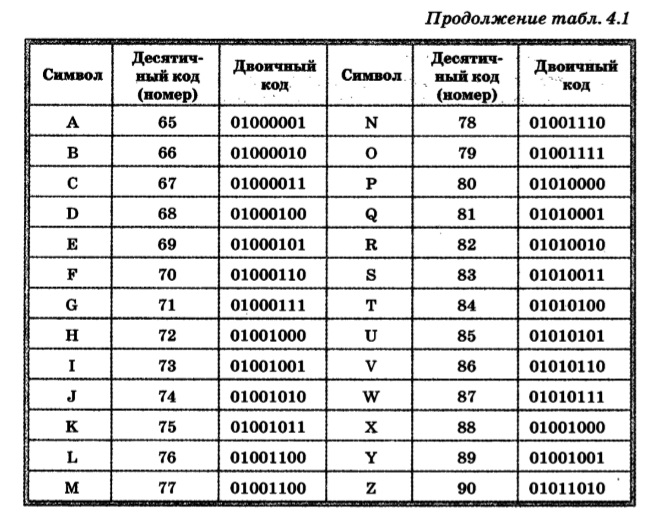 Эти два числа полностью определяют диапазон ключа, которым можно выразить такой двоичный код. Давайте рассмотрим возможности упомянутой формы записи. При использовании данного вида беззнакового ключа, состоящего из восьми разрядов, диапазон возможных чисел составит от 0 до 255. Шестнадцатиразрядный код будет иметь диапазон от 0 до 65535. В восьмиразрядных процессорах для хранения и записи таких чисел используют два сектора памяти, которые располагаются в соседних адресатах. Работу с такими ключами обеспечивают специальные команды.

Прямые целые знаковые коды

В данном виде двоичных ключей старший разряд используется для записи знака числа. Нуль соответствует плюсу, а единица — минусу. В результате введения данного разряда диапазон закодированных чисел смещается в отрицательную сторону. Получается, что восьмиразрядный знаковый целый двоичный ключ может записать числа в диапазоне от -127 до +127. Шестнадцатиразрядный – в диапазоне от -32767 до +32767. В восьмиразрядных микропроцессорах для хранения подобных кодов используют два соседних сектора.

Недостатком такой формы записи является то, что знаковые и цифровые разряды ключа необходимо обрабатывать раздельно. Алгоритмы программ, работающих с этими кодами, получаются очень сложными. Для изменения и выделения знаковых разрядов необходимо применять механизмы маскировки этого символа, что способствует резкому увеличению размеров программного обеспечения и уменьшению его быстродействия. С целью устранения данного недостатка был введен новый вид ключа – обратный двоичный код.

Знаковый обратный ключ

Данная форма записи отличается от прямых кодов только тем, что отрицательное число в ней получается путем инвертирования всех разрядов ключа. При этом цифровые и знаковые разряды идентичны. Благодаря этому, алгоритмы работы с таким видом кодов существенно упрощаются. Однако обратный ключ требует специальный алгоритм для распознавания символа первого разряда, вычисления абсолютной величины числа. А также восстановления знака результирующего значения. Более того, в обратном и прямом кодах числа для записи нуля используют два ключа.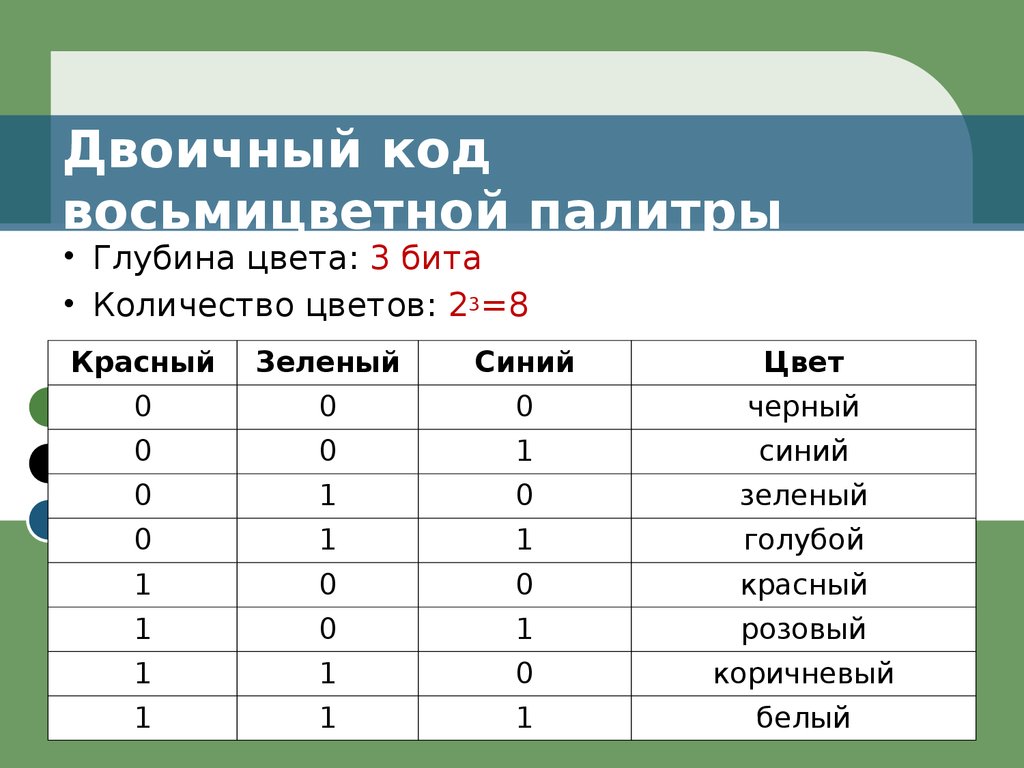 Несмотря на то что это значение не имеет положительного или отрицательного знака.

Знаковый дополнительный код двоичного числа

Данный вид записи не имеет перечисленных недостатков предыдущих ключей. Такие коды позволяют проводить непосредственное суммирование как положительных, так и отрицательных чисел. При этом не проводится анализ знакового разряда. Все это стало возможным благодаря тому факту, что дополнительные числа представляют собой естественное кольцо символов, а не искусственные образования, такие как прямые и обратные ключи. Более того, важным фактором является, то что произвести вычисления дополнений в двоичных кодах чрезвычайно просто. Для этого достаточно к обратному ключу добавить единицу. При использовании данного вида знакового кода, состоящего из восьми разрядов, диапазон возможных чисел составит от -128 до +127. Шестнадцатиразрядный ключ будет иметь диапазон от -32768 до +32767. В восьмиразрядных процессорах для хранения таких чисел также используют два соседних сектора.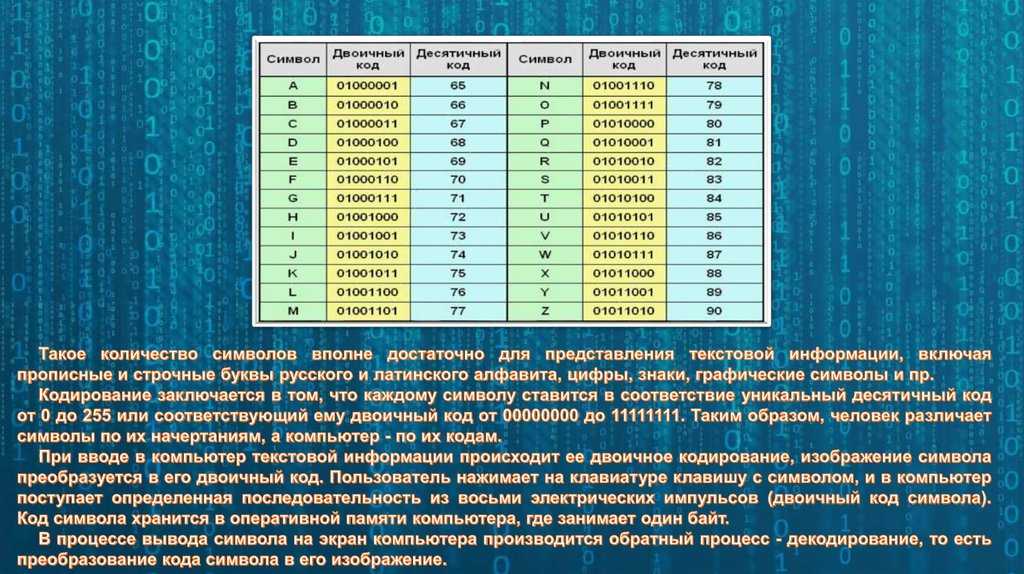

Двоичный дополнительный код интересен наблюдаемым эффектом, который называют явлением распространения знака. Давайте разберемся, что это значит. Данный эффект заключается в том, что в процессе преобразования однобайтового значения в двухбайтовое достаточно каждому биту старшего байта назначить значения знаковых битов младшего байта. Получается, что для хранения знакового символа числа можно воспользоваться старшими битами. При этом значение ключа совершенно не изменяется.

Код Грея

Данная форма записи, по сути, является одношаговым ключом. То есть в процессе перехода от одного значения к другому меняется всего лишь один бит информации. При этом погрешность при считывании данных приводит к переходу от одного положения к другому с незначительным смещением по времени. Однако получение совершенно неверного результата углового положения при таком процессе полностью исключается. Достоинством такого кода является его способность зеркально отображать информацию. Например, инвертируя старшие биты, можно просто менять направление отсчета.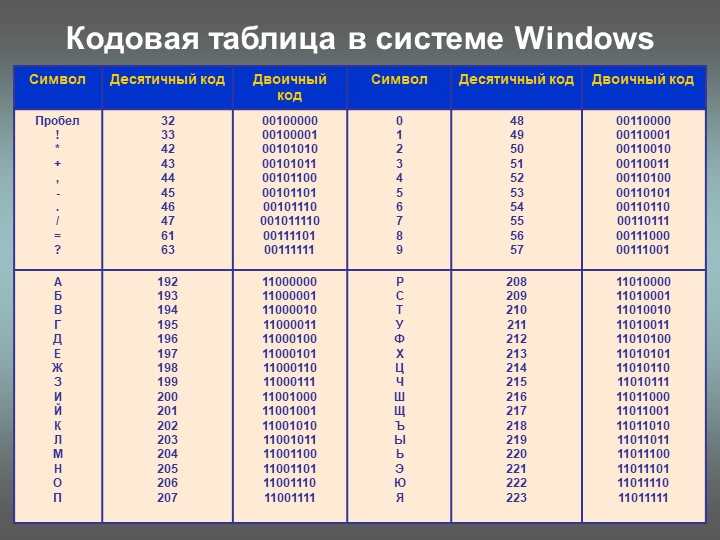 Это происходит благодаря управляющему входу Complement. При этом выдаваемое значение может быть как возрастающим, так и спадающим при одном физическом направлении вращения оси. Так как информация, записанная в ключе Грея, имеет исключительно кодированный характер, который не несет реальных числовых данных, то перед дальнейшей работой требуется предварительно преобразовать его в обычную бинарную форму записи. Осуществляется это с помощью специального преобразователя – декодера Грей-Бинар. Данное устройство легко реализуется на элементарных логических элементах как аппаратным, так и программным способом.

Код Грея-Экспресс

Стандартный одношаговый ключ Грей подходит для решений, которые представлены в виде чисел, возведенных в степень два. В случаях, где необходимо реализовывать иные решения, из такой формы записи вырезают и используют только средний участок. В результате сохраняется одношаговость ключа. Однако в таком коде началом числового диапазона не является нуль. Он смещается на заданное значение. В процессе обработки данных от генерируемых импульсов отнимают половину разницы между начальным и редуцированным разрешением.

Представление дробного числа в двоичном ключе с фиксированной запятой

В процессе работы приходится оперировать не только целыми цифрами, но и дробными. Такие числа можно записывать с помощью прямых, обратных и дополнительных кодов. Принцип построения упомянутых ключей такой же, как и у целых. До сих пор мы считали, что двоичная запятая должна находиться справа от младшего разряда. Но это не так. Она может располагаться и слева от старшего разряда (в таком случае в качестве переменной можно записывать исключительно дробные числа), и посередине переменной (можно записывать смешанные значения).

Представление двоичного кода с плавающей запятой

Такая форма применяется для записи больших чисел, либо наоборот — очень малых. В качестве примера можно привести межзвездные расстояния или размеры атомов и электронов. При вычислении таких значений пришлось бы применять двоичный код с очень большой разрядностью. Однако нам нет необходимости учитывать космические расстояние с точностью до миллиметра. Поэтому форма записи с фиксированной запятой в данном случае неэффективна. Для отображения таких кодов используется алгебраическая форма. То есть число записывается как мантисса, умноженная на десять в степени, отображающей нужный порядок числа. Следует знать, что мантисса не должна быть больше единицы, а после запятой не должен записываться ноль.

Это интересно

Считается, что двоичное исчисление было изобретено в начале 18-го века математиком из Германии Готфридом Лейбницем. Однако, как недавно открыли ученые, задолго до этого аборигены полинезийского острова Мангареву использовали данный вид арифметики. Несмотря на то что колонизация практически полностью уничтожила оригинальные системы исчисления, ученые восстановили сложные двоичные и десятичные виды счета. Кроме того, ученый Когнитивист Нуньес утверждает, что кодирование двоичным кодом применялось в древнем Китае еще в 9-м веке до н.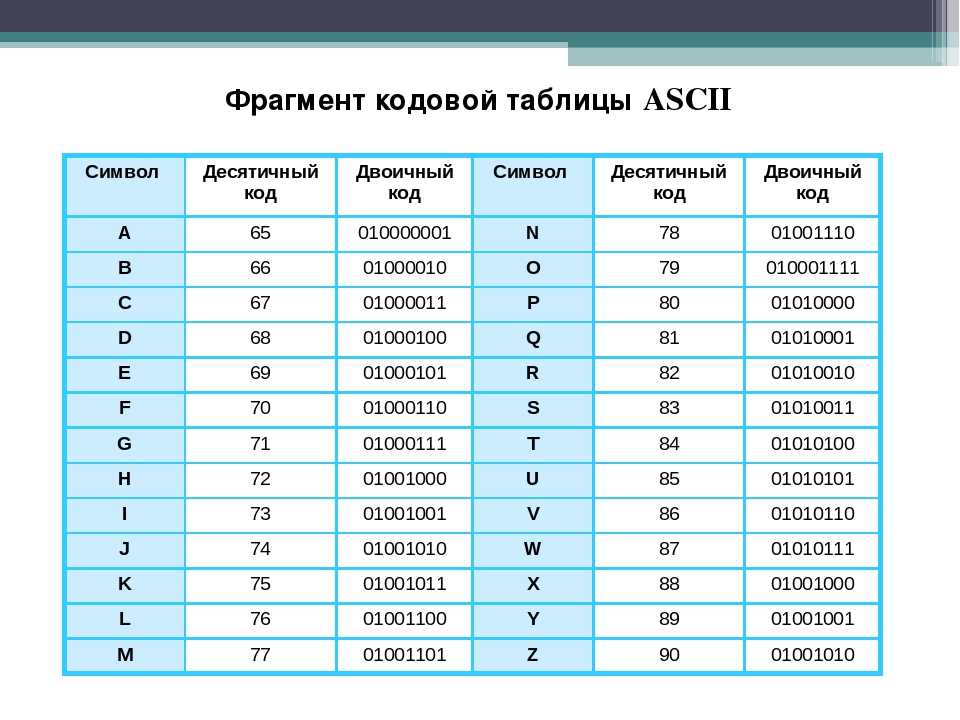 э. Другие древние цивилизации, например, индейцы майя, также использовали сложные комбинации десятичных и бинарных систем для отслеживания временных интервалов и астрономических явлений.

кодировка — Разница между двоичным и байт кодом?

Небольшая историческая справка.

В самых первых компьютерах (1940-е годы) команды и данные хранились раздельно. Данные располагались в памяти, а команды задавались перемычками на лицевой панели. Из-за этого некоторые команды нельзя было реализовать в принципе. Например, нельзя было передать управление на команду, адрес которой хранится в памяти. Сейчас с помощью таких косвенных вызовов работают виртуальные методы в Java/C++/C#.

Группа инженеров предложила несколько архитектурных принципов, которые помогли сделать компьютеры проще и в то же время мощнее. Один из них гласит, что и программы и данные хранятся в оперативной памяти. Поскольку компьютер не хранит ничего кроме чисел, процессор «видит» программу именно как массив чисел.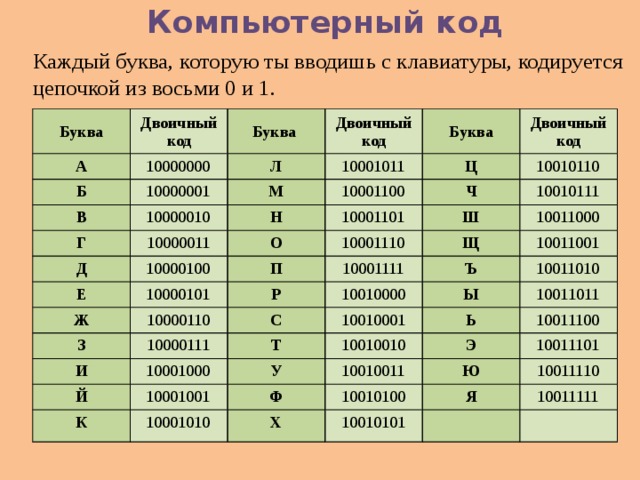

Сейчас эти принципы называются архитектурой Фон Неймана по имени американского математика, который был участником группы, разработавшей первые компьютеры. Большая историческая несправедливость состоит в том, что Фон Нейман не руководил этой группой, и, скорее всего, не придумал ни одного из предложенных принципов. Но в опубликованной статье его фамилия стояла первой, и именно поэтому принципы получили такое название.

Числа хранятся в двоичном виде (ещё один принцип архитектуры Фон Неймана). Минимальной единицей хранения является байт. Я читал, что существовали компьютеры с 7-битными и 9-битными словами, но никогда их не видел. Насколько я знаю, уже в конце 60-х годов победил 8-битный байт.

Вот пример машинного кода и его представления на языке Ассемблера. Я нашёл его в Google. Слева указан порядковый номер (адрес) первого байта команды. Во второй колонке мы видим байты команды, они записаны в восьмеричной системе счисления. В третьей колонке мнемоники Ассемблера, которые упрощают восприятие программы человеком. Некоторые команды занимают один байт, а некоторые два. В этом примере нет команд, которые занимают три, четыре и больше байт, но такие команды также встречаются.

004: 003 010       lbl adda    #8      immediate value decimal
006: 103 010           addb    #010    same thing in octal
010: 024 001           lda     b       memory reference
012: 235 220           stx     (ptr)   indirect reference
014: 306 204           ora     data,x  indexed
016: 337 220           lnega   (ptr),x indirect/indexed
020:               # jumps and calls
020: 344 004           jmp     lbl     unconditional jump
022: 043 030           jane    lbl2-2  jump if a not equal 0
024: 257 221           jxgt    (ptr+one) jump indirect if x gt
026: 364 041           call    sub     call to subroutine
030: 174 220           cbeq    (ptr)   call indirect if b eq 0
032:               # set and skips
032:                   lbl2
032: 122 204           set1    fox,2  set bit 2 of data to 1
034: 272 205           skp0    data+1,7  skip if bit 7 is 0
036:               # shifts and rotates
036: 001               shra    1+SHIFT   shift a right 4 plcs
037: 361               rolb    2       rotate b left 2 places
040: 000               hlt             halt
041: 000               sub db 0            return address
042: 200               nop             no op
043: 023 222           lda #0222
045: 123 144           ldb #100
047: 360               sys             system call (extension)
050: 023 222           sysp 0222,100   system call using parms
052: 123 144
054: 360
055: 354 041           jmp (sub)       return

Именно это и есть двоичный код, который «понимает» процессор.

Теперь о байт-коде. Основной проблемой двоичного кода является его специфичность. Два разных устройства, например, ноутбук и мобильный телефон, имеют разные процессоры и разные наборы команд.

Если мы захотим написать для них программу, нам придётся писать две программы. Традиционно проблема переносимости решается с помощью языков высокого уровня и компиляторов. Хороший компилятор — это сложная программа, которую долго разрабатывать и трудно поддерживать. Если наш компилятор имеет создавать код для пяти разных процессоров, в нём пять разных оптимизаторов и пять генераторов кода.

Проблему переносимости и сложности можно решить с помощью промежуточной виртуальной машины. Она должна иметь архитектуру низкого уровня, чтобы её можно было просто реализовать. С другой стороны, она должна включать в себя возможности современных процессоров, чтобы не проседать в производительности.

Виртуальный процессор работает также, как и реальный: он видит массив чисел, и воспринимает их как команды для выполнения. Байт-код внешне совершенно идентичен двоичному коду. Вот пример байт-кода виртуальной машины Java:

000: 03        iconst_0
001: 3b        istore_0
002: 84 00 01  iinc 0, 1
005: 1a        iload_0
006: 05        iconst_2
007: 68        imul
010: 3b        istore_0
011: a7 ff f9  goto -7

Единственная разница заключается в том, что двоичный код исполняет физический процессор, а байт-код — очень простая программа-интерпретатор. Впрочем, насколько я знаю, существуют физические процессоры, которые умеют выполнять байт-код Java-машины, так что разница между ними может быть и совсем условной.

Что такое двоичный код

Великолепным примером двоичного кода могут служить любые пары антонимов, к примеру, «да/нет», «белое/черное», «включено/выключено» и т.д.

Три двоичных разряда могут иметь следующий вид: 000, 001, 010, 011, 100, 101, 110 и 111.

Увеличение разрядности на единицу приведет к удвоению числа комбинаций в позиционном двоичном коде.

При двух символах (смотри примеры выше) мы имеем 4 комбинации, при трех – 8 комбинаций, при четырех – 16 комбинаций, при n символах – 2ⁿ комбинаций.

Например, в двоичной системе счисления единицу можно представить по-разному: 1, 01, 001, 0001 и т.д.

Нумерация двоичных разрядов осуществляется справа налево.

Примеры двоичного кода

С помощью трех двоичных разрядов можно обозначить восемь десятичных чисел от 0 до 7:

0 = 000
1 = 001
2 = 010
3 = 011
4 = 100
5 = 101
6 = 110
7 = 111

Эта таблица отражает перевод десятичных чисел в двоичный код.

Фото 1. Выключатели — прекрасный пример двоичного кода

Чтобы перевести двоичный код обратно в десятичный, нужно 1-ый разряд двоичного кода умножить на 1 (или на 2⁰), 2-ой разряд – на 2 (или на 2¹), третий разряд – на 4 (или на 2²), n-ый разряд — на 2^n-1, а затем сложить полученные значения.

Примеры:

111 → 1 * 2² + 1 * 2¹ + 1 * 2⁰ = 4 + 2 + 1 = 7

101 → 1 * 2² + 0 * 2¹ + 1 * 2⁰ = 4 + 0 + 1 = 5

Зачем нужен двоичный код

Основное назначение двоичного кода – шифрование и кодирование информации.

Допустим, нам необходимо закодировать фразу «ХОЛОДНОЕ ЛЕТО».

Установим произвольные соответствия букв двоичному коду: Х – 000, О – 001, Л – 010, Д – 011, Н – 100, Е – 101, Т – 111.

Фото 2. Двоичный код лежит в основе двоичной системы счисления

Тогда закодированная фраза примет следующий вид: 000001010001011100001101010101111001 (36 символов).

Для сокращения длины кода может применяться неравномерный двоичный код.

Данный пример указывает на проблемы с использованием непродуманных комбинаций двоичного кода.

Виды двоичных кодов

При этом значение минимального числа в n-разрядном двоичном коде будет равно 0, а максимального вычисляться по формуле 2ⁿ-1.

К примеру, для шестнадцатиразрядного кода допустимыми будут значения чисел от 0 до 65535.

На практике приходится решать задачи посложнее.

Фото 3. С помощью двоичного кода можно закодировать все что угодно

В частности, для определения знака числа используется старший разряд в слове.

Как следствие, программный код увеличивается в объеме, а скорость его работы замедляется.

Видео о двоичном коде:

Что такое двоичный код? Как это работает? (Объяснение двоичного кода)

Итак, вам интересно, как работает двоичный код, а?

Если вы изучаете информатику или программирование, понимание двоичного кода является частью основ, которые вы должны изучить.

Но с чего начать? Как проще всего понять двоичную систему?

Возможно, вы знаете, что двоичная система основана на единицах и нулях. Эти две цифры лежат в основе всех технических гаджетов вокруг нас.

Так что, даже если вы не изучаете программирование, знание того, как работает двоичный код, поможет вам понять окружающий мир.

В этом руководстве я покажу вам простой способ разобраться в двоичной системе. Я поделюсь с вами тем, что я узнал о тех простых единицах и нулях, которые заставляют вращаться наш наполненный технологиями мир.

Начнем!

Вот несколько статей по теме, которые могут оказаться полезными:

Учитесь программировать быстрее: изучение основ информатики для компьютерного программирования
26 лучших веб-сайтов для изучения программирования для начинающих
8 важных моментов, которые нужно знать перед изучением программирования Я могу получить небольшую комиссию, если вы купите по одной из моих ссылок, без каких-либо дополнительных затрат для вас. Спасибо за Вашу поддержку!
Содержание
Зачем вам понимать, как работает двоичный код?
Что такое двоичный код?
Что означают все 1 и 0?
Как компьютеры хранят данные?
Как работает двоичный код?
Где можно узнать больше о двоичном коде и информатике?
Часто задаваемые вопросы: Как работает двоичный код?
Зачем вам понимать, как работает двоичный код?
Но если двоичный код понимается только компьютерами, зачем вам изучать его побольше?
Вы абсолютно правы. Вы (скорее всего) никогда не будете писать компьютерные программы в двоичном коде.
Вместо этого такие разработчики, как вы и я, используют более удобные языки программирования, чтобы давать инструкции компьютерам.
Тем не менее, двоичный код, вероятно, является наиболее фундаментальной концепцией, лежащей в основе программирования и информатики. Это то, что заставляет каждый компьютер работать так, как он работает.
В общем, двоичный код позволяет нам общаться с компьютерами и давать им инструкции.
И хотя языки программирования, которые вы используете для написания кода, мы надеемся, далеки от двоичного кода, они все же переводятся в двоичный код, чтобы компьютеры могли интерпретировать их и запускать ваши программы.
Эти 1 и 0 определяют, как компьютеры принимают входные данные, хранят и обрабатывают информацию, а также производят выходные данные для своих пользователей — это вы и я.
Таким образом, понять хотя бы основы того, что такое бинарник и как он работает, не только интересно и довольно увлекательно, но и весьма полезно.
Но не беспокойтесь, если концепция двоичного кода поначалу покажется вам абстрактной и трудной для понимания.
Важно то, что вы знаете, как такой простой язык может быть переведен в самые сложные компьютерные программы и информационные структуры, которые вы видите и используете ежедневно.
☝️ вернуться к содержанию ☝️
Что такое двоичный код?
Что же такое двоичный код? Как именно работает двоичный код?
Как может очень сложная компьютерная программа состоять только из 1 и 0?
Для упрощения вы можете думать о двоичном формате как о способе сообщить компьютеру, должен ли переключатель быть включен или выключен. Таким образом, 1 означает «включено», 0 означает «выключено».
Но постойте: о каком выключателе идет речь?
Как включенный или выключенный переключатель влияет на то, что делают компьютеры?
Чтобы лучше понять это, давайте посмотрим, как работают компьютеры:
Компьютеры выполняют четыре основные функции:
Принимают входные данные
Информация о хранении
Информация о процессе
Результаты вывода
Это четыре основные задачи, которые должна выполнять машина, чтобы быть компьютером.
Например, когда вы печатаете на своем компьютере, ваши пальцы, ударяющие по клавиатуре, вводят компьютер.
Ваш компьютер волшебным образом знает, как преобразовать определенную клавишу в нужную букву.
Наконец компьютер выдал вывод: вы видите на экране нужную букву.
Какое отношение это имеет к двоичному коду?
Читайте также: Информатика 101: что такое компьютер?
☝️ вернуться к содержанию ☝️
Что означают все 1 и 0?
Эти 1 и 0, или переключатели, о которых я упоминал выше, — это то, как ваш компьютер хранит и обрабатывает данные.
В те дни, когда были построены самые первые компьютеры, они имели настоящие лампочки, чтобы обеспечить вывод для своих пользователей. Пользователь увидит, что определенный свет включается, чтобы указать на определенный тип вывода или сообщения от компьютера.
То же самое происходит и сейчас, когда вы ведете машину и загорается лампочка газа. Это выход из вашей машины, говорящий, что вы должны сойти с автострады и как можно скорее найти заправочную станцию.
Итак, с компьютером эти 1 и 0 могут быть чем угодно в современных компьютерах. Но обычно они представляют собой числа, буквы и другие символы.
Суть в том, что эта простая концепция включения или выключения переключателя может превратиться во что-то действительно сложное .
Даже самые сложные современные компьютеры работают в соответствии с этим очень простым, рудиментарным машинным языком, где 1 и 0 представляют два состояния: либо ВКЛ, либо ВЫКЛ.
Но чтобы это произошло, ваш компьютер, очевидно, имеет дело не только с одним включенным или выключенным переключателем.
Читайте также: Как начать изучать программирование? 6 советов для начинающих
☝️ вернуться к содержанию ☝️
Как компьютеры хранят данные?
Прежде чем мы углубимся в то, как на самом деле работают двоичный код и двоичные числа и как можно расшифровать простую двоичную последовательность, давайте сначала рассмотрим один фундаментальный момент, касающийся хранения данных.
Как я упоминал выше, компьютеры используют входные данные для хранения и обработки информации. Эта информация или данные являются основным компонентом работы любого компьютера.
Теперь, когда вы заглянете внутрь компьютера, вы увидите кучу цепей и электрических проводов. Они несут всю информацию внутри компьютера, доставляя ее в нужное место для хранения или обработки.
Но как хранить или представлять информацию с помощью электричества?
Единицы и нули, которые мы только что обсуждали, представляют наименьшую единицу данных, которую понимает компьютер.
Один переключатель, включенный или выключенный, — это то, что нам нужно для хранения одного бит данных.
Следовательно, бит является фундаментальной, базовой единицей информации. Достаточно указать два разных варианта либо «вкл», либо «выкл».
Также это может означать «верно» или «ложно», или просто «да» или «нет».
Я знаю, всего два варианта не дают нам слишком много возможностей… Но это хорошее начало!
С помощью одной лампочки мы можем хранить 1 бит информации.
С 10 лампочками мы могли бы сделать 10 бит.
Итак, если бы у нас было достаточно лампочек, мы могли бы хранить любое количество данных, какое захотим, в цифровой форме.
Читайте также: Зачем изучать программирование? 12 Преимущества обучения программированию
Хранение данных в битах: простой пример
Конечно, в наши дни для хранения данных в компьютерах используются другие методы и технологии, а не простые лампочки.
Использование лампочек не только заняло бы слишком много места, но также было бы трудно хранить данные: выключение компьютера, использующего только лампочки, означало бы потерю данных при отключении питания.
Таким образом, вместо лампочек компьютеры хранят биты данных, например, удерживая электроны в конденсаторах. Ваш компьютер использует эту технологию в памяти DRAM.
Итак, сколько именно лампочек поместится в вашу DRAM?
Предположим, ваш компьютер имеет, например, 4 ГБ DRAM.
Один ГБ равен приблизительно миллиарду байтов. Или, если быть более точным, 1 ГБ — это 2 ³⁰ байт. А 1 байт = 8 бит.
Это означает, что ваши 4 ГБ DRAM содержат 2 ³⁰ x 4 x 8 = 34 359 738 368 бит.
Это 34 миллиарда лампочек — и мы говорим здесь только о вашей DRAM, а не о вашем жестком диске емкостью 2 ТБ!
Итак, очевидно, что современные компьютеры могут делать гораздо больше, чем решать, включать ли отдельный свет или нет.
Несмотря на то, что двоичный код состоит только из 1 и 0, он может представлять самые сложные компьютерные программы.
☝️ вернуться к содержанию ☝️
Как работает двоичный код?
Итак, что значит иметь 34 миллиарда битов для хранения и представления информации?
Чтобы понять, что эти биты могут сделать для нас, давайте подробнее рассмотрим двоичную систему счисления .
Двоичная система счисления использует только 0 и 1 для представления любых дальнейших числовых значений, а также других типов данных.
Во-первых, давайте быстро напомним, как «обычные» числа, к которым мы привыкли…
Знакомство с десятичной системой счисления
Числа от 0 до 9, которые мы с вами выучили в школе, составляют десятичную систему счисления .
Вы можете использовать любую комбинацию этих 10 цифр для представления числового значения.
Кроме того, вы знаете, как выполнять сложения, вычитания и другие базовые математические вычисления с использованием этих чисел относительно быстро.
В десятичной системе каждая цифра в определенном числе представляет собой 1, 10, 100 и т. д., начиная с правой стороны.
Итак, с числом 216, например, мы имеем:
A 6, представляющий единицы
A 1, представляющий 10-й
A 2, представляющий 100-й
различают эти три «уровня» цифр:
1-е: единицы представляют, сколько раз числовое значение включает 10 ⁰
10-е: 10-е обозначают 10 ¹
1000 ²
Итак, вы видите здесь закономерность?
10 в степени 0, 1, 2 и так далее.
Мы просто увеличиваем степень числа 10 по мере увеличения нашего числа. Поэтому десятичную систему также называют системой счисления с основанием 10 .
И для моих дорогих собратьев-знатоков языка:
Слово «десятичный» происходит от латинского слова decem «десять», а «двоичный» происходит от латинского слова bi , означающего «два» в качестве префикса. .
Теперь посмотрим, чем двоичная система счисления отличается от десятичной.
Как понимать двоичную систему счисления?
В двоичной системе вместо степеней 10 мы используем степени двойки.
Как и в приведенном выше десятичном примере, давайте подумаем о том, что означают разные позиции в числе.
Предполагая, что у нас есть двоичное число с несколькими цифрами, мы можем снова начать с правой части:
1. из этих цифр просто говорит нам, является ли цифра «включенной» или «выключенной».
  Когда вы видите «1», это означает, что значение этой цифры включено в числовое значение, которое мы хотим представить.
  Если вы видите «0», значение не должно быть включено.
  Как «расшифровать» двоичное число? Простой двоичный пример
  Итак, как мы можем представить число, которое мы только что видели в десятичной системе счисления, 216 , в двоичном виде?
  Давайте попробуем!
  Во-первых, давайте начнем с рассмотрения степени числа 2 в приведенном выше списке. Нам нужно найти наибольшее значение , которое на меньше , чем значение 216.
  Мы видим, что это 128, поэтому в этом случае нам нужно 8 двоичных цифр, начиная с 2 ⁰.до 2 ⁷ . Вы можете увидеть эти 8 точек на изображении ниже.
  Поскольку 128 «включено» в наш номер, давайте обозначим это цифрой «1» вместо 128 на изображении ниже.
  Затем давайте выполним простое вычитание: 216 – 128 = 88.
  Опять же, давайте повторим первый шаг и найдем наибольшее значение, которое меньше этого остатка 88. Мы видим, что это 64-е, поэтому мы ставим «1» в цифре для 2 ⁶ .
  Теперь снова вычтем: 88 – 64 = 24.
  Итак, возвращаясь к первому шагу, мы видим, что следующая цифра, для которой нам нужно использовать «1», — это разряд 16, или 2 ⁴ .
  Мы просто продолжаем повторять эти шаги, чтобы выяснить, какие двоичные цифры получают значение «1» или «0».
  Наконец, мы получаем следующую двоичную последовательность:
  1 1 0 1 1 0 0 0
  Таким образом, эта двоичная последовательность чисел на самом деле ничего не значит для нас с вами, поскольку мы не привыкли к двоичной системе.
  Подсчитаем значения степеней двойки для каждой цифры и сложим их вместе:
  128 + 64 + 0 + 16 + 8 + 0 + 0 + 0
  = 216
  Итак, мы получили правильное число что мы хотели отобразить в двоичном виде: 216.
  Большой успех!
  Очевидно, нам нужно на несколько цифр больше, чем в десятичной системе, но значение числа точно такое же. И это то, чего мы хотели добиться!
  Думать и считать в двоичных числах, конечно, несколько сложно, поскольку мы привыкли к системе счисления, основанной на степенях 10.
  Но, несмотря на фундаментальную идею наличия только двух состояний, представляющих два значения, либо «включено», либо «выключено», двоичная система так же хороша, как и десятичная система для отображения чисел.
  Но как двоичный код работает с другими видами информации, такой как текст, изображения или звук?
  Оказывается, все эти типы информации также могут быть представлены в двоичном коде!
  Представление текста в двоичном коде
  В двоичном коде мы можем использовать простые числа для представления различных букв алфавита. Таким образом, «А» может быть «1», «В» может быть «2» и так далее.
  Таким образом, мы можем представить любое слово или абзац текста как последовательность этих чисел. Затем компьютер может сохранить эти числа в качестве информации, используя сигналы «включено» или «выключено».
  Итак, всякий раз, когда вы читаете текст на своем телефоне или компьютере, то, что вы видите на экране, основано на подобном двоичном коде.
  Представление изображений и графики в двоичном коде
  Подобно представлению алфавита в числах, мы можем сделать то же самое для изображений и других графических носителей.
  Изображение, отображаемое на вашем экране, состоит из пикселей. Каждый пиксель изображения имеет числовое значение, которое определяет цвет, который он должен отображать.
  Учитывая, что одно изображение может состоять из миллионов пикселей, мы говорим об огромном количестве информации!
  ☝️ вернуться к содержанию ☝️
  Где узнать больше о двоичном коде и информатике?
  Если вы хотите научиться программировать, вы также должны понимать, что происходит внутри вашего компьютера.
  Таким образом, если вы новичок в программировании, обязательно найдите время, чтобы ознакомиться с некоторыми основами информатики.
  Впрочем, никаких дополнительных навыков не требуется. Основы достаточно.
  Как только вы поймете, как работает компьютер внутри, научиться программировать будет намного проще.
  А когда вы знакомы с тем, как компьютер обрабатывает данные, вы также можете писать более качественный и эффективный код.
  Чтобы помочь вам начать изучение информатики, я собрал ниже свои любимые учебные пособия и курсы:
  1: Основы работы с компьютером (Codecademy)
  Основы работы с компьютером на Codecademy рассказывает о том, как работают компьютеры, важном оборудовании, способах устранения неполадок и многом другом. Курс
  «Основы работы с компьютером» является частью курса «Введение в ИТ». Если вы новичок в информатике и программировании, ознакомьтесь с полным учебным планом, чтобы найти еще больше полезных уроков и модулей.
  Вот еще один интересный курс Codecademy для вас:
  Двоичные коды и базовые значения — это быстрый курс для начинающих. Он знакомит вас с логикой баз и помогает понять, как различные базы работают на практике.
  Если вы еще не знакомы с Codecademy, прочитайте мой полный обзор Codecademy здесь.
  2: CS101 Bootcamp: Introduction to Computer Science & Software (Udemy)
  CS101 Bootcamp — это короткий, но интенсивный курс для начинающих по Udemy для изучения основ компьютерных наук.
  Чтобы пройти этот курс, вам не нужны технические знания в области компьютерных наук, поэтому он идеально подходит для начинающих.
  Если вы использовали смартфон или компьютер в прошлом, этого достаточно, чтобы начать этот быстрый двухчасовой курс.
  К концу курса вы поймете основы баз данных, мобильных приложений и программирования.
  Более того, вы даже сможете написать свои собственные базовые программы и приложения.
  Если вы не знакомы с Udemy, ознакомьтесь с моим полным обзором Udemy здесь.
  3: Информатика 101: Освоение теории программирования (Udemy)
  Информатика 101: Освоение теории программирования on — это всеобъемлющий курс информатики для начинающих.
  Если вы хотите овладеть теорией CS, что настоятельно рекомендуется для любого программиста, этот курс является идеальным выбором.
  К концу этого курса вы будете знакомы с тем, как работает двоичный код, и сможете анализировать и использовать различные алгоритмы.
  4: CS50’s Introduction to Computer Science (Гарвардский колледж)
  CS50’s Introduction to Computer Science из Гарвардского колледжа — мой любимый бесплатный курс по основам CS для начинающих. С более чем 2 000 000 студентов по всему миру (и это число продолжает расти), это один из самых популярных курсов информатики.
  Если вы хотите изучить информатику, разработку мобильных приложений и игр, бизнес-технологии и искусство программирования, CS50 — идеальное место для начала.
  Профессор отлично все объясняет, поэтому вы никогда не почувствуете, что остались позади.
  Вы попадете в лекционные залы Гарварда, где сможете просмотреть полнометражные видеоролики с лекциями и выполнить наборы упражнений, которые помогут вам применить то, что вы изучаете.
  5: Ускоренный курс информатики (YouTube)
  Ускоренный курс информатики — это бесплатный курс из 40 уроков для начинающих.
  Каждый урок длится около 10–15 минут и знакомит вас с такими важными основами, как:
  Булева логика
  Что такое двоичный код
  Как компьютеры вычисляют
  Регистры и оперативная память
  Основы программирования
  0
  2 и многое другое
  
  6: Основы работы с компьютером (Treehouse)
  Если вы спешите, Основы работы с компьютером в Team Treehouse — это идеальное введение в информатику.
  Всего за 55 минут вы изучите множество основ информатики, в том числе краткий урок по двоичному коду и тому, как работает двоичный код когда вы запускаете свои компьютерные программы.
  Также вы узнаете основы обработки данных, как работает память, что означает двоичный код в CS и как работают компьютерные программы.
  7: Введение в теоретическую информатику (Udacity)
  Введение в теоретическую информатику в Udacity — еще один из моих любимых.
  Этот бесплатный курс среднего уровня поможет вам углубить свое понимание алгоритмов и решения проблем.
  Кроме того, вы получите мощные инструменты для решения самых сложных алгоритмических задач на практике.
  ☝️ вернуться к содержанию ☝️
  Часто задаваемые вопросы: Как работает двоичный код?
  Что такое двоичная система счисления?
  Двоичная система счисления — это система счисления, в основе которой лежит число 2. В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, то есть 0 и 1.
  Как двоичный код работает в компьютерных программах?
  В компьютерных программах двоичные числа представлены только двумя символами или цифрами, то есть нулем «0» и одной «1». Любое числовое значение может быть представлено как двоичное значение, состоящее только из 0 и 1. Имея достаточное количество двоичного кода, мы можем представить любое желаемое значение и хранить миллионы и миллиарды битов данных, используя только эти два числа.
  Почему система счисления называется двоичной?
  «Би» на латыни означает «два». Поскольку в двоичной системе есть только два варианта, 0 и 1, одна цифра в двоичном числе может представлять только две разные вещи или значения. Все числа состоят из двух цифр 0 и 1.
  Что означает 11111111 в двоичном формате?
  11111111 равно 255 в десятичной системе счисления. Чтобы найти десятичный эквивалент в двоичном, последовательно делите 255 на 2, пока частное не станет равным 0. Затем вы можете получить двоичный эквивалент, записывая остаток на каждом шаге деления снизу вверх.
  ☝️ вернуться к содержанию ☝️
  Заключительные мысли: Что такое двоичный код и как работает двоичный код – Объяснение двоичного кода
  Надеюсь, вы все еще со мной!
  Я знаю, что эта тема несколько абстрактна, если вы новичок в информатике. И может быть трудно представить себе ситуацию, когда вам нужно знать, как работает двоичный код.
  Потому что правда такова:
  Когда вы пишете код и программы для своего компьютера, вы не имеете дело непосредственно с этими двоичными числами. Скорее всего, вы будете использовать язык программирования, который поможет вам выполнять работу проще и быстрее.
  Однако вы столкнетесь с тем, что могут сделать для вас все эти 1 и 0. Вы пишете и читаете текст, создаете и просматриваете изображения, а также смотрите видео и другие медиафайлы на своем компьютере.
  Двоичный код является основой всего, что делают компьютеры:
  Получение входных данных
  Хранение информации
  Обработка информации
  Получение выходных данных
  Неважно, насколько сложной или изощренной является компьютерная программа или система. вниз только 1 и 0.
  Знание того, как работает двоичный код и что означает двоичная система, поможет вам понять, как работают компьютеры, и как разработчику писать лучший код.
  Вот несколько статей по теме, которые могут оказаться полезными:
  10 мифов о кодировании, которые следует игнорировать
  этот пост о двоичном коде и о том, как работает двоичный код, полезен? Напишите мне в комментариях ниже!
  P. S. Поделитесь им с другими, чтобы они тоже могли узнать о двоичном коде. Спасибо!
  Удачного кодирования!
  – Микке
  Четыре типа двоичного кода и их использование
  Даже если вы не замечаете, различные типы двоичного кода используются во всех компьютерных приложениях.
  Компьютеры могут понимать и общаться только с использованием двоичной системы счисления (0 и 1).
  Но есть одно предостережение: существует не один тип двоичного кода.
  Давайте рассмотрим их в этой статье.
  Содержание
  Что такое двоичный код?
  Двоичный код — это любые данные, текст или компьютерные инструкции, представленные с использованием двухсимвольной системы. Эти два числовых символа — 0 и 1. Компьютеры и цифровые электронные устройства могут обмениваться данными только с помощью нулей и единиц. Например, текст в вашем мобильном приложении на английском языке, но есть фоновая система кодирования, которая переводит эти слова в двоичные числа для обработки компьютером.
  В этой статье вы узнаете о взвешенном коде , невзвешенном коде, двоично-десятичном коде, коде Excess-3, коде Грея, буквенно-цифровом коде и кодах обнаружения ошибок с использованием метода четности.
  Начнем с различных классификаций двоичных кодов.
  Типы двоичного кода
  Каждый из различных типов двоичного кода имеет определенные свойства и применение в компьютерах и цифровой электронике. Например, двоично-десятичный (BCD) код обеспечивает быстрое и эффективное преобразование десятичных чисел в двоичные.
  Four types of binary code:
  Weighted binary code
  Non-weighted binary code
  Alphanumeric code
  Error detection code
  Weighted binary code
  Weighted binary code is двоичный код, подчиняющийся системе позиционных весов. Это система, в которой каждой цифре соответствует цифра 9. 0017 удельный вес в зависимости от его положения.
  Двоичные веса
  Двоичные веса — это значения, присваиваемые двоичным числам в зависимости от их положения в двоичном коде. Они помогают легко преобразовывать двоичные числа в десятичные числа.
  Чтобы преобразовать 10110 в десятичную систему, рассмотрите веса этого двоичного кода.
  16 , 8 , 4 , 2 , 1
  Эти значения происходят от 2 в степени их двоичной позиции: 2 ⁴ , 2³ , 2² , 2¹ , 2⁰ , начиная со старшего бита (MSB) до младший значащий бит (LSB).
  Мы будем рассматривать только веса, соответствующие 1 в 10110, потому что 0 возвращают 0 после умножения. Теперь добавим веса. 2 + 4 + 16 = 22
  Вы можете проверить ответ на нашем двоично-десятичном калькуляторе.
  Двоично-десятичный код (BCD)
  Код BCD является примером взвешенного двоичного кода. Он также известен как 8421 код . В методе кодирования BCD каждая десятичная цифра представляется четырехбитным двоичным числом. Двоично-десятичный код позволяет нам легко преобразовывать десятичные числа в их двоичные эквиваленты.
  Мы можем представить 16 чисел, используя систему счисления BCD. (от 0000 до 1111). Однако используются только первые 10 комбинаций. Последние 6 кодовых комбинаций (от 1010 до 1111) являются недопустимыми и могут вызвать машинное исключение или неопределенное поведение в зависимости от компьютерной реализации арифметики BCD.
  Проверьте двоичные часы, чтобы увидеть классную реализацию двоично-десятичного двоичного кода.
  Вот таблица, показывающая систему BCD. Более продвинутые пользователи двоичного кода имеют эту таблицу в своей памяти.
  Decimal BCD
  0 0000
  1 0001
  2 0010
  3 0011
  4 0100
  5 0101
  6 0110
  7 0111
  8 1000
  9 1001
  Применение взвешенного двоичного кода ) код обеспечивает удобное отображение
  функций ввода/вывода в цифровых схемах
  Взвешенный двоичный код используется в сложных математических вычислениях
  Невзвешенный двоичный код
  Невзвешенный код используется для специальных приложений, где не требуется двоичный вес. Невзвешенный код не использует позиционные веса для преобразования двоичного кода в другие системы, такие как десятичная, шестнадцатеричная, восьмеричная или любая другая система. Примеры невзвешенного кода включают код избытка-3, код и код Грея .
  Код Excess-3
  Код Excess-3 также известен как код XS-3 . Код Excess-3 — это невзвешенный код, полученный из кода 8421 BCD. Каждое число в коде 8421 увеличивается на 9.0017 0011 для получения кода XS-3. 3 является десятичным эквивалентом 0011, отсюда и название XS-3.
  Вот таблица, показывающая, как код Excess-3 получается из кода 8421 BCD.
  Decimal BCD XS Code
  (+0011)
  0 0000 0011
  1 0001 0100
  2 0010 0101
  3 0011 0110
  4 0100 0111
  5 0101 1000
  6 0110 1001
  7 0111 1010
  8 1000 1011
  9 1001 1100
  Gray Code
  Gray code is a non-weighted code that is used as a unit distance code . Его нельзя использовать для любых арифметических операций, таких как сложение, вычитание, умножение и деление (булевы алгебраические операции). Код Грея реализует уникальную систему, в которой для каждого десятичного числа изменяется только один бит. Это обеспечивает выравнивание и синхронность, тем самым снижая частоту ошибок.
  Вот таблица, показывающая код Грея.
  5
  5
  50784 0101
  Decimal BCD Gray Code
  0 0000 0000
  1 0001 0001
  2 0010 0011
  3 0011 0010
  4 0100 0110
  0111
  6 0110 0101
  7 0111 0100
  8 1000 1100
  9 1001 1111
  Применение невзвешенного двоичного кода
  - Невзвешенные двоичные коды идеально подходят для обнаружения ошибок , поскольку они следуют организованной последовательности возрастания. 9&.
    Буквенно-цифровой код представляет собой как цифры, так и буквенные символы. Наиболее распространенными типами буквенно-цифрового кода являются EBCDIC и ASCII.
    EBCDIC
    EBCDIC означает Расширенный двоично-десятичный код обмена. Код EBCDIC — это 8-битный код, который в основном используется в мейнфреймах IBM и компьютерных операционных системах IBM среднего класса.
    ASCII
    ASCII означает Американский стандартный код для обмена информацией. Код ASCII — это 7-битный код, используемый в небольших компьютерах. Код ASCII представляет числа от 0 до 9, девяносто пять заглавных и строчных букв алфавита, знаки препинания и пробел. Всего ASCII кодирует 128 символов.
    Коды обнаружения ошибок (код четности)
    Когда данные или инструкции передаются в электронном виде, существует вероятность ошибок во время передачи данных в виде скремблирования или повреждения данных. Чтобы избежать этого, используются коды обнаружения ошибок.
    Код обнаружения ошибки добавляет к сообщению дополнительные данные перед отправкой, и это определяет, было ли сообщение повреждено во время передачи данных.
    Код четности — это код обнаружения ошибок, в котором к сообщению добавляется дополнительный бит (называемый битом четности), чтобы количество нулей и единиц было четным или нечетным в зависимости от типа четности.
    Преобразование двоичного кода онлайн
    Как мы видели в этой статье, тип двоичного кода, используемый компьютерами и электронными системами, может относиться к любой из этих четырех категорий: взвешенные, невзвешенные, буквенно-цифровые коды и коды обнаружения ошибок.
    Не забудьте использовать наш преобразователь двоичного кода в ascii для преобразования двоичного кода в текст или наоборот.
    Двоичный код | Объяснение двоичной системы
    Двоичный код (или двоичная система) вездесущ в компьютерных технологиях, и некоторые люди до сих пор помнят его со своих уроков математики. Этот код представляет сложные вещи только с двумя состояниями. Это часто трудно понять людям, которые знакомы только с десятичной системой и ее десятью цифрами. В то же время бинарный код имеет свои преимущества, и о нем также необходимо знать с технической точки зрения.
    Содержание
    1. Что такое двоичный код?
    2. История двоичной системы: от Лейбница до компьютерных систем
    3. Понимание двоичного кодирования: как работает компьютер?
    Что такое двоичный код?
    Большинство людей используют десятичную систему с десятью цифрами от 0 до 9. Чтобы выразить большое число, вы добавляете еще одну «позицию»: так что число больше, чем самая большая цифра в десятичной системе, 9, нуждается новая позиция: «1». Начиная с самого начала, мы получаем позицию 1 плюс первую цифру десятичной системы «0». Эти две цифры вместе отображаются как 10 или «десять». Двоичная система работает точно так же. Тем не менее, у вас есть только две цифры (или два состояния), доступные в соответствии с латинским префиксом «bi»: 0 и 1, вкл. и выкл., светлое и темное, истинное и ложное. Как и в десятичной системе, большие числа представляются с использованием большего количества позиций.
    Люди обычно знакомы с двоичной системой в контексте компьютеров, где все работает на единицах и нулях. Так хранятся данные и выполняются вычисления. Однако этот способ вычисления и представления информации также используется в других ситуациях. Всякий раз, когда мы получаем информацию через одно из двух состояний, это в основном двоичный код. Свет на электронном устройстве может сказать нам, работает ли оно, будучи выключенным (состояние 1) или включенным (состояние 2).
    Объединяя эти состояния включения/выключения вместе, вы можете передавать гораздо более сложную информацию. Например, система письма для слепых Брайля основана на двоичном коде. В этой системе каждый символ представлен сеткой из шести точек. Комбинации выпуклых точек (1/вкл) и плоских пробелов (0/выкл) представляют разные символы.
    История двоичной системы: от Лейбница до компьютерных систем
    Хотя двоичный код уже использовался в классической древности для передачи информации, двоичная система в том виде, в каком мы ее знаем сегодня, не была введена до конца 17 века, когда она был задуман Готфрид Вильгельм Лейбниц. Этот философ и математик (и де-факто ученый широкого профиля) искал метод преобразования логических терминов (т. е. истинных и ложных) в математическую систему и сделал это, используя систему единиц и нулей, используемую до сих пор.
    Несколькими десятилетиями ранее английский философ Фрэнсис Бэкон уже начал размышлять о том, как можно представить текст с помощью двоичного кода. Третий ученый, Джордж Буль , наконец, разработал булеву алгебру, основанную на двоичной системе, примерно через полтора века после Лейбница. Эта система логических операторов до сих пор очень важна в компьютерных науках.
    В 20 веке цифровая техника получила окончательное развитие, и были выпущены первые электронные счетные машины. Перед пионерами вычислительной техники стояла задача перевести числа и буквы в систему, которую могли понять компьютеры. Для этого был создан двоичный код, поскольку абстракции единиц и нулей могут быть переведены в физических состояний . Например, в электротехнике вы можете использовать 1, если есть напряжение, и 0, если напряжения нет.
    Перфокарты также используют двоичную систему для передачи информации. Эти карты могут представлять определенное количество символов с использованием отверстия или отсутствия отверстия. Это позволяет хранить информацию постоянно и при этом быть машиночитаемой. Перфокарты уже использовались до изобретения компьютеров, например, в ткацких станках и механических музыкальных машинах.
    На первый взгляд двоичный код и двоичная система кажутся синонимами. Однако, как только вы поймете, что такое код, вы увидите разницу. А код — это контролируемый перевод символов. Каждому символу в оригинале назначается отдельный символ или строка символов. Это позволяет конвертировать туда и обратно. Между тем, система автономна и не нуждается в сравнении с другой системой. Например, если вы выполняете вычисления в двоичной системе, вам не нужно обращаться к десятичной системе для получения результатов.
    Оба могут быть найдены в электронной обработке данных (EDP). Например, эту кодировку можно найти в Код ASCII . Все буквы латинского алфавита, а также некоторые другие символы могут быть представлены семью позициями и двумя состояниями (1 и 0). Однако, поскольку это не может представлять почти все символы в мире, вы также можете использовать UTF-8, который использует от одного до четырех 8-битных байтов.
    Понимание двоичного кодирования: как работает компьютер?
    Компьютерные системы распознают битов устройства и байтов. Бит — это позиция в коде, которая может быть либо 1, либо 0. Его имя представляет собой сочетание «двоичной цифры». Один байт — это восемь таких битов. Компьютеры — это в основном вычислительные машины, которые работают с этими единицами, как калькулятор. Для выполнения расчета десятичные числа переводятся в двоичную систему.
    В байтах десятичное число 5 можно представить следующим образом: 00000101 . Ведущие нули в начале двоичного числа не влияют на значение и только обеспечивают сохранение фиксированного формата с восемью позициями.
    Как и в десятичной системе, каждая цифра соответствует степени . Однако, в отличие от нашей обычной системы, которая использует основание 10 для вычислений, двоичная система использует основание 2. Первая позиция соответствует 2 ⁰ , второй до 2 ¹ , третий до 2 ² и так далее. A byte corresponding to the decimal number 23 can be read as follows:
    2 ⁷
    2 ⁶
    2 ⁵
    2 ⁴
    2 ³
    2 ²
    2 ¹
    2 ⁰
    0
    0
    0
    1
    0
    1
    1
    1
    Таким образом имеем (десятичное число): 2 ⁴ + 2 ² + 2 ¹ + 2 ⁰ = 16 + 4 + 2 + 1 = 23
    9000 в десятичной системе: 1100 + 1010 = 10110. Что происходит при расчете? Для простоты сложение может быть построено так же, как и в письменном расчете. Вы считаете справа налево.
    - 0 + 0 = 0
    - 0 + 1 = 1
    - 1 + 0 = 1
    - 1 + 1 = 0. Перенись 1
    - 03.09.19
    - Веб -разработка
    33930202020211111311111111111111111111111111111311111111111311111113111111311111311113111311131113113111131113111311131
  311311311311311311107
2. .

Статьи по теме

ASCII: объяснение и примеры

06.04.2022
Ноу-хау

Каждый день мы работаем с текстом на ПК, смартфонах и планшетах и ожидаем, что перед нами на мониторе появятся буквы, цифры и символы. Дело в том, что за этой повседневной функцией стоит многолетняя система кодирования. С 19В 60-х годах ASCII определил, как компьютеры интерпретируют наш ввод. Мы объясняем, как работает код ASCII.

ASCII: объяснение и примеры

UTF-8: сетевой стандарт

27.02.2019
Создание сайта

UTF-8 — это метод кодировки символов Unicode, который, как утверждается, охватывает все современные языки обработки данных. Формат значительно повлиял на международное цифровое общение. Но что именно означает «UTF-8»? А что особенного в UTF-8 в наборе символов Unicode? Здесь вы можете узнать, на какой структуре основано кодирование, и какие байты разрешены в стандарте…

UTF-8: сетевой стандарт

Спецификация: что такое метка порядка байтов?

31.10.2019
Веб-разработка

Как информация на самом деле читается? Некоторым ответ кажется очевидным – слева направо. Однако для представителей многих культур противоположное направление считается нормальным. Все это условности, которые компьютеры не понимают. Итак, в каком порядке следует читать байты? Метка порядка байтов (BOM) решает эту проблему.

Спецификация: что такое метка порядка байтов?

Шестнадцатеричная система счисления

04.11.2021
Ноу-хау

Что такое шестнадцатеричные числа и почему они являются одними из самых важных обозначений в ИТ? В вычислительной технике шестнадцатеричная система используется для представления больших чисел как можно меньшим числом цифр. Продолжайте читать, чтобы узнать об основах системы счисления и о том, в чем разница между шестнадцатеричными числами и двоичными или десятичными числами.

Шестнадцатеричная система

Что такое двоичный код? (с картинками)

Джереми Лаукконен

Дата последнего изменения: 13 сентября 2022 г.

Двоичный код позволяет упростить представление информации. В двоичном коде всего две цифры: единица и ноль. Типичные двоичные коды будут использовать строки из единиц и нулей для представления букв, цифр или других понятий. Примером могут служить двоичные представления американского стандартного кода для обмена информацией (ASCII), где каждая строка из восьми символов может представлять любой из 256 различных вариантов. Двоичные коды часто используются в вычислительной технике и другой электронике, хотя они также присутствовали на протяжении всей истории человечества в других формах.

Двоичный код использует только единицы и нули для базового компьютерного программирования.

Чтобы двоичный код представлял текст, инструкции компьютерного процессора или другую информацию, он должен быть разделен на отдельные строки. Их часто называют битовыми строками, и они могут быть либо фиксированными, либо динамическими по длине. В этом контексте бит относится к каждой двоичной цифре, поэтому строка из восьми символов двоичного кода будет содержать восемь битов информации. Используя различные кодировки или наборы символов, такие битовые строки могут представлять множество разных вещей.

Одной из форм двоичного кода является шрифт Брайля, в котором для представления букв или цифр используются группы из шести точек.

Компьютеры и другая электроника используют так называемые триггерные схемы для представления информации в двоичном коде. Эти схемы могут различаться по конструкции, хотя обычно они должны существовать в двух дискретных состояниях. В вычислениях схема триггера обычно представляет собой единицу с положительным напряжением и ноль без напряжения. Ранние примеры этой конструкции включали использование громоздких электронных ламп, а более поздние прорывы привели к таким элементам, как транзисторы и микрочипы. Такие компоненты, как динамическая память с произвольным доступом (DRAM), могут использовать триггерные схемы для хранения двоичных кодов.

Сложные формы данных также могут храниться в двоичном коде, часто в виде дискретных строк по восемь битов каждая. Двоичный файл может быть чем угодно, от простого текстового документа до исполняемой программы, а содержащиеся в нем данные будут представлены теми же единицами и нулями, что и любой двоичный код. Поскольку двоичный файл может содержать изображения, звуки или практически любую другую информацию, они обычно включают заголовок, который компьютер может использовать для целей идентификации.

Двоичные коды существуют гораздо дольше, чем современные компьютеры, и примеры данных, представленных двумя дискретными состояниями, встречаются на протяжении большей части истории человечества. Древняя концепция фэн-шуй использует несколько бинарных наборов в виде символов яо, каждый из которых представляет инь или ян. Нигерийское племя также использовало двоичный набор из круга или двух линий для представления информации на протяжении тысячелетий. Другой формой двоичного кода, не связанной с вычислениями, является шрифт Брайля, в котором для представления букв или цифр используются группы из шести точек. Каждая точка может находиться в одном из двух состояний: приподнятом или плоском, чтобы слепые могли их прочитать.

Примером могут служить двоичные представления американского стандартного кода для обмена информацией (ASCII), где каждая строка из восьми символов может представлять любой из 256 различных вариантов.

Начало работы с двоичным кодом — McAuliffe-Shepard Discovery Center

01 апреля 2020 г. 01 апреля 2020 г.

/ Гость

Из этого введения в кодирование вы узнаете, как компьютеры хранят информацию в числовом формате, и проверьте свои навыки чтения и записи в двоичном формате!

01001000 01100101 01101100 01101100 01101111 00100001

Этот набор чисел выглядит как случайный беспорядок? Хотите верьте, хотите нет, но эти цифры содержат специальное сообщение для вас!

Хотите научиться читать? Как и любой код, для расшифровки смысла сообщения нужен только правильный ключ…

Код — это система общения, в которой слова, буквы или символы заменяются ДРУГИМИ словами, буквами, символами и даже изображениями. Смысл сообщения скрыт, если читатель не знает, что представляет собой каждый фрагмент кода. Чтобы понять закодированное сообщение, вам нужно выполнить некоторый перевод: перейти от того, что в сообщении говорится , к тому, что это означает .

Например, если я дам вам следующий код:

вы можете читать и писать некоторые слова, используя только эти фигуры.

Вы бы написали КОМНАТА так:

И вы бы написали ДВЕРЬ так:

Попробуйте!

Используйте формы или символы, чтобы придумать свой собственный код и использовать его для написания своего имени. Чтобы сделать еще один шаг, попробуйте использовать цвета для обозначения верхнего и нижнего регистра.

В мире существует множество видов кода. Например, шрифт Брайля использует систему выпуклых выступов для обозначения букв, что позволяет слепым людям считывать информацию с поверхности кончиками пальцев. Азбука Морзе использует точки и тире — электронные сигналы, которые очень короткие или немного длиннее, если вы их слышите, — для написания слов.

Компьютеры используют систему, называемую двоичным кодом , для отправки, получения и хранения информации.

Слово «двоичный» означает, что что-то имеет ДВА варианта. В двоичном коде сообщения передаются с помощью комбинации всего двух символов: цифры 1 и цифры 0.

Провода передают информацию

через компьютер

в виде электричества.

Когда двоичный код передается в виде последовательности 1 и 0, каждая цифра в последовательности называется бит . 8 бит подряд называется байт .

Компьютер, который может понимать только сообщения, состоящие из одной цифры, например, 1 = включено и 0 = выключено , имеет емкость обработки одного бита. Этот компьютер может отправлять и получать только два возможных сообщения: либо 1 , либо 0 . Он может выполнять только две команды.

Компьютер, который понимает двузначные сообщения, имеет двухбитную вычислительную мощность. Теперь есть ЧЕТЫРЕ возможных сообщения, которые он может отправлять и получать: 00 , 01 , 10 и 11 . Обратите внимание, что добавление всего лишь одного бита к последовательности удвоило вычислительную мощность компьютера.

Если мы добавим еще одну цифру — отправку трехбитных сообщений — компьютер теперь сможет понять ВОСЕМЬ возможных сообщений: 000 , 001 , 010 , 011 , 100 19017 100 , 110 и 111 . Мы снова удвоили мощность обработки.

Увеличение числа битов позволяет компьютеру выполнять больше и более сложные команды.

Большинство компьютеров отправляют и получают сообщения, используя 8-битный двоичный код — каждая буква и знак препинания представлены последовательностью единиц и нулей длиной 8 цифр. Чтобы прочитать код в 8-битном двоичном коде, вам нужен только ключ:

Помните длинную серию единиц и нулей в начале этого урока?

01001000 01100101 01101100 01101100 01101111 00100001

Это сообщение записано в 8-битном двоичном коде, и приведенная выше таблица является ключом, который нам нужен для его расшифровки. Мы можем использовать таблицу для перевода кода из групп 1 и 0 в буквы, которые они представляют. We can see from the key that:

01001000 =

01100101 =

01101100 =

01101111 =

или

00100001 =

Сообщение 01001000 01100101 01101100 01101100 01101111 00100001 в двоичном коде переводится как H e l l o ! на английском языке.

Для компьютера каждый символ этого сообщения будет равен 8 битам — или 1 байту — памяти. Все сообщение длиной 6 символов потребует 8 x 6 = 48 байтов (6 бит) памяти.

Напишите свое имя в двоичном формате

Используйте двоичный код, чтобы написать свое имя, представляя каждую букву серией затемненных и пустых кружков вместо единиц и нулей. Затемненный кружок представляет 1, а пустой кружок представляет 0.

нажмите здесь, чтобы просмотреть рабочий лист

Сделайте двоичный браслет или ожерелье

Создайте бумажный браслет со своими инициалами в двоичном формате и носите свои знания в области кодирования на всеобщее обозрение! Чтобы сделать еще один шаг, нанижите вместе настоящие бусины на кусок шнура или ершик для чистки труб. Решите, какой цвет бусин представляет собой 1, а какой — 0 (аналогично темным и пустым кружкам в упражнении выше), и напишите свое полное имя, используя бусины. Вы даже можете добавить разные цвета для верхнего и нижнего регистра.

нажмите здесь, чтобы просмотреть рабочий лист

Какие еще объекты можно использовать для отправки сообщений в двоичном виде? На этом веб-сайте мы нашли пример, в котором слова пишутся с помощью гороха и моркови!

Участвуете дома? Поделись фотографией своей работы!

Отметьте нас на

Facebook , Instagram (@msdiscoverycenter) и Твиттер (@msdiscoverycntr)

01 апреля 2020 г. / гостевой пользователь/ / Источник

Модуль дистанционного обучения, STEM-деятельность на дому

дистанционное обучение, дистанционное обучение, онлайн-обучение, STEM, обучение STEM, STEM в действии, кодирование, двоичный код, технология

Гость

блестящих проектов с двоичным кодом для детей

Коллин Розенталь Размещено: 24.07.2022 24.07.2022 Обновлено: 24.07.2022

Могут ли дети выучить двоичный код? Они точно могут! Давайте изучим и поймем основы двоичного кода. Двоичный код — это способ, с помощью которого компьютер понимает, что ему нужно делать, используя код для чтения и передачи информации. Вы можете увидеть в приветственном сообщении ниже, как буквы представлены в двоичном коде.

ДВОИЧНЫЙ БЛЕСТЯЩИЙ!

Отказ от ответственности: эта статья может содержать комиссионные или партнерские ссылки. Как партнер Amazon я зарабатываю на соответствующих покупках.
Не видите наши видео? Отключите все блокировщики рекламы, чтобы наш видеопоток был виден. Или посетите наш канал на YouTube, чтобы узнать, загружено ли туда видео. Мы потихоньку загружаем наши архивы. Спасибо!

WELCOME TO BINARY

01010111 01000101 01001100 01000011 01001111 010001101 01000101
01010100 01001111 01000010 01001001 01001110 01000001 01010010 01011001

Что такое двоичный код?

Ну, начнем с самого слова. Би означает два. Бинар — это нечто, состоящее из 2-х частей. В случае кода bi относится к нулям и единицам, которые являются единственными двумя числами, составляющими двоичный код. Каждая появляющаяся последовательность из восьми цифр напрямую связана с буквой в алфавите. Например, 01000001 — это двоичная заглавная буква А.

Давайте представим это как игру красный-зеленый свет. Мы знаем, что когда мы слышим «красный свет», мы останавливаемся, а когда мы слышим «зеленый свет», мы идем — компьютер понимает различные последовательности чисел и преобразует их в язык. Вы можете найти похожие коды из двух частей и в других областях! Азбуку Морзе можно использовать, отправляя длинные и короткие световые или звуковые сигналы, которые можно перевести на язык. Азбука Морзе использовалась много до того, как появилась возможность озвучивать радиосигналы. Другим примером является шрифт Брайля, используемый слабовидящими. Буквы, цифры и знаки препинания представлены на странице приподнятыми и опущенными выступами.

Как работает двоичный код?

Откуда мы знаем, что обозначают нули и единицы? В таблице ниже приведен основной перевод алфавита в двоичном коде для заглавных букв, строчных букв и цифр от одного до десяти.

Мы можем использовать эту таблицу, чтобы проводить всевозможные забавные мероприятия с нашими детьми дома или с учениками в школе. Я включил пакет с некоторыми готовыми, минимальными подготовительными действиями, чтобы практиковать этот увлекательный код с детьми. Есть 5 занятий, так что вы можете легко включить их в неделю занятий по программированию! Отличная идея для летнего лагеря STEM!

ДВОИЧНЫЙ КОД ПРОЕКТ ИДЕИ ДЛЯ ДЕТЕЙ

Двоичный код для печати

Для некоторых из этих действий с двоичным кодом требуются рабочие листы для печати. Просто введите свой адрес электронной почты в форму, чтобы разблокировать печатную форму. Печатная форма идеально подходит для классной комнаты или лагеря STEM.

Напишите и раскрасьте свое имя в двоичном формате

Предложите детям выбрать 2 цвета — они могут использовать мелки, цветные карандаши или фломастеры! Раскрасьте два прямоугольника, помеченные цифрами 0 и 1, — это поможет им легко ориентироваться во время работы. Затем попросите их написать свое имя сбоку распечатанной таблицы. Каждая буква должна соответствовать строке в таблице. Используя таблицу двоичного алфавита, заполните нули и единицы, соответствующие каждой букве вашего имени. Наконец, раскрасьте коробки.

Изготовление браслета с двоичным кодом

Для этого задания нам понадобятся бусины трех цветов и ершик для труб. Как и в первом упражнении, у нас будет код и цвет детей, но на этот раз только их инициалы. Теперь, когда они знают код своих инициалов, попросите их выбрать бусинки для обозначения нулей и единиц. Не волнуйтесь, если ваши бусины не соответствуют цветам ваших маркеров — есть круги, которые они могут раскрасить, чтобы представить бусины, или они могут просто поместить бусину в каждый круг, чтобы они знали, что есть что. Есть три круга: нули, единицы и пробелы.

Загните один конец ершика, чтобы шарики не соскальзывали во время работы. Я начал и закончил свой браслет бусинкой-пространством, чтобы показать разделение. Просто нанижите бусины в том порядке, в котором вы написали свой код инициалов. Поместите пробел между каждой буквой. Когда вы закончите, вы можете скрутить два конца вокруг друг друга, чтобы завершить браслет.

Двоичные компьютерные шутки

Знаете, что получится, если скрестить жука и компьютер? Используйте свою таблицу, чтобы перевести двоичный код и узнать кульминацию! Есть две шутки для детей, чтобы перевести.

Секретное сообщение в двоичном коде

Объедините детей в пары и попросите их написать секретное сообщение в двоичном коде. Когда они закончат, они могут поменяться со своим партнером и посмотреть, смогут ли они перевести сообщение. Я предлагаю, чтобы дети написали свое сообщение на другом листе бумаги, чтобы у них была простая ссылка, пока они пишут свой код.

Binary Scavenger Hunt

Попросите детей перевести подсказки, а затем найти предметы дома или в классе!

Быстрая и простая минимальная подготовительная неделя программирования! Закрепление кода в течение недели поможет детям действительно понять, как нули и единицы представляют разные буквы. Хотите знать, как еще вы могли бы включить этот код? А как насчет списков правописания? Если вы заставляете своих детей каждую неделю записывать слова, которые они пишут, почему бы не перевести их в код — еще лучше, если у вас есть имена собственные, им придется помнить, что прописные и строчные буквы представлены по-разному.

2 ⁷	2 ⁶	2 ⁵	2 ⁴	2 ³	2 ²	2 ¹	2 ⁰
0	0	0	1	0	1	1	1

Виды двоичных кодов

Двоичный код это в информатике

Примеры двоичных чисел [ править | править код ]

Пример «доисторического» использования кодов [ править | править код ]

Примеры двоичного кода

Зачем нужен двоичный код

Виды двоичных кодов

1. Введение

5. Бит и байт

Двоичные коды — CoderLessons.com

Преимущества двоичного кода

Классификация двоичных кодов

Взвешенные коды

Невзвешенные коды

Код избытка-3

пример

Серый код

Применение кода Грея

Двоичный код (BCD)

Преимущества кодов BCD

Недостатки кодов BCD

Буквенно-цифровые коды

Коды ошибок

Разновидности и длина двоичного кода. Алгоритм считывания двоичного кода

Как составляется двоичная форма записи?

Виды двоичных кодов

Беззнаковый двоичный код

Прямые целые знаковые коды

Знаковый обратный ключ

Знаковый дополнительный код двоичного числа

Код Грея

Код Грея-Экспресс

Представление дробного числа в двоичном ключе с фиксированной запятой

Представление двоичного кода с плавающей запятой

Это интересно

кодировка — Разница между двоичным и байт кодом?

Что такое двоичный код

Примеры двоичного кода

Зачем нужен двоичный код

Виды двоичных кодов

Что такое двоичный код? Как это работает? (Объяснение двоичного кода)

Содержание

Зачем вам понимать, как работает двоичный код?

Что такое двоичный код?

Что означают все 1 и 0?

Как компьютеры хранят данные?

Хранение данных в битах: простой пример

Как работает двоичный код?

Знакомство с десятичной системой счисления

Как понимать двоичную систему счисления?

Как «расшифровать» двоичное число? Простой двоичный пример

Представление текста в двоичном коде

Представление изображений и графики в двоичном коде

Где узнать больше о двоичном коде и информатике?

1: Основы работы с компьютером (Codecademy)

2: CS101 Bootcamp: Introduction to Computer Science & Software (Udemy)

3: Информатика 101: Освоение теории программирования (Udemy)

4: CS50’s Introduction to Computer Science (Гарвардский колледж)

5: Ускоренный курс информатики (YouTube)

6: Основы работы с компьютером (Treehouse)

7: Введение в теоретическую информатику (Udacity)

Часто задаваемые вопросы: Как работает двоичный код?

Заключительные мысли: Что такое двоичный код и как работает двоичный код – Объяснение двоичного кода

Четыре типа двоичного кода и их использование

Что такое двоичный код?

Типы двоичного кода

Four types of binary code:

Weighted binary code

Двоичные веса

Двоично-десятичный код (BCD)

Применение взвешенного двоичного кода ) код обеспечивает удобное отображение

Невзвешенный двоичный код

Код Excess-3

Gray Code

Применение невзвешенного двоичного кода

EBCDIC

ASCII

Коды обнаружения ошибок (код четности)

Преобразование двоичного кода онлайн

Двоичный код | Объяснение двоичной системы