НОУ ИНТУИТ | Лекция | Двоичные числа и двоичная арифметика
Аннотация: Рассматривается двоичная система счисления как частный случай позиционной системы и основные правила двоичной арифметики.
Ключевые слова: вес, целое число, запись, аналогия, выражение, логический, основание, связь, восьмеричная система счисления, обратный код, дополнительный код, прямой, система счисления, сложение, вычитание
Принцип представления чисел в позиционных системах счисления
Позиционной называется система счисления, в которой вес разряда числа определяется его позицией в записи числа [1].
Вспомним нашу привычную десятичную систему счисления, в которой мы с детства производим все расчеты. Уже в начальной школе мы привыкли к терминам «единицы», «десятки», «сотни», «тысячи», «десятые», «сотые», «тысячные» и не задумываемся над тем, что они означают вес разряда, выраженный в виде числа, равного , где — целое число. Например, число 125, 46 можно представить в виде суммы:
Например, число 125, 46 можно представить в виде суммы:
сотни десятки единицы десятые доли сотые доли
Аналогично любое число в десятичной системе счисления можно представить в виде подобной суммы:
где — количество знаков в целой части числа, — количество знаков в дробной части числа, — вес -го разряда, — весовой коэффициент для -го разряда числа.
Количество возможных вариантов значения коэффициента в десятичной системе счисления равно , поскольку для записи чисел в ней используются десять знаков — арабские цифры «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9».
Основание системы счисления — это число, равное количеству знаков, которые используются в этой системе для записи чисел.
Для числа в системе счисления с основанием выражение (11.1) преобразуется к виду:
| Название системы счисления | Основание системы счисления | Знаки, использующиеся для записи чисел |
|---|---|---|
| Двоичная | 2 | 0, 1 |
| Троичная | 3 | 0, 1, 2 |
| Четверичная | 4 | 0, 1, 2, 3 |
| … | … | … |
| Восьмеричная | 8 | |
| … | … | … |
| Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| … | … | … |
| Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
| … | … |
Запись двоичного числа, как будет показано ниже, как правило, довольно длинна и громоздка, поэтому для более короткой записи двоичных чисел применяются восьмеричные и шестнадцатеричные числа. Выбор именно этих систем обусловлен тем, что их основания равны целой степени числа 2. Основание восьмеричной системы , а основание шеснадцатиричной системы — это . Для записи шестнадцатеричных чисел арабских цифр не хватает, поэтому используются первые шесть заглавных букв латинского алфавита.
Итак, далее мы подробно рассмотрим именно эти позиционные системы — двоичную, восьмеричную, шестнадцатеричную и их связь с привычной нам десятичной системой счисления.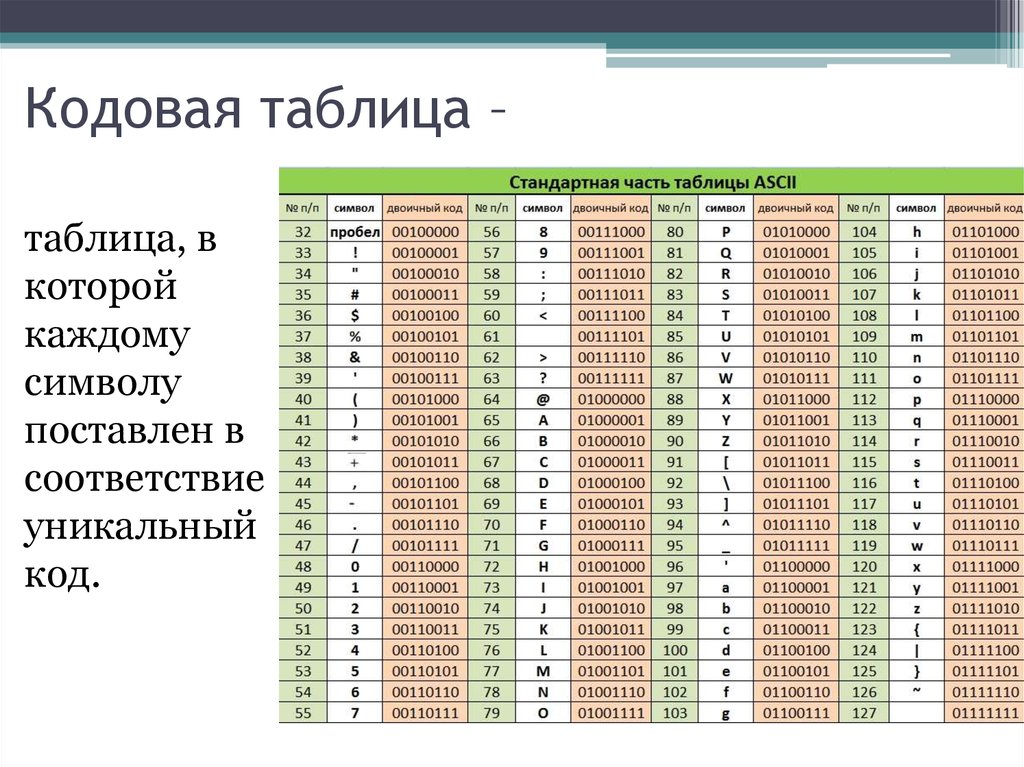
Приведем примеры записи чисел в указанных системах и найдем их десятичные эквиваленты по формуле (11.2).
Для двоичного числа:
Здесь и далее будем придерживаться следующего правила: числа в двоичной, восьмеричной и шестнадцатеричной системах записываются с указанием основания, десятичные — без этой записи.
Для восьмеричного числа:
Для шестнадцатеричного числа:
Из рассмотренных примеров видно, что общая формула (11.2) может использоваться для перевода числа из системы счисления с любым основанием в десятичную.
Перевод чисел из одной системы счисления в другую
Перевод из десятичной системы в любую другую. Перевод целых чисел
Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).
| a) | б) | в) |
Проверка:
- в двоичном коде: ;
- в восьмеричном коде ;
- в шестнадцатеричном коде — .
В рассмотренном примере при переводе вместо коэффициента используется его десятичный эквивалент в соответствии с таблицей 11. 2.
2.
Перевод из двоичной системы в шестнадцатеричную (восьмеричную)
Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.
Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы (табл. 11.2).
| Двоичная группа | Шестнадцатеричный знак | Десятичный эквивалент | Двоичная группа | Восьмеричный знак |
|---|---|---|---|---|
| 0000 | 0 | 0 | 000 | 0 |
| 0001 | 1 | 1 | 001 | 1 |
| 0010 | 2 | 2 | 010 | 2 |
| 0011 | 3 | 3 | 011 | 3 |
| 0100 | 4 | 4 | 100 | 4 |
| 0101 | 5 | 5 | 101 | 5 |
| 0110 | 6 | 6 | 110 | 6 |
| 0111 | 7 | 7 | 111 | 7 |
| 1000 | 8 | 8 | ||
| 1001 | 9 | 9 | ||
| 1010 | A | 10 | ||
| 1011 | B | 11 | ||
| 1100 | C | 12 | ||
| 1101 | D | 13 | ||
| 1110 | E | 14 | ||
| 1111 | F | 15 |
- перевод в шестнадцатеричную систему:
- перевод в восьмеричную систему:
Перевод из шестнадцатеричной (восьмеричной) системы в двоичную
Обычно программы в машинных кодах записаны в шестнадцатеричной системе счисления, реже — в восьмеричной. При необходимости отдельные числа такой программы записываются в двоичном коде, например, при рассмотрении форматов регистров, кодов операции команд и т.п. В этом случае нужен обратный перевод из шестнадцатеричной (восьмеричной) системы счисления в двоичную по следующему правилу.
Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).
Примеры:
- intuit.ru/2010/edi»>для шестнадцатеричного числа: ;
- для восьмеричного числа: .
Как показано в примерах, крайние нули слева и справа при желании можно не писать, но такое сокращение делается уже после перевода в двоичную систему.
Глава 31. Двоичная система исчисления . Введение в электронику
ЦЕЛИ
После изучения этой главы студент должен быть в состоянии:
• Описать двоичную систему счисления.
• Перечислить значения разрядов для каждого бита двоичного числа.
• Преобразовывать двоичные числа в десятичные.
• Преобразовывать десятичные числа в двоичные.
• Преобразовывать десятичные числа в двоично-десятичный код.
• Преобразовывать числа в двоично-десятичном коде в десятичные.
Система счисления — это не более, чем код.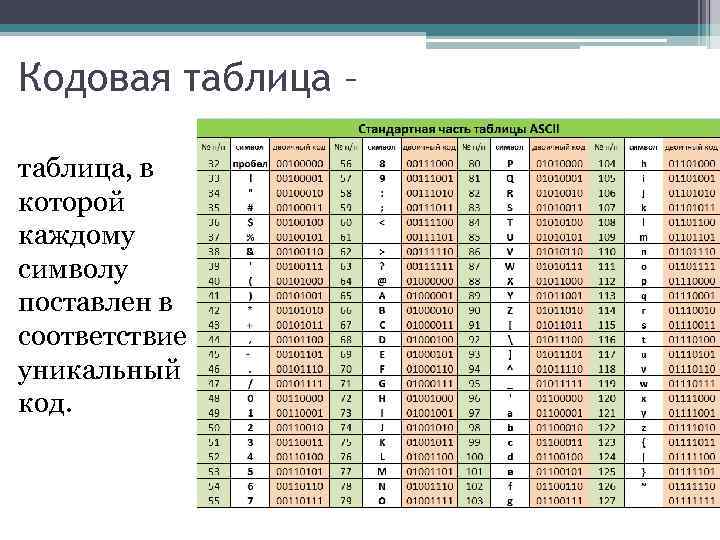 Для каждой отдельной величины существует приписанный ей символ. Когда код известен, можно выполнять вычисления. Это возможно с помощью арифметики и высшей математики.
Для каждой отдельной величины существует приписанный ей символ. Когда код известен, можно выполнять вычисления. Это возможно с помощью арифметики и высшей математики.
Простейшей системой счисления является двоичная. Двоичная система содержит только две цифры — 0 и 1. Эти цифры имеют такое же значение, как и в десятичной системе счисления.
Двоичная система счисления используется в цифровых и микропроцессорных цепях благодаря ее простоте. Двоичные данные представляются двоичными цифрами, называемыми битами. Термин бит означает двоичная цифра (разряд) (binary digit).
31-1. ДВОИЧНЫЕ ЧИСЛА
Десятичная система счисления называется системой с основанием 10, поскольку она использует десять цифр от 0 до 9. Двоичная система — это система с основанием два, поскольку она использует две цифры, 0 и 1. Положение 0 или 1 в двоичном числе показывает их значение в числе и называется значением разряда или его весом. Значения разрядов двоичного числа увеличиваются как степени 2.
Значения разрядов двоичного числа увеличиваются как степени 2.
Счет в двоичной системе начинается с чисел 0 и 1. Как и в десятичной системе счисления, каждая двоичная цифра отличается от предыдущей на единицу. Сумма единицы и нуля дает единицу, а сумма двух единиц дает нуль, и при этом прибавляется единица в старшем разряде. На рис. 31-1 показана последовательность двоичных чисел, образованная по описанному алгоритму.
Рис. 31-1. Десятичные числа и эквивалентные двоичные числа.
Для определения наибольшего значения, которое может быть представлено данным количеством разрядов с основанием 2, используйте следующую формулу:
Наибольшее число = 2n — 1,
где n — число битов (или число использованных значений разрядов).
ПРИМЕР: два бита могут быть использованы для счета от 0 до 3, так как
2n — 1 = 22 — 1 = 4–1 = 3.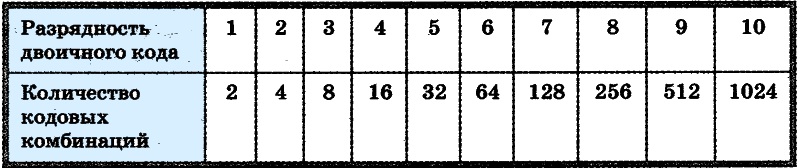
Четыре бита необходимы для счета от 0 до 15, так как
2n — 1 = 24 — 1 = 16 — 1 = 15.
31-1. Вопросы
1. В чем преимущество двоичной системы счисления перед десятичной при использовании в цифровых цепях?
2. Как определить наибольшее значение двоичного числа при заданном числе разрядов?
3. Каково наибольшее значение двоичного числа с:
а. 4 битами,
б. 8 битами,
в. 12 битами,
г. 16 битами.
31-2. ПРЕОБРАЗОВАНИЕ ДВОИЧНЫХ ЧИСЕЛ В ДЕСЯТИЧНЫЕ И НАОБОРОТ
Как установлено, двоичное число представляет собой число с весом каждого разряда. Значение двоичного числа может быть определено суммированием произведений каждой цифры на вес ее разряда. Метод вычисления двоичного числа показан на следующем примере:
Метод вычисления двоичного числа показан на следующем примере:
ПРИМЕР:
Число 45 является десятичным эквивалентом двоичного числа 101101.
Дробные числа также могут быть представлены в двоичной форме путем размещения двоичных цифр справа от двоичной запятой, так же как и десятичные цифры размещаются справа от десятичной запятой. Все цифры справа от запятой имеют вес, представленный отрицательными степенями 2 или дробными значениями разрядов.
Степень 2 ∙ Значение разряда
25 = 32
24 = 16
23 = 8
22 = 4
21 = 2
20 = 1
десятичная запятая
2-1 = 1/21 = 1/2 = 0,5
2-2 = 1/22 = 1/4 = 0,25
2-3 = 1/23 = 1/8 = 0,125
2-4 = 1/24 = 1/16 = 0,0625
ПРИМЕР: Определить десятичное значение двоичного числа 111011,011.
При работе с цифровым оборудованием часто бывает необходимо преобразовывать числа из двоичной системы в десятичную, и наоборот. Наиболее популярный способ преобразования десятичных чисел в двоичные — это последовательное деление десятичного числа на 2, с записью остатка после каждого деления. Остатки, взятые в обратном порядке, образуют двоичное число.
ПРИМЕР: Преобразовать 11 в двоичное число последовательным делением на 2. (Самый Младший Разряд).
(1/2 = 0 означает, что 1 не делится на 2, так что 1 является остатком). Десятичное число 11 равно 1011 в двоичной системе.
Этот процесс может быть упрощен путем записи чисел упорядоченным образом, как это показано на примере преобразования 25 в двоичное число.
ПРИМЕР:
Десятичное число 25 равно двоичному числу 11001. Дробные числа преобразовываются по другому: число умножается на 2 и целая часть записывается как двоичная дробь.
Дробные числа преобразовываются по другому: число умножается на 2 и целая часть записывается как двоичная дробь.
ПРИМЕР: Преобразовать десятичную дробь 0,85 в двоичную дробь последовательным умножением на 2.
Умножение на 2 продолжается до тех пор, пока не будет достигнута необходимая точность. Десятичная дробь 0,85 равна 0,110110 в двоичной форме.
ПРИМЕР: Преобразовать десятичное число 20,65 в двоичное число. Разделите 20,65 на целую часть 20 и дробную 0,65 и примените описанные выше методы.
Десятичное 20 — двоичному 10100
и
Комбинируя два числа, получим 20,6510 = 10100,10100112.
Это 12-разрядное число является приближенным, потому что преобразование дроби было прервано после получения 7 разрядов.
31-2. Вопросы
1. Чему равно значение каждого разряда 8-разрядного двоичного числа?
2. Чему равно значение каждого разряда для 8 разрядов правее десятичной точки?
3. Преобразуйте следующие двоичные числа в десятичные:
а. 1001;
б. 11101111;
в. 11000010;
г. 10101010,1101;
д. 10110111,0001.
4. В чем состоит процесс преобразования десятичных чисел в двоичные?
5. Преобразуйте следующие десятичные числа в двоичные:
а. 27;
б. 34,6;
в. 346;
г. 321,456;
д. 7465.
31-3. КОД 8421
Код 8421 — это двоично-десятичный код (ДДК), состоящий из четырех двоичных разрядов.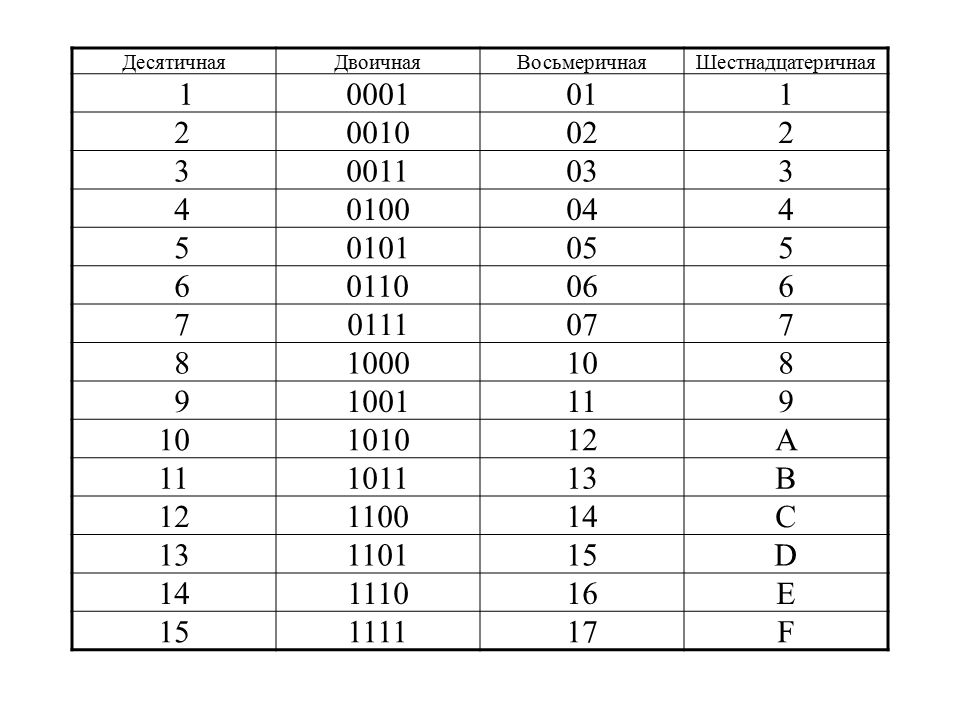 Он используется для представления цифр от 0 до 9. Обозначение 8421 относится к двоичному весу 4 разрядов.
Он используется для представления цифр от 0 до 9. Обозначение 8421 относится к двоичному весу 4 разрядов.
Степени 2: 23 22 21 20
Двоичный вес: 8 4 2 1
Основным достоинством этого кода является то, что он допускает легкое преобразование из десятичной формы в двоичную, и наоборот. Поэтому двоично-десятичный код используется всегда, если не оговорено другое.
Каждая десятичная цифра (от 0 до 9) представляется двоичной комбинацией следующим образом:
Хотя с помощью четырех двоичных разрядов можно представить 16 чисел (24), шесть кодовых комбинаций для чисел, больших 9 (1010,1011,1100, 1101, 1110 и 1111), в коде 8421 не используются.
Для того чтобы выразить любое десятичное число с помощью кода 8421, замените каждую десятичную цифру соответствующим 4-разрядным кодом.
ПРИМЕР: Преобразовать следующие десятичные числа в двоично-десятичный код: 5, 13, 124, 576, 8769.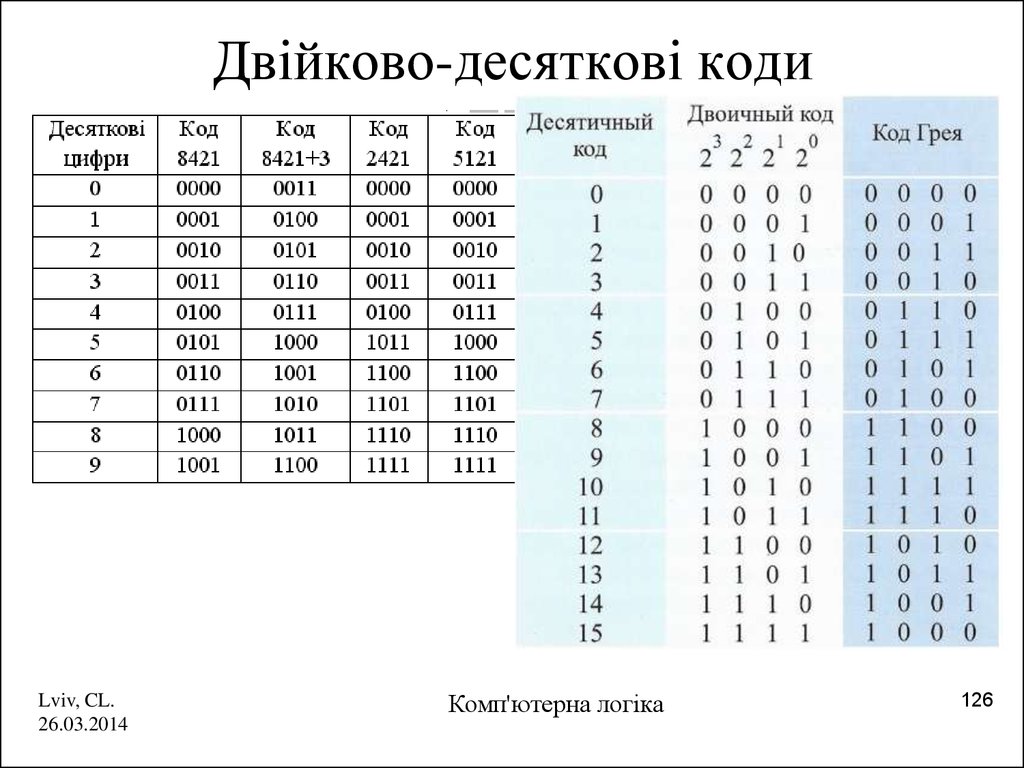
Для преобразования числа из двоично-десятичного кода в десятичную систему, разбейте число на группы по 4 разряда. После этого запишите десятичные цифры, соответствующие каждой 4-разрядной группе.
ПРИМЕР: Преобразуйте числа, записанные двоично-десятичным кодом в десятичную систему: 10010101, 1001000, 1100111, 1001100101001, 1001100001110110.
Замечание: Если в крайней группе слева не хватает разрядов до четырех, то к ней добавляются нули.
31-3. Вопросы
1. Что такое код 8421 и как он используется?
2. Преобразуйте следующие десятичные числа в двоично-десятичный код:
а. 17;
б. 100;
в. 256;
г. 778;
д. 8573.
3. Преобразуйте следующие двоично-десятичные коды в десятичные числа:
Преобразуйте следующие двоично-десятичные коды в десятичные числа:
а. 1000 0010;
б. 0111 0000 0101;
в. 1001 0001 0011 0100;
г. 0001 0000 0000 0000;
д. 0100 0110 1000 1001.
РЕЗЮМЕ
• Двоичная система счисления — это простейшая система счисления.
• Двоичная система счисления содержит две цифры — 0 и 1.
• Двоичная система счисления используется для представления данных в цифровых и компьютерных системах.
• Двоичные данные представляются двоичными разрядами, которые называются битами.
• Термин бит происходит от названия двоичный разряд (binary digit)
• Значение каждого более высокого разряда двоичного числа увеличивается как степень 2.
• Наибольшее число, которое может быть представлено данным количеством разрядов в двоичной системе равно 2n — 1, где n — количество разрядов.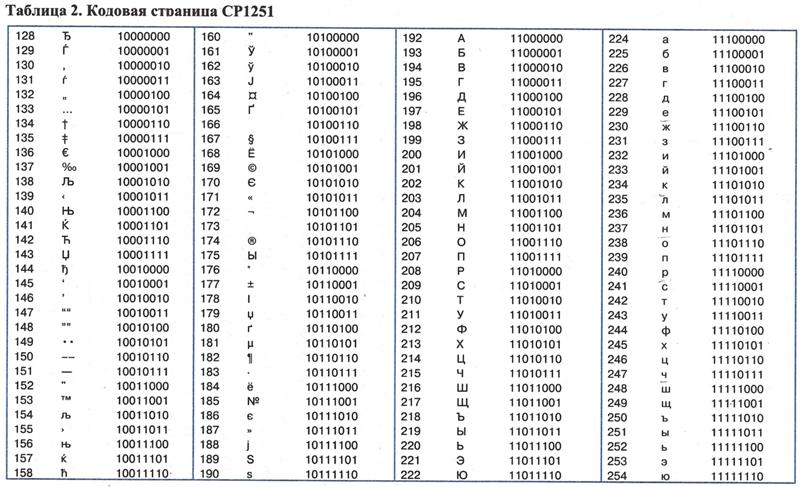
• Значение двоичного числа может быть определено суммированием произведений каждой цифры на вес ее разряда.
• Дробные числа представляются отрицательными степенями 2.
• Для преобразования десятичного числа в двоичное, десятичное число последовательно делится на 2, и после каждого деления записывается остаток. Эти остатки, расположенные в обратном порядке, образуют двоичное число.
• Код 8421 или двоично-десятичный код используется для представления цифр от 0 до 9.
• Достоинством двоично-десятичного кода является возможность легкого преобразования чисел из десятичной формы в двоичную и наоборот.
Глава 31. САМОПРОВЕРКА
1. Запишите в двоичной форме десятичные числа от 0 до 27.
2. Сколько двоичных разрядов нужно для представления десятичного числа 100?
3. Опишите процесс преобразования десятичного числа в двоичное число.
4. Преобразуйте следующие двоичные числа в десятичные:
а. 100101,001011;
б. 111101110,11101110;
в. 10000001,00000101.
5. Опишите процесс преобразования десятичных чисел в двоично-десятичный код.
6. Преобразуйте следующие двоично-десятичные коды в десятичные числа:
а. 0100 0001 0000 0110;
б. 1001 0010 0100 0011;
в. 0101 0110 0111 1000.
Двоичный код | Определение, цифры и факты
- Связанные темы:
- кодировка
Просмотреть весь соответствующий контент →
двоичный код , код, используемый в цифровых компьютерах, основанный на двоичной системе счисления, в которой есть только два возможных состояния, выключено и включено, обычно обозначаемое 0 и 1. В то время как в десятичной системе, в котором используется 10 цифр, каждая позиция цифры представляет степень числа 10 (100, 1000 и т. д.), в двоичной системе каждая позиция цифры представляет степень числа 2 (4, 8, 16 и т. д.). Двоичный кодовый сигнал представляет собой серию электрических импульсов, которые представляют собой числа, символы и операции, которые необходимо выполнить. Устройство, называемое часами, посылает регулярные импульсы, а такие компоненты, как транзисторы, включаются (1) или выключаются (0), чтобы пропускать или блокировать импульсы. В двоичном коде каждое десятичное число (0–9) представлен набором из четырех двоичных цифр или битов. Четыре основные арифметические операции (сложение, вычитание, умножение и деление) могут быть сведены к комбинациям основных булевых алгебраических операций над двоичными числами. ( См. в таблице ниже, как десятичные числа от 0 до 10 представлены в двоичном формате.)
В то время как в десятичной системе, в котором используется 10 цифр, каждая позиция цифры представляет степень числа 10 (100, 1000 и т. д.), в двоичной системе каждая позиция цифры представляет степень числа 2 (4, 8, 16 и т. д.). Двоичный кодовый сигнал представляет собой серию электрических импульсов, которые представляют собой числа, символы и операции, которые необходимо выполнить. Устройство, называемое часами, посылает регулярные импульсы, а такие компоненты, как транзисторы, включаются (1) или выключаются (0), чтобы пропускать или блокировать импульсы. В двоичном коде каждое десятичное число (0–9) представлен набором из четырех двоичных цифр или битов. Четыре основные арифметические операции (сложение, вычитание, умножение и деление) могут быть сведены к комбинациям основных булевых алгебраических операций над двоичными числами. ( См. в таблице ниже, как десятичные числа от 0 до 10 представлены в двоичном формате.)
| десятичный | бинарный | преобразование |
|---|---|---|
| 0 | 0 | 0 ( 2 0 ) |
| 1 | 1 | 1 ( 2 0 ) |
| 2 | 10 | 1 ( 2 1 ) + 0 ( 2 0 ) |
| 3 | 11 | 1 ( 2 1 ) + 1 ( 2 0 ) |
| 4 | 100 | 1 ( 2 2 ) + 0 ( 2 1 ) + 0 ( 2 0 ) |
| 5 | 101 | 1 ( 2 2 ) + 0 ( 2 1 ) + 1 ( 2 0 ) |
| 6 | 110 | 1 ( 2 2 ) + 1 ( 2 1 ) + 0 ( 2 0 ) |
| 7 | 111 | 1 ( 2 2 ) + 1 ( 2 1 ) + 1 ( 2 0 ) |
| 8 | 1000 | 1 ( 2 3 ) + 0 ( 2 2 ) + 0 ( 2 1 ) + 0 ( 2 0 ) |
| 9 | 1001 | 1 ( 2 3 ) + 0 ( 2 2 ) + 0 ( 2 1 ) + 1 ( 2 0 ) |
| 10 | 1010 | 1 ( 2 3 ) + 0 ( 2 2 ) + 1 ( 2 1 ) + 0 ( 2 0 ) |
Редакторы Британской энциклопедии Эта статья была недавно отредактирована и дополнена Адамом Августином.
Что такое двоично-десятичный код и как он используется?
К
- Рахул Авати
Двоично-десятичный код — это система записи цифр, которая присваивает четырехзначный двоичный код каждой цифре от 0 до 9 в десятичном (с основанием 10) числе. Проще говоря, двоично-десятичный код — это способ преобразования десятичных чисел в их двоичные эквиваленты. Однако двоично-десятичное представление — это не то же самое, что простое двоичное представление.
Подробнее о двоично-десятичном коде В двоично-десятичном формате каждая цифра десятичного числа с основанием 10 представляется как группа из четырех двоичных цифр или битов. Любое число или цифра с основанием 10 могут быть представлены в двоичной системе счисления с использованием двоично-десятичной системы счисления.
Каждая цифра кодируется отдельно. Полный номер сначала разделяется на отдельные цифры. Затем эти цифры представляются их эквивалентными 4-битными двоично-десятичными кодами, как показано в этой таблице истинности.
Как правило, десятичное кодирование в двоичное с использованием двоично-десятичного кода может быть выполнено с использованием либо 4-битных, либо 8-битных эквивалентов. Однако обычно предпочтительнее использовать 4-битный эквивалент, который эффективно представляет десятичные значения от 0 до 9.
Арифметические операции, такие как умножение и сложение, необходимы для преобразования действительных двоичных чисел в десятичные. Однако в двоично-десятичном формате возможны только 10 различных комбинаций (см. таблицу выше) в каждой 4-битной двоичной последовательности. Это делает двоично-десятичные числа более простым способом представления десятичных чисел.
Следующие числа не считаются двоично-десятичными: 1010, 1011, 1100, 1101, 1110 и 1111.
Представление больших цифр и чисел в двоично-десятичном кодеВ десятичной системе все числа больше 9 состоят из двух и более цифр. В двоично-десятичной системе эти числа выражаются поразрядно.
Пример 1
Десятичное число = 1764
Двоично-десятичное представление представлено следующим образом:
1 | 7 | 6 | 4 |
0001 | 0111 | 0110 | 0100 |
Пример 2
Десятичное число = 238
Двоично-десятичное представление представлено следующим образом:
2 | 3 | 8 |
0010 | 0010 | 0010 |
Пример 3
Десятичное число = 1895
Двоично-десятичное представление представлено следующим образом:
1 | 8 | 9 | 5 |
0001 | 1000 | 1001 | 0101 |
Двоично-десятичное представление числа отличается от его простого двоичного представления. Например, в двоичной форме десятичная величина 1895 отображается как 11101100111. В двоично-десятичной форме она отображается как 0001100010010101.
Например, в двоичной форме десятичная величина 1895 отображается как 11101100111. В двоично-десятичной форме она отображается как 0001100010010101.
Двоичные эквиваленты для каждого из приведенных выше примеров всегда идут слева направо. Другие битовые шаблоны иногда используются в двоично-десятичном формате для представления специальных символов, относящихся к конкретной системе, таких как знак (положительный или отрицательный), условие ошибки или условие переполнения.
Преимущества и области применения двоично-десятичной системы счисления Двоично-десятичная система позволяет обойти ограничения по размеру, налагаемые на целочисленную арифметику. Он также обеспечивает простое преобразование между машиночитаемыми и удобочитаемыми цифрами. По сравнению с двоичной системой кодировать и декодировать двоично-десятичные числа проще. Таким образом, двоично-десятичный код предлагает быструю и эффективную систему для преобразования десятичных чисел в двоичные числа.
Двоично-десятичный код полезен в цифровых дисплеях, где может быть сложно манипулировать большими числами или отображать их. Поскольку в двоично-десятичном коде каждая цифра рассматривается как отдельная подсхема, манипулирование данными в таких устройствах становится проще. Доступны интегральные схемы, сконфигурированные для вывода двоично-десятичных чисел на такие дисплеи.
Двоично-десятичная система преобразования также используется в некоторых приложениях с валютой, где представления с плавающей запятой не совсем точны.
Ограничения двоично-десятичных чисел Несмотря на свои преимущества, двоично-десятичный код имеет определенные ограничения. Например, представление десятичного числа в виде двоично-десятичного числа требует дополнительных битов памяти в памяти компьютера, что делает его неэффективным способом хранения чисел. Это также требует повышенной сложности схемы по сравнению со стандартной двоичной системой. Двоично-десятичный код также может быть расточительным, поскольку многие 4-битные состояния (от 10 до 16) не используются.
Другое ограничение двоично-десятичных чисел заключается в том, что выполнение арифметических задач с использованием двоично-десятичных чисел может быть громоздким, поскольку ни одна цифра не может превышать 9. Следовательно, добавление двух десятичных цифр в двоично-десятичном числе может создать бит переноса, равный 1, который необходимо добавить к следующей группе из 4 битов, чтобы получить правильное двоично-десятичное представление.
Типы двоично-десятичныхСуществует два типа двоично-десятичных чисел.
Неупакованный двоично-десятичный код
В распакованных двоично-десятичных числах каждая 4-битная двоично-десятичная группа хранится в отдельном регистре внутри компьютера. Недостатком здесь является то, что если регистры имеют размер 8 бит или больше, пространство тратится впустую для хранения двоично-десятичных чисел.
Упакованный двоично-десятичный код
В упакованных двоично-десятичных числах один 8-битный регистр хранит две двоично-десятичных цифры.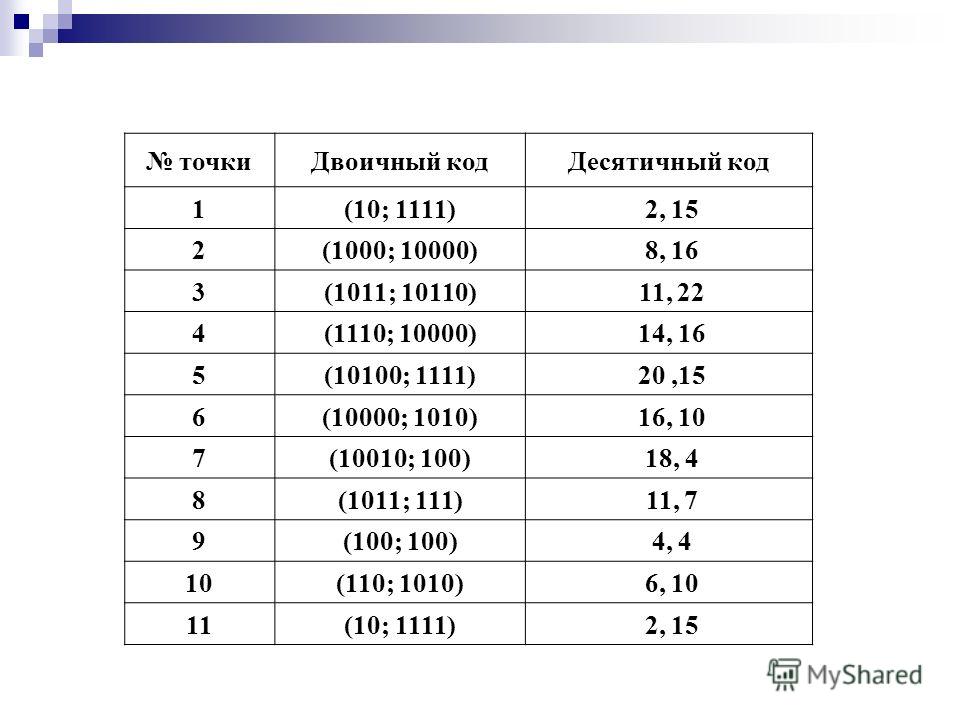 Сдвигая число в верхнем регистре влево четыре раза, а затем добавляя числа в верхнем и нижнем регистрах, процесс объединяет две двоично-десятичные цифры, что позволяет хранить их в одном регистре.
Сдвигая число в верхнем регистре влево четыре раза, а затем добавляя числа в верхнем и нижнем регистрах, процесс объединяет две двоично-десятичные цифры, что позволяет хранить их в одном регистре.
В простом двоичном представлении целое число преобразуется в двоичную форму путем многократного деления числа на 2. В двоично-десятичном коде каждая отдельная цифра преобразуется в двоичную. Затем 4-битный двоичный эквивалент каждой цифры записывается вместе.
Вот пример:
- Десятичное число 234.
- В двоичном формате 234 = 11101010
- В двоично-десятичном коде число 234 записывается следующим образом:
- 2 = 0010, 3 = 0011, 4 = 0100
- Следовательно, 234 = 001000110100
See also: Extended Binary Coded Decimal Interchange Code , encoding and decoding , hexadecimal , big-endian and little-endian , globally unique identifier , универсальный уникальный идентификатор и Американский стандартный код для обмена информацией .
Последнее обновление: июнь 2022 г.
Продолжить чтение О двоично-десятичном кодировании- Объяснение двоичных и шестнадцатеричных чисел для разработчиков
- Будущее за разведкой угроз ИИ, и будущее уже сейчас
- Применяйте лучшие практики использования политики как кода для получения преимуществ
- 2 метода обработки данных для лучшего машинного обучения
- Сравнение 6 лучших языков программирования
словарь данных
Словарь данных — это набор описаний объектов данных или элементов в модели данных, на которые могут ссылаться программисты и другие лица.
Сеть
- доступность сети
Доступность сети — это время безотказной работы сетевой системы в течение определенного интервала времени.
- NFV MANO (управление и оркестрация виртуализации сетевых функций)
NFV MANO (управление виртуализацией и оркестровкой сетевых функций), также называемый MANO, представляет собой архитектурную основу для …
- Сетевой коммутатор
Сетевой коммутатор соединяет устройства в сети друг с другом, позволяя им общаться путем обмена пакетами данных.
Безопасность
- GPS-глушение
Подавление сигналов GPS — это использование устройства, передающего частоту, для блокирования или создания помех радиосвязи.
- контрольная сумма
Контрольная сумма — это значение, представляющее количество битов в передаваемом сообщении и используемое ИТ-специалистами для обнаружения.
 ..
.. - информация о безопасности и управление событиями (SIEM)
Управление информацией о безопасности и событиями (SIEM) — это подход к управлению безопасностью, который объединяет информацию о безопасности …
ИТ-директор
- доказательство концепции (POC)
Доказательство концепции (POC) — это упражнение, в котором работа сосредоточена на определении того, можно ли превратить идею в реальность.
- зеленые ИТ (зеленые информационные технологии)
Green IT (зеленые информационные технологии) — это практика создания и использования экологически устойчивых вычислений.
- ориентир
Контрольный показатель — это стандарт или точка отсчета, которые люди могут использовать для измерения чего-либо еще.
HRSoftware
- самообслуживание сотрудников (ESS)
Самообслуживание сотрудников (ESS) — это широко используемая технология управления персоналом, которая позволяет сотрудникам выполнять множество связанных с работой .
 ..
.. - платформа обучения (LXP)
Платформа обучения (LXP) — это управляемая искусственным интеллектом платформа взаимного обучения, предоставляемая с использованием программного обеспечения как услуги (…
- Поиск талантов
Привлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса …
Отдел обслуживания клиентов
- привлечения клиентов
Взаимодействие с клиентами — это средство, с помощью которого компания устанавливает отношения со своей клиентской базой, чтобы повысить лояльность к бренду и …
- прямой электронный маркетинг
Прямой маркетинг по электронной почте — это формат кампаний по электронной почте, в котором отдельные рекламные объявления рассылаются целевому списку …



 1.
Параметры позиционных систем счисления
1.
Параметры позиционных систем счисления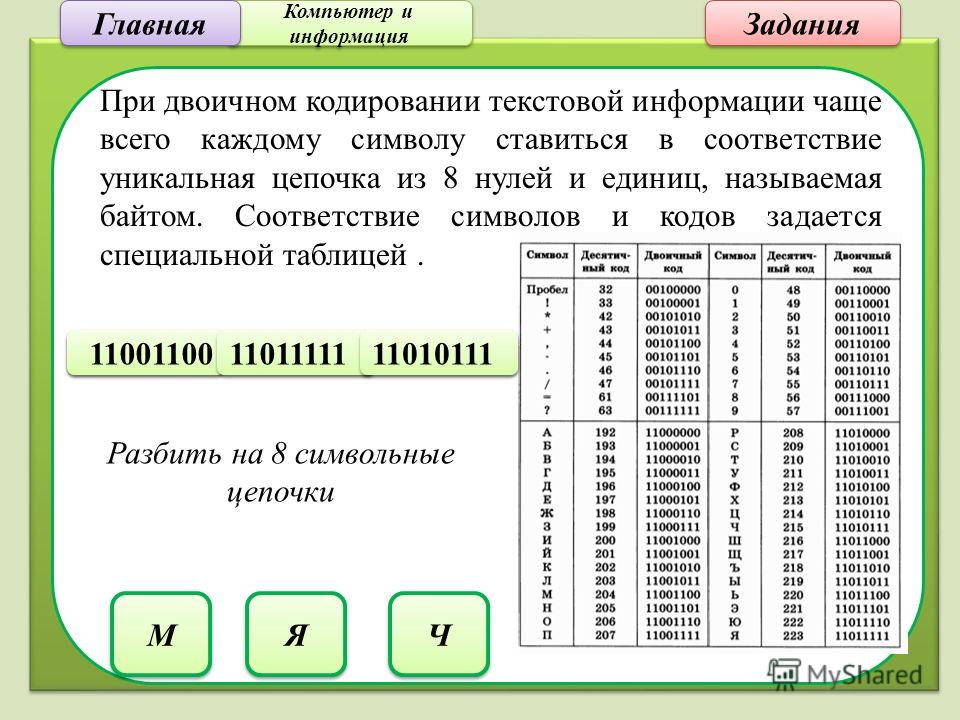 2.
Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков
2.
Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков ..
.. ..
..