3.2. Логические элементы

Современные компьютеры представляют собой технические системы, отличающиеся сложной структурой, большим числом электронных элементов и электромеханических деталей, а также сложностью выполняемых функций. Поэтому изучение компь­ютера целесообразно начать с рассмотрения простейших частей, из которых он состоит. При множестве электронных элементов (миллионы), используемых в компьютере, число их типов срав­нительно невелико (десятки и сотни). Дело в том, что все уст­ройства (например, оперативная память) имеют регулярную структуру, т.е. состоят из большого числа повторяющихся (ти­повых) схем.

Преобразование информации в компьютере выполняется при помощи электронных схем, имеющих различную сложность. По функциональной сложности принято делить электронные схемы компьютера на элементы, узлы (блоки) и устройства.

Элемент — это простейшая часть компьютера, выполняющая операции над двоичными цифрами (битами).

Основные элементы могут быть логическими или элементами памяти. Логические эле­менты выполняют двоичные (бинарные) операции, на основе которых осуществляются практически все преобразования инфор­мации. В качестве логических элементов используются элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ и т.д. Элементы памяти чаще всего представляют собой триггеры различных ти­пов: RS-, JK-, D— или Г-триггеры. Кроме логических элементов и элементов памяти в состав компьютера входят вспомогательные элементы, усиливающие или формирующие сигналы стандарт­ной формы.

Узлы (блоки) состоят из элементов и выполняют операции над байтами или словами, состоящими из нескольких байтов. К типо­вым узлам компьютера относятся регистры, счетчики, суммато­ры, дешифраторы, селекторы, мультиплексоры и др. Несколько узлов могут объединяться в функциональные блоки (например, блок сумматора может включать в себя собственно сумматор и регистр сумматора).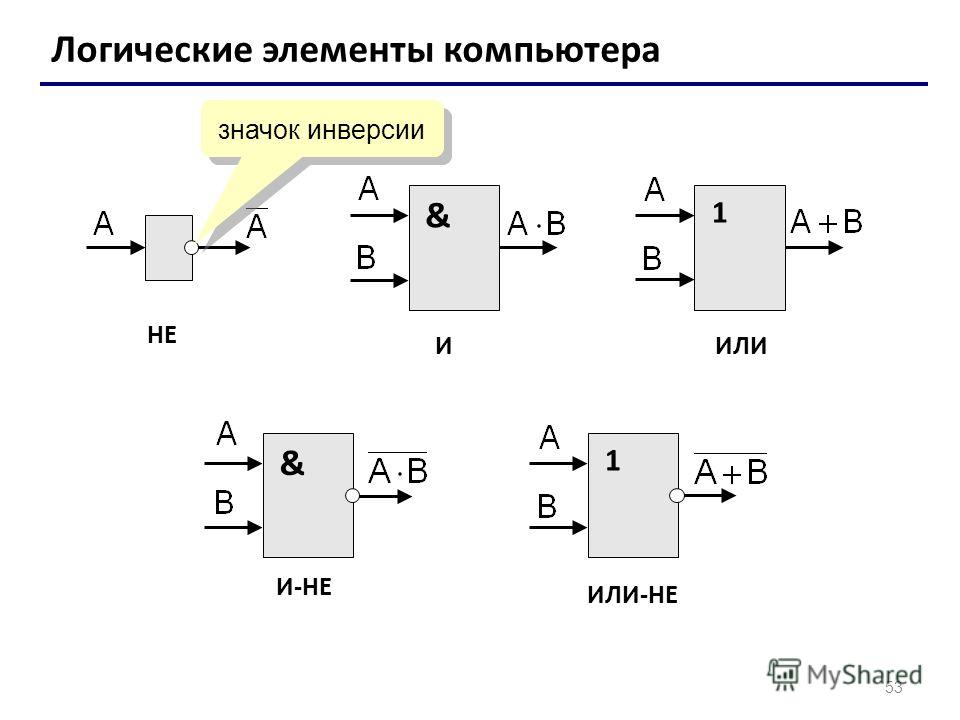

Устройства компьютера строятся из элементов и узлов и вы­полняют определенный набор однотипных операций. К устрой­ствам относятся запоминающие устройства, арифметико-логиче­ское устройство, центральное устройство управления, устройства ввода и вывода. Устройства компьютера конструктивно выполня­ют отдельно или несколько устройств объединяют в один конст­руктивный блок (например, системный блок может объединять устройство управления, арифметико-логическое устройство и ус­тройства памяти).

В зависимости от состава узлы могут быть комбинационного (комбинационные схемы — КС) или накапливающего типа (ав­томаты с памятью, последовательные схемы).

Узлы комбинационного типа состоят из логических элементов. Их главная особенность заключается в том, что выходной сигнал (Y) зависит только от комбинации входных сигналов (X) в дан­ный момент времени, при этом каждой комбинации сигналов на входе соответствует выходной сигнал (рис.

3.1, а). Выходной сиг­нал может измениться только при получении другого входного сигнала. При неоднократном повторении одного и того же вход­ного сигнала значение выходного также повторяется, поэтому ком­бинационная схема фактически осуществляет перекодировку вход­ных сигналов в выходные. Несмотря на кажущуюся примитивность логики работы комбинационных схем, все основные преобразо­вания информации в компьютере выполняются с их помощью. Это объясняется тем, что в основе преобразования данных в ком­пьютере заложено выполнение логических операций.

Автоматы с памятью состоят из логических элементов и эле­ментов памяти (рис. 3.1,

б). Информация, записанная в памяти автомата, называется состоянием автомата (0. Выходной сигнал автомата в общем случае зависит от сигнала на входе и состояния автомата, поэтому при одном и том же входном сигнале автомат может выдавать различные выходные сигналы. При работе автома­та в его памяти накапливается обобщенная информация о всех входных сигналах, поступивших к данному моменту времени, поэтому состояние автомата и выходной сигнал зависят от всей предыстории входных сигналов. Наличие памяти позволяет авто­мату выполнять не только отдельные операции, но и последова­тельности взаимосвязанных операций, т.е. заданные алгоритмы обработки данных. Компьютер в целом представляет собой слож­ный автомат с памятью большой емкости. Для понимания орга­низации компьютера и процессов преобразования информации в нем необходимо изучить логику работы его составных частей, прежде всего состав и работу элементов и типовых узлов.

Логические элементы выполняют преобразования информации, которые описываются логическими функциями. Логическая функция и ее аргументы могут принимать только два значения: «О» и «1». Зависимость значений логической функции от значе­ний ее аргументов можно задать с помощью таблицы истинно­сти (табл. 3.1).

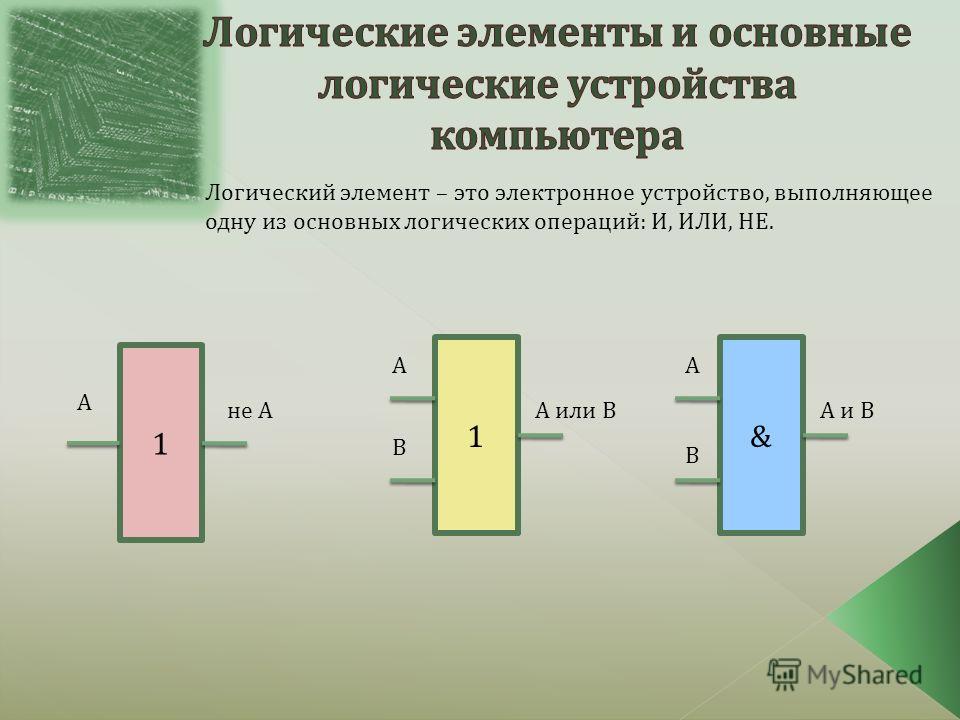
Логическая функция И (логическое умножение, конъюнкция)

F(x_u х₂) — х_х х₂ принимает значение «1», если оба аргумента рав­ны «1», а функция ИЛИ (логическое сложение, дизъюнкция) F{x_h х₂) = *i v х₂ — если один или несколько аргументов равны «1».

Функция НЕ (инверсия, отрицание) принимает значение «1», если аргумент равен «О» и наоборот. Таким образом, значения функций И, ИЛИ и НЕ определяются в соответствии с обычным смыслом слов «и», «или» и «не». Число входов элементов ИЛИ и И совпадает с числом аргументов соответствующей функции. Ус­ловные графические обозначения (УГО) элементов И, ИЛИ и НЕ на функциональных схемах приведены на рис. 3.2.

Условное графическое обо­значение элемента выполняют в виде прямоугольника, в левом верхнем углу которого указыва­ют обозначение выполняемой функции. Входы элемента обо­значают линиями слева, выхо­ды — справа.

Элементы И, ИЛИ и НЕ со­ставляют функционально пол­ную систему, т. е. из них можно составить любую комбинационную (логическую) схему. Логичес­кие элементы, выполненные в виде интегральных схем, обычно реализуют логические функции И—НЕ (штрих Шеффера) или ИЛИ—НЕ (стрелка Пирса). Каждый из этих элементов обладает свойством функциональной полноты.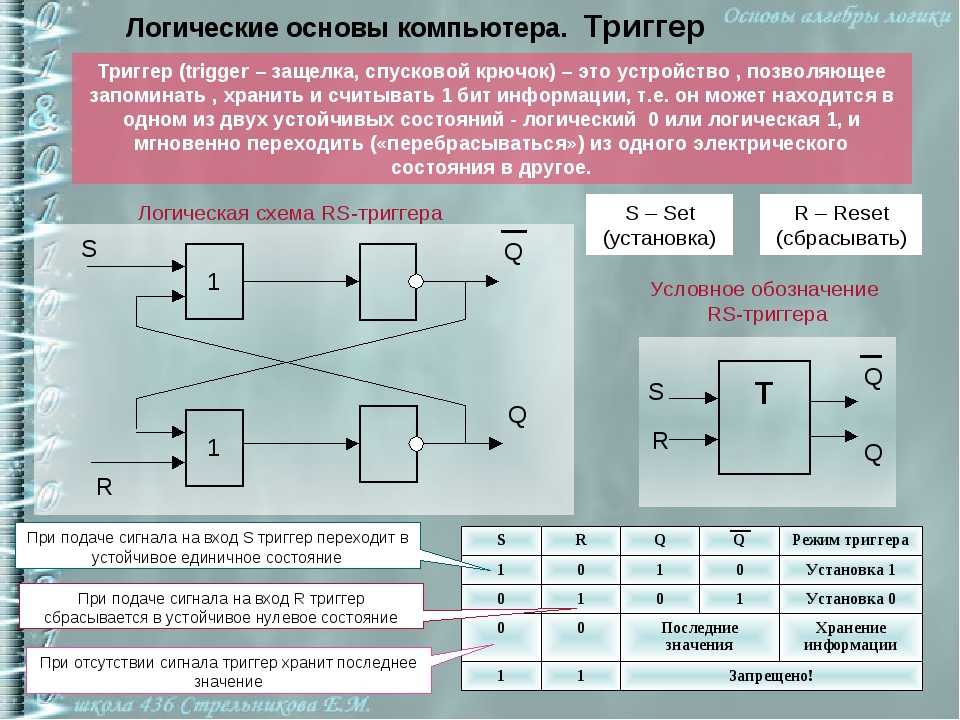

Обозначения элементов И—НЕ и ИЛИ—НЕ на функциональных схемах, а также приме­ры их реализации приведены на рис. 3.3.

Элементы И на два входа часто используют в качестве ключей (вентилей), которые управляют передачей данных между двумя схемами (рис. 3.4).

При передаче одноразрядных данных (см. рис. 3.4, а) один вход элемента И является информационным, а второй — управляю­щим. На информационный вход поступают одноразрядные данные

D от источника А. Если на управляющем входе сигнал «Пере­дать» равен «О», то на приемник В поступает сигнал «О» независи­мо от значения данных D. Если сигнал «Передать» равен «1», то сигнал на выходе элемента И совпадает с информационным сиг­налом и на вход приемника поступают данные D.

При передаче многоразрядных данных (см. рис. 3.4, б) каждый разряд данных проходит через отдельный элемент И, а сигнал «Передать» подается одновременно на управляющие входы всех ключей.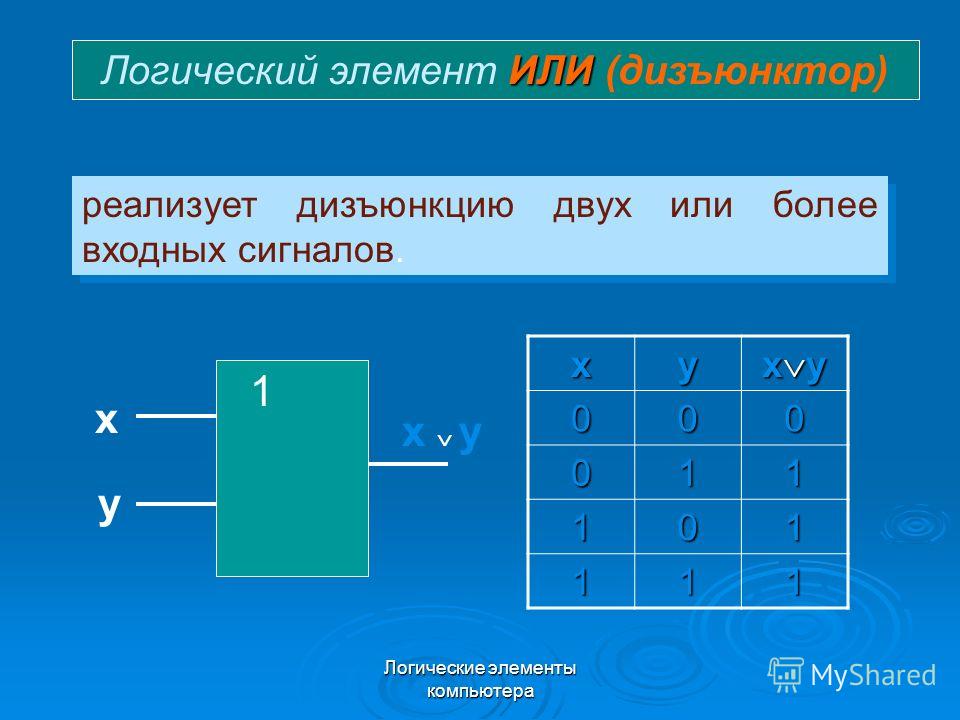

Общие сведения о триггерах. Для хранения информации в ком­пьютере могут использоваться различные типы элементов памяти. В зависимости от способа хранения информации элементы памя­ти могут быть статическими, позволяющими хранить двоичную информацию сколь угодно долго, и динамическими, хранящими информацию в течение ограниченного отрезка времени. Для дли­тельного хранения информации в динамических элементах памя­ти необходимо периодически восстанавливать ее (регенерировать). Динамические элементы памяти применяют при построении уст­ройств памяти. Здесь рассматриваются статические элементы па­мяти, которые используют в схемах процессора. В качестве стати­ческих элементов памяти в настоящее время применяют тригге­ры.

Основу триггера составляет бистабильная ячейка, имеющая два устойчивых состояния. Бистабильные ячейки могут быть постро­ены на двух логических элементах И—НЕ или ИЛИ—НЕ, соеди­ненных перекрестными связями (рис. 3.5).

Существование двух устойчивых состояний бистабильной ячейки объясняется наличием в ее схеме обратных связей, позволяющих сигналу с выхода элемента поступать на его же вход через второй элемент. Так, если на рис. 3.5, а сигнал на верхнем выходе равен а б

«1» и на оба входа подается сигнал «О», то сигнал «1» с выхода элемента 1 поступает на вход элемента 2 и формирует на его вы­ходе сигнал «О». Этот сигнал поступает на вход элемента 1 и под­держивает такое состояние схемы, делая его устойчивым. В этом состоянии на выходе элемента 1 сигнал равен «1», а на выходе элемента 2 сигнал равен «О».

Для изменения состояния схемы необходимо подать на верх­ний вход элемента 1 сигнал «1». При этом на выходе элемента 1 сигнал становится равным «О». Тогда на выходе элемента 2 фор­мируется сигнал «1», который вместе с единичным входным сиг­налом устанавливает выходной сигнал элемента 1 равным «О». Та­кое состояние схемы также является устойчивым и после того, как сигнал на входе элемента 1 станет равным «О». В этом состоя­нии на выходе элемента 1 сигнал равен «О», а на выходе элемента 2 — «1». При поступлении сигнала «1» на вход элемента 2 проис­ходит возвращение схемы в начальное состояние. Таким образом, схема имеет два устойчивых состояния, которые можно устанавли­вать подачей сигнала «1» на вход элемента 1 или 2. Аналогично работает бистабильная ячейка на элементах И—НЕ (см. рис. 3.5, б).

Триггер — это цифровая электронная схема с двумя устойчи­выми состояниями, которые устанавливаются при подаче соот­ветствующей комбинации входных сигналов и сохраняются.

Кроме бистабильной ячейки в состав триггера входит схема управления (рис. 3.6). Схема управления — это комбинационная схема, при помощи которой осуществляется запись информации в триггер (изменение состояний триггера). Конкретный вид схемы управления зависит от типа триггера.

Триггер имеет два выхода: прямой и инверсный (Q и Q). Сиг­налы на выходах триггера всегда имеют различные значения. Если на прямом выходе сигнал равен «1», то на инверсном — «О» и наоборот. Состояние триггера определяется значением сигнала на gрямом выходе (Q). Если сигнал на прямом выходе равен «1», то триггер находится в состоянии «1». Можно также сказать, что со­стояние триггера — это информация, записанная в триггере. Та­ким образом, если триггер находится в состоянии «1», то в нем записана единица.

Триггеры могут быть асинхронными или синхронными. В асин­хронных триггерах используются только основные или информа­ционные входы. Изменение состояния асинхронного триггера мо­жет происходить в произвольные моменты времени, определяе­мые изменениями сигналов на информационных входах.

В синхронных триггерах кроме информационных входов имеется вход синхронизации. На этот вход подается сигнал синхрониза­ции С, который выполняет функции сигнала, разрешающего пе­реключение триггера из одного состояния в другое. Если сигнал синхронизации С равен «О», то состояние синхронного триггера не изменяется при любой комбинации сигналов на информаци­онных входах. Для переключения синхронного триггера необходи­мо подать на информационные входы определенную, зависящую от типа триггера, комбинацию сигналов и, кроме того, устано­вить значение сигнала С, равное «1».

Логика переключения триггера определяется его типом и зави­сит от числа и назначения входов. Наиболее часто в цифровой тех­нике используют RS-, JK-, D— и Г-триггеры, а также комбиниро­ванные триггеры. Буквами R, S, J, К, D и Т обозначаются инфор­мационные входы триггеров (X

При R = 0 и S = 0 состояние триггера не меняется. Такой ре­жим называется режимом хране­ния. В случае если R = 0 и S = 1 триггер переходит в состояние «1» независимо от того, в каком состоянии он находился до из­менения входных сигналов. При R = 1 и £ = 0 триггер переходит в состояние «0». Таким образом, для записи «1» в RS—триггер не­обходимо подать на его входы сигналы R = 0 и S = 1, для записи «0» — сигналы R = 1 и S = 0. -триггер. Этот триггер имеет дополнительно вход С, на который поступает синхросигнал. Информационные сигна­лы R и S могут изменять состояние триггера только при значении синхросигнала С = 1. Таблица переходов синхронного ДО-триггера состоит из двух частей. Первая часть таблицы описывает переходы триггера при С = 1 и совпадает с таблицей переходов асинхронно­го триггера (см. табл. 3.2). Когда С = 0, триггер не меняет своего

состояния при любой комбина-Таблица34 иии сигналов на информацион­ных входах и логика его пере-Переходы синхронного АУ-триггера ходов может быть.

Отметим, что при С = 0 раз­решенными являются любые комбинации входных сигналов, в том числе R — 1, 5=1.

На рис. 3.8 приведены фун­кциональные схемы синхрон­ных .Кб’-триггеров, реализован­ных на элементах И—НЕ и

И—ИЛИ—НЕ, и их условное графическое обозначение.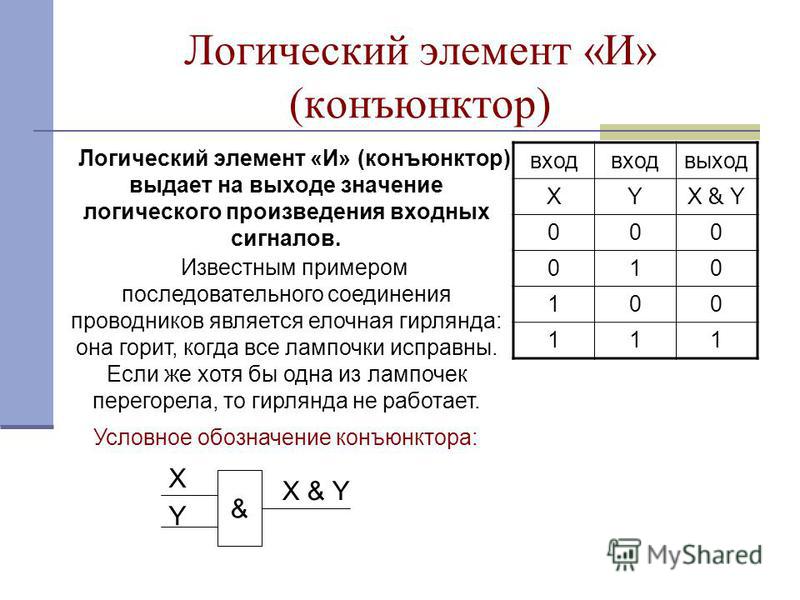 Кроме ос­новных входов R и S там показаны дополнительные входы R_x и S_uкоторые являются асинхронными. При подаче сигналов на них состояние триггера может изменяться независимо от значения сигнала С. Следует отметить, что в каждый момент времени мож­но управлять переходами триггера только с помощью синхронных или асинхронных входов.

Двухтактный .К.У-трштер. Триггеры используются в различных узлах ЭВМ, между которыми осуществляется передача информа­ции. Устойчивая работа цепочки триггеров происходит только в том случае, когда запись новой информации в триггер произво­дится после считывания прежней и передачи ее в следующий по цепочке триггер.

Это возможно при использовании двух серий синхроимпуль­сов, сдвинутых относительно друг друга на полпериода. Такой прин­цип управления и синхронизации применяется в двухтактных триг­герах. Двухтактные триггеры используются в сдвигающих регист­рах, а также в качестве элементов памяти в цифровых автоматах с памятью для устранения эффекта гонок.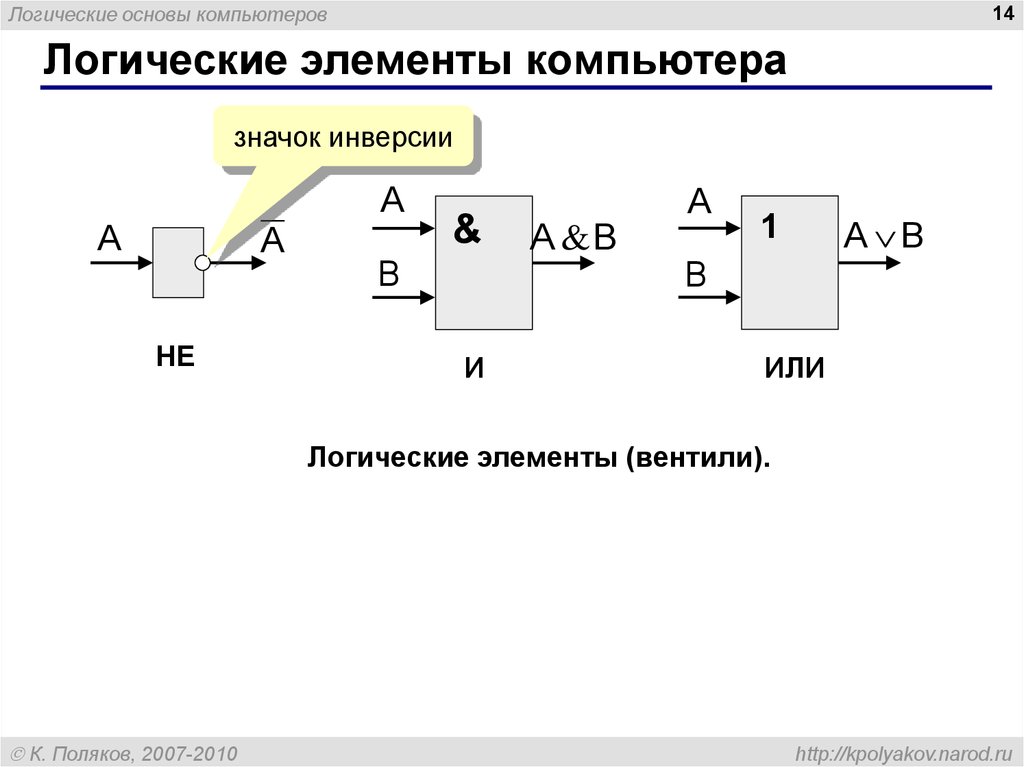 -триггера в «0» или «1» независимо от при­сутствия сигнала на входе С в схему вводят прямые или инверсные входы R и £ асинхронной установки (рис. 3.10, а) и отображают их на УГО (рис. 3.10, б).

Асинхронный и синхронный D-триггеры. В вычислительной тех­нике широко применяют D-триггеры, которые реализуют функ­цию временной задержки входного сигнала. Также 2)-триггеры имеют один информационный вход. Логика работы асинхронного Х>-триггера описывается таблицей переходов (табл. 3.5).

В асинхронном D-триггере состояние (выходной сигнал) Q_l+lповторяет значение входного сигнала D„ поэтому асинхронный D-триггер по существу не является элементом памяти и рассмат­ривается только как основа для построения синхронного D-триг-гера.

Функциональная схема и УГО синхронного Я-триггера, пост­роенного на основе синхронного 7?6*-триггера, показаны на рис. -триггера в D-триггер сигнал D пода­ется на вход непосредственно, а на вход R — через инвертор. Если при С = 1 на вход D подать сигнал «1», то триггер перейдет в состояние «1», а при подаче сигнала D = 0 в триггер будет записан «О». Таким образом, для записи в .D-триггер единицы на вход D нужно подать сигнал «1», а для записи нуля — сигнал «О» (так как триггер синхронный, на вход С необходимо в обоих случаях пода­вать сигнал «1»). Это делает D-триггер удобным для использова­ния в схемах статической памяти, так как для записи достаточно иметь одну линию на разряд данных. При этом сигнал С является общим для всех разрядов записываемых данных.

Логику работы синхронного Х)-триггера описывает табл. 3.6. Эту логику можно охарактеризовать выражением «что надо записать в .D-триггер, то и подается на его вход».

Наличие входа синхронизации позволяет записывать новые дан­ные в триггер только в определенные моменты времени (при С= 1). В промежутках между ними данные в триггере сохраняются без изменения. При чтении данных из триггера его состояние также не меняется.

J-триггер. Этот триггер имеет один информационный вход. Ло­гику работы асинхронного Г-триггера характеризует таблица пе­реходов (табл. 3.7).

При Г = 1 асинхронный Г-триггер меняет свое состояние на противоположное, а при Г= О состояние триггера не изменяется. (Аналогичную логику работы имеет кнопочный выключатель на-

Логические элементы ЭВМ

Логические элементы ЭВМ.

Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию. Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ и другие, (называемые также вентилями), а также триггер.

Система элементов ЭВМ — набор логических элементов, позволяющий реализовать любую функционально-логическую схему электронной вычислительной машины. Минимальный (по числу типов элементов) функционально полный (с точки зрения выполнения логических операций) набор состоит из элементов типа «и» — «не» либо «или» — «не»; такие элементы позволяют построить простейший элемент памяти ЭВМ — статический Триггер. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу различных устройств компьютера. Обычно у логических элементов (вентилей) бывает от двух до восьми входов и один или два выхода.

Применяемые в ЭВМ системы элементов содержат, кроме того, ряд специальных элементов для формирования сигналов, их усиления, временной задержки и т. д. Как правило, в систему элементов вводится несколько модификаций основного логического элемента, различающихся коэффициентом разветвления на входе и выходе или некоторыми дополнительными схемными возможностями. Это позволяет получить большую эффективность и гибкость при конструировании функциональных схем, сократить число уровней логики, увеличить эффективное быстродействие устройств ЭВМ и т. д. Все элементы одной системы выполняются совместимыми по уровням сигналов, временным характеристикам, требованиям к источникам питания.

По типу сигналов, используемых для представления информации (логических переменных), системы элементов подразделяют на импульсные, потенциальные и импульсно-потенциальные. Импульсные системы элементов применялись в основном в ранних образцах ЭВМ (преимущественно 1-го поколения — компьютеры на электронных лампах, вроде тех, что были в старых телевизорах). В ЭВМ 2-го (вместо электронных ламп использовались транзисторы, а в качестве устройств памяти стали применяться магнитные сердечники, впервые появилось то, что сегодня называется операционной системой) и особенно 3-го поколения (десятки и сотни транзисторов заменились одним кристаллом полупроводника) применяются потенциальные и импульсно-потенциальные системы элементов.

В вычислительных машинах коды нуля и единицы представляются электрическими сигналами, имеющими два различных состояния.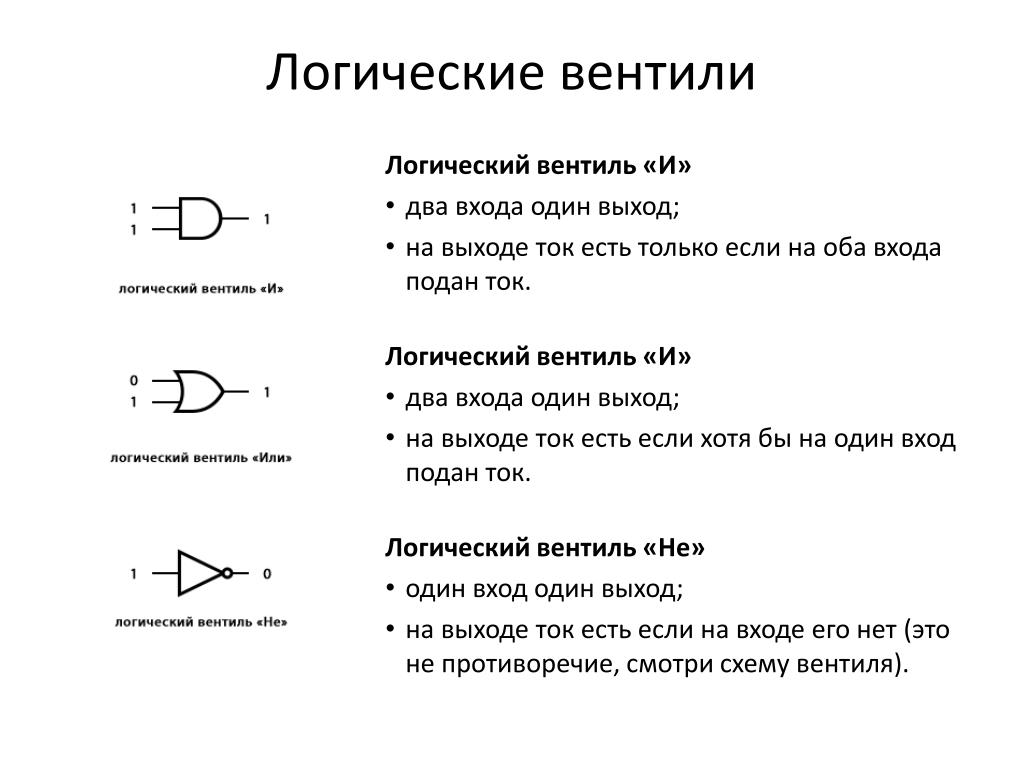 Наиболее распространенными способами физического представления информации являются импульсный и потенциальный:

• импульс или его отсутствие;

• высокий или низкий потенциал;

• высокий потенциал или его отсутствие.

При импульсном способе отображения код единицы идентифицируется наличием электрического импульса, код нуля — его отсутствием (впрочем, может быть и наоборот). Импульс характеризуется амплитудой и длительностью, причем длительность должна быть меньше временного такта машины.

При потенциальном способе отображения код единицы — это высокий уровень напряжения, а код нуля — отсутствие сигнала или низкий его уровень. Уровень напряжения не меняется в течение всего такта работы машины. Форма и амплитуда сигнала при этом во внимание не принимаются, а фиксируется лишь сам факт наличия или отсутствия потенциала.

Вышесказанное обусловило то, что для анализа и синтеза схем в компьютере при алгоритмизации и программировании решения задач широко используется математический аппарат алгебры логики, оперирующий также с двумя понятиями «истина» или «ложь».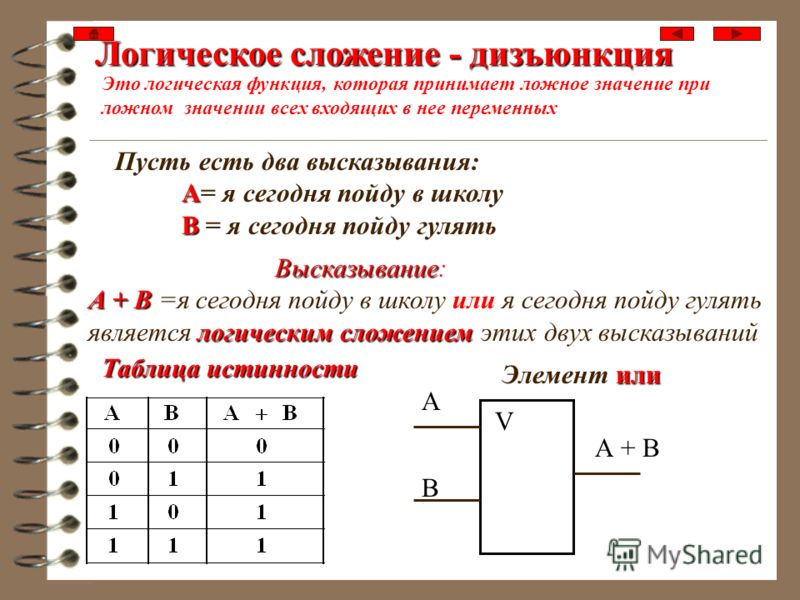

Бинарная логика

Основой цифровой техники служат три логические операции, лежащие в основе всех выводов компьютера. Иногда эти операции И, ИЛИ, НЕ называют «тремя китами машинной логики». Познакомимся с ними подробнее.

При записи тех или иных логических выражений используется специальный язык, который принят в математической логике. Основоположником математической логики является великий немецкий математик Готфрид Вильгельм Лейбниц (1646 — 1716 гг.). Он сделал попытку построить универсальный язык, с помощью которого споры между людьми можно было бы разрешать посредством вычислений. На заложенном Лейбницем фундаменте ирландский математик Джордж Буль построил здание новой науки — математической логики, — которая в отличие от обычной алгебры оперирует не числами, а высказываниями. В честь Д.Буля логические переменные в языке программирования Паскаль впоследствии назвали булевскими.

Высказывание — это любое утверждение, относительно которого можно сказать истинно оно или ложно, т.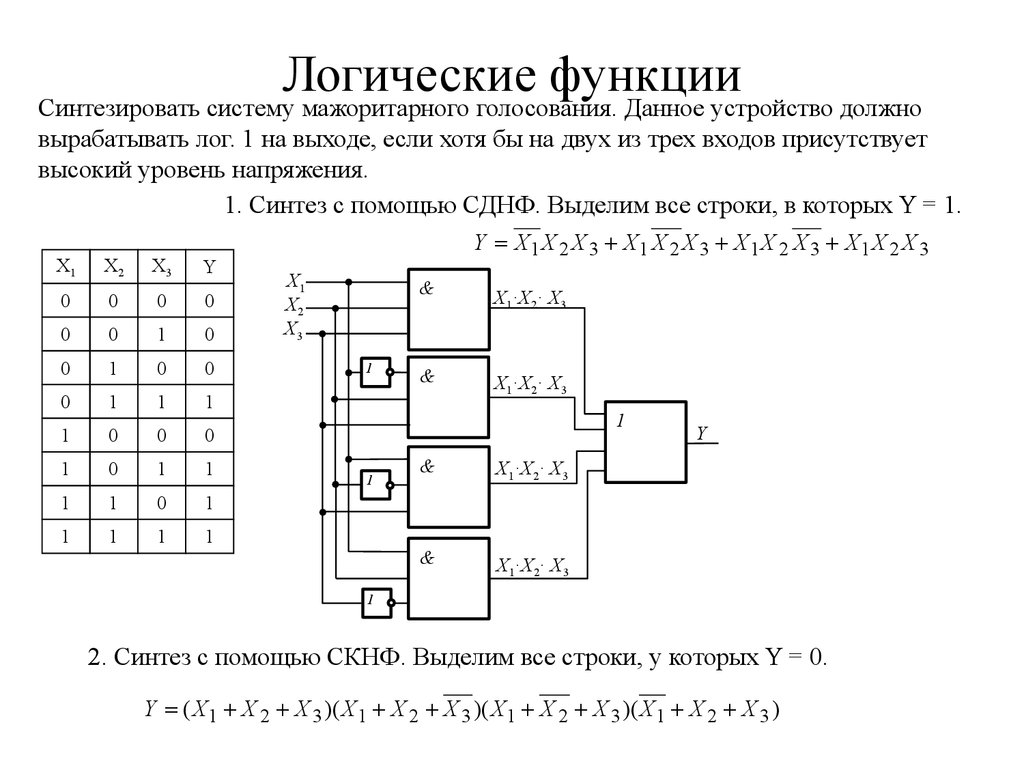 е. соответствует оно действительности или нет.

Таким образом по своей сути высказывания фактически являются двоичными объектами и поэтому часто истинному значению высказывания ставят в соответствие 1, а ложному — 0. Например, запись А = 1 означает, что высказывание А истинно.

Высказывания могут быть простыми и сложными. Простые соответствуют алгебраическим переменным, а сложные являются аналогом алгебраических функций. Функции могут получаться путем объединения переменных с помощью логических действий.

Самой простой логической операцией является операция НЕ, по-другому ее часто называют отрицанием, дополнением или инверсией и обозначают NOT_X. Результат отрицания всегда противоположен значению аргумента. Логическая операция НЕ является унарной, т.е. имеет всего один операнд. В отличие от нее, операции И (AND) и ИЛИ (OR) являются бинарными, так как представляют собой результаты действий над двумя логическими величинами.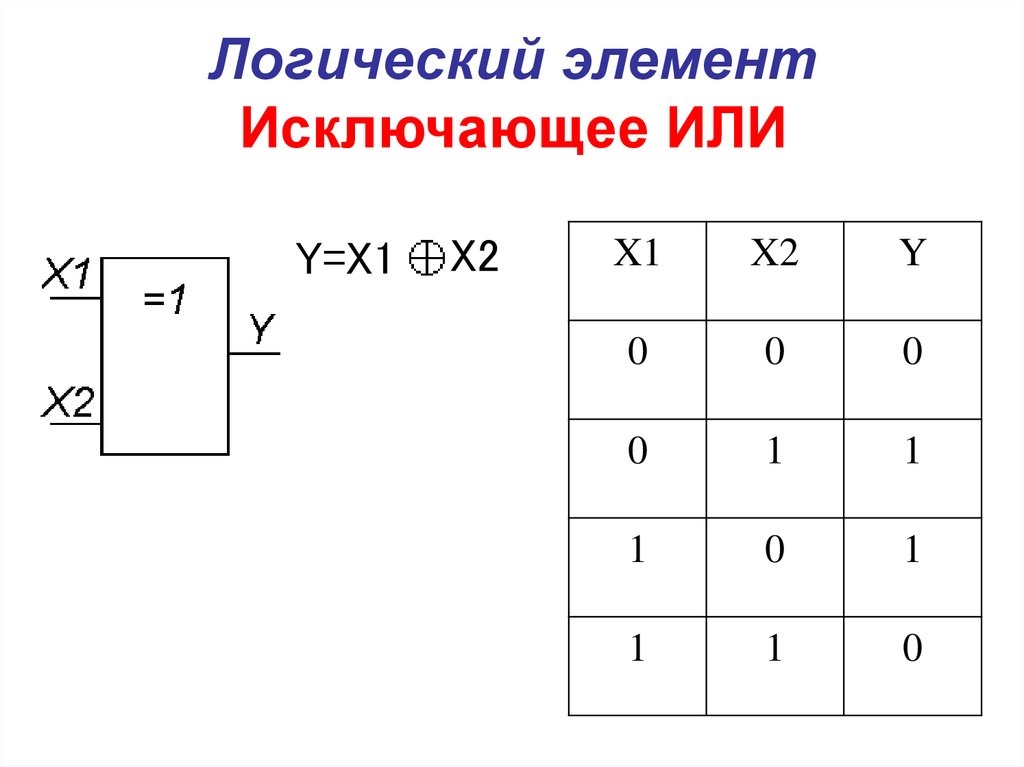

X	not X
0	1
1	0

Логическое И еще часто называют конъюнкцией, или логическим умножением (не правда ли, таблица для этой операции похожа как две капли воды на двоичную таблицу умножения?), а ИЛИ -дизъюнкцией, или логическим сложением.

Операция И имеет результат «истина» только в том случае, если оба ее операнда истинны. Операция ИЛИ «менее привередлива» к исходным данным. Она дает «истину», если значение «истина» имеет хотя бы одни из операндов. Разумеется, в случае, когда справедливы оба аргумента одновременно, результат по-прежнему истинный.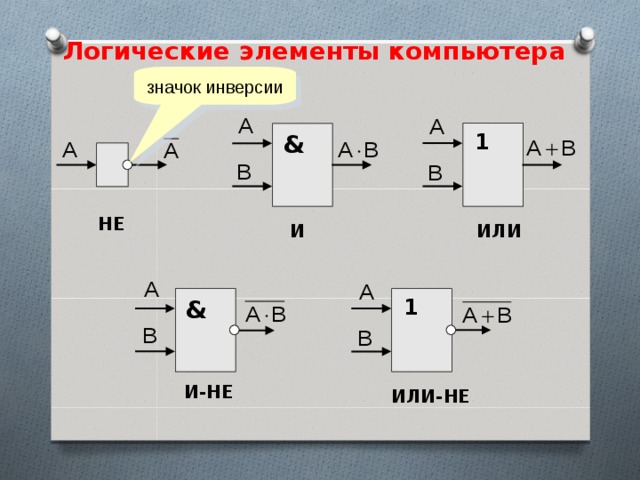

X	Y	X and Y	X or Y	X xor Y
0	0	0	0	0
0	1	0	1	1
1	0	0	1	1
1	1	1	1	0

Операции И, ИЛИ, НЕ образуют полную систему логических операций, из которой можно построить сколь угодно сложное логическое выражение.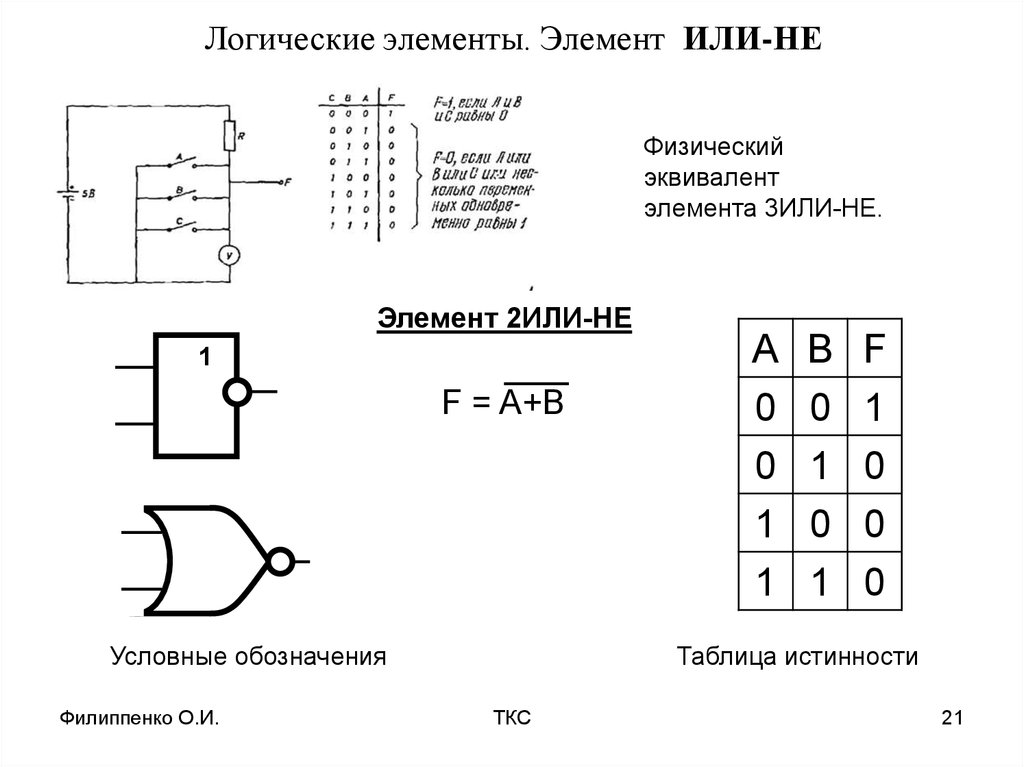 В вычислительной технике также часто используется операция исключающее ИЛИ (XOR), которая отличается от обыкновенного ИЛИ только при Х=1 и Y=1. Операция XOR фактически сравнивает на совпадение два двоичных разряда. Хотя теоретически основными базовыми логическими операциями всегда называют именно И, ИЛИ, НЕ, на практике по технологическим причинам в качестве основного логического элемента используется элемент И-НЕ. На базе элементов И-НЕ могут быть скомпонованы все базовые логические элементы (И, ИЛИ, НЕ), а значит и любые другие, более сложные.

Рис. 1. Логические элементы ИЛИ, И, НЕ в схемном представлении

Цифровые логические схемы: определение, применение и типы

Содержание

В настоящее время компьютеры и другие цифровые устройства основаны на электронных схемах. Если вы ничего не знаете о цифровых схемах, не волнуйтесь, мы здесь для вас.

Цифровые схемы состоят из транзисторов и других компонентов для создания логических элементов. Логические элементы можно комбинировать для создания логических схем, таких как сумматоры, мультиплексоры, счетчики и декодеры, которые решают определенные задачи, такие как сложение чисел или декодирование входной строки в осмысленный выход.

Цифровые схемы являются основой компьютеров. Они используются для различных целей, начиная от простых логических вентилей и заканчивая сложными микропроцессорами, отвечающими за выполнение инструкций на компьютере.

Расскажите нам больше о цифровых логических схемах с помощью этой статьи:

Цифровые логические схемы являются основой цифровых систем. Эти логические схемы представляют собой набор логических вентилей, которые показывают логическую эквивалентность между двумя разными группами двоичных чисел.

Эти цифровые логические схемы используют 0 и 1 для условий включения/выключения, где 0 означает состояние включения, а 1 — состояние отключения.

Цифровые логические схемы — это цифровые устройства, которые используют логические вентили, АЛУ, микропроцессоры, ОЗУ, ПЗУ для управления другими схемами. Это особая форма логической схемы, которая обрабатывает числовые значения 0 и 1.

Как работают цифровые схемы?

Цифровая схема преобразует ряд чисел в другой ряд чисел. Он предназначен для предоставления только одного выхода для любого заданного входа, и на выходе будет либо 0 В, либо 5 В. Это схема, которая использует дискретные значения напряжения для представления данных.

Наиболее распространенные цифровые схемы основаны на двоичной системе счисления, хотя в некоторых системах используются недвоичные значения. Цифровая схема содержит переключатели, которые либо включены, либо выключены. Он обрабатывает информацию как последовательность «1» и «0».

Почему мы используем цифровые схемы?

Цифровая схема — это электронная схема, которая использует дискретные количества информации, такие как логические уровни (т. е. не непрерывный диапазон, как аналоговый сигнал), для обработки информации и выполнения функций. Мы используем цифровую схему, потому что она может изменять уровень напряжения от 0В до 5В, что очень удобно для использования с микроконтроллером.

Цифровая схема — это способ хранения информации. Он использует двоичный код, в котором всего две цифры: ноль и единица. Цифровые схемы используются в калькуляторах, компьютерах, телевизорах и многих других устройствах.

Почему цифровые схемы также называют логическими схемами?

Цифровые схемы также называют логическими схемами, поскольку они выполняют логические операции над цифровыми сигналами. Цифровые схемы используют логические элементы, такие как И, ИЛИ, НЕ, НЕ-И и ИЛИ, для выполнения необходимых цифровых операций.

Цифровая схема — это схема, содержащая цифровую логику. Цифровые схемы являются наиболее распространенной физической реализацией булевой алгебры и двоичной арифметики и лежат в основе всех современных компьютеров.

Это связано с тем, что цифровые схемы в основном используются для обработки данных, которые имеют только два значения, например, истинное или ложное.

Другими словами, можно сказать, что основной функцией цифровой схемы является обработка информации, управляющей двоичной системой. Цифровые схемы называются логическими, потому что они выполняют логические операции и дают результаты, которые можно интерпретировать как истинные или ложные.

Каковы основные концепции цифровых схем и систем?

Цифровая схема, также известная как цифровая электроника, представляет собой отрасль электроники, которая выполняет различные задачи для выполнения множества требований с помощью цифровых сигналов. В основном эта схема используется для преодоления недостатков аналоговых систем.

Аналоговые системы медленнее, и полученные данные могут содержать ошибку. Схема разработана с использованием двоичных логических элементов, таких как ИЛИ, исключающее ИЛИ, НЕ, И-НЕ, ИЛИ, И. Эти логические элементы известны выполнением логических операций.

Эта конструкция помогает схеме переходить из одного состояния в другое. Входной сигнал, используемый для этой схемы, имеет цифровую форму, которая представляет собой двоичный формат 0 и 1.

Схема может быть двух видов: комбинационная или последовательная. Сначала он был запущен путем разработки более поздних электронных ламп, транзисторно-транзисторной логики TTL, логики с эмиттерной связью и логических реле CMOS.

Основные строительные блоки цифровых схем:

Логические элементы являются основным компонентом цифровых схем, которые могут выполнять преобразование двоичной информации. Цифровая схема содержит сеть из нескольких логических вентилей, которые взаимосвязаны друг с другом.

Каждые ворота имеют свой символ, которым они представлены, и алгебраическая функция определяет их работу. Таблица истинности может определить связь между выходными и входными переменными каждого вентиля. Временная диаграмма определяет возвратно-поступательное движение сигнала логических вентилей.

Основы аналоговых и цифровых электронных схем:

Интегральная схема является пульсом многих поколений современных инноваций в области электроники. Многие компании участвуют в проектировании, чтобы работать лучше, а также в разработке и производстве, чтобы предоставить больше новых кремниевых технологий, благодаря которым инженеры могут создавать новые ИС с хорошим функциональным оборудованием с хорошей производительностью и мощностью, новыми и лучшими электронными инновациями.

Ожидается, что глобальный объем данных увеличится с 897 эксабайт в 2020 году до 392 540 эксабайт к 2030 году, поскольку бизнес становится все более цифровым и, таким образом, поглощает и создает данные.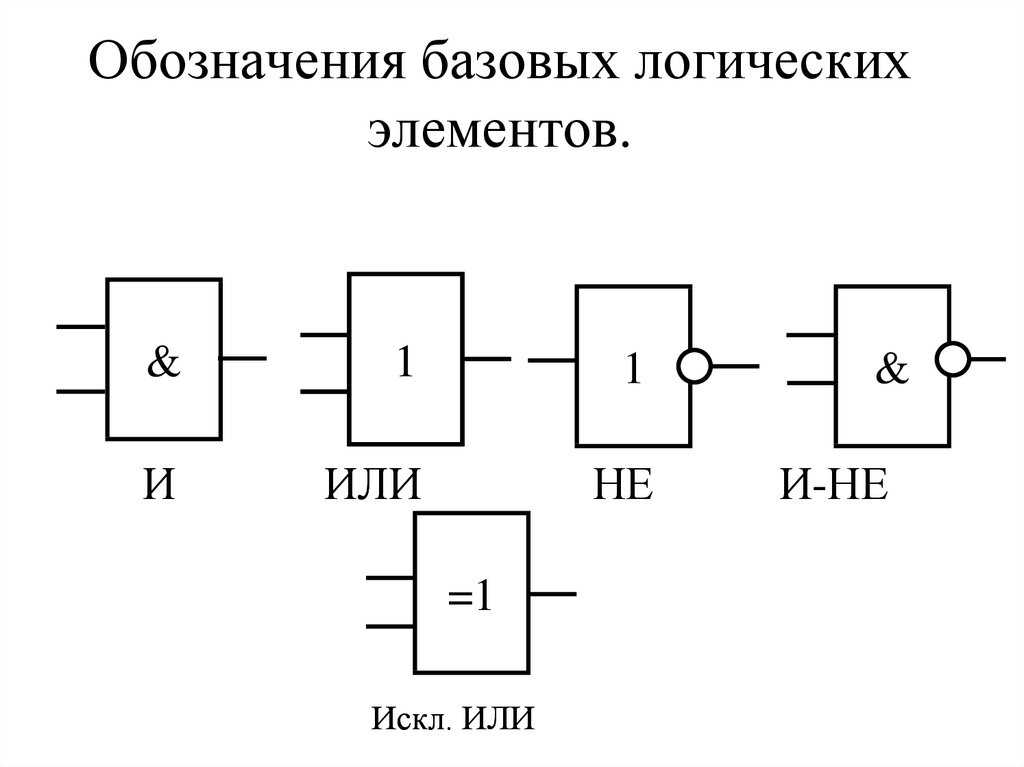

И ИС будут расти только тогда, когда они будут увеличиваться и расти во всем мире, как космические ракеты. Чтобы поставлять больше и производить больше, нам нужен хороший поставщик и надежный партнер, преданный делу компании, который предлагает лучшее решение на сегодняшний день и обеспечивает более совершенную разработку новых технологий, чтобы сделать компании более успешными.

Типы цифровых логических схем:

Кратко остановимся на некоторых типах цифровых логических схем:

1. Синхронные системы:

каждый компонент системы в данный момент определяет состояние во все последующие моменты времени. Асинхронная система — это система, в которой события и процессы происходят регулярно и повторяются.

Синхронные системы включают часы, наши циркадные ритмы и периодические явления, такие как приливы и волны. В электронике асинхронная система — это система, в которой временное поведение различных элементов связано друг с другом.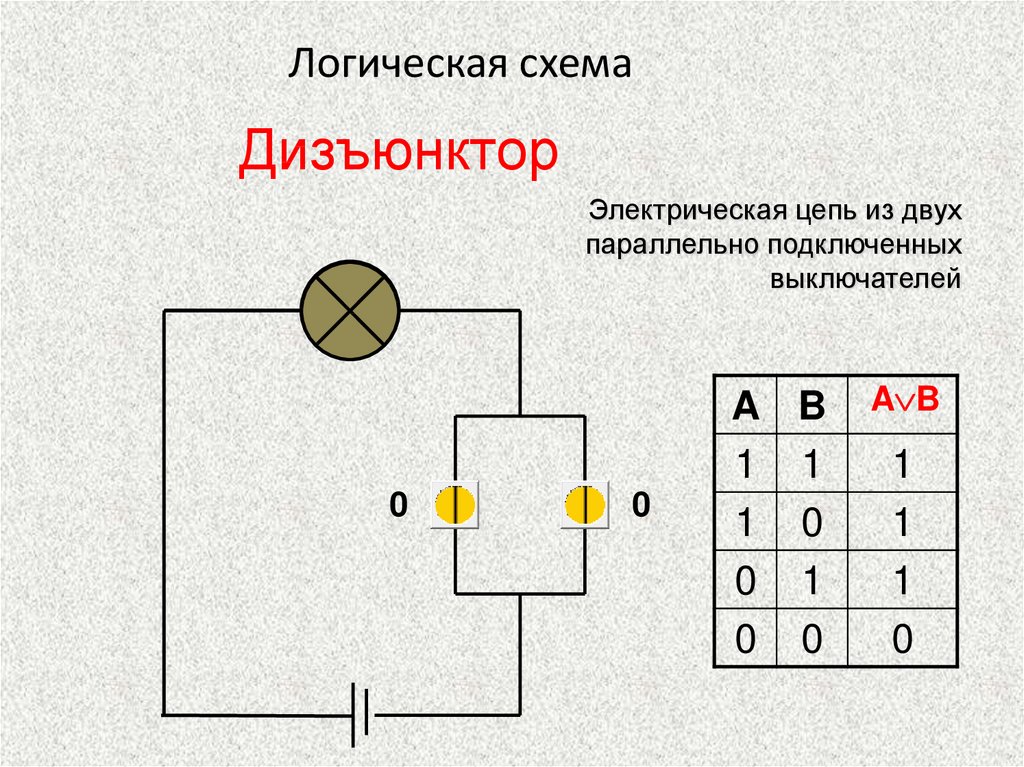 Время событий в синхронных системах зависит от часов сигналов.

2. Асинхронные системы:

Асинхронные системы отправляют сообщения и выполняют операции параллельно без необходимости ждать ответа. Это означает, что разные процессы могут происходить одновременно; то есть несколько функций могут выполняться одновременно.

Асинхронный означает отсутствие или возможность появления одновременно. Асинхронная система — это набор взаимодействующих частей, которые не имеют общего состояния и поэтому могут выполняться независимо.

3. Комбинационные логические схемы:

Комбинационная логика — это форма цифровой логики, в которой входной шаблон применяется к схеме, а выходной шаблон зависит только от этого входного шаблона. Логические элементы, несомненно, являются одним из самых основных и важных строительных блоков цифровых схем.

Они обычно используются для выполнения операций с двоичными сигналами. С другой стороны, комбинированные логические схемы — это электронные или компьютерные схемы, предназначенные для реализации булевых функций или логических процедур.

Эти схемы представляют собой схемы, которые выполняют свои операции только с входными сигналами.

4. Последовательные сети:

Сеть последовательности — это тип эквивалентной сети баланса, который используется для системы баланса мощности. Инвестиции и предполагаемые рабочие условия устанавливаются таким образом, чтобы в напряжении и токе могла присутствовать только одна составляющая последовательности.

Эти сети используются для расчета несимметричных повреждений, присутствующих в различных частях или точках сети энергосистемы.

Схемы аналого-цифровых преобразователей

Аналого-цифровые преобразователи (АЦП) и цифро-аналоговые преобразователи (ЦАП) — это схемы, преобразующие один вид информации в другой.

Аналого-цифровой преобразователь (АЦП) представляет собой электронную схему, преобразующую аналоговый сигнал в цифровую форму. Другое преобразование, известное как цифро-аналоговый преобразователь (ЦАП), преобразует цифровое слово в аналоговый сигнал.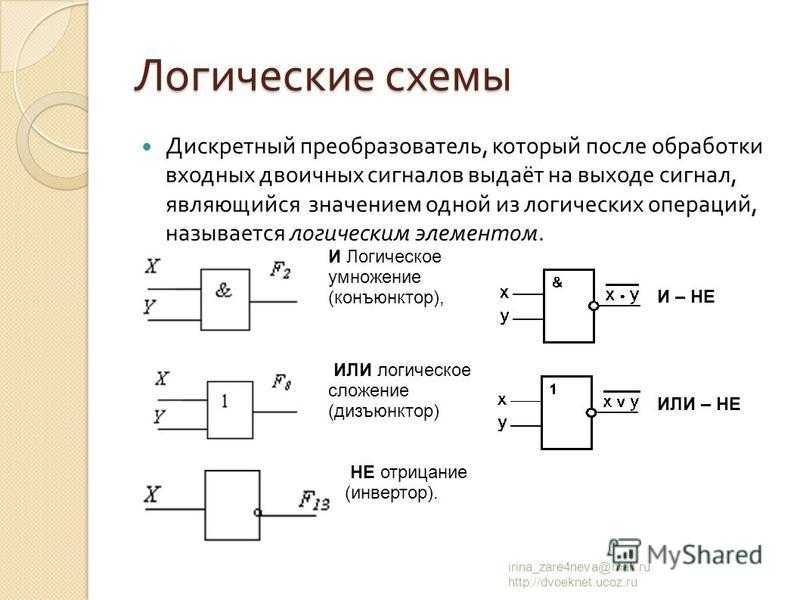

Вместе эти две схемы используются во многих приложениях, включая хранение, передачу и обработку данных. Он преобразует непрерывный поток аналоговых значений в дискретные цифровые значения. Затем это цифровое представление сохраняется в памяти или обрабатывается другими цифровыми системами.

Аналоговые и цифровые схемы :

Аналоговые и цифровые схемы являются основными строительными блоками всей современной электроники. Ключевое различие между аналоговой и цифровой электроникой заключается в представлении информации в виде сигналов.

Цифровые схемы представляют информацию в виде различных значений напряжения, таких как 0 В и 5 В, которые соответствуют «ложь» и «истина» в булевой логической системе. Аналоговая схема — это схема, которая представляет информацию в виде непрерывного диапазона напряжения.

Аналоговая схема — это схема, которая использует непрерывный диапазон значений для передачи информации. Напротив, цифровая схема представляет информацию дискретными шагами или уровнями.

В чем разница между цифровыми схемами и цифровой электроникой?

Цифровые схемы и цифровая электроника — это одно и то же, но они используются по-разному. Оба метода манипулируют двоичными сигналами для создания логических функций, но они также генерируют схемы переключения или логические вентили в цифровой электронике.

Цифровая электроника в основном основана на уровнях напряжения. Цифровые схемы, с другой стороны, преобразуют сигналы в форму, которую может обработать компьютер или микропроцессор. Он использует логические вентили для управления цифровыми сигналами.

С другой стороны, цифровые схемы — это устройства, которые используются для выполнения логических операций с цифровыми сигналами с использованием этих логических элементов. Цифровые схемы — это электрические схемы, в которых используются дискретные уровни напряжения, такие как двоичная (с основанием 2) логика.

Наиболее распространенный тип схем в компьютерных системах.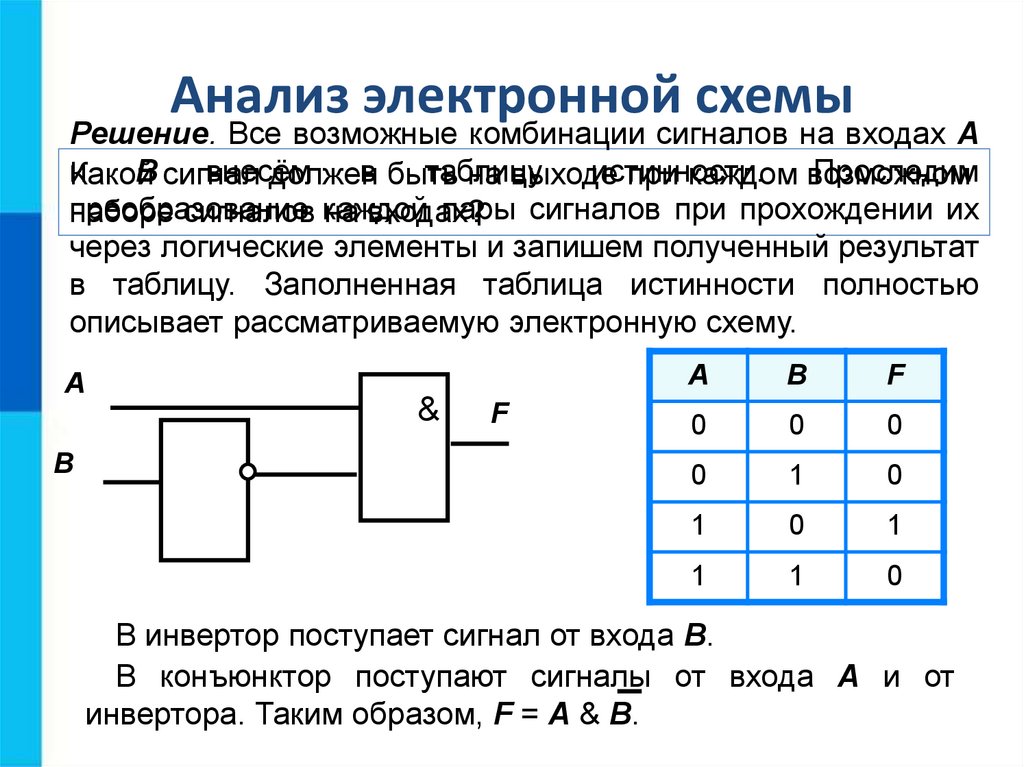 Напротив, цифровая электроника — это электронные схемы, используемые для создания цифровых схем (например, компьютеров).

Цифровая электроника имеет дело с цифровыми интегральными схемами (ИС), которые выполняют определенные вычислительные функции с использованием двоичных чисел. Цифровые схемы в основном состоят из логических вентилей.

Их также называют комбинационными схемами, потому что выходы зависят исключительно от текущих входов и не зависят от истории входов.

Цифровые ИС содержат множество транзисторов, резисторов, конденсаторов, диодов и т. д., предназначенных для выполнения определенных операций, таких как сложение, умножение, сдвиг и т. д.

Что такое проектирование цифровых интегральных схем?

Проектирование цифровых интегральных схем — это процесс проектирования схем, выполняющих логические операции с использованием цифровых схем. Это делается путем создания двух или более электронных устройств и их соединения проводами.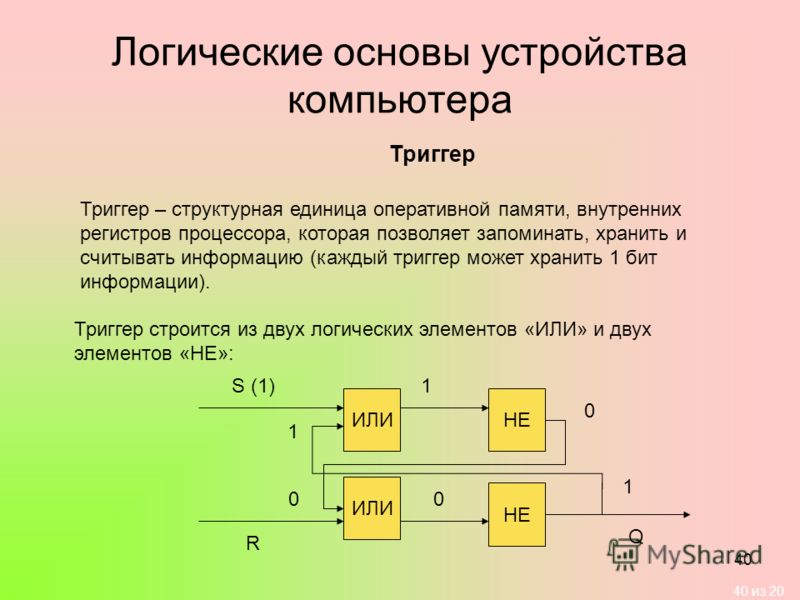

Наиболее распространенная цифровая логическая система представляет собой набор транзисторов, соединенных в последовательность логических элементов, управляющих двоичными числами (0 и 1).

Эти двоичные числа представляют информацию, которую будет обрабатывать схема.

Процесс проектирования аналоговых и цифровых схем. Он предполагает междисциплинарный подход к области электротехники. Целью этой деятельности является предоставление новых электронных продуктов или обновление существующих продуктов.

Проектирование цифровых интегральных схем — это метод проектирования электронных схем, с помощью которого цифровые сигналы преобразуются в эквивалентные двоичные коды, а полученные коды используются в качестве входных данных для создания аппаратных средств из этих двоичных кодов.

Почему цифровые схемы должны быть двоичными?

Цифровые схемы известны как основа современной электроники. Они повсюду в нашем мире — в наших телефонах, компьютерах, автомобилях и т.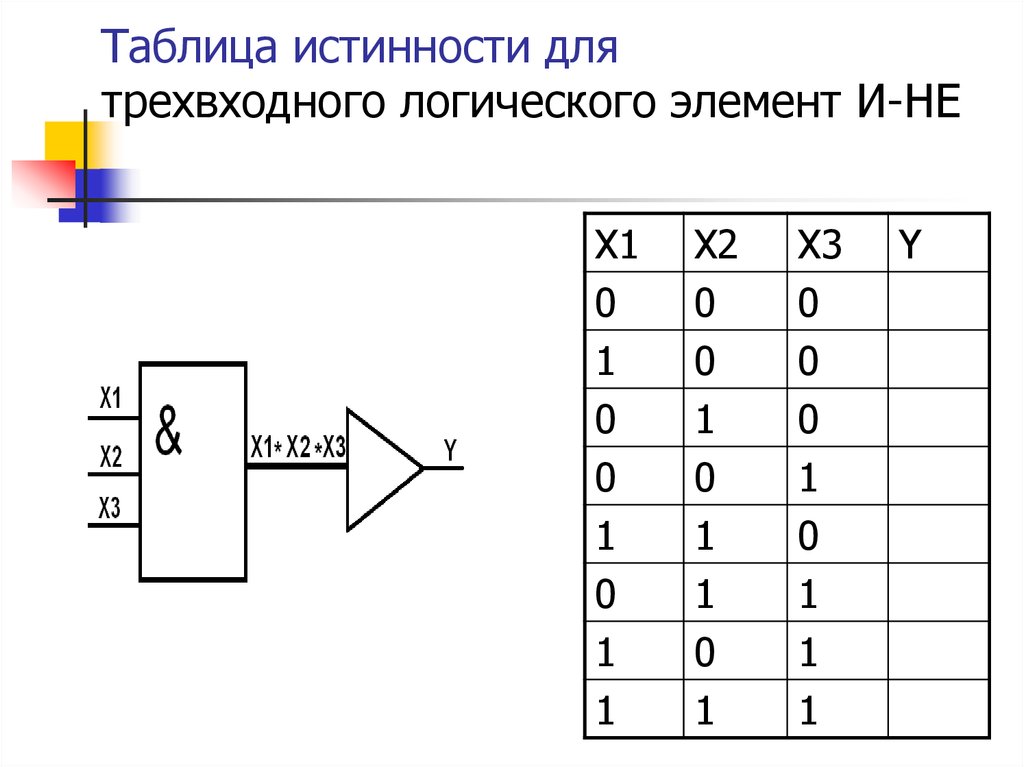 д. Вы когда-нибудь задумывались, почему все они двоичные?

Ответ заключается в том, что цифровые схемы используют двоичную логику, потому что это самый простой способ манипулирования информацией. Основным преимуществом цифровых схем по сравнению с аналоговыми является точность и скорость.

Из чего состоит цепь?

Цепи по праву можно считать неотъемлемой частью нашей повседневной жизни. Цепь можно правильно назвать путем или соединением, которое формируется между различными точками.

Это может быть физический путь, например маршрут, по которому вы каждый день едете на работу, или это могут быть электрические соединения в вашем телефоне. Схема — это электронное устройство, которое может быть изготовлено из различных компонентов.

Он использует электрический ток для передачи энергии, данных или сигнала от одного компонента к другому.

Цепь состоит из полупроводников, соединенных проводами. Полупроводники — это материалы, которые могут проводить электричество при определенных условиях, в то время как изоляторы не пропускают электричество.

Цепь — это путь, по которому движутся электроны при движении через материал. В него входят проволока, бусины, металлические полоски и другие материалы. Когда электроны движутся по проводу, они проходят через разные части цепи.

Почему мы используем резистор в цепях?

Резистор — это электрический компонент, препятствующий протеканию тока в цепи. Обычно он находится последовательно с другими электронными компонентами, такими как конденсаторы и катушки индуктивности, и образует часть электронной схемы.

Резисторы являются одним из наиболее распространенных компонентов электрических цепей. Они бывают разных форм, размеров и упаковок.

Их основная цель — ограничить ток в цепи путем преобразования части его в тепло. Их основная цель — ограничить протекание тока в цепи путем преобразования части его в тепло. Узнайте больше о резисторах.

Лучшие тренажеры для цифровых логических вентилей Производитель, поставщик и экспортер:

Tesca Technologies Pvt. Ltd. является одним из самых известных производителей, поставщиков и экспортеров широкого спектра цифровых логических схем по всему миру. У нас есть возможности для реализации проектов «под ключ» для международных тендеров с отличной технической и маркетинговой поддержкой.

Брошюра Tesca Technologies Получить сейчас

Логические вентили | Учебное пособие по архитектуре компьютера

Двоичная информация представлена ​​в цифровых компьютерах физическими величинами, называемыми сигнализирует . Электрические сигналы, такие как напряжения, существуют в компьютере в одном из двух распознаваемых состояний. Два состояния представляют собой двоичную переменную, которая может быть равна 1 или 0.

Например, конкретный цифровой компьютер может использовать сигнал 3 вольта для представления двоичного числа 1 и 0,5 вольта для представления двоичного числа 0 . Теперь входные клеммы цифровых схем будут принимать двоичные сигналы только 3 и 0,5 вольта для представления двоичного ввода и вывода, соответствующих 1 и 0 соответственно.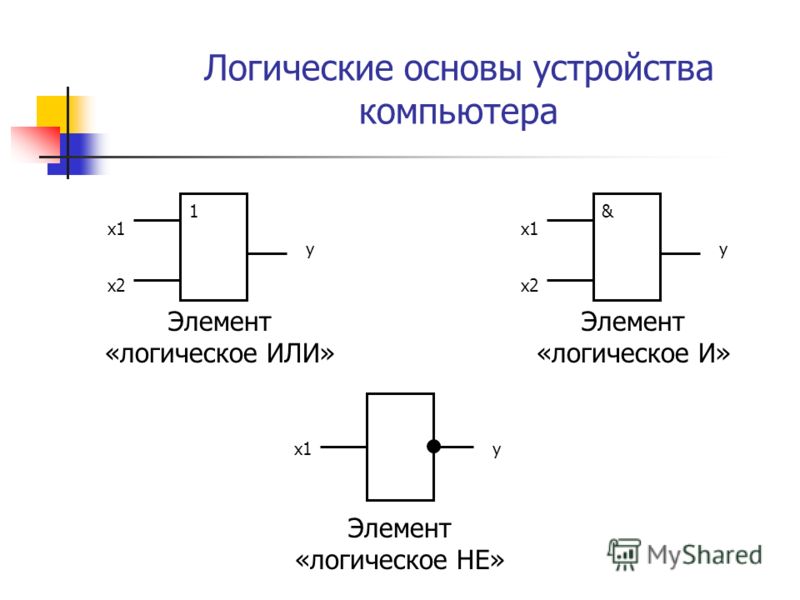

Итак, теперь мы знаем, что на уровне ядра компьютер общается в виде сигналов 0 и 1 , которые являются ничем иным, как низким и высоким сигналами напряжения.

Но как над этими сигналами выполняются различные операции? Это делается с использованием другой логики Gates .

---

Что такое ворота?

Двоичная логика имеет дело с двоичными переменными и с операциями, которые имеют логический смысл. Он используется для описания в алгебраической или табличной форме манипуляций, выполняемых логическими схемами, называемыми 9.0215 ворота .

Ворота представляют собой аппаратные блоки, которые создают графические символы, и их работа может быть описана с помощью алгебраического выражения. Отношение ввода-вывода двоичных переменных для каждого вентиля может быть представлено в табличной форме с помощью таблицы истинности.

Самые простые логические элементы: И и включительно ИЛИ с несколькими входами и НЕ с одним входом.

Каждый вентиль с более чем одним входом чувствителен к логическому 0 или логической 1 на любом из своих входов, генерируя выход в соответствии со своей функцией. Например, логический элемент И с несколькими входами чувствителен к логическому 0 на любом из своих входов, независимо от любых значений на других входах.

Различные логические элементы:

1. И
2. ИЛИ
3. НЕ
4. НЕ-И
5. НИ
6. Исключающее ИЛИ
7. Исключающее ИЛИ

---

Элемент И

Элемент И выполняет логическую функцию И, то есть выход равен 1, если вход A и вход B равны 1; в противном случае выводится 0.

Алгебраический символ функции И такой же, как символ умножения обычной арифметики.

Мы можем либо использовать точку между переменными, либо объединить переменные без символа операции между ними. Элементы И могут иметь более двух входов, и по определению выход равен 1 тогда и только тогда, когда все входы равны 1.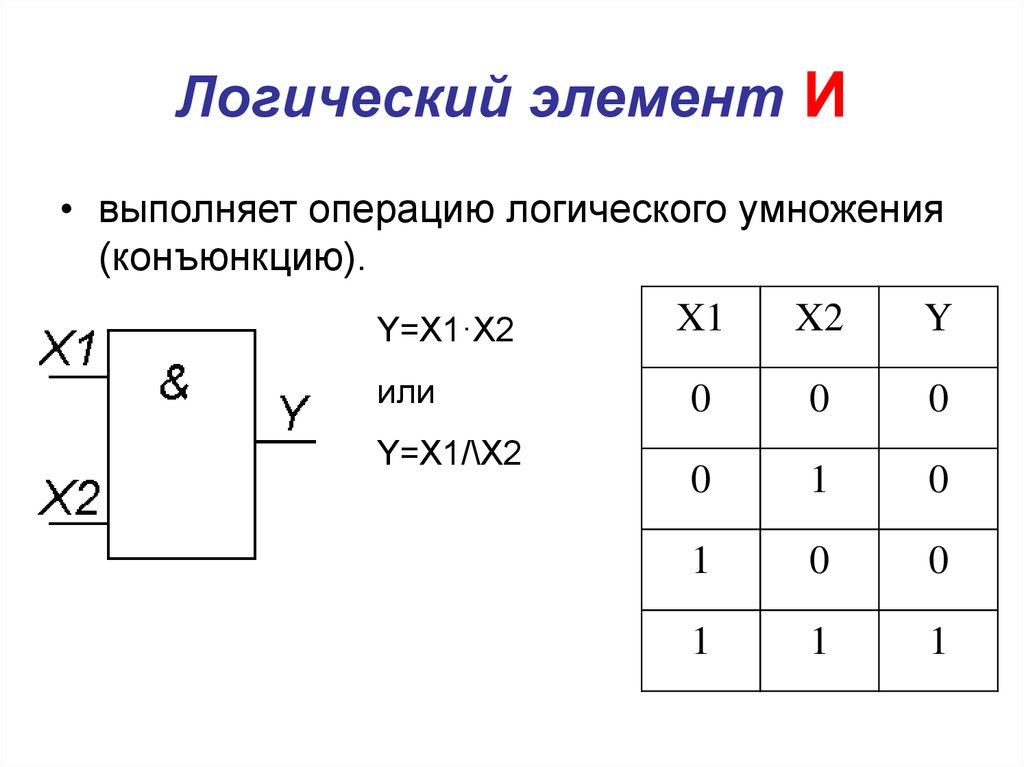

---

Элемент ИЛИ

Элемент ИЛИ производит функцию включающего ИЛИ; то есть выход равен 1, если вход A или вход B или оба входа равны 1; в противном случае выход равен 0.

Алгебраический символ функции ИЛИ равен + , аналогично арифметике дополнение .

Элементы ИЛИ могут иметь более двух входов, и по определению выход равен 1, если любой вход равен 1.

---

Элемент инвертора (НЕ)

Схема инвертора инвертирует логический смысл двоичного сигнала. Он производит НЕ, или функцию дополнения.

Алгебраический символ, используемый для логического дополнения, представляет собой штрих или черту над переменным символом.

---

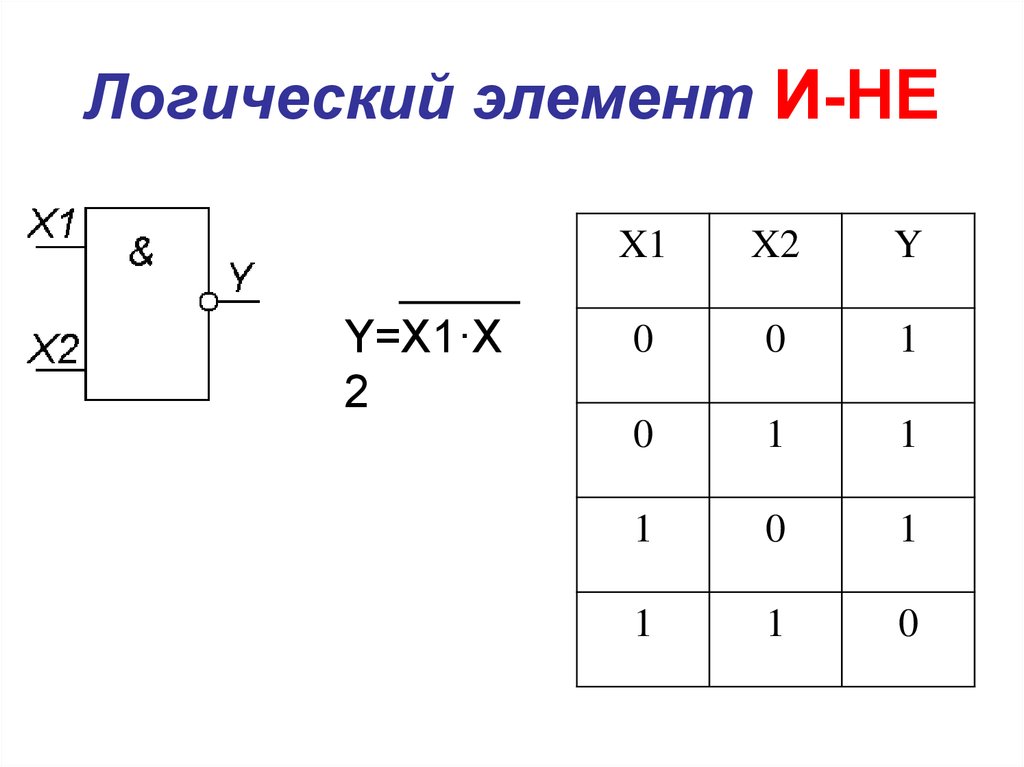
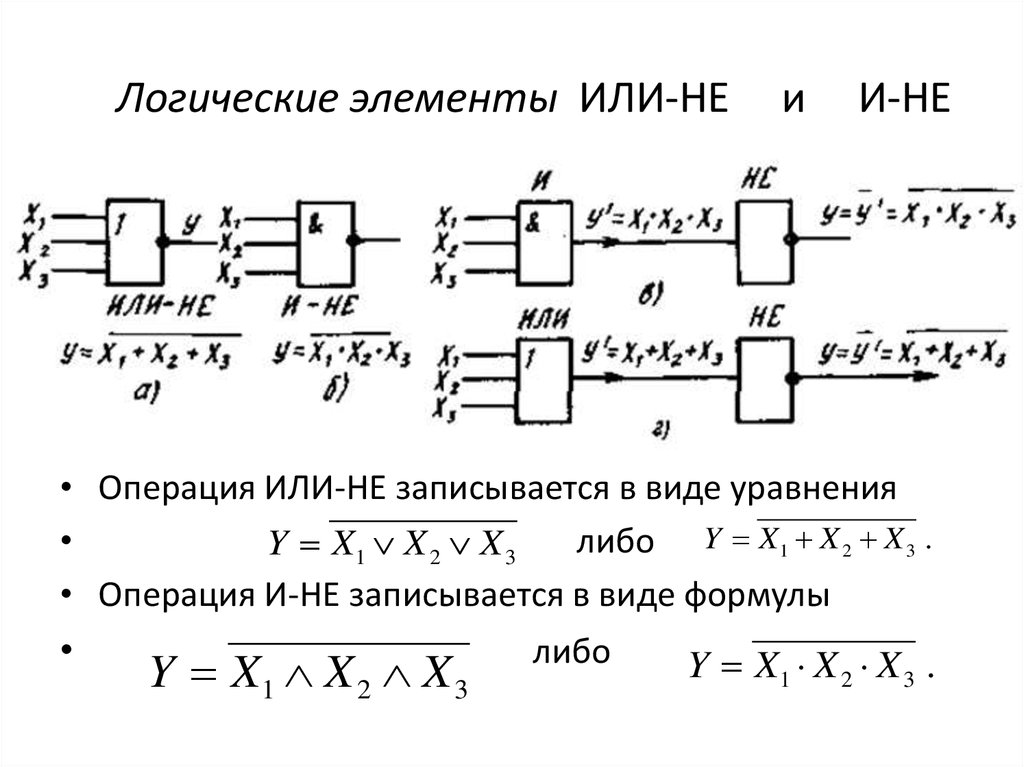
Ворота И-НЕ

Функция НЕ-И является дополнением к функции И, на что указывает графический символ, состоящий из графического символа И, за которым следует маленький кружок.

Обозначение НЕ-И происходит от аббревиатуры НЕ-И.

---

Схема ИЛИ-НЕ

Схема ИЛИ-НЕ является дополнением схемы ИЛИ и использует графический символ ИЛИ, за которым следует маленький кружок.