Бинарные числа: двоичная система счисления
Бинарные числа — это числа из двоичной системы счисления, имеющей основание 2. Она непосредственно реализована в цифровой электронике, используется в большинстве современных вычислительных устройств, включая компьютеры, мобильные телефоны и разного рода датчики. Можно сказать, что все технологии нашего времени построены на бинарных числах.
Запись чисел
Любое число, сколь бы большим оно ни было, в двоичной системе записывается посредством двух символов: 0 и 1. Например цифра 5 из всем знакомой десятичной системы в двоичной будет представлено как 101. Бинарные числа могут быть обозначены префиксом 0b или амперсандом (&), например: &101.
Во всех системах счисления, исключая десятичную, символы читаются по одиночке, то есть взятое в пример 101 читается как «один ноль один».
Перевод из одной системы в другую
Программисты, постоянно работающие с двоичной системой счисления, на ходу могут перевести бинарное число в десятичное.
Это действительно можно сделать и без всяких формул, особенно если человек имеет представление о том, как работает самая малая часть компьютерного «мозга» — бит.
Цифра ноль так же обозначает 0, а цифра один в двоичной системе тоже будет единицей, но что делать дальше, когда цифры закончились? Десятичная система «предложила» бы в таком случае ввести термин «десяток», а в бинарной системе это будет называться «двойка».
Если 0 это &0 (амперсанд — обозначение двоичной системы), 1 = &1, то 2 будет обозначаться как &10. Тройку тоже можно записать в двух разрядах, она будет иметь вид &11, то есть одна двойка и одна единица. Возможные комбинации исчерпаны, и в десятичной системе на этом этапе вводятся сотни, а в двоичной — «четверки». Четыре — это &100, пять — &101, шесть — &110, семь — &111. Следующая, более крупная единица счета — это восьмерка.
Можно заметить особенность: если в десятичной системе разряды умножаются на десять (1, 10, 100, 1000 и так далее), то в двоичной, соответственно, на два: 2, 4, 8, 16, 32.
Это соответствует размеру флеш-карт и прочих накопителей, использующихся в компьютерах и других устройствах.
Что такое бинарный код
Числа, представленные в двоичной системе счисления, называются бинарными, однако в таком виде можно представить и не числовые значения (буквы и символы). Таким образом, в цифрах можно закодировать слова и тексты, правда вид они будут иметь не столь лаконичный, ведь для записи всего одной буквы потребуется несколько нолей и единиц.
Но каким образом компьютерам удается считывать такое количество информации? На самом деле все проще, чем кажется. Люди, привыкшие к десятичной системе счисления, сначала переводят двоичные числа в более привычные, и только потом производят с ними какие-либо манипуляции, а в основе компьютерной логики изначально лежит бинарная система чисел. Единице в технике соответствует высокое напряжение, а нулю — низкое, либо для единицы напряжение есть, а для ноля вообще отсутствует.
Бинарные числа в культуре
Ошибкой будет считать, что двоичная система счисления — это заслуга современных математиков.
Хотя бинарные числа и являются основополагающими в технологиях нашего времени, использовались они уже очень давно, причем в разных уголках планеты. Используются длинная линия (единица) и прерывистая (ноль), кодирующие восемь символов, означающих восемь стихий: небо, землю, гром, воду, горы, ветер, огонь и водоем (массу воды). Этот аналог 3-битных цифр описывался в классическом тексте книги Перемен. Триграммы составляли 64 гексаграммы (6-битные цифры), порядок которых в книге Перемен был расположен в соответствии с двоичными цифрами от 0 до 63.
Этот порядок был составлен в одиннадцатом веке китайским ученым Шао Юном, хотя нет доказательств того, что он действительно понимал двоичную систему счисления в целом.
В Индии еще до нашей эры тоже применялись бинарные числа в математической основе для описания поэзии, составленные математиком Пингалой.
Узелковая письменность инков (кипу) считается прообразом современных баз данных. Именно они впервые применили не только бинарный код числа, но и не числовые записи в двоичной системе.
Узелковое письмо кипу характерно не только первичными и дополнительными ключами, но и использованием позиционных чисел, кодированием с помощью цвета и сериями повторений данных (циклами). Инки впервые применили способ ведения бухгалтерского учета, называемый двойной записью.
Первый из программистов
Двоичную систему счисления, основанную на цифрах 0 и 1, описал и знаменитый ученый, физик и математик, Готфрид Вильгельм Лейбниц. Он увлекался древней китайской культурой и, изучая традиционные тексты книги Перемен, заметил соответствие гексаграмм бинарным числам от 0 до 111111. Он восхитился свидетельствам подобных достижений в философии и математике для того времени. Лейбница можно назвать первым из программистов и информационных теоретиков. Именно он обнаружил, что если записать группы двоичных чисел вертикально (одно под другим), то в получившихся вертикальных столбцах чисел будут регулярно повторяться ноли и единицы. Это позвонило ему предположить, что возможно существование совершенно новых математических законов.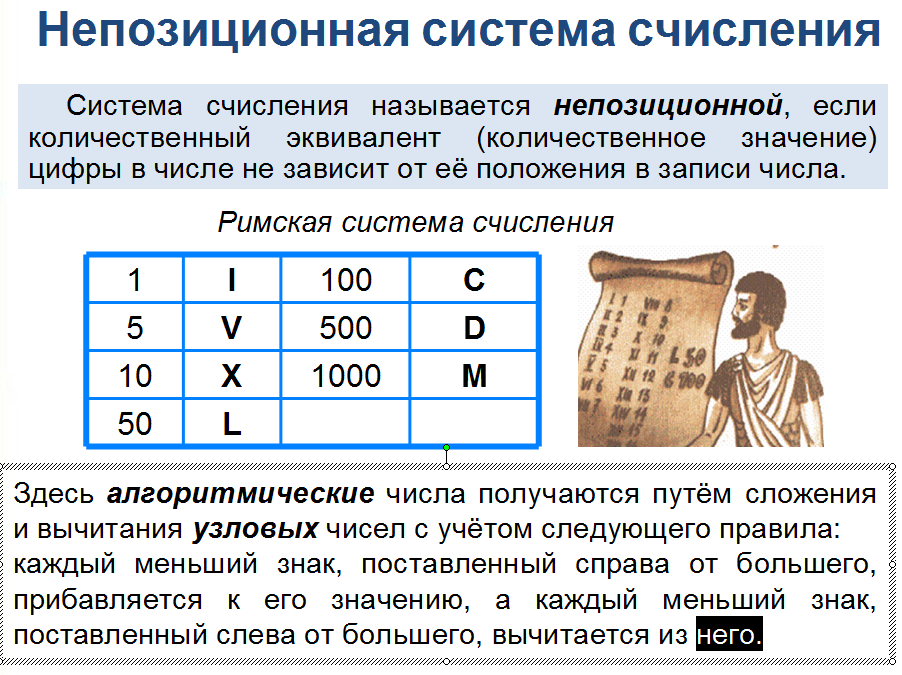
Лейбниц понял и то, что бинарные числа оптимальны для применения в механике, основой которой должна быть смена пассивных и активных циклов. На дворе был 17 век, а этот великий ученый изобрел на бумаге вычислительную машину, работавшую на основе его новых открытий, однако быстро понял, что цивилизация еще не достигла такого технологического развития, и в его время создание такой машины будет невозможным.
Двоичное счисление — SBP-Program
Автор: Субботин Б.П.
- Перевод двоичного числа в десятичное
- Двоичные дроби
- Перевод дробного двоичного числа в десятичное
- Двоичная система счисления: как сравнить два числа?
- Двоичная система счисления: сложение
- Двоичная система счисления: вычитание
- Двоичная система счисления: умножение
- Двоичная система счисления: деление
Двоичное счисление имеет в своей основе только две цифры: 0 и 1. Все числа записывают с помощью этих двух цифр. Основание двоичной системы счисления равно двум.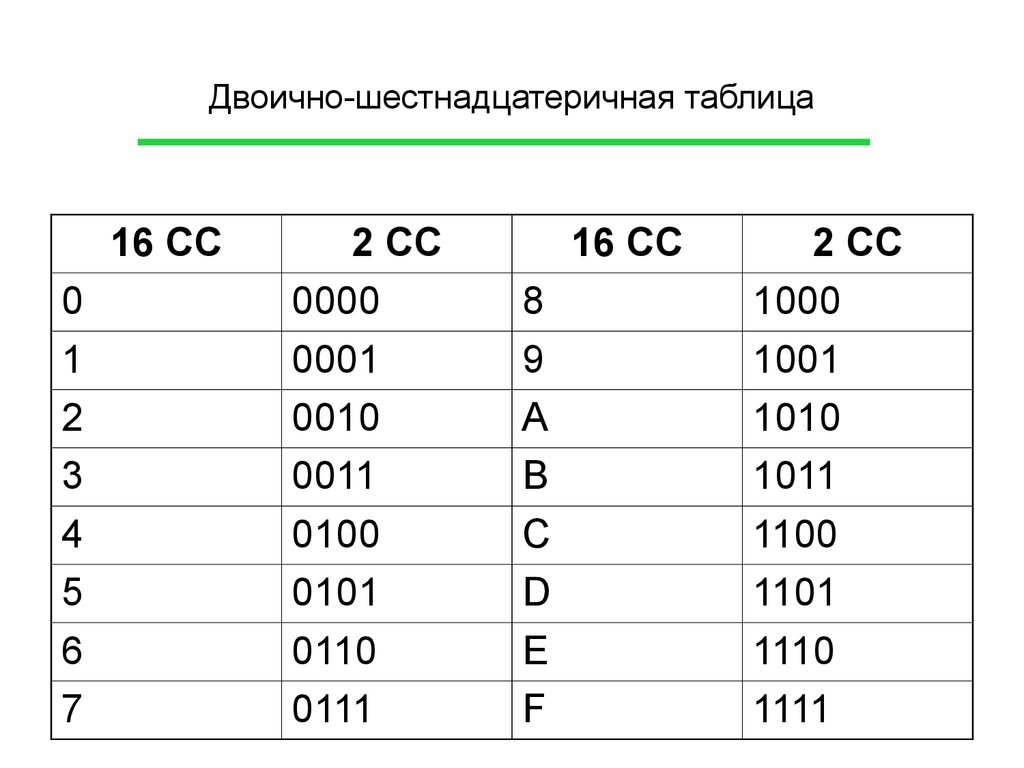
Двоичная система счисления применяется в компьютерной технике. Бит — это наименьшая единица информации. Слово «бит», по-английски bit, происходит от «binary digit», что значит «двоичная цифра». Бит может быть единицей или нулём, ведь в двоичной системе счисления имеются только две цифры: 0 и 1.
Двоичное счисление относится к позиционным системам счисления. Это значит, что значение двоичного числа связано с позициями цифр в нём. Пример: двоичные числа 1101 и 1011 составлены из одинакового количества единиц и нулей, но позиции их различны, значит и числа различны.
Вот таблица позиций числа 1101:
Теперь таблица позиций числа 1011:
Номера позиций начинаются с нуля.
Перевод двоичного числа в десятичное
Основание двоичной системы счисления равно двум, это мы будем использовать. Каждую двоичниую цифру в двоичном числе умножим на два в степени, равной номеру позиции двоичной цифры в числе. Для примера возьмём числа из предыдущего раздела: 1101 и 1011 и найдём их десятичные эквиваленты.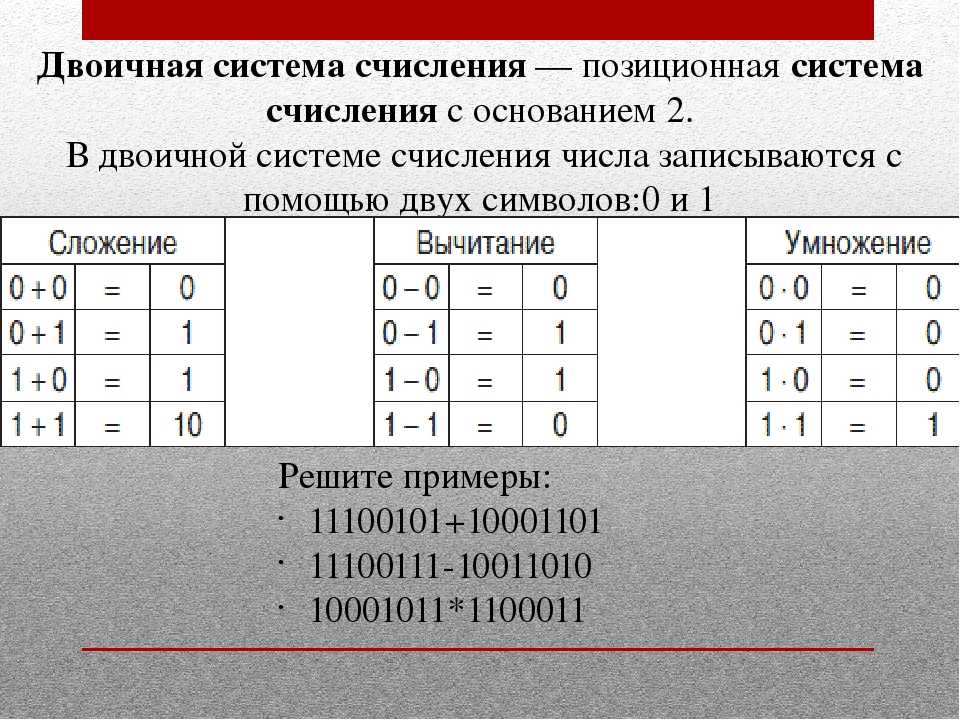
Вот таблица позиций числа 1101:
Степени 2 равны номеру позиции.
Итак, двоичное число 1101 равно 13 в десятичной системе счисления.
Теперь число 1011. Его таблица позиций:
Степени 2 равны номеру позиции.
Итак, двоичное число 1011 равно 11 в десятичной системе счисления.
Наверх
Двоичные дроби
Дроби в двоичной системе счисления записывают как и в десятичной:
1101,1101
Таблица позиций числа 1101,1101
Позиции дробной части начинаются с -1.
Наверх
Перевод дробного двоичного числа в десятичное
Переведём двоичное дробное число 1101,1101 в десятичную дробь.
Таблица позиций числа 1101,1101
Степени 2 равны номеру позиции.
Итак, двоичное число 1101,1101 равно 13,8125 в десятичной системе счисления.
Наверх
Двоичная система счисления: как сравнить два числа?
Двоичные числа сравнивают также, как и в десятичной системе счисления, примеры:
100 > 10
100 < 110
111 < 1111
111 < 1000
Наверх
Двоичная система счисления: сложение
Правила сложения двоичных чисел аналогичны правилам в десятичной системе счисления.
Таблица сложения в двоичной системе счисления:
1 + 1 = 10
1 + 0 = 1 и 0 + 1 = 1
0 + 0 = 0
Здесь все числа двоичные.
Пример в двоичной системе счисления:
1 + 0 = 1
Переведём левую и правую части этого равенства в десятичную систему:
1 * 20 + 0 * 20 = 1 * 20
получаем в десятичной системе:
1 + 0 = 1
Пример:
Сложим числа 1001 и 10. Складывать будем «столбиком», как и в десятичной системе счисления:
Пример:
Сложим 100 и 100:
Пример:
Сложим 101 и 101:
Наверх
Двоичная система счисления: вычитание
Таблица вычитания двоичных чисел:
10 — 1 = 1
1 — 0 = 1
1 — 1 = 0
0 — 0 = 0
Здесь все числа двоичные.
Пример в двоичной системе счисления:
10 — 1 = 1
Переведём левую и правую части этого равенства в десятичную систему:
1 * 21 + 0 * 20 — 1 * 20 = 1 * 20
получаем в десятичной системе:
2 + 0 — 1 = 1
Пример.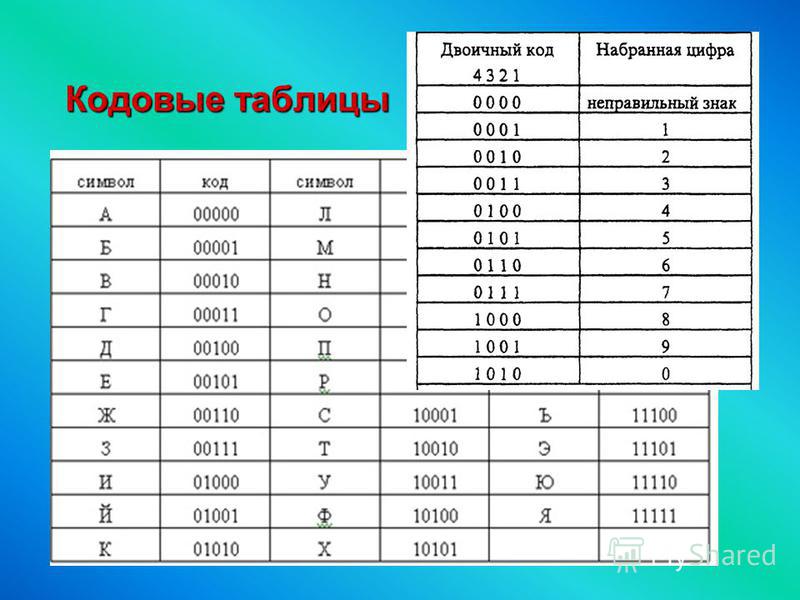
Вычтем из числа 100 число 10. Вычетать будем «столбиком», как и в десятичной системе счисления:
Здесь сначала из правого нуля в 100 вычли ноль, а после, чтоб из среднего нуля в 100 вычесть 1, мы заняли 1 из позиции 3. Всё как в десятичной системе, но в нашем распоряжении только 0 и 1 и таблица вычитания.
Пример. Вычтем из числа 1001 число 10.
Пример. Вычтем из числа 1000 число 1.
Наверх
Двоичная система счисления: умножение
1 * 1 = 1
1 * 0 = 0 и 0 * 1 = 0
0 * 0 = 0
Здесь все числа двоичные.
Пример. Умножать будем «столбиком», как и в десятичной системе счисления:
Пример:
Наверх
Двоичная система счисления: деление
Используя таблицу вычитания и таблицу умножения для двоичных чисел, делим подобно тому, как мы делим десятичные числа.
Пример деления двоичных чисел:
| ]]> | ]]> |
Наверх
Что такое двоичный код и как он используется в вычислениях?
По
- Рахул Авати
Двоичный описывает схему нумерации, в которой есть только два возможных значения для каждой цифры — 0 или 1 — и является основой для всего двоичного кода, используемого в вычислительных системах.
Термин двоичный также относится к любой системе цифрового кодирования/декодирования, в которой есть ровно два возможных состояния. В памяти, хранении, обработке и передаче цифровых данных значения 0 и 1 иногда называют low и high соответственно. В транзисторах 1 означает поток электричества, а 0 означает отсутствие потока электричества.
Двоичная система счисления была усовершенствована в 17 веке Готфридом Лейбницем. В математике и вычислительных системах двоичная цифра или бит — это наименьшая единица данных. Каждый бит имеет единственное значение либо 1, либо 0, что означает, что он не может принимать никакое другое значение.
Компьютеры могут представлять числа с помощью двоичного кода в виде цифровых единиц и нулей внутри центрального процессора (ЦП) и ОЗУ. Эти цифровые числа являются электрическими сигналами, которые либо включены, либо выключены внутри ЦП или ОЗУ.
Поскольку двоичная система использует только две цифры или бита и представляет числа с использованием различных комбинаций единиц и нулей, она известна как система с основанием 2 . Здесь 1 означает «включено» или «истинно», а 0 означает «выключено» или «ложно».
Напротив, десятичная система счисления представляет собой систему с основанием 10 , где каждое возможное место в числе может быть одним из 10 цифр (0-9). В многозначном числе крайняя правая цифра стоит на первом месте, цифра рядом с ней слева — на 10-м месте, цифра левее — на 100-м месте и так далее.
Пример
В четырехзначном числе 1980 вот места, занимаемые каждой цифрой.
| 1 | 9 | 8 | 0 |
1000 место | 100 место | 10 место | 1 место |
Двоичная система счисления является основой всех вычислительных систем и операций. Он позволяет устройствам хранить, получать доступ и манипулировать всеми типами информации, направляемой в ЦП или память и из них. Это позволяет разрабатывать приложения, которые позволяют пользователям делать следующее:
- просмотр веб-сайтов;
- создавать и обновлять документы;
- играть в игры;
- просмотра потокового видео и других видов графической информации; программное обеспечение доступа
- ; и
- выполнять расчеты и анализ данных.
Двоичная схема цифровых единиц и нулей предлагает простой и элегантный способ работы компьютеров. Он также предлагает эффективный способ управления логическими схемами и определения истинного (1) и ложного (0) состояний электрического сигнала.
Двоичная система является основным языком вычислительных систем. Внутри этих систем двоичное число состоит из последовательности восьми битов. Эта серия известна как байт . В двоичной схеме положение каждой цифры определяет ее десятичное значение. Таким образом, зная положение каждого бита, двоичное число можно преобразовать в десятичное число.
В десятичных числах каждое дополнительное место умножается на 10 при движении справа налево (первое место, 10-е место, 100-е место и т. д.). Но в двоичных числах каждое дополнительное место при движении справа налево умножается на два. Два приведенных ниже примера поясняют эту идею.
Пример 1
Вот как вычисляются десятичные значения для 8-битного (байтового) двоичного числа 01101000.
В этом номере первая цифра крайняя справа, а восьмая цифра крайняя левая. Цифры со второй (0) по седьмую (1) читаются справа налево.
Битовая позиция | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Бит | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
Двоично-десятичный расчет (экспонента) | 2 0 | 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 | 2 7 |
Десятичное значение (x2) | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
По мере увеличения позиции бита с единицы до восьми предыдущее десятичное значение умножается на два.
Вот почему первый бит имеет значение 1, второй бит имеет значение 2, третий бит имеет значение 4 и так далее.
Окончательное значение десятичного числа вычисляется путем сложения отдельных значений из приведенной выше таблицы. Однако следует добавлять только те значения, в которых бит равен 1. Эти значения представляют положение «включено». Нули представляют положение «выключено», поэтому они не учитываются при вычислении десятичного значения.
Итак, для двоичного числа 01101000 десятичное значение вычисляется следующим образом:
8 + 32 + 64 = 104
Пример 2
Вот как вычисляются десятичные значения для двоичного числа 11111111.
Битовая позиция | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Бит | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Двоично-десятичный расчет (экспонента) | 2 0 | 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 | 2 7 |
Десятичное значение | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
В этом двоичном числе каждый бит имеет значение 1, поэтому складываются все отдельных значений.
Итак, для этого числа , десятичное значение следующее:
1 + 2 + 4 + 8 + 16+ 32 + 64 +128 = 255
Представление десятичных чисел в двоичном форматеКак упоминалось ранее, двоичная система счисления работает только с 1 и 0. Однако положение только этих двух цифр может представлять гораздо больше чисел. Примеры в предыдущем разделе показывают, как любое десятичное число от 0 до 255 может быть представлено с помощью двоичных чисел. Числа больше 255 также можно представить, добавив больше битов к 8-битному двоичному числу.
Вот десятичные числа от нуля до 20 и их двоичные эквиваленты.
| Десятичное число | Двоичный номер | Десятичное число | Двоичный номер |
0 | 0 | 11 | 1011 |
1 | 1 | 12 | 1100 |
2 | 10 | 13 | 1101 |
3 | 11 | 14 | 1110 |
4 | 100 | 15 | 1111 |
5 | 101 | 16 | 10000 |
6 | 110 | 17 | 10001 |
7 | 111 | 18 | 10010 |
8 | 1000 | 19 | 10011 |
9 | 1001 | 20 | 10100 |
10 | 1010 | — | — |
Преобразование двоичных чисел в текстовые символыДвоичные числа можно преобразовать в текстовые символы, используя коды американского стандарта для обмена информацией (ASCII) для хранения информации в ОЗУ или ЦП компьютера. Приложения с поддержкой ASCII, такие как текстовые процессоры, могут считывать текстовую информацию из ОЗУ или ЦП. Они также могут хранить текстовую информацию, которая затем может быть извлечена пользователем позднее. Коды ASCII хранятся в таблице ASCII, состоящей из 128 текстовых или специальных символов. Каждый символ имеет соответствующее десятичное значение.
символов ASCII включают символы a-z, A-Z, 0-9 и набор знаков препинания. В первом примере предыдущего раздела двоичное число равно 01101000 (десятичное число 104). В ASCII это число будет h в нижнем регистре. Чтобы образовать слова, нужно добавить больше букв к h . В двоичном выражении это означает добавление дополнительных двоичных чисел к двоичному числу для ч .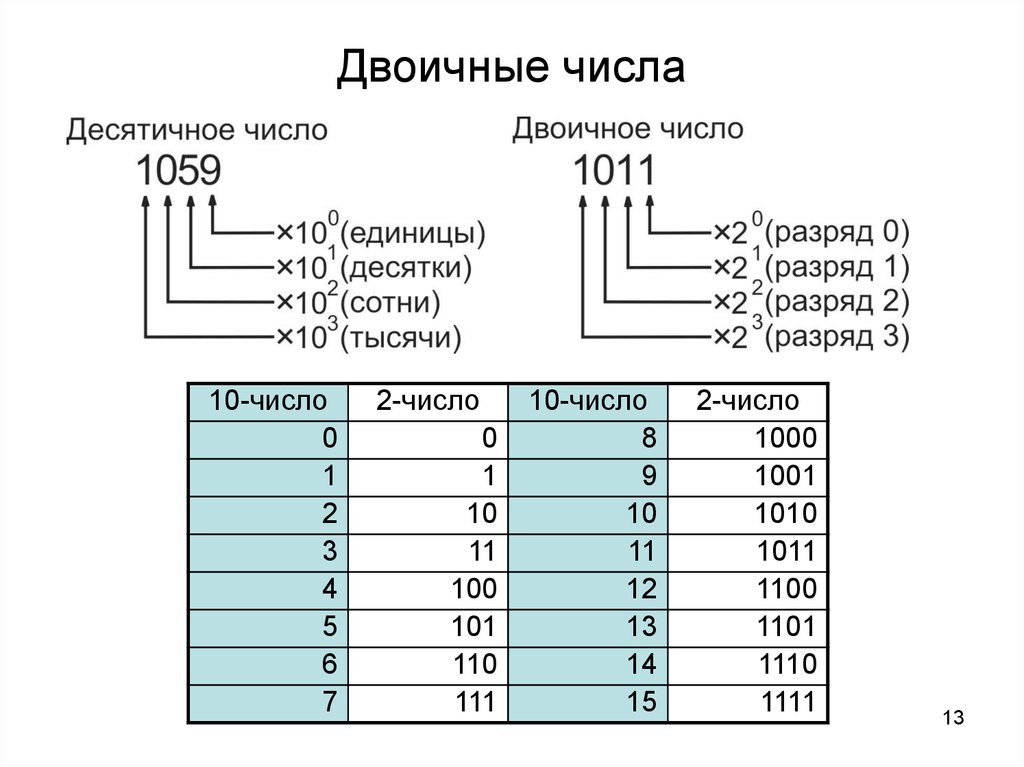
Пример
Двоичный код строчной буквы ASCII i равно 01101001. Итак, чтобы создать слово hi , двоичное число для i добавляется к двоичному числу для h . Это дает следующее двоичное число:
.01101000 + 01101001 = 0110100001101001
В десятичном выражении десятичные числа для h и i равны 104 и 105 соответственно.
Другими распространенными примерами преобразования двоичных чисел в текстовый код ASCII являются следующие.
| Двоичный номер | Десятичное число | Код ASCII |
110000 | 48 | 0 |
1000001 | 65 | А (верхний регистр) |
1111111 | 127 | Клавиша DEL |
11011 | 27 | Клавиша ESC |
См.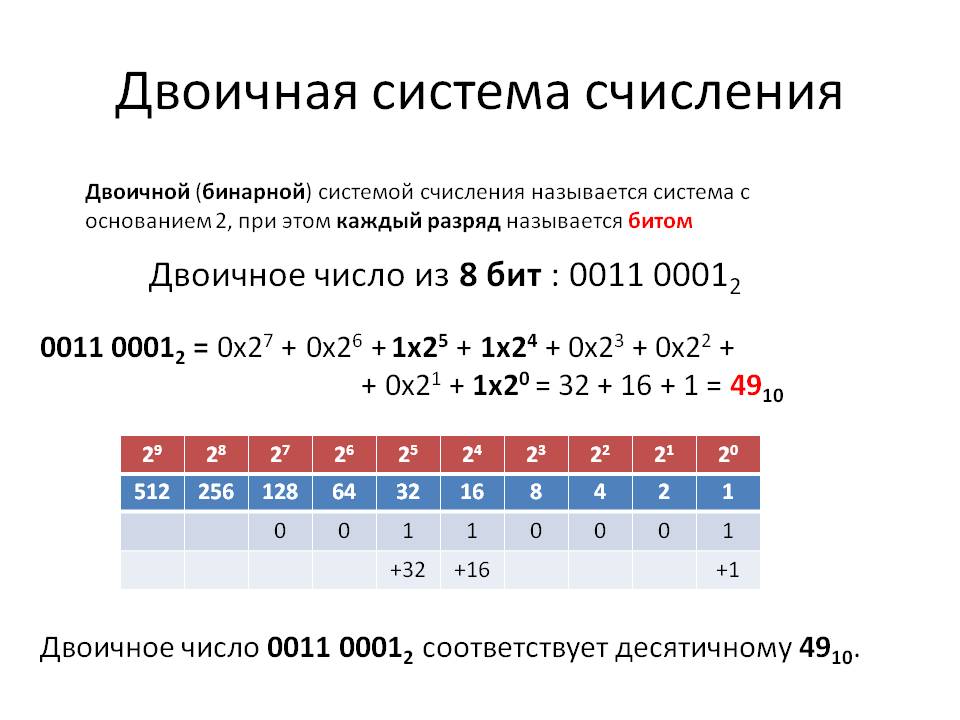
также: Символы ASCII ; киби, меби, гиби, теби, пеби и эксби ; кодирование и декодирование ; старший бит или байт ; и Расширенный двоично-десятичный код обмена .
Последнее обновление: май 2022 г.
Продолжить чтение о бинарнике- Объяснение двоичных и шестнадцатеричных чисел для разработчиков
- Новые функции Java 7: двоичная запись и литеральная инициализация переменных
- Введение в бинарное сравнение для этичных хакеров
- ТБ и ГБ: терабайт больше гигабайта?
- Преобразование двоичного кода в десятичный
функция как служба
«Функция как услуга» (FaaS) — это модель облачных вычислений, которая позволяет клиентам облачных вычислений разрабатывать приложения и развертывать функции и взимать плату только при выполнении функций.
ПоискСеть
- восточно-западный трафик
Трафик Восток-Запад в контексте сети — это передача пакетов данных с сервера на сервер в центре обработки данных.
- CBRS (Гражданская широкополосная радиослужба)
Служба широкополосной радиосвязи для граждан, или CBRS, представляет собой набор операционных правил, заданных для сегмента общего беспроводного спектра и …
- частный 5G
Private 5G — это технология беспроводной сети, которая обеспечивает сотовую связь для случаев использования частных сетей, таких как частные …
ПоискБезопасность
- одноразовый пароль на основе времени
Одноразовый пароль на основе времени (TOTP) — это временный код доступа, сгенерированный алгоритмом, который использует текущее время дня как один …
- Что такое модель безопасности с нулевым доверием?
Модель безопасности с нулевым доверием — это подход к кибербезопасности, который по умолчанию запрещает доступ к цифровым ресурсам предприятия и .
.. - RAT (троянец удаленного доступа)
RAT (троян удаленного доступа) — это вредоносное ПО, которое злоумышленник использует для получения полных административных привилегий и удаленного управления целью …
..ПоискCIO
- организационные цели
Организационные цели — это стратегические задачи, которые руководство компании устанавливает для определения ожидаемых результатов и руководства …
- пространственные вычисления
Пространственные вычисления широко характеризуют процессы и инструменты, используемые для захвата, обработки и взаимодействия с трехмерными данными.
- Пользовательский опыт
Дизайн взаимодействия с пользователем (UX) — это процесс и практика, используемые для разработки и внедрения продукта, который обеспечит положительные и …
SearchHRSoftware
- Поиск талантов
Привлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса .
.. - удержание сотрудников
Удержание сотрудников — организационная цель сохранения продуктивных и талантливых работников и снижения текучести кадров за счет стимулирования …
- гибридная рабочая модель
Гибридная модель работы — это структура рабочей силы, включающая сотрудников, работающих удаленно, и тех, кто работает на месте, в офисе компании…
..SearchCustomerExperience
- CRM (управление взаимоотношениями с клиентами) аналитика
Аналитика CRM (управление взаимоотношениями с клиентами) включает в себя все программные средства, которые анализируют данные о клиентах и представляют…
- разговорный маркетинг
Диалоговый маркетинг — это маркетинг, который привлекает клиентов посредством диалога.
- цифровой маркетинг
Цифровой маркетинг — это общий термин для любых усилий компании по установлению связи с клиентами с помощью электронных технологий.
Информатика: Двоичная система счисления
Урок 3: Двоичная система счисления
/en/computer-science/hardware-and-software/content/
Двоичная система счисления
На протяжении всей истории почти каждая цивилизация использовала десятичную систему счисления с 10 цифры : от нуля до девяти. Все числа, которые мы можем придумать, используют некоторую комбинацию этих 10 цифр.
Однако компьютеры работают иначе. Вместо этого они используют систему счисления, в которой всего две цифры : единица и ноль. Эта система называется двоичной , и ваш компьютер использует ее все время.
Посмотрите видео ниже, чтобы узнать больше о том, как компьютеры используют двоичные файлы.
Компьютерам нужна информация, чтобы делать то, что они делают.
Эта цифровая информация, или данных , состоит из чего-то, что называется битами . Bit — это сокращение от двоичной цифры , что означает, что каждый бит на самом деле представляет собой просто одно число: либо один или ноль .
Эти биты можно комбинировать для создания более крупных единиц, таких как байты, мегабайты и т. д., которые мы используем для измерения наших файлов. Чем больше файл, тем больше в нем битов. Так что что-то вроде видео высокого разрешения на самом деле состоит из миллионов и миллионов единиц и нулей.
Но как именно эти единицы и нули объединяются и позволяют компьютеру функционировать? Давайте подумаем о двоичном коде как о выключателе света . Представьте, что единица представляет собой выключатель света на , а ноль представляет на . В бинарном режиме свет либо включен, либо выключен, без каких-либо других возможных состояний.
