Двоичная система счисления | Digital Music Academy
Если в десятичной системе счисления числа записываются с помощью десяти различных символов (от 0 до 9), то в двоичной системе — с помощью всего двух символов: 0 и 1. Такая система необходима для всех устройств, в которых информация представлена в виде последовательностей двух возможных состояний носителя, а это практически вся современная вычислительная техника.
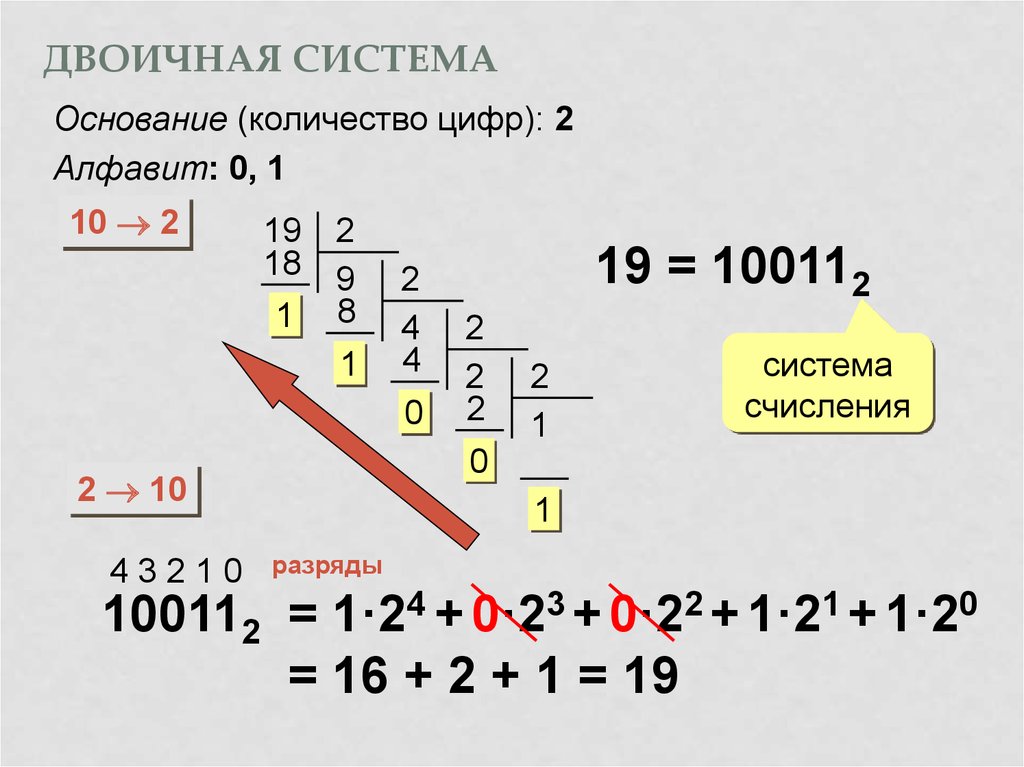
Так же, как в десятичной системе разряды являются степенями основания 10, в двоичной системе разряды являются степенями основания 2:
| 10 000 000 000 | 1 000 000 000 | 100 000 000 | 10 000 000 | 1 000 000 | 100 000 | 10 000 | 1000 | 100 | 10 | 1 |
| 1010 | 109 | 108 | 107 | 106 | 105 | 104 | 102 | 101 | 100 |
| 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 210 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
При этом значением числа будет сумма значений всех разрядов.
Например, переведем в привычный десятичный вид двоичное число
1 * 25 + 1 * 24 + 0 * 23 + 0 * 22 + 0 * 21 + 1 * 20 = 49
Или то же самое чуть иначе:
1 * 32 + 1 * 16 + 0 * 8 + 0 * 4 + 0 * 2 + 1 * 1 = 49
Или так:
В современных вычислительных системах информация представлена не в виде непрерывного потока двоичных символов (условных нолей и единиц), а за единицу информации, как правило, принимается байт (byte).
Байт состоит из восьми битов (т.е. это восьмиразрядное двоичное число), соответственно, он имеет 256 (28) возможных значений.
Именно поэтому стандартные варианты разрядности кратны восьми. Например, для операционных систем это 32 или 64 разряда (или бита), а для цифрового звука: 8, 16, 24 и 32.
Важно не запутаться в трех основных значениях, которые определяются разрядностью числа: количество возможных значений, максимальное значение и значение старшего бита/разряда.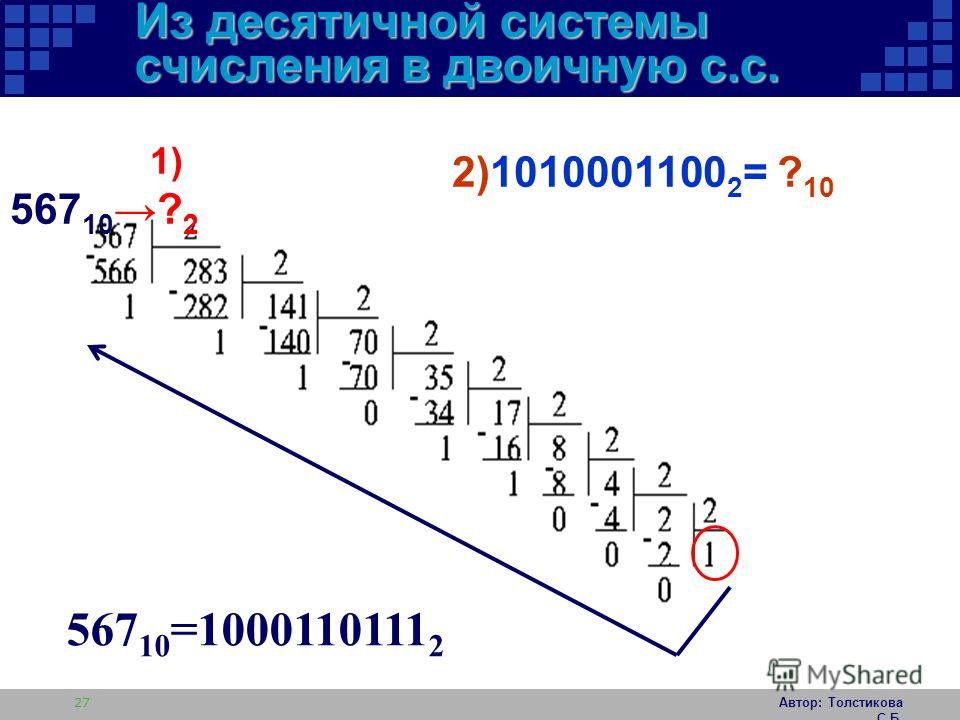
Например, для 8-разрядного числа количество возможных значений = 256 (0 — 255), максимальное значение = 255, а значение старшего бита = 128.
Cистемы счисления, Двоичные (бинарные системы)
Степени точности
Системы счисления, которые вы используете, влияют на точность некоторых расчетов. Один из примеров можно увидеть в извлечении квадратного корня из 3 в десятичной системе. Используйте метод из второй части для извлечения квадратного корня из 2.
ПРИБЛИЖЕНИЯ
Обратите внимание, что каждое «место» в десятичной системе дает лучшее приближение к квадратному корню из 3. Чтобы проверить это, посмотрите, как возведение в квадрат извлаченного корня приблизит вас к значенbю, с которого вы извлекали корень: 3.
На первом месте 1, что в квадрате даст только 1 — ошибка на 2 единицы по сравнению с истинным значением — 3. Если бы использовалось 2, ответ был бы точнее: квадрат 2 это 4 — ошибка только на 1. Но наше правило, приведенное внизу, остается верным.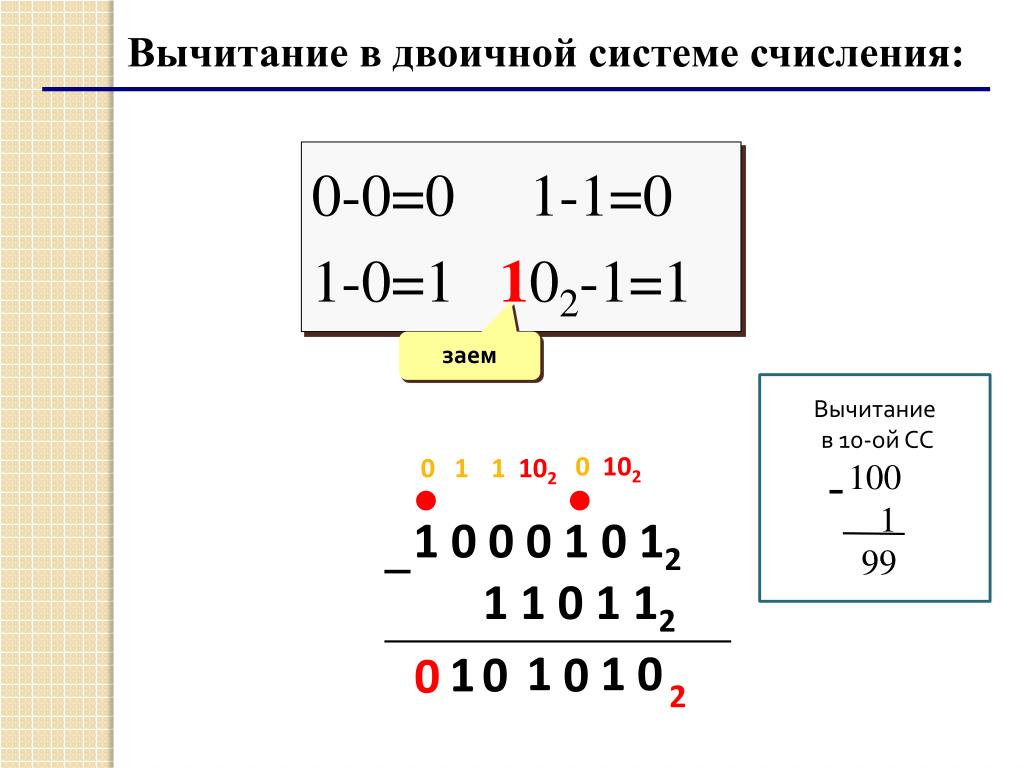
Второе «место» дает более точный результат. Квадрат 1.7 равен 2.89, что уменьшает ошибку до 0.11. Третье «место», 1.73 в квадрате дает 2.9929 — ошибка в 0.0071. Четвертое место, 1.732 еще ближе к истине, так как это число, возведенное в квадрат дает 2.999824 — ошибка в 0.000176.
Дроби в расширенных системах счисления
Если вы использовали семеричную сисему, дробь 1/7 была бы 0.1 — полностью точным с только одной цифрой после запятой (не десятичной запятой, если эта система семеричная). В десятичной системе дробь, что получается в результате деления на 7, не является такой простой.
Дроби и десятичные числа
Эти задачи должны заставить вас задуматься о точности и надежности цифр. Что означает ошибка в одну миллионную? Будете ли Вы использовать (что маловероятно) семеричную систему вместо десятичной, чтобы проверить как точно 1/7?
Порядки величин
Порядки величин начинают собой совершенно новую концепцию в области математики.
Чтобы показать другую сторону этой концепции, предположим, что Вам необходимо получить область, состоящую из идеального квадрата. Для получения области более точных размеров, необходимо добавить или вычесть немного к или от обоих измерений. Начиная с квадрата с размерами L в каждом направлении, вы либо добавляете или вычитаете небольшие кусочки S. Изменение площади может проводиться двумя длинными прямоугольниками (размеры L и S) и одного намного меньшего квадрата со стороной S. Чем меньше S по сравнению с L, тем меньше S в квадрате, по сравнению с SL.
Вы можете расширить этот подход к аналогичным изменениям кубического объема. Теперь, начиная с большого куба, имеющего стороны L, необходимо добавить или вычесть 3 плитки с размерами L х L x S, три длинных параллелепипеда с размерами L х S х S, и один маленький куб со стороной S. Если S равно 1/10 от L (или гораздо меньше), то S в кубе составляет 1/1000 от L в кубе.
ПОРЯДКИ ВЕЛИЧИН
Вы можете продемонстрировать такую же самую прогрессию алгебраически.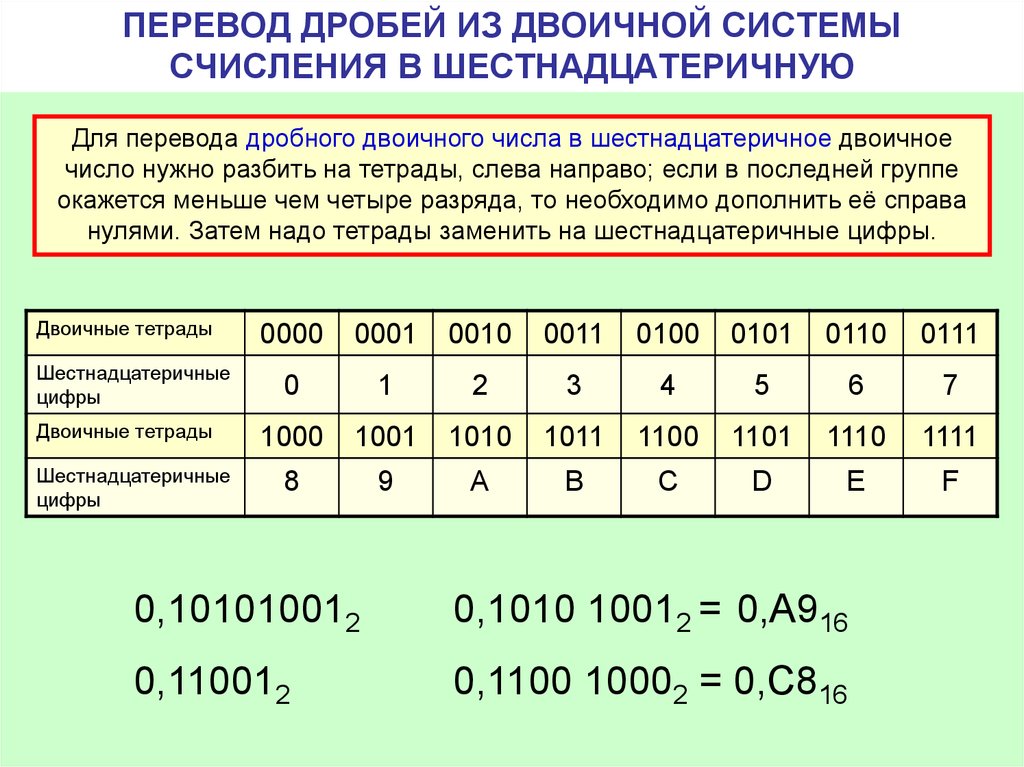
Тем не менее, продолжая работать в нашей знакомой десятичной системе, Вы заменяете различные значения a и показываете, как меняется его изменения последовательных степеней (1 +a). Если это 0.1, последовательные степени начинают «перетекать» в предыдущие «места». До 4-й степени, первые две цифры есть 1.1, 1.2, 1.3, но в 4-й степени 1,5 будет ближе.
Если a равно 0,01, более высокие степени не влияют на первый член, который в настоящее время во втором знаке после запятой. Оставьте его за вторым местом, первые два места есть 1,01, 1,02, 1,03 и 1,04. Дальнейшие члены 4-й степени только достигают 1,0406 на 4-м месте.
Однако, если a равно 0.2, следующие члены влияют на более ранние.
Цифры в квадратиках демонстрируют это.
Системы счисления
Перед изобретением электронных цифровых устройств использовались счетные машины. Числа, которые можно было видеть через окошко, были похожи на те, которые мы сейчас видим на дисплее калькуляторов. Если бы Вы подняли крышку счетной машины, Вы бы увидели, как работает механизм счетной машины, что могло бы помочь Вам понять в общем системы счисления.
Самое правое колесико ведет отсчет 0 до 9 в десятичной системе. Когда оно доходит 9, оно перейдет от 9 до 0 и одновременно передвинет следующее колесико с 0 до 1. Каждый раз, когда первое колесо переходит от 9 до 0, следующее колесико будет переходить на 1 больше, пока оно не возвратиться к 9. Тогда, два колесика будут означать 99. Когда в этот раз первое колесико перейдет от 9 до 0, следующее колесико также перейдет от 9 до 0, а третье колесико передвинется от 0 до 1, и таким образом счетная машина покажет 100.
Двенадцатеричная система
Десятеричная система не единственная, которую Вы можете использовать.
Давно, некоторые народы использовали двенадцатеричную систему, считая до 12 вместо десяти. Для того чтобы использовать эту систему в счетных машинах, необходимо было бы добавить два числа на каждом колесике. На колесиках, нарисованных внизу, дополнительные два символа t и e, обозначающие десять и одиннадцать. Современные цифровые системы чаще используют системы с основанием 16, которые называются шестнадцатеричные системы.
Первые шесть букв алфавита вместе с однозначными числами полностью формируют ряд до числа 15.
Десятичная
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Шестнадцатеричная
0 1 2 3 4 5 6 7 8 9 A B C D E F
В десятичной системе «10» (один ноль) означает десять. В двенадцатеричной системе «10» означает двенадцать. В шестнадцатеричной «10» означает шестнадцать. Чтобы получить немного практики в различных системах счисления, попробуйте пользоваться некоторое время двенадцатеричной системой.
Преобразование из десятичной системы в двенадцатеричную
Зачем работать в двенадцатеричной системе, когда она никогда не используется? Потому что что-то незнакомое заставляет вас думать, оно помогает вам понять почему это не используется. Шестнадцатеричная система основана на двоичной (основание два), но ее не так просто использовать в системах, использующих большие базы чисел. Итак, посмотрим на преобразование десятичной системы в двенадцатеричную.
Чтобы узнать, скольки раз по двенадцать состоит число, Вы делите число (например 143131, как показано на рисунке ниже) на 12 в в знакомой Вам десятичной системе. Остаток после деления на 12 записывается слева в двенадцатеричной система. Затем разделите число на 12 еще раз. На этот раз остаток равен одиннадцать. В двенадцатеричной систем все числа до одиннадцати должны использовать одну цифру, так что для 11 используется буква е.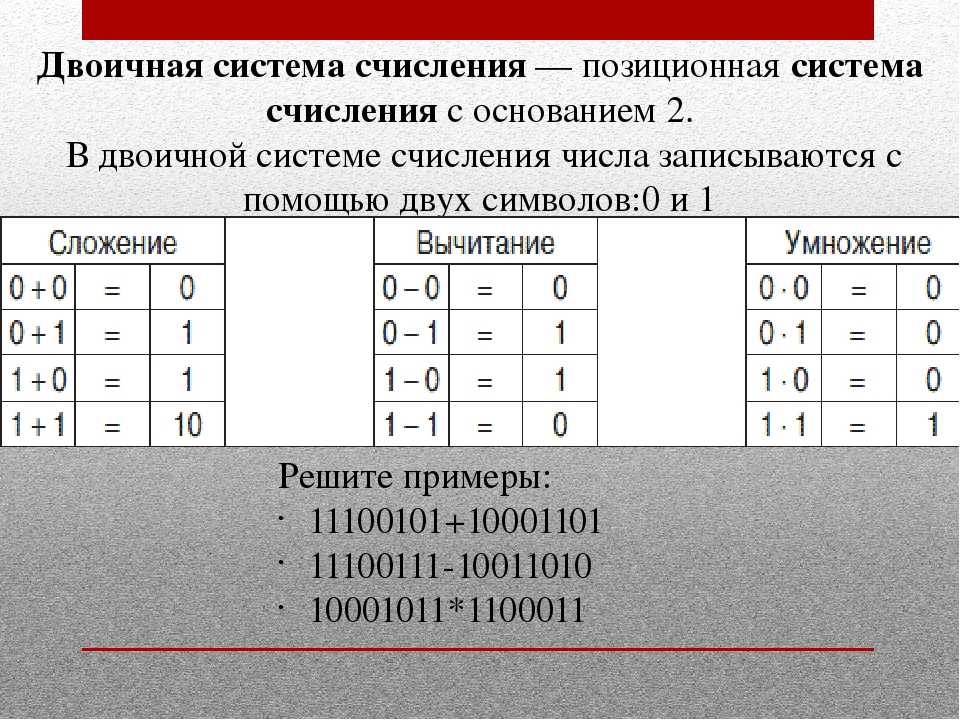
Вы можете сами далее проследить за правильностью вычислений в остальной части этого преобразования. Двенадцатеричный эквивалент десятичному числу 143131 есть 6t9e7.
Преобразование десятичного числа 143131 в двенадцатеричное
Переход от двенадцатеричной системы в десятичную
Как преобразовать число из двенадцатеричной системы в десятичную? Просто сделать обратный процесс. Двенадцатеричное число разделить на десять столько раз, сколько необходимо. Вам потребуется, как минимум колонка десяти из двенадцатеричной таблицы умножения. Вы, вероятно, были знакомы с двенадцатью колонками, чтобы сделать это довольно легко. Тем не менее, таким образом Вы должны использовать колонку десяти в двенадцатиричной системе счисления. Эта система не знакома, и поэтому заставит вас думать.
Пойдем ниже по колонке десяти. Десять раз по два есть 18. Это означает, что 1 двенадцать и 8, что вы обычно называете двадцать. Двенадцать и восемь в сумме дают двадцать, не так ли? Далее, десять раз по 3 есть 26, что означает 2 двенадцать и 6.
Два на двенадцать дает 24 и с шестью дает результат, который обычно называют 30. Пройдите до конца самостоятельно.
ДВЕНАДЦАТИРИЧНАЯ ТАБЛИЦА УМНОЖЕНИЯ
Преобразование двенадцатеричного 6 +9e7 в десятичное
Двоичное счисление
Трудность в работе с двоичной системой состоит в том, что каждое место имеет только два «значения»: 0 и 1. Вы не можете посчитать «до» чего-то, а затем перейти к следующему месту. Если у вас уже есть 1, следующая цифра 1 преобразует его обратно в 0, и даст 1 следующему месту. Если у вас есть ряд единиц, то добавление еще одной единицы преобразует все единицы обратно в 0, и присвоит следующему месту 1 (справа налево).
В панели окошек ниже, десятичный эквивалент числа заменен двоичными числами. В двоичной системе в любом месте будет либо 1, либо 0.
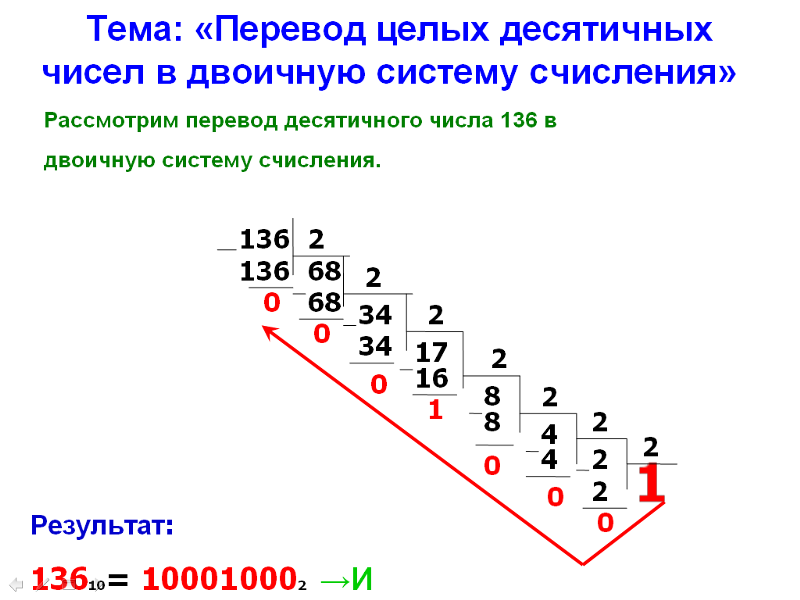
Преобразование десятичных чисел в двоичные
Здесь значения места в двоичном системе, которые имеют 1 вместо 0, приведены в виде десятичных чисел.
Начнем с числа в десятичной форме, 1546. Во-первых, 11-я двоичная колонка является 1024, что ставит 1 в 11-м столбце двоичного файла. Вычтите 1024 из 1546, останется 522. Следующая, 10-я колонка в двоичной системе составляет 512, поэтому вычитаем 512 из 522, остается 10, что ставит 1 в 10-м столбце двоичного файла. От 10 колонки налево следующий двоичный знак использует 4-ю колонку, что соответствует 8. Таким образом, мы пропускаем колонки с 9-й по 5-ю, ставим 1 в 4-м столбце и вычитаем 8 из 10 (остаток 2). 2 ставит 1 во 2-м столбце двоичного файла, и таким образом заканчивается преобразование.
Для завершения предыдущего раздела в следующей таблице приведены двоичные эквиваленты десятичных чисел от 1 до 30.
Умножение в двоичной системе
Хотя Вы вводите данные в калькулятор или компьютер в знакомой десятичной системе счисления, все они используют двоичную систему для выполнения математических функций. Попробуем проделать умножение чисел, как делает это калькулятор.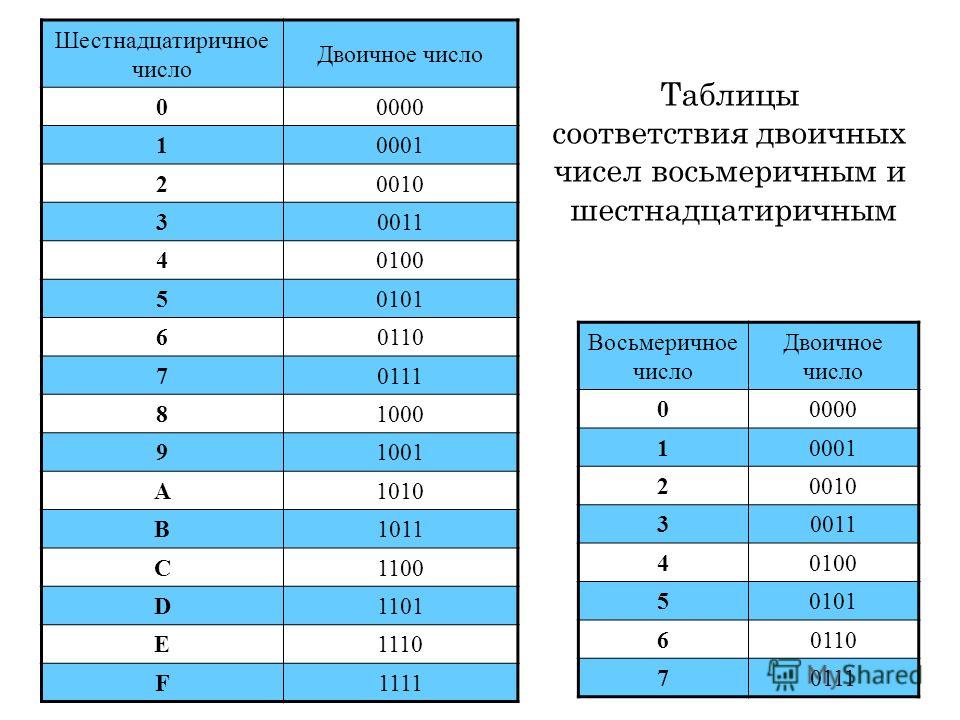
Предположим, вы умножаете 37 на 27. Во-первых, необходимо преобразовать каждое число в двоичную систему, что и делает калькулятор, когда вы вводите цифры. Я буду упрощать этот процесс, преобразовав числа в настоящие двоичные, а не в би-пятеричные, которые облегчают задачу для калькулятора, но делают ее более трудной для понимания. Но с этим разберемся позже.
Ниже приведено преобразование 37 в 27 в чистой двоичной системе.
Здесь есть умножение в двоичной системе, изложенное также, как обычные способы умножения, но в системе, где не допускаются цифры больше чем 1. Каждая цифра должна быть равно 1 или 0. И в действительности процесс сводится к тому, чтобы сложить последовательности цифр, которые представляют 37, и последовательность где 1-цифра есть 27.
Четыре единицы в 27, и поэтому три единицы в 37 (с «вкраплениями» нулей) вводятся 4 раза в нужных местах (для представления «27 раз») и слагаются. Вы можете их все добавить сразу. Тем не менее, калькулятор делает это последовательно.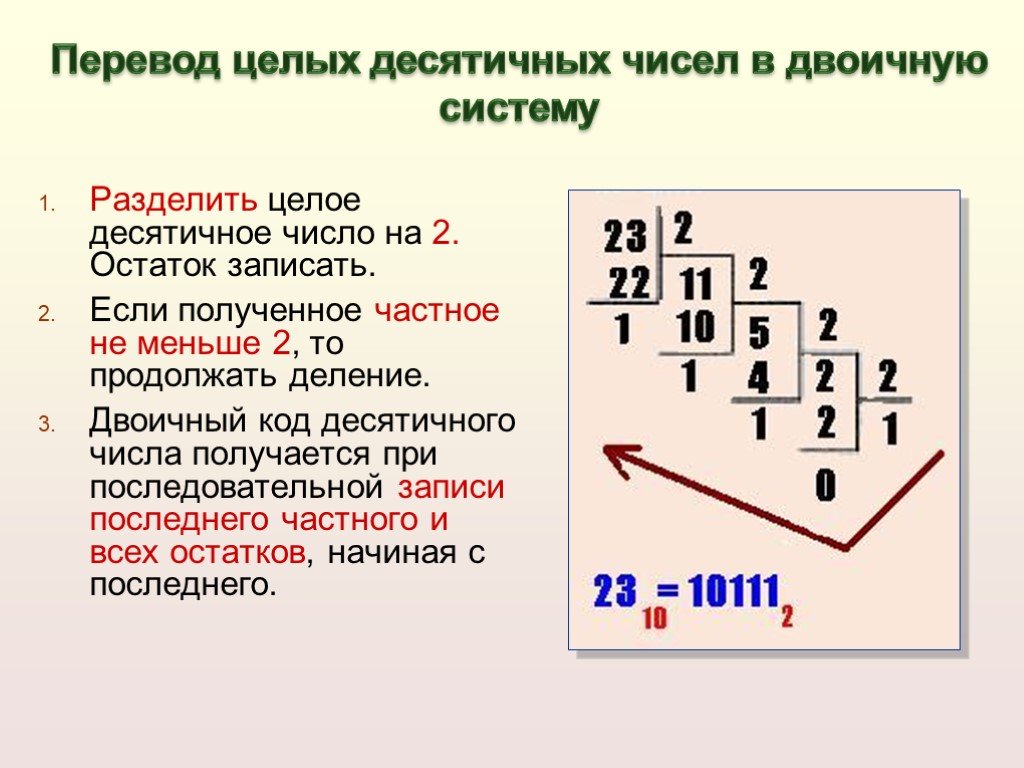
Каждые две сложенные единицы превращаются в 0 и добавляют 1 до следующего места слева.
Двигаясь справа налево, видно, что у первых трёх позиций в сумме есть только одна единица. На четвёртой позиции есть две единицы, которые в сумме дают 0 этой позиции и добавляют единицу к пятой позиции, у которой уже есть собственная единица, так что здесь ставится 0 и единица переходит на шестую позицию. Но у этой позиции уже есть две единицы, поэтому здесь остается единица, которая также добавляется к единице на седьмом месте, где снова есть две единицы. Эта позиция теперь также имеет единицу, которая перемещается на восьмое место. На восьмой позиции эта единица остается и это окончательное перемещение, спровоцированное перемещением справа налево. Оставшиеся две позиции имеют по единице, которые и занимают их. Таким образом, получился результат — двоичное число 1111100111.
Преобразуйте двоичное число назад в десятичное, подставляя десятичный эквивалент каждой позиции, где есть единица.
Для проверки, умножьте 37 на 27 старым длинным способом.
«Каким длинным путем?» спросите Вы. Двоичный путь и так кажется довольно длинный. Единственная причина, того, что калькулятор делает это так быстро, это то, что он выполняет миллионы операций в секунду. Поэтому, этим долгим методом калькулятор считает быстрее, чем вы считаете методом, который гораздо короче.
Умножение 37 на 27 двоичным способом
ДВОИЧНОЕ УМНОЖЕНИЕ
Альтернативное двоичное преобразование
Вот еще один способ преобразования десятичных чисел в двоичные. Он использует таблицу двоичных эквивалентов чисел от 1 до 9 для каждого десятичного места. Для иллюстрации этого способа два числа для деления, приведенного ниже, преобразованы в двоичные (см. таблицы ниже).
Обратите внимание, что двоичные эквиваленты для конкретной цифры не имеют никакого отношения друг к другу — от одной колонки к другой. Вы не можете передвинуть десятичную точку или умножить на десять, как Вы делаете подобный сдвиг в двоичной системе.
Я вернусь к тому как калькуляторы или компьютеры справляются с этой проблемой чуть позже.
Деление двоичных чисел
Деление двоичных чисел на самом деле есть повторяющееся вычитание. 37 в двоичной системе 1000001.
Для преобразования двоичного числа обратно в десятичное, используйте вычитание в двоичной системе и применяйте таблицы из предыдущего раздела. Первое вычитание есть двоичное число 100-а, что оставляет 11101. Для двоичного числа 20-ти, что оставляет 1001, вычитается двоичное 9. Работая так через двоичные, после деления 4773 на 37 частное есть 129.
АЛЬТЕРНАТИВНОЕ ДВОИЧНОЕ ПРЕОБРАЗОВАНИЕ
ДЕЛЕНИЕ 4773 на 37
1001010100101 на 100101
Специальная двоичная система для калькуляторов
Вы заметили, что двоичные числа для различных чисел в десятичной системе меняются на каждой позиции, что делает преобразование сложным. При вводе цифры на калькуляторе, первая цифра появляется справа. При вводе следующей цифры, первая цифра перемещается влево и новая цифра появляется справа от нее.
Если бы калькулятор преобразовывал бы двоичную последовательность в новую с получением следующей цифры, система была бы очень сложной.
Так, калькулятор выделяет 4 двоичных места для каждого десятичного знака, для чего требуется немного больше «пространства» в памяти калькулятора, чем потребовался бы чистый двоичный код. По сути дела, калькулятор теперь «работает» в десятичной системе, но использует 4 «бита» двоичной системы для каждой десятичной позиции.
Показатели степеней
В любой системе счисления — двоичной, восьмеричной, десятичной или шестнадцатеричной (или даже в других, которые используются в очень узких сферах), место цифры указывает степень числа, на котором основывается эта система. В двоичной системе, позиция, где появляется единица, представляет некоторую степень числа 2. На 4-й позиции это третья степень числа 2, что равно 8. Вот сравнение степеней 2 и степеней 10.
На этом примере Вы можете увидеть некоторые правила использования показателей степеней, которые помогают нам идти короткими путями в умножении и делении.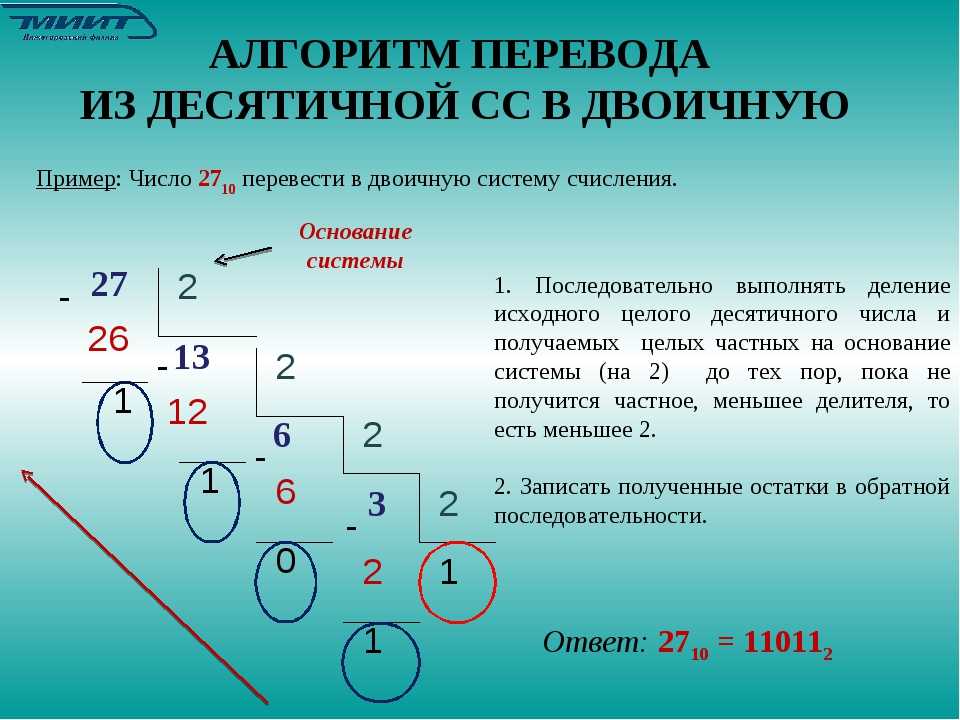
Во-первых, помните, что умножение и деление это укороченные методы выполнения повторяющихся операция сложения и вычитания. Теперь, степени являются укороченными методами для многократного умножения и деления.
Предположим, что Вы должны умножить xa на xb. Произведение равно x(a+b). Вы можете легко это увидеть, если Вы напишите x умноженное на само себя a раз, и тогда умножить результат на x, умноженной само на сабя b раз. Общее число раз, которое Вы умножали x само на себя, равно (a + b) раз. Для иллюстрации, предположим, что a равно 3 и b равно 2; x3 умноженное на x2 дает x5. В численном значении, 23 равно 8, 22 равно 4, и 25 равно 32. 8 x 4 = 32. Это проверка.
Теперь попробуем деление. Разделяя xa на xb, частное есть xa-b. Вы можете проверить этот ответ, умножая x само на себя a раз как числитель дроби и используя x умноженное само на себя b раз в знаменателе.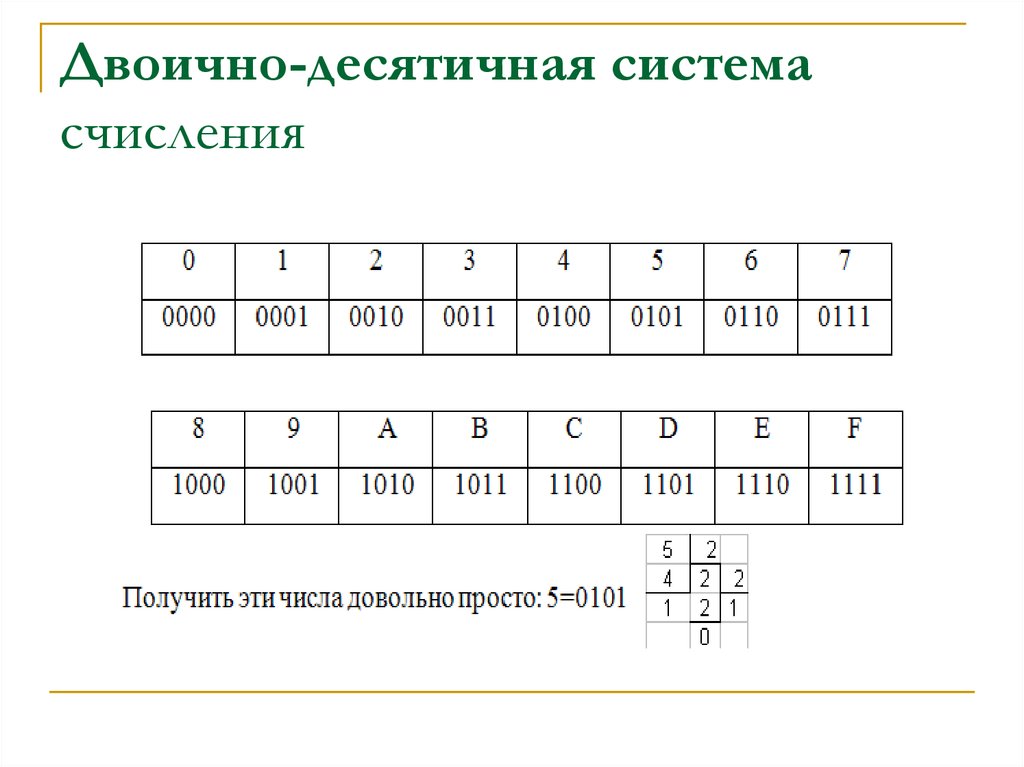
Вы можете сократить b раз в знаменателе и оставить остаток х-ов в знаменателе, что равно (a — b) раз. Для иллюстрации, пусть a = 5 и b = 2. x5 разделенное на x2 равняется x3. Если вы использовали 2 для x, x5 равно 32, x2 равно 4, и x3 равно 8. 32 разделенное на 4 равно 8.
Арифметические корни: инверсия степеней
Здесь вы должны понимать разницу между инверсией числа и инверсией степени. Отрицательная степеннь есть инверсией или обратной величиной числа, возведенного в степень, определенную индексом. Арифметические корни есть противоположность возведению в степень. Например, из-за того, что 22 равно 4, то 41/2 равно 2; 23 равно 8, а 81/3 равно 2; 24 равно 16, а 161/4 равно 2 и так далее.
Дробные показатели степеней означают арифметические корни. Степень 3/2 четырех есть 8 — квадратный корень 4 есть 2, и 23 равно 8.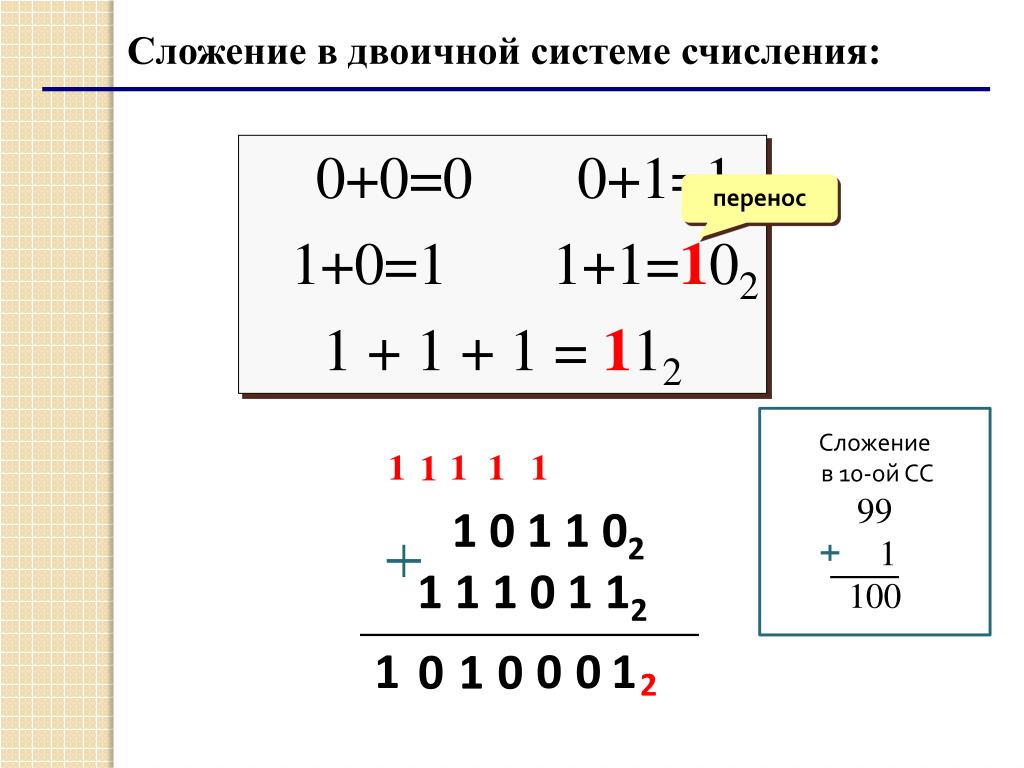
Обратный процесс, 82/3 равно 4. Вы можете найти другие корни чисел используя квадратные корни. Например, 21/2 (квадратный корень двух) равно 1.414 и так далее; 81/2 равно удвоенному значению предыдущего. Почему? Так как 41/2 равно 2 и 21/2 равно 1.414, (2 раза по 4)1/2 равно 81/2 (удвоенное 1.414), что равно 2.828.
Вообще, Вы не ограничены квадратными корнями, да и вообще какими-либо конкретными корнями. Теперь, совершенно новая область чисел открыта для Вас.
Арифметический корень n-й степени и степени чисел
Представление арифметических корней n-й степени есть возвращением к практически устаревшему способу написания арифметических корней. Перед тем, как описанные в предыдущем разделе обозначения дробных степеней вошли в моду, было принято использовать число на знаком квадратного корня, для указания значения корня. Таким образом, просто знак корня перед х представлял собой квадратный корень из х, такой же, как х /.
Написание цифры 3 над знаком корня означало кубический корень из х. Написание небольших n или любой другой буквы или цифры над знаком корня также обозначало конкретный корень.
Если число под знаком корня имело степень b и значение a стояло над знаком корня, это могло бы быть записано как: xb/a. Длинный знак корня над членами a2 + b2 есть корнем всего выражения. Это выражение может быть записано как: (a2 + b2)1/2.
Вопросы и задачи
Примечание: эти вопросы и задачи расположены в случайном порядке. Если у Вас есть трудности с какой-то задачей, попробуйте решить другую, а затем вернуться к нерешенной задаче. Задачи составлены таким образом, что Вы должны проявлять определенную инициативу в применении принципов, которые были рассмотрены ранее.
1. Найдите десятичный эквивалент дроби 1/37. Определите ошибку преобразования, которая возникает, когда десятичный эквивалент преобразуется до трех значащих цифр.
2. Используя двойную систему, умножьте 15 на 63 и преобразуйте результат обратно в десятичное число. Проверьте свой результат непосредственно умножением десятичных чисел.
3. Используя двоичную систему, разделите 1922 на 31 и преобразовать результат обратно в десятичной число. Проверьте свой результат непосредственно умножением десятичных чисел.
4. Найдите значения следующих выражений:
(a) 163/4 (b) 2430,8 (c) 251,5
(d) 642/3 (e) 3434/3
5. Преобразуйте следующие числа из десятичных в двоичные. В качестве проверки, преобразуйте их также обратно в десятичные.
(a) 62 (b) 81 (c) 111
(d) 49 (e) 98 (f) 222
(g) 650 (h) 999 (i) 2000
6. Преобразуйте следующие числа из десятичных в двоичные. В качестве проверки, преобразуйте их также обратно в десятичные.
(a) 101 (b) 1111 (c) 10101
(d) 111100 (e) 110111000110
7. Умножьте 129 на 31 в десятичной системе. Умножьте двоичные эквиваленты этих чисел. Предположим, что была сделана ошибка во второй цифре справа во втором числа в десятичном результате, поэтому 129 умножается на 41, а не на 31. Предположим, что подобная ошибка произошла в двоичной системе, поэтому вторая цифра справа во втором числе меняется на противоположную. Сравните относительную погрешность в десятичной системе с ошибкой в двоичной системе счисления.
8. Подсчитайте значение выражения (a2 + b2)1/2 для следующих значений:
(a) a = 4 и b = 3 (b) a = 12 и b = 5
(c) a = 24 и b = 7 (d) a = 40 и b = 9
(e) a = 60 и b = 11 (f) a = 84 и b = 13
(g) a= 112 и 6= 15
Что общего имеет каждая пара?
9. Подсчитайте значение выражения (a2 + b2)1/2 для следующих значений:
(a) a = 8 и b = 6 (b) a = 15 и b = 8
(c) a = 24 и b = 10 (d) a = 35 и b = 12
(e) a = 48 и b = 14 (f) a = 63 и b = 16
Что общего имеет каждая пара?
10.
Запишите как простые десятичные числа, без дробей, следующие выражения:
(a) 1002 (b) 1001/2
(c) 100-2 (d) 100-1/2
Из этих четырёх значений, найдите значения следующих выражений методом сложения и вычитания степеней:
(e) 1003/2 (f) 1005/2
(g) 100-3/2 (h) 100-5/2
11. Используя на калькуляторе только клавишу вычисления квадратного корня, найдите следующие значения по крайней мере с тремя цифрами после запятой:
(a) 1001/4 (b) 1001/8
(c) 1001/16 (d) 1001/32
12. Если значение степени в d) предыдущей задачи делить пополам, то есть 1/64, 1/128, 1/256, 1/512, и так далее, к какому числу будет стремиться выражение? Почему?
13. Найдите значения до трех верных десятичных цифр после запятой для следующих:
(a) 320,1 (b) 320,2 (c) 320,3
(d) 320,4 (e) 320,5 (f)320,6
(g) 320,7 (h) 320,8 (i) 320,9
14.
Посчитайте значения следующих выражений, используя калькулятор, если Вы хотите. Где возможно, посчитайте значения выражений хотя бы до трёх десятичных цифр после запятой:
(a) (102 — 26)1/2 (b) (362 — 83)1/2 (c) (282 — 212)1/3
(d) (52 — 32)1/4 (e) (172 — 152)1/6 (f) 65611/2
(g) 6561-1/2 (h) 65611/4 (i) 6561-1/4
(j) 65611/8 (k) 6561-1/8
Почему двоичные числа?
Чтобы понять, почему компьютеры используют двоичные числа, нам придется коснуться совсем других тем. Мы поговорим о первых компьютерах, транзисторах, троичной логике, электричестве, квантовых компьютерах и оптоволокне.
Самый известный десятичный компьютер.
Два первых компьютера оказали огромное влияние на информатику.
Один из них ENIAC, а другой EDVAC. Оба от одних и тех же изобретателей: Джона Мочли и Джона Преспера Эккерта.
ENIAC был первым программируемым компьютером, и он использовал десятичную систему. Закончили строить в 1945, он стоил почти 0,5 млн долларов, что эквивалентно 6 млн долларов в 2020 году, и имел длину 30 метров.
EDVAC сильно отличался от ENIAC и больше походил на наши нынешние компьютеры. Во-первых, вместо десятичной системы использовалась двоичная.
Интересно, что изобретатели уже думали о втором, даже не закончив первый. Разработка ENIAC закончилась в 1945 году, а в 1944 году было отправлено предложение по EDVAC.
Изобретатели, должно быть, заметили изъян в архитектуре EDVAC. Возможно, одним из недостатков была десятичная система.
Аппаратное обеспечение компьютера поддерживает двоичный код.
Ранние компьютеры, такие как ENIAC и EDVAC, использовали электронные лампы для выполнения вычислений. Эти лампы потребляют много энергии и очень быстро нагреваются.
В 1947 году был изобретен транзистор, и все компьютеры, начиная с 60-х годов, использовали транзисторы вместо электронных ламп.
И вакуумные лампы, и транзистор — это устройства, контролирующие прохождение электричества. Поэтому инженеры используют их для создания логических вентилей, фундаментальных элементов компьютерных систем.
Эти компоненты не очень надежны с точки зрения точного количества электричества, которое они контролируют. Например, они не подходят для перехода с 1,5 вольта на 2,5 вольта, а затем на -2 вольта.
Когда мы используем двоичный код, нам нужно разделить электричество, проходящее через транзистор, на два сегмента, один из которых означает 0, а другой — 1.
Определить напряжение легко, потому что сегменты большие. Неважно, что транзисторы плохо контролируют количество. Вместо этого представьте, что мы хотели определить десятичное число: 9.0003
Наличие десяти сегментов для идентификации каждого из чисел делает его более подверженным ошибкам.
Компьютер, работающий с десятью сегментами, менее надежен, чем компьютер, управляющий двумя сегментами.
Тернарный компьютер
Как насчет использования трех ведер вместо двух? Наверное, так же задавались вопросом в МГУ в 1958 году. Вот и построили «Сетунь», самую современную троичную ЭВМ.
Сетунь использовал троичную логику вместо двоичной. Вместо 0 и 1 он работал с -1, 0 и +1, также определяемыми как «-», «0» и «+».
Компьютер «Сетунь» работал хорошо, и пока непонятно, почему его перестали выпускать. В результате тернарный компьютер на время канул в лету. Однако изобретение оптических волокон вернуло возможность троичного компьютера.
Оптические волокна совместимы с тройными системами. Легко идентифицируются три состояния: «0», когда света нет, и две ортогональные поляризации света для «-» и «+». Хотя это кажется возможным, многие другие проблемы в оптических вычислениях еще не решены.
Некоторые ученые-компьютерщики, такие как Даниэль Кнут, считают, что троичная логика вернется из-за ее элегантности и эффективности.
Например, нам нужно меньше компонентов для хранения того же объема данных в троичной системе, чем в двоичной. Это сделало бы компьютер дешевле и более энергоэффективным.
Теоретически троичный компьютер возможен и даже более элегантен и производительен, чем двоичный, но при создании его аппаратного обеспечения возникает множество проблем.
Квантовый компьютер
А как насчет квантовых компьютеров? Используют ли они двоичный код? До сих пор они делают.
Основным элементом квантового компьютера является кубит — квантовый бит, — и он использует двоичную систему 0 и 1. Кроме того, кубит обладает особыми свойствами, такими как суперпозиция и запутанность. Тем не менее, система счисления Кубита по-прежнему двоичная.
Ответ в аппаратной части или в логике?
Информатика, электротехника и математика пересекаются. В этом и заключается ответ на вопрос «Почему двоичный?».
Мы знаем, что бинарные системы используют больше компонентов и больше энергии, но они более надежны.
Мы также знаем, что транзисторы дешевы и энергоэффективны, но ненадежны для измерений.
Комбинация транзистора и двоичной системы на данный момент стала идеальной.
Спасибо за прочтение, не будьте чужим 👋
GIMTEC — это информационный бюллетень, который я хотел бы иметь раньше в своей карьере программиста.
Каждую вторую среду я делюсь статьей на тему, которую вы не узнаете на работе.
Присоединяйтесь к более чем 3000 подписчикам ниже.
Спасибо за подписку! Письмо с подтверждением отправлено.
Проверьте папку СПАМ, если вы не получили его в ближайшее время.
Извините, произошла ошибка 🤫.
Попробуйте еще раз и свяжитесь со мной по адресу llorenc[at]gimtec.io, если это не сработает. Спасибо!
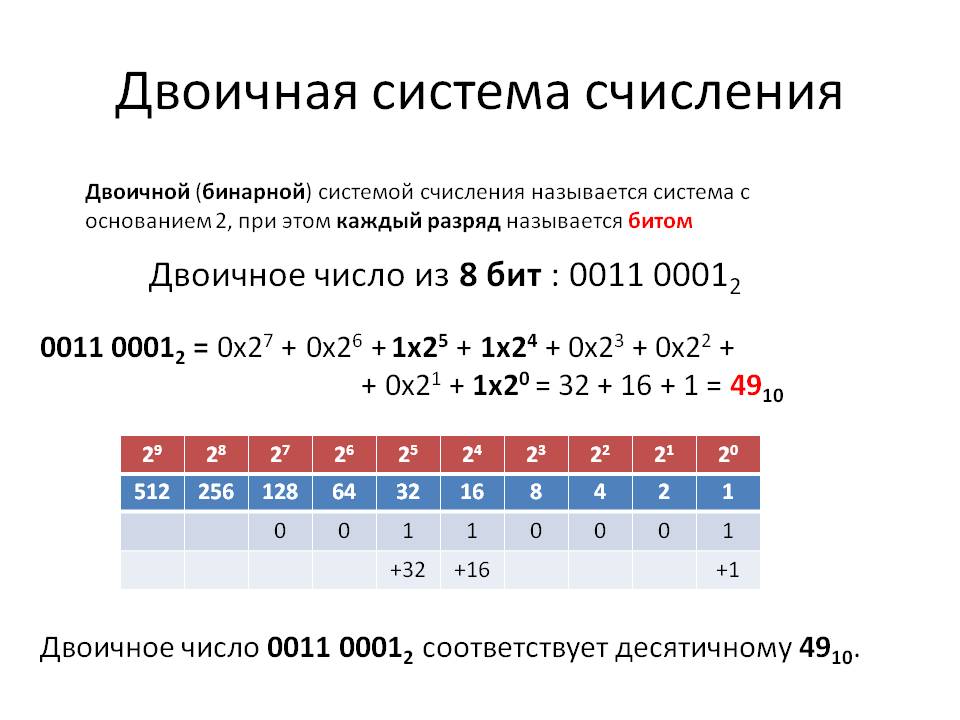
| Двоичный код — настолько просто, что это может сделать компьютер Хотя каждый современный компьютер обменивается и обрабатывает информацию в единицах и нулях двоичной системы счисления, а не в более громоздкой десятизначной десятичной системе, эта идея не нова. Австралийские аборигены считали по два, и многие племена африканского буша отправляли сложные сообщения, используя сигналы барабана на высоких и низких тонах. Азбука Морзе также использует две цифры (точки и тире) для представления алфавита. Готфрид Лейбниц заложил современные основы перехода от десятичной системы к двоичной еще в 1666 году, а Джон Атанасов, профессор физики из Колледжа штата Айова, к 1939 году построил прототип двоичного компьютера. Тем временем Клод Шеннон, Конрад Цузе и Джордж Стибиц размышляли в своих уголках мира, размышляя о преимуществах сочетания двоичных чисел с булевой логикой. Сегодня, конечно, и почти в каждом компьютере, построенном с 1950-х годов, двоичная система заменила десятичную систему (которая на самом деле появилась только потому, что было удобно уметь считать на пальцах) и расширила возможности цифрового компьютера до невероятной степени. . По сути, двоичный код упрощает обработку информации. Поскольку всегда должно быть не менее двух символов, чтобы система обработки могла различать значение или цель, двоичная система является наименьшей системой счисления, которую можно использовать. Процессор компьютера должен распознавать только два состояния, включено или выключено, но (с оттенком лейбницевского мистицизма) из этого состояния «включено-выключено», «да-нет» все течет — точно так же, как переключатель всегда должен быть разомкнут или выключен. закрыт, или электрический поток включен или выключен, двоичная цифра всегда должна быть единицей или нулем. Если затем расположить переключатели в соответствии с булевыми ориентирами, эти две простые цифры могут создавать схемы, способные выполнять как логические, так и математические операции. Сокращение десятичного числа до двоичного действительно увеличивает длину числа, но это более чем компенсируется увеличением скорости, памяти и использования. Особенно утилизация. Помните, что компьютеры не всегда имеют дело с чистыми числами или логикой. Изображения и звук должны быть сначала сведены к числовым эквивалентам, которые, в свою очередь, должны быть снова декодированы для получения конечного результата. Итак, как это работает? Это не так уж и сложно, на самом деле. Двоичные числа используют те же правила, что и десятичные — значение любой цифры всегда зависит от ее положения в целом числе. Все сводится к базам. Десятичная система использует десятичную систему счисления, так что каждый раз, когда число перемещается на одну позицию влево в цифре, оно увеличивается в десятой степени (например, 1, 10, 100 и т. д.). Двоичный, с другой стороны, использует основание два, поэтому каждое движение влево увеличивает значение на степень двойки (например, 1, 2, 4 и т. д.). Чтобы преобразовать десятичную систему в двоичную или наоборот, вам нужно только посмотреть на место цифры в целом числе и сложить ее значение. Простой. Двоичный против десятичного
Преобразование Чтобы преобразовать десятичное число в двоичное, вам нужно только продолжать вычитать наибольшую степень двойки. Здесь десятичное число 200 представлено как 11001000 (один х 128, один х 64, нет 32, нет 16, один х 8, нет 4, нет 2, нет 1) Из двоичного в десятичный еще проще — просто сложите столбцы.
 . . . . . . . . . . . . . . . . . . .Добавление Опять же, сложение отличается от десятичного только тем, что оно использует основание два.
Единственный трюк здесь состоит в том, чтобы помнить, что — это с основанием 2, тогда как в десятичном виде 1 + 1 = 2 без переноса в следующий столбец, в двоичном — 1 + 1 9.  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
