Добротность — это… Что такое Добротность?
Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
Общая формула для добротности любой колебательной системы:
,
где:
- — резонансная частота колебаний
- — энергия, запасённая в колебательной системе
- — рассеиваемая мощность.
Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.
Для Колебательного контура в RLC цепях:
- ,
где , и — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.
Для электрической цепи гораздо проще измерить амплитуду (ток или напряжение), чем энергию или мощность. Поскольку мощность и энергия пропорциональны квадрату амплитуды осцилляции, полоса на АЧХ будет от пика (примерно −3 дБ, а 1/2 это −6 дБ). Поэтому чаще используется другое эквивалентное определение добротности, которое связывает ширину амплитудной резонансной кривой по уровню с круговой частотой резонанса :
,
где: — коэффициент затухания, равный полуширине резонансной кривой, — число колебаний за время релаксации.
Метрологические аспекты
Ссылки
Литература
См. также
Измеритель добротности
8. Идеальный и реальный колебательные контура. Основные характеристики колебательного контура (свободные колебания, частота и период свободных колебаний, характеристическое сопротивление, добротность)
Контур состоит из катушки и конденсатора. Идеальный колебательный контур состоит из катушки и конденсатора, но в нём нет сопротивления потерь.
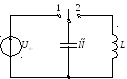
 .
. Во 2 положении конденсатор начинает
разряжаться на катушку, и энергия
переходит в энергию магнитного поля
катушки 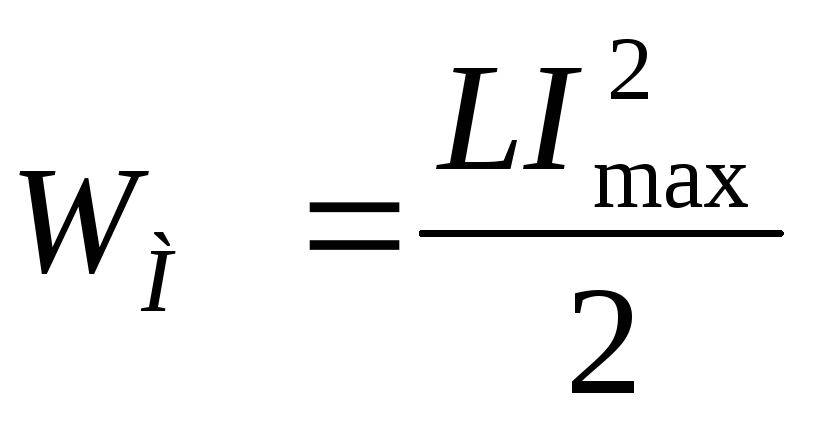 .
.
В катушке возникает ЭДС самоиндукции, которая поддерживает ток, и конденсатор снова заряжается, но в другом направлении. Энергия опять переходит в энергию электрического поля конденсатора.
Вывод:конденсатор и катушка
обмениваются энергией, т. е. происходит
колебание энергии. Такие колебания
называются

Эти колебания будут незатухающими. Их амплитуда мс течением времени не будет уменьшаться, т. к. нет сопротивления потерь, и энергия из контура не уходит. Выведем формулу частоты и периода свободных колебаний:
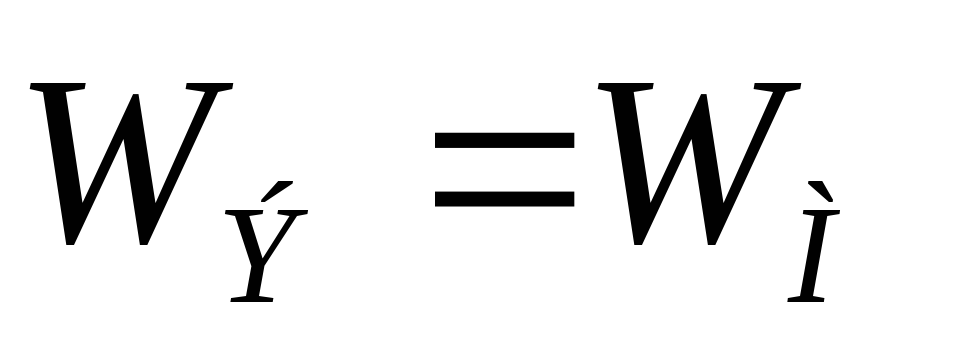
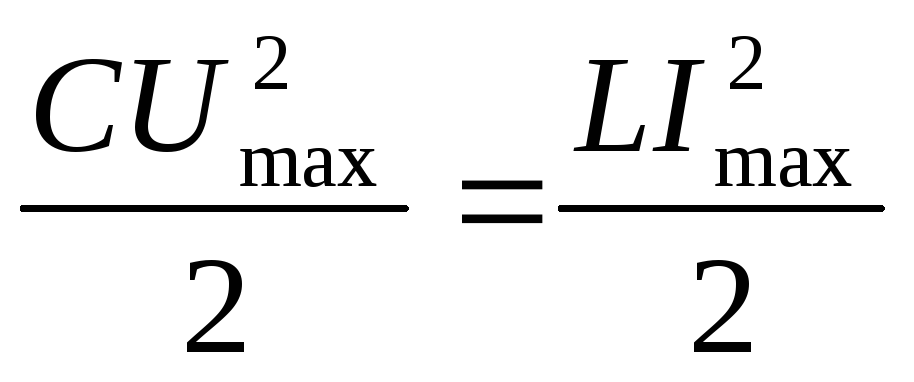
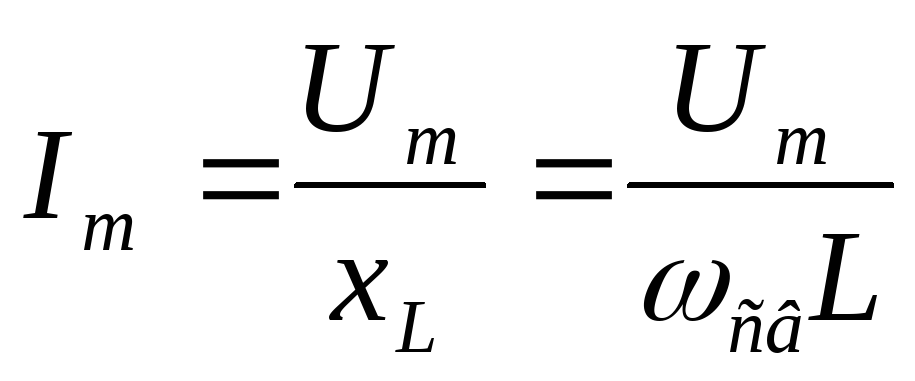
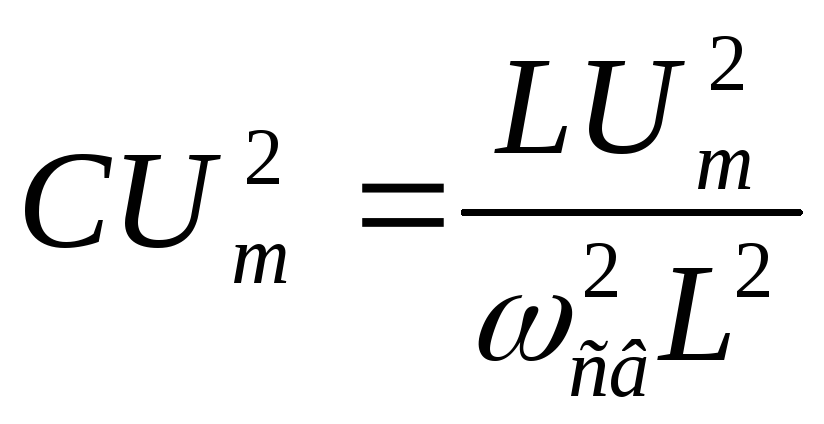
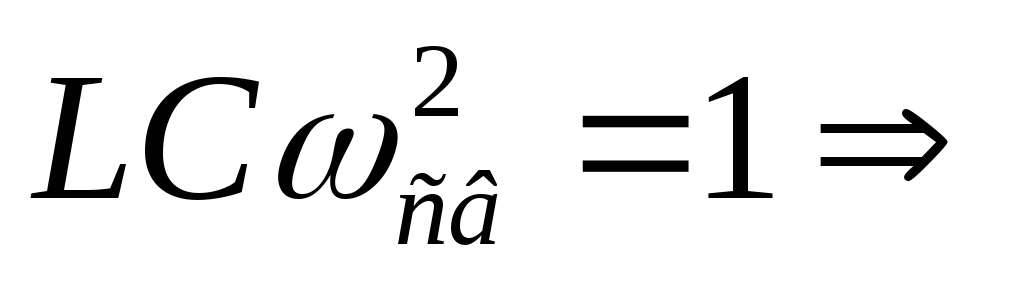
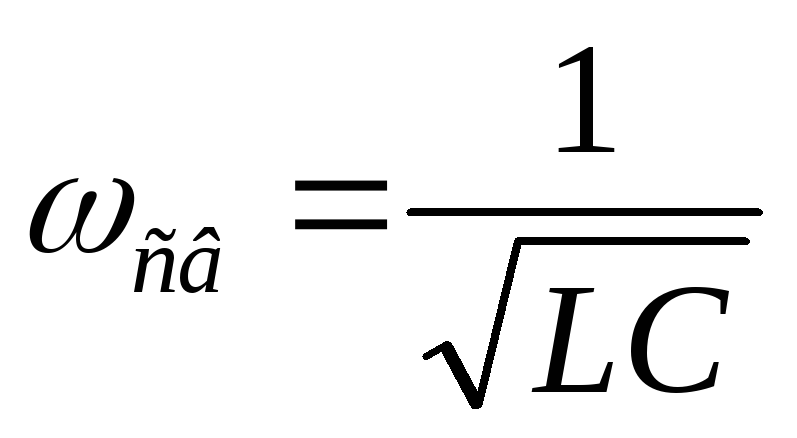
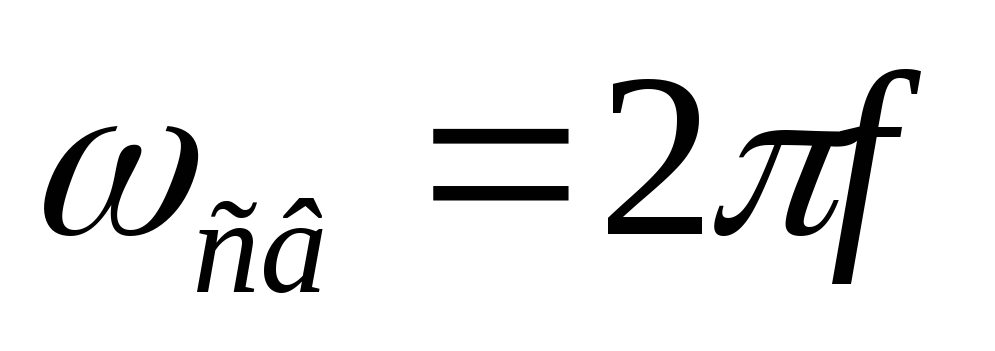
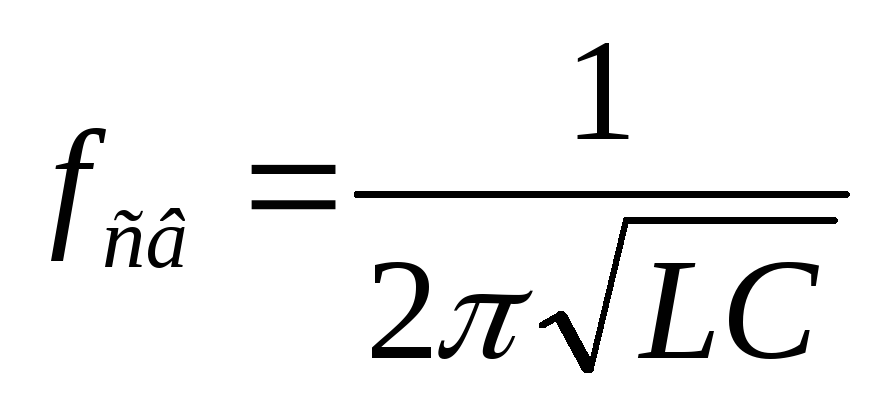
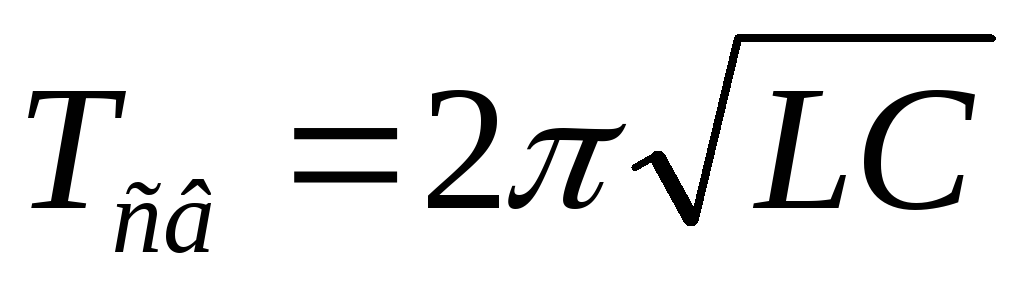
Вывод:частота и период свободных колебаний зависят отLиC, но не зависят от величины приложенного напряжения.
Рассчитаем сопротивление катушки и конденсатора на частоте свободных колебаний.
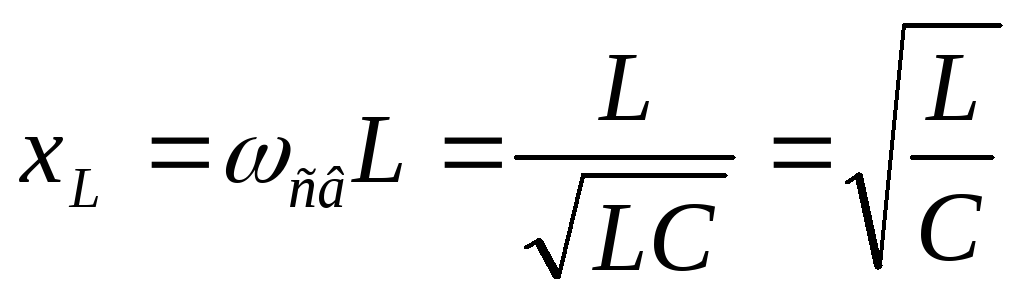
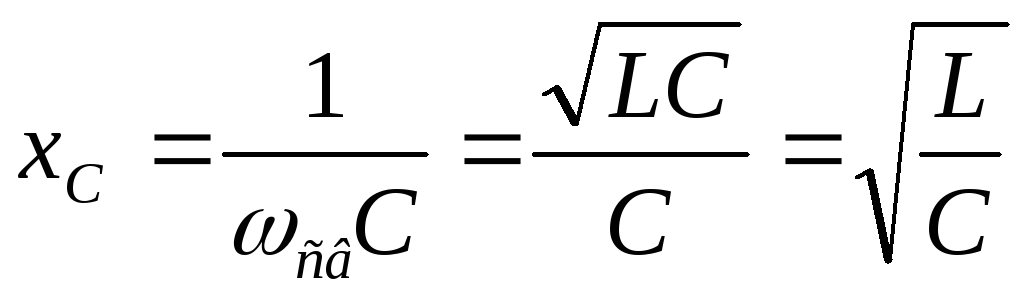
Вывод:сопротивление катушки и конденсатора на частоте свободных колебаний называется характеристическим:
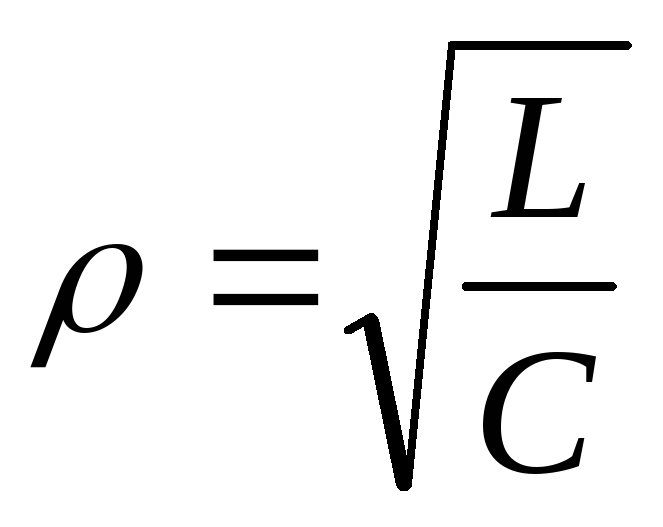
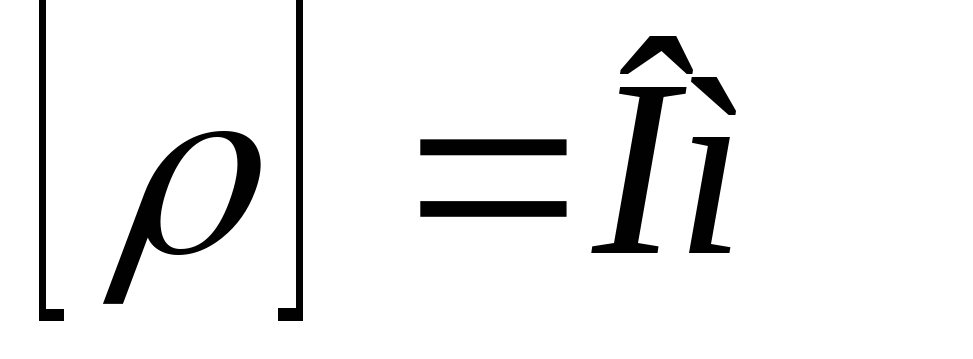
В реальном контуре существует сопротивление потерь, поэтому колебания будут затухающими, их амплитуда с течением времени будет уменьшаться, т. к. часть энергии будет уходить через сопротивление потерь.
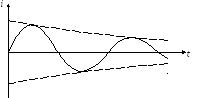
Отношение характеристического сопротивления к резистивному называется добротность:
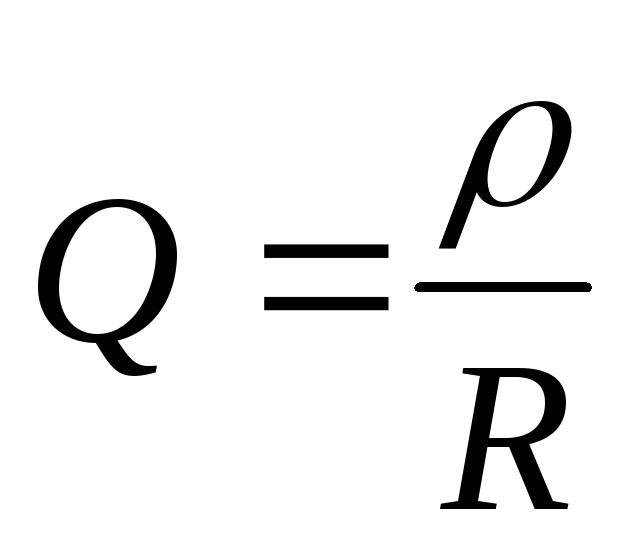
В обычных контурах она составляет единицы – десятки.
Добротность характеризует качество контура. Чем выше добротность, тем медленнее происходят затухания. Величина, обратная добротности, обозначается d—затухание контура:
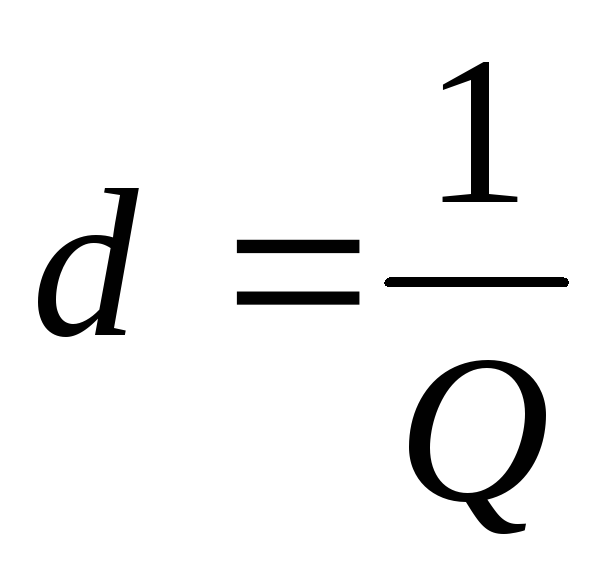
9. Принципиальная схема последовательного колебательного контура. Резонанс напряжений в последовательном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе напряжений. Резонансная частота, добротность. Настройка колебательного контура в резонанс
Резонанс напряжений
Колебания называются вынужденными, если они происходят под действием источника.
Контур называется последовательным, если катушка и конденсатор соединены последовательно с источником:
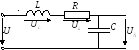
Резонансомназывается такое
состояние цепи, когда ток и напряжение
на входе совпадают по фазе, =>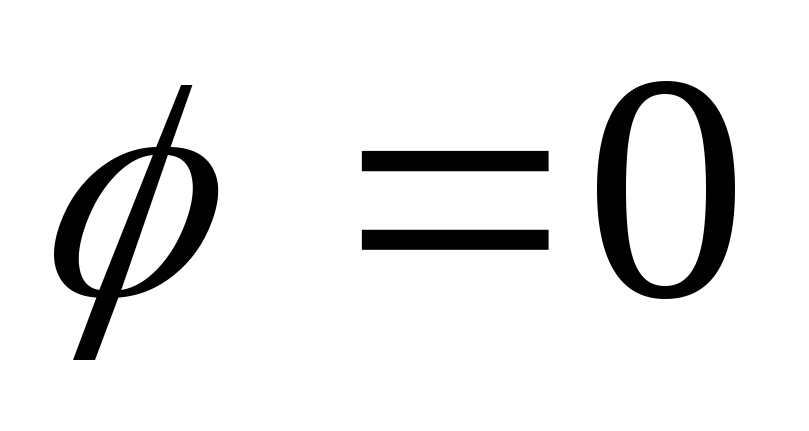 .
.
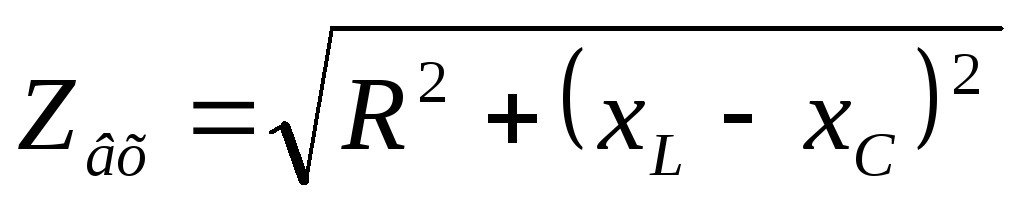
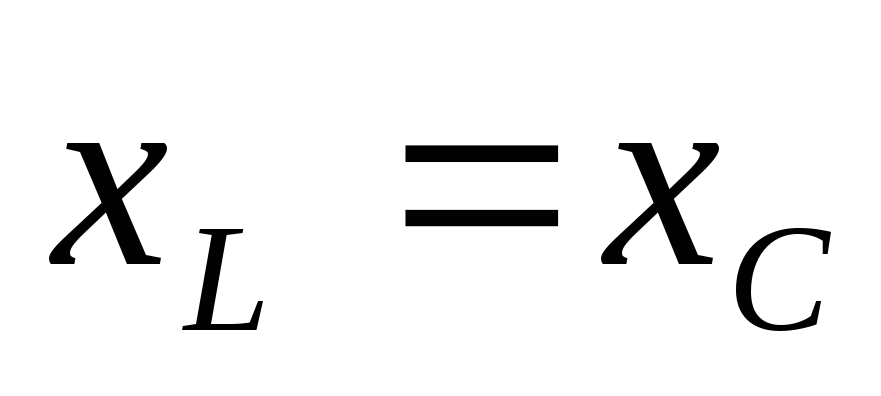 — условие резонанса напряжений (
— условие резонанса напряжений (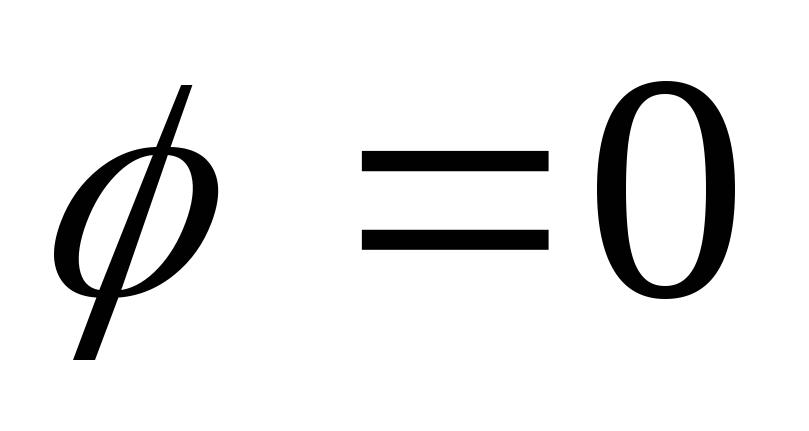 ).
).
Обычно все параметры цепи, относящиеся к резонансу, записываются с индексом 0, => сопротивление контура в момент резонанса
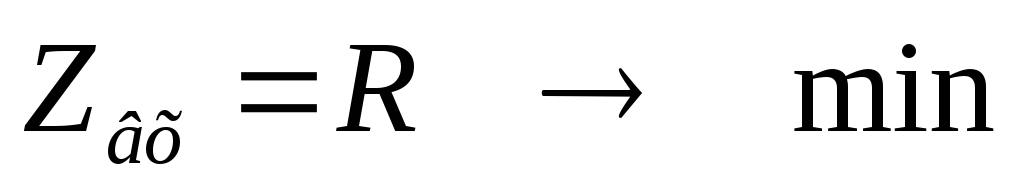
Сопротивление последовательного контура в момент резонанса минимально.
Свойства цепи при резонансе напряжений
При резонансе напряжений в контуре течёт максимальный ток.
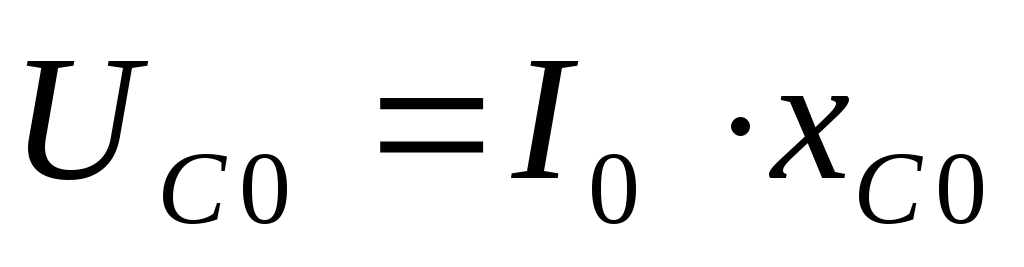
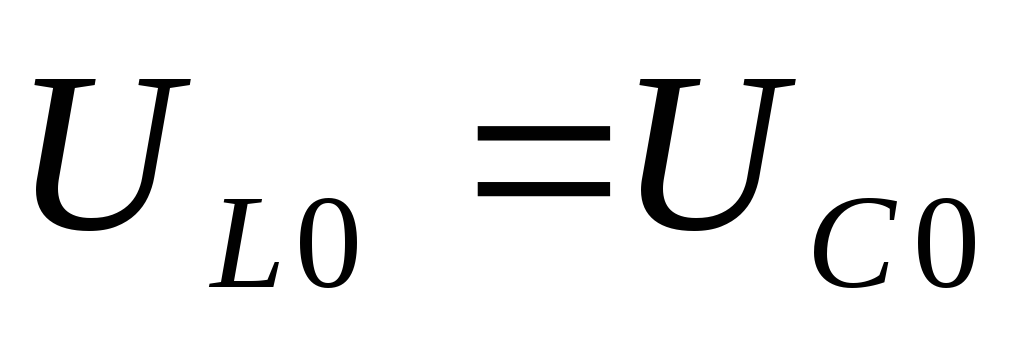
На практике 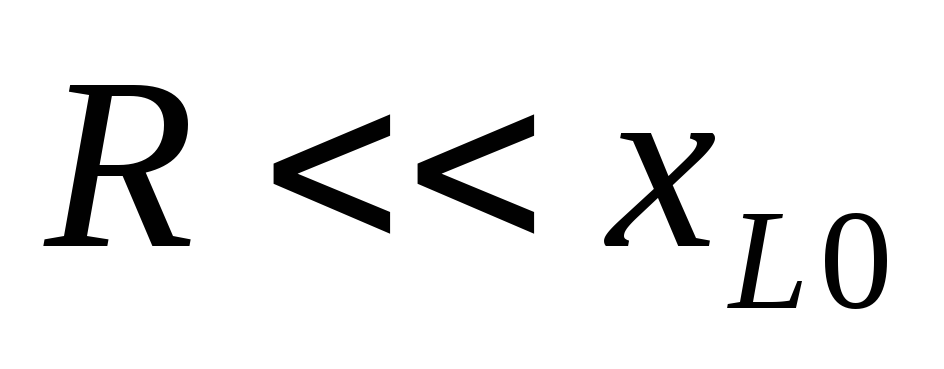 и
и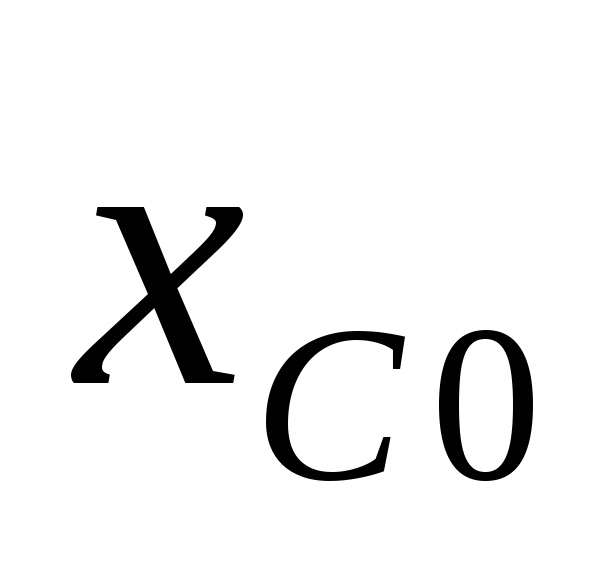 ,
=>
,
=>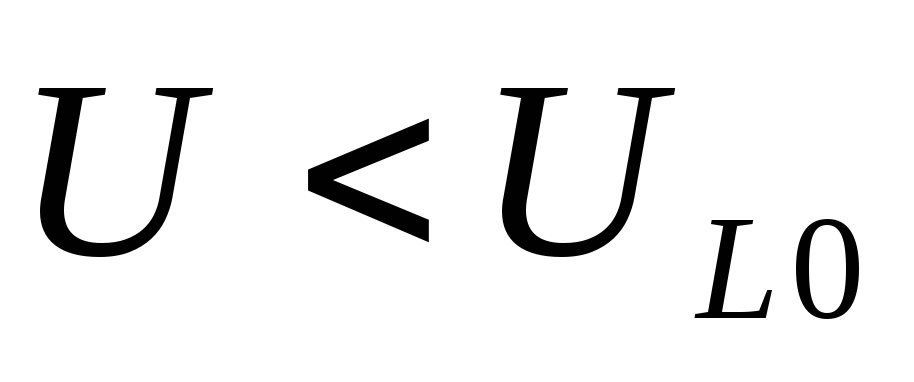 и
и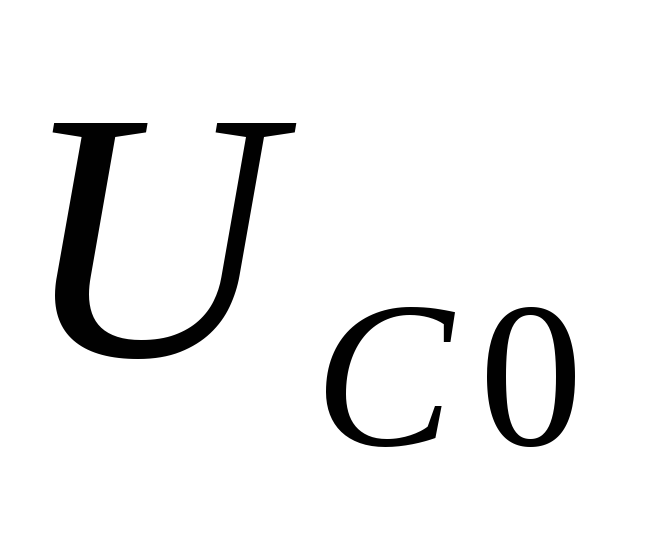
Вывод:это явление и называется резонанс напряжений, потому что напряжение на идеальной катушке и конденсаторе больше, чем напряжение на входе в момент резонанса.
Нарисуем векторную диаграмму:
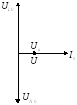
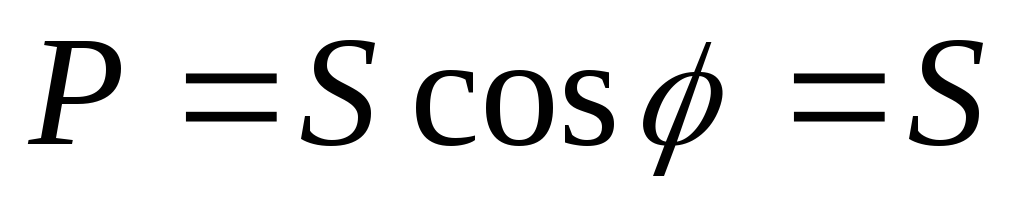
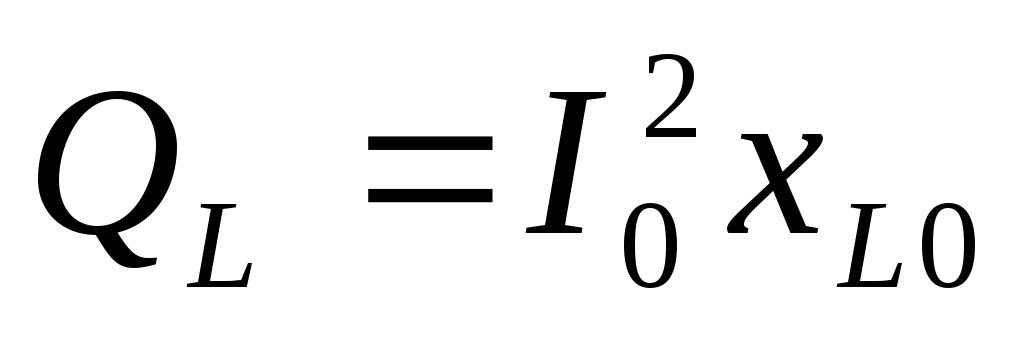
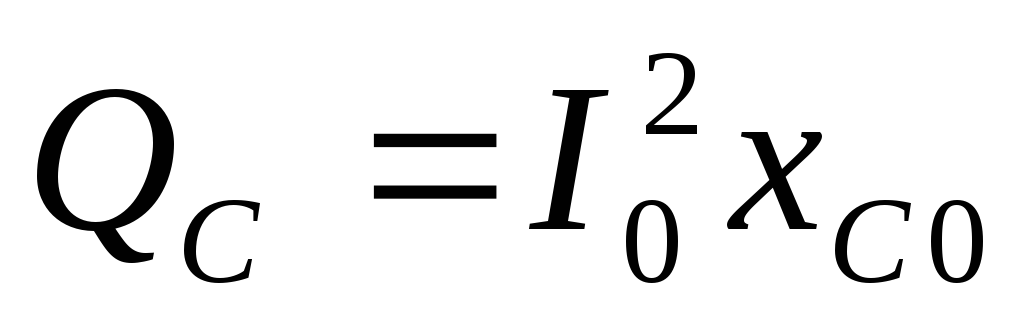
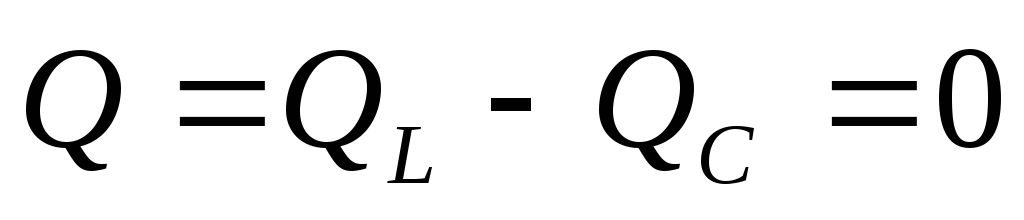
Выводы:
Т. к.
 ,
то от источника потребляется только
активная мощность.
,
то от источника потребляется только
активная мощность. — катушка и конденсатор обмениваются
энергией, а т. к.
— катушка и конденсатор обмениваются
энергией, а т. к.  ,
то с источником обмена энергией не
происходит.
,
то с источником обмена энергией не
происходит.
Резонансная частота, добротность последовательного контура
Выведем формулу резонансной частоты:
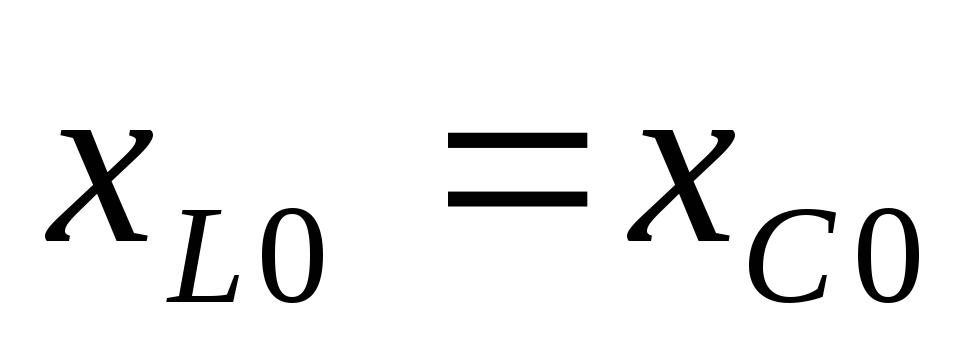

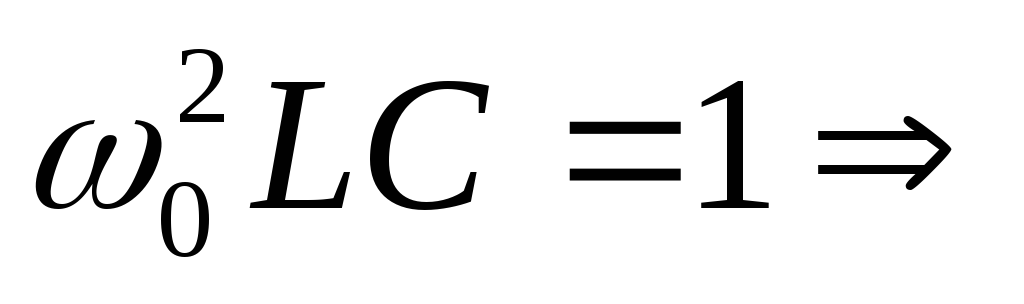
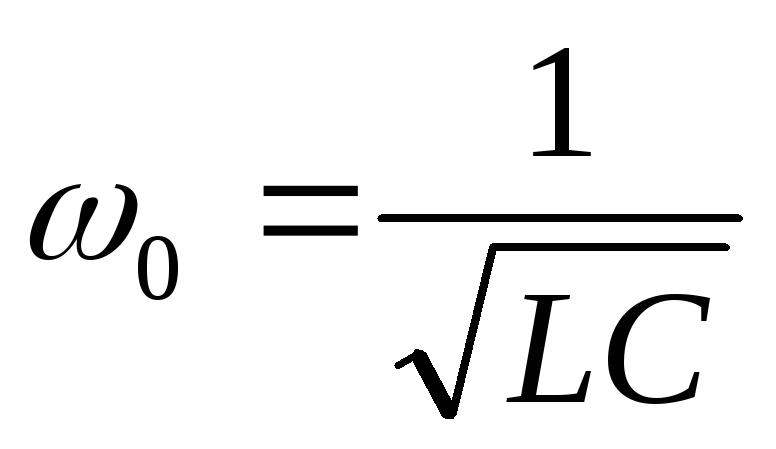
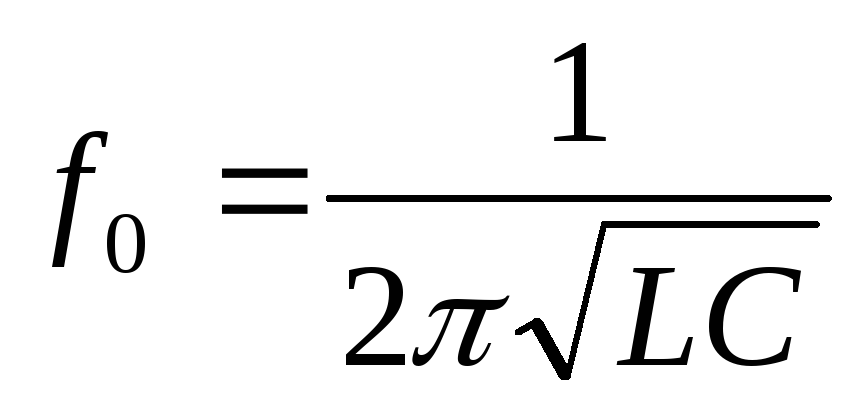
Вывод:резонанс напряжений наступает
тогда, когда частота питающего напряжения
равна частоте собственных колебаний
контура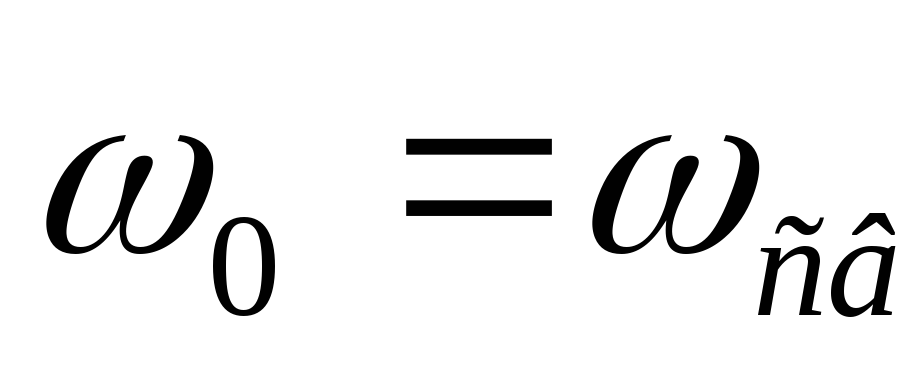 .
.
Настроить контур в резонанс можно:
изменяя L или C, при этом подгоняем частоту собственных колебаний под частоту питающего напряжения;
можно изменять частоту питания, подгоняя её под частоту собственных колебаний контура.
Т. к.  ,
то можно записать, что
,
то можно записать, что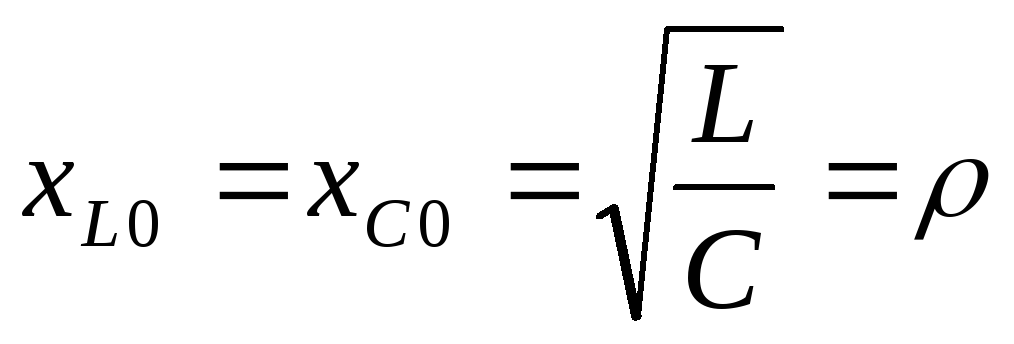 .
.
Сопротивление катушки и конденсатора на резонансной частоте равно характеристическому сопротивлению контура.
Формула добротности:
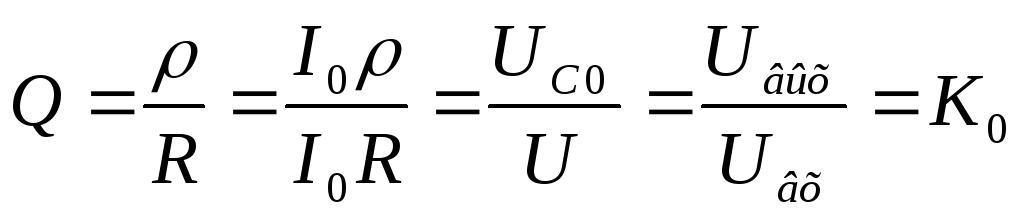
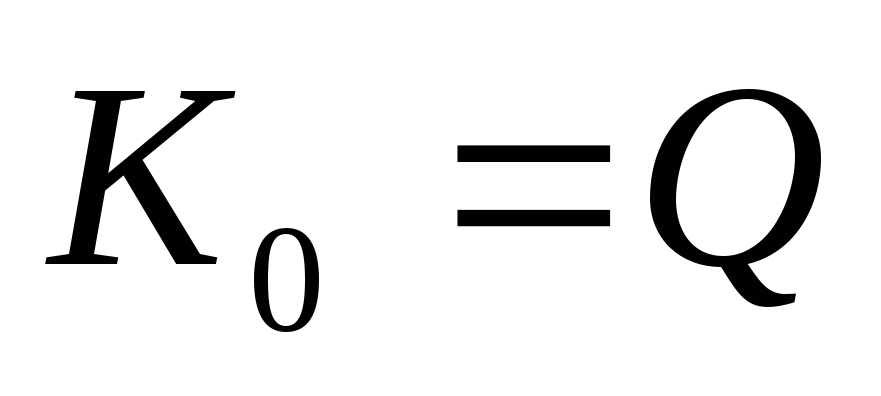
Вывод: добротность в последовательном контуре показывает, во сколько раз напряжение на выходе больше, чем на входе в момент резонанса.
10. Расстройка колебательного контура. Виды расстроек. Входные АЧХ и ФЧХ последовательного колебательного контура. Характер реактивного сопротивления последовательного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной
Расстройка— отклонение частоты от резонансной. Различают:
Абсолютная расстройка — разность текущей частоты и резонансной:
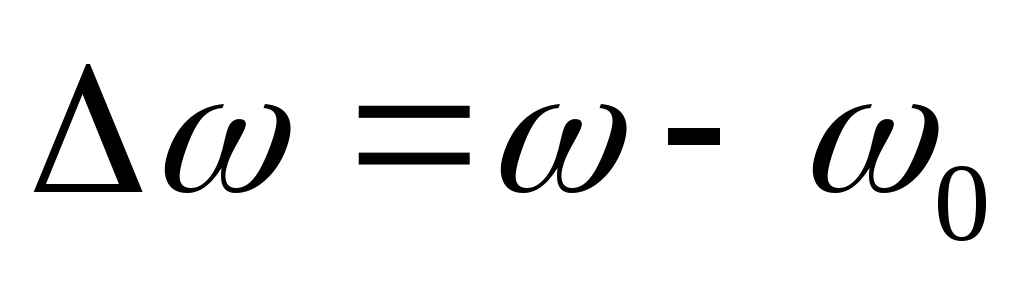
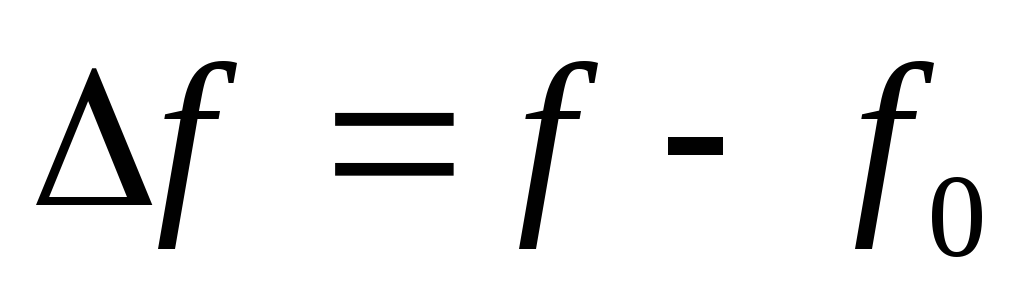
Расстройка может и положительной и отрицательной.
Относительная расстройка — отношение абсолютной расстройки к резонансной частоте:
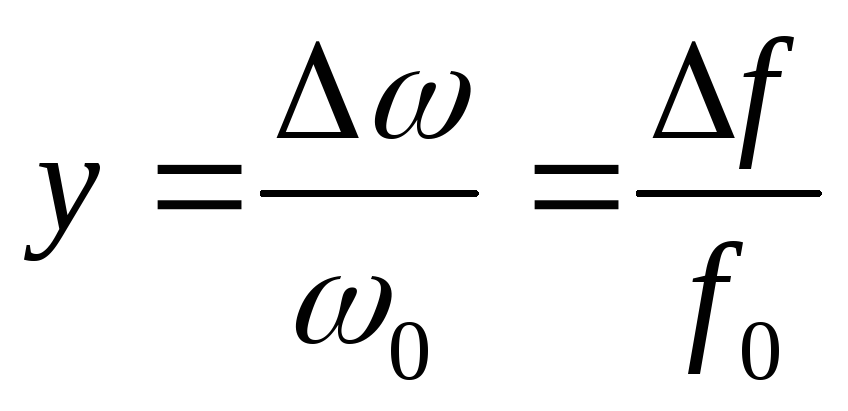
Обобщённая расстройка — отношение реактивного сопротивления xк резистивному:
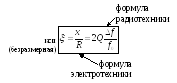
Обычно входные характеристики строят от расстройки.
Входные АЧХ и ФЧХ последовательного контура
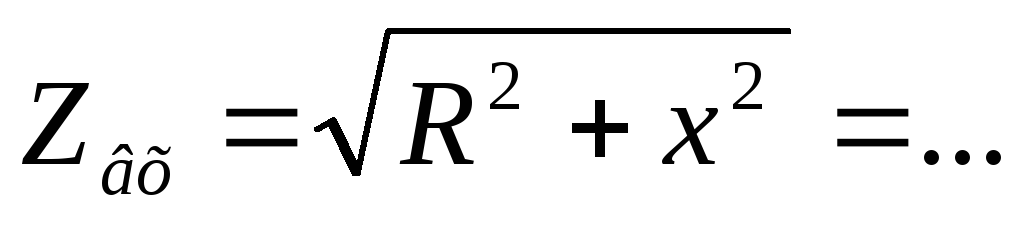 ,где
,где 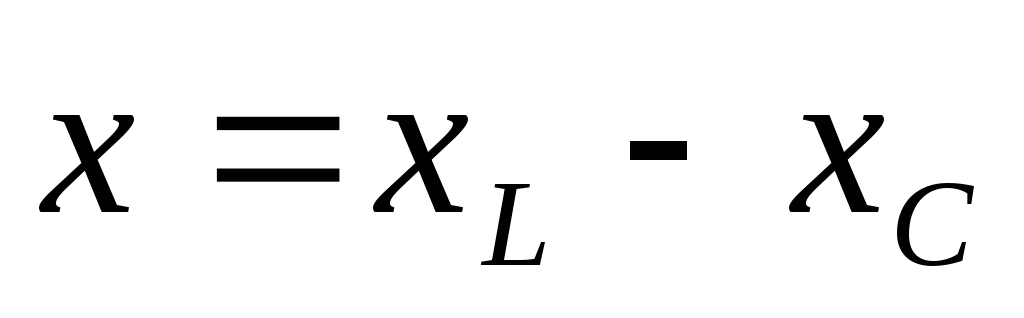
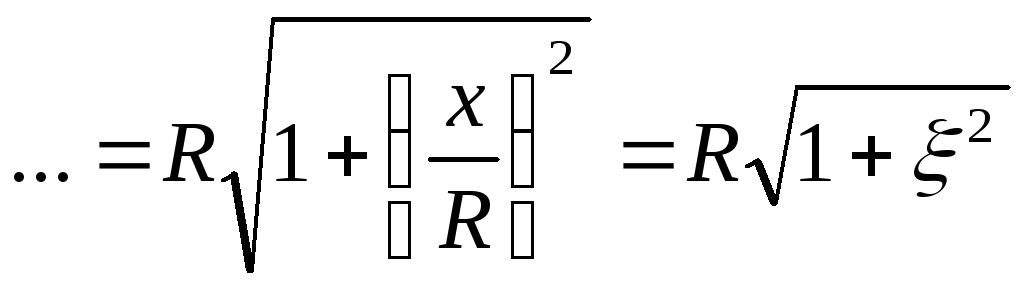
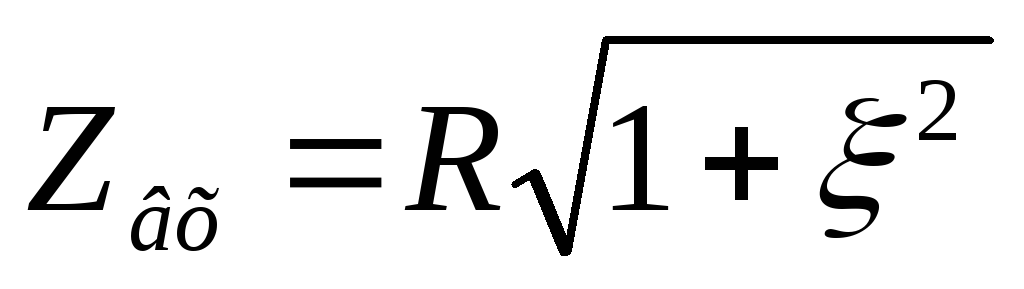 — формула входной АЧХ последовательного
контура
— формула входной АЧХ последовательного
контура
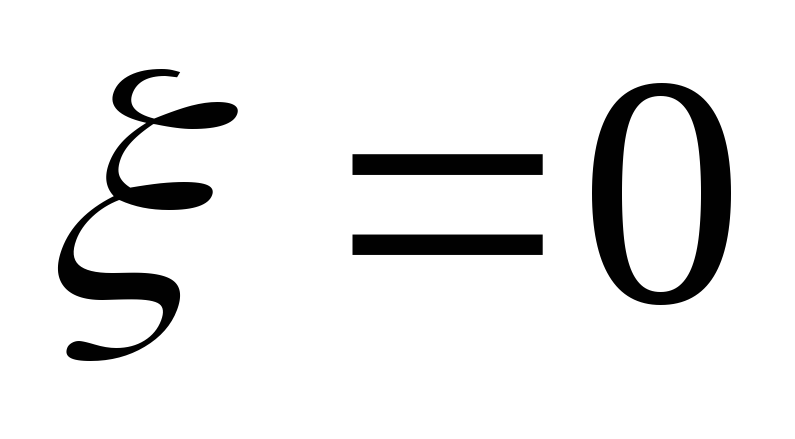

(на резонансной частоте все расстройки равны 0)
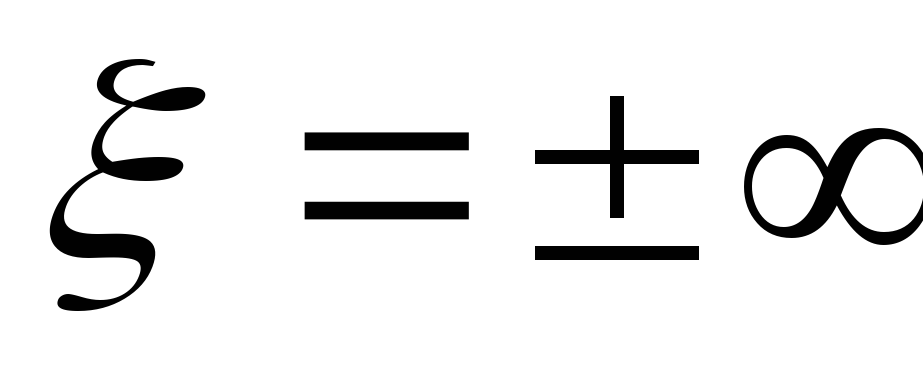
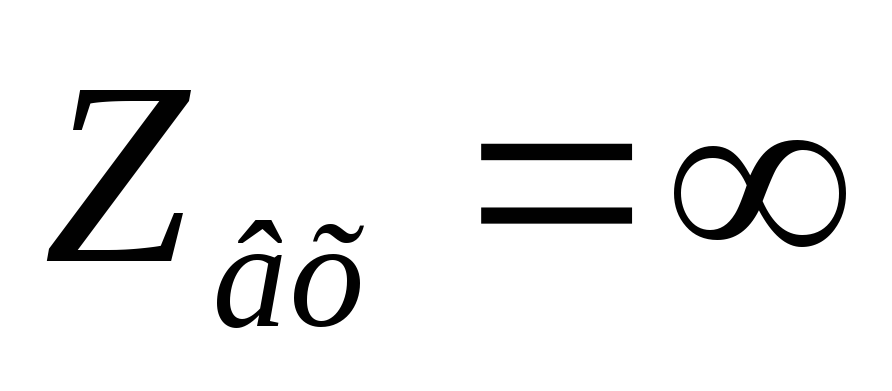
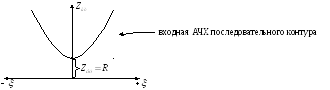
Вывод:на резонансной частоте
сопротивление последовательного контура
имеет наименьшее значение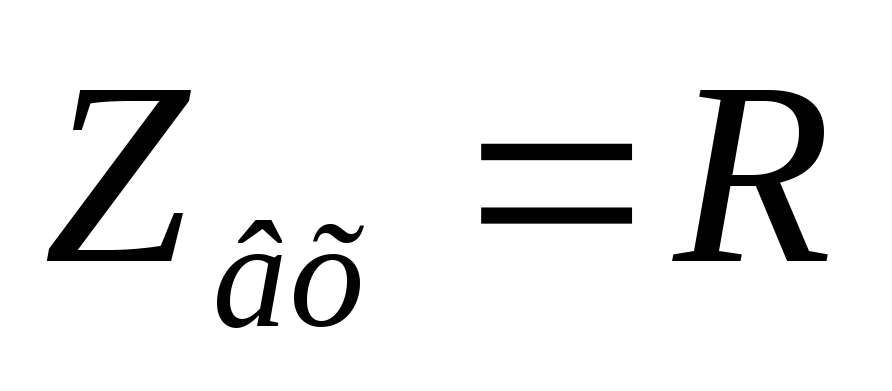 .
По мере увеличения расстройки сопротивление
контура возрастает.
.
По мере увеличения расстройки сопротивление
контура возрастает.
ФЧХ:
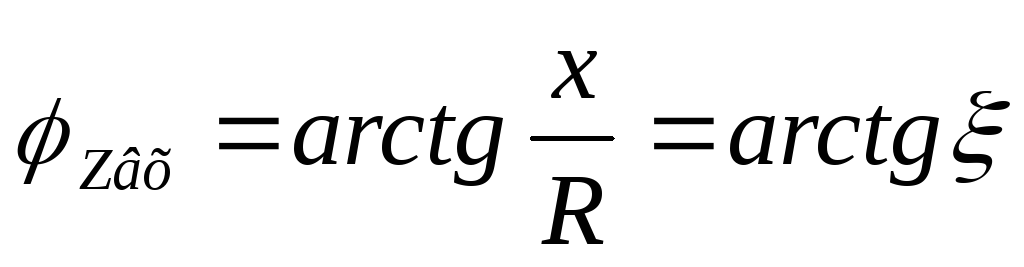
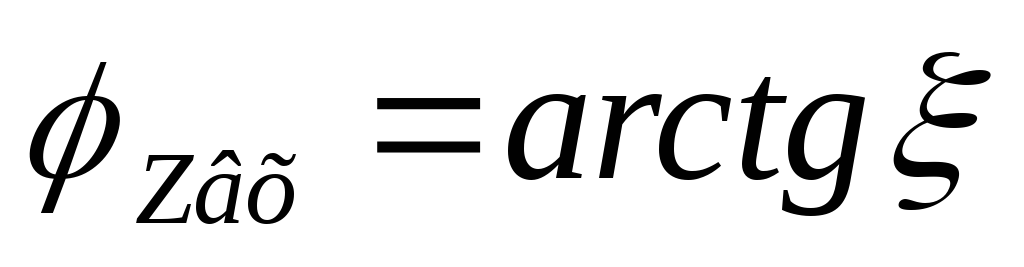 — формула входной ФЧХ последовательного
контура
— формула входной ФЧХ последовательного
контура
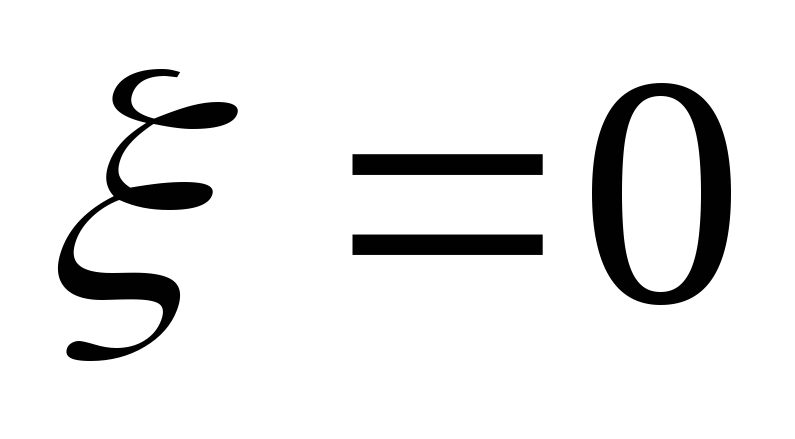
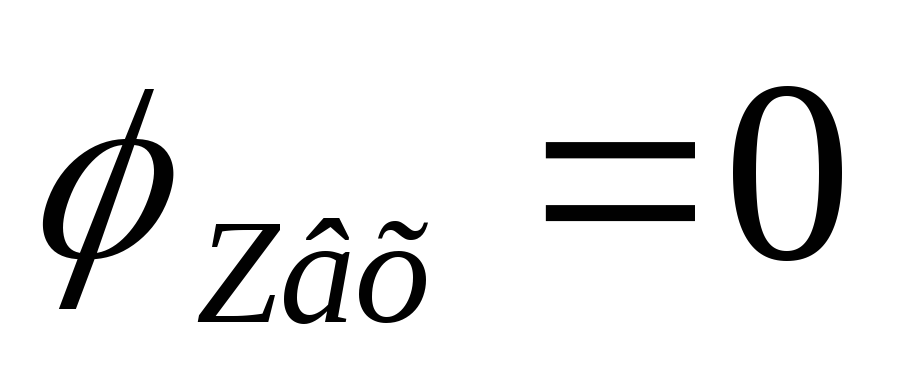
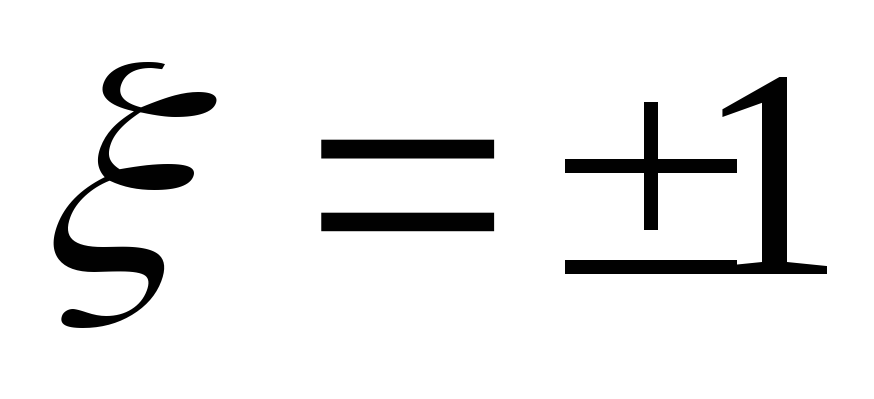
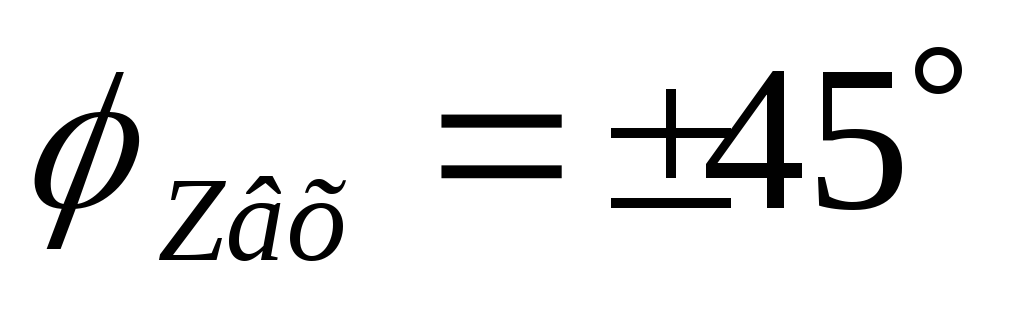
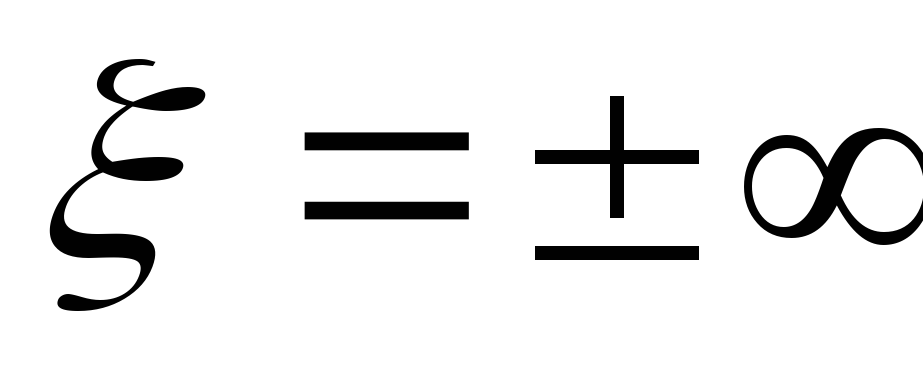
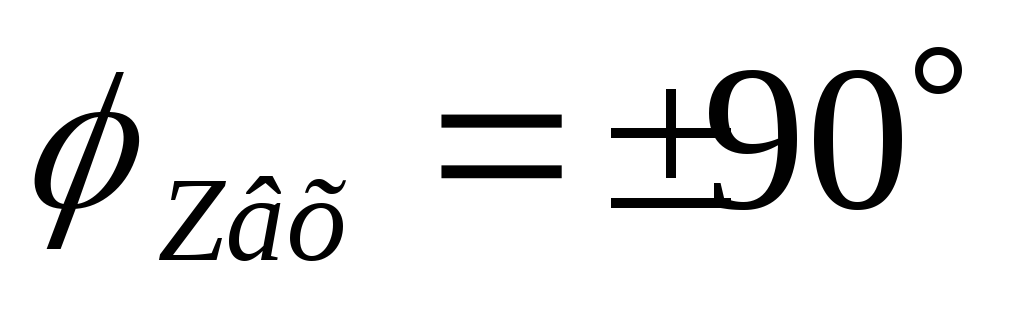
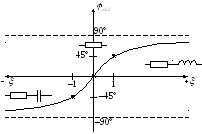
Вывод:на резонансной частоте
последовательный контур имеет чисто
активное сопротивление: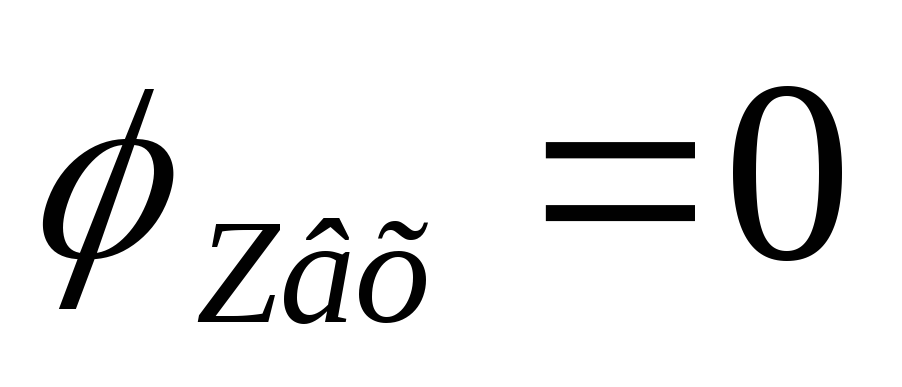 .
На частотах меньше резонансной характер
сопротивления активно-емкостной, т. к.
.
На частотах меньше резонансной характер
сопротивления активно-емкостной, т. к.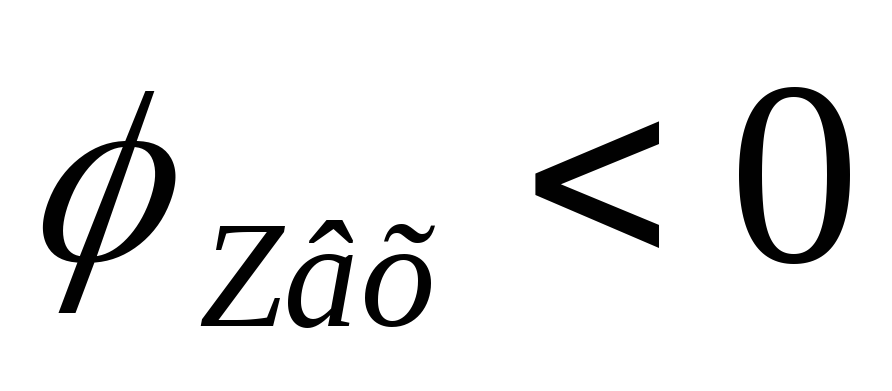 .
На частотах больше резонансной характер
сопротивления активно-индуктивный:
.
На частотах больше резонансной характер
сопротивления активно-индуктивный: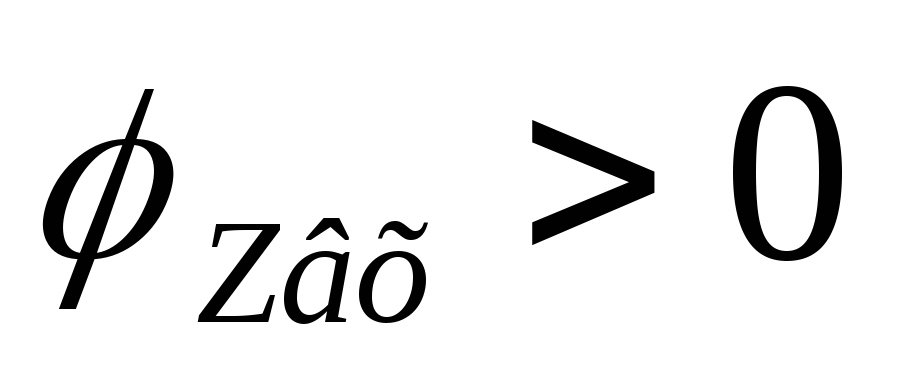 .
.
КАКОЙ ПРИЕМНИК ЛУЧШЕ? | Техника и Программы
Как известно селективность приемника создается колебательными контурами, а чувствительность определяется числом каскадов усиления до детектора. Начнем с селективных свойств одиночного колебательного контура. Мы уже говорили, что селективность характеризует ослабление сигнала мешающей радиостанции, работающей на частоте f, по сравнению с сигналом полезной радиостанции, частота которой совпадает с резонансной частотой контура fрез. Обозначает селективность Se. Селективность Se показывает, во сколько раз будет ослаблена амплитуда сигнала посторонней радиостанции U по сравнению с амплитудой полезного сигнала Upe3 при одинаковой амплитуде этих сигналов Se=Upe3/U.
Однако надо подчеркнуть, что на селективность Se влияют не только селективные свойства контура, но и так называемая расстройка Дf, которая показывает, насколько далеко отстоит по частоте сигнал посторонней радиостанции от резонансной частоты контура Дf=f — fрез.
При расчете селективности расстройку определяют в процентах: Af%= = [(f—fpeз)/fpeз] 100% = (Дf /fpeз) 100%.
Чем дальше отстоит частота посторонней радиостанции от резонансной частоты, т. е. чем больше расстройка, тем значительнее ослабление мешающего сигнала (рис. 29).
Часто селективность определяют не в относительных единицах, а в децибелах Se (AB)=201gSe.
Отчего же зависят селективные свойства колебательного контура? В основном от добротности Q его катушки индуктивности. Конденсатор контура, если он хорошего качества (например, воздушный, слюдяной или керамический) вносит небольшие электрические потери, и поэтому добротность контура я основном определяется добротностью катушки. Чем больше добротность Q, тем круче идут ветви резонансной характеристики контура (рис. 30). Добротность катушки индуктивности зависит от многих факторов: потерь электрической энергии в проводах при прохождении по нему тока высокой частоты, потерь в изоляции проводов, в каркасе катушки, в магнитном сердечнике и т. п.
Рис. 30. Резонансные характеристики контуров с различными Q
Рис. 31. Селективность колебательного контура в зависимости от добротности Q и расстройки Дf
Причем эти потери тем выше, чем на более высокой частоте работает контур. Ориентировочно добротность катушек различных диапазонов следующая: в ДВ Q = 10 — 25, в СВ Q = 25 — 40, в KB Q = 80 — 1120. Казалось бы, при переходе от ДВ к KB из-за увеличения частоты и роста потерь добротность катушки должна падать, однако практически получается наоборот, поскольку катушки диапазона KB имеют малое число витков и провод большого сечения.
Предположим, что имеется колебательный контур с катушкой определенной добротности, которую измерили при помощи куметра или определили по паспорту. Найдем теперь его селективность. На рис. 31 приведены кривые, позволяю-. щие определить Se колебательного контура при небольших расстройках, т. е, когда (Дf/fPe3)100%<l0%.
При больших расстройках селективность приближенно можно подсчитать по формуле
Se = Q[(f/fPe3) — (fрез/f)]
Для примера сделаем следующий расчет: определим селективность по соседнему и зеркальному каналам для контура добротностью Q = 50, работающего в СВ диапазоне на частоте 1,5 МГц (селективность всегда определяют на максимальной частоте диапазона, потому что чем выше частота, тем больше полоса пропускания при той же добротности контура. При уходе на Дf=10 кГц от резонансной частоты fрез= 1500 кГц расстройка, выраженная в процентах, составит:
Далее на горизонтальной оси графика, приведенного на рис. 31, находим точку, соответствующую расстройке 0,66%. Но, взглянув на график, можно сказать
варанее, что при такой небольшой расстройке контур будет очень ослаблять сигнал посторонней радиостанции. Если все же надо определить селективность контура при такой расстройке, то ее можно подсчитать по формуле
Какая же это селективность! Сигнал с частотой, отличающейся на 10 кГц от резонансной (т. е. сигнал соседней станции), проходит почти так же хорошо, как и сигнал принимаемой станции.
При помощи такого же простейшего расчета можно убедиться, что селективность по соседнему каналу входного контура на KB диапазоне вообще ничтожно мала. Но вот на ДВ положение с селективностью по соседнему каналу несколько изменяется. Если рассчитать селективность контура на какой-нибудь частоте ДВ диапазона, например на частоте 400 кГц, то расстройка на 10 кГц от этой частоты составит:
Примем, что на ДВ диапазоне добротность контура Q= 100. Из точки на горизонтальной оси графика (рис. 31), соответствующей расстройке 2,5%, восстановим перпендикуляр и продолжим его до пересечения с кривой Q=100. Через точку их пересечения проведем горизонтальную линию до пересечения с вертикальными осями графика и определим селективность контура при данной расстройке на ДВ диапазоне, т. е. для частоты 410 или 390 кГц. Селективность на этих частотах по отношению к частоте 400 кГц составляет около 15 дБ,
По результатам расчетов делаем вывод: селективность колебательного контура при малой расстройке невелика. Но она увеличится, если между антенной и детектором включить два колебательных контура: между антенной и входом усилителя радиочастоты (УРЧ) и между УРЧ и детектором Д (рис. 32).
Рис. 32. Включение двух колебательных контуров, настроенных на частоту принимаемого сигнала
Безусловно селективность при этом увеличится (рис. 33). Чтобы определить результирующую характеристику приемника по высокой частоте (от антенного входа до входа детектора), надо перемножить ординаты резонансных характеристик отдельных контуров — значения напряжений на обоих контурах на данной частоте. Как видно из рисунка, результирующая характеристика обладает значительно большей крутизной скатов, чем характеристики отдельных контуров (на рис. 33 вертикальный масштаб результирующей характеристики уменьшен в 10 раз). Этим и объясняется возрастание селективности приемника при увеличении числа колебательных контуров. Если, например, ослабление Uve3/U сигнала входным контуром на частоте расстройки 16 кГц составляло 1/0,3=3,3, то ослабление при такой же расстройке по результирующей характеристике равно 1/0,092=10,9.
Следует обратить внимание на то, что в результате увеличения общей селективности сузится полоса пропускания высокочастотного тракта приемника — это хорошо видно на рис. 33. Подсчитать полосу пропускания Я для такого случая можно по формуле П=0,б4fmin/Q.
Рис. 33. Увеличение селективности и сужение полосы пропускания приемника при включении двух колебательных контуров, настроенных на частоту принимаемого сигнала
Посмотрим теперь, как обстоит дело с селективностью и полосой пропускания в простейшем приемнике, работающем по схеме прямого усиления. Такой приемник содержит один или несколько каскадов УРЧ, причем на входе каждого из каскадов (в том числе и детекторного) включен колебательный контур. Каждый колебательный контур (они все настроены на одну частоту) ослабляет сигналы с частотами, отличающимися от резонансной. Чем больше таких контуров-фильтров, тем значительнее будут ослаблены сигналы соседних по частоте радиостанций и тем выше будет селективность приемника. Таким образом, если включить как можно больше контуров, то можно получить любую необходимую селективность. Но в действительности это не так просто «делать. Ведь при перестройке приемника на другую радиостанцию все колебательные контуры придется перестраивать. Однако добиться, чтобы большое число колебательных контуров имело совершенно одинаковые параметры, очень трудно. Поэтому при перестройке контуров общей ручкой блока конденсаторов переменной емкости настройка контуров неизбежно «расходится». В результате полоса пропускания увеличивается, а следовательно ухудшается селективность приемника. Кроме того при этом уменьшаются усиление приемника и его чувствительность к сигналам в приемной антенне. Ведь колебания в контуре имеют наибольшую амплитуду на резонансной частоте, и если частота какого-либо контура сдвинута относительно частоты сигнала, то контур реагирует на его колебания слабее, чем в случае, когда резонансная частота совпадает с частотой сигнала.
Рис. 34. Резонансная характеристика колебательного контура с добротностью Q== 160 и резонансной частотой f рез =10 МГц
Но предположим, что все же удалось так точно изготовить колебательные контуры и блок конденсаторов настройки, что при перестройке все колебательные контуры настраиваются на одну и ту же частоту. Все равно, это не спасает положения. Дело в том, что полоса пропускания контура зависит от частоты,, на которой он работает, причем чем выше частота, тем шире полоса пропуска-, ния: n=f/Q. При перестройке колебательного контура на более высокие частоты полоса пропускания расширяется, а на более низкие — сужается (добротность контура Q практически остается постоянной). Если в середине диапазона полоса пропускания выбрана такой, что обеспечено достаточно естественное: воспроизведение передачи, а помехи со-стороны других радиостанций незначительны, то на высокочастотном участке диапазона полоса пропускания может стать слишком большой, и помехи от других радиостанций будут очень заметными. Наоборот, на низкочастотном; конце диапазона полоса пропускания может сузиться настолько, что ухудшится естественность воспроизведения радиопередачи.
На рис. Э4 изображена резонансная характеристика колебательного контура с добротностью Q= 160 на частоте 10 МГц. Несмотря даже на такую большую добротность, характеристика контура на высоких частотах выглядит весьма пологой. Полоса пропускания на уровне 0,7 составляет 60 кГц. А нужно не более 10 кГц. Конечно при такой широкой полосе пропускания все составляющие спектра полезного сигнала хорошо пройдут через приемник, но и селективность приемника будет чрезвычайно низкой. Собственно, о какой селективности может идти речь, если в приемнике с одинаковой громкостью будут одновременно слышны шесть радиостанций! А полоса пропускания на уровне 0,1 составляет 220 кГц!
Рис. 35. Принципиальная схема (а) и формы резонансной характеристики (б) двухконтурного полосового фильтра
Итак, приемник прямого усиления не может одновременно обеспечить необходимую полосу пропускания и хорошую отстройку от соседних по частоте радиостанций. Самым лучшим с позиций селективности и хорошего качества воспроизведения передачи будет такой приемник, форма резонансной характеристики которого напоминает букву П (плоская вершина и отвесные боковые-склоны.) Обычно степень приближения формы резонансной характеристики к идельной оценивают так называемым коэффициентом прямоугольности, который представляет собой отношение ширины полосы пропускания на каком-то определенном уровне (обычно на уровне 0,1) к полосе, отсчитываемой на уровне-0,7: Кп = 2Дf0,1/2Дf0,7.
Естественно, идеальный приемник должен иметь Kп = 1- Для приемников-прямого усиления даже при очень большом числе одиночных колебательных контуров этот коэффициент составляет не менее 3,9. Конечно, это плохо, причем чем выше частота, на которой работает приемник, тем больше коэффициент прямоугольности. Как же уменьшить коэффициент прямоугольности приемника, т. е. как сделать форму его резонансной характеристики более прямоугольной? Вообще говоря, резонансную П-образную характеристику можно получить, если заменить одиночные резонансные контуры группами из двух связанных контуров (рис. 35,а). Такие сиетемы называются полосовыми фильтрами с индуктивной (трансформаторной) связью. Полосовые фильтры равномерно пропускают колебания определенной полосы частот, отсекая остальные, не попадающие в их полосу пропускания. Ширина полосы пропускания, а также возможность отсеивания мешающих сигналов определяется добротностью контуров L1C1 и L2C2, а кроме того индуктивной связью (коэффициентом связи) между этими контурами.
Форма резонансной характеристики таких фильтров при различных коэффициентах связи показана на рис. 35,6. Кривая 1 соответствует слабой связи между контурами. Характеристика в этом случае во многом напоминает по форме характеристику одиночного контура, коэффициент прямоугольности которого около 10. Если связь увеличивать, например сближением контурных катушек, то крутизна склонов характеристики будет увеличиваться (кривая 2). При некоторой критической связи характеристика будет иметь вид кривой 3, которая соответствует наибольшей высоте резонансной характеристики при коэффициенте прямоугольности 3,2 — 3,5. При связи между контурами выше критической на характеристике возникают два горба и появляется провал на резонансной частоте (кривая 4)., причем чем сильнее связь, тем значительнее высота горбов и глубже впадина (кривая 5). При связи чуть больше критической характеристика полосового фильтра очень напоминает прямоугольную (П-образную), так как крутизна склонов велика, а провал почти не заметен. Коэффициент прямоугольности такой системы контуров уменьшается до 2,3 — 2,5.
Однако нельзя все колебательные контуры приемника прямого усиления просто заменить подобными полосовыми фильтрами и тем самым сделать его резонансную характеристику П-образной. Ведь тогда при перестройке приемника с одной частоты на другую придется перестраивать и эти фильтры. И дело даже не в том, что это очень сложно осуществить на практике (придется перестраивать одновременно шесть и даже больше контуров), самое главное в том, что с изменением частоты будет изменяться полоса пропускания фильтров. Поэтому на низкочастотном участке диапазона она будет меньше, а на высокочастотном — больше необходимой. Но и это не все. Предположим, что приемник должен работать в KB диапазоне. В приемнике прямого усиления принимаемый сигнал усиливается в усилителе, работающем на частоте этого сигнала. На частотах выше нескольких мегагерц большую роль играют различные паразитные связи между каскадами усилителя, которые могут привести к самовозбуждению усилителя, т. е. усилитель превращается в генератор паразитных колебаний, создающих помехи. Поэтому трудно сделать высокочастотный усилитель с большим коэффициентом усиления, а ведь для приема дальних станций необходимо очень большое усиление принимаемого сигнала.
Реализовать преимущества полосового фильтра возможно лишь в том случае, если он работает на неизменной (фиксированной) частоте. Но для этого надо сигнал принимаемой радиостанции преобразовать в колебания такой частоты, на которую настроены контуры полосового фильтра. Тогда преобразованный по частоте сигнал радиостанции можно будет подать в усилитель с полосовыми фильтрами, форма резонансной характеристики которого П-образна, т. е. коэффициент прямоугольности составляет 1,6 и даже меньше. Приемник, работающий по такой схеме, обладает хорошими параметрами, имеет большую чувствительность, поскольку усиление принимаемого сигнала осуществляется двумя усилителями на разных частотах: на частоте принимаемого сигнала УРЧ, а затем усилителем с полосовыми фильтрами на промежуточной частоте. Результирующее усиление может быть весьма значительным, так как оно происходит на разных частотах, причем основное усиление осуществляется в усилителе с полосовыми фильтрами, который обычно работает на частоте ниже частоты СВ диапазона (на так называемой промежуточной частоте). Именно по такой схеме работают супергетеродинные радиоприемники.
Как же преобразовать сигналы принимаемой частоты в колебания промежуточной частоты? Такое преобразование происходит в специальном блоке супергетеродинного приемника, называемом преобразователем частоты. Чтобы произвести преобразование, надо сигнал принимаемой радиостанции «смешать» с колебаниями высокочастотного гетеродина (генератора), имеющегося в блоке преобразователя частоты. При смешении колебаний возникнут так называемые биения, т. е. новые колебания, частота которых равна разности частот смешивающих колебаний (одновременно с колебаниями разностной частоты образуются и колебания суммарной частоты, но о них мы поговорим позднее). Естественно, что для нашего случая частота этих колебаний должна быть равна промежуточной частоте fп. Это достигается выбором соответствующей частоты гетеродина fr, при которой fa=fr — fc (fc — частота принимаемой радиостанции).
Однако следует предупредить, что преобразование — это не только вычитание колебаний различных частот. Если например два колебания разных частот пропустить через резистор, то никакого преобразования не получится. Сумма или разность двух колебаний не содержит и не создает какого-либо нового колебания, если смешение происходит в линейной цепи. Для преобразования необходимы условия, при которых биения, возникающие при сложении или вычитании колебаний, превратились бы в реальное колебание. Такие условия будут в том случае, если смешение колебаний происходит в нелинейной цепи, параметры которой (или один параметр) изменяются в зависимости от приложенного напряжения или тока.
Простейшим нелинейным элементом может быть полупроводниковый диод. Его характеристика — зависимость тока, проходящего через диод от приложенного к диоду напряжения — нелинейна. Когда полярность напряжения совпадает с полярностью диода, нарастание тока через диод линейно следует за нарастанием напряжения. Если полярность приложенного напряжения не совпадает с полярностью диода, то он заперт, и ток уже не следует за нарастанием напряжения. Другими словами, в области положительных напряжений диод обладает некоторой крутизной характеристики (крутизна характеристики — это отношение малого приращения тока Дi к вызвавшему его малому приращению напряжения Ди, т. е. S = Дi/Дu, мА/В), а в области отрицательных напряжений крутизна характеристики равна нулю. Следовательно, крутизна характеристики диода изменяется в зависимости от знака приложенного напряжения — она нелинейна.
При воздействии на прибор с нелинейной характеристикой двух колебаний с разной частотой на выходе прибора возникают биения — колебания разностной частоты fn=fr — fc. Такие биения представляют собой периодическое (о частотой fa) изменение амплитуды напряжения на выходе нелинейного прибора от ыг + «с до ит — «с (огибающая на рис. 36). Частота этого изменения fn = fr — fc и является промежуточной частотой.
Рис. 36. Биения промежуточной частоты fa на выходе преобразователя в результате смещения колебаний с частотами fc и fr
Рис. 37. Преобразователь частоты на диоде
Следует заметить, что на выходе преобразователя возникает не только колебание разностной частоты fг — fc, но и колебание суммарной частоты fг+fс, колебание с частотой гетеродина fг, а также колебание с частотой сигнала fc. К этому надо добавить, что в реальном приемнике на вход преобразователя подаются не только колебания с частотой сигнала fс, но и другие сигналы, и они тоже образуют биения с колебаниями гетеродина. Словом, на выходе преобразователя имеются колебания множества частот. Как же выделить необходимые нам колебания с частотой fn=fr — fc?
Представьте, что в цепь диода, на котором происходит смешение колебаний принимаемого сигнала и гетеродина, включен колебательный контур LC (рис. 37], Этот контур не окажет заметного сопротивления колебаниям с частотами сигнала, гетеродина и суммарной частоты fr+fc, так как контур сильно расстроен относительно этих частот. Сигнал же с промежуточной частотой fn=fr — fc выделится на контуре, так как контур настроен на эту частоту и обладает на ней значительным сопротивлением. Таким образом на выходе фильтра возникает напряжение с промежуточной частотой fп, которое затем будет подано на вход усилителя промежуточной частоты (УПЧ).
Рис. 38. Преобразование спектра принимаемого сигнала в спектр сигнала промежуточной частоты
Как уже было сказано, при AM радиостанция излучает не только сигнал несущей частоты, но и целую полосу колебаний шириной 2fB (fB — наивысшая частота модуляции). С каждым из этих колебаний колебания гетеродина образуют биения, поэтому и несущая частота радиостанции, и все боковые частоты, образующиеся при модуляции, преобразуются по частоте (рис. 38). В УПЧ попадают только те колебания, частота которых равна промежуточной Iп. Как было показано, колебания с частотой fn возникают в результате биения с разностной частотой fг — fс. Но это произойдет только в том случае, если частота гетеродина точно на частоту fп выше частоты сигнала принимаемой радиостанции, иначе разностная частота fг — fс не будет равна частоте fп и поэтому не попадет в УПЧ. Однако из этого следует, что при перестройке приемника для приема другой радиостанции с частотой foi, необходима перестройка и гетеродина на частоту fn, чтобы сохранилось равенство fri — fa=fn.
Таким образом настройка приемника зависит от настройки гетеродина. Другими словами, чтобы приемник оказался способен принимать радиостанцию с частотой fс, необходимо настроить гетеродин на частоту fг. Поясним это на примере. Если к входу преобразователя присоединить антенну, то на нем окажутся, например, сигналы от радиостанции с частотами fc1, fc2 и fс3 (рис. 39). Предположим, что приемник должен принимать радиостанцию, работающую на частоте fс2. Для этого гетеродин надо настроить на частоту fC2, чтобы разностная частота fр2=fг2 — fс2 была равна промежуточной fп, на которую настроены фильтры УПЧ. Только в этом случае преобразованный по частоте спектр сигнала радиостанции fC2 попадает в полосу пропускания этих фильтров и пройдет к детектору радиоприемника. Сигналы радиостанций fc1 и fсз тоже образуют с колебаниями гетеродина разностные частоты fpi и }рз, однако их преобразованные по частоте спектры окажутся, как это видно из рис. 39, за пределами полосы пропускания фильтров УПЧ.
Рис. 39. Проникновение в полосу пропускания фильтров промежуточной частоты преобразованного спектра радиостанции, частота которой fc. отличается от частоты гетеродина fr на частоту fр, равную fn
Если необходимо перестроить приемник на прием другой радиостанции, например fa, частота которой ниже частоты, радиостанции fci, то соответственно гетеродин должен быть настроен на более низкую частоту fг1, причем такую, чтобы образовавшаяся разностная частота fri — fci была равна fn. В результате уменьшения частоты гетеродина разностная частота fP2 также уменьшается и уже не будет равна частоте fп. В этом случае преобразованный по частоте спектр сигнала радиостанции fC2 выйдет за пределы полосы пропускания фильтров УПЧ, а его место займет спектр сигнала радиостанции fci. Радиоприемник окажется настроенным на частоту радиостанции fci.
13. Подключение параллельного колебательного контура к источникам напряжения и тока. Избирательность параллельного колебательного контура
Питание параллельного контура от источника напряжения и источника тока
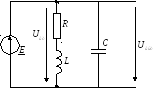

Если параллельный контур питается от
источника напряженияс малым внутренним
сопротивлением, то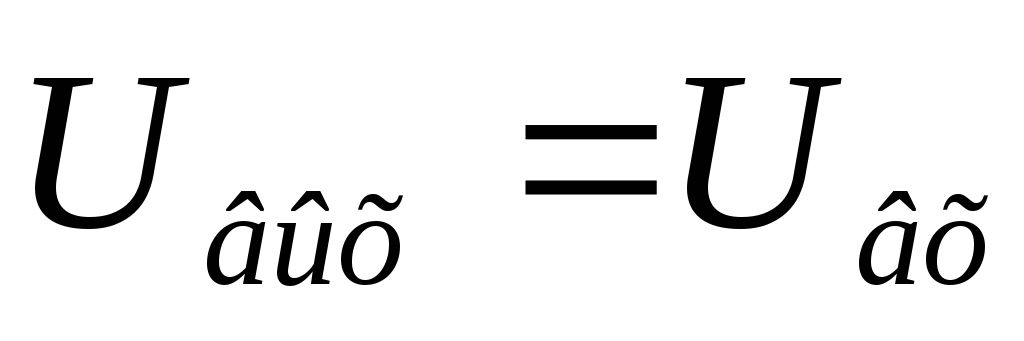 (видно из схемы), избирательности по
напряжению нет.
(видно из схемы), избирательности по
напряжению нет.
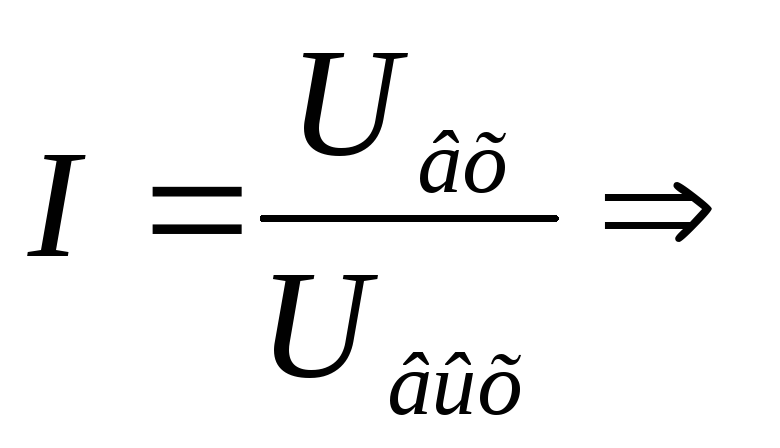 в момент резонанса будет минимальный
ток.
в момент резонанса будет минимальный
ток.
Вывод:при питанииот источника напряженияс малым внутренним сопротивлением параллельный контур обладаетизбирательностью по току, но не обладает избирательностью по напряжению.
Чтобы он обладал избирательностью по
напряжению, последовательно с ним
включают очень большое внутреннее
сопротивление 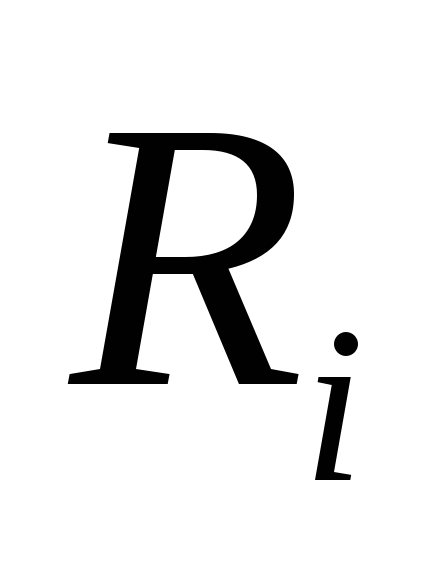 ,
которое:
,
которое:
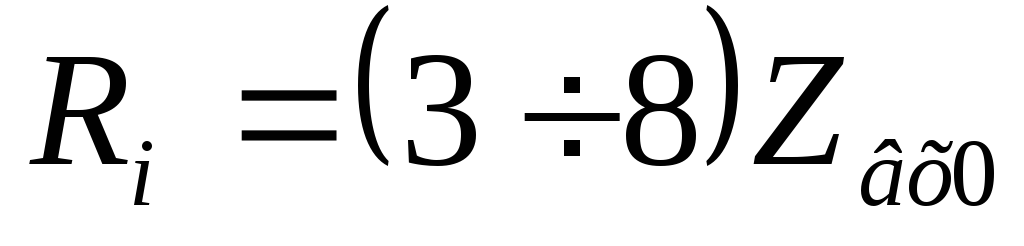
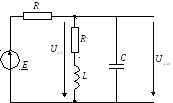
При этом источник напряжения превращается в источник тока, ток которого не зависит от сопротивления нагрузки.

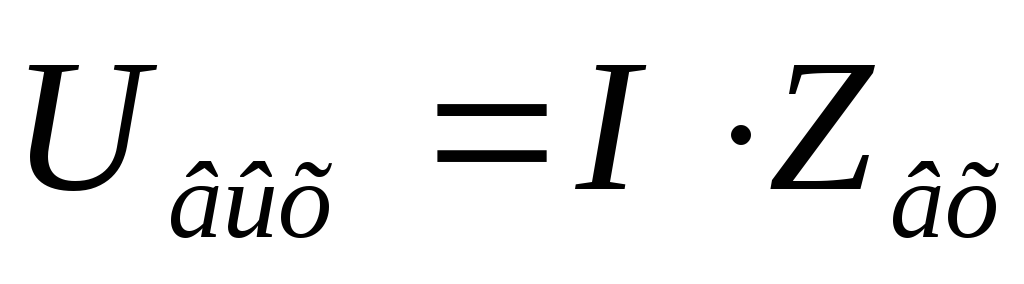 ,
а т. к.
,
а т. к.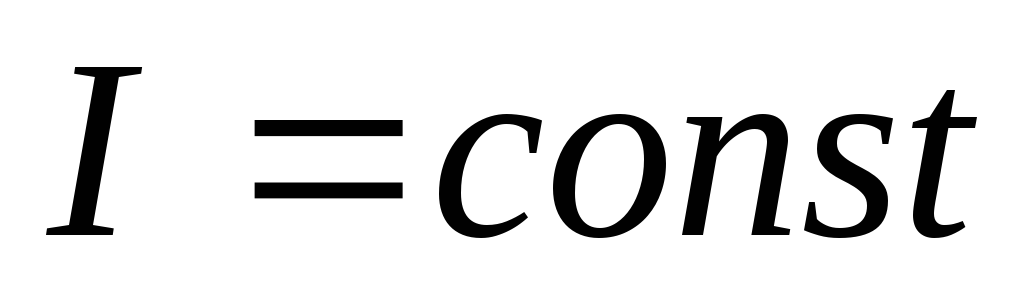 ,
то
,
то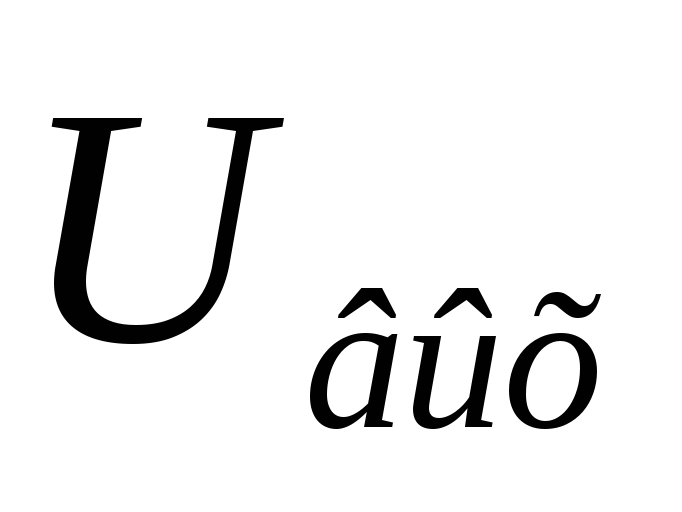 будет повторять по форме
будет повторять по форме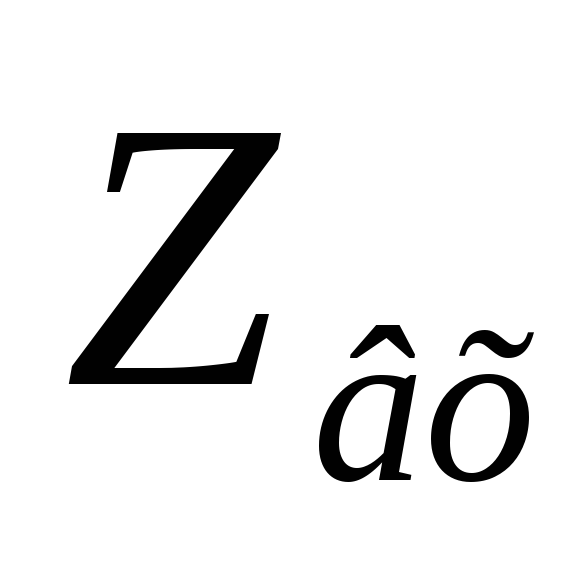 .
.
Вывод:если параллельный контур питаетсяот источника тока, то он обладаетизбирательностью по напряжению.
14. Входные ачх и фчх параллельного колебательного контура. Характер реактивного сопротивления параллельного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной

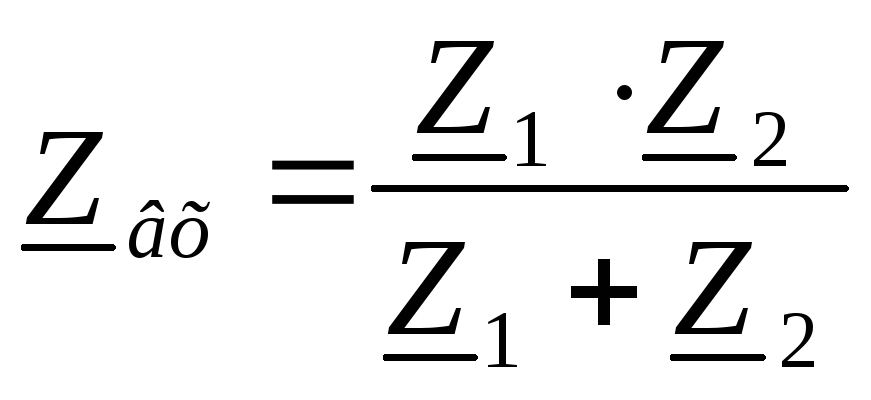
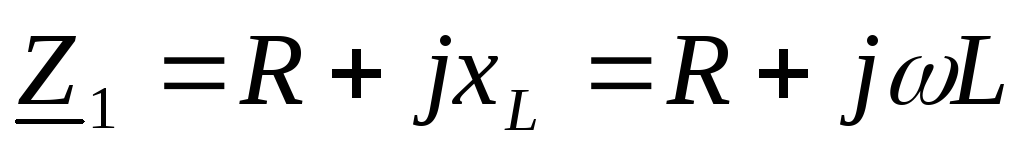
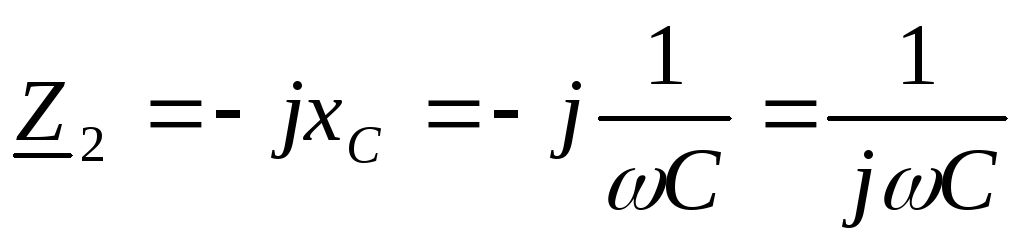
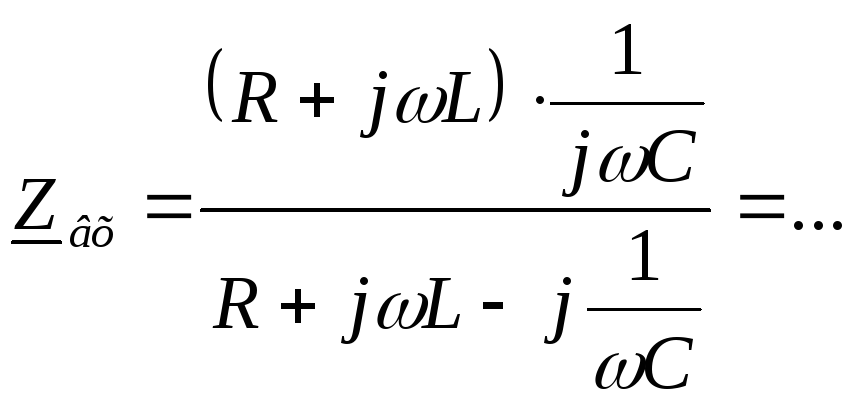
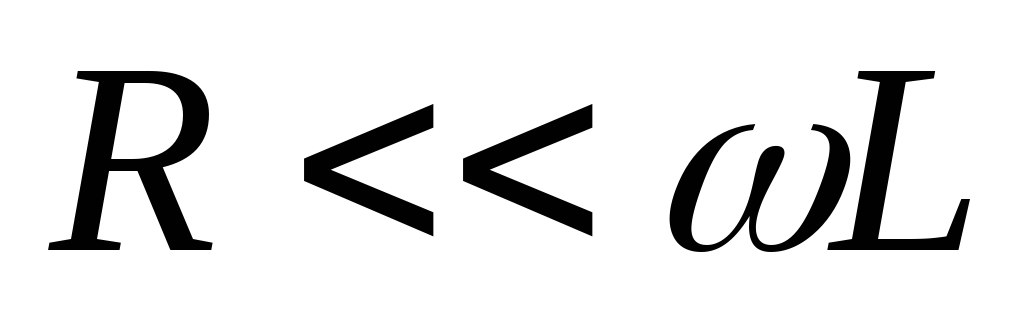 ,
и в числителе им можно пренебречь
,
и в числителе им можно пренебречь
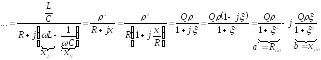
Воспользовавшись формулой 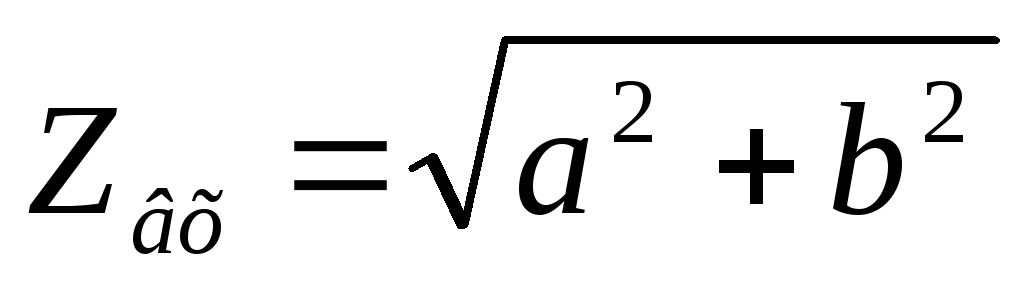 ,
получим формулу входной АЧХ параллельного
контура:
,
получим формулу входной АЧХ параллельного
контура:
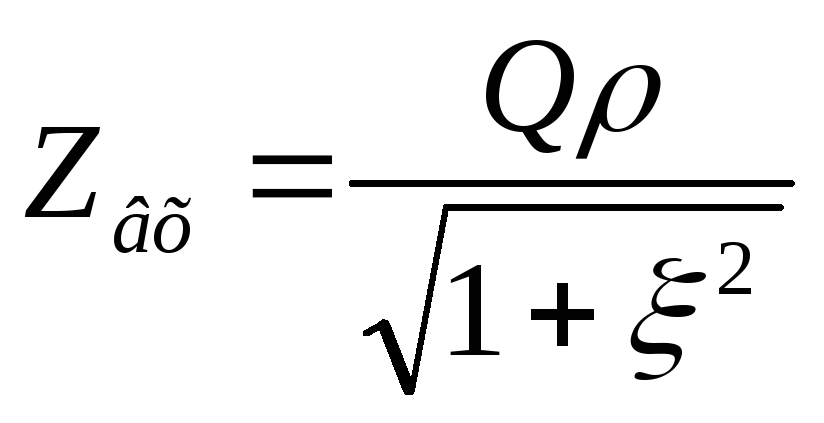 — формула входной АЧХ параллельного
контура
— формула входной АЧХ параллельного
контура
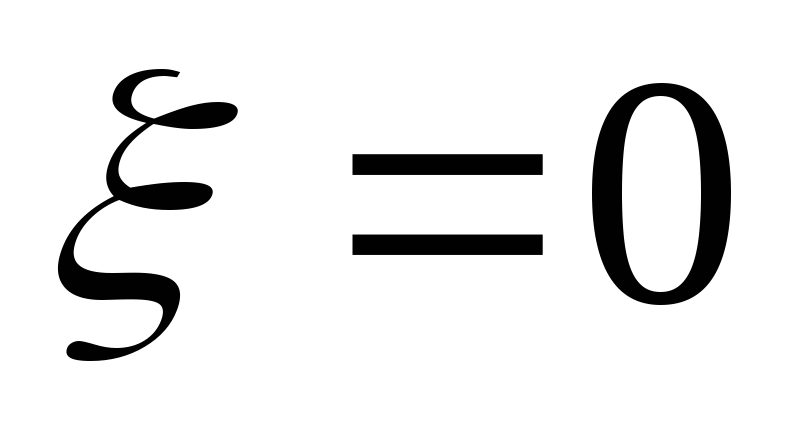
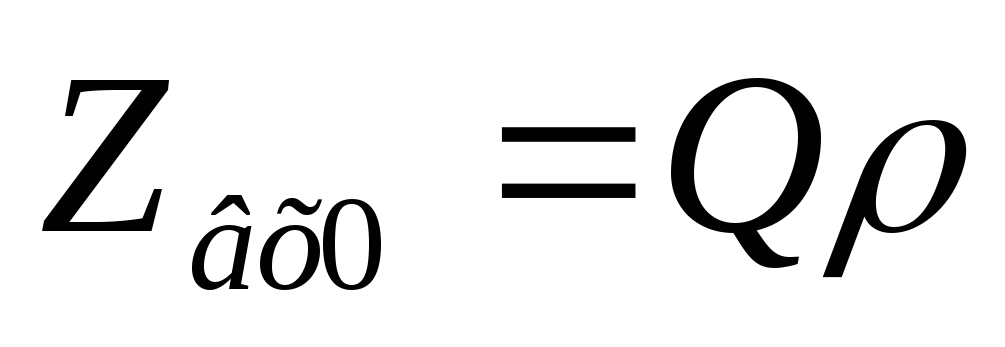
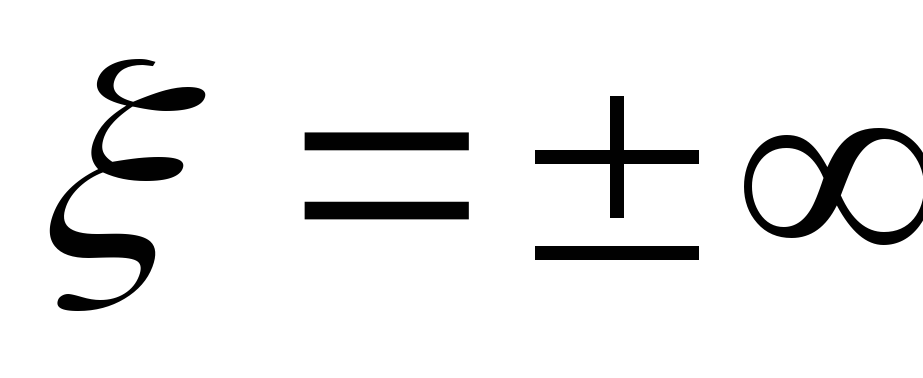
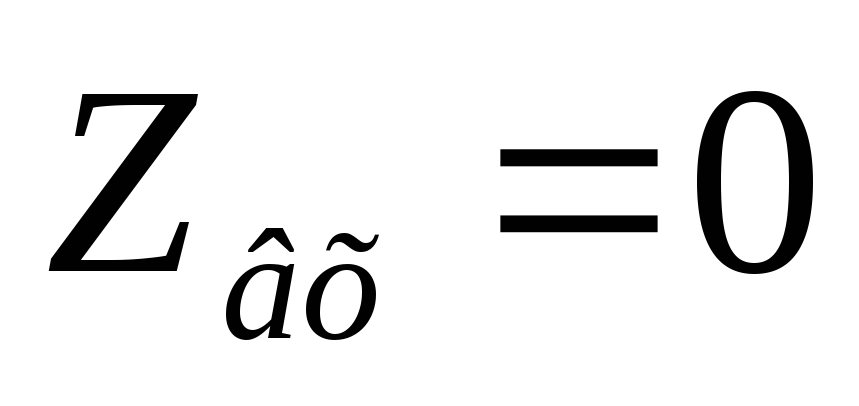

Вывод:параллельный контур имеет максимальное сопротивление на резонансной частоте. По мере увеличения расстройки сопротивление параллельного контура падает.
ФЧХ:
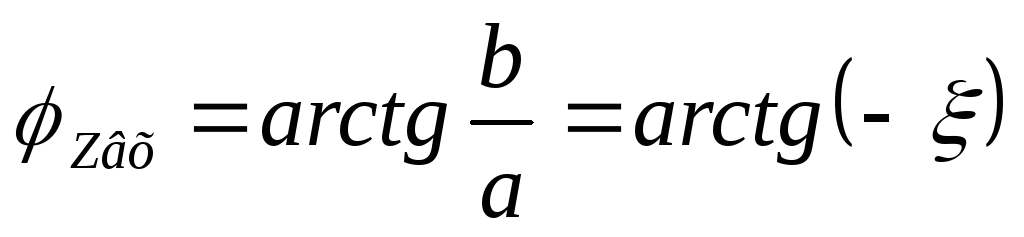
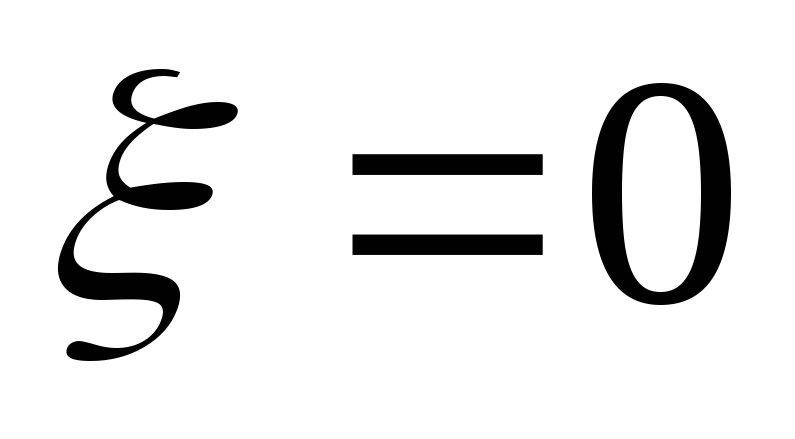
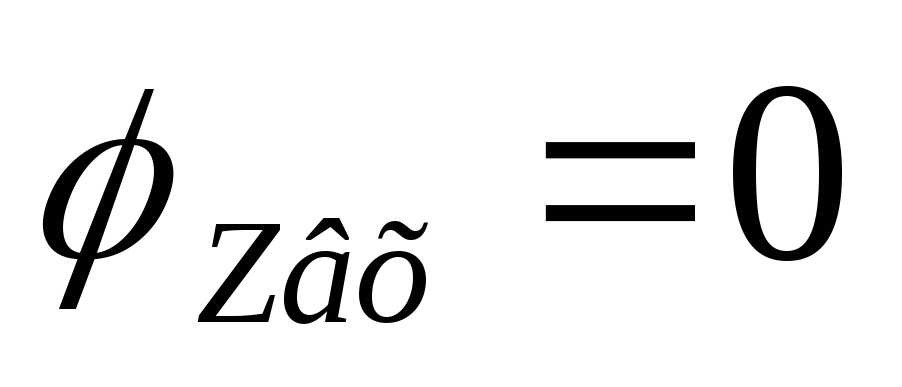
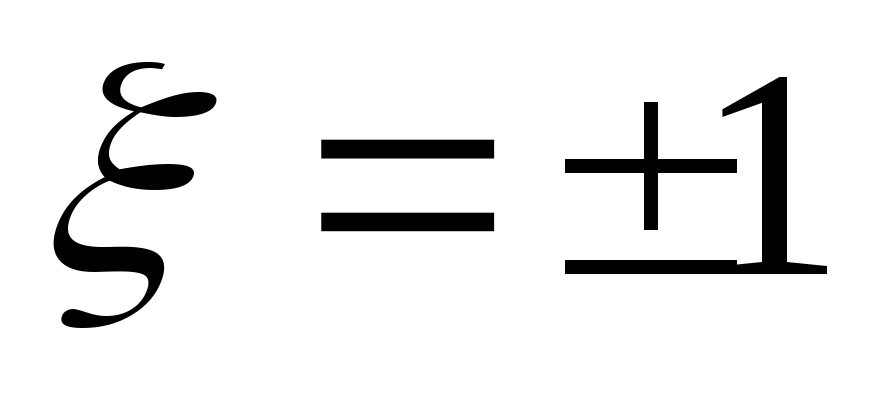
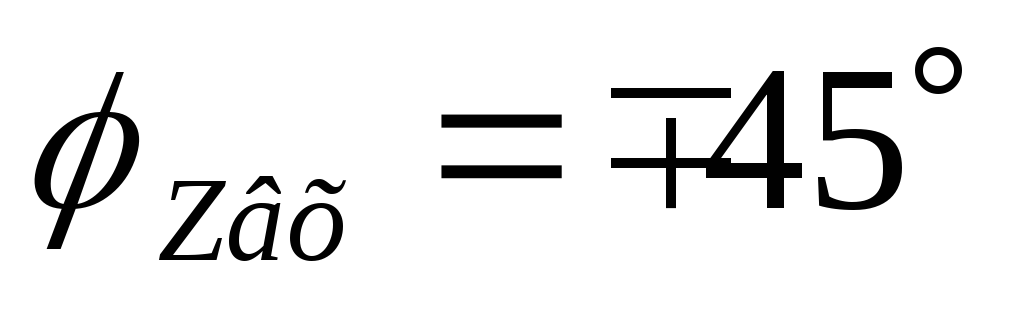
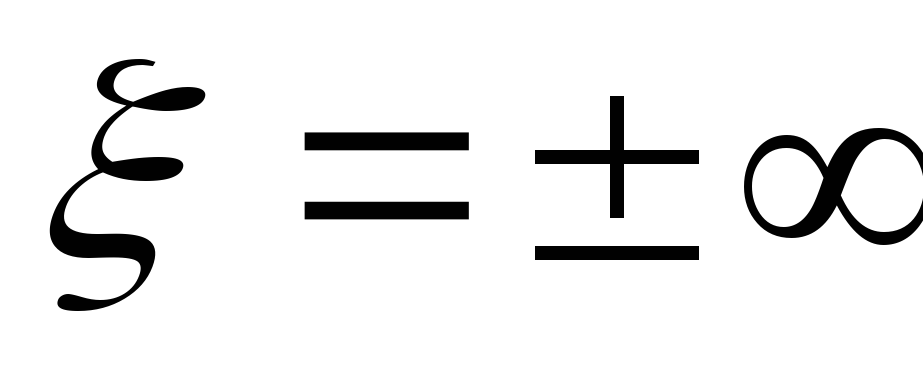
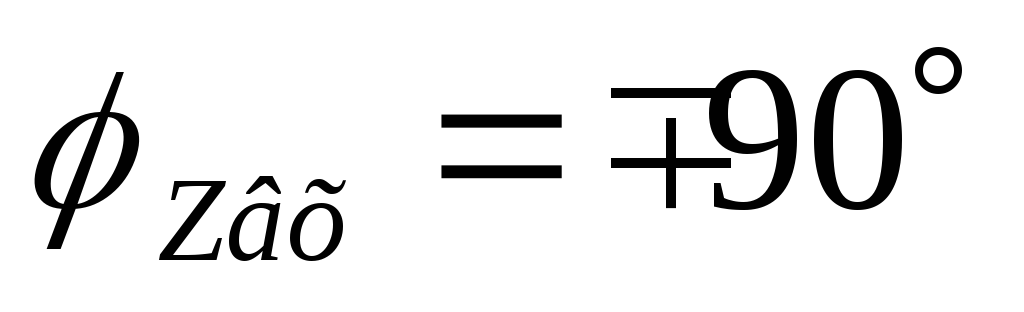
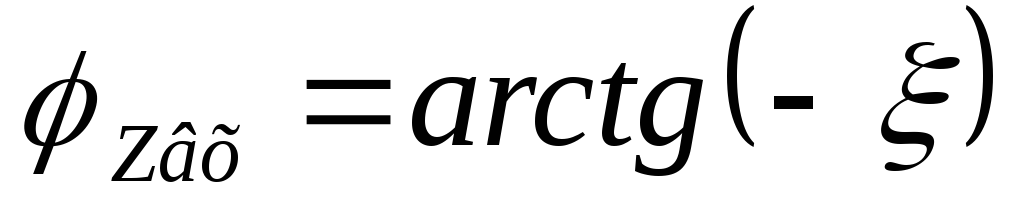 — входная ФЧХ параллельного контура
— входная ФЧХ параллельного контура
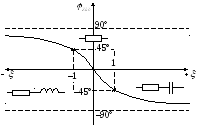
Вывод:на резонансной частоте
сопротивление контура чисто активное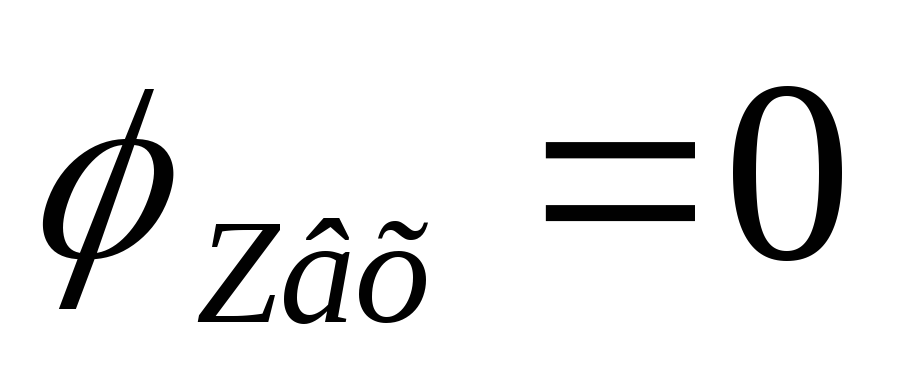 .
На частотах больше резонансной —
активно-емкостное,
.
На частотах больше резонансной —
активно-емкостное,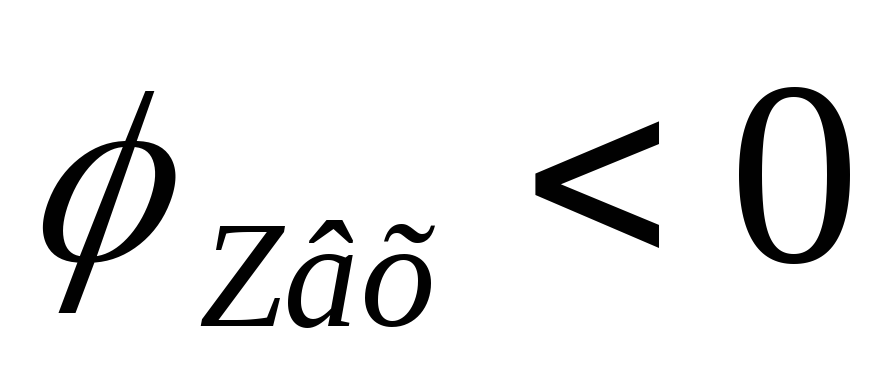 ,
а на частотах меньше резонансной —
активно-индуктивное,
,
а на частотах меньше резонансной —
активно-индуктивное,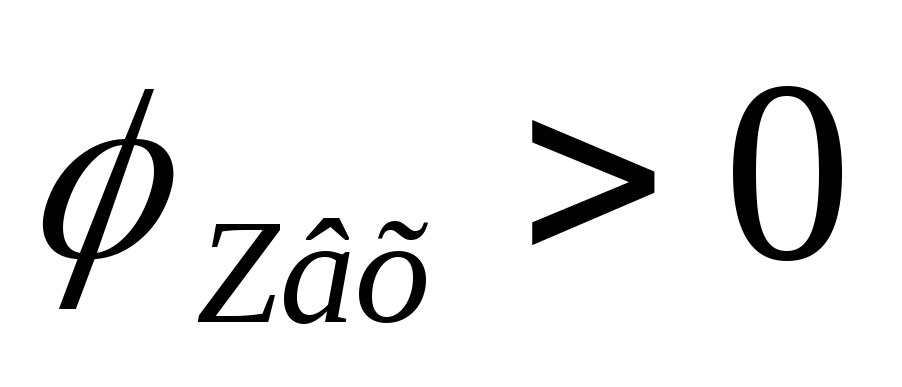 .
.
15. Передаточные ачх параллельного колебательного контура. Эквивалентная добротность, полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы
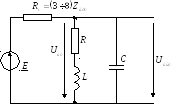
Для этой схемы вводят понятие эквивалентной добротности:
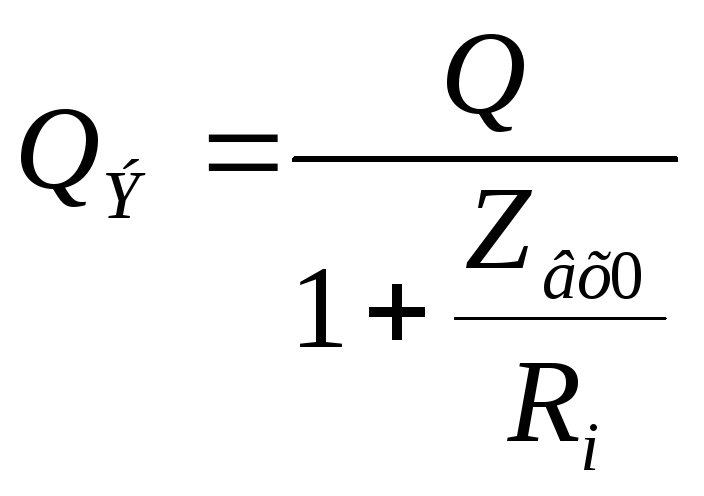 ,
где
,
где
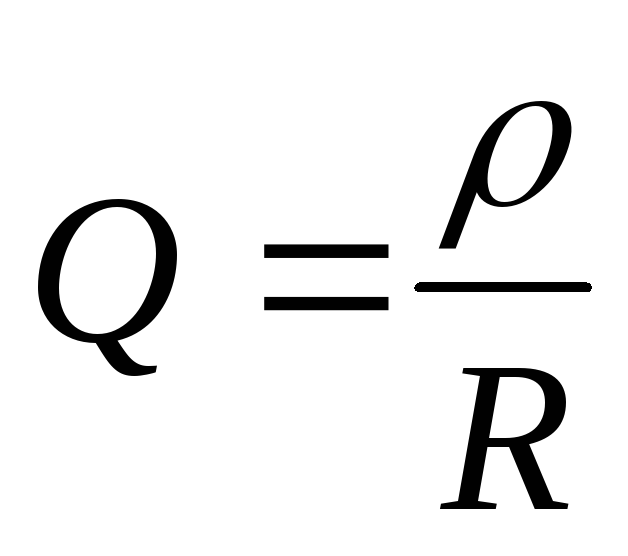 — собственная добротность параллельного
контура
— собственная добротность параллельного
контура
Появляется понятие эквивалентной обобщённой расстройки:
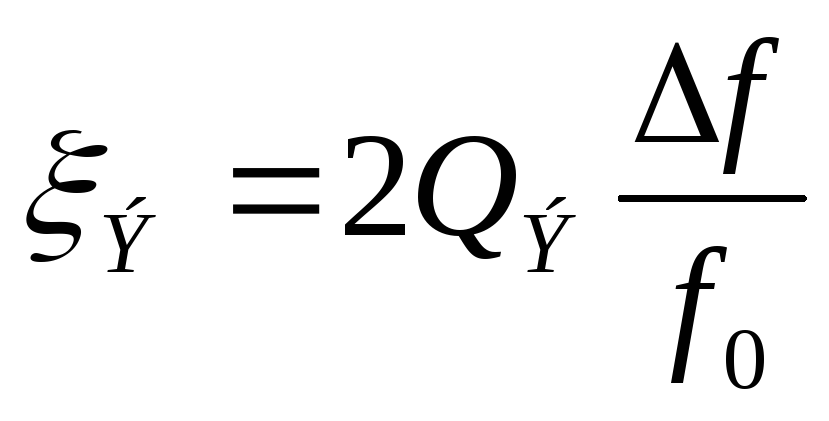 ,
,
тогда передаточная АЧХ параллельного контура в абсолютных координатах рассчитывается:
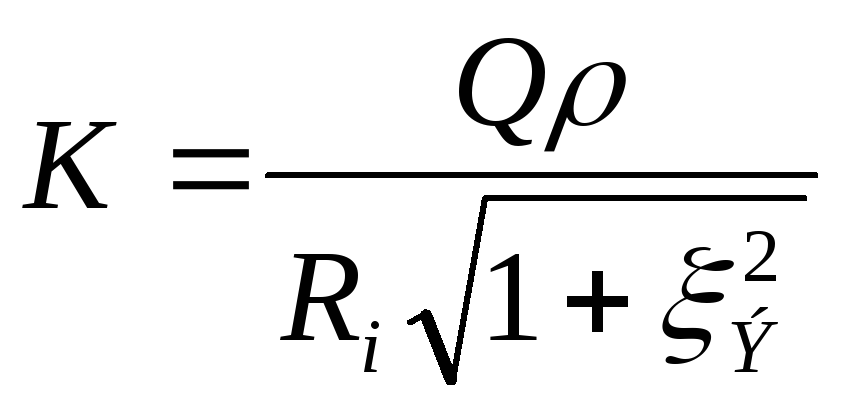 ,
где
,
где
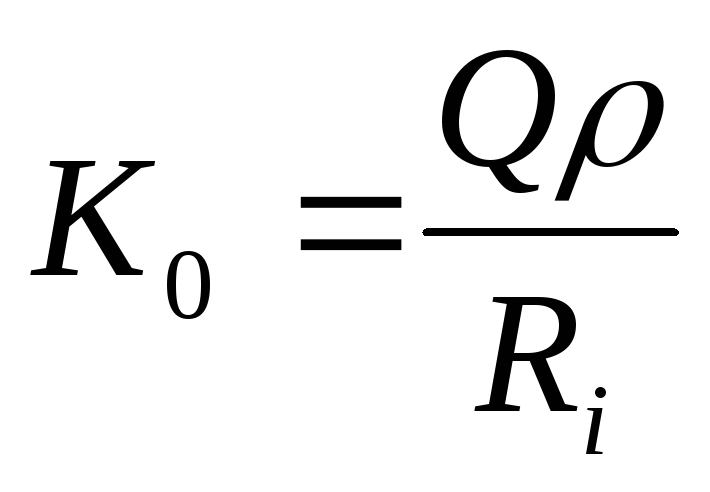
Передаточная АЧХ в относительных координатах параллельного контура имеет вид:
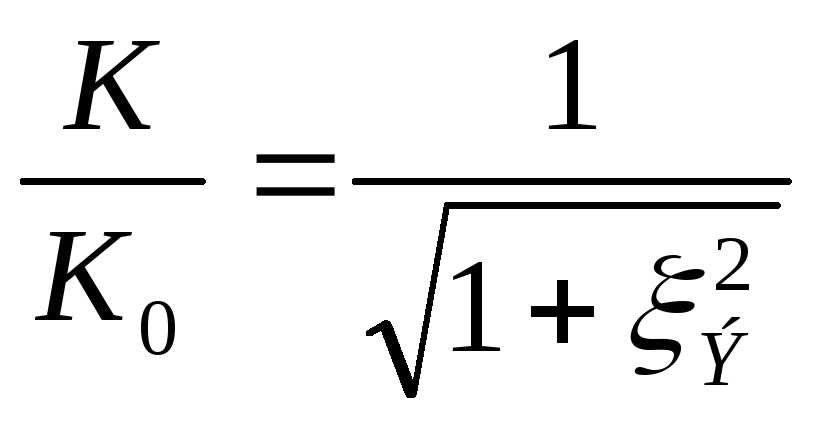
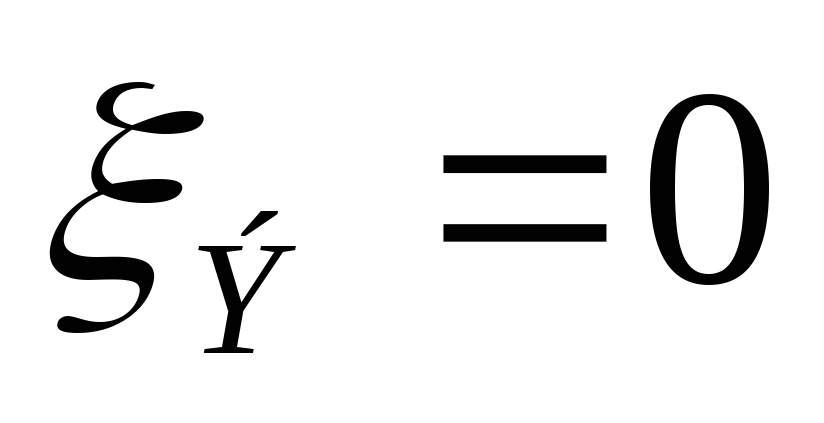
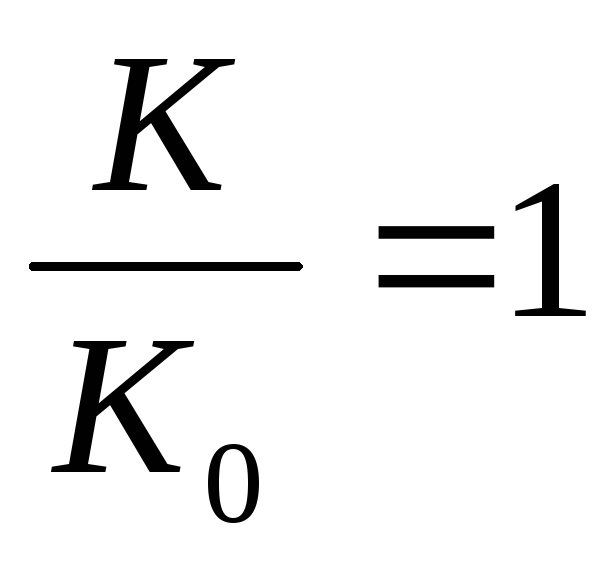
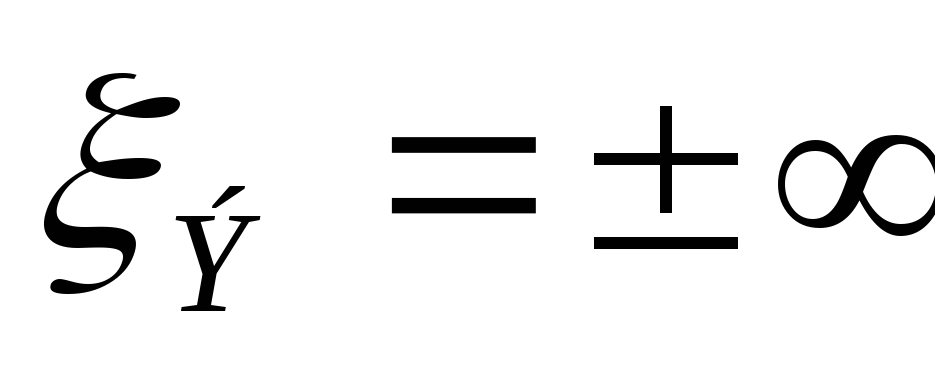
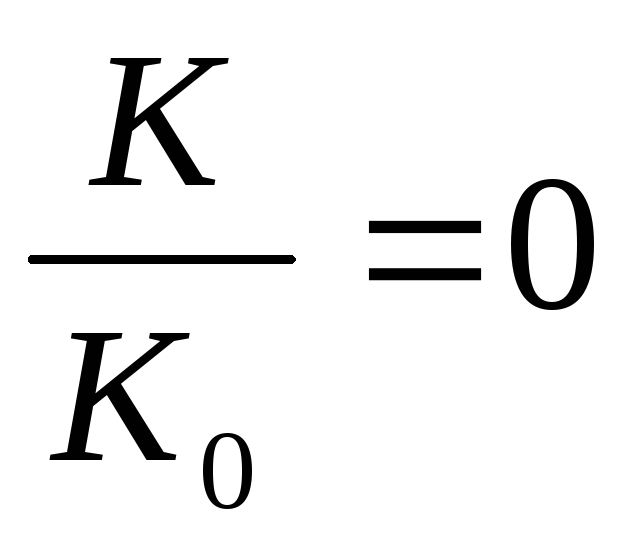

Для этой схемы токи ветвей и общий ток в момент резонанса можно рассчитать по формулам:
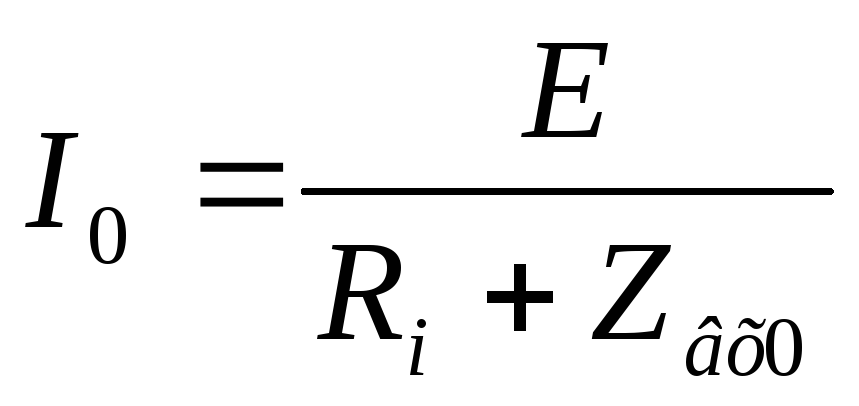
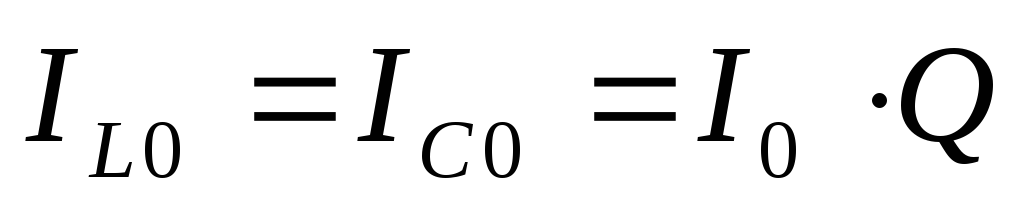
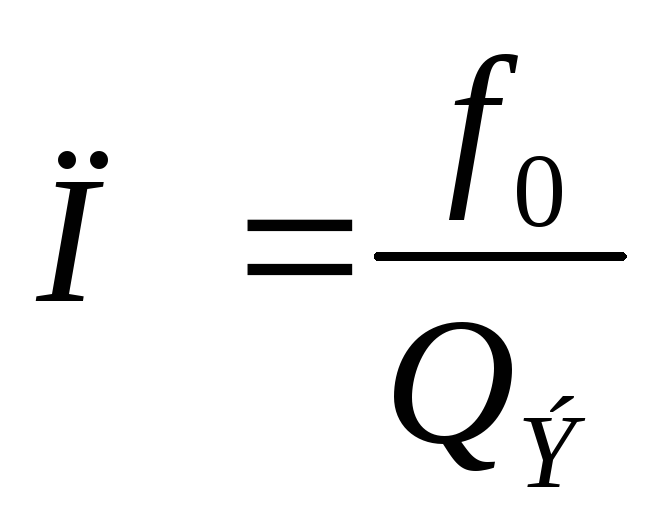
16. Виды параллельных колебательных контуров. Контуры с неполным включением
Автотрансформаторное (неполное) включение контура
Схема контура I-го вида
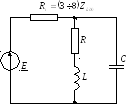
Эта цепь удовлетворительно работает,
если соблюдается условие 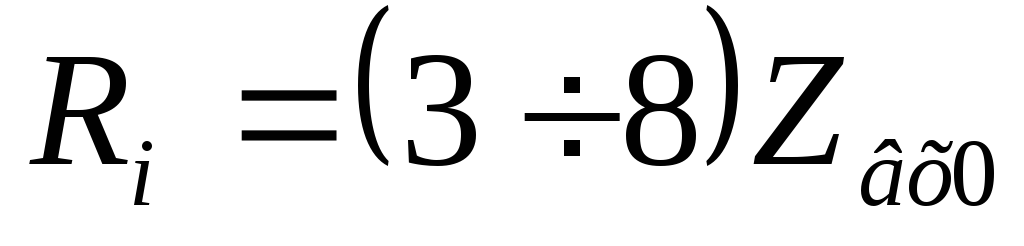 .
.
На практике 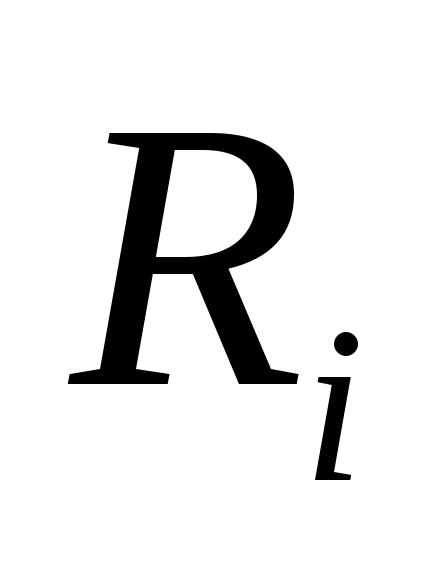 — внутреннее сопротивление лампы или
транзистора, т. е. вполне определённая
величина.
— внутреннее сопротивление лампы или
транзистора, т. е. вполне определённая
величина.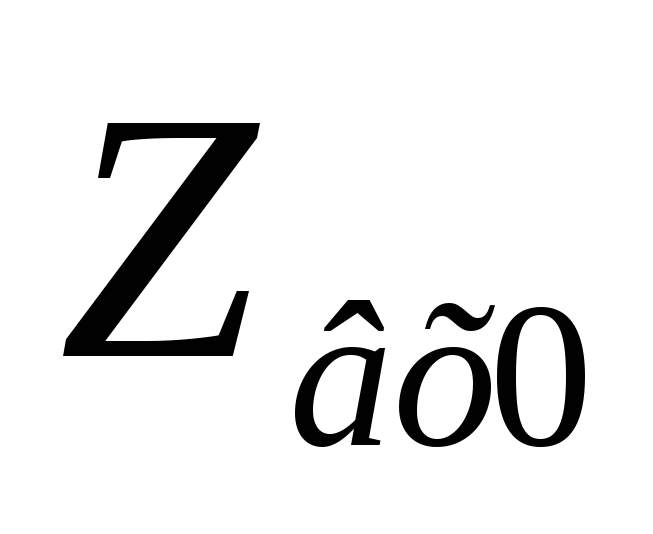 — тоже определённая величина, поэтому
это равенство может не соблюдаться.
— тоже определённая величина, поэтому
это равенство может не соблюдаться.
Чтобы это равенство соблюдалось,
уменьшают 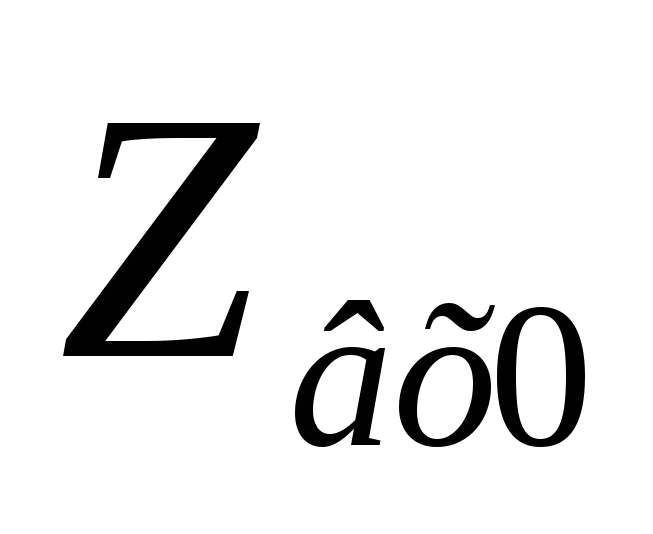 .
Для этого используютнеполное
(автотрансформаторное) включение
контура. Часть индуктивности катушки
или ёмкости конденсатора переносят из
одной ветви в другую так, чтобы общая
ёмкость или индуктивность контура, а
значит и резонансная частота, не
изменились.
.
Для этого используютнеполное
(автотрансформаторное) включение
контура. Часть индуктивности катушки
или ёмкости конденсатора переносят из
одной ветви в другую так, чтобы общая
ёмкость или индуктивность контура, а
значит и резонансная частота, не
изменились.
Схема контура II-го вида
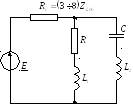
Вводят понятие коэффициент включения контура:
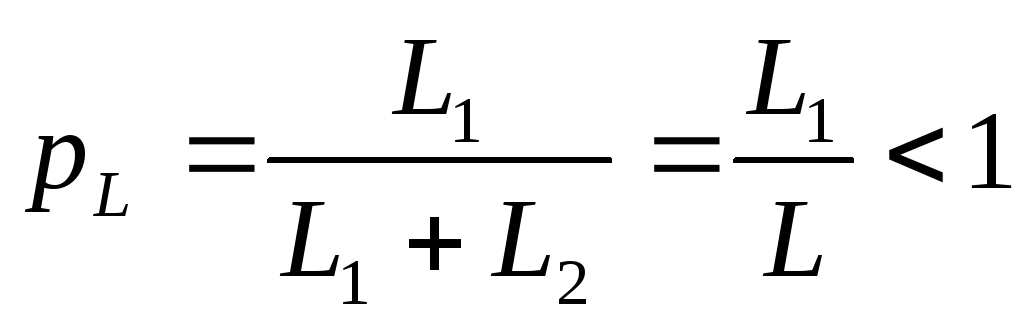
Доказано, что 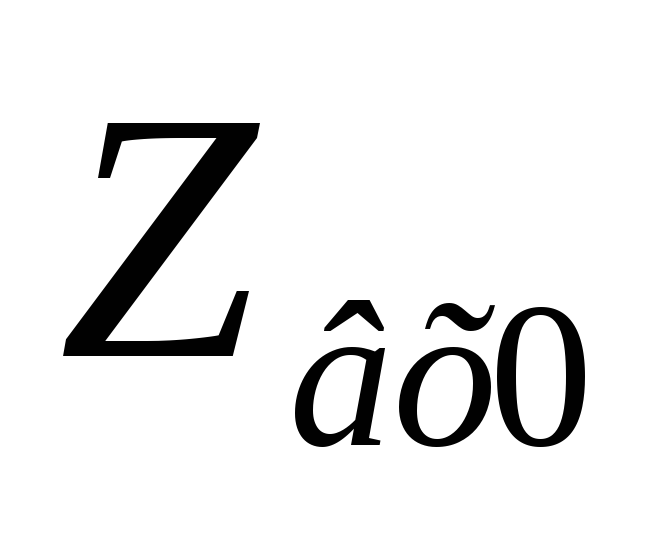 контура II вида равно:
контура II вида равно:
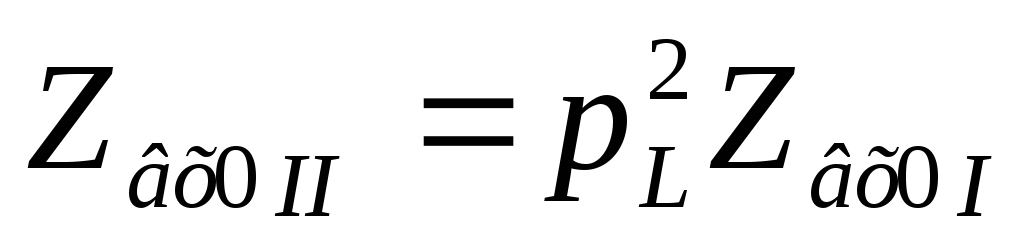
Т. к. 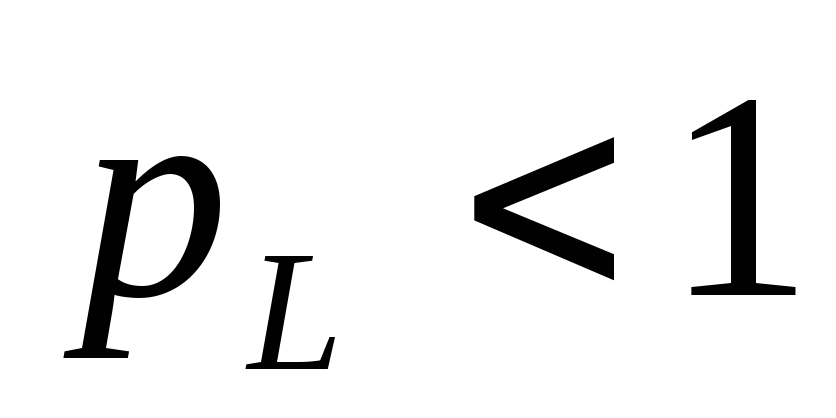 ,
то
,
то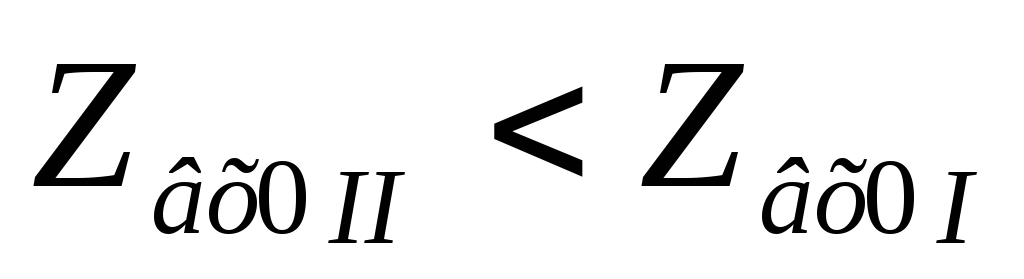
Схема контура III вида

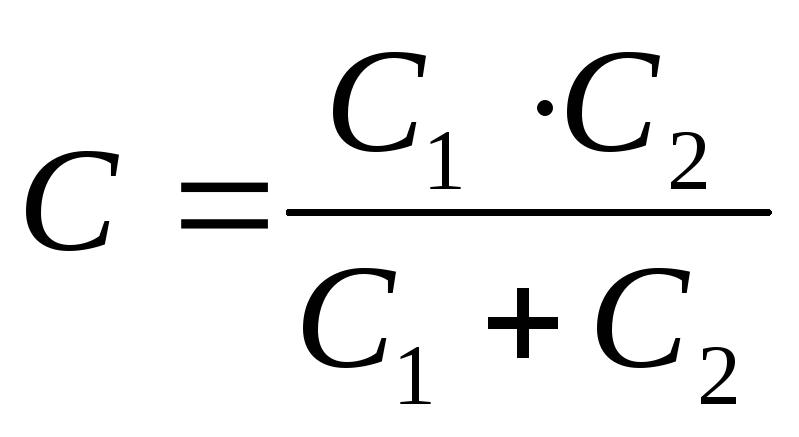
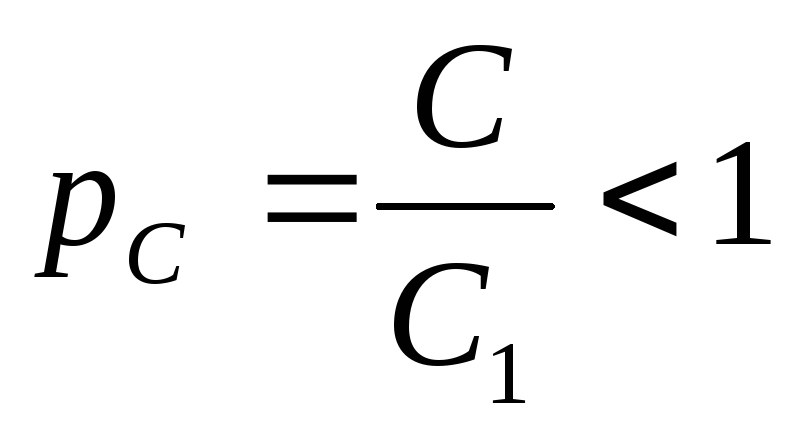
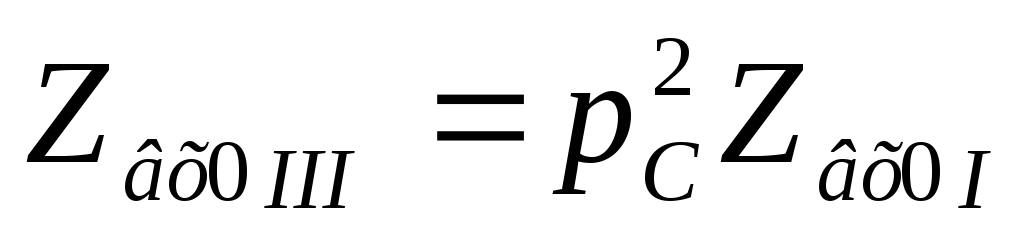
Т. к. 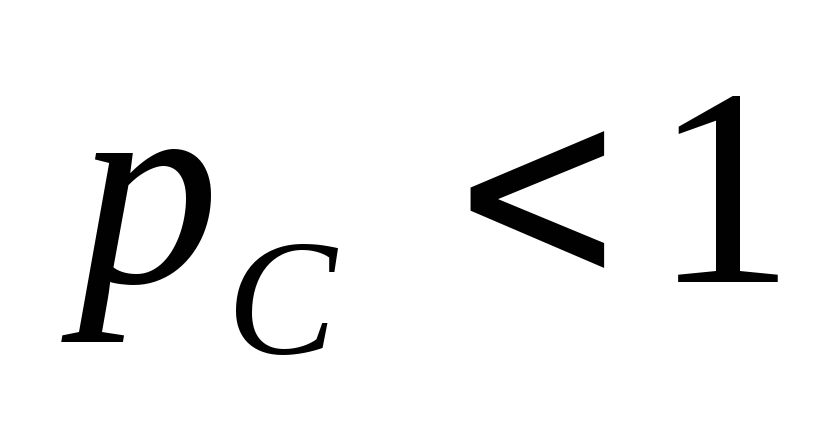 ,
то
,
то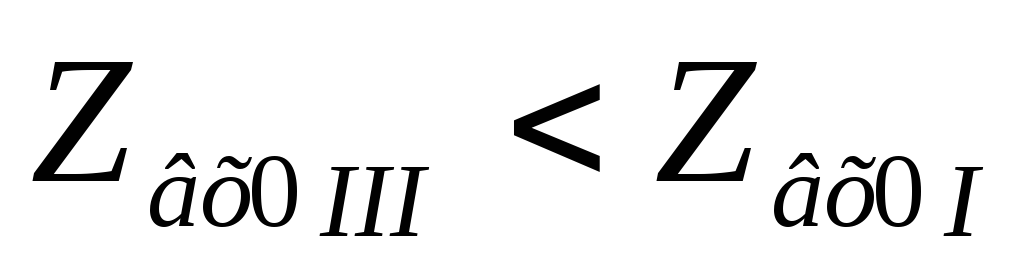
Неполное включение контура служит для уменьшения входного сопротивления контура на резонансной частоте.
Дополнение. Сравнение последовательного и параллельного контуров
Последовательный контур | Параллельный контур |
1. Резонанс напряжений
| 1. Резонанс токов
|
2.
| 2.
|
3. | 3. |
4. В последовательном контуре добротность показывает, во сколько раз напряжение на реактивных элементах (на выходе) больше, чем напряжение на входе. Поэтому это явление называется резонанс напряжений. | 4. В параллельном контуре добротность показывает, во сколько раз ток ветвей больше общего тока в момент резонанса. Поэтому это явление называется резонанс токов. |
17. Электронные аналоги колебательных контуров. Электронный колебательный контур, его избирательные свойства. Достоинства электронного колебательного контура по сравнению с пассивными колебательными контурами. Гиратор
Электронный колебательный контур
Начертим схему последовательного контура, чтобы на выходе стоял резистор:
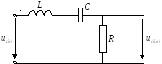
Известно, что последовательный контур обладает избирательностью по напряжению. Докажем, при каких условиях это будет. Рассмотрим, какой вид имеет комплексная передаточная характеристика контура:
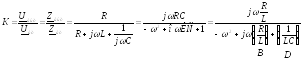
Вывод:если знаменатель комплексного
коэффициента передачи цепи имеет вид
квадратного уравнения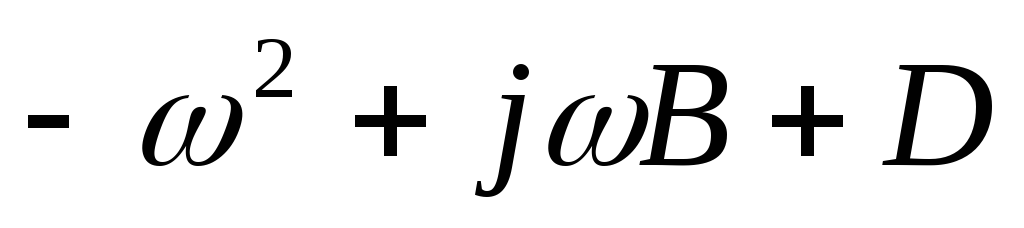 ,
то эта цепь обладает избирательностью
по напряжению. Выражают некоторые
величины черезBиD:
,
то эта цепь обладает избирательностью
по напряжению. Выражают некоторые
величины черезBиD:
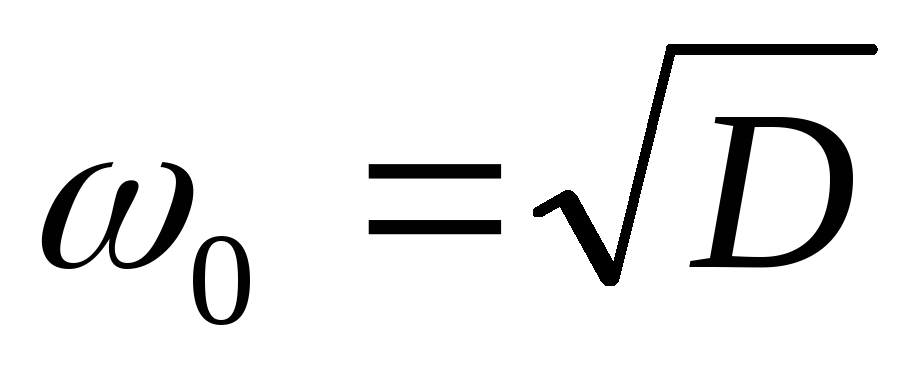
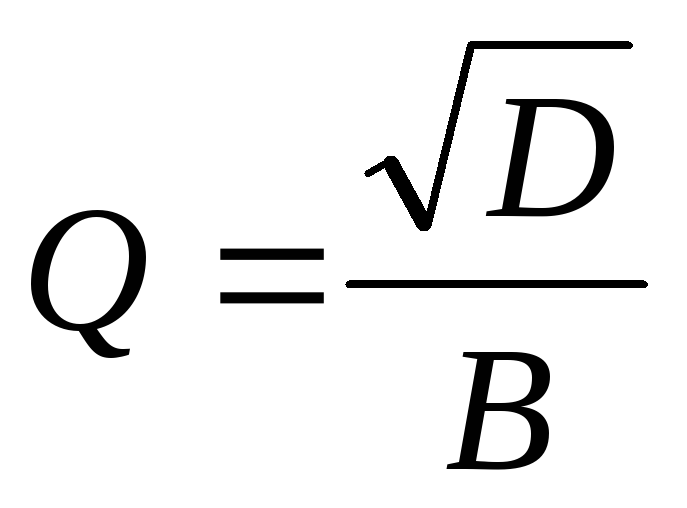
Можно получить избирательные свойства цепи, используя активные элементы ОУ с отрицательными обратными связями:
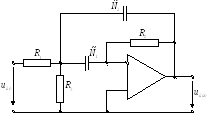
Для этой цепи рассчитан комплексный
коэффициент передачи, считая 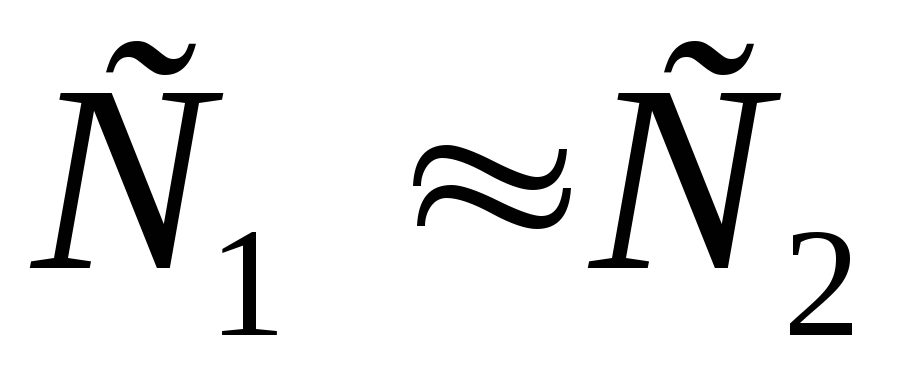 :
:
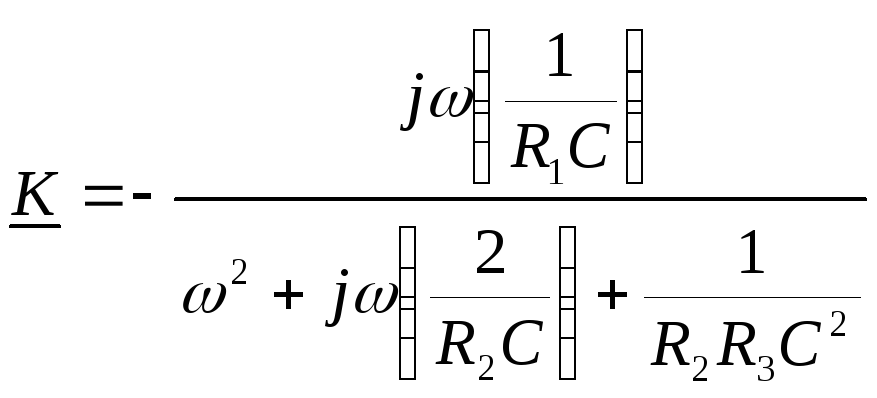
Из формулы видно, что знаменатель передаточной функции имеет вид квадратного уравнения, значит электронный контур обладает избирательностью по напряжению, и егопередаточная характеристика имеет резонансный вид:

Рассчитаем некоторые величины через коэффициенты BиD:
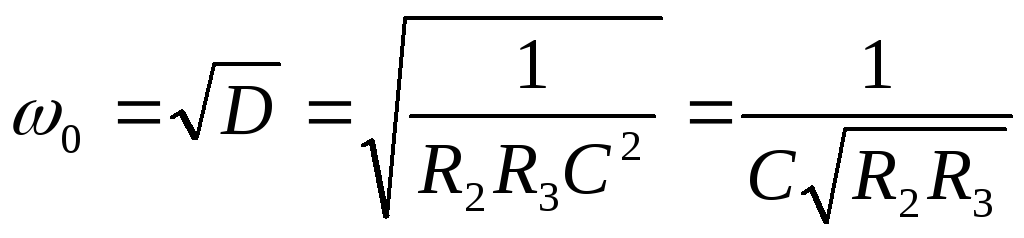
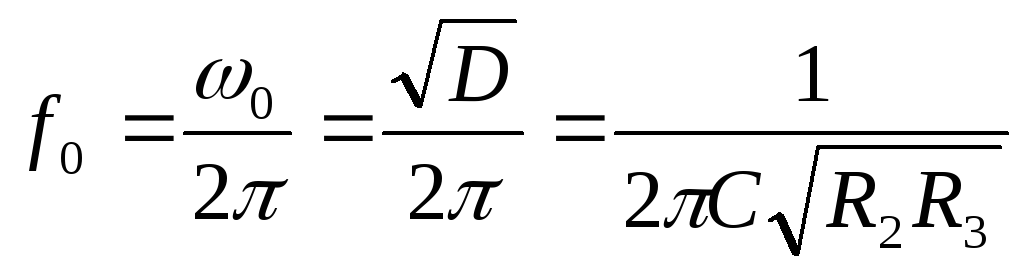
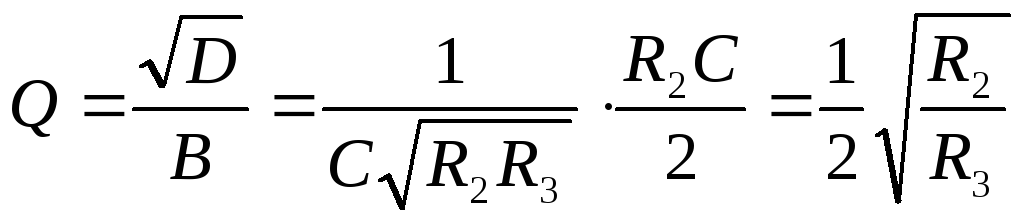
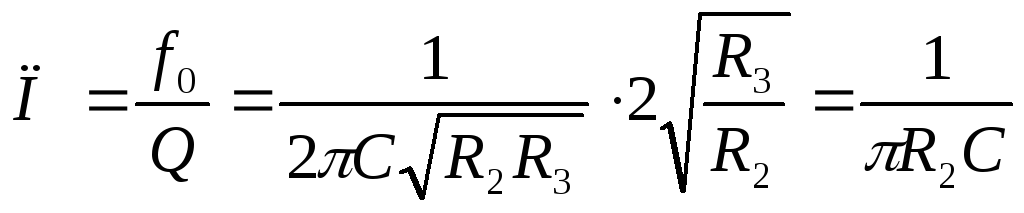
Электронный контур имеет следующие преимущества перед обычными контурами:
можно регулировать
 ,
, ,QиПрезисторами;
,QиПрезисторами;большое входное сопротивление
 кОм, малое выходное сопротивление;
кОм, малое выходное сопротивление;схема компактная, т. к. нет катушек индуктивности.
Электронная индуктивность (гиратор)
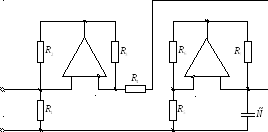
Обычные катушки индуктивности обладают рядом недостатков:
сказываются помехи, создаваемые магнитными полями других катушек или цепей;
большие габариты;
магнитная проницаемость, а значит и индуктивность катушки, зависят от частоты, поэтому используют схему, состоящую из активных элементов (ОУ), резисторов и конденсаторов.
Электронные цепи, обладающие индуктивными
свойствами, называются гираторами.
Если считать все сопротивленияRприблизительно одинаковыми, то входное
сопротивление такой цепи: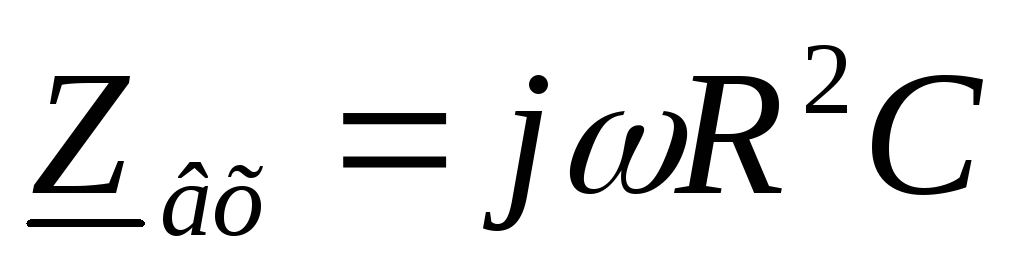 .
.
Известно, что входное сопротивление
индуктивности 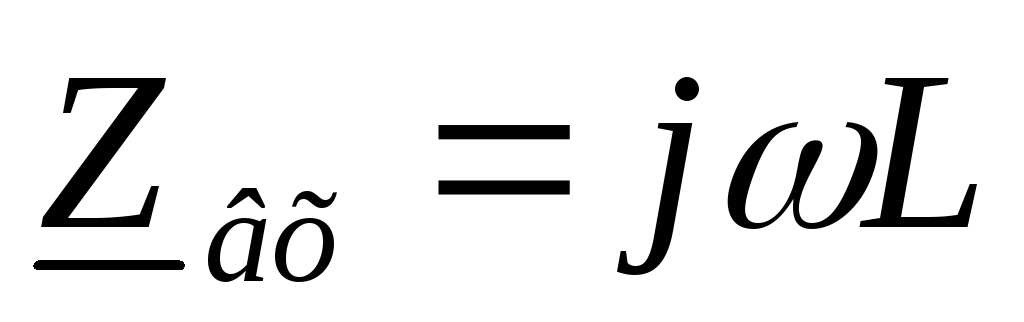 ,
значит входное сопротивление такой
цепи изменяется по закону индуктивности,
где в качествеLЭсуществует:
,
значит входное сопротивление такой
цепи изменяется по закону индуктивности,
где в качествеLЭсуществует:
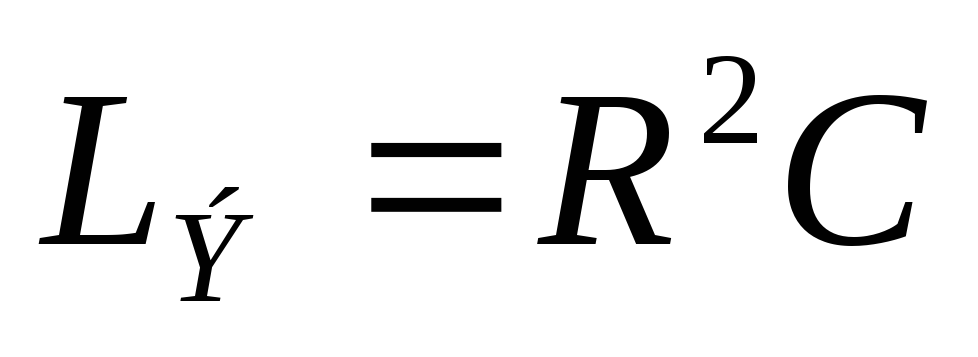 ,
тогда
,
тогда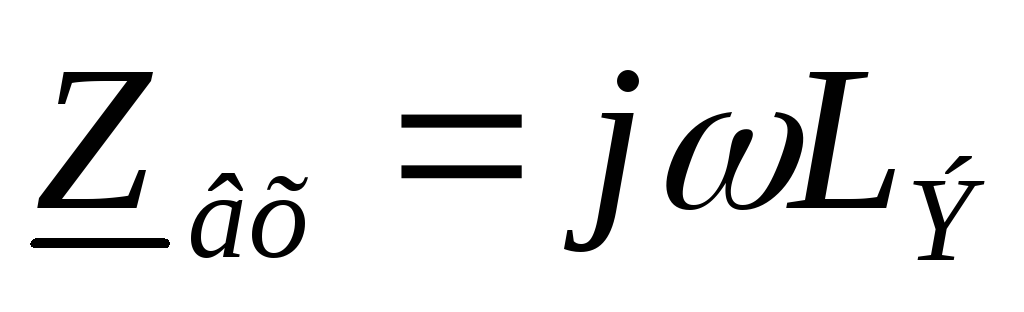 .
.
Электронная индуктивность имеет малые габариты, может быть выполнена в микроэлектронном исполнении и не подвержена влиянию внешних электромагнитных полей.
18. Реактивные двухполюсники. Определение. Одно-, двух-, трехэлементные реактивные двухполюсники. Построение характеристик, χ = F(ω), φ = F(ω). Нулевые и полюсные частоты
Реактивные двухполюсники
Реактивными двухполюсникаминазываются цепи, имеющие 2 входных зажима и состоящие из индуктивностей и емкостей.
Главной зависимостью двухполюсника
является зависимость его реактивного
сопротивления от частоты, т. е. 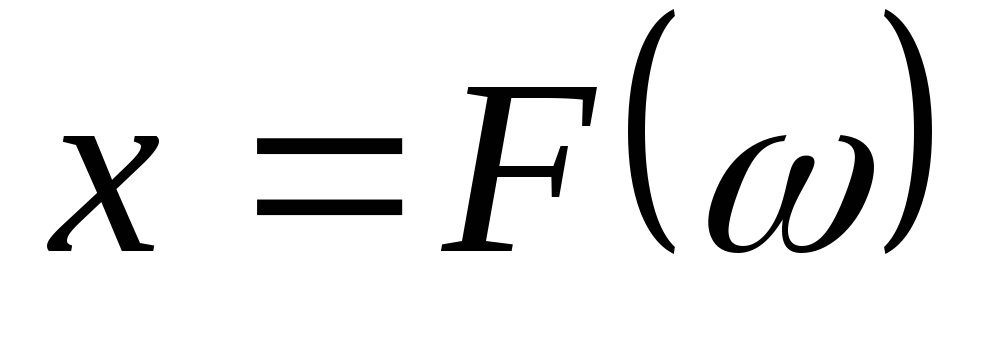 ,
гдеx— реактивное сопротивление.
,
гдеx— реактивное сопротивление.
Одноэлементные реактивные двухполюсники

Двухэлементные реактивные двухполюсники
Последовательное соединение L и C
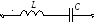
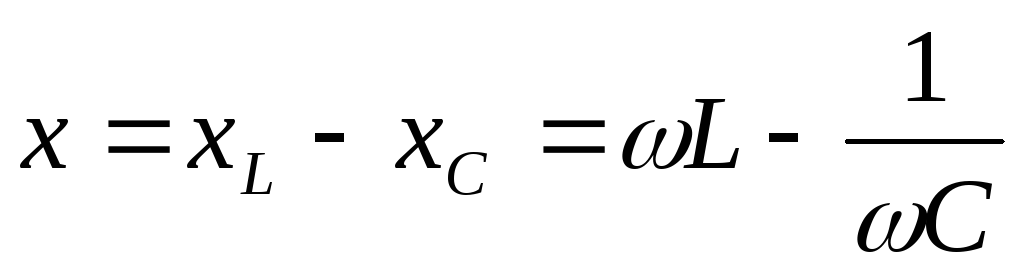
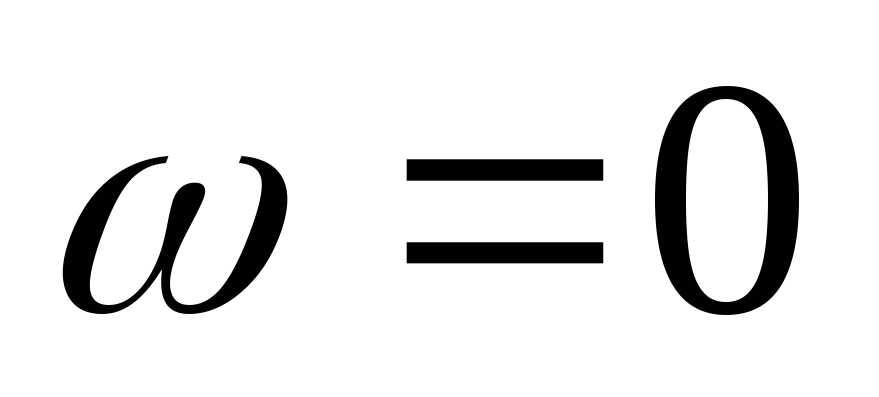
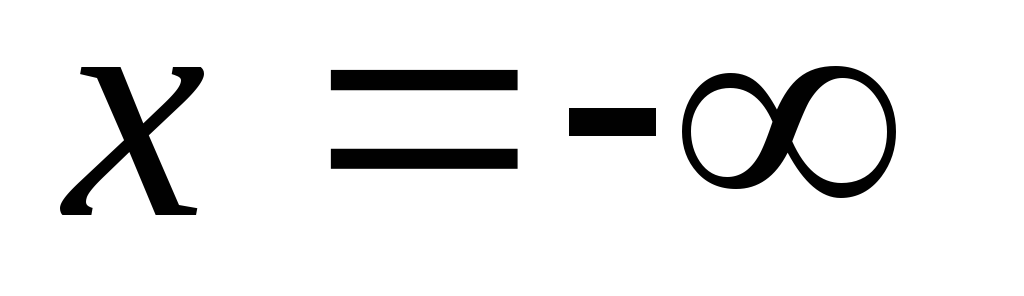
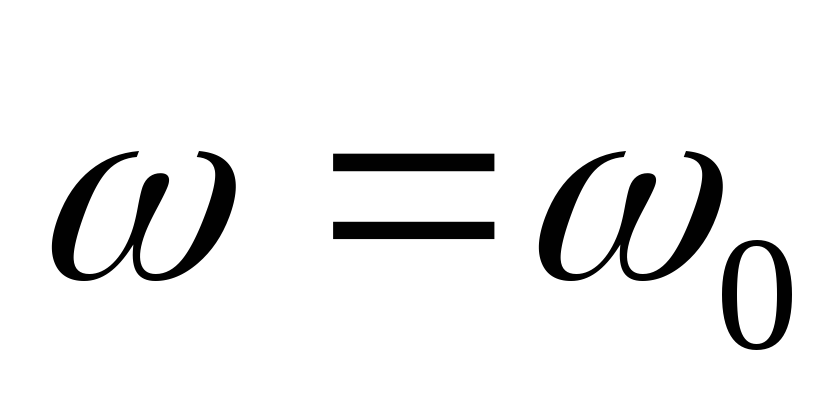
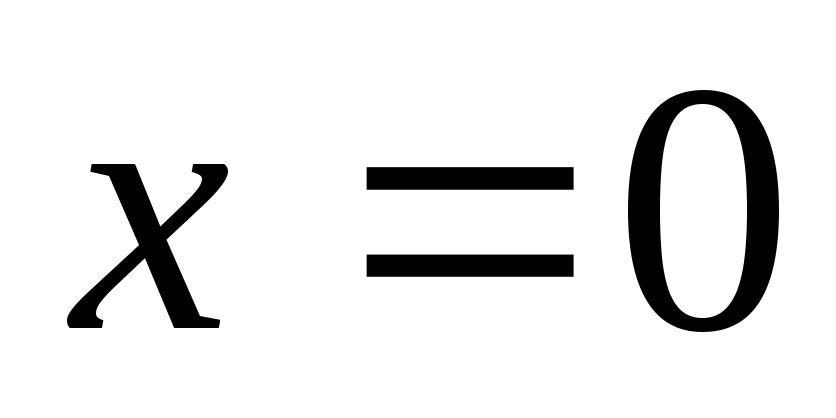
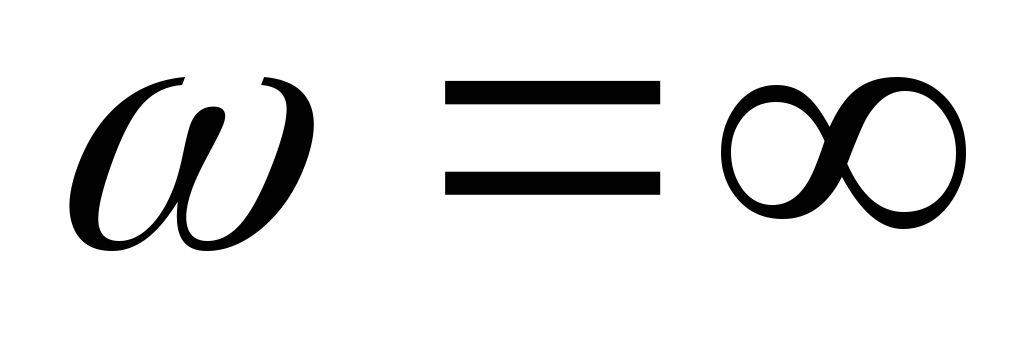
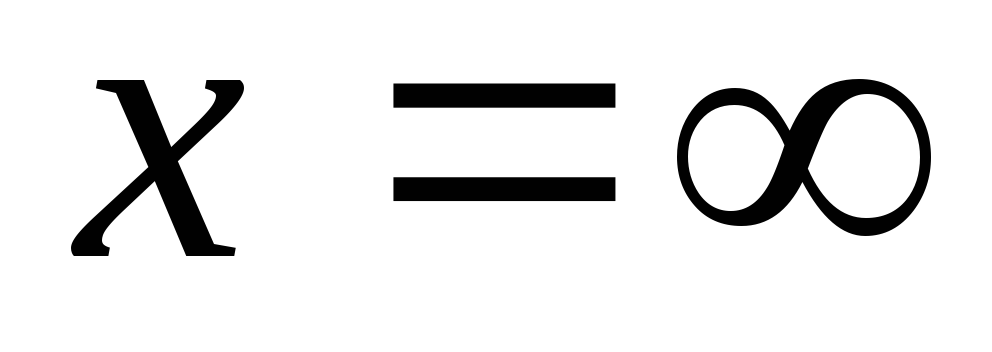

На некоторой частоте 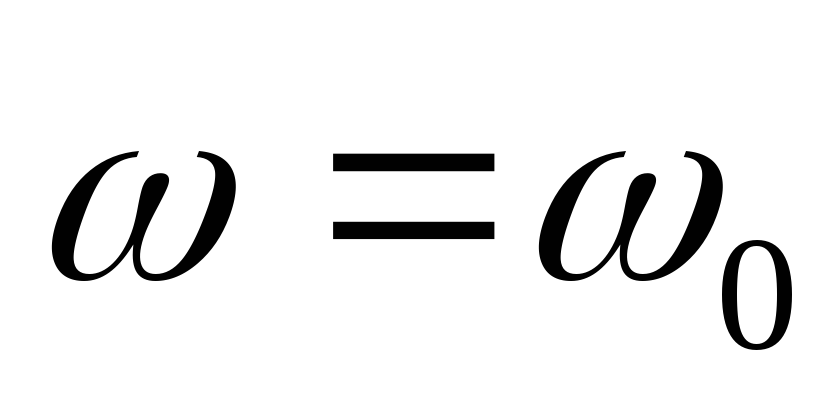
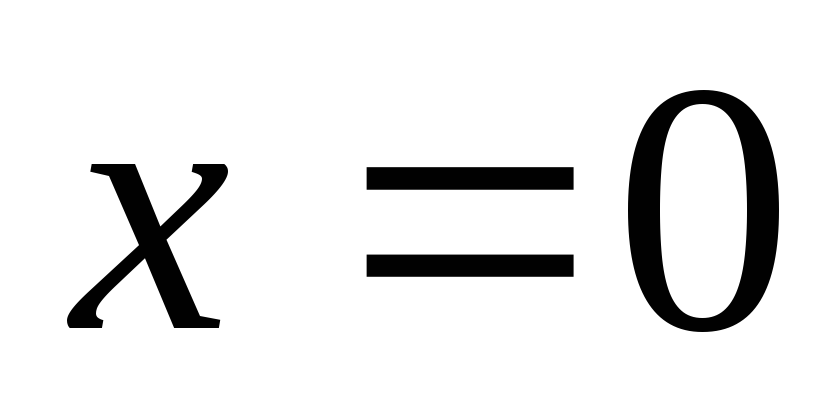 .
Наступает резонанс напряжений. Такие
частоты называютсянулями функции
.
Наступает резонанс напряжений. Такие
частоты называютсянулями функции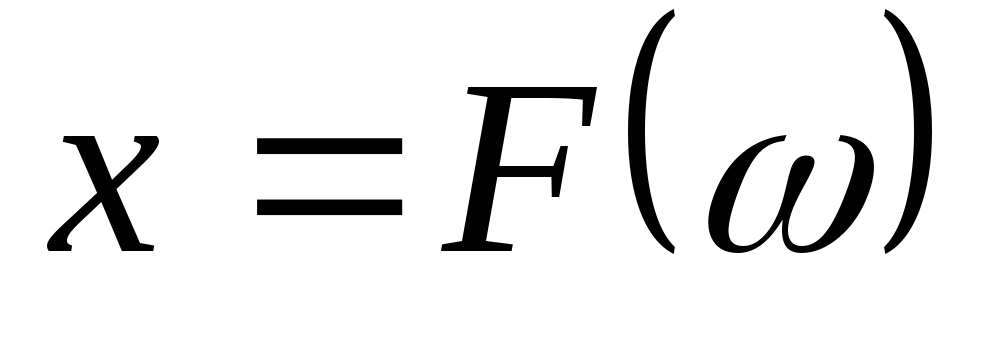 и обозначаются кружком
и обозначаются кружком  .
.
Признак последовательного двухполюсника:
нет пути прохождения постоянному току.
Параллельное соединение L и C

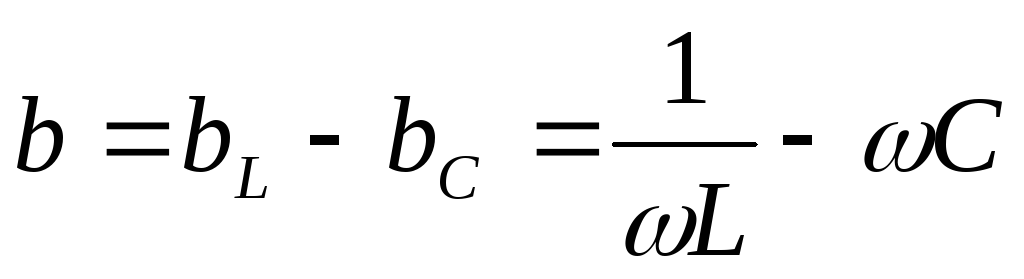
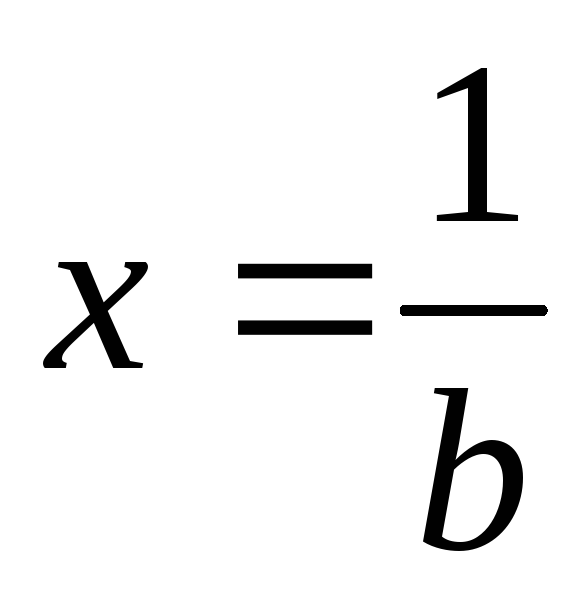
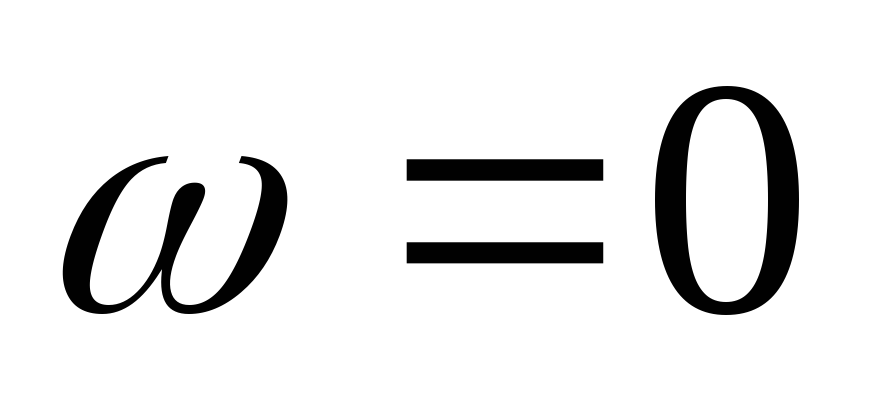
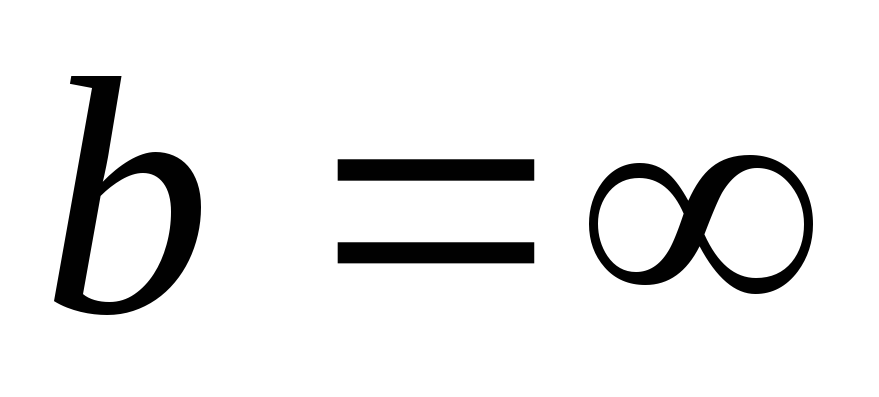
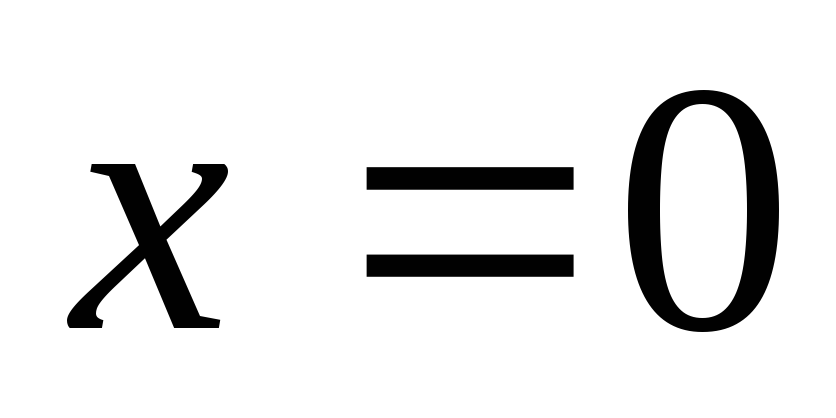
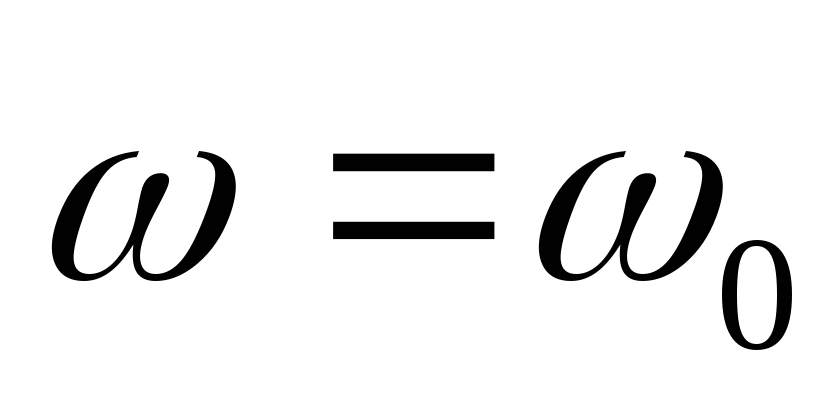
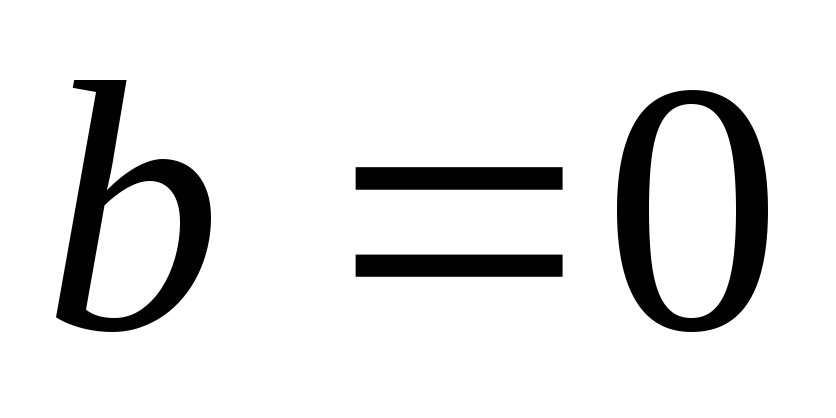
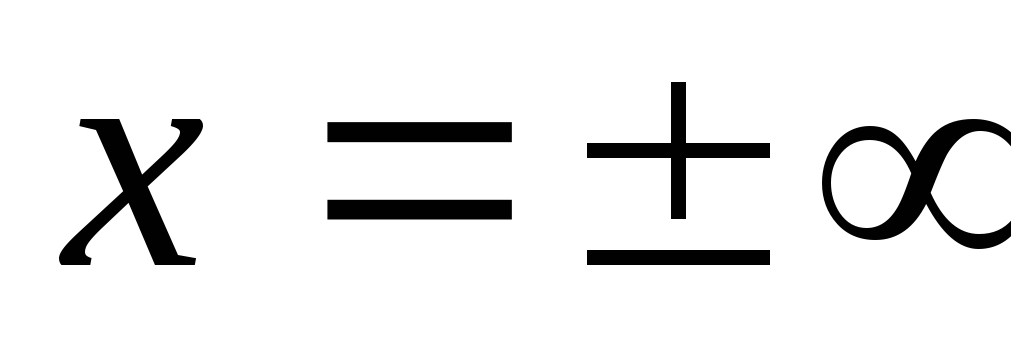

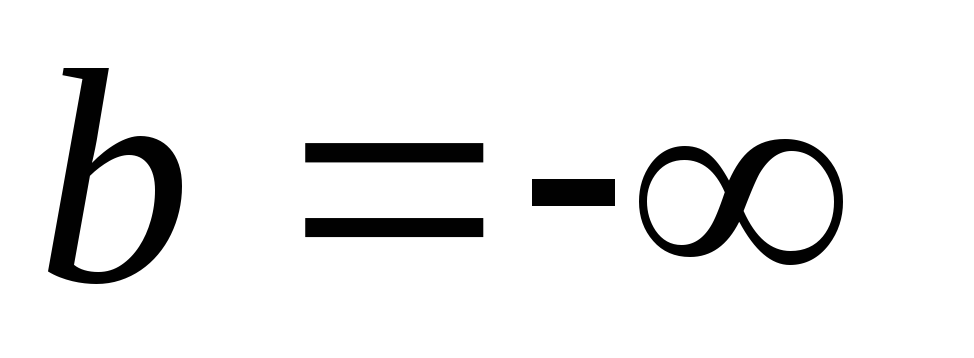
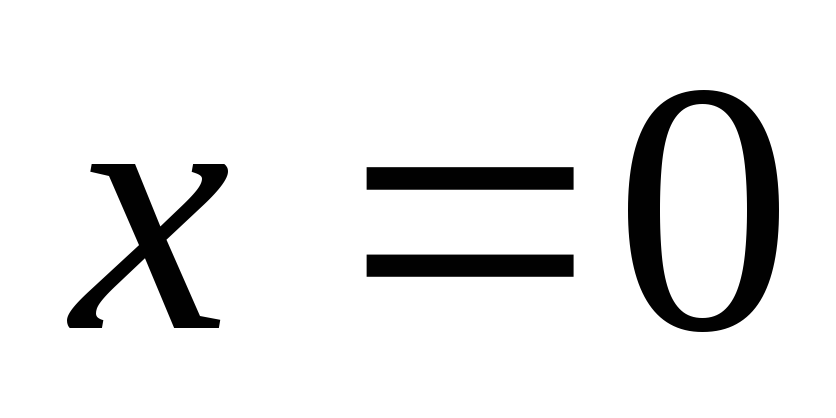
На некоторой частоте 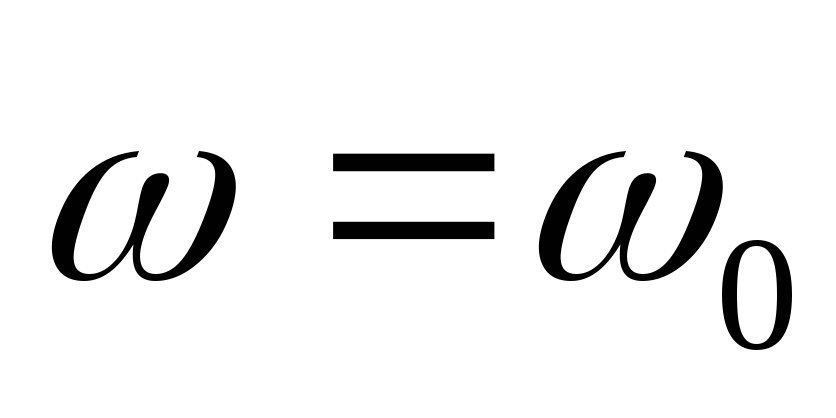 наступает резонанс токов,
наступает резонанс токов,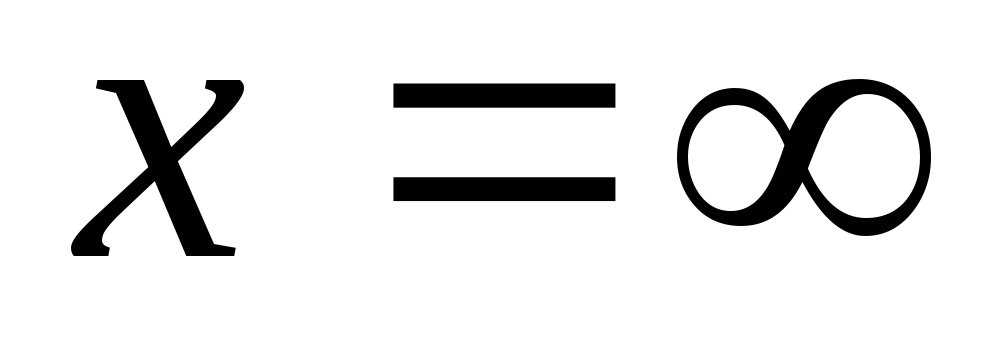 .
Такие частоты называютсяполюсами
функции
.
Такие частоты называютсяполюсами
функции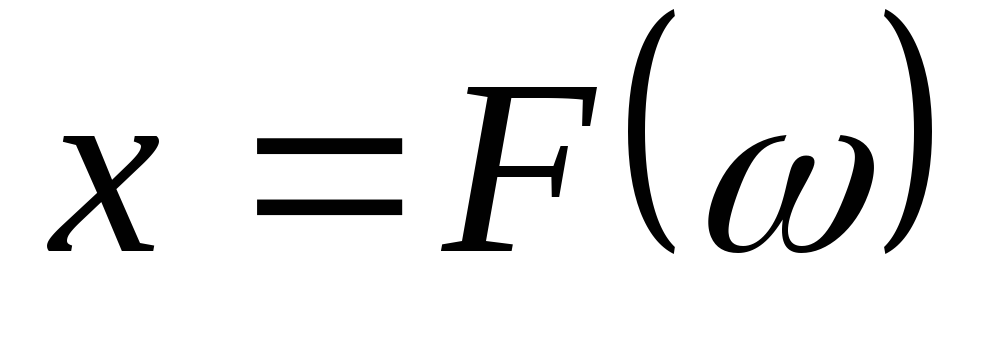 и обозначаются крестиком
и обозначаются крестиком  .
.
Признак параллельности двухполюсника:
Есть путь прохождения постоянному току.
Трёхэлементные реактивные двухполюсники
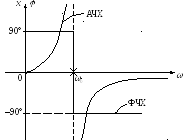
Порядок построения характеристик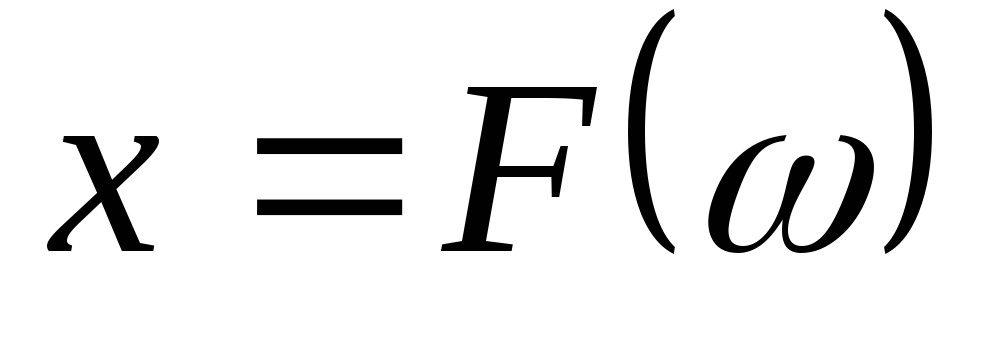 :
:
Резонансных частот на 1 меньше числа элементов.
Нулевые и полюсные частоты всегда чередуются.
Если есть путь прохождения постоянному току, то первым будет резонанс токов, характеристика начинается с нулевого сопротивления.
Если постоянный ток не проходит, то первым будет резонанс напряжений, т. е. характеристика начинается из
 .
.
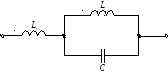
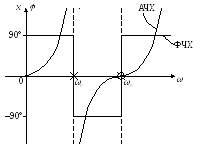
Постоянный ток по данной цепи проходит, значит первым будет резонанс токов, характеристика начинается с 0. Это собственный резонанспараллельного контура LC. Вторым будет резонанс напряжений. Эторезонанс между L0 и параллельным контуром, когда его сопротивление носит емкостной характер.
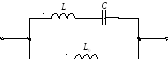
Т. к. есть путь для прохождения постоянного тока, то первым будет резонанс токов. Характеристика начинается с 0. Это коллективный резонанспараллельного контура междуL0и последовательным контуром, когда его сопротивление носит емкостной характер. Вторым будет резонанс напряжений. Этособственный резонанспоследовательного контура. Входная АЧХ и ФЧХ будут такими же, как и для пункта 1.

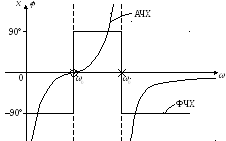
Т. к. нет пути прохождения постоянному току, первым будет резонанс напряжений. Это собственный резонанспоследовательного контура LC. Вторым будет резонанс токов. Этоколлективный резонансмеждуC0и последовательным контуром, когда его сопротивление носит индуктивный характер.

Т. к. нет пути для прохождения постоянного тока, то первым будет резонанс напряжений. Это коллективный резонансмеждуC0и параллельным контуром, когда его сопротивление носит индуктивный характер. Вторым будет резонанс токов. Этособственный резонанспараллельного контура.


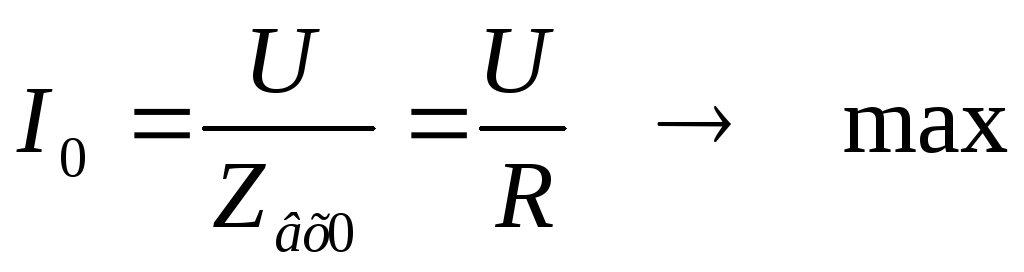
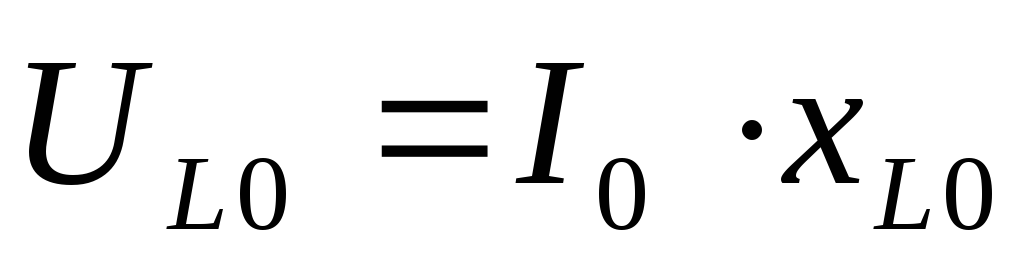
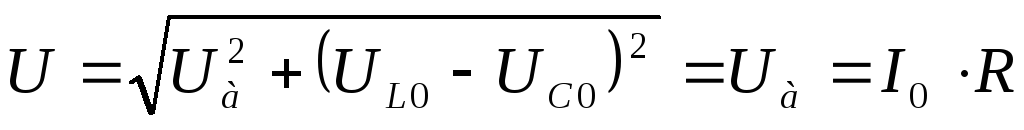
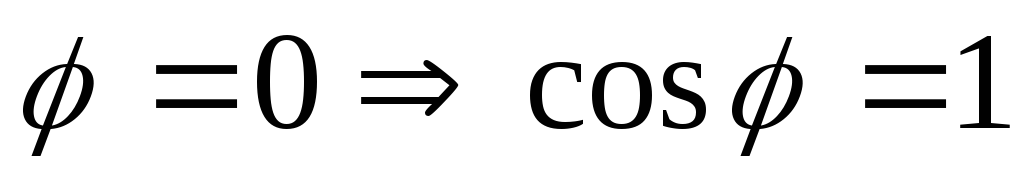
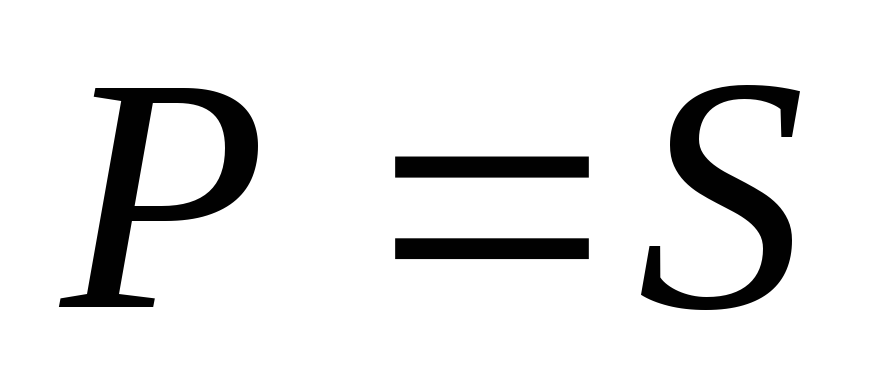 ,
то от источника потребляется только
активная мощность.
,
то от источника потребляется только
активная мощность.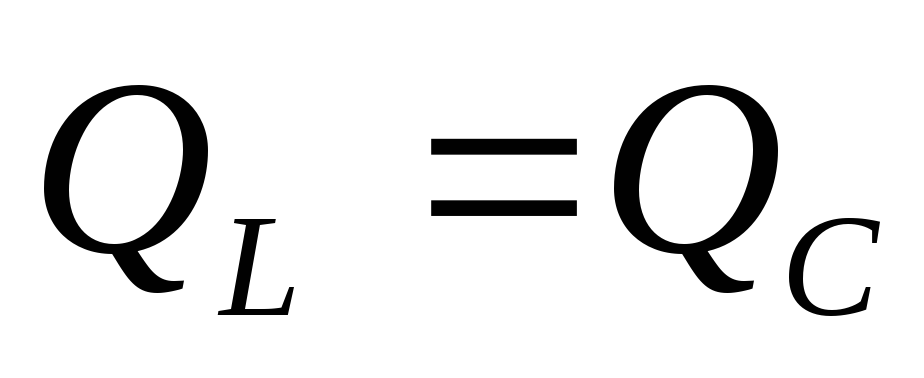 — катушка и конденсатор обмениваются
энергией, а т. к.
— катушка и конденсатор обмениваются
энергией, а т. к. 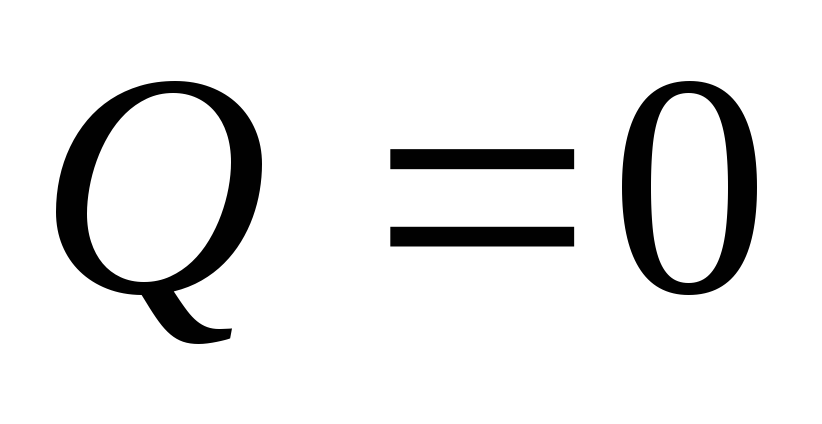 ,
то с источником обмена энергией не
происходит.
,
то с источником обмена энергией не
происходит.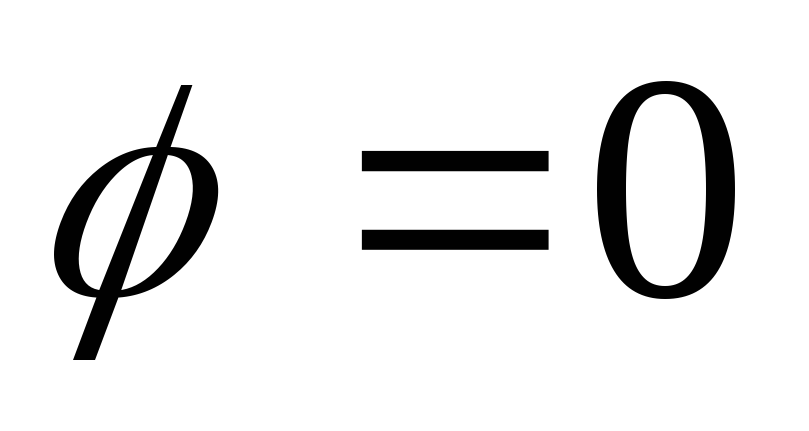
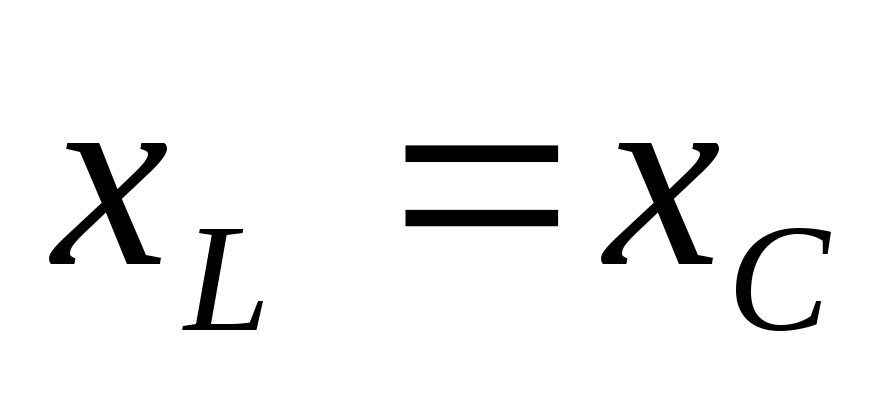
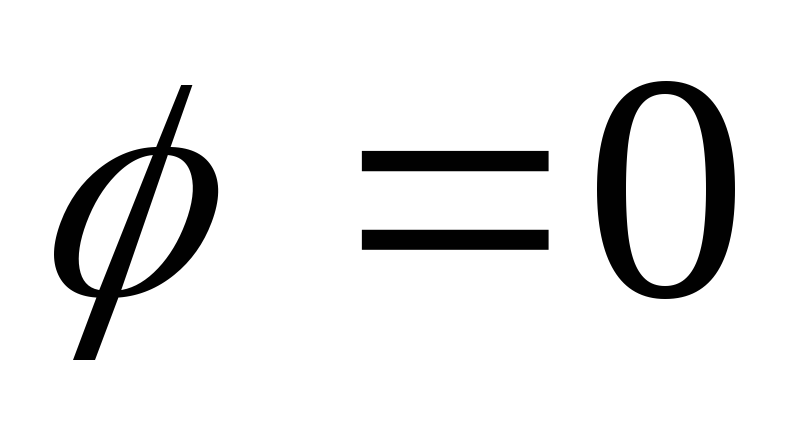
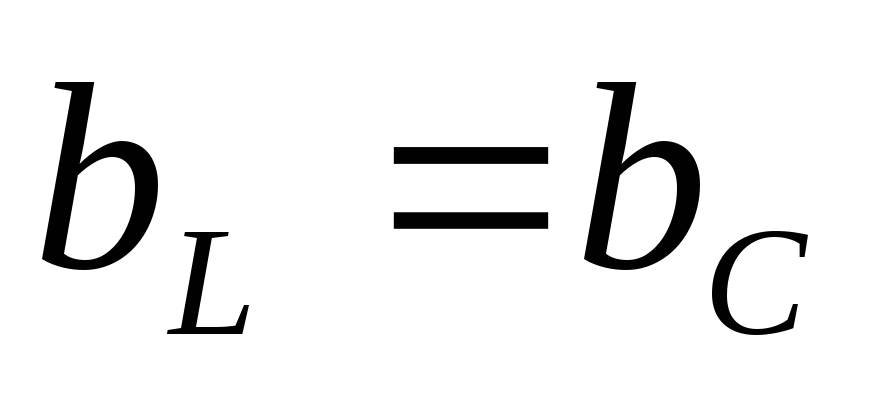
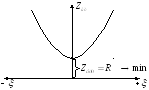
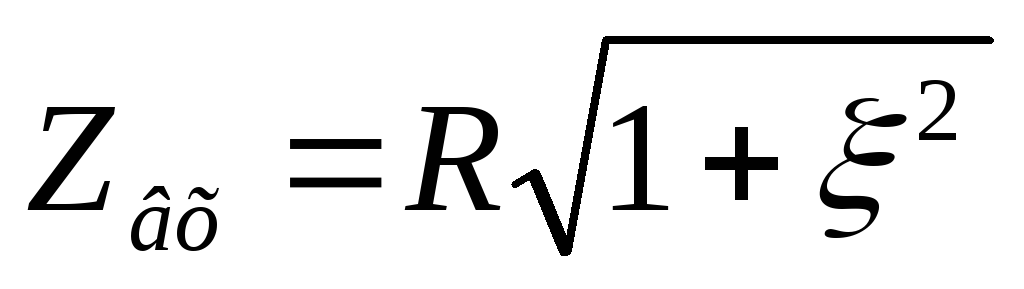

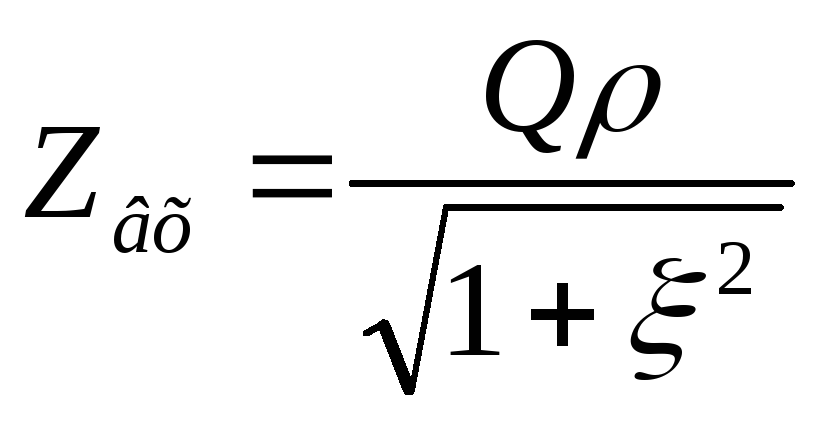
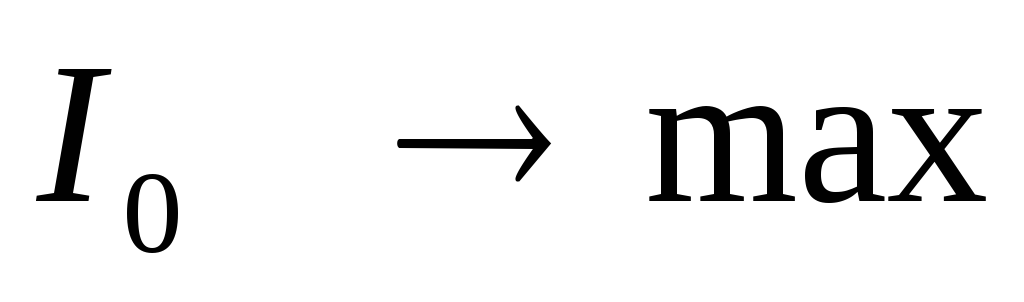

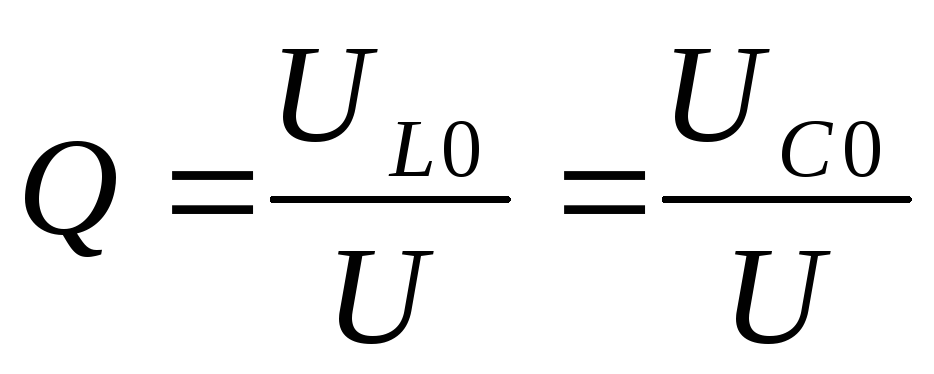
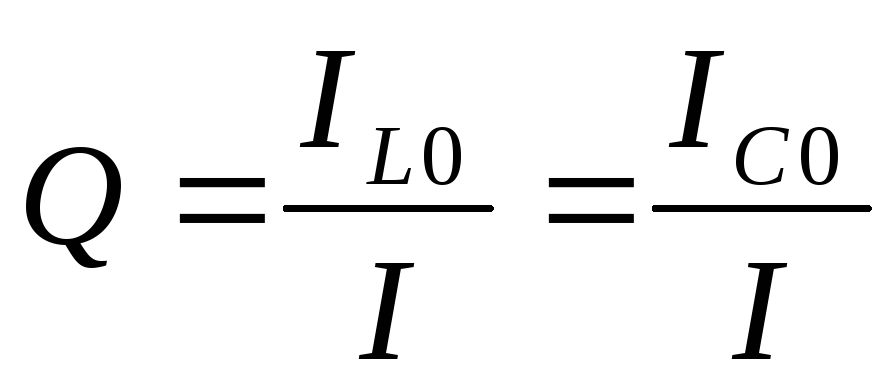
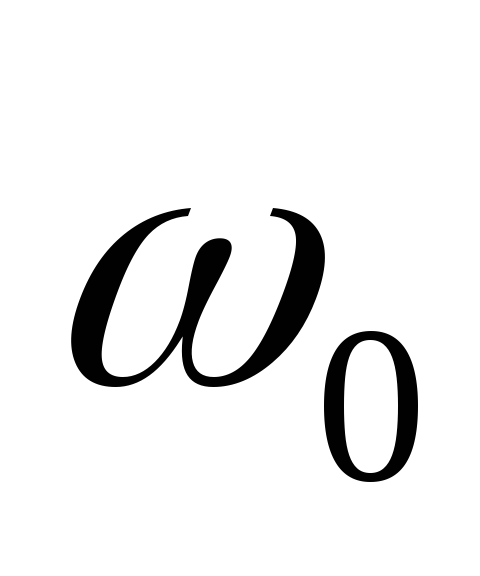 ,
,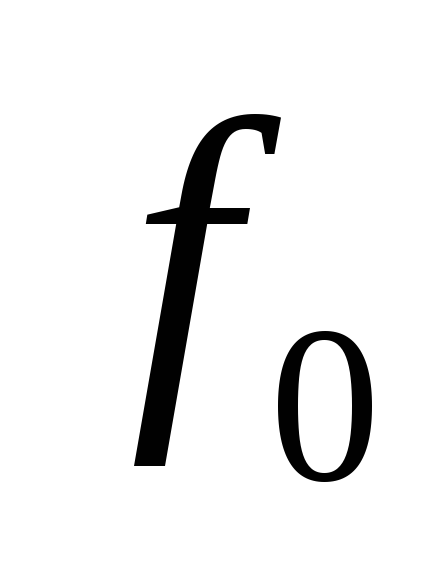 ,QиПрезисторами;
,QиПрезисторами;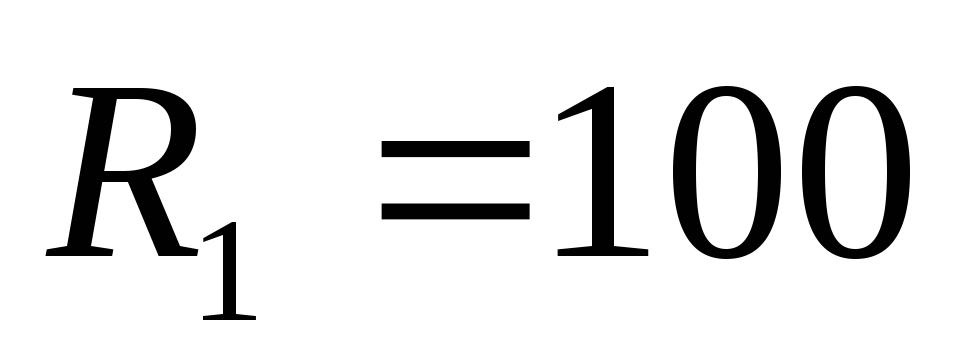 кОм, малое выходное сопротивление;
кОм, малое выходное сопротивление; .
.