Скалярное произведение векторов. Профильный уровень 11 класс онлайн-подготовка на Ростелеком Лицей
Длина вектора. Расстояние между точками
Мы продолжаем расширять модель вектора для трехмерного пространства. На прошлом уроке мы рассмотрели определение вектора с использованием двух подходов (геометрического и алгебраического), ввели основные операции (сложение и вычитание векторов, умножение вектора на число), рассмотрели некоторые свойства.
Также мы определили длину вектора как длину соответствующего отрезка с использованием теоремы Пифагора: длина вектора равна корню из суммы квадратов его координат (утверждение остается верным, независимо от количества этих самых координат) (см. рис. 1):
Рис. 1. Вектор
Если вектор задан координатами начала и конца, то его собственные координаты находятся как разности координат этих точек (см. рис. 2):
Рис. 2. Вектор
Таким образом, формула длины вектора через его координаты эквивалентна утверждению, что расстояние между двумя точками находится как корень из суммы квадратов попарных разностей их координат:
Для трехмерного пространства ситуация повторяется абсолютно. Т. к. длина вектора – это длина диагонали прямоугольного параллелепипеда с измерениями, равными координатам вектора, то его длина находится как корень квадратный из суммы квадратов его координат (см. рис. 3):
Т. к. длина вектора – это длина диагонали прямоугольного параллелепипеда с измерениями, равными координатам вектора, то его длина находится как корень квадратный из суммы квадратов его координат (см. рис. 3):
Рис. 3. Вектор
Если две точки заданы своими координатами, то мы можем их рассматривать как начало и конец вектора (см. рис. 4):
Тогда мы можем найти координаты вектора и его длину, т. е. расстояние между точками:
Рис. 4. Вектор
Скалярное произведение векторов
Вспомним задачу о нахождении работы силы по перемещению объекта.
Задача 1. Мальчик тащит санки за веревку по горизонтальной поверхности. Чему равна работа силы натяжения по перемещению санок (см. рис. 5)?
Рис. 5. Иллюстрация к задаче 1
Решение
Если мы умножим силу на расстояние, то ответ будет верным только в том случае, если веревка натянута строго горизонтально, т. е. векторы силы и перемещения сонаправлены (см. рис. 6).
векторы силы и перемещения сонаправлены (см. рис. 6).
Рис. 6. Иллюстрация к задаче 1
Если же веревка натянута под углом, то за перемещение отвечает не сама сила, а ее проекция на вектор перемещения (грубо говоря, помогает тянуть нам только та часть силы, которая действует вдоль перемещения, она и совершает работу) (см. рис. 7):
Рис. 7. Иллюстрация к задаче 1
Длина проекции равна длине вектора силы, умноженной на косинус угла между силой и перемещением (см. рис. 8):
Рис. 8. Иллюстрация к задаче 1
Тогда:
Ответ: .
Рассуждая таким образом, в планиметрии мы ввели понятие скалярного произведения двух векторов. Произведение двух векторов равно произведению модуля одного вектора на проекцию второго вектора на первый (см. рис. 9):
Рис. 9. Векторы и
Если нам известны длины векторов и угол между ними, то формула для вычисления скалярного произведения имеет вид:
Часто для обозначения модуля вектора используют просто букву , подчеркивая, что длина вектора и длина соответствующего отрезка – это одно и то же:
Результатом скалярного произведения является число.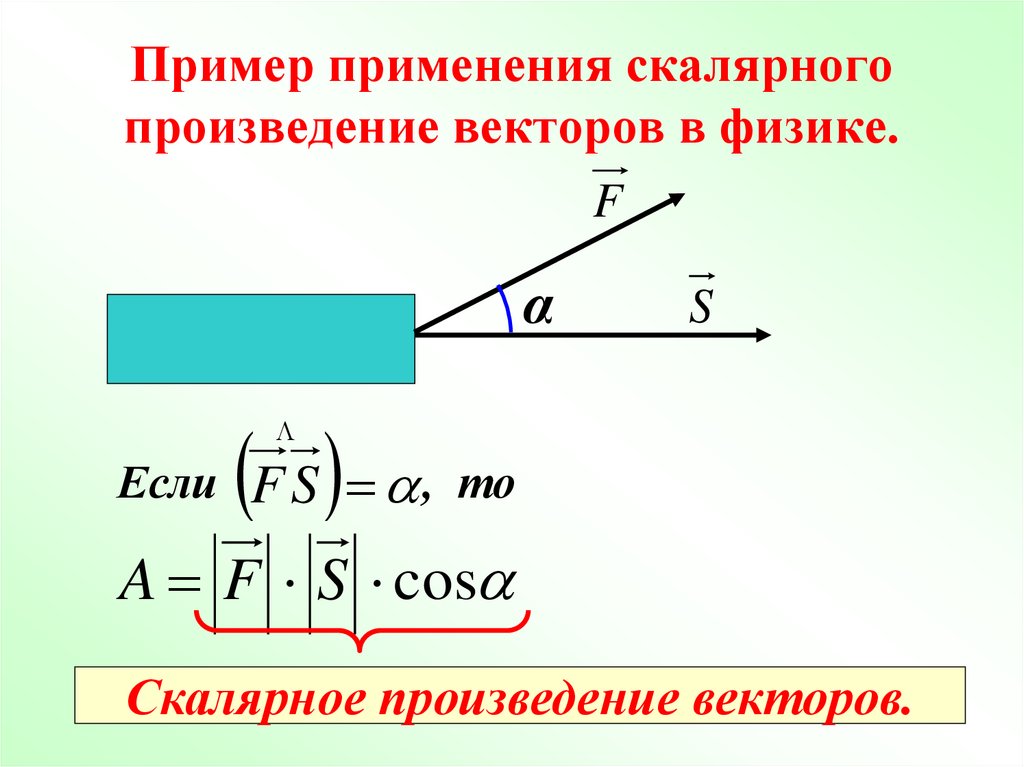 В примере с санками – это работа силы, величина скалярная. Очевидно, для скалярного произведения справедлив переместительный закон (если поменять местами сомножители, то результат не изменится):
В примере с санками – это работа силы, величина скалярная. Очевидно, для скалярного произведения справедлив переместительный закон (если поменять местами сомножители, то результат не изменится):
Все вышесказанное нам известно из планиметрии. Если мы возьмем два вектора в пространстве и совместим их начала, то они будут лежать в одной плоскости (см. рис. 10).
Рис 10. Векторы и лежат в одной плоскости
Следовательно, для них будет справедливо то же самое определение скалярного произведения:
Физический смысл скалярного произведения остается тем же самым.
Разница появляется только в описании через координаты, т. к. в планиметрии у вектора две координаты, а в пространстве – три:
Произведение вектора на себя называют скалярным квадратом. Подставим его в формулу скалярного произведения:
Таким образом, скалярный квадрат вектора равен квадрату его длины.
Скалярное произведение в координатах
Если вектор задан координатами, то мы можем найти его скалярный квадрат, так как уже умеем искать его длину:
Итак, скалярный квадрат вектора равен сумме квадратов его координат:
Рассмотрим теперь, как выражается скалярное произведение двух произвольных векторов через их координаты. Мы это уже делали в планиметрии, и результат будет аналогичным. Тем не менее повторим эти рассуждения.
Мы это уже делали в планиметрии, и результат будет аналогичным. Тем не менее повторим эти рассуждения.
Пусть два вектора, и не коллинеарны. Совместим их в общее начало. Построим вектор (см. рис. 11).
Рис. 11. Вектор
По теореме косинусов имеем:
Если векторы коллинеарны, то данное равенство окажется верным и для него. Таким образом, дальнейшие рассуждения верны для любой пары векторов.
Выражение – это скалярное произведение векторов. Тогда имеем:
Выразим скалярное произведение:
В правой части равенства у нас только скалярные квадраты векторов. Мы умеем находить их через координаты. Сделаем это:
Упростим выражение и получим:
Итак, мы получили формулу, знакомую нам из планиметрии: скалярное произведение векторов равно сумме попарных произведений их соответствующих координат.
Если в формулу скалярного произведения подставить один и тот же вектор , то получим знакомую уже формулу скалярного квадрата.
Итак, повторим:
1. С геометрической точки зрения скалярное произведение двух векторов равно произведению их длин на косинус угла между ними:
2. С алгебраической точки зрения скалярное произведение равно сумме попарных произведений их соответствующих координат:
Теперь мы можем сформулировать основные свойства скалярного произведения:
, причем , при . Оно непосредственно следует из того:
Переместительный закон, который следует как из геометрической, так и из алгебраической интерпретации произведения:
Распределительный закон, который следует из координатной формы записи скалярного произведения:
Сочетательный закон, который очень легко доказать, используя как геометрическую, так и координатную формы скалярного произведения (сделайте это самостоятельно):
В самом деле: в формуле для вычисления скалярного произведения фигурирует косинус угла между векторами. Т. к. данный угол может принимать значения только от до , то единственное значение, при котором косинус равен , это .
Т. к. данный угол может принимать значения только от до , то единственное значение, при котором косинус равен , это .
Угол между векторами
Если мы знаем длины векторов и угол между ними, то мы можем найти скалярное произведение по формуле:
Пример. Найти скалярное произведение двух векторов, длины которых равны и , а угол равен .
Решение
:
Вспоминаем: если сила и перемещение сонаправлены, то работа силы (которая и равна скалярному произведению векторов силы и перемещения) максимальна и равна произведению их модулей.
:
Как только веревка санок поднимается, проекция силы на перемещение уменьшается, уменьшается и работа силы. В данном случае в два раза.
:
Если сила направлена вертикально вверх, то работа такой силы по перемещению санок равна нулю.
:
Веревка направлена вверх и назад, горизонтальная проекция силы препятствует движению, работа отрицательна.
:
Сила направлена прямо противоположно перемещению. Работа отрицательна и максимальна по модулю (мы мешали движению как могли сильно) (см. рис. 12).
Рис. 12. Иллюстрация к примеру
Ответ: .
Задача может быть и обратной. Известны длины векторов и скалярное произведение. Тогда мы можем найти угол между векторами. В самом деле:
Тогда:
Эта формула позволяет найти угол между векторами. Проблема в том, что если длина векторов часто может быть известна из постановки задачи, то скалярное произведение вряд ли. Другое дело, если нам известны координаты векторов. Тогда мы можем найти и их длины, и их скалярное произведение.
Задача 2.
Решение
В силу симметрии куба не важно, между каким ребром и диагональю искать угол.
Найдем угол между ребром и диагональю , а для этого рассмотрим соответствующие векторы. Свяжем с кубом систему координат так, чтобы точка совместилась с началом координат (см. рис. 13).
рис. 13).
Рис. 13. Иллюстрация к задаче 2
Координаты вектора , координаты вектора . Найдем косинус угла между векторами:
Найдем угол:
Ответ: .
Рассмотрим еще одну задачу на применение скалярного произведения, а более подробно сделаем это уже на практическом уроке.
Задача 3. Доказать, что четыре точки являются вершинами квадрата (см. рис. 14). Найти его площадь:
Рис. 14. Иллюстрация к задаче 3
Решение
Для начала докажем, что данный четырехугольник – параллелограмм. Рассмотрим векторы противоположных сторон:
Векторы противоположных сторон равны, следовательно, они имеют равную длину и параллельны. Но это признак параллелограмма.
Осталось показать, что смежные стороны перпендикулярны. Найдем координаты вектора:
Перемножим векторы и :
Скалярное произведение векторов равно нулю, следовательно, векторы перпендикулярны.
Осталось найти площадь. Перемножим длины смежных сторон:
Перемножим длины смежных сторон:
Ответ: .
Список литературы
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11класс. Учебник. – АО «Издательство “Просвещение”».
- Мордкович А.Г., Смирнова И.М. Математика. Базовый уровень. 11 класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА».
- Погорелов А.В. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 класс. Базовый и углубленный уровни. Учебник. – АО «Издательство “Просвещение”».
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru
- Интернет-портал webmath.ru
- Интернет-портал math34.ru
Домашнее задание
- Найти длину вектора , если и .
- Даны векторы и . Найти значение , при котором .
- Доказать, что четырехугольник с вершинами есть параллелограмм.
 =a→·npa→b→=b→·npb→a→ показывает, что npb→a→ — это числовая проекция a→ на b→, npa→a→- проекция b→ на a→ соостветсвенно.
=a→·npa→b→=b→·npb→a→ показывает, что npb→a→ — это числовая проекция a→ на b→, npa→a→- проекция b→ на a→ соостветсвенно.Сформулируем определение произведения для двух векторов:
Скалярное произведение двух векторов a→ на b→ называют произведение длины вектора a→ на проекцию b→ на направление a→ или произведение длины b→ на проекцию a→ соответственно.
Скалярное произведение в координатах
Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.
Скаларное произведение двух векторов на плоскости, в трехмерном простарнстве называют сумму координат заданных векторов a→ и b→.
При вычислении на плоскости скаларного произведения заданных векторов a→=(ax,ay), b→=(bx,by) в декартовой системе используют:
a→,b→=ax·bx+ay·by,
для трехмерного пространства применимо выражение:
a→,b→=ax·bx+ay·by+az·bz.
Фактически это является третьим определением скалярного произведения.
Докажем это.
 )==ax·bx+ay·by+az·bz
)==ax·bx+ay·by+az·bz– соответственно для векторов трехмерного пространства.
Скалярное произведение векторов с координатами говорит о том, что скалярный квадрат вектора равен сумме квадратов его координат в пространстве и на плоскости соответственно. a→=(ax,ay,az), b→=(bx,by,bz) и (a→,a→)=ax2+ay2.
Скалярное произведение и его свойства
Существуют свойства скалярного произведения, которые применимы для a→,b→ и c→:
- коммутативность (a→,b→)=(b→,a→);
- дистрибутивность(a→+b→,c→)=(a→,c→)+(b→,c→), (a→+b→,c→)=(a→,b→)+(a→,c→);
- сочетательное свойство (λ·a→,b→)=λ·(a→,b→),(a→,λ·b→)=λ·(a→,b→), λ — любое число;
- скалярный квадрат всегда больше нуля (a→,a→)≥0, где (a→,a→)=0 в том случае, когда a→ нулевой.
Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел.
Доказать свойство коммутативности (a→,b→)=(b→,a→). Из определения имеем, что (a→,b→)=ay·by+ay·by и (b→,a→)=bx·ax+by·ay.
 )=3·7·cos60°=3·7·12=212
)=3·7·cos60°=3·7·12=212Ответ:(a→,b→)=212.
Пример 3Заданны векторы a→=(1,-1,2-3), b→=(0,2,2+3). Чему равно скалярной произведение.
Решение
В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи:
(a→,b→)=ax·bx+ay·by+az·bz==1·0+(-1)·2+(2+3)·(2+3)==0-2+(2-9)=-9
Ответ: (a→,b→)=-9
Пример 4Найти скалярное произведение AB→ и AC→. На координатной плоскости заданы точки A(1,-3), B(5,4), C(1,1).
Решение
Для начала вычисляются координаты векторов, так как по условию даны координаты точек:
AB→=(5-1,4-(-3))=(4,7)AC→=(1-1,1-(-3))=(0,4)
Подставив в формулу с использованием координат, получим:
(AB→,AC→)=4·0+7·4=0+28=28.
Ответ: (AB→,AC→)=28.
Пример 5Заданы векторы a→=7·m→+3·n→ и b→=5·m→+8·n→, найти их произведение.m→ равен 3 и n→ равен 2 единицам, они перпендикулярные.
Решение
(a→,b→)=(7·m→+3·n→, 5·m→+8·n→). Применив свойство дистрибутивности, получим:
(7·m→+3·n→, 5·m→+8·n→)==(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)
Выносим коэффициент за знак произведения и получим:
(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)==7·5·(m→,m→)+7·8·(m→,n→)+3·5·(n→,m→)+3·8·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)
По свойству коммутативности преобразуем:
35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(m→,n→)+24·(n→,n→)==35·(m→,m→)+71·(m→,n→)+24·(n→,n→)
В итоге получим:
(a→,b→)=35·(m→,m→)+71·(m→,n→)+24·(n→,n→).
 )+24·n→2==35·32+71·3·2·cosπ2+24·22=411.
)+24·n→2==35·32+71·3·2·cosπ2+24·22=411.Ответ: (a→,b→)=411
Если имеется числовая проекция.
Пример 6Найти скалярное произведение a→и b→. Вектор a→ имеет координаты a→=(9,3,-3), проекция b→ с координатами (-3,-1,1).
Решение
По условию векторы a→ и проекция b→ противоположно направленные, потому что a→=-13·npa→b→→, значит проекция b→ соответствует длине npa→b→→, при чем со знаком «-»:
npa→b→→=-npa→b→→=-(-3)2+(-1)2+12=-11,
Подставив в формулу, получим выражение:
(a→,b→)=a→·npa→b→→=92+32+(-3)2·(-11)=-33.
Ответ: (a→,b→)=-33.
Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.
Пример 7Какое значение должна принять λ при заданном скалярном произведении a→=(1,0,λ+1) и b→=(λ,1,λ) будет равным -1.
Решение
Из формулы видно, что необходимо найти сумму произведений координат:
(a→,b→)=1·λ+0·1+(λ+1)·λ=λ2+2·λ.
В дано имеем (a→,b→)=-1.
 )=5·3·cos(45°)=1522.
)=5·3·cos(45°)=1522.Ответ: A=1522.
Пример 9Материальная точка, перемещаясь из M(2,-1,-3) в N(5,3λ-2,4) под силой F→=(3,1,2), совершила работа равную 13 Дж. Вычислить длину перемещения.
Решение
При заданных координатах вектора MN→ имеем MN→=(5-2, 3λ-2-(-1), 4-(-3))=(3, 3λ-1,7).
По формуле нахождения работы с векторами F→=(3,1,2) и MN→=(3, 3λ-1,7) получим A=(F⇒, MN→)=3·3+1·(3λ-1)+2·7=22+3λ.
По условию дано, что A=13Дж, значит 22+3λ=13. Отсюда следует λ=-3, значит и MN→=(3,3λ-1,7)=(3,-10,7).
Чтобы найти длину перемещения MN→ , применим формулу и подставим значения:
MN→=32+(-10)2+72=158.
Ответ: 158.
Автор: Ирина Мальцевская
Преподаватель математики и информатики.
 Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспортаСвойства скалярного произведения векторов
Скалярное произведение двух векторов.
В физике работа А постоянной силы F при прямолинейном движении материальной точки из положения В в положение С (рис. 52) вычисляется по формуле
Эта формула вектору силы F и вектору перемещения ВС ставит в соответствие скалярную величину — работу. Величину А называют скалярным произведением векторов F и \(\overrightarrow{BC}\). Скалярное произведение может быть определено для любых двух векторов. Оно широко используется в физике и в математике.
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Если из двух векторов хотя бы один нулевой, то скалярное произведение этих векторов принимается равным нулю.
Скалярное произведение векторов а и b обозначается а • b.
 Итак, по определению
Итак, по определениюа • b = | а | • | b | cos\(\widehat{(a; b)}\). (1)
Если а = b, то скалярное произведение принимает вид а • a и называется скалярным квадратом вектора а и обозначается символом a2. Очевидно, что a2 = а • a = |а|2.
Как известно, проекция вектора b на ось, направление которой совпадает с направлением вектора а, выражается формулой
прab = | b | cos\(\widehat{(a; b)}\). (2)
Используя формулы (1) и (2), можно записать
а • b = | а | npab. (3)
Таким образом, скалярное произведение двух векторов равно произведению длины одного из них и проекции второго вектора на направление первого.

Аналогично получается формула а • b = | b | npba.
Задача 1. Известно, что | а | = 2, | b | = 1/3 , \(\widehat{(a; b)}\) = 150°. Найти а • b .
По формуле (1) находим
а • b = | а | • | b | cos\(\widehat{(a; b)}\) = 2 • 1/3 • 150°
Задача 2. Найти всевозможные скалярные произведения базисных векторов i и j прямоугольной декартовой системы координат на плоскости.
По определению скалярного произведения
i • j = | i | • | j | cos 90° = 1 • 1 • 0 = 0,
i2 = i • i = | i | • | i | cos 0° = 1 • 1 • 1 = 1.

Аналогично j • i = 0, j2 = 1.
Задача 3. Какой знак имеет скалярное произведение векторов а и b, если
90° < \(\widehat{(a; b)}\) < 180°?Так как в формуле а • b = | а | • | b | cos \(\widehat{(a; b)}\) числа | а | и | b | неотрицательны, знак а • b зависит от знака косинуса.
В промежутке ] 90°; 180°] cos \(\widehat{(a; b)}\) < 0, поэтому а • b < 0.
Задача 4. В каком промежутке находится величина угла между векторами а и b, если а • b > 0?
Так как а • b > 0, то | а | =/= 0, | b | =/= 0 и cos \(\widehat{(a; b)}\) > 0. Отсюда \(\widehat{(a; b)}\) \(\in\) [0°; 90° [.
Свойства скалярного произведения векторов
1.
 Скалярное умножение векторов обладает переместительным свойством:
Скалярное умножение векторов обладает переместительным свойством:а Х b = b Х а. (1)
Так как
\(\widehat{(a; b)}\) = \(\widehat{(b; a)}\) и | а | Х | b | = | b | Х | а |,
то
а Х b = | а | Х | b | cos \(\widehat{(a; b)}\) = | b | Х | а | cos\(\widehat{(b; a)}\) = b Х а.
Если а = 0 или b = 0, то по определению скалярного произведения а Х b = 0 и b Х а = 0, т. е. а Х b = b Х а
2. Скалярное умножение векторов обладает сочетательным свойством по отношению к умножению вектора на число:
(ka) Х b = k (а Х b). (2)
Обозначим \(\widehat{(a; b)}\) = φ и \(\widehat{(ka; b)}\) = φ1.

Если k > 0, то \(\widehat{(a; b)}\) = \(\widehat{(ka; b)}\), т. е. φ = φ1 и тогда
(ka) Х b = | kа | Х | b | cos φ1 = k | а | Х | b | cos φ = k (а Х b).
Если k < 0, то ka \(\uparrow\downarrow\) a и φ1 = 180° Ч φ, и тогда
(ka) Х b = | kа | Х | b | cos φ1 = | k | Х | а | Х | b | cos (180° Ч φ) =
= Ч k Х | а | Х | b |(Ч cos φ) == k | а | Х | b | cos φ = k (а Х b)
Если k = 0 или a = 0, или b = 0, то
(ka) Х b = 0 и k (а Х b) = 0, и поэтому (ka) Х b =k (а Х b).

3. Скалярное умножение векторов обладает распределительным свойством относительно сложения векторов
а Х (b + с) = а Х b + а Х c. (3)
Если a = 0, то свойство (3) очевидно.
Пусть a =/= 0. Тогда
а Х (b + с) = | a | Х npa(b + c) = | a | Х (npab + npac) =
= | a | Х npab + | a | Х npac = а Х b + а Х c.В ходе доказательства были использованы известные свойства проекции вектора на ось.
Заметим, что из (1) и (3) следует формула
(a + b) Х c = a Х c + b Х c. (4)
Сходство свойств скалярного произведения векторов со свойствами произведения действительных чисел позволяет легко производить вычисления и преобразования со скалярными произведениями.

Задача. Доказать тождество
(a + b) 2 = а2 + 2a Х b + b2.
Используя свойства (1) и (4) скалярного произведения, получаем
(a + b) 2 = (a + b) Х (a + b) = (a + b) Х а + (a + b) Х b =
= aХa + bХa + aХb + bХb = а2 + aХb + aХb + b2 == а2 + 2a Х b + b2
Теорема. Для того чтобы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю:
(а =/= 0, b =/= 0, a Х b = 0 ) <==> a ⊥ b. (5)
Необходимость.
 Пусть a ⊥ b. Тогда
Пусть a ⊥ b. Тогдаφ = \(\widehat{(a; b)}\) = 90° и a Х b = | а | Х | b | Х cos 90° = 0.
Достаточность. Пусть a Х b = 0 , а =/= 0, b =/= 0.
Так как а =/= 0, b =/= 0, то | а | =/= 0, | b | =/= 0, а так как | а | Х | b | Х cos φ = 0, то cos φ = 0 и, следовательно, φ = 90°, т. е. a ⊥ b.
Скалярное произведение векторов, заданных своими координатами
Пусть на плоскости имеется некоторая прямоугольная декартова система координат и пусть заданы векторы а = (x1 ; y1 ) и b = (x2 ; y2). Так как
a = x1i + y1 j, b = x2i + y2 j,
то, используя соответствующие свойства скалярного умножения векторов, получаем
а • b = (x1 + y1 j) • (x2i + y2 j) = (x1x2) i 2 + (x1y2) i • j + (y1x2) j • i+ (y1y2) j 2.

Очевидно, что i 2 = j 2 = 1 и i • j = j • i = 0, поэтому
а • b = x1x2 + y1y2. (1)
Пусть теперь в пространстве имеется некоторая прямоугольная декартова система координат и заданы векторы
а = (x1 ; y1 ; z1) , b = (x2 ; y2; z2).
Аналогично предыдущему получим
а • b = x1x2 + y1y2+ z1z2. (2)
Итак, скалярное произведение двух векторов равно сумме произведений одноименных координат этих векторов.
Задача 1. Вычислить а • b , если а = 2i + 3j, b = — 5i + j.

а • b = (2i + 3j) • (- 5i + j) = 2 • (-5) + 3 • l = — 7.
Задача 2. Вычислить а • b, если а = (2; -3; 4), b = (5; 7;-1).
а • b = 2 • 5 + (-3) • 7 + 4 • (- 1) = — 15.
Задача 3. Найти длину вектора а = (х; у; z).
Применяя формулу (2) при b = a, получим
а2 = а • а = хх + уу + zz = х2 + у2 + z2.
С другой стороны, согласно определению скалярного произведения получаем
а2 = а • а = | а | • | а | cos 0 = | а | 2
Следовательно,
$$ |a| = \sqrt{x^2 + y^2 + z^2} $$
Скалярное произведение векторов — справочник для студентов и школьников
Определение
Скалярное произведение двух ненулевых векторов \(\ \overline{a} \) и \(\ \overline{b} \) представляет собой число, равное произведению длин этих векторов и косинуса угла между ними:
\(\ \overline{a} \overline{b}=\overline{a} \cdot \overline{b}=(\overline{a}, \overline{b})=|\overline{a}||\overline{b}| \cos (\overline{a}, \overline{b}) \)
Пример
- Задание.
 {2}
\) и называется скалярным квадратом.
{2}
\) и называется скалярным квадратом.3. Если \(\ \overline{a} \neq \overline{0} \) , то \(\ (\overline{a}, \overline{b})=|\overline{a}| \cdot \Pi p_{\overline{a}} \overline{b} \)
4. Если \(\ \overline{a} \neq \overline{0} \) и \(\ \overline{b} \neq \overline{0} \) и \(\ (\overline{a}, \overline{b})=0 \), то \(\ \overline{a} \perp \overline{b} \). Обратное также верно.
5. \(\ (\overline{a}+\overline{b}, \overline{c})=(\overline{a}, \overline{c})+(\overline{b}, \overline{c}) \)
6. \(\ (\lambda \overline{a}, \overline{b})=\lambda(\overline{a}, \overline{b}) \)
7. \(\ (\alpha \overline{a}+\beta \overline{b}, \gamma \overline{c}+\delta \overline{d})=\alpha \gamma(\tilde{a}, \overline{c})+\alpha \delta(\overline{a}, \overline{d})+\beta \gamma(\overline{b}, \overline{c})+\beta \delta(\overline{b}, \overline{d}) \)
Если векторы \(\ \overline{a} \) и \(\ \overline{b} \) задаются своими координатами: \(\ \overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right), \overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right) \) , то их скалярное произведение вычисляется по формуле:
\(\ (\overline{a}, \overline{b})=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3} \)
Определение
Скалярное произведение векторов, заданное его координатами, равно сумме произведений соответствующих координат.
 {\circ}
\)
{\circ}
\) - A является скалярной величиной и обозначением работы;
- a представляет собой вектор перемещения (смещения) материальной точки;
- F определяется, как вектор силы, которая оказывает воздействие на данную точку;
- ϕ является углом силы F, действующим к смещению a.
- Если вычислить скалярное произведение вектора a¯ самого на себя, то результат в любом случае будет положительным, либо имеет нулевое значение: a¯·a¯=a¯2=a¯, a¯≥0. Выражение a¯·a¯=a¯2=a¯, a¯ является скалярным квадратом вектора a¯.
- Нулевое значение скалярного произведения вектора самого на себя возможно лишь в том случае, когда рассматривается нулевой вектор: a¯·a¯=0⇔=a¯=0¯.
- Значение скалярного произведения вектора самого на себя представляет собой квадрат модуля заданного вектора: a¯·a¯=a¯2=a¯2.

- Действие по поиску скалярного произведения является коммуникативным, то есть: a¯, b¯=b¯, a¯.
- В том случае, когда скалярное произведение пары ненулевых векторов имеет нулевое значение, данные вектора являются ортогональными, то есть перпендикулярными: a¯, b¯=0, a¯, b¯≠0¯⇔a¯⊥b¯.
- λa¯, b¯=λ·a¯, b¯
- Действие по поиску результата скалярного произведения векторов является дистрибутивным, то есть: a¯+b¯, c¯=a¯, c¯+b¯, c¯.
- Знак скалярного произведения зависит от значения угла между векторами. В том случае, когда угол, разделяющий вектора, является острым, скалярное произведение имеет знак плюс, то есть обладает положительным значением. Это объясняется положительным значением косинуса острого угла. Если вектора составляют тупой угол, то скалярное произведение данных векторов будет иметь знак минус, то есть являться отрицательным. Причиной этому служит отрицательное значение величины косинуса тупого угла. Справедливыми являются и обратные утверждения.
- Угол между сонаправленными векторами составляет 0°.
 В таком случае скалярное произведение этих векторов обладает положительным значением. Вектора, имеющие противоположные направления, разделены углом в 180°. Тогда скалярное произведение данных векторов обладает отрицательным значением.
В таком случае скалярное произведение этих векторов обладает положительным значением. Вектора, имеющие противоположные направления, разделены углом в 180°. Тогда скалярное произведение данных векторов обладает отрицательным значением. - скалярное произведение векторов или скалярное произведение
- векторное произведение векторов или перекрестное произведение
- Свойство 1: Скалярное произведение двух векторов коммутативно, т. е. a.b = b.a = ab cos θ.
- Свойство 2: Если a.b = 0 , то ясно видно, что либо b , либо a равно нулю или cos θ = 0,
\(\begin{array}{l}\Rightarrow \theta=\frac{\pi}{2}.\end{array} \)
Предполагает, что любой из векторов равен нулю или они перпендикулярны друг другу . - Свойство 3: Также мы знаем, что с помощью скалярного произведения векторов (p a ).(q b )=(p b ).(q a )=pq a.b
8
- Свойство 4: Скалярное произведение вектора на себя представляет собой квадрат величины вектора, т.
 е. a.a = a.a cos 0 = a 2
е. a.a = a.a cos 0 = a 2 - Свойство 5: Скалярное произведение также подчиняется закону распределения, т. е. a.(b + c) = a.b + a.c
- Свойство 6: В терминах ортогональных координат для взаимно перпендикулярных векторов видно, что
\(\begin{array}{l}\hat{i}.\hat{i} = \hat{j}.\hat {j} = \шляпа{к}.\шляпа{к} = 1\конец{массив} \)
- Свойство 7: С точки зрения единичных векторов, если
\(\begin{array}{l}a = a_{1}\hat{i}+ a_{2}\hat{j}+a_{3} \ шляпа {k} \ и \ b = b_ {1} \ шляпа {i} + b_ {2} \ шляпа {j} + b_ {3} \ шляпа {k} \ конец {массив} \)
затем\(\begin{array}{l}a.b = (a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k}).(b_1 \hat{i} + b_2 \hat{ j} + b_3 \шляпа{к})\конец{массив} \)
- Свойство 4: Скалярное произведение вектора на себя представляет собой квадрат величины вектора, т.
- линейная алгебра
- $<0$, если угол тупой ,
- $>0$ если угол острый ,
- $=0$, если $a$ и $b$ ортогональны .
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2588
- Гилберт Стрэнг и Эдвин «Джед» Герман
- OpenStax
- Вычислить скалярное произведение двух заданных векторов.
- Определить, перпендикулярны ли два заданных вектора.
- Найдите направляющие косинусы заданного вектора.
- Объясните, что подразумевается под векторной проекцией одного вектора на другой вектор, и опишите, как ее вычислить.
- Вычислите работу, совершаемую данной силой.

- Найдите скалярное произведение \(\vecs{ u}=⟨3,5,2⟩\) и \(\vecs{ v} =⟨−1,3,0⟩\).
- Найдите скалярное произведение \(\vecs{ p}=10\hat{\textbf i}−4 \hat{\textbf j}+7 \hat{\textbf k}\) и \(\vecs{ q} = −2 \ шляпа {\ textbf i} + \ шляпа {\ textbf j} +6 \ шляпа {\ textbf k}. \)
- Подсказка
Умножьте соответствующие компоненты, а затем сложите их произведения.
- Ответить
\(7\)
- Коммутативное свойство \[\vecs{ u}⋅\vecs{ v}=\vecs{ v}⋅\vecs{ u} \nonumber \]
- Распределительное свойство \[\vecs{ u}⋅(\vecs{ v}+\vecs{ w})=\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ w} \номер\]
- Ассоциативное свойство \[c(\vecs{ u}⋅\vecs{ v})=(c\vecs{ u})⋅\vecs{ v}=\vecs{ u}⋅(c\vecs{ v} ) \номер\] 92 \номер \]
- \(( \vecs{a} ⋅ \vecs{b}) \vecs{c} \)
- \(\vecs{a}⋅(2\vecs{c})\) 92\)
- Подсказка
Используйте уравнение \ref{dot2}.
- Ответить
\(θ≈0,22\) рад
- Подсказка
Векторы \(\vecs{ p}\) и \(\vecs{ q}\) ортогональны тогда и только тогда, когда \(\vecs{ p}⋅\vecs{ q}=0\).
- Ответить
\(х=5\)
- \(\vecs{v}\) и \(\mathbf{\шляпа i}\)
- \(\vecs{v}\) и \(\mathbf{\hat j}\)
- \(\vecs{v}\) и \(\mathbf{\шляпа k}\)
- \(\vecs{v}\) и \(\mathbf{\шляпа i}\)
- \(\vecs{v}\) и \(\mathbf{\hat j}\)
- \(\vecs{v}\) и \(\mathbf{\шляпа k}\)
- Подсказка
\(\mathbf{\hat i}=⟨1,0,0⟩, \mathbf{\hat j}=⟨0,1,0⟩,\) и \(\mathbf{\hat k}=⟨0 ,0,1⟩\)
- Ответить
\(а. α≈1,04\) рад; б. \(β≈2,58\) рад; в. \(γ≈1,40\) рад
- Подсказка
Используйте четырехмерные векторы для стоимости, цены и проданного количества.
- Ответить
Продажи = 15 685,50 долларов США; прибыль = 14 073,15
долларов США- \(\vecs{v}=⟨3,5,1⟩\) и \(\vecs{u}=⟨−1,4,3⟩\)
- \(\vecs{v}=3\mathbf{\шляпа i}−2\mathbf{\шляпа j}\) и \(\vecs{u}=\mathbf{\шляпа i}+6\mathbf{\ шапка j}\)
- Подсказка
Начните с нахождения проекции \(\vecs{ v}\) на \(\vecs{ u}\).
- Ответить
\(\vecs{v}=\vecs{p}+\vecs{q},\) где \(\vecs{p}=\dfrac{18}{5}\mathbf{\hat i}+\dfrac {9}{5}\mathbf{\hat j}\) и \(\vecs{q}=\dfrac{7}{5}\mathbf{\hat i}−\dfrac{14}{5}\mathbf {\ шляпа j} \)
- Подсказка
Вычислить скалярную проекцию \(\vecs{w}\) на \(\vecs{v}\).
- Ответить
21 узел
- Подсказка
Используйте определение работы как скалярного произведения силы и расстояния.
- Ответить
150 фут-фунт
- Скалярное произведение двух векторов \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) и \(\vecs{ v}=⟨v_1,v_2,v_3 ⟩\) равно \(\vecs{u}⋅\vecs{v}=u_1v_1+u_2v_2+u_3v_3\).
 92\)
92\) - Скалярное произведение двух векторов может быть иначе выражено как \(\vecs{ u}⋅\vecs{ v}=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ.\) Эта форма скалярного произведения полезно для нахождения меры угла, образованного двумя векторами.
- Векторы \(\vecs{ u}\) и \(\vecs{ v}\) ортогональны, если \(\vecs{ u}⋅\vecs{ v}=0\).
- Углы, образованные ненулевым вектором и осями координат, называются углами направления для вектора. Косинусы этих углов называются 9.2}\vecs{ и}\). Величина этого вектора известна как скалярная проекция из \(\vecs{v}\) на \(\vecs{u}\), заданная выражением \(\text{comp}_\vecs{u}\ vecs{v}=\dfrac{\vecs{u}⋅\vecs{v}}{‖\vecs{u}‖}\).
- Работа совершается, когда к объекту прикладывается сила, вызывающая его перемещение. Если сила представлена вектором \(\vecs{F}\), а перемещение представлено вектором \(\vecs{s}\), то выполненная работа \(W\) определяется формулой (W=\vecs{F}⋅\vecs{s}=∥\vecs{F}∥‖\vecs{s}‖\cos θ.
 \)
\) - Скалярное произведение \(\vecs{ u}\) и \(\vecs{ v}\)
- Косинус образуемого угла по \(\vecs{u}\) и \(\vecs{v}\)
- Векторная проекция \ (\vecs{v}\) на 92}\vecs{ u}\)
- Скалярная проекция \(\vecs{ v}\) на \(\vecs{ u}\)
\(\text{comp}_\vecs{ u}\vecs{v}=\dfrac{\vecs{ u}⋅\vecs{v}}{‖\vecs{ u}‖}\)
- Работа, совершаемая силой \(\vecs{ F}\) для перемещения объекта через вектор смещения \(\vecd{PQ}\)
\(W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ\)
Глоссарий
- Углы направления
- углы, образованные ненулевым вектором и осями координат
- направление косинусов
- косинусы углов, образованных ненулевым вектором и осями координат
- скалярное произведение или скалярное произведение
- \(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3\), где \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) и \(\vecs{ v}=⟨ v_1,v_2,v_3⟩\)
- скалярная проекция
- величина векторной проекции вектора
- ортогональные векторы
- векторов, образующих прямой угол при размещении в стандартном положении
- векторная проекция
- составляющая вектора, следующего заданному направлению
- работа силы Работой
- обычно считается количество энергии, необходимое для перемещения объекта; если мы представим приложенную силу вектором \(\vecs{F}\), а перемещение объекта вектором \(\vecs{s}\), то работа, выполненная силой, будет скалярным произведением \ (\vecs{F}\) и \(\vecs{s}\).

Авторы и авторство
Эта страница под названием 12.3: The Dot Product распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа ООР или издатель
- ОпенСтакс
- Показать страницу Содержание
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- углы направления
- направление косинусов
- скалярный продукт
- внутренний продукт
- ортогональных векторов
- скалярное произведение
- скалярная проекция
- источник@https://openstax.
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 - Точечный продукт
- векторная проекция
- работа, совершенная силой
Объяснение урока: скалярное произведение в 3D
В этом объяснении мы узнаем, как найти скалярное произведение двух векторов в 3D.
Скалярное произведение, также называемое скалярным произведением, поскольку оно дает скалярную величину, не вектор, это один из способов перемножения векторов.
Вероятно, вы уже знакомы с нахождением скалярного произведения на плоскости. (2Д). Возможно, вы узнали, что скалярное произведение ⃑𝐴 и ⃑𝐵 определяется как ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖×‖‖⃑𝐵‖‖×𝜃cos, где 𝜃 — угол между двумя векторами ⃑𝐴 и ⃑𝐵.
Немного поэкспериментировав с геометрией, можно показать, что его можно вычислить из компоненты обоих векторов: ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵, где 𝐴 и 𝐵 — 𝑥-компоненты ⃑𝐴 и ⃑𝐵, а 𝐴 и 𝐵 — их 𝑦-компоненты.

Рассмотрим два вектора ⃑𝐴 и ⃑𝐵, которые образуют углы 𝜃 и 𝜃 с положительное направление оси 𝑥 соответственно.
Тогда угол между ними равен 𝜃=𝜃−𝜃. При условии 𝐴 = ‖⃑𝐴⃑𝐴⃑𝐴⃑𝐴𝜃, 𝐴 = ‖⃑𝐴⃑𝐴⃑𝐴⃑𝐴𝜃, 𝐵 = ‖⃑𝐵⃑𝐵⃑𝐵⃑𝐵, 𝐵 = ‖⃑𝐵⃑𝐵⃑𝐵⃑𝐵, cossincossin мы находим, что 𝐴𝐵+𝐴𝐵 = ‖⃑𝐴⃑𝐴⃑𝐴‖⋅ ‖‖⃑𝐵⃑𝐵⃑𝐵𝜃𝜃+‖⃑𝐴⃑𝐴⃑𝐴⋅ ⋅ ‖⃑𝐵⃑𝐵𝜃𝜃 = ‖⃑𝐴⃑𝐴‖⋅‖⃑𝐵⃑𝐵⃑𝐵 коскоссинскоскоссинсин
Используя тригонометрическое тождество вычитания coscoscossinsin(𝛼−𝛽)=𝛼𝛽+𝛼𝛽, находим, заменив 𝛼 на 𝜃 и 𝛽 с 𝜃, что coscoscossinsincoscossinsin(𝜃−𝜃)=𝜃𝜃+𝜃𝜃=𝜃𝜃+𝜃𝜃.
Поскольку 𝜃=𝜃−𝜃 𝐴𝐵+𝐴𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖𝜃=⃑𝐴⋅⃑𝐵.cos
Переходя к 3D-векторам, определение скалярного произведения не изменилось.
Определение: скалярное произведение двух трехмерных векторов где 𝜃 — угол между ⃑𝐴 и ⃑𝐵.
Давайте посмотрим на наш первый пример и применим определение скалярного произведения.
Пример 1. Нахождение скалярного произведения двух векторов по данным Норма одного из них, составные части другого и Угол между Ними
Допустим ⃑𝐴=(−1,2,7), ‖‖⃑𝐵‖‖=13, а угол между двумя векторов составляет 135∘.
 Найдите ⃑𝐴⋅⃑𝐵 с точностью до сотых.
Найдите ⃑𝐴⋅⃑𝐵 с точностью до сотых.Ответить
Мы знаем, что ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖𝜃cos. Мы уже знаем ‖‖⃑𝐵‖‖ и угол 𝜃. Поэтому нам нужно найти ‖‖⃑𝐴‖‖ используя компоненты ⃑𝐴: ‖‖⃑𝐴‖‖=𝐴+𝐴+𝐴=√(−1)+2+7=√54.
Теперь, подставив это значение в наше уравнение для ⃑𝐴⋅⃑𝐵, мы нашли ⃑𝐴⋅⃑𝐵=√54⋅13⋅135≃−67.55.cos∘
Практическое руководство. Вычисление скалярного произведения с использованием компонентов вектора
Скалярное произведение трехмерных векторов вычисляется с использованием компонентов вектора вектора так же, как и в 2D, а именно, ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵, где индексы 𝑥, 𝑦 и 𝑧 обозначим компоненты вдоль 𝑥-, 𝑦-, и 𝑧-оси.
Применим этот метод на следующем примере.
Пример 2. Нахождение скалярного произведения двух заданных векторов Их компоненты
Учитывая, что ⃑𝐴=(−6,−3,5) и ⃑𝐵=(7,−4,−1), определить ⃑𝐴⋅⃑𝐵.
Ответ
Здесь мы вычисляем скалярный продукт, используя ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵, где индексы 𝑥, 𝑦 и 𝑧 обозначим компоненты вдоль 𝑥-, 𝑦-, и 𝑧-оси.
 Таким образом, мы имеем
⃑𝐴⋅⃑𝐵=(−6)⋅7+(−3)⋅(−4)+5⋅(−1)=−42+12+(−5)=−35.
Таким образом, мы имеем
⃑𝐴⋅⃑𝐵=(−6)⋅7+(−3)⋅(−4)+5⋅(−1)=−42+12+(−5)=−35.Теперь, когда мы знаем, как определяется скалярный продукт и как его вычислить, используя компонентов векторов, давайте посмотрим на свойства скалярного произведения.
Поскольку скалярное произведение является произведением величин векторов, умноженных косинусом угла между ними, он равен нулю, когда косинус угла между обоими векторами равен нулю. Это происходит, когда угол между ними 90∘ или −90∘ (или 270∘), то есть, когда они перпендикулярны.
Свойство: Скалярное произведение двух перпендикулярных векторов
Скалярное произведение двух перпендикулярных векторов равно нулю. И наоборот, когда скалярное произведение двух векторов равно нулю, то эти два вектора перпендикулярны.
Чтобы вспомнить, у каких углов косинус равен нулю, вы можете визуализировать единичный круг, помня, что косинус — это 𝑥-координата точки P, связанная с угол 𝜃.
Мы собираемся использовать это свойство в следующих двух примерах.

Пример 3. Поиск недостающих компонентов ортогональных векторов
Для какого значения 𝑘 являются векторами ⃑𝐴=(7,−7𝑘,−6) и ⃑𝐵=(7,−3,𝑘) перпендикуляр?
Ответ
Если два вектора перпендикулярны, то угол между ними равен 90∘ или −90∘ (или 270∘). В обоих случаях косинус угла между ними равен нуль. Следовательно, скалярное произведение двух векторов равно нулю. В этом вопрос, значит ⃑𝐴⋅⃑𝐵=0; то есть, 𝐴𝐵+𝐴𝐵+𝐴𝐵=0.
Следовательно, имеем 7⋅7+(−7𝑘)⋅(−3)+(−6)⋅𝑘=049+21𝑘−6𝑘=0𝑘=-4915.
Пример 4. Определение перпендикулярных и параллельных векторов
Что из следующего верно для векторов ⃑𝐴=(−3,7,−8) и ⃑𝐵=(−6,−1,−1)?
- Они параллельны.
- Они перпендикулярны.
- Они не параллельны и не перпендикулярны.
Ответ
Если ⃑𝐴 и ⃑𝐵 параллельны, то существует число 𝑘 такое, что ⃑𝐴=𝑘⃑𝐵. Мы было бы −3=−6𝑘7=−𝑘−8=−𝑘.
Очевидно, нет значения 𝑘, которое бы подтверждало три уравнения, поскольку мы получить три различных решения для каждого из них 12,−7,8а.
 Поэтому,
⃑𝐴 и ⃑𝐵 не параллельны.
Поэтому,
⃑𝐴 и ⃑𝐵 не параллельны.Если ⃑𝐴 и ⃑𝐵 перпендикулярны, то их скалярное произведение равно нулю. Давайте работать их точечный продукт: ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵=(−3)⋅(−6)+7⋅(−1)+(−8)⋅(−1)=18+(−7)+8=19.
Их скалярное произведение не равно нулю; следовательно, ⃑𝐴 и ⃑𝐵 не перпендикулярны .
Правильный ответ: ⃑𝐴 и ⃑𝐵 не параллельны и не перпендикулярны.
Другие свойства скалярного произведения возникают из-за того, что косинус угол между двумя векторами является одним из его факторов. Например, учитывая, что функция косинуса четная с периодом 360∘, это означает, что не имеет значения, если берем угол от ⃑𝐴 к ⃑𝐵 или с ⃑𝐵 на ⃑𝐴, потому что coscoscos𝜃=(−𝜃)=(360−𝜃).
Следовательно, скалярное произведение коммутативно: ⃑𝐴⋅⃑𝐵=⃑𝐵⋅⃑𝐴.
Кроме того, скалярное произведение двух коллинеарных векторов равно плюс или минус произведению их величины. Действительно, рассмотрим сначала два коллинеарных вектора ⃑𝐴 и ⃑𝐵, угол между которыми равен нулю: ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖⋅0=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖, потому что поскольку cos0=1.

Теперь рассмотрим два коллинеарных вектора ⃑𝐴 и ⃑𝐵, причем угол между ними 180∘ (т. е. два вектора указывают в противоположных направлениях): ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖⋅180=−‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖, cos∘ поскольку cos180=−1∘.
Отсюда следует, что скалярное произведение вектора на самого себя дает квадрат его величины. Это можно легко проверить с помощью того, как мы вычисляем скалярное произведение: ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵, так ⃑𝐴om⃑𝐴 = 𝐴𝐴+𝐴𝐴+𝐴𝐴 = 𝐴+𝐴+𝐴.
, так как ‖⃑𝐴⃑𝐴⃑𝐴 = 𝐴+𝐴+𝐴, мы находим, что ⃑𝐴⋅⃑𝐴=‖‖⃑𝐴‖‖.
Как и умножение, скалярное произведение является дистрибутивным: (⃑𝐴+⃑𝐵)⋅⃑𝐶=⃑𝐴⋅⃑𝐶+⃑𝐴⋅⃑𝐶.
Кроме того, у нас есть (𝑘⃑𝐴)⋅⃑𝐵=⃑𝐴⋅(𝑘⃑𝐵)=𝑘⃑𝐴⋅⃑𝐵.
Воспользуемся этими свойствами, чтобы ответить на следующий вопрос.
Пример 5: Использование распределения скалярного произведения
Если ⃑𝐴 и ⃑𝐵 — два перпендикулярных единичных вектора, находить (3⃑𝐴−⃑𝐵)⋅(−2⃑𝐴+⃑𝐵).
Ответ
Во фразе «⃑𝐴» есть две части информации и ⃑𝐵 два перпендикулярные единичные векторы».
 Во-первых, векторы перпендикулярны,
что означает, что их скалярное произведение равно нулю. Второй
что они являются единичными векторами, что означает, что они имеют величину 1. Теперь, используя распределительное свойство скалярного произведения, мы находим, что
(3⃑𝐴−⃑𝐵)⋅(−2⃑𝐴+⃑𝐵)=−6⃑𝐴⋅⃑𝐴+3⃑𝐴⋅⃑𝐵+2⃑𝐵⋅⃑𝐴−⃑𝐵⋅⃑𝐵.
Во-первых, векторы перпендикулярны,
что означает, что их скалярное произведение равно нулю. Второй
что они являются единичными векторами, что означает, что они имеют величину 1. Теперь, используя распределительное свойство скалярного произведения, мы находим, что
(3⃑𝐴−⃑𝐵)⋅(−2⃑𝐴+⃑𝐵)=−6⃑𝐴⋅⃑𝐴+3⃑𝐴⋅⃑𝐵+2⃑𝐵⋅⃑𝐴−⃑𝐵⋅⃑𝐵.Поскольку векторы перпендикулярны, члены 3⃑𝐴⋅⃑𝐵 и 2⃑𝐵⋅⃑𝐴 равны нулю.
Также мы знаем, что ⃑𝐴⋅⃑𝐴=‖‖⃑𝐴‖‖=1 так как ⃑𝐴 является единичным вектором. То же самое относится к ⃑𝐵. Следовательно, мы находим, что (3⃑𝐴−⃑𝐵)⋅(−2⃑𝐴+⃑𝐵)=−6−1=−7.
Ключевые точки
- Скалярное произведение векторов ⃑𝐴 и ⃑𝐵 определяется как ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖×‖‖⃑𝐵‖‖×𝜃, потому что где 𝜃 — угол между двумя векторами ⃑𝐴 и ⃑𝐵.
- Скалярное произведение 3D-векторов можно рассчитать с помощью векторов компоненты: ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵.
- Продукт DOT имеет следующие свойства:
- ⃑𝐴⋅⃑𝐵 = ⃑𝐵⋅⃑𝐴 (коммутативность),
- ⃑𝐴⋅⃑𝐴 = ‖⃑𝐴⃑𝐴⃑𝐴⃑𝐴,
- ⃑𝐴⋅⃑𝐵 = 0, если и только если ⃑𝐴 ⃑𝐴 ⃑𝐴 и ⃑𝐵 перпендикулярно,
- (⃑𝐴+⃑𝐵) ⋅⃑𝐶 = ⃑𝐴om⃑𝐶+⃑𝐴om⃑𝐶 (распределение),
- (𝑘⃑𝐴) ⋅⃑𝐵 = ⃑𝐴om (𝑘⃑𝐵) = 𝑘⃑𝐴om⃑𝐵, где 𝑘 реальное число.

Векторное умножение: скалярное произведение
С технической точки зрения скалярное произведение является своего рода скалярным произведением. Это означает, что это операция, которая берет два вектора и «умножает» их. вместе, и производит скаляр. Однако нам не нужен скалярный продукт двух векторы для получения любого скаляра. Было бы хорошо, если бы продукт мог предоставить значимой информации о векторах в терминах скаляров.
Что мы подразумеваем под «значимым»? Рад, что вы спросили. Для начала поищем скалярные величины, которые могут характеризовать вектор. Одним из простых примеров этого является длина , или величина вектора v , обычно обозначаемая | против |. Каждый из 2- и 3-мерных векторов, которые мы обсуждали, имеет длина, а длина является скалярной величиной. Например, чтобы найти длину вектор ( a , b , c ), нам просто нужно вычислить расстояние между началом координат и точка ( a , b , c ).
 (Идея та же самая в двух измерениях). Наше измерение
даст скалярное значение величины без направления — , а не другой
вектор! Этот тип скаляры звучит как вид значимой информации,
точечный продукт может предоставить нам.
(Идея та же самая в двух измерениях). Наше измерение
даст скалярное значение величины без направления — , а не другой
вектор! Этот тип скаляры звучит как вид значимой информации,
точечный продукт может предоставить нам.Компонентный метод
Теорема Пифагора говорит нам, что длина вектора ( а , б , в ) есть данный . Это дает нам представление о том, как мы можем определить скалярное произведение. Например, если нам нужно скалярное произведение вектора v = ( v 1 , v 2 , v 3 ) с собой ( v · v ) дать информацию о нас v , имеет смысл требовать, чтобы это выглядело так:
в · v = v 1 v 1 + v 2 v 2 + v 3 v 3 Следовательно, скалярное произведение вектора на самого себя дает величину вектора в квадрате.

Хорошо, это то, что мы хотели, но теперь царит новый вопрос: что такое точка произведение между двумя разными векторами? Важно помнить, что как бы мы ни определяли общее правило, оно должно сводиться к тому, когда мы подключаем два одинаковых вектора. На самом деле, @@Equation @@ уже написано наводя на размышления, чтобы указать, что общее правило для скалярного произведения между двумя векторов U = ( U 1 , U 2 , U 3 ) и v = ( V 57157157157157157157157157157915759тели1557157157157571571571549 . . 3 ) может быть:
u · v = u 1 v 1 + u 2 v 2 + u 3 v 3 Это уравнение точно соответствует формуле скалярного произведения двух Трехмерные векторы.
 (Обратите внимание, что количество, полученное справа, является скаляр, , хотя мы больше не можем сказать, что это представляет собой длину
either vector.) For 2-dimensional vectors, u = ( u 1 , u 2 ) and v = ( v 1 , v 2 ), мы
есть:
(Обратите внимание, что количество, полученное справа, является скаляр, , хотя мы больше не можем сказать, что это представляет собой длину
either vector.) For 2-dimensional vectors, u = ( u 1 , u 2 ) and v = ( v 1 , v 2 ), мы
есть:u · v = u 1 v 1 + u 2 v 2 Снова подставив u = v , мы восстановим квадрат длины вектора в двух измерениях.
Геометрический метод
Так что же дает скаляр, полученный при скалярном произведении u . v представляете? Мы можем получить представление о том, что происходит, взглянув на скалярное произведение вектора.
 с единичными векторами. В Unit Vectors мы определили единицу
векторы i , j и k для трехмерного случая. В двух измерениях мы имеем только i = (1, 0) и j = (0, 1). (Пока мы будем работать в двух измерениях, так как такие векторы легче представить графически.) Скалярные произведения вектора v = ( v 1 , v 2 ) с единичными векторами i и j определяются по формуле:
с единичными векторами. В Unit Vectors мы определили единицу
векторы i , j и k для трехмерного случая. В двух измерениях мы имеем только i = (1, 0) и j = (0, 1). (Пока мы будем работать в двух измерениях, так как такие векторы легче представить графически.) Скалярные произведения вектора v = ( v 1 , v 2 ) с единичными векторами i и j определяются по формуле:V · I = V 1 1 + V 2 0 = 0 = 8 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 8888 8888 8888 8888 88888. v · j = v 1 0 + v 5 9 591 5 9 5918 2 1087 2 Другими словами, скалярное произведение v с i выделяет компонент v в направлении x , и точно так же скалярное произведение на с на выделяет компонент на , лежащий в направлении на .
 Это
так же, как вычисление величины проекции v на оси x и y соответственно.
Это
так же, как вычисление величины проекции v на оси x и y соответственно.Это может показаться не слишком захватывающим, поскольку в некотором смысле мы уже знали об этом, как только как мы записали наш вектор с точки зрения компонентов. Но что было бы, если бы вместо компонентов нам были даны только направление и величина вектора и , как на следующем рисунке?
Рисунок %: Вектор v с длиной l и направлением, заданным углом θ .В этом случае, заметив образовавшиеся два прямоугольных треугольника и вспомнив правила из тригонометрии находим, что v · i и v · j можно вычислить по-другому. А именно:
v · i = | против | cos θ v · j = | против | sin θ = l cos(90 — θ ) Что произойдет, если мы возьмем скалярное произведение v с общим вектором, лежащим чисто в направлении x (т.
 е. не обязательно единичный вектор)? Мы можем написать
такой вектор как w = ( w 1 , 0) = w 1 (1, 0) = w 1 i , а
величина w | с | = ш 1 . Следовательно, w = | с | и . Используя приведенное выше правило
для скалярного произведения между v и i , находим, что:
е. не обязательно единичный вектор)? Мы можем написать
такой вектор как w = ( w 1 , 0) = w 1 (1, 0) = w 1 i , а
величина w | с | = ш 1 . Следовательно, w = | с | и . Используя приведенное выше правило
для скалярного произведения между v и i , находим, что:v · w = | против || с | cos θ На самом деле это уравнение в общем случае выполняется: если мы возьмем v и w произвольными векторы в двух или трех измерениях, и пусть θ будет углом между их, мы находим, что эта версия формулы скалярного произведения точно согласуется с формула компонента, которую мы нашли ранее.
Геометрически скалярное произведение v · w равно | против || с | cos θ .
Обратите внимание, что когда векторы лежат в одном направлении, θ = 0 и cos θ достигает своего максимального значения 1. (В частности, это случай то два вектора совпадают, что восстанавливает наше первоначальное требование для скалярный продукт: v · v = | против | 2 .) Фактически, для векторов одинаковой величины чем меньше угол между ними, тем больше будет их скалярное произведение. Это в этом смысле мы можем сказать, что скалярное произведение дает информацию о том, как во многом два вектора «перекрываются». Например, если два вектора перпендикулярны друг друга (т.е. они вообще не «перекрываются»), угол между ними равен 90 градусов. Поскольку cos 90 90 155 o 90 156 = 0, их скалярное произведение равно нулю.
Краткое изложение правил скалярного произведения
Таким образом, правила скалярных произведений 2- и 3-мерных векторов по компонентам это:
u · v = u 1 v 1 + u 2 v 2 u · v = u 1 v 1 + u 2 v 2 + u 3 v 3 Правило для векторов, заданных с точки зрения величины и направления (либо в 2 или 3 измерения), где θ обозначает угол между ними, составляет:
в · в = | против || с | cos θ Что такое скалярное произведение?
К
- Роберт Шелдон
Скалярное произведение, также называемое скалярным произведением, является мерой того, насколько точно совпадают два вектора с точки зрения направлений, которые они указывают.
 Мера представляет собой скалярное число (одно значение), которое можно использовать для сравнения двух векторов и понимания влияния изменения положения одного или обоих из них. Скалярный продукт получается путем выполнения математических расчетов векторных свойств.
Мера представляет собой скалярное число (одно значение), которое можно использовать для сравнения двух векторов и понимания влияния изменения положения одного или обоих из них. Скалярный продукт получается путем выполнения математических расчетов векторных свойств.Вектор — это величина, которая имеет как направление, так и величину (длину вектора). На рис. 1 показаны два вектора ( a и b ) на двумерной декартовой плоскости. Вектор a имеет величину 8 и расположен под углом 115 градусов к оси x (движется против часовой стрелки). Вектор b имеет звездную величину 10 и расположен под углом 45 градусов к оси x. Угол между двумя векторами, представленный греческой буквой тета (θ), составляет 70 градусов, что вычисляется путем вычитания 45 градусов из 115 градусов.
Рис. 1. Диаграмма, показывающая два вектора (a и b) на двумерной декартовой плоскости.Если известна величина двух векторов и угол между ними, легко вычислить скалярное произведение.
 Скалярный продукт представлен точкой между двумя векторными ссылками, в данном случае a и b , как показано в следующей формуле:
Скалярный продукт представлен точкой между двумя векторными ссылками, в данном случае a и b , как показано в следующей формуле:а • б
Полное уравнение для нахождения скалярного произведения несколько сложнее. Это влечет за собой умножение величины вектора a на величину вектора b , а затем произведение на косинус (cos) угла между векторами, как показано в следующем уравнении:
а • б = |а| × |б| × cos(θ)
Вертикальные полосы показывают, что эти значения являются модулями вектора. Иногда вместо одинарных стержней используются двойные стержни. Если значения с рисунка 1 подставить в уравнение, можно быстро вычислить скалярное произведение для этих двух векторов, как показано в следующем уравнении:0005
a • b = 8 × 10 × cos(70 градусов)
a • b = 8 × 10 × 0,342
a • b = 27,36Косинус угла округлен до трех знаков после запятой, поэтому конечный результат (27,36) является лишь приблизительным, хотя и близким.

Если величина двух векторов и угол между ними неизвестны, используйте следующую формулу для вычисления скалярного произведения:
a • b = (a 91 587 x 91 588 × b 91 587 x 91 588) + (a 91 587 y 91 588 × b 91 587 y 91 588)
Рис. 2. Диаграмма с добавлением длин векторов, отраженных на каждой оси, к рис. 1.В этом случае умножьте длины векторов, поскольку они проецируются на оси x и оси y декартовой плоскости. Чтобы лучше понять, как это работает, рассмотрите рис. 2, который был обновлен по сравнению с рис. 1, чтобы включить длины векторов, отраженные на каждой оси.
Vector a измеряет -3,4 по оси x и 7,3 по оси y. (Эти числа были округлены до одного десятичного знака в меньшую сторону.) Вектор b измеряет 7,1 по оси x и 7,1 по оси y. Для этого вектора измерения одинаковы по каждой оси, потому что вектор находится под углом 45 градусов. Эти суммы можно подставить в следующую новую формулу:
.
a • b = (a 91 587 x 91 588 × b 91 587 x 91 588 ) + (a 91 587 y 91 588 × b 91 587 y 91 588 )
a • b = (-3,4 × 7,1) + (7,3 × 7,1)
a • b = -24,12 + 51,83
а • b = 27,71Поскольку числа были округлены, окончательная цифра немного отличается от предыдущей (27,36), но они достаточно близки, чтобы продемонстрировать, как можно использовать два разных метода для вычисления скалярного произведения для пары векторов.
Аналогичный подход можно использовать для вычисления скалярного произведения векторов в трехмерном пространстве. Для этого измените формулу следующим образом, чтобы включить третье измерение (представленное осью Z):
a • b = (a x × b x ) + (a y × b y ) + (a z × b z )
Формула теперь включает в свои расчеты ось Z, но исходные компоненты остаются прежними. Чтобы проверить обновленную формулу, предположим, что оба вектора измеряют 5 по оси Z. Теперь расчеты будут выглядеть следующим образом:
a • b = -(3,4 × 7,1) + (7,3 × 7,1) + (5 x 5)
a • b = -24,12 + 51,83 + 25
a • b = 52,71Неудивительно, что скалярное произведение равно 52,71, что на 25 больше, чем 27,71 в предыдущем вычислении.
 Число 25 является результатом добавления компонента a z × b z (5 x 5) к уравнению для включения трехмерного пространства.
Число 25 является результатом добавления компонента a z × b z (5 x 5) к уравнению для включения трехмерного пространства.Скалярное произведение используется в таких областях, как физика, математика и другие области, способами, которые имеют практическое применение в реальном мире. Например, скалярное произведение можно использовать при установке солнечной панели на крыше. Сравнивая угол наклона солнца с углом панели, инженеры могут рассчитать наилучшее положение панели, чтобы максимизировать количество солнечной энергии, поглощаемой в течение дня.
См. также: Математические символы
Последнее обновление: октябрь 2022 г.
Продолжить чтение О точечном произведении (скалярном произведении)- 11 навыков работы с данными для машинного обучения и искусственного интеллекта
- 18 инструментов обработки данных, которые следует рассмотреть в 2022 году
- 8 лучших приложений для обработки данных и варианты использования для бизнеса
- Наука о данных, машинное обучение и искусственный интеллект: как они работают вместе
управление мобильными устройствами
Программное обеспечениедля управления мобильными устройствами (MDM) позволяет ИТ-администраторам контролировать, защищать и применять политики на смартфонах, планшетах и других конечных устройствах.

Сеть
- коаксиальный кабель
Коаксиальный кабель — это тип медного кабеля, специально изготовленного с металлическим экраном и другими компонентами, предназначенными для блокирования сигнала …
- мегагерц (МГц)
Мегагерц (МГц) — это множитель, равный одному миллиону герц (106 Гц). Герц — стандартная единица измерения частоты в …
- Стандарты беспроводной связи IEEE 802
IEEE 802 — это набор сетевых стандартов, которые охватывают спецификации физического уровня и уровня канала передачи данных для таких технологий, как…
Безопасность
- SOAR (организация безопасности, автоматизация и реагирование)
Управление безопасностью, автоматизация и реагирование, или SOAR, представляет собой набор совместимых программ, который позволяет организации.
 ..
.. - цифровая подпись
Цифровая подпись — это математический метод, используемый для проверки подлинности и целостности сообщения, программного обеспечения или цифрового…
- судо (су ‘делать’)
Sudo — это утилита командной строки для Unix и операционных систем на базе Unix, таких как Linux и macOS.
ИТ-директор
- хорошие навыки
Твердые навыки — это определенные способности, способности и наборы навыков, которыми человек может обладать и демонстрировать взвешенно.
- управление корпоративными проектами (EPM)
Управление корпоративными проектами (EPM) представляет собой профессиональные практики, процессы и инструменты, используемые для управления несколькими …
- Управление портфелем проектов: руководство для начинающих
Управление портфелем проектов — это формальный подход, используемый организациями для выявления, определения приоритетов, координации и мониторинга проектов .
 ..
..
HRSoftware
- пассивный кандидат
Пассивный кандидат (пассивный кандидат на работу) — это любой работник, который не ищет работу активно.
- проверка сотрудников
Проверка сотрудников — это процесс проверки, проводимый работодателями для проверки биографических данных и проверки информации о новом…
- Эффект хоторна
Эффект Хоторна — это изменение поведения участников исследования в ответ на их знание о том, что они …
Отдел обслуживания клиентов
- квалифицированный маркетолог лид (MQL)
Квалифицированный маркетолог (MQL) — это посетитель веб-сайта, уровень вовлеченности которого указывает на то, что он может стать клиентом.
- автоматизация маркетинга
Автоматизация маркетинга — это тип программного обеспечения, которое позволяет компаниям эффективно ориентироваться на клиентов с помощью автоматизированного маркетинга .

Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Угол между векторами Длина (модуль) вектора Координаты вектора. Направляющие косинусы Проекция вектора на ось
Направляющие косинусы Проекция вектора на ось
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Как ⭐ найти скалярное произведение векторов по координатам: теорема и доказательство
Физический смысл скалярного произведения
Распространенное понятие такое, как скалярное произведение обладает физическим смыслом. Его можно объяснить так, что работа А является результатом умножения силы F, которая производится постоянно во время движения тела, вектора а и составляющий с направлением силы F угол ϕ:
Его можно объяснить так, что работа А является результатом умножения силы F, которая производится постоянно во время движения тела, вектора а и составляющий с направлением силы F угол ϕ:
A=∣F∣·∣a∣=∣F∣·∣a∣·cosϕ
В качестве презентации введенного понятия рассмотрим рисунок:
Источник: matematicus.ru
На рисунке изображены следующие величины, с которыми можно часто встретиться в классе на уроках алгебры, геометрии и физики при рассмотрении различных теорем и доказательств:
В качестве примера разберем простую задачу. Предположим, что имеется два вектора а и b с длинами 3 м и 2 м соответственно. Угол между этими векторами составляет 120 градусов. Требуется определить, чему равно скалярное произведение этих векторов.
Решение будет выглядеть следующим образом:
a·b=∣a∣·∣b∣·cos(ϕ)=3·2·cos(120)=−3м2
Основные определения
Определение 1Системой координат называют метод определения положения и перемещения точки или тела с использованием чисел и других символов.
Определение 2Координаты представляют собой совокупность чисел, определяющих положение некого объекта относительно прямой, плоскости, поверхности, либо пространства.
Определение 3Скаляр является величиной, полностью определяемой в какой-либо системе координат с помощью одного числа или функции.
Определение 4Вектор является направленным отрезком прямой, для которого известны точки начала и конца.
Если вектор начинается в точке А, а заканчивается в точке В, то его обозначают, как AB→. Допускается обозначение вектора с помощью малых латинских букв, над которыми изображены стрелочки или черточки, к примеру, a→.
Определение 5Скалярное произведение пары векторов a¯ и b¯, отличных от нуля, представляет собой число, равное произведению длин данных векторов на косинус угла между ними:
a¯b¯=a¯·b¯=(a¯,b¯)=|a¯||b¯|cos(a¯,b¯)
Пример 2Рассмотрим типичный пример. Требуется продемонстрировать, как будет вычисляться скалярное произведение векторов a¯ и b¯. Данные векторы обладают длинами 2 и 3 соответственно, а разделяет их угол в 60°.
Требуется продемонстрировать, как будет вычисляться скалярное произведение векторов a¯ и b¯. Данные векторы обладают длинами 2 и 3 соответственно, а разделяет их угол в 60°.
Запишем условие задания:
|a¯|=2
|b¯|=3
(a¯,b¯)
В результате:
a¯·b¯=(a¯,b¯)=2·3·cos60°=6·12=3
Примечание 1Особым случаем является равенство какого-либо из векторов a¯ или b¯ нулевому вектору. Тогда (a¯,b¯)=0.
Скалярное произведение пары векторов характеризуется следующими свойствами:
Формулы скалярного произведения векторов заданных координатами
Формула 1В том случае, когда векторы a¯ и b¯ характеризуются координатами:
a¯=a1;a2;a3,
b¯=b1;b2;b3
Скалярное произведение данных векторов модно определить с помощью следующей формулы:
(a¯,b¯)=a1b1+a2b2+a3b3
Определение 6Скалярным произведением векторов, которые заданы собственными координатами, называют сумму произведений соответствующих им координат.
Пример 3Рассмотрим пример. Попробуем определить скалярное произведение двух векторов с координатами:
a¯=(3;-1)
b¯=(-2;7)
Воспользуемся уже знакомой формулой:
a¯b¯=3·(-2)+(-1)·7=-6-7=-13
Формула 2Определить, какой длиной обладает вектор a¯=a1;a2;a3 с собственными координатами, можно с помощью формулы:
|a¯|=a12+a22+a32
Определение 7Длина, или модуль вектора с заданными собственными координатами является корнем квадратным из суммы квадратов координат.
Рассмотрим типичный пример. Представим, что требуется найти длину вектора с заданными координатами:
a¯=(-4;3)
Воспользуемся записанной выше формулой и получим:
|a¯|=(-4)2+32=16+9=25=5
Формула 3Формула для расчета угла, который разделяет два вектора a¯=a1;a2;a3,b¯=b1;b2;b3:
cos(a¯,b¯)=(a¯;b¯)|a¯|·|b¯|=a1b1+a2b2+a3b3a12+a22+a32·b12+b22+b32
Пример 5Постараемся решить задачу. Требуется вычислить угол, расположенный между двух векторов a¯=(1;3)иb¯=(1;0).
Воспользуемся записанной формулой и выполним вычисления:
cos(a¯,b¯)=1·1+3·012+(3)2·12+02=12
(a¯,b¯)=arccos12=60°
Примеры задач на вычисление скалярного произведения векторов
Задача 1Даны два вектора с определенными координатами, скалярное произведение которых требуется вычислить:
a¯=(-1;2) и b¯=(2;1)
Решение
Заметим, что для векторов указаны координаты. Применим соответствующую формулу. В процессе выполним умножение соответствующих координат и найдем их сумму:
(a¯,b¯)=-1·2+2·1=-2+2=0
В итоге произведение обладает нулевым значением.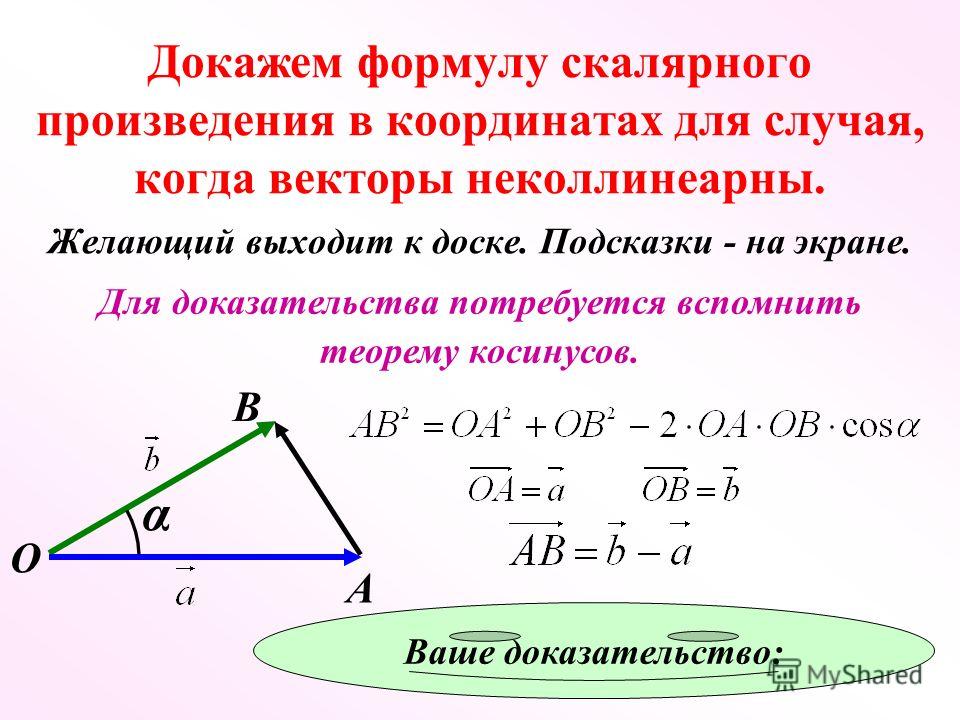 Данный результат означает, что векторы расположены перпендикулярно относительно друг друга, или являются ортогональными. Запишем ответ.
Данный результат означает, что векторы расположены перпендикулярно относительно друг друга, или являются ортогональными. Запишем ответ.
Ответ: (a¯,b¯)=0
Задача 2В пространстве задана пара векторов, которые имеют определенное в нем начало и конец:
A = (1;3;-2), B = (-1;4;1), C = (2; 1; -2)
Необходимо вычислить, чему равно скалярное произведение векторов AB¯ и AC¯.
Решение
В данном случае не получится найти скалярное произведение векторов, так как имеются лишь заданные в условии точки. По этой причине сначала следует определить непосредственно сами векторы AB¯ и AC¯. Для этого вычислим разность конца и начала каждого вектора, то есть найдем разность соответствующих координат данных точек:
AB¯=(-1-1;4-3;1-(-2))=(-2;1;3)
AC¯=(2-1;1-3;-2-(-2))=(1;-2;0)
Далее можно приступать к вычислению скалярного произведения найденных векторов:
(AB¯,AC¯)=-2·1+1·(-2)+3·0=-2-2+0=-4
Ответ: (AB¯,AC¯)=-4
Задача 3Даны вектора, скалярное произведение которых требуется определить:
a¯=-1; 2; 3, b¯=2; 0; -1.
Решение
Воспользуемся уже знакомой формулой, согласно которой скалярное произведение пары векторов соответствует сумме произведений их координат, которые определены:
a¯, b¯=-1·2+2·0+3·-1=-2+0-3=-5
Ответ: a¯, b¯=-5.
Задача 4Дана пара векторов:
a¯=x; -1 и b¯=3; 2
Необходимо вычислить такие значения х, при которых записанные векторы являются ортогональными, то есть векторы расположены перпендикулярно по отношению друг к другу.
Решение
Условие задачи, то есть ортогональность заданных векторов, выполняется лишь в том случае, когда скалярное произведение этих векторов обладает нулевым значением. Найдем его по уже известной формуле:
a¯·b¯=x·3+-1·2=3x-2=0⇒3x=2⇒x=23
Ответ: x=23
Задача 5Дан некий треугольник с равными друг другу сторонами ∆ABC. Длины его сторон составляют 1. Требуется определить, чему равно:
AB→·BC→+BC→·CA→+CA→·AB→
Решение
Ответ: =-32
Задача 6Имеется пара векторов, которые являются неколлинеарными:
a и b
Нужно определить вектор x, который будет компланарен заданным векторам a и b, а также соответствует следующей системе уравнений:
Решение
Заметим, что в том случае, когда вектора a и b являются неколлинеарными, данные вектора составляют базис относительно плоскости. Какой-либо компланарный вектор для данных векторов допустимо представить в следующем виде:
Какой-либо компланарный вектор для данных векторов допустимо представить в следующем виде:
x=λa+μb
Используя записанное соотношение, изменим вид начальной системы из условий задачи:
Найдем решения записанной системы:
В результате получим нужный вектор:
x=(b·b)a+(a·b)b(a·a)(b·b)-(a·b)2
Ответ: x=(b·b)a+(a·b)b(a·a)(b·b)-(a·b)2
Задача 7Имеется некий параллелограмм OACB. Для этой геометрической фигуры предусмотрены следующие параметры:
длина |OA|=a
длина |OB|=b
угол ∠AOB=α
Необходимо найти, чему равна длина d диагонали OC параллелограмма, а также определить значение косинусов углов, которые расположены между диагональю и сторонами параллелограмма.
Решение
Заметим, что:
OC→=OA→+OB→
В результате длина диагонали составит:
Углы, которые разделяют диагональ и стороны параллелограмма, можно вычислить таким образом:
Ответ: a2+b2+2abcosα,a+bcosαa2+b2+2abcosα,acosα+ba2+b2+2abcosα.
Скалярный продукт двух векторов
Вектор — это величина, которая имеет как величину, так и направление. Над векторами можно выполнять некоторые математические операции, такие как сложение и умножение. Умножение векторов можно выполнить двумя способами, т. е. скалярным произведением на и перекрестным произведением. В этой статье вы узнаете скалярное произведение двух векторов с помощью примеров.
Над векторами можно выполнять некоторые математические операции, такие как сложение и умножение. Умножение векторов можно выполнить двумя способами, т. е. скалярным произведением на и перекрестным произведением. В этой статье вы узнаете скалярное произведение двух векторов с помощью примеров.
Определение скалярного произведения можно дать двумя способами, то есть алгебраически и геометрически. Алгебраически скалярный продукт определяется как сумма произведений соответствующих записей двух последовательностей чисел. Геометрически это произведение евклидовых величин двух векторов и косинуса угла между ними. Оба определения эквивалентны при работе с декартовыми координатами. Тем не менее, скалярное произведение двух векторов — это произведение величины двух векторов и cos угла между ними. Напомним, что векторы умножаются двумя способами
. Разница между обоими методами заключается лишь в том, что при использовании первого метода мы получаем в качестве результата скалярное значение, а при использовании второго метода полученное значение снова является вектором по своей природе.
Скалярное произведение двух векторов a и b величины |a| и |б| задается как |a||b| cos θ, где θ представляет собой угол между векторами a и b , взятый в направлении векторов.
Мы можем выразить скалярное произведение как:
а.б=|а||б| cosθ
, где |а| и |б| представляют величину векторов a и b , тогда как cos θ обозначает косинус угла между обоими векторами, а a.b указывает скалярное произведение двух векторов.
В случае, когда любой из векторов равен нулю, угол θ не определяется и в таком сценарии a.b задается равным нулю.
Проекция векторов
Известно, что BP является проекцией вектора a на вектор b в направлении вектора 9.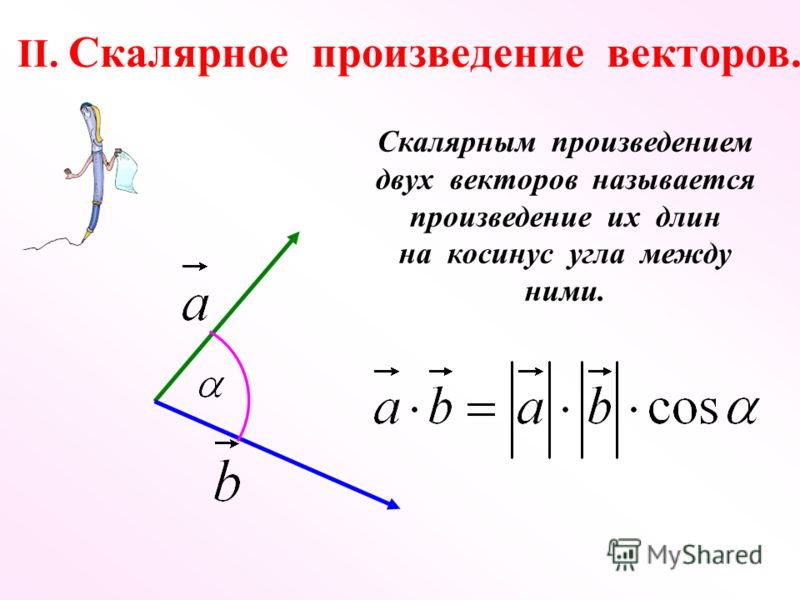 0007 b определяется как |a| потому что θ.
0007 b определяется как |a| потому что θ.
Аналогично, проекция вектора b на вектор a в направлении вектора a определяется выражением |b| потому что θ.
Проекция вектора a в направлении вектора b выражается как
\(\begin{массив}{l} BP = \frac{a.b}{|b|}\end{массив} \)
\(\begin{array}{l}\Rightarrow \overrightarrow{BP} = \frac{a.b}{|b|} × \hat{b}\end{array} \) 92}б\конец{массив} \)
Аналогично, проекция вектора b в направлении вектора a выражается как
\(\begin{array}{l}BQ = \frac{a.b}{|a|}\end{array} \)
\(\begin{array}{l}\Rightarrow \overrightarrow{BQ} = \frac{a.b}{|a|} \times \hat{a}\end{array} \)
\(\begin{array}{l}\Rightarrow \overrightarrow{BQ} = \frac{a.b}{|a|} \frac{a}{|a|}\end{array} \)
\(\begin{array}{l}\Rightarrow \overrightarrow{BQ} = \frac{a. 2}a\end{array} \)
2}a\end{array} \)
Таким образом, мы видим, что скалярное произведение двух векторов есть произведение модуля одного вектора на разрешенную составляющую другого в направлении первого вектора.
Свойства скалярного произведения вектора:
\(\begin{array}{l}\Rightarrow a_1b_1 + a_2b_2 + a_3b_3 = ab\ cos\theta\end{массив} \)
Также проверьте: Векторный продукт
Скалярное произведение двух векторов Примеры вопросов
Пример 1: Пусть есть два вектора [6, 2, -1] и [5, -8, 2]. Найдите скалярное произведение векторов.
Найдите скалярное произведение векторов.
Решение:
Даны векторы: [6, 2, -1] и [5, -8, 2] равны a и b соответственно.
а.б = (6)(5) + (2)(-8) + (-1)(2)
а.б = 30 – 16 – 2
а.б = 12
Пример 2: Пусть есть два вектора |a|=4 и |b|=2 и θ = 60°. Найдите их скалярное произведение.
Решение:
a.b = |a||b|cos θ
a.b = 4,2 cos 60°
аб = 4,2 × (1/2)
а.б = 4
линейная алгебра — Какая польза от скалярного произведения двух векторов?
спросил
Изменено 6 месяцев назад
Просмотрено 60 тысяч раз
$\begingroup$
Предположим, у вас есть два вектора a и b , из которого вы хотите получить скалярное произведение, теперь это делается довольно просто, беря каждую соответствующую координату каждого вектора, перемножая их, а затем складывая результат вместе. В конце выполнения нашей операции у нас остается постоянное число.
В конце выполнения нашей операции у нас остается постоянное число.
Мой вопрос, поэтому, что мы можем сделать с этим числом, почему мы, так сказать, вычисляем его? Я имею в виду, что это кажется мне почти бесполезным по сравнению с перекрестным произведением двух векторов (где вы получаете фактический вектор).
$\endgroup$
3
$\begingroup$
Re: «[точечный продукт] кажется мне почти бесполезным по сравнению с векторным произведением двух векторов».
См. статью Википедии о скалярном произведении, чтобы узнать больше о значении скалярного произведения и графических изображениях, которые помогают визуализировать значение скалярного произведения (в частности, геометрическую интерпретацию). Кроме того, вы узнаете больше о том, как он используется. Например, прокрутите вниз до «Физики» (в связанной записи), чтобы прочитать некоторые из ее применений: 9T.\;$
Например, прокрутите вниз до «Физики» (в связанной записи), чтобы прочитать некоторые из ее применений: 9T.\;$
Но скалярное произведение также имеет эквивалентное геометрическое определение :
В евклидовом пространстве евклидов вектор — это геометрический объект, обладающий как величиной, так и направлением. Вектор можно изобразить в виде стрелки. Его величина — это его длина, а его направление — это направление, на которое указывает стрелка. Величина вектора A обозначается $\|\mathbf{A}\|.$ Скалярное произведение двух евклидовых векторов A и B определяется как
$$\mathbf A\cdot\mathbf B = \|\mathbf A\|\,\|\mathbf B\|\cos\theta,\quad\text{где $\theta$ — угол между $A $ и $B.$} \tag{1}$$
С помощью $(1)$, например, мы видим, что можем вычислить (определить) угол между двумя векторами, зная их координаты: $$\cos \theta = \frac{\mathbf A\cdot\mathbf B}{\|\mathbf A\|\,\|\mathbf B\|}$$
$\endgroup$
6
$\begingroup$
Первоначальная мотивация геометрическая: скалярное произведение можно использовать для вычисления угла $\alpha$ между двумя векторами $a$ и $b$:
$a\cdot b=|a|\cdot|b|\cdot \cos(\alpha)$.
Обратите внимание, что знак этого выражения зависит только от косинуса угла, поэтому скалярное произведение равно
Другой важный частный случай появляется, когда $a=b$: Корень скалярного произведения вектора с самим собой имеет длину 92$.
Есть еще одно интересное применение скалярного произведения в сочетании с перекрестным произведением: если у вас есть три вектора $a$, $b$ и $c$, они определяют параллелепипед, и вы можете вычислить его (со знаком) объем $V$ следующим образом, используя так называемое скалярное тройное произведение:
$V=(a\times b)\cdot c$
(Обратите внимание, что это обобщение $|a\times b|$ площадь параллелограмма, заданного $a$ и $b$.)
$\endgroup$
4
$\begingroup$
Прежде чем ответить на ваш вопрос, я хочу сказать, что это очень хороший вопрос, и вы правы, ожидая, что точечный продукт имеет смысл/значение.
Во-первых, важно думать о векторах отдельно от их координат. Хотя верно то, что мы часто представляем векторы как серию координат вдоль четко определенных осей, это делается исключительно из вычислительных соображений. Вектор как идея «существует» в пространстве без какой-либо предопределенной системы координат. Я говорю это, потому что существует два определения скалярного произведения, одно из которых равно 9.0262 без координат (т. е. $\mathbf a\cdot\mathbf b = \|\mathbf a\|\,\|\mathbf b\|\cos\theta$), а другой основан на координатах (т. a\cdot\mathbf b = \sum_i{a_i b_i}$). Из этих двух скалярное произведение лучше всего рассматривать с точки зрения первого, поскольку оно не зависит от системы координат. (Относительно легко показать, что последнее может быть получено из первого, но в этом выводе есть неявное предположение, что система координат, используемая для представления скалярного произведения, равна ортогональный .)
Во-вторых, учитывая бескоординатное определение, фундаментальная идея скалярного произведения состоит в том, что проекция . Тем самым он дает единственное число, которое указывает компонент вектора в направлении другого вектора. Ваше наблюдение о несхожести между точечным и перекрестным произведением 90 262 является 90 263 правильным, однако скалярное произведение 90 262 также используется для создания вектора 90 263, оно просто делает это покомпонентно. Предположим, что у нас есть вектор $\mathbf v$, представленный своими компонентами в заданной системе координат. Далее предположим, что у нас есть ортонормированный базис, определенный в той же системе координат, что и набор вектор-столбцов $\{\mathbf u_1, \mathbf u_2, \ldots, \mathbf u_n\}$. Наконец, предположим, что мы хотим представить $\mathbf v$ в этом базисе как $\mathbf w$. Вопрос в том, как мы это делаем? Конечно, мы используем скалярное произведение! Таким образом, первый компонент $\mathbf w$ будет тогда $w_1 = \mathbf u_1\cdot \mathbf v$, а второй компонент будет $w_2 = \mathbf u_2\cdot \mathbf v$ и так далее. (Обратите внимание, что поскольку $\|\mathbf u_i\| = 1$, мы имеем $\mathbf u_1\cdot \mathbf v= \|\mathbf v\|\cos\theta_i$.
Тем самым он дает единственное число, которое указывает компонент вектора в направлении другого вектора. Ваше наблюдение о несхожести между точечным и перекрестным произведением 90 262 является 90 263 правильным, однако скалярное произведение 90 262 также используется для создания вектора 90 263, оно просто делает это покомпонентно. Предположим, что у нас есть вектор $\mathbf v$, представленный своими компонентами в заданной системе координат. Далее предположим, что у нас есть ортонормированный базис, определенный в той же системе координат, что и набор вектор-столбцов $\{\mathbf u_1, \mathbf u_2, \ldots, \mathbf u_n\}$. Наконец, предположим, что мы хотим представить $\mathbf v$ в этом базисе как $\mathbf w$. Вопрос в том, как мы это делаем? Конечно, мы используем скалярное произведение! Таким образом, первый компонент $\mathbf w$ будет тогда $w_1 = \mathbf u_1\cdot \mathbf v$, а второй компонент будет $w_2 = \mathbf u_2\cdot \mathbf v$ и так далее. (Обратите внимание, что поскольку $\|\mathbf u_i\| = 1$, мы имеем $\mathbf u_1\cdot \mathbf v= \|\mathbf v\|\cos\theta_i$. ) Если затем мы подумаем о векторе $ \mathbf w$ определены как таковые, мы имеем 9T\mathbf v$$
) Если затем мы подумаем о векторе $ \mathbf w$ определены как таковые, мы имеем 9T\mathbf v$$
Наконец, мы заключаем, что скалярное произведение играет ключевую роль в преобразовании вектора из одного базиса в другое и что скалярное произведение скрыто в определении умножения матриц в этом одно из представлений о матрично-векторном произведении состоит в том, что каждый элемент произведения представляет собой скалярное произведение между строкой слева и столбцом справа.
Надеюсь, это поможет.
$\endgroup$
1
$\begingroup$
Скалярный продукт является важным ингредиентом матричного продукта. Произведение двух матриц $A$ и $B$ (совместимых размеров, т. е. число столбцов матрицы $A$ равно числу строк матрицы $B$) представляет собой матрицу, $(i, j)$ которой является скалярным произведением $i$-й строки таблицы $A$ и $j$-го столбца таблицы $B$. {t}$ имеет в своей позиции $(i, j)$ количество студентов, принимающих как $c_{i}$, так и $c_{j}$.
{t}$ имеет в своей позиции $(i, j)$ количество студентов, принимающих как $c_{i}$, так и $c_{j}$.
Эта матрица, конечно, полезна при составлении расписания занятий.
$\endgroup$
$\begingroup$
Геометрическая идея скалярного произведения была затронута, но есть обширное обобщение этого произведения в геометрической алгебре , алгебре не только ориентированных линий (векторов), но плоскостей, объемов и т. д. (называемых лезвиями). ).
В геометрической алгебре у нас есть обобщенное скалярное произведение вектора $a$ и другого лезвия $B$, обозначаемое $a \cdot B$. Это произведение имеет простую геометрическую интерпретацию как часть $B$, ортогональная проекции $a$, с величиной $|a||B|| \cos \theta|$, где $\theta$ угол $a$ образует со своей проекцией в $B$.
(Примечание: на самом деле $a \cdot B$ также ортогонален $a$, не только его проекция в $B$, но размышление об этом приводит к некоторым трудностям, а размышление о том, что перпендикулярно проекции нет. )
)
Если $B$ является 2-лопастным (также называемым бивектором ), то вы должны быть в состоянии представить это непосредственно: если $a$ целиком лежит в $B$, то $a \ cdot B$ — это просто вектор, перпендикулярный $a$ в $B$. Если $a$ не лежит целиком в $B$, то его можно разложить на касательную и нормальную части. Мы отбрасываем нормальную часть, и к тангенциальной части применяется предыдущая логика.
Если $B$ является трехмерным лезвием (тривектором), то в трехмерном пространстве $a$ должно лежать в $B$ (поскольку не существует трехмерного объема, который не может быть охвачен вектором), и произведение $a \cdot B$ — это «двойственная по Ходжем» плоскость, перпендикулярная $a$.
В этом свете скалярное произведение векторов может оказаться наиболее неинтуитивной частью этого рассуждения. Когда вы берете скалярное произведение, остается только скаляр — не остается вектора или другого многомерного объекта, который был бы ортогонален $a$. Опять же, именно поэтому я подчеркиваю, что $a \cdot B$ — это часть $B$, ортогональная проекция $a$ на $B$.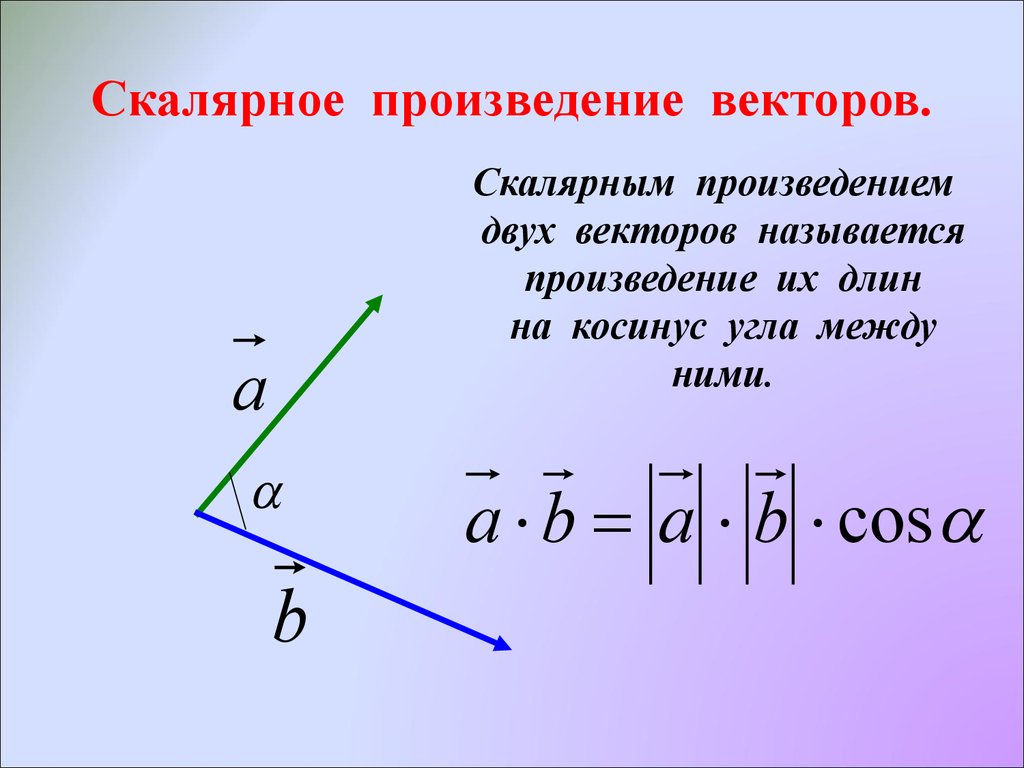 Когда $B$ является вектором, ясно, что нет другого вектора или чего-то еще, что могло бы быть ортогональным проекции $a$, поскольку $B$ и эта проекция параллельны, поэтому результат обязательно будет просто скаляром.
Когда $B$ является вектором, ясно, что нет другого вектора или чего-то еще, что могло бы быть ортогональным проекции $a$, поскольку $B$ и эта проекция параллельны, поэтому результат обязательно будет просто скаляром.
$\endgroup$
$\begingroup$
Когда вычисляют A.B , происходят два измерения: измерение того, насколько мал угол между ними, и как долго A и Б ар. AB в основном означает длину проекции A на B , при этом эта длина масштабируется на абсолютную длину B .
Один из способов интерпретации скалярного произведения состоит в том, чтобы подумать, как максимизировать или минимизировать скалярное произведение между двумя векторами. Предположим, мы пытаемся максимизировать скалярное произведение между двумя векторами, которые мы можем изменить:
Скалярное произведение будет увеличиваться по мере уменьшения угла между двумя векторами. Скалярный продукт A.B также будет увеличиваться по мере увеличения абсолютных длин A и B . Это связано с тем, что по мере того, как A становится больше, его проекционная длина будет больше, а по мере увеличения длины B масштабирование проекции A будет увеличиваться, учитывая, что B абсолютная длина будет действовать как скейлер длины проекции A .
Скалярный продукт A.B также будет увеличиваться по мере увеличения абсолютных длин A и B . Это связано с тем, что по мере того, как A становится больше, его проекционная длина будет больше, а по мере увеличения длины B масштабирование проекции A будет увеличиваться, учитывая, что B абсолютная длина будет действовать как скейлер длины проекции A .
Следовательно, в задачах, где желательно максимизировать или минимизировать размер векторов и минимизировать отклонение или угол между ними, может быть полезно количественное определение с помощью скалярного произведения.
$\endgroup$
$\begingroup$
Я не вижу здесь достаточно простых английских ответов, если честно. Один простой пример: в стелс-игре вы можете определить, находится ли объект в пределах 90-градусной прямой видимости чего-либо или нет.
$\endgroup$
12.3: Скалярный продукт — Математика LibreTexts
Цели обучения
Если мы прикладываем силу к объекту, чтобы объект двигался, мы говорим, что сила совершает работу. Раньше мы рассматривали постоянную силу и предполагали, что сила приложена в направлении движения объекта. В этих условиях работу можно выразить как произведение силы, действующей на объект, и расстояния, которое этот объект перемещает. Однако в этой главе мы увидели, что и сила, и движение объекта могут быть представлены векторами.
В этом разделе мы разработаем операцию, называемую скалярным произведением, которая позволяет вычислить работу в случае, когда вектор силы и вектор движения имеют разные направления. Скалярное произведение, по сути, говорит нам, какая часть вектора силы приложена в направлении вектора движения. Скалярное произведение также может помочь нам измерить угол, образованный парой векторов, и положение вектора относительно осей координат. Он даже обеспечивает простой тест, чтобы определить, пересекаются ли два вектора под прямым углом.
Скалярный продукт и его свойства
Мы уже научились складывать и вычитать векторы. В этой главе мы исследуем два типа умножения векторов. Первый тип векторного умножения называется скалярным произведением, основанным на обозначениях, которые мы для него используем, и определяется следующим образом:
В этой главе мы исследуем два типа умножения векторов. Первый тип векторного умножения называется скалярным произведением, основанным на обозначениях, которые мы для него используем, и определяется следующим образом:
Определение: скалярное произведение
скалярное произведение векторов \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) и \(\vecs{ v}=⟨v_1,v_2,v_3⟩\) задается суммой произведений компонент
\[\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3. \nonumber \]
Обратите внимание, что если \(u\) и \(v\) являются двумерными векторами, скалярное произведение вычисляется аналогичным образом. Таким образом, если \(\vecs{ u}=⟨u_1,u_2⟩\) и \(\vecs{ v}=⟨v_1,v_2⟩,\), то
\[\vecs{ u}⋅\vecs{ v }=u_1v_1+u_2v_2. \nonumber \]
Когда два вектора объединяются при сложении или вычитании, результатом является вектор. Когда два вектора объединяются с помощью скалярного произведения, результатом является скаляр. По этой причине скалярное произведение часто называют числом 9. 0262 скалярное произведение. Его также можно назвать внутренним продуктом .
0262 скалярное произведение. Его также можно назвать внутренним продуктом .
Пример \(\PageIndex{1}\): вычисление скалярных произведений
Раствор :
а. Подставляем компоненты вектора в формулу скалярного произведения:
\[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &=3(−1)+5(3)+2(0) \\[4pt] &=−3+15+0 \\[4pt] &=12. \end{выравнивание*}\]
б. Расчет такой же, если векторы записываются с использованием стандартных единичных векторов. У нас все еще есть три компонента для каждого вектора, которые нужно подставить в формулу скалярного произведения:
\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=p_1q_1+p_2q_2+p_3q_3 \\[4pt ] &=10(−2)+(−4)(1)+(7)(6) \\[4pt] &=−20−4+42 \\[4pt] &=18. \end{align* }\]
\end{align* }\]
Упражнение \(\PageIndex{1}\)
Найдите \(\vecs{ u}⋅\vecs{ v}\), где \(\vecs{ u}=⟨2,9,−1⟩\) и \(\vecs{v}=⟨−3,1,−4⟩.\)
Подобно сложению и вычитанию векторов, скалярное произведение имеет несколько алгебраических свойств. Мы докажем три из этих свойств, а остальные оставим в качестве упражнений.
Свойства скалярного произведения
Пусть \(\vecs{ u}\), \(\vecs{ v}\) и \(\vecs{ w}\) — векторы, и пусть \(c\) быть скаляром.
Доказательство
Пусть \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) и \(\vecs{ v}=⟨v_1,v_2,v_3⟩. \) Тогда
\) Тогда
\[ \begin{ выровнять*} \vecs{ u}⋅\vecs{ v} &=⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &= v_1u_1+v_2u_2+v_3u_3 \\[4pt] &= ⟨v_1,v_2,v_3⟩⋅⟨u_1,u_2,u_3⟩ \\[4pt] &=\vecs{ v}⋅\vecs{ u}.\end{align *}\]
Ассоциативное свойство похоже на ассоциативное свойство для умножения действительных чисел, но обратите особое внимание на разницу между скалярными и векторными объектами:
\[ \begin{align*} c(\vecs{ u}⋅\vecs{ v}) &=c(u_1v_1+u_2v_2+u_3v_3) \\[4pt] &=c(u_1v_1)+c(u_2v_2) +c(u_3v_3) \\[4pt] &=(cu_1)v_1+(cu_2)v_2+(cu_3)v_3 \\[4pt] &=⟨cu_1,cu_2,cu_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt ] &=c⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=(c\vecs{ u})⋅\vecs{ v}.\end{align*}\]
Доказательство того, что \(c(\vecs{ u}⋅\vecs{ v})=\vecs{ u}⋅(c\vecs{ v})\), аналогично.
Четвертое свойство показывает связь между величиной вектора и его скалярным произведением на самого себя: 92.\end{align*}\]
□
Обратите внимание, что определение скалярного произведения дает \(\vecs{ 0}⋅\vecs{ v}=0. \) По свойству iv. если \(\vecs{ v}⋅\vecs{ v}=0,\), то \(\vecs{ v}=\vecs{ 0}.\)
\) По свойству iv. если \(\vecs{ v}⋅\vecs{ v}=0,\), то \(\vecs{ v}=\vecs{ 0}.\)
Пример \(\PageIndex{2}\): Использование Свойства скалярного произведения
Пусть \(\vecs{ a}=⟨1,2,−3⟩\), \(\vecs{ b}=⟨0,2,4⟩\) и \(\vecs { c} =⟨5,−1,3⟩\).
Найдите каждый из следующих продуктов.
Раствор
а. Обратите внимание, что это выражение запрашивает скалярное число, кратное \(\vecs{ c}\) на \(\vecs{ a}⋅\vecs{ b}\):
\[ \begin{align*} (\vecs{ a}⋅\vecs{ b})\vecs{ c} &=(⟨1,2,−3⟩⋅⟨0,2,4⟩)⟨5,−1,3⟩ \\[4pt] &=( 1(0)+2(2)+(−3)(4))⟨5,−1,3⟩ \\[4pt] &=−8⟨5,−1,3⟩ \\[4pt] &= ⟨−40,8,−24⟩.\end{align*}\]
б. Это выражение представляет собой скалярное произведение вектора \(\vecs{ a}\) и скаляра, кратного 2\(\vecs{ c}\):
\[ \begin{align*} \vecs{ a}⋅(2\ vecs{ c}) &=2(\vecs{a}⋅\vecs{c}) \\[4pt] &=2(⟨1,2,−3⟩⋅⟨5,−1,3⟩) \\ [4pt] &=2(1(5)+2(-1)+(-3)(3)) \\[4pt] &=2(-6)=-12. \end{align*}\] 92=53\)
\end{align*}\] 92=53\)
Использование скалярного произведения для нахождения угла между двумя векторами
Когда два ненулевых вектора помещаются в стандартное положение в двух или трех измерениях, они образуют между собой угол (рис. \(\PageIndex{1}\) ). Скалярное произведение позволяет найти меру этого угла. Это свойство является результатом того факта, что мы можем выразить скалярное произведение через косинус угла, образованного двумя векторами.
Рисунок \(\PageIndex{1}\): Пусть \(θ\) — угол между двумя ненулевыми векторами \(\vecs{ u}\) и \(\vecs{ v}\), такой, что \(0≤θ≤π\).Вычисление скалярного произведения
Скалярное произведение двух векторов — это произведение величины каждого вектора на косинус угла между ними:
\[\vecs{ u}⋅\vecs{ v}=‖\ vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{evaldot} \]
Доказательство
Поместите векторы \(\vecs{ u}\) и \(\vecs{ v}\) в стандартное положение и рассмотрим вектор \(\vecs{ v}−\vecs { u}\) (Рисунок \(\PageIndex{2}\)). Эти три вектора образуют треугольник с длинами сторон \(‖\vecs{ u}‖,‖\vecs{ v}‖\) и \(‖\vecs{ v}−\vecs{ u}‖\). 92−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] −2\vecs{ u}⋅\vecs{ v} &=−2‖\vecs{ u}‖‖ \vecs{ v}‖\cos θ \\[4pt] \vecs{ u}⋅\vecs{ v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \end{align*}\]
Эти три вектора образуют треугольник с длинами сторон \(‖\vecs{ u}‖,‖\vecs{ v}‖\) и \(‖\vecs{ v}−\vecs{ u}‖\). 92−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] −2\vecs{ u}⋅\vecs{ v} &=−2‖\vecs{ u}‖‖ \vecs{ v}‖\cos θ \\[4pt] \vecs{ u}⋅\vecs{ v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \end{align*}\]
□
Мы можем использовать форму скалярного произведения в уравнении \ref{evaldot}, чтобы найти меру угла между двумя ненулевыми векторами, перестроив уравнение \ref{evaldot} для решения для косинуса угла:
\[\cos θ=\dfrac{\vecs{u}⋅\vecs{v}}{‖\vecs{u}‖‖\vecs{v}‖}. \метка{точка2} \]
Используя это уравнение, мы можем найти косинус угла между двумя ненулевыми векторами. Поскольку мы рассматриваем наименьший угол между векторами, мы предполагаем \(0°≤θ≤180°\) (или \(0≤θ≤π\), если мы работаем в радианах). Арккосинус уникален в этом диапазоне, поэтому мы можем определить меру угла \(θ\).
Пример \(\PageIndex{3}\): нахождение угла между двумя векторами
Найдите меру угла между каждой парой векторов. 2}} \\[4pt] &=\dfrac{-2}{\sqrt{3}\sqrt{14}} =\ dfrac{−2}{\sqrt{42}}. \end{выравнивание*}\] 92}} \\[4pt] &=\dfrac{0}{\sqrt{65}\sqrt{36}}=0.\end{align*}\]
2}} \\[4pt] &=\dfrac{-2}{\sqrt{3}\sqrt{14}} =\ dfrac{−2}{\sqrt{42}}. \end{выравнивание*}\] 92}} \\[4pt] &=\dfrac{0}{\sqrt{65}\sqrt{36}}=0.\end{align*}\]
Теперь \(\cos θ=0\ ) и \(0≤θ≤π\), поэтому \(θ=π/2\).
Упражнение \(\PageIndex{3}\)
Найдите меру угла в радианах, образованного векторами \(\vecs{ a}=⟨1,2,0⟩\) и \(\vecs{ б}=⟨2,4,1⟩\). Округлить до сотых.
Угол между двумя векторами может быть острым \((0<\cos θ<1),\), тупым \((−1<\cos θ<0)\) или прямым \((\cos θ=− 1)\). Если \(\cos θ=1\), то оба вектора имеют одинаковое направление. Если \(\cos θ=0\), то векторы в стандартном положении образуют прямой угол (рисунок \(\PageIndex{3}\)). Мы можем формализовать этот результат в виде теоремы об ортогональных (перпендикулярных) векторах.
Рисунок \(\PageIndex{3}\): (a) Острый угол имеет \(0<\cos θ<1\). (b) Тупой угол имеет \(−1<\cos θ<0.\) (c) Прямая линия имеет \(\cos θ=−1\). (d) Если векторы имеют одинаковое направление, \(\cos θ=1\). (e) Если векторы ортогональны (перпендикулярны), \(\cos θ=0.\)
(b) Тупой угол имеет \(−1<\cos θ<0.\) (c) Прямая линия имеет \(\cos θ=−1\). (d) Если векторы имеют одинаковое направление, \(\cos θ=1\). (e) Если векторы ортогональны (перпендикулярны), \(\cos θ=0.\)Ортогональные векторы
Ненулевые векторы \(\vecs{u}\) и \(\vecs{v}\) являются ортогональными векторами тогда и только тогда, когда \(\vecs{u}⋅\vecs{v}= 0.\)
Доказательство
Пусть \(\vecs{u}\) и \(\vecs{v}\) ненулевые векторы, и пусть \(θ\) обозначает угол между ними. Сначала предположим, что \(\vecs{u}⋅\vecs{v}=0.\)Затем
\[‖\vecs{u}‖‖\vecs{v}‖\cos θ=0. \nonumber \]
Однако \(‖\vecs{u}‖≠0\) и \(‖\vecs{v}‖≠0,\), поэтому мы должны иметь \(\cos θ=0\). Следовательно, \(θ=90°\) и векторы ортогональны.
Теперь предположим, что \(\vecs{u}\) и \(\vecs{v}\) ортогональны. Тогда \(θ=90°\) и мы имеем
\[ \begin{align*} \vecs{u}⋅\vecs{v} &=‖\vecs{ u}‖‖\vecs{ v}‖\ cos θ \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖\cos 90° \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖(0 ) \\[4pt] &=0. \end{align*}\]
\end{align*}\]
□
Термины ортогональные, перпендикулярные, и нормальные указывают на то, что математические объекты пересекаются под прямым углом. Использование каждого термина определяется главным образом его контекстом. Мы говорим, что векторы ортогональны, а прямые перпендикулярны. Срок нормальный используется чаще всего при измерении угла, выполненного с плоскостью или другой поверхностью.
Пример \(\PageIndex{4}\): определение ортогональных векторов
Определите, являются ли \(\vecs{p}=⟨1,0,5⟩\) и \(\vecs{q}=⟨10,3 ,−2⟩\) — ортогональные векторы.
Решение
Используя определение, нам нужно только проверить скалярное произведение векторов:
\[ \vecs{ p}⋅\vecs{ q}=1(10)+(0)(3)+ (5)(-2)=10+0-10=0. \nonumber \]
Поскольку \(\vecs{p}⋅\vecs{q}=0,\) векторы ортогональны (рис. \(\PageIndex{4}\)).
Рисунок \(\PageIndex{4}\): Векторы \(\vecs{ p}\) и \(\vecs{ q}\) образуют прямой угол, когда их начальные точки совпадают.
Упражнение \(\PageIndex{4}\)
Для какого значения \(x\) \(\vecs{ p}=⟨2,8,−1⟩\) ортогонально \(\vecs{ q} =⟨x,−1,2⟩\)?
Пример \(\PageIndex{5}\): измерение угла, образованного двумя векторами
Пусть \(\vecs{ v}=⟨2,3,3⟩.\) Найдите меры углов, образованных двумя векторами следующие векторы.
Решение
а. Пусть α будет углом, образованным \(\vecs{ v}\) и \(\mathbf{\hat i}\): 92}\sqrt{1}}=\dfrac{3}{\sqrt{22}} \\[4pt]γ &=\arccos\dfrac{3}{\sqrt{22}}≈0,877\,\text{ рад.} \end{align*}\]
Упражнение \(\PageIndex{5}\)
Пусть \(\vecs{ v}=⟨3,−5,1⟩. \) Найдите меру углы, образованные каждой парой векторов.
\) Найдите меру углы, образованные каждой парой векторов.
Угол, который вектор образует с каждой из осей координат, называемый углом направления, очень важен в практических вычислениях, особенно в таких областях, как инженерия. Например, в космонавтике угол запуска ракеты должен определяться очень точно. Очень маленькая ошибка в угле может привести к тому, что ракета отклонится от курса на сотни миль. Углы направления часто рассчитываются с помощью скалярного произведения и косинусов углов, называемых направляющими косинусами. Поэтому мы определяем как эти углы, так и их косинусы.
Поэтому мы определяем как эти углы, так и их косинусы.
Определение: углы направления
Углы, образованные ненулевым вектором и осями координат, называются углами направления для вектора (рисунок \(\PageIndex{5}\)). Косинусы этих углов называются косинусами направления .
Рисунок \(\PageIndex{5}\): Угол \(α\) образован вектором \(\vecs{ v}\) и единичным вектором \(\mathbf{\hat i}\). Угол β образован вектором \(\vecs{v}\) и единичным вектором \(\mathbf{\hat j}\). Угол γ образован вектором \(\vecs{v}\) и единичным вектором \(\mathbf{\hat k}\).В примере \(\PageIndex{5}\) направляющие косинусы \(\vecs{ v}=⟨2,3,3⟩\) равны \(\cos α=\dfrac{2}{\sqrt{ 22}}, \cos β=\dfrac{3}{\sqrt{22}},\) и \(\cos γ=\dfrac{3}{\sqrt{22}}\). Углы направления \(\vecs{v}\) равны \(α=1,130\) рад, \(β=0,877\) рад и \(γ=0,877\) рад.
До сих пор мы в основном фокусировались на векторах, связанных с силой, движением и положением в трехмерном физическом пространстве. Однако векторы часто используются более абстрактно. Например, предположим, что продавец фруктов продает яблоки, бананы и апельсины. В данный день он продает 30 яблок, 12 бананов и 18 апельсинов. Он может использовать количественный вектор \(\vecs{ q}=⟨30,12,18⟩,\) для представления количества фруктов, которое он продал в тот день. Точно так же он может захотеть использовать ценовой вектор \(\vecs{ p}=⟨0,50,0,25,1⟩,\), чтобы указать, что он продает свои яблоки по 50 центов за штуку, бананы по 25 центов за штуку и апельсины по 1 доллар за штуку. В этом примере, хотя мы все еще можем изобразить эти векторы, мы не интерпретируем их как буквальное представление положения в физическом мире. Мы просто используем векторы для отслеживания отдельных фрагментов информации о яблоках, бананах и апельсинах.
Однако векторы часто используются более абстрактно. Например, предположим, что продавец фруктов продает яблоки, бананы и апельсины. В данный день он продает 30 яблок, 12 бананов и 18 апельсинов. Он может использовать количественный вектор \(\vecs{ q}=⟨30,12,18⟩,\) для представления количества фруктов, которое он продал в тот день. Точно так же он может захотеть использовать ценовой вектор \(\vecs{ p}=⟨0,50,0,25,1⟩,\), чтобы указать, что он продает свои яблоки по 50 центов за штуку, бананы по 25 центов за штуку и апельсины по 1 доллар за штуку. В этом примере, хотя мы все еще можем изобразить эти векторы, мы не интерпретируем их как буквальное представление положения в физическом мире. Мы просто используем векторы для отслеживания отдельных фрагментов информации о яблоках, бананах и апельсинах.
Эта идея может показаться немного странной, но если мы будем рассматривать векторы просто как способ упорядочивания и хранения данных, мы обнаружим, что они могут быть весьма мощным инструментом. Возвращаясь к продавцу фруктов, давайте подумаем о скалярном произведении \(\vecs{ q}⋅\vecs{ p}\). Мы вычисляем его, умножая количество проданных яблок (30) на цену одного яблока (50 центов), количество проданных бананов на цену одного банана и количество проданных апельсинов на цену одного апельсина. Затем мы складываем все эти значения вместе. Итак, в этом примере скалярный продукт говорит нам, сколько денег было у продавца фруктов в продажах в этот конкретный день.
Возвращаясь к продавцу фруктов, давайте подумаем о скалярном произведении \(\vecs{ q}⋅\vecs{ p}\). Мы вычисляем его, умножая количество проданных яблок (30) на цену одного яблока (50 центов), количество проданных бананов на цену одного банана и количество проданных апельсинов на цену одного апельсина. Затем мы складываем все эти значения вместе. Итак, в этом примере скалярный продукт говорит нам, сколько денег было у продавца фруктов в продажах в этот конкретный день.
Когда мы используем векторы более общим образом, нет причин ограничивать число компонентов тремя. Что, если продавец фруктов решит начать продавать грейпфруты? В этом случае он хотел бы использовать четырехмерные векторы количества и цены для представления количества проданных яблок, бананов, апельсинов и грейпфрутов и их цены за единицу. Как и следовало ожидать, чтобы вычислить скалярное произведение четырехмерных векторов, мы просто складываем произведения компонентов, как и раньше, но сумма состоит из четырех членов вместо трех.
Пример \(\PageIndex{6}\): Использование векторов в экономическом контексте
Магазин товаров для вечеринок AAA продает приглашения, сувениры для вечеринок, украшения и предметы общественного питания, такие как бумажные тарелки и салфетки. Когда AAA покупает свой инвентарь, она платит 25 центов за упаковку за приглашения и сувениры для вечеринок. Украшения стоят 50 центов AAA за штуку, а предметы общественного питания — 20 центов за упаковку. AAA продает приглашения по 2,50 доллара за упаковку и сувениры для вечеринок по 1,50 доллара за упаковку. Украшения продаются по 4,50 доллара за штуку, а предметы общественного питания по 1,25 доллара за упаковку.
В течение мая в магазине товаров для вечеринок AAA было продано 1258 приглашений, 342 сувенира для вечеринок, 2426 украшений и 1354 предмета общественного питания. Используйте векторы и скалярные произведения, чтобы рассчитать, сколько денег AAA заработала на продажах в мае месяце. Какую прибыль получил магазин?
Решение
Векторы стоимости, цены и количества: p} &=⟨2. 50,1.50,4.50,1.25⟩ \\[4pt] \vecs{q} &=⟨1258,342,2426,1354⟩. \end{выравнивание*}\]
50,1.50,4.50,1.25⟩ \\[4pt] \vecs{q} &=⟨1258,342,2426,1354⟩. \end{выравнивание*}\]
Продажи AAA в мае можно рассчитать с помощью скалярного произведения \(\vecs{ p}⋅\vecs{ q}\). У нас есть
\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=⟨2.50,1.50,4.50,1.25⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] & =3145+513+10917+1692,5 \\[4pt] &= 16267,5. \end{align*}\]
Итак, в мае ААА заработала 16 267,50 долларов. Чтобы рассчитать прибыль, мы должны сначала подсчитать, сколько ААА заплатила за проданные товары. Мы используем скалярное произведение \(\vecs{c}⋅\vecs{q}\), чтобы получить
\[ \begin{align*} \vecs{ c}⋅\vecs{ q} &=⟨0,25,0,25,0,50,0,20⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] &=314,5+ 85,5+1213+270,8 \\[4pt] &=1883,8. \end{align*}\]
Итак, AAA заплатила 1 883,80 долларов за проданные товары. Таким образом, их прибыль равна
\[\vecs{ p}⋅\vecs{ q}−\vecs{ c}⋅\vecs{ q}=16267,5−1883,8=14383,7. \nonumber \]
Таким образом, в мае магазин товаров для вечеринок AAA заработал 14 383,70 долларов США.
Упражнение \(\PageIndex{6}\)
1 июня магазин товаров для вечеринок AAA решил повысить цену на сувениры для вечеринок до 2 долларов за упаковку. Они также сменили поставщиков своих приглашений и теперь могут покупать приглашения всего за 10 центов за упаковку. Все остальные их расходы и цены остаются прежними. Если ААА продаст 1408 приглашений, 147 подарков для вечеринок, 2112 украшений и 1894 пункта общественного питания в июне месяце, используйте векторы и точечные произведения, чтобы рассчитать их общий объем продаж и прибыль за июнь.
Проекции
Как мы видели, сложение объединяет два вектора для создания результирующего вектора. Но что, если нам дан вектор и нужно найти его составные части? Мы используем векторные проекции для выполнения противоположного процесса; они могут разбить вектор на его компоненты. Величина векторной проекции является скалярной проекцией. Например, если ребенок тянет ручку тележки под углом 55°, мы можем использовать проекции, чтобы определить, какая сила на ручке фактически двигает тележку вперед (\(\PageIndex{6}\)) . Мы вернемся к этому примеру и научимся его решать после того, как увидим, как вычислять проекции.
Величина векторной проекции является скалярной проекцией. Например, если ребенок тянет ручку тележки под углом 55°, мы можем использовать проекции, чтобы определить, какая сила на ручке фактически двигает тележку вперед (\(\PageIndex{6}\)) . Мы вернемся к этому примеру и научимся его решать после того, как увидим, как вычислять проекции.
Определение: вектор и проекция
Проекция вектора \(\vecs{ v}\) на \(\vecs{ u}\) — это вектор с меткой \(\text{proj}_\vecs{ u} \vecs{ v}\) на рисунке \(\PageIndex{7}\). Он имеет ту же начальную точку, что и \(\vecs{ u}\) и \(\vecs{ v}\), и то же направление, что и \(\vecs{ u}\), и представляет компонент \(\vecs { v}\), который действует в направлении \(\vecs{ u}\). Если \(θ\) представляет собой угол между \(\vecs{ u}\) и \(\vecs{ v}\), то по свойствам треугольников мы знаем длину \(\text{proj}_ \vecs{ u}\vecs{ v}\) равно \(\|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs{ v}‖\cos θ. \) Когда выражая \(\cos θ\) через скалярное произведение, это становится 92}\vecs{у}. \nonumber \]
\) Когда выражая \(\cos θ\) через скалярное произведение, это становится 92}\vecs{у}. \nonumber \]
Длина этого вектора также известна как скалярная проекция из \(\vecs{ v}\) на \(\vecs{ u}\) и обозначается как
\[\| \text{proj}_\vecs{u}\vecs{v}\|=\text{comp}_\vecs{u}\vecs{v}=\dfrac{\vecs{u}⋅\vecs{v} }{‖\vecs{ u}‖.} \nonumber \]
Рисунок \(\PageIndex{7}\): Проекция \(\vecs{ v}\) на \(\vecs{ u}\) показывает компонента вектора \(\vecs{ v}\) в направлении \(\vecs{ u}\).Пример \(\PageIndex{7}\): поиск проекций
Найдите проекцию \(\vecs{ v}\) на \(\vecs{ u}\).
Раствор
а. Подставим компоненты \(\vecs{ v}\) и \(\vecs{ u}\) в формулу проекции:
\[\begin{align*} \text{proj}_\vecs{ u }\vecs{ v} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{⟨ −1,4,3⟩⋅⟨3,5,1⟩}{∥⟨−1,4,3⟩∥^2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{−3 +20+3}{(−1)^2+4^2+3^2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{20}{26}⟨−1,4, 3⟩ \\[4pt] &=⟨−\dfrac{10}{13},\dfrac{40}{13},\dfrac{30}{13}⟩. \end{выравнивание*}\] 92}(\mathbf{\шляпа i}+6\mathbf{\шляпа j}) \\[4pt] &= -\dfrac{9}{37}(\mathbf{\шляпа i}+6\mathbf{\ шляпа j}) \\[4pt] &= -\dfrac{9}{37}\mathbf{\hat i}-\dfrac{54}{37}\mathbf{\hat j}.\end{align*} \]
\end{выравнивание*}\] 92}(\mathbf{\шляпа i}+6\mathbf{\шляпа j}) \\[4pt] &= -\dfrac{9}{37}(\mathbf{\шляпа i}+6\mathbf{\ шляпа j}) \\[4pt] &= -\dfrac{9}{37}\mathbf{\hat i}-\dfrac{54}{37}\mathbf{\hat j}.\end{align*} \]
Иногда бывает полезно разложить векторы, то есть разбить вектор на части в виде суммы. Этот процесс называется -разложением вектора на компоненты. Проекции позволяют нам идентифицировать два ортогональных вектора, имеющих желаемую сумму. Например, пусть \(\vecs{ v}=⟨6,−4⟩\) и пусть \(\vecs{ u}=⟨3,1⟩.\) Мы хотим разложить вектор \(\vecs{ v }\) на ортогональные компоненты, так что один из векторов компонентов имеет то же направление, что и \(\vecs{ u}\). 92}\vecs{ u} \\[4pt] = \dfrac{18−4}{9+1}\vecs{ u} \\[4pt] = \dfrac{7}{5}\vecs{ u}= \dfrac{7}{5}⟨3,1⟩=⟨\dfrac{21}{5},\dfrac{7}{5}⟩. \end{align*}\]
Теперь рассмотрим вектор \(\vecs{ q}=\vecs{ v}−\vecs{ p}.\) У нас есть
\[\begin{align*} \vecs { q} =\vecs{ v}−\vecs{ p} \\[4pt] = ⟨6,−4⟩−⟨\dfrac{21}{5},\dfrac{7}{5}⟩ \\[ 4pt] = ⟨\dfrac{9}{5},−\dfrac{27}{5}⟩. \end{align*}\]
\end{align*}\]
Очевидно, по тому, как мы определили \(\vecs{ q}\), имеем \(\vecs{ v}=\vecs{ q}+\vecs{ p},\ ) и
\[\begin{align*}\vecs{ q}⋅\vecs{ p} =⟨\dfrac{9}{5},−\dfrac{27}{5}⟩⋅⟨\dfrac{21}{5 },\dfrac{7}{5}⟩ \\[4pt] = \dfrac{9(21)}{25}+−\dfrac{27(7)}{25} \\[4pt] = \dfrac{ 189}{25}−\dfrac{189}{25}=0. \end{align*}\]
Следовательно, \(\vecs{ q}\) и \(\vecs{ p}\) ортогональны.
Пример \(\PageIndex{8}\): преобразование векторов в компоненты
Выразите \(\vecs{ v}=⟨8,−3,−3⟩\) в виде суммы ортогональных вектора имеют то же направление, что и \(\vecs{ u}=⟨2,3,2⟩.\) 92}⟨2,3,2⟩ \\[4pt] &=\dfrac{1}{17}⟨2,3,2⟩ \\[4pt] &=⟨\dfrac{2}{17},\dfrac {3}{17},\dfrac{2}{17}⟩. \end{align*} \nonumber \]
Затем
\[ \begin{align*} \vecs{q} &=\vecs{v}-\vecs{p}=⟨8,-3,- 3⟩−⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩\\[4pt] &=⟨\dfrac{134}{17},−\ dfrac{54}{17},−\dfrac{53}{17}⟩. \end{align*} \nonumber \]
Чтобы проверить нашу работу, мы можем использовать скалярное произведение, чтобы убедиться, что векторы \(\vecs{ p}\) и \(\vecs{ q}\) являются ортогональными векторами:
\[ \begin{align*}\vecs{ p}⋅\vecs{ q}&=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩ ⋅⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩\\[4pt] &=\dfrac{268}{289}-\dfrac{162}{289}-\dfrac{106}{289}=0. \end{align*} \nonumber \]
\end{align*} \nonumber \]
Затем
\[\vecs{ v}=\vecs{ p}+\vecs{ q}=⟨\dfrac{2}{17},\dfrac{3 }{17},\dfrac{2}{17}⟩+⟨\dfrac{134}{17},-\dfrac{54}{17},-\dfrac{53}{17}⟩. \nonumber \]
Упражнение \(\PageIndex{7}\)
Выразите \(\vecs{ v}=5\mathbf{\hat i}−\mathbf{\hat j}\) в виде суммы ортогональных такие, что один из векторов имеет то же направление, что и \(\vecs{u}=4\mathbf{\hat i}+2\mathbf{\hat j}\).
Пример \(\PageIndex{9}\): Скалярная проекция скорости
Контейнеровоз выходит из порта и движется \(15°\) к северу от востока. Его двигатель развивает на этом пути скорость 20 узлов (см. следующий рисунок). Кроме того, океанское течение перемещает корабль на северо-восток со скоростью 2 узла. Учитывая и двигатель, и течение, с какой скоростью корабль движется в направлении \(15°\) к северу от востока? Округлите ответ до двух знаков после запятой.
следующий рисунок). Кроме того, океанское течение перемещает корабль на северо-восток со скоростью 2 узла. Учитывая и двигатель, и течение, с какой скоростью корабль движется в направлении \(15°\) к северу от востока? Округлите ответ до двух знаков после запятой.
Решение
Пусть \(\vecs{ v}\) будет вектором скорости, создаваемой двигателем, и пусть \(\vecs{w}\) будет вектором скорости течения. Мы уже знаем \(‖\vecs{ v}‖=20\) вдоль нужного маршрута. Нам просто нужно добавить скалярную проекцию \(\vecs{w}\) на \(\vecs{v}\). Получаем
\[ \begin{align*} \text{comp}_\vecs{ v}\vecs{w}=\dfrac{\vecs{ v}⋅\vecs{w}}{‖\vecs{ v }‖} \\[4pt] =\dfrac{‖\vecs{ v}‖‖\vecs{ w}‖\cos(30°)}{‖\vecs{ v}‖} =‖\vecs{ w}‖ \cos(30°) =2\dfrac{\sqrt{3}}{2}=\sqrt{3}≈1,73\,\text{узлы.}\end{align*}\]
Судно движется со скоростью 21,73 узла в направлении \(15°\) к северо-востоку.
Упражнение \(\PageIndex{8}\)
Повторите предыдущий пример, но предположите, что океанское течение движется на юго-восток, а не на северо-восток, как показано на следующем рисунке.
Работа
Теперь, когда мы понимаем точечные произведения, мы можем увидеть, как применять их в реальных ситуациях. Чаще всего скалярное произведение двух векторов применяется для расчета работы.
Из физики мы знаем, что работа совершается, когда объект перемещается под действием силы. Когда сила постоянна и приложена в том же направлении, в котором движется объект, тогда мы определяем проделанную работу как произведение силы на расстояние, которое проходит объект: \(W=Fd\). Мы видели несколько примеров этого типа в предыдущих главах. Теперь представьте, что направление силы отличается от направления движения, как в примере с ребенком, тянущим тележку. Чтобы найти совершенную работу, нужно умножить составляющую силы, действующей в направлении движения, на величину перемещения. Скалярный продукт позволяет нам сделать именно это. Если представить приложенную силу вектором \(\vecs{ F}\), а перемещение объекта вектором \(\vecs{ s}\), то работа, выполненная силой , является скалярным произведением \(\vecs{F}\) и \(\vecs{s}\).
Скалярный продукт позволяет нам сделать именно это. Если представить приложенную силу вектором \(\vecs{ F}\), а перемещение объекта вектором \(\vecs{ s}\), то работа, выполненная силой , является скалярным произведением \(\vecs{F}\) и \(\vecs{s}\).
Определение: постоянная сила
Когда к объекту приложена постоянная сила, так что объект движется по прямой из точки \(P\) в точку \(Q\), работа \(W\), выполненная сила \(\vecs{ F}\), действующая под углом θ от линии движения, равна
\[W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F }∥∥\vecd{PQ}∥\cos θ. \nonumber \]
Вернемся к проблеме детской тележки, представленной ранее. Предположим, ребенок тянет тележку с силой 8 фунтов на ручке под углом 55° . Если ребенок протащит тележку на 50 футов, найдите работу силы (рисунок \(\PageIndex{8}\)).
Рисунок \(\PageIndex{8}\): Горизонтальная составляющая силы представляет собой проекцию \(\vecs{ F}\) на положительную ось \(x\).Имеем
\[W=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ=8(50)(\cos(55°))≈229\,\text{ft⋅lb. } \nonumber \]
} \nonumber \]
В стандартных единицах США мы измеряем величину силы \(∥\vecs{ F}∥\) в фунтах. Величина вектора смещения \(∥\vecd{PQ}∥\) говорит нам, как далеко переместился объект, и измеряется в футах. Таким образом, общепринятой единицей измерения труда является футо-фунт. Один футо-фунт — это количество работы, необходимой для перемещения объекта весом 1 фунт на расстояние 1 фут по прямой. В метрической системе единицей измерения силы является ньютон (Н), а единицей измерения величины работы — ньютон-метр (Н·м) или джоуль (Дж).
Пример \(\PageIndex{10}\): Расчет работы
Конвейерная лента создает силу \(\vecs{ F}=5\mathbf{\hat i}−3\mathbf{\hat j}+\ mathbf{\hat k}\), который перемещает чемодан из точки \((1,1,1)\) в точку \((9,4,7)\) по прямой. Найдите работу, совершенную конвейерной лентой. Расстояние измеряется в метрах, а сила измеряется в ньютонах.
Решение
Вектор смещения \(\vecd{PQ}\) имеет начальную точку \((1,1,1)\) и конечную точку \((9,4,7)\):
\[\vecd{PQ}=⟨9−1,4−1,7−1⟩=⟨8,3,6⟩=8\mathbf{\шляпа i}+3 \mathbf{\шляпа j}+6\mathbf{\шляпа k}. \nonumber \]
\nonumber \]
Работа есть точечный продукт силы и перемещения:
\[\begin{align*} W &=\vecs{ F}⋅\vecd{PQ} \\[4pt] &= (5\ mathbf {\ шляпа i} −3 \ mathbf {\ шляпа j} + \ mathbf {\ шляпа k}) ⋅ (8 \ mathbf {\ шляпа i} +3 \ mathbf {\ шляпа j} +6 \ mathbf {\ шляпа k}) \\[4pt] = 5(8)+(−3)(3)+1(6) \\[4pt] &=37\,\text{N⋅m} \\[4pt] &= 37\,\text{J} \end{align*}\]
Упражнение \(\PageIndex{9}\)
Постоянная сила в 30 фунтов, приложенная под углом 60°, тянет ручную тележку на расстояние 10 футов по земле. Какую работу совершает эта сила?
Ключевые понятия
Ключевые уравнения
\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ\)
\(\cos θ=\dfrac{\vecs{ u}⋅\vecs{v}}{‖\vecs{ u}‖‖\vecs{v}‖}\)


 =a→·npa→b→=b→·npb→a→ показывает, что npb→a→ — это числовая проекция a→ на b→, npa→a→- проекция b→ на a→ соостветсвенно.
=a→·npa→b→=b→·npb→a→ показывает, что npb→a→ — это числовая проекция a→ на b→, npa→a→- проекция b→ на a→ соостветсвенно. )==ax·bx+ay·by+az·bz
)==ax·bx+ay·by+az·bz )=3·7·cos60°=3·7·12=212
)=3·7·cos60°=3·7·12=212 )+24·n→2==35·32+71·3·2·cosπ2+24·22=411.
)+24·n→2==35·32+71·3·2·cosπ2+24·22=411.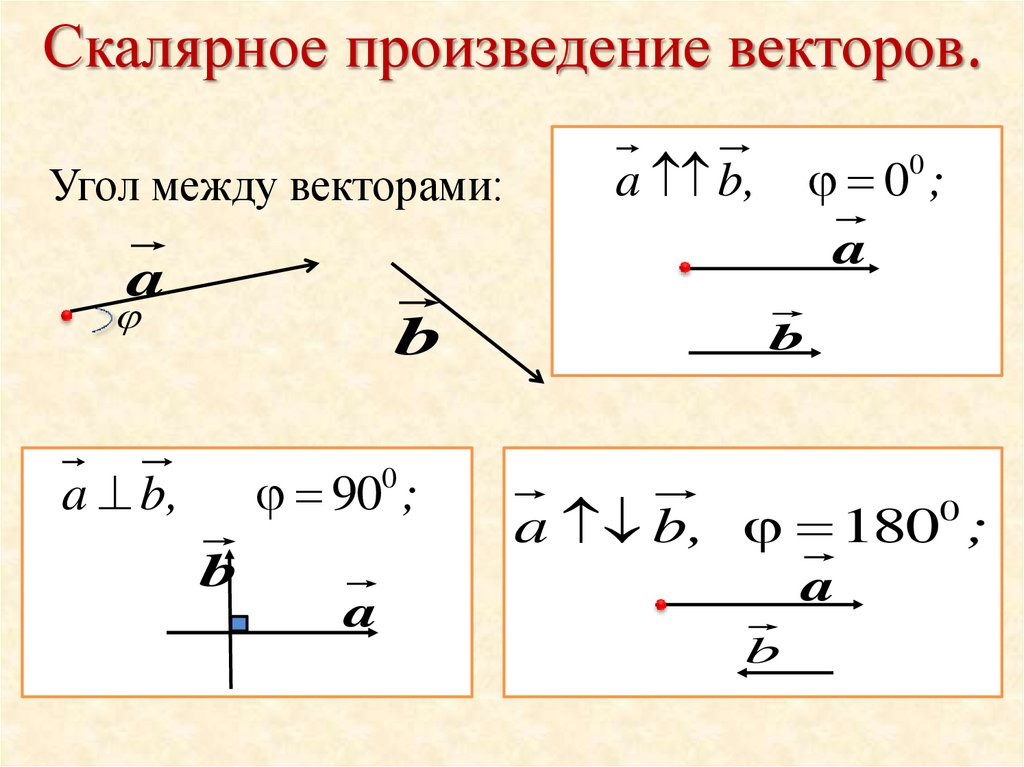 )=5·3·cos(45°)=1522.
)=5·3·cos(45°)=1522. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта Итак, по определению
Итак, по определению

 Скалярное умножение векторов обладает переместительным свойством:
Скалярное умножение векторов обладает переместительным свойством:

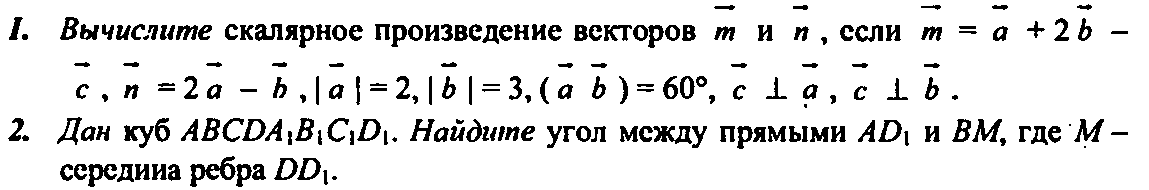
 Пусть a ⊥ b. Тогда
Пусть a ⊥ b. Тогда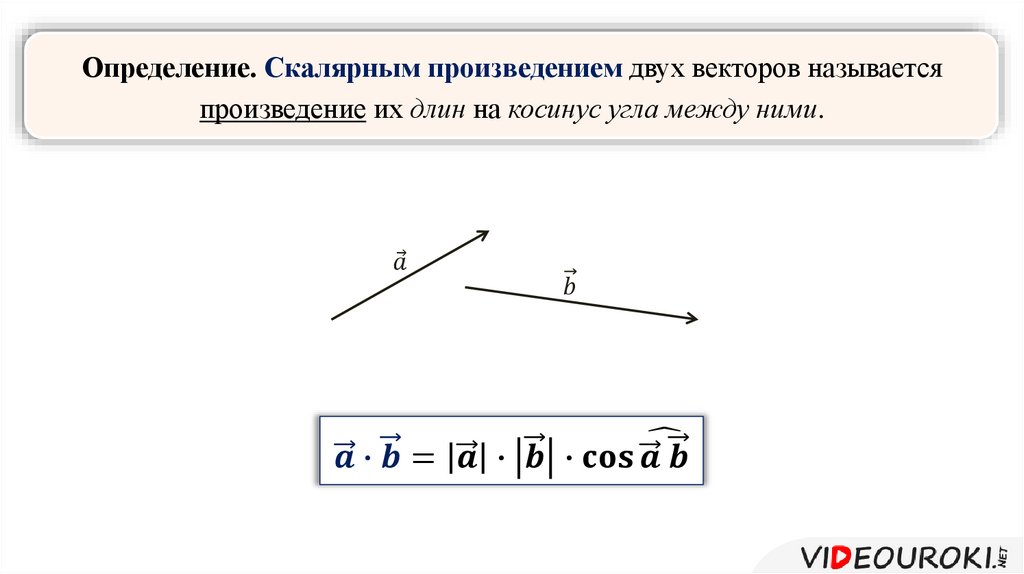

 {2}
\) и называется скалярным квадратом.
{2}
\) и называется скалярным квадратом. {\circ}
\)
{\circ}
\)
 В таком случае скалярное произведение этих векторов обладает положительным значением. Вектора, имеющие противоположные направления, разделены углом в 180°. Тогда скалярное произведение данных векторов обладает отрицательным значением.
В таком случае скалярное произведение этих векторов обладает положительным значением. Вектора, имеющие противоположные направления, разделены углом в 180°. Тогда скалярное произведение данных векторов обладает отрицательным значением. е. a.a = a.a cos 0 = a 2
е. a.a = a.a cos 0 = a 2 