Как сложить два вектора по правилу треугольника?
Как сложить два вектора по правилу треугольника?
Правило треугольника
- Для того чтобы сложить два вектора →a и →b (рис. 3, а) нужно переместить вектор →b параллельно самому себе так, чтобы его начало совпадало с концом вектора →a (рис. …
- При помощи правила треугольника можно сложить два параллельных вектора →a и →b (рис. …
- Для того чтобы сложить два вектора →a и →b (рис.
Как происходит сложение векторов?
Сложение нескольких векторов производится следующим образом: первый вектор складывается со вторым, затем их сумма складывается с третьим вектором и т. д. Сумма нескольких векторов не зависит от того, в каком порядке они складываются.
Что можно сказать о координатах коллинеарных векторов?
Два вектора коллинеарны, если отношения их координат равны. .
.. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору. N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Как проверить что векторы образуют базис?
Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор нельзя разложить по данному базису.
Как узнать какую тройку образуют векторы?
Векторы образуют правую тройку ( ).
Что такое Некомпланарные вектора?
Некомпланарные векторы Три вектора называются некомпланарными, если концы равных им векторов, отложенных от одной точки, не лежат в одной плоскости с их общим началом.
Что такое Компланарные прямые?
Иногда компланарными называют те точки (или другие объекты), которые лежат на (принадлежат) одной плоскости. … Тогда параллельные или пересекающиеся прямые будут компланарны, а скрещивающиеся прямые — нет.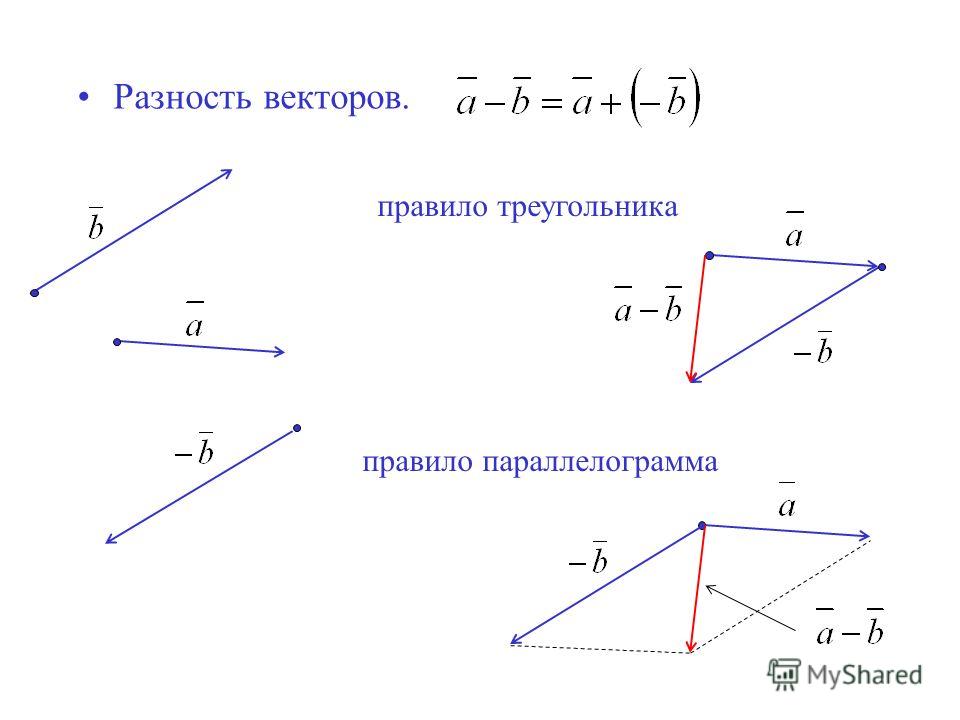
Как можно вычислить координаты вектора?
Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Как построить векторы в пространстве?
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z: … Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости.
Как найти координаты точки в треугольнике?
Координаты точки пересечения биссектрис треугольника (центра вписанной окружности) определяются соотношениями: x0=ax1+bx2+cx3a+b+c,y0=ay1+by2+cy3a+b+c, где a=BC, b=AC, c=AB.
Как найти координаты вектора по точкам?
Теория. Координаты вектора по двум точкам Определеие.
Чтобы найти координаты вектора AB, зная координаты его начальной точки А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Сложение векторов — ZNZN
Добавить в конспект
НАВИГАЦИЯ ПО СТРАНИЦЕ
ПОЛНЫЙ ОТВЕТ
БЕЗ ВОДЫ
Без воды — краткий вариант ответа,
легко понять и запомнить
Верно ли утверждение?
Тупая зубрёжка работает. Даже когда надо выучить массу новых сведений. Поэтому если готовиться к экзамену в ночь перед экзаменом, можно легко получить наивысший балл.
Верно!
Такой подход – прямой билет на станцию «пересдача». Освой метод флэш-карточек, и тогда к экзаменам не придётся открывать конспект с ощущением, что всё забыто.
Верно ли утверждение?
Тупая зубрёжка работает. Даже когда надо выучить массу новых сведений. Поэтому если готовиться к экзамену в ночь перед экзаменом, можно легко получить наивысший балл.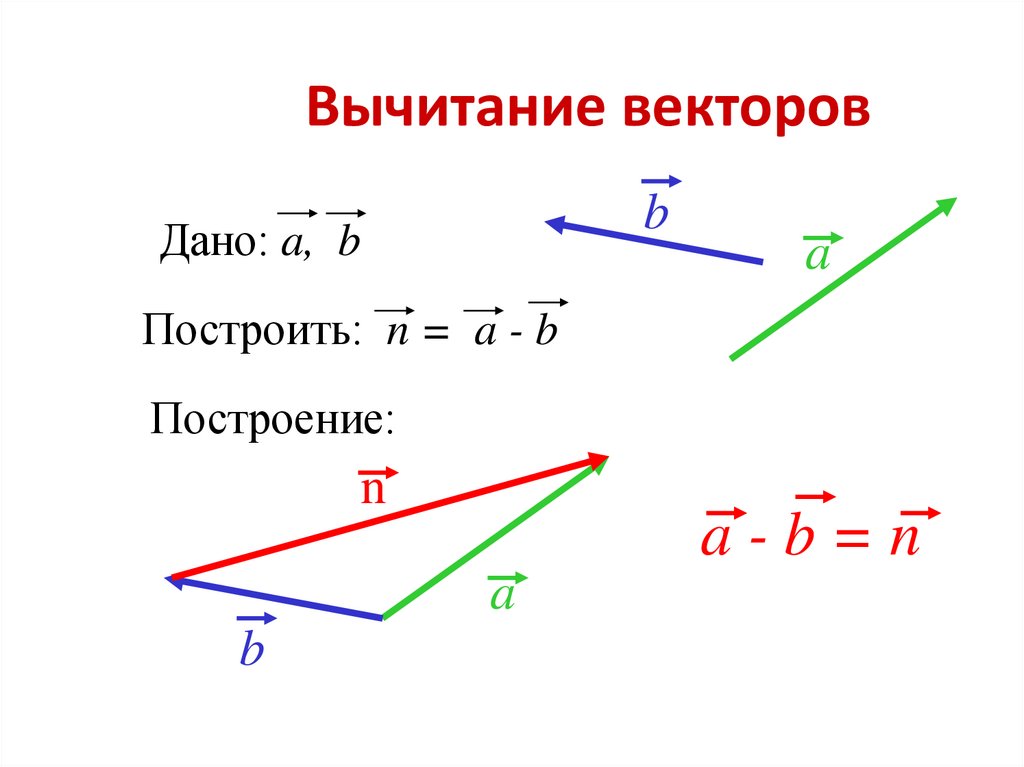
Верно!
Такой подход – прямой билет на станцию «пересдача». Освой метод флэш-карточек, и тогда к экзаменам не придётся открывать конспект с ощущением, что всё забыто.
Коллинеарные векторы — векторы, лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.
Нулевой вектор — любая точка плоскости, обозначается как нуль со стрелкой сверху.
Над векторами можно выполнять множество операций, но самая основная из них – сложение.
Сложение векторов
Векторные величины изображаются направленными отрезками (векторами) могут складываться по 3 правилам:
Правило треугольника.
Правило параллелограмма.
Правило многоугольника.
1. Правило треугольника
Для этого нужно начало вектора (рис. 1 а) совместить с концом вектора , их суммой будет вектор (рис. 1 б), соединяющий начало вектора с концом вектора .
Рисунок 1. Правило треугольника
2. Правило параллелограмма
Для того чтобы сложить два вектора по правилу параллелограмма, необходимо:
Взять произвольную точку А.
Отложить от точки векторы и .
Построить на векторах и параллелограмм.
Диагональ параллелограмма и будет суммой векторов (рис. 2)
Рисунок 2. Правило параллелограмма
3. Правило многоугольника
Если начало очередного вектора соединить с концом предыдущего, то получим ломаную линию (рис. 3). Вектор , проведенный из начала первого вектора в конец последнего, является суммой нескольких векторов (в данном случае четырех): ܽ
Рисунок 3. Правило многоугольника
Верно ли утверждение?
Тупая зубрёжка работает. Даже когда надо выучить массу новых сведений. Поэтому если готовиться к экзамену в ночь перед экзаменом, можно легко получить наивысший балл.
Верно!
Такой подход – прямой билет на станцию «пересдача».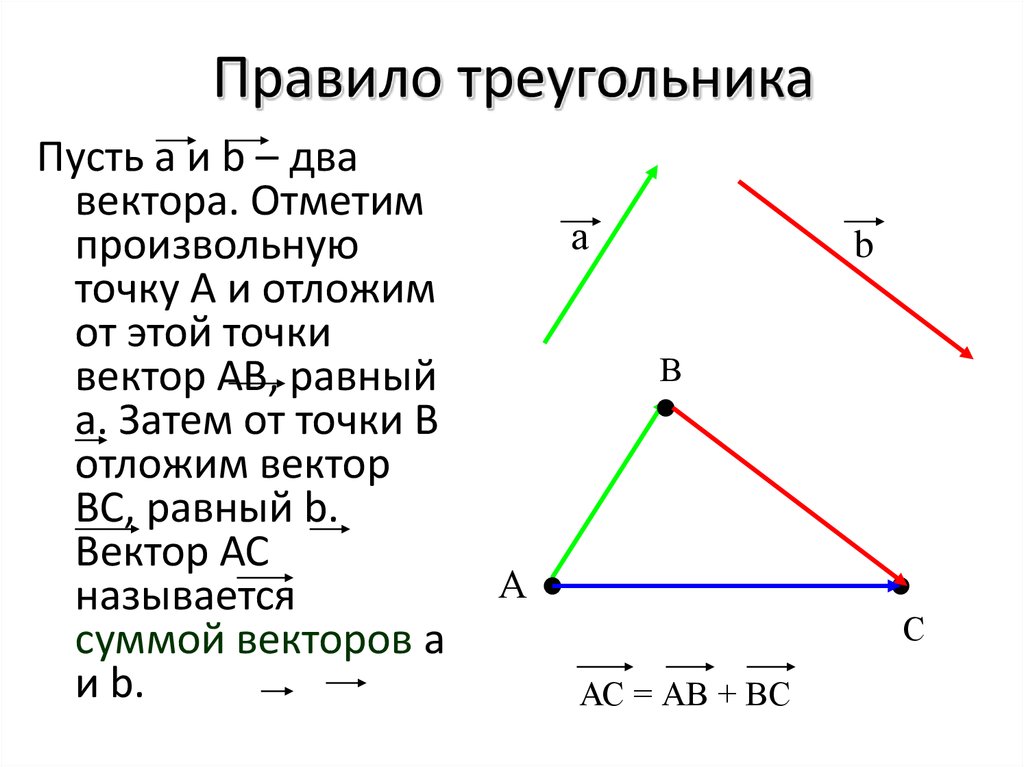
Освой метод флэш-карточек, и тогда к экзаменам не придётся открывать конспект с ощущением, что всё забыто.
Верно ли утверждение?
Тупая зубрёжка работает. Даже когда надо выучить массу новых сведений. Поэтому если готовиться к экзамену в ночь перед экзаменом, можно легко получить наивысший балл.
Верно!
Такой подход – прямой билет на станцию «пересдача». Освой метод флэш-карточек, и тогда к экзаменам не придётся открывать конспект с ощущением, что всё забыто.
Добавление векторов | Superprof
В этой статье мы обсудим, как складывать и вычитать векторы. Но прежде чем перейти к обсуждению сложения и вычитания векторов, сначала давайте определим векторы.
Вектор относится к величине, которая описывается величиной, а также направлением. Он изображен алфавитом со стрелкой вправо вверху. Например, и т. д. используются для представления векторов.
Другими словами, мы можем сказать, что векторы относятся к геометрическим представлениям величины и направления.
Величина и направление изображаются прямыми стрелками, которые начинаются с одной точки на оси координат и заканчиваются в другой точке. Величина векторов на самом деле является их длиной. Эта длина представляет некоторое значение, так что вектор сопоставим с другим вектором. Стрелки векторов показывают, что они имеют направление. Это основное различие между скаляром и вектором, поскольку скаляры — это величины без направления.
Ключевые моменты, которые следует помнить для векторов
Некоторые из ключевых моментов, которые вы должны помнить для векторов:
- Двумя компонентами векторов являются величина и направление.
- Примеры векторов в реальной жизни включают ускорение, расстояние, силу и скорость, потому что эти термины описываются как величиной, так и направлением.
- Мы определяем векторы не только по их величине, но и по их ориентации, соответствующей набору координат.
- Когда мы пытаемся анализировать векторы, мы часто разбиваем их на разные части или компоненты.
Для двумерных векторов эти части являются горизонтальными и вертикальными. С другой стороны, для трехмерных векторов часть величины одинакова, однако мы изображаем часть направления в терминах x, y и z.
Для двумерных векторов эти части являются горизонтальными и вертикальными. С другой стороны, для трехмерных векторов часть величины одинакова, однако мы изображаем часть направления в терминах x, y и z.Лучшие репетиторы по математике
Поехали
Сложение двух векторов
Для сложения двух векторов и , вы должны соединить хвост одного вектора с головой другого вектора, как показано на рисунке ниже .
Сумма вектора представлена как на рисунке выше и равна расстоянию от конца первого вектора до начала второго вектора.Правило параллелограмма
Вы также можете использовать правило параллелограмма для сложения векторов. Для этого нарисуйте векторы так, чтобы их хвосты (начальные точки) совпадали друг с другом. После этого следует начертить линии, чтобы получился параллелограмм. Диагональ, идущая от начальной точки к противоположной вершине параллелограмма, является результатом этого сложения.
Это правило показано на рисунке ниже.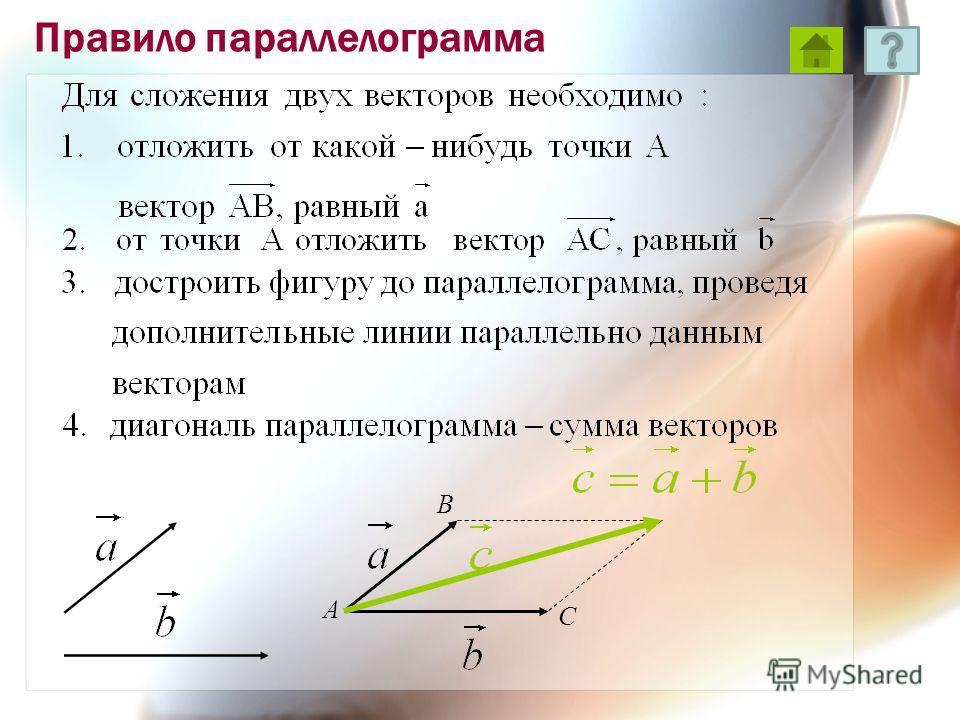
Видно, что хвосты векторов и совпадают друг с другом. Затем из головок обоих векторов мы нарисовали линии, чтобы получить параллелограмм. В конце мы нарисовали диагональ от начальной точки до противоположной вершины, которая изображена зеленой линией. Эта диагональ является результатом сложения и математически представляется как .
Если вам даны два вектора и , то как вы будете складывать эти векторы?
Ну, дополнение простое. Все, что вам нужно сделать, это сложить компоненты векторов следующим образом:
Свойства сложения векторов
Некоторые свойства сложения векторов приведены ниже:
Ассоциативное свойство
Ассоциативное свойство сложения векторов: математически обозначается как:
Коммутативность
Коммутативность сложения векторов математически представляется как:
Аддитивное свойство
Согласно аддитивному свойству сложения векторов, если к вектору добавить нулевой вектор, то результатом будет сам вектор:
Аддитивное обратное или противоположное свойство векторы говорят, что:
Вычитание векторов
Теперь, когда вы знаете, как складывать два вектора, вам может быть интересно, как вычесть два вектора, потому что сложение и вычитание векторов тесно связаны.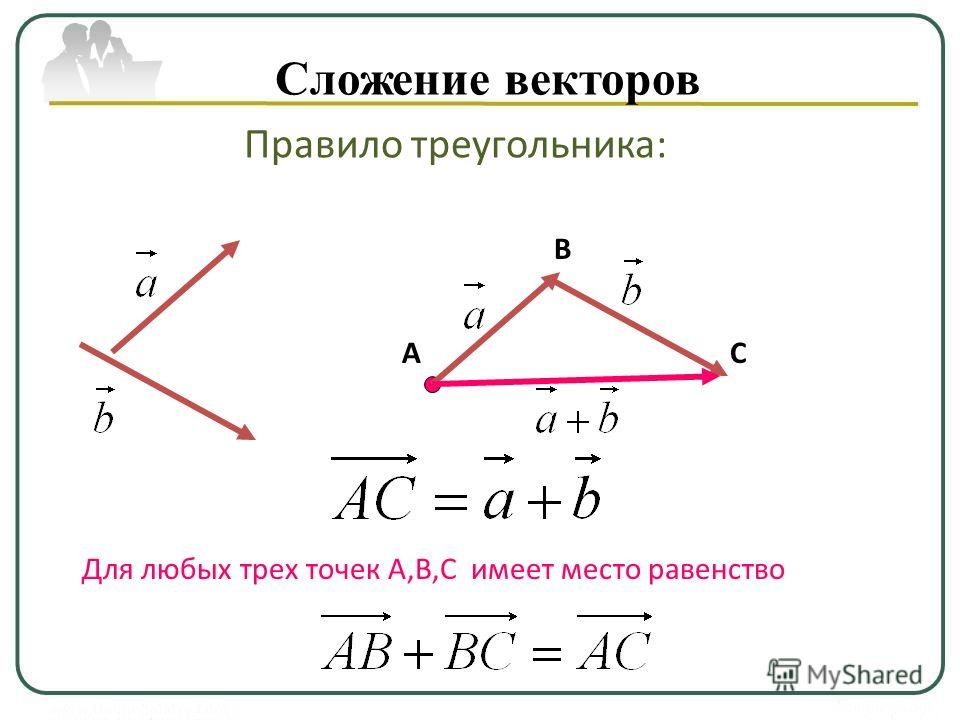
Меняется только знак между компонентами. Изображение вычитания через треугольник показано на рисунке ниже:
Чтобы вычесть два вектора и , нужно сложить вектор с противоположностью вектора
Математически это представляется как:
В следующем разделе мы решим несколько примеров, связанных со сложением векторов.
Найдите репетитора по математике рядом со мной на Superprof.
Пример 1
Если и то найти и .
Решение
=
Теперь узнаем . Для этого перепишем как
Если , то
Пример 2
Если и то найти и .
Решение
=
Теперь узнаем . Для этого перепишем как
Если , то
Пример 3
Если и то найдем и .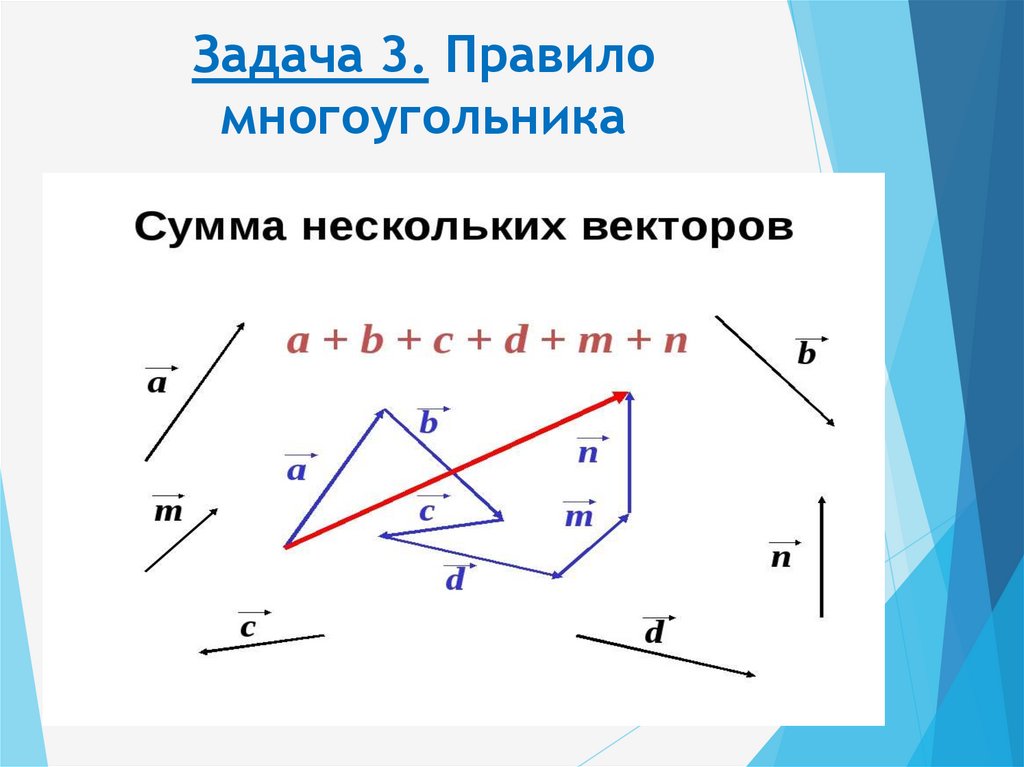
Решение
=
Теперь узнаем . Для этого перепишем как
Если , то
Пример 4
Если и то найдем и .
Решение
=
Сейчас узнаем . Для этого перепишем как
Если , то
Пример 5
Если и то найдем и .
Решение
=
Теперь узнаем . Для этого перепишем как
Если , то
| ;; Складываем два вектора | |
| (определение add-vec-simple [[x1 y1] [x2 y2]] | |
| [(+ х1 х2) (+ у1 у2)]) | |
| ;; Сложите два или более векторов вместе (первая попытка) | |
| (определить add-vec-better [[x1 y1] & args] | |
| (цикл [x x1 y y1 больше аргументов] | |
| (если (пусто? больше) | |
| [х у] | |
| (recur (+ x (первый (первый больше)) | |
| (+ у (второй (первый больше))) | |
| (остальное больше))))) | |
;; Сложите два или более векторов вместе. | |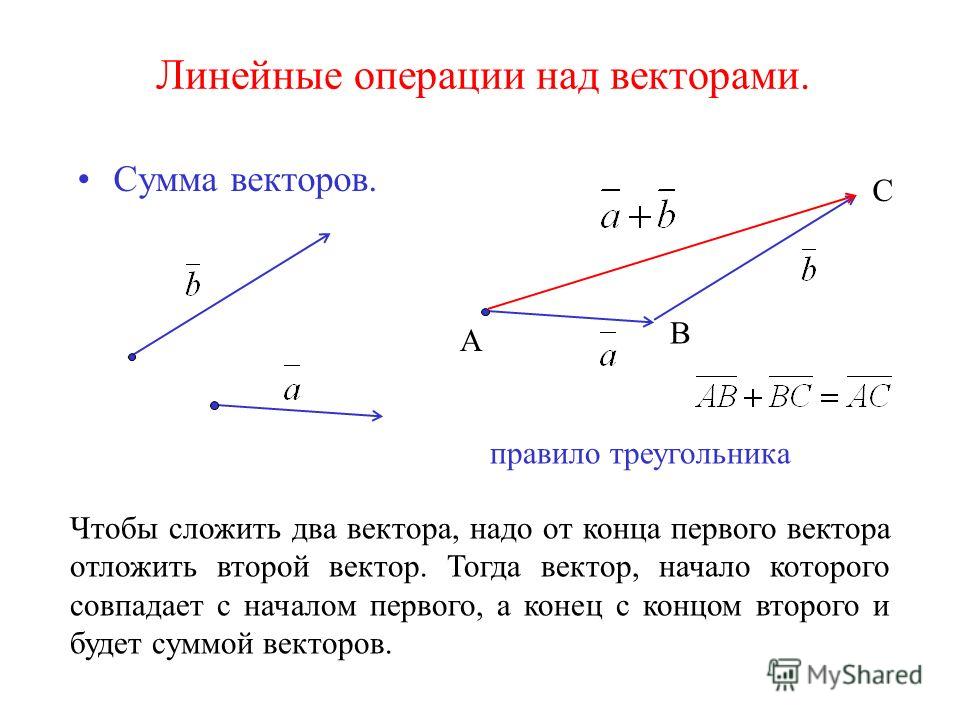
| ;; (Лучшая попытка. Использует деструктурирование, чтобы сделать его более читабельным и более сухим.) | |
| (определить add-vec-better2 [[x y] & args] | |
| «Добавить два или более векторов вместе» | |
| (цикл [x1 x y1 y больше аргументов] | |
| (если (пусто? больше) | |
| [x1 у1] | |
| (пусть [[x2 y2] (сначала больше)] ;;получить главный вектор | |
| (повторяется (+ х1 х2) | |
| (+ у1 у2) | |
| (остальное больше))))) | |
;;Более общая версия, позволяющая добавлять векторы любого размера, например трехмерные. | |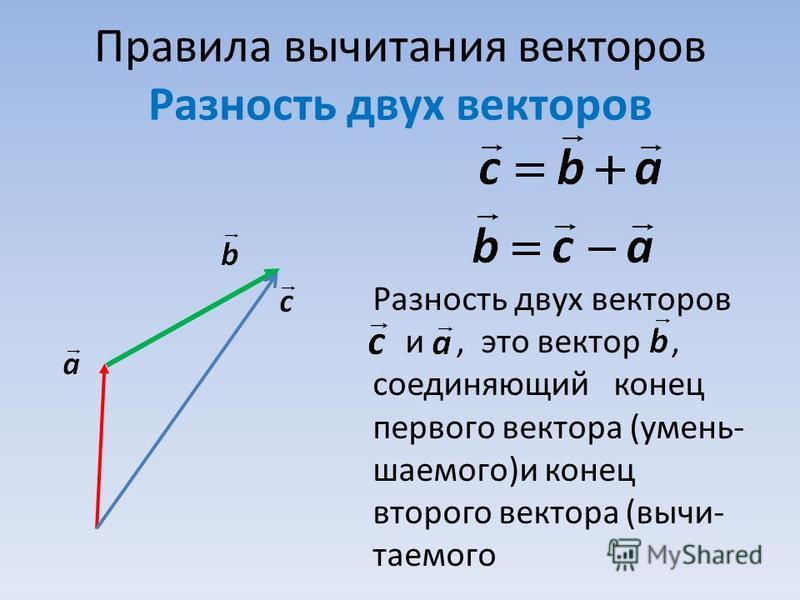
| (определить add-vec-better3 [& args] | |
| «Добавить два или более векторов вместе» | |
| (цикл [координаты (первые аргументы) больше (остальные аргументы)] | |
| (если (пусто? больше) | |
| (век координаты) | |
| (recur (карта + координаты (сначала больше)) | |
| (остальное больше))))) | |
| ;;ОБНОВЛЕНИЕ. Работая над более общей версией выше, я обнаружил, что карта может сделать это: | |
| (vec (карта + [1 2] [1 2] [1 2])) | |
| ;: возвращает [3 6] | |
| (vec (карта + [1 2 3] [1 2 3] [1 2 3])) | |
| ;: возвращает [3 6 9] | |
| ;;И mapv возвращает вектор: | |
| (мапв + [1 2 3] [1 2 3] [1 2 3]) | |
| ;: возвращает [3 6 9] | |
| ;;Поэтому add-vec можно записать кратко так: | |
| (определить add-vec [& args] | |
| «Добавить два или более векторов вместе» | |
| (когда (последовательность аргументов) | |
| (применить карту + аргументы))) | |
| ;;Вывод: | |
;;не стоит* знать.  |