PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Физика для средних специальных учебных заведений

Жданов Л. С., Жданов Г. Л. Физика для средних специальных учебных заведений: Учебник.—4-е изд., испр.—М.: Наука. Главная редакция физико-математической литературы, 1984. — 512 с. Содержание и расположение материала соответствуют программе по физике для техникумов на базе 8 классов средней школы, утвержденной в 1977 году. Изложение материала ведется на основе Международной системы единиц (СИ). В полном соответствии с содержанием курса составлен «Сборник задач и упражнений по физике для средних специальных учебных заведений», под редакцией Р. А. Гладковой (6-е изд. 1983 г.). Для учащихся средних специальных учебных заведений, ПТУ, общеобразовательных школ, слушателей и преподавателей подготовительных отделений вузов, а также лиц, занимающихся самообразованием. Оглавление ВВЕДЕНИЕ § 1.2. Физика и техника. § 1.3. Понятие о величине и измерении. Физические величины. § 1.4. Прямое и косвенное измерения. § 1.5. Звездное небо и его видимое вращение. § 1.6. Угловые измерения на небе. § 1.7. Определение расстояний до небесных тел на основе измерения параллаксов. § 1.8. Основные единицы времени и их связь с движением Земли. § 1.9. Правило вывода единиц физических величин из формул. Международная система единиц СИ. § 1.10. Плотность вещества. Раздел I. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕПЛОТА Глава 2. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ СТРОЕНИЯ ВЕЩЕСТВА § 2.2. Диффузия. § 2.3. Силы молекулярного взаимодействия. § 2.4. Кинетическая и потенциальная энергия молекул. § 2.5. Агрегатное состояние вещества. § 2.6. Понятие о температуре и внутренней энергии тела. Глава 3. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗООБРАЗНОГО СОСТОЯНИЯ ВЕЩЕСТВА § 3.2. Броуновское движение. § 3.3. Измерение скорости движения молекул газа. Опыт Штерна. § 3.4. Распределение молекул по скоростям их хаотического движения. § 3.5. Размеры и массы молекул и атомов. § 3. 6. Постоянная Авогадро и постоянная Лошмидта. § 3.7. Число столкновений и длина свободного пробега молекул в газе. § 3.8. Давление газа. Манометры. § 3.9. Понятие вакуума. § 3.10. Межзвездный газ. Глава 4. ИДЕАЛЬНЫЙ ГАЗ. АБСОЛЮТНАЯ ТЕМПЕРАТУРА И ЕЕ СВЯЗЬ С ЭНЕРГИЕЙ МОЛЕКУЛ ГАЗА § 4.2. Основное уравнение молекулярно-кинетической теории газов. § 4.3. Зависимость давления газа от температуры при постоянном объеме. § 4.4. Абсолютный нуль. § 4.5. Термодинамическая шкала температур. Абсолютная температура. § 4.6. Связь между температурой и кинетической энергией молекул газа. Постоянная Больцмана. Глава 5. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА § 5.2. Объединенный газовый закон. Приведение объема газа к нормальным условиям. § 5.3. Молярная газовая постоянная. Определение числового значения постоянной Больцмана. § 5.4. Уравнение Клапейрона — Менделеева. Плотность газа. § 5.5. Зависимость средней квадратичной скорости молекул газа от температуры. § 5.6. Изохорический процесс. § 5.7. Изобарический процесс. § 5.8. Изотермический процесс. § 5.9. Внутренняя энергия идеального газа. § 5.10. Работа газа при изменении его объема. Физический смысл молярной газовой постоянной. Глава 6. ИЗМЕНЕНИЕ ВНУТРЕННЕЙ ЭНЕРГИИ. ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ § 6.2. Теплообмен. § 6.3. Виды теплообмена. § 6.4. Изменение внутренней энергии при нагревании и охлаждении. § 6.5. Уравнение теплового баланса при теплообмене. § 6.6. Подсчет теплоты, выделяемой при сжигании топлива. К. п. д. нагревателя. § 6.7. Изменение внутренней энергии при выполнении механической работы. Опыт Джоуля. § 6.8. Закон сохранения и превращения энергии в механике. § 6.9. Закон сохранения и превращения энергии в механических и тепловых процессах. § 6.10. Первое начало термодинамики. § 6.11. Применение первого начала термодинамики к изопроцессам в идеальном газе. § 6.12. Адиабатный процесс. § 6.13. Понятие о строении Солнца и звезд. Глава 7. ПЕРЕХОД ВЕЩЕСТВА ИЗ ЖИДКОГО СОСТОЯНИЯ В ГАЗООБРАЗНОЕ И ОБРАТНО § 7.2. Испарение. § 7.3. Теплота парообразования. Глава 8. СВОЙСТВА ПАРОВ. КИПЕНИЕ. КРИТИЧЕСКОЕ СОСТОЯНИЕ ВЕЩЕСТВА § 8.2. Свойства паров, насыщающих пространство. § 8.3. Свойства паров, не насыщающих пространство. § 8.4. Процесс кипения жидкости. § 8.5. Зависимость температуры кипения жидкости от внешнего давления. Точка кипения. § 8.6. Уравнение теплового баланса при парообразовании и конденсации. § 8.7. Перегретый пар и его использование в технике. § 8.8. Критическое состояние вещества. § 8.9. Сжижение газов и использование жидких газов в технике. Глава 9. ВОДЯНОЙ ПАР В АТМОСФЕРЕ § 9.2. Абсолютная и относительная влажность воздуха. Точка росы. § 9.3. Приборы для определения влажности воздуха. § 9.4. Понятие об атмосферах планет. Глава 10. СВОЙСТВА ЖИДКОСТЕЙ § 10.2. Поверхностный слой жидкости. § 10.3. Энергия поверхностного слоя жидкости. Поверхностное натяжение. § 10.4. Сила поверхностного натяжения. § 10.5. Смачивание. Краевой угол. § 10.6. Мениск. Давление, создаваемое искривленной поверхностью жидкости. § 10.7. Капиллярность. Капиллярные явления в природе и технике. § 10.8. Понятие о вязкости среды. Ламинарное течение жидкости. § 10.9. Закон Ньютона для внутреннего трения. Динамическая вязкость. § 10.10. Аморфные вещества. Глава 11. СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДЕФОРМАЦИИ § 11.2. Анизотропия кристаллов. Пространственная решетка и ее дефекты. § 11.3. Виды кристаллических структур. § 11.4. Виды деформаций. § 11.5. Механическое напряжение. § 11.6. Упругость, пластичность, хрупкость и твердость. § 11.7. Закон Гука. Модуль упругости. § 11.8. Энергия упруго деформированного тела. Глава 12. ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ. СУБЛИМАЦИЯ. ДИАГРАММА СОСТОЯНИЙ ВЕЩЕСТВА § 12.2. Удельная теплота плавления. § 12.3. Изменение объема и плотности вещества при плавлении и отвердевании. § 12.4. Зависимость температуры и теплоты плавления от давления. Точка плавления. § 12.5. Уравнение теплового баланса при плавлении и кристаллизации. § 12.6. Растворы и сплавы. Охлаждающие смеси. § 12.7. Испарение твердых тел (сублимация). § 12.8. Диаграмма состоянии вещества. Тройная точка. Глава 13. ТЕПЛОВОЕ РАСШИРЕНИЕ ТЕЛ § 13.2. Линейное расширение твердых тел при нагревании. § 13.3. Объемное расширение тел при нагревании. Зависимость плотности вещества от температуры. § 13.4. Особенности теплового расширения твердых тел. § 13.5. Некоторые особенности теплового расширения жидкостей. § 13.6. Значение теплового расширения тел в природе и технике. Раздел II. ОСНОВЫ ЭЛЕКТРОДИНАМИКИ Глава 14. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ЗАКОН КУЛОНА § 14.2. Явления, подтверждающие сложное строение атома. § 14.3. Опыты Резерфорда. Ядерная модель строения атома. § 14.4. Понятие о строении атомов различных химических элементов. § 14.5. Электризация при соприкосновении незаряженных тел. 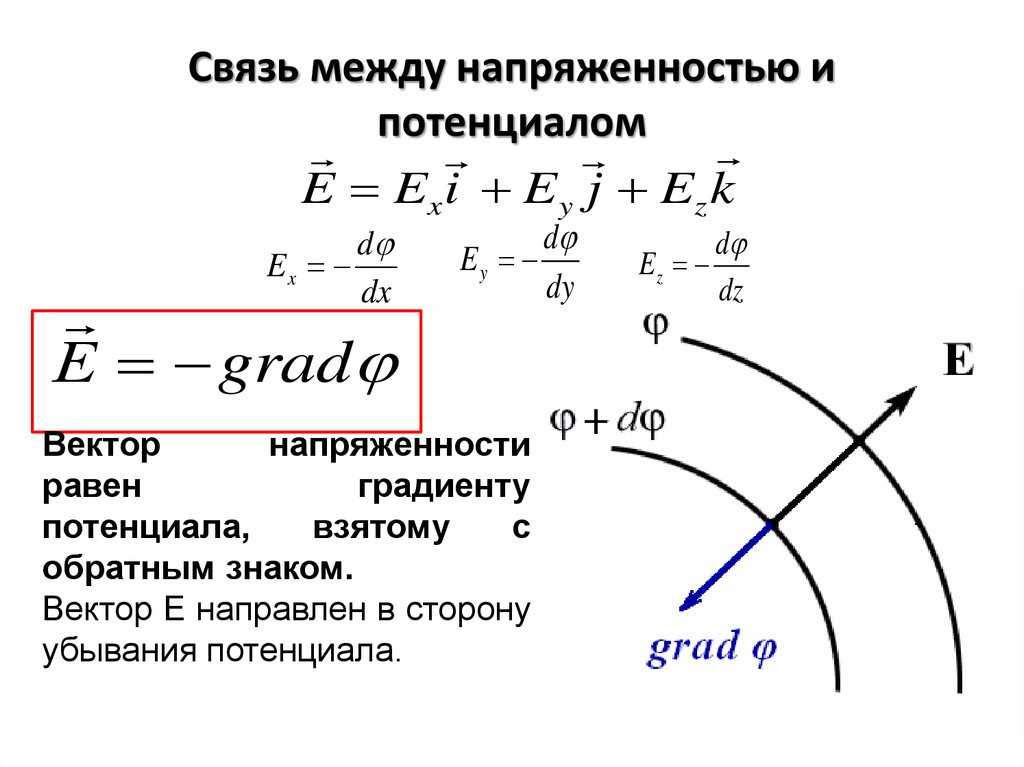§ 14.6. Сила взаимодействия электрических зарядов. Закон Кулона. § 14.7. Диэлектрическая проницаемость среды. § 14.8. Международная система единиц СИ в электричестве. Электрическая постоянная. § 14.9. Электроскоп. Глава 15. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ § 15.2. Напряженность электрического поля. § 15.3. Линии напряженности электрического поля. § 15.4. Однородное поле. Поверхностная плотность заряда. § 15.5. Работа электрического поля при перемещении заряда. Потенциальная энергия заряда. § 15.6. Потенциал. Разность потенциалов и напряжение. Эквипотенциальные поверхности. § 15.7. Связь между напряженностью поля и напряжением. Градиент потенциала. § 15.8. Проводник в электрическом поле. § 15.9. Электрометр. § 15.10. Диэлектрик в электрическом поле. Поляризация диэлектрика. § 15.11. Понятие о сегнетоэлектриках. § 15.12. Пьезоэлектрический эффект. § 15.13. Электроемкость проводника. § 15.14. Условия, от которых зависит электроемкость проводника. § 15.15. Конденсаторы. § 15.16. Соединение конденсаторов в батарею. § 15.17. Энергия заряженного конденсатора. Плотность энергии электрического поля. § 15.18. Опыт Милликена. Глава 16. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА § 16.2. Сила тока и плотность тока в проводнике. § 16.3. Замкнутая электрическая цепь. § 16.4. Электродвижущая сила источника электрической энергии. § 16.5. Внешняя и внутренняя части цепи. § 16.6. Закон Ома для участка цепи без э. д. с. Сопротивление проводника. Падение напряжения. § 16.7. Зависимость сопротивления от материала, длины и площади поперечного сечения проводника. § 16.8. Зависимость сопротивления от температуры. § 16.9. Сверхпроводимость. § 16.10. Эквивалентное сопротивление. § 16.11. Последовательное соединение потребителей энергии тока. § 16.12. Параллельное соединение потребителей энергии тока § 16.13. Закон Ома для всей цепи. § 16.14. Соединение одинаковых источников электрической энергии в батарею. § 16.15. Закон Ома для участка цепи с э. д. с. и для всей цепи при нескольких э. д. с. Глава 17. РАБОТА, МОЩНОСТЬ И ТЕПЛОВОЕ ДЕЙСТВИЕ ЭЛЕКТРИЧЕСКОГО ТОКА § 17.2. Мощность электрического тока. § 17.3. Тепловое действие электрического тока. Закон Джоуля — Ленца. § 17.4. Короткое замыкание. Практическое применение теплового действия тока. Глава 18. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ § 18.2. Контактная разность потенциалов. § 18.3. Термоэлектродвижущая сила. § 18.4. Явление Пельтье. § 18.5. Применение термоэлектрических явлений в науке и технике. Глава 19. ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ § 19.2. Электролиз. § 19.3. Электролиз, сопровождающийся растворением анода. § 19.4. Количество вещества, выделяющегося при электролизе. Первый закон Фарадея. § 19.5. Второй закон Фарадея. Определение заряда иона. § 19.6. Использование электролиза в технике. § 19.7. Гальванические элементы. § 19.8. Аккумуляторы. § 19.9. Применение гальванических элементов и аккумуляторов в технике. Явление электрокоррозии. Глава 20. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ И В ВАКУУМЕ § 20.2. Зависимость силы тока в газе от напряжения. § 20.3. Электрический разряд в газе при атмосферном давлении. § 20.4. Электрический разряд в разреженных газах. Газосветные трубки и лампы дневного света. § 20.5. Излучение и поглощение энергии атомом. § 20.6. Катодные лучи. § 20.7. Понятие о плазме. § 20.8. Электрический ток в вакууме. § 20.9. Двухэлектродная лампа (диод). § 20.10. Трехэлектродная лампа (триод). § 20.11. Электронно-лучевая трубка. Глава 21. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ § 21.2. Чистые (беспримесные) полупроводники. Термисторы. § 21.3. Примесные полупроводники. § 21.4. Электронно-дырочный переход. § 21.5. Полупроводниковый диод. § 21.6. Полупроводниковый триод (транзистор). Глава 22. ЭЛЕКТРОМАГНЕТИЗМ § 22.2. Магнитное поле как особый вид материи. § 22.3. Магниты. § 22.4. Линии магнитной индукции. Понятие о вихревом поле. § 22.5. Магнитное поле прямолинейного тока, кругового тока и соленоида. § 22.6. Сравнение магнитных свойств соленоида и постоянного магнита. § 22.7. Сила взаимодействия параллельных токов. Магнитная проницаемость среды. § 22.8. Определение ампера. Магнитная постоянная. § 22.9. Действие магнитного поля на прямолинейный проводник с током. § 22.10. Однородное магнитное поле. § 22.11. Магнитный момент контура с током. § 22.12. Работа при перемещении проводника с током в магнитном поле. Магнитный поток. § 22.13. Индукция магнитного поля, создаваемая в веществе проводниками с током различной формы. § 22.14. Напряженность магнитного поля и ее связь с индукцией и магнитной проницаемостью среды. § 22.15. Парамагнитные, диамагнитные и ферромагнитные вещества. § 22.16. Намагничивание ферромагнетиков. Электромагнит. § 22.17. Работа и устройство амперметра и вольтметра. § 22.18. Сила Лоренца. Движение заряда в магнитном поле. § 22.19. Постоянное и переменное магнитные поля. Глава 23. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 23.2. Явление электромагнитной индукции. § 23.3. Э. д. с. индукции, возникающая в прямолинейном проводнике при его движении в магнитном поле. Правило правой руки. § 23.4. Опыты Фарадея. § 23.5. Закон Ленца для электромагнитной индукции. Объяснение диамагнитных явлений. § 23.6. Величина э. д. с. индукции. § 23.7. Вихревое электрическое поле и его связь с магнитным полем. § 23.8. Вихревые токи. § 23.9. Роль магнитных полей в явлениях, происходящих на Солнце и в космосе. § 23.10. Явление самоиндукции. Э. д. с. самоиндукции. § 23.11. Энергия магнитного поля. Раздел III. КОЛЕБАНИЯ И ВОЛНЫ Глава 24. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ § 24.2. Условия возникновения колебаний. § 24.3. Классификация колебательных движений тела в зависимости от действующей на него силы. § 24.4. Параметры колебательного движения. § 24.5. Величины, характеризующие мгновенное состояние колеблющейся точки. § 24.6. Гармоническое колебание. § 24.7. Уравнение гармонического колебания и его график. § 24.8. Математический маятник. § 24.9. Законы колебания математического маятника. Формула маятника. § 24.10. Физический маятник. § 24.11. Практические применения маятников. § 24.12. Упругие колебания. Превращение энергии при колебательном движении. § 24.13. Распространение колебательного движения в упругой среде. § 24.14. Перенос энергии бегущей волной. § 24.15. Поперечные и продольные волны. § 24.16. Волна и луч. Длина волны. § 24.17. Скорость распространения волн и ее связь с длиной волны и периодом (частотой) колебаний. § 24.18. Сложение колебаний, происходящих по одной прямой. § 24.19. Отражение волн. § 24.20. Стоячие волны. § 24.21. Интерференция волн. § 24.22. Сложение колебаний с кратными частотами. Разложение сложного колебания на гармонические составляющие. § 24.23. Вынужденные колебания. Механический резонанс и его роль в технике. Глава 25. ЗВУК И УЛЬТРАЗВУК § 25.3. Громкость и интенсивность звука. § 25.4. Высота тона и тембр звука. § 25.5. Интерференция звуковых волн. § 25.6. Отражение и поглощение звука. § 25.7. Звуковой резонанс. § 25.8. Ультразвук и его применение в технике. Глава 26. ПЕРЕМЕННЫЙ ТОК § 26.2. Понятие об устройстве индукционных генераторов. § 26.3. Действующие значения э. д. с., напряжения и силы переменного тока. § 26.4. Индуктивность и емкость в цепи переменного тока. § 26.5. Преобразование переменного тока. Трансформатор. § 26.6. Индукционная катушка. § 26.7. Трехфазный ток. § 26.8. Получение, передача и распределение электрической энергии в народном хозяйстве СССР. Глава 27. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ § 27.2. Затухающие электромагнитные колебания. Электрический резонанс. § 27.3. Получение незатухающих колебаний с помощью лампового генератора. § 27.4. Токи высокой частоты и их применение. § 27.5. Электромагнитное поле как особый вид материи. § 27.6. Открытый колебательный контур. Излучение. § 27.7. Электромагнитные волны. Скорость их распространения. § 27.8. Опыты Герца. § 27.9. Изобретение радио А С. Поповым. Радиотелеграфная связь. § 27.10. Радиотелефонная связь. Амплитудная модуляция. § 27.11. Устройство простейшего лампового радиоприемника с усилителем низкой частоты. § 27.12. Понятие о радиолокации. Раздел IV. ОПТИКА. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ Глава 28. ПРИРОДА СВЕТА. РАСПРОСТРАНЕНИЕ СВЕТА § 28.2. Понятие об электромагнитной теории света. Диапазон световых волн. § 28.3. Понятие о квантовой теории света. Постоянная Планка. § 28.4. Источники света. § 28.5. Принцип Гюйгенса. Световые лучи. § 28.6. Скорость распространения света в вакууме. Опыт Майкельсона. § 28.7. Скорость распространения света в различных средах. Глава 29. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА § 29.2. Законы отражения света. § 29.3. Зеркальное и диффузное отражение. Плоское зеркало. § 29. 4. Сферические зеркала. § 29.5. Построение изображений, получаемых с помощью сферических зеркал. Формула сферического зеркала. § 29.6. Законы преломления света. § 29.7. Абсолютный показатель преломления и его связь с относительным показателем преломления. § 29.8. Полное отражение света. Предельный угол. § 29.9. Прохождение света через пластинку с параллельными гранями и через трехгранную призму. Призма с полным отражением. Глава 30. ЛИНЗЫ. ПОЛУЧЕНИЕ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ЛИНЗ § 30.2. Главные фокусы и фокальные плоскости линзы. § 30.3. Оптическая сила линзы. § 30.4. Построение изображения светящейся точки, расположенной на главной оптической оси линзы. § 30.5. Вывод формулы для сопряжеппых точек тонкой линзы. § 30.6. Построение изображения светящейся точки, расположенной на побочной оптической оси линзы. § 30.7. Построение изображений предмета, создаваемых линзой. § 30.8. Линейное увеличение, полученное с помощью линзы. § 30.9. Недостатки линз. Выясним, какие существенные недостатки встречаются у линз. Глава 31. ОПТИЧЕСКИЕ ПРИБОРЫ. ГЛАЗ § 31.2. Фотографический аппарат. § 31.3. Глаз как оптическая система. § 31.4, Длительность зрительного ощущения. § 31.5. Угол зрения. § 31.6. Расстояние наилучшего зрения. Оптические дефекты глаза. § 31.7. Увеличение оптического прибора. Лупа. § 31.8. Микроскоп. § 31.9. Труба Кеплера. Телескопы. § 31.10. Труба Галилея. Бинокль. Глава 32. ЯВЛЕНИЯ, ОБЪЯСНЯЕМЫЕ ВОЛНОВЫМИ СВОЙСТВАМИ СВЕТА § 32.2. Цвета тонких пленок. § 32.3. Интерференция в клинообразной пленке. Кольца Ньютона. § 32.4. Интерференция света в природе и технике. § 32.5. Дифракция света. § 32.6. Дифракционная решетка и дифракционный спектр. Измерение длины световой волны. § 32.7. Поляризация волн. § 32.8. Поляризация света. Поляроиды. § 32.9. Поляризация при отражении и преломлении света. Глава 33. ФОТОМЕТРИЯ § 33.2. Световой поток. § 33.3. Сила света. Единицы силы света и светового потока. § 33.4. Освещенность. § 33.5. Яркость. § 33.6. Законы освещенности. § 33.7. Сравнение силы света двух источников. Фотометр. Люксметр. Глава 34. ИЗЛУЧЕНИЕ И СПЕКТРЫ. РЕНТГЕНОВСКИЕ ЛУЧИ § 34.2. Разложение белого света призмой. Сплошной спектр. § 34.3. Сложение спектральных цветов. Дополнительные цвета. § 34.4. Цвета тел. § 34.5. Ультрафиолетовая и инфракрасная части спектра. § 34.6. Роль ультрафиолетовых и инфракрасных лучей в природе. Их применение в технике. § 34.7. Приборы для получения и исследования спектров. § 34.8. Виды спектров. § 34.9. Спектры поглощения газов. Опыты Кирхгофа. § 34.10. Закон теплового излучения Кирхгофа. § 34.11. Законы теплового излучения Стефана — Больцмана, Вина, Планка. § 34.12. Спектры Солнца и звезд. Их связь с температурой. § 34.13. Спектральный анализ. § 34.14. Понятие о принципе Доплера. § 34.15. Рентгеновские лучи и их практическое применение. § 34.16. Шкала электромагнитных волн. § 34.17. Виды космического излучения. Глава 35. ЯВЛЕНИЯ, ОБЪЯСНЯЕМЫЕ КВАНТОВЫМИ СВОЙСТВАМИ ИЗЛУЧЕНИЯ § 35.2. Давление световых лучей. Опыты П. Н. Лебедева. § 35.3. Тепловое действие света. § 35.4. Химическое действие света. § 35.5. Использование химического действия света при фотографировании. Понятие о квантовой природе химического действия излучения. § 35.6. Внешний фотоэлектрический эффект. Опыты Столетова. § 35.7. Законы внешнего фотоэффекта. § 35.8. Объяснение фотоэффекта на основе квантовой теории. § 35.9. Фотоэлементы с внешним фотоэффектом. § 35.10. Внутренний фотоэффект. § 35.11. Фотосопротивления. § 35.12. Фотоэлементы с внутренним фотоэффектом. § 35.13. Использование фотоэлементов в науке и технике. § 35.14. Понятие о телевидении. § 35.15. Понятие о теории Бора. Строение атома водорода. § 35.16. Излучение и поглощение энергии атомами. § 35.17. Явление люминесценции. § 35.18. Понятие о квантовых генераторах. Глава 36. ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 36.2. Экспериментальные основы специальной теории относительности Эйнштейна. Постулаты Эйнштейна. § 36.3. Понятие одновременности. § 36.4. Относительность понятий длины и промежутка времени § 36.5. Теорема сложения скоростей Эйнштейна. § 36.6. Масса и импульс в специальной теории относительности. § 36.7. Связь между массой и энергией. Уравнение Эйнштейна. § 36.8. Связь между импульсом и энергией. Импульс и энергия фотонов. Раздел V. ФИЗИКА АТОМНОГО ЯДРА Глава 37. СТРОЕНИЕ АТОМНОГО ЯДРА § 37.2. Радиоактивность. § 37.3. Понятие о превращении химических элементов. § 37.4. Понятие об энергии и проникающей способности радиоактивного излучения. § 37.5. Эффект Вавилова — Черенкова. § 37.6. Открытие искусственного превращения атомных ядер. § 37.7. Открытие нейтрона. § 37.8. Состав атомного ядра. Запись ядерных реакций. § 37. 9. Изотопы. § 37.10. Понятие о ядерных силах. § 37.11. Дефект массы атомных ядер. Энергия связи. Глава 38. КОСМИЧЕСКИЕ ЛУЧИ. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ § 38.2. Открытие позитрона. § 38.3. Нейтрино. § 38.4. Открытие новых элементарных частиц. § 38.5. Классификация элементарных частиц. § 38.6. Античастицы. Взаимные превращения вещества и поля. § 38.7. Гипотеза кварков. Глава 39. АТОМНАЯ ЭНЕРГИЯ И ЕЕ ИСПОЛЬЗОВАНИЕ § 39.2. Деление тяжелых атомных ядер. § 39.3. Цепная реакция деления. Ядерный взрыв. § 39.4. Ядерный реактор. § 39.5. Развитие ядерной энергетики в СССР. § 39.6. Понятие о термоядерной реакции. Энергия Солнца и звезд. § 39.7. Понятие об управляемой термоядерной реакции. § 39.8. Получение радиоактивных изотопов и их применение. Раздел VI. ОСНОВНЫЕ СВЕДЕНИЯ ПО АСТРОНОМИИ Глава 40. СТРОЕНИЕ И РАЗВИТИЕ ВСЕЛЕННОЙ § 40.2. Происхождение и развитие небесных тел. § 40.3. Понятие о космологии.

Документ без названия

Документ без названия

Работа сил электростатического поля

Сила, действующая на точечный заряд, находящийся в поле другого неподвижного точечного заряда, является центральной. Направление силы, действующей в любой точке пространства на заряд, проходит через центр заряда, создающего поле, а значение силы зависит только от расстояния до этого заряда    до точки наблюдения. (Например, поле силы тяжести является полем центральных сил).

Рис. 3,1

 

Если тело поставлено в такие условия, что в каждой точке пространства оно подвержено воздействию других тел с силой, закономерно изменяющейся от точки к точке, то говорят, что это тело находится в поле сил. Центральное поле сил потенциально. Убедимся, что электрическое поле потенциально. Вычислим работу, которая совершается силами поля неподвижного точечного заряда q над перемещающимся в этом поле точечным зарядом  (рис. 3.1). Работа на элементарном пути  равна:  или
,
так как . Отсюда на пути 1–2
                         (1)
Видно, что работа не зависит от пути, по которому перемещался в электрическом поле заряд q’, а зависит лишь от начального и конечного положений этого заряда (от r1 и r2). Следовательно, силы, действующие на заряд q’ в поле неподвижного заряда q, являются консервативными, а поле этих сил потенциальным. Этот вывод легко распространяется на поле любой системы неподвижных зарядов, так как сила , действующая на точечный заряд q‘ в таком поле, может по принципу суперпозиции быть представлена в виде , где – сила, обусловленная i-м зарядом создающей поле системы. Работа в этом случае равна алгебраической сумме работ, совершаемых отдельными силами: . Каждое из слагаемых в правой части этого выражения не зависит от пути. Поэтому не зависит от пути и работа А.
Из механики известно, что работа потенциальных сил на замкнутом пути равна нулю. Работа, совершаемая силами поля над зарядом q’ при обходе по замкнутому контуру, может быть представлена как , где –проекция вектора  на направление элементарного перемещения , то, следовательно:
                                       (2)
Это соотношение должно выполняться для любого замкнутого контура. Следует иметь в виду, что (21) справедливо только для электростатического поля. Поле движущихся зарядов (т.е. поле, изменяющееся со временем) не является потенциальным. Следовательно, условие (21) для него не выполняется.
Выражение вида  называется циркуляцией вектора  по данному контуру. Таким образом, характерным для электростатического поля является то, что циркуляция вектора напряженности по любому замкнутому контуру равна нулю.

Теорема о циркуляции вектора напряженности электростатического поля
Итак, мы утверждаем, что циркуляция вектора  в любом электростатическом поле равна нулю, т.е. . Это утверждение называют теоремой о циркуляции вектора .
Пусть в заданном поле с напряженностью  перемещается заряд по замкнутому пути 1а2б1. Для доказательства теоремы разобьем произвольный замкнутый путь на две части 1а2 и 2б1 (см. рисунок). Найдем работу по перемещению заряда q из точки 1 в точку 2. Так как работа в заданном поле не зависит от формы пути, то работа по перемещению заряда по пути 1а2 равна работе по перемещению заряда по пути 1б2  или    

Рисунок 3.2
Из сказанного выше следует, что

(Интегралы по модулю равны, но знаки противоположны). Тогда работа по замкнутому пути:
                                      (3)
или                                               (4)                                         
Поле, обладающее такими свойствами, называется потенциальным. Любое электростатическое поле является потенциальным.

Потенциальная энергия и потенциал электростатического поля

Тело, находящееся в поле потенциальных сил, обладает потенциальной энергией, за счет которой совершается работа силами поля. Следовательно, работа может быть представлена как разность значений потенциальных энергий, которыми обладает заряд q’ в точках 1 и 2 поля заряда q

Можно показать также, что, так как ,
.
Отсюда для потенциальной энергии заряда  в поле заряда q получаем:
                              (6)
Значение const в (6) обычно выбирают таким образом, чтобы при удалении заряда q’ на бесконечность () потенциальная энергия обращалась в нуль. При этом условии получается, что
                                        (7)
Будем считать q’ пробным зарядом. Тогда потенциальная энергия, которой обладает пробный заряд, зависит не только от его значения , но и от значения q и r,  определяющих поле. Следовательно, эта энергия может быть использована для описания поля, подобно тому, как была использована для этой цели сила, действующая на пробный заряд.
Разные пробные заряды ,  будут обладать в одной и той же точке поля различной энергией ,  и т.д. Однако отношение   будет для всех зарядов одно и то же. Величина
                                          (8)
называется потенциалом поля в данной точке и используется наряду с напряженностью поля , для описания электрических полей.
Как следует из (8) потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.
Таким образом, для потенциального поля точечного заряда получаем следующее выражение:
                                    (9)
Если поле создано системой точечных зарядов q1, q2, …, qn, находящихся на расстояниях соответственно r1, r2,…, rn до точки поля, в которой находится заряд , то работа, совершаемая силами этого поля над зарядом , будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности:
.
Но каждая из работ  равна:

где расстояние от заряда  до начального положения    заряда , расстояние от заряда  до конечного положения   заряда .
Следовательно:
.
Сопоставляя это выражение с соотношением , получаем для потенциальной энергии заряда  в поле системы зарядов выражение:
,                                   (10)
откуда
.                                 (11).
Следовательно, потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Из соотношения  вытекает, что заряд , находящийся в точке поля с потенциалом , обладает потенциальной энергией . Следовательно, работа сил поля над зарядом  может быть выражена через разность потенциалов:
                     (12)
Таким образом, работа, совершаемая над зарядом силами поля, равна произведению заряда на разность потенциалов в начальной и конечной точках. Если заряд  из точки с потенциалом  удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет равна
 или ,
т. е, потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки поля в бесконечность, или работе, которую надо совершить против сил электрического поля для того, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля.
За единицу потенциала следует принять потенциал в такой точке поля, для перемещения заряда в которую  из бесконечности необходимо совершить работу, равную
1 Джоулю (система единиц “Си”)

Связь между напряженностью электростатического поля и потенциалом

Напряженность электрического поля – величина, численно равная силе, действующей на заряд. Потенциал  – величина, численно равная потенциальной энергии заряда. Таким образом, между этими величинами должна существовать связь, аналогичная связи между потенциальной энергией и силой (т.е. ). Работа сил поля над зарядом  на отрезке пути  может быть представлена как , а убыль потенциальной энергии заряда, которая при этом будет возникать: . Откуда из равенства  находим:
 или ,                                    (21)
где через  обозначено произвольно выбранное направление.
Тогда,
, , ,                      (22)
Откуда
,                            (23)
где орты координатных осей, т. е., единичные вектора. Вектор с компонентами , где скалярная функция координат  называется градиентом функции  и обозначается символом  (или , где  – оператор набла). Таким образом, градиент потенциала:
                               (24)
и из (23) и (24) следует ,  что
                                   (25)

Так как градиент – это вектор, показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой, то градиентом потенциала  (где r–радиус-вектор) называется вектор, направленный в сторону наиболее быстрого возрастания потенциала, численно равный быстроте его изменения на единицу длины в этом направлении.
Поскольку  – векторная величина, то его модуль выражается как:
,                     (26)
подобно тому, как модуль вектора :
                                 (27)
Знак “–” (25) указывает на то, что напряженность  направлена в сторону убывания потенциала. Формула (25) позволяет по известным значениям  найти напряженность поля в каждой точке или решить обратную задачу, т.е., по заданным значения  в каждой точке найти разность потенциалов между двумя произвольными точками поля.

Эквипотенциальные поверхности

Потенциал электростатического поля представляет собой функцию, меняющуюся от точки к точке. Однако, во всяком реальном случае можно выделить совокупность точек, потенциалы которых одинаковы.
Геометрическое место точек постоянного потенциала называется поверхностью равного потенциала или эквипотенциальной поверхностью.
Возьмем равномерно заряженную бесконечную плоскость (рис. 3.6). Поле, создаваемое такой плоскостью однородно, а линии напряженности нормальны к плоскости. Отсюда следует, что работа перемещения заряда из некоторой точки В1 в любую другую точку В2, находящуюся на таком же расстоянии от заряженной поверхности, что и точка В1 равна нулю. Действительно, при перемещении некоторого заряда q по прямой В1В2 сила, действующая на заряд со стороны поля, будет все время перпендикулярна к перемещению, а, следовательно, ее работа равна нулю. Но эта работа может быть представлена, с другой стороны, в виде:
,                               (28)
где  и  – соответственно потенциалы точек В1 и В2. Отсюда, так как  А = 0, то =, т.е., потенциалы точек, равноудаленных от заряженной плоскости, одинаковы. Таким образом, поверхности равного потенциала (эквипотенциальные поверхности) являются плоскостями, параллельными заряженной плоскости. Если плоскость заряжена положительно, то значение потенциала убывает по мере удаления от заряженной плоскости. Очевидно, что поверхности равного потенциала расположены симметрично по обе стороны от заряженной плоскости.
Эквипотенциальные поверхности поля точечного заряда это сферы с радиусом r , центр которых находится в центре точечного заряда, т. е.  (рис. 3.7). На рис. 3.6 и рис. 3.7 вектор напряженности  перпендикулярен эквипотенциальным поверхностям.
Покажем, что вектор напряженности перпендикулярен эквипотенциальной поверхности. Рассмотрим работу по перемещению заряда по поверхности равного потенциала на малом участке пути ?S (рис. 3.7). При этом,  работа электрической силы  на данном пути будет:
,                            (29)
где α – угол между направлением силы f  и перемещением ?S. С другой стороны, эта работа может быть выражена как произведение величины перемещающегося заряда на разность потенциалов в начальном и конечном положениях заряда, т.е. .
Так как перемещение идет по эквипотенциальной поверхности, то разность потенциалов   и , или cosα = 0, значит α = 900 т.е. угол между направлением силы  и перемещением ?S равен 900. Но , т.е. направления  и  совпадают, поэтому угол между  и ?S, α=900 т.е. направление вектора напряженности электростатического поля всегда перпендикулярно к эквипотенциальной поверхности.
Эквипотенциальных поверхностей вокруг заряженного тела можно провести сколько угодно много. По густоте эквипотенциальных поверхностей можно судить о величине , однако  при условии, что разность потенциалов между двумя соседними эквипотенциальными поверхностями равна постоянной величине.
Формула       выражает связь потенциала с напряженностью и позволяет по известным значениям φ найти напряженность поля в каждой точке. Можно решить и обратную задачу, т.е. по известным значениям  в каждой точке поля найти разность потенциаловмежду двумя произвольными точками поля. Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, может быть, вычислена как:

С другой стороны работу можно представить в виде:
, тогда
Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, т.к. работа сил поля не зависит от пути.
При обходе по замкнутому контуру  получим:

т. е. пришли к известной нам теореме о циркуляции вектора напряженности: циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.
Поле, обладающее этим свойством, называется потенциальным.
Из обращения в нуль циркуляции вектора  следует, что линии  электростатического поля не могут быть замкнутыми: они начинаются на положительных зарядах (истоки) и на отрицательных зарядах заканчиваются (стоки) или уходят в бесконечность.
Обобщим теорему Гаусса и теорему о циркуляции вектора напряженности электростатического поля  в вакууме. Так как , а   , то  .  Поскольку   (- оператор Лапласа), то для потенциала φ получим выражение  или  , которое называется уравнением Пуассона.
Это уравнение позволяет по известному распределению заряда  и заданным граничным условием для потенциала φ  определить  значения  во всех точках поля, а затем по формуле   найти напряженность    поля, т. е. решить прямую задачу электростатики.

Потенциал поля точечного заряда: .

потенциал Диполя

Найдем потенциал, создаваемый в точке P(r) двумя равными по величине зарядами противоположных знаков, расположенными на небольшом расстоянии друг от друга вблизи начала координат.

Рис. 3.1

Если расстояние l между зарядами мало по сравнению с расстоянием до точки P, то такая система зарядов называется диполем. Учитывая, что l<<r, можно приближенно положить: Тогда потенциал диполя равен

(3.1)

где обозначено ql=p или

(3.2)

где вектор p определен как p=ql и называется электрическим моментом диполя или дипольным моментом.
Найдем в полярной системе координат компоненты Er и Eq вектора напряженности поля, создаваемого диполем. Для этого воспользуемся известной связью между напряженностью поля и потенциалом:

(3.3) Выразим оператор набла в полярной системе координат . Подставляя j из (3.1), будем иметь: (3.4)

Рис. 3.2

Тогда квадрат модуля вектора напряженности равен

а модуль

(3.5)

Выразим вектор E через радиус вектор r и вектор дипольного момента p. Для этого применим соотношение (3.3) к потенциалу диполя в виде (3.2). Ввиду громоздкости выкладок, найдем векторE покомпонентно



По аналогии можно получить


Тогда окончательно будем иметь

(3.6)

Полученное выражение не зависит от системы координат и выражает вектор напряженности поля через известные вектора p и r.

Потенциал системы зарядов

Рис. 3.3

Пусть вблизи начала координат находится некоторое количество точечных зарядов. Определим потенциал поля, создаваемого этими зарядами в точке P, расположенной на большом удалении (по сравнению с расстояниями между зарядами) от начала координат. В силу принципа суперпозиции потенциал всей совокупности зарядов равен сумме потенциалов, создаваемых в данной точке поля каждым из зарядов в отдельности: (3. 7)

Для определения расстояния от i-того заряда до точки P воспользуемся теоремой косинусов (см. рис. 3.3):

Учитывая, что ri/ro << 1, выражение в скобках можно представить как (1+Δx), где Δx — малая величина, по степеням которой можно сделать разложение в ряд. Ограничиваясь линейными по ri/roчленами, получим следующее выражение:

Тогда для потенциала (3.7) будем иметь

Величинаназывается электрическим дипольным моментом системы зарядов.
Окончательно для потенциала системы зарядов, расположенной вблизи начала координат, в удаленной от нее точке, характеризуемой радиус-вектором r, имеем

(3.8)

Как следует из полученного выражения, при не равном нулю суммарном заряде потенциал определяется в основном первым членом, стоящим в скобках в (3. 8), потому что он ~1/r, тогда как второй член ~1/r2. Однако во многих важных случаях суммарный заряд системы равен нулю, как это имеет место, например, для молекулы. Расположение же зарядов может быть таково, что дипольный момент системы отличен от нуля. Тогда потенциал определяется вторым членом. Заметим, что и при равном нулю дипольном моменте потенциал системы, вообще говоря, не равен нулю, а определяется членами высших порядков в разложении по степеням ri/ro. Напомним, что речь все время идет о потенциале в точках, расположенных на большом удалении от системы.

 

 

Проводники в электростатическом поле. Школьный курс физики

Главная | Физика 10 класс | Проводники в электростатическом поле

Свободные заряды.

Что происходит с телами, если их зарядить или поместить в электрическое поле? Проще всего ответить на этот вопрос, если рассмотреть случай проводника. В проводниках, к которым в первую очередь относятся металлы, имеются заряженные частицы, которые способны перемещаться внутри проводника под действием внешнего электрического поля. По этой причине заряды этих частиц называют свободными. В металлах носителями свободных зарядов являются электроны. Свободные электроны участвуют в тепловом (хаотическом) движении, подобно молекулам газа, и могут перемещаться по всему объёму металла в любом направлении.

Электростатическое поле внутри проводника.

Обобщим основные свойства электростатического поля внутри проводника.

1. Пpu равновесии зарядов на проводнике поле внутри проводника отсутствует. Это связано с тем, что свободные электроны в металлическом проводнике, помещённом в электростатическое поле, под действием сил поля будут перемещаться в направлении, противоположном его напряжённости. На рисунке 9.45 изображён проводник ABCD, находящийся в однородном электростатическом поле, напряжённость которого направлена слева направо. На поверхности проводника AC появляется избыточный отрицательный заряд, а на другой, BD, — избыточный положительный заряд.

Таким образом, проводник, помещённый в однородное электростатическое поле, электризуется. При этом заряды, появляющиеся на поверхности проводника, создадут внутри проводника своё электростатическое поле напряжённостью . Силовые линии данного поля показаны пунктиром на рисунке 9.45.

Рис. 9.45

Они направлены противоположно силовым линиям внешнего электростатического поля. Перемещение зарядов будет происходит до тех пор, пока напряжённость результирующего электростатического поля внутри проводника не станет равной нулю ¹.

---

¹ Утверждение об отсутствии поля внутри проводника справедливо как для незаряженного проводника, помещённого во внешнее электростатическое поле, так и для проводника, которому сообщён некоторый избыточный заряд.

В этом состоит явление электростатической индукции. Появившиеся на поверхности проводника заряды (их называют индуцированными) создают своё поле, которое накладывается на внешнее электростатическое поле и его компенсирует.

Для доказательства того факта, что внутри заряженного проводника или полости в проводнике электрическое поле отсутствует, Фарадей предложил прибор, называемый клеткой Фарадея (рис. 9.46).

Рис. 9.46

Он состоит из двух цилиндров, выполненных из проволочной сетки и расположенных внутри друг друга на основании из формованного пластика. Внешний цилиндр является экраном. Он позволяет наблюдать за тем, что происходит внутри внутреннего цилиндра (собственно клетки). Клетка закреплена на изолированных стержнях (изоляторах). Разность потенциалов такой конструкции с Землёй была настолько сильной, что при приближении к ней тел, соединённых с земной поверхностью, с внешней поверхности клетки вылетали искры.

В одном из опытов Фарадей сам располагался внутри клетки с очень чувствительным электроскопом. При этом электроскоп внутри клетки не показывал никакого отклонения. Другими словами, внутри клетки не действуют никакие электрические силы, хотя на наружной поверхности накапливался значительный заряд. Так было убедительно доказано, что электростатического поля внутри проводника нет.

На этом свойстве основана так называемая электростатическая защита. Для того чтобы защитить чувствительные к электрическому полю приборы, их заключают в металлические ящики.

2. Рассмотрим более подробно ещё один вид электризации тел — электризацию через влияние. Для этого проведём опыт.

Исследования физических явлений опытным путём

При приближении наэлектризованного тела к лёгкому проводнику, например к лёгкому бузиновому цилиндру, подвешенному па нити, на нём появятся индуцированные заряды обоих знаков (рис. 9.47).

Рис. 9.47

Заряд противоположного знака будет притягиваться к телу, а одноимённый — отталкиваться. Так как последний находится на стороне цилиндра, более удалённой от тела, то равнодействующей этих сил будет сила притяжения. Под действием этой силы цилиндр притянется к телу. При их соприкосновении индуцированный заряд противоположного знака нейтрализуется частью заряда тела, равного ему по величине. На цилиндре останется заряд того же знака, что и на теле. Так как цилиндр теперь имеет заряд одного знака с телом, то он оттолкнётся от тела, что и наблюдается на опыте.

3. Внутри проводника при равновесии зарядов не только напряжённость поля равна нулю, равен нулю и заряд. Весь статический заряд проводника сосредоточен на его поверхности.

Объяснить скапливание заряда на поверхности проводника одним отталкиванием одноимённых зарядов нельзя. Кавендиш экспериментально доказал, что заряд проводника целиком распределяется на его поверхности. Для этого он поместил заряженный проводящий шар на изолирующей подставке внутрь сферы, образованной двумя металлическими полусферами, плотно соединёнными друге другом.

В одной из полусфер было сделано маленькое отверстие, через которое можно было соединить заряженный шар и полусферы металлической проволокой (рис. 9.48).

Рис. 9.48

После соединения шара и полусфер проволокой полусферы раздвигались и измерялся заряд шара. Он оказался равным нулю.

4. Силовые линии электростатического поля вне проводника в непосредственной близости к его поверхности перпендикулярны поверхности. Если бы это было не так, то имелась бы составляющая напряжённости поля вдоль поверхности проводника. Она вызывала бы перемещение зарядов вдоль поверхности. Но это противоречит необходимому равновесному распределению зарядов на поверхности заряженного проводника.

5. Поверхность любого проводника в электростатическом поле яв ляется эквипотенциальной. Это связано с тем, что силовые линии электрического поля перпендикулярны поверхности проводника.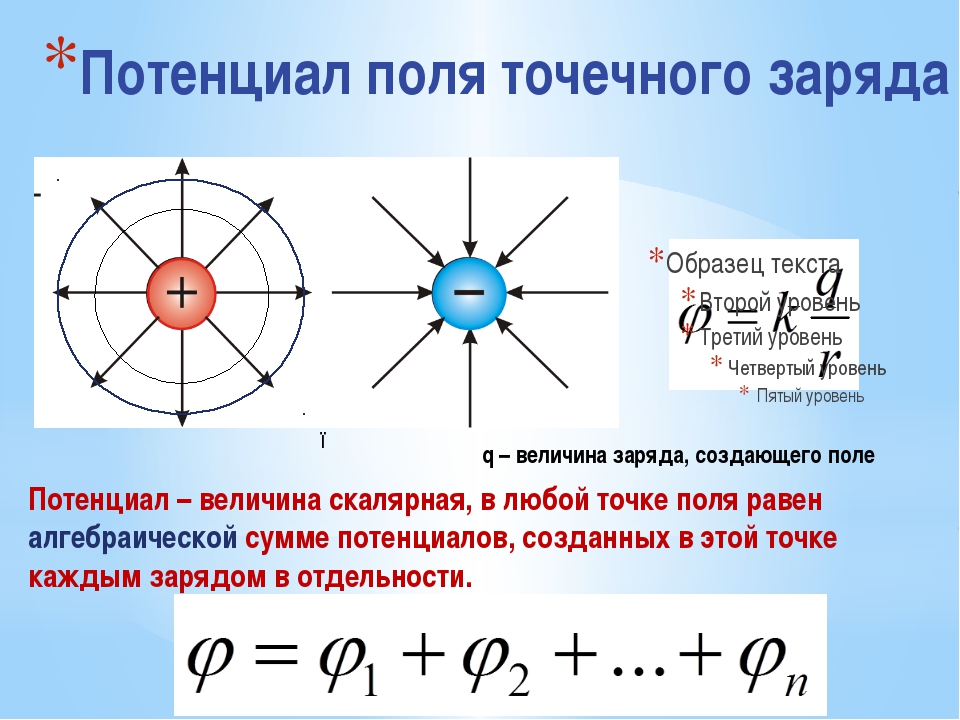 Причём не только поверхность, но и все точки внутри проводника имеют один и тот же потенциал. Напряжённость ноля внутри проводника равна нулю, поэтому равна нулю и разность потенциалов между любыми точками проводника.

6. Многочисленные эксперименты свидетельствуют о том, что напряжённость электростатического поля зависит от кривизны поверхности. Чем сильнее искривлена поверхность, тем больше поверхностная плотность заряда (см. § 61 «Напряжённость поля различной конфигурации зарядов») в этом месте. На острие заряженного проводника поверхностная плотность заряда может стать настолько большой, что заряды начинают с него «стекать».

Причина этого явления состоит в большой напряжённости и значительной неоднородности электростатического поля вблизи острия. В сильном поле нейтральные молекулы воздуха поляризуются, коснувшись острия, молекулы приобретают одинаковый с ним заряд и отталкиваются от него. Заряженные молекулы удаляются от острия с большими скоростями, чем они приближались к нему, и увлекают за собой другие молекулы воздуха. Возникает так называемый «электрический ветер», которым можно даже погасить зажжённую свечу. В демонстрационном приборе — колесе Франклина — «электрический ветер», образующийся при стекании зарядов с остриёв, приводит во вращение изогнутые спицы с остриями на концах (рис. 9.49).

Рис. 9.49

Вопросы:

1. Почему заряды в проводниках называют свободными?

2. Объясните, почему при равновесии зарядов на проводнике электростатическое поле внутри проводника отсутствует.

3. В чём состоит явление электростатической индукции?

4. Какой вывод можно сделать на основе опытов с клеткой Фарадея?

5. Какой способ электризации тел называют электризацией через влияние?

6. Почему поверхность проводника является эквипотенциальной?

Вопросы для обсуждения:

1. Если коснуться стержня заряженного электроскопа пальцем, то электроскоп разрядится. Произойдёт ли то же самое, если вблизи электроскопа находится заряженное тело?

2. Металлический заряженный цилиндр соединён с электроскопом. Наличие каких зарядов покажет электроскоп в тех случаях, когда:

а) в цилиндр вносится положительно заряженный шарик, не соприкасающийся с ним;

б) заряженным шариком касаются внутренней поверхности цилиндра?

Пример решения задачи

Положительный точечный заряд, модуль которого равен 3 ∙ 10 ^-7 Кл, находится на расстоянии 5 см от поверхности незаряженного проводящего шара радиусом 3 см. Определите потенциал поверхности шара. Найдите модуль заряда, который появится на шаре при его заземлении.

Рис. 9.50

В созданном зарядом q электрическом поле незаряженный шар электризуется. В результате на его поверхности появляются индуцированные заряды —q_инд и ÷q_инд. Используя формулу для потенциала поля точечного заряда, запишем:

Подставляя числовые данные, получим:

Определим модуль заряда, который появится на шаре при его заземлении (рис. 9.51).

Рис. 9.51

Шар заземлён, поэтому φ₀ = 0, так же, как и потенциал любой точки шара (положительный заряд уйдёт в землю). C учётом этого запишем:

Подставляя числовые данные, получим:

Ответ: φ₀ ≈ 3,4 • 10 ⁴ В, Q ≈ 1,1 • 10 ^-7 Кл.

Упражнения:

1. К заряженному электрометру подносят с большого расстояния отрицательно заряженный предмет. По мере приближения предмета показания электрометра сначала уменьшаются, а с некоторого момента вновь увеличиваются. Заряд какого знака был на электрометре?

2. Допустим, в вашем распоряжении имеются два изолированных металлических шара одинакового диаметра. Каким образом можно на них получить равные по модулю заряды:

а) разноимённые;

б) одноимённые?

3. Две металлические концентрические сферы радиусами 15 и 30 см расположены в воздухе. На внутренней сфере расположен заряд, равный -20 нКл. При этом потенциал внешней сферы равен 450 В. Вычислите напряжённость и потенциал электростатического поля в точках, удалённых от центра сфер:

а) на 10 см;

б) 20 см;

в) 36 см.

4. Металлический шар радиусом 3,2 см, заряженный до потенциала 100 В, находится далеко от других заряженных тел и Земли. Чему будет равен модуль заряда на шаре, если его соединить длинным проводником с незаряженным металлическим шаром радиусом 32 см?

Предыдущая страницаСледующая страница

Определение расположения эквипотенциален и построение силовых линий электрических полей

ЦЕЛЬ РАБОТЫ: определение расположения эквипотенциален и построение силовых линий электрических полей.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ.

Между напряженностью электрического доля и электрическим потенциалом существует интегральная и дифференциальная связь:

j₁ — j₂ = ∫Еdl   (1)

E = -gradj   (2)

Электрическое поле может быть представлено графически двумя способами, дополняющими друг друга: с помощью эквипотенциальных поверхностей и ли­ний напряженности (силовых линий).

Поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Линия пересечения ее с плоскостью чертежа называется эквипотенциалью. Силовые линии — линии, касательные к которым в каждой точке совпадают с направлением вектора Е. На рисунке 1 пунктирными линиями показаны эквипотенциали, сплошными — силовые линии электрического поля.

 

Рис.1

Разность потенциалов между точками 1 и 2 равна 0, так как они находятся на одной эквипотенциали. В этом случае из (1):

∫Еdl = 0 или ∫Еdlcos(Edl) = 0   (3)

Поскольку Е и dl в выражении (3) не равны 0, то cos(Edl) = 0. Следовательно, угол между эквипотенциалью и силовой линией составляет p/2.

Из дифференциальной связи (2) следует, что силовые линии всегда направлены в сторону убывания потенциала.

Величина напряженности электрического поля определяется «густотой» сило­вых линий. Чем гуще силовые линии, тем меньше расстояние между эквипотенциалями, так что силовые линии и эквипотенциали образуют «криволинейные квадраты». Исходя из этих принципов, можно построить картину силовых линий, располагая картиной эквипотенциалей, и наоборот.

Достаточно полная картина эквипотенциалей поля позволяет рассчитать в раз­ных точках значение проекции вектора напряженности Е на выбранное направ­ление х, усредненное по некоторому интервалу координаты ∆х:

Е_{ср. ∆х} = — ∆j/∆х,

где ∆х — приращение координаты при переходе с одной эквипотенциали на дру­гую,

∆j — соответствующее ему приращение потенциала,

Е_{ср. ∆х} — среднее значение Е_х между двумя потенциалами.

ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКА ИЗМЕРЕНИЙ.

Для моделирования электрического поля удобно использовать аналогию, су­ществующую между электрическим полем, созданным заряженными телами и электрическим полем постоянного тока, текущего по проводящей пленке с одно­родной проводимостью. При этом расположение силовых линий электрического поля оказывается аналогично расположению линий электрических токов.

То же утверждение справедливо для потенциалов. Распределение потенциалов поля в проводящей пленке такое же, как в электрическом поле в вакууме.

В качестве проводящей пленки в работе используется электропроводная бума­га с одинаковой во всех направлениях проводимостью.

На бумаге устанавливаются электроды так, чтобы обеспечивался хороший кон­такт между каждым электродом и проводящей бумагой.

Рабочая схема установки приведена на рисунке 2. Установка состоит из модуля II, выносного элемента I, индикатора III, источника питания IV. Модуль служит для подключения всех используемых приборов. Выносной элемент представляет собой диэлектрическую панель 1, на которую помещают лист белой бумаги 2, по­верх нее — лист копировальной бумаги 3, затем — лист электропроводящей бумаги 4, на котором крепятся электроды 5. Напряжение на электроды подается от моду­ля II с помощью соединительных проводов. Индикатор III и зонд 6 используются для определения потенциалов точек на поверхности электропроводящей бумаги.

В качестве зонда применяется провод со штекером на конце. Потенциал j зонда равен потенциалу той точки поверхности электропроводящей бумаги, которой он касается. Совокупность точек поля с одинаковым потенциалом и есть изображе­ние эквипотенциали поля. В качестве источника питания IV используется блок питания ТЕС – 42, который подключается к модулю с помощью штепсельного разъема на задней стенке модуля. В качестве индикатора Ш используется вольт­метр В7 – 38.

 

Рис. 2.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1.  Установить на панели 1 лист белой бумаги 2. На него положить копироваль­ную бумагу 3 и лист электропроводящей бумаги 4 (рис.2).

2.  Установить на электропроводящей бумаге электроды 5 и закрепить гайками.

3.  Подключить к модулю блок питания IV (ТЕС – 42) с помощью штепсельного разъема на задней стенке модуля.

4.  С помощью двух проводников подключить индикатор III (вольтметр В7 – 38) к гнездам «PV» на лицевой панели модуля. Нажать соответствующую кнопку на вольтметре для измерения постоянного напряжения (рис.2).

5.  С помощью двух проводников подключить электроды 5 к модулю П.

6.  Подключить зонд (провод с двумя штекерами) к гнезду на лицевой панели модуля.

7.  Подключить стенд к сети 220 В. Включить общее питание стенда.

Электростатика. Потенциал — презентация онлайн

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

Физика. 2 курс. 3 семестр, специалитет
Лекция 2. Электростатика. Потенциал.
В.И. Читайкин
кандидат физико-математических наук
доцент
План лекции
Наименование раздела
Номер
слайда
Введение
3
Раздел 1. Понятие потенциала
4
Раздел 1.1. Работа сил электростатического поля
9
Раздел 2. Примеры: потенциал и напряжённость для
«типовых» электрических зарядов
11
2
Введение
Во второй лекции продолжается изучение раздела «Электростатика».
Будет введена ещё одна важная характеристика электростатического поля –
потенциал φ и установлена его связь с понятием напряжённости
электростатического поля Е, рассмотренном в первой лекции.
Понятия потенциала φ и напряжённости электростатического поля Е
позволяют определить и рассчитывать практически важные характеристики:
— работу сил поля,
— собственно потенциал точечного, сферического и других зарядов,
а также будут широко использоваться в других разделах «Электромагнетизма».
3
Раздел 1. Понятие потенциала
4
1. Понятие потенциала
Потенциал — характеристика электростатического поля, создаваемого зарядом q на
расстоянии r от этого заряда. Потенциал, наряду с напряжённостью (см. лекцию 1), являются
характеристиками электростатического поля.
Напряжённость (Е)
Е – это сила Кулона в расчёте на «пробный»
положительный заряд q0 (или qпр)
Потенциал (φ)
φ – это потенциальная энергия в расчёте на
«пробный» положительный заряд q0 (или qпр)
φ
F – сила Кулона (см. лекцию 1)
W – потенциальная энергия поля, W = F·r
Размерность [Е] – В/м
Размерность [φ] – В = 1 Дж/Кл
Е – векторная величина
φ – скалярная величина
Е – силовая характеристика поля
φ – энергетическая характеристика поля
Связь между напряжённостью и потенциалом:
— для постоянного по пространству поля: Е = φ / r или φ = E·r
— для переменного по пространству поля: E = — dφ/dr или φ = — ∫Edr
5
1. Понятие потенциала
Важное различие между напряжённостью Е и потенциалом φ: обе величины
уменьшаются по мере удаления от заряда q, создавшего поле. Но напряжённость Е убывает
быстрее, чем потенциал φ.
φ
Е
Е
~ r-2 (синия линия)
φ
~ r-1 (красная линия)
Заряд q находится в точке О
График Е(r) спадает «круче», чем график φ(r)
6
1. Понятие потенциала
Эквипотенциальная поверхность – это поверхность (в 3D-пространстве) или линия
(в 2D-пространстве), во всех точках которой потенциал φ имеет одно и то же значение.
Точечный заряд: φ ~ r-1
эквипотенциальные линии в 2D-пространстве
– концентрические круги
Два разноимённых точечных заряда:
эквипотенциальные линии в 2D-пространстве
образуют более сложную картину.
7
1. Понятие потенциала
Разность потенциалов
Каждой окружности (эквипотенциальной линии) радиуса r
соответствует определённое значение потенциала φ
.
Разность потенциалов: U = φi – φi+1.
Например, разность потенциалов между эквипотенциальными
линиями с радиусами r1 и r2:
U12 = φ1 – φ2
(принято: среда – вакуум, ε=1)
Важный вывод: Разность потенциалов точек, расположенных на
одной эквипотенциальной линии (поверхности) равна нулю, т. к. в этом
случае r1 = r2.
8
1. Понятие потенциала
1.1. Работа сил электростатического поля определяется при перемещении какоголибо заряда q0 в поле заряда q из одной точки в другую (1→2), т.е. с одной эвкипотенциальной
поверхности радиуса r1 на другую радиуса r2.
А = q0·(φ1 – φ2) = q0·
q
Важный вывод:
Траектория перемещения заряда q0 в поле заряда q
может быть любой, сколь угодно запутанной, например, красная
линия на рисунке.
Но совершённая при этом работа А будет
определяться только разностью потенциалов начальной
точки 1 и конечной точки 2. Т.е. для обеих траекторий
перемещения (кратчайшей и запутанной) работа будет одинаковой.
●1
q0
●2
Траектории перемещения
заряда q0 в поле центрального
заряда q из точки 1 в точку 2:
синий цвет – кратчайшая,
красный цвет – запутанная.
9
1. Понятие потенциала
1.1. Работа сил электростатического поля: важной следствие
Из вывода, сделанного на предыдущем слайде, вытекает
следующее:
Если траектория перемещения заряда q0 во внешнем электростатическом поле будет замкнутой (начальная и конечная точки
совпадают – жёлтая линия), то совершаемая при этом работа
будет равна нулю.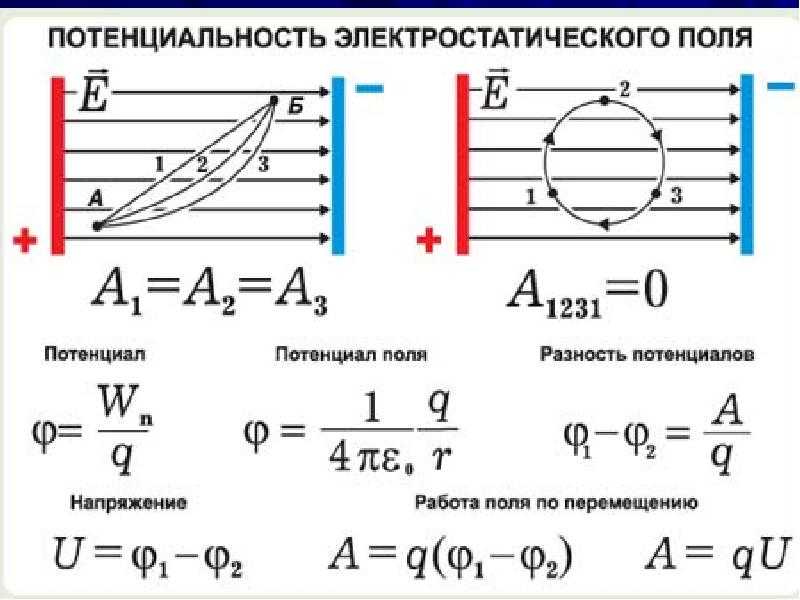
dA = d A = 0.
L – длина замкнутой траектории
Элементарная работа dA, совершаемая полем Е на элементарном
участке траектории dl, равна dA = E·dl .
Теорема о циркуляции вектора напряжённости:
Для замкнутой траектории справедливо утверждение:
dA =
q
q0
Замкнутая траектория
перемещения заряда q0 во
внешнем поле центрального
заряда q : жёлтая линия.
= 0. = 0.
10
Раздел 2. Примеры: потенциал и напряжённость
для «типовых» электрических зарядов
11
1. Примеры: «типовые» заряды
«Типовые» заряды и электрическое поле, создаваемое ими, будут подробно
рассматриваться на семинарских занятиях.
Здесь приведены качественные рисунки для некоторых таких зарядов.
Прошу:
1. Ответить на вопрос: шар полый
или сплошной?
2. Нарисовать потенциал и
напряжённость для бесконечно
тонкого заряженного цилиндра
(проводник).
12
1. Примеры: «типовые» заряды
Подсказка для первого вопроса.
13
Спасибо за внимание

English     Русский Правила

Электрическая потенциальная энергия (U) и электрический потенциал (В): (Примечания к C

Электрическая потенциальная энергия (U) и электрический потенциал (V): ( Заметки из лекций C. Erkals PHYS 221 )

 

электрическое поле между его большими пластинами. Это достигается подключением каждой пластины к одному из выводов источник питания (например, аккумулятор).

 

 

 

Рисунок 1: Электрическое поле создается заряженными пластинами разделены расстоянием l. обвинения на пластинах +Q и Q.

 

Рис. 2: Электрический заряд q перемещается из точки A в направлении точка B с внешней силой T против электрической силы qE.

 

Рис. 3, 4: При перемещении на расстояние d его потенциальная энергия в точке B равна qEd относительно точки A.

 

Рис. 5. При выходе из положения B (T = 0) оно ускоряется к нижней пластине. Как он движется по направлению к нижней пластине ее потенциальная энергия уменьшается, а ее кинетическая энергия увеличивается. Когда он достигает нижней пластина (где мы можем выбрать Потенциальную энергию равной нулю), ее потенциал энергия в точке A полностью преобразуется в кинетическую энергию в точке B:

 

 

Обратите внимание, что qEd — это работа, совершаемая полем в виде заряда. движется под действием силы qE из В в А. Здесь m — масса заряда q, а v — его скорость при достижении точка А. Здесь мы предполагали, что электрические поле однородное! Работа, проделанная полем E:

 

 

 

 

Давайте вспомним теорему о кинетической энергии-работе (рабочая энергия принцип):

 

 

 

где мы ввели понятие потенциальной энергии и консервативная сила (сила, под действием которой можно определить потенциальную энергию так, что совершенная работа зависит только от разницы потенциальной энергии функция оценивается в конечных точках).

 

Эмпирическое правило для принятия решения о том, является ли EPE возрастание:

Если заряд движется в направлении, в котором он нормально двигаться, его электрическая потенциальная энергия уменьшается. Если заряд перемещается в направлении, противоположном чтобы он нормально двигался, его электрическая потенциальная энергия увеличивается. Эта ситуация аналогична ситуации постоянное гравитационное поле (g = 9,8 м/с ² ). Когда вы поднимаете предмет, вы увеличивает свою гравитационную потенциальную энергию. Точно так же, когда вы опускаете объект, его гравитационная энергия уменьшение.

 

Общая формула для разности потенциалов:

 

Работа, совершаемая полем E при воздействии на заряд q для перемещения это из точки А в точку Б определяется как разность электрических потенциалов между точки A и B:

 

 

Ясно, что потенциальная функция V может быть поставлена ​​в соответствие каждой точка в пространстве, окружающем распределение заряда (например, параллельная тарелки). Приведенная выше формула обеспечивает простой рецепт для расчета работы, совершаемой при перемещении заряда между двумя точками где мы знаем величину разности потенциалов. Приведенные выше утверждения и формула справедливы независимо от пути, по которому перемещается заряд. Особый интерес представляет потенциал точечного заряда Q. Его можно найти, просто выполнив интегрирование по простому пути (например, по прямой) из точки A чье расстояние от Q равно r до бесконечности. Путь выбирается по радиальной линии так, чтобы становится просто Edr. Поскольку электрическое поле Q равно кОм/р, заряжать. Обратите внимание, что потенциальная функция скалярная величина, в отличие от электрического поля, являющегося векторной величиной. Теперь мы можем определить электрический потенциал энергия системы зарядов или зарядовых распределений. Предположим, мы вычисляем работу, совершенную против электрические силы при перемещении заряда q из бесконечности в точку на расстоянии r от заряд Q. Работа определяется:

 

 

Обратите внимание, что если q отрицательно, его знак должен использоваться в уравнение! Таким образом, система состоящий из отрицательного и положительного точечных зарядов, имеет отрицательный потенциальная энергия.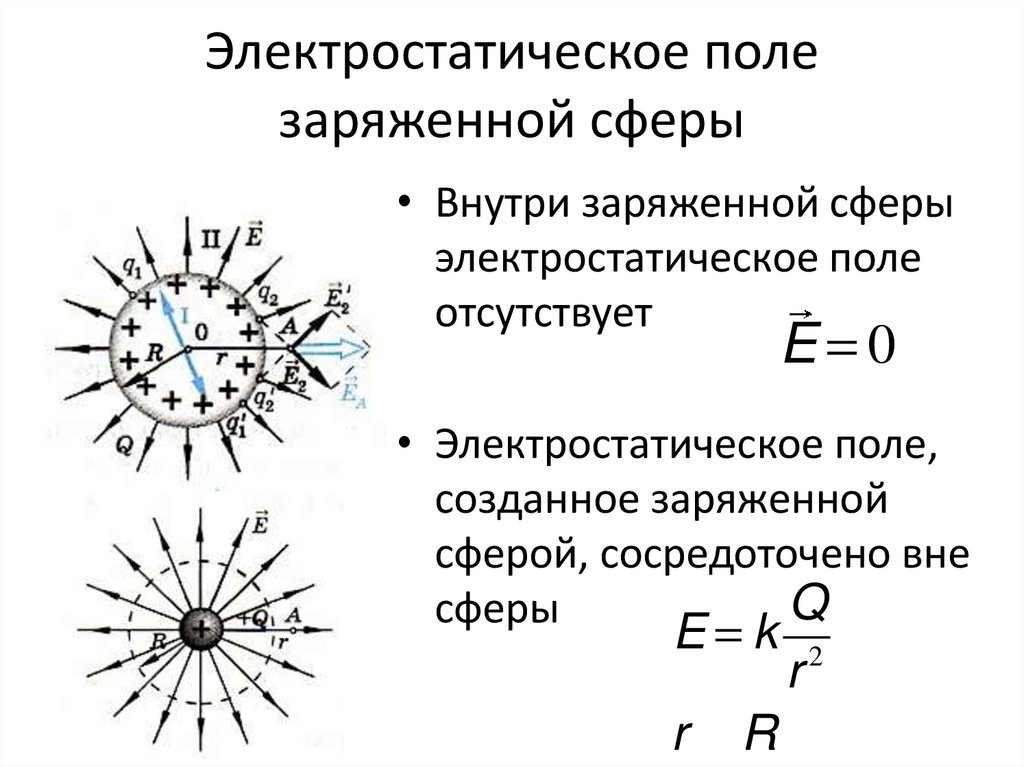

Отрицательная потенциальная энергия означает, что необходимо совершить работу против электрического поля при раздвигании зарядов!

Теперь рассмотрим более общий случай, связанный с потенциал в окрестности ряда зарядов, как показано на рисунке ниже:

 

Пусть r ₁ ,r ₂ ,r ₃ расстояния зарядов до точки поля А, и r ₁₂ , r ₁₃ , r ₂₃ представляют расстояние между зарядами. Электрический потенциал в точке А равен:

 

 

Пример:

Если мы принесем заряд Q из бесконечности и поместим его в точку А проделанная работа будет:

 

 

Полная электрическая потенциальная энергия этой системы зарядов, а именно работа, необходимая для приведения их в текущую позицию, может быть рассчитывается следующим образом: сначала принесите q1 (ноль работы, так как нет заряда вокруг еще), то в поле q1 вносим q2, то в поля q1 и q2 принести Q3. Добавьте всю работу, необходимую для вычислить общую работу. Результат будет:

 

 

 

Определение электрического поля по электрическому потенциалу:

 

Составляющая E в любом направлении является отрицательной скорость изменения потенциала с расстоянием в этом направлении:

 

Символ называется градиентом. Электрическое поле – это градиент электрического потенциала. Линии электрического поля всегда перпендикулярно эквипотенциальным поверхностям.

 

Эквипотенциальные поверхности:

Это воображаемые поверхности, окружающие заряд. распределение. В частности, если распределение заряда сферическое (точечный заряд или равномерно заряженная сфера), поверхности сферические, концентрические с центром заряда распределение. Линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Уравнение подразумевает, что из-за отрицательный знак, направление E противоположно направлению, в котором V увеличивается; E направлена ​​от высших к низшим уровням V (от высших потенциал к более низкому потенциалу). Другой Другими словами, градиент скаляра (в данном случае поля E) нормальен к поверхности постоянного значения (эквипотенциальная поверхность) скаляра и в направлении максимальная скорость изменения постоянного скаляра. Помните об этом утверждении, когда будете проводить эксперимент.

B5: Работа электрического поля и электрического потенциала

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5880

• Джеффри В. Шник
• Колледж Святого Ансельма

Когда заряженная частица перемещается из одного положения в электрическом поле в другое положение в том же электрическом поле, электрическое поле совершает работу над частицей. Проделанная работа консервативна; следовательно, мы можем определить потенциальную энергию для случая силы, действующей со стороны электрического поля. Это позволяет нам использовать понятия работы, энергии и сохранения энергии при анализе физических процессов с участием заряженных частиц и электрических полей.

Мы определили работу, совершаемую силой над частицей, как произведение силы вдоль пути на длину пути, при условии, что когда составляющая силы вдоль пути различна на разных участках пути, нужно разбить путь на отрезки, на каждом из которых сила вдоль пути имеет одно значение для всего отрезка, вычислить работу, совершенную на каждом отрезке, и сложить результаты.

Исследуем работу, совершаемую электрическим полем над заряженной частицей при ее движении в электрическом поле в достаточно простом случае однородного электрического поля. Например, рассчитаем работу, совершаемую положительно заряженной частицей с зарядом q при ее движении из точки \(P_1\) в точку \(P_3\)

по пути: «Из \(P_1\) прямо в точку \(P_2\) и оттуда прямо в \(P_3\)». Обратите внимание, что нам не говорят, что заставляет частицу двигаться. В данной задаче нас это не волнует. Возможно, заряженная частица находится на конце кварцевого стержня (кварц — хороший изолятор), и человек, держащий стержень за другой конец, перемещает стержень так, чтобы заряженная частица двигалась, как указано.

На первом участке пути, от \(P_1\) до \(P_2\), сила на заряженную частицу перпендикулярна пути.

Сила не имеет составляющей на пути, поэтому она вообще не действует на заряженную частицу, когда заряженная частица движется из точки \(P_1\) в точку \(P_2\).

\[W_{12}=0 \nonumber \]

Из \(P_2\) частица попадает прямо в \(P_3\).

На этом отрезке пути (от \(P_2\) до \(P_3\)) сила действует точно в том же направлении, что и частица.

Таким образом, работа равна произведению величины силы на длину сегмента пути:

\[W_{23}=Fb \nonumber \]

Величина силы равна заряду частицы, умноженному на величину электрического поля \(F = qE\), поэтому

\[W_{ 23}=qEb \nonumber \]

Таким образом, работа, совершаемая электрическим полем над заряженной частицей при движении частицы из точки \(P_1\) в \(P_3\) по заданному пути, равна

\[ W_{123}=W_{12}+W_{23} \номер \]

\[W_{123}=0+qEb \неномер \]

\[W_{123}=qEb \неномер \]

Теперь посчитаем работу, совершаемую заряженной частицей, если она совершает такое же смещение (из \(P_1\) в \(P_3\) ), но движется по прямому пути, прямо из \(P_1\) в \(P_3\).

Сила, действующая на положительно заряженную частицу в том же направлении, что и электрическое поле, вектор силы составляет угол \(\theta\) с направлением пути и выражение

\[W=\vec{ F} \cdot \vec{\Delta r} \nonumber \]

для работы становится

\[W_{13}=F c \, cos \theta \nonumber \]

\[W_{13}=qE c \, cos \theta \nonumber \]

Анализ заштрихованного треугольника на следующей диаграмме :

мы находим, что \(cos \theta=\frac{b}{c}\). Подставляя это в наше выражение для работы ( \(W_{13}=qE c \, cos \theta\) ) получаем

\[W_{13}=qEc \frac{b}{c} \nonumber \]

\[W_{13}=qEb \nonumber \]

Это тот же результат, который мы получили для работы, совершаемой электрическим полем над заряженной частицей при движении частицы между теми же двумя точками (из \(P_1\) в \(P_3\) ) по другому пути (\(P_1\) в \(P_2\) в \(P_3\) ). Как оказалось, проделанная работа одинакова независимо от того, какой путь проходит частица на пути из \(P_1\) в \(P_3\). Я не хочу тратить время на то, чтобы доказывать это здесь, но я хотел бы исследовать еще один путь (не столько для получения результата, сколько для повторения важного момента о том, как вычислить работу). Ссылаясь на схему:

Рассчитаем работу, совершаемую электрическим полем над частицей с зарядом \(q\), при движении частицы из \(P_1\) в \(P_3\) по пути «из \(P_1\ ) прямо в \(P_4\), из \(P_4\) прямо в \(P_5\) и из \(P_5\) прямо в \(P_3\)». От \(P_1\) до \(P_4\) сила действует точно в том же направлении, что и направление, в котором частица движется по траектории, поэтому

\[W_{14}=F(b+d) \номер \]

\[W_{14}=qE(b+d) \неномер \]

От точки \(P_4\) до \(P_5\) сила, действующая на заряженную частицу со стороны электрического поля, направлена ​​под прямым углом к ​​траектории, поэтому на отрезке эта сила не действует на заряженную частицу \( P_4\) до \(P_5\).

\[W_{45}=0 \nonumber \]

На отрезке от \(P_5\) до \(P_3\),

сила направлена ​​прямо противоположно направлению, в котором частица движется. Это означает, что работа, совершаемая силой электрического поля над заряженной частицей при движении частицы из \(P_5\) в \(P_3\), равна отрицательному значению величины силы, умноженной на длину сегмента пути. Таким образом

\[W_{53}=-Fd \nonumber \]

\[W_{53}=-qEd \nonumber \]

и

\[W_{1453}=W_{14}+W_{45 }+W_{53} \без номера \]

\[W_{1453}=qE(b+d)+0+(-qEd) \без номера \]

\[W_{1453}=qEb \без номера \]

Как было объявлено, мы получаем тот же результат для работы, проделанной над частицей, когда она движется от \(P_1\) к \(P_3\) вдоль «\(P_1\) к \(P_4\) к \(P_5\ ) в \(P_3\)», как и в двух других путях.

Всякий раз, когда работа, совершаемая над частицей силой, действующей на эту частицу, когда эта частица движется из точки \(P_1\) в точку \(P_3\), одинакова, независимо от того, какой путь частица выбирает на пути из \(P_1\) до \(P_3\), мы можем определить функцию потенциальной энергии для силы. Функция потенциальной энергии — это присвоение значения потенциальной энергии каждой точке пространства. Такое задание позволяет вычислить работу, совершаемую над частицей силой при движении частицы из точки \(P_1\) в точку \(P_3\), просто вычитая значение потенциальной энергии частицы в точке \(P_1 \) от значения потенциальной энергии частицы в точке \(P_3\) и взятия отрицательного результата. Другими словами, работа, совершаемая над частицей силой электрического поля при переходе частицы из одной точки в другую, есть как раз отрицательная величина изменения потенциальной энергии частицы.

При определении функции потенциальной энергии для случая частицы с зарядом \(q\) в однородном электрическом поле \(\vec{E}\) (бесконечный набор векторов, каждый из которых указывает в одну и ту же направление и каждая из которых имеет одну и ту же величину \(E\) ), мы в значительной степени полагаемся на ваше понимание гравитационной потенциальной энергии околоземной поверхности. Около поверхности земли, как мы говорили еще в первом томе этой книги, существует однородное гравитационное поле (векторное поле силы на массу), направленное вниз. Частица массы \(m\) в этом поле имеет силу «\(mg\) вниз», действующую на нее в любом месте вблизи поверхности земли. В этом случае потенциальная энергия частицы массы \(m\) определяется выражением \(mgy\), где \(mg\) — величина направленной вниз силы, а \(y\) — высота, на которой частица выше произвольно выбранного контрольного уровня. Для простоты сравнения со случаем электрического поля мы теперь описываем опорный уровень для гравитационной потенциальной энергии как плоскость, перпендикулярную гравитационному полю \(g\), поле вектора силы на массу; и; мы называем переменную \(y\) расстоянием «вверх поля» (расстоянием в направлении, противоположном направлению гравитационного поля), на котором частица находится от плоскости отсчета. (Итак, мы называем направление, в котором указывает гравитационное поле, направление, которое, как вы знаете, направлено вниз, направлением «нижнего поля».)

Теперь перейдем к случаю однородного электрического поля. Как и в случае с приземным поверхностным гравитационным полем, сила, действующая на свою жертву со стороны однородного электрического поля, имеет одну и ту же величину и направление в любой точке пространства. Конечно, в случае с электрическим полем сила равна \(qE\), а не \(mg\), и характеристика жертвы, которая имеет значение, — это заряд \(q\), а не масса \(m\). Мы называем направление, в котором указывает электрическое поле, направлением «слабого поля», а противоположное направление направлением «сильного поля». Теперь мы произвольно определяем плоскость, перпендикулярную электрическому полю, как плоскость отсчета для электрической потенциальной энергии частицы с зарядом \(q\) в электрическом поле. Если мы назовем \(d\) расстоянием, на котором заряженная частица удалена от плоскости в направлении сильного поля, то потенциальная энергия частицы с зарядом \(q\) определяется выражением

\[U=qEd \nonumber \]

где

\(U\) — электрическая потенциальная энергия заряженной частицы,

\(q\) — заряд частицы,

\(E \) — это величина каждого вектора электрического поля, составляющего однородное электрическое поле, а

\(d\) — это «сильное поле», на котором частица находится от эталонной плоскости \(U = 0\).

Убедимся, что это выражение для функции потенциальной энергии дает результат, полученный нами ранее для работы, совершаемой над частицей с зарядом \(q\) однородным электрическим полем, изображенным на следующей диаграмме, когда частица движется из \ (P_1\) до \(P_3\)

Как видите, я решил (для собственного удобства) определить опорную плоскость так, чтобы она находилась в самом нижнем положении, имеющем отношение к проблеме. При таком выборе частица заряда \(q\), когда она находится в \(P_1\), имеет потенциальную энергию \(qEb\) (поскольку точка \(P_1\) находится на расстоянии \(b\) «сильного поля» от плоскости отсчета) и, когда она находится в \(P_3\), частица заряда \(q\) имеет потенциальную энергию \(0\), так как \(P_3\) находится на плоскости отсчета.

\[W_{13}=-\Дельта U \номер\]

\[W_{13}=-(U_3-U_1) \без номера \]

\[W_{13}=-(0-qEb) \без номера \]

\[W_{13}=qEb \без номера \]

Это действительно результат, который мы получили (для работы электрического поля над частицей с зарядом \(q\) при перемещении этой частицы из \(P_1\) в \(P_3\)) другой три способа, которыми мы рассчитали эту работу.

---

Эта страница под названием B5: Работа, проделанная электрическим полем и электрическим потенциалом, распространяется под лицензией CC BY-SA 2.5 и была создана, изменена и/или курирована Джеффри В. Шником через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Джеффри В. Шник

   Лицензия

   CC BY-SA

   Версия лицензии

   2,5

   Показать оглавление

   нет

2. Теги

   1. источник@http://www. cbphysics.org

Электрический потенциал

Электрический (или электростатический) потенциал можно определить как работу, проделанную для переноса единичного положительного заряда из бесконечности в эту точку поля; единица заряда, связанная со статическим (неизменным во времени) электрическим полем

Измеряется в вольт (В) .

Это скалярная величина .

Разность электрических потенциалов между двумя точками известна как разность потенциалов или напряжение .

Вы привыкли жить в материальном измерении, в котором объекты «тяготеют» к точке или от нее из-за градиента ландшафта вокруг них. Неподвижный мяч всегда будет катиться вниз по склону, если его положить на наклонную поверхность, и останется неподвижным на ровной поверхности.

Подумайте об «электрическом измерении». Тот, где заряды создают пейзаж, на который реагируют все заряженные объекты.

Посмотрите на приведенное выше определение электрического потенциала и подумайте о нем с точки зрения гравитационного потенциала. Мы могли бы сказать, что гравитационное потенциальное (положение в гравитационном поле) — это потенциальная энергия на единицу веса, связанная с гравитационным полем — эти два параметра сопоставимы

Размерность материи	Электрический размер
Высота над уровнем моря (м)	Электрический потенциал (В)
Гравитационная потенциальная энергия (Нм = Дж) = mgh = вес x рост	Электрическая потенциальная энергия (CV = J) = заряд x электрический потенциал
Вес (Н)	Заряд (С)

 

Если вы думаете об электрическом поле как о «ландшафте для заряда» — холмах и долинах, которые заставят свободно «катящийся» заряд ускоряться и/или замедляться по мере его прохождения через него, то вы можно думать об электрическом потенциале как о «высоте» различных точек на этом «ландшафте» 9. 0015

Вы можете нанести точки эквипотенциала вокруг заряда, чтобы получить «контурную карту» этого электрического ландшафта. Говорят, что точка в пространстве, находящаяся на бесконечном расстоянии от любого заряда, находится при нулевом напряжении. На трехмерной диаграмме выше вы видите это как «плоскость» — плоскую область в ландшафте электрического измерения, уходящую в бесконечность. Посмотрите, как на трехмерной диаграмме показан более крутой градиент поля между зарядами, что соответствует более близким контурным линиям. Градиент поля называется напряженностью электрического поля или напряженностью электрического поля .

Электрический потенциал является скалярной величиной. Это доставляет людям проблемы, потому что имеет знак (положительный или отрицательный). Вы должны думать о знаке как об указании того, находится ли эта точка в пространстве выше или ниже нулевой плоскости.

Чтобы вычислить потенциал точки, на которую воздействуют поля нескольких зарядов , вам нужно выяснить, какое влияние оказывает каждый заряд на высоту «рельефа» в этой точке. Положительный заряд поднимет его выше нуля, а отрицательный заряд поднимет ниже нуля. Вы просто суммируете «корректировку электрической высоты» вместе, чтобы получить окончательное значение.

Пример вопроса:

Каков электростатический потенциал в точке X?

по уравнению:

определите потенциал в точке X от каждого из зарядов.

Результат положительного заряда равен 1,12 x 10 ⁴ вольт (точка X поднимается за счет наличия этого заряда), а результат отрицательного заряда равен -1,12 x 10 ⁴ вольт (точка X опускается за счет наличие этого заряда). Их сумма представляет собой нулевой потенциал (X имеет нулевой потенциал — тот же уровень, который был бы, если бы вообще не было зарядов!).

Пару лет назад вопрос с несколькими вариантами ответов вызвал много беспокойства. Это был тип истинного/ложного, и утверждение, которое многие считали верным, было следующим:

«Электрический потенциал равен нулю, когда напряженность электрического поля равна нулю»

Это ЛОЖНОЕ утверждение, но многие студенты не могли понять, что оно было ложным.

Напряженность или напряженность электрического поля является вектором, поэтому, если равные притяжения или толчки воздействуют на «пробную частицу» в точке пространства, на которую вы смотрите, они компенсируют друг друга. НО потенциал в этой точке пространства будет подвержен изменению потенциала из-за влияния всех зарядов в данной местности. Посмотрите на схему.

Положительные заряды толкают положительный тестовый заряд с одинаковой силой, компенсируя эффект ускорения. Таким образом, напряженность электрического поля в этой точке равна нулю, НО оба заряда влияют на электрический потенциал точки X. Наличие одного из них затрудняет перенос единичного положительного заряда из бесконечности, а наличие второго удваивает как тяжело!. Эта точка в «электрическом пространстве» как бы поднимается в два раза выше благодаря наличию вторых зарядов.

Электрический потенциал можно рассматривать как «давление». в следующей аналогии: если два человека толкают воздушный шар, по одному с каждой стороны, с одинаковой силой, общая сила будет равна нулю — чистой силы нет, но давление в воздушном шаре выше, чем при приложении истинной нулевой силы.

 

Потенциальная электрическая энергия — физические ресурсы MCAT

Все физические ресурсы MCAT

8 диагностических тестов 303 практических теста Вопрос дня Карточки Учитесь по концепции

Физическая помощь MCAT » Физика » Электричество и магнетизм » Электростатика и электрические поля » Electric Potential Energy

Если электрическая потенциальная энергия между двумя одинаковыми зарядами увеличивается в четыре раза, опишите изменение расстояния между частицами.

Возможные ответы:

Расстояние увеличилось в четыре раза

Расстояние не изменилось

Расстояние увеличилось вдвое

Расстояние уменьшилось вдвое

Расстояние было разделено на четыре части

Правильный ответ:

Расстояние было разделено на четыре части

Пояснение:

Электрическая потенциальная энергия определяется уравнением .

Электрическая потенциальная энергия обратно пропорциональна расстоянию между двумя зарядами. Если энергия увеличилась в четыре раза, то (расстояние между двумя одинаковыми зарядами) должно было уменьшиться пропорционально.

Чтобы энергия увеличилась в четыре раза, радиус нужно разделить на четыре.

Сообщить об ошибке

Для следующего:

Если заряд +4e удерживается на месте в 3 морских милях от заряда -5e, который также удерживается на месте. Чему равна потенциальная энергия системы?

Возможные ответы:

Правильный ответ:

Объяснение:

 

Учитывая уравнение и подставляя значения e и k, мы получаем, что

Важно помнить, что заряд указан в вопросе и должен быть включен в формулу путем умножения каждого заряда на это значение.

Сообщить об ошибке

Что из следующего неверно относительно электрического потенциала?

Возможные ответы:

Все утверждения верны

Положительный полюс батареи имеет более высокий электрический потенциал, чем отрицательный

Отрицательный заряд, перемещающийся из области с низким потенциалом в область с высоким потенциалом, будет ускоряться

Когда положительный заряд перемещается из области с низким потенциалом в область с высоким потенциалом, электрическое поле совершает над зарядом положительную работу

Электрический потенциал может быть выражен в единицах Вольт или джоуль на кулон

Правильный ответ:

Когда положительный заряд перемещается из области с низким потенциалом в область с высоким потенциалом, электрическое поле совершает над зарядом положительную работу

Объяснение:

Положительный тестовый заряд естественным образом перейдет от высокого потенциала к низкому. Если его перемещать в противоположном направлении, то электрическое поле будет совершать работу против его движения (отрицательная работа). Это видно из уравнения для работы электрического поля:

— работа, совершаемая электрическим полем, — заряд, — разность потенциалов. Если положительно (конечный потенциал выше начального потенциала) и также положительно, то работа, совершаемая полем, отрицательна.

Сообщить об ошибке

Какую работу необходимо совершить, чтобы свести три заданных заряда из бесконечности в углы равностороннего треугольника со стороной 1 см?

Возможные ответы:

Правильный ответ:

Объяснение:

Соответствующие уравнения:

Шаг 1: Поскольку работа по сборке зарядов равна их потенциальной энергии в этом расположении, найдите потенциальную энергию между каждой парой зарядов. Работа равна изменению потенциальной энергии; поскольку заряды начинаются на бесконечном расстоянии, изначально потенциальная энергия равна нулю.

Стоимость 1 и 2

Плата 1 и 3

Заряды 2 и 3

Шаг 2: все эти потенциальные затраты.

Сообщить об ошибке

Стандартная розетка переменного тока способна подавать ток. Какое максимально возможное напряжение выдает розетка.

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку данное напряжение представляет собой среднеквадратичное напряжение, мы должны умножить напряжение на  , чтобы найти максимальное напряжение.

Определяем, что максимальное напряжение, выдаваемое розеткой, равно .

Сообщить об ошибке

Уведомление об авторских правах

Все физические ресурсы MCAT

8 Диагностические тесты 303 практических теста Вопрос дня Карточки Учитесь по концепции

MCQ по физике для класса 12 с ответами Глава 2 Электростатический потенциал и емкость

Бесплатная загрузка в формате PDF вопросов с несколькими вариантами ответов CBSE Physics для класса 12 с ответами Глава 2 Электростатический потенциал и емкость. MCQ по физике для 12-го класса Глава с ответами Загрузка в формате PDF была подготовлена ​​на основе последней модели экзамена. Учащиеся могут решить MCQ класса 12 NCERT по физике, электростатическому потенциалу и емкости в формате Pdf с ответами, чтобы узнать свой уровень подготовки.

1. Какое из следующих утверждений верно?
(а) Электростатическая сила является консервативной силой.
(b) Потенциал в точке — это работа, совершаемая на единицу заряда при перемещении заряда из любой точки в бесконечность.
(c) Электростатическая сила неконсервативна
(d) Потенциал есть произведение заряда и работы.

Ответ

Ответ: a

---

2. 1 вольт эквивалентен

Ответ

Ответ: c

---

3. Работа, совершаемая для переноса единичного положительного заряда с бесконечного расстояния в точку на расстоянии x от положительного заряда Q, равна W. Тогда потенциал в этой точке равен

Ответ

Ответ: b

---

4. Рассмотрим однородное электрическое поле в направлении z. Потенциал является константой
(а) для любого x для данного z
(b) для любого y для данного z
(c) на плоскости x-y для данного z
(d) все эти

Ответ

Ответ: д

---

5. Эквипотенциальные поверхности
(а) ближе в областях больших электрических полей по сравнению с областями более низких электрических полей.
(б) будет теснее возле острых краев проводника.
(c) всегда будут располагаться через равные промежутки.
(d) оба варианта (a) и (b) верны.

Ответ

Ответ: д

---

6. В области постоянного потенциала
(а) электрическое поле однородно.
(б) электрическое поле равно нулю.
(c) внутри области не может быть заряда.
(d) и (b), и (c) верны.

Ответ

Ответ: д

---

7. Пробный заряд перемещается из точки с более низким потенциалом в точку с более высоким потенциалом. Потенциальная энергия пробного заряда будет
(а) остаются прежними
(б) увеличиваются
(в) уменьшаются
(г) обнуляются

Ответ

Ответ: в

---

8. Электрический диполь с моментом \(\vec{p}\) помещен в однородное электрическое поле \(\vec{E}\) . Тогда
(i) крутящий момент на диполе равен \(\vec{p} \times \overrightarrow{\mathrm{E}}\)
(ii) потенциальная энергия системы равна \(\vec{p} . \overrightarrow{\mathrm{E}}\)
(iii) результирующая сила на диполе равна нулю. Выберите верный вариант.
(a) (i), (ii) и (iii) верны
(b) (i) и (iii) верны и (ii) неверны
(c) только (i) верны
(d) (i) и (ii) верны и (iii) неверны

Ответ

Ответ: b

---

9. Если проводник имеет потенциал V ≠ 0 и больше нигде снаружи нет зарядов, то
(а) должны быть заряды на поверхности или внутри самого проводника.
(b) в теле проводника не может быть никакого заряда.
(c) заряды должны быть только на поверхности.
(d) и (a), и (b) верны.

Ответ

Ответ: c

---

10. Какое из следующих утверждений неверно для идеального проводника?
(а) Поверхность проводника является эквипотенциальной поверхностью.
(b) Электрическое поле сразу за поверхностью проводника перпендикулярно поверхности.
(c) Заряд, переносимый проводником, всегда равномерно распределен по поверхности проводника.
(d) Ни один из них.

Ответ

Ответ: д

---

11. Диэлектрическая проницаемость металла равна
(а) нулю
(б) бесконечно
(в) 1
(г) 10

Ответ

Ответ: б

---

12. При замене воздуха диэлектрической средой постоянной К максимальная сила притяжения между двумя зарядами, разделенными расстоянием
(а) увеличивается в К раз
(б) остается неизменной
(в) уменьшается в К раз
( г) увеличивает K ^-1 раз

Ответ

Ответ: c

---

13. В конденсаторе с параллельными пластинами емкость увеличивается, если
(a) площадь пластины уменьшается.
(б) расстояние между пластинами увеличивается.
(в) площадь пластины увеличена.
(d) диэлектрическая проницаемость постоянно уменьшается.

Ответ

Ответ: c

---

14. Плоский воздушный конденсатор заряжается до разности потенциалов V вольт. После отключения зарядной батареи расстояние между пластинами конденсатора увеличивают с помощью изолирующей ручки. В результате разность потенциалов между пластинами
(а) увеличивается
(б) уменьшается
(в) не изменяется
(г) становится равным нулю

Ответ

Ответ: а

---

15. Два одинаковых конденсатора соединены параллельно, заряжены до потенциала V, разделены и затем соединены последовательно, плюсовая пластина одного соединена с минусовой пластиной другого. Какие из следующих утверждений верно?
(a) Заряды на соединенных вместе свободных пластинах уничтожены.
(б) Энергия, запасенная в этой системе, увеличивается.
(c) Разность потенциалов между свободными пластинами составляет 2В.
(d) Разность потенциалов остается постоянной.

Ответ

Ответ: c

---

16. Конденсатор имеет диэлектрик между обкладками и подключен к источнику постоянного тока. Аккумулятор теперь отключен, а затем удален диэлектрик, тогда емкость
(а) увеличится.
(b) запасенная энергия уменьшится.
(c) электрическое поле увеличится.
(d) напряжение уменьшится.

Ответ

Ответ: c

---

17. Два сферических проводника емкостью C каждый заряжены до потенциалов V и -V. Затем они соединяются тонкой проволокой. Потеря энергии
(a) ноль
(b) \(\frac{1}{2}\)CV ²
(c) CV ²
(d) 2 CV ²

Ответ

Ответ: с

---

Мы надеемся, что данные MCQ по физике для 12 класса с ответами Глава 2 Электростатический потенциал и емкость помогут вам. Если у вас есть какие-либо вопросы относительно физического электростатического потенциала и емкости MCQ класса 12 CBSE Pdf, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.

CBSE MCQ по физике для 12 класса с ответами

Содержание

MCQ по физике для 12 класса

Физика — один из самых сложных предметов для учащихся. Подготовка к физике тоже непростая задача. Подготовка к вашей работе по физике требует последовательности, тяжелой работы и некоторой практики. Что касается практической части, вам не о чем беспокоиться, потому что здесь, в Adda247, мы вас поддержим. Мы все знаем о ваших трудностях при подготовке к доскам. Чтобы помочь вам в достижении ваших целей, мы составили список MCQ, которые помогут вам в подготовке к MCQ 12 класса CBSE по физике. Этот пост также включает решения для вопросов MCQ по физике класса 12 CBSE. Прежде чем идти, ознакомьтесь с важными вопросами MCQ по физике CBSE Class 12 с ответами и желаю удачи в вашем тесте по физике CBSE Class 12!

MCQ 12 класса по физике с ответом 2023

Q. Электрическое поле в точке изменяется как r° для
(a) электрический диполь
(b) точечный заряд
(c) плоский бесконечный слой заряда
(г) линейный заряд бесконечной длины

Ответ: (в) плоский бесконечный слой заряда

Q.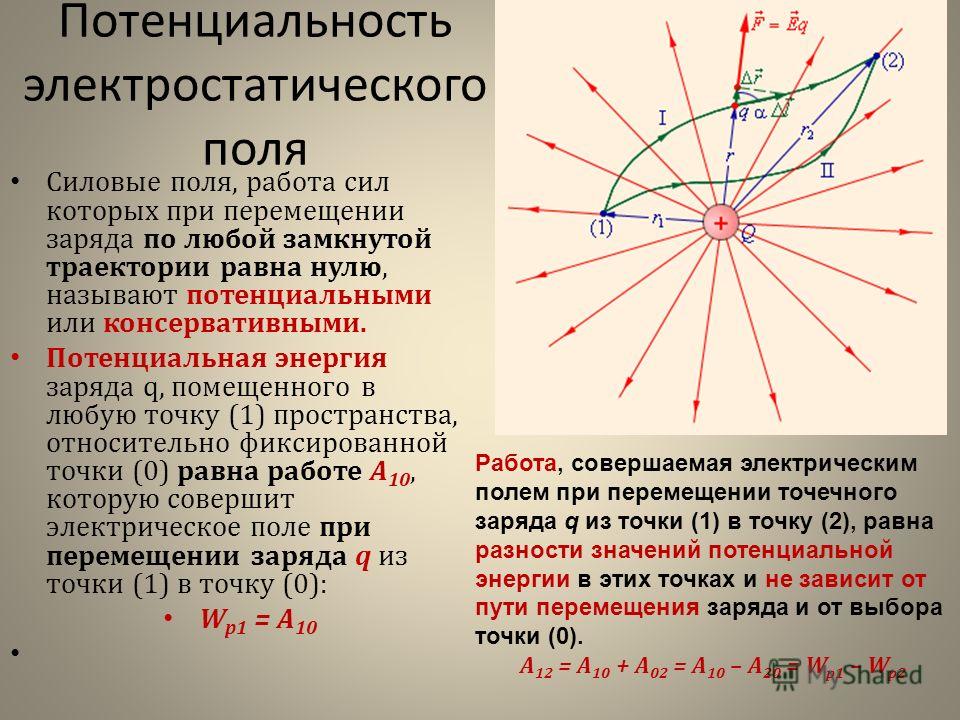 Положительно заряженная частица выходит из состояния покоя в однородном электрическом поле. Электрическая потенциальная энергия заряда
(а) остается постоянной, поскольку электрическое поле однородно.
(б) увеличивается, потому что заряд движется вдоль электрического поля.
(в) уменьшается, потому что заряд движется вдоль электрического поля.
(г) уменьшается, потому что заряд движется против электрического поля.

Ответ: (в) уменьшается, потому что заряд движется вдоль электрического поля.

В. На рисунках показаны некоторые эквипотенциальные линии, распределенные в пространстве. Заряженный предмет перемещается из точки А в точку В.
(а) Работа, совершенная на рис. (и), является наибольшей.
(b) Работа, выполненная на рис. (ii), наименьшая.
(c) Проделанная работа одинакова на рис. (i), рис. (ii) и рис. (iii).
(d) Работа, выполненная на рис. (iii), больше, чем на рис. (ii), но равна работе на рис. (i).

Ответ: (c) Выполненная работа одинакова на рис. (i), рис. (ii) и рис. (iii).

Q. Эквипотенциальными на большом расстоянии от совокупности зарядов, общая сумма которых не равна нулю, являются приблизительно
(a) сферы
(b) плоскости
(c) параболоиды
(d) эллипсоиды

Ответ: (a) сферы

Q. Две маленькие сферы, каждая из которых несет заряд q, расположены на расстоянии r метров друг от друга. Если одну из сфер обвести вокруг другой по круговой траектории радиуса r, то совершенная работа будет равна
(а) сила между ними × r
(б) сила между ними × 2πr
(в) сила между ними/2πr
(d) ноль

Ответ: (d) ноль

Прочтите: MCQ 12 класса по математике

В. Заряд, текущий в проводнике, изменяется со временем как:
q = αt +12 βt² + 16 γt³
Где α, β, γ — положительные константы. Тогда начальный ток (l) определяется условием:
(a) l = α
(b) l = α²
(c) l = α ^-1
(d) Ни один из этих

Ответ: (a) l = α

Q. Конденсатор имеет емкость C и реактивное сопротивление X, если емкость и частота удвоятся, то реактивное сопротивление будет
(a) 4X
(b) X/2
(c) X /4
(г) 2Х

Ответ: (в) Х/4

В. Ниже приведены два утверждения, помеченные как Утверждение (A) и Причина (R)

Утверждение: Мы не можем представить конфигурацию магнитного поля с тремя полюсами крутящий момент на себя за счет собственного поля.

Выберите наиболее подходящий ответ из приведенных ниже вариантов:

(a) И A, и R верны, и R является правильным объяснением A

(b) И A, и R верны, но R нет правильное объяснение А.

(c) A верно, но R ложно.

(d) А ложно, и R тоже ложно.

Ответ: (b) И A, и R верны, но R не является правильным объяснением A.

(b) на частицах существует заряд

(c) на частице существует минимально допустимый заряд

(d) заряд, который составляет долю кулона на частице

Ответ- (d)

Q. Единицей электрического дипольного момента является

(a) ньютон

(b) кулон

(c) фарад

5 дебай Ответ (d)

Q. Заряд – это свойство, связанное с материей, благодаря которой он производит и испытывает

(a) только электрические эффекты

(b) только магнитные эффекты

(c) как электрические, так и магнитные эффекты

(d) Ничего из перечисленного

Ответ- (c)

Q.   Электрический диполь с моментом ?⃗  находится в однородном электрическом поле ?⃗  . Тогда

(i) крутящий момент на диполе ?⃗ ×E→

(ii) потенциальная энергия системы ?⃗ . E→

(iii) равнодействующая сила на диполе диполь равен нулю. Выберите верный вариант.

(a) (i), (ii) и (iii) верно

(b) (i) и (iii) верно и (ii) неверно

(c) только (i) верно

(d) (i) и (ii) верно и (iii) неверно

Ответ- (b)

Вопрос. пластинчатый конденсатор, емкость увеличивается, если

(a) площадь пластины уменьшается.

(б) расстояние между пластинами увеличивается.

(в) площадь пластины увеличена.

(г) диэлектрическая проницаемость постоянно уменьшается.

Ответ- (c)

В. Плоский воздушный конденсатор заряжается до разности потенциалов V вольт. После отключения зарядной батареи расстояние между пластинами конденсатора увеличивают с помощью изолирующей ручки. В результате разность потенциалов между пластинами

(а) увеличивается

(б) уменьшается

(в) не изменяется

(г) становится равным нулю заряжены до потенциала V и -V. Затем они соединяются тонкой проволокой. Потери энергии

(a) ноль

(b) ½ CV²

(c) CV²

(d) 2 CV²

Ответ- (c)

1 Два одинаковых конденсатора. соединенные параллельно, заряженные до потенциала V, разделенные и затем соединенные последовательно, положительная пластина одного соединена с отрицательной пластиной другого. Какие из следующих утверждений верно?

(a) Заряды на соединенных вместе свободных пластинах уничтожаются.

(b) Энергия, запасенная в этой системе, увеличивается.

(c) Разность потенциалов между свободными пластинами составляет 2В.

(d) Разность потенциалов остается постоянной.

Ответ- (c)

В. В области потенциал представлен как V(x,y,z)= 6x – 8xy – 8y + 6yz, где V в вольтах, а x,y,z находятся в метрах. Электрическая сила, действующая на заряд в 2 Кл, расположенный в точке (1,1,1), равна-

(a) 6√5 N

(b) 30 N

(c) 24 N

(D) 4√35 N

Ответ- (D)

9961 Q Электрон летит с равномерной скоростью вдоль оси длинного соленоида с током. Какие из следующих утверждений верно?

(а) Электрон будет ускоряться вдоль оси.
(b) Траектория электрона будет круговой вокруг оси.
(c) Электрон будет испытывать силу под углом 45° к оси и, следовательно, будет двигаться по винтовой траектории.
(г) Электрон будет продолжать двигаться с постоянной скоростью вдоль оси соленоида.

Ответ: (г) Электрон будет продолжать двигаться с постоянной скоростью вдоль оси соленоида.

В. Что из следующего неверно относительно циклотрона?

(a) Это машина для ускорения заряженных частиц или ионов до высоких энергий.
(b) Циклотрон использует совместно электрические и магнитные поля для увеличения энергии заряженных частиц.
(c) Работа циклотрона основана на том факте, что время одного оборота иона не зависит от его скорости или радиуса его орбиты.
(г) Заряженные частицы и ионы в циклотроне могут двигаться по любой произвольной траектории.

Ответ: (d) Заряженные частицы и ионы в циклотроне могут двигаться по любой произвольной траектории.

В. Какая из следующих независимых величин не используется для определения магнитного поля Земли?

(a) Магнитное склонение (θ).

(б) Магнитный провал (δ).

(c) Горизонтальная составляющая поля Земли (ЧД).

(d) Вертикальная составляющая поля Земли (BV).

Ответ (d)

В. Что из следующего верно относительно магнитного монополя?

(а) Магнитный монополь существует.

(b) Магнитный монополь не существует.

(c) Магнитные монополи имеют постоянное значение импульса монополя.

(г) Импульс монополя увеличивается из-за увеличения его расстояния от поля.

Ответ (b)

В. Что из следующего не показывает существенное различие между электростатическим экранированием проводящей оболочкой и магнитостатическим экранированием?

(a) Линии электростатического поля могут заканчиваться зарядами, а проводники имеют свободные заряды.

(b) Линии магнитного поля могут заканчиваться, но проводники не могут их заканчивать.

(c) Линии магнитного поля не могут заканчиваться на каком-либо материале, и идеальное экранирование невозможно.

(d) Оболочки из материалов с высокой проницаемостью могут использоваться для отклонения линий магнитного поля от внутренней области.

Ответ- (б)

В. Проницаемость парамагнитного вещества:

(а) очень большая
(б) малая, но больше единицы
(в) меньше единицы
(г) отрицательный

Ответ: (б) мало, но больше единицы

В. Вертикальная составляющая магнитного поля Земли . на месте в √3 раза больше горизонтальной составляющей
значение угла падения в этом месте
(а) 30°
(б) 45°
(в) 60°
(г) 90°

Ответ: (в) 60°

Q. В данном месте земной поверхности горизонтальная составляющая магнитного поля Земли равна 2 × 10 ^3-5 Тл, а результирующее магнитное поле равно 4 × 10 ^3-5 Тл. Угол падения в этом месте is
(a) 30°
(b) 60°
(c) 90°
(d) 45°

Ответ: (b) 60°

В. Какое из следующих свойств указывает на свойство ферромагнитных веществ?
(a) Ферромагнитные свойства зависят от температуры
(b) Ферромагнитные свойства не зависят от температуры.
(c) При достаточно высокой температуре ферромагнетик становится диамагнетиком.
(d) При низкой температуре ферромагнетик становится парамагнетиком.

Ответ: (а) Ферромагнитные свойства зависят от температуры

Q. Первичное происхождение магнетизма лежит в
(а) атомный ток и собственный спин электронов.
(b) полярная и неполярная природа молекул.
(c) Принцип запрета Паули.
(d) электроотрицательная природа материалов.

Ответ: (а) атомный ток и собственный спин электронов.

В. Если катушку А заставить вращаться вокруг вертикальной оси (рисунок). В B ток не течет, если A покоится. Ток в катушке А, когда ток в В (в момент t = 0) течет против часовой стрелки, а катушка А в этот момент, t = 0, находится в таком положении, как показано на рисунке, составляет

(а) постоянный ток по часовой стрелке.
(б) переменный ток по часовой стрелке.
(c) переменный ток против часовой стрелки.
(d) постоянный ток против часовой стрелки.

Ответ: (а) постоянный ток по часовой стрелке.

В. Цилиндрический стержневой магнит вращается вокруг своей оси (рисунок). Проволока соединена с осью и выполнена через контакт, касающийся цилиндрической поверхности. Тогда

(а) в амперметре А протекает постоянный ток.
(б) через амперметр А ток не течет.
(c) через амперметр A протекает переменный синусоидальный ток с периодом времени T = 2πω
(d) через амперметр протекает изменяющийся во времени несинусоидальный ток.

Ответ: (б) ток через амперметр А не течет.

Ответ: (c) искрение

Q. Напряженность электрического поля, создаваемая бесконечным цилиндром радиуса R и имеющим заряд q на единицу длины на расстоянии rr r(r > R) от его оси, равна
(а) прямо пропорциональна r².
(b) прямо пропорционально r ³ .
(в) обратно пропорциональна r.
(d) обратно пропорциональна r².

Ответ: (d) обратно пропорциональна r².

В. В L.C.R. серия а.с. цепи, ток
(a) всегда находится в фазе с напряжением
(b) всегда отстает от напряжения генератора
(c) всегда опережает напряжение генератора
(d) Ни один из этих

Ответ: (d) Нет из них

В. Последовательная цепь LCR, подключенная к источнику E, находится в резонансе. Тогда напряжение на
(a) R равно нулю
(b) R равно приложенному напряжению
(c) C равно нулю
(d) L равно приложенному напряжению

Ответ: (b) R равно приложенному напряжению

Ом. Электрическое поле внутри сферической оболочки с однородной поверхностной плотностью заряда
(а) равно нулю.
(б) постоянная, меньше нуля.
(в) прямо пропорционально расстоянию от центра.
(d) ни один из этих

Ответ: (a) ноль.

В. Ниже приведены два утверждения, помеченные как Утверждение (A) и Причина (R)

Утверждение: В высоких широтах можно увидеть разноцветные завесы света, свисающие с больших высот
Причина: Высокая энергия заряженные частицы Солнца отклоняются в полярные области магнитным полем Земли

Выберите наиболее подходящий ответ из предложенных ниже вариантов:

(a) И A, и R верны, и R является правильным объяснением A

(b) И A, и R верны, но R не является правильным объяснением A.

(c) A верно, но Р неверно.

(d) А ложно, и R тоже ложно.

Ответ: (a) И A, и R верны, и R является правильным объяснением A

Q. Ниже приведены два утверждения, помеченные как Утверждение (A) и Причина (R)

Утверждение: Конденсатор подключен к источнику постоянного тока. Его реактивное сопротивление бесконечно.
Причина: реактивное сопротивление конденсатора определяется как χ _c  = 1/ωC.

Выберите наиболее подходящий ответ из приведенных ниже вариантов:

(a) И A, и R верны, и R является правильным объяснением A

(b) И A, и R верны, но R нет правильное объяснение A.

(c) A верно, но R ложно.

(d) А ложно, и R тоже ложно.

Ответ: (a) И A, и R верны, и R является правильным объяснением A

Q. Температурный коэффициент сопротивления провода 0,00125°С ^-1 . При 27°С его сопротивление равно 1 Ом. Температура провода, при которой его сопротивление становится равным 2 Ом, составляет:
(а) 1400 К
(б) 854°С
(в) 1127 К
(г) 1154 К.

Ответ: (б) 854° C

Q. Нагревательный элемент электронагревателя должен быть изготовлен из материала, который должен иметь:
(a) низкое удельное сопротивление и низкую температуру плавления.
(b) высокое удельное сопротивление и высокая температура плавления.
(в) высокое удельное сопротивление и низкая температура плавления.
(d) низкое удельное сопротивление и высокая температура плавления.

Ответ: (а) низкое удельное сопротивление и низкая температура плавления.

Q. Эффективная мощность ламп мощностью 60 Вт и 40 Вт, соединенных последовательно, равна:
(a) 24 Вт
(b) 20 Вт
(c) 100 Вт
(d) 80 Вт.

Ответ: (a) 24 Вт

Q. Эффективная мощность ламп мощностью 60 Вт и 40 Вт, соединенных параллельно, равна:
(а) 24 Вт
(б) 20 Вт
(в) 100 Вт
(г) 80 Вт

Ответ: (а) 24 Вт

(а) максимум
(б) минимум
(в) ноль
(г) бесконечность

Ответ: (б) минимум

В. При резонансной частоте амплитуда тока в последовательном LCR-контуре равна
(а) максимум
(б) минимум
(в) ноль
(г) бесконечность

Ответ: (a) максимум

В. При настройке мы изменяем емкость конденсатора в цепи настройки таким образом, чтобы резонансная частота цепи стала почти равной частоте принимаемого радиосигнала. Когда это происходит, …А… с частотой сигнала конкретной радиостанции в цепи максимальна. Здесь A относится к
(a) резонансной частоте
(b) импедансу
(c) амплитуде тока
(d) реактивному сопротивлению

Ответ: (c) амплитуда тока

В. Каков угол наклона в месте, где горизонтальная составляющая магнитного поля Земли равна вертикальной?
(a) 0°
(b) 30°
(c) 45°
(d) 90°

Ответ: (c) 45°

ферриты?
(a) Электропроводность
(b) Проницаемость
(c) Магнитная восприимчивость
(d) Все вышеперечисленное

Ответ: (a) Электропроводность

Q. Единица потока в СИ:
(a) Ом
(b) Вебер
(c) Тесла
(d) Нет

Ответ: (b) Вебер 9016 9046 Q. Размерное представление плотности магнитного потока: А ^-2 ]
(г) [МТ ^-2 А ^-1 ]

Ответ: (б) [МЛТ ^-2 A ^-1 ]

Q. Петля из прямых ребер имеет шесть углов в A(0, 0, 0), B(L, 0, 0) C(L, L, 0), D(0,L,0), E(0,L,L) и F(0,0,L). В области присутствует магнитное поле B = B _o  ( i+k )T. Поток, проходящий через контур ABCDEFA (в таком порядке), равен

(a) B _o L² Wb.
(б) 2B _или L² Вб.
(c) √2B _или L² Wb.
(d) 4B _или L² Wb.

Ответ: (б) 2В _или L² Вб.

В. В катушке, не подключенной к внешнему источнику напряжения, возникает ЭДС. Это не связано с тем, что
(a) катушка находится в изменяющемся во времени магнитном поле.
(б) катушка, движущаяся в изменяющемся во времени магнитном поле.
(в) катушка, движущаяся в постоянном магнитном поле.
(г) катушка неподвижна во внешнем пространственно-переменном магнитном поле, которое не меняется во времени.

Ответ: (г) катушка неподвижна во внешнем пространственно-переменном магнитном поле, которое не меняется во времени.

Q. Ниже приведены два утверждения, помеченные как Утверждение (A) и Причина (R)

Утверждение (A) Напряженность поля между такими листами, имеющими одинаковую и противоположную однородную поверхностную плотность заряда, становится постоянной.

Причина(R): Интенсивность поля не зависит от расстояния между тонкими листами.

Выберите наиболее подходящий ответ из приведенных ниже вариантов:

(a) И A, и R верны, и R является правильным объяснением A

(b) И A, и R верны, но R не является правильным объяснением A.

(c) A верно, но R ложно.

(d) А ложно, и R тоже ложно.

Ответ: (a) И A, и R верны, и R является правильным объяснением A

Q. Ниже приведены два утверждения, помеченные как Утверждение (A) и Причина (R)

Утверждение: В последовательном резонансном контуре LCR импеданс равен омическому сопротивлению.
Причина: при резонансе индуктивное сопротивление превышает емкостное сопротивление.

Выберите наиболее подходящий ответ из приведенных ниже вариантов:

(a) И A, и R верны, и R является правильным объяснением A

(b) И A, и R верны, но R нет правильное объяснение A.

(c) A верно, но R ложно.

(d) А ложно, и R тоже ложно.

Ответ: (b) И A, и R верны, но R не является правильным объяснением A.

В. Ниже приведены два утверждения, помеченные как Утверждение (A) и Причина (R)

Утверждение: Конденсатор подключен к источнику постоянного тока. Его реактивное сопротивление бесконечно.
Причина: реактивное сопротивление конденсатора определяется как χ _c  = 1/ωC.

Выберите наиболее подходящий ответ из приведенных ниже вариантов:

(a) И A, и R верны, и R является правильным объяснением A

(b) И A, и R верны, но R нет правильное объяснение А.

(c) A верно, но R ложно.

(d) А ложно, и R тоже ложно.

Ответ: (a) Оба A и R верны, и R является правильным объяснением A

Q. Сила на единицу заряда известна как
(a) электрический поток
(b) электрическое поле
(c) электрический потенциал
(d) электрический ток

Ответ: (b) электрическое поле

В. Какое из следующих утверждений о законе Гаусса неверно?
(а) Закон Гаусса верен для любой замкнутой поверхности.
(b) Член q в правой части закона Гаусса включает сумму всех зарядов, заключенных на поверхности.
(c) Закон Гаусса не очень полезен при расчете электростатического поля, когда система обладает некоторой симметрией.
(d) Закон Гаусса основан на обратной квадратичной зависимости от расстояния, содержащейся в законе Кулона

Ответ: (c) Закон Гаусса не очень полезен при расчете электростатического поля, когда система имеет некоторую симметрию.

В. В области постоянного потенциала
(а) электрическое поле однородно.
(б) электрическое поле равно нулю.
(c) внутри области не может быть заряда.
(d) и (b), и (c) верны.

Ответ: (d) и (b), и (c) верны.

Q. Рассмотрим однородное электрическое поле в направлении z. Потенциал является константой
(а) для любого x для данного z
(b) для любого y для данного z
(c) на плоскости x-y для данного z
(d) все эти

Ответ: (d) все эти

В. Какой из следующих цветов белого света отклоняется больше всего при прохождении через призму?
(a) Красный свет
(b) Фиолетовый свет
(c) Желтый свет
(d) Оба (a) и (b)

Ответ: (b) Фиолетовый свет

Q. Ток проводимости такой же, как ток смещения, когда источник
(a) только переменный ток
(b) только постоянный ток
(c) либо переменный, либо постоянный ток
(d) ни постоянного, ни переменного тока

Ответ: (c) либо переменного, либо постоянного тока

Q. Если проводник имеет потенциал V ≠ 0 и снаружи нет никаких зарядов, то
(a) должны быть заряды на поверхности или внутри себя.
(b) в теле проводника не может быть никакого заряда.
(c) заряды должны быть только на поверхности.
(d) оба варианта (a) и (b) верны.

Ответ: (c) заряды должны быть только на поверхности.

Q. Переменное напряжение (В) представлено уравнением cot ωt
(d) V(t) = Vm tan ωt

Ответ: (b) V(t) = Vm sin ωt

Q. Подвижность электронов проводимости больше, чем у дырок, так как электроны больше, чем у дырок, так как электроны.
(а) заряжены отрицательно.
(b) легче
(c) требуют меньше энергии для движения через кристаллическую решетку.
(d) Претерпевать меньшее количество столкновений.

Ответ: (в) требуют меньше энергии для движения через кристаллическую решетку.

Q. Мираж – это явление, обусловленное
(а) преломлением света
(б) отражением света
(в) полным внутренним отражением света
(г) дифракцией света.

Ответ: (c) полное внутреннее отражение света

Q. Фотоэлектроны получают при облучении цинка излучением 3100 Å. Для увеличения кинетической энергии вылетающих фотоэлектронов.
(а) следует увеличить интенсивность излучения.
(b) следует увеличить длину волны излучения.
(c) необходимо уменьшить длину волны излучения.
(d) следует увеличить как длину волны, так и интенсивность излучения.

Ответ: в) необходимо уменьшить длину волны излучения.

В. В чисто емкостной цепи, если частота источника переменного тока удвоится, то его емкостное сопротивление будет
(a) останется прежним
(b) вдвое
(c) вдвое
(d) ноль

Ответ: (c) вдвое

Q. Если проводимость полупроводника обусловлена ​​только разрывом ковалентной зоны вследствие теплового возбуждения , то полупроводник называется:
(а) собственный
(б) внешний
(в) акцепторный
(г) ни один из этих

Ответ: (а) собственный

Q. Если переменная частота переменного тока источник подключен к конденсатору, то с уменьшением частоты ток смещения будет
(a) увеличение
(b) уменьшение
(c) остается неизменным
(d) сначала уменьшение, затем увеличение

Ответ: (b) уменьшение

магнитное поле находится с помощью
(a) правила левой руки Флеминга
(b) правила правой руки Флеминга
(c) правила Ампера
(d) правила правой руки

Ответ: (b) правила правой руки Флеминга

В. Соленоид подключен к батарее так, что через него протекает постоянный ток. Если в соленоид вставить железный сердечник, ток будет
(a) увеличить
(b) уменьшить
(c) оставить без изменений
(d) сначала увеличить, затем уменьшить

Ответ: (b) уменьшить

MCQ класса 12 по физике за семестр 1 Ожидаемый вопрос

MCQ CBSE Class 12 Physics MCQ 2023 QNA

Почему физика такая сложная?

Физика сложна для учащихся, потому что они должны одновременно соревноваться с различными представлениями, такими как эксперименты, формулы и вычисления, графики и концептуальные объяснения.

Что мы в основном изучаем в физике?

Квантовая механика используется для изучения очень маленьких объектов, а общая теория относительности используется для изучения всего космоса.

С точки зрения непрофессионала, что такое физика?

Физика изучает энергию и материю в пространстве и времени, а также их взаимосвязь.

Является ли физика разновидностью математики?

Физика и математика всегда были переплетены, и многие исторические личности были и физиками, и математиками.