Векторы движения — Windows drivers
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
- Чтение занимает 2 мин
Если изображение не находится внутри рисунка (элемент бпиЦинтра структуры DXVA_PictureParameters равен нулю), векторы движения включаются в структуру команд элемента управления макроблокк.
Количество векторов движения, включаемых в структуру, зависит от типа изображения (например, B Picture или P Picture). Кроме того, если используется выбор изображений на основе макроблокк (как определено в H. 263-приложении U), то для каждого вектора движения также включается индекс выбора изображения в структуре управляющей команды макроблокк.
Пространство, зарезервированное для векторов движения в каждой структуре команд элемента управления макроблокк, обычно является объемом, необходимым для четырех векторов движения. Каждый вектор движения задается с помощью структуры
Если обмк используется (элемент бпикобмк структуры DXVA_PictureParameters равен 1), а рисунок не является частью статьи Pb (элемент бпикбинпб этой структуры равен нулю), пространство для 10 векторов движения, а также дополнительное пространство, необходимое для выровняйте по 16-байтовой границе, включено.
Если ОБМК используется (элемент бпикобмк структуры DXVA_PictureParameters равен 1), а рисунок является частью статьи Pb (элемент бпикбинпб этой структуры равен 1), пространство для 11 векторов движения, а также дополнительное пространство, необходимое для совмещения с 16-байтовой границей, включено.
Если ОБМК не используется (элемент бпикобмк структуры DXVA_PictureParameters равен нулю), рисунок является частью статьи Pb (элемент бпикбинпб этой структуры равен 1), а четыре вектора движения на макроблокк разрешены (элемент
Практика. Решение задач. Векторы. Уравнения прямой и окружности 9 класс онлайн-подготовка на Ростелеком Лицей |
Решение задач, связанных с векторами
Задача 1.
Доказать, что сумма любого набора векторов, для которых конец одного совпадает с началом следующего, равна вектору, соединяющему начало первого вектора и конец последнего:
Решение.
Для набора из двух векторов этот факт мы уже знаем – это просто правило треугольника (см. рис. 1):
Рис. 1. Правило треугольника
Получается, что мы собираемся доказать обобщение правила треугольника – и это действительно так. Утверждение, которое мы доказываем, называется правилом многоугольника. Интуитивно оно понятно: если мы движемся по маршруту: , то итоговое перемещение всегда будет составлять вектор (см. рис. 2).
Рис. 2. Правило многоугольника:
Проведем строгое доказательство правила многоугольника. Для этого воспользуемся методом математической индукции (см. урок). Вспомним его идею: если мы умеем доказывать утверждение для какого-то начального значения параметра (база), а также умеем доказывать, что если утверждение верно при , то оно верно и при (индукционный переход), то мы доказали, что утверждение верно для всех натуральных значениях .
В нашем примере база уже доказана (для двух векторов – правило треугольника). Осталось доказать переход: если утверждение верно для набора из векторов, то оно будет верно и для набора из вектора (тогда раз верно для векторов, то верно и для векторов, раз верно для векторов, то верно и для векторов и т. д.).
Пусть для любого набора из векторов, удовлетворяющих условию, верно утверждение правила многоугольника (см. рис. 3):
Рис. 3. Правило многоугольника
Рассмотрим теперь набор из вектора, у которых конец каждого вектора совпадает с началом следующего. Выделим из него набор из первых векторов – для него верно утверждение (по нашему предположению):
Тогда интересующая нас сумма:
Но эта сумма равна по правилу треугольника. Значит, для набора из векторов утверждение тоже верно. Переход доказан, значит, доказано и правило многоугольника.
Доказано.
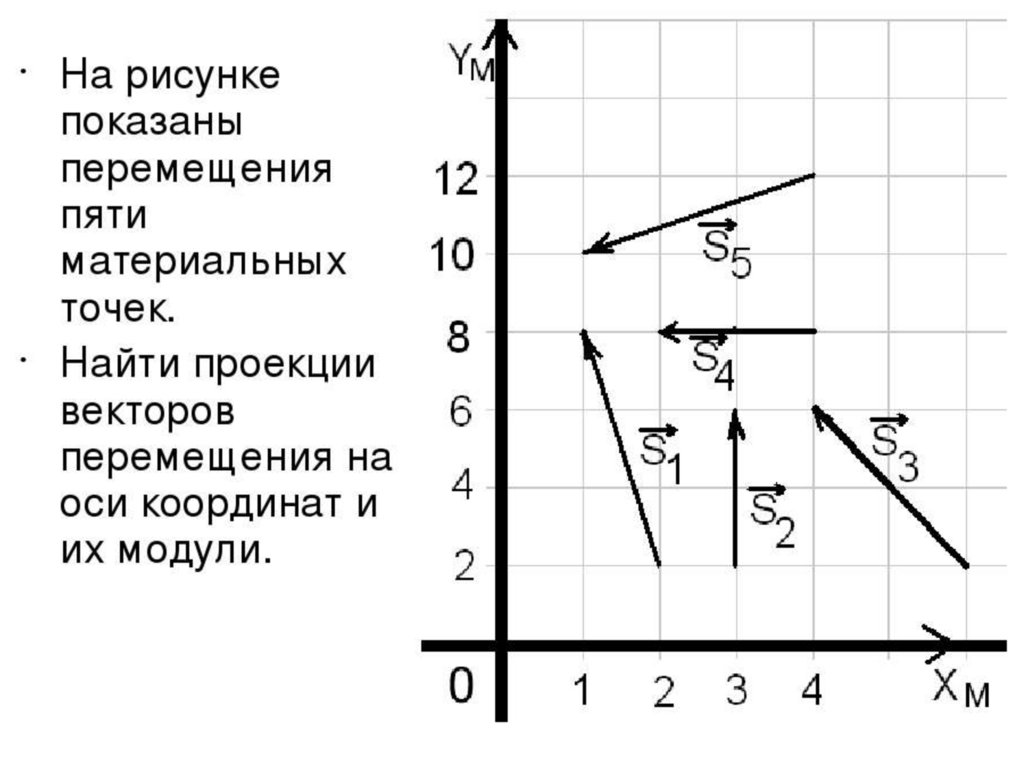
Задача 2. Сколько различных векторов задают стороны трапеции?
Решение.
Посмотрим на трапецию (см. рис. 4).
Рис. 4. Трапеция
Понятно, что каждая сторона задает два различных вектора, направленных в противоположные стороны (см. рис. 5). Т. е. всего набирается векторов.
Рис. 5. Каждая сторона трапеции задает два различных вектора, направленных в противоположные стороны
Не может ли быть среди них равных? Равные векторы должны быть равны по длине и сонаправлены:
Боковые стороны трапеции не параллельны ( по определению трапеции), следовательно, векторы, которые задаются двумя боковыми сторонами, не могут быть равны: , т. к. они не коллинеарны. Конечно, не параллельны и соседние стороны: , значит, соответствующие векторы не коллинеарны.
Векторы, которые задаются двумя основаниями, не могут быть равны по длине, т. к. основания в трапеции не равны друг другу: (в противном случае у трапеции две стороны были бы равны и параллельны, т. е., по признаку, трапеция должна была бы оказаться параллелограммом – противоречие):
Таким образом, стороны трапеции задают ровно неравных друг другу векторов.
Ответ: векторов.
Задача 3. Векторы задаются сторонами правильного пятиугольника (см. рис. 6). Равны ли эти векторы? Найти суммы:
Рис. 6. Иллюстрация к задаче 3
Решение.
Равны ли эти векторы? Конечно, нет. У всех этих векторов равна длина (по определению правильного многоугольника):
Но среди них нет сонаправленных, все векторы различны:
Найдем сумму . Здесь все просто, по правилу многоугольника эта сумма равна вектору (см. рис. 7):
Рис. 7. Правило многоугольника:
Чему равна сумма ? По правилу треугольника (см. рис. 8):
Рис. 8. Правило треугольника:
Аналогично (см. рис. 9):
Рис. 9. Правило треугольника:
Найдем сумму .Пока мы не можем использовать ни одного из известных нам правил сложения. Надо соединить последовательно два вектора. Например, к вектору приставить вектор, равный (см. рис. 10).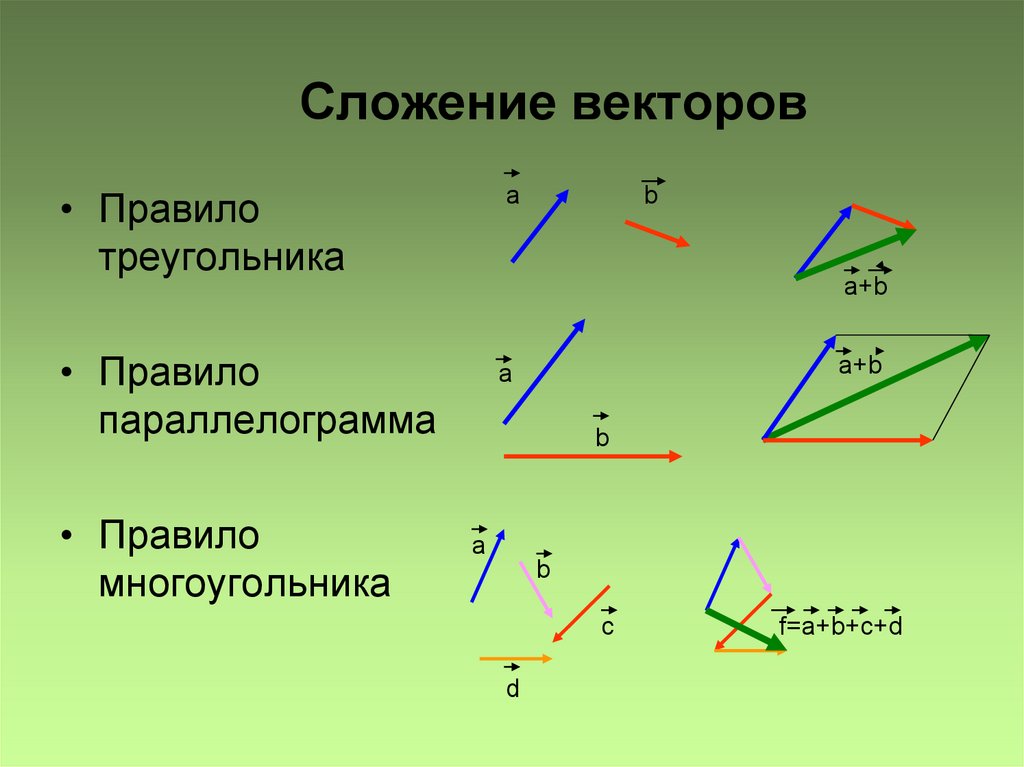
Рис. 10. К вектору приставлен вектор, равный
Обозначим точку пересечения диагоналей и – точку (см. рис. 11).
Рис. 11. Точка – точка пересечения диагоналей и
Казалось бы, подходящий кандидат – вектор . Надо убедиться, что он в самом деле равен вектору , т. е. надо показать, что и .
Рассмотрим четырехугольник (см. рис. 12).
Рис. 12. Четырехугольник
Из того, что пятиугольник – правильный, следует, что и .
Продлим стороны и до пересечения (см. рис. 13).
Рис. 13. Продленные стороны и пересекаются в точке
Углы и тоже будут равны друг другу (как смежные равным углам), т. е. треугольник равнобедренный.
Но тогда прямые и отсекают равные отрезки на двух сторонах углов:
(см. рис. 14), следовательно, они параллельны (обратная теорема Фалеса): .
Рис. 14. Прямые и отсекают равные отрезки на двух сторонах углов
Абсолютно аналогично можно доказать, что .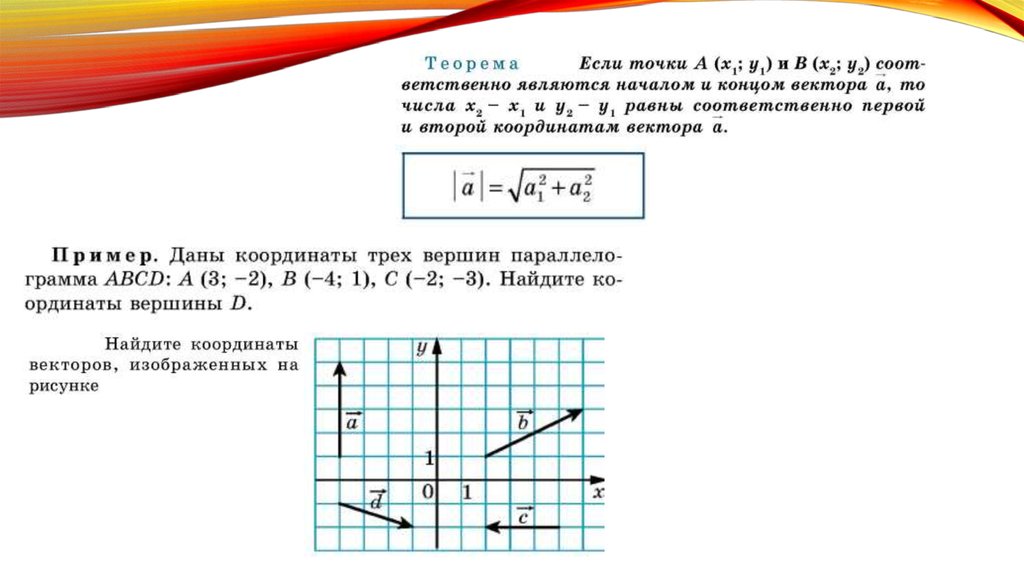
Значит, – параллелограмм, но тогда векторы (по свойству параллелограмма):
Следовательно:
Ответ: нет, , , , .
Другой способ доказательства того, что
Векторы задаются сторонами правильного пятиугольника . Доказать, что .
Доказательство.
Т. к. – правильный пятиугольник, то вокруг него можно описать окружность (в любой правильный многоугольник можно вписать и вокруг любого правильного многоугольника можно описать окружность).
Т. к. все стороны правильного пятиугольника равны , то они отсекают на окружности равные дуги (по свойству равных хорд, стягивающих дуги) (рис. 15): , градусные меры которых равны:
Рис. 15. Равные стороны правильного пятиугольника отсекают на окружности равные дуги
Тогда вписанные углы равны как вписанные углы, опирающиеся на равные дуги:
Из равенства углов следует параллельность (по признаку параллельных прямых: накрест лежащие углы равны), а из равенства углов следует параллельность .
Тогда, по определению, – параллелограмм:
Доказано.
Решение задач, связанных с длинами векторов
Когда мы измеряем длину пройденного пути (см. рис. 16), то нам не важно, как именно это сделать: посчитать длины каждого из участков и потом их сложить: – или посчитать длину всего пути: – результат будет одним и тем же.
Рис. 16. Путь
А вот с перемещениями не так. Если вы поехали из в , а потом – из в (см. рис. 17), то итоговое перемещение будет равняться , а его длина (т. к. вы вернулись в исходную точку), а вот длина каждого из перемещений по отдельности равна , но .
Рис. 17. Перемещения и
Получаем, что для длин векторов не работает привычное для нас свойство аддитивности (когда сумма измерений частей равна измерению целого): сумма длин векторов практически никогда не будет равна длине суммы этих векторов.
Задача 4. Доказать неравенство:
Рис.
18. Иллюстрация к задаче 4
Доказательство.
Это векторная форма неравенства треугольника: длина любой стороны треугольника меньше суммы длин двух других его сторон. Т. е. в случае неколлинеарных векторов (которые образуют треугольник) неравенство строгое:
Если же векторы коллинеарны, то треугольник не образуется (см. рис. 19).
Рис. 19. Треугольник не образуется, если векторы коллинеарны
Для противоположно направленных векторов неравенство тоже будет строгим:
Равенство мы получим только в случае сонаправленных векторов (треугольник не образуется) (см. рис. 20):
Рис. 20. Треугольник не образуется, если векторы сонаправлены
Кстати, этот факт иногда используется для доказательства того, что три точки лежат на одной прямой: если модуль суммы векторов и равен сумме их модулей:
, то точки , и лежат на одной прямой, причем находится между и .
Доказано.
Итак, важно не путать модуль суммы и сумму модулей: и .
Задача 5. В прямоугольном треугольнике катеты , .Вычислить:
Решение.
Модули векторов – это длины соответствующих отрезков, поэтому:
Т. к. векторы не сонаправлены , то результат должен оказаться меньше предыдущего:
По правилу треугольника:
Гипотенуза треугольника равна (несложно вычислить по теореме Пифагора), тогда:
Разность длин векторов вычислить несложно:
Найдем теперь модуль разности . Разность двух векторов с общим началом – это вектор, соединяющий их концы и направленный к уменьшаемому, т. е.:
Тогда:
Этот результат можно было получить и по-другому:
Но мы знаем, что , поэтому:
Этот модуль мы только что уже нашли.
Ответ: .
Задача 6. Парашютист спускался со скоростью м/с. Ветром его начинает сносить в сторону со скоростью м/с. Какова его реальная скорость ? Под каким углом к вертикали спускается парашютист?
Рис.
21. Иллюстрация к примеру 6
Решение.
Скорость – векторная величина. Т. к. парашютист имеет две скорости в различных направлениях, то результирующая (истинная скорость) находится как векторная сумма первых двух:
Найдем ее, используя правило параллелограмма (в нашем случае параллелограмм – это прямоугольник (см. рис. 22)):
Рис. 22. Прямоугольник
Значение реальной скорости – это длина вектора, т. е. диагонали прямоугольника:
Ее можно найти, используя теорему Пифагора:
м/с
Тангенс искомого угла между вертикалью и реальной скоростью равен, по определению, отношению противолежащего катета к прилежащему:
Острый угол, который соответствует такому тангенсу, равен .
Ответ: м/с, .
Решение задач, связанных с уравнениями прямой и окружности
Вторую часть урока мы посвятим решению задач, связанных с уравнениями прямой и окружности.
Вспомним, что общее уравнение прямой (см.
рис. 23) имеет вид:
При этом сразу два коэффициента, и не могут одновременно равняться :
Рис. 23. График прямой
Общее уравнение окружности имеет вид:
,
где – координаты центра окружности, а – ее радиус (см. рис. 24).
Рис. 24. График окружности с центром в точке и радиусом
Задача 7. Определить, какие из данных точек принадлежат окружности и прямой .
Решение.
Чтобы увидеть, принадлежит ли данная точка окружности, прямой или любой другой линии, заданной уравнением, не нужно строить изображение этой линии и отмечать сами точки. Достаточно просто подставить координаты точки в уравнение линии. Сама идея уравнения линии: все точки, координаты которых удовлетворяют этому уравнению, принадлежат линии, остальные – нет:
|
Точка |
||
|
Точка не лежит на окружности |
Точка лежит на прямой |
|
|
Точка лежит на окружности |
Точка не лежит на прямой |
|
|
Точка лежит на окружности. |
Точка лежит на прямой. Попутно получили, что точка – точка пересечения (или точка касания) прямой и окружности |
|
|
Точка не лежит на окружности. |
Точка не лежит на прямой. |
Теперь изобразим обе линии и точки. Чтобы начертить прямую, нужно знать две точки, через которые она проходит. Но мы две такие точки и знаем – и .
Окружность строим с центром в точке и радиусом .
Рис. 25. На графике изображены точки с координатами , окружность, заданная уравнением , и прямая, заданная уравнением
Ответ: точка лежит только на прямой, точка – только на окружности, точка – точка пересечения прямой и окружности, точка не лежит ни на одной из двух линий.
Задача 8. Найти точки пересечения окружности и прямой с осями координат и друг с другом.
Решение.
Точка пересечения двух линий – это точка, которая принадлежит одновременно им обеим, т. е. ее координаты должны удовлетворять одновременно уравнениям обеих линий. Или, если перевести на математический язык, они должны являться решением соответствующей системы уравнений.
Найдем сначала точки пересечения прямой и окружности. Составляем систему уравнений и решаем ее.
Получаем две точки пересечения:
В принципе, при решении данной задачи можно обойтись без чертежа, но с ним проще и нагляднее (да и для самоконтроля он полезен). Поэтому построим окружность (мы знаем, что ее центр имеет координаты , а ее радиус равен ) (см. рис. 26):
Рис. 26. График окружности с центром в точке с координатами и радиусом, равным
Прямую мы можем построить по двум точкам ее пересечения с окружностью, которые мы нашли: (см. рис.
27).
Рис. 27. График прямой, пересекающей окружность с центром в точке с координатами и радиусом, равным , в точках с координатами
Уже видно, что мы «случайно» нашли точку пересечения прямой с осью и одну из точек пересечения окружности с осью :
Ось является прямой и задается уравнением , ось задается уравнением . Чтобы найти точки пересечения данных в условии прямой и окружности с осями координат, поступим точно так же – решим соответствующие системы уравнений.
Пересекаем окружность и ось :
Получаем:
Откуда находим две точки пересечения:
Аналогично находим точки пересечения окружности и оси :
Получаем:
Откуда находим две точки пересечения:
Осталось найти координаты точек пересечения с осями прямой из условия. Используем ту же самую идею – решаем две соответствующие системы.
Система состоит из уравнения прямой и уравнения оси :
Получили уже известную нам точку:
Система состоит из уравнения прямой и уравнения оси :
Получили точку (см.
рис. 28):
Рис. 28. На графике отмечены точки пересечения окружности и прямой с осями координат и друг с другом
Ответ: точки пересечения окружности с осями координат: . Точки пересечения прямой с осями координат: . Точки пересечения окружности и прямой: .
Решение геометрических задач алгебраическими методами
В последней задаче рассмотрим, как алгебраические методы (в нашем случае использование координат) помогают при решении сугубо геометрических задач.
Задача 9. Доказать, что центром описанной окружности прямоугольного треугольника является середина гипотенузы (см. рис. 29).
Рис. 29. Иллюстрация к задаче 9
Доказательство.
То, что центр гипотенузы является центром описанной окружности, означает, что точка (этот самый центр) находится на одинаковом расстоянии от всех вершин треугольника (см. рис. 30).
Рис. 30. Точка находится на одинаковом расстоянии от всех вершин треугольника
Докажем, что так оно и есть.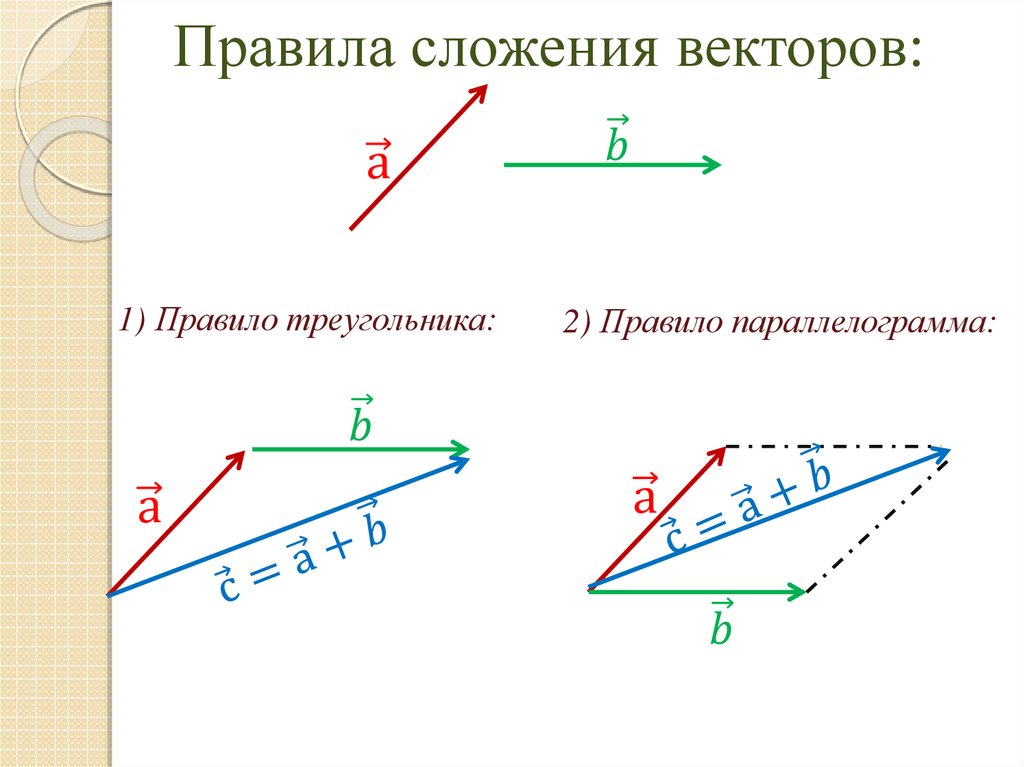
Введем систему координат и расположим треугольник так, чтобы его катеты лежали на координатных осях, а вершина прямого угла совпадала с началом координат (см. рис. 31).
Рис. 31. В системе координат катеты прямоугольного треугольника лежат на координатных осях, а вершина прямого угла совпадает с началом координат
Пусть длины катетов равны и . Тогда мы знаем координаты всех вершин (см. рис. 32):
Рис. 32. Вершины треугольника имеют координаты
Найдем координаты точки – середины гипотенузы. Координаты середины отрезка – это среднее арифметическое координат концов:
Тогда точка имеет координаты (см. рис. 33):
Рис. 33. Точка имеет координаты
Вычислим длины трех отрезков , и , используя формулу для нахождения расстояния между двумя точками:
Получаем:
Видим, что длины всех трех отрезков одинаковы, причем равны половине гипотенузы:
Значит, точка – центр описанной окружности (см.
рис. 34).
Рис. 34. , точка – центр описанной окружности
Доказано.
Заключение
В дальнейшем мы свяжем эти два инструмента – векторы и координаты – и научимся использовать их связь для решения более сложных задач.
Список литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 9 класс. Учебник. – М.: «Просвещение», 2017.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия. 9 класс. Учебник. – М.: «Просвещение», 2018.
- Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия. 9 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал webmath.ru (Источник)
- Интернет-портал kursoteka.ru (Источник)
- Интернет-портал yaklass.ru (Источник)
Домашнее задание
1.
Точки расположены так, что . Доказать, что для любой точки справедливо равенство:
2. Даны точки . Доказать, что диагонали четырехугольника взаимно перпендикулярны.
3. Даны точки и . Найти множество всех точек , для каждой из которых:
Как определить, является ли вектор линейной комбинацией других векторов
Идея линейной комбинации векторов очень важна для изучения линейной алгебры. Мы можем использовать линейные комбинации для понимания остовных множеств, пространства столбцов матрицы и многих других тем. Одним из самых полезных навыков при работе с линейными комбинациями является определение того, когда один вектор является линейной комбинацией заданного набора векторов.
реклама
Предположим, что у нас есть вектор \(\vec{v}\) и мы хотим узнать ответ на вопрос «является ли \(\vec{v}\) линейной комбинацией векторов \(\vec{ a}_{1}\), \(\vec{a}_{2}\) и \(\vec{a}_{3}\)?». Используя определение линейной комбинации векторов, этот вопрос можно сформулировать следующим образом:
Существуют ли скаляры \(x_{1}\), \(x_{2}\) и \(x_{3}\) такие, что:
\(\vec{v} = x_1\vec{a}_{ 1 }+x_2\vec{a}_{2}+ x_3\vec{a}_{3}\)?
Если векторы находятся в \(R^n\) для некоторого \(n\), то на этот вопрос можно ответить, используя эквивалентную расширенную матрицу:
\(\left[ \begin{array}{ccc|c} \vec{a}_1 & \vec{a}_2 & \vec{a}_3 & \vec{v} \\ \end{array} \right ]\)
Если эта матрица представляет собой непротиворечивую систему уравнений, то мы можем сказать, что \(\vec{v}\) является линейной комбинацией других векторов.
Пример
Определить, является ли вектор \(\begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix}\) линейной комбинацией векторов:
\(\begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix}\), \(\begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix}\), \(\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix}\) и \(\begin{bmatrix} -4 \\ 6 \\ 1 \\ \end{bmatrix}\)
Решение
Помните, что это означает, что мы хотим найти константы \(x_{1}\), \(x_{2}\), \(x_{3}\) и \(x_{4}\) так что:
\(\begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix} = x_{1}\begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix} + x_{2} \begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix} + x_{3}\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix} + x_{4}\begin {bmatrix}-4\6\1\\end{bmatrix}\)
Это векторное уравнение эквивалентно расширенной матрице. Составляя эту матрицу и уменьшая количество строк, мы находим, что:
\(\left[ \begin{array}{cccc|c} 2 & 1 & 8 & -4 & 5 \\
0 & 4 & 1 & 6 & 3 \\
1 & 3 & 1 & 1 & 0 \ \
\ конец {массив} \ справа]
\)
Эквивалент:
\(\left[ \begin{array}{cccc|c} 1 & 0 & 0 & -\dfrac{103}{29} & -\dfrac{74}{29} \\
0 & 1 & 0 & \ dfrac{42}{29} & \dfrac{13}{29} \\
0 & 0 & 1 & \dfrac{6}{29} & \dfrac{35}{29} \\
\end{массив} \Правильно]\)
Хотя это и некрасиво, эта матрица НЕ содержит такой строки, как \(\begin{bmatrix} 0 & 0 & 0 & 0 & c \\ \end{bmatrix}\), где \(c \neq 0 \), что указывало бы на то, что базовая система несовместима.
Следовательно, основная система непротиворечива (имеет решение), что означает, что векторное уравнение также непротиворечиво.
Итак, мы можем сказать, что \(\begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix}\) является линейной комбинацией других векторов.
Пошаговый процесс
В общем, если вы хотите определить, является ли вектор \(\vec{u}\) линейной комбинацией векторов \(\vec{v}_{1}\), \(\vec{v}_ {2}\), … , \(\vec{v}_{p}\) (для любого целого числа \(p > 2\)) вы сделаете следующее.
Шаг 1
Настройка расширенной матрицы
\(\left[ \begin{array}{cccc|c} \vec{v}_1 & \vec{v}_2 & \cdots & \vec{v}_p & \vec{u} \\ \end{array } \right]\)
и уменьшить строку.
Шаг 2
Используйте сокращенную форму матрицы, чтобы определить, представляет ли расширенная матрица непротиворечивую систему уравнений. Если это так, то \(\vec{u}\) является линейной комбинацией остальных. В противном случае это не так.
На втором этапе важно помнить, что система уравнений непротиворечива, если существует одно решение ИЛИ много решений.
Количество решений не важно, главное, чтобы было хотя бы одно решение. Это означает, что существует по крайней мере один способ записать данный вектор как линейную комбинацию других.
Запись вектора в виде линейной комбинации других векторов
Иногда вас могут попросить записать вектор в виде линейной комбинации других векторов. Это требует той же работы, что и выше, с еще одним шагом. Вам нужно использовать решение векторного уравнения, чтобы написать, как векторы комбинируются, чтобы создать новый вектор.
Давайте начнем с более простого случая, чем тот, который мы делали раньше, а затем вернемся к нему, так как он немного сложнее.
Пример
Запишите вектор \(\vec{v} = \begin{bmatrix} 2 \\ 4 \\ 2 \\ \end{bmatrix}\) в виде линейной комбинации векторов:
\(\begin{bmatrix} 2 \ \ 0 \\ 1 \\ \end{bmatrix}\), \(\begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix}\) и \(\begin{bmatrix} -2 \ \ 0 \\ 0 \\ \end{bmatrix}\)
Решение
Шаг 1
Мы настраиваем нашу расширенную матрицу и уменьшаем ее по строкам.
\(
\left[ \begin{array}{ccc|c} 2 & 0 & -2 & 2 \\
0 & 1 & 0 & 4 \\
1 & 0 & 0 & 2 \\
\end{ массив} \справа]
\)
эквивалентно
\(
\left[ \begin{array}{ccc|c} 1 & 0 & 0 & 2 \\
0 & 1 & 0 & 4 \\
0 & 0 & 1 & 1 \\
\end{array } \справа]
\)
Шаг 2
Определяем, представляет ли матрица непротиворечивую систему уравнений.
Основанная на уменьшенной матрице базовая система непротиворечива. Опять же, это потому, что нет строк со всеми нулями в коэффициентной части матрицы и единственного ненулевого значения в дополнении. (вы также можете использовать количество точек разворота в качестве аргумента.)
В отличие от предыдущего, мы не только хотим проверить, что у нас есть линейная комбинация. Мы хотим показать саму линейную комбинацию. Это означает, что нам нужно реальное решение. В данном случае есть только один:
\(x_1 = 2\), \(x_2 = 4\), \(x_3 = 1\)
Используя эти значения, мы можем записать \(\vec{v}\) как:
\(\vec{v} = \begin{bmatrix} 2 \\ 4 \\ 2 \\ \end{bmatrix} = (2)\begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix} + (4)\begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} + (1)\begin{bmatrix} -2 \\ 0 \\ 0 \\ \end{bmatrix}\)
Теперь давайте вернемся к нашему первому примеру (с сумасшедшими дробями), но немного изменим инструкции.
Пример
Запишите вектор \(\vec{v} = \begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix}\) в виде линейной комбинации векторов:
\(\begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix}\), \(\begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix}\), \ (\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix}\) и \(\begin{bmatrix} -4 \\ 6 \\ 1 \\ \end{bmatrix}\)
Когда мы сделали шаг 1, у нас была следующая работа. Это показало, что эквивалентное векторное уравнение было непротиворечивым, и подтвердило, что \(\vec{v}\) является линейной комбинацией других векторов.
\(\left[ \begin{array}{cccc|c} 2 & 1 & 8 & -4 & 5 \\
0 & 4 & 1 & 6 & 3 \\
1 & 3 & 1 & 1 & 0 \\
\end{массив} \right]
\)
Эквивалент:
\(\left[ \begin{array}{cccc|c} 1 & 0 & 0 & -\dfrac{103}{29} & -\dfrac{74}{29} \\
0 & 1 & 0 & \ dfrac{42}{29} & \dfrac{13}{29} \\
0 & 0 & 1 & \dfrac{6}{29} & \dfrac{35}{29} \\
\end{массив} \Правильно]\)
Что, если бы мы захотели записать линейную комбинацию.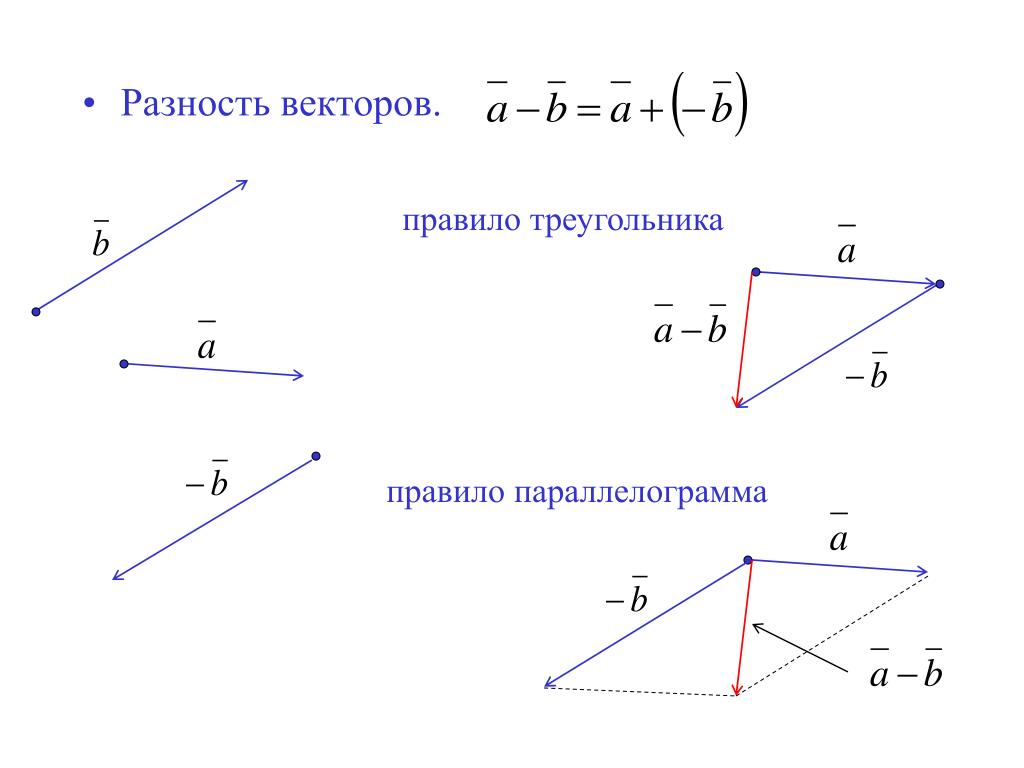
Этот пример отличается от предыдущего тем, что существует бесконечно много решений векторного уравнения.
Присмотревшись к этой расширенной матрице, мы увидим, что имеется одна свободная переменная \(x_{4}\). Если мы выпишем уравнения, мы получим:
\(x_1 – \left(\dfrac{103}{29}\right)x_4 = -\dfrac{74}{29}\)
\(x_2 + \left(\dfrac{42}{29}\right)x_4 = \dfrac{13}{29}\)
\(x_3 + \left(\dfrac{6}{29}\right)x_4 = \dfrac{35}{29}\)
Поскольку \(x_{4}\) — свободная переменная, мы можем присвоить ей любое значение и найти решение этой системы уравнений. Действительно «хорошее» значение было бы равно нулю. Если \(x_4 = 0\), то:
\(x_1 – \dfrac{103}{29}(0) = -\dfrac{74}{29}\)
\(x_2 + \dfrac{42}{29}(0) = \dfrac{13}{29}\)
\(x_3 + \dfrac{6}{29}(0) = \dfrac{35}{29}\)
Используя это решение, мы можем записать \(\vec{v}\) как линейную комбинацию других векторов.
\(\vec{v} = \begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix} = \left(-\dfrac{72}{29}\right)\begin{bmatrix} 2 \ \ 0 \\ 1 \\ \end{bmatrix} + \left(\dfrac{13}{29}\right)\begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix} + \left( \dfrac{35}{29}\right)\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix} + (0)\begin{bmatrix} -4 \\ 6 \\ 1 \\ \end{bmatrix}\)
Это было бы одно решение, но поскольку \(x_4\) бесплатен, их бесконечно много.
Для каждого возможного значения \(x_4\) у вас есть другой правильный способ записать \(\vec{v}\) как линейную комбинацию других векторов. Например, если \(x_4 = 1\):
\(\begin{align}x_1 &= -\dfrac{74}{29} + \dfrac{103}{29} \\ &= \dfrac{29}{29} \\ &= 1\end{align} \)
\(\begin{align}x_2 &= \dfrac{13}{29} – \dfrac{42}{29}\\ &= -\dfrac{29}{29} \\ &= -1\end{align}\)
\(\begin{align}x_3 &= \dfrac{35}{29} – \dfrac{6}{29}\\ &= \dfrac{29}{29} \\ &= 1\end{align}\ )
Используя это, мы также можем написать:
\(\vec{v} = \begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix} = (1)\begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix} + (-1)\begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix} + (1)\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix} + (1 )\begin{bmatrix} -4 \\ 6 \\ 1 \\ \end{bmatrix}\)
Как хорошо? (примечание: обычно мы не записываем 1 в уравнении, показывающем линейную комбинацию. Я оставил его там, чтобы вы могли видеть, где оказалось каждое число из решения).
Опять же, у подобной задачи бесконечно много ответов.
Все, что вам нужно сделать, это выбрать значение для свободных переменных, и у вас будет одно конкретное решение, которое вы сможете использовать при написании линейной комбинации.
Когда вектор НЕ является линейной комбинацией других
Стоит рассмотреть один пример, когда вектор не является линейной комбинацией некоторых заданных векторов. Когда это произойдет, мы получим расширенную матрицу, указывающую на противоречивую систему уравнений.
Пример
Определить, является ли вектор \(\begin{bmatrix} 1 \\ 2 \\ 1 \\ \end{bmatrix}\) линейной комбинацией векторов:
\(\begin{bmatrix} 1 \\ 1 \\ 0 \\ \end{bmatrix}\), \(\begin{bmatrix} 0 \\ 1 \\ -1 \\ \end{bmatrix}\), и \(\begin{bmatrix} 1\\ 2 \\ — 1 \\ \end{bmatrix}\).
Решение
Шаг 1
Мы настраиваем нашу расширенную матрицу и уменьшаем ее по строкам.
\(
\left[ \begin{array}{ccc|c} 1 & 0 & 1 & 1 \\
1 & 1 & 2 & 2 \\
0 & -1 & -1 & 1 \\
\end{массив} \right]
\)
эквивалентно:
\(
\left[ \begin{array}{ccc|c} 1 & 0 & 1 & 0 \\
0 & 1 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array } \справа]
\)
Шаг 2
Определяем, представляет ли матрица непротиворечивую систему уравнений.
Учитывая форму последней строки, эта матрица представляет противоречивую систему уравнений. Это означает, что нет никакого способа записать этот вектор как линейную комбинацию других векторов. Вот именно — больше нечего сказать! Это будет наш вывод каждый раз, когда сокращение строки приводит к строке с нулями и ненулевым значением в увеличении.
Учебное пособие – линейные комбинации и пролет
Нужно больше практики с линейными комбинациями и пролетом? Это 40-страничное учебное пособие поможет! Он включает в себя объяснения, примеры, практические задачи и полные пошаговые решения.
Получить учебное пособие
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и наборы задач.
Подпишитесь, чтобы время от времени получать электронные письма (раз в пару или три недели), сообщающие о новинках!
Linear Combinations and Span
Let v 1 , v 2 ,…, v r be vectors in R n .
линейная комбинация этих векторов представляет собой любое выражение вида
где коэффициенты k 1 , k 2 ,…, k r являются скалярами.
Пример 1 : Вектор v = (−7, −6) является линейной комбинацией векторов v 1 = (−2, 3) и v 2 = (1, 4 ), так как v = 2 v 1 − 3 v 2 . Нулевой вектор также является линейной комбинацией v 1 и v 2 , поскольку 0 = 0 v 1 + 0 2 4 4 В самом деле, легко видеть, что нулевой вектор в R n is always a linear combination of any collection of vectors v 1 , v 2 ,…, v r from R n .
The set of all linear combinations of a collection of vectors v 1 , v 2 ,…, v r from R n называется пролетом из { v 1 , v 2 ,…, v r } . 5 } Этот набор, обозначенный SPAN { V 1 , V 2 ,…, V R }, всегда является субпасом R 
Пример 2 : Промежуток множества {(2, 5, 3), (1, 1, 1)} является подпространством R 3 , состоящая из всех линейных комбинаций векторов v 1 = (2, 5, 3) и v 2 = (1, 1, 1). Это определяет плоскость в R 3 . Поскольку вектор нормали к этой плоскости в n = v 1 x v 2 = (2, 1, −3), уравнение этой плоскости имеет вид 2 x + y − 3 z = d для некоторой константы д . Поскольку плоскость должна содержать начало координат — это подпространство — d должно быть равно 0. Это плоскость в примере 7.
Пример 3 : Подпространство R 2 , натянутое на векторы i = (1, 0) и j = (0, 1), есть все R 2 1 каждый 90901 , потому что вектор в R 2 может быть записан как линейная комбинация i и j :
Let v 1 , v 2 ,…, v r −1 , v r be vectors in R n .
Если V R — это линейная комбинация V 1 , V 2 ,…, V 9 111112111121111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111тели .
То есть, если какой-либо из векторов в данной коллекции является линейной комбинацией других, то его можно отбросить, не затрагивая диапазон. Следовательно, чтобы получить наиболее «эффективный» остовный набор, найдите и исключите все векторы, которые зависят от других (то есть могут быть записаны в виде их линейной комбинации).
Пример 4 : Пусть v 1 = (2, 5, 3), v 2 = (1, 1, 1) и v 3 = (3, 15) ). Так как v 3 = 4 v 1 − 5 v 2 ,
То есть, поскольку v 3 является линейной комбинацией v 1 и v 2 , его можно исключить из коллекции, не затрагивая диапазон.
Геометрически вектор (3, 15, 7) лежит в плоскости, натянутой на V 1 и V 2 (см. Пример 7 выше), поэтому добавление множества V 3 к линейным сочетаниям V 1 . вектора от этой плоскости. Обратите внимание, что V 1 является линейной комбинацией V 2 и В 3 (с В 1 = 5/4.1 V 1 = 5/4.1 V 1 = 5/4.1 V 1 = 5/4.1 V 1 = 5.102331. 3 ) и В 2 — это линейная комбинация В 1 и В 2 3 (с V 2 3 (с V 2 3 (с V 2 3 (с V 9 2 3 (с V 9 2 3 .
