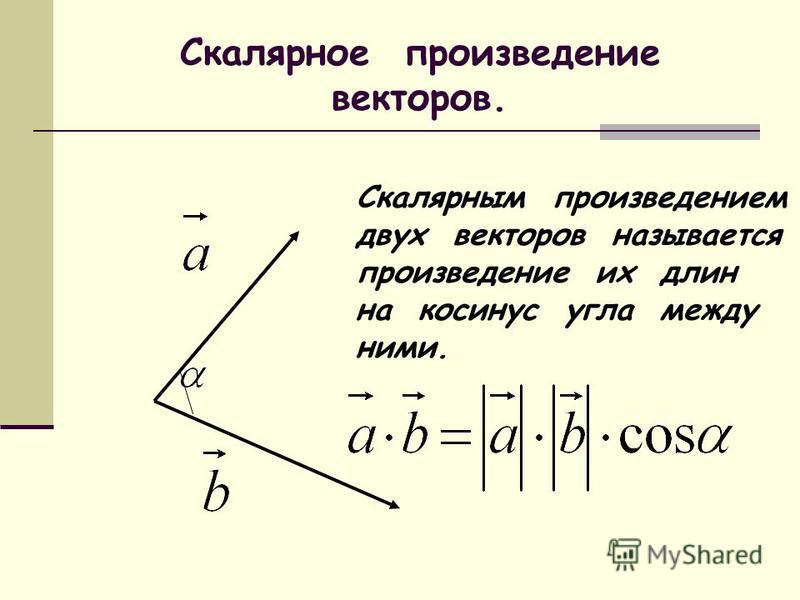
определения, свойства, формулы, примеры и решения
Определение векторного произведения
Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a→, b→, c→ в трехмерном пространстве.
Отложим для начала векторы a→, b→, c→ от одной точки. Ориентация тройки a→, b→, c→ бывает правой или левой, в зависимости от направления самого вектора c→. От того, в какую сторону осуществляется кратчайший поворот от вектора a→ к b→ с конца вектора c→, будет определен вид тройкиa→, b→, c→.
Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a→, b→, c→ называется правой, если по часовой стрелке – левой.
Далее возьмем два не коллинеарных вектора a→ и b→. Отложим затем от точки A векторы AB→=a→ и AC→=b→. Построим вектор AD→=c→, который одновременно перпендикулярный одновременно и AB→ и AC→. Таким образом, при построении самого вектора AD→=c→ мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).
Упорядоченная тройка векторов a→, b→, c→ может быть, как мы выяснили правой или левой в зависимости от направления вектора.
Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Определение 1Векторным произведением двух векторов a→ и b→ будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
- если векторы a→ и b→ коллинеарны, он будет нулевым;
- он будет перпендикулярен и вектору a→ и вектору b→ т.е. ∠a→c→=∠b→c→=π2 ;
- его длина определяется по формуле: c→=a→·b→·sin∠a→,b→;
- тройка векторов a→, b→, c→ имеет такую же ориентацию, что и заданная система координат.
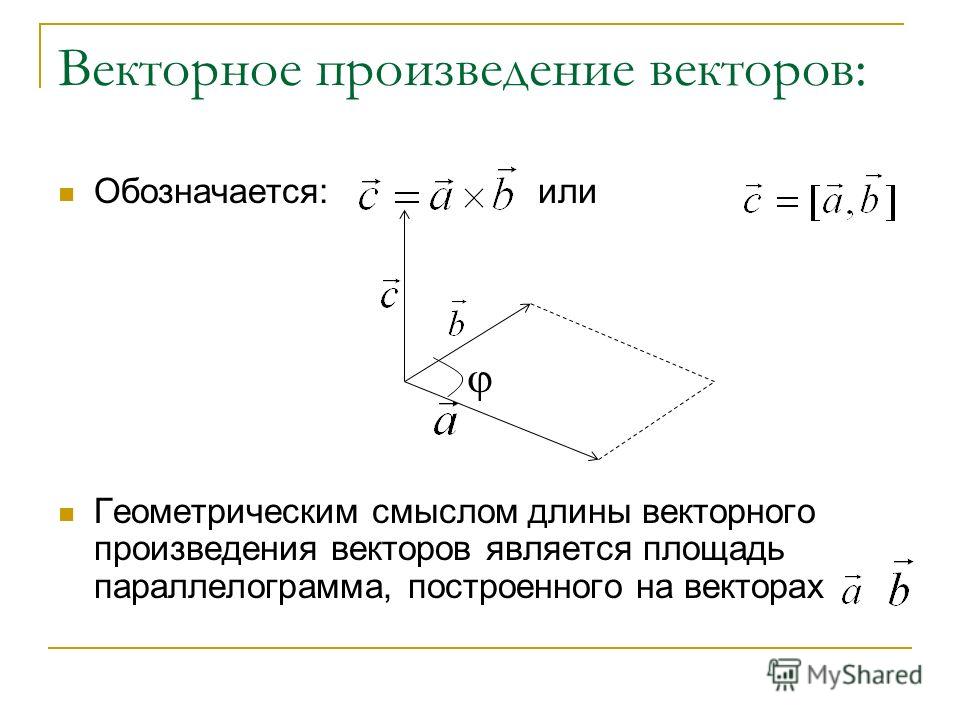
Векторное произведение векторов a→ и b→ имеет следущее обозначение: a→×b→.
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.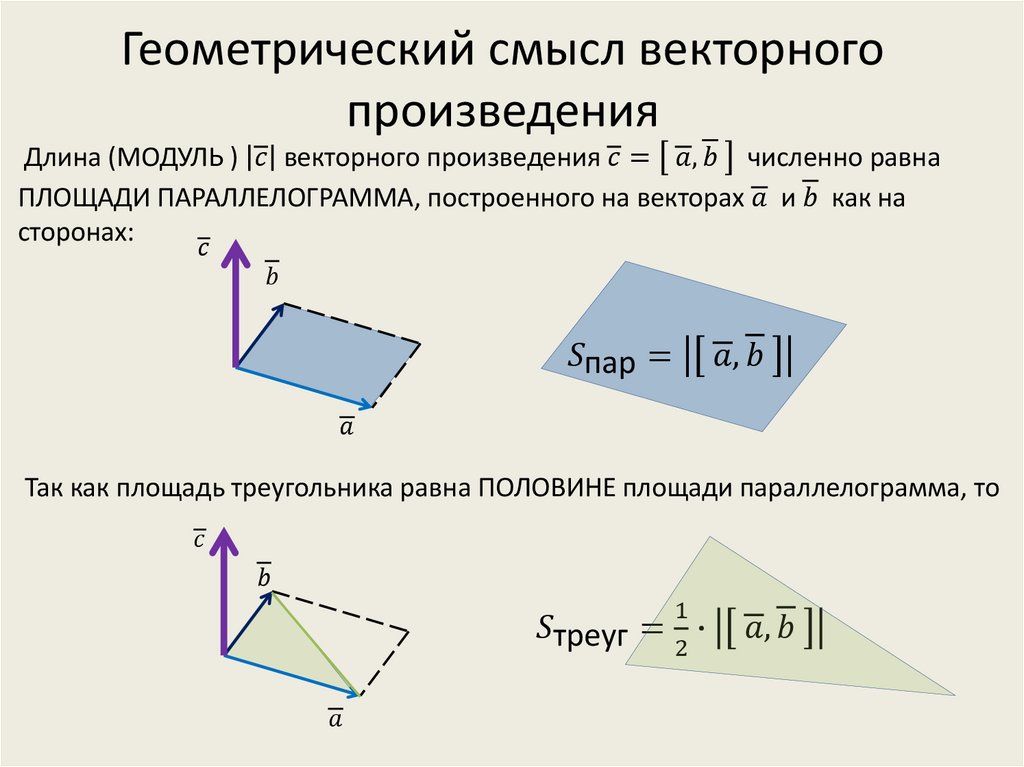
В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a→=(ax; ay; az) и b→=(bx; by; bz)
Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i→, j→, k→, вторая строка содержит координаты вектора a→, а третья – координаты вектора b→ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c→=a→×b→=i→j→k→axayazbxbybz
Разложив данный определитель по элементам первой строки, получим равенство: c→=a→×b→=i→j→k→axayazbxbybz=ayazbybz·i→-axazbxbz·j→+axaybxby·k→==a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→
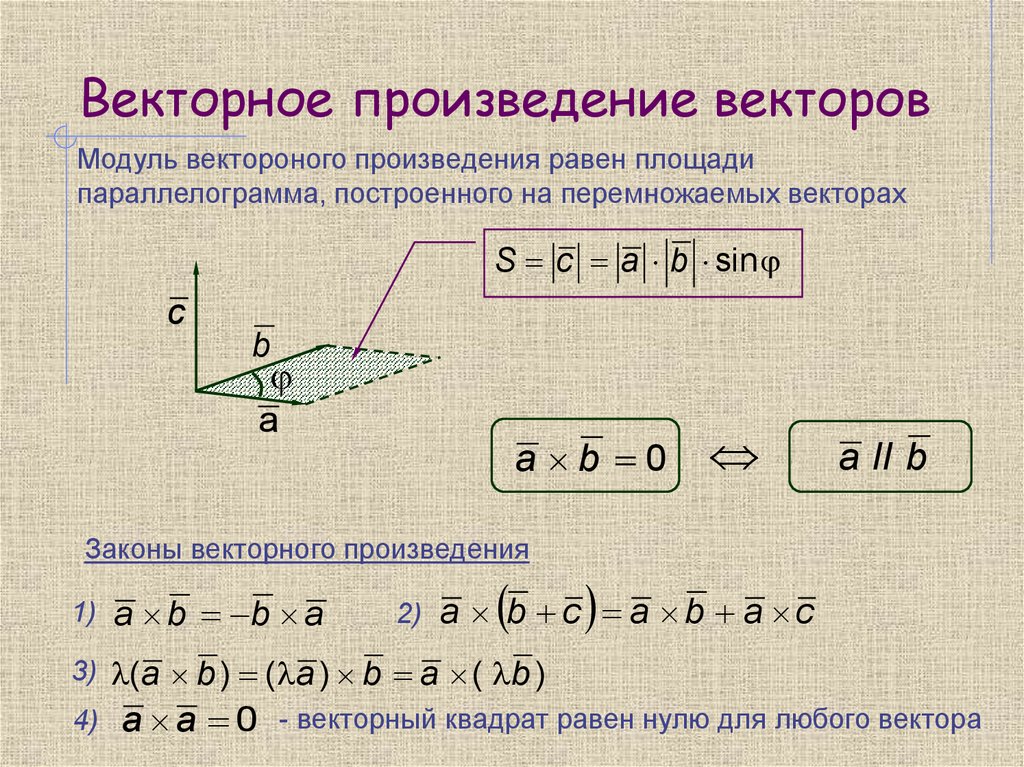
Свойства векторного произведения
Известно, что векторное произведение в координатах представляется как определитель матрицы c→=a→×b→=i→j→k→axayazbxbybz, то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:
- антикоммутативность a→×b→=-b→×a→;
- дистрибутивность a(1)→+a(2)→×b=a(1)→×b→+a(2)→×b→ или a→×b(1)→+b(2)→=a→×b(1)→+a→×b(2)→;
- ассоциативность λ·a→×b→=λ·a→×b→ или a→×(λ·b→)=λ·a→×b→, где λ — произвольное действительное число.

Данные свойства имеют не сложные доказательства.
Для примера можем доказать свойство антикоммутативности векторного произведения.
Доказательство антикоммутативностиПо определению a→×b→=i→j→k→axayazbxbybz и b→×a→=i→j→k→bxbybzaxayaz. А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно,a→×b→=i→j→k→axayazbxbybz =-i→j→k→bxbybzaxayaz=-b→×a→, что и доказывает антикоммутативность векторного произведения.
Векторное произведение – примеры и решения
В большинстве случаев встречаются три типа задач.
В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулойc→=a→·b→·sin∠a→,b→ .
Пример 1Найдите длину векторного произведения векторов a→ и b→, если известноa→=3, b→=5, ∠a→,b→=π4.
Решение
С помощью определения длины векторного произведения векторов a→ и b→ решим данную задач: a→×b→=a→·b→·sin∠a→,b→=3·5·sinπ4=1522.
Ответ: 1522.
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a→=(ax; ay; az) и b→=(bx; by; bz).
Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a→ и b→, а их разложения по координатным векторам вида
Рассмотрим следующие примеры.
Пример 2В прямоугольной системе координат заданы два вектора a→=(2; 1; -3), b→=(0; -1; 1). Найдите их векторное произведение.
Решение
По второму определению найдем векторное произведение двух векторов в заданных координатах:a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→==(1·1-(-3)·(-1))·i→+((-3)·0-2·1)·j→+(2·(-1)-1·0)·k→==-2i→-2j→-2k→.
Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a→×b→=i→j→k→axayazbxbybz=i→j→k→21-30-11=-2i→-2j→-2k→.
Ответ: a→×b→=-2i→-2j→-2k→.
Пример 3Найдите длину векторного произведения векторов i→-j→ и i→+j→+k→, где i→, j→, k→ — орты прямоугольной декартовой системы координат.
Решение
Для начала найдем координаты заданного векторного произведения i→-j→×i→+j→+k→ в данной прямоугольной системе координат.
Известно, что векторы i→-j→ и i→+j→+k→ имеют координаты (1; -1; 0) и (1; 1; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i→-j→×i→+j→+k→=i→j→k→1-10111=-i→-j→+2k→.
Следовательно, векторное произведение i→-j→×i→+j→+k→ имеет координаты (-1; -1; 2) в заданной системе координат.
Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i→-j→×i→+j→+k→=-12+-12+22=6.
Ответ: i→-j→×i→+j→+k→=6. .
.
В прямоугольной декартовой системе координат заданы координаты трех точек A(1,0,1), B(0,2,3), C(1,4,2) . Найдите какой-нибудь вектор, перпендикулярный AB→ и AC→ одновременно.
Решение
Векторы AB→ и AC→ имеют следующие координаты (-1; 2; 2) и (0; 4; 1) соответственно. Найдя векторное произведение векторов AB→ и AC→, очевидно, что оно является перпендикулярным вектором по определению и к AB→ и к AC→, то есть, является решением нашей задачи. Найдем его AB→×AC→=i→j→k→-122041=-6i→+j→-4k→.
Ответ: -6i→+j→-4k→. — один из перпендикулярных векторов.
Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.
Пример 5Векторы a→ и b→ перпендикулярны и их длины равны соответственно 3 и 4. Найдите длину векторного произведения 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→.
Решение
По свойству дистрибутивности векторного произведения мы можем записать 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→
По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→==3·a→×a→+3·(-2)·a→×b→+(-1)·b→×a→+(-1)·(-2)·b→×b→==3·a→×a→-6·a→×b→-b→×a→+2·b→×b→
Векторные произведения a→×a→ и b→×b→ равны 0, так как a→×a→=a→·a→·sin0=0 и b→×b→=b→·b→·sin0=0, тогда 3·a→×a→-6·a→×b→-b→×a→+2·b→×b→=-6·a→×b→-b→×a→.
Из антикоммутативности векторного произведения следует -6·a→×b→-b→×a→=-6·a→×b→-(-1)·a→×b→=-5·a→×b→..
Воспользовавшись свойствами векторного произведения, получаем равенство 3·a→-b→×a→-2·b→==-5·a→×b→.
По условию векторы a→ и b→ перпендикулярны, то есть угол между ними равен π2. Теперь остается лишь подставить найденные значения в соответствующие формулы: 3·a→-b→×a→-2·b→=-5·a→×b→==5·a→×b→=5·a→·b→·sin(a→,b→)=5·3·4·sinπ2=60.
Ответ: 3·a→-b→×a→-2·b→=60.
Геометрический смысл векторного произведения
Длина векторного произведения векторов по орпеделению равна a→×b→=a→·b→·sin∠a→,b→. Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов a→ и b→, отложенные от одной точки, на синус угла между ними sin∠a→,b→.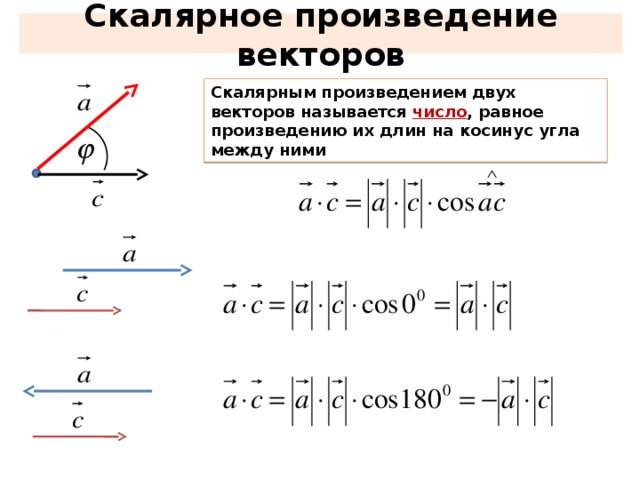
Это и есть геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.
Определение 3Под моментом силы F→, приложенной к точке B, относительно точки A будем понимать следующее векторное произведение AB→×F→.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
§23. Векторное произведение векторов
Определение 1. Векторным произведением двух ненулевых неколлинеарных векторов называется вектор , такой что:
длина вектора равна произведению длин этих векторов на синус угла между ними:
вектор перпендикулярен этим векторам и
векторы , образуют базис того же типа, что и векторы (правый базис).

Если же векторы коллинеарны или хотя бы один из них нулевой вектор, то их векторное произведение есть нулевой вектор
Обозначение: или
Теорема 1. (О геометрическом смысле векторного произведения). Длина векторного произведения двух ненулевых неколлинеарных векторов равна площади параллелограмма, построенного на этих векторах.
Доказательство.
Следствие. Площадь ∆C выражается формулой:
Теорема доказана.
Теорема 2. Для того, чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было нулевым вектором:
Доказательство.
Необходимость. Пусть ,
тогда согласно определению 1 либо ,
либо ,
либо ,
либо ,
либо .
Во всех этих случаях вектора коллинеарны по определению.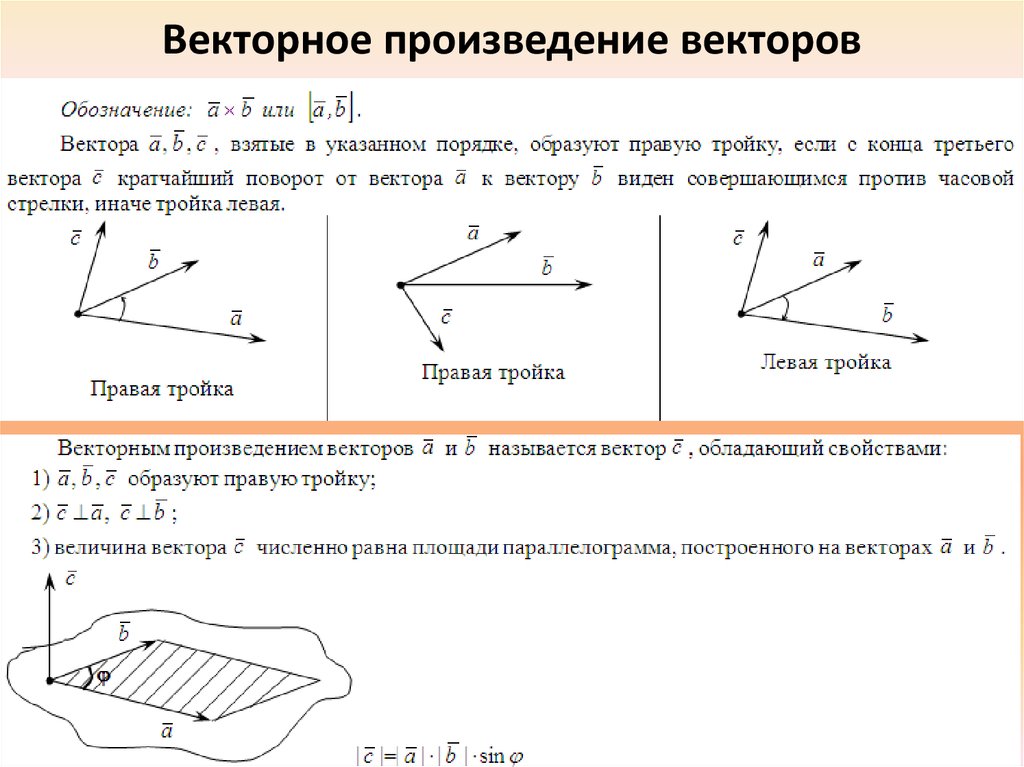
Достаточность. Пусть , тогда снова по определению 1
Теорема доказана.
Следующие три теоремы сформулируем без доказательства.
Теорема 3. Векторное произведение антикоммутативно (антисимметрично):
Теорема 4. Векторное произведение ассоциативно относительно скалярного множителя:
Теорема 5. Векторное произведение дистрибутивно относительно суммы векторов:
Теорема 6.
Доказательство.
Доказательство следует из определения 1.
Пусть, например, , тогда имеем:
⟹⟹.
Замечание. Достаточно запомнить первую формулу, вторая получается из первой, а третья – из второй с помощью круговой или циклической замены векторов
Теорема 7. (О координатах векторного произведения). Если в прямоугольном базисе (ортогональном) ( и , то
Доказательство.
Воспользуемся определением координат вектора и теоремами 3, 4, 5 и 6:
(см. определение определителя 3-его порядка)
Теорема доказана.
Пример. Вычислить площадь треугольника с вершинами А(-1,0,-1), В(0,2,-3), С(4,4,1).
Решение.
,
По следствию из теоремы 1 имеем:(кв.ед.).
Определение 1. Смешанным произведением трёх векторов называется число, равное скалярному произведению векторного произведения векторов на вектор .
Обозначение. (
Можно показать, что
Теорема 1. Абсолютная величина (модуль) смешанного произведения трёх неколлинеарных векторов равна объёму параллелепипеда, построенного на этих векторах.
Доказательство.
Введём обозначения: , ∠(
Тогда имеем:
( (1)
По теореме 1 из §2 имеем:
(2)
Пусть — высота параллелепипеда (.
Из ∆
Случай 1:
Случай 2:
В обоих случаях получаем:
. (3)
Подставляя значения (2) и (3) в формулу (1), окончательно получаем:
(
Итак,
. (4)
Теорема доказана.
Следствие 1.
. (5)
Доказательство следствия.
Следствие доказано.
Следствие 2. Знак смешанного произведения тройки некомпланарных векторов соответствует её ориентации, то есть если тройка правая, то , если тройка левая, то
Следствие 3. Три вектора коллинеарны тогда и только тогда, когда их смешанное произведение равно нулю.
Доказательство следствия.
Если
тройка векторов коллинеарная, то объём
параллелепипеда, построенного на
векторах этой тройки, равно нулю. Обратно,
если VПАР = 0,
то вектора тройки коллинеарны.
Обратно,
если VПАР = 0,
то вектора тройки коллинеарны.
Следствие доказано.
Замечание. Из трёх неколлинеарных векторов , можно составить шесть упорядоченных троек: причём первые три тройки векторов образуют правый базис, а последние три – левый базис (большой, указательный, средний пальцы).
При перестановке любых двух векторов в каждой из первых троек получается копия – либо из трёх последних, поэтому в результате меняется ориентация упорядоченных троек векторов.
Если в упорядоченной тройке векторов осуществить циклическую перестановку векторов, то непосредственной проверкой убедимся, что при этом ориентация упорядоченной тройки векторов не меняется.
Из
теоремы 1 следует, что при перестановке
векторов в упорядоченной тройке модуль
скалярного произведения не меняется,
так как во всех случаях он равен объёму
одного и того же параллелепипеда. Так
же от скалярного произведения зависит
ориентации
тройки
векторов.
Так
же от скалярного произведения зависит
ориентации
тройки
векторов.
Следствие 4.
(6)
Пример.
Используя формулу (6), то есть определение 1 дано корректно.
Теорема 2.
Теорема 3.
Доказательства теорем 2 и 3 следуют из свойств определителя 3-го порядка; мы их опускаем (см. теорему 4).
Теорема 4. Если в ортонормированном базисе
то
(7)
Доказательство. .
Теорема доказана.
Векторное и смешанное произведения векторов с примерами решения
Содержание:
Векторное произведение
Определение: Тройка векторов
Пример:
Рис. 13. Правая (а) и левая (б) тройки векторов.
Определение: Векторным произведением векторов называется вектор который:
- по модулю численно равен площади параллелограмма, построенного на векторах
- перпендикулярен плоскости, в которой лежат вектора
- тройка векторов является правой.

Замечание: Из определения векторного произведения следует, что направление вектора определяется по правилу правого винта: при вращении вектора к вектору правый винт движется в направлении вектора Вычислим площадь параллелограмма, построенного на векторах (Рис. 14):
Рис. 14. Площадь параллелограмма, определяющего длину вектора из треугольника АВС высота тогда следовательно, длина вектора равна где -угол между векторами
Векторное произведение векторов обладает следующими свойствами:
- 1.
- 2. ;
- 3. ;
- 4. Если вектор коллинеарен вектору то их векторное произведение равно нулю:
Замечание: Свойство 4. определяет второе условие коллинеарности векторов.
Формула для векторного произведения векторов через проекции перемножаемых векторов
Теорема: Пусть и .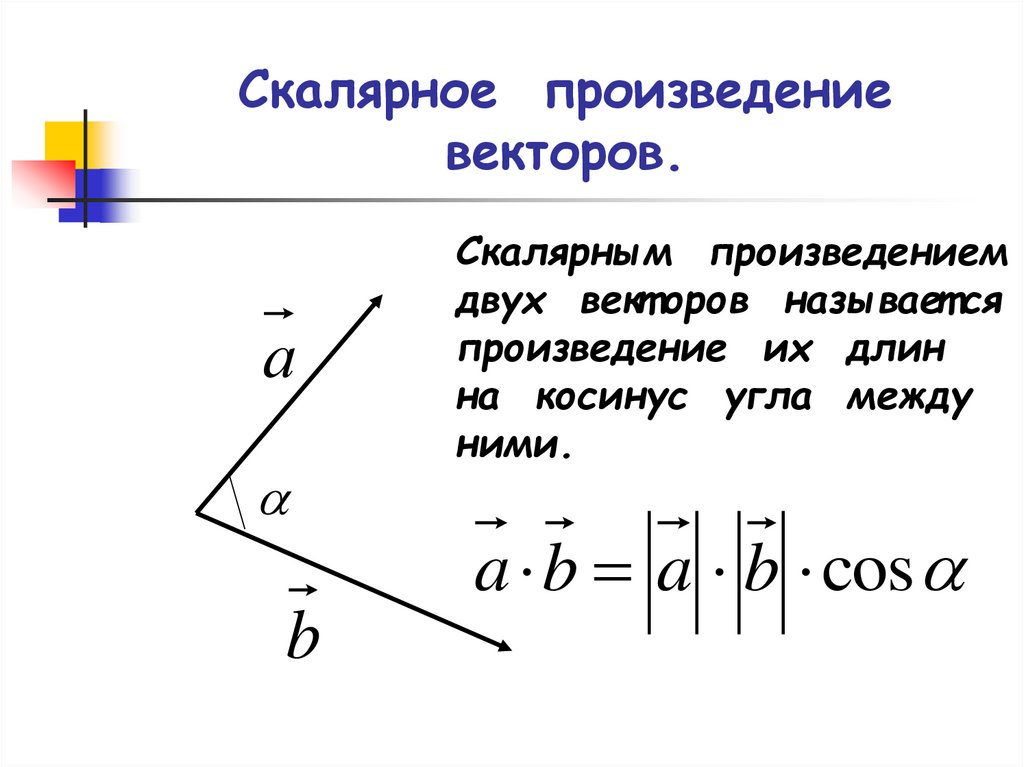 Тогда
Тогда
Доказательство: Запишем вектора в декартовом базисе: и Для доказательства формулы теоремы составим таблицу векторных произведений ортов осей:
Используя эту таблицу, вычислим векторное произведение векторов
Отсюда следует, что Для запоминания этих формул существует мнемоническое правило: надо запомнить переход проекций от одной к другой (Рис. 15):
Рис. 15. Циклический переход от одной координаты к другой.
Для нахождения, например проекции надо взять компонент у первого вектора и умножить на компоненту z второго вектора, а затем вычесть их произведение, обменяв местами обозначение компонент. Аналогично поступают при нахождении двух других проекций вектора С другой стороны, полученную формулу можно записать в виде
Полученное выражение представляет собой раскрытие определителя III порядка по элементам первой строки, то есть окончательно можно записать, что
Пример:
Найти, при каком значении параметра m вектор коллинеарен вектору
Решение:
Согласно свойству 4. для векторного произведения (пункт 1 Лекция № 6) найдем векторное произведение заданных векторов
для векторного произведения (пункт 1 Лекция № 6) найдем векторное произведение заданных векторов
Так как вектор должен быть нулевым, то все его проекции должны быть равными нулю, следовательно, m = 2.
- Заказать решение задач по высшей математике
Пример:
Найти векторное произведение векторов
Решение:
Пример:
Найти векторное произведение векторов
Решение:
Приложения векторного произведения
1. Физика. Пусть точка начала вектора закреплена, а к его концу приложена сила тогда момент этой силы будет равен (Рис. 16). Рис. 16. Момент силы
2. Геометрия. Пусть даны три разные точки и Требуется вычислить площадь треугольника
Введем в рассмотрение вектора (Рис. 17).
Рис. 17. Площадь треугольника
Проекции этих векторов равны:
Так как площадь треугольника составляет половину от площади параллелограмма, площадь которого равна модулю векторного произведения векторов то
Пример:
Даны три точки Вычислить площадь треугольника
Решение:
Введем в рассмотрение вектора вычислим их векторное произведение Следовательно, площадь треугольника равна
3. Тригонометрия. Выведем формулу для
Тригонометрия. Выведем формулу для
Пусть в плоской декартовой системе координат даны векторы которые образуют с положительным направлением оси Ох углы соответственно (Рис. 18):
Рис. 18. Синус суммы двух углов.
Проекции векторов равны Используя формулу для векторного произведения векторов и свойство 4. для определителей (см. Лекция № 7), получим Раскрыв этот определитель по элементам третьего столбца, имеем
Длина этого вектора равна По определению векторного произведения его длина равна Сравнивая две полученные формулы, получаем формулу для синуса суммы двух углов. В частности, при получаем, что синус удвоенного угла равен
Смешанное произведение векторов
Определение: Смешанным произведением векторов называется число равное векторному произведению умноженному скалярно на вектор т.е.
Получим формулу для вычисления смешанного произведения
Обменяв местами первую строку со второй, а затем и с третьей, получим окончательную формулу
Таким образом, смешанное произведение векторов представляет собой определитель III порядка, откуда следуют его свойства:
1. , т.е. вектора, входящие в смешанное произведение, можно циклически перестав.!ять местами, поэтому зачастую смешанное произведение пишут без знаков abc.
, т.е. вектора, входящие в смешанное произведение, можно циклически перестав.!ять местами, поэтому зачастую смешанное произведение пишут без знаков abc.
2. Смешанное произведение векторов равно объему параллелепипеда, построенного на этих векторах, взятого со знаком «+», если тройка векторов правая, и со знаком «-», если тройка векторов левая (Рис. 19):
Рис. 19. Объем параллелепипеда, построенного на векторах
Так как
3. Если вектора , и компланарны (лежат в одной плоскости или параллельных плоскостях), то их смешанное произведение равно нулю, т.е. .
Замечание: Свойство 3. определяет условие компланарности трех векторов, т.е. если то вектора и лежат в одной плоскости или параллельных плоскостях.
Пример:
Доказать, что вектора компланарны.
Решение:
Согласно формуле, определяющей смешанное произведение векторов, имеем
Пример:
Даны 4 точки Вычислить объем параллелепипеда.
Решение:
Составим векторы Вычислим объем параллелепипеда Положительность вычисленного объема указывает на то, что вектора и образуют правую тройку.
Пример:
Чему равен объём пирамиды с вершинами А, В, С и D (координаты точек А, В, С и D взять из VIII.). Найти длину высоту, которая опущена из точки А на основание BCD.
Решение:
Объём пирамиды равен Используя векторы из VIII., которые имеют координаты вычислим объём параллелепипеда Следовательно, объём пирамиды с вершинами А, В, С и D равен
С другой стороны, её объём по формуле из средней школы равен
Вычислим площадь треугольника BCD, лежащего в основании пирамиды: Вычислим векторное произведение этих векторов Найдём длину этого вектора Следовательно, площадь треугольника BCD равна Тогда длина высоты, опущенной из точки А на основание BCD, равна
Перекрестное произведение векторов в R-программировании
В математике перекрестное произведение или также известное как векторное произведение представляет собой бинарную операцию над двумя векторами в трехмерном пространстве и обозначается символом ‘ х ‘. Для двух линейно независимых векторов a и b перекрестное произведение a × b представляет собой вектор, который перпендикулярен обоим векторам a и b и, следовательно, нормален к плоскости, содержащей их.
Для двух линейно независимых векторов a и b перекрестное произведение a × b представляет собой вектор, который перпендикулярен обоим векторам a и b и, следовательно, нормален к плоскости, содержащей их.
Пусть мы дали два вектора,
и,
Где,
I: Вектор блока вдоль X направления
j: . вдоль направлений z
Тогда векторное произведение рассчитывается как:
где
— коэффициенты единичного вектора вдоль направлений i, j и k.
Пример:
Даны два вектора A и B,
A = 3i + 5j + 4k,
и
B = 2i + 7j + 5k 9001 4 ? 7)i + (4 ? 2 – 3 ? 5)j + (3 ? 7 – 5 ? 2)k
= (?3)i + (?7)j + (11)k
Перекрестное произведение в языке R
R предоставляет очень эффективный метод вычисления перекрестного произведения двух векторов. Используя метод cross() , доступный в 9Библиотека 0003 pracma . Эта функция вычисляет перекрестное или векторное произведение векторов в трех измерениях. В случае матриц он берет первое измерение длины 3 и вычисляет перекрестное произведение между соответствующими столбцами или строками.
Используя метод cross() , доступный в 9Библиотека 0003 pracma . Эта функция вычисляет перекрестное или векторное произведение векторов в трех измерениях. В случае матриц он берет первое измерение длины 3 и вычисляет перекрестное произведение между соответствующими столбцами или строками.
Syntax: cross(x, y)
Parameters:
x: numeric vector or matrix
y: numeric vector or matrix
# Taking Input as Vectors
Example 1:
R
[1] -3 -7 11 Example 2: R
Вывод: [1] -458 797 -29
# Taking Input as Matrix Example 1: R
Вывод: [ 1] [ 2] [ 3] [1, ] -4 14 -8 [2, ] -6 0 4 [3, ] 54 -36 -10 Пример 2: R
Вывод: [ 1] [ 2] [ 3] [1, ] -649 2624 61 [2, ] -3592 232 36 [3, ] 54 225 -242 Mathwords: перекрестное произведениеMathwords: перекрестное произведение
3D-перекрестное произведение • Информатика и машинное обучение3D-перекрестное произведение (также известное как 3D-внешнее произведение или векторное произведение ) двух векторов \(\mathbf{a}\) и \(\mathbf {b}\) определяется только на трехмерных векторах как другой вектор \(\mathbf{a}\times\mathbf{b}\), который ортогонален плоскости, содержащей как \(\mathbf{a}\), так и \ (\mathbf{b}\) и имеет величину 9\circ\), как \(\sin\theta=1\). Другое определение перекрестного произведения сохраняет направление векторного произведения в единичном векторе \(\hat{\mathbf{n}}\) перпендикулярно \(\mathbf{a}\) и \(\mathbf{ b}\) такое, что: \[\mathbf{a}\times\mathbf{b}=\hat{\mathbf{n}}|\mathbf{a}||\mathbf{b}|\sin\ theta\] Отсюда также очевидно, что коллинеарные векторы \(\mathbf{a}\) и \(\mathbf{b}\) приводят к \(\sin\theta=0\) и, таким образом, \(\mathbf {а}\раз\mathbf{b} = \mathbf{0}\) Чтобы получить векторное произведение, мы используем определитель, аналогичный вычислению 2D perp-product или perp-product с использованием определителя: \[\begin{array}{rl} \mathbf{a}\times\ mathbf{b} &= \left|\begin{array}{ccc}\hat{\mathbf{x}}&\hat{\mathbf{y}}&\hat{\mathbf{z}}\\ a_x & a_y & a_z\\ b_x & b_y & b_z \end{массив} \right|\\ &= (a_yb_z-a_zb_y)\hat{\mathbf{x}} - (a_zb_x-a_xb_z)\hat{\mathbf{y} } + (a_xb_y-a_yb_x)\hat{\mathbf{z}}\\ &= \left(\begin{array}{c} a_yb_z-a_zb_y\\ a_zb_x-a_xb_z\\ a_xb_y-a_yb_x \end{массив}\ справа) \end{массив}\] С \(\hat{\mathbf{x}}, \hat{\mathbf{y}}\) и \(\hat{\mathbf{z}}\) в качестве ортонормированного базиса. Свойства перекрестного произведенияСуществует два возможных варианта вычисления перекрестного произведения, каждый из которых представляет собой отрицание другого. Это делает векторное произведение некоммутативным и, следовательно, антикоммутативным/антисимметричным. Выбранный определяется по правилу правой руки. Если ваш указательный палец \(\mathbf{a}\), ваш средний палец \(\mathbf{b}\), то ваш большой палец - это положительных перекрестное произведение \(\mathbf{a}\times\mathbf{b}\). \[\mathbf{a}\times\mathbf{b}=-(\mathbf{b}\times\mathbf{a}) = (-\mathbf{b})\times\mathbf{a}\] Аддитивное распределение\[\mathbf{a}\times(\mathbf{b}+\mathbf{c}) = \mathbf{a}\times\mathbf{b}+\mathbf{a}\times\ mathbf{c}\] \[(\mathbf{a}+\mathbf{b})\times\mathbf{c} = \mathbf{a}\times\mathbf{c}+\mathbf{b}\ times\mathbf{c}\] Тождество Гросмана или двойное векторное произведениеЛевая ассоциация \[(\mathbf{a}\times\mathbf{b})\times\mathbf{c} = (\mathbf{a}\cdot\mathbf{c})\mathbf{b} - (\mathbf{ b}\cdot\mathbf{c})\mathbf{a}\] Правильная ассоциация \[\mathbf{a}\times(\mathbf{b}\times\mathbf{c}) = (\mathbf {a}\cdot\mathbf{c})\mathbf{b} - (\mathbf{a}\cdot\mathbf{b})\mathbf{c}\] Идентификация лжи\[\mathbf{a }\times(\mathbf{b}\times\mathbf{c}) + \mathbf{c}\times(\mathbf{a}\times\mathbf{b}) + \mathbf{b}\times(\mathbf {c}\times\mathbf{a}) = \mathbf{0}\] Ассоциация точка-крест\[\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c}) = (\mathbf{a}\times\mathbf{b})\cdot\mathbf {c} \] Скалярная ассоциация\[(\alpha\mathbf{a})\cdot(\beta\mathbf{b}) = (\alpha\beta)(\mathbf{a}\times\mathbf {b})\] \[\alpha(\mathbf{a}\times\mathbf{b}) = (\alpha\mathbf{a})\times\mathbf{b} = \mathbf{a}\ раз(\альфа\mathbf{b})\] Нормальность\[(\mathbf{a}\times\mathbf{b})\cdot\mathbf{a} = (\mathbf{a}\times\ mathbf{b})\cdot\mathbf{b} = 0\] Нильпотент\[\mathbf{a}\times\mathbf{a}=\mathbf{0}\] \[\mathbf{a}\times\mathbf{0} = \mathbf{0}\ times\mathbf{a} = \mathbf{0}\] Тождество Якоби\[\mathbf{a}\times(\mathbf{b}\times\mathbf{c}) + \mathbf{b}\ times(\mathbf{c}\times\mathbf{a}) + \mathbf{c}\times(\mathbf{a}\times\mathbf{b}) = \mathbf{0}\] Тождество Лагранжа\[(\mathbf{a}\times\mathbf{b})\cdot(\mathbf{c}\times\mathbf{d}) = (\mathbf{a}\cdot\mathbf{c})(\ mathbf{b}\cdot\mathbf{d}) - (\mathbf{a}\cdot\mathbf{d})(\mathbf{b}\cdot\mathbf{c})\] 92\theta \end{array}\] Отсюда следует определение перекрестного произведения: \[|\mathbf{a}\times\mathbf{b}|=|\mathbf{a}||\ mathbf{b}|\sin\theta\] Что работает, поскольку угол между \(\mathbf{a}\) и \(\mathbf{b}\) всегда находится в диапазоне от 0° до 180° и, следовательно, \( \sin\theta\geq 0\). ПриложенияНормаль к треугольникуНаиболее распространенное применение перекрестного произведения — создание вектора, ортогонального двум другим векторам. Предположим, у нас есть три точки \(P\), \(Q\) и \(R\) и мы хотим сгенерировать единичный вектор \(\hat{\mathbf{n}}\), который ортогонален плоскости, образованной три точки. Теперь \(\mathbf{a}=Q-P\) и \(\mathbf{b}=RP\) и нормаль можно найти с помощью \(\mathbf{n}=\mathbf{a}\times\mathbf {б}\). Направление нормали обычно выбирается так, чтобы оно указывало изнутри наружу нашего объекта. Интересно, что длина \(|\mathbf{n}|\) здесь равна удвоенной площади треугольника (поскольку половина параллелограмма, образованного \(\mathbf{a}\) и \(\mathbf{b} \) — наш треугольник). Расстояние между двумя прямыми Рассмотрим две прямые в пространстве \(\ell_1\) и \(\ell_2\) такие, что точка \(\ell_1\) проходит через \(P_1\) и параллельна вектору \(\ mathbf{v}_1\) и \(\ell_2\) проходит через \(P_2\) и параллелен \(\mathbf{v}_2\). Если линии пересекаются, расстояние равно \(d=0\). Если они параллельны, то \(d\) соответствует расстоянию между точками \(P_2\) и \(\ell_1\): \[d=\frac{\|\overrightarrow{P_1P_2}\times \mathbf{v}_1\|}{\|\mathbf{v}_1\|}\] Если прямые не параллельны и не пересекаются (косые прямые), то пусть \(\mathbf{n}=\ mathbf{v}_1\times\mathbf{v}_2\) — вектор, перпендикулярный обеим прямым. Проекция вектора на \(\mathbf{n}\) дает \(d\): \[d=\frac{|\overrightarrow{P_1P_2}\cdot\mathbf{n}|}{\|\mathbf{n}\|}\] Проверить параллельность двух векторов Аналогично скалярному произведению , перекрестное произведение можно использовать, чтобы определить, параллельны ли два вектора \(\mathbf{a}\) и \(\mathbf{b}\), что имеет место, когда \(\mathbf{a}\times\mathbf {b}=\mathbf{0}\). Этот результат следует непосредственно из определения длины векторного произведения, поскольку \(\sin(\theta)=0\) для 0° и 180°. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





 0116
0116  В результате перекрестного произведения двух векторов получается вектор, который
ортогонален обоим
векторы перемножаются. Величина
векторное произведение двух векторов находится по формуле |u × v| = |и| |в| грех θ,
где θ — меньший угол между
векторы.
В результате перекрестного произведения двух векторов получается вектор, который
ортогонален обоим
векторы перемножаются. Величина
векторное произведение двух векторов находится по формуле |u × v| = |и| |в| грех θ,
где θ — меньший угол между
векторы.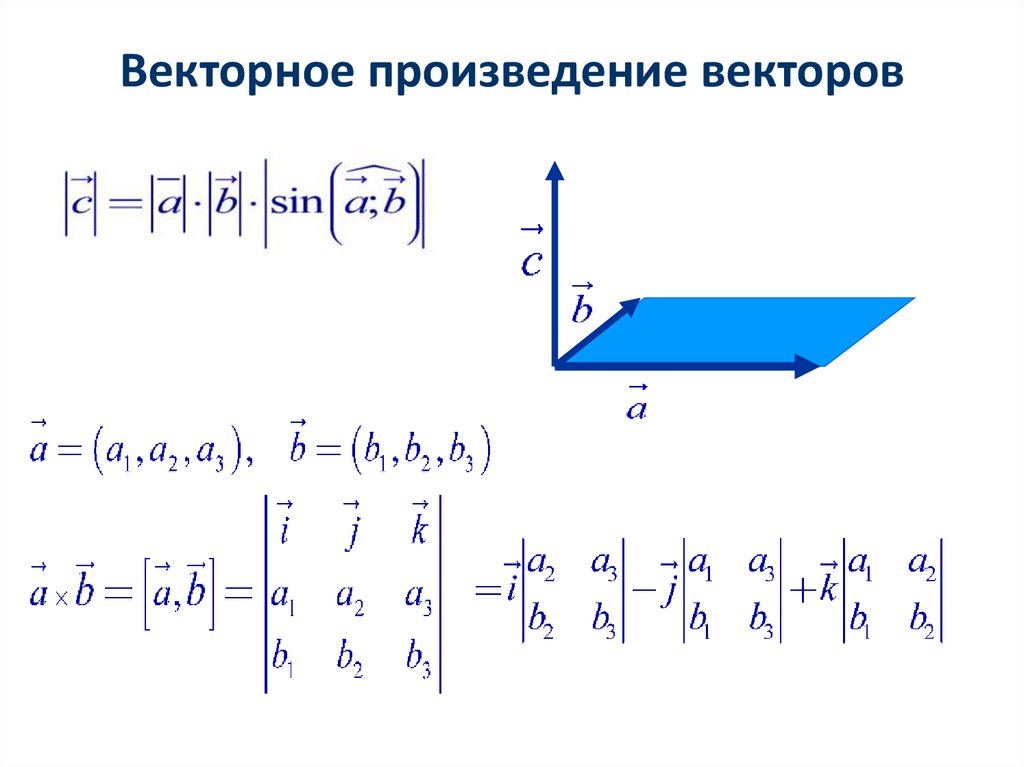

 Мы хотим вычислить наименьшее расстояние \(d\) между двумя линиями.
Мы хотим вычислить наименьшее расстояние \(d\) между двумя линиями.