Удельное сопротивление проводника – формула, определение, таблица для расчета

4.7

Средняя оценка: 4.7

Всего получено оценок: 99.

4.7

Средняя оценка: 4.7

Всего получено оценок: 99.

Проводниками в физике называют материалы, общим свойством которых является способность хорошо проводить электрический ток. Большое количество свободных носителей электрического заряда (электронов и ионов), имеющееся в проводниках, при воздействии на них электрического поля, создает направленное, упорядоченное перемещение, то есть электрический ток. Величины токов для разных проводников с одинаковыми геометрическими размерами и одинаковой напряженностью электрического поля могут существенно отличаться. Физическая величина, характеризующая способность различных материалов по разному проводить электрический ток, называется удельным электрическим сопротивлением.

Вспомним закон Ома

Основным законом, устанавливающим связь между электрическим напряжением U, током I и сопротивлением R, является закон Ома:

$ I = {U \over R} $ (1).

Закон был открыт немецким ученым Георгом Омом в 1826 г. экспериментальным путем. Ученый измерял величину тока при различных напряжениях, которое он варьировал с помощью гальванических батарей, меняя их количество.

От чего зависит величина сопротивления

R ?

Дальнейшие эксперименты показали, что:

• Величина R прямо пропорциональна длине проводника, то есть чем больше длина проводник L, тем больше тем больше его сопротивление, причем зависимость линейная, то есть R∼ L;
• Величина R , обратно пропорциональна поперечной площади проводника S, то есть $ R ∼ {1\over S } $;
• Поскольку у проводников из разных материалов с одинаковыми размерами
  S и L сопротивления отличались, то была введена физическая величина, названная удельным сопротивлением ρ.

Рис. 1. Проводник длиной L, поперечным сечением S и током I

Тогда выражение для величины сопротивления приобрело следующий вид:

$ R = ρ * {L\over S} $ (2). 2]}\over [м]} $ (5).

Тогда числовые значения ρ, становятся более удобными для восприятия. Например, удельное сопротивление железа ρ_ж = 130000 (Ом*м) = 0,13 (Ом*мм²)/м. В справочниках данные приводятся в этом в последнем, более компактном представлении.

Температурная зависимость

ρ(Т)

Для большинства материалов проведены многочисленные эксперименты по измерению значений удельных сопротивлений. Данные по большинству проводников можно найти в справочных таблицах.

Удельное сопротивление металлов и сплавов, Ом*мм²/м

(при Т = 20⁰С)

Серебро	0,016	Бронза (сплав)	0,1
Медь	0,017	Олово	0,12
Золото	0,024	Сталь (сплав)	0,12
Алюминий	0,028	Свинец	0,21
Иридий	0,047	Никелин (сплав)	0,42
Молибден	0,054	Манганин (сплав)	0,45
Вольфрам	0,055	Константан (сплав)	0,48
Цинк	0,06	Титан	0,58
Латунь (сплав)	0,071	Ртуть	0,958
Никель	0,087	Нихром (сплав)	1,1
Платина	0,1	Висмут	1,2

Чаще всего приводятся значения ρ при нормальной, то есть комнатной температуре 20⁰С. Но оказалось, что при повышении температуры удельное сопротивление возрастает по линейному закону в соответствии с формулой:

$ ρ(Т) = ρ0 * (1 + α*T)$ (6),

где: ρ₀ — удельное сопротивление проводника при температуре 0⁰С,

α — температурный коэффициент удельного сопротивления, который тоже имеет для каждого вещества свое, индивидуальное, значение. Из формулы (6) следует, что коэффициент α имеет размерность [ ⁰C^-1 ] или [ 1\⁰C ].

Рис. 2. Температурная зависимость удельного сопротивления проводника

В соответствии с законом Джоуля-Ленца при протекании электрического тока т выделяется тепло, а значит происходит рост температуры проводника. Кроме этого, в зависимости от области применения, электрические приборы могут работать как при пониженных (минусовых), так и при высоких температурах. Для точных расчетов электрических цепей необходимо учитывать зависимость ρ(Т).

Величину α для конкретного материала можно узнать из справочной литературы.

Рис. 3. Справочные значения температурного коэффициента удельного сопротивления проводников

Что мы узнали?

Итак, мы узнали, что величина, характеризующая способность различных материалов по разному проводить электрический ток, называется удельным электрическим сопротивлением. Приведена формула (3) для определения удельного сопротивления проводника ρ. Линейная температурная зависимость удельного сопротивления ρ(Т) описывается формулой (6).

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Максим Разуваев

  3/10

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 99.

---

А какая ваша оценка?

Формула расчета электрического сопротивления проводника. Чем больше сечение провода тем меньше сопротивление? Расчет по диаметру

Содержание:

При проектировании электрических сетей в квартирах или частных домах в обязательном порядке выполняется расчет сечения проводов и кабелей. Для проведения вычислений используются такие показатели, как значение потребляемой мощности и сила тока, которая будет проходить по сети. Сопротивление не принимается в расчет из-за малой протяженности кабельных линий. Однако этот показатель необходим при большой длине ЛЭП и перепадах напряжения на различных участках. Особое значение имеет сопротивление медного провода. Такие провода все чаще используются в современных сетях, поэтому их физические свойства должны обязательно учитываться при проектировании.

Понятия и значение сопротивления

Электрическое сопротивление материалов широко используется и учитывается в электротехнике. Данная величина позволяет установить основные параметры проводов и кабелей, особенно при скрытом способе их прокладки. В первую очередь устанавливается точная длина проложенной линии и материал, использованный для производства провода. Вычислив первоначальные данные, вполне возможно измеряемого кабеля.

По сравнению с обычной электрической проводкой, в электронике параметрам сопротивления придается решающее значение. Оно рассматривается и сопоставляется в совокупности с другими показателями, присутствующими в электронных схемах. В этих случаях неправильно подобранное сопротивление провода, может вызвать сбой в работе всех элементов системы. Такое может произойти, если для подключения к блоку питания компьютера воспользоваться слишком тонким проводом. Произойдет незначительное снижение напряжения в проводнике, что вызовет некорректную работу компьютера.

Сопротивление в медном проводе зависит от многих факторов, и в первую очередь от физических свойств самого материала. Кроме того, учитывается диаметр или сечение проводника, определяемые по формуле или специальной таблице.

Таблица

На сопротивление медного проводника оказывают влияние несколько дополнительных физических величин. Прежде всего должна учитываться температура окружающей среды. Всем известно, что при повышении температуры проводника, наблюдается рост его сопротивления. Одновременно с этим происходит снижение силы тока из-за обратно пропорциональной зависимости обеих величин.

В первую очередь это касается металлов с положительным температурным коэффициентом. Примером отрицательного коэффициента является вольфрамовый сплав, применяющийся в лампах накаливания. В этом сплаве сила тока не снижается даже при очень высоком нагреве.

Как рассчитать сопротивление

Для расчетов сопротивления медного провода существует несколько способов. К наиболее простым относится табличный вариант, где указаны взаимосвязанные параметры. Поэтому, кроме сопротивления, определяется сила тока, диаметр или сечение провода.

Во втором случае используются разнообразные . В каждый из них вставляется набор физических величин медного провода, с помощью которых получаются точные результаты. В большинстве подобных калькуляторов используется в размере 0,0172 Ом*мм 2 /м. В некоторых случаях такое усредненное значение может повлиять на точность вычислений.

Наиболее сложным вариантом считаются ручные вычисления, с использованием формулы: R = p x L/S, в которой р — удельное сопротивление меди, L — длина проводника и S — сечение этого проводника. Следует отметить, что сопротивление медного провода таблица определяет, как одно из наиболее низких. Более низким значением обладает лишь серебро.

Содержание:

Появление электрического тока наступает при замыкании цепи, когда на зажимах возникает разность потенциалов. Перемещение свободных электронов в проводнике осуществляется под действием электрического поля. В процессе движения, электроны сталкиваются с атомами и частично передают им свою накопившуюся энергию. Это приводит к уменьшению скорости их движения. В дальнейшем, под влиянием электрического поля, скорость движения электронов снова увеличивается. Результатом такого сопротивления становится нагревание проводника, по которому течет ток. Существуют различные способы расчетов этой величины, в том числе и формула удельного сопротивления, применяющаяся для материалов с индивидуальными физическими свойствами.

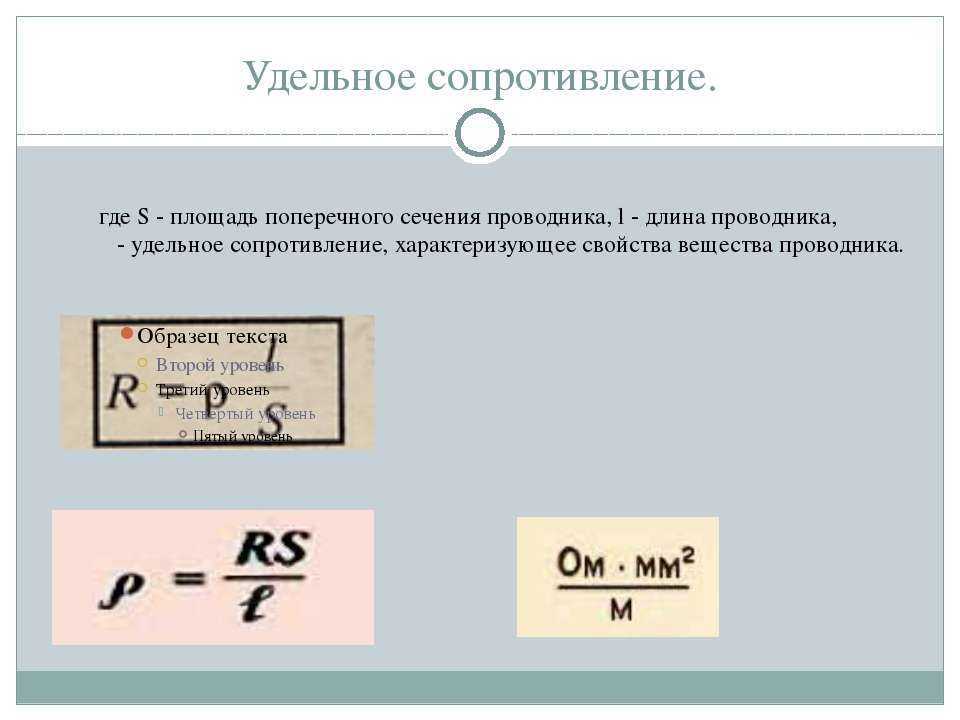
Электрическое удельное сопротивление

Суть электрического сопротивления заключается в способности того или иного вещества превращать электрическую энергию в тепловую во время действия тока. Данная величина обозначается символом R, а в качестве единицы измерения используется Ом. Значение сопротивления в каждом случае связано со способностью того или иного .

В процессе исследований была установлена зависимость от сопротивления. Одним из основных качеств материала становится его удельное сопротивление, меняющееся в зависимости от длины проводника. То есть, с увеличением длины провода, возрастает и значение сопротивления. Данная зависимость определяется как прямо пропорциональная.

Другим свойством материала является площадь его поперечного сечения. Она представляет собой размеры поперечного среза проводника, независимо от его конфигурации. В этом случае получается обратно пропорциональная связь, когда с увеличением площади поперечного сечения уменьшается .

Еще одним фактором, влияющим на сопротивление, является сам материал. Во время проведения исследований была обнаружена различная сопротивляемость у разных материалов. Таким образом, были получены значения удельных электрических сопротивлений для каждого вещества.

Выяснилось, что самыми лучшими проводниками являются металлы. Среди них самой низкой сопротивляемостью и высокой проводимостью обладают и серебро. Они применяются в наиболее ответственных местах электронных схем, к тому же медь имеет сравнительно низкую стоимость.

Вещества, удельное сопротивление которых очень высокое, считаются плохими проводниками электрического тока. Поэтому они используются в качестве изоляционных материалов. Диэлектрические свойства более всего присущи фарфору и эбониту.

Таким образом, удельное сопротивление проводника имеет большое значение, поскольку с его помощью можно определить материал, из которого был изготовлен проводник. Для этого измеряется площадь сечения, определяется сила тока и напряжение. Это позволяет установить значение удельного электрического сопротивления, после чего, с помощью специальной таблицы можно легко определить вещество. Следовательно, удельное сопротивление относится к наиболее характерным признакам того или иного материала. Этот показатель позволяет определить наиболее оптимальную длину электрической цепи так, чтобы соблюдался баланс .

Формула

На основании полученных данных можно сделать вывод, что удельным сопротивлением будет считаться сопротивление какого-либо материала с единичной площадью и единичной длиной. То есть сопротивление, равное 1 Ом возникает при напряжении 1 вольт и силе тока 1 ампер. На этот показатель оказывает влияние степень чистоты материала. Например, если к меди добавить всего лишь 1% марганца, то ее сопротивляемость увеличится в 3 раза.

Удельное сопротивление и проводимость материалов

Проводимость и удельное сопротивление рассматриваются как правило при температуре 20 0 С. Эти свойства будут отличаться у различных металлов:

• Медь . Чаще всего применяется для изготовления проводов и кабелей. Она обладает высокой прочностью, стойкостью к коррозии, легкой и простой обработкой. В хорошей меди доля примесей составляет не более 0,1%. В случае необходимости медь может использоваться в сплавах с другими металлами.
• Алюминий . Его удельный вес меньше, чем у меди, однако у него более высокая теплоемкость и температура плавления. Чтобы расплавить алюминий, потребуется энергии значительно больше, чем для меди. Примеси в качественном алюминии не превышают 0,5%.
• Железо . Наряду с доступностью и дешевизной, этот материал обладает высоким удельным сопротивлением. Кроме того, у него низкая устойчивость к коррозии. Поэтому практикуется покрытие стальных проводников медью или цинком.

Отдельно рассматривается формула удельного сопротивления в условиях низких температур. В этих случаях свойства одних и тех же материалов будут совершенно другими. У некоторых из них сопротивляемость может упасть до нулевой отметки. Такое явление получило название сверхпроводимости, при которой оптические и структурные характеристики материала остаются неизменными.

То как влияет материал проводника учитывается при помощи удельного сопротивления, которое принято обозначать буквой греческого алфавита ρ и являет собой сопротивление проводника сечением 1 мм2 и длинной 1м. У серебра наименьшее удельное сопротивление ρ = 0,016 Ом.мм2/м. Ниже приводятся значения удельного сопротивления для нескольких проводников:

• Сопротивление кабеля для серебра — 0,016,
• Сопротивление кабеля для свинеца — 0,21,
• Сопротивление кабеля для меди — 0,017,
• Сопротивление кабеля для никелина — 0,42,
• Сопротивление кабеля для люминия — 0,026,
• Сопротивление кабеля для манганина — 0,42,
• Сопротивление кабеля для вольфрама — 0,055,
• Сопротивление кабеля для константана — 0,5,
• Сопротивление кабеля для цинка — 0,06,
• Сопротивление кабеля для ртути — 0,96,
• Сопротивление кабеля для латуни — 0,07,
• Сопротивление кабеля для нихрома — 1,05,
• Сопротивление кабеля для стали — 0,1,
• Сопротивление кабеля для фехрали -1,2,
• Сопротивление кабеля для бронзы фосфористой — 0,11,
• Сопротивление кабеля для хромаля — 1,45

Так как в состав сплавов входят разные количества примесей, то удельное сопротивление может изменятся. 2

• где d — это диаметр провода.

Измерить диаметр провода можно микрометром либо штангенциркулем,но если их нету под рукой,то можно плотно намотать на ручку (карандаш) около 20 витков провода, затем измерить длину намотанного провода и разделить на количество витков.

Для определения длинны кабеля,которая нужна для достижения необходимого сопротивления,можно использовать формулу:

l=(S?R)/ρ

Примечания:

1.Если данные для провода отсутствуют в таблице,то берется некоторое среднее значение.Как пример,провод из никелина который имеет диаметр 0,18 мм площадь сечения равна приблизительно 0,025 мм2, сопротивление одного метра 18 Ом, а допустимый ток 0,075 А.

2.Данные последнего столбца,для другой плотности тока, необходимо изменить. Например при плотности тока 6 А/мм2, значение необходимо увеличить вдвое.

Пример 1 . Давайте найдем сопротивление 30 м медного провода диаметром 0,1 мм.

Решение . С помощью таблицы берем сопротивление 1 м медного провода, которое равно 2,2 Ом. Значит, сопротивление 30 м провода будет R = 30.2,2 = 66 Ом.

Расчет по формулам будет выглядеть так: площадь сечения: s= 0,78.0,12 = 0,0078 мм2. Поскольку удельное сопротивление меди ρ = 0,017 (Ом.мм2)/м, то получим R = 0,017.30/0,0078 = 65,50м.

Пример 2 . Сколько провода из манганина у которого диаметр 0,5 мм нужно чтобы изготовить реостат, сопротивлением 40 Ом?

Решение . По таблице выбираем сопротивление 1 м этого провода: R= 2,12 Ом: Чтобы изготовить реостат сопротивлением 40 Ом, нужен провод, длина которого l= 40/2,12=18,9 м.

Расчет по формулам будет выглядеть так. Площадь сечения провода s= 0,78.0,52 = 0,195 мм2. Длина провода l = 0,195.40/0,42 = 18,6 м.

Одним из физических свойств вещества является способность проводить электрический ток. Электропроводимость (сопротивление проводника) зависит от некоторых факторов: длины электрической цепи, особенностей строения, наличия свободных электронов, температуры, тока, напряжения, материала и площади поперечного сечения.

Протекание электрического тока через проводник приводит к направленному движению свободных электронов. Наличие свободных электронов зависит от самого вещества и берется из таблицы Д. И. Менделеева, а именно из электронной конфигурации элемента. Электроны начинают ударяться о кристаллическую решетку элемента и передают энергию последней. В этом случае возникает тепловой эффект при действии тока на проводник.

При этом взаимодействии они замедляются, но затем под действием электрического поля, которое их ускоряет, начинают двигаться с той же скоростью. Электроны сталкиваются огромное количество раз. Этот процесс и называется сопротивлением проводника.

Следовательно, электрическим сопротивлением проводника считается физическая величина, характеризующая отношение напряжения к силе тока.

Что такое электрическое сопротивление: величина, указывающая на свойство физического тела преобразовывать энергию электрическую в тепловую, благодаря взаимодействию энергии электронов с кристаллической решеткой вещества. По характеру проводимости различаются:

1. Проводники (способны проводить электрический ток, так как присутствуют свободные электроны).
2. Полупроводники (могут проводить электрический ток, но при определенных условиях).
3. Диэлектрики или изоляторы (обладают огромным сопротивлением, отсутствуют свободные электроны, что делает их неспособными проводить ток).

Обозначается эта характеристика буквой R и измеряется в Омах (Ом) . Применение этих групп веществ является очень значимым для разработки электрических принципиальных схем приборов.

Для полного понимания зависимости R от чего-либо нужно обратить особое внимание на расчет этой величины.

Расчет электрической проводимости

Для расчета R проводника применяется закон Ома, который гласит: сила тока (I) прямо пропорциональна напряжению (U) и обратно пропорциональна сопротивлению.

Формула нахождения характеристики проводимости материала R (следствие из закона Ома для участка цепи): R = U / I.

Для полного участка цепи эта формула принимает следующий вид: R = (U / I) — Rвн, где Rвн — внутреннее R источника питания.

Способность проводника к пропусканию электрического тока зависит от многих факторов: напряжения, тока, длины, площади поперечного сечения и материала проводника, а также от температуры окружающей среды.

В электротехнике для произведения расчетов и изготовления резисторов учитывается и геометрическая составляющая проводника.

От чего зависит сопротивление: от длины проводника — l, удельного сопротивления — p и от площади сечения (с радиусом r) — S = Пи * r * r.

Формула R проводника: R = p * l / S.

Из формулы видно, от чего зависит удельное сопротивление проводника: R, l, S. Нет необходимости его таким способом рассчитывать, потому что есть способ намного лучше. Удельное сопротивление можно найти в соответствующих справочниках для каждого типа проводника (p — это физическая величина равная R материала длиною в 1 метр и площадью сечения равной 1 м².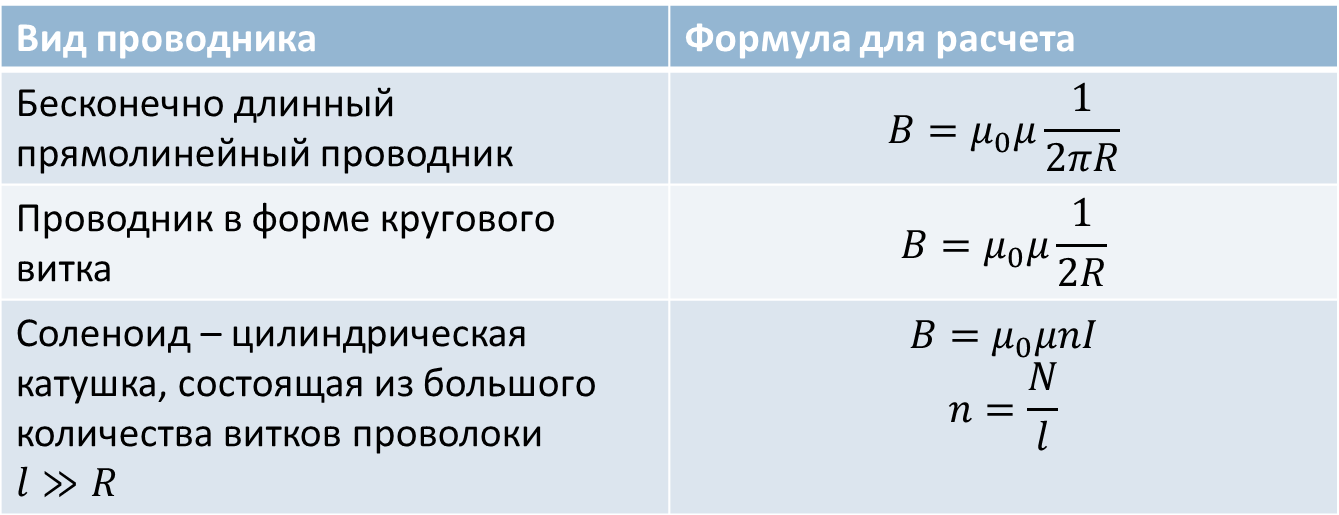

Однако этой формулы мало для точного расчета резистора, поэтому используют зависимость от температуры.

Влияние температуры окружающей среды

Доказано, что каждое вещество обладает удельным сопротивлением, зависящим от температуры.

Для демонстрации это можно произвести следующий опыт. Возьмите спираль из нихрома или любого проводника (обозначена на схеме в виде резистора), источник питания и обычный амперметр (его можно заменить на лампу накаливания). Соберите цепь согласно схеме 1.

Схема 1 — Электрическая цепь для проведения опыта

Необходимо запитать потребитель и внимательно следить за показаниями амперметра. Далее следует нагревать R, не отключая, и показания амперметра начнут падать при росте температуры. Прослеживается зависимость по закону Ома для участка цепи: I = U / R. В данном случае внутренним сопротивлением источника питания можно пренебречь: это не отразится на демонстрации зависимости R от температуры. Отсюда следует, что зависимость R от температуры присутствует.

Физический смысл роста значения R обусловлен влиянием температуры на амплитуду колебаний (увеличение) ионов в кристаллической решетке. В результате этого электроны чаще сталкиваются и это вызывает рост R.

Согласно формуле: R = p * l / S, находим показатель, который зависит от температуры (S и l — не зависят от температуры). Остается p проводника. Исходя из это получается формула зависимости от температуры: (R — Ro) / R = a * t, где Ro при температуре 0 градусов по Цельсию, t — температура окружающей среды и a — коэффициент пропорциональности (температурный коэффициент).

Для металлов «a» всегда больше нуля, а для растворов электролитов температурный коэффициент меньше 0.

Формула нахождения p, применяемая при расчетах: p = (1 + a * t) * po, где ро — удельное значение сопротивления, взятое из справочника для конкретного проводника. В этом случае температурный коэффициент можно считать постоянным. Зависимость мощности (P) от R вытекает из формулы мощности: P = U * I = U * U / R = I * I * R. Удельное значение сопротивления еще зависит и от деформаций материала, при котором нарушается кристаллическая решетка.

При обработке металла в холодной среде при некотором давлении происходит пластическая деформация. При этом кристаллическая решетка искажается и растет R течения электронов. В этом случае удельное сопротивление также увеличивается. Этот процесс является обратимым и называется рекристаллическим отжигом, благодаря которому часть дефектов уменьшается.

При действии на металл сил растяжения и сжатия последний подвергается деформациям, которые называются упругими. Удельное сопротивление уменьшается при сжатии, так как происходит уменьшение амплитуды тепловых колебаний. Направленным заряженным частицам становится легче двигаться . При растяжении удельное сопротивление увеличивается из-за роста амплитуды тепловых колебаний.

Еще одним фактором, влияющим на проводимость, является вид тока, проходящего по проводнику.

Сопротивление в сетях с переменным током ведет себя несколько иначе, ведь закон Ома применим только для схем с постоянным напряжением. Следовательно, расчеты следует производить иначе.

Полное сопротивление обозначается буквой Z и состоит из алгебраической суммы активного, емкостного и индуктивного сопротивлений.

При подключении активного R в цепь переменного тока под воздействием разницы потенциалов начинает течь ток синусоидального вида. В этом случае формула выглядит: Iм = Uм / R, где Iм и Uм — амплитудные значения силы тока и напряжения. Формула сопротивления принимает следующий вид: Iм = Uм / ((1 + a * t) * po * l / 2 * Пи * r * r).

Емкостное сопротивление (Xc) обусловлено наличием в схемах конденсаторов. Необходимо отметить, что через конденсаторы проходит переменный ток и, следовательно, он выступает в роли проводника с емкостью.

Вычисляется Xc следующим образом: Xc = 1 / (w * C), где w — угловая частота и C — емкость конденсатора или группы конденсаторов. Угловая частота определяется следующим образом:

1. Измеряется частота переменного тока (как правило, 50 Гц).
2. Умножается на 6,283.

Индуктивное сопротивление (Xl) — подразумевает наличие индуктивности в схеме (дроссель, реле, контур, трансформатор и так далее). Рассчитывается следующим образом: Xl = wL, где L — индуктивность и w — угловая частота. Для расчета индуктивности необходимо воспользоваться специализированными онлайн-калькуляторами или справочником по физике. Итак, все величины рассчитаны по формулам и остается всего лишь записать Z: Z * Z = R * R + (Xc — Xl) * (Xc — Xl).

Для определения окончательного значения необходимо извлечь квадратный корень из выражения: R * R + (Xc — Xl) * (Xc — Xl). Из формул следует, что частота переменного тока играет большую роль, например, в схеме одного и того же исполнения при повышении частоты увеличивается и ее Z. Необходимо добавить, что в цепях с переменным напряжением Z зависит от таких показателей:

1. Длины проводника.
2. Площади сечения — S.
3. Температуры.
4. Типа материала.
5. Емкости.
6. Индуктивности.
7. Частоты.

Следовательно и закон Ома для участка цепи имеет совершенно другой вид: I = U / Z . Меняется и закон для полной цепи.

Расчеты сопротивлений требуют определенного количества времени, поэтому для измерений их величин применяются специальные электроизмерительные приборы, которые называются омметрами. Измерительный прибор состоит из стрелочного индикатора, к которому последовательно включен источник питания.

Измеряют R все комбинированные приборы , такие как тестеры и мультиметры. Обособленные приборы для измерения только этой характеристики применяются крайне редко (мегаомметр для проверки изоляции силового кабеля).

Прибор применяется для прозвонки электрических цепей на предмет повреждения и исправности радиодеталей, а также для прозвонки изоляции кабелей.

При измерении R необходимо полностью обесточить участок цепи во избежание выхода прибора из строя. Для это необходимо предпринять следующие меры предосторожности:

В дорогих мультиметрах есть функция прозвонки цепи, дублируемая звуковым сигналом, благодаря чему нет необходимости смотреть на табло прибора.

Таким образом, электрическое сопротивление играет важную роль в электротехнике. Оно зависит в постоянных цепях от температуры, силы тока, длины, типа материала и площади поперечного сечения проводника . В цепях переменного тока эта зависимость дополняется такими величинами, как частота, емкость и индуктивность. Благодаря этой зависимости существует возможность изменять характеристики электричества: напряжение и силу тока. Для измерений величины сопротивления применяются омметры, которые используются также и при выявлении неполадок проводки, прозвонки различных цепей и радиодеталей.

В домашних условиях мы часто применяем переносные удлинители – розетки для временного (как правило остающееся на постоянно ) включения бытовых приборов: электронагревателя, кондиционера, утюга с большими токами потребления.
Кабель для этого удлинителя обычно выбирается по принципу – что попало подруку, а это не всегда соответствует необходимым электрическим параметрам.

В зависимости от диаметра (или от поперечного сечения провода в мм. кв.)провод обладает определенным электрическим сопротивлением для прохождения электрического тока.

Чембольше поперечное сечение проводника, тем меньше его электрическое сопротивление, тем меньше падение напряжения на нем. Соответственно меньше потеря мощности в проводе на его нагрев.

Проведем сравнительный анализпотери мощности на нагрев в проводе в зависимости от его поперечного сечения. Возьмем наиболее распространенные в быту кабели с паперечным сечением: 0,75; 1,5; 2,5 мм.кв. для двух удлинителей с длиной кабеля: L = 5 м. и L = 10м .

Возьмем для примера нагрузку в виде стандартного электронагревателя с электрическими параметрами:
— напряжение питания U = 220 Воль т ;
— мощность электронагревателя Р = 2,2 КВт = 2200 Вт ;
— ток потребления I = P / U = 2200 Вт / 220 В = 10 А.

Из справочной литературы, возьмем данные сопротивлений 1 метра провода разных поперечных сечений.

Приведена таблица сопротивлений 1 метра провода изготовленного из меди и алюминия.

Посчитаем потерю мощности, уходящей на нагрев для поперечного сечения провода S = 0,75 мм.кв. Провод изготовлен из меди.

Сопротивление 1 метра провода (из таблицы) R 1 = 0,023 Ом.
Длина кабеля L = 5 метров.
Длина провода в кабеле (туда и обратно)2 · L =2 · 5 = 10 метров .
Электрическое сопротивление провода в кабеле R = 2 · L · R 1 = 2 · 5 · 0,023 = 0,23 Ом.

Падение напряжения в кабеле при прохождении тока I = 10 A будет: U = I · R = 10 А · 0,23 Ом = 2,3 B .
Потеря мощности на нагрев в самом кабеле составит:P = U · I = 2,3 В · 10 А = 23 Вт .

Если длина кабеляL = 10 м . (того же сечения S = 0,75 мм.кв .),потеря мощности в кабеле составит 46 Вт . Это составляет примерно 2 % мощности потребляемой электронагревателем от сети.

Для а кабеляс алюминиевыми жилами того же сечения S = 0,75 мм.кв . показания увеличиваютсяи составляютдля L = 5 м-34,5 Вт. Для L = 10 м— 69 Вт.

Все данные расчетовдля кабелей сечением 0,75; 1,5; 2,5 мм.кв. для длины кабелейL = 5 и L = 10 метров,приведены в таблице.
Где: S – сечение провода в мм.кв.;
R 1 – сопротивление 1 метра провода в Ом;
R -сопротивление кабеля в Омах;
U – падение напряжения в кабеле в Вольтах;
Р – потеря мощности в кабеле в ватах или в процентах.

Какие же выводы нужно сделать из этих расчетов?

• — При одном и том же поперечном сечении, медный кабель имеет больший запас надежности и меньше потерь электрической мощности на нагрев провода Р .
• — С увеличением длины кабеля увеличиваются потери Р . Чтобы скомпенсировать потеринеобходимо увеличить поперечное сечение проводов кабеля S .
• — Кабель желательно выбирать в резиновой оболочке, а жилы кабеля многожильными .

Для удлинителя желательно использовать евро-розетку и евро-вилку. Штырьки евро-вилки имеют диаметр 5 мм . У простой электрической вилки диаметр штырьков 4 мм . Евро-вилки рассчитаны на больший ток, чем простые розетка и вилка. Чем больше диаметр штырьков вилки, тем больше площадь контакта в месте соединения вилки и розетки, следовательно меньшее переходное сопротивление. Это способствует меньшему нагревув месте соединения вилки и розетки.

Длина проводника и провисание – столбы и провода

Одним из непонятных аспектов линий электропередач является эффект, который может оказать добавление проводника небольшой длины в пролет на провисание.

Хорошо известно, что контактная сеть является лучшим способом моделирования изгиба кабеля линии электропередач.

«Хотя имеющиеся в продаже провода и кабели не являются действительно гибкими, на очень коротких пролетах они будут соответствовать контактной сети больше, чем любой другой кривой. В более длинных пролетах проводники можно считать действительно гибкими, поскольку они будут провисать в форме контактной сети».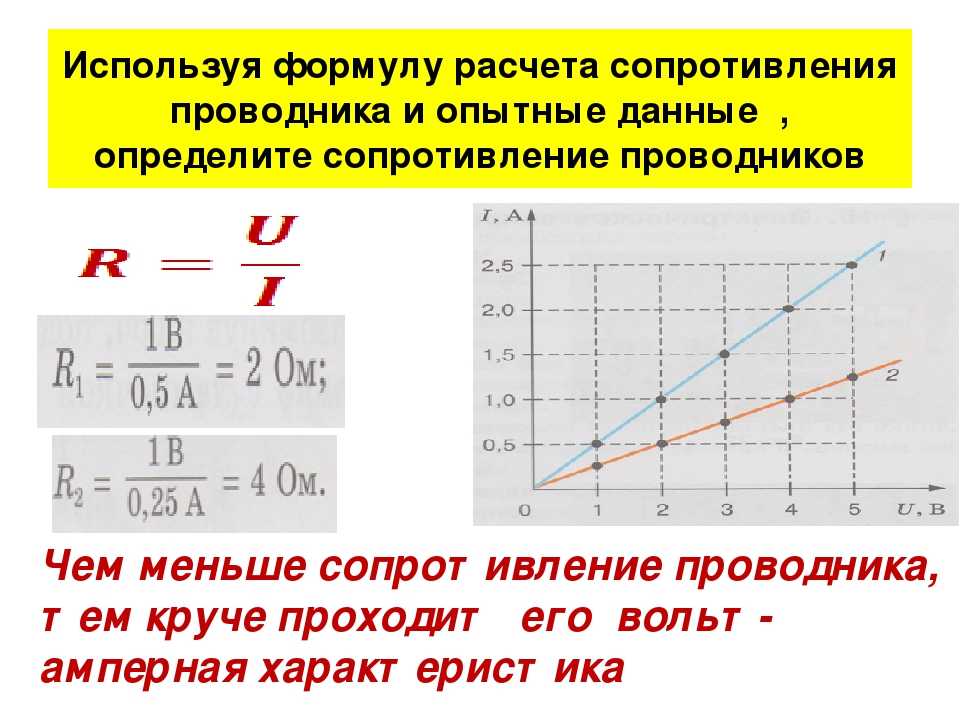 Х Фарр, 9 лет0007 Руководство по проектированию линий электропередач , Денвер, Министерство внутренних дел США, 1980, с. 15

Чтобы удовлетворить свое любопытство, я провел простой эксперимент с цепочкой ожерелья. С помощью кронштейнов для моделирования столбов я измерил провисание и соответствующую длину цепи.

Размеры, которые я снял с модели:

9{2}}\тег{R21}\)

 

\(D=C\left ( ch\frac{L}{2C}-1 \right )\tag{R38}\)

 

Используя уравнение R38 для расчета постоянной контактной сети по провисанию, а затем R21 для определения длины цепи по постоянной контактной сети, я получаю следующие результаты:

Длина пролета	436 мм
провисание 20 мм	Длина цепи 439 мм
провисание 40 мм

Провисание	Цепная постоянная	Расчетная длина цепи	Измеренная длина цепи
20 мм	1,19	438 мм	439мм
40 мм	0,60	446 мм	446 мм
60 мм	0,405	457 мм	457 мм

Я могу заметить, что модель контактной сети предсказывает «длину проводника под напряжением» (длину цепи) в пределах моих экспериментальных допусков.

Теперь рассмотрим некоторые реалистичные примеры:

Пролет 80 м лунного проводника, натянутого при 10% CBL, температура 15°, стандартная температура 15°. Провисание составляет 1,406 м. Длина проводника 80,066м.

Если мы добавим 20 мм проводника к пролету, то есть длина составит 80,086 м, константа контактной сети будет равна 498,1. Расчетный прогиб 1,607 м, на 20 см больше!

Пролет 300 м Raisen натянут при 18% CBL. Прогиб 4,845 м, длина проводника 300,209 м.

Добавление 100-мм проводника увеличивает провисание с 1,06 м до 5,909 м

	Диапазон	Натяжение	Прогиб (м)	Длина проводника (м)	Дополнительный проводник	Новый прогиб (м)	Увеличение провисания (м)
Луна	80	10 % CBL, 15°	1.406	80.066	20 мм	1,607	0,201
Райзен	300	18% ХП, 15°	4,845	300. 209	100 мм	5.909	1,06

Библиография

Farr H, Руководство по проектированию линий электропередач , Министерство внутренних дел США, 1980
Jwa Y, Sohn G, Модель роста кусочно-цепной кривой для трехмерной реконструкции линии электропередач , Фотограмметрическая инженерия и дистанционное зондирование, том. 78, № 12, декабрь 2012 г., стр. 1227–1240
Мадаан Р., Каесс М., Шерер С., Многоракурсная реконструкция проводов с использованием модели контактной сети , Университет Карнеги-Меллона, https://www.ri.cmu .edu/publications/multi-view-reconstruction-of-wires-using-a-catenary-model-2/
AS/NZS7000, Standards Australia, Sydney, 2016
AmBrSoft Calculators+ , http://www.ambrsoft.com/TrigoCalc/Sphere/Arc_.htm (по состоянию на 22 июля 2020 г.)

 

Электрическая длина

Электрическая длина линий передачи модели с сосредоточенными параметрами для кабелей работают достаточно хорошо.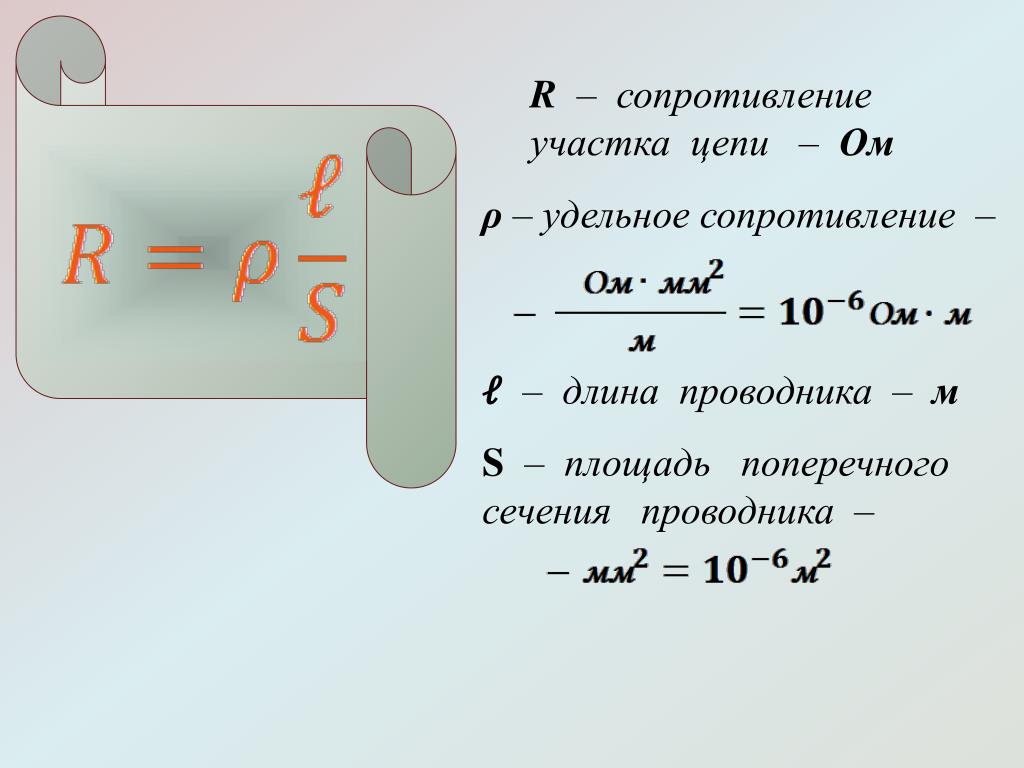 Но по мере увеличения частоты мы приходим к тому, что даже при различных сосредоточенных модели соглашаются, они не могут точно предсказать, что происходит в реальных кабелях. На этих частотах мы нужно много более сложная математически модель кабеля, называемая теория линий передачи. На очень высоких частотах особой разницы нет какую модель мы использовать, так как мощность всех моделей — и самого кабеля — будет близка к нулю.

Частота, на которой необходимо переключиться с моделей с сосредоточенными параметрами на передачу линия модели различаются в зависимости от длины кабеля. Когда модель с сосредоточенными параметрами подходит ну, мы говорим кабель электрически короткий. Когда модель с сосредоточенными параметрами не подходит, мы говорим кабель электрически длинный или является линией передачи.

На уроках физики студентов учат о бегущих волнах. Это могут быть волны на поверхности океана, звуковых волн, радиоволн, световых волн или электрических волн в длинном провод. Независимо от типа волны, некоторые параметры, описывающие ее, – частота f, скорость распространения v и длина волны λ. Когда мы измеряем волна в определенной точке пространства, мы часто хотим знать, как далеко эта точка находится от источник волны, х. Если мы сфотографируем волну в момент времени, это может выглядеть как рисунок ниже. Горизонтальная ось здесь — это расстояние, а не время. Обратите внимание, что эта фотография не говорит вам о частоте волны.

Связь между скоростью, частотой и длиной волны определяется формулой \[v = f\лямбда \] Если скорость измеряется в метрах в секунду, а частота в циклов/секунду, то λ имеет единицы измерения метры/цикл.

Мы определяем, является ли кабель электрически коротким или длинным, сравнивая его длины к длине волны λ. Если длина большая короче длины волны, то кабель электрически короткий. Если длина сравнима с длиной волны или длиннее ее, то кабель электрически длинный. Мы будем считать, что кабель электрически длинный, если его длина превышает 10 %. λ, и короткой, когда ее длина составляет менее 10% длины λ.

Чтобы определить, является ли кабель электрически коротким или длинным, нам необходимо знать скорость распространения и частоту, поэтому мы можем определить длину волны λ.

Последнее замечание: все эти расчеты основаны на электрической волне. синусоида.

В других разделах мы проведем более точные расчеты относительно скорость распространения в кабеле. Этот раздел предназначен только для несколько общих руководящих принципов.

Электроэнергия обычно передается по коммуникационному кабелю со скоростью значительная часть скорости света. Скорость часто описывают с использованием коэффициента скорости VF троса. 8}{\rm{м/с}}} \справа)$$ Если кабель связи представляет собой две обычные жилы (медь, алюминий), разделенные общедоступной изоляцией (полиэтилен, нейлон, воздух), и кабель не подходит близко к черному материалу (железу, стали) то коэффициент скорости обычно находится в диапазоне от 50% до 99%.

Если известны индуктивность и емкость кабеля, можно приблизительно коэффициент скорости как \[v = \left( {VF} \right)c \ cong \ frac {1}{{\ sqrt {L’C’}}}\] Широко расставленные провода с воздушной изоляцией имеют наибольшую индуктивность, самая низкая емкость и, следовательно, самые высокие коэффициенты скорости — приближается к VF=100%. Близко расположенные провода, разделенные изолятором с высокая диэлектрическая проницаемость, самая низкая индуктивность и самая высокая емкость, опережая самые низкие коэффициенты скорости — обычно порядка 50%.

Некоторые напряжения, используемые в электрических системах, являются либо синусоидами, либо очень близкими к синусоидам. В этих случаях это просто вопрос измерения или поиска. до стандарта, чтобы найти частоту, которую они используют. Вот несколько примеров:

• Постоянный ток (0 Гц). Все кабели кажутся электрически короткими при использовании для передачи постоянного напряжения или постоянного тока. Делая это заявление, я предполагаю, что вы никогда не включить или выключить уровень постоянного тока. Точнее, когда вы его включаете — вам нужно распознать, что кабель будет иметь переходную характеристику. Во время этого нестационарным, электрически короткие модели могут оказаться бесполезными. Но как только переходный процесс закончился, можно вернуться к модели с электрическим замыканием. такая же осторожность применяется при отключении напряжения — будет переходный процесс в течение этого времени электрически короткие модели линии не могут быть точный.
• Силовая передача (от 50 Гц до 60 Гц). Большое количество электричества электроэнергия производится и транспортируется по всему миру с частотой 50 Гц и 60 Гц. В более специализированных приложениях и приложениях на короткие расстояния могут использоваться более высокие частоты. Передача энергии постоянного тока становится все более распространенной, но по-прежнему встречается в меньшинстве. когда речь идет о системах передачи электроэнергии.
• Голос низкого качества (от 300 Гц до 3 кГц). Люди производят звуковые волны в воздухе, и микрофоны могут преобразовывать эти колебания давления воздуха на колебания напряжения. Когда мы свистнем, волна может быть близко к синусоиде. Но обычно наши голоса производят волны, которые не синусоидальный. Однако мы можем точно смоделировать этот сигнал, добавив куча синусоид. Если мы используем только синусоидальные волны в диапазоне 300 Гц до 3 кГц, мы можем воспроизводить звук низкого качества, который вы слышите на старых телефонных системах и при прослушивании радиопередач AM. Звук явно искажен или приглушен. Но вы все равно можете идентифицировать человека, говорящего, и разобрать слова, которые они говорят. В случае с музыкой вы можете узнавать, какие инструменты играют, а также мелодию или основную структуру музыки. Но это звучит не так хорошо, как личное присутствие.
• Высококачественный звук (от 20 Гц до 20 кГц). В наших ушах есть маленькие волоски которые действуют как камертоны, которые реагируют на синусоидальные волны от 20 Гц до 20 кГц. Высококачественные системы записи и воспроизведения музыки, как правило, быть в состоянии производить синусоидальные волны во всем этом диапазоне частот. Иногда они также производят более низкие частоты, но их больше ощущают, чем слышат.
Радио
• AM (1 МГц). АМ-радиопередатчики производят сигналы, которые близки к идеальной синусоиде, но немного отличаются от нее. Они используют частоты от 530 кГц до 1,7 МГц.
• Коротковолновое радио (от 3 МГц до 30 МГц). Некоторые радиопередатчики предназначены для практически глобальный охват без использования спутников. Эти коротковолновые радиопередатчики производят сигналы, близкие к синусоиде.
• FM-радио (100 МГц). FM-радиопередатчики издают сигналы, близко к идеальной синусоиде, но немного отличается от нее. Они используют частоты от 88 МГц до 108 МГц.
• Мобильные телефоны (от 0,5 ГГц до 40 ГГц). Мобильные телефоны передают и принимают сигналы, очень похожие на синусоидальные. Они используют широкий диапазон частот, в зависимости от провайдера, формата телефона и поколения. Текущий используемые частоты включают 0,6, 0,7, 0,8, 0,85, 1,7, 2,1, 2,5, 1,9, 2.1, 28, 39 ГГц.
• WiFi (2,4 ГГц и 5 ГГц). Беспроводной интернет, WiFi, передатчики производят сигналы, которые очень похожи на синусоидальные волны, около 2,4 ГГц или 5 ГГц.
• Микроволновые печи (2,4 ГГц). Микроволны производят мощные синусоидальные волны которые должны содержаться в духовке, но часто просачиваются в некоторой степени.
• Системы спутниковой навигации (от 1,2 ГГц до 1,6 ГГц). Спутниковые навигационные системы, такие в качестве GPS (США), ГЛОНАСС (Россия), BeiDou (Китай), Galileo (Европейский Союз), NavIC (Индия) и QZSS (Япония) производят сигналы, близкие к синусоидальным. волны. Они используют синусоидальные волны в диапазоне частот примерно от 1,2 ГГц до 1,6 ГГц.
• Инфракрасный свет (от 300 ГГц до 400 ТГц). Системы оптической связи, как правило, использовать инфракрасный свет, который находится чуть ниже частотного диапазона видимого света. Обычно они не пытаются избежать обнаружения человеческими глазами. Это просто волоконно-оптические кабели, которые они используют, более прозрачны для инфракрасного света, чем они для видимого света.

Существуют различные системы, которые дают названия частотным диапазонам без указания какое-либо конкретное приложение. Одна из систем именования приведена ниже.

• ELF, от 3 до 30 Гц, сверхнизкая частота
• SLF, от 30 Гц до 300 Гц, сверхнизкая частота
• ULF, от 300 Гц до 3 кГц, сверхнизкая частота
• СНЧ, от 3 кГц до 30 кГц, очень низкая частота
• НЧ, от 30 кГц до 300 кГц, низкая частота
• MF, от 300 кГц до 3 МГц, сверхнизкая частота
• ВЧ, от 3 МГц до 30 МГц, высокая частота
• ОВЧ, от 30 МГц до 300 МГц, очень высокая частота
• УВЧ, от 300 МГц до 3 ГГц, сверхвысокая частота
• СВЧ, от 3 до 30 ГГц, сверхвысокая частота
• КВЧ, от 30 до 300 ГГц, сверхвысокая частота
• THF, от 300 ГГц до 3 ТГц, чрезвычайно высокая частота

Предположим, вас попросили спроектировать аудиосистему для аудитории. Это будут иметь кабели длиной от десятков до нескольких сотен метров. Вам нужно относиться к ним как к линиям передачи?

Высококачественный звуковой сигнал использует частоты от 20 Гц до 20 кГц. Как кабели становятся длиннее, именно на высоких частотах в первую очередь необходимо будет используйте теорию линий передачи, так что давайте начнем с нее. Предположим, что кабель имеет скорость коэффициент 50%, что делает скорость около v = 1,5×10⁠ ⁸ м/с. Поместите эту скорость и f = 20 × 10⁠ ³ Гц в $$v = f\лямбда $$ чтобы найти длину волны около 7,5 км, или чуть меньше 5 миль.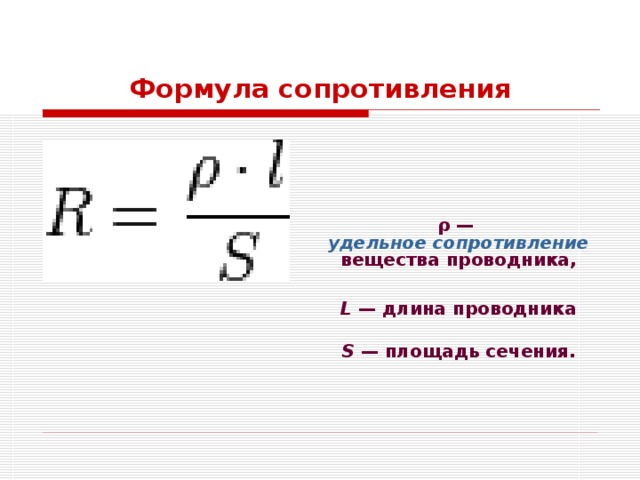 Кабель будет выглядеть электрически длинным, когда он превышает 750 метров или около полумили длинная.

При анализе кабелей нет необходимости использовать теорию линий передачи. Также не будет необходимости рассматривать теорию линий передачи для любого из печатные платы и другие провода внутри используемых вами электронных устройств.

Мобильный телефон передает сигналы на частоте 1 ГГц. Этот сигнал нужно передать с одной печатной платы на другую внутри телефона. Кабель соединение двух досок имеет длину несколько сантиметров (дюйм или два). Нужно ли рассматривать этот кабель как линию передачи?

Предположим, что кабель имеет скорость коэффициент 50%, что делает скорость примерно v = 1,5×10⁠ ⁸ м/с. Поместите эту скорость и f = 1 × 10⁠ ⁹ Гц в $$v = f\лямбда $$ чтобы найти длину волны около 16 см, или 6 дюймов. Кабель будет выглядеть электрически длинным, если его длина превышает 1,6 см или около половины дюйма. Если ваш кабель может быть длиной до 2 см или одного дюйма, то вам нужно лечить это как линия передачи.

Обратите внимание, что это справедливо даже для дорожек на печатной плате. Если цепь след длиннее примерно полдюйма, его нужно рассматривать как передачу линия. При проектировании печатных плат на этих частотах принято рассматривать каждую трасса как линия передачи.

Предположим, что по проводу передаются случайные цифровые данные со скоростью передачи данных 1 Мбит/с. (один мегабит в секунду). Мы будем называть эту скорость передачи данных f _б , т.е. f _b =1×10⁠ ⁶ бит/сек.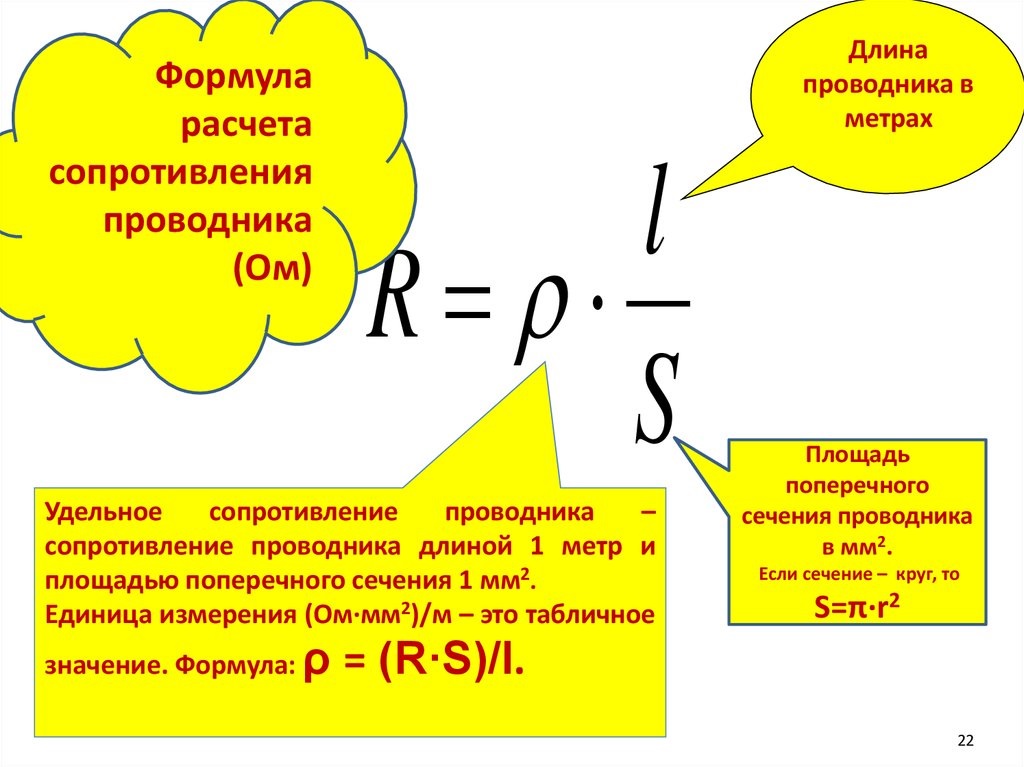 Образец сигнала будет выглядеть так

Хотя этот сигнал не похож на синусоиду, его можно точно смоделировать суммируя большое количество синусоид. Для идеального цифрового сигнала данных выше, синусоидальные волны будут варьироваться от постоянного тока до бесконечной частоты. Это означает длина волны самой высокой частоты синусоиды равна нулю, поэтому все кабели — неважно насколько короткие, нужно рассматривать как линии передачи.

Цифровые сигналы в реальном мире не выглядят точно так же, как идеальные сигналы выше. Они могут больше походить на красную линию ниже:

Обратите внимание, что фактические формы сигналов не перескакивают мгновенно с одного напряжения на другое. еще один. Это связано, в частности, с емкостью, индуктивностью и сопротивлением кабель. Единственный способ мгновенно изменить напряжение на конденсаторе — это ввести бесконечное количество тока в него. Если вы хотите получить бесконечный ток через резистор, нужно бесконечное напряжение — которого у вас нет.

При описании реального цифрового сигнала мы можем говорить о его времени нарастания, Т _Р . Это время, необходимое для перехода сигнала из одного уровня на другой.

Обратите внимание, что в некоторых системах время нарастания для перехода от логического 0 к логическому 1 такое же, как время спада для перехода от логической 1 обратно к логическому 0 — как есть в рисунок выше. Однако это зависит от системы. Существуют логические семьи, в которых время нарастания отличается от времени спада. В этом случае используйте более короткий из двух раз для расчетов электрической длины.

Иногда время нарастания не ясно, так как фактический сигнал может никогда не достичь идеальный уровень. В этих случаях вы можете захотеть определить окончание времени нарастания. как момент времени, когда форма сигнала «близка» к другому уровню. Ошибка в 10% от разницы между двумя логическими уровнями — один из способов сделать это.

Многие логические семейства четко определяют диапазоны напряжений, которые считаются действительные уровни логического 0 и логической 1. В этом случае вы можете использовать эти пороги.

Точное определение времени нарастания не так критично для расчетов обсуждалось здесь. Это расчеты по порядку величины.

Частоты, используемые случайным цифровым сигналом, находятся в диапазоне от постоянного тока (ноль герц) до f _H , где $${f_H} \ приблизительно {1 \over {{T_R}}}$$ В приведенном выше уравнении, если единицы на T _R больше секунд, чем единиц на f _H будет число циклов в секунду, также известное как герц.

Вы хотите передать сигнал данных со скоростью 100 Мбит/с по кабелю длиной 100 метров. Можете ли вы смоделировать кабель, используя простую модель с сосредоточенными параметрами, или вы должны использовать теория линий передачи?

Сначала найдите самую высокую частоту в сигнале данных. { — 99}{\rm{Гц}}$$ Обратите внимание, что самая высокая частота в герцах в десять раз превышает скорость передачи данных в битах в секунду. это удобно соотношение, которое нужно помнить, если вы хотите, чтобы цифровые сигналы выглядели примерно так:

Если мы предположим, что коэффициент скорости кабеля равен 50%, то мы можем найти длину волны используя уравнения ниже. Нас действительно волнует одна десятая длины волны, так как это длина, на которой кабель становится электрически длинный $$\выравнивание{ & v = f \ лямбда \ cr & (VF)c = f\лямбда\cr & (0,5)(3 х {10^8}) = {10^9}\лямбда\кр & \ лямбда = 0,15 \ кр & {\ lambda \ over {10}} = 0,015 \cr} $$

Кабель длиной 100 метров имеет длину более 600 длин волн или более 6000 раз дольше, чем требуется, чтобы считаться электрически длинным. Нет сомнений в том, что В этом случае необходимо использовать теорию линий передачи.

Приведенные расчеты показывают, почему часто не стоит тратить время на беспокоиться о точном определении времени нарастания. Даже если бы кто-то удвоил или сократил в два раза меньше первоначального определения времени нарастания, это не повлияет на окончательный вывод.

В предыдущих разделах кабель считался электрически коротким, когда он короче 10% длины волны для самой высокой частоты, с которой вы работаете. с использованием. Это приближение хорошо работает, когда импеданс источника близок к или менее волновое сопротивление кабеля Z ₀ . если ты не знаю Z ₀ , но можно рассчитать индуктивность кабеля и емкость, вы можете аппроксимировать Z ₀ как \[{Z_0} \ cong \ sqrt {\ frac {{L’}} {{C’}}} \]

Когда импеданс источника больше, чем Z ₀ , тогда предлагаю использовать перемещение разделительной линии между электрически короткими и длинными из λ/10 до \[\ frac{\lambda}{{10}}\left( {\frac{{{Z_0}}}{{{R_s}}}} \right)\]

Например, посмотрите на коаксиальный кабель с Z ₀ =50 Ом, скорость коэффициент VF=60%, управляемый источником с внутренним сопротивлением R _s =50 Ом сопротивление. Если источник генерирует синусоиду с частотой 10 МГц, длина волны в кабель \[\lambda = \frac{v}{f} = \frac{{\left( {VF} \right)c}}{f} = 18\;{\rm{метры}}\] Это делает любой кабель длиной более 1,8 метра электрически длинным.

Теперь предположим, что источник заменен на источник с внутренним сопротивлением R _с = 10 кОм. Теперь кабель становится электрически длинным в 1,8(50/10000)=9 миллиметров.

Люди, обеспокоенные тем, что их кабели могут выглядеть как линии передачи, часто используют источники с внутренним сопротивлением, близким к Z ₀ кабеля. В этих случаях не нужно беспокоиться об этом поправочном коэффициенте.