1.2.2.Дифференцирующие rc-цепи.
П ростейшая дифференцирующая RC-цепь образуется из интегрирующей заменой конденсатора на резистор (рис.1.28).
Рис.1.28.Простейшая дифференцирующая RC-цепь.
Н апряжение на выходе цепи будет определяться падением напряжения на резисторе R: UВЫХ(t)=UR(t)=I(t)R. Зависимость I(t) была нами приведена на рис.1.17. Следовательно, напряжение на выходе будет иметь вид, представленный на рис.1.29 (окончание импульса входного напряжения означает отрицательный скачок напряжения).
Рис.1.29.Сигналы на входе и выходе дифференцирующей RC-цепи.
Цепь
называется дифференцирующей, поскольку
ток через конденсатор можно определить
как производную от приложенного
напряжения. Действительно, как было
показано, ,
отсюда .
Поскольку , .
Как и в случае с интегрирующей цепочкой,
можно считать, что дифференцирование
входного напряжения происходит лишь в
первый момент входного импульса.
Изменение напряжения на выходе дифференцирующей RC-цепочки можно определить, зная изменение напряжения на выходе интегрирующей RC-цепи, т.к. и . Действительно, вычитая из UГ(t) (рис.1.19а) напряжение UC(t)=UВЫХ(t) (рис.1.19в), получаем UR(t). Таким же образом можно поступить, если нужно рассчитать более сложные дифференцирующие цепи.
Р ассмотрим пример усложнённой дифференцирующей RC-цепи с резистором, включённым параллельно конденсатору (рис.1.30).
Рис.1.30. Дифференцирующая RC-цепь с дополнительным резистором, включенным параллельно конденсатору.
В
первый момент подачи прямоугольного
импульса напряжение на конденсаторе
не может измениться. По этой причине
все входное напряжение будет приложено
к резистору R При этом зарядка конденсатора будет
происходить с постоянной времени .
При воздействии отрицательного скачка
напряжения переходной процесс будет
происходить аналогично (рис.1.31).
При этом зарядка конденсатора будет
происходить с постоянной времени .
При воздействии отрицательного скачка
напряжения переходной процесс будет
происходить аналогично (рис.1.31).
Р ис.1.31. Входной и выходной импульс дифференцирующей RC-цепи с дополнительным резистором, включенным параллельно конденсатору.
1.2.3.RC-цепи с двумя конденсаторами.
Рассмотрим теперь RC-цепи, включающие в себя два конденсатора и один резистор. Пример такой цепи приведён на рис.1.32.
Р ис.1.32.RC-цепь с двумя конденсаторами и одним резистором.
При подаче входного прямоугольного импульса в первый момент напряжения на конденсаторах будут равны 0, а всё входное напряжение будет приложено к резистору R, что вызовет ток I(0)=UГ/R.
Этим
током конденсаторы будут заряжаться.
При действии положительного скачка
напряжения и t=∞
на конденсаторах установятся такие
напряжения, которые создадут на правой
пластине конденсатора С Нейтрализоваться эти заряды не могут,
т.к. приложено внешнее напряжение UГ.
Следовательно, QС1=QC2.
Выразим заряды на конденсаторах через
напряжения на них и значения их ёмкостей:
C1UC1=C2UC2.
Поскольку UГ=UC1+UC2 (тока при t=∞
через конденсаторы не протекает, поэтому
напряжение на резисторе равно 0), получаем:
C
Нейтрализоваться эти заряды не могут,
т.к. приложено внешнее напряжение UГ.
Следовательно, QС1=QC2.
Выразим заряды на конденсаторах через
напряжения на них и значения их ёмкостей:
C1UC1=C2UC2.
Поскольку UГ=UC1+UC2 (тока при t=∞
через конденсаторы не протекает, поэтому
напряжение на резисторе равно 0), получаем:
C
Постоянную
времени заряда конденсаторов можно
рассчитать, зная чему равна ёмкость
двух последовательно включённых
конденсаторов. Эту ёмкость можно
определить по тому заряду, который
накопится в конденсаторе С2 при приложении к двум последовательно
соединённым конденсаторам напряжения
UГ :
Q2=C1C2/(C1+C2)UГ=Q1.
Т аким образом, зарядка конденсатора будет происходить с постоянной времени . Импульс на выходе рассмотренной RC-цепи приведён на рис.1.33. Как видим, данная цепь с двумя конденсаторами ведет себя как интегрирующая цепочка (сравните рис.1.33 и рис.1.25).
Рис.1.33. Импульс на входе и выходе RC-цепи, представленной на рис.1.32.
Д ругой пример RC-цепи с двумя конденсаторами приведён на рис.1.34.
Рис.1.34.RC-цепь
с двумя конденсаторами.
В
данном случае при скачках входного
напряжения конденсаторы будут заряжаться
через внутреннее сопротивление генератора
импульсов. Если мы положим, что генератор
входного напряжения идеальный, то его
внутреннее сопротивление равно 0. Это
значит, что скачок входного напряжения
вызовет скачок напряжения на выходе,
причём, как это было показано выше: .
Затем будет происходить перезаряд
конденсаторов: конденсатор С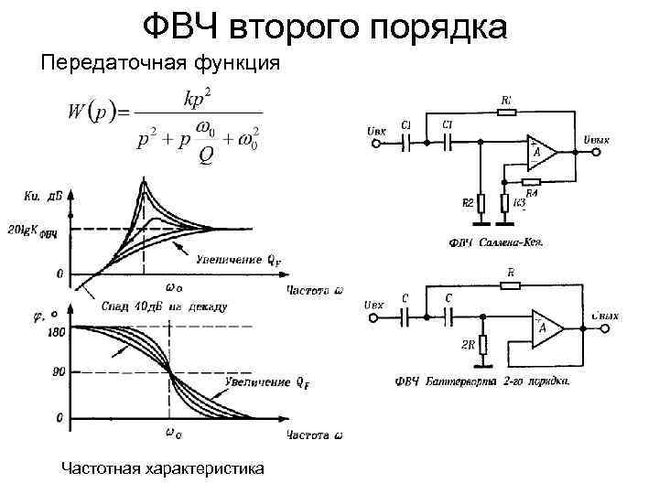 Перезаряд конденсаторов будет происходить
через включённый параллельно с ними
резистор R,
т.е. постоянная времени перезаряда
конденсаторов будет равна: τ=(С1+С2)R.
Входной и выходной импульсы приведены
на рис.1.35. Как видим, данная цепь с двумя
конденсаторами ведёт себя как
дифференцирующая цепочка (сравните
рис.1.35 и 1.29).
Перезаряд конденсаторов будет происходить
через включённый параллельно с ними
резистор R,
т.е. постоянная времени перезаряда
конденсаторов будет равна: τ=(С1+С2)R.
Входной и выходной импульсы приведены
на рис.1.35. Как видим, данная цепь с двумя
конденсаторами ведёт себя как
дифференцирующая цепочка (сравните
рис.1.35 и 1.29).
Рис.1.35. Входной и выходной импульсы цепи, приведённой на рис.1.34.
Р ассмотрим RC-цепь, соединяющую два резистора и два конденсатора (рис.1.36).
Рис.1.36. RC-цепь, содержащая два резистора и два конденсатора.
В
момент положительного скачка входного
напряжения конденсатор С2 зарядится до напряжения .
В последующее время будет происходить
перезаряд конденсаторов с постоянной
времени τ=(С1+С2)R1R2/(R1+R2)
(конденсаторы и резисторы при перезарядке
конденсаторов будут включены параллельно). При t=∞
напряжение на выходе будет стремиться
к уровню: (конденсаторы при t=∞
не будут определять падение напряжения
на резисторах). В зависимости от того,
какое напряжение U
При t=∞
напряжение на выходе будет стремиться
к уровню: (конденсаторы при t=∞
не будут определять падение напряжения
на резисторах). В зависимости от того,
какое напряжение U
Р ис.1.37. Входной и выходные сигналы цепи, приведённой на рис.1.36.
Урок 17. Как работает Интегрирующая и Дифференцирующая RC-цепь Самое понятное объяснение
содержание видео
Рейтинг: 4.0; Голоса: 1
Как работает интегрирующая и дифференцирующая RC-цепь Самое понятное объяснение
Объясняется, как работает интегрирующая и дифференцирующая RC-цепь на реальных примерах.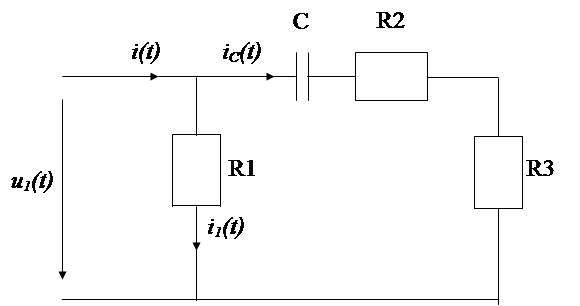 Такие RC-цепи занимают особое место в электрических цепях. Часто они образуют паразитные связи, тогда от них всяческие пытаются избавится или свести к минимуму их воздействие. Однако в большинстве случаев они имеют очень полезное практическое применение.
Дифференцирующая RC-цепь используется для фильтрации сигналов высоких частот, то есть она пропускает сигналы высокой частоты и срезает сигналы низкой частоты. Поэтому дифференцирующую RC-цепь еще называют фильтром высоких частот ФВЧ. На входе ФВЧ устанавливается конденсатор, а выходной сигнал снимается с резистора.
Интегрирующая RC-цепь работает наоборот пропускает преимущественно сигналы низкой частоты и снижает уровень сигналов высокой частоты. Поэтому интегрирующую RC-цепь относят к фильтру низких частот ФНЧ.
В сложных электрических схемах одновременно протекают переменные и постоянные токи. Для нормальной работы определенного электронного узла нужно, чтобы через него протекал либо чисто постоянных ток, либо чисто переменный ток.
Такие RC-цепи занимают особое место в электрических цепях. Часто они образуют паразитные связи, тогда от них всяческие пытаются избавится или свести к минимуму их воздействие. Однако в большинстве случаев они имеют очень полезное практическое применение.
Дифференцирующая RC-цепь используется для фильтрации сигналов высоких частот, то есть она пропускает сигналы высокой частоты и срезает сигналы низкой частоты. Поэтому дифференцирующую RC-цепь еще называют фильтром высоких частот ФВЧ. На входе ФВЧ устанавливается конденсатор, а выходной сигнал снимается с резистора.
Интегрирующая RC-цепь работает наоборот пропускает преимущественно сигналы низкой частоты и снижает уровень сигналов высокой частоты. Поэтому интегрирующую RC-цепь относят к фильтру низких частот ФНЧ.
В сложных электрических схемах одновременно протекают переменные и постоянные токи. Для нормальной работы определенного электронного узла нужно, чтобы через него протекал либо чисто постоянных ток, либо чисто переменный ток.
Дата: 2020-09-04
← Урок 16. Как работает RC-цепь РЕАЛЬНО САМОЕ ПОНЯТНОЕ ОБЪЯСНЕНИЕ!
Надежная схема бесперебойного питания от аккумулятора →
Похожие видео
ПОТОП — ПРИЧИНА восстания ДЕКАБРИСТОВ!
• Альтернативная история
Как выносили тело Сталина из Мавзолея. Чего боялся Хрущев. Как советский народ на это отреагировал
• Загадки истории
Путешествие по настоящей России. Пинежье Русское географическое общество
• Русское географическое общество
СУДОРОГИ в ногах, СВОДИТ ноги, КРУТИТ НОГИ по ночам или днём. ЧТО ДЕЛАТЬ? + Ответы на вопросы.
• Доктор Евдокименко
Какое будущее нас ждет? — Жак Фреско
• Жак Фреско и Проект Венера
Путешествие по настоящей России. На реке Пинеге Русское географическое общество
• Русское географическое общество
Комментарии и отзывы: 10
Михаил
Очень подробно, но все равно местами непонятно.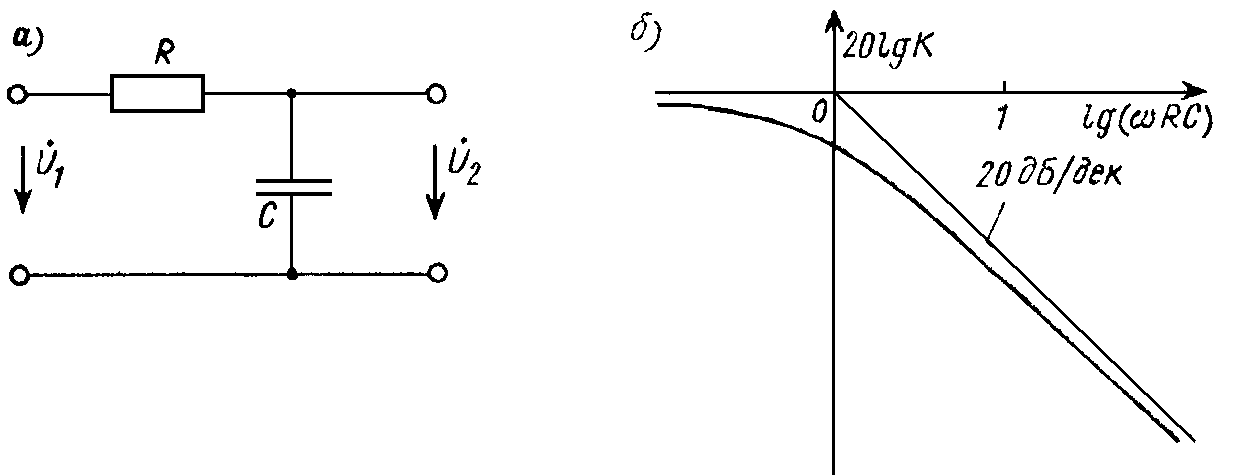 Хочу понять как рассчитать ток, который протекает через конденсатор. Есть формула, по которой определяется сопротивление Xc конденсатора, в котором нет времени, есть формула для определения времени t, необходимое для достижения напряжения конденсатора равное 63% от напряжения источника питания, t=RC. Из какой формулы следует что ток через конденсатор в начальный момент времени максимальный? I=U/R. Вопрос какое U и какое R подставлять в формулу чтобы получить ток через конденсатор в разные моменты времени?
Хочу понять как рассчитать ток, который протекает через конденсатор. Есть формула, по которой определяется сопротивление Xc конденсатора, в котором нет времени, есть формула для определения времени t, необходимое для достижения напряжения конденсатора равное 63% от напряжения источника питания, t=RC. Из какой формулы следует что ток через конденсатор в начальный момент времени максимальный? I=U/R. Вопрос какое U и какое R подставлять в формулу чтобы получить ток через конденсатор в разные моменты времени?
ильфат
Когда в школе учился все время думал, почему изучал алгебру, в котором формулы даже не нужныв в жизни, зачем детей мучают лишними предметами, лучше эти формулы на прямой касались электронике и другим предметам, тогда восприятие детей больше понимали для чего и куда в жизне пригодиться. Извените у меня восприятие туго доходит, пока воображу в голове как все происходит не смогу понять, посмотрел до этого два ролика и час до половину пока, завтра досмотрю, устал слышать слова конденсатор, так и не понял куда пригодиться конденсатор и зачем нужен
Radio
Классное видео, все понял, кроме одного. После 28-й минуты не понял, почему в интегрирующей цепи, убирается синусоидальный сигнал. Каким образом R его забирает( Если можете подскажите, спасибо.
После 28-й минуты не понял, почему в интегрирующей цепи, убирается синусоидальный сигнал. Каким образом R его забирает( Если можете подскажите, спасибо.
Вот по диференциирующей цепи, где 1-м стоит C, который не пропускает постоянный ток и фильтрует его — здесь я понял, но в интегрирующей что-то не доганяю Вас ребята)
Vlad
С дифференцирующей цепью непонятно. Почему при изменении тау меняется и амплитуда? Она ведь не должна меняться, меняться должна только форма сигнала, амплитуда же не должна меняться, т. к. на разряженном конденсаторе в первоначальный момент времени сопротивление равно нулю, разве не так? От чего в таком случае зависит величина амплитуды?
Эдуард
Привет от выпускника радиотехнич. факультета 60-х годов и преподават. института радиоэлектроники впоследствии. Неплохо излагаете, но при подачи имп. на входе цепи у нас потечёт ток. Я говорил студенту, что у нас ничего не потечёт, а вот в цепи будет. Неплохо, неплохо. кто заказчик уроков.
Михаил
Ещё вопрос. А куда девается заряд конденсатора при изменении направления протекания тока? Ведь в момент переключения тока конденсатор имеет заряд, почему он не оказывает влияние на время заряда конденсатора и конденсатор себя ведёт так как будто он полностью разряжен!
А куда девается заряд конденсатора при изменении направления протекания тока? Ведь в момент переключения тока конденсатор имеет заряд, почему он не оказывает влияние на время заряда конденсатора и конденсатор себя ведёт так как будто он полностью разряжен!
Nick
Спасибо за видео. Но мне кажется что в конце автор не правильно указал 28: 52. Так как мы снимаем напряжение с конденсатора, а значит это интегрирующая RC цепь, т. е будет проходить только переменная составляющая, потому что конденсатор не проводит постоянный ток. Или я не прав?
Иванов
Автор, твои видосы супер, смотрю и учусь. Но есть одна поправочка: натуральная дробь выглядит так 3/14 и читается как три четырнадцатых, десятичная дробь выглядит так 3, 14 и читается как три целых четырнадцать сотых. Думаю ты и сам это прекрасно знаешь.
Vasia
Объяснено ооочень понятно, а алени, именно алени, через а, что пишут свои корректировки, идите лесом, это для начинающих, а книжного поноса хватает в книгах и ВУЗах. Огромное спасибо Автору, делайте и далее такие видео. Всего Вам самого хорошего.
Огромное спасибо Автору, делайте и далее такие видео. Всего Вам самого хорошего.
Den
Интересный материал, но в конце не совсем было понятно, а именно работа rc цепей для отсечения постоянной либо переменной составляющий. Правильно ли я понимаю, что при небольшой ёмкости интегрирующая цепь будет повторять синусоиду?
Прохождение импульсов через линейные цепи
радиоликбез
Понятие о переходных процессах. Электрические цепи реальных радиотехнических схем обычно содержат сопротивления, индуктивности и емкости. В таких цепях связь между напряжением и током имеет сложный характер. Объясняется это тем, что емкость и индуктивность обладают способностью накапливать и отдавать электроэнергию. Этот процесс не может протекать скачкообразно. При изменении напряжения в такой цепи ток изменяется с некоторой задержкой во времени. Эти процессы, связанные с изменением запаса энергии в цепях с реактивными элементами при воздействии импульса, называются переходными.
Действие импульсного напряжения на цепь RС. Предположим, что на входе цеди, содержащей конденсатор С и резистор R (рис, 164, а), действует последовательность прямоугольных импульсов (pиc. 154,б). В момент появления на входе RC цепи переднего фронта импульса в ней потечет наибольший ток Im =Um /R (рис, 154,в).
По мере заряда конденсатора результирующее напряжение в схеме up=Um—uc уменьшается, соответственно уменьшается зарядный ток ta. Уменьшение тока происходит по экспоненциальному закону, Ток заряда iз создает на резисторе R падение напряжения (рис. 154, г). С уменьшением тока экспоненциально снижается напряжение на резисторе R. Напряжение на конденсаторе uc по мере
|
Рис. 154. Воздействие прямоугольного импульса на дифференцирующую цепь: а — схема, б — форма импульса на входе, в —форма тока в цепи, г —форма напряжении на резисторе, д — то же, на конденсатора,е —форма импульса на выходе при τ0≥tи, ж — то же при τ0≤ tи |
его заряда экспоненциально возрастает (рис. 154, д) и к некоторому моменту достигает наибольшего значении Um после чего остается постоянным на все время действия плоской вершины входного импульса. Время, в течение которого напряженно на С и R достигает амплитудного значении, зависит от величины сопротивления резистора R и емкости конденсатора С. Чем меньше эти величины, тем быстрее заканчивается переходный процесс.
154, д) и к некоторому моменту достигает наибольшего значении Um после чего остается постоянным на все время действия плоской вершины входного импульса. Время, в течение которого напряженно на С и R достигает амплитудного значении, зависит от величины сопротивления резистора R и емкости конденсатора С. Чем меньше эти величины, тем быстрее заканчивается переходный процесс.
После спада входного импульса конденсатор разряжается через резистор R. Скорость изменения разрядного тока ip (рис. 164, в) и напряжения un (рис. 154, г) такая же, как и при заряде, а на выходе формируется задний фронт (спад) импульса. Направление тока и полярность напряжения на резисторе в этом случае станут противоположными.
Оценку длительности переходного процесса ведут с помощью постоянной времени цепи
Рис. 155. Воздействие прямоугольного импульса на интегрирующую цепь:а— схема, б— форма импульса на входе, в — то же, на выходе, г — зависимость формы импульса от соотношения τ0/tи
С увеличением τ0 длительность переходных процессов возрастает.
Практически переходные процессы в схеме закапчиваются по истечении промежутка времени t = (2,3+3)τ0.
Форма выходного напряжении зависит от значения τ0 (рис. 154, г, е, ж). При τ0»tи (рис. 154,е) конденсатор за время действия входного импульса не успевает зарядиться, и форма выходного сигнала лишь незначительно отличает-ся от формы входного. С такими параметрами (τ0»tи) цепь часто используют в схемах импульсных устройств как разделительную (переходную) между усилительными каскадами. При τ0<tи заряд и разряд конденсатора происходят за время, немного меньшее длительности импульса, поэтому выходное напряженно имеет вид двух узких разнополярных импульсов (рис. 164, ж).
Как очевидно из рис. 164, а, цепи из элементов RC в различных комбинациях могут быть использованы для преобразования формы импульсов. В зависимости от того, с какого элемента снимается сигнал (с R или С), цепь называют дифференцирующей или интегрирующей.
Дифференцирующие цепи. Цепь, показанная на рис. 154, а называется дифференцирующей, поскольку при τ0<tи выходное напряжение пропорционально производной от входного и служит для получения кратковременных остроконечных импульсов напряжения, часто используемых для запуска формирующих устройств. Чем меньше τ0, тем больше скорость изменения напряжения и тем острее будут импульсы напряжения на выходе дифференцирующей цепи.
На работу дифференцирующей цепи существенно влияет входная (паразитная) емкость Сп последующей цепи, которая вызывает уменьшение амплитуды выходного напряжения Uвых. Чтобы уменьшить влияние Сп на выходной сигнал, выбирают емкость цепи C≥(5-10) Сп.
Пример. Длительность импульса tи=5 мкс. Рассчитать элементы дифференцирующей цепи.
В дифференцирующей цепи τ0≪tи. Примем τ0=RС=0,1 tи=0,1×5=0,5 мкс, т.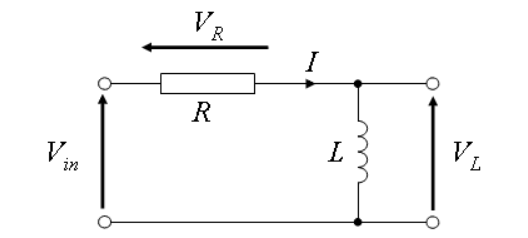 е, tи ≫3τ0. Задаемся величиной R=10 кОм, тогда емкость
е, tи ≫3τ0. Задаемся величиной R=10 кОм, тогда емкость
Интегрирующие цепи. Если в цепи RC выходное напряжение снимается с емкости (рис. 155, а), то при τ0≫tи выходной сигнал пропорционален интегралу от входного, и такая цепь называется интегрирующей. Если постоянная времени RC цепи выбрана равной или больше длительности прямоугольного импульса (рис. 155,б) напряжения на входе (τ0≫tи), то на выходе RC цепи возникает импульс с растянутым фронтом и спадом (рис. 155, в). При воздействии на вход такой цепи кратковременного импульса напряжения на выходе образуется более широкий импульс.
|
Рис. 156. Цепи на RL элементах:а —дифференцирующая, б — интегрирующа |
Интегрирующие цепи применяют для увеличения длительности импульса. Кроме того, их используют в схемах генерирования пилообразного напряжения, селекции импульсов по длительности и т. д. Чем больше то при неизменной длительности входного импульса tи, тем больше растянут импульс на выходе (рис. 155, г). Амплитуда импульса при этом уменьшается, так как конденсатор не успевает полностью зарядиться за время действия входного импульса.
д. Чем больше то при неизменной длительности входного импульса tи, тем больше растянут импульс на выходе (рис. 155, г). Амплитуда импульса при этом уменьшается, так как конденсатор не успевает полностью зарядиться за время действия входного импульса.
Дифференцирование и интегрирование может также осуществляться с помощью цепей RL. Поскольку реактивное действие индуктивности противоположно емкости, то в RL-цепях при дифференцировании выходной сигнал снимается с индуктивности (рис. 156, а), а при интегрировании — с резистора (рис. 156, б). Цепи RL применяют сравнительно редко, так как они содержат дорогую моточную деталь.
Читайте также: Параметры периодической последовательности импульсов
Стр 1 из 2Следующая ⇒ Лабораторная работа №1 Исследование характеристик дифференцирующей цепи
1.
Теоретические основы
Дифференцирующей называется электрическая цепь, в которой выходная величина пропорциональна производной от входной величины. Простейшими дифференцирующими цепями могут служить цепи с емкостью или индуктивностью (рис.2.1).
Рис.2.1 Простейшие дифференцирующие цепи В цепи с емкостью
Принимая uc(t) за входную величину, а ток ic(t) – за выходную, получим дифференцирующую цепь. В цепи с индуктивностью Принимая iL(t) за входную величину, а uL(t) – за выходную, получим дифференцирующую цепь. Использовать ток как входную или выходную величину практически затруднительно, так как в первом случае необходимо иметь стабильный источник тока, а во втором для его измерения необходимо включить последовательно дополнительное сопротивление, которое оказывает влияние на процесс.
Условие, при котором rC-цепь выполняет операцию дифференцирования, вытекает из уравнения
Если принять то При синусоидальном входном напряжении уравнение цепи в комплексной форме
По условию дифференцирования
тогда
или При несинусоидальной форме напряжения U1(t) условие дифференцирования должно быть выполнено для всех гармонических составляющих входного сигнала. При этом условием дифференцирования является
где ωВ – частота наивысшей гармоники, которой нельзя пренебречь.
Идеальное дифференцирование прямоугольного импульса показано на рис. 2.2,а. Амплитуда выходного сигнала u2(t)бесконечно велика.
Рис.2.2 Идеальное (а) и реальное (б) дифференцирование прямоугольного импульса
График напряжения u2(t)на выходе реальной дифференцирующей цепи показан на рис.2.2,б. Напряжение u2(t)представляет собой импульсы экспоненциальной формы с чередующейся полярностью. За длительность выходного импульса принимают время, равное утроенному значению постоянной времени цепи . Амплитуда импульсов равна величине входного напряжения. Сравнение временных диаграмм реальной и идеальной дифференцирующей цепи (рис.1,а и 1,б) показывает, что при уменьшении τдлительность импульсов u2(t)сокращается и кривая u2(t)стремится по форме к производной входного напряжения. Величина τ называется постоянной времени цепи и соответствует изменению выходного напряжения на 63% от исходного (e-1 = 0.37). Очевидно, что время изменения выходного напряжения зависит от сопротивления резистора и емкости конденсатора и, соответственно, постоянная времени цепи пропорциональна этим значениям, т. Дифференцирующая цепь называется еще укорачивающей, так как длительность выходных импульсов значительно меньше, чем входных.
Допустим, конденсатор разряжен. При подаче на вход RC-цепи импульса напряжения конденсатор сразу же начнет заряжаться током, проходящим через него самого и резистор. Сначала ток будет максимальным, затем по мере увеличения заряда конденсатора постепенно уменьшится до нуля по экспоненте. Когда через резистор проходит ток, на нем образуется падение напряжения, которое определяется, как U=i R, где i-ток заряда конденсатора. Поскольку ток изменяется экспоненциально, то и напряжение будет изменяться также — экспоненциально от максимума до нуля. Падение напряжения на резисторе как раз и является выходным, величину которого можно определить по формуле Uвых = U0e-t/τ. Передаточная функция цепи (коэффициент передачи) — равна отношению комплексной амплитуды сигнала на выходе к комплексной амплитуде сигнала на входе: , где — фазово-частотная характеристика, — амплитудно-частотная характеристика цепи. Импульсная характеристика g(t) —реакция цепи на действие сигнала в виде δ-функций, т. е. это сигнал на выходе, если сигнал на входе есть d-функция. при . При этом g(t) = 0 при t < 0 – выходной сигнал не может возникнуть ранее момента появления входного сигнала. Импульсная характеристика цепи и передаточная функция связаны преобразованием Фурье: Переходная характеристика цепи h(t) — является откликом на сигнал, называемый единичным скачком: h(t) = 1 при t >0, h(t) = 0 при t < 0, при этом Для дифференцирующей цепи: Комплексный коэффициент передачи: , Передаточная функция: ФЧХ: ; АЧХ: Импульсная характеристика: Рис.2.3 АЧХ (а) и ФЧХ (б) идеального дифференциатора Условие хорошего дифференцирования сигнала: для синусоидального колебания с частотой w дифференцирование осуществляется при условии, что частота его много меньше величины 1/RC. Подставляя в выражение для передаточной функции K(p) вместо р комплексную величину jω, мы получаем однозначную зависимость между передаточной функцией и частотными характеристиками звена. При этом комплексная величина K(jω) есть функция частоты, и называется амплитудно-фазовой характеристикой (АФХ). При построении K(jω) в прямоугольной системе координат — комплексной плоскости — получаем годограф амплитудно-фазовой характеристики, где частота ω входит как параметр. Примерный вид годографа АФХ показан на рис. 2.4. Каждой точке такого годографа соответствует определенная частота ω, как и помечено на рисунке. Рис.2.4 Амплитудно-фазовая характеристика
АФЧХ реального дифференцирующего звена приведена на рис. 2.5. Рис.
Годограф описывает полуокружность с радиусом, стремящимся к ¥ при T стремящимся к 0. При этом годограф прижимается к положительной мнимой полуоси и становится практически неотличим от годографа идеального дифференцирующего звена. Частота w*=1/T считается максимальной, при которой еще реальное дифференцирующее звено работает «почти как идеальное». При достаточно низких частотах реальное дифференцирующее звено близко к идеальному. 12Следующая ⇒ ©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов. |
Простейшие линейные цепи | Политех в Сети
Лабораторная работа №3
Цель работы — изучить частотные, фазовые и переходные характеристики дифференцирующих и интегрирующих цепей, выяснить взаимосвязь между частотными и временными характеристиками этих цепей на примере прохождения через эти цепи гармонических и импульсных сигналов.
Приборы и модули: электронный осциллограф, генератор звуковых частот, универсальный лабораторный стенд, модули № 1, 2, 6.
Сведения из теории.
Любые радиотехнические устройства содержат линейные цепи. Линейной называется цепь, описываемая линейным алгебраическим или дифференциальным уравнением с постоянными коэффициентами. Для линейной цепи справедлив принцип суперпозиции и следствие этого принципа — закон Ома. К простейшим линейным цепям относятся RС -цепи. Если выходом RС -цепи является резистор ее называют дифференцирующей, если конденсатор — интегрирующей.
Различают переходное состояние RС -цепи, соответствующее процессу установления напряжений и токов, и установившееся (стационарное) — когда закон изменения всех напряжений и токов в цепи с точностью до постоянных величин совпадает с действующим на входе напряжением.
Стационарный режим работы RС -цепи описывается коэффициентом передачи, амплитудно-частотной и фазово — частотной характеристиками, переходной процесс — переходной характеристикой.
Рассмотрим дифференцирующую цепь.
Коэффициент передачи RС -цепи (рис.1) для гармонического сигнала имеет вид:
где:
— граничная частота, при которой реактивное сопротивление становится равным активному; T=RC — постоянная времени. Зависимость модуля коэффициентапередачи от частоты называется амплитудно – частотной характеристикой (рис.2).
Рис. 1. Дифференцирующая цепь
Рис. 2. Амплитудно — частотная характеристика дифференцирующей цепи
Зависимость сдвига Фаз между выходным и входным напряжениями от частоты называется фазово — частотной характеристикой (рис.3).
Рис. 3. фазово — частотная характеристика дифференцирующей цепи
Фазовый сдвиг объясняется наличием в цепи реактивного элемента — конденсатора.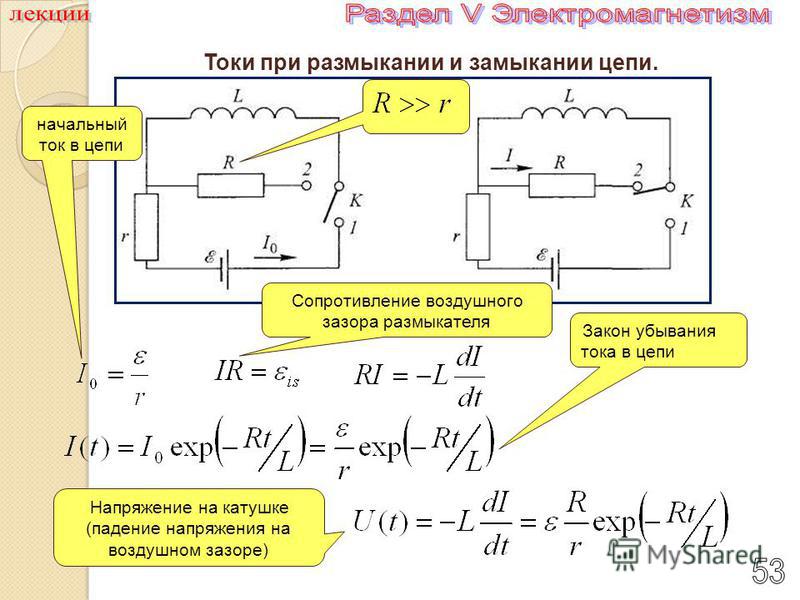
Рис.2, 3 показывают, что дифференцирующая цепь передает с коэффициентом передачи близким к 1 и с фазовым сдвигом близким к нулю сигналы высоких частот, а на низких частотах значительно ослабляет сигналы и выходные сигналы опережают по фазе входные сигналы. Т. о. дифференцирующая цепь является фильтром высоких частот.
Зависимость, коэффициента передачи от частоты можно объяснить, рассматривая дифференцирующую цепь как делитель входного напряжения. Одно плечо делителя — частотно-зависимое реактивное сопротивление конденсатора
Другое – активное опротивление R. С увеличением частоты уменьшается сопротивление конденсатора и падение напряжения на нем UC. Поскольку U1=UR+UC (U1 — входное напряжение), то уменьшение UC сопровождается возрастанием (на выходе RС-цепи).
Переходные процессы в дифференцирующей цепи удобно рассматривать, анализируя осциллограммы напряжений на R И С При подаче на вход RС — цепи прямоугольных импульсов. Переходная характеристика
Представляет собой отклик цепи или изменение напряжения во времени на выходе RС -цепи при подаче на вход единичного скачка напряжения. Постоянная времени T=RC — время, за которое напряжение на выходе дифференцирующей цепи уменьшается в E раз по сравнению с начальным значением единичного скачка (т. е. до уровня 0,37). Величина T определяет скорость заряда (разряда) конденсатора С.
При различных T Дифференцирующая цепь по — разному передает входные импульсы.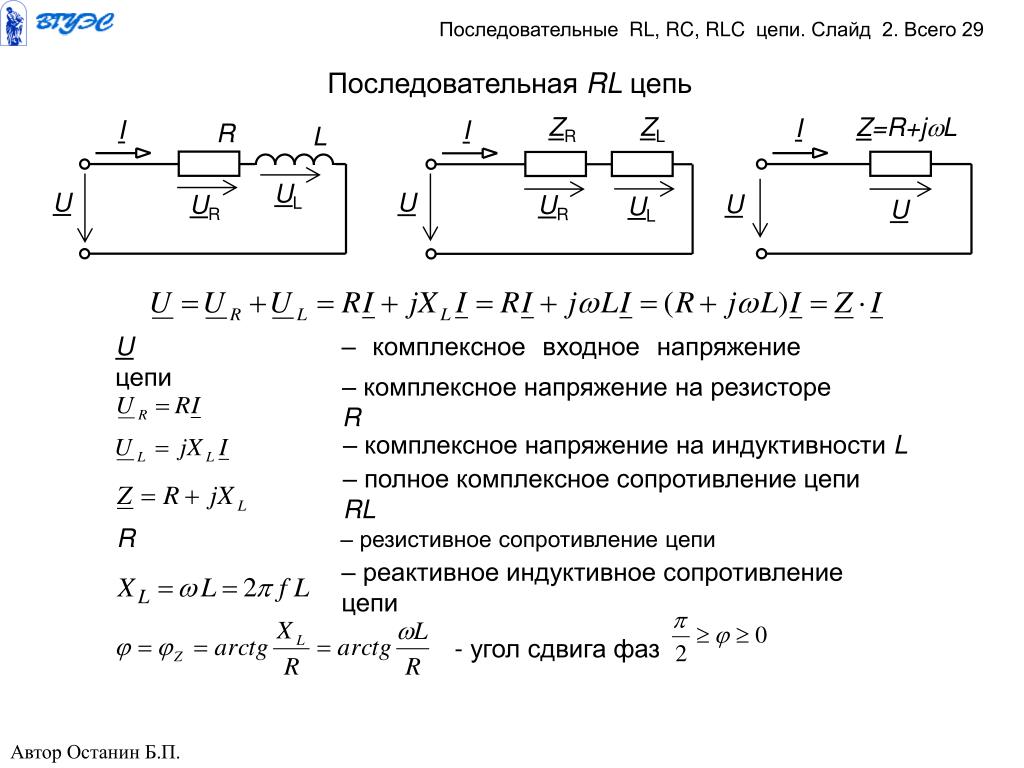 Это видно из уравнения для RС — цепи.
Это видно из уравнения для RС — цепи.
Или
В зависимости от соотношения между и возможны два различных случая.
Если (T велико по сравнению с 1/W), То или U1»U2.
Если (T Мало по сравнению с 1/W)
То или.
Если на вход цепи вместо гармонического сигнала поступает прямоугольный импульс, то в зависимости от соотношения между T и длительностью входного импульса TU, Дифференцирующая цепь либо с определенными искажениями передает входной импульс, либо с определенной степенью точности его дифференцирует.
Осциллограммы напряжений для случая T>TU Приведены на рис.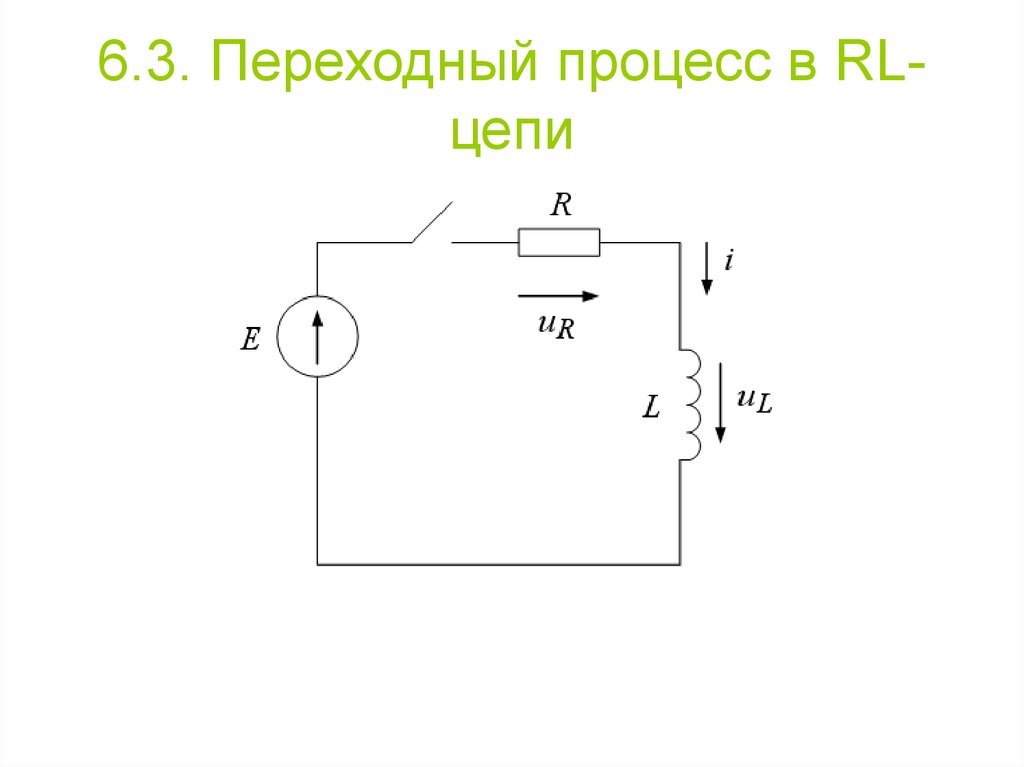 4.
4.
В начальный момент времени на выходе цепи (на резисторе R) регистрируется скачок напряжения равный U1 , напряжение же на конденсаторе равно 0. Затем начинается заряд конденсатора с постоянной времени T и напряжение на R. Уменьшается. К моменту окончания входного импульса конденсатор не успевает зарядиться до амплитудного значения входного импульса. Начало разряда конденсатора приводит к скачкообразному изменению направления тока в цепи, что вызывает появление выброса напряжения противоположной полярности на резисторе.
Рис.4. Осциллограммы напряжений на элементах дифференцирующей цепи для случая T>TU.
Для случая T<<TU осциллограммы напряжений приведены на рис. 5.
5.
Рис.5. Осциллограммы напряжений на элементах дифференцирующей цепи для случая T<<TU
Рассматривая прямоугольный импульс в соответствии с преобразованием Фурье как сумму бесконечного множества гармонических составляющих и связывая передачу фронта и спада импульса с прохождением через RС—Цепь высокочастотных составляющих спектра (сопротивление конденсатора близко к нулю) а передачу вершины — с прохождением низкочастотных составляющих спектра (сопротивление конденсатора становится существенным), можно объяснить осциллограммы на рис.4 с позиций спектрального анализа сигналов сложной формы.
В соответствии с преобразованием Фурье сигнал U1 действующий на входе RC-цепи, можно представить через спектральную функцию Ŝ(ω):
Спектр одиночного прямоугольного импульса длительностью TU является непрерывным и содержит «все частоты» от 0 до бесконечности (рис.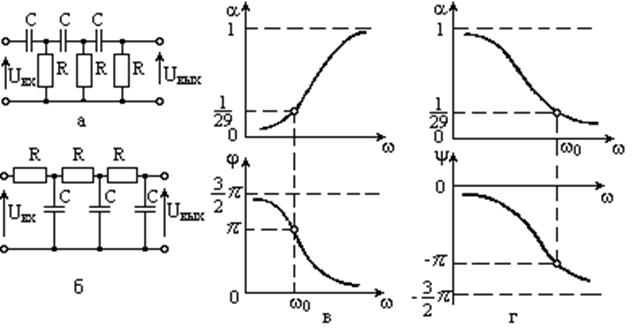 6).
6).
Рис.6. Спектр одиночного прямоугольного импульса.
Входной сигнал, представляющий собой функцию времени, и может изменяться быстрее, чем изменяется мгновенно значение самой высокочастотной составляющей его спектра. Наиболее быстрые изменения сигнала во времени, соответству ющие фронту и спаду прямоугольного импульса, связаны прохождением через RС—Цепь высокочастотных составляющих спектра. Медленные изменения сигнала во времени соответствующие плоской части импульса — вершине, связаны прохождением через RС-цепь низкочастотных составляющи спектра.
Анализируя частотные и переходные характеристики для различных постоянных времени (рис.7), можно установит взаимосвязь между частотной и переходной характеристикам дифференцирующей цепи.
Рис.7. Частотные и переходные характеристики дифференцирующих цепей с различными постоянными времени τ1>τ2.
Из частотных характеристик видно, что чем меньше постоянная (τ1>τ2) времени тем с меньшим коэффициентом передаются низкие частоты и тем меньше отличается RС-цепь от идеальной дифференцирующей цепи, коэффициент передачи которой для низких частот равен 0. Это же подтверждается и переходными характеристиками дифференцирующей цепи. Чем меньше постоянная времени, тем больше скол (спад) вершины импульса, что связано с уменьшением коэффициента передачи цепи на низких частотах. А чем больше скол вершины импульса, тем больше выходное напряжение напоминает по форме производную от входного сигнала (единичного скачка). В этом случае заряд и разряд конденсатора происходит быстро за время τ, гораздо меньшее длительности импульса и конденсатор успевает быстро зарядиться до амплитуды входного импульса. Напряжение на выходе дифференцирующей цепи напоминает при этом производную от входного напряжения.
Рассмотрим интегрирующую цепь.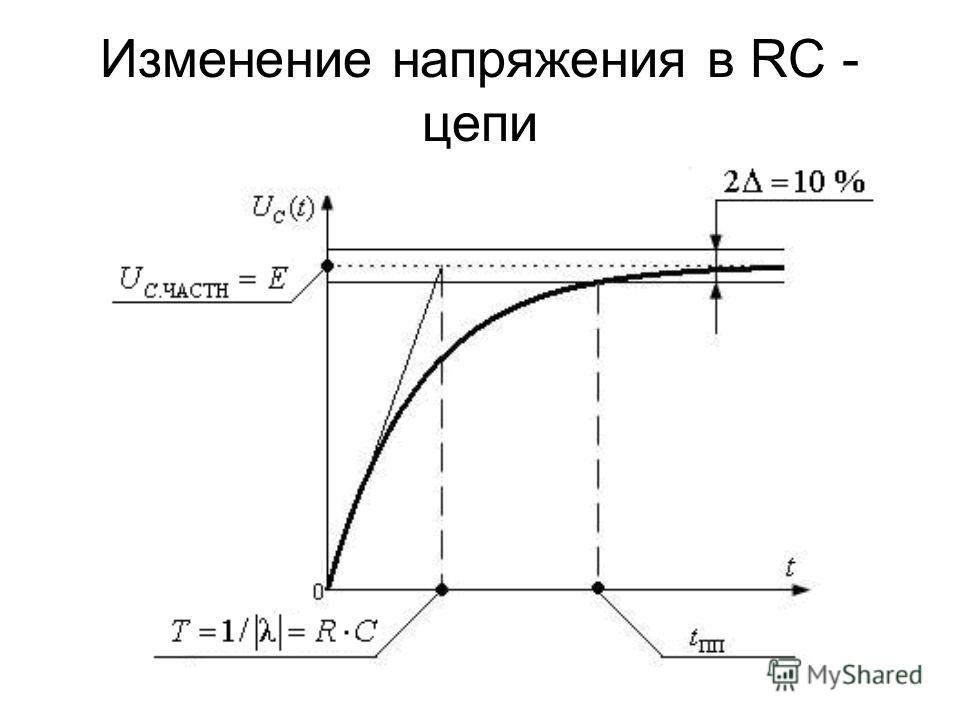
Рис.8. Интегрирующая цепь.
Коэффициент передачи цепи (рис. 8) для гармонического сигнала записывается:
Модуль коэффициента передачи:
А фазово-частотная характеристика,
Где — граничная частота;τ — постоянная времени.
Соответствующие этим выражениям амплитудно-частотная и фазово-частотная характеристики интегрирующей цепи представлены на рис.9.10.
Рис.9. Амплитудно-частотная ха — Рис.10. Фазово-частотная
Рактеристика интегрирующей характеристика интегриру-
Цепи. ющей цепи.
Из графиков на рис. 9 и 10 видно, что интегрирующая цепь с коэффициентом передачи близким к 1 и фазовым сдвигом к о передает низкочастотные сигналы и значительно ослабляет высокочастотные сигналы.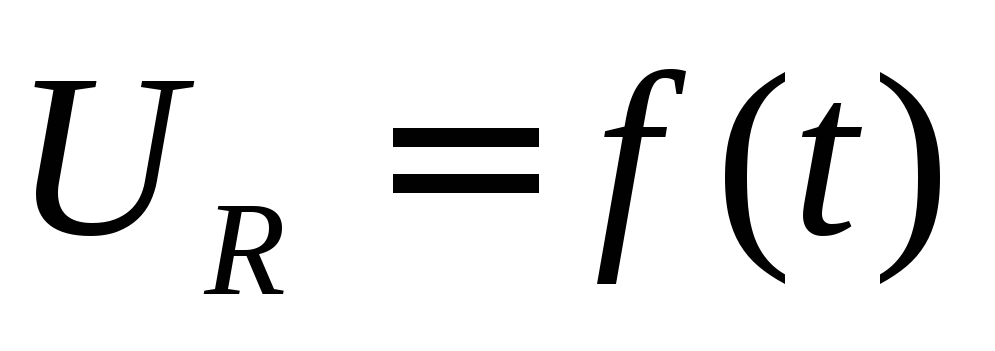 Последние отстают по фазе от входных сигналов, т. е. интегрирующая цепь является фильтром низких частот. Переходные процессы в интегрирующей цепи можно проанализировать подавая на вход прямоугольный импульс длительностью TU. Из уравнения для интегрирующей цепи:
Последние отстают по фазе от входных сигналов, т. е. интегрирующая цепь является фильтром низких частот. Переходные процессы в интегрирующей цепи можно проанализировать подавая на вход прямоугольный импульс длительностью TU. Из уравнения для интегрирующей цепи:
видно, что цепь по разному перелает входные сигналы при различных постоянных времени. При τ<<TU
т. е. RС-цепь с небольшими искажениями передаёт входной сигнал на выход. Когда же τ>>TU
(напряжение на выходе RС-цепи примерно пропорционально
Интегралу от входного напряжения).
Осциллограммы напряжений для этих случаев приведены на
рис. 11, 12 соответственно.
11, 12 соответственно.
Рис.11.Осциллограммы напряжений Рис.12.Осциллограммы напряжений
На элементах интегрирующей на элементах интегрирующей
Цепи для случая τ<<TU. цепи для случая τ>>TU.
Переходная характеристика интегрирующей цепи представляет собой отклик этой цепи или изменение напряжения во времени на ее выходе при подаче на вход единичного скачка напряжения.
Аналитическое выражение для переходной характеристики
интегрирующей цепи записывается в виде
Где τ — это время, в течение которого напряжение на выходе интегрирующей цепи нарастает до уровня 0,63 максимального значения.
Анализируя частотные и переходные характеристики интегрирующих цепей с различными постоянными времени (рис.13), можно установить взаимосвязь между частотной и переходной характеристиками интегрирующей цепи.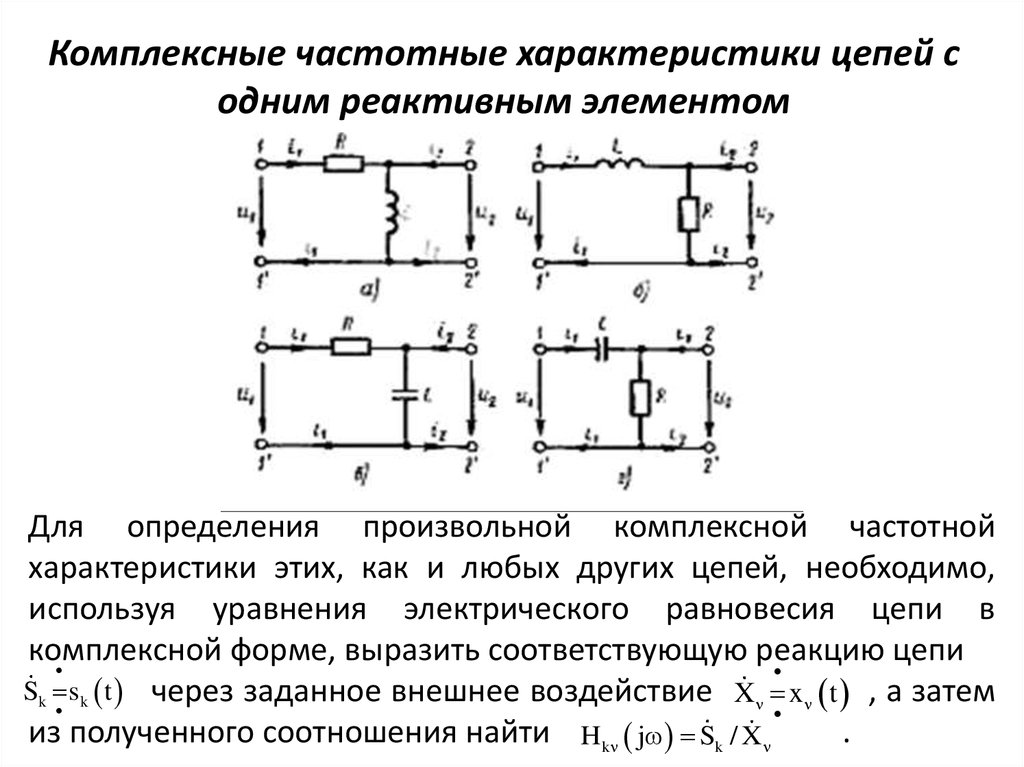
Рис.13. Амплитудно-частотные и переходные характеристики интегрирующих цепей с различными постоянными времени.
Чем больше постоянная времени τ (τ1>τ2), тем с меньшим коэффициентом передаются на выход интегрирующей цепи высокочaстотные составляющие спектра сигнала и тем меньше отличается выходное напряжение интегрирующей цепи от интеграла от входного напряжения.
Задания и методические рекомендации
1.Изучите амплитудно-частотную и переходную характеристики дифференцирующей цепи. ( R=22 КОм, С = 5,1 нФ Модули №1, №2)
1.1. Рассчитайте постоянную времени цепи τ и граничную частоту F1
1.2. Рассчитайте значение модуля коэффициента передачи и сдвиг фазы для частоты F=F1.
1. 3. Соберите схему, показанную на рис. 14.
3. Соберите схему, показанную на рис. 14.
Рис.14. Схема для исследования дифференцирующей цепи.
1.4. При постоянной амплитудные напряжения UВх=1В На входе RС -цепи измерьте UВых на частотах 0,5; 1; 1,5; 2; 4; 8; 16 кГц.. Все измерения проводите при помощи осциллографа. Вычислите значения модуля коэффициента передачи для указанных частот. Данные запишите в таблицу 1. Табл. 1
1.5. На этих же частотах измерьте сдвиг фазы φ между выходным и входным сигналами RС-Цепи, используя осциллограф в режиме внешней синхронизации. Синхронизируйте осциллограф входным сигналом. Подключите вход «Y» осциллографа ко входу исследуемой RС-цепи и установите длительность развертки такой, чтобы половина периода синусоиды занимала почти всю рабочую часть экрана (отрезок «А» на рис.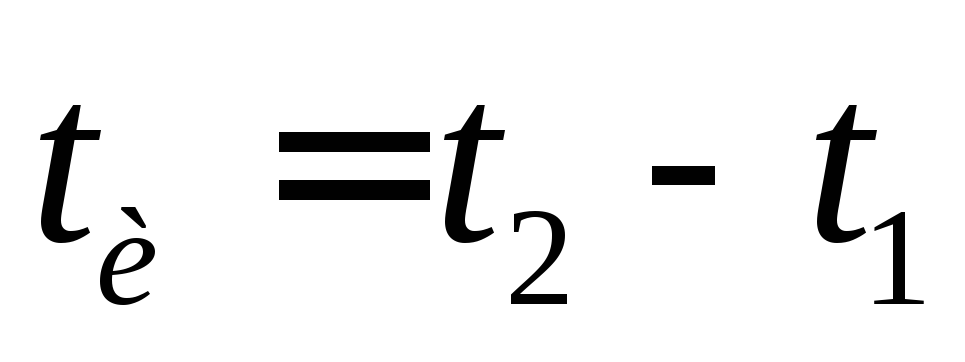 15). При этом необходимо отцентрировать изображение так, чтобы горизонтальная линия в центре экрана, осциллографа являлась бы горизонтальной осью симметрии входного синусоидального сигнала. Измерьте отрезок «А«, пользуясь ручками «стабильность», «уровень» и «↔» и совместите переход сигнала через ноль с пересечением горизонтальной оси симметрии экрана осциллографа с одной из вертикальных линий экрана. Подключив «Y» вход осциллографа к выходу RС-цепи, заметьте временной сдвиг выходного сигнала по отношению ко входному по нулевым переходам и измерьте отрезок «B«, соответствующий этому временному сдвигу. Вычислите для всех частот сдвиг фазы.
15). При этом необходимо отцентрировать изображение так, чтобы горизонтальная линия в центре экрана, осциллографа являлась бы горизонтальной осью симметрии входного синусоидального сигнала. Измерьте отрезок «А«, пользуясь ручками «стабильность», «уровень» и «↔» и совместите переход сигнала через ноль с пересечением горизонтальной оси симметрии экрана осциллографа с одной из вертикальных линий экрана. Подключив «Y» вход осциллографа к выходу RС-цепи, заметьте временной сдвиг выходного сигнала по отношению ко входному по нулевым переходам и измерьте отрезок «B«, соответствующий этому временному сдвигу. Вычислите для всех частот сдвиг фазы.
Результаты измерений и вычислений запишите в таблицу 1.
1.6. По данным таблицы постройте амплитудно-частотную и фазово-частотную характеристики дифференцирующей цепи.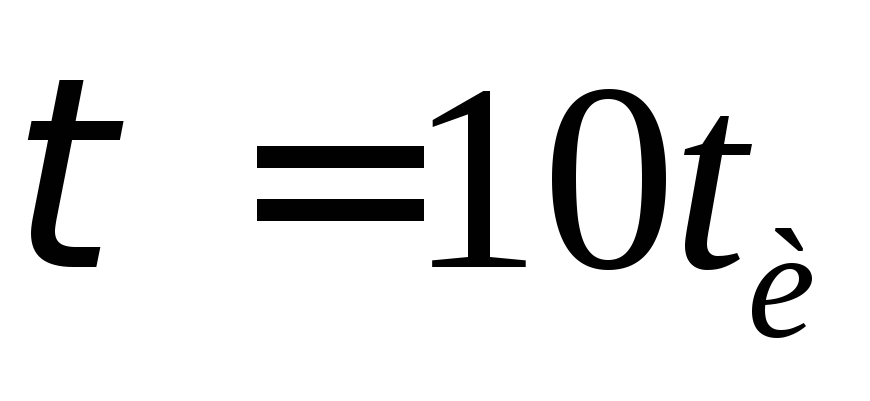 По каждой из них определите постоянную времени τ. Объясните характер изменения характеристик в области низких и высоких частот.
По каждой из них определите постоянную времени τ. Объясните характер изменения характеристик в области низких и высоких частот.
Рис.15. Измерение сдвига фаз между входным и выходным напряжениями
1.7. Получите на экране переходную характеристику дифференцирующей цепи. Для этого ко входу RС-цепи вместо генератора звуковых частот подключите генератор прямоугольных импульсов (Модуль 6). Используйте осциллограф в режиме внешней синхронизации, запуская развертку входным импульсом. Зарисуйте переходную характеристику и измерьте постоянную времени τ. Сравните измеренные значения с вычислениями.
1.8. Зарисуйте и объясните переходные характеристики дифференцирующей цепи для различных постоянных времени ( R=22 кОм; 100 кОм; 470 кОм; С=5,1 нф) .
2. Из тех же элементов R и C Соберите интегрирующую цепь. Снимите для нее и постройте амплитудно-частотную, фазовую и переходную характеристики.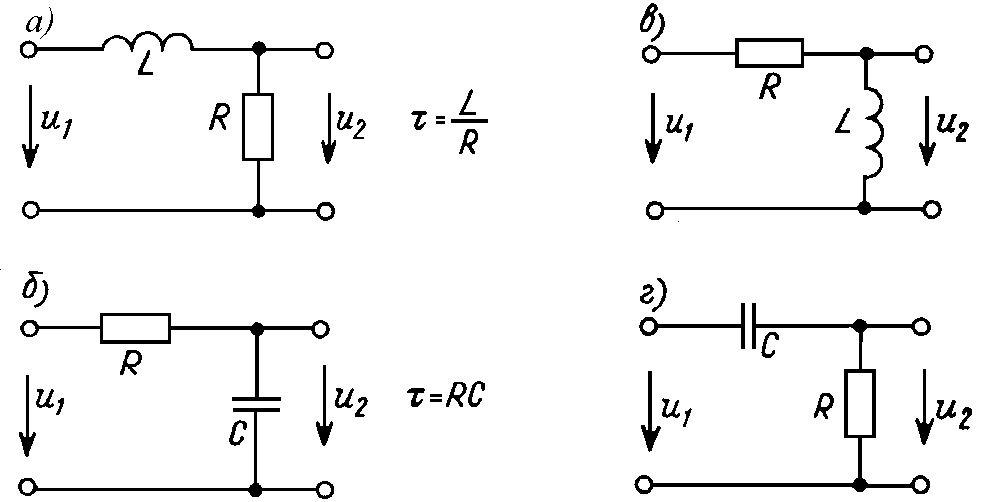 Обьясните характер их изменения. Зарисуйте и обьясните переходные характеристики интегрирующей цепи для различных постоянных времени.
Обьясните характер их изменения. Зарисуйте и обьясните переходные характеристики интегрирующей цепи для различных постоянных времени.
Оформление результатов
В отчет включите принципиальные электрические схемы, расчетные формулы, таблицы измеренных и рассчитанных результатов, графики и выводы по результатам.
Контрольные вопросы
1. Какие цепи называются линейными?
2. Какое из записанных соотношений между постоянными времени τ и длительностью входного импульса TUСоответствует условию лучшего дифференцирования входного импульса? лучшего интегрирования?
1) τ=tU ; 2) τ>>tU ; 3) τ<tU ; 4) τ<<tU ; 5) τ>tU.
3*. Нарисуйте векторные диаграммы для тока и напряжений в дифференцирующей и интегрирующей цепях. Обьясните причину наличия фазового сдвига между выходным и входным напряжениями.
4. Объясните взаимосвязь между амплитудно-частотной и переходной характеристиками дифференцирующей и интегрирующей RС—Цепей.
5. К интегрирующей цепи R=1 кОм, С=1000 мкф подключено постоянное напряжение 1В. Какого значения напряжения на выходе цепи достигает через 3 секунды? Через время равное τ?
Литература
1. В. Н. Ушаков. Основы радиоэлектроники и радиотехнические устройства, 1976
2. М. К. Ефимчик, С. С. Шушкевич. Основы радиоэлектроники, 1981.
3. А. А. Харкевич. Основы радиотехники, 1963.
5.5. Простейшие радиотехнические цепи. 5. Радиотехнические цепи. Радиотехнические цепи и сигналы. Учебное пособие
5.5.1. Пассивные апериодические цепи
5.5.2. Пассивные частотно-избирательные цепи
5.5.3. Активные линейные цепи
5.5.1. Пассивные апериодические цепи
При классификации радиотехнических цепей было отмечено, что по признаку наличия в цепи источника энергии цепи подразделяются на пассивные и активные.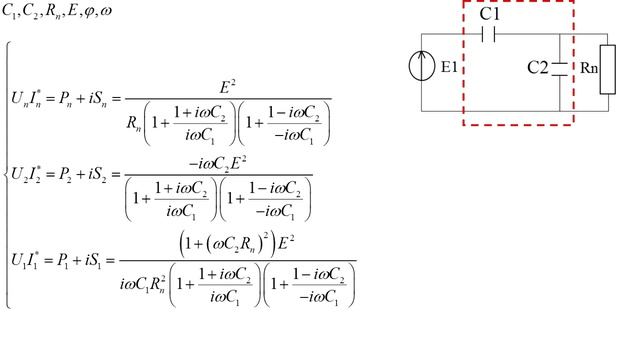 Начнем с рассмотрения пассивных цепей первого порядка, т.е. цепей содержащих один реактивный элемент (емкость или индуктивность). На основе этих цепей строятся как простейшие активные цепи, так и более сложные радиотехнические устройства.
Начнем с рассмотрения пассивных цепей первого порядка, т.е. цепей содержащих один реактивный элемент (емкость или индуктивность). На основе этих цепей строятся как простейшие активные цепи, так и более сложные радиотехнические устройства.
Выше в качестве примера линейной цепи при рассмотрении методов анализа приводилась RC-цепь, которая получила название интегрирующей цепи. Рассмотрим еще одну RC-цепь, называемую дифференцирующей цепью, определим ее характеристики и сравним с характеристиками интегрирующей цепи.
Определение характеристик цепей можно проводить любым из рассмотренных выше методов. Так, например, при определении частотных характеристик цепей в данном случае удобно представить ту или иную цепь в виде делителя напряжения, в состав которого входят комплексные сопротивления и . Временные характеристики (переходную и импульсную) можно рассчитать как методом интеграла наложения, так и операторным методом.
В таблице 5 представлены схемы интегрирующей и дифференцирующей цепи, дифференциальные уравнения, которыми описываются цепи, аналитические выражения комплексного коэффициента передачи , амплитудно-частотных , фазо-частотных , а также переходных и импульсных характеристик и их графические изображения.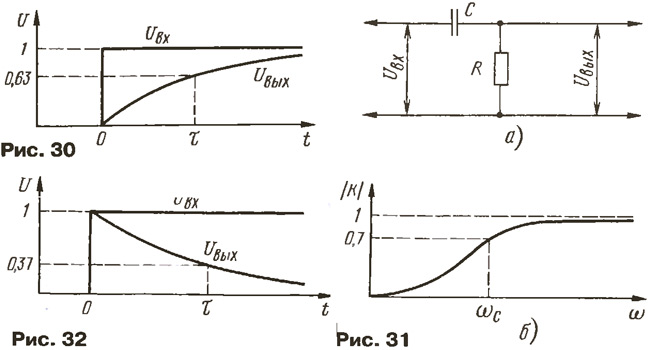
Анализ графиков АЧХ цепей показывает, что интегрирующая цепь пропускает нижние частоты и задерживает верхние, т.е. является фильтром нижних частот (ФНЧ). Дифференцирующая цепь наоборот пропускает верхние частоты и тем самым является фильтром верхних частот (ФВЧ).
Форма временных (переходной и импульсной) характеристик определяет характер переходных процессов. Для рассматриваемых цепей переходные характеристики представляют собой монотонно возрастающую (для интегрирующей цепи) и монотонно убывающую (для дифференцирующей цепи) функции. Это определило название цепей как апериодических.
Обратимся к выражению для комплексного коэффициента передачи интегрирующей цепи. При комплексный коэффициент передачи
.
Так как входной и выходной сигналы связаны соотношением
,
то при указанном условии
. (5.40)
Но оператор является оператором интегрирования. Тогда применяя обратное преобразование Фурье, получим
,
т. е. цепь выполняет функцию интегрирования входного сигнала.
е. цепь выполняет функцию интегрирования входного сигнала.
Аналогично для дифференцирующей цепи при
и (5.41)
Таблица 5
Как известно, оператор – это оператор дифференцирования. Очевидно, обратное преобразование Фурье обеих частей (5.41) дает
.
Таким образом, рассмотренные простейшие RC-цепи осуществляют соответственно приближенное интегрирование и дифференцирование входных сигналов.
В заключение отметим, что в качестве интегрирующих и дифференцирующих цепей могут выступать и RL-цепи, где реактивными элементами являются индуктивности. Схемы этих цепей также представляют собой делители напряжения, с той лишь разницей, что в интегрирующей цепи выходной сигнал снимается с резистора, а в дифференцирующей – с индуктивности.
5.5.2. Пассивные частотно-избирательные цепи
К пассивным частотно-избирательным цепям относятся колебательные контуры. Простейший колебательный контур содержит резистор R, индуктивность L и емкость C.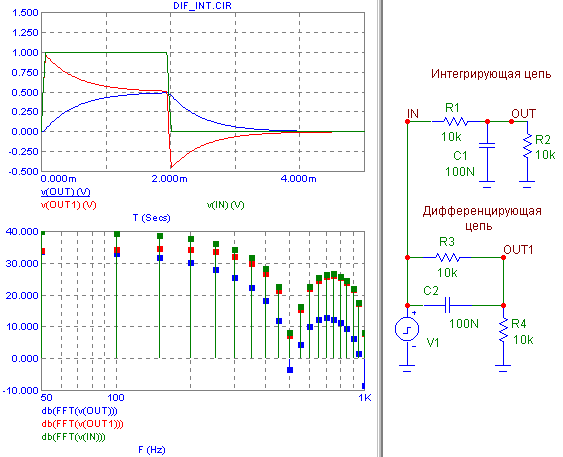 Если в контуре элементы R, L и C соединены последовательно, то такой контур называется последовательным, а если соединены параллельно – параллельным колебательным контуром.
Если в контуре элементы R, L и C соединены последовательно, то такой контур называется последовательным, а если соединены параллельно – параллельным колебательным контуром.
Рис.5.6
Один из вариантов последовательного колебательного контура изображен на рис. 5.6. Так же, как и предыдущие цепи, рассматриваемый контур можно представить как делитель напряжения. Тогда
комплексный коэффициент передачи контура
,
или с учетом того, что , и :
. (5.42)
Из этого выражения следует, что комплексный коэффициент передачи имеет максимум при
, (5.43)
т.е. последовательный колебательный контур из совокупности сигналов разных частот выделяет один, который имеет частоту . Это явление, как известно, называется резонансом, а частота – резонансной частотой.
Резонансная частота определяется из условия (5.43):
или . (5.44)
Рассмотрим основные характеристики последовательного колебательного контура.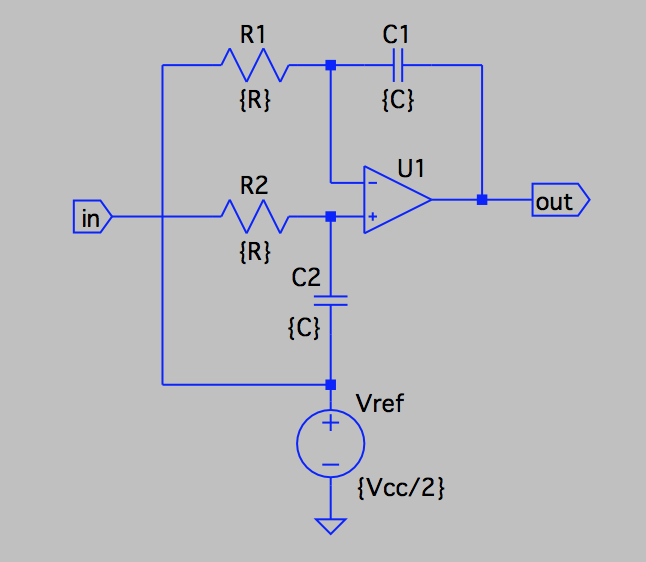
Характеристическим сопротивлением называется значение сопротивления одного из реактивных элементов (индуктивности или емкости) при резонансной частоте
. (5.45)
Добротностью контура называется отношение характеристического сопротивления к резистивному
. (5.46)
Поясним физический смысл добротности. Из (5.42) при имеем
.
Тогда с учетом (5.46) можно записать
. (5.47)
Таким образом, добротность показывает во сколько раз напряжение на индуктивности или емкости (выходной сигнал) больше, чем приложенное входное напряжение. Затуханием контура называется безразмерная величина, обратная добротности
.
Постоянная времени контура
, (5.48)
характеризует инерционность контура. Очевидно, чем больше (чем больше ), тем медленнее протекают переходные процессы в контуре.
Возвратимся к (5.42) и представим это выражение с учетом (5. 44) в виде
44) в виде
.
Обозначая
,
после несложных преобразований получим
.
Рассмотрим поведение комплексного коэффициента передачи в окрестности резонансной частоты, т.е. при . Тогда величина :
, (5.49)
где – абсолютная расстройка, представляет собой так называемую удвоенную относительную расстройку. С учетом этого выражение для комплексного коэффициента передачи можно представить как функцию удвоенной относительной расстройки в следующем виде
. (5.50)
Амплитудно-частотная характеристика
, (5.51)
а фазо-частотная характеристика
. (5.52)
На рис. 5.7 изображены графики АЧХ и ФЧХ рассматриваемого колебательного контура в окрестности резонансной частоты.
Рис. 5.7
Полосой пропускания контура называется диапазон частот, в пределах которого . Очевидно, равенство в этом выражении соответствует граничным частотам и полосы пропускания.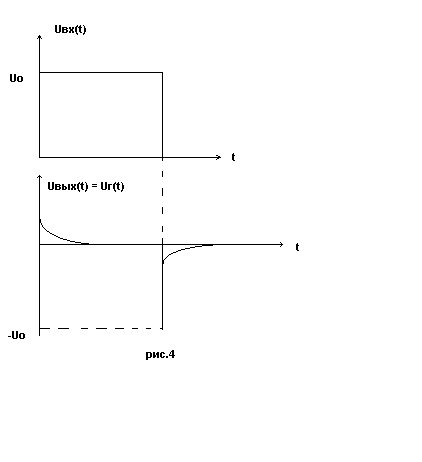 Эти частоты находятся в результате решения уравнения
Эти частоты находятся в результате решения уравнения
. (5.53)
Решение этого уравнения дает
, ,
или с учетом (5.49)
, .
Тогда полоса пропускания контура определяется по формуле
. (5.54)
В заключение составим дифференциальное уравнение последовательного колебательного контура. Напряжение, приложенное к контуру:
, (5.55)
где – напряжение на резисторе, – напряжение на индуктивности, – напряжение на конденсаторе. Но напряжение на конденсаторе является выходным сигналом . С другой стороны напряжение на резисторе , а напряжение на индуктивности . Ток, протекающий через контур, можно выразить через напряжение на конденсаторе
.
Тогда напряжение на индуктивности
,
и на резисторе
.
Подстановка этих выражений в (5.55) дает соотношение
.
Разделим обе части этого уравнения на . Тогда уравнение принимает вид
Тогда уравнение принимает вид
, (5.56)
где – коэффициент затухания.
Применив к обеим частям уравнения (5.56) преобразование Лапласа, можно получить выражение для передаточной функции
. (5.57)
Нетрудно заметить, что замена в (5.57) на приводит к выражению (5.42).
Параллельный колебательный контур представляет собой параллельное соединение , и элементов (рис. 5.8). Входным сигналом такого контура является ток , а выходным – напряжение на элементах контура. Согласно закону Ома комплексное значение напряжения на элементах контура
.
В свою очередь комплексное сопротивление есть величина, обратная комплексной проводимости. При параллельном соединении , и комплексная проводимость равна
, (5.58)
или
. (5.59)
Проводя суммирование дробей, и вычисляя обратное значение суммы, получим
. (5.60)
Как и в последовательном контуре, резонанс в параллельном колебательном контуре, как это следует из (5. 60), имеет место при условии .
60), имеет место при условии .
Характеристическое сопротивление контура описывается выражением (5.45). Что касается добротности , то в отличие от (5.46) для параллельного контура она определяется выражением
. (5.61)
Отсюда постоянная времени контура
. (5.62)
Вводя параметр и проводя аналогичные рассуждения, как и в случае последовательного контура, после несложных преобразований получим выражение для в окрестности резонансной частоты:
. (5.63)
Очевидно, амплитудно-частотная характеристика
, (5.64)
носит такой же характер, как и для последовательного контура (5.51). Поэтому график АЧХ параллельного контура совпадает по форме с кривой рис. 5.7а. Фазо-частотная характеристика имеет вид
. (5.65)
На рис. 5.9 приведен график ФЧХ параллельного контура. Полоса пропускания и граничные частоты и определяются аналогично этим же параметрами последовательного контура. При составлении дифференциального уравнения следует учесть, что входной сигнал – ток
При составлении дифференциального уравнения следует учесть, что входной сигнал – ток
, (5.66) где ; ; – токи, протекающие через соответствующие элементы, – напряжение на контуре, являющееся выходным сигналом .
Подстановка этих выражений в (5.65) дает
.
Дифференцирование левой и правой частей приводит к результату
, (5.67)
где – коэффициент затухания.
Передаточная функция параллельного контура описывается выражением
. (5.68)
5.5.3. Активные линейные цепи
Типичным примером активной цепи является усилитель, собранный на n-p-n транзисторе с общим эмиттером. Если нагрузкой усилителя служит R-цепь, то такой усилитель является апериодической активной цепью, а если нагрузкой служит колебательный контур – частотно-избирательной активной цепью.
Рис. 5.10
На рис. 5.10 представлена упрощенная принципиальная схема частотно-избирательной активной цепи.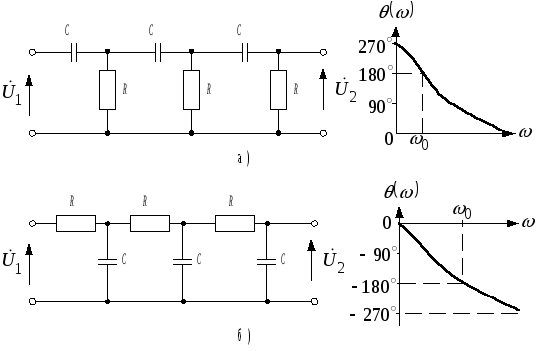 При достаточно малой амплитуде входного сигнала такую цепь можно считать линейной (линейным усилителем малых сигналов). Этот случай мы и рассмотрим.
При достаточно малой амплитуде входного сигнала такую цепь можно считать линейной (линейным усилителем малых сигналов). Этот случай мы и рассмотрим.
Для определения характеристик рассматриваемой активной цепи составим ее эквивалентную схему. Транзистор можно представить в
виде источника тока управляемого напряжением . Величина тока в этом случае составит
, (5.69)
где – крутизна характеристики транзистора (крутизна управления), имеющая размерность . Как известно, источник тока можно представить как параллельное соединение идеального источника и внутреннего сопротивления, в качестве которого выступает внутреннее сопротивление транзистора . Тогда эквивалентная схема рассматриваемой цепи принимает вид (рис. 5.11).
Рис.5.11
Так же, как и для пассивной цепи (параллельного контура) комплексный коэффициент передачи:
.
совпадает с комплексным сопротивлением . Вместе с тем, для рассматриваемой цепи комплексная проводимость определяется выражением
, (5. 70)
70)
где – эквивалентное сопротивление контура с учетом внутреннего сопротивления транзистора. Сравнение (5.70) с (5.59) показывает, что комплексный коэффициент передачи рассматриваемой цепи описывается выражением (5.60) с той лишь разницей, что вместо собственного сопротивления параллельного контура здесь выступает
. (5.71)
Очевидно, исходя из эквивалентной схемы, добротность рассматриваемого усилителя составит величину
. (5.72)
Так как , то включение параллельного контура в качестве нагрузки усилителя приводит к уменьшению его добротности, что объясняется шунтирующим свойством транзистора.
Аналогично комплексный коэффициент передачи как функция удвоенной относительной расстройки ε описывается выражением
, (5.73)
а амплитудно-частотная и фазо-частотная характеристики – соответственно выражениями:
, (5.74)
. (5.75)
Полоса пропускания рассматриваемого усилителя определяется в соответствии с (5. 54), где вместо фигурирует
54), где вместо фигурирует
. (5.76)
Очевидно, так как включение параллельного контура в качестве нагрузки усилителя приводит к уменьшению его добротности до , это в свою очередь обуславливает расширение полосы пропускания.
напряжение — Дифференциатор и интегратор — без операционного усилителя
Может кто-нибудь сказать мне, почему мы должны использовать операционные усилители для этой функции?
Вот два коротких, но исчерпывающих ответа — в первом операционный усилитель считается подключенным к источнику входного напряжения; во втором считается подключенным к конденсатору:
ОУ копирует падение напряжения VC на конденсаторе и добавляет его к входному напряжению VIN для компенсации VC; в результате ток не зависит от Vc. Копия используется как выходное напряжение; поэтому нагрузка не влияет на входной ток, поскольку он питается от отдельного источника напряжения.
Операционный усилитель служит «вспомогательным» источником напряжения VC, подключенным последовательно к конденсатору.

Но если вы все же хотите узнать всю правду о знаменитой схеме, рекомендую вам прочитать мой рассказ ниже. Я нарисовал серию из трех картинок, чтобы проиллюстрировать это.
Когда мы пытаемся улучшить схему, в какой-то момент мы сталкиваемся с противоречием . Например, в скромной RC-интегрирующей схеме ОП — рис. 1, с одной стороны, источник ввода «хочет», чтобы падение напряжения на конденсаторе было незначительным, чтобы не влиять на входной ток (как также отмечают другие комментарии) . Однако, с другой стороны, следующий этап «хочет», чтобы это напряжение было достаточно большим для правильной работы.
Рис. 1. RC-цепь, действующая как несовершенная интегрирующая цепь
В принципе, есть два способа решения противоречий схемы — через компромисс (используется условно мыслящими схемотехниками, инженерами, техниками, любителями… ) и через новую идею (используется творчески мыслящими изобретателями). Первое решение представляет собой лишь количественное улучшение, а второе — качественно новая идея, ведущая к изобретательству.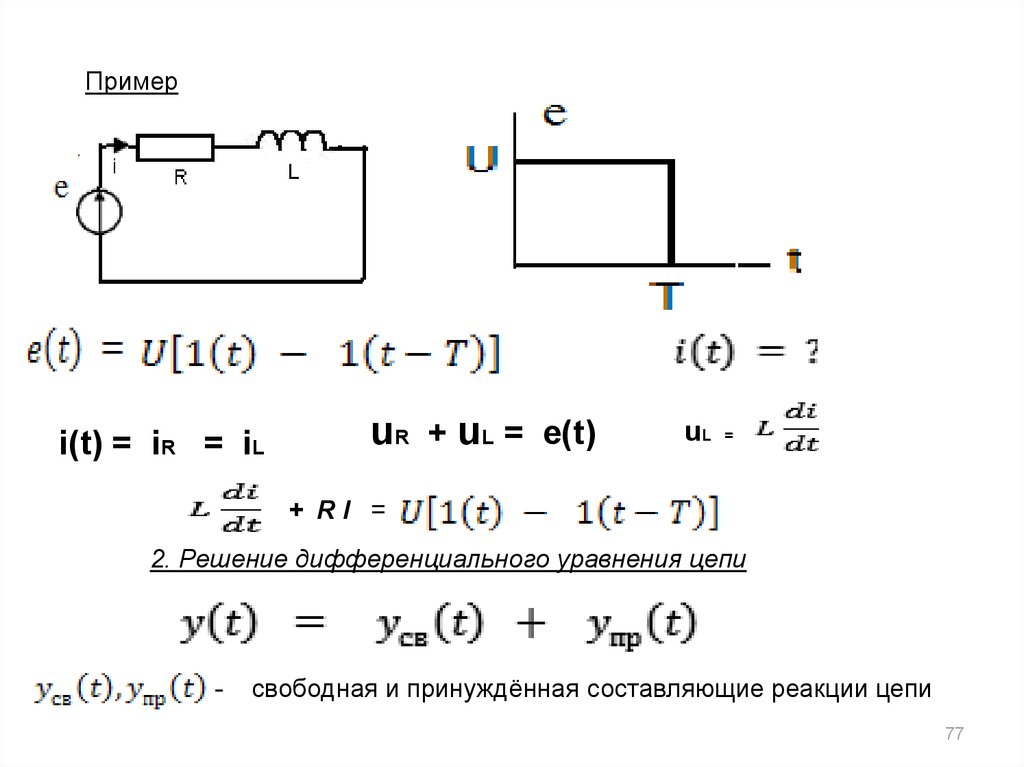 Рассмотрим два подхода в RC-интегрирующей схеме ОП.
Рассмотрим два подхода в RC-интегрирующей схеме ОП.
Компромиссное решение
Во-первых, мы можем умеренно увеличить R, C или оба (так называемая постоянная времени R.C), чтобы не допустить сильного увеличения выходного напряжения. Таким образом, мы найдем компромисс между линейностью и величиной выходного напряжения… но мы не можем ожидать большого результата.
Еще одно простое решение — значительно увеличить постоянную времени RC, а затем усилить сигнал… но это также увеличит шум. Очевидно, нужна более умная идея…
Изобретательное решение
Умная идея. Мы можем позаимствовать эту идею из жизни, где мы компенсируем убытки за счет эквивалентного дохода . В этом случае падение напряжения VC на конденсаторе является такой потерей, поскольку оно вычитается из входного напряжения VIN и в цепи остается действующее напряжение VIN — VC. Он создает постепенно уменьшающийся ток I = (VIN — VC)/R, который меньше желаемого постоянного тока I = VIN/R.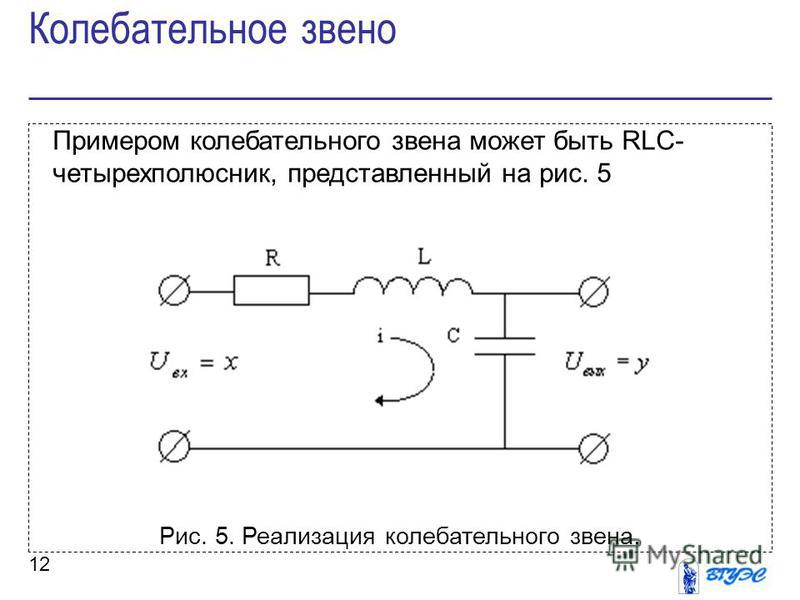
Концептуальная схема. Следуя нашей жизненной философии, мы решили компенсировать «вредное» падение напряжения VC добавлением к входному напряжению эквивалентного напряжения VC. Для этого к источнику входного напряжения последовательно и в том же направлении подключаем следующий источник напряжения — Рис. 2.
Рис. 2. Следующий источник напряжения VOA = VC последовательно добавляет свое напряжение к VIN таким образом компенсация нежелательного падения напряжения VC.
Его напряжение добавляется к VIN: таким образом, он компенсирует VC и ток не изменяется при зарядке конденсатора — I = (VIN — VC + VC)/R = VIN/R. В результате противоречие разрешается, и мы получаем идеальную линейность в сочетании с высоким выходным напряжением.
Реализация операционного усилителя. Источник компенсирующего напряжения может быть реализован повторителем с плавающим напряжением… но гениальное решение известного инвертирующего усилителя на ОУ может быть получено путем применения отрицательной обратной связи — Рис.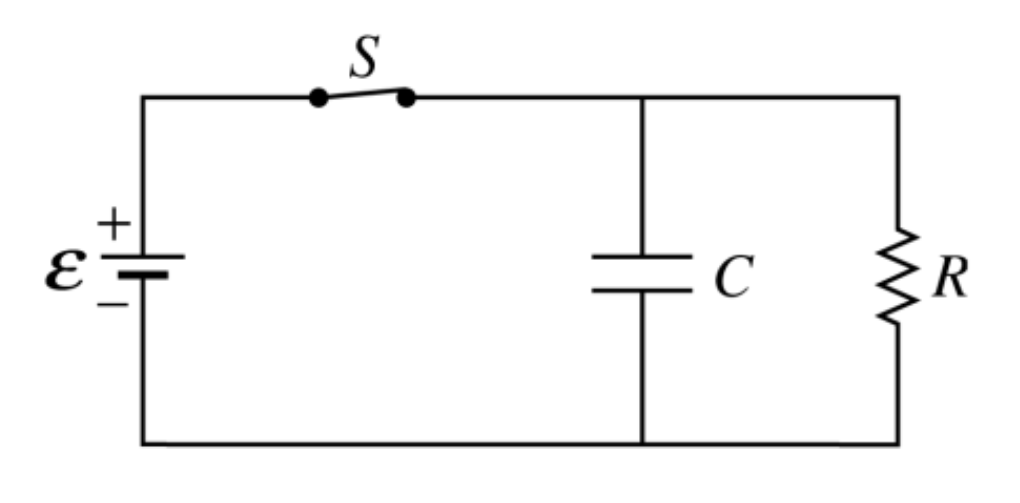 3.
3.
Рис. 3. В ОУ -выход операционного усилителя действует как источник компенсирующего напряжения (явно показан только отрицательный источник питания V-).
Здесь операционный усилитель регулирует свое выходное напряжение, чтобы сделать его равным VC, наблюдая разницу между ними на своих входах и поддерживая ее почти нулевой. Если неинвертирующий вход операционного усилителя заземлен (это не обязательно), знаменитая 9На инвертирующем входе появляется виртуальная земля 0021 .
Как вы видели выше, идея инвертирующего интегратора операционного усилителя чрезвычайно проста. Это просто усовершенствованная RC-интегральная схема , в которой дополнительный источник напряжения (наподобие маленькой регулируемой «батарейки»), вырабатывающий напряжение VC, подключен последовательно к источнику входного напряжения, чтобы помочь ему. В результате падение напряжения на резисторе R равно входному напряжению VIN, а входной ток I = VIN/R зависит только от VIN.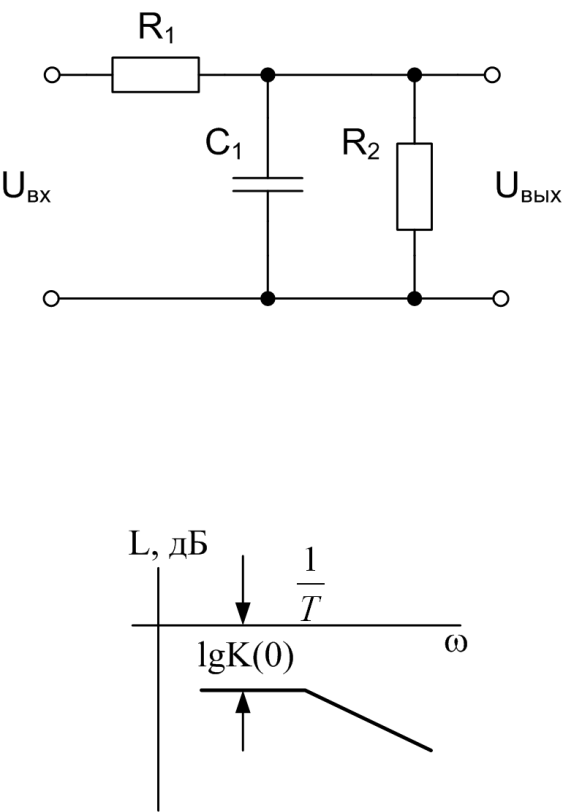
В завершение своего рассказа хочу поделиться интересным психологическим феноменом — на что способны люди во имя непринятия чужой идеи… какой бы простой она ни была… только потому, что она ничья, а чье-то… Чтобы проиллюстрировать это, я расположил в хронологическом порядке основные материалы, которые я опубликовал, посвященные этой простой, но умной идее.
Первые догадки об этой идее возникли в моей голове еще в конце 80-х, а ясно стало в 1992, когда я набросал его на листе формата А5 и добавил в свою коллекцию схемных идей…
Пожелтевший лист из моего архива идей — на болгарском языке. Переведенный текст: (дата 07.05.92) Заголовок: Активный интегратор с объяснением «антивольтаж». Объяснение: Операционный усилитель создает «анти-напряжение» и подает его последовательно на Uc. В результате ток I в цепи (через С) постоянен и равен I = E/R. Конденсатор заряжен линейно (Uc).
Меня интересовала не сама идея, какой бы умной она ни была, а вывод универсальных принципов преобразования несовершенных пассивных схем в совершенные схемы операционных усилителей. мне удалось это сделать в 1997 на университетской конференции Электроника’97 с моим материалом Как преобразовать пассивные схемы в активные и с тех пор продвигаю его.
мне удалось это сделать в 1997 на университетской конференции Электроника’97 с моим материалом Как преобразовать пассивные схемы в активные и с тех пор продвигаю его.
В 2001 году мы с моими студентами провели в лаборатории очень интересный эксперимент с использованием «управляемого человеком операционного усилителя» (мы сделали его с помощью батарейки и потенциометра). Мы выбрали большую постоянную времени (C = 1000 мкФ, R = 10 кОм), чтобы напряжение на конденсаторе медленно возрастало. Один из студентов медленно двигал движок потенциометра в противоположном направлении, чтобы поддерживать нулевое напряжение на 9.0021 виртуальная земля . В результате напряжение на потенциометре изменялось линейно. К сожалению, я сделал только одну фотографию плохого качества, где детали плохо видны.
В 2004 году я включил эту идею в свой веб-курс по базовой электронике.
Чтобы сделать его более привлекательным, в 2004 году я создал интерактивный конструктор схем, основанный на этом принципе: рассказы на доске на моем сайте Circuit fantasia и посвятил этому принципу несколько рассказов:
Как построить RC-интегратор на операционном усилителе?
Генератор рампы
В 2008 году я провел свой очередной веб-дидактический эксперимент, загрузив лабораторные занятия с участием моих учеников в викибук Circuit Idea. Вот моя история об интеграторе:
Вот моя история об интеграторе:
Как сделать идеальный RC-интегратор
В 2009 году я обобщил этот принцип в философию всех схем инвертирования операционных усилителей и создал викиучебник по компенсации напряжения. На странице обсуждения я рассказал историю этой идеи.
В 2010 году мне удалось объединить этот принцип с противоположным бутстрэппингом и обобщить их с помощью теоремы Миллера из Википедии:
Теорема Миллера
форумы в том числе SE EE. Вот некоторые из моих материалов:
2011 Какова цель операционного усилителя в схеме интегратора? — СЭ ЕЕ
2013 Можем ли мы виртуально увеличить емкость до бесконечности? — Исследовательские ворота
2015 Мое понимание RC-цепей нарушено — SE EE
2020 Как работает интегратор операционных усилителей? — ГП ЕЕ
2020 Зарядка конденсатора в RC-цепи — SE EE
2021 Что делает конденсатор? — SE EE
… до сих пор… всего 30 лет…
И как вы думаете, что получилось?
То же, что и здесь, в комментариях и чатах под этим вопросом. .. и каким он будет после моей очередной попытки показать насколько проста идея интегратора ОУ… и всех инвертирующих схем с отрицательный отзыв — просто маленькая «батарейка» последовательно с конденсатором …
.. и каким он будет после моей очередной попытки показать насколько проста идея интегратора ОУ… и всех инвертирующих схем с отрицательный отзыв — просто маленькая «батарейка» последовательно с конденсатором …
Дифференциальная схема. дифференцирующая цепь. Условия дифференцирования и интегрирования
Дифференцирующие цепи применяют, когда требуется преобразовать напряжение заданной формы в сигнал ip, изменяющийся по закону
где — коэффициент пропорциональности.
Простейшая дифференцирующая RC-цепь аналогична интегрирующей RC-цепи и отличается только тем, что выходное напряжение снимается не с конденсатора, а с активного сопротивления (рис. 6.19)., а). Напряжение на его выходе
Напряжение конденсатора.
Если т. е. -цепь успешно выполняет дифференцирование только в этом случае.
Оценим приближенно погрешность, вносимую членом , для чего продифференцируем выражение для , приняв
Подставляя (6. 98) в (6.96), получаем необходимо, чтобы
98) в (6.96), получаем необходимо, чтобы
(6.100)
т. е. необходимо уменьшить постоянную времени -цепи). Это требование противоположно требованию к интегрирующей схеме, где постоянная времени была увеличена для точного интегрирования.
Выходной сигнал в дифференцирующей цепи, как и в интегрирующей, уменьшается с увеличением точности соответствующего преобразования. Действительно, уменьшение постоянной времени в дифференцирующей цепи приводит к уменьшению члена, что вызывает ошибку дифференцирования. При этом уровень выходного сигнала уменьшается пропорционально уменьшению .
При дифференцировании наибольшая ошибка получается во время нарастания (или среза) импульса. Это связано с тем, что при этих процессах наибольшее значение имеет вторая производная, выражающая скорость изменения крутизны фронта (или среза).
Наименьшая ошибка возникает в те интервалы времени, в которых скорость изменения входного напряжения постоянна.
Рис. 6.19. Дифференциальная цепь (а) и диаграммы изменения напряжения на отдельных ее участках (б, в, г)
Дифференциальная цепь (а) и диаграммы изменения напряжения на отдельных ее участках (б, в, г)
Выясним возможности и условия дифференциации — по схеме синусоидального изменяющегося напряжения.
При точном дифференцировании этот сигнал должен изменяться по закону
(6.101)
Таким образом, выходное напряжение должно быть сдвинуто по фазе на 90° относительно входного. В реальной RC-цепи амплитуда и фаза отличаются от соответствующих значений идеальной дифференцирующей цепи. Выходное напряжение
и фазовый угол
(6.103)
Для того, чтобы можно было дифференцировать синусоидально изменяющееся напряжение с частотой , необходимо выполнить условие Однако это также уменьшает значение выходного сигнала. Поэтому приходится ограничиваться компромиссным решением, при котором выходной сигнал и фазовая ошибка не выходят за допустимые значения.
Если, например, принять , то фазовая ошибка дифференцирования составит 14°. Такие фазовые искажения выходного сигнала можно считать допустимыми в ряде общих приложений. В этом случае значение выходного сигнала мало зависит от , так как да 1, поэтому его можно считать близким к теоретическому.
В этом случае значение выходного сигнала мало зависит от , так как да 1, поэтому его можно считать близким к теоретическому.
При дифференциации импульса активная ширина его спектра ограничивается частотой. Если неравенство выполняется при , то оно обязательно будет выполнено и при . Это позволяет на основе активной ширины спектра определить требования к постоянной времени дифференцирующей цепи:
Для грубой оценки активной ширины спектра при равных длительностях нарастания и спада импульса можно использовать приближенное выражение
(6.105)
где для импульсов, для которых , т. е. для наиболее часто встречающихся.
Тогда, подставив в (6.104) значение , получим
Таким образом, постоянная времени дифференцирующей схемы общего назначения должна быть примерно в десять раз меньше активного времени нарастания дифференцируемого импульса.
При дифференциации однополярного импульса на выходе дифференцирующей цепи формируется двухполярный импульс. Поэтому длительность импульса выходного напряжения любой одной полярности меньше длительности дифференцируемого импульса, и рассматриваемая схема обеспечивает операцию укорочения.
Поэтому длительность импульса выходного напряжения любой одной полярности меньше длительности дифференцируемого импульса, и рассматриваемая схема обеспечивает операцию укорочения.
Пусть на вход RC-цепи (рис. 6.19, а) действует идеальный прямоугольный импульс, который поступает в момент времени (рис. ). При этом конденсатор С начинает заряжаться и напряжение на нем изменяется по закону
Зарядный ток, протекающий через сопротивление R, создает на выходе RC-цепи экспоненциальный импульс положительной полярности, который полностью затухает до конец входного импульса. После окончания входного импульса достигнутое равновесие в цепи нарушается. Происходит разряд конденсатора через резистор R и источник импульсов. Выходной импульс отрицательной полярности, возникающий при разряде конденсатора, отличается от рассмотренного только полярностью.
Таким образом, при укорочении прямоугольного импульса на выходе схемы получаются экспоненциальные импульсы напряжения положительной и отрицательной полярности, высота которых равна высоте входных импульсов. Длительность выходных импульсов определяется постоянной времени. Если измеряется на уровне , то определяется из выражения
Длительность выходных импульсов определяется постоянной времени. Если измеряется на уровне , то определяется из выражения
Иногда длительность активного импульса измеряется на уровне:
Постоянная времени дифференцирующей цепи при укорочении импульсов выбирается значительно больше, чем при выполнении операции точного дифференцирования.
Его значение находится исходя из требуемой длительности активного импульса, заданной на уровне .
В реальных случаях приходится учитывать внутреннее сопротивление источника, к которому подключается рассматриваемая цепь (рис. 6.20, и). При этом характер процессов в -цепи не меняется. Однако увеличение активного сопротивления цепи приводит к увеличению постоянной времени. Это ограничивает возможность получения коротких импульсов. Кроме того, уменьшаются зарядный и разрядный токи i конденсатора, что приводит к уменьшению выходного напряжения. Максимальное значение выходного напряжения находится из уравнения
Во многих радиоустройствах используются простые схемы, выполняющие функцию дифференцирования или интегрирования входного сигнала, либо преобразования спектрального состава этого сигнала. Цепи первого типа называются соответственно дифференцирующими и интегрирующими , а цепи второго типа называются фильтрами . К фильтрам относятся схемы, которые могут пропускать только сигналы определенного частотного диапазона, и не пропускать (существенно ослаблять) сигналы, не принадлежащие этому диапазону. Если схема пропускает все сигналы с частотами меньше некоторой граничной частоты f гр, то она называется фильтр нижних частот (ФНЧ). Цепь, пропускающая почти без затухания все сигналы с частотами выше определенной частоты среза f gr, называется фильтром верхних частот (ФВЧ) ) . Помимо них существуют еще фильтры, пропускающие только сигналы, принадлежащие определенному частотному диапазону от f gr1 до f gr2, и ослабляющие сигналы всех частот ff gr2. Такие фильтры называются полосовыми (ПФ). Фильтры, пропускающие сигналы всех частот, кроме заданного диапазона, ограниченного частотами f gr1 и f gr2, называются ректор (шквал).
Цепи первого типа называются соответственно дифференцирующими и интегрирующими , а цепи второго типа называются фильтрами . К фильтрам относятся схемы, которые могут пропускать только сигналы определенного частотного диапазона, и не пропускать (существенно ослаблять) сигналы, не принадлежащие этому диапазону. Если схема пропускает все сигналы с частотами меньше некоторой граничной частоты f гр, то она называется фильтр нижних частот (ФНЧ). Цепь, пропускающая почти без затухания все сигналы с частотами выше определенной частоты среза f gr, называется фильтром верхних частот (ФВЧ) ) . Помимо них существуют еще фильтры, пропускающие только сигналы, принадлежащие определенному частотному диапазону от f gr1 до f gr2, и ослабляющие сигналы всех частот ff gr2. Такие фильтры называются полосовыми (ПФ). Фильтры, пропускающие сигналы всех частот, кроме заданного диапазона, ограниченного частотами f gr1 и f gr2, называются ректор (шквал).
На рис. 3. показаны простейшие дифференцирующие схемы.
3. показаны простейшие дифференцирующие схемы.
Коэффициент передачи схемы на рис. 3, а равен:
Обозначим: а (2.4)
Тогда (2.3.) можно переписать:
(2.5)
Модуль коэффициента передачи напряжения:
(2.6)
При частоте активное сопротивление цепи R и реактивное равны и , (2.7)
т.е. на этой частоте выходное напряжение по модулю меньше входного напряжения.
Для схемы на рис. 3б аналогично можно получить:
(2.8)
Обозначая или , (2.9)
Выражение (2.8.) приводится к виду:
,
что полностью совпадает с (2.5.). Поэтому модуль коэффициента передачи напряжения также будет определяться соотношением (2.6). При частоте, определяемой (2.9), активное и реактивное сопротивления цепи также будут равны, поэтому справедливо и соотношение (2.7).
Преобразуем выражение (2.5):
(2.10)
Комплексный коэффициент передачи напряжения определяет отношение не только амплитуд входного и выходного напряжений по формуле (2.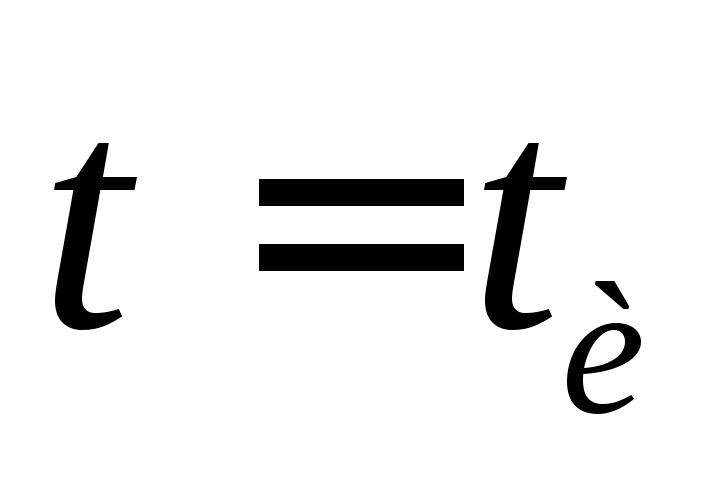 6), но и фазовый сдвиг между ними. Из (2.10) очевидно, что откуда
6), но и фазовый сдвиг между ними. Из (2.10) очевидно, что откуда
Выражение (2.6.) определяет амплитудно-частотную характеристику (АЧХ), а (2.11.) — фазо-частотную характеристику (PFC) дифференциальные цепи. Вид этих характеристик показан на рис.4.
На частотах, как следует из рис. 5, представляющего собой частотную зависимость активного и реактивного сопротивлений цепи,
,
и так можно определить ток в цепи
Выходное напряжение при это условие будет
(2.12)
Соотношение (2.12) показывает, что схема на рис. 3а действительно выполняет функцию дифференцирования входного напряжения при выполнении условия.
В дифференцирующей цепи (рис. 11.2, а) постоянная времени должна быть малой по сравнению с длительностью импульса. Эта схема используется в тех случаях, когда импульсы относительно большой длительности должны быть преобразованы в короткие импульсы запуска с крутым фронтом. Схема удерживает крутой фронт импульса в той же полярности и по существу ведет себя как фильтр верхних частот, ослабляя низкочастотные составляющие импульса и пропуская высокочастотные составляющие импульса.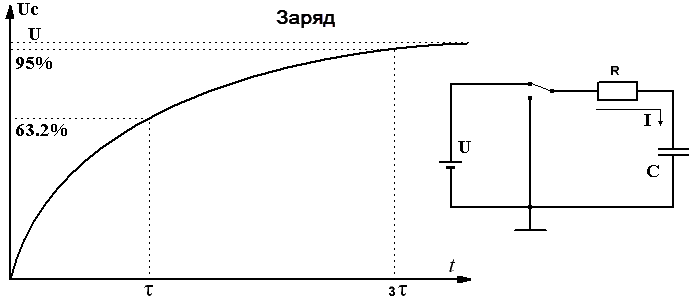
Когда к конденсатору приложено напряжение, ток, протекающий через него, пропорционален производной напряжения, приложенного к конденсатору e с:
(11.4)
При малой постоянной времени сопротивление резистора намного больше реактивного сопротивления конденсатора. Следовательно, выходное напряжение, равное падению напряжения на резисторе, приблизительно выражается формулой
(11.5)
На рис. 11.2.6 и в показаны формы импульсов на входе и выходе дифференцирующей цепи соответственно. С начального момента импульса и на протяжении всей его длительности на вход схемы подается постоянное напряжение. Если конденсатор Ci не был заряжен в момент подачи входного импульса, то в первый момент через конденсатор, как и через резистор R1, будет протекать большой ток. Таким образом, на резисторе сразу появляется большое падение напряжения, из-за чего фронт импульса на выходе нарастает очень быстро (рис. 11.2, в). По мере зарядки конденсатора ток, протекающий через него, уменьшается со скоростью, зависящей от постоянной времени цепи. При малой постоянной времени конденсатор быстро заряжается и ток по цепи перестает течь. Таким образом, при полном заряде конденсатора напряжение на резисторе Р 1 падает до нуля. В конце импульса входное напряжение падает до нуля, и конденсатор начинает разряжаться. Ток разрядки конденсатора имеет противоположное направление по сравнению с током заряда, поэтому направление тока через резистор также противоположно току заряда. Поэтому на выходе теперь появится отрицательный всплеск напряжения.
При малой постоянной времени конденсатор быстро заряжается и ток по цепи перестает течь. Таким образом, при полном заряде конденсатора напряжение на резисторе Р 1 падает до нуля. В конце импульса входное напряжение падает до нуля, и конденсатор начинает разряжаться. Ток разрядки конденсатора имеет противоположное направление по сравнению с током заряда, поэтому направление тока через резистор также противоположно току заряда. Поэтому на выходе теперь появится отрицательный всплеск напряжения.
Рис. 11.2. Дифференциальная схема (а) и форма входного импульса (б) и выход (в) цепи.
На практике на вход дифференцирующей цепи обычно подаются импульсы. Если на вход дифференцирующей цепи подать синусоидальные колебания, то их форма не изменится, но сместится фаза выходного колебания и уменьшится амплитуда этих колебаний на величины, зависящие от частоты входного сигнала . Другой тип дифференцирующей цепи можно получить, заменив С 1 резистором, а R 1 индуктивностью.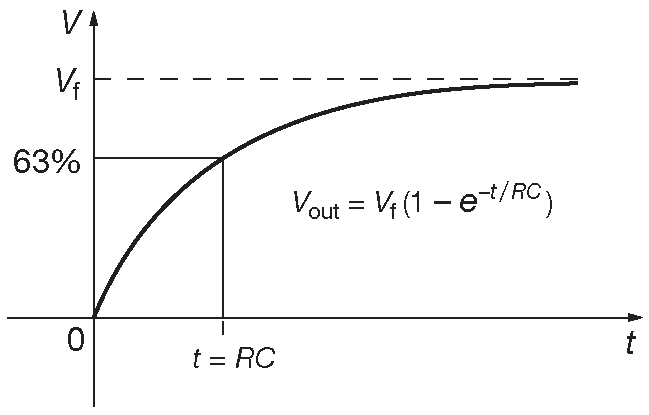 В такой схеме фактором, определяющим качество дифференциации, также является постоянная времени. Как и в интегрирующей схеме, омическое сопротивление катушки индуктивности ухудшает характеристики схемы. Поэтому такая цепочка используется довольно редко.
В такой схеме фактором, определяющим качество дифференциации, также является постоянная времени. Как и в интегрирующей схеме, омическое сопротивление катушки индуктивности ухудшает характеристики схемы. Поэтому такая цепочка используется довольно редко.
Сложные электронные устройства состоят из простых схем. Рассмотрим цепь, состоящую из последовательно соединенных резистора и конденсатора с генератором идеального напряжения, показанного на рис. 3.3.
Рис.3.3. Цепь дифференцирующая
Если выходное напряжение снимается с резистора, то схема называется дифференцирующей, если с конденсатора — интегрирующей. Эти линейные цепи характеризуются стационарными и переходными характеристиками. Это связано с тем, что изменение величины действующего в цепи напряжения приводит к тому, что токи и напряжения на разных участках цепи приобретают новые значения. Изменение состояния цепи происходит не мгновенно, а через определенный промежуток времени. Поэтому различают стационарное состояние и переходное состояние электрической цепи.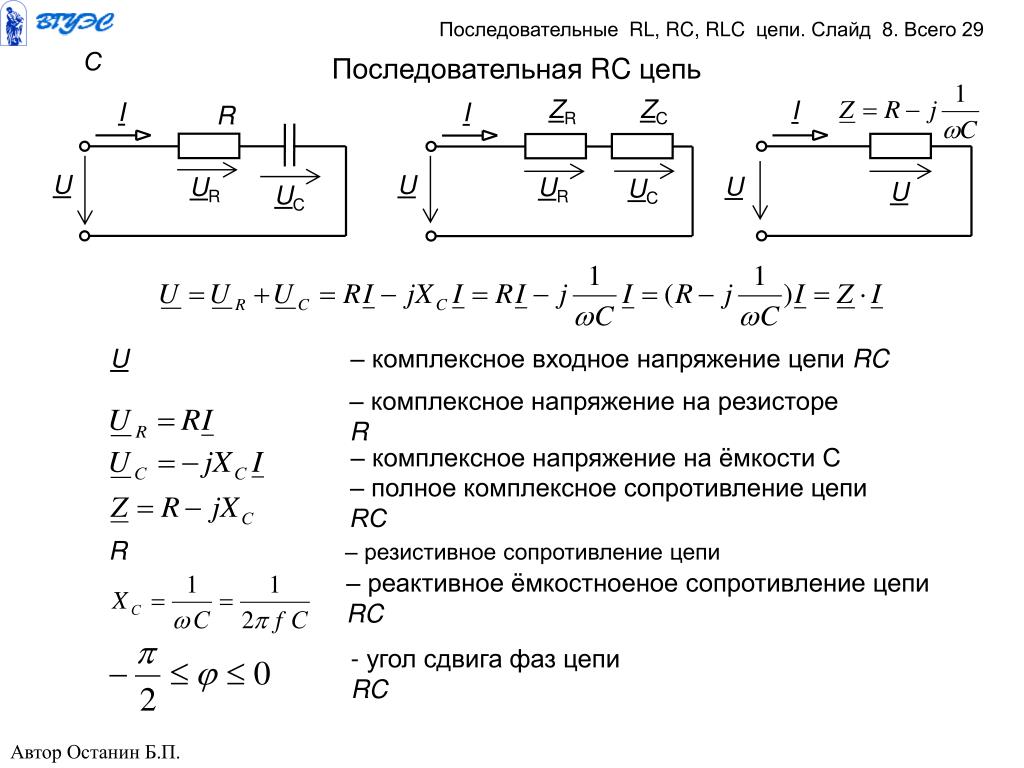
Электрические процессы считаются установившимися (стационарными), если закон изменения всех напряжений и токов совпадает, с точностью до постоянных значений, с законом изменения напряжения, действующего в цепи от внешнего источника. В противном случае цепь считается находящейся в переходном (нестационарном) состоянии.
Стационарные характеристики включают амплитудно-частотную и фазовую характеристики линейной цепи.
Нестационарное состояние линейной цепи описывается переходной характеристикой.
Предположим, что на вход схемы подключен генератор идеального напряжения. На основании второго закона Кирхгофа для дифференцирующей цепи можно написать дифференциальное уравнение, связывающее напряжение и ток в ветвях цепи:
(3.2)
Так как напряжение на выходе цепи, то:
( 3.3)
Подставив значение тока в интеграл, получим:
(3.4)
Продифференцируем левую и правую части последнего уравнения по времени:
(3.5)
Перепишем это уравнение в следующем виде:
, (3. 6)
6)
Где = – параметр цепи, называемый постоянной времени цепи.
В зависимости от значения постоянной времени возможны два различных соотношения между первым и вторым членами в правой части уравнения.
Если постоянная времени велика по сравнению с периодом гармонических сигналов >> или с длительностью импульсов >>, которые можно подать на вход этой схемы, то
А напряжение на выходе схемы повторяет входное напряжение с небольшим искажением:
Если постоянная времени мала по сравнению с периодом гармонических сигналов
Отсюда выходное напряжение равно:
Таким образом, в зависимости от значения постоянной времени такая схема может либо передавать входной сигнал на выход с определенными искажениями, либо дифференцировать его с определенной степенью точности. В этом случае форма выходного сигнала будет другой. Ниже на рис. 3.4 показано входное напряжение, напряжение на резисторе и конденсаторе для случаев, когда постоянная времени велика, а постоянная времени мала.
НО Б
Рис. 3.4. Напряжения на элементах дифференцирующей цепи при ( А ) и ( Б )
В начальный момент времени на резисторе появляется скачок напряжения, равный амплитуде входного сигнала, а затем конденсатор начинает заряжаться, при этом напряжение на резисторе будет уменьшаться.
При постоянной времени конденсатор не успевает зарядиться до амплитуды входного импульса и схема передает входной сигнал на выход с небольшим искажением. В
Теперь определим коэффициент передачи дифференцирующей цепи. Комплексный коэффициент передачи дифференцирующей цепи при подаче на вход гармонического сигнала равен:
. (3.11)
Обозначим соотношение , где – частота среза полосы пропускания дифференцирующего контура.
Выражение для коэффициента передачи примет вид:
Модуль коэффициента передачи равен:
. (3.13)
— частота среза полосы пропускания, при которой модуль реактивного сопротивления становится равным значению активного сопротивления, а коэффициент передачи контура равен .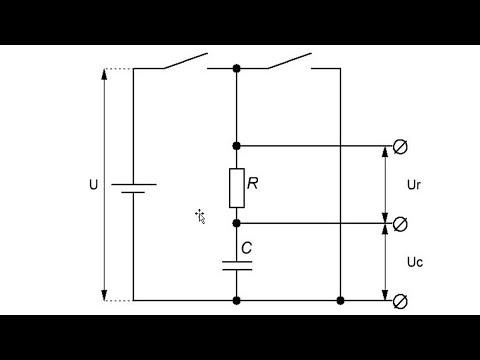 Зависимость модуля коэффициента передачи от частоты называется амплитудно-частотной характеристикой (АЧХ).
Зависимость модуля коэффициента передачи от частоты называется амплитудно-частотной характеристикой (АЧХ).
Зависимость фазового угла между выходным и входным напряжениями от частоты называется фазовой характеристикой (ФЧХ). Фазовая характеристика:
Ниже на рис. 3.5 приведены АЧХ и ФЧХ дифференцирующей цепи:
Рис. 3.5. Амплитудно-частотная и фазовая характеристики
Дифференциальная цепь
Из амплитудно-частотной характеристики видно, что прохождение сигналов через дифференцирующую цепь сопровождается уменьшением амплитуд низкочастотных составляющих ее спектра . Цепь дифференциатора представляет собой фильтр верхних частот.
Из фазовой характеристики видно, что фазы низкочастотных составляющих сдвинуты на больший угол, чем фазы высокочастотных составляющих.
Переходную характеристику дифференцирующей цепи можно получить, подав на вход напряжение в виде одиночного скачка. Комплексный коэффициент усиления
Дифференциальные цепи — схемы, в которых выходное напряжение пропорционально производной входного напряжения. Эти схемы решают две основные задачи преобразования сигналов: получение импульсов очень малой длительности (укорочение импульсов), которые используются для запуска управляемых преобразователей электрической энергии, триггеров, одиночных вибраторов и других устройств; выполнение математической операции дифференцирования (получение производной по времени) сложных функций, заданных в виде электрических сигналов, что часто встречается в вычислительной технике, аппаратуре автоматического управления и т. д.
Эти схемы решают две основные задачи преобразования сигналов: получение импульсов очень малой длительности (укорочение импульсов), которые используются для запуска управляемых преобразователей электрической энергии, триггеров, одиночных вибраторов и других устройств; выполнение математической операции дифференцирования (получение производной по времени) сложных функций, заданных в виде электрических сигналов, что часто встречается в вычислительной технике, аппаратуре автоматического управления и т. д.
Схема емкостной дифференцирующей цепи показана на рис. 1. Входное напряжение прикладывается ко всей цепи, а выходное напряжение снимается с резистора R. Ток, протекающий через конденсатор, связан с напряжением на нем известным соотношением i C = C (dU C / dt ). Учитывая, что через резистор R протекает такой же ток, запишем выходное напряжение
Если U ВЫХОД
Значение t = RC называется постоянной времени цепи. Из курса электричества известно, что конденсатор заряжается (разряжается) через резистор по экспоненциальному закону. Через промежуток времени t = t = RC конденсатор заряжается на 63 % от приложенного входного напряжения, через t = 2,3 t — до 90 % U IN и после 4,6 т — до 99 % U IN.
Через промежуток времени t = t = RC конденсатор заряжается на 63 % от приложенного входного напряжения, через t = 2,3 t — до 90 % U IN и после 4,6 т — до 99 % U IN.
Пусть на вход дифференцирующей цепи (рис. 1) (рис. 2, а) подан прямоугольный импульс длительностью t I . Пусть t ˆ = 10 т. Выходной сигнал при этом будет иметь вид, показанный на рис. 2, г. Ведь в начальный момент времени напряжение на конденсаторе равно нулю и мгновенно измениться не может. Поэтому все входное напряжение подается на резистор. Затем конденсатор заряжается экспоненциально уменьшающимся током. При этом напряжение на конденсаторе увеличивается, а напряжение на резисторе уменьшается так, что в каждый момент времени выполняется равенство U ВХ = U С + U ВЫХ. Через промежуток времени t ³ 3 t конденсатор зарядится почти до входного напряжения, зарядный ток прекратится и выходное напряжение станет равным нулю.
Когда входной импульс закончится (U ВХ = 0), конденсатор начнет разряжаться через резистор R и входную цепь.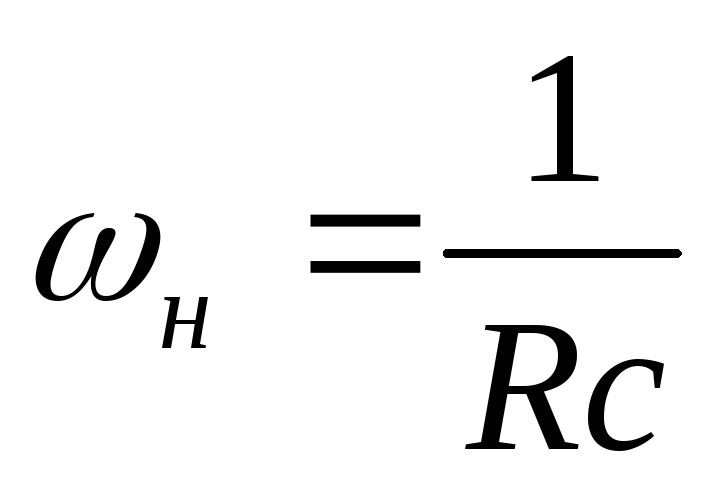 Направление разрядного тока противоположно направлению зарядного тока, поэтому полярность напряжения на резисторе обратная. По мере разрядки конденсатора напряжение на нем уменьшается, а вместе с ним уменьшается и напряжение на резисторе R. В результате получаются укороченные импульсы (при t ˆ > 4¸5 RC). Изменение формы импульса при других соотношениях длительности импульса и постоянной времени показано на рис. 2б, в.
Направление разрядного тока противоположно направлению зарядного тока, поэтому полярность напряжения на резисторе обратная. По мере разрядки конденсатора напряжение на нем уменьшается, а вместе с ним уменьшается и напряжение на резисторе R. В результате получаются укороченные импульсы (при t ˆ > 4¸5 RC). Изменение формы импульса при других соотношениях длительности импульса и постоянной времени показано на рис. 2б, в.
Интегральная схема Схема, выходное напряжение которой пропорционально интегралу входного напряжения по времени. Интегрирующие схемы (рис. 3) отличаются от дифференцирующих схем (рис. 1) тем, что выходное напряжение снимается с конденсатора. Когда напряжение на конденсаторе C пренебрежимо мало по сравнению с напряжением на резисторе R, т. е. U OUT = U C
Применение операционного усилителя в качестве схемы дифференциатора
В этом учебном пособии мы изучим работу и реализацию операционного усилителя в качестве дифференциатора или усилителя-дифференциатора.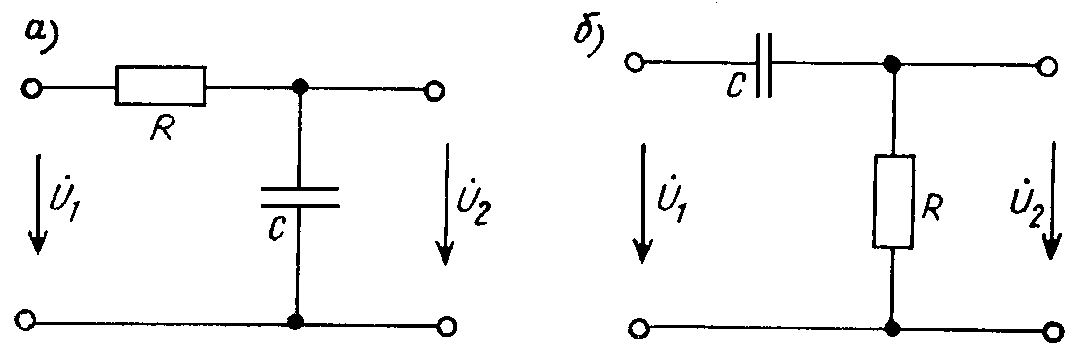 Усилитель-дифференциатор может быть пассивным или активным в зависимости от компонентов, используемых в его конструкции. Настройка операционного усилителя в качестве дифференциатора или усилителя-дифференциатора в основном использует операционный усилитель в качестве фильтра верхних частот и используется в схемах формирования волны, частотных модуляторах и т. д.
Усилитель-дифференциатор может быть пассивным или активным в зависимости от компонентов, используемых в его конструкции. Настройка операционного усилителя в качестве дифференциатора или усилителя-дифференциатора в основном использует операционный усилитель в качестве фильтра верхних частот и используется в схемах формирования волны, частотных модуляторах и т. д.
Мы уже обсуждали операционный усилитель в качестве интегратора в другом руководстве, где мы узнали, как настроить операционный усилитель в качестве интегратора. Здесь мы проведем аналогичный анализ, но на этот раз для операционного усилителя в качестве дифференциатора.
Для получения дополнительной информации о высокочастотных пассивных фильтрах см. «Пассивные высокочастотные RC-фильтры» и «Активный высокочастотный фильтр». Вы можете найти основы операционных усилителей в разделе «Основы операционных усилителей».
Контур
Введение
Дифференциатор на операционном усилителе или дифференцирующий усилитель представляет собой схему, обратную схеме интегратора. Он создает выходной сигнал, мгновенная амплитуда которого пропорциональна скорости изменения приложенного входного напряжения.
Он создает выходной сигнал, мгновенная амплитуда которого пропорциональна скорости изменения приложенного входного напряжения.
Математически говоря, выходной сигнал Дифференциатора является первой производной входного сигнала. Например, если входной сигнал является пилообразным, то выход схемы с операционным усилителем в качестве дифференциатора будет простым постоянным током (поскольку скорость изменения линейно изменяющегося сигнала постоянна). Точно так же, если входной сигнал является синусоидой, то выходной сигнал также является синусоидой, но с разностью фаз 90 0 .
[адсенс1]
Дифференциатор только с RC-цепью называется пассивным дифференциатором, тогда как дифференциатор с активными компонентами схемы, такими как транзисторы и операционные усилители, называется активным дифференциатором. Активные дифференциаторы имеют более высокое выходное напряжение и гораздо меньшее выходное сопротивление, чем простые RC-дифференциаторы.
Дифференциатор на операционном усилителе — это инвертирующий усилитель, в котором последовательно с входным напряжением используется конденсатор. Дифференциальные цепи обычно разрабатываются так, чтобы реагировать на треугольные и прямоугольные входные сигналы.
Дифференциаторы имеют ограничения по частоте при работе с синусоидальными входами; схема ослабляет все низкочастотные компоненты сигнала и пропускает на выходе только высокочастотные компоненты. Другими словами, схема ведет себя как фильтр верхних частот.
Идеальная схема дифференциального операционного усилителя
Дифференцирующий усилитель на операционном усилителе использует конденсатор, включенный последовательно с источником входного напряжения, как показано на рисунке ниже.
Для входа постоянного тока входной конденсатор C 1 после достижения своего потенциала не может принимать никаких зарядов и ведет себя как разомкнутая цепь. Неинвертирующий вход ОУ подключен к земле через резистор R comp , обеспечивающий компенсацию входного смещения, а инвертирующий вход подключен к выходу через резистор обратной связи R f .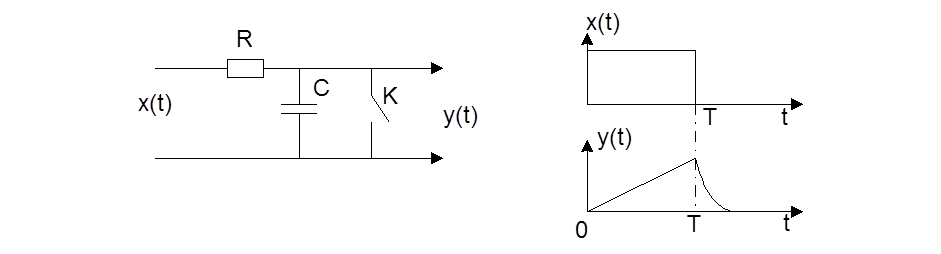
Таким образом, схема ведет себя как повторитель напряжения.
[адсенс2]
Когда на вход подается положительное напряжение, ток I протекает через конденсатор C 1 , как показано на рисунке. Поскольку ток, протекающий во внутреннюю цепь операционного усилителя, равен нулю, фактически весь ток I протекает через резистор R f . Выходное напряжение равно
В вых = – (I * R f )
Здесь это выходное напряжение прямо пропорционально скорости изменения входного напряжения.
На рисунке узел «X» практически заземлен, а узел «Y» также имеет потенциал земли, т. е. В X = V Y = 0 .
Со стороны входа ток I может быть представлен следующим образом: ) / дт}
Со стороны выхода ток I определяется как:
Приравняв два приведенных выше уравнения тока, получим:
C 1 {d(V в ) / dt} = -V из / R f
V вых = -C 1 R f {d(V в ) / dt}
Вышеприведенное уравнение показывает, что выход C 1 R f умножает на дифференцирование входного напряжения. Произведение C 1 R f называется постоянной времени RC цепи дифференциатора. Отрицательный знак указывает, что выход не совпадает по фазе на 180 0 по отношению к входу.
Произведение C 1 R f называется постоянной времени RC цепи дифференциатора. Отрицательный знак указывает, что выход не совпадает по фазе на 180 0 по отношению к входу.
Основным преимуществом такой схемы активного дифференцирующего усилителя является малая постоянная времени, необходимая для дифференцирования.
Входные и выходные сигналы
Теперь посмотрим на выходные сигналы для различных входных сигналов. Когда ступенчатый входной сигнал (уровень постоянного тока) с амплитудой V m подается на дифференциатор операционного усилителя, выходной сигнал может быть математически выражен как V м ) / dt}
Для простоты предположим, что произведение C 1 R f равно единице.
Следовательно, V out = 0, поскольку амплитуда V m постоянна и d(V m ) / dt = 0,
конечное количество времени, чтобы подняться от 0 вольт до V m вольт. Следовательно, выходные данные выглядят как пик в момент времени t = 0, как показано на рисунке ниже.
Следовательно, выходные данные выглядят как пик в момент времени t = 0, как показано на рисунке ниже.
Если входной сигнал дифференциатора изменить на меандр, выходной сигнал будет состоять из положительных и отрицательных пиков, соответствующих зарядке и разрядке конденсатора, как показано на рисунке ниже.
Для входного синусоидального сигнала, который математически представляется как V (t) = V m sin ωt, где V m — амплитуда входного сигнала, а t — период, выходной сигнал дифференциатора равен дается как
V из = – C 1 R f {d(V m sin ωt) / dt}
Для простоты предположим, что произведение C 1 R f равно единице.
В вых = – В м . ω. cos ωt
Таким образом, выходной сигнал дифференциатора для входного синусоидального сигнала представляет собой косинусоидальный сигнал, а входные и выходные сигналы показаны на рисунке ниже.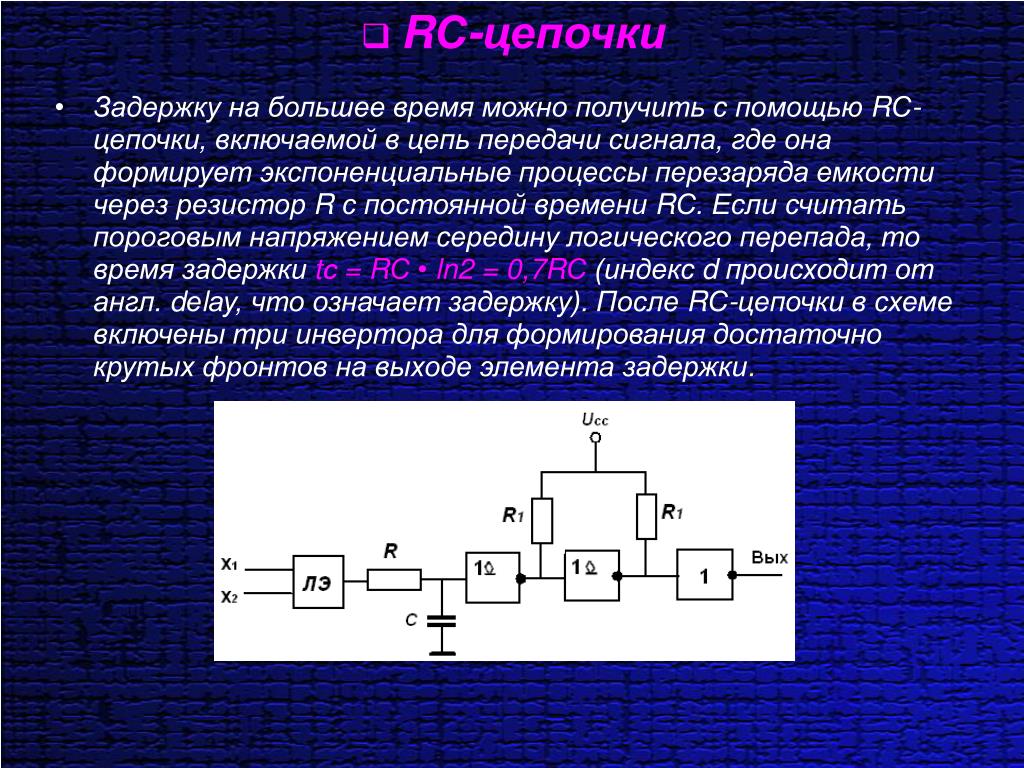
Частотная характеристика идеального дифференциатора
Коэффициент усиления дифференциатора на операционном усилителе напрямую зависит от частоты входного сигнала. Следовательно, для входов постоянного тока, где f = 0, выход также равен нулю. Когда частота входного сигнала увеличивается, выходной сигнал также увеличивается. Частотная характеристика идеального дифференциатора показана на рисунке ниже.
Частота f 1 — это частота, для которой усиление дифференциатора становится равным единице. Из рисунка видно, что для частоты меньше f 1 коэффициент усиления меньше единицы. Для f 1 усиление становится равным единице (0 дБ), а за пределами f 1 усиление увеличивается на 20 дБ за декаду.
Практическая схема дифференциатора на операционном усилителе
Для идеального дифференциатора усиление увеличивается с увеличением частоты. Таким образом, на некоторых более высоких частотах дифференциатор может стать нестабильным и вызвать колебания, которые приводят к шуму.
Этих проблем можно избежать или исправить с помощью практической схемы дифференциатора, в которой используется резистор R 1 , включенный последовательно с входным конденсатором, и конденсатор C f , включенный параллельно резистору обратной связи, как показано на рисунке ниже.
Выходное напряжение практической схемы дифференцирующего усилителя на ОУ задается как
т.е. выходное напряжение C 1 R f кратное дифференцирование входного напряжения.
Добавление резистора R 1 и конденсатора С f стабилизирует схему на более высоких частотах, а также уменьшает влияние помех на схему.
Частотная характеристика практического дифференциатора
Коэффициент усиления практического дифференциатора увеличивается с увеличением частоты и на определенной частоте f 1 коэффициент усиления становится равным единице (0 дБ). Коэффициент усиления продолжает увеличиваться со скоростью 20 дБ за декаду, пока входная частота не достигнет частоты f 2 .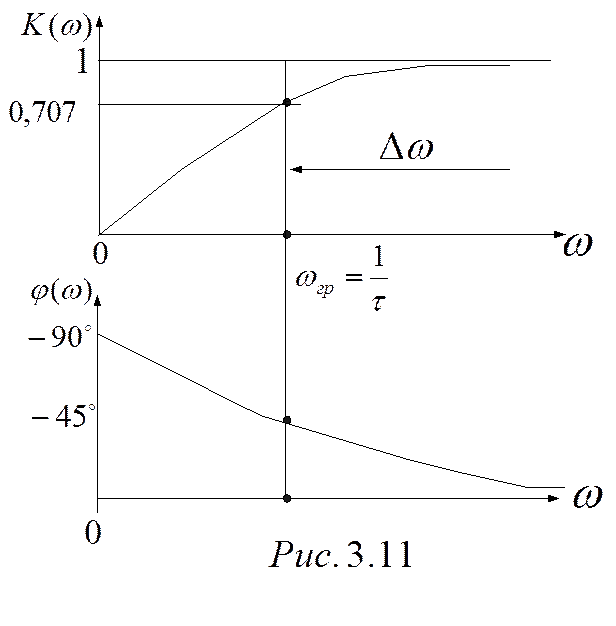
За пределами этой частоты входного сигнала усиление дифференциатора начинает уменьшаться со скоростью 20 дБ за декаду. Этот эффект обусловлен добавлением резистора R 1 и конденсатора C f . Кривая частотной характеристики практического дифференциатора показана на рисунке ниже.
Применение дифференциатора операционных усилителей
- Дифференцирующие усилители чаще всего предназначены для работы с треугольными и прямоугольными сигналами. Дифференциаторы
- также находят применение в качестве цепей формирования волны для обнаружения высокочастотных составляющих во входном сигнале.
Краткое описание операционного усилителя в качестве дифференциатора
- Дифференцирующий усилитель на операционном усилителе представляет собой схему инвертирующего усилителя, в которой используются реактивные компоненты (обычно конденсатор, а не катушка индуктивности).
- Дифференциатор выполняет математическую операцию дифференцирования входного сигнала по времени, т.
 е. мгновенное выходное напряжение пропорционально скорости изменения входного сигнала.
е. мгновенное выходное напряжение пропорционально скорости изменения входного сигнала. - Дифференциальные цепи обычно используются для работы с треугольными и прямоугольными сигналами. При работе с синусоидальными входами дифференцирующие цепи имеют ограничения по частоте.
10.3: Дифференциаторы — Инженерные тексты LibreText
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3609
- Джеймс М. Фиоре
- Муниципальный колледж Mohawk Valley
Дифференциаторы выполняют дополнительную функцию по отношению к интегратору. Базовая форма дифференциатора показана на рисунке \(\PageIndex{1}\). Выходное напряжение является разностью входного напряжения. Это очень полезно для определения скорости изменения сигнала во времени. Например, можно найти скорость по заданному расстоянию и ускорение по заданной скорости. Это может быть очень полезно при управлении технологическим процессом.
Выходное напряжение является разностью входного напряжения. Это очень полезно для определения скорости изменения сигнала во времени. Например, можно найти скорость по заданному расстоянию и ускорение по заданной скорости. Это может быть очень полезно при управлении технологическим процессом.
Рисунок \(\PageIndex{1}\): основное отличие
По сути, дифференциатор имеет тенденцию усиливать быстрые переходы сигнала. Если форма входного сигнала не меняется (т. Е. Постоянный ток), наклон равен нулю, и, следовательно, выходной сигнал дифференциатора равен нулю. С другой стороны, резкое изменение сигнала, такое как нарастающий фронт прямоугольной волны, приводит к очень большому наклону, и поэтому выходной сигнал дифференциатора будет большим. Чтобы создать различие, соответствующее устройство должно быть связано со схемой операционного усилителя. Такой подход был использован с интегратором, и здесь он остается в силе. По сути, у нас остаются те же два варианта: использовать либо катушку индуктивности, либо конденсатор. Опять же, с конденсаторами, как правило, несколько легче работать, чем с катушками индуктивности, и поэтому они предпочтительнее. Единственная разница между интегратором и дифференциатором заключается в положении конденсатора. Вместо того, чтобы размещать его в позиции \(R_f\), конденсатор будет помещен в позицию \(R_i\). Получившаяся схема показана на рисунке \(\PageIndex{2}\).
Опять же, с конденсаторами, как правило, несколько легче работать, чем с катушками индуктивности, и поэтому они предпочтительнее. Единственная разница между интегратором и дифференциатором заключается в положении конденсатора. Вместо того, чтобы размещать его в позиции \(R_f\), конденсатор будет помещен в позицию \(R_i\). Получившаяся схема показана на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\): Простой дифференциатор операционного усилителя.
Анализ начинается с основного уравнения конденсатора (уравнение 10.2.1):
\[i(t) = C \frac{dv(t)}{dt} \nonumber \]
Мы уже знаем из предыдущей работы, что выходное напряжение появляется через \(R_f\), хотя и инвертировано.
\[V_{out} = −V_{Rf} \номер\]
Также по закону Ома
\[V_{Rf} = iR_{f} \номер\]
Используя приближение, согласно которому весь входной ток протекает через \(R_f\) (поскольку входной ток операционного усилителя равен нулю), а затем подставив ток в уравнение 10.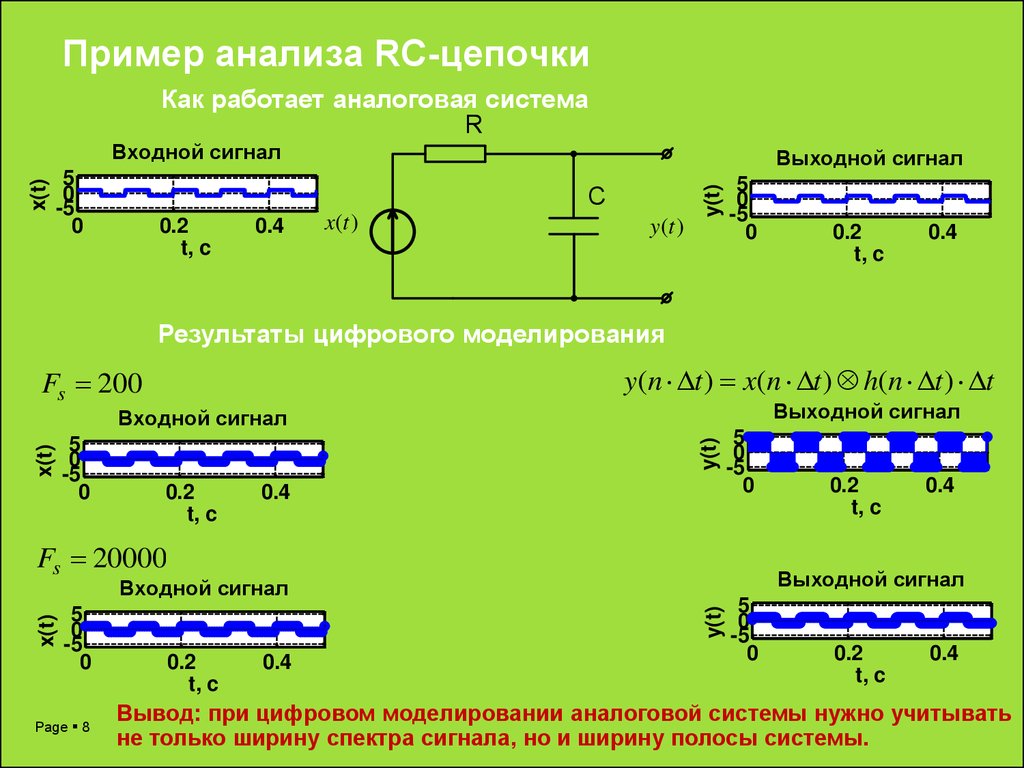 2.1, мы найдем
2.1, мы найдем
\[V_{out}(t) = −R_f C \frac{dv (t)}{dt} \nonumber \]
Беглый осмотр схемы показывает, что все входное напряжение падает на конденсаторе, потому что инвертирующий вход операционного усилителя представляет собой виртуальную землю. Имея это в виду, мы приходим к окончательному уравнению выходного напряжения
.\[V_{out}(t) = −R_f C \frac{dV_{i n}(t)}{dt} \label{10.8} \]
Как и в случае с интегратором, к основной форме добавляется ведущая константа. Опять же, можно масштабировать выход по мере необходимости с помощью цепей усиления или ослабления.
10.3.1: Точность и полезность дифференциации
Уравнение \ref{10.8} является точным отражением отклика схемы, пока основные предположения остаются в силе. Как и в случае с интегратором, практические соображения ограничивают рабочий диапазон схемы. Если цепь анализируется в дискретных точках в частотной области, ее можно смоделировать как инвертирующий усилитель со следующим уравнением усиления:
\[A_v = − \frac{R_f}{X_C} = −2 \pi f C R_f \номер\]
Обратите внимание, что с уменьшением частоты X_C растет, что снижает коэффициент усиления. И наоборот, при повышении входной частоты значение X_C падает, что приводит к увеличению усиления. Этот рост будет продолжаться до тех пор, пока не пересечет характеристику операционного усилителя без обратной связи. Результирующая амплитудная характеристика показана на рисунке \(\PageIndex{3}\).
И наоборот, при повышении входной частоты значение X_C падает, что приводит к увеличению усиления. Этот рост будет продолжаться до тех пор, пока не пересечет характеристику операционного усилителя без обратной связи. Результирующая амплитудная характеристика показана на рисунке \(\PageIndex{3}\).
Рисунок \(\PageIndex{3}\): Ответ простого дифференциатора.
Этот отклик является зеркальным отражением основного отклика интегратора и имеет наклон 6 дБ на октаву. Обратите внимание, что коэффициент усиления по постоянному току равен нулю, поэтому проблемы, создаваемые входными токами смещения и смещения, не так серьезны, как в интеграторе. Из-за этого нет ограничений на то, насколько низкой может быть входная частота, за исключением влияния отношения сигнал/шум. Однако на высоком уровне все значительно отличается. Как только отклик схемы отклоняется от идеальных 6 дБ на октаву, дифференциация больше не происходит.
10.3.2: Оптимизация дифференциатора
Есть несколько проблем с общим дифференциатором на рисунке \(\PageIndex{2}\). Во-первых, вполне возможно, что схема может стать нестабильной на более высоких частотах. Кроме того, основная форма амплитудной характеристики предполагает усиление высоких частот, что увеличивает относительный уровень шума. Обе эти проблемы могут быть уменьшены путем предоставления искусственной верхней предельной частоты \(f_{high}\). Эта настройка может быть достигнута путем шунтирования \(R_f\) небольшим конденсатором. Это уменьшает усиление высоких частот и, следовательно, уменьшает шум. Полученный ответ показан на рисунке \(\PageIndex{4}\).
Во-первых, вполне возможно, что схема может стать нестабильной на более высоких частотах. Кроме того, основная форма амплитудной характеристики предполагает усиление высоких частот, что увеличивает относительный уровень шума. Обе эти проблемы могут быть уменьшены путем предоставления искусственной верхней предельной частоты \(f_{high}\). Эта настройка может быть достигнута путем шунтирования \(R_f\) небольшим конденсатором. Это уменьшает усиление высоких частот и, следовательно, уменьшает шум. Полученный ответ показан на рисунке \(\PageIndex{4}\).
Рисунок \(\PageIndex{4}\): Ответ частично оптимизированного дифференциатора.
Находим \(f_{high}\) стандартным образом:
\[f_{high (fdbk)} = \frac{1}{2 \pi R_f C_f} \label{10.9} \]
\(f_{high}\) представляет самую высокую частоту для дифференциации. Это точка точности 50%. Для более высокой точности входная частота должна быть значительно ниже \(f_{high}\). Примерно при 0,1 \(f_{high}\) точность уравнения \ref{10.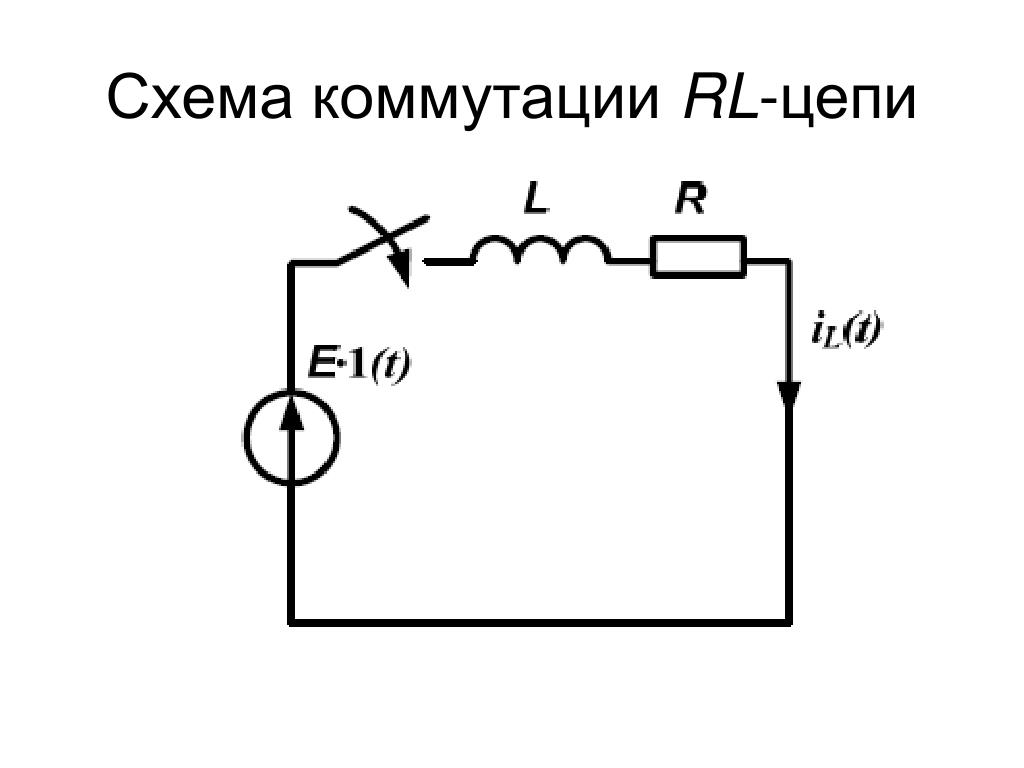 8} составляет около 99%. Как правило, вы должны быть несколько более консервативны в оценке точности, чем с интегратором. Это связано с тем, что сложные волны содержат гармоники выше основной гармоники. Несмотря на то, что основная гармоника может находиться в пределах диапазона высокой точности, верхние гармоники могут не соответствовать этому диапазону.
8} составляет около 99%. Как правило, вы должны быть несколько более консервативны в оценке точности, чем с интегратором. Это связано с тем, что сложные волны содержат гармоники выше основной гармоники. Несмотря на то, что основная гармоника может находиться в пределах диапазона высокой точности, верхние гармоники могут не соответствовать этому диапазону.
Другая серьезная проблема базовой схемы заключается в том, что входное сопротивление обратно пропорционально входной частоте. Это связано с тем, что \(X_C\) является единственным коэффициентом входного импеданса. Это может представлять проблему на более высоких частотах, поскольку импеданс будет приближаться к нулю. Чтобы обойти эту проблему, резистор может быть включен последовательно с входным конденсатором, чтобы установить минимальное значение импеданса. К сожалению, это также создаст верхнюю частоту разрыва, \(f_{high}\).
\[f_{high (in)} = \frac{1}{2 \pi R_f C} \label{10.10} \]
Результирующий ответ показан на рисунке \(\PageIndex{5}\). Эффективное \(f_{высокое}\) для системы будет меньшим из уравнений \ref{10.9} и \ref{10.10}.
Эффективное \(f_{высокое}\) для системы будет меньшим из уравнений \ref{10.9} и \ref{10.10}.
Рисунок \(\PageIndex{7}\): Реакция практического дифференциатора.
Готовый практический дифференциатор показан на рисунке \(\PageIndex{8}\). Обратите внимание, что на неинвертирующем входе может потребоваться резистор компенсации смещения, хотя он и не показан.
Рисунок \(\PageIndex{8}\): Практический отличительный признак.
10.3.3: Анализ дифференциаторов с помощью непрерывного во времени метода
Непрерывный во времени метод будет использоваться, когда входной сигнал может быть легко записан во временной области (например, синусоидальные волны). Для более сложных сигналов, таких как треугольная волна, будет использоваться метод дискретного времени. Непрерывный метод приведет непосредственно к представлению формы выходного сигнала во временной области. Конкретные координаты напряжения/времени не будут оцениваться.
Пример \(\PageIndex{1}\)
Определите полезный диапазон для дифференцирования в схеме на рисунке \(\PageIndex{9}\). Также определите выходное напряжение, если входной сигнал представляет собой синусоидальный сигнал с пиковым значением 2 В на частоте 3 кГц.
Также определите выходное напряжение, если входной сигнал представляет собой синусоидальный сигнал с пиковым значением 2 В на частоте 3 кГц.
Рисунок \(\PageIndex{9}\): дифференциатор для примера \(\PageIndex{1}\).
Верхний предел полезного диапазона частот будет определяться нижней из двух сетей \(RC\).
\[f_{high (fdbk)} = \frac{1}{2 \pi R_f C_f} \\ f_{high (fdbk)} = \frac{1}{2 \pi \times 5 k \times 100 pF} \\ f_{high (fdbk)} = 318,3 кГц \\ f_{high (in)} = \frac{1}{2 \pi R_f C} \\ f_{high (in)} = \frac{1 }{2 \pi \times 100 \times 10 нФ} \\ f_{high (in)} = 159.2 кГц \номер \]
Таким образом, верхний предел равен 159,2 кГц. Помните, что точность на этом пределе относительно низкая, и нормальная работа обычно будет на несколько октав ниже этого предела. Обратите внимание, что входная частота составляет 3 кГц, поэтому должна быть получена высокая точность. Во-первых, запишите \(V_{in}\) как выражение во временной области:
\[V_{in}(t) = 2 \sin 2 \pi 3000 t \\ V_{out}(t) = −R_f C \frac{dV_{in} (t)}{dt} \\ V_{out}(t) = −5 k \times 10 нФ \frac{d 2 \sin 2 \pi 3000t}{dt} \\ V_ {out}(t) = −10^{−4} \frac{d \sin 2 \pi 3000t}{dt} \\ V_{out}(t) = −1,885 \cos 2 \pi 3000t \nonumber \] 9{\circ}\).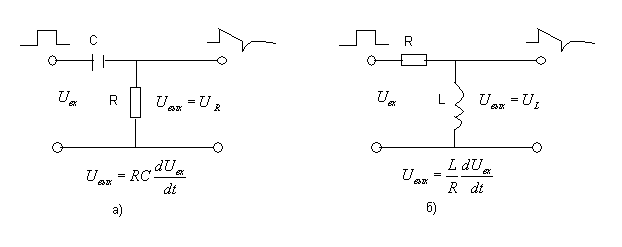 Обратите внимание, что входная частота не изменилась, но изменилась амплитуда. Дифференциатор работает с наклоном 6 дБ на октаву, поэтому видно, что выходная амплитуда прямо пропорциональна входной частоте. Если этот пример повторить с частотой 6 кГц, выходная амплитуда будет удвоена по сравнению с текущим значением.
Обратите внимание, что входная частота не изменилась, но изменилась амплитуда. Дифференциатор работает с наклоном 6 дБ на октаву, поэтому видно, что выходная амплитуда прямо пропорциональна входной частоте. Если этот пример повторить с частотой 6 кГц, выходная амплитуда будет удвоена по сравнению с текущим значением.
Компьютерное моделирование
Моделирование Multisim для схемы примера \(\PageIndex{1}\) показано на рисунке \(\PageIndex{10}\). Обратите внимание на отличную корреляцию фазы и амплитуды выходного сигнала. Как и в случае моделирования интегратором, выходной график анализа переходных процессов запускается после установления начальных условий.
Рисунок \(\PageIndex{10a}\): Дифференциатор в Multisim.
Рисунок \(\PageIndex{10b}\): Входные и выходные сигналы дифференциатора.
10.3.4: Анализ дифференциаторов с помощью дискретного по времени метода
Для более сложных сигналов иногда бывает целесообразно разбить сигнал на отдельные фрагменты, дифференцировать каждую часть, а затем объединить результаты. Идея состоит в том, чтобы разбить сигнал на эквивалентные прямолинейные сегменты. Дифференциация прямолинейного отрезка приведет к константе (т. Е. Наклону, который не меняется за это время). Процесс повторяется до тех пор, пока не будет завершен один цикл входного сигнала. Результирующие уровни затем объединяются графически для получения формы выходного сигнала.
Идея состоит в том, чтобы разбить сигнал на эквивалентные прямолинейные сегменты. Дифференциация прямолинейного отрезка приведет к константе (т. Е. Наклону, который не меняется за это время). Процесс повторяется до тех пор, пока не будет завершен один цикл входного сигнала. Результирующие уровни затем объединяются графически для получения формы выходного сигнала.
Часто сигналы симметричны, и требуется выполнить только часть вычислений: изменение знака — это все, что потребуется для частей зеркального отображения. Например, треугольная волна может быть разбита на сегмент положительной линии и сегмент отрицательной линии. Наклоны должны быть равными, изменилось только направление (то есть знак). Прямоугольную волну можно разбить на четыре части: положительный фронт, статическое положительное значение, отрицательный фронт и статическое отрицательное значение. «Плоские» участки имеют нулевой наклон, поэтому необходимо выполнить только одно вычисление, и это положительный фронт. Мы рассмотрим обе эти формы волны в следующих двух примерах.
Пример \(\PageIndex{2}\)
Нарисуйте форму выходного сигнала для схемы, показанной на рисунке \(\PageIndex{9}\), если входной сигнал представляет собой пиковый треугольный сигнал с напряжением 3 В и частотой 4 кГц.
Во-первых, обратите внимание, что входная частота находится в пределах полезного диапазона этой схемы, рассчитанного в примере \(\PageIndex{1}\). (Обратите внимание, что высшие гармоники по-прежнему будут находиться вне допустимого диапазона, но внесенная ошибка будет незначительной.)
Треугольная волна может быть разбита на положительную и отрицательную части. В любом случае общее изменение напряжения составит 6 В за один полупериод. Период сигнала равен
\[T = \frac{1}{4 кГц} \\ T = 250 \mu s \nonumber \]
Следовательно, для положительной части изменение на 6 вольт будет видно в 125 \(\mu \) с (-6 В за 125 \(\мю\)с для отрицательной части). Наклон равен
\[Slope = \frac{6 V}{125 \mu s} \\ Slope = 48000 V/s \nonumber \]
Что, как выражение во временной области, равно
\[V_{ in}(t) = 48000t \nonumber \]
Подстановка этого уравнения в уравнение \ref{10. 8} дает
8} дает
\[V_{out}(t) = −R_f C \frac{dV_{in}(t)} {dt} \\ V_{out}(t) = −5 k \times 10 nF \frac{d 48000 t}{dt} \\ V_{out}(t) = −2,4 V \nonumber \]
В течение от \(t = 0\) до \(t = 125 мкс\)с выход составляет -2,4 В. Дифференциация второй половины волны аналогична, но дает положительный выход, +2,4 В. В результате получается прямоугольная волна 4 кГц с пиковым напряжением 2,4 В. Результирующий сигнал показан на рисунке \(\PageIndex{11}\).
Рисунок \(\PageIndex{11}\): Входные/выходные сигналы.
Компьютерное моделирование
Некоторые схемы более чувствительны к выбору операционного усилителя, чем другие, и последствия неправильного выбора не всегда могут быть сразу очевидны без предварительного построения или моделирования схемы. Хороший пример этого показан на рисунке \(\PageIndex{12}\). Multisim использовался для создания анализа переходных процессов для схемы из примера \(\PageIndex{2}\) с двумя разными операционными усилителями. Точное дифференцирование требует от операционного усилителя превосходной высокочастотной характеристики. В первом моделировании используется операционный усилитель 741. Это устройство не особенно быстрое. В результате форма выходного сигнала страдает от чрезмерного выброса и звона. Кроме того, довольно очевидно ограничение скорости нарастания, замедляющее переходы формы выходного сигнала. Напротив, использование LF411 в той же схеме дает гораздо лучший отклик. Некоторое превышение все еще существует, но его величина ограничена, как и звон. Кроме того, ограничение скорости нарастания значительно снижается. Ясно, что второй результат гораздо ближе к идеальному расчету, чем первый прогон.
В первом моделировании используется операционный усилитель 741. Это устройство не особенно быстрое. В результате форма выходного сигнала страдает от чрезмерного выброса и звона. Кроме того, довольно очевидно ограничение скорости нарастания, замедляющее переходы формы выходного сигнала. Напротив, использование LF411 в той же схеме дает гораздо лучший отклик. Некоторое превышение все еще существует, но его величина ограничена, как и звон. Кроме того, ограничение скорости нарастания значительно снижается. Ясно, что второй результат гораздо ближе к идеальному расчету, чем первый прогон.
Рисунок \(\PageIndex{12a}\): Мультисим-схема дифференциатора.
Рисунок \(\PageIndex{12b}\): Входные и выходные сигналы с использованием 741.
Рисунок \(\PageIndex{12c}\): Входные и выходные сигналы с использованием LF411.
Пример \(\PageIndex{3}\)
Повторить пример \(\PageIndex{2}\) с пиковым напряжением 3 В и квадратной частотой 4 кГц в качестве входного сигнала.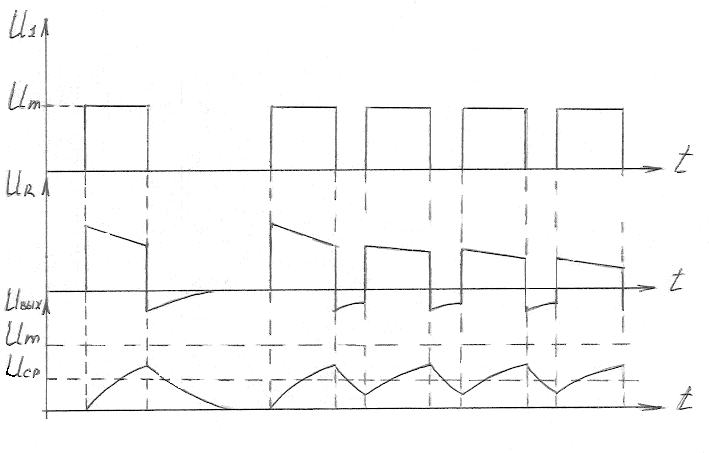 6 t \nonumber \] 96 t}{dt} \\ V_{out}(t) = −250V \nonumber \]
6 t \nonumber \] 96 t}{dt} \\ V_{out}(t) = −250V \nonumber \]
Очевидно, что при использовании стандартного операционного усилителя и источника питания \(\pm 15\) V ограничение будет происходить вблизи -13,5 В. Для отрицательного переднего фронта будет виден аналогичный результат (рассчитано +250 В с ограничением на +13,5 В). Результирующий сигнал показан на рисунке \(\PageIndex{13}\). Обратите внимание, что пики формы выходного сигнала также будут ограничены скоростью нарастания операционного усилителя дифференциатора.
Рисунок \(\PageIndex{13}\): Дифференцированная прямоугольная волна (обратите внимание на отсечение выходного сигнала).
Пример \(\PageIndex{4}\)
На рисунке \(\PageIndex{14}\) показан дифференциатор, получающий сигнал от LVDT или дифференциального трансформатора с линейной переменной 1 . LVDT можно использовать для точного измерения положения объектов со смещением менее одной тысячной дюйма. Это может быть полезно в автоматизированной производственной системе.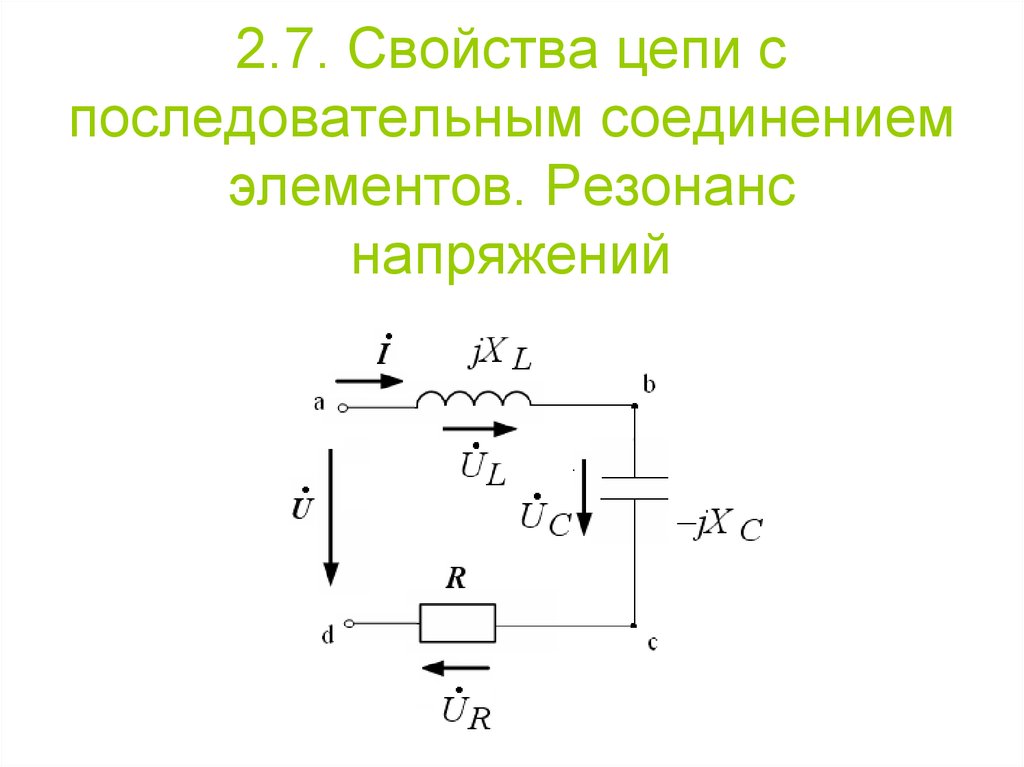 Дифференцируя этот сигнал положения, можно получить сигнал скорости. Вторая дифференциация вызовет ускорение. Если LVDT создает волну, показанную на рисунке \(\PageIndex{14}\), определите кривую скорость/время для отслеживаемого объекта.
Дифференцируя этот сигнал положения, можно получить сигнал скорости. Вторая дифференциация вызовет ускорение. Если LVDT создает волну, показанную на рисунке \(\PageIndex{14}\), определите кривую скорость/время для отслеживаемого объекта.
Рисунок \(\PageIndex{14a}\): Схема дифференциатора с LVDT.
Сначала проверьте верхний предел частоты для цепи.
\[f_{high( fdbk )} = \frac{1}{2 \pi R_f C_f} \\ f_{high( fdbk )} = \frac{1}{2 \pi \times 40 k \times 2 nF } \\ f_{high(fdbk)} = 1,99 кГц \\ f_{high(in)} = \frac{1}{2 \pi R_i C} \\ f_{high(in)} = \frac{1 }{2 \pi \times 250 \times 500 nF} \\ f_{high( in )} = 1,273 кГц \nonnumber \]
Предел будет меньшим из двух или 1,273 кГц. Это намного выше медленно меняющегося входного сигнала, и, следовательно, должна быть возможна высокая точность.
Рисунок \(\PageIndex{14b}\): Сигнал, создаваемый LVDT.
Эту волну можно анализировать кусочно. Участки линейного изменения будут давать постоянные выходные уровни, а плоские участки будут давать на выходе 0 В (т. е. скорость изменения равна нулю).
е. скорость изменения равна нулю).
Для первой секции
\[Slope = \frac{2V}{0.2s} \\ Slope = 10V/s \nonumber \]
Что, как выражение во временной области, равно
\[V_ {in} (t) = 10 t \\ V_{out}(t) = −R_f C \frac{dV_{in} (t)}{dt} \\ V_{out}(t) = −40 k \ раз 500 нФ \frac{d 10t}{dt} \\ V_{out}(t) = −0,2V \nonumber \]
Таким образом, в течение от \(t = 0\) до \(t = 0,2\) с выход составляет −0,2 В. Период времени между 0,2 с и 0,5 с дает выход 0 В. Для отрицательного идущая часть,
\[Наклон = \frac{−4V}{0.2s} \\ Slope = −20V/s \quad \text{ таким образом,} \\ V_{i n} (t) = −20 t \\ V_{out}(t) = −R_f C \frac{dV_{i n} (t)}{dt} \\ V_{out}(t) = −40 k 500 нФ \frac{d 20t}{dt} \ \ V_{out}(t) = 0,4 В \nonumber \]
Выходное напряжение составляет 0,4 В между 0,5 и 0,7 с. Третья секция имеет тот же наклон, что и первая секция, и также дает уровень -0,2 В. Форма выходного сигнала показана на рисунке \(\PageIndex{15}\).
Рисунок \(\PageIndex{15}\): Выход дифференциатора.
Каталожные номера
1 LVDT — это трансформатор с двумя вторичными обмотками и подвижным сердечником. Сердечник соединен с валом, который, в свою очередь, приводится в действие каким-либо внешним объектом. Движение сердечника изменяет взаимную индуктивность между первичной и вторичной обмотками. Несущий сигнал подается на первичную обмотку, а изменение взаимной индуктивности изменяет силу сигнала, наводимого на вторичные обмотки. Это изменение сигнала преобразуется демодулятором в простое напряжение постоянного тока. Результирующий потенциал постоянного тока пропорционален положению сердечника и, следовательно, пропорционален положению измеряемого объекта.
Эта страница под названием 10.3: Дифференциаторы распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М. Фиоре с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.
; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джеймс М. Фиоре
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- source@http://www.
 dissidents.com/resources/OperationalAmplifiersAndLinearICs_3E.pdf
dissidents.com/resources/OperationalAmplifiersAndLinearICs_3E.pdf
- source@http://www.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Integrator & Differentiator-B Технический университет Вопросы и ответы
Integrator & Differentiator-B Технический университет Вопрос и ответ
Q1. Объясните работу фильтра нижних частот RC, как он может действовать как интегратор.
Ключ ответа: цепь(2), рабочая+частотная характеристика(4), действовать как интегратор(5), выход(1)
Чтобы узнать, как подготовить ключ ответа, перейдите по ссылке.
Рассмотрим RC-цепь первого порядка. Он может действовать как фильтр нижних частот и позволяет пропускать только низкочастотные сигналы.
Р
| Рис. 1 |
, где,
AC -Source, который обеспечивает входные (Vin)
— выходы
AC — AC, который обеспечивает входные (vin)
— выходы
AC — AC, который обеспечивает входные (vin)
— выходы
. в сериале с Вин.
Реактивное сопротивление конденсатора Xc =
где, f – частота входного переменного тока c — емкость конденсатора C
Уравнение показывает, что Xc обратно пропорциональна частоте f. Итак,
При низкочастотном входном сигнале Xc становится очень большим. Таким образом, Xc >> R. Следовательно, падение напряжения на конденсаторе, который является выходом, очень велико. Аналогичным образом при высоком
частота, Xc << R. Таким образом, выход низкий.
Таким образом, Xc >> R. Следовательно, падение напряжения на конденсаторе, который является выходом, очень велико. Аналогичным образом при высоком
частота, Xc << R. Таким образом, выход низкий.
| Частотная характеристика первого порядка Фильтр нижних частот |
Подводя итог:
Для низкочастотного переменного тока / для постоянного тока — Vc >> VR — большее выходное напряжение
Для высокочастотного переменного тока — Vc << VR -- меньшее выходное напряжение
Эта схема обеспечивает высокое выходное напряжение для низкочастотных входов и ослабляет выходное напряжение для высокочастотные входные сигналы. Вот почему он имеет название «низкий проход». фильтр’.
Интегратор Интегратор выдает результат, пропорциональный интегралу от его входа.
Сама низкочастотная RC-цепь действует как интегратор при соблюдении одного условия. Давайте проверим это условие.
Уравнение для выходного напряжения на рис. 1:1263
Преобразование Лапласа s=jw и w=2πf (w-omega)
В приведенном выше уравнении, если мы принимаем условие wRC >> 1, тогда , в знаменатель 1+jwRC почти равен jwRC. Тогда уравнение принимает вид
Перестановка,
Здесь 1/RC принимается за константу
Обратное преобразование Лапласа,
Уравнение выше
показывает, что Vout пропорционально интегралу входного напряжения. Итак, если мы
иметь RC-цепь нижних частот, которая удовлетворяет условию wRC
>> 1, он будет выступать в роли интегратора.
Для достижения хорошей интеграции должны быть выполнены следующие условия :
- Постоянная времени RC схемы должна быть очень большой по сравнению с периодом времени входного сигнала.

- Значение R должно быть в 10 или более раз больше, чем Xc.
Выход интегратора для входа прямоугольной волны представляет собой треугольную волну.
Q2. Объясните работу фильтра верхних частот RC, как он может действовать как дифференциатор.
Ключ ответа: цепь(2), рабочая+частотная характеристика(4), интегратор(5), выход(1)
Чтобы узнать, как подготовить ключ ответа, перейдите по ссылке.
Рассмотрим RC-цепь первого порядка. Он может действовать как фильтр верхних частот и позволяет пропускать только высокочастотные сигналы.
Принципиальная схема:Вход — источник переменного тока, выход — через резистор. Содержит одну пару R&C.
где
AC – источник переменного тока, обеспечивающий вход (Vin)
Output – выходное напряжение
Резисторы (R) и конденсаторы (C) соединены последовательно с Vin.
Напряжение на R принимается за выходное напряжение. Посмотрим, что случилось с этим напряжением при низком и высокие частоты.
Для высоких частот ввод:
Хс очень мала (Xc обратно пропорциональна частоте). Так что Vc тоже низкий. Итак, Vc << V R, , где V R — выходное напряжение. В заключение, для высокочастотного входа выход выше.
Для низкочастотного входа:
Xc очень высокое. Vc также высокое. Следовательно
для более низких частот V R << Vc. Таким образом, выходное напряжение В R гораздо меньше для низкочастотного входа.
| Частотная характеристика фильтра высокого прохода |
Суммирование:
для высокой частоты вход .


 Цель работы: овладение методами измерения основных характеристик линейной цепи (звена).
Цель работы: овладение методами измерения основных характеристик линейной цепи (звена). Следовательно, входной и выходной величинами целесообразно выбирать напряжения, при этом используются rC — и rL – цепи. На практике широкое распространение получила rC — цепь.
Следовательно, входной и выходной величинами целесообразно выбирать напряжения, при этом используются rC — и rL – цепи. На практике широкое распространение получила rC — цепь.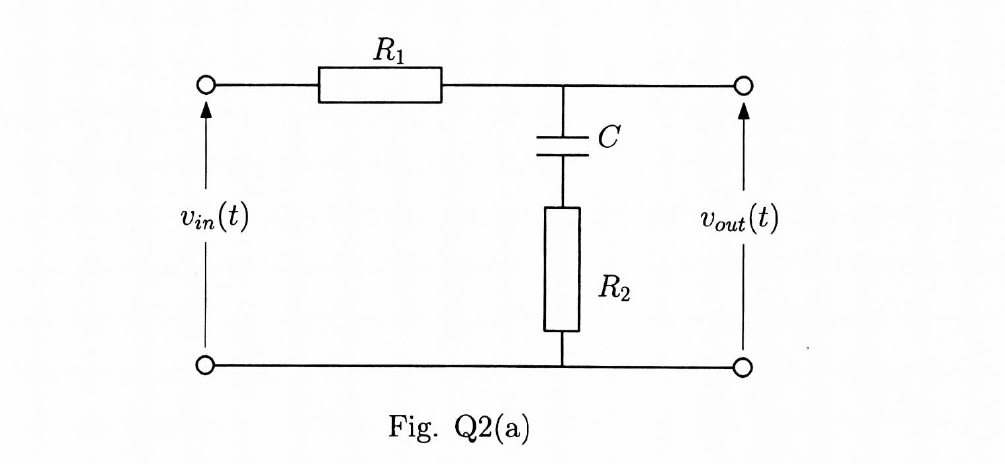
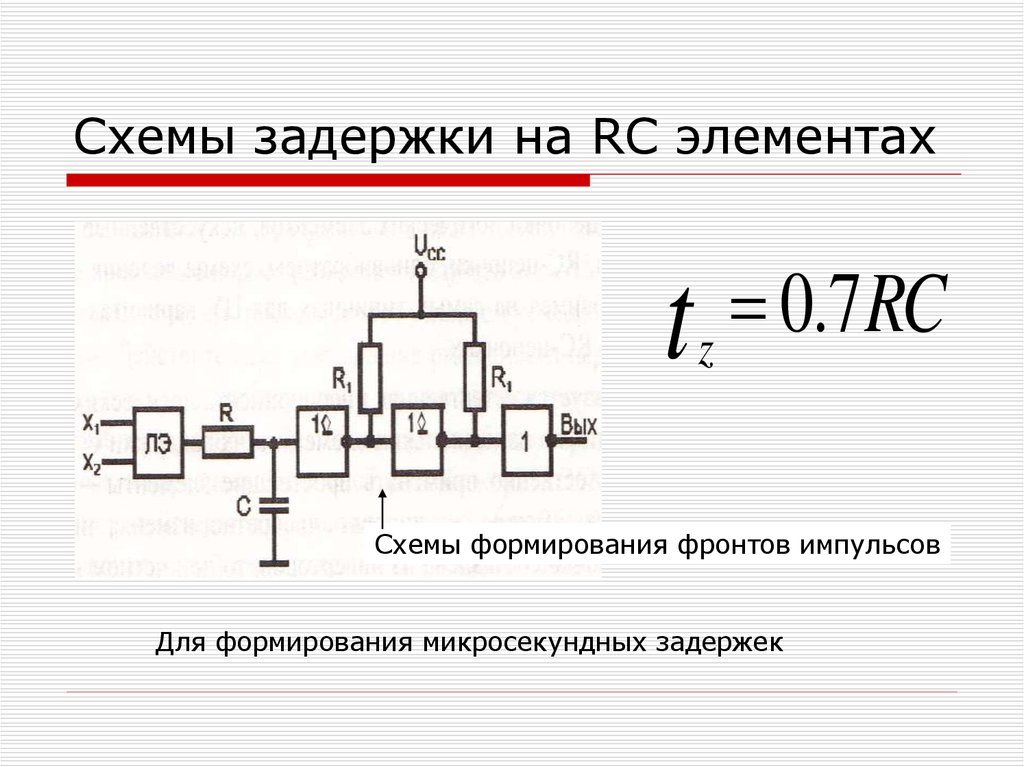 е. τ = RC (в секундах).
е. τ = RC (в секундах).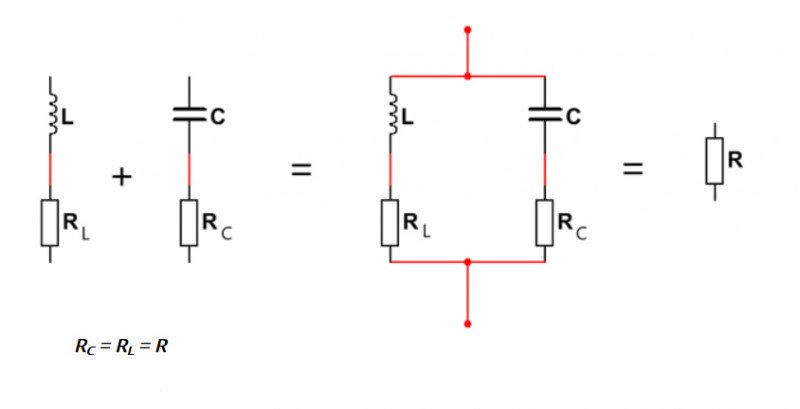
 Если на входе действует сложный сигнал, то он будет хорошо дифференцироваться, если наивысшая частота в спектре входного сигнала много меньше граничной частоты цепочки.
Если на входе действует сложный сигнал, то он будет хорошо дифференцироваться, если наивысшая частота в спектре входного сигнала много меньше граничной частоты цепочки.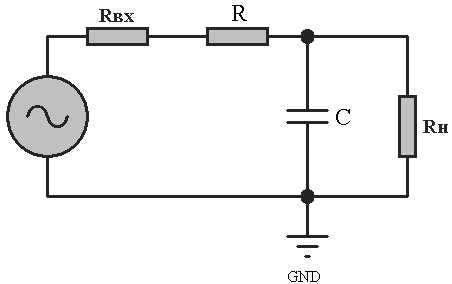 2.5 Годограф АФЧХ реального дифференцирующего звена
2.5 Годограф АФЧХ реального дифференцирующего звена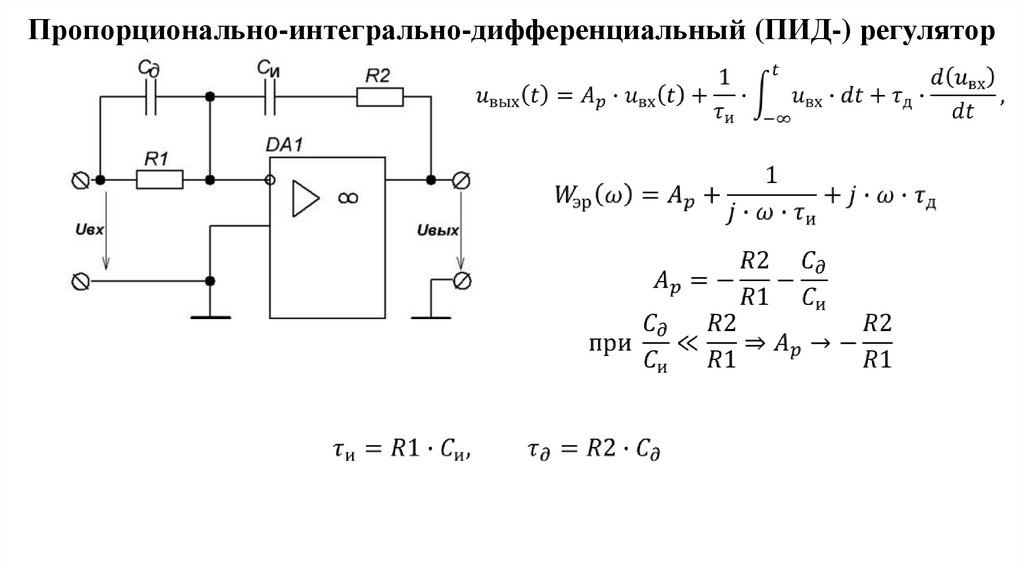
 е. мгновенное выходное напряжение пропорционально скорости изменения входного сигнала.
е. мгновенное выходное напряжение пропорционально скорости изменения входного сигнала.