1.14. Дифференцирующие цепи
ОСНОВЫ ЭЛЕКТРОНИКИ
Конденсаторы и цепи переменного тока
Подразделы: 1.12 1.13 1.14 1.15
Рассмотрим схему, изображенную на рис. 1.36. Напряжение на конденсаторе С равно Uвх — U, поэтому
I = Cd(Uвх-U)/dt=U/R.
Рис. 1.36.
Если резистор и конденсатор выбрать так, чтобы сопротивление R и емкость С были достаточно малыми и выполнялось условие dU/dt « dUвхdt, то
C(dUвх/dt) = U/R или U(t) = RC[dUвх(t)/dt].
Таким образом, мы получили, что выходное напряжение пропорционально скорости изменения входного сигнала.
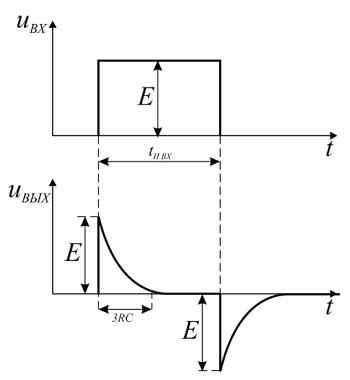
Для того чтобы выполнялось условие dU/dt « dUвхdt, произведение RC должно быть небольшим, но при этом сопротивление R не должно быть слишком малым, чтобы не «нагружать» вход (при скачке напряжения на входе изменение напряжения на конденсаторе равно нулю и R представляет собой нагрузку со стороны входа схемы). Более точный критерий выбора для R и С мы получим, когда изучим частотные характеристики. Если на вход схемы подать прямоугольный сигнал, то сигнал на выходе будет иметь вид, представленный на рис. 1.37.
Более точный критерий выбора для R и С мы получим, когда изучим частотные характеристики. Если на вход схемы подать прямоугольный сигнал, то сигнал на выходе будет иметь вид, представленный на рис. 1.37.
Рис. 1.37. Выходной сигнал (верхний), снимаемый с дифференциатора, на вход которого подается прямоугольный сигнал.
Дифференцирующие цепи удобно использовать для выделения переднего и заднего фронтов импульсных сигналов, и в цифровых схемах можно иногда встретить цепи, подобные той, которая показана на рис. 1.38. Дифференцирующая RC — цепь генерирует импульсы в виде коротких пиков в моменты переключения входного сигнала, а выходной буферный усилитель преобразует эти импульсы в короткие прямоугольные импульсы. В реальных схемах отрицательный пик бывает небольшим благодаря встроенному в буфер диоду (речь об этом элементе пойдет в разд. 1.25).
Рйс. 1.38. Выделение переднего фронта импульса.
Рйс. 1.39. Паразитная емкостная связь.
Паразитная емкостная связь. Иногда схема неожиданно начинает проявлять дифференцирующие свойства, причем в ситуациях, где они совершенно нежелательны. При этом можно наблюдать сигналы, подобные показанным на рис. 1.39. Первый сигнал (а точнее, импульсная помеха) может возникнуть при наличии емкостной связи между рассматриваемой линией и схемой, в которой присутствует прямоугольный сигнал; причиной появления подобной помехи может служить отсутствие оконечного резистора в линии. Если же резистор есть, то следует либо уменьшить сопротивление источника сигналов для линии, либо найти способ ослабления емкостной связи с источником сигналов прямоугольной формы. Сигнал второго типа можно наблюдать в цепи, по которой должен проходить сигнал прямоугольной формы, при наличии дефекта в контакте с этой цепью, например, в щупе осциллографа. Небольшая емкость, возникающая при плохом контакте, и входное сопротивление осциллографа образуют дифференцирующую цепь. Если вы обнаружили, что ваша схема «что-то» дифференцирует, то сказанное может помочь вам найти причину неисправности и устранить ее.
Подразделы: 1.12 1.13 1.14 1.15
Индуктивности и трансформаторы
1.2.2.Дифференцирующие rc-цепи.
П ростейшая дифференцирующая RC-цепь образуется из интегрирующей заменой конденсатора на резистор (рис.1.28).
Рис.1.28.Простейшая дифференцирующая RC-цепь.
Н апряжение на выходе цепи будет определяться падением напряжения на резисторе R: UВЫХ(t)=UR(t)=I(t)R. Зависимость I(t) была нами приведена на рис.1.17. Следовательно, напряжение на выходе будет иметь вид, представленный на рис.1.29 (окончание импульса входного напряжения означает отрицательный скачок напряжения).
Рис.1.29.Сигналы на входе и выходе дифференцирующей RC-цепи.
Цепь
называется дифференцирующей, поскольку
ток через конденсатор можно определить
как производную от приложенного
напряжения. Действительно, как было
показано, ,
отсюда .
Поскольку , .
Как и в случае с интегрирующей цепочкой,
можно считать, что дифференцирование
входного напряжения происходит лишь в
первый момент входного импульса.
Изменение напряжения на выходе дифференцирующей RC-цепочки можно определить, зная изменение напряжения на выходе интегрирующей RC-цепи, т.к. и . Действительно, вычитая из UГ(t) (рис.1.19а) напряжение UC(t)=UВЫХ(t) (рис.1.19в), получаем UR(t). Таким же образом можно поступить, если нужно рассчитать более сложные дифференцирующие цепи.
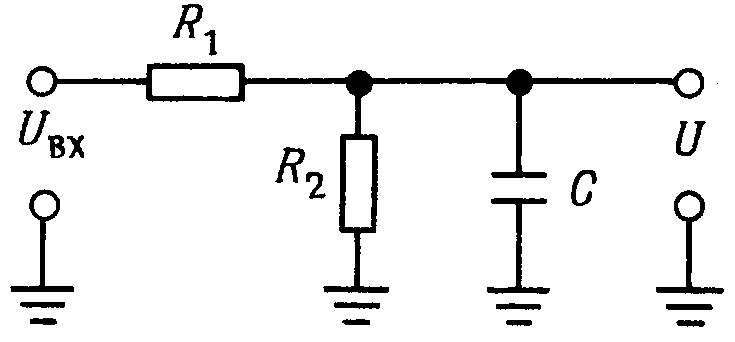
Р ассмотрим пример усложнённой дифференцирующей RC-цепи с резистором, включённым параллельно конденсатору (рис.1.30).
Рис.1.30. Дифференцирующая RC-цепь с дополнительным резистором, включенным параллельно конденсатору.
В
первый момент подачи прямоугольного
импульса напряжение на конденсаторе
не может измениться. По этой причине
все входное напряжение будет приложено
к резистору R2,
т.е. на выходе произойдет скачок
напряжения, равный UГ.
При t=∞
и действии положительного скачка
напряжения напряжение на резисторе R2 будет уменьшаться и достигнет уровня .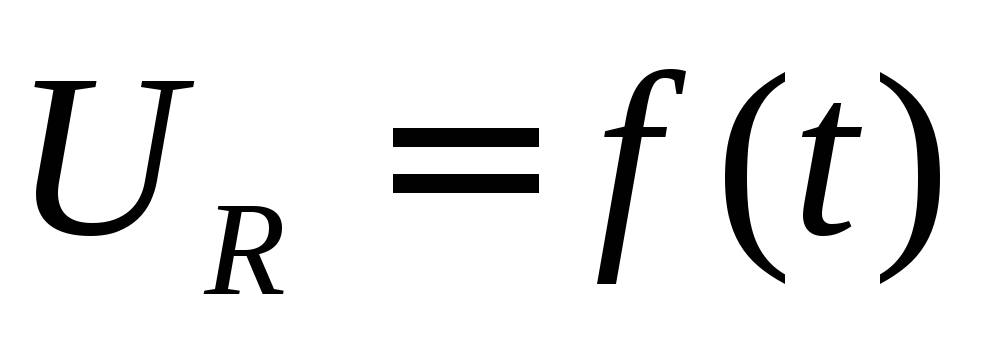 При этом зарядка конденсатора будет
происходить с постоянной времени .
При воздействии отрицательного скачка
напряжения переходной процесс будет
происходить аналогично (рис.1.31).
При этом зарядка конденсатора будет
происходить с постоянной времени .
При воздействии отрицательного скачка
напряжения переходной процесс будет
происходить аналогично (рис.1.31).
Р ис.1.31. Входной и выходной импульс дифференцирующей RC-цепи с дополнительным резистором, включенным параллельно конденсатору.
1.2.3.RC-цепи с двумя конденсаторами.
Рассмотрим теперь RC-цепи, включающие в себя два конденсатора и один резистор. Пример такой цепи приведён на рис.1.32.
Р ис.1.32.RC-цепь с двумя конденсаторами и одним резистором.
При подаче входного прямоугольного импульса в первый момент напряжения на конденсаторах будут равны 0, а всё входное напряжение будет приложено к резистору R, что вызовет ток I(0)=UГ/R.
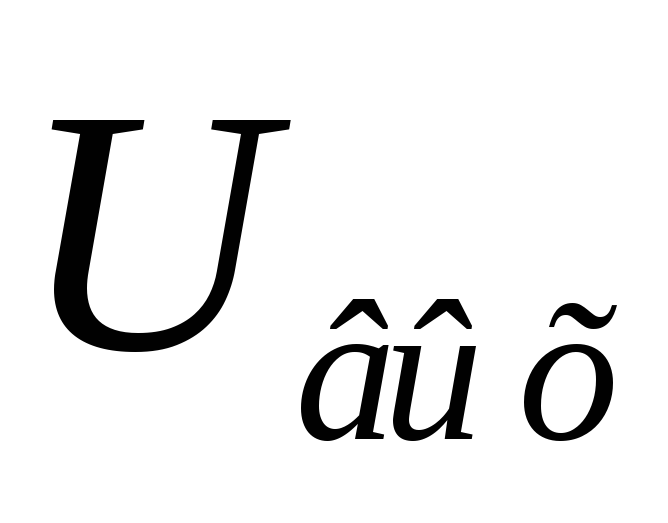 Нейтрализоваться эти заряды не могут,
т.к. приложено внешнее напряжение UГ.
Следовательно, QС1=QC2.
Выразим заряды на конденсаторах через
напряжения на них и значения их ёмкостей:
C1UC
Нейтрализоваться эти заряды не могут,
т.к. приложено внешнее напряжение UГ.
Следовательно, QС1=QC2.
Выразим заряды на конденсаторах через
напряжения на них и значения их ёмкостей:
C1UC Постоянную
времени заряда конденсаторов можно
рассчитать, зная чему равна ёмкость
двух последовательно включённых
конденсаторов. Эту ёмкость можно
определить по тому заряду, который
накопится в конденсаторе С2 при приложении к двум последовательно
соединённым конденсаторам напряжения
U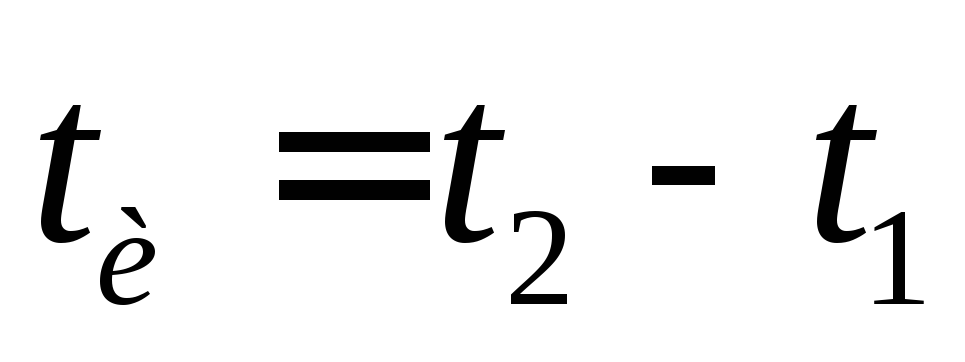 Если приложить
напряжение UГ к некому конденсатору с ёмкостью СЭКВ — эквивалентной ёмкости двух после-довательно
включённых конденсаторов, то накопленный
заряд будет равен: QЭКВ=СЭКВUГ0.
Приравнивая QЭКВ=Q2=Q1,
получаем: СЭКВUГ=С1С2/(C1+C2)UГ или СЭКВ=С1С2/(С1+С2).
Если приложить
напряжение UГ к некому конденсатору с ёмкостью СЭКВ — эквивалентной ёмкости двух после-довательно
включённых конденсаторов, то накопленный
заряд будет равен: QЭКВ=СЭКВUГ0.
Приравнивая QЭКВ=Q2=Q1,
получаем: СЭКВUГ=С1С2/(C1+C2)UГ или СЭКВ=С1С2/(С1+С2).
Т аким образом, зарядка конденсатора будет происходить с постоянной времени . Импульс на выходе рассмотренной RC-цепи приведён на рис.1.33. Как видим, данная цепь с двумя конденсаторами ведет себя как интегрирующая цепочка (сравните рис.1.33 и рис.1.25).
Рис.1.33. Импульс на входе и выходе RC-цепи, представленной на рис.1.32.
Д ругой пример RC-цепи с двумя конденсаторами приведён на рис.1.34.
Рис.1.34.RC-цепь
с двумя конденсаторами.
В
данном случае при скачках входного
напряжения конденсаторы будут заряжаться
через внутреннее сопротивление генератора
импульсов. Если мы положим, что генератор
входного напряжения идеальный, то его
внутреннее сопротивление равно 0. Это
значит, что скачок входного напряжения
вызовет скачок напряжения на выходе,
причём, как это было показано выше: .
Затем будет происходить перезаряд
конденсаторов: конденсатор С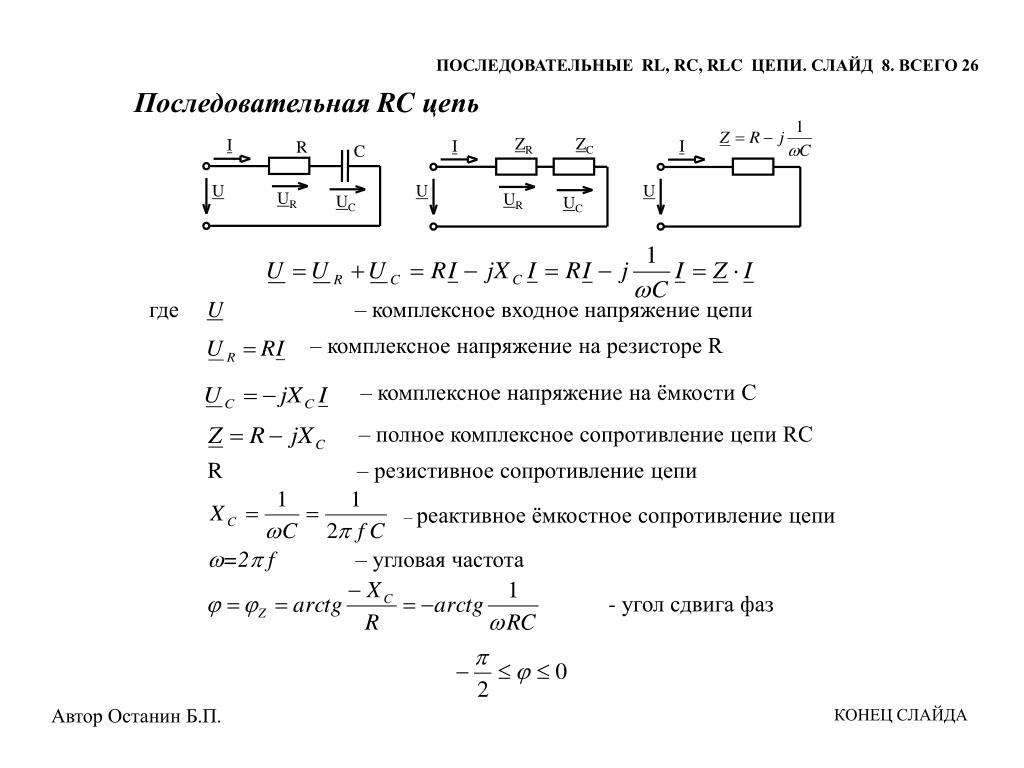 Перезаряд конденсаторов будет происходить
через включённый параллельно с ними
резистор R,
т.е. постоянная времени перезаряда
конденсаторов будет равна: τ=(С1+С2)R.
Входной и выходной импульсы приведены
на рис.1.35. Как видим, данная цепь с двумя
конденсаторами ведёт себя как
дифференцирующая цепочка (сравните
рис.1.35 и 1.29).
Перезаряд конденсаторов будет происходить
через включённый параллельно с ними
резистор R,
т.е. постоянная времени перезаряда
конденсаторов будет равна: τ=(С1+С2)R.
Входной и выходной импульсы приведены
на рис.1.35. Как видим, данная цепь с двумя
конденсаторами ведёт себя как
дифференцирующая цепочка (сравните
рис.1.35 и 1.29).
Рис.1.35. Входной и выходной импульсы цепи, приведённой на рис.1.34.
Р ассмотрим RC-цепь, соединяющую два резистора и два конденсатора (рис.1.36).
Рис.1.36. RC-цепь, содержащая два резистора и два конденсатора.
В
момент положительного скачка входного
напряжения конденсатор С2 зарядится до напряжения .
В последующее время будет происходить
перезаряд конденсаторов с постоянной
времени τ=(С1+С2)R1R2/(R1+R2)
(конденсаторы и резисторы при перезарядке
конденсаторов будут включены параллельно).
Р ис.1.37. Входной и выходные сигналы цепи, приведённой на рис.1.36.
ДифференциаторRC Схемотехника — Блог DCAClab
ДифференциаторRC:
Дифференциатор RC представляет собой серию, соединяющую сеть RC. Его выходные данные используются для математических процессов.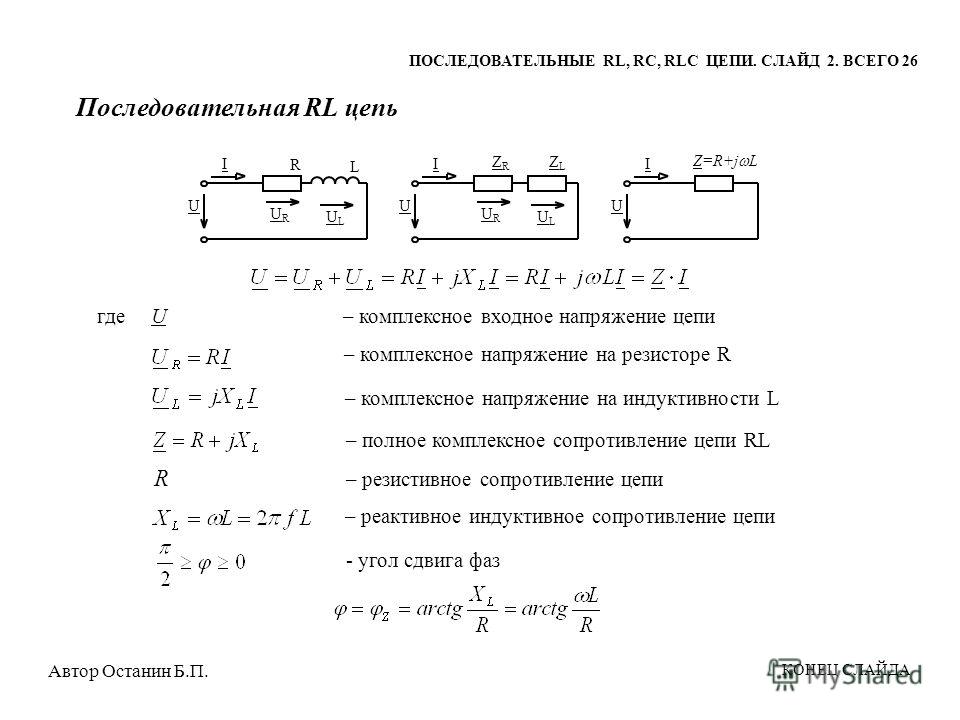 Дифференциатор RC представляет собой емкость, последовательно соединенную с сопротивлением. Это частотно-зависимое устройство, в котором реактивное сопротивление включено последовательно с постоянным сопротивлением. Как и в схеме интегратора, выходное напряжение зависит от постоянной времени цепи RC и входной частоты.
Дифференциатор RC представляет собой емкость, последовательно соединенную с сопротивлением. Это частотно-зависимое устройство, в котором реактивное сопротивление включено последовательно с постоянным сопротивлением. Как и в схеме интегратора, выходное напряжение зависит от постоянной времени цепи RC и входной частоты.
Радиоуправляемый дифференциатор Схема:
Цепь, в которой выходное напряжение прямо пропорционально производной входного, называется дифференцирующей схемой.
Дифференциальная цепь представляет собой простую последовательную RC-цепь, в которой выход подключается к резистору R.
Таким образом, если постоянный ток. или постоянный вход применяется к такой схеме, выход будет равен нулю.
На рис.1 показана типовая дифференцирующая цепь.
Для достижения хорошей дифференциации должны быть выполнены следующие два условия:
- Постоянная времени RC цепи должна быть намного меньше периода времени входной волны.

- Значение X C должно быть в 10 или более раз больше, чем R на рабочей частоте.
При выполнении этих условий выход через R будет производной от входа.
Пусть e i — входное переменное напряжение
И пусть i — результирующий переменный ток.
Заряд q на конденсаторе C в любой момент равен
Теперь
Или
Поскольку реактивное сопротивление емкости намного больше, чем R, входное напряжение можно считать равным емкости конденсатора. напряжение с незначительной погрешностью, т.е.
Итак,
Выходное напряжение,
Отсюда
Прямоугольная волна на входе:
Рис.2
На участке входного прямоугольного сигнала его амплитуда резко меняется, поэтому дифференцированная волна будет представлять собой острый узкий импульс, как показано на рис.2.
Однако во время постоянной части CB входа выход будет равен нулю, потому что производная константы равна нулю.
Давайте посмотрим на физическое объяснение такого поведения схемы.
Поскольку постоянная времени RC цепи очень мала по отношению к период входной волны и X C >>R,
Конденсатор полностью заряжается в начале каждого полупериода входной волны.
В течение оставшейся части полупериода выход схемы будет равен нулю, поскольку напряжение на конденсаторе (e c ) нейтрализует входное напряжение, и через R не может протекать ток.
Таким образом, мы получим резкий импульс на выходе в начале каждого полупериода входной волны, а в оставшуюся часть полупериода входной волны выход будет равен нулю.
Такие импульсы широко используются в электронных схемах, например. в телевизионных передатчиках и приемниках, в мультивибраторах для инициирования действия и т. д.
Рис. 3: Входная прямоугольная волнаВыходная форма волны RC:
при ширине импульса (а в нашем примере выше это 0,1 x 10 мс = 1 мс) или меньше мы можем получить требуемые выбросы на выходе, и чем меньше постоянная времени RC для данной ширины импульса, тем острее будут выбросы.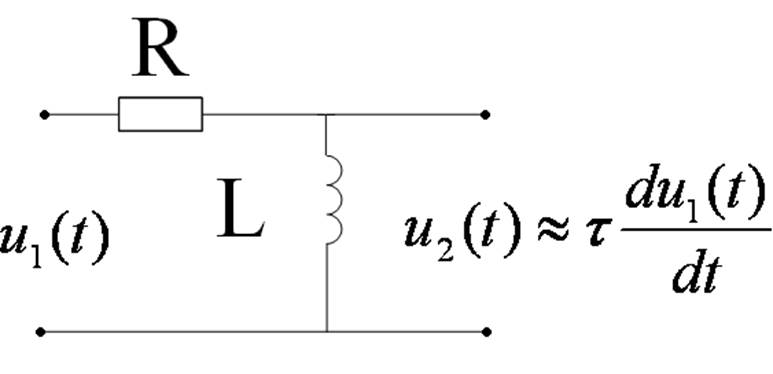 Таким образом, точная форма выходного сигнала зависит от значения постоянной времени RC.
Таким образом, точная форма выходного сигнала зависит от значения постоянной времени RC.
Вывод:
В этом учебном пособии по RC-дифференциатору мы видели, что входной сигнал подается на одну сторону конденсатора, а выходной — на резистор. Схема дифференциатора используется для создания триггерных или пиковых импульсов для приложений схемы синхронизации.
Когда на эту RC-цепь подается ступенчатая прямоугольная волна, она создает на выходе сигнал совершенно другой формы. Форма выходного сигнала в зависимости от периодического времени T (и, следовательно, частоты ƒ) входного прямоугольного сигнала и от значения постоянной времени RC-цепи.
Когда периодическое время формы входного сигнала аналогично или меньше (более высокая частота) постоянной времени RC-цепи, форма выходного сигнала напоминает форму входного сигнала, т. е. прямоугольный профиль. Когда периодическое время входного сигнала намного больше (более низкая частота) постоянной времени цепи RC, выходной сигнал напоминает узкие положительные и отрицательные пики.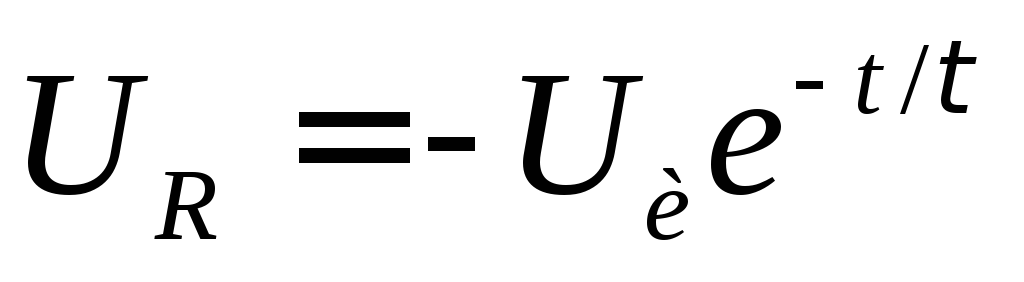
Положительный выброс на выходе создается передним фронтом входной прямоугольной волны, а отрицательный выброс на выходе создается задним фронтом входной прямоугольной волны. Тогда выход RC-цепи дифференциатора зависит от скорости изменения входного напряжения, поскольку эффект очень похож на математическую функцию дифференцирования.
Live Simulation: RC дифференциатор Circuit
See My All Simulation
Нравится:
Нравится Загрузка…
Дифференциаторы — Формирование волны — Основы электроники
Формирование волны
5 Дифференциация является прямой противоположностью интеграции. В РЦ интегратора, выход снимается с конденсатора. В дифференциале, выход берется через резистор. Аналогично, это означает, что когда В качестве дифференциатора используется цепь RL, берется дифференцированный выход через индуктор.
Применение закона Кирхгофа показывает взаимосвязь между формами волны
через резистор и конденсатор в последовательной сети.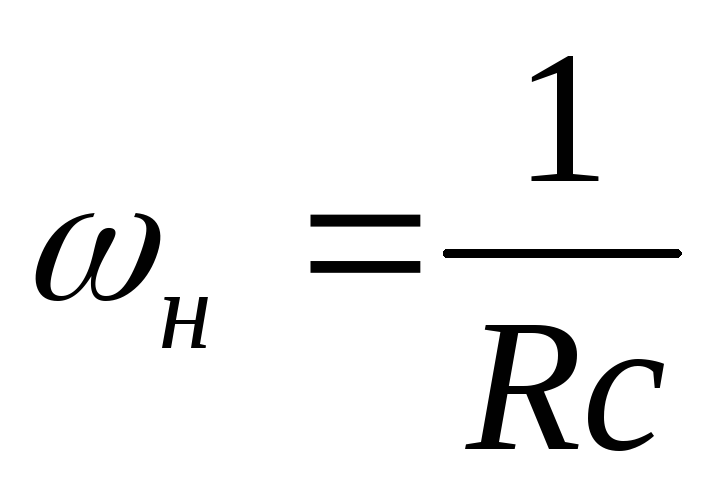 Поскольку сумма
падение напряжения в замкнутом контуре должно равняться общему приложенному напряжению,
графическая сумма сигналов напряжения в замкнутом контуре должна равняться приложенному
форма волны. На рисунке ниже показана схема дифференциатора с выходным сигналом.
через переменный резистор.
Поскольку сумма
падение напряжения в замкнутом контуре должно равняться общему приложенному напряжению,
графическая сумма сигналов напряжения в замкнутом контуре должна равняться приложенному
форма волны. На рисунке ниже показана схема дифференциатора с выходным сигналом.
через переменный резистор.
RC-цепь в качестве дифференциатора.
Краткосрочный дифференциатор с постоянной выдержкой времени
С переменным резистором, установленным на 1000 Ом, и номиналом конденсатора 0,01 мкФ, постоянная времени цепи 10 мкс. Поскольку входной сигнал имеет длительность 100 мкс, замыкание короткое схема с постоянной временем.
В первый момент времени в короткозамкнутой цепи напряжение на конденсаторе равен 0. Ток протекает через резистор и вызывает Максимальное напряжение, которое должно быть на нем. Это показано в первый момент времени на графике рисунка ниже.
Прямоугольная волна применяется к короткому постоянному дифференциатору.
Когда конденсатор начинает накапливать заряд, напряжение на
резистор начнет уменьшаться. В конце первой постоянной времени
напряжение на резисторе уменьшится на величину, равную
до 63,2 процента приложенного напряжения. Поскольку приложено 100 вольт, напряжение
на резисторе после 1 τ будет равно 36,8 вольта. После
вторая постоянная времени, напряжение на резисторе упадет до
13,5 вольт. В конце третьей постоянной времени в Р будет 5 вольт, а в конце четвертой постоянной времени 2 вольта. В
конце пятой постоянной времени напряжение на резисторе будет очень
близко к 0 вольт. Поскольку постоянная времени равна 10 микросекундам,
потребуется в общей сложности 50 микросекунд, чтобы полностью зарядить конденсатор и остановить
протекание тока в цепи.
В конце первой постоянной времени
напряжение на резисторе уменьшится на величину, равную
до 63,2 процента приложенного напряжения. Поскольку приложено 100 вольт, напряжение
на резисторе после 1 τ будет равно 36,8 вольта. После
вторая постоянная времени, напряжение на резисторе упадет до
13,5 вольт. В конце третьей постоянной времени в Р будет 5 вольт, а в конце четвертой постоянной времени 2 вольта. В
конце пятой постоянной времени напряжение на резисторе будет очень
близко к 0 вольт. Поскольку постоянная времени равна 10 микросекундам,
потребуется в общей сложности 50 микросекунд, чтобы полностью зарядить конденсатор и остановить
протекание тока в цепи.
Как показано на рисунке выше, наклон кривой заряда будет очень резким.
Напряжение на резисторе будет оставаться равным 0 вольт до конца
100 микросекунд. В это время приложенное напряжение внезапно падает до 0, и
теперь конденсатор будет разряжаться через резистор. В это время
разрядный ток будет максимальным, что приведет к развитию большого разрядного напряжения
через резистор. Это показано как отрицательный всплеск на рисунке выше.
Поскольку ток течет от конденсатора, который теперь действует как источник,
уменьшается экспоненциально, напряжение на резисторе также будет уменьшаться.
Напряжение резистора будет экспоненциально уменьшаться до 0 вольт за 5 постоянных времени.
Все это действие разряда займет в общей сложности 50 микросекунд.
кривая разряда также показана на рисунке выше. В конце
200 микросекунд действие начинается снова. Форма выходного сигнала, взятая через
резистор в этой короткой цепи с постоянной выдержкой времени является примером
дифференциация. При применении прямоугольной волны положительные и отрицательные пики
производятся на выходе. Эти всплески приблизительно соответствуют скорости изменения
входной прямоугольной волны.
Это показано как отрицательный всплеск на рисунке выше.
Поскольку ток течет от конденсатора, который теперь действует как источник,
уменьшается экспоненциально, напряжение на резисторе также будет уменьшаться.
Напряжение резистора будет экспоненциально уменьшаться до 0 вольт за 5 постоянных времени.
Все это действие разряда займет в общей сложности 50 микросекунд.
кривая разряда также показана на рисунке выше. В конце
200 микросекунд действие начинается снова. Форма выходного сигнала, взятая через
резистор в этой короткой цепи с постоянной выдержкой времени является примером
дифференциация. При применении прямоугольной волны положительные и отрицательные пики
производятся на выходе. Эти всплески приблизительно соответствуют скорости изменения
входной прямоугольной волны.
Дифференциатор средней постоянной времени
Выход через резистор в RC-цепи со средней постоянной времени
показано на рисунке ниже. Значение переменного резистора было
увеличилось до значения 10000 Ом.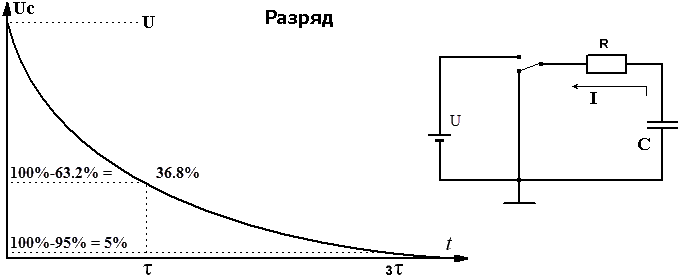 Это означает, что постоянная времени
схема равна длительности входного импульса или 100 мкс.
Для ясности формы сигналов напряжения развивались как на резисторе, так и на
показаны конденсаторы. Как и прежде, сумма напряжений на резисторе и
конденсатор должен быть равен приложенному напряжению 100 вольт.
Это означает, что постоянная времени
схема равна длительности входного импульса или 100 мкс.
Для ясности формы сигналов напряжения развивались как на резисторе, так и на
показаны конденсаторы. Как и прежде, сумма напряжений на резисторе и
конденсатор должен быть равен приложенному напряжению 100 вольт.
Выходы напряжения в среднем постоянном дифференциаторе времени.
В первый момент времени импульс амплитудой 100 вольт длительностью
применяется 100 микросекунд. Поскольку конденсатор не может быстро реагировать на
при изменении напряжения все приложенное напряжение ощущается на резисторе.
На рисунке выше показано напряжение на резисторе ( v R ).
должно быть 100 вольт, а напряжение на конденсаторе ( v C ) равно
быть 0 вольт. Со временем конденсатор заряжается. Как конденсатор
напряжение увеличивается, напряжение на резисторе уменьшается. С тех пор, как
конденсатору разрешается заряжаться за 100 мкс (равно 1 т в этой цепи) конденсатор будет заряжаться до 63,2 процента приложенного
напряжение в конце 1 τ , или 63,2 вольта. Поскольку закон Кирхгофа должен
постоянно соблюдать, напряжение на резисторе должно быть равно
разница между приложенным напряжением и зарядом на
конденсатор (100 — 63,2 вольта), или 36,8 вольта.
Поскольку закон Кирхгофа должен
постоянно соблюдать, напряжение на резисторе должно быть равно
разница между приложенным напряжением и зарядом на
конденсатор (100 — 63,2 вольта), или 36,8 вольта.
В конце первых 100 микросекунд входное напряжение резко падает. до 0 вольт. Заряд на конденсаторе (-63,2 вольта) становится источником и все напряжение развивается на резисторе в первый момент.
Конденсатор разряжается в течение следующих 100 микросекунд. Напряжение на резистор уменьшается с той же скоростью, что и напряжение на конденсаторе, и общее напряжение поддерживается на уровне 0. Это экспоненциальное уменьшение напряжения резистора показано в течение вторых 100 микросекунд на рисунке выше. Конденсатор будет разрядить 63,2 процента своего заряда до значения 23,3 вольта в конце вторые 100 микросекунд. Напряжение на резисторе увеличится в плюсе. направление до значения -23,3 вольта, чтобы поддерживать общее напряжение на уровне 0 вольт.
По истечении 200 микросекунд входное напряжение снова резко возрастает до
100 вольт. Так как конденсатор не может реагировать на увеличение 100 вольт
мгновенно на резисторе происходит изменение 100 вольт.
напряжение на резисторе резко возрастает с -23,3 вольта до +76,7 вольта.
Теперь конденсатор начнет заряжаться в течение 100 микросекунд. Напряжение будет
уменьшается на резисторе. Это действие заряда и разряда будет продолжаться
на многие циклы. Наконец, напряжение на конденсаторе возрастет и
падают на равные суммы как выше, так и ниже примерно 50-вольтового уровня. Резистор
напряжение также будет повышаться и понижаться на равные величины примерно до уровня 0 вольт.
Так как конденсатор не может реагировать на увеличение 100 вольт
мгновенно на резисторе происходит изменение 100 вольт.
напряжение на резисторе резко возрастает с -23,3 вольта до +76,7 вольта.
Теперь конденсатор начнет заряжаться в течение 100 микросекунд. Напряжение будет
уменьшается на резисторе. Это действие заряда и разряда будет продолжаться
на многие циклы. Наконец, напряжение на конденсаторе возрастет и
падают на равные суммы как выше, так и ниже примерно 50-вольтового уровня. Резистор
напряжение также будет повышаться и понижаться на равные величины примерно до уровня 0 вольт.
Дифференциатор с длительной постоянной выдержкой времени
Если увеличить постоянную времени цепи RC-дифференциатора, чтобы
это длинная постоянная схема, выходной сигнал дифференциатора будет казаться более
как ввод. Постоянная времени цепи может быть изменена либо
увеличение значения емкости или сопротивления. В этой цепи время
постоянная будет увеличиваться за счет увеличения значения сопротивления от
от 10 000 до 100 000 Ом. Увеличение значения сопротивления приведет к
постоянная времени 1000 микросекунд. Постоянная времени в 10 раз больше
длительность входного импульса. Выход этой долговременной постоянной схемы
показано на рисунке ниже.
Увеличение значения сопротивления приведет к
постоянная времени 1000 микросекунд. Постоянная времени в 10 раз больше
длительность входного импульса. Выход этой долговременной постоянной схемы
показано на рисунке ниже.
Выходное напряжение в дифференциаторе с длительной постоянной времени.
В первый момент времени импульс амплитудой 100 вольт и длительностью применяется 100 микросекунд. Поскольку конденсатор не может реагировать мгновенно к изменению напряжения ощущается все приложенное напряжение через резистор. Со временем конденсатор заряжается и напряжение на резисторе уменьшится. С тех пор, как конденсатору разрешено заряжаться в течение 100 микросекунд, конденсатор будет плата только за 1/10 от 1 τ или до 9,5 % приложенного напряжения. Напряжение на резисторе должно быть равно разнице между приложенное напряжение и заряд на конденсаторе (100 — 9,5 вольт), или 90,5 вольт.
В конце первых 100 мкс входного сигнала приложенное напряжение внезапно
падает до 0 вольт, изменение 100 вольт.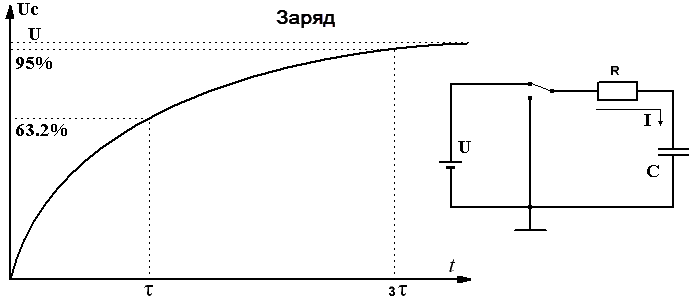 Так как конденсатор не может
реагировать на столь быстрое изменение напряжения, он становится источником 9,5 вольт. Этот
вызывает ощущение напряжения -9,5 на резисторе в первый момент
время. Сумма напряжений на двух компонентах теперь равна 0 вольт.
Так как конденсатор не может
реагировать на столь быстрое изменение напряжения, он становится источником 9,5 вольт. Этот
вызывает ощущение напряжения -9,5 на резисторе в первый момент
время. Сумма напряжений на двух компонентах теперь равна 0 вольт.
В течение следующих 100 микросекунд конденсатор разряжается. Общая схема напряжение поддерживается на уровне 0 за счет уменьшения напряжения на резисторе при с той же скоростью, что и разрядка конденсатора. Это экспоненциальное уменьшение в напряжении резистора показано в течение вторых 100 микросекунд работы. Конденсатор теперь разрядит 9,5% своего заряда до значения 8,6. вольт. По истечении вторых 100 мкс напряжение на резисторе подняться в положительном направлении до значения -8,6 вольт для поддержания общее напряжение цепи при 0 вольт.
По истечении 200 мкс входное напряжение снова резко возрастает до
100 вольт. Поскольку конденсатор не может реагировать на изменение 100 вольт
мгновенно на резисторе происходит изменение 100 вольт.