|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Интересное: Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является. Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 2 дифференциальная форма закона Ома. где:
интегральная форма Вычислим Rчерез — удельное сопротивление материала: I=U/R=US/l следуетчтоU= Il /S E=U/l=Il /Sl=(I/S )* следуетI/S=E/ 1/ = следует что
9 вопрос При движении частицы в магнитном поле сила Лоренца не совершает работу , так как она всегда перпендикулярна скорости . отсюда следует что угол равен 90 градусов и значит cosравен 0 A=FScos £=0 ( A=qVBsinβ*cos£) (A=F*r- скалярное произведение)
10 вопрос dFA= IdlBsin £ Два прямых противоположно направленных тока будут отталкиваться друг от друга Предположим , что они оба бесконечной длины dF21= -I1dl (µ0I2 /2pir) dF12=I2dl (-µ0I1/ 2 pi r) dF21=dF12 Сила взаимодействия двух проводников с токами : F= µ0I1I2dl / 2 pir = µ0I1I2/ 2 pir ( одинаковая длина проводника) µ0— магнитная постоянная; I1I2– силы токов ; r – расстояние между проводниками
17. Закон Фарадея [править] Согласно закону электромагнитной индукции Фарадея (в СИ): где — электродвижущая сила, действующая вдоль произвольно выбранного контура, — магнитный поток через поверхность, натянутую на этот контур. Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца: Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток. Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом: где — электродвижущая сила, — число витков, — магнитный поток через один виток, — потокосцепление катушки. Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. · В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)[1]. Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство продолжает соблюдаться, но ЭДС в левой части теперь не сводится к (которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула верна так же, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника). 16.
Индукцио́нный ток — электрический ток, возникающий в замкнутом проводящем контуре при изменении потока магнитной индукции, пронизывающего этот контур. Величина и направление индукционного тока определяются законом электромагнитной индукции и правилом Ленца. Магни́тный пото́к — поток как интеграл вектора магнитной индукции через конечную поверхность . Определяется через интеграл по поверхности при этом векторный элемент площади поверхности определяется как где — единичный вектор, нормальный к поверхности. Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади: где α — угол между вектором магнитной индукции и нормалью к плоскости площади. Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру: Поток через поверхность и ЭДС в контуре [править] Определение поверхностного интеграла предполагает, что поверхность Σ поделена на мелкие элементы. Векторное поле F(r, t) определено во всём пространстве, а поверхность Σ ограничена кривой ∂Σ, движущейся со скоростью v. По этой поверхности производится интегрирование поля. Закон электромагнитной индукции Фарадея использует понятие магнитного потока ΦB через замкнутую поверхность Σ, который определён через поверхностный интеграл: где dA — площадь элемента поверхности Σ(t), B — магнитное поле, а B·dA — скалярное произведение B и dA. Предполагается, что поверхность имеет «устье», очерчённое замкнутой кривой, обозначенной ∂Σ(t). Закон индукции Фарадея утверждает, что когда поток изменяется, то при перемещении единичного положительного пробного заряда по замкнутой кривой ∂Σ совершается работа , величина которой определяется по формуле: где — величина электродвижущей силы (ЭДС) в вольтах, а ΦB — магнитный поток в веберах. Для плотно намотанной катушки индуктивности, содержащей N витков, каждый с одинаковым магнитным потоком ΦB, закон индукции Фарадея утверждает, что: где N — число витков провода, Φ Закон Ленца [править] Заряд q в проводнике на левой стороне петли испытывает силу Лоренца q v × B k = −q v B(xC − w / 2) j (j, k — единичные векторы в направлениях y и z; см. векторное произведение векторов), что вызывает ЭДС (работу на единицу заряда) v ℓ B(xC− w / 2) по всей длине левой стороны петли. На правой стороне петля аналогичное рассуждение показывает, что ЭДС равнаv ℓ B(xC + w / 2). Две противоположные друг другу ЭДС толкают положительный заряд по направлению к нижней части петли. В случае, когда поле  Используя правило правой руки, мы получаем, что поле B, создаваемое током, противоположно приложенному полю.[13]ЭДС, вызывающая ток, должна увеличиваться по направлению против часовой стрелки (в отличие от тока). Складывая ЭДС в направлении против часовой стелки вдоль петли мы находим:
⇐ Предыдущая12 Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… |
ниже).
Каждый элемент связан с вектором dA, величина которого равна площади элемента, а направление — по нормали к элементу во внешнюю сторону.
Направление электродвижущей силы определяется законом Ленца.
1 2 3 Байланысты:
1 2 3 ©melimde.com 2022 | Басты бет |
33 Kb.
6) какЗаконов постоянного тока.
Электрический ток. Мощность и плотность тока. ЭДС и напряжение. Закон Ома. Закон Ома для однородного участка цепи. Закон Ома для неоднородного участка цепи в интегральной форме. Закон Ома для полной цепи. Закон Ома в дифференциальной форме. Законы постоянного тока. Электрический ток. Мощность и плотность тока. ЭДС и напряжение. Закон Ома. Закон Ома для однородного участка цепи. Закон Ома для неоднородного участка цепи в интегральной форме. Закон Ома для полной цепи. Закон Ома в дифференциальной форме.ЗАКОНЫ ПОСТОЯННЫЙ ТОК
§ 1 Электрический ток .
Мощность и плотность тока.
ЭДС и напряжение
I. Любое упорядоченное (направленное) движение электрических зарядов, называемое электрическим током .
При внешнем электрическом поле E в проводнике начинают двигаться заряды, т.е. генерируется электрический ток. При этом положительные заряды движутся поперек поля, а отрицательные — против поля. Примите за направление тока направление движения положительных зарядов. Для возникновения и существования электрического тока необходимы два условия:
1) наличие свободных носителей заряда (т.е. вещество должно быть проводником или полупроводником при высоких температурах),
2) Наличие внешнего электрического поля.
Для количественной характеристики электрического тока вводится — сила тока — скалярная физическая величина, равная количеству электрического заряда, переносимого в единицу времени через поперечное сечение S .— для постоянного тока и
— для переменного тока.
Ток, сила и направление которого не меняются со временем, называется постоянным.
Плотность тока — векторная физическая величина, численно равная силе тока, протекающего через единицу площади перпендикулярно току.
— для постоянного тока и
— для переменного тока.
II. К участку рассматриваемого проводника поступает ток I , необходимый для поддержания постоянной разности потенциалов между этими точками проводника. Для поддержания постоянной разности потенциалов концы проводника необходимо подключить к источнику питания. Источник тока работает по перемещению электрических зарядов по цепи. Эту работу совершают внешние силы — силы не электростатического происхождения, действующие на заряды со стороны источника питания. Природа внешних сил может быть
разные (кроме фиксированных платежей):
1) химическая реакция — в гальванических элементах (батареях), аккумуляторных батареях,
2) Электромагнитные — в генераторах. Генератор может использовать а) механическую энергию — гидро, б) атомную — ядерный реактор) тепловую — ТЭЦ, з) приливов — ПЭС, Г) ветер — ветряная электростанция и т.д.
3) использование фотоэффекта — фотонапряжение в калькуляторах и солнечных батареях4) пьезоэлектрическое — пьезоЭДС, например пьезозажигалка,
5) контактный потенциал — термоЭДС в термопарах и т.
д.
Поле внешних сил, электрические заряды движутся внутри источника питания против сил электростатического поля, в результате чего по клемме источника тока и поддерживается разностью потенциалов в цепи ток.
ЭДС определяется работой внешних сил по перемещению единицы положительного заряда по замкнутому контуру.
Двусторонняя сила равна:
где — поле внешних сил. Работа внешних сил по перемещению заряда q на замкнутом участке цепи равна:
т.е. ЭДС циркуляции равна вектору напряженности внешних сил. На участке 1 — 2 (см. рисунок) кроме внешних сил сила, действующая на электростатическое поле
т.е. результирующая сила на участке 1 — 2 равна
, затем
Для замкнутого контура
Напряжение U на участке 1 -2 называется физической величиной, определяемой работой, совершаемой суммарным полем электростатических (кулоновских) и внешних сил при перемещении единичного положительного заряда по данному участку цепи
в
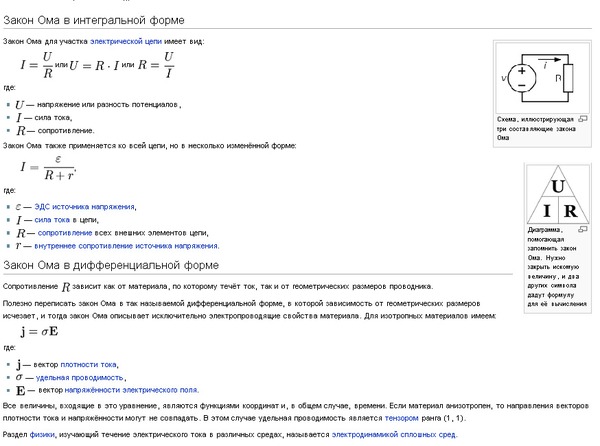
§ 2 Закон Ома
1.
Закон Ома для однородного участка цепи.Называется однородная область, свободная от ЭМП.
Ток на однородном участке цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению цепи
1 Ом — сопротивление проводника, по которому при напряжении 1 В 1 А протекает ток.
Г —
электропроводность. (Сименс).
Сопротивление R проводника зависит от его размера и формы, а также материала проводника.,
где ρ — удельное сопротивление проводника — сопротивление на единицу длины проводника.
ℓ — длина провода; S — площадь поперечного сечения проводника.
2. Закон Ома для неоднородного участка цепи
Неоднородным называется участок цепи, содержащий ЭДС.
— Закон Ома для неоднородного участка цепи в интегральной форме
3.
Закон Ома для замкнутой цепи (полной цепи).
где R — сопротивление внешней цепи, Ом0051 r — импеданс источника ЭДС, затем
-Закон Ома для полной цепи
4. Закон Ома в дифференциальной форме
σ — электропроводность;
—
Закон Ома в дифференциальной форме.
Плотность тока прямо пропорциональна напряженности электрического поля Е . Коэффициент пропорциональности σ — электропроводность.
К списку лекций
ЗаконОма — Electronics-Lab.com
Введение
Фундаментальное соотношение между током, напряжением и сопротивлением известно как закон Ома и, вероятно, является самым известным и элементарным физическим законом электроники. Именно в 1827 году немецкий физик Георг Симон Ом впервые публикует в книге « Die galvanische Kette, mathematisch bearbeitet » (на английском языке: математическое исследование гальванической цепи) ранняя форма закона, который позже получит его имя.
В первом разделе мы представим макроскопический закон Ома, который представляет собой форму, которая демонстрируется учащимся в начале процесса обучения.
Во втором разделе мы увидим, что различные формы уравнения могут быть адаптированы в зависимости от топологии цепи и характера ее источника, в частности, при рассмотрении режима переменного тока.
Более сложные концепции представлены в третьем разделе, где мы сосредоточимся на мезоскопическом определении уравнения, известного как локальное выражение закона Ома .
Презентация
Рассмотрим электрический ток I, протекающий через резистор R, который создает разность потенциалов U на его клеммах:
рис. 1: Ток, проходящий через резистор, создает напряжение на его клеммах Закон Ома устанавливает простую линейную зависимость между эти три параметра, такие как U=R×I . Любой электрический компонент, который соответствует закону Ома, может быть помечен как омический проводник и имеет вольт-амперную характеристику, как показано на рис.
2 :
Важно отметить, что закон Ома является эмпирическим , что означает, что он получен из экспериментальных наблюдений, а не из теории.
Макроскопическая форма широко используется в электронных схемах, и ее очень полезно знать. Мы можем вычислить неизвестный параметр (например, R), зная два других параметра (например, U и I). Более того, это позволяет записать выражение для рассеиваемой мощности в резисторе в виде P=R×I 2 .
Эквивалентность в режиме переменного тока
Закон Ома можно обобщить, когда ток и напряжение имеют синусоидальную форму. В этом случае мы используем комплексное обозначение для записи закона, такого как U=Z×I , где Z представляет собой комплексное сопротивление набора линейных компонентов (резистор, конденсатор и катушка индуктивности).
В резисторе
Если мы снова рассмотрим схему, представленную на рис.
1 в режиме переменного тока, закон Ома можно записать в виде u(t)=Ri(t) где i(t)=I×sin(ωt) , u(t)=U×sin(ωt+φ), а I, U — амплитуды соответствующих сигналов. Однако, поскольку разность фаз в чисто резистивной составляющей равна нулю, получаем U=RI .
В режиме переменного тока выражение закона Ома в резисторе аналогично тому, как в режиме постоянного тока.
В катушке индуктивности
При рассмотрении реактивных элементов все обстоит немного иначе, начнем с катушки индуктивности:
рис. 3: Переменное напряжение и ток на катушке индуктивности LСогласно закону Ленца, напряжение u(t), создаваемое индуктор пропорционален как индуктивности, так и вариациям тока i(t), как показано в уравнении 1 :
уравнение 1: Зависимость между напряжением и током в катушке индуктивности Из Уравнения 1 можно показать зависимость между током и напряжением можно записать u(t)=Lω×Isin(ωt+φ) .
Демонстрация становится еще проще, если использовать сложные обозначения и знать, что операция вывода в комплексной области аналогична умножению на jω, которое состоит в умножении фазора i(t) на ω и переходе к вращению φ=+π/2 рад (см. руководство по фазовым диаграммам и алгебре).
Таким образом, в катушке индуктивности сигналы тока и напряжения сдвинуты по фазе на Δφ=+π/2 рад. Поскольку напряжение обычно считается эталонным, его выражение остается неизменным (u(t)=U×sin(ωt)), а ток можно записать i(t)=I×sin(ωt+φ).
Закон Ома для катушки индуктивности можно записать в виде U=LωI ; φ=+π/2 рад.
В конденсаторе
Наконец, рассмотрим конденсатор в режиме переменного тока:
рис. 4: Напряжение переменного тока и ток на конденсаторе емкостью C В этой конфигурации заряд конденсатора является функцией времени и выражается как q(t)=C×u(t) . Поскольку i(t)=dq(t)/dt, мы можем показать непосредственно или с помощью комплексных обозначений, что i(t)=-Cω×Usin(ωt+φ).
Если мы снова рассмотрим напряжение как опорный сигнал, фазовый сдвиг здесь равен Δφ=-π/2 рад , поэтому выражение для тока есть i(t)=I×sin(ωt- ф).
Закон Ома для конденсатора можно записать в виде U=I/Cω ; φ=-π/2 рад.
Локальная форма
В этом разделе мы обсудим более сложную концепцию, известную как локальная форма закона Ома . Прежде чем представить эту специальную форму, нам необходимо ввести и определить некоторые понятия. Мы хотим отметить, что далее векторы выделены жирным шрифтом, а скаляры — нет.
Представление и определения
Локальная форма может быть применена к промежуточной пространственной шкале между микроскопической и макроскопической, известной как мезоскопическая шкала . Обычно считается, что мезоскопический масштаб достаточно велик, чтобы содержать большое количество частиц в элементарном объеме (в нашем случае электронов), но достаточно мал, чтобы такие параметры, как давление и температура, оставались локальными.
Мы обычно называем электроны «носителями заряда» или просто «носителями», они определяются плотностью носителей n e , их вектором скорости v , элементарным зарядом e и их массой m e .
Из этих параметров мы можем определить важный вектор j известный как плотность тока будет j =-en e v . Термин -en e также известен как плотность заряда и обозначается как ρ e .
Модель Drude
Рассмотрим омический проводник сечения S, на который подается определенное напряжение V, эта разность потенциалов индуцирует электрическое поле E, заставляющее носитель проводника двигаться:
рис. 5: Схематическое изображение сил (выделено красным) и поля внутри омического проводникаДвижение носителей определяется двумя силами, действующими в противоположных направлениях:
- Электрическая сила -e E стремится сдвинуть электроны в направлении, противоположном электрическому полю (то же направление для положительно заряженных носителей) .
- Сила трения -k v , стремящаяся замедлить электроны. Эта сила обусловлена неподвижными зарядами, составляющими кристаллическую решетку омического проводника, в которую с определенной вероятностью врезаются электроны. Параметр k — постоянная величина, зависящая от материала, рассматриваемого в качестве проводника.
Модель Друде (1900) состоит из учета этих двух сил и применения второго закона Ньютона к носителям:
eq 2: Второй закон Ньютона в модели ДрудеВыражение локальной формы
Мы можем изменить Уравнение 2 и записать k/m=1/τ, где τ — параметр времени релаксации омического проводника:
В постоянном режиме (t>>τ) это дифференциальное уравнение первого порядка принимает следующее выражение как решение:
Наконец, плотность тока может быть переписана следующим образом: =σ E .
Локальная форма особенно полезна для изучения электрических свойств в микроскопическом масштабе.
Электрическое сопротивление и макроскопический закон Ома
Электрическое поле в омическом проводнике можно записать E =(V/L) n , где n является единичным вектором в том же направлении, что и E .
Электрический ток I определяется как:
Сила тока (Кл/с) действительно может быть понята как сумма плотности тока (Кл/м 2 /с) на сечении (м 2 ).
Для топологии, представленной в Рис. 5 , предыдущее выражение можно упростить до I=σES . При замене поля E на V/L получаем:
Наконец, мы можем заключить, что локальная форма закона Ома позволяет нам получить как макроскопический закон Ома, так и определение сопротивления R=L/(σS). Также можно отметить, что 1/σ можно заменить на ρ , которое определяется как удельное сопротивление омического проводника.
Однако упрощение интегрального выражения опирается на две сильные гипотезы: проводимость σ постоянна в материале, а плотность тока Дж коллинеарна оси материала и равномерна.
В принципе, эти две гипотезы можно получить, если предположить, что материал изотропен (однородность во всех ориентациях).
В общем случае, для любой топологии и если материал анизотропный, сопротивление можно вычислить по следующей формуле:
Заключение
В этом руководстве основное внимание уделяется известному физическому закону, известному как закон Ома . Резюме дается в первом разделе, где показаны его структура, определение, последствия и использование.
Второй раздел дает более общую форму закона, когда источник питания работает в режиме переменного тока. При рассмотрении трех элементарных составляющих электроники мы понимаем, что форма закона в режиме переменного тока для резистора не меняется, а для реактивных составляющих записывается иначе.
В заключительном разделе мы представляем локальную форму закона Ома , адаптированную для промежуточной шкалы между макроскопическим и микроскопическим миром: мезоскопической шкалы.
