Дифференцирующая (укорачивающая) и разделительная RC-цепи — Мегаобучалка

 

Дифференцирующей цепью называют такую цепь, сигнал на выходе которой имеет значения, пропорциональные в каждый момент производной от входного сигнала. Следовательно, . Коэффициент К должен выражаться в секундах, в противном случае размерность левой и правой частей равенства не будет одинакова. Идеальным дифференцирующим устройством можно считать конденсатор С или катушку L. Например, при использовании конденсатора С можно считать входным сигналом напряжение на нём , а выходным — ток в цепи. Эти переменные связаны известным соотношением , т.е. ток в цепи пропорционален производной от входного напряжения. Однако использовать эту схему для практических целей нельзя, так как она не содержит элемента, который обеспечивал бы какую-либо регистрацию значений тока, измерение его значений.

Для того чтобы получить выходной сигнал в форме, удобной для наблюдения или регистрации, в цепь последовательно включают токочувствительный прибор с внутренним сопротивлением

R. В простейшем случаи это может быть резистор R, напряжение на котором пропорционально току .

Рассмотренная RC-цепочка может выполнять функции как дифференцирующей (укорачивающей) при , так и разделительной цепи, если .

На рис.1.11 показаны графики напряжений и такой цепочки.

 

а) б)

Рисунок 1.11 — а) режим 1 – , б) режим 2 –

 

Рассмотрим два режима:

I. Дифференцирующая цепь — , при этом возможны два варианта: а) ; б) ;

II. Разделительная цепь — , при этом также: а) ; б) .

I. Рассмотрим дифференцирующую цепочку под воздействием импульсной последовательности (рис.1.12).

 

Рисунок 1.12 — Принципиальная схема укорачивающей RC-цепочки

 

При импульсе конденсатор С заряжается под воздействием зарядного тока , при паузе — разряжается, обуславливая разрядный ток . При этом .

Допустим ,тогда им можно пренебречь ( ).

Рассмотрим режим I, вариант а): , .

После окончания импульса (момент времени ) .

В период паузы ( ) разряд конденсатора С получается полный (см. рис.1.13.), т.к. ;

;

.

Тогда

;

 

При получим:

 

.

 

Рисунок 1.13 — Зависимости (t) и (t)

 

Значит, получена идеальная дифференцирующая цепь. Следовательно, для того чтобы цепь была дифференцирующей необходимо выполнение трёх условий:

 

1) ;

2) ;

3) ;

 

При этом график напряжения при наличии импульсной последовательности на входе будет иметь следующий вид (рис.1.14):

Режим I, вариант б): , :

 

Рисунок 1.14 — График напряжения дифференцирующей цепи при наличии импульсной последовательности на входе

 

Графики напряжений и приведены на рис.1.15. В этом режиме с момента времени имеют место, в отличие от варианта а), новые начальные условия . Такой режим называют режимом негармонических возмущений.

 

Рисунок 1.15 — Зависимости (t) и (t); режим I, вариант б): ,

 

В период импульса переходные процессы аналогичны рассмотренным в варианте а), а в период паузы конденсатор С не успевает разрядиться до нуля за время , поэтому нулевые начальные условия не выполняются и для дифференцирующей цепочки такой вариант неприемлем.

Режим II при , обеспечивает вариант разделительной цепочки.

В момент времени , после действия импульса, (см. рис.1.16) , а в момент времени имеют место нулевые начальные условия. Сигнал на выходе повторяет сигнал на входе. Следовательно, такая цепочка является разделительной.

 

Рисунок 1.16 — Зависимости (t) и (t); режим II при ,

 

Режим II, при , , аналогичен варианту б) режима I, поскольку в момент времени также имеют место новые, ненулевые начальные условия (рис.1.17) (режим негармонических возмущений). Для разделительной цепи такой вариант неприемлем.

 

Рисунок 1.17 — Зависимости (t) и (t); режим II при ,

 

Цифровая электроника | Страница 8 из 32

Разделительная дифференцирующая RC-цепь

Электрическая принципиальная схема разделительной дифференцирующей RC-цепи и её временные диаграммы представлены на рис. 2.6.

Рис. 2.6. Разделительная дифференцирующая RC-цепь и временные диаграммы напряжений.

Как было показано ранее, меняется по закону:

для 0 ?t ?t_и,

  для t >t_и.

При  рассматриваемая RC-цепь выполняет функции разделительной цепи, назначение которой передать входное напряжение с наименьшими искажениями и отделить при этом постоянную составляющую. Абсолютная величина завала вершины равна напряжению на конденсаторе в момент t_и снятия входного импульса, т.е.

.

Для случая , с учетом рассмотренного ранее разложения функции  при  получаем:

.

Оценкой качества разделительной цепи является величина относительного завала вершины g, которая определяется как:

.

Таким образом, завал вершины, а значит искажение входного импульса, тем меньше, чем больше постоянная времени цепи t при данном t_и. Если величина завала вершины несравненно мала, то импульс передается без искажения.

Рис. 2.7. Диаграммы входного и выходного напряжений разделительной цепи.

Из временной диаграммы рис. 2.7 видно, что амплитуда последовательности импульсов выходного напряжения постоянна, но при этом импульсы смещаются относительно нулевого уровня. В установившемся режиме площади под графиком S₊ положительной и S_— отрицательной областей последовательности импульсов окажутся равными друг другу: S₊ = S_—.

Доказать этот факт можно, рассмотрев диаграмму тока, протекающего через резистор (рис.2.8). Очевидно, что i₁t₁ — это заряд Q_и, переносимый через емкость за время действия импульса на входе, а i₂(t₂—t₁) – заряд Q_п, переносимый через емкость за время паузы между импульсами, т.е. в обратном направлении. Тогда общий заряд, переносимый через емкость за время, равное периоду импульса будет равен:

.

Поскольку постоянная составляющая через емкость не проходит , следовательно,  или . Поскольку , а сопротивление – величина постоянная, то значит и равны S₊ и S_— на диаграмме U_вых. Таким образом, для разделительной цепи необходимо выполнение условия: .

Рис. 2.8. Диаграмма тока, протекающего через резистор разделительной RC-цепи.

Поскольку , а , то

Продифференцируем обе части полученного уравнения. Получим

Так как , то .

Рассмотрим случай . Поскольку , то можно записать . Тогда

.

Из полученной формулы следует название такой цепи – дифференцирующая. Для дифференцирующей цепи должно выполняться условие , т.е. конденсатор должен успевать быстро перезаряжаться при данном t_и. Диаграммы входного и выходного напряжений дифференцирующей цепи для последовательности импульсов представлены на рис. 2.9.

Рис. 2.9. Диаграммы входного и выходного напряжений дифференцирующей RC-цепи.

RC-цепь — Википедия

Материал из Википедии — свободной энциклопедии

RC цепь интегрирующего типа

RC-цепь — электрическая цепь, состоящая из конденсатора и резистора. Её можно рассматривать как делитель напряжения с одним из плеч, обладающих ёмкостным сопротивлением переменному току.

Интегрирующая RC-цепь

Реакция интегрирующей цепи на единичное ступенчатое воздействие. Осциллограммы, снятые с последовательной RC цепи.
R — 1500 Ом — желт.
С — 100нФ — син.
τ = 150us

Если входной сигнал подаётся к V_in, а выходной снимается с V_c (см. рисунок), то такая цепь называется цепью интегрирующего типа.

Реакция цепи интегрирующего типа на единичное ступенчатое воздействие с амплитудой V определяется следующей формулой:^[1]

Vc(t)=V0(1−e−t/RC).{\displaystyle \,\!V_{c}(t)=V_{0}\left(1-e^{-t/RC}\right).}

Таким образом, постоянная времени τ этого апериодического процесса будет равна

τ=RC.{\displaystyle \tau =RC.}

Интегрирующие цепи пропускают постоянную составляющую сигнала, отсекая высокие частоты, то есть являются фильтрами нижних частот. При этом чем выше постоянная времени τ{\displaystyle \tau }, тем ниже частота среза. В пределе пройдёт только постоянная составляющая. Это свойство используется во вторичных источниках питания, в которых необходимо отфильтровать переменную составляющую сетевого напряжения. Интегрирующими свойствами обладает кабель из пары проводов, поскольку любой провод является резистором, обладая собственным сопротивлением, а пара идущих рядом проводов ещё и образуют конденсатор, пусть и с малой ёмкостью. При прохождении сигналов по такому кабелю, их высокочастотная составляющая может теряться, причём тем сильнее, чем больше длина кабеля.

Применения

Дифференцирующая RC-цепь

Дифференцирующая RC-цепь получается, если поменять местами резистор R и конденсатор С в интегрирующей цепи. При этом входной сигнал идёт на конденсатор, а выходной снимается с резистора. Для постоянного напряжения конденсатор представляет собой разрыв цепи, то есть постоянная составляющая сигнала в цепи дифференцирующего типа будет отсечена. Такие цепи являются фильтрами верхних частот. И частота среза в них определяется всё той же постоянной времени τ{\displaystyle \tau }. Чем больше τ{\displaystyle \tau }, тем ниже частота, которая может быть без изменений пропущена через цепь.

Дифференцирующие цепи имеют ещё одну особенность. На выходе такой цепи один сигнал преобразуется в два последовательных скачка напряжения вверх и вниз относительно базы с амплитудой, равной входному напряжению. Базой является либо положительный вывод источника, либо «земля», в зависимости от того, куда подключён резистор. Когда резистор подключён к источнику, амплитуда положительного выходного импульса будет в два раза выше напряжения питания. Этим пользуются для умножения напряжения, а также, в случае подключения резистора к «земле», для формирования двуполярного напряжения из имеющегося однополярного.

Применение

См. также

Примечания

Изучение характеристик интегрирующей и дифференцирующей RC-цепей

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Рыбинская Государственная Авиационная Технологическая Академия

имени П.А. Соловьева

Факультет радиоэлектроники и информатики

Кафедра «Радиоэлектронные и телекоммуникационные системы»

                            лабораторная работа

прохождение  сигналов  через

простейшие  RC-цепи

Студенты:                                                        Силаев А.Ю. Соловьев П.Е.

Преподаватель:                                                Ландо В.С.

Рыбинск  2007

Цель работы – изучение характеристик интегрирующей и дифференцирующей RC-цепей, исследование изменения формы видеоимпульсов при прохождении через эти цепи.

1. Интегрирующая RC-цепь.

Схема цепи приведена на рисунке 1.

 

Коэффициент передачи такой цепи равен:

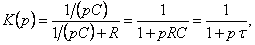
где 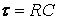– постоянная времени цепи.

Частотный коэффициент передачи цепи получим заменой :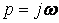

Построим для заданных значений: , , .

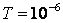Графики амплитудно-частотной характеристики находятся из формулы:

                                   , 

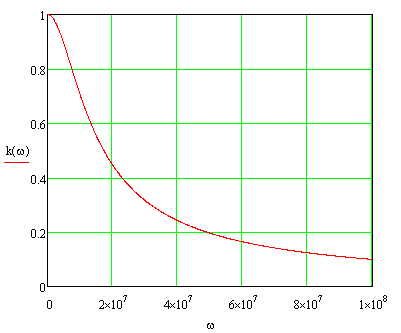
Рис.2 – Амплитудно – частотная характеристика цепи.

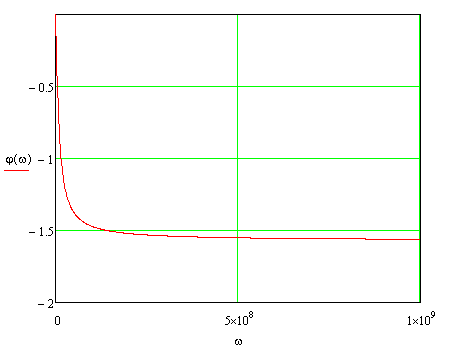
Графики фазочастотной характеристики находятся из формулы:

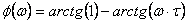
Рис.3 – фазочастотная характеристика цепи.

Коэффициент передачи цепи и ее импульсная характеристика связаны преобразованием Лапласа: . Найдем импульсную характеристику, учитывая, что 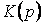 имеет одну особую точку (полюс) .

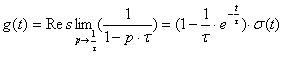
где – функция включения, показывающая, что импульсная характеристика равна нулю при отрицательных значениях t.

График импульсной характеристики будет выглядеть так:

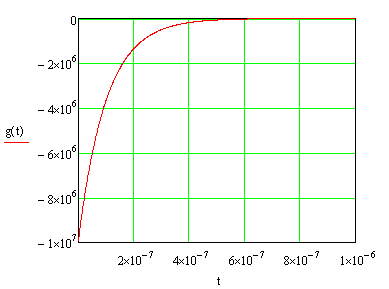
Рис.4 – импульсная характеристика цепи.

Интегрируя импульсную характеристику, найдем переходную характеристику цепи:

График переходной характеристики будет выглядеть так:

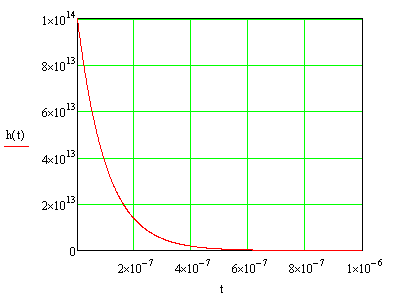
Рис.5 –импульсная характеристика цепи.

2. Дифференцирующая RC-цепь.

ИССЛЕДОВАНИЕ ДИФФЕРЕНЦИРУЮЩИХ И

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

ИНТЕГРИРУЮЩИХ ЦЕПЕЙ

 

Цель работы: экспериментально определить формы сигналов на выходе дифференцирующих и интегрирующих цепей при различных воздействиях.

 

Домашнее задание

1 Изучите по [1] тему «Дифференцирующие и интегрирующие цепи».

2 Подготовьте бланк отчета.

3 Подготовьте ответы на вопросы для самопроверки.

4 Рассчитайте величину резистивного сопротивления R, чтобы схема (рисунок 11а) была дифференцирующей, если величина емкости конденсатора С_А = 28,3нФ, частота повторения сигналов f = 2 кГц.

5 Рассчитайте величину резистивного сопротивления R, чтобы схема (рисунок 11б) была дифференцирующей, если величина индуктивности катушки L

A = 44мГн, частота повторения сигналов f = 2кГц.

6 Рассчитайте величину резистивного сопротивления R, чтобы схема (рисунок 11г) была интегрирующей, если величина емкости конденсатора С_A=28,3нФ, частота повторения сигнала f=2кГц.

7 Занесите полученные величины сопротивлений в таблицу 11.1 в графы R_диф или R_инт.

 

Вопросы для самопроверки

1 Какими пассивными элементами можно реализовать дифференцирующую цепь? Нарисуйте схемы.

2 Какими пассивными элементами можно реализовать интегрирующую цепь? Нарисуйте схемы.

3 Как зависит коэффициент передачи дифференцирующей цепи от частоты?

4 Как зависит коэффициент передачи интегрирующей цепи от частоты?

5 Какие недостатки пассивных дифференцирующих и интегрирующих цепей по сравнению с активными?

6 Дайте изображение активной дифференцирующей цепи. Докажите, что эта цепь дифференцирует.

7 Дайте изображение активной интегрирующей цепи. Докажите, что эта цепь интегрирует.

8 Какой формы сигнал получается после дифференцирования сигнала треугольной формы? После интегрирования?

9 Докажите при каких условиях цепь RC дифференцирует? Интегрирует?

10 Докажите при каких условиях цепь RL дифференцирует? Интегрирует?

Приборы и оборудование

1 Лабораторный стенд ЛКТЦ.

2 Соединительные провода (7 шт.).

 

Порядок выполнения работы

1 Проверка подготовки студентов к лабораторной работе по вопросам для самопроверки.

2 Подготовка лабораторной установки к работе, получение инструктажа по технике безопасности.

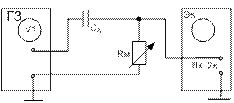
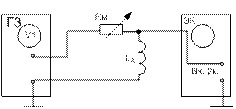
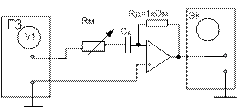
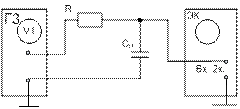
2.1 Ознакомиться с элементами, из которых собирают исследуемую цепь (рисунки 11а, 11б, 11в, 11г): генератором на блоке Г3, осциллографом, операционным усилителем на плате активных элементов, элементами С_А, L_А, Rм, Rд.

2.2 Собрать электрическую цепь по схеме (рисунок 11 а).

2.3 Поставьте переключатели в следующие позиции:

– на блоке Г1 тумблер в положение «ВНУТР»;

– на блоке Г2 переключатель формы сигнала в третью позицию ;

– на блоке Г3 тумблеры в положения «НОРМ» и «10В»;

– на блоке «ЭК» тумблер «КАНАЛ» установите в среднее положение;

– ослабление обоих каналов в положение 1:10;

– тумблеры синхронизации «1-ый КАНАЛ» и «ВХОД Х» в положение «ВНУТР»;

– регуляторы «ПОДСТРОЙКА» поверните против часовой стрелки до упора.

2.4 Пригласите преподавателя проверить собранную цепь.

2.5 Включить тумблеры в следующей последовательности: «СЕТЬ», «ГЕНЕРАТОР», «КОММУТАТОР-ОСЦИЛЛОГРАФ».

 

а)

б)

 

в)

г)

 

Рисунок 11 – Схемы для исследования пассивных

дифференцирующих (а, б), активной

дифференцирующей (в) и интегрирующей цепи (г)

 

3 Проведите исследования пассивных дифференцирующих цепей (рисунки 11а, 11б). Для этого:

3.1 На блоке генератора Г3 ручкой регулировка напряжения установите по верхней шкале вольтметра PV1 напряжение на входе цепи от 2 В до 4 В по вашему выбору. Поддерживайте величину этого напряжения во всех опытах!

3.2 На магазине сопротивлений установите сопротивление, ближайшее к величине, рассчитанной в пункте 4 домашнего задания.

3.3 С помощью регуляторов «УСИЛЕНИЕ Х», «РАЗВЕРТКА», «УСИЛЕНИЕ 1-ГО КАНАЛА», «РАСХОЖДЕНИЕ», «↔», «↨» установите изображение сигнала первого канала вверху экрана (это сигнал, подаваемый на вход дифференцирующей цепи) размахом 2 – 4 клетки.

3.4 Получите изображение второго канала (это сигнал, получаемый на выходе дифференцирующей цепи) размахом 2 – 4 клетки. Используйте регулятор «УСИЛЕНИЕ 2-ГО КАНАЛА».

3.5 Ручкой «РАСХОЖДЕНИЕ» наложите изображения сигналов одно на другое и зарисуйте эти изображения в таблице 11.1 (входной и выходной сигналы разными цветами).

3.6 Определите коэффициент передачи исследуемой цепи (К= ).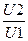

Внимание! При проведении данного исследования не трогайте больше регуляторы «УСИЛЕНИЯ» 1 и 2 каналов. Нажмите кнопку «ТАРИР» 1-го канала и держите ее все время измерений. На экране появится сигнал прямоугольной формы. Регулятором «ТАРИР-НАПРЯЖЕНИЕ» установите размах этого сигнала величиной в 1 клетку. По верхней шкале вольтметра PV1 снимите величину напряжения. Это напряжение соответствует величине сигнала в 1 клетку. 1 клетка – «N» вольт (где «N»-снятое вами напряжение). Отпустите кнопку «ТАРИР». Чтобы узнать величину напряжения U1 надо показание вольтметра «N» умножить на число клеток, которое занимает сигнал 1 канала.

3.7 Проделайте пункт 3.6 для второго канала. Определите величину U2 (нажимаете и держите кнопку «ТАРИР»-2-ого канала).

3.8 Занесите померенные данные в таблицу 11.1

3.9 Повторите пункты 3.4-3.8 для сигналов следующих форм: , .

Внимание! Чтобы получить сигнал данной формы , надо поставить переключатель формы в 7-ую позицию и использовать нижний регулятор «ПОДСТРОЙКА».

3.10 Соберите электрическую цепь по схеме (рисунок 11б).

3.11 На магазине сопротивлений установите сопротивление, ближайшее к величине, рассчитанной в пункте 5 домашнего задания.

3.12 Повторите пункты 3.4 – 3.8 для сигналов треугольной и пилообразной формы.

Внимание! Чтобы получить сигнал пилообразной формы, надо использовать нижний регулятор «ПОДСТРОЙКА».

4 Проведите исследование активной дифференцирующей цепи. Для этого:

4.1 Соберите электрическую цепь по схеме (рисунок 11в)

 

Таблица 11.1 – экспериментальные данные исследования дифференцирующих и интегрирующих цепей

 

 

4.2 На магазине сопротивлений установите величину сопротивления 40 – 80 Ом. Это сопротивление необходимо для нейтрализации влияния индуктивности соединительных проводов. Включите тумблер «ПЛАТА ЭЛЕМЕНТОВ».

4.3 Повторите пункты 3.4 – 3.8 для сигналов синусоидальной и треугольной формы.

5 Проведите исследование пассивной интегрирующей цепи. Для этого:

5.1 Соберите электрическую цепь по схеме (рисунок 11г). В качестве резистора «R» возьмите на панели пассивных элементов резистор, ближайший по значению к величине, рассчитанной в пункте 6 домашнего задания.

5.2 Повторите пункты 3.4 – 3.8 для сигналов синусоидальной, треугольной, прямоугольной формы.

6 После снятия данных и представления их преподавателю выключите стенд в следующей последовательности: «КОММУТАТОР-ОСЦИЛЛОГРАФ», «ГЕНЕРАТОР», «СЕТЬ».

 

Содержание отчета

1 Наименование и цель работы.

2 Выполненное домашнее задание (пункт 4, 5, 6).

3 Схемы исследования (рисунки 11 а, 11 б, 11 в, 11 г).

4 Заполненная таблица с графиками входных и выходных сигналов, измерений и вычислений.

5 Ответы на контрольные вопросы (по указанию преподавателя).

6 Выводы по работе.

 

Контрольные вопросы

1 Дайте определение дифференцирующей цепи.

2 Дайте определение интегрирующей цепи.

3 Приведите график дифференцирования однополярного прямоугольного импульса.

4 Приведите график интегрирования однополярного прямоугольного импульса.

5 Запишите условия дифференцирования пассивных дифференцирующих цепей RC и RL.

6 Запишите условия интегрирования пассивных интегрирующих цепей RC и RL.

7 Укажите достоинства активных дифференцирующих и интегрирующих цепей по сравнению с пассивными.

8 Почему дифференцирующую цепь называют укорачивающей цепью?

9 Почему интегрирующую цепь называют удлиняющей цепью?

 

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Дифференцирующими называют четырехполюсники, мгновенное значение напряжения на выходе которых пропорционально производной по времени от мгновенного значения напряжения на входе (u₂~ ).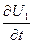

Пассивную дифференцирующую цепь можно составить с помощью элементов RC и RL (рисунок 11.2).

а) 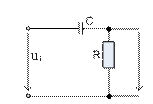б)

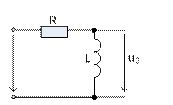
Рисунок 11.2 – Пассивные дифференцирующие цепи.

 

Дифференцируют цепи при условии, если их коэффициент передачи К<<1.

Так как идеальную дифференцирования получить невозможно, то критерием для соотношения между Х_C и R, X_L и R выбирают следующее:

– для схемы рисунка 11.2 а R≤ ,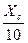

– для схемы рисунка 11.2 б Х_L≤ .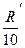

Интегрирующими называют четырехполюсники, мгновенное значение напряжения на выходе которых пропорционально интегралу от мгновенного значения напряжения на входе (u₂~∫u₁dt).

Пассивную интегрирующую цепь можно составить также с помощью элементов RC и RL (рисунок 11.3).

а) 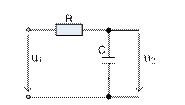б)

 

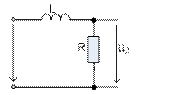
Рисунок 11.3 – Пассивные интегрирующие цепи

 

Интегрируют цепи также при условии, если их коэффициент передачи К<<1.

Так как идеальную интегрирования получить невозможно, то критерием для соотношения между Х_C и R, Х_L и R выбирают следующее:

– для схемы рисунка 11.3 а Х_C≤ ,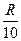

– для схемы рисунка 11.3 б R≤

Пассивные дифференцирующие и интегрирующие цепи имеют малый коэффициент передачи по напряжению, т.е. малое выходное напряжение, что на практике представляет значительные неудобства. От этого недостатка свободны активные (АRC) дифференцирующие и интегрирующие цепи (рисунки 11.4 и 11.5).

Рисунок 11.4 – Активная дифференцирующая цепь

 

 

Рисунок 11.5 – Активная интегрирующая цепь

 

Литература

1 Добротворский, И. Н. Теория электрических цепей / И. Н. Добротворский. – М. : Радио и связь, 1989. – С. 400 – 410.

 

 

ЛАБОРАТОРНАЯ РАБОТА № 12

Рекомендуемые страницы:

дифференцирующая rc-цепь — со всех языков на русский

дифференцирующая индуктивно-резистивная цепь — дифференцирующая LR цепь — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы дифференцирующая LR цепь EN… …   Справочник технического переводчика

дифференцирующая цепь — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN differentiating network …   Справочник технического переводчика

дифференцирующая цепь — diferencijuojamoji grandinė statusas T sritis fizika atitikmenys: angl. differentiating circuit vok. Differenzierkreis, m; Differenzierschaltung, f rus. дифференцирующая схема, f; дифференцирующая цепь, f pranc. circuit différentiel, m …   Fizikos terminų žodynas

дифференцирующая цепь — diferencijavimo grandinė statusas T sritis automatika atitikmenys: angl. differentiating circuit vok. Differentiationskreis, m; differenzierender Kreis, m; Differenzierkreis, m rus. дифференцирующая цепь, f pranc. circuit de différentiation, m;… …   Automatikos terminų žodynas

дифференцирующая схема — diferencijuojamoji grandinė statusas T sritis fizika atitikmenys: angl. differentiating circuit vok. Differenzierkreis, m; Differenzierschaltung, f rus. дифференцирующая схема, f; дифференцирующая цепь, f pranc. circuit différentiel, m …   Fizikos terminų žodynas

RC-цепь — RC цепь  электрическая цепь, состоящая из конденсатора и резистора. Содержание 1 Интегрирующая RC цепочка 1.1 Применения …   Википедия

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ — совокупности соединенных определенным образом элементов и устройств, образующих путь для прохождения электрического тока. Теория цепей раздел теоретической электротехники, в котором рассматриваются математические методы вычисления электрических… …   Энциклопедия Кольера

Differenzierkreis — diferencijuojamoji grandinė statusas T sritis fizika atitikmenys: angl. differentiating circuit vok. Differenzierkreis, m; Differenzierschaltung, f rus. дифференцирующая схема, f; дифференцирующая цепь, f pranc. circuit différentiel, m …   Fizikos terminų žodynas

Differenzierschaltung — diferencijuojamoji grandinė statusas T sritis fizika atitikmenys: angl. differentiating circuit vok. Differenzierkreis, m; Differenzierschaltung, f rus. дифференцирующая схема, f; дифференцирующая цепь, f pranc. circuit différentiel, m …   Fizikos terminų žodynas

circuit différentiel — diferencijuojamoji grandinė statusas T sritis fizika atitikmenys: angl. differentiating circuit vok. Differenzierkreis, m; Differenzierschaltung, f rus. дифференцирующая схема, f; дифференцирующая цепь, f pranc. circuit différentiel, m …   Fizikos terminų žodynas

diferencijuojamoji grandinė — statusas T sritis fizika atitikmenys: angl. differentiating circuit vok. Differenzierkreis, m; Differenzierschaltung, f rus. дифференцирующая схема, f; дифференцирующая цепь, f pranc. circuit différentiel, m …   Fizikos terminų žodynas

RC-цепь — Википедия

Материал из Википедии — свободной энциклопедии

RC цепь интегрирующего типа

RC-цепь — электрическая цепь, состоящая из конденсатора и резистора. Её можно рассматривать как делитель напряжения с одним из плеч, обладающих ёмкостным сопротивлением переменному току.

Интегрирующая RC-цепь

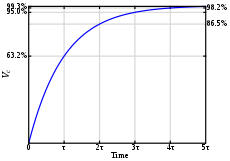Реакция интегрирующей цепи на единичное ступенчатое воздействие. Осциллограммы, снятые с последовательной RC цепи.
R — 1500 Ом — желт.
С — 100нФ — син.
τ = 150us

Если входной сигнал подаётся к V_in, а выходной снимается с V_c (см. рисунок), то такая цепь называется цепью интегрирующего типа.

Реакция цепи интегрирующего типа на единичное ступенчатое воздействие с амплитудой V определяется следующей формулой:^[1]

Vc(t)=V0(1−e−t/RC).{\displaystyle \,\!V_{c}(t)=V_{0}\left(1-e^{-t/RC}\right).}

Таким образом, постоянная времени τ этого апериодического процесса будет равна

τ=RC.{\displaystyle \tau =RC.}

Интегрирующие цепи пропускают постоянную составляющую сигнала, отсекая высокие частоты, то есть являются фильтрами нижних частот. При этом чем выше постоянная времени τ{\displaystyle \tau }, тем ниже частота среза. В пределе пройдёт только постоянная составляющая. Это свойство используется во вторичных источниках питания, в которых необходимо отфильтровать переменную составляющую сетевого напряжения. Интегрирующими свойствами обладает кабель из пары проводов, поскольку любой провод является резистором, обладая собственным сопротивлением, а пара идущих рядом проводов ещё и образуют конденсатор, пусть и с малой ёмкостью. При прохождении сигналов по такому кабелю, их высокочастотная составляющая может теряться, причём тем сильнее, чем больше длина кабеля.

Применения

Дифференцирующая RC-цепь

Дифференцирующая RC-цепь получается, если поменять местами резистор R и конденсатор С в интегрирующей цепи. При этом входной сигнал идёт на конденсатор, а выходной снимается с резистора. Для постоянного напряжения конденсатор представляет собой разрыв цепи, то есть постоянная составляющая сигнала в цепи дифференцирующего типа будет отсечена. Такие цепи являются фильтрами верхних частот. И частота среза в них определяется всё той же постоянной времени τ{\displaystyle \tau }. Чем больше τ{\displaystyle \tau }, тем ниже частота, которая может быть без изменений пропущена через цепь.

Дифференцирующие цепи имеют ещё одну особенность. На выходе такой цепи один сигнал преобразуется в два последовательных скачка напряжения вверх и вниз относительно базы с амплитудой, равной входному напряжению. Базой является либо положительный вывод источника, либо «земля», в зависимости от того, куда подключён резистор. Когда резистор подключён к источнику, амплитуда положительного выходного импульса будет в два раза выше напряжения питания. Этим пользуются для умножения напряжения, а также, в случае подключения резистора к «земле», для формирования двуполярного напряжения из имеющегося однополярного.

Применение

См. также

Примечания