Диэлектрическая проницаемость постоянная: Диэлектрическая проницаемость — Википедия – Диэлектрическая проницаемость — Википедия — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Диэлектрическая проницаемость — Википедия

Диэлектри́ческая проница́емость — коэффициент, входящий в математическую запись закона Кулона для силы взаимодействия точечных зарядов q1{\displaystyle q_{1}} и q2{\displaystyle q_{2}}, находящихся в однородной изолирующей (диэлектрической) среде на расстоянии r12{\displaystyle r_{12}} друг от друга:

F=14πεa⋅|q1q2|r122{\displaystyle F={\frac {1}{4\pi \varepsilon _{a}}}\cdot {\frac {|q_{1}q_{2}|}{r_{12}^{2}}}},

а также в уравнение связи вектора электрической индукции с напряжённостью электрического поля:

D=εaE{\displaystyle \mathbf {D} =\varepsilon _{a}\mathbf {E} }

в рассматриваемой среде^[1]. Вводятся абсолютная (а) и относительная (r, от англ. relative — относительный) проницаемости:

εa=ε0εr{\displaystyle \varepsilon _{a}=\varepsilon _{0}\varepsilon _{r}},

где ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная^[2]. Cам термин «диэлектрическая проницаемость» применяется и для εr{\displaystyle \varepsilon _{r}}, и для εa{\displaystyle \varepsilon _{a}}; ради краткости, одну из этих величин (в российской литературе чаще εr{\displaystyle \varepsilon _{r}}, в англоязычной εa{\displaystyle \varepsilon _{a}}) переобозначают как ε{\displaystyle \varepsilon } (из контекста всегда ясно, о чём идёт речь). Величина εr{\displaystyle \varepsilon _{r}} безразмерна, а εa{\displaystyle \varepsilon _{a}} по размерности совпадает с ε0{\displaystyle \varepsilon _{0}} (в Международной системе единиц (СИ): фарад на метр, Ф/м).

Проницаемость εr{\displaystyle \varepsilon _{r}} показывает, во сколько раз сила взаимодействия двух электрических зарядов в конкретной среде меньше, чем в вакууме, для которого εr=1{\displaystyle \varepsilon _{r}=1}. Отличие проницаемости от единицы обусловлено эффектом поляризации диэлектрика под действием внешнего электрического поля, в результате которой создаётся внутреннее противоположно направленное поле. В области низких частот ω{\displaystyle \omega } значение проницаемости реальных сред εr>1{\displaystyle \varepsilon _{r}>1}, обычно оно лежит в диапазоне 1—100, но для сегнетоэлектриков составляет десятки и сотни тысяч. Как функция частоты электрического поля величина εr(ω){\displaystyle \varepsilon _{r}(\omega )} слегка возрастает на участках вне линий поглощения данного материала, однако вблизи линий резко спадает, из-за чего высокочастотная диэлектрическая проницаемость ниже статической. Имеет место связь проницаемости и показателя преломления вещества: для немагнитной непоглощающей среды n2(ω)=εr(ω){\displaystyle n^{2}(\omega )=\varepsilon _{r}(\omega )}.

Относительная диэлектрическая проницаемость εr{\displaystyle \varepsilon _{r}} является одним из «электромагнитных параметров» среды, влияющих на распределение компонент напряжённости электромагнитного поля в пространстве и описывающих среду в материальных уравнениях электродинамики (уравнениях Максвелла).

$\varepsilon _{r}$ Схематическое изображение ориентации диполей в диэлектрической среде под воздействием электрического поля

Абсолютная диэлектрическая проницаемость вакуума[править | править код]

Электрическая постоянная, она же «абсолютная диэлектрическая проницаемость вакуума», в системе единиц СИ равна ε0≈8,85⋅10−12{\displaystyle \varepsilon _{0}\approx 8{,}85\cdot 10^{-12}} Ф/м (имеет размерность L⁻³M⁻¹T⁴I²). В системе СГС эта же постоянная составляет ε0=1/4π{\displaystyle \varepsilon _{0}=1/4\pi }, однако часто в СГС вообще не задействуют ε0{\displaystyle \varepsilon _{0}}, надлежащим образом адаптируя формулы (скажем, закон Кулона: F=εr−1⋅|q1q2|/r122{\displaystyle F=\varepsilon _{r}^{-1}\cdot |q_{1}q_{2}|/r_{12}^{2}}). Электрическая постоянная связана с магнитной постоянной и скоростью света в вакууме:

ε0μ0=c−2{\displaystyle \varepsilon _{0}\mu _{0}=c^{-2}}

Ниже все формулы приводятся для СИ, а символ ε{\displaystyle \varepsilon } используется как замена εr{\displaystyle \varepsilon _{r}} (εa=ε0ε{\displaystyle \varepsilon _{a}=\varepsilon _{0}\varepsilon }).

Эффект поляризации диэлектрика и проницаемость[править | править код]

Под воздействием электрического поля в диэлектрике имеет место поляризация — явление, связанное с ограниченным смещением зарядов или поворотом электрических диполей. Данное явление характеризует вектор электрической поляризации P{\displaystyle \mathbf {P} }, равный дипольному моменту единицы объёма диэлектрика. В отсутствие внешнего поля диполи ориентированы хаотично (см. верхний рис.), за исключением особых случаев спонтанной поляризации в сегнетоэлектриках. При наличии поля диполи в большей или меньшей степени поворачиваются (нижний рис.), в зависимости от восприимчивости χ(ω){\displaystyle \chi (\omega )} конкретного материала, а восприимчивость, в свою очередь, определяет проницаемость ε(ω){\displaystyle \varepsilon (\omega )}. Помимо дипольно-ориентационного, имеются и другие механизмы поляризации. Поляризация не изменяет суммарного заряда в любом макроскопическом объёме, однако она сопровождается появлением связанных электрических зарядов на поверхности диэлектрика и в местах неоднородностей. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле, как правило, направленное против внешнего наложенного поля. В итоге тот факт, что εa≠ε0{\displaystyle \varepsilon _{a}\neq \varepsilon _{0}}, является следствием электрической поляризации материалов.

Роль диэлектрической проницаемости среды в физике[править | править код]

идеальным диэлектриком (диэлектриком без поглощения, диэлектриком без потерь), для неё ε{\displaystyle \varepsilon } определяет такие вторичные параметры, как коэффициент преломления среды, скорость распространения, фазовую скорость и коэффициент укорочения длины электромагнитной волны в среде, волновое сопротивление среды. Относительная диэлектрическая проницаемость реальных диэлектриков (диэлектриков с потерями, диэлектриков с поглощением, для которых σ>0{\displaystyle \sigma >0}) также влияет на значение тангенса угла диэлектрических потерь и погонное затухание электромагнитной волны в среде. Относительная диэлектрическая проницаемость среды влияет на электрическую ёмкость расположенных в ней проводников: увеличение ε{\displaystyle \varepsilon } приводит к увеличению ёмкости. При изменении ε{\displaystyle \varepsilon } в пространстве (то есть если ε{\displaystyle \varepsilon } зависит от координат) говорят о неоднородной среде, зависимость ε{\displaystyle \varepsilon } от частоты электромагнитных колебаний — одна из возможных причин дисперсии электромагнитных волн, зависимость ε{\displaystyle \varepsilon } от напряженности электрического поля — одна из возможных причин нелинейности среды. Если среда является анизотропной, то в материальном уравнении ε{\displaystyle \varepsilon } будет не скаляром, а тензором. При использовании метода комплексных амплитуд в решении системы уравнений Максвелла и наличии потерь в среде (σ>0{\displaystyle \sigma >0}) оперируют комплексной диэлектрической проницаемостью.

Таким образом, ε{\displaystyle \varepsilon } является одним из важнейших «электромагнитных параметров» соответствующей среды.

Диэлектрическая проницаемость непоглощающей среды[править | править код]

Проницаемость и связанные с ней величины[править | править код]

Применительно к диэлектрической среде без потерь действует цепочка соотношений:

D=ε0E+P=ε0(1+χ)E=ε0εE{\displaystyle \mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P} =\varepsilon _{0}(1+\chi )\mathbf {E} =\varepsilon _{0}\varepsilon \mathbf {E} }.

В большинстве случаев χ{\displaystyle \chi } и, соответственно, ε{\displaystyle \varepsilon } — это просто безразмерные константы конкретного материала. В вакууме χ{\displaystyle \chi } равно нулю.

Особая ситуация возникает для нелинейных сред, когда ε{\displaystyle \varepsilon } зависит от величины поля E{\displaystyle E}; такое возможно в сравнительно сильных полях. В сегнетоэлектриках возможно появление спонтанной поляризации, а именно сохранение P≠0{\displaystyle \mathbf {P} \neq 0} после снятия ранее наложенного внешнего поля.

Распределение электрического поля в пространстве с различными диэлектриками находится из численного решения уравнения Максвелла

∇⋅D(r)=ρ(r){\displaystyle {\boldsymbol {\nabla }}\cdot \mathbf {D(r)} =\rho (\mathbf {r} )}

или уравнения Пуассона для электрического потенциала φ{\displaystyle \varphi }

∇(ε(r)∇φ(r))=−ε0−1ρ(r){\displaystyle {\boldsymbol {\nabla }}\left(\varepsilon (\mathbf {r} ){\boldsymbol {\nabla }}\varphi (\mathbf {r} )\right)=-\varepsilon _{0}^{-1}\rho (\mathbf {r} )},

где ρ(r){\displaystyle \rho (\mathbf {r} )} обозначает плотность свободных зарядов. На незаряженной границе двух диэлектрических сред отношение нормальных компонент напряжённости поля En{\displaystyle E_{n}} с обеих сторон равно обратному отношению значений проницаемости сред.

В ситуации однородного диэлектрика его наличие приводит к снижению электрического поля E(r){\displaystyle \mathbf {E} (\mathbf {r} )} в ε{\displaystyle \varepsilon } раз, по сравнению со случаем вакуума при том же распределении свободных зарядов. Помимо закона Кулона, практически важным примером является конденсатор любой геометрии, заряд (не разность потенциалов!) обкладок которого фиксирован.

Проницаемость в оптическом диапазоне частот[править | править код]

Диэлектрическая проницаемость, совместно с магнитной, определяют фазовую скорость распространения электромагнитной волны в рассматриваемой среде, а именно:

ε0ε(ω)μ0μ(ω)=vph−2{\displaystyle \varepsilon _{0}\varepsilon (\omega )\mu _{0}\mu (\omega )=v_{ph}^{-2}}.

Показатель преломления диэлектрика без потерь можно выразить как квадратный корень из произведения его магнитной и диэлектрической проницаемостей:

n(ω)=μ(ω)⋅ε(ω){\displaystyle n(\omega )={\sqrt {\mu (\omega )\cdot \varepsilon (\omega )}}}

Для немагнитных сред μ=1{\displaystyle \mu =1}. Значения ε{\displaystyle \varepsilon } для актуального в данном контексте оптического диапазона могут очень сильно отличаться от статических значений: как правило, ε{\displaystyle \varepsilon } намного ниже, чем для статического поля. Однако, если рассматривать оптический диапазон частот сам по себе, то в нём с ростом ω{\displaystyle \omega } величина ε{\displaystyle \varepsilon } (а значит, и n{\displaystyle n}) чаще всего возрастает. Такое поведение показателя преломления («синий свет преломляется сильнее красного») является случаем так называемой нормальной дисперсии. С противоположной ситуацией аномальной дисперсии можно столкнуться вблизи полос поглощения, но такой случай не может рассматриваться как случай без потерь.

Тензор проницаемости анизотропных сред[править | править код]

Диэлектрическая проницаемость связывает электрическую индукцию D{\displaystyle \mathbf {D} } и напряжённость электрического поля E{\displaystyle \mathbf {E} }. В электрически анизотропных средах компонента вектора напряжённости Ei{\displaystyle E_{i}} может не только влиять на ту же самую компоненту вектора электрической индукции Di{\displaystyle D_{i}}, но и порождать другие его компоненты Dj(j≠i){\displaystyle D_{j}(j\neq i)}. В общем случае проницаемость является тензором, определяемым из следующего соотношения (в записи использовано соглашение Эйнштейна):

Di=ε0εijEj{\displaystyle D_{i}=\varepsilon _{0}\varepsilon _{ij}E_{j}}

или, иначе,

D=εaE{\displaystyle \mathbf {D} ={\boldsymbol {\varepsilon }}_{a}\mathbf {E} }

где жирный шрифт использован для векторных и тензорных величин, а

E=E1e1+E2e2+E3e3{\displaystyle \mathbf {E} =E_{1}\mathbf {e} _{1}+E_{2}\mathbf {e} _{2}+E_{3}\mathbf {e} _{3}} — вектор напряжённости электрического поля,

D=D1e1+D2e2+D3e3{\displaystyle \mathbf {D} =D_{1}\mathbf {e} _{1}+D_{2}\mathbf {e} _{2}+D_{3}\mathbf {e} _{3}} — вектор электрической индукции,

εa=ε0εij{\displaystyle {\boldsymbol {\varepsilon }}_{a}=\varepsilon _{0}\varepsilon _{ij}} — тензор абсолютной диэлектрической проницаемости.

В изотропном случае любая компонента вектора напряженности Ei{\displaystyle E_{i}} влияет только на Di{\displaystyle D_{i}}, при этом εij= δijε{\displaystyle \varepsilon _{ij}=~\delta _{ij}\varepsilon }, где δij{\displaystyle \delta _{ij}} — символ Кронекера, поэтому уравнения Максвелла могут быть записаны с использованием скалярной диэлектрической проницаемости (ε{\displaystyle \varepsilon } — просто коэффициент в уравнении).

Статическая проницаемость некоторых диэлектриков[править | править код]

Значение ε{\displaystyle \varepsilon } вакуума равно единице, для реальных сред в статическом поле ε>1{\displaystyle \varepsilon >1}. Для воздуха и большинства других газов в нормальных условиях значение ε{\displaystyle \varepsilon } близко к единице в силу их низкой плотности. В статическом электрическом поле для большинства твёрдых или жидких диэлектриков значение ε{\displaystyle \varepsilon } лежит в интервале от 2 до 8, для жидкой воды значение ε{\displaystyle \varepsilon } достаточно высокое, 88 при 0∘{\displaystyle 0^{\circ }}. А у твердого льда ε{\displaystyle \varepsilon } больше и составляет 97 при 0∘{\displaystyle 0^{\circ }}. Это объясняется тем, что переход атома Н от одного О-атома к другому вызывает перестройку ковалентных и водородных связей у обоих этих О-атомов и в их в окрестности. В результате вся сеть ковалентных и водородных связей во льду сильно флуктуирует, и это приводит к аномально высокой поляризуемости льда, превосходя диэлектрическую проницаемость жидкой воды^[3]. Значение ε{\displaystyle \varepsilon } велико для веществ с молекулами, обладающими большим электрическим дипольным моментом. Значение ε{\displaystyle \varepsilon } сегнетоэлектриков составляет десятки и сотни тысяч.

Диэлектрическая проницаемость — Википедия

Материал из Википедии — свободной энциклопедии

F=14πεa⋅|q1q2|r122{\displaystyle F={\frac {1}{4\pi \varepsilon _{a}}}\cdot {\frac {|q_{1}q_{2}|}{r_{12}^{2}}}},

а также в уравнение связи вектора электрической индукции с напряжённостью электрического поля:

D=εaE{\displaystyle \mathbf {D} =\varepsilon _{a}\mathbf {E} }

εa=ε0εr{\displaystyle \varepsilon _{a}=\varepsilon _{0}\varepsilon _{r}},

Абсолютная диэлектрическая проницаемость вакуума

ε0μ0=c−2{\displaystyle \varepsilon _{0}\mu _{0}=c^{-2}}

Видео по теме

Эффект поляризации диэлектрика и проницаемость

Роль диэлектрической проницаемости среды в физике

Относительная диэлектрическая проницаемость ε{\displaystyle \varepsilon } среды, наряду с её относительной магнитной проницаемостью μ{\displaystyle \mu } и удельной электропроводностью σ{\displaystyle \sigma }, влияет на распределение напряжённости электромагнитного поля в пространстве и используется при описании среды в системе уравнений Максвелла. Среду со значениями μ=1{\displaystyle \mu =1} и σ=0{\displaystyle \sigma =0} называют идеальным диэлектриком (диэлектриком без поглощения, диэлектриком без потерь), для неё ε{\displaystyle \varepsilon } определяет такие вторичные параметры, как коэффициент преломления среды, скорость распространения, фазовую скорость и коэффициент укорочения длины электромагнитной волны в среде, волновое сопротивление среды. Относительная диэлектрическая проницаемость реальных диэлектриков (диэлектриков с потерями, диэлектриков с поглощением, для которых σ>0{\displaystyle \sigma >0}) также влияет на значение тангенса угла диэлектрических потерь и погонное затухание электромагнитной волны в среде. Относительная диэлектрическая проницаемость среды влияет на электрическую ёмкость расположенных в ней проводников: увеличение ε

Диэлектрическая проницаемость | энергетик

Вернутся в раздел ⇒ Законы электротехники коротко

Диэлектрическая проницаемость — величина, характеризующая диэлектрические свойства среды — её реакцию на электрическое поле:

D = εF
В большинстве диэлектриков при не очень сильных полях диэлектрическая проницаемость не зависит от поля Е. В сильных же электрических полях (сравнимых с внутриатомными полями), а в некоторых диэлектриках в обычных полях зависимость D от Е — нелинейная.

Так же диэлектрическая проницаемость показывает, во сколько раз сила взаимодействия F между электрическими зарядами в данной среде меньше их силы взаимодействия F_o в вакууме:

Относительная диэлектрическая проницаемость вещества может быть определена путем сравнения ёмкости тестового конденсатора с данным диэлектриком (C_x) и ёмкости того же конденсатора в вакууме (C_o):

Таблица значений диэлектрической проницаемости для твердых тел:

Таблица значений диэлектрической проницаемости для жидкостей:

Таблица значений диэлектрической проницаемости для газов:

Обозначение в формуле:

D — электрическая индукция в среде;

ε — диэлектрическая проницаемость среды;

E — напряжённость электрического поля;

F₀ — сила взаимодействия между зарядами в среде;

F — сила взаимодействия между зарядами в вакууме;

C_x — ёмкость конденсатора в среде;

C₀ — ёмкость конденсатора в вакууме.

Ещё картинки на тему диэлектрическая проницаемость:

Относительная диэлектрическая проницаемость Википедия

F=14πεa⋅|q1q2|r122{\displaystyle F={\frac {1}{4\pi \varepsilon _{a}}}\cdot {\frac {|q_{1}q_{2}|}{r_{12}^{2}}}},

а также в уравнение связи вектора электрической индукции с напряжённостью электрического поля:

D=εaE{\displaystyle \mathbf {D} =\varepsilon _{a}\mathbf {E} }

εa=ε0εr{\displaystyle \varepsilon _{a}=\varepsilon _{0}\varepsilon _{r}},

Новый документ в формате RTF (2)

Диэлектри́ческая проница́емость среды — физическая величина, характеризующая свойства изолирующей (диэлектрической) среды и показывающая зависимостьэлектрической индукции от напряжённости электрического поля.

Определяется эффектом поляризации диэлектриков под действием электрического поля (и с характеризующей этот эффект величиной диэлектрической восприимчивости среды).

Различают относительную и абсолютную диэлектрические проницаемости.

Относительная диэлектрическая проницаемость ε является безразмерной и показывает, во сколько раз сила взаимодействия двух электрических зарядов в среде меньше, чем в вакууме. Эта величина для воздуха и большинства других газов в нормальных условиях близка к единице (в силу их низкой плотности). Для большинства твёрдых или жидких диэлектриков относительная диэлектрическая проницаемость лежит в диапазоне от 2 до 8 (для статического поля). Диэлектрическая постояннаяводы в статическом поле достаточно высока — около 80. Велики её значения для веществ с молекулами, обладающими большим электрическим дипольным моментом. Относительная диэлектрическая проницаемость сегнетоэлектриков составляет десятки и сотни тысяч.

Абсолютная диэлектрическая проницаемость в зарубежной литературе обозначается буквой ε, в отечественной преимущественно используется сочетани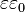е , где 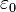— электрическая постоянная. Абсолютная диэлектрическая проницаемость используется только в Международной системе единиц (СИ), в которой индукция и напряжённость электрического поля измеряются в различных единицах. В системе СГС необходимость в введении абсолютной диэлектрической проницаемости отсутствует. Абсолютная диэлектрическая постоянная (как и электрическая постоянная) имеет размерность L⁻³M⁻¹T⁴I². В единицах Международной системы единиц (СИ): [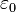]=Ф/м.

Следует отметить, что диэлектрическая проницаемость в значительной степени зависит от частоты электромагнитного поля. Это следует всегда учитывать, поскольку таблицы справочников обычно содержат данные для статического поля или малых частот вплоть до нескольких единиц кГц без указания данного факта. В то же время существуют и оптические методы получения относительной диэлектрической проницаемости по коэффициенту преломления при помощи эллипсометров и рефрактометров. Полученное оптическим методом (частота 10¹⁴ Гц) значение будет значительно отличаться от данных в таблицах.

Рассмотрим, например, случай воды. В случае статического поля (частота равна нулю), относительная диэлектрическая проницаемость при нормальных условияхприблизительно равна 80. Это имеет место вплоть до инфракрасных частот. Начиная примерно с 2 ГГц ε_r начинает падать. В оптическом диапазоне ε_r составляет приблизительно 1,8. Это вполне соответствует факту, что в оптическом диапазоне показатель преломления воды равен 1,33.^[1] В узком диапазоне частот, называемом оптическим, диэлектрическое поглощение падает до нуля, что собственно и обеспечивает человеку механизм зрения^[^{источник не указан 1252 дня}^] в земной атмосфере, насыщенной водяным паром. С дальнейшим ростом частоты свойства среды вновь меняются. О поведении относительной диэлектрической проницаемости воды в диапазоне частот от 0 до 10¹² (инфракрасная область) можно прочитать на [1] (англ.)

Диэлектрическая проницаемость диэлектриков является одним из основных параметров при разработке электрических конденсаторов. Использование материалов с высокой диэлектрической проницаемостью позволяют существенно снизить физические размеры конденсаторов.

Ёмкость конденсаторов определяется:

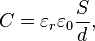
где ε_r — диэлектрическая проницаемость вещества между обкладками, ε_о — электрическая постоянная, S — площадь обкладок конденсатора, d — расстояние между обкладками.

Параметр диэлектрической проницаемости учитывается при разработке печатных плат. Значение диэлектрической проницаемости вещества между слоями в сочетании с его толщиной влияет на величину естественной статической ёмкости слоев питания, а также существенно влияет на волновое сопротивлениепроводников на плате.

УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ электрическое, физическая величина , равная электрическому сопротивлению (см.СОПРОТИВЛЕНИЕ ЭЛЕКТРИЧЕСКОЕ) R цилиндрического проводника единичной длины (l = 1м) и единичной площади поперечного сечения (S =1 м²).. r = R S/l. В Си единицей удельного сопротивления является Ом^.м. Удельное сопротивление могут выражать также в Ом^.см. Удельное сопротивление является характеристикой материала, по которому протекает ток, и зависит от материала, из которого он изготовлен. Удельное сопротивление, равное r = 1 Ом^.м означает, что цилиндрический проводник, изготовленный из данного материала, длиной l = 1м и с площадью поперечного сечения S = 1 м² имеет сопротивление R = 1 Ом^.м. Величина удельного сопротивления металлов (см. МЕТАЛЛЫ), являющихся хорошими проводниками (см. ПРОВОДНИКИ), может иметь значения порядка 10^—⁸ – 10^—⁶Ом^.м (например, медь, серебро, железо и т. д.). Удельное сопротивление некоторых твердых диэлектриков (

см. ДИЭЛЕКТРИКИ) может достигать значения 10¹⁶-10¹⁸Ом.м (например, кварцевое стекло, полиэтилен, электрофарфор и др.). Величина удельного сопротивления многих материалов (особенного полупроводниковых материалов (см.ПОЛУПРОВОДНИКОВЫЕ МАТЕРИАЛЫ)) существенно зависит от степени их очистки, наличия легирующих добавок, термических и механических обработок и т. д. Величина s, обратная удельному сопротивлению , называется удельной проводимостью: s = 1/r Удельная проводимость измеряется в сименсах (см. СИМЕНС (единица проводимости)) на метр См/м. Удельное электрическое сопротивление (проводимость) является скалярной величиной для изотропного вещества; и тензорной — для анизотропного вещества. В анизотропным монокристаллах анизотропия электропроводности является следствием анизотропии обратной эффективной массы ( см. ЭФФЕКТИВНАЯ МАССА) электронов и дырок.

1-6. ЭЛЕКТРОПРОВОДНОСТЬ ИЗОЛЯЦИИ

При включении изоляции кабеля или провода на постоянное напряжение U через нее проходит ток i, изменяющийся во времени (рис. 1-3). Этот ток имеет постоянные составляющие — ток проводимости (i_∞ ) и ток абсорбции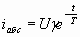, где γ — проводимость, соответствующая току абсорбции; Т — время, в течение которого ток i

абс спадает до 1/e своего первоначального значения. При бесконечно большом времени i_абс →0 и i = i_∞ . Электропроводность диэлектриков объясняется наличием в них некоторого количества свободных заряженных частиц: ионов и электронов.

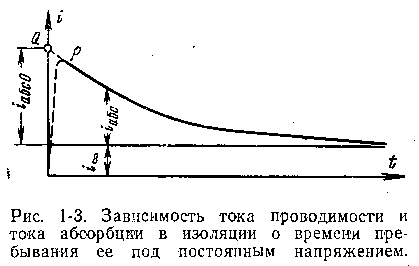
Наиболее характерна для большей части электроизоляционных материалов ионная электропроводность, которая возможна за счет неизбежно присутствующих в изоляции загрязнений (примеси влаги, солей, щелочей и т. п.). У диэлектрика с ионным характером электропроводности строго соблюдается закон Фарадея — пропорциональность между количеством прошедшего через изоляцию электричества и количеством выделившегося при электролизе вещества.

При повышении температуры удельное сопротивление электроизоляционных материалов уменьшается и характеризуется формулой

где_ρ_о , А и В — постоянные для данного материала; Т- температура, °К.

Большая зависимость сопротивления изоляции от влаги имеет место у гигроскопичных изоляционных материалов, главным образом волокнистых (бумага, хлопчатобумажная пряжа и др.). Поэтому волокнистые материалы подвергаются сушке и пропитке, а также защите влагостойкими оболочками.

Сопротивление изоляции может уменьшаться с повышением напряжения за счет образования в изоляционных материалах объемных зарядов. Создающаяся при этом добавочная электронная проводимость приводит к увеличению электропроводности. Существует зависимость проводимости от напряжения в очень сильных полях (закон Я. И. Френкеля):

где γ_о — проводимость в слабых полях; а — постоянная. Все электроизоляционные материалы характеризуются определенными значениями проводимости изоляции G. В идеале проводимость изоляционных материалов равна нулю. У реальных изоляционных материалов проводимость на единицу длины кабеля определяют по формуле

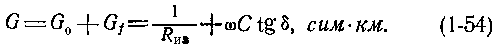
В кабелях, имеющих сопротивление изоляции более , 3-10¹¹ ом-м и кабелях связи, где потери на диэлектрическую поляризацию значительно больше тепловых потерь, проводимость определяют по формуле

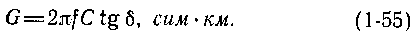
Проводимость изоляции в технике связи является электрическим параметром линии, характеризующим потери энергии в изоляции жил кабелей. Зависимость величины проводимости от частоты приведена на рис. 1-1. Величина, обратная проводимости — сопротивление изоляции, представляет собой отношение приложенного к

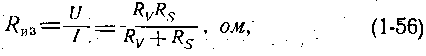
изоляции напряжения постоянного тока (в вольтах) к току утечки (в амперах), т. е.

где R_V — объемное сопротивление изоляции, численно определяющее препятствие, создаваемое прохождению тока в толще изоляции; R_S — поверхностное сопротивление, определяющее препятствие прохождению тока по поверхности изоляции.

Практической оценкой качества применяемых изоляционных материалов является удельное объемное сопротивление ρ_V выражаемое в омо-сантиметрах (ом*см). Численно ρ_V равно сопротивлению (в омах) куба с ребром 1 см из данного материала, если ток проходит через две противоположные грани куба. Удельное поверхностное сопротивление ρ_S численно равно сопротивлению поверхности квадрата (в омах), если ток подводится к электродам, ограничивающим две противоположные стороны этого квадрата.

Сопротивление изоляции одножильного кабеля или провода определяют по формуле

Абсорбционными токами называются токи смещения различных видов замедленной поляризации. Абсорбционные токи при постоянном напряжении протекают в диэлектрике до момента установления равновесного состояния, изменяя свое направление при включении и выключении напряжения. При переменном напряжении абсорбционные токи протекают в течение всего времени нахождения диэлектрика в электрическом поле.

Влажностные свойства диэлектриков

Влагостойкость – это надежность эксплуатации изоляции при нахождении ее в атмосфере водяного пара близкого к насыщению. Влагостойкость оценивают по изменению электрических, механических и других физических свойств после нахождения материала в атмосфере с повышенной и высокой влажностью; по влаго- и водопроницаемости; по влаго- и водопоглощаемости.

Влагопроницаемость – способность материала пропускать пары влаги при наличии разности относительных влажностей воздуха с двух сторон материала.

Влагопоглощаемость – способность материала сорбировать воду при длительном нахождении во влажной атмосфере близкой к состоянию насыщения.

Водопоглощаемость – способность материала сорбировать воду при длительном погружении его в воду.

Тропикостойкость и тропикализация оборудования – защита электрооборудования от влаги, плесени, грызунов.

Тепловые свойства диэлектриков

Для характеристики тепловых свойств диэлектриков используются следующие величины.

Нагревостойкость – способность электроизоляционных материалов и изделий без вреда для них выдерживать воздействие высокой температуры и резких смен температуры. Определяют по температуре, при которой наблюдается существенное изменение механических и электрических свойств, например, в органических диэлектриках начинается деформация растяжения или изгиба под нагрузкой.

Теплопроводность – процесс передачи тепла в материале. Характеризуется экспериментально определяемым коэффициентом теплопроводности λ_т. λ_т – количество теплоты, переданной за одну секунду через слой материала толщиной в 1 м и площадью поверхности – 1 м² при разности температур поверхностей слоя в 1 °К. Коэффициент теплопроводности диэлектриков изменяется в широких пределах. Самые низкие значения λ_т имеют газы, пористые диэлектрики и жидкости (для воздуха λ_т = 0,025 Вт/(м·К), для водыλ_т = 0,58 Вт/(м·К)), высокие значения имеют кристаллические диэлектрики (для кристаллического кварца λ_т = 12,5 Вт/(м·К)). Коэффициент теплопроводности диэлектриков зависит от их строения (для плавленого кварца λ_т = 1,25 Вт/(м·К)) и температуры.

Тепловое расширение диэлектриков оценивают температурным коэффициентом линейного расширения: 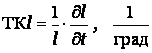. Материалы с малым тепловым расширением, имеют, как правило, более высокую нагревостойкость и наоборот. Тепловое расширение органических диэлектриков значительно (в десятки и сотни раз) превышает расширение неорганических диэлектриков. Поэтому стабильность размеров деталей из неорганических диэлектриков при колебаниях температуры значительно выше по сравнению с органическими.

1. Абсорбционные токи

В общем случае электрический ток j в диэлектрике представляет собой сумму сквозного тока j_ск и тока абсорбции j_аб

j = j_ск + j_аб.

Ток абсорбции можно определить через ток смещения j_см — скорость изменения вектора электрической индукции D

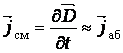
Сквозной ток определяется переносом (движением) в электрическом поле различных носителей заряда.

2. Электронная электропроводность характеризуется перемещением электронов под действием поля. Кроме металлов она присутствует у углерода, оксидов металлов, сульфидов и др. веществ, а также у многих полупроводников.

3. Ионная – обусловлена движением ионов. Наблюдается в растворах и расплавах электролитов – солей, кислот, щелочей, а также во многих диэлектриках. Она подразделяется на собственную и примесную проводимости. Собственная проводимость обусловлена движением ионов, получаемых при диссоциации^[1] молекул. Движение ионов в электрическом поле сопровождается электролизом^[2] – переносом вещества между электродами и выделением его на электродах. Полярные жидкости диссоциированы в большей степени и имеют большую электропроводность, чем неполярные.

В неполярных и слабополярных жидких диэлектриках (минеральные масла, кремнийорганические жидкости) электропроводность определяется примесями.

4. Молионная электропроводность – обусловлена движением заряженных частиц, называемых молионами. Наблюдают ее в коллоидных системах, эмульсиях^[3], суспензиях^[4]. Движение молионов под действием электрического поля называют электрофорезом. При электрофорезе, в отличие от электролиза, новых веществ не образуется, меняется относительная концентрация дисперсной фазы в различных слоях жидкости. Электрофоретическая электропроводность наблюдается, например, в маслах, содержащихэмульгированную воду.

Относительная диэлектрическая проницаемость — это… Что такое Относительная диэлектрическая проницаемость?

Проверить информацию.

Необходимо проверить точность фактов и достоверность сведений, изложенных в этой статье.
На странице обсуждения должны быть пояснения.

Относи́тельная диэлектри́ческая проница́емость среды ε — безразмерная физическая величина, характеризующая свойства изолирующей (диэлектрической) среды. Связана с эффектом поляризации диэлектриков под действием электрического поля (и с характеризующей этот эффект величиной диэлектрической восприимчивости среды). Величина ε показывает, во сколько раз сила взаимодействия двух электрических зарядов в среде меньше, чем в вакууме. Относительная диэлектрическая проницаемость воздуха и большинства других газов в нормальных условиях близка к единице (в силу их низкой плотности). Для большинства твёрдых или жидких диэлектриков относительная диэлектрическая проницаемость лежит в диапазоне от 2 до 8 (для статического поля). Диэлектрическая постоянная воды в статическом поле достаточно высока — около 80. Велики её значения для веществ с молекулами, обладающими большим электрическим диполем. Относительная диэлектрическая проницаемость сегнетоэлектриков составляет десятки и сотни тысяч.

Измерение

Относительная диэлектрическая проницаемость вещества ε_r может быть определена путем сравнения ёмкости тестового конденсатора с данным диэлектриком (C_x) и ёмкости того же конденсатора в вакууме (C_o):

Практическое применение

Ёмкость конденсаторов определяется:

где ε_r — диэлектрическая проницаемость вещества между обкладками, ε_о — электрическая постоянная, S — площадь обкладок конденсатора, d — расстояние между обкладками.

Зависимость от частоты

Рассмотрим, например, случай воды. В случае статического поля (частота равна нулю), относительная диэлектрическая проницаемость при нормальных условиях приблизительно равна 80. Это имеет место вплоть до инфракрасных частот. Начиная примерно с 2 ГГц ε_r начинает падать. В оптическом диапазоне ε_r составляет приблизительно 1,8. Это вполне соответствует факту, что в оптическом диапазоне показатель преломления воды равен 1,33.^[1] В узком диапазоне частот, называемом оптическим, диэлектрическое поглощение падает до нуля, что собственно и обеспечивает человеку механизм зрения^{[источник не указан 665 дней]} в земной атмосфере, насыщенной водяным паром. С дальнейшим ростом частоты свойства среды вновь меняются. О поведении относительной диэлектрической проницаемости воды в диапазоне частот от 0 до 10¹² (инфракрасная область) можно прочитать на [1] (англ.)

Примечания

↑ Справочник по элементарной физике. Кошкин Н. И., Ширкевич М. Г. М.: Наука, 1972. — 256с.

См. также

Значения диэлектрической проницаемости для некоторых веществ

Вещество	Химическая формула	Условия измерения	Характерное значение ε_r
Алюминий	Al	1 кГц	-1300 + 1,3·10¹⁴i
Серебро	Ag	1 кГц	-85 + 8·10¹²i
Вакуум	—	—	1
Воздух	—	Нормальные условия, 0,9 МГц	1,00058986 ± 0,00000050
Углекислый газ	CO₂	Нормальные условия	1,0009
Тефлон	—	—	2,1
Нейлон	—	—	3,2
Полиэтилен	[-СН₂-СН₂-]_n	—	2,25
Полистирол	[-СН₂-С(С₆Н₅)Н-]_n	—	2,4-2,7
Каучук	—	—	2,4
Битум	—	—	2,5-3,0
Сероуглерод	CS₂	—	2,6
Парафин	С₁₈Н₃₈ − С₃₅Н₇₂	—	2,0-3,0
Бумага	—	—	2,0-3,5
Электроактивные полимеры	−	−	2-12
Эбонит	(C₆H₉S)₂	−	2,5-3,0
Плексиглас (оргстекло)	—	—	3,5
Кварц	SiO₂	—	3,5-4,5
Диоксид кремния	SiO₂	−	3,9
Бакелит	—	—	4,5
Бетон	−	−	4,5
Фарфор	−	−	4,5-4,7
Стекло	−	−	4,7 (3,7-10)
Стеклотекстолит FR-4	—	—	4,5-5,2
Гетинакс	—	—	5-6
Слюда	—	—	7,5
Резина	−	−	7
Поликор	98 % Al₂O₃	—	9,7
Алмаз	−	−	5,5-10
Поваренная соль	NaCl	−	3-15
Графит	C	−	10-15
Керамика	−	−	10-20
Кремний	Si	−	11.68
Бор	B	−	2.01
Аммиак	NH₃	20 °C	17
		0 °C	20
		−40 °C	22
		−80 °C	26
Спирт этиловый	C₂H₅OH или CH₃-CH₂-OH	−	27
Метанол	CH₃OH	−	30
Этиленгликоль	HO—CH₂—CH₂—OH	−	37
Фурфурол	C₅H₄O₂	−	42
Глицерин	HOCH₂CH(OH)-CH₂OH или C₃H₅(OH)₃	0 °C	41,2
		20 °C	47
		25 °C	42,5
Вода	H₂O	200 °C	34,5
		100 °C	55,3
		20 °C	81
		0 °C	88
Плавиковая кислота	HF	0 °C	83,6
Формамид	HCONH₂	20 °C	84
Серная кислота	H₂SO₄	20-25 °C	84-100
Перекись водорода	H₂O₂	−30 °C — +25 °C	128
Синильная кислота	HCN	(0-21 °C)	158
Двуокись титана	TiO₂	—	86-173
Титанат кальция	CaTiO₃	—	170
Титанат стронция	SrTiO₃	—	310
Барий-стронций титанат	—	—	500
Титанат бария	BaTiO₃	(20-120 °C)	1250-10000
Цирконат-титанат свинца	(Pb[Zr_xTi_1-x]O₃, 0<x<1)		500-6000
Сополимеры	—	—	до 100000

Ссылки

Диэлектрическая проницаемость различных веществ, в т.ч. основных диэлектриков.

Диэлектрик	ε	примечание
Алмаз, С	5,7
Аммиак Nh4 (жид.)	16,90 22,4	(-33°С)
Анилин C6H7N	6,89
Анизол C7H8O (метилфениловый эфир)	4,33
Ацетофенон C8H8O	17,39
Ацетонитрил C2h4N	38,0
Бакелит	4,5
Бальза (дерево)	1,4
Бензин	2
Бензол C6H6	2,23 — 2,27	(20°С — 25°С)
Бетон	4,5
Битум	2,5 — 3
Бумага	2,0 — 3,5
Бумага конденсаторная	2,5 — 2,55
Вода	81	при +20°C
Воздух	1,0001959
Гексан C6h24	1,89
Гетинакс	5 — 6
Гидрат целлюлозы	6,0	(20°С)
Германий, Ge	16 — 16,4
Дерево	2,04 — 7,3	В зависимости от типа древесины
1,4-Диоксан C4H8O2	2,21
Каучук	2,4
Кварц, Si02	3,5 — 4,5
Керосин	2,1
Кристаллическая сера	3,75 — 4,45	В соответствии с ориентацией
Kaмeнная соль, NaCl	6,3
Кремний, Si	11,7
Керамика конденсаторная	10 — 200	радиотехническая
Лёд, Н20 (водяной лед)	73	при -5°С
Масло Вазелиновое	2	Лампадное
Масло трансформаторное	2,2
Масло касторовое	4,6 — 4,8
Метанол Ch5O	32,63	метиловый спирт
Муравьиная кислота Ch3O2	57,0 (20°С) 58,0 (16°С)
Метатитанат бария	2000
Мрамор	7,0 — 8
Нитробензол C6H5O2N	34,85 (25°С) 34,82 (30°С)
Нитрометан Ch4O2N	38,6 (25°С) 35,9 (30°С)
Резина мягкая	2,5
Резина	7,0
Рутил, Ti02	170	вдоль оптической оси
Сегнетова соль	500
Серная кислота h3SO4	101
Сероуглерод CS2	2,64
Силиконовая резина	2,8
Скипидар	2,2
Слюда	5,7 — 11,5
Соль NaCl	5,9	монокристалл, Кулинарные соли
Стекло оконное = плавленый кварц	3,8
Стекло	3,8 — 19	В зависимости от типа стекла
Стеклотекстолит	5,5
Текстолит	7,5
Тефлон = фторопласт 4	2,1
Толуол C7H8	2,3 — 2,4
Трихлорметан (хлороформ) CHCl3	4,81 — 4,64
Триметилметанол C4h20O	9,3
Трицианэтилцеллюлоза	13	(20°С )
Титанат бария, ВаТi03	4000 при 20°С	перпендикулярно оптической оси
Оргстекло	3,5
Полиэтилен	2,25 — 2,4
Парафин	2,0 — 2,3
Пенополистирол	1,03
Полиамид	5,0
Полипропилен	2,3
Полиуретаны	6,7-7,5	(20°С)
Полистирол	2,4 — 2,6
Полихлорвинил	2,9 — 3,0
Плексиглас	3,4 — 3,5
Шеллак	3,5
Фанера	4,0
Фарфор	4,4 — 4,7
Фторид лития LiF	9	монокристалл
Формамид Ch4ON	110	(20°С)
Хлористый водород HCl	4,97	Газ
Хлорбензол C6H5Cl	5,62
Хлористый водород HCl	4,97
Целлулоид	3,0
Цемент	2,0
Циклогексан C6h22	2,0
Эбонит	2,5 — 4,0
Эпоксидные смолы отвержденные	4,4-4,8	(20°С)
Этанол C2H6O этиловый спирт	25,0 (20°С) 24,30 (25°С)
Эфир	1
Янтарь	2,6 — 2,8

Диэлектрическая проницаемость — Википедия

Абсолютная диэлектрическая проницаемость вакуума[править | править код]

Эффект поляризации диэлектрика и проницаемость[править | править код]

Роль диэлектрической проницаемости среды в физике[править | править код]

Диэлектрическая проницаемость непоглощающей среды[править | править код]

Проницаемость и связанные с ней величины[править | править код]

Проницаемость в оптическом диапазоне частот[править | править код]

Тензор проницаемости анизотропных сред[править | править код]

Статическая проницаемость некоторых диэлектриков[править | править код]

Диэлектрическая проницаемость — Википедия

Абсолютная диэлектрическая проницаемость вакуума

Видео по теме

Эффект поляризации диэлектрика и проницаемость

Роль диэлектрической проницаемости среды в физике

Диэлектрическая проницаемость | энергетик

Относительная диэлектрическая проницаемость Википедия

Новый документ в формате RTF (2)

Относительная диэлектрическая проницаемость — это… Что такое Относительная диэлектрическая проницаемость?

Измерение

Практическое применение

Зависимость от частоты

Примечания

См. также

Значения диэлектрической проницаемости для некоторых веществ

Ссылки

Диэлектрическая проницаемость различных веществ, в т.ч. основных диэлектриков.

Диэлектрическая проницаемость различных веществ, в т.ч. основных диэлектриков.

alexxlab

Добавить комментарий Отменить ответ

Рубрики