Диаметр окружности круга • как найти ⬅️ формула
Поможем понять и полюбить математику
Начать учиться
316.2K
В школьных задачах за шестой класс обязательно есть задания по поиску диаметра круга или шара. В статье мы подробно рассмотрим этот вопрос и способы его решения.
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Записывайтесь на онлайн-курсы по математике для детей и подростков!
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
Отметить точки пересечения прямой и окружности.
Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
Теперь осталось измерить диаметр круга при помощи линейки.
 Получилось!
Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
420.1K
Как найти площадь прямоугольника
К следующей статье
183.6K
Таблица умножения: поможем выучить легко и быстро
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Знак диаметра
В тех случаях, когда требуется указать размер диаметра, используют знак в виде окружности с линией « Этот символ наносят перед размерным числом.
Этот символ наносят перед размерным числом.
Примеры использования знака диаметра:
Знаки диаметра на деталях вращения цилиндрической и конической формы
Размеры наносимые при недостатке места
на размерной линии
Обозначение размеров при недостатке места
для стрелок
Диаметр – это длинна отрезка прямой соединяющей поверхности окружности. Отрезок диаметра, в любом случае проходит только через центр окружности. Обозначают его обычно латинской буквой «Ø». Если радиус окружности умножить на два, суммой будет диаметр. Все объемные тела, имеющие сферическую форму, а также те, хотя бы одно из возможных сечений которых представляет собой круг, обозначаются символами диаметра. Слово «диаметр» произошло от греческого слова «diametros» – поперечник.
Пример обозначения четырёх отверстий
с указанием диаметра
На технических чертежах диаметры обозначаются символом в виде перечеркнутой окружности «Ø».
В сечение конус представляет собой прямоугольный треугольник, один из катетов которого параллелен или сосен телу вращения. Его параметры имеют следующими обозначениями: «D» – больший диаметр, «d» – меньший диаметр, «L» – длина. На чертеже диаметры конуса обозначаются цифрами, перед которыми ставятся знаки «Ø» а числовое значение длинны без буквенных обозначений.
К наиболее распространенным деталям с цилиндрическими поверхностями, относятся валы различного назначения. Цилиндрические тела, образованные вращением прямоугольника около одной из его сторон обозначаются диаметром. Гладкие валы имеют некоторые конструктивные особенности, и разделяются на разновидности: прямые, ступенчатые односторонние, ступенчатые двусторонние и тяжелые. К примеру, валы асинхронных двигателей, в которых ротор сопрягается с валом методом запрессовки на наибольший его диаметр, а по обеим сторонам имеются ступени под подшипники, вентиляторы, и шкивы.
ØПример нанесения знака диаметра
на сферической поверхности
К деталям с коническими поверхностями относятся инструментальные переходные втулки, у которых наружная и внутренняя поверхность конические. Такие втулки обеспечивают высокую точность центрирования и быстродействие смены инструмента с достаточной жёсткостью при использовании их на станках. Переходные втулки бывают короткие и длинные.
Конические инструментальные детали данного типа называются «конус Морзе» и делятся на номера. Углы, длины и диаметры переходных втулок можно взять из специальных таблиц. В табличных данных используются буквенные обозначения такие как – «
Углы, длины и диаметры переходных втулок можно взять из специальных таблиц. В табличных данных используются буквенные обозначения такие как – «d» меньший диаметр, «D» большой диаметр, «L» длина детали. На чертежах диаметры и длины обозначаются цифровыми значениями, причём перед числами диаметра ставится знак «Ø
«Конус Морзе» – помимо переходных втулок применяется при изготовлении хвостовиков спиральных свёрл, концевых фрез, приспособлений и оправок. Инструментальные конусы фиксируются за счёт упругой и пластической деформации. Для реализации таких соединений в шпинделях фрезерных и токарных станков, предусмотрены конические отверстия для установки вспомогательного инструмента. Кроме того у токарного станка пиноль задней бабки имеет такое же коническое отверстие.
В технике используются большое количество деталей и их элементов для обозначения, которых используется знак диаметра. Для стандартных размеров диаметров используются параметрический ряд, в который входят стандартные размеры.
Какие единицы измерения диаметра?
••• DedMityay/iStock/GettyImages
Мэтью Пердью
Окружность — это геометрический объект, характеризуемый как линия точек на плоскости, равноудаленных от одной точки. По сути, для описания размера круга используются три различных значения измерения — радиус, диаметр и длина окружности. Диаметр, в частности, описывается как длина линии между двумя точками на окружности, которая пересекает центральную точку; он равен удвоенному значению радиуса. Единицы, используемые для описания диаметра, в конечном итоге зависят от контекста, в котором он измеряется и сообщается.
Метрические единицы
Наиболее распространенными единицами научных измерений являются те, которые определены в метрической системе. Единицы линейного измерения, такие как диаметр, указываются в метрах. Значение также может быть указано в различных производных счетчика в зависимости от измеряемого объекта, включая миллиметры, сантиметры и километры. Например, километры были бы предпочтительными единицами измерения, используемыми для сообщения диаметра Земли, тогда как миллиметры или сантиметры были бы идеальными единицами измерения диаметра монеты.
Единицы линейного измерения, такие как диаметр, указываются в метрах. Значение также может быть указано в различных производных счетчика в зависимости от измеряемого объекта, включая миллиметры, сантиметры и километры. Например, километры были бы предпочтительными единицами измерения, используемыми для сообщения диаметра Земли, тогда как миллиметры или сантиметры были бы идеальными единицами измерения диаметра монеты.
Традиционные единицы
В Соединенных Штатах метрическая система обычно не используется для обычных измерений. Вместо этого используются обычные единицы, такие как фунты для измерения веса и дюймы для линейных измерений. Таким образом, диаметр в ненаучных ситуациях может быть указан в дюймах, футах или милях в зависимости от соответствующего размера измеряемого круглого объекта.
Единицы диаметра в расчете длины окружности
Длина окружности описывает меру расстояния вокруг края окружности. Он рассчитывается как измеренный диаметр соответствующего круга, умноженный на математическую константу пи. Сообщаемая единица окружности зависит от единицы, используемой для диаметра. Таким образом, длина окружности, рассчитанная с использованием диаметра в дюймах, также будет указана в дюймах.
Он рассчитывается как измеренный диаметр соответствующего круга, умноженный на математическую константу пи. Сообщаемая единица окружности зависит от единицы, используемой для диаметра. Таким образом, длина окружности, рассчитанная с использованием диаметра в дюймах, также будет указана в дюймах.
Единицы измерения диаметра в расчете площади
Площадь круга рассчитывается как квадрат диаметра, умноженный на одну четвертую постоянной числа пи. Поэтому единицы площади представляются как квадратные единицы измерения диаметра. Например, площадь круга, вычисленная с диаметром в сантиметрах, будет указана в квадратных сантиметрах.
Статьи по теме
Ссылки
- Matisfun.com: Circle
Об авторе
Мэтт Пердью — студент-медик аллопатической медицинской школы США. Начиная с 2010 года он начал писать научные статьи для eHow. Он также был автором статьи для медицинского журнала, посвященной текущим рекомендациям по сканированию костей для диагностики остеопороза.
Вопрос Видео: Измерение диаметра и толщины монеты
Стенограмма видео
Измеренные диаметр и толщина монеты составляют 2,4 сантиметра и 2,36 миллиметра соответственно. Какой из следующих инструментов лучше всего использовать для измерения этих длин? (A) стандартный метр, (B) метровая лента, (C) обычная линейка или (D) штангенциркуль.
Прежде чем мы рассмотрим эти отдельные инструменты, давайте сначала посмотрим на монету. Диаметр монеты — это ее ширина от одного конца до другого, что в данном случае составляет 2,4 сантиметра. Но монеты — это не просто плоские круги, на которых обычно изображают очень богатых и очень мертвых людей. Нет, у них тоже есть толщина. Глядя на это сбоку, толщина монеты — это расстояние от передней до задней стороны монеты, которое составляет 2,36 миллиметра. Таким образом, инструмент, который может лучше всего измерять эти длины, должен уметь измерять сантиметры, миллиметры и доли миллиметров.
Начнем со стандартного счетчика.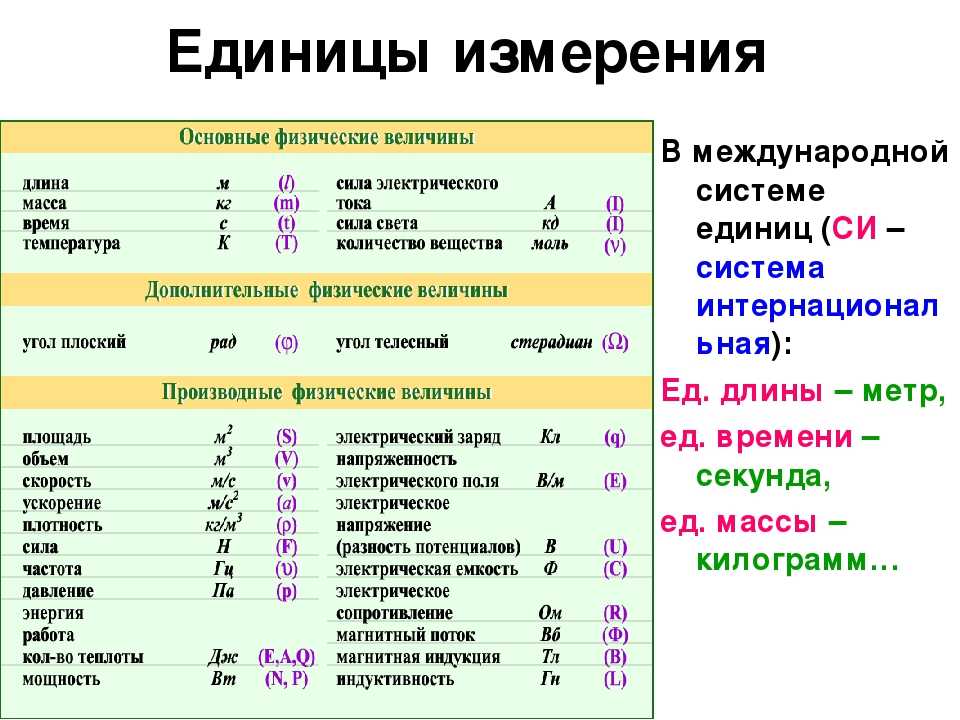
Однако проблема с измерением толщины монеты все еще существует, так как стандартный счетчик может измерять только полные миллиметры, а не доли миллиметров. Так что стандартный счетчик, вероятно, не лучший выбор. Те же принципы применимы и к обычной линейке, поскольку она похожа на метровую линейку, только короче. Он по-прежнему измеряет только сантиметры и полные миллиметры, а это означает, что это не лучший инструмент для измерения этой монеты.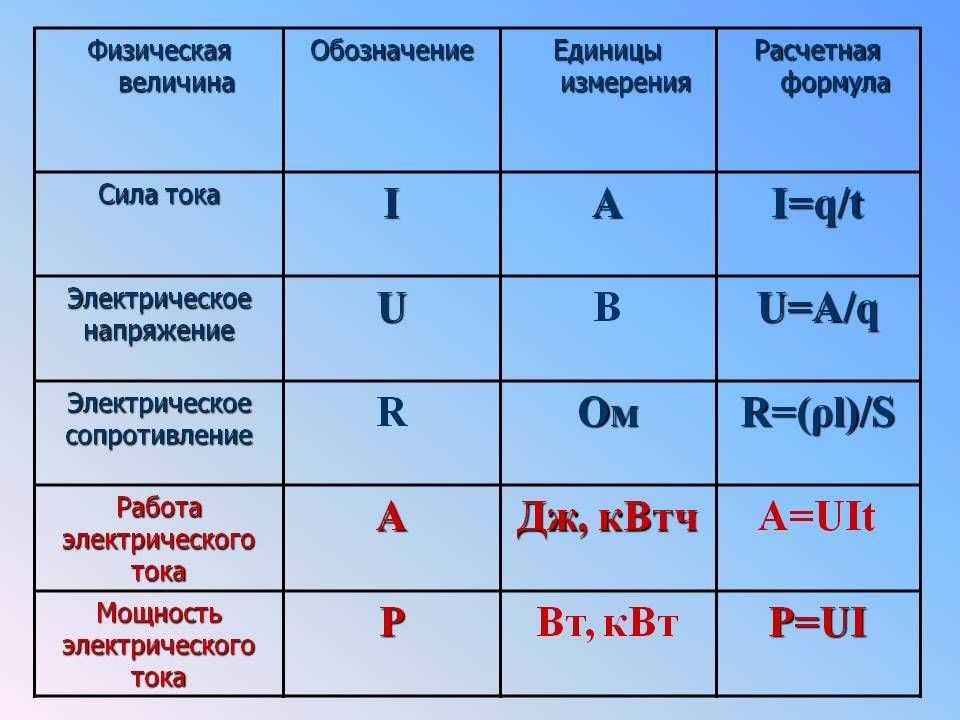


 Получилось!
Получилось!