АМПЛИТУДНЫЕ ДЕТЕКТОРЫ НА ОУ в устройствах на микросхемах

Амплитудный детектор представляет собой выпрямитель, на выходе которого включен накопительный конденсатор. Амплитудныйдетектор на ОУ представляет собой однополупериодный выпрямитель на ОУ, нагруженный на конденсатор.

В отличие от выпрямителей-детекторов, используемых для питания радиоэлектронных узлов, амплитудные детекторы предназначены для запоминания экстремальных значений входного сигнала.

В типовой схеме амплитудного детектора при возрастании уровня входного напряжения напряжение на накопительном конденсаторе С1 (рис. 16.1) возрастает. В случае последующего снижения уровня этого напряжения напряжение на конденсаторе С1 остается неизменным (т. е. запоминается). Заряд на конденсаторе сохраняется в течение времени, определяемого током утечки конденсатора, либо повышается при условии возрастания напряжения на входе устройства выше предыдущего экстремального значения [16.1,16.2].

Для того, чтобы произвести сброс заряда конденсатора С1, рис. 16.1, и подготовить устройство для последующего цикла работы используют импульс сброса, подаваемый на управляющий вход электронного ключа, например, полевого транзистора, подключенного параллельно накопительному конденсатору.

Двухкаскадный амплитудный детектор положительного уровня, рис. 16.2—16.4, представляет собой более совершенное устройство: он

Рис. 16.4. Схема модифицированного двухкаскадного амплитудного детектора с цепью сброса

Рис. 16.3. Схема модифицированного амплитудного детектора

Усовершенствования схем амплитудных детекторов коснулись и цепей сброса накопительного конденсатора. Одна из подобных схем приведена на рис. 16.4 [16.2].

содержит повторитель напряжения на микросхеме DA2. Это минимизирует влияние сопротивления нагрузки на саморазряд накопительного (запоминающего) конденсатора С1. Одновременно повышается точность преобразования.

Для снижения токов утечки конденсатора С1 через обратносмещенный диод VD2 в схеме модифицированного амплитудного детектора, представленной на рис. 16.3, использован дополнительный диод VD3 и резистор R3 [16.2].

Практическая схема милливольтметра переменного тока на микросхеме DAI NE531 с использованием прецизионного выпрямителя приведена на рис. 16.5 [16.3].

Для использования в бытовой радиоаппаратуре была разработана специализированная микросхема К157ДА1. Микросхема представляла собой двухканальный двухполупериодный выпрямитель среднего уровня аудиосигналов для использования в звуковоспроизводящей стереофонической аппаратуре. В состав микросхемы К157ДА1 (рис. 16.6, [16.4]) входили:

♦    два идентичных канала, содержащих предусилитель на ОУ и преобразователь двуполярного сигнала;

♦  схема стабилизации питающего напряжения.

Питание микросхема могла получать от двуполярного источника напряжения ±(3—20) В при суммарном потреблении тока при отсутствии входного сигнала до 1,6 мА. Коэффициент усиления микросхемы по напряжению при напряжении питания ±15 В — 7—10 до верхней границы частоты не ниже 100 кГц. Выходное напряжение — до 9 В при токе нагрузки 2,5—6,0 мА. Выводы 8 и 14 микросхемы — выводы делителя обратной связи. Выводы 9 и 13 — выводы детектора для соединения с общей шиной (рис. 16.6).

Пример использования микросхемы К157ДА1 для индикации уровня аудиосигнала стереофонического усилителя приведен на рис. 16.7 [16.4].

Поскольку двуполярное питание микросхемы малоприемлемо при ее работе в нестационарных условиях, для однополярного питания микросхемы К157ДА1 была предусмотрена схема включения, приведенная на рис. 16.8 [16.4].

Устройство обеспечивает одноканальную регистрацию квазипиковых значений входного сигнала. Время интеграции определяется RC-произведением интегрирующей цепочки и для приведенных на рис. 16.8 номиналах близка 10 мс. Время разряда конденсатора СЗ примерно равно 300 мс.

Рис. 16.7. Типовая схема включения микросхемы К157ДА1 в качестве двухканального двухполупериодного выпрямителя среднего значения аудиосигнала

Рис. 16.8. Типовая схема включения микросхемы К157ДА1 при однополярном питании

Рис. 16.9. Схема индикатора среднего значения сигнала на микросхеме К157ДА 7

Для измерения среднего уровня сигнала, более точно отвечающего слуховому восприятию и оценке громкости сигнала, может быть использован индикатор, схема которого представлена на рис. 16.9 [16.4]. Коэффициент преобразования микросхемы в таком включении около 50 мкА/В, его можно регулировать подстройкой потенциометра R2.

Шустов М. А., Схемотехника. 500 устройств на аналоговых микросхемах. — СПб.: Наука и Техника, 2013. —352 с.

Чувствительный амплитудный детектор | Техника радиоприёма

Способ детектирования, примененный в описанных выше приемниках (см. Схема на трех транзисторах и Карманный приемник), хорошо себя зарекомендовал и навел на мысль о разработке более чувствительного амплитудного детектора для других конструкций. Известно, что диодные и транзисторные амплитудные детекторы, используемые в радиовещательных приемниках AM сигналов, обладают невысокой чувствительностью. Их коэффициент передачи быстро уменьшается при уровнях сигнала ниже 100 мВ. Связано это с квадратичностью характеристики при малых сигналах: амплитуда продетектированного сигнала пропорциональна квадрату амплитуды входного сигнала РЧ.

Гораздо большую чувствительность и больший динамический диапазон имеют активные детекторы, собранные на операционных усилителях (ОУ). Они получили некоторое распространение в измерительной технике, но так и не стали применяться в радиоприемниках, вероятно, из-за сложности, дороговизны и ограниченного частотного диапазона. Используя высокочастотный транзистор и диоды, удалось разработать амплитудный детектор с высокой чувствительностью, содержащий минимум деталей.

Схема детектора показана на рис. 4.17. Он представляет собой обычный резистивный усилительный каскад, в котором в цепи смещения базы транзистора VT1 вместо резистора установлен кремниевый диод VD1. Цепочка R2C2 фильтрует сигнал ЗЧ на выходе детектора от радиочастотных пульсаций. В отсутствие сигнала напряжение на коллекторе транзистора автоматически устанавливается около 1-1,1 В: оно равно сумме напряжений открывания диода и перехода база — эмиттер транзистора. Ток транзистора определяется напряжением питания и сопротивлением резистора нагрузки R1, I

o = (U_п — 1,1 В) / R1. При номинале резистора, указанном на схеме, и напряжении питания 3 В ток составляет около 0,5 мА, но его можно сделать и значительно меньше, увеличив сопротивление резистора.

Ток базы транзистора составляет не более нескольких микроампер, он протекает через диод в прямом направлении, устанавливая его на пороге открывания, на участке с максимальной кривизной вольтамперной характеристики, что и требуется для хорошего детектирования. Динамическое сопротивление диода составляет в этой точке десятки килоом — оно незначительно снижает усиление транзисторного каскада.

При поступлении на вход детектора AM сигнала положительные полуволны, выделяющиеся на нагрузке R1, выпрямляются диодом и увеличивают потенциал базы, открывая транзистор. Емкость разделительного конденсатора С1 должна быть значительно больше емкости обычных разделительных конденсаторов радиочастотных каскадов, чтобы он не успевал разряжаться током базы за период колебаний. Коллекторный ток открывающегося транзистора возрастает, а его коллекторное напряжение уменьшается. Максимумы положительных полуволн коллекторного напряжения оказываются как бы «привязанными» к уровню +1 В, в то время как огибающая отрицательных полуволн промодулирована удвоенной амплитудой напряжения ЗЧ. Осциллограмма коллекторного напряжения точно такая же, как на рис. 4.11.

Отфильтрованное цепочкой R2C2 среднее напряжение, соответствующее закону модуляции, поступает на выход. Его максимальный размах составляет 0,5 В, далее наступает ограничение. Параметры детектора таковы: при входном сигнале 3 мВ с глубиной модуляции 80% выходное напряжение ЗЧ составляет 180 мВ. Искажения огибающей визуально почти незаметны, к тому же они резко уменьшаются с понижением глубины модуляции. Входное сопротивление детектора невелико и составляет сотни ом, поэтому сигнал на него лучше подавать от эмиттерного (истокового) повторителя, но можно и от обычного апериодического каскада с резистором нагрузки не более 1-2 кОм. Выходное сопротивление детектора определяется суммарным сопротивлением резисторов R1 и R2, поэтому желательно, чтобы входное сопротивление УЗЧ, подключенного к выходу детектора, составляло не менее 20 кОм.

Коэффициент передачи детектора и его выходное напряжение ЗЧ можно повысить вдвое, установив еще один диод, как показано на рис. 4.18. Резистор нагрузки детектора R2 присоединен к проводу питания, обеспечивая небольшой начальный ток через дополнительный диод VD2, чтобы вывести его на участок с максимальной кривизной характеристики. Этот диод выпрямляет отрицательные полуволны коллекторного напряжения, и потенциал верхней по схеме обкладки фильтрующего конденсатора С2 повторяет их огибающую.

Этот детектор вносит несколько большие нелинейные искажения, но развивает то же напряжение ЗЧ (180 мВ) при входном сигнале 1,5 мВ, а начинает детектировать при входных сигналах в сотни микровольт. Для сравнения была измерена чувствительность апериодического УРЧ (на том же транзисторе с тем же сопротивлением нагрузки 3,9 кОм), нагруженного на диодный детектор по схеме удвоения напряжения — она получилась втрое хуже, хотя схема получается сложнее и содержит больше элементов.

Постоянную составляющую продетектированного сигнала можно использовать в системе автоматической регулировки усиления (АРУ), учитывая, что в детекторе по схеме рис. 4.17 она изменяется по мере увеличения уровня сигнала от 1,1 до 0,55 В, а в детекторе по схеме на рис. 4.18 — от 1,65 до 0,55 В. Это позволяет управлять смещением кремниевых транзисторов УРЧ или УПЧ непосредственно с выхода детектора. При отсутствии сигнала смещение максимально, а при наличии сигнала уменьшается, снижая усиление каскадов. Дополнительная польза такого решения в том, что напряжение смещения будет мало зависеть от напряжения питания, поскольку детектор выступит в роли его стабилизатора.

Максимальная частота сигнала для обоих детекторов составляет около 3 МГц, поэтому их можно использовать в ДСВ приемниках прямого усиления и в супергетеродинах со стандартным значением ПЧ 450-470 кГц. Представляется интересным объединить этот детектор с описанным ранее истоковым повторителем для магнитной антенны, схема которого дана на рис. 4.6. Должен получиться довольно чувствительный приемник без усилителей напряжения РЧ.

Читать дальше — Приемник на биполярных транзисторах с АРУ

ДЕТЕКТОРЫ С НЕЛИНЕЙНЫМИ ПЕРЕДАТОЧНЫМИ ХАРАКТЕРИСТИКАМИ — КиберПедия

 

Пиковый детектор на транзисторах. При отсутствии на входе AM сигнала транзисторы VT1 и VT2 (рис. 8.14) закрыты. Напряжение на конденсаторах CI и С2 равно нулю. Входной сигнал через эмиттерный повторитель на транзисторе VT1 проходит на базу транзистора VT2. Импульс отрицательной полярности проходит через два транзисторных перехода. Через переход база — коллектор заряжается конденсатор С2, а через переход база — эмиттер — конденсатор С1. В этом случае транзистор работает как два диода. При отсутствии входного сигнала конденсатор С1 разряжается через переход база — эмиттер VT3 и резистор R2. Напряжение на конден­саторе С2 остается без изменения. Если последующий входной им­пульс будет иметь большую амплитуду, чем предыдущий, то вновь откроется два перехода транзистора VT2 и произойдет заряд коненсаторов до нового уровня входного сигнала. В том случае, если входной импульс будет меньше по амплитуде, то откроется толь ко переход база — эмиттер. Тран зистор VT2 работает как триод Конденсатор С2 разряжается че­рез транзистор VT2 на конденса­тор С1. Процесс разряда будет происходить до тех пор, пока по­тенциалы этих конденсаторов не сравняются. Напряжение на них будет равно амплитуде входного сигнала. Постоянная времени за­ряда конденсатора С2 равна 2,5 мкс, постоянная времени раз­ряда — 40 или 0,6 мкс в зависимости от режима работы транзи­стора VT2. Точность детектирования огибающей не хуже 2,5% при частоте 100 кГц. Минимальная амплитуда входного сигнала 20 мВ.

Рис. 8.14 Рис. 8.15

Рис. 8.16

 

Частотно-зависимый амплитудный детектор. Выходной сигнал детектора (рис. 8.15, а) снимается с диагонали моста, который включен в цепь ООС ОУ. Коэффициент передачи детектора зависит от элементов ООС R3, R2 и С, а также от сопротивления компен­сирующего резистора R1. Коэффициент передачи определяется вы­ражением

На рис. 8.15,6 приведена зависимость выходного напряжения от частоты.

Квадратичный детектор с аппроксимацией.Детектор (рис. 8.16) состоит из двух симметричных устройств. На вход ОУ DA1 прихо­дит отрицательная полярность входного сигнала, а на вход ОУ DA2 — положительная. Когда входной сигнал отрицательной поляр­ности имеет уровень меньше 1 В, коэффициент усиления микросхемы определяется отношением R₆/R₁ и равен единице. Как только вход­ной сигнал превысит уровень 1 В открывается транзистор VT1 и коэффициент усиления усилителя меняется. На выходе интеграль­ной микросхемы DA1 сигнал удваивается. При дальнейшем увели­чении входного сигнала будут последовательно открываться осталь­ные транзисторы. Таким образом, квадратичная зависимость выход­ного сигнала будет аппроксимирована линейными участками. Воз-рая половина схемы для положительной полярности входного сиг­нала работает аналогичным образом. Верхняя граничная частота входного сигнала определяется граничной частотой работы ОУ.

ЧАСТОТНЫЕ ДЕТЕКТОРЫ

 

Детектор на дифференцирующем каскаде. В основу ча­стотного детектора (рис. 8.17, а) положен каскад усилителя с не­равномерной частотной характеристикой. Коэффициент усиления усилителя равен oR₂Ci. К коллектору транзистора VJ2 подключен детектор. Постоянное напряжение на выходе детектора пропорцио­нально частоте входного сигнала. На рис. 7.17, а показаны три гра­фика зависимости выходного сигнала от частоты при различных емкостях конденсатора CL Линейная зависимость наблюдается для емкости 6 нФ. На частоте 100 кГц коэффициент передачи де­тектора равен 100.

Рис. 8.17

Рис 8.18

Детектор с фазовым звеном. Частотный детектор (рис 8 18) построен по принципу синхронного детектирования Входной сиг­нал через транзистор VT1 проходит на базы транзисторов VT2 и VT3 Транзистор VT2 совместно с элементами С! и R6 образуют фазосдвнгающин каскад Цепочка R6 и С1 имеет частоту среза 1 кГц На этой частоте выходной сигнал транзистора VT2 сдвинут на 90° относительно входного сигнала В каскаде на транзисторе VT3 входной сигнал усиливается и ограничивается Этот сигнал управляет работой полевого транзистора VT4, который работает в ключевом режиме и управляет цепью, через которую проходит сдвинутый по фазе входной сигнал Интегратор на элементах R11 и С4 выделяет постоянную составляющую Зависимость постоянной составляющей от частоты входного сигнала, имеющего амплитуду 2 В, приведена на рис 8 18

Активные частотные детекторы. Четыре схемы частотных де­текторов (рис 8 19) построены по одному принципу Частотно-за­висимым элементом в схемах является RC цепочка Сигнал на ре­зисторе R2 в схеме рис 819, с сдвинут относительно входного сигнала на определенный фазовый угол Фазовый сдвиг зависит от частоты входного сигнала Сигнал на базе управляет транзистором VT, выходной ток которого заряжает конденсатор С2 Значение тока определяется сопротивлением резистора R1 Функции интегри­рования выходного сигнала выполняют элементы RI, C2 Кроме того, резистор R1 является элементом фазосдвигающей цепочки

В схеме рис 819,6 фазосдвигающая цепочка построена на эле­ментах R1, С1, а интегрирующая цепочка — на R2, С2. Частотные характеристики обоих детекторов имеют в области низких частот неравномерный участок, который ограничивает рабочий диапазон устройства Чтобы уменьшить этот участок, в следующих схемах включен дополнительный транзистор На рис 819, в детектор имеет частотную характеристику, неравномерный участок которой пере­мещен к частотам менее 2 кГц Введение дополнительного транзи­стора в схеме с ОБ позволило создать детектор (рис 819, г), ча­стотная характеристика которого является линейной и имеет большую крутизну, чем все предыдущие Амплитуда входного сиг­нала равна 3 В Все схемы проиллюстрированы частотными зави­симостями выходного напряжения

Детектор с фазовым мостом. В основе частотного детектора (рис 8 20, а) лежат две схемы мостового фазовращателя и балансного фазового детектора Фазовращатель собран на Rl, R2 и С1.С2, а фазовый детектор состоит из следующих элементов VD1, VD2, R3, R4, СЗ, С4 Выходное напряжение фазовращателя используется ках коммутирующее напряжение для детектора При изменении ча­стоты входного сигнала от 0 до оо сдвиг фазы выходного сигнала на выходе фазовращателя будет меняться от 0 до 180° Для частоты w=1/RС = 2,1 МГц сдвиг фазы будет равен 90°. Для этого сдвига фазы на выходе детектора будет нулевое напряжение. При других значениях фазового сдвига напряжение на выходе детектора является положительным или отрицательным. Коэффициент передачи детектора в зависимости от частоты сигнала определяется выраже­нием U_BЫХ/U_{вых max}=(w₀² — w²)/(w₀² +w²). На рис. 8.20, б приведена характеристика детектора.

Рис 8.19

 

Рис. 8.20

 

Рис. 8.21

 

Частотный детектор на интегральной микросхеме К224ДС2. Принципиальная схема микросхемы приведена на рис. 8.21, а. Сим­метричный детектор отношений (рис. 8.21,6) предназначен для ра­боты с частотой от 6 до 20 МГц. Для симметрирования плеч детек­тора между выводами 3, 5 включен резистор R.

 

ФАЗОВЫЕ ДЕТЕКТОРЫ

 

Детектор на дифференциальном усилителе. Детектор (рис. 8.22) построен на дифференциальном усилителе, входящем в микросхему, к выходу которого подключены два транзистора, осу­ществляющие функции повторителя и преобразователя уровня. На один вход усилителя поступает исследуемый сигнал, на вход управ­ления — опорный сигнал. Амплитудная характеристика детектора линейна при амплитудах входного сигнала до 50 мВ. Частотный диапазон работы от единиц герц до мегагерц.

Рис. 8.22

 

Детектор на ограничителях. Фазовый детектор (рис 823 а) со­стоит из двух усилительных каскадов, работающих в режиме насы­щения. На первый вход подается исследуемый сигнал а на вто­рой — сигнал с опорной частотой. В коллекторах транзисторов появ­ляется сигнал прямоугольной формы. Когда в коллекторах транзи­сторов VT1 и VT2 сигнал положительной полярности а в коллек­торах VT3 и VT4 — отрицательной, то на входе диода будет нуле­вой сигнал. Это случай совпадения сигналов по фазе При сдвиге сигналов на 2л в коллекторах транзисторов будут совпадать по времени положительные и отрицательные импульсы. На входе диода будет сигнал той же полярности, что и в коллекторах транзисто­ров. Отрицательный полупериод сигнала пройдет через диод и на выходе фильтра выделится постоянная составляющая Длитель­ность импульсов положительной и отрицательной полярностей бу­дет пропорциональна фазовому сдвигу между сигналами В прин­ципе можно образовать выходной сигнал и от положительных им­пульсов. На рис. 8.23, б приведена характеристика детектора

 

Рис. 8.23

 

Детектор на интегральной микросхеме К122УД1. Детектор собран на дифференциальном усилителе интегральной микросхемы К122УД1 (рис. 8.24). Сигнал на Входе 1 (база одного из двух транзисторов дифференциальной пары микросхемы) формирует на двух выходах сигналы, сдвинутые по фазе на 180°. Сигнал, кото­рый подается на Вход 2 (база транзистора микросхемы), форми­рует сигналы, совпадающие по фазе. При фазовом сдвиге сигналов, равном 90°, на входах и выходах микросхемы образуются одина­ковые сигналы. После выпрямления на выходе детектора будет нуль. Для совпадающих по фазе входных сигналов на выходах дифферен­циального усилителя будет максимальный разбаланс по амплиту­де. В этом случае после детектирования формируется максимальное отрицательное напряжение. При сдвиге по фазе на 180° между входными сигналами на выходе схемы формируется максимальное положительное напряжение. Для других фазовых соотношений между входными сигналами на выходе будет устанавливаться промежуточное значение. Детектор работает при входных сигналах с амплитудой до 1 В на частотах от 1 кГц до 1 МГц.

Рис. 8.24

 

Фазовый детектор с амплитудными ограничителями. Фазовый детектор (рис. 8.25) состоит из двух детекторов AM сигнала, кото­рые построены на ОУ DA1 и DA2. Если на входах действуют сиг­налы U₁ — А (t)соs[wt+ф(t)] и U₂ = Acoswt, то на выходе детекто­ра после ОУ DA3, работающего в схеме дифференциального интегратора, будет сигнал, равный среднему значению выходных напря­жений ОУ DAI и DA2. Для A>A(t) U_вых = 2/п A(t) cos Ф(t). Де­тектор работает в широком диапазоне частот. Верхняя граничная частота определяется частотными свойствами ОУ Нижняя гранич­ная частота зависит от параметров интегратора. В детекторе можно применить любой ОУ. Детектор с ОС. Входной фазомодулированный сигнат подается на входы ОУ DA1 (рис. 8.26).

Рис. 8.25

Рис. 8.26

 

Выходной сигнал этого усилителя зависит от состояния полевого транзистора. Если транзистор за­крыт, то выходной сигнал равен нулю. При открытом состоянии транзистора входной сигнал проходит на выход DA1. Управление полевым транзистором осуществляется интегральной микросхемой DA3, выполняющей функции ограничителя. На вход этой схемы по­ступает сигнал с фазосдвигающего устройства, построенного на интегральной микросхеме DA2. Коэффициент передачи фазосдвига­ющего каскада равен К= l/(l+jwC₂R₈). Частота cpeзa цепочки может быть определена из равенства w₀ = R₈С₂=1. Для подстрой­ки фазы сигнала служит потенциометр R8. В результате входной сигнал с частотой w₀ будет создавать нулевой сигнал на выходе интегратора Я₄С,. При изменении входного сигнала по фазе на вы ходе интегратора образуется сигнал, который дополнительно усили­вается интегральной микросхемой DA4.

Фазовый детектор на переключателях. Фазовый детектор (рис. 8.27) состоит из двухполупернодного детектора усилителя и схемы управления. Детектор сигнала состоит из аналоговых ключей на полевых транзисторах VT1-VT3 и ОУ DA1. При открывали транзисторов VT1 и VT2 входной сигнал проходит через ОУ DA1 инвертируется. Коэффициент усиления усилителя равен единице При закрывании VT1 и VT2 открывается VT3. Через транзтотор VT3 входной сигнал проходит на вход ОУ DA2. Управление детек тором осуществляется входными сигналами с транзисторов VT5 и VT6.

Для балансировки ОУ DA2 при отсутствии входного сигнал служит потенциометр R15. В цепь ОС этого ОУ включен конденсатор, выполняющий функции интегратора. Его емкость определяется частотой входного сигнала. Схема управления собрана на транзи­сторах VT4 — VT6. Фазовый детектор может работать в диапазоне частот от 50 Гц до 20 кГц. Чувствительность схемы выше 120 мВ/град. Дрейф нуля меньше 60 мВ.

Рис. 8.27

 

ОДНОТАКТНЫЕ ДЕТЕКТОРЫ

 

Транзисторный детектор. Детектор (на рис. 8.28, а) по­строен на одном транзисторе, который выполняет функции ключа. При отсутствии опорного сигнала входной сигнал отрицательной полярности открывает переход база — коллектор транзистора. Сиг­нал на выходе отсутствует. Входной сигнал положительной поляр­ности запирает переход коллектор — база. В этом случае опорный сигнал открывает транзистор. Ток входного сигнала проходит через эмиттер-коллекторную цепь. При различных фазовых соотношениях между входным и опорным сигналами амплитуда сигнала на выходе будет меняться. Выходной сигнал меняется и от амплитуды входно­го сигнала. Эти зависимости показаны на рис. 8.28, б, в. Частота сигналов 10 кГц, амплитуда входного сигнала 1 В, опорного — 2 В. Для компенсации постоянного уровня отрицательной полярно­сти предназначен резистор R5.

Рис. 8.28

Рис. 8.29

 

Конденсаторный детектор. Синхронный детектор (рис. 8.29, а) построен по принципу интегрального накопления заряда на конден­саторе. Во время отрицательной полуволны опорного сигнала тран­зистор VT2 открыт. Входной сигнал заряжает конденсатор С1 через резистор R1. Во время положительного полупериода транзистор VT2 закроется, a VT1 откроется. Накопленный заряд на конденса­торе С2 будет приложен к интегрирующей цепочке R₃C₂. В резуль­тате на выходе будет выделена постоянная составляющая. Зави­симость выходного сигнала от фазового сдвига между входным и опорным сигналами показана на рис. 8.29,6. Если вместо резистора R3 поставить диод VD, то получим однополярную характеристику. Амплитуда входного сигнала 1 В, частота 50 кГц. Амплитуда опор­ного гармонического сигнала 2 В.

Детектор с электронным переключателем. В синхронном детек­торе (рис. 8.30, а) роль управляющего элемента выполняет полевой транзистор. В качестве интегратора применяется ОУ с конденсато­ром в цепи ОС. Когда транзистор открыт, на выходе появляется сигнал, соответствующий среднему значению входного сигнала. Амплитуда этого сигнала регулируется в широких пределах сопро­тивлениями резисторов R1 и R2. Емкость конденсатора также влияет на выходной сигнал. На рис. 8.30, б приведена зависимость коэф­фициента передачи детектора от частотного сдвига между выходным и опорным сигналами.

Рис. 8.30

Рис. 8.31

 

Детектор на интегральной микросхеме К122УД1. Детектор (рис. 8.31, а) собран на дифференциальном усилителе. Входной сиг­нал подается на базу усилительного транзистора, а опорный — на базу токозадающего транзистора. Выходной сигнал является ре­зультатом взаимодействия двух сигналов. Он зависит от амплитуды входного и опорного сигналов, а также от фазового сдвига между ними.

Эта схема может применяться для детектирования AM и ФМ сигналов. Амплитудно-модулированный сигнал требует стабилиза­ции фазы между сигналами, а ФМ сигнал — стабилизации амплитуд сигналов. Кроме того, детектор может применяться и для детекти­рования ЧМ сигналов. В этом случае необходимо изменить схему, связанную с транзистором VT. Изображенная схема предназначена для выявления амплитудных изменений входного сигнала. Она яв­ляется узкополосной. На рис. 8.31,6 — г проиллюстрированы зависи­мости выходного напряжения детектора от опорного и входного на­пряжений, а точнее, разности фаз между ними.

 

ДВУХТАКТНЫЕ ДЕТЕКТОРЫ

 

Двухтактный детектор. В качестве управляющих элемен­тов в детекторе (рис. 8.32) используют два транзистора. Противо­фазные сигналы управления отрицательной полярности подаются на базы транзисторов. Когда один транзистор закрыт отрицательным импульсом, в базе другого — нулевой потенциал и транзистор от­крыт. С помощью транзисторов осуществляется прерывание вход­ного сигнала. Сигнал с эмиттеров транзисторов подается на ОУ. С помощью резисторов R5 и R7 устанавливается необходимый коэф­фициент усиления (K=10). Подбором резисторов R6 и R8 вырав­нивают амплитуды сигналов, которые проходят на выход ОУ. Детектор работает на частотах до сотен килогерц.

Рис. 8.32

 

Детектор на полевых транзисторах. Детектор (рис. 8.33) состоит из двух ключей и ОУ. В качестве ключей применены полевые тран­зисторы, позволяющие коммутировать сигналы низкого уровня. Минимальный входной сигнал равен 10 мВ, управляющий сигнал подается на затворы полевых транзисторов, сигнал положительной полярности на неинвертирующий вход ОУ, а отрицательная поляр­ность входного сигнала — на инвертирующий вход усилителя. В ре­зультате на выходе ОУ формируется сигнал положительной по­лярности. Регулировка коэффициента усиления осуществляется резистором R3. Входное сопротивление детектора более 40 кОм, а выходное менее 200 Ом. Граничная частота входного сигнала 20 кГц. Погрешность преобразования менее 0,5%.

Синхронные фильтр и детектор. В состав синхронного детекто­ра (рис. 8.34) входит синхронный фильтр, построенный на элемен­тах R1, С1, С2 и управляемый транзисторами микросхемы DA1.

Рис. 8.33 Рис. 8.34

 

Эти транзисторы поочередно открываются импульсным напряжением с амплитудой 2 В. Операционный усилитель детектирует сигналы фильтра, в результате чего на выходе появляется постоянная состав­ляющая. Коэффициент передачи схемы равен 20, температурный дрейф 0,1%/град. Постоянная времени приблизительно 1,5 с. Мак­симальная амплитуда входного сигнала ±0,5 В. Температурный дрейф нуля 20 — 50 мкВ/град.

Высокочастотный синхронный детектор.В синхронном детекто­ре (рис. 8.35) перемножающим элементом является микросхема DA1. Интегральная микросхема DA2 преобразует парафазный сиг­нал перемножителя в однофазный. При этом значительно ослабля­ются синфазные помехи, которые могут быть в цепях питания. На нулевой выходной потенциал схема настраивается с помощью по­тенциометра R12.

Синхронный детектор работает на частоте 30 МГц. Исследуе­мый сигнал с частотой модуляции 2 — 20 МГц и амплитудой 150 мкВ — 250 мВ подается на Вход 1. Опорный сигнал с ампли­тудой 0,1 В подается на Вход 2. Максимальная амплитуда выход­ного сигнала равна 0,3 В. Нелинейность частотной характеристики менее 3%, а нелинейность амплитудной характеристики 2%. Верх­няя граничная частота модуляции входного сигнала определяется полосой пропускания ОУ DA2. На выходе этого усилителя включе­ны два фильтра, которые ослабляют составляющие с частотами 30 и 60 МГц более чем на 60 дБ. Эти составляющие появляются в ре­зультате перемножения входного и опорного сигналов в интеграль­ной микросхеме DA1.

Для устранения возбуждения микросхемы DA2 необходимо включить между контактами 2 и 4 конденсатор емкостью 16 пФ и между контактами 2 и 12 — резистор сопротивлением 100 Ом и конденсатор емкостью 56 пФ.

Детектор на перемножителе. Основой синхронного детектора (рис. 8.36) является микросхема DA3. На Вход 2 детектора по­дается преобразуемый сигнал, а на Вход 1 — опорный сигнал. Для линеаризации рабочей характеристики детектора опорный сигнал, проходит на микросхему DA3 через логарифмический каскад. Этот каскад построен по дифференциальной схеме на DA2 с диодной нагрузкой в коллекторах (DA1). Такое включение позволяет создать режим работы микросхемы DA3 по постоянному току, обеспечивая хорошую температурную стабилизацию и высокий коэффициент по­давления опорного сигнала на выходе микросхемы DA3. Амплитуда опорного сигнала равна 0,5 В. Балансировка перемножителя по по­стоянному току осуществляется потенциометрами JR3 и R13. Когда опорный сигнал равен нулю, то с помощью резистора КЗ добивают­ся максимального подавления преобразуемого сигнала. С помощью резистора R13 добиваются максимального подавления опорного сигнала при нулевом сигнале на Входе 1. Выходной парафазный сигнал перемножителя подается на микросхему DA4, которая до­полнительно усиливает его в 10 раз, что позволяет существенно ослабить влияние синфазной помехи в цепи питания и уменьшить дрейф нуля.

Рис. 8.35

Рис. 8.36

 

Детектор работает в диапазоне частот от 20 Гц до 2 МГц. Неравномерность коэффициента передачи в этом диапазоне менее 3%. Амплитуда преобразуемого сигнала меняется от 0,2 мВ до 0,5 В при точности преобразования 1%. При увеличении амплитуды сигнала до 1 В точность преобразования снижается до 3%.

 

Глава 9

ПРЕЦИЗИОННЫЕ ВЫПРЯМИТЕЛИ НА ОУ в устройствах на микросхемах

Прецизионные или высокоточные выпрямители, в отличие от диодных выпрямителей, идеально выполняют функцию выпрямления: один из полупериодов без искажений присутствует на выходе устройства, другой практически незаметен. Есть и еще одно существенное отличие: амплитуда выходного сигнала прецизионного выпрямителя может превышать амплитуду входного, к тому же ее можно регулировать.

Прецизионные или идеальные выпрямители на основе ОУ могут быть выполнены по схемам, представленным на рис. 15.1 и рис. 15.2 [15.1— 15.3]. На выходе первого из них (рис. 15.1) формируются сигналы отрицательной полярности, второго (рис. 15.2) — положительной. Напряжения, снимаемые с выходов выпрямителя, отличаются на величину падения напряжения на открытом кремниевом диоде (0,6—0,7 В). Для германиевых диодов эта разница близка к 0,25—0,3 В.

Прецизионные неинвертирующие выпрямители (рис. 15.3 и 15.4) на основе ОУ имеют более высокое входное сопротивление.

Выпрямитель на ОУ, схема которого представлена на рис. 15.5, обеспечивает эквивалентное снижение падения прямого напряжения на выпрямительных диодах до 1000 раз. Это существенно повышает точность преобразования и позволяет детектировать сигналы с амплитудой в несколько милливольт [15.4]. Частотные свойства детектора (выпрямителя) определяются свойствами ОУ, диодов VD1 и VD2.

Однополупериодные выпрямители достаточно просты, однако им присущи явно выраженные недостатки:

Рис. 15.5. Схема выпрямителя на ОУ с выходами положительного и отрицательного уровня

♦    возможность полезного использования лишь одного полупериода входного напряжения;

♦  высокое выходное сопротивление;

♦    необходимость использования ОУ с защитой от короткого замыкания нагрузки и т. д.

Более совершенны двухполупери- одные выпрямители. Схемы таких выпрямителей, работающих с неза- земленной и заземленной нагрузкой, приведены на рис. 15.6—15.11 [15.3].

Рис. 15.6. Схема двухполу- периодного выпрямителя на ОУ с незаземленной нагрузкой

Рис. 15.3. Прецизионный выпрямитель

Рис. 15.4. Вариант схемы прецизионного выпрямителя

Двухполупериодный выпрямитель, представленный на рис. 15.6, обычно используют в качестве аналогового вольтметра переменного напряжения, включив в качестве нагрузки магнитоэлектрический микроамперметр.

Для прецизионного двухполупериод- ного выпрямителя (рис. 15.7) при посту-

плении на вход положительной полуволны входного напряжения диод VD1 запирается. ОУ работает в режиме неинвертирующего усилителя с коэффициентом передачи, равном R3/R1.

Рис. 75.7. Схема двухполупериодного выпрямителя на ОУ с заземленной нагрузкой

R3

Рис. 75.8. Схема усовершенствованного двухполупериодного выпрямителя на ОУ с заземленной нагрузкой

При R3=R1 этот коэффициент равен единице, и выходное напряжение равно входному U_Bblx=U_BX. При поступлении на вход устройства отрицательной полуволны соответствующей амплитуды диод VD1 открывается, схема работает в режиме инвертирующего усилителя с коэффициентом передачи, равном единице, U =-U .

вых.              вх.

Недостаток схемы очевиден: при малом входном напряжении отрицательной поляр- ^{ности и}вь„*-и_в,.

Точность преобразования при малом входном напряжении отрицательной полярности можно повысить, используя схемное решение, рис. 15.8 [15.3]. Отличается схема тем, что в качестве диода VD1 (рис. 15.7) использован идеальный диод на ОУ DA2. Схема также не лишена недостатков: она имеет разное входное сопротивление для сигналов разной полярности.

Варианты схем двухполупериодных выпрямителей приведены на рис. 15.9 и 15.10 [15.4].

На рис. 15.11 приведена очередная схема прецизионного двухполупериодного выпрямителя, состоящая из однополупериодного выпрямителя на ОУ DA1 (см. рис. 15.1) и сумматора на ОУ DA2 [15.3].

Рис. 15.9. Схема двухполупериодного выпрямителя на двух ОУ

Рис. 15.10. Схема усовершенствованного двухполупериодного выпрямителя

Примечание.

Рис. 75.7 7. Схема прецизионного двухполупериодного выпрямителя на двух ОУ

Этот выпрямитель имеет равное входное сопротивление для разнополярных сигналов, но отличается повышенной сложностью.

Можно показать, что напряжение на выходе однополупери- одного выпрямителя U_l равно:

Примеры практического выполнения прецизионных одно- и двухпо- лупериодного выпрямителей на микросхемах ΝΕ531/SE531 приведены на рис. 15.12 и 15.13 [15.5].

Прецизионный двухполупери- одный выпрямитель может быть выполнен и на микросхемах AD820, рис. 15.14 [15.3].

Высокочастотный двухполупе- риодный выпрямитель-детектор сигналов на микросхеме AD8036 (AD8037), рис. 15.15, идеально

Рис. 75.75. Схема высокочастотного выпрямителя-детектора сигналов на микросхеме AD8036

работает вплоть до частот 20 МГц. Амплитуда входных сигналов — до 1 В, сопротивление нагрузки — 100 Ом. При необходимости чувствительность устройства может быть повышена подбором номиналов резисторов R1 и R2.

Шустов М. А., Схемотехника. 500 устройств на аналоговых микросхемах. — СПб.: Наука и Техника, 2013. —352 с.

Пиковые детекторы

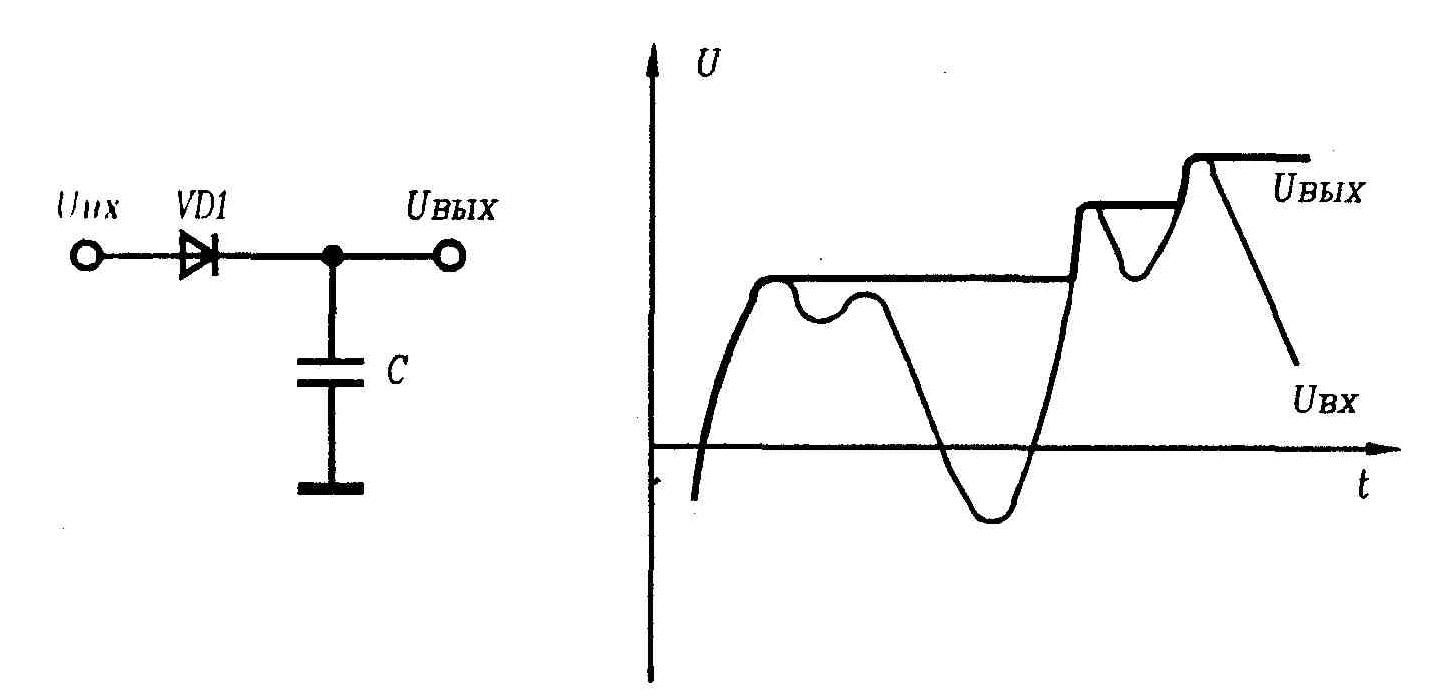
Пиковые детекторы предназначены для измерения максимального за некоторый отрезок времени значения сигнала. Работу пикового детектора можно пояснить на примере простой схемы, состоящей из идеальных диода и конденсатора (рис. 1.29) [1, 3, 5, 7, 12].

Пиковые детекторы могут работать в двух различных режимах – слежения и хранения. В режиме слежения входной сигнал больше ранее запомненного пикового значения, и выходное напряжение детектора соответствует входному до тех пор, пока входное напряжение не начнет снижаться. В этот момент устройство переходит в режим хра­нения, в котором будет оставаться до тех пор, пока входное напряжение вновь не превысит ранее достигнутого уровня. Показанный на рис. 1.29 простой детектор имеет несколько недо­статков. Во-первых, зафиксированное выходное напряжение не остается постоянным из-за разряда конденсатора. Во-вторых, при выборе емкости конденсатора приходится учитывать два противоречивых требования: уменьшения скорости спада и повышения скорости нарастания.

Простой двухкаскадный пиковый детектор изображен на рис. 1.30. В этой схеме ОУ А₁заряжает конденсатор до пикового значения, а ОУА₂выполняет роль буферного повторителя. Когда входное напряжение пре­высит хранимое на конденсатореС, тогда выходное напряжение ОУА₁начнет уве­личиваться, а конденсатор – заряжаться через диодVD₁. Таким образом, пока напряжениеU_вхрастет, петля обратной связи ОУА₁замкнута через диодVD₁и напряжение на конденсатореСотслеживает входное. Как только входное напряжение начинает уменьшаться, ОУА₁ переходит в состояние отрицательного насыщения, поскольку цепь его обратной связи размыкается. КонденсаторСоказывается изолированным от выхода А₁и хранит установившееся на нем напряжение.

0

а б

Рис. 1.29. Простейшая схема пикового детектора: а– схема;б– эпюры входного и выходного напряжений

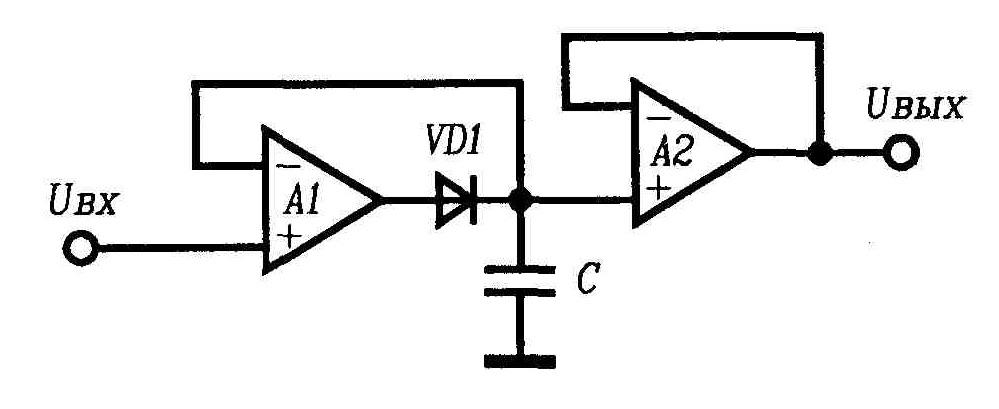
Рис. 1.30. Простой двухкаскадный пиковый детектор

Одной из основных причин изменения заряда конденсатора в режиме хранения являются входные токи ОУ, протекающие через конденсатор и изменяющие накопленный на нем заряд. В этой схеме конденсатор Ссоединен со входами обоих ОУ. Поэтому для данной схемы целесообразно выбирать ОУ с полевыми вхо­дами, имеющие малые входные токи. Кроме того, входной сигнал про­ходит через два ОУ –А₁иА₂, и поэтому прихо­дится выбирать ОУ также с малыми входными напряжениями смещения.

Можно предложить несколько вариантов улучшения базовой схемы (рис. 1.30). В частности, на рис. 1.31 показан инверти­рующий пиковый детектор с усилением сигнала. Конденсатор разряжа­ется через резистор R₂на виртуальную землю – инвертирующий вход ОУА₁. Спад выходного напряжения в режиме хранения определяется экспоненциальным разрядом конденсатора с постоянной времениCR₂. Каскад на ОУА₁представляет собой однополупериодный выпрямитель. Отметим, что диод VD2 обеспечивает отрицательную обратную связь ОУА₁в режиме хранения. Это предот­вращает насыщение усилителяА₁и значительно сокращает время пере­хода в режим отслеживания сигнала. ДиодVD₂ повышает быстродействие схемы.

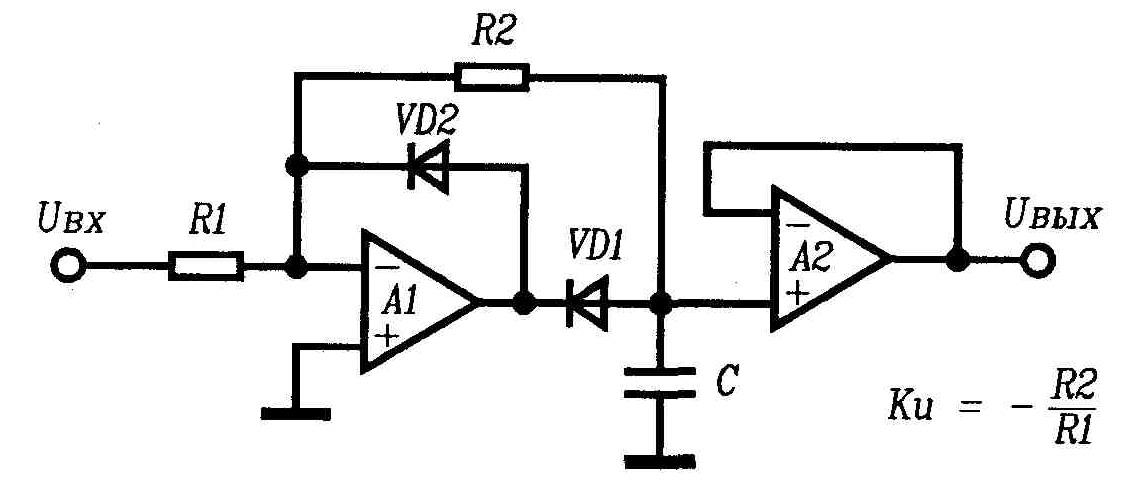
Рис. 1.31. Инвертирующий пиковый детектор

На рис. 1.32 приведена схема пикового детектора с общей обратной связью. При работе этой схемы в режиме слежения диод VD₁ открыт и конденсаторСзаряжается до напряженияU_вх. Сигнал обратной связи поступает на ОУА₁с буферного ОУА₂. При снижении входного напряжения оно становится меньшеU_вых. В результате выходное напря­жениеА₁становится отрицательным, диодVD₁ закрывается и схема пере­ходит в режим хранения. Из-за наличия резистораR₁и диодаVD₂(сопротивление резистораR₁обычно составляет около 10 кОм), выходное напряжение ОУА₁ограничивается на уровне, меньшем выходного (хра­нимого) напряжения на величину прямого падения на диоде. Быстро­действие этой схемы ниже, чем у двухкаскадной, но она обладает лучшими параметрами по смещению и точности хра­нения.

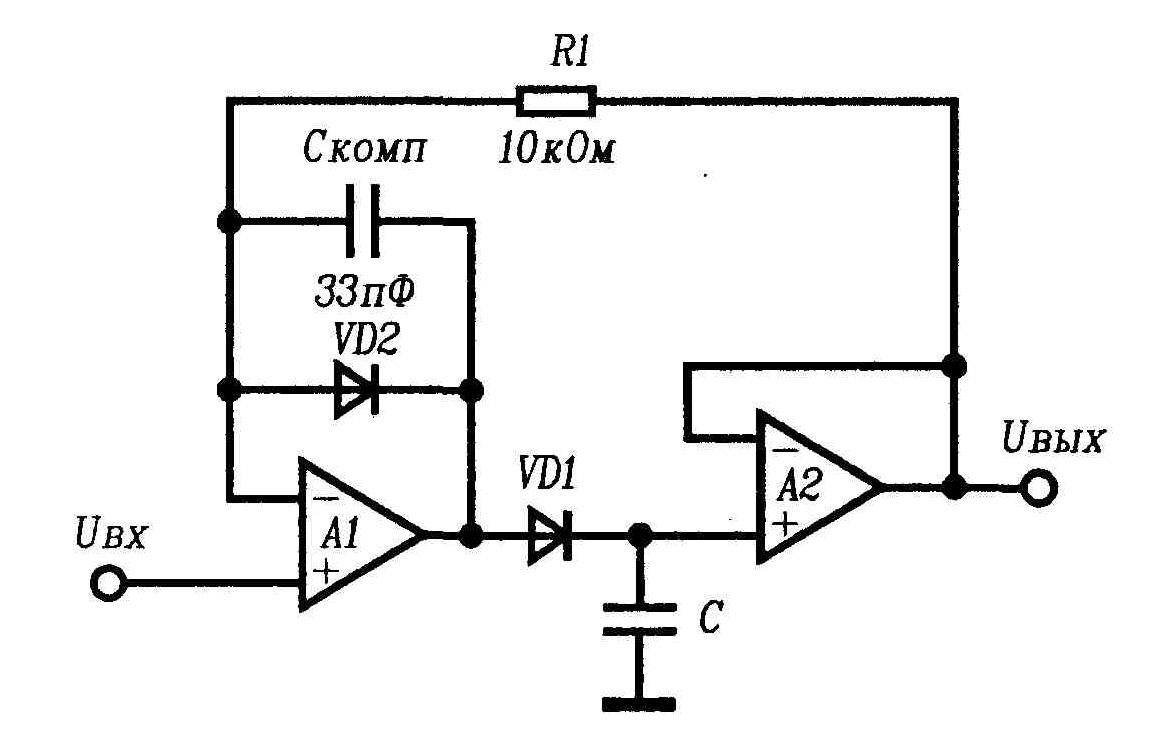
Рис. 1.32. Пиковый детектор с общей обратной связью

В данной схеме к запоминающему конденсатору подсоединен только один вход ОУ, поэтому влияние входных токов усилителей уменьшается, и скорость спада выходного напряжения оказывается меньше. Поскольку схема охвачена общей обратной связью с выхода на вход ОУ А₁, выход­ное смещение определяется только этим ОУ.

В заключение отметим, что можно построить быстродействующий пиковый детектор с длительным хранением, включая последовательно два каскада: с малым временем нарастания и малой скоростью спада (рис. 1.33, а).

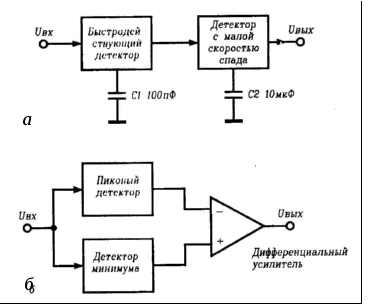
Рис. 1.33. Разновидности пиковых детекторов: а– комбинированный быстродействующий детектор;б– детектор размаха

Наконец, можно построить детектор размаха, используя пиковый детектор, детектор минимума и дифференциальный усилитель (рис. 1.33, б).

Пиковый детектор

1. Радиоэлектроника
2. Схемотехника
3. Основы электроники и схемотехники
4. Том 3 – Полупроводниковые приборы

1. Книги / руководства / серии статей
2. Основы электроники и схемотехники. Том 3. Полупроводниковые приборы

Добавлено 4 марта 2017 в 18:00

Сохранить или поделиться

Пиковый детектор – это последовательное соединение диода и конденсатора, выдающее постоянное напряжение, равное пиковому значению приложенного сигнала переменного напряжения. Схема показана на рисунке ниже с соответствующим списком соединений SPICE.

Источник переменного напряжения, подключенный к пиковому детектору, заряжает конденсатор до пикового значения на входе. Диод пропускает положительные «полупериоды», заряжая конденсатор до пика формы сигнала. Когда мгновенное значение входного сигнала становится ниже «пикового» постоянного напряжения, хранящегося в конденсаторе, диод будет смещен в обратном направлении, блокируя протекания тока из конденсатора обратно в источник. Таким образом, конденсатор сохраняет пиковое значение даже тогда, когда мгновенное значение входного сигнала падает до нуля. С другой стороны, пиковый детектор является однополупериодным выпрямителем с подключенным к выходу фильтрующим конденсатором.

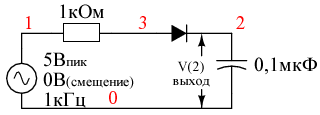Пиковый детектор: Диод пропускает положительные полуволны, заряжая конденсатор до пикового напряжения (ниже на значение прямого напряжения диода)

*SPICE 03441.eps
C1 2 0 0.1u
R1 1 3 1.0k
V1 1 0 SIN(0 5 1k)
D1 3 2 diode
.model diode d
.tran 0.01m 50mm
.end

Процесс зарядки конденсатора до пикового значения занимает несколько периодов сигнала (рисунок ниже) из-за включенного последовательно резистора (постоянная времени RC-цепи). Почему конденсатор не заряжается до полных 5 вольт? Он зарядился бы до 5 вольт, если бы использовался «идеальный диод». Однако, кремниевый диод обладает прямым падением напряжения 0,7В, которое вычитается из пика 5В на входе.

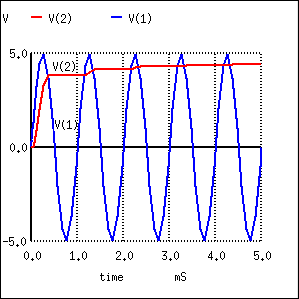Пиковый детектор: Конденсатор заряжается до пикового значения за несколько периодов

Схема на рисунке выше может представлять собой источник питания постоянного тока на базе однополупериодного выпрямителя. Сопротивление будет составлять несколько Ом, вместо 1 кОм, и представлять вторичную обмотку трансформатора, заменяющую источник напряжения и резистор. При этом должен использоваться конденсатор «фильтра» большей емкости. Источник питания, работающий на частоте 60 Гц, с фильтром в несколько сотен мкФ может обеспечить ток порядка до 100 мА. Источники питания редко выполняются на базе однополупериодных выпрямителей из-за сложности фильтрации полуволны.

Пиковый детектор может использоваться в детекторном приемнике.

Оригинал статьи:

Теги

ДетекторДиодОбучениеПиковый детекторЭлектроника

Сохранить или поделиться

На сайте работает сервис комментирования DISQUS, который позволяет вам оставлять комментарии на множестве сайтов, имея лишь один аккаунт на Disqus.com.

В случае комментирования в качестве гостя (без регистрации на disqus.com) для публикации комментария требуется время на премодерацию.

Детектор скрытой проводки на ОУ TL074

Этот материал написан посетителем сайта, и за него начислено вознаграждение. В процессе ремонта в квартире столкнулся с необходимостью сверления стен для навешивания разного вида ящиков и крепления труб, а так как электропроводка в квартире разведена слегка необычно (провода в шпаклевке могут находиться в неожиданных местах, и проходить по диагонали комнаты) — решил собрать несложный детектор проводки, чтобы не повредить провода, так как замена проводки не входит в планы текущего ремонта.

Учитывая свою задачу и отсутствие времени, выбор я остановил на самом простом варианте — электростатическом детекторе.

В интернет присутствует великое множество вариантов схем простых детекторов, например:

— на транзисторе КП303 (очень просто)
http://radiomaster.com.ua/2021-prostye-detektory-skrytoy-provodki.html

— на транзисторах КП103 и КТ3107
http://www.freeseller.ru/2009/12/14/prostojj-iskatel-skrytojj-provodki.html

— на транзисторах КП103 и КТ315
http://subscribe.ru/archive/tech.electronics/200012/17205406.html

— на транзисторах КП103, КТ203 и КТ315
http://forum.fazanol.ru/showthread.php?p=11843

— на транзисторах ВС547
http://radioskot.ru/publ/detektor_provodki/1-1-0-218

— на базе микросхемы К561ЛА7
http://www.amatar.by/news-print-169.html
http://radioskot.ru/publ/detektor/1-1-0-209

— на базе операционного усилителя TL074 и транзисторов BC817
http://bsvi.ru/detektor-skrytoj-provodki/

Наибольший интерес представляют последние три схемы, и так как давно обратил внимание на схему автора BSVi, но всё не было времени собрать её — решил воплотить в железе именно его творение.

Схема BSVi основана на базе операционного усилителя с низким уровнем шумов TL074 (детектор напряжения + генератор), и высокочастотных биполярных npn транзисторов BC817 (усилитель).

(кликните по картинке для увеличения)

Предоставленный автором файл не годится для распечатки и изготовления печатной платы, так как в нем не соблюдаются размеры (плата получится на 12% больше необходимого размера). По этой причине необходимо либо скопировать и уменьшить картинку печатной платы с 1609х1162 до 1417х1024 точек, либо воспользоваться приготовленной мной:

(кликните по картинке для увеличения)
Плата детектора скрытой проводки

Я изготовил два устройства, поэтому дальше фотографии будут часто дублироваться.

Фото с накатанными дорожками:

После травления плат:

После смывки тонера (качество плат не очень высокое, так как использовал старый картридж, и одну плату передержал):

Распаянная плата:

Подключены провода, светодиод, кнопка, переменный резистор:

Прибор № 1 в сборе (пилотная версия):

Прибор № 2 в сборе (в сравнении с первой версией — выполнен кабель менеджмент ):

Особенности реализации:
1) При изготовлении использовал односторонний текстолит, поэтому на плате 4 перемычки (отлично видны на фото).
2) Все элементы SMD — формата 0805, иногда можно использовать 1206 (для сравнения — на фото 3,3кОм резистор формата 1206).
3) Вместо R8 номиналом 9,1 МОм — использовал 10 МОм.
4) Резистор R4 использовал переменный Wh248-1A-2 A, 100кОм, 3pin, прямой — очень чувствительный к перегреву, паять нужно в одно касание, иначе постоянно пропадает контакт, и прибор начинает пищать без остановки.
5) Пьезоэлемент необходимо использовать без встроенного генератора (например излучатель без генератора PKM44EW: 70dB, 500Hz-20KHz; размер 44х14мм).
6) Светодиод обычный 5мм, красный, подключен через резистор 390 Ом (ограничивающий ток резистор выбран с огромным запасом по мощности, так как меньше просто не было под рукой).
7) Использовал следующие транзисторы:
— прибор №1: PMBT5551 (NPN;160V;0.6A;250mW;100MHz;h31=30-250)
— прибор №2: BC817-40 (NPN;45V;0.5A;250mW;170MHz;h31=250-600)

Субъективно — на транзисторах BC817-40 работает громче, звук резче (проверял на одих и тех же пьезо пищалках).

Прибор не требует настройки, работает сразу после сборки. Отлично обнаруживает провода под напряжением (проверял на глубине до 50мм). Единственное замечание — также реагирует на металлические предметы не под напряжением (выборочно), а также на некоторые участки стен (кирпичная кладка — красный прочный кирпич, черный внутри, арматуры в стенах нет, почему пищит прибор — пока не разобрался).

Потребление прибора 22,5мА, около 15мА из которых приходится на светодиод, и около 7,5мА на сам прибор. Размышляю о целесообразности отказа от светодиода.

Автору схемы (BSVi) — мои благодарности.

С вопросами сюда:
https://forums.overclockers.ru/viewtopic.php?f=25&t=350340&start=260

Детектор

— Wikipédia, livre enciclopédia

Origem: Wikipédia, livre enciclopédia.

Os detectores são aparelhos ou máquinas cuja finalidade é de assinalar a presença de uma substância ou de um corpo emterminado meio ambiente. Por outras palavras é um dispositivo que muda de estado na presença de um elemento ou de uma situação para o qual foi especificamente conbido.

O trabalho que os físicos fazem для идентификации partícula que passou pelo детектор, эквивалентный манеру, как alguém que estuda as pegadas deixada na lama.Tamanho, forma, direcção e profundidade da marca deixadas podem revelar o tipo de animal que a provocou. Как partículas também deixam traços que a identity.

Actualmente os detectores da física de partículas são constituídos por várias camadas de sub-detectores, cada um especializado num specific tipo departículas.

Na física utilizam-se Principalmente três tipos de sub-detectores:

• detectores de movimento — detectam e revelam o traço deixado pela partícula;
• калориметров — парам, поглощает и лечит партиейную энергию;
• detectores de Identificação — Identificam o tipo da partícula utilizando várias técnicas.

Para ajudar aidentificar as partículas, os detectores normalmente utilizam campos magnéticos que tem a capacity de encurvar as partículas. A partir da curvatura os físicos podem calcular o momento da partícula e ajudar aidentificá-la. Quanto mais forte é o momento menos elas encurvam.

Детекторы движения [редакторы | editar código-fonte]

Os detectores de movimento revelam a paris departículas electricamente carregas pelo traço que deixam.Efeito idêntico ao de um avião que não se vê pela altura a que voa, mas sabe-se que é um pelo rastro que deixa no céu.

Calorímetros [редактор | editar código-fonte]

Os calorímetros medem a energia deixada por uma partícula que os atravessa. Normalmente desenhado parar ou Absorver a partícula resultante da colisão, forçando-a depositar toda a sua energia dentro do детектор. Tipicamente, são aparelhos feitos em camadas de material muito denso, tal como o chumbo, e camadas de um elemento activo , como o argão.Os calorímetros electromagnéticos medem a energia de partículas de luz — elétrão e fotão — quando interagem com partículas carregada electricamente dentro da matéria. Адронные калориметры измеряют энергию адронов (частиц, содержащих кварки, такие как протоны и нейтроны), когда они взаимодействуют с атомными ядрами.

Детекторы идентификации [редактор | editar código-fonte]

Os Deteores de Identificação são de dois tipos:

• Radiacção Cherenkov : средство, выбрасывающее материал, который используется в качестве частичного материала;
• Radiacção de transição : esta radiação é produzida por uma partícula carregada muito rápida quando atravessa a barreira entre dois isoladores eléctricos com Diferentes resistências à corrente eléctrica.O fenómeno está ligado com a energia da partícula e distingue diferentes tipos departículas.

Comerciais [редактор | editar código-fonte]

Científicos [редактор | editar código-fonte]

Em física são muito utilizados na Detecção de partículas em labratórios como os de SLAC, de Fermilab ou do CERN. Vão de pequenos aparelhos com alguns Centímetros a gigantescos aparelhos com centenas de toneladas como os do LHC no CERN.

As câmaras [editar | editar código-fonte]

Детекторы ОС [editar | editar código-fonte]

Os contadores [редактор | editar código-fonte]

.Детектор

— перевод — Англо-галисийский словарь

^ru Итак, чтобы проверить это, мы использовали машину, которую мы назвали Детектором Blicket.

ted2019 ^gl Configuración do Resumo das tarefas

^en Порядок миграции, наблюдаемый детектором, показан на рисунке 3: маленькие многозарядные катионы мигрируют быстро, а маленькие многозарядные анионы прочно удерживаются.

WikiMatrix ^gl Dá soporte para ler ficheiros FITS en Kst.Название

^en Такие линзы могут использоваться в высокоскоростных детекторах движения и сверхтонких многонаправленных камерах.

jw2019 ^gl Díxitos racionais

^en Рентгеновские лучи, проходящие через объект, улавливаются детектором (фотопленкой или цифровым детектором) позади него.

WikiMatrix ^gl Gardar a Configuración do Teclado

^en Это детектор, который мы обучили на 80 различных классах в наборе данных Microsoft COCO.

ted2019 ^gl Un fito é un evento planificado que indica que se complete un resultado important ou un conxunto de resultados relacionados entresi (polo xeral sinalando a fin dun período). Un fito é unha actividade con duración nula e sen esforzo & ie; os fitos non teñen un traballo asociado a eles. É unha marca no plano de traballos que indica que algún traballo foi completetado

^en Выходной сигнал детектора отправляется на устройство вывода и обработки данных, такое как интегратор или компьютер.

WikiMatrix ^gl CARY (Radio; англ. Grella

^en Другие бинарные соединения ниобия включают нитрид ниобия (NbN), который становится сверхпроводником при низких температурах и используется в детекторах инфракрасного света.

WikiMatrix ^gl Corpo da Mensaxe

^en В датчике использовался стрип-детектор, в котором четыре полоски индий-висмута были расположены крест-накрест, а четыре полоски были расположены в виде логарифмических спиралей.

WikiMatrix ^gl Максимальное число Que & kbruch; usará como denominador común nosercios. De un mínimo de # a un máximo de

^en Уровень радиации в различных частях здания контролировался путем сверления отверстий в реакторе и установки длинных металлоискательских трубок.

WikiMatrix ^gl Converter & en

^en Астрономы наблюдают за объектами в инфракрасной части электромагнитного спектра с помощью оптических компонентов, включая зеркала, линзы и твердотельные цифровые детекторы.

WikiMatrix ^gl Perfil importado do ficheiro%

^en Кристина использовала наши детекторы Blicket.

QED ^gl confianza marxinal

^en Если в следующий раз трассировка лучей будет сделана так, как если бы световая волна (в понимании классической физики) была достаточно широкой, чтобы пройти оба пути, то трассировка лучей точно предсказывает появление максимумы и минимумы на экране детектора, когда много частиц проходят через устройство и постепенно «рисуют» ожидаемую интерференционную картину.

WikiMatrix ^gl Rosa Clarocolor

^en Следовательно, комбинация этикеток, которую можно использовать, зависит от длины волны лампы (ей) или лазера (ов), используемых для возбуждения флуорохромов, и от доступных детекторов.

WikiMatrix ^gl Inverte as core dunha imaxeComment

^en Детектор дыма: ионизационный детектор дыма включает в себя крошечную массу радиоактивного америция-241, который является источником альфа-излучения.

WikiMatrix ^gl Gravar como & Modelo

^en На оси абсцисс отложено время удерживания, а на оси ординат — сигнал (например, полученный спектрофотометром, масс-спектрометром или множеством других детекторов. ), соответствующий ответу, создаваемому аналитами, покидающими систему.

WikiMatrix ^gl Prema para trocar todas as fontes

^en Прямое пропорциональное наведение по прямой видимости использовало информацию от детектора для маневра и аннулирования любых изменений прямой видимости.

WikiMatrix ^gl Descoñecido

^en Увеличение количества лазеров и детекторов позволяет метить множественные антитела и более точно идентифицировать целевую популяцию по их фенотипическим маркерам.

WikiMatrix ^gl Amosar miniatura nunha fiestra

^en Заряд рассеивается примерно за 0,2 секунды, но он может быть автоматически обновлен по данным, полученным детектором.

WikiMatrix ^gl A xanela Principal de & kgeography

^en Разработан портативный детектор метана, который, установленный в транспортном средстве, может обнаруживать избыточные уровни метана в окружающей атмосфере и отличать природный метан от гниющей растительности или утечки навоза и газа.

WikiMatrix ^gl A imaxinacíon dos informáticos semella ilimitadaCando se trata de atopar novas prestacións

^en Мы сталкиваемся с ними внутри гигантских детекторов.

QED ^gl Editar или Bloco AppInfo

^en Это перекрытие или «перетекание» возникает в результате использования флуоресцентных красителей, которые можно измерить более чем в одном детекторе; этот вторичный эффект коррелирует с константой, известной как коэффициент перелива.

WikiMatrix ^gl Mensaxe de colaboración

^en Первоначально в телескопах использовался человеческий глаз.

WikiMatrix ^gl Abrir nesta & fiestra

^en Хорошо известный мысленный эксперимент предсказывает, что если детекторы частиц расположены на щелях, показывая, через какую щель проходит фотон, интерференционная картина исчезнет.

WikiMatrix ^gl GenerateOpenvpnKeyDialog: sen nome de ficheiro.Детектор

— перевод — Англо-галисийский словарь

^ru Итак, чтобы проверить это, мы использовали машину, которую мы назвали Детектором Blicket.

ted2019 ^gl Configuración do Resumo das tarefas

^en Порядок миграции, наблюдаемый детектором, показан на рисунке 3: маленькие многозарядные катионы мигрируют быстро, а маленькие многозарядные анионы прочно удерживаются.

WikiMatrix ^gl Dá soporte para ler ficheiros FITS en Kst.Название

^en Такие линзы могут использоваться в высокоскоростных детекторах движения и сверхтонких многонаправленных камерах.

jw2019 ^gl Díxitos racionais

^en Рентгеновские лучи, проходящие через объект, улавливаются детектором (фотопленкой или цифровым детектором) позади него.

WikiMatrix ^gl Gardar a Configuración do Teclado

^en Это детектор, который мы обучили на 80 различных классах в наборе данных Microsoft COCO.

ted2019 ^gl Un fito é un evento planificado que indica que se complete un resultado importante ou un conxunto de resultados relacionados entre si (polo xeral sinalando a fin dun período). Un fito é unha actividade con duración nula e sen esforzo & ie; os fitos non teñen un traballo asociado a eles. É unha marca no plano de traballos que indica que algún traballo foi completetado

^en Выходной сигнал детектора отправляется на устройство вывода и обработки данных, такое как интегратор или компьютер.

WikiMatrix ^gl CARY (Radio; англ. Grella

^en Другие бинарные соединения ниобия включают нитрид ниобия (NbN), который становится сверхпроводником при низких температурах и используется в детекторах инфракрасного света.

WikiMatrix ^gl Corpo da Mensaxe

^en В датчике использовался стрип-детектор, в котором четыре полоски индий-висмута были расположены крест-накрест, а четыре полоски были расположены в виде логарифмических спиралей.

WikiMatrix ^gl Максимальное число Que & kbruch; usará como denominador común nosercios. De un mínimo de # a un máximo de

^en Уровень радиации в различных частях здания контролировался путем сверления отверстий в реакторе и установки длинных металлоискательских трубок.

WikiMatrix ^gl Converter & en

^en Астрономы наблюдают за объектами в инфракрасной части электромагнитного спектра с помощью оптических компонентов, включая зеркала, линзы и твердотельные цифровые детекторы.

WikiMatrix ^gl Perfil importado do ficheiro%

^en Кристина использовала наши детекторы Blicket.

QED ^gl confianza marxinal

^en Если в следующий раз трассировка лучей будет сделана так, как если бы световая волна (в понимании классической физики) была достаточно широкой, чтобы пройти оба пути, то трассировка лучей точно предсказывает появление максимумы и минимумы на экране детектора, когда много частиц проходят через устройство и постепенно «рисуют» ожидаемую интерференционную картину.

WikiMatrix ^gl Rosa Clarocolor

^en Следовательно, комбинация этикеток, которую можно использовать, зависит от длины волны лампы (ей) или лазера (ов), используемых для возбуждения флуорохромов, и от доступных детекторов.

WikiMatrix ^gl Inverte as core dunha imaxeComment

^en Детектор дыма: ионизационный детектор дыма включает в себя крошечную массу радиоактивного америция-241, который является источником альфа-излучения.

WikiMatrix ^gl Gravar como & Modelo

^en На оси абсцисс отложено время удерживания, а на оси ординат — сигнал (например, полученный спектрофотометром, масс-спектрометром или множеством других детекторов. ), соответствующий ответу, создаваемому аналитами, покидающими систему.

WikiMatrix ^gl Prema para trocar todas as fontes

^en Прямое пропорциональное наведение по прямой видимости использовало информацию от детектора для маневра и аннулирования любых изменений прямой видимости.

WikiMatrix ^gl Descoñecido

^en Увеличение количества лазеров и детекторов позволяет метить множественные антитела и более точно идентифицировать целевую популяцию по их фенотипическим маркерам.

WikiMatrix ^gl Amosar miniatura nunha fiestra

^en Заряд рассеивается примерно за 0,2 секунды, но он может быть автоматически обновлен по данным, полученным детектором.

WikiMatrix ^gl A xanela Principal de & kgeography

^en Разработан портативный детектор метана, который, установленный в транспортном средстве, может обнаруживать избыточные уровни метана в окружающей атмосфере и отличать природный метан от гниющей растительности или утечки навоза и газа.

WikiMatrix ^gl A imaxinacíon dos informáticos semella ilimitadaCando se trata de atopar novas prestacións

^en Мы сталкиваемся с ними внутри гигантских детекторов.

QED ^gl Editar или Bloco AppInfo

^en Это перекрытие или «перетекание» возникает в результате использования флуоресцентных красителей, которые можно измерить более чем в одном детекторе; этот вторичный эффект коррелирует с константой, известной как коэффициент перелива.

WikiMatrix ^gl Mensaxe de colaboración

^en Первоначально в телескопах использовался человеческий глаз.

WikiMatrix ^gl Abrir nesta & fiestra

^en Хорошо известный мысленный эксперимент предсказывает, что если детекторы частиц расположены на щелях, показывая, через какую щель проходит фотон, интерференционная картина исчезнет.

WikiMatrix ^gl GenerateOpenvpnKeyDialog: sen nome de ficheiro.