Делитель напряжения в цепи обратной связи
Добавлено 22 ноября 2018 в 23:36
Сохранить или поделиться
Если мы добавим делитель напряжения в схему отрицательной обратной связи так, чтобы на инвертирующий вход подавалась только часть выходного напряжения, а не полная его величина, выходное напряжение будет кратно входному напряжению (помните, схема подключения питания к операционному усилителю снова пропущена для простоты):
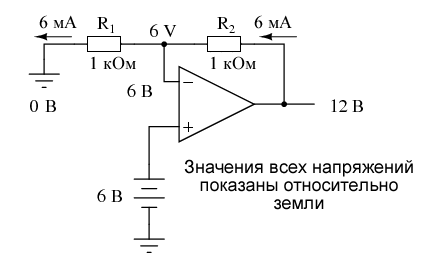Эффект отрицательной обратной связи с делителем напряженияЕсли R1 и R2 равны, а Vвх равно 6 вольт, операционный усилитель будет выдавать любое напряжение, необходимое для падения 6 вольт на резисторе R1 (чтобы сделать напряжение на инвертирующем входе равным 6 вольтам, а также сохранить разность напряжений между входами равной нулю). С делителем напряжения 1:2 из резисторов R
Другой способ анализа этой схемы – начать с вычисления величины и направления тока через R1, зная напряжение на обеих сторонах (и, следовательно, при помощи вычитания напряжение на R1) и сопротивление R1. Так как левая сторона R1 связана с землей (0 вольт), а правая сторона имеет потенциал 6 вольт (из-за отрицательной обратной связи, поддерживающей эту точку, равной Vвх), мы видим, что имеем на R1 напряжение 6 вольт. Это дает нам ток 6 мА через R1 слева направо. Поскольку мы знаем, что оба входа операционного усилителя имеют чрезвычайно высокий импеданс, мы можем с уверенностью предположить, что они не будут добавлять или вычитать какой-либо ток через делитель. Другими словами, мы можем рассматривать R
Исследуя последнюю иллюстрацию, можно задаться вопросом: «Где проходит этот ток 6 мА?». Последняя иллюстрация не показывает весь путь прохождения тока, но на самом деле он начинается с положительного вывода источника питания постоянного напряжения, через выходной транзистор(ы) операционного усилителя, через выходной вывод операционного усилителя, через R
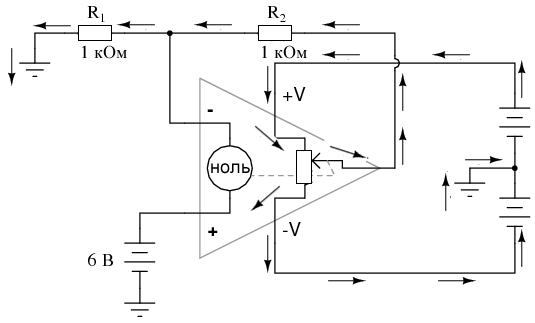Отрицательная обратная связь с делителем напряжения на примере модели операционного усилителяМы можем изменить коэффициент усиления по напряжению в этой схеме, просто регулируя значения R1 и R2 (изменяя часть выходного напряжения, которая подается обратно на инвертирующий вход). Коэффициент усиления можно рассчитать по следующей формуле:
\[A_V = {R_2 \over R_1} + 1\]
Обратите внимание, что коэффициент усиления по напряжению для этой схемы усилителя никогда не может быть меньше 1. Если бы мы должны были понизить значение R
Также обратите внимание, что полярность выходного сигнала совпадает с полярностью входного сигнала, как и в повторителе напряжения. Положительное входное напряжение приводит к положительному выходному напряжению и наоборот (относительно земли). По этой причине эта схема называется
Как и с повторителем напряжения, мы видим, что дифференциальный коэффициент усиления ОУ не имеет значения, если он очень велик. Напряжения и токи в этой схеме вряд ли изменились бы вообще, если бы коэффициент усиления ОУ составлял бы 250000 вместо 200000. Это резко контрастирует со схемами усилителей на отдельных транзисторах, где бета отдельных транзисторов сильно влияла на общий коэффициент усиления усилителя. С отрицательной обратной связью у нас есть система самокорректирования, которая усиливает напряжение в соответствии с соотношением, установленным резисторами обратной связи, а не коэффициентами усиления, внутренними для операционного усилителя.
Давайте посмотрим, что произойдет, если мы сохраним отрицательную обратную связь через делитель напряжения, но подадим входное напряжение в другое место:
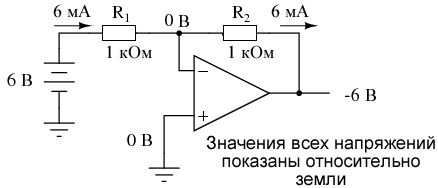Схема усилителя с отрицательной обратной связью с делителем напряжения и подачей входного сигнала на инвертирующий входПри соединении неинвертирующего входа с землей отрицательная обратная связь также удерживает напряжение на инвертирующем входе на нуле вольт. По этой причине инвертирующий вход упоминается в этой схеме как
Мы можем изменить общий коэффициент усиления по напряжению этой схемы, просто регулируя значения R1 и R2 (изменяя часть выходного напряжения, которая подается обратно на инвертирующий вход). Коэффициент усиления можно рассчитать по следующей формуле:
\[A_V = -{R_2 \over R_1}\]
Обратите внимание, что коэффициент усиления этой схемы может быть меньше 1, в зависимости от отношения R2 к R1. Также обратите внимание, что выходное напряжение всегда имеет полярность, противоположную полярности входного напряжения. Положительное входное напряжение приводит к отрицательному выходному напряжению и наоборот (относительно земли). По этой причине данная схема называется
Эти две схемы усилителей, которые мы только что исследовали, служат для умножения или деления величины напряжения входного сигнала. Именно так математические операции умножения и деления обычно обрабатываются в аналоговой компьютерной схемотехнике.
Резюме
- Подключая инвертирующий (-) вход операционного усилителя напрямую к выходу, мы получаем отрицательную обратную связь, которая дает нам схему повторителя напряжения. Подключая эту отрицательную обратную связь через резисторный делитель напряжения (подавая часть выходного напряжения на инвертирующий вход), выходное напряжение становится кратным входному напряжению.
- Схема операционного усилителя с отрицательной обратной связью и подачей входного сигнала на неинвертирущий (+) вход называется неинвертирующим усилителем. Выходное напряжение будет такой же полярности, как и входное. Коэффициент усиления по напряжению определяется следующей формулой: AV = (R2/R1) + 1.
- Схема операционного усилителя с отрицательной обратной связью и подачей входного сигнала на «нижнюю часть» резисторного делителя напряжения, с неинвертирующим (+) входом, соединенным с землей, называется инвертирующим усилителем. Его выходное напряжение будет противоположной полярности, чем входное напряжение. Коэффициент усиления по напряжению определяется следующей формулой: AV = -R2/R1.
Оригинал статьи:
Теги
Делитель напряженияИнвертирующий усилительНеинвертирующий усилительОтрицательная обратная связьОУ (операционный усилитель)Повторитель напряженияУчебникЭлектроникаСохранить или поделиться
Что такое делитель напряжения
Делители напряжения получили широкое распространение в электронике, потому что именно они позволяют оптимальным образом решать задачи регулировки напряжения. Существуют различные схематичные решения: от простейших, например, в некоторых настенных светильниках, до достаточно сложных, как в платах управления переключением обмоток нормализаторов сетевого напряжения.
Что такое делитель напряжения? Формулировка проста – это устройство, которое в зависимости от коэффициента передачи (настраивается отдельно) регулирует значение выходного напряжения относительно входного.
Раньше на прилавках магазинов часто можно было встретить светильник-бра, рассчитанный на две лампы. Его особенностью являлось то, что сами лампы были рассчитаны на работу с напряжением 127 Вольт. При этом вся система подключалась к бытовой электросети с 220 В и вполне успешно работала. Никаких чудес! Все дело в том, что способ соединения проводников формировал не что иное, как делитель напряжения. Вспомним основы электротехники, а именно параллельное и последовательное соединение потребителей. Как известно, при последовательном способе включения сила тока равна, а напряжение изменяется (вспоминаем закон Ома). Поэтому в примере со светильником однотипные лампы включены последовательно, что дает уменьшение питающего их напряжения в два раза (110 В). Также делитель напряжения можно встретить в устройстве, распределяющем сигнал с одной антенны на несколько телевизоров. На самом деле примеров много.
Давайте рассмотрим простейший делитель напряжения на основе двух резисторов R1 и R2. Сопротивления включены последовательно, на свободные выводы подается входное напряжение U. Из средней точки проводника, соединяющего резисторы, есть дополнительный вывод. То есть получается три конца: два – это внешние выводы (между ними полное значение напряжения U), а также средний, формирующий U1 и U2.
Выполним расчет делителя напряжения, воспользовавшись законом Ома. Так как I = U / R, то U является произведением тока на сопротивление. Соответственно, на участке с R1 напряжение составит U1, а для R2 составит U2. Ток при этом равен (последовательное соединение). Учитывая закон для полной цепи, получаем, что питающее U является суммой U1+U2.
Чему же равен ток при данных условиях? Обобщая уравнения, получаем:
I = U / (R1+R2).
Отсюда можно определить значение напряжения (U exit) на выходе делителя (это может быть как U1, так и U2):
U exit = U * R2 / (R1+R2).
Для делителей на регулируемых сопротивлениях существует ряд важных особенностей, которые необходимо учитывать как на этапе расчетов, так и при эксплуатации.
Прежде всего, такие решения нельзя использовать для регулировки напряжения мощных потребителей. Например, таким способом невозможно запитать электродвигатель. Одна из причин – это номиналы самих резисторов. Сопротивления на киловатты если и существуют, то представляют собой массивные устройства, рассеивающие внушительную часть энергии в виде тепла.
Значение сопротивления подключенной нагрузки не должно быть меньше, чем электрическое сопротивление схемы самого делителя, в противном случае всю систему потребуется пересчитывать. В идеальном варианте различие R делителя и R нагрузки должно быть максимально большим. Важно точно подобрать значения R1 и R2, так как завышенные номиналы повлекут за собой излишнее падение напряжения, а заниженные будут перегреваться, затрачивая энергию на нагрев.
Рассчитывая делитель, обычно подбирают значение его тока в несколько раз (например, в 10) больше, чем ампераж подключаемой нагрузки. Далее, зная ток и напряжение, вычисляют суммарное сопротивление (R1+R2). Далее по таблицам подбирают ближайшие стандартные значения R1 и R2 (учитывая их допустимую мощность, чтобы избежать чрезмерного нагрева).
1. Делители напряжения | 5. Схемы делителей и законы Кирхгофа | Часть1
1. Делители напряжения
Делители напряжения
Давайте проанализируем простую последовательную цепь и определим напряжения на каждом из ее резисторов:
Зная сопротивления каждого из резисторов, мы можем вычислить общее сопротивление цепи (которое для последовательной цепи будет равно сумме отдельных сопротивлений):
Теперь, используя закон Ома (I = U/R), определяем общую силу тока, которая будет одинакова на всех компонентах нашей последовательной цепи:
Из этой таблицы видно, что напряжения на резисторах пропорциональны их сопротивлениям (учитывая, что сила тока через все резисторы одинакова). Заметьте, напряжение на резисторе R2 в два раза больше напряжения на резисторе R1, так же как и сопротивление R2 в два раза больше сопротивления R1.
Если мы изменим общее напряжение цепи, то увидим, что эта пропорциональность сохранится:
Несмотря на увеличение напряжение источника питания, напряжение на резисторе R2 по прежнему в два раза больше напряжения на резисторе R1.
Произведя несколько подобных наблюдений становится очевидным, что напряжение на каждом из резисторов составляет фиксированную пропорцию от общего напряжения. Например, при напряжении батареи 45 вольт, напряжение на резисторе R1 составляло 10 вольт. Когда напряжение батареи было увеличено до 180 вольт (в 4 раза), напряжение на резисторе R1 так же увеличилось в 4 раза (с 10 до 40 вольт). Как видите, соотношение между напряжением на резисторе R1 и общим напряжением не изменилось:
Соотношения других напряжений с увеличением напряжения питания так же не изменятся:
Из за способности последовательной цепи пропорционально распределять общее напряжение по резистивным компонентам, ее часто называют делителем напряжения. Немного поколдовав с математикой, можно получить формулу для определения напряжения на любом резисторе, имея только значения сопротивлений отдельных резисторов, общего напряжения и общего сопротивления:
Полученная нами формула известна как формула делителя напряжения, с ее помощью легче рассчитывать напряжения последовательной цепи, чем производить аналогичные расчеты с использованием закона Ома.
Используя эту формулу можно повторно проанализировать приведенную выше схему, и определить ее напряжения произведя меньшее количество действий:
Делители напряжения нашли широкое применение в схемах измерительных приборов, где определенные комбинации соединенных последовательно резисторов используются для «деления» напряжения на нужные пропорции, необходимые для измерения разных величин того же напряжения.
Одним из устройств, часто используемых в качестве делителя напряжения, является потенциометр. Потенциометр представляет собой проводник с большим омическим сопротивлением (резистор), снабженный скользящим контактом:
Условное обозначение потенциометра представляет собой вертикальный символ резистора с примыкающей к нему стрелкой — скользящим контактом. Если скользящий контакт переместить ближе к контакту 1, то сопротивление между ними будет меньше, чем сопротивление между скользящим контактом и контактом 2. Если скользящий контакт переместить ближе к контакту 2, то эффект будет противоположным. Сопротивление между контактами 1 и 2 будет постоянным, независимо от положения скользящего контакта:
На рисунке ниже показана конструкция двух типов потенциометров, роторного и линейного:
Некоторые линейные потенциометры приводятся в действие посредством прямолинейного движения рычага или слайд-кнопки. Другие, как тот, который изображен на рисунке — посредством отвертки, для более точной настройки. Такие потенциометры называют еще «подстроечными». Следует отметить, что не у всех линейных потенциометров назначение выводов соответствует показанным на рисунке. У некоторых, вывод скользящего контакта находится посередине, между выводами конечных контактов.
На следующей фотографии изображен реальный ротационный потенциометр с открытыми для просмотра скользящим контактом и резистивным элементом. Рукоятка этого потенциометра повернута таким образом, что его скользящий контакт почти касается левого вывода резистивного элемента:
А здесь показан тот же самый потенциометр, но его скользящий контакт повернут против часовой стрелки в другую сторону:
Если постоянное напряжение приложить к контактам резистивного элемента потенциометра, то скользящий контакт выступит в роли своеобразного «крана», с помощью которого можно регулировать величину этого напряжения на выходе прибора:
По аналогии с фиксированным делителем напряжения, пропорциональность деленного потенциометром напряжения является исключительно функцией сопротивления, а не приложенного напряжения. Иными словами, если ручкой потенциометра установить его скользящий контакт строго посередине резистивного элемента, то на выходе мы получим ровно половину от приложенного напряжения, независимо от его величины. Можно сказать, что потенциометр функционирует как регулируемый делитель напряжения, в котором пропорциональность деленного напряжения устанавливается положением скользящего контакта.
Такая функция потенциометра очень полезна для получения регулируемого напряжения от фиксированного источника, например батареи. Если собранная вами схема требует напряжение, которое меньше напряжения имеющейся батареи, то вы можете подключить к этой батарее выводы резистивного элемента потенциометра, и ручкой «выставить» нужное напряжение между скользящим контактом и одним из конечных контактов:
Такое применение потенциометра при проектировании электрических схем пользуется большой популярностью.
На следующей фотографии показаны небольшие потенциометры, которые обычно применяются в бытовых электроприборах и различных радиолюбительских схемах:
Самый левый и самый правый потенциометры могут устанавливаться непосредственно на макетную или печатную плату. Средние устройства предназначены для установки на плоскую панель, со схемой они соединяются при помощи проводов.
Ниже показаны специализированные потенциометры:
как рассчитать формулой на резисторах
В электронике, радиотехнике, робототехнике, системотехнике и ещё ряде практических дисциплин важно добиться оптимальных значений для рабочих компонентов. Именно для этого и используются всевозможные элементы, как-то резисторы, транзисторы, тиристоры, конденсаторы и множество подобных им.
Что это
Делитель напряжения — это устройство, позволяющее получать из большего напряжения (как постоянного, так и переменного) меньшее. При построении схемы используется, как минимум, два элемента сопротивления. Если их величины одинаковые, то на выходе полученное значение составит половину значения на входе. В других случаях конечный результат определяется с помощью формул.
Делитель напряжения
Эти устройства особенно необходимы, если проводятся высоковольтные испытания электрооборудования. Дело в том, что большинство измерительных приборов предназначены для использования, если значение не превышает 1000В. Чтобы выполнить поставленную задачу и используется рассматриваемое устройство. Тогда полученное значение умножается на коэффициент и получается фиксируемое значение.
Разновидности
Разным сопротивлением выдерживается разная нагрузка. Но при этом существуют делители, отличающиеся не только по своим основным, но и по дополнительным параметрам. Несмотря на все эти нюансы и тонкости, главным является один — электрическое сопротивление.
Резисторные
Могут использоваться и для постоянного, и для переменного тока. Резисторы предназначены для низкого напряжения. Их нельзя использовать, если речь заходит о питании мощных машин. Самый простой вариант исполнения предусматривает последовательное соединение двух резисторов.
Резисторные делители напряжения
Как рассчитать делитель напряжения на резисторах? Для этого используется первый закон Кирхгофа и положения Ома. Так, величина тока, протекающая через резисторы, будет одинаковой. И для каждого из них необходимо рассчитывать получаемое значение. Падение при этом прямо пропорциональное величинам тока и сопротивления.
Емкостные
Это устройство предусматривает, что решено подключать конденсаторы для деления. Простейшая схема также состоит из двух элементов, соединённых последовательно. Такое решение популярно, если делается многоуровневый инвертор напряжения. Без них немыслимо ни одно направление силовой электроники. Например, работа электроподвижного состава.
Расчёт значения емкостного делителя
Расчет емкостного делителя напряжения в теории является более лёгким делом, нежели его реализация на практике. Ведь на пути стоит сложность невозможности обеспечения ситуации, когда конденсаторы разряжаются равномерно. Из-за этого, как бы не старались, не получиться добиться, чтобы напряжение распределялось поровну. Так, чем сильнее разряжен один конденсатор, тем ощутимее разница будет на другом. Ведь напряжение в этом случае определяется как результат деления заряда на емкость.
Создаваемые с конденсаторами схемы работают очень нестабильно. При их создании всегда должно предусматриваться создание узлов подзарядки. Они используются для выравнивания напряжения на конденсаторах.
Индуктивные
Широко применяются в измерительных устройствах. Являются масштабными электромагнитными преобразователями. В процессе работы могут возникать погрешности. Их источник — неравенство активных сопротивления и индуктивностей из-за рассеяния разных секций обмоток, переход напряжения на коммутационные и соединительные элементы, шунтирующие взаимовоздействия обмоток, проявление емкости нагрузки и паразитных факторов. Если возникают проблемы с самого начала, вероятнее всего, проблема именно в последнем.
Индуктивные делители
Важно! Дополнительно паразитные емкости являются основной причиной возникновения частотной погрешности, что ограничивается использование индуктивных делителей напряжения на высоких частотах. Самые простейшие варианты имеют довольно много недостатков. Но использование на индуктивных делителях напряжений микропроцессоров позволяет использовать алгоритм уравновешивания.
Формула расчёта делителя напряжения
Самый простой вариант в использовании — схема, построенная на резисторах. Для неё рассчитываются значения по каждому элементу. В таком случае формула расчёта: UR1 = I * R1 и UR2 = I * R2.
UR1 и UR2 показывают, как упадёт напряжение. Их сумма равна параметрам источника питания. Часто необходимо подсчитать ток. Для этого используют формулу: I = Uпит / (R1+R2).
Для лучшего понимания расчета резистивного делителя напряжения подойдёт небольшой пример. Допустим, что создана схема, в которой источник составляет 10 А и используются элементы на 20 000 и 80 000 Ом. В таком случае расчёт будет выглядеть следующим образом: I = 10 / (20 000 + 80 000) = 0,0001 А = 0,1 мА.
Формулы для расчёта значений
Результат этой формулы уже можно подставлять, чтобы узнать требуемые показатели:
- UR1 = 0,0001 * 20 000 = 2 В;
- UR2 = 0,0001 * 80 000 = 8 В.
Если немного изменить расчет делителя напряжения, то можно получить универсальную формулу: UR1 / R1 = Uпит / (R1+R2). За рамки был вынесен ток. Из формулы получается, что UR1 равно: = Uпит * R1 / (R1+R2). Как проверить правдивость этих размышлений? А очень просто — необходимо поставить данные и посмотреть, сходятся ли они с уже полученными значениями:
- UR1 = 10 * 20000 / (20000+80000) = 2 В;
- UR2 = 10 * 80000 / (20000+80000) = 8 В.
Как видно, получаемые значения совпадают. Это говорит о том, что расчеты правильные.
Как работает
На практике использование устройств несколько сложнее, чем просто рассчитать требуемые значения для элементов. Использование схемы замещения для делителей напряжения усложняет реалистичный учет фазовых и амплитудных характеристик. Эта проблема может быть решена исключительно экспериментальным путём. Затруднительно так сделать только если наблюдаются очень высокие частоты.
Графическое изображение работы
В качестве доступной альтернативы используется экспериментальное определение реакции схемы на прямоугольный импульс. Его суть — наблюдение за состоянием, когда на входе происходит скачкообразное изменение напряжения. При единичном воздействии можно наблюдать особенности работы благодаря переходной функции измерительной схемы.
Реакция определяется двумя способами:
- Первый предполагает, что на вход полностью собранной схемы подают периодически импульсы с амплитудой в 100В (50 или 100 раз в секунду). Фронт их нарастания должен составлять меньше 10-9 с. Получение таких импульсов не является делом сложным. Для этого можно воспользоваться механическими коммутаторами с герконом или ртутным реле. На выходе схемы измеряется реакция посредством осциллографа, на котором присутствует широкополосной усилитель, величина пропускания которого составляет до 109 Гц.
- Второй способ используется для схем, у которых напряжение составляет несколько десятков киловольт. В таком случае делают крутой срез посредством малоиндуктивного искрового промежутка, помещенного в условия сжатого газа. На выходе с помощью обычного осциллографа записывается реакция. Также вместо среза часто обращаются к использованию разряда заряженного кабеля и волнового сопротивления через искровой промежуток.
Описывая работу делителей напряжения, нельзя обойти вниманием постоянную времени. Чтобы правильно измерять показатели быстропротекающих процессов, необходимо добиться различия в 5-10 раз. Постоянная времени делителя должна быть меньше характеристического времени процесса. Если не получить разницу в 5-10 раз, то будут фиксироваться различные искажения. Наиболее вероятные — это затягивание фронта вместе с уменьшением амплитуды сигнала на выходе в сравнении с расчетными показателями.
Важно! При выборе делителя в первую очередь внимание обращают на его возможное влияние, оказываемое на источник напряжения, равно как и искажения основного параметра при измерении. Например, в случае использования обычных ГИН допустимыми считаются резисторные, емкостные и смешанные устройства, но только при соблюдении оговоренных условий. К таковым относятся значения емкости плеча высокого напряжения и сопротивление.
Схема
Вот четыре варианта возможного исполнения:
Схема интегрального делителя напряжения
Можно добиться разных значений, изменяя схему подключения и ориентируясь на задачи. Каждый элемент можно использовать как регулятор для напряжения, необходимо только правильно выстроить цепь, чтобы были отображены именно необходимые данные.
Область применения
Делитель очень важен в схемотехнике. Он может использоваться как простейший электрический фильтр или же быть параметрическим стабилизатором напряжения. Они могут выполнять роль электромеханических запоминающих устройств, которые помнят величину угла поворота реостата. Особенность делителей напряжения в том, что они могут хранить информацию неограниченное количество времени, хотя и не используются широко, поскольку присутствуют более совершенные средства. Современное использование заключается в следующем:
Коммерческое изделие
- Создание в усилителях цепей обратной связи. Резистивный делитель напряжения может использоваться для задания коэффициента усиления каскадов.
- Простейшие электрические фильтры.
- Усилители напряжения. Это возможно при условии, что второе сопротивление больше или равно первому, которое отрицательное. Подобное используется в туннельных диодах.
- Параметрический стабилизатор напряжения. Поработать с входным значением можно, если как нижнее плечо делителя используется стабилитрон.
Только перечисленным дело не ограничивается. Возможности применения делителя напряжения придумывает человек, использующий их в рамках доступных физических возможностей.
Делитель напряжения — это простое техническое устройство, что в определённых случаях бывает очень полезным. Выбор и создание конкретного прибора должен отталкиваться от поставленных технических целей.
