Шестнадцатиричная система счисления – умножение, вычитание в таблице
4.1
Средняя оценка: 4.1
Всего получено оценок: 185.
4.1
Средняя оценка: 4.1
Всего получено оценок: 185.
Для записи адресов и содержимого ячеек памяти компьютера используется шестнадцатеричная система счисления. Запись числовых значений в шестнадцатеричной системе счисления, а также выполнение арифметических операций над ними имеет ряд особенностей, о чем можно прочитать в данной статье.
Что такое шестнадцатеричная система счисления
Шестнадцатеричная система счисления использует для записи числовых значений шестнадцать символов: арабские цифры от 0 до 9 и буквы латинского алфавита A, B, C, D, E, F. Соответственно, основанием такой системы счисления будет число 16.
При использовании шестнадцатеричных чисел следует помнить, что в числовом ряду шестнадцатеричных чисел после числа 9 идет А, а после F следует двузначное число 10.
Перевод 16 –10
Для прямого перевода шестнадцатеричного числа в десятичную систему удобно пользоваться развернутой формой записи, когда число представляют в виде суммы, в которой слагаемые получаются путем умножения символа разряда (числа или числового эквивалента буквы) на 16 в степени соответствующего разряда.
Обратный перевод выполняется последовательным делением десятичного числа на 16 и взятия остатков от деления. Причем полученные остатки в диапазоне от 10 до 15 надо заменить соответствующей буквой.
Выполняя обратный перевод, следует помнить, что результирующее значение получают путем записи полученных от деления остатков в обратном порядке, начиная с последнего частного. Каждый остаток от деления должен получаться всегда меньше шестнадцати.
Например: 500 / 16 = 31 (остаток 4)
31 / 16 = 1 (остаток 15 заменяем на букву F)
Таким образом, получено шестнадцатеричное число 1F4.
Перевод 16 – 2
Для перевода шестнадцатеричного числа в десятичную систему каждую его цифру заменяют группой из четырех нулей и единиц, которую принято называть «тетрадой». Для перевода обычно пользуются таблицей соответствия шестнадцатеричных символов и двоичных тетрад.
Рис. 1. Таблица соответствия шестнадцатеричных чисел и их двоичных и десятичных эквивалентовНапример, 1F4 = (0001)(1111)(0100).
Арифметические действия в шестнадцатеричной системе счисления
Сложение и вычитание
Операции сложения и вычитания удобно выполнять с использованием таблицы сложения шестнадцатеричных чисел. И сложение или вычитание выполняются поразрядно, начиная с младшего разряда.
Если при сложении двух чисел одинакового разряда получается двузначное число, то значение его старшего разряда (единицу) добавляют в старший разряд.
Например, 1F + 2D = 4C.
Сначала складываются значения младших разрядов F + D. По таблице получается двузначное число1С, единицу старшего разряда которого переносим и добавляем к сумме следующих по величине разрядов суммируемых шестнадцатеричных чисел.
Сумма цифр старших разрядов 1 + 2 равна 3 и еще прибавляется переносимая единица, то есть получается в сумме 4.
Таким образом, получается число 4C.
При выполнении вычитания часто возникает ситуация, когда необходимо выполнять заем из старшего разряда, если уменьшаемое конкретного разряда меньше вычитаемого. Тогда занимается единица из старшего разряда. Значение разности смотрится по таблице.
Тогда занимается единица из старшего разряда. Значение разности смотрится по таблице.
Например, 2D – 1F = E.
Сначала находят разность цифр младших разрядов, то есть D – F (в десятичном представлении 13-15). Уменьшаемое меньше вычитаемого, поэтому происходит заем единицы из старшего разряда исходного числа. То есть вычисляют разность 1D – F = E.
После выполненных манипуляций с младшими разрядами переходят к следующим по величине. В текущем примере следует вычислить 2 – 1. Но ранее произошел заем единицы и в старшем разряде уменьшаемого остается не 2, а 1. Поэтому вычисляется разность 1 – 1 = 0.
Умножение и деление
Умножать и делить числа в шестнадцатеричной системе следует также поразрядно. При вычислениях удобно пользоваться таблицей умножения шестнадцатеричной системы счисления.
Рис. 3. Таблица умножения шестнадцатеричных чиселНапример, 1С * 2 = 38. Используя распределительный закон умножения: (10 + С) * 2 = 10 * 2 + С * 2 = 20 + 18 = 38
Операция деления также выполняется столбиком с использованием таблицы умножения: 1С / 2 = Е.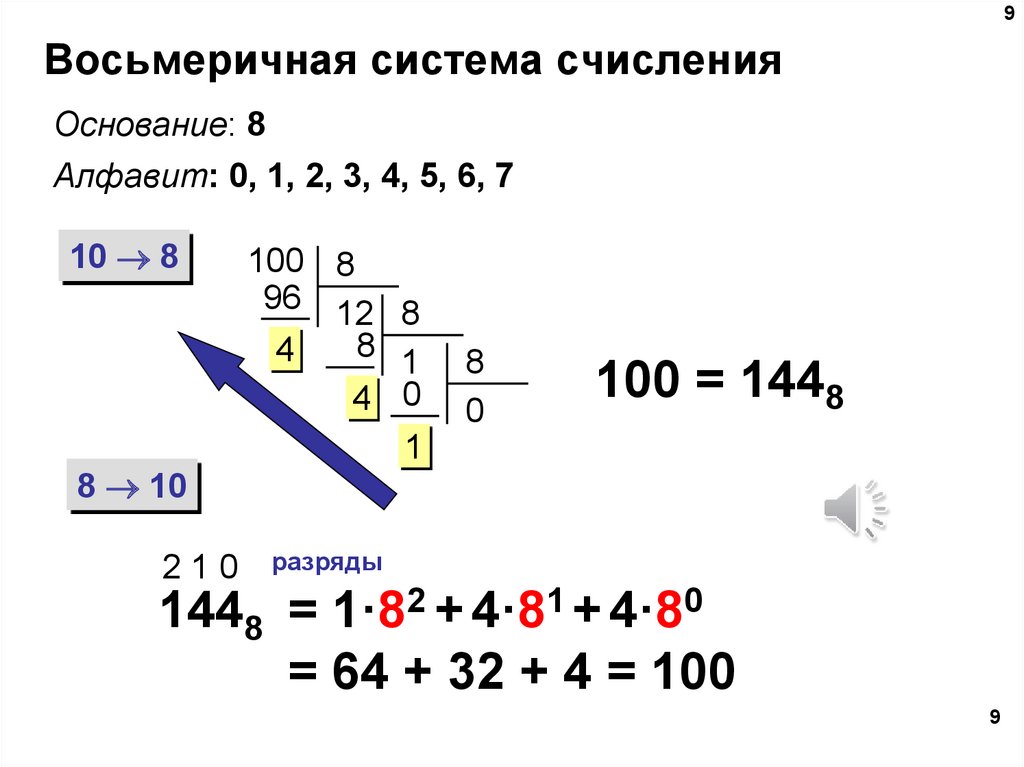
Что мы узнали?
В шестнадцатеричной системе счисления для записи числовых значений используются цифры от 0 до 9 и латинские буквы от A до F. Прямой перевод шестнадцатеричного числа в десятичную систему выполняется с использованием развернутой формы записи числа. Обратный перевод выполняется путем деления и записи остатков. Каждую шестнадцатеричную цифру в числе можно заменить тетрадой двоичных чисел. Арифметические операции в шестнадцатеричной системе удобнее всего выполнять поразрядно с использованием таблиц сложения и умножения шестнадцатеричных чисел
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Роман Журавлев
10/10
Татьяна Лазарева
10/10
Коля Приходько
8/10
Андрей Букин
10/10
Игорь Карабута
1/10
Александра Цалко
8/10
Оценка статьи
4. 1
1
Средняя оценка: 4.1
Всего получено оценок: 185.
А какая ваша оценка?
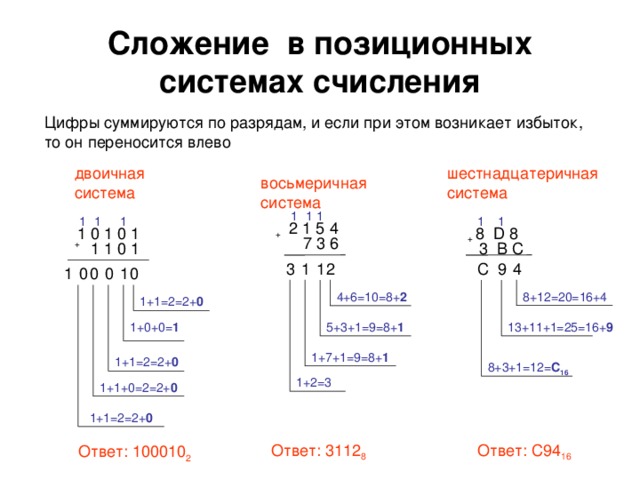
Арифметические действия в различных системах счисления.
Примечание: Сложение:
Пример: Сложить 1001001110 и 100111101 в двоичной системе счисления
Ответ: 1110001011 Сложить F3B и 5A в шестнадцатеричной системе счисления
Ответ: FE0 Самое главное, не забывайте про то, что у вас в распоряжении только цифры данной системы счисления, так же не забывайте про переходы между разрядными слагаемыми.
Вычесть из 1001001110 число 100111101 в двоичной системе счисления
Ответ: 100010001 Вычесть из F3B число 5A в шестнадцатеричной системе счисления
Ответ: D96 Самое главное, не забывайте про то, что у вас в распоряжении только цифры данной системы счисления, так же не забывайте про переходы между разрядными слагаемыми. Умножение в других системах счисления происходит точно так же, как и мы привыкли умножать.
Пример: Умножить 10111 на число 1101 в двоичной системе счисления
Ответ: 100101011 Умножить F3B на число A в шестнадцатеричной системе счисления
Ответ: 984E Ответ: 984E Самое главное, не забывайте про то, что у вас в распоряжении только цифры данной системы счисления, так же не забывайте про переходы между разрядными слагаемыми. Деление в других системах счисления происходит точно так же, как и мы привыкли делить.
Пример:Разделить 1011011 на число 1101 в двоичной системе счисления
Ответ: 111 Разделить F3B на число 8 в шестнадцатеричной системе счисления
Ответ: DEF Самое главное, не забывайте про то, что у вас в распоряжении только цифры данной системы счисления, так же не забывайте про переходы между разрядными слагаемыми. НЕПОЗИЦИОННЫЕ Непозиционные системы счисления
Таким образом, этот единственный символ имеет значение единицы, из которой последовательным сложением получается необходимое число:
Модификацией единичной системы является система с основанием, в которой есть символы не только для обозначения единицы, но и для степеней основания. Например, если за основание взято число 5, то будут дополнительные символы для обозначения 5, 25, 125 и так далее. Примером такой системы с основанием 10 является древнеегипетская, возникшая во второй половине третьего тысячеления до новой эры. В этой системе имелись следующие иероглифы:
Числа получались простым сложением, порядок следования мог быть
любым. Так, для обозначения, например, числа 3815, рисовали три цветка
лотоса, восемь пальмовых листов, одну дугу и пять шестов. Более сложные
системы с дополнительными знаками — старая греческая, римская. Новогреческая и древнерусская системы использовали в качестве цифр 27 букв алфавита, где ими обозначалось каждое число от 1 до 9, а также десятки и сотни. Такой подход обеспечил возможность записывать числа от 1 до 999 без повторений цифр. В старорусской системе для обозначения больших чисел использовались специальные обрамления вокруг цифр. В качестве словесной системы номерации до сих пор практически
везде используется непозиционная. Словесные системы нумерации сильно
привязаны в языку, и общие их элементы в основном относятся к общим
принципам и названиям больших чисел (триллион и выше). Общие принципы,
положенные в основу современных словесных нумераций вредполагают
формирование обозначения посредством сложения и умножения значений
уникальных названий. В качестве словообразующих корней в основном используются названия для чисел первого десятка и степеней десяти:
Второй десяток нередко образуется модификацией названий первого — в русском это добавление в конце суффиксоила Среди больших чисел как правило названия имеют степени тысячи:
Другие степени десяти практически вышли из употребления — 104 — тьма, мириада и т. д. Прочие числа образуются комбинированием набора слов с использованием сложения и перемножения их значений. При этом выполняемая операция зависит от типа языкового согласования слов: семнадцать тысяч — это 17·1000 = 17 000, а тысяча семнадцать — это 1000+17 = 1017. |
Системы счисления
Перед математиками и
конструкторами в 50-х годах XX столетия встала
задача найти такие системы счисления, которые бы
отвечали требованиям разработчиков ЭВМ и
программного обеспечения. В результате были
созданы “машинные” системы счисления:
— двоичная;
— восьмеричная;
— шестнадцатеричная.
Каждая из этих систем использует определенный
набор символов языка, которыми записываются
данные — символы алфавита.
В двоичной системе счисления их всего два: 0 и
1.
В восьмеричной системе их восемь:
0,1,2,3,4,5,6,7.
В шестнадцатеричной — шестнадцать: арабские
цифры 0-9, и символы латинского алфавита от А до
F. Причем символ А соответствует 10, В =11 и т.д
, F=15.
Каждая система счисления из
машинной группы применяется в различных случаях,
а именно, двоичная – для организации
преобразования информации, восьмеричная и
шестнадцатеричная – для представления машинных
кодов в удобном виде.
Десятичная система применяется для ввода данных
и вывода на устройства печати и на экран
дисплея.
Двоичная система счисления
Обработка информации в ПК основа
на обмене электрическими сигналами между
различными устройствами компьютера. Эти сигналы
возникают в определенной последовательности. ПК
“различает” два уровня этих сигналов – высокий
(1) и низкий (0). Таким образом, любая
информация в вычислительной технике
представляется как набор (код) двух символов 0 и
1. Каждый такой набор нулей и единиц называется
двоичным кодом. Количество информации,
кодируемое двоичной цифрой – 0 или 1 –
называется битом. Бит является единицей
измерения информации.
Эти сигналы
возникают в определенной последовательности. ПК
“различает” два уровня этих сигналов – высокий
(1) и низкий (0). Таким образом, любая
информация в вычислительной технике
представляется как набор (код) двух символов 0 и
1. Каждый такой набор нулей и единиц называется
двоичным кодом. Количество информации,
кодируемое двоичной цифрой – 0 или 1 –
называется битом. Бит является единицей
измерения информации.
Двоичная система счисления обладает такими же свойствами, что и десятичная, только для представления чисел используется не 10 цифр, а всего 2. Эта система счисления тоже является позиционной.
Официальное рождение двоичной
арифметики связано с именем Г.В. Лейбница,
опубликовавшего в 1703 г. статью, в которой он
рассмотрел правила выполнения арифметических
действий над двоичными числами.
статью, в которой он
рассмотрел правила выполнения арифметических
действий над двоичными числами.
Из истории известен курьезный случай с
восьмеричной системой счисления. Шведский король
Карл XII в 1717 году увлекался восьмеричной
системой счисления, считал ее более удобной, чем
десятичная, и намеревался королевским приказом
ввести ее как общепринятую. Неожиданная смерть
короля помешала осуществить столь необычное
намерение.
Восьмеричная и шестнадцатиричная системы счисления
Двоичные числа – длинные
последовательности 0 и 1 – очень неудобны для
восприятия. В связи с этим двоичные числа стали
разбивать на группы по три (триада) или четыре
(тетрада) разряда. Из трех нулей и единиц можно
составить восемь различных двоичных чисел, а из
четырех – шестнадцать. Для кодирования 3 бит
требуется 8 цифр, и поэтому взяли цифры от 0 до
7, т.е. в соответствии с определением получили
алфавит 8-ной системы счисления.
Для кодирования 3 бит
требуется 8 цифр, и поэтому взяли цифры от 0 до
7, т.е. в соответствии с определением получили
алфавит 8-ной системы счисления.
|
Восьмеричный алфавит |
Двоичное число (триада) |
|
0 |
000 |
|
1 |
001 |
|
2 |
010 |
|
3 |
011 |
|
4 |
100 |
|
5 |
101 |
|
6 |
110 |
|
7 |
111 |
Для кодирования 4 бит необходимо
16 знаков, для чего используются 10 цифр
десятичной системы и 6 первых букв латинского
алфавита.
|
Шестнадцатеричный алфавит |
Двоичное число (тетрада) |
|
0 |
0000 |
|
1 |
0001 |
|
2 |
0010 |
|
3 |
0011 |
|
4 |
0100 |
|
5 |
0101 |
|
6 |
0110 |
|
7 |
0111 |
|
8 |
1000 |
|
9 |
1001 |
|
A |
1010 |
|
B |
1011 |
|
C |
1100 |
|
D |
1101 |
|
E |
1110 |
|
F |
1111 |
Представление чисел в различных системах счисления
|
10-ная |
2-ная |
8-ная |
16-ная |
|
0 |
00 |
0 |
0 |
|
1 |
01 |
1 |
1 |
|
2 |
10 |
2 |
2 |
|
3 |
11 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
A |
|
11 |
1011 |
13 |
B |
|
12 |
1100 |
14 |
C |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
E |
|
15 |
1111 |
17 |
F |
|
16 |
10000 |
20 |
10 |
ПЕРЕВОД ЧИСЕЛ ИЗ N-РИЧНОЙ СИСТЕМЫ В ДЕСЯТИЧНУЮ
Перевод чисел из одной системы счисления в
другую выполняет компьютер. Эти операции
выполняются по определенным правилам.
Эти операции
выполняются по определенным правилам.
Перевод числа из двоичной системы
счисления в десятеричную:
1) пронумеровать двоичный код начиная с младшего
разряда (его номер равен 0) к старшему;
2) записать двоичное число как сумму
произведений веса каждого разряда на основание
системы счисления исходного числа (2) в степени,
соответствующей номеру разряда;
3) выполнить вычисление произведений и суммы.
Например,
1010112 = 1*25+0*24+1*23+0*22+1*21+1*20
= 32+0+8+0+2+1=4310
Перевод числа из любой n-ричной системы счисления в десятеричную выполняется с описанным выше правилом (следует учесть, что для каждой системы счисления основание системы свое).
Задание:
Выполните перевод следующих чисел в десятичную:
123708 — ?10
ПЕРЕВОД ЧИСЕЛ ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ В N-РИЧНУЮ
Перевод числа из десятеричной в двоичную систему счисления:
1) выполнить последовательное
деление десятичного числа, а затем получаемых
целых частных на основание системы счисления, в
которую переводится число (2). Деление
выполняется в записью целого частного и целого
остатка от деления до тех пор, пока целое
частное не будет равно 0.
Деление
выполняется в записью целого частного и целого
остатка от деления до тех пор, пока целое
частное не будет равно 0.
2) записать код числа, записывая остатки от
деления, начиная с последнего из целых остатков
(в обратном порядке) символами алфавита
требуемой системы счисления.
|
Например,4210 — ?2 4210 = 1010102 |
Перевод числа из десятеричной в n-ричную систему счисления:
1) выполнить последовательное
деление десятичного числа, а затем получаемых
целых частных на основание системы счисления, в
которую переводится число (n). Деление
выполняется в записью целого частного и целого
остатка от деления до тех пор, пока целое
частное не будет равно 0.
Деление
выполняется в записью целого частного и целого
остатка от деления до тех пор, пока целое
частное не будет равно 0.
2) записать код числа, записывая остатки от
деления, начиная с последнего из целых остатков
(в обратном порядке) символами алфавита
требуемой системы счисления.
Задание:
выполните перевод десятичных чисел 54 и 782
в 8-ричную и 16-ричную системы счисления каждое.
ПЕРЕВОД ЧИСЕЛ ИЗ ДВОИЧНОЙ СИСТЕМЫ В ВОСЬМЕРИЧНУЮ И ШЕСТНАДЦАТЕРИЧНУЮ
Правило перевода чисел из двоичной системы счисления в восьмеричную:
влево и вправо от запятой
двоичное число разбивается на двоичные триады,
при необходимости крайние группы дополняются
нулями; каждая триада заменяется соответствующей
цифрой восьмеричного алфавита (см. таблицу).
таблицу).
|
100010011,112 = ?8 |
100 |
010 |
011, |
1102 |
=423,68 |
|
|
4 |
2 |
3 |
6 |
Правило перевода чисел из двоичной системы счисления в шестнадцатеричную:
влево и вправо от запятой
двоичное число разбивается на двоичные тетрады,
при необходимости крайние группы дополняются
нулями; каждая тетрада заменяется
соответствующей цифрой шестнадцатеричного
алфавита (см. таблицу).
таблицу).
|
11111100011,1010102 = ?16 |
0111 |
1110 |
0011, |
1010 |
1000 |
= 7Е3,А816 |
|
|
7 |
Е |
3 |
А |
8 |
При переводе чисел из
восьмеричной и шестнадцатеричной систем
счисления в двоичную достаточно заменить каждую
цифру соответственно двоичной триадой или
тетрадой.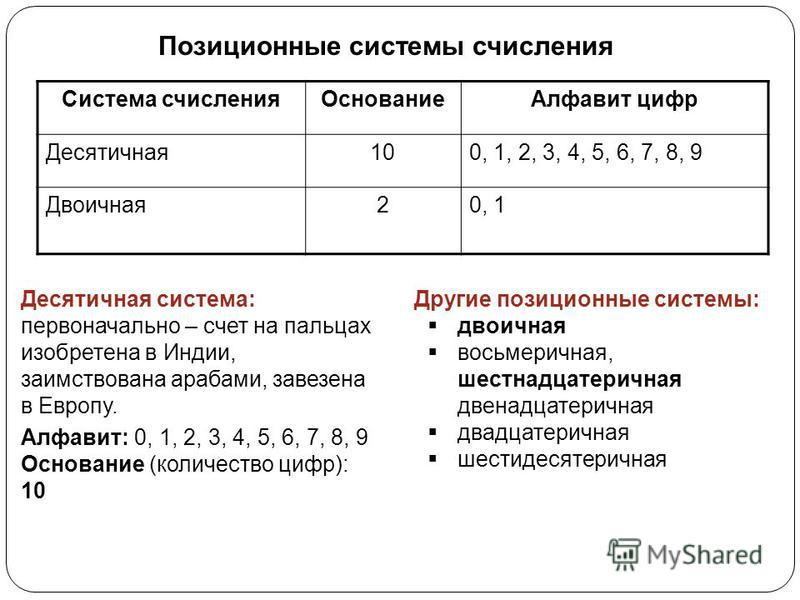 При этом незначащие нули
отбрасываются.
При этом незначащие нули
отбрасываются.
Примеры: 324,78 — ? 2
3 2 4, 78 = 11010100,1112
Е4А1, В516 — ?2
Е 4 А 1, В 516 =
1110010010100001,101101012
ПЕРЕВОД ЧИСЕЛ ИЗ ВОСЬМЕРИЧНОЙ И ШЕСТНАДЦАТЕРИЧНОЙ СИСТЕМЫ В ДВОИЧНУЮ
При переводе чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную достаточно заменить каждую цифру соответственно двоичной триадой или тетрадой. При этом незначащие нули отбрасываются.
Примеры:
|
324,78 — ? 2 |
3 |
2 |
4, |
78 = |
11010100,1112 |
|
|
|
011 |
010 |
100 |
111 |
|
Е4А1, В516 — ?2 |
Е |
4 |
А |
1, |
В |
516 = |
1110010010100001,101101012 |
|
|
1110 |
0100 |
1010 |
0001 |
1011 |
0101 |
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ В ДВОИЧНОЙ СИСТЕМЕ
С цифрами двоичного числа можно
выполнять арифметические операции. При этом
выполняются правила двоичной арифметики:
При этом
выполняются правила двоичной арифметики:
|
0+0=0 |
0*0=0 |
|
1+0=1 |
1*0=0 |
|
0+1=1 |
0*1=0 |
|
1+1= 0 (+ перенос единицы
|
1*1= 1 |
Все арифметические операции над
двоичными числами можно свести к 2-м операциям:
сложению и сдвигу кодов. Это позволяет
технически реализовать четыре арифметических
действия в одном арифметико-логическом
устройстве, используя одни и те же электронные
схемы. Впрочем, и в десятичной арифметике в
конечном итоге выполняются те же действия –
сложение и сдвиг.
Это позволяет
технически реализовать четыре арифметических
действия в одном арифметико-логическом
устройстве, используя одни и те же электронные
схемы. Впрочем, и в десятичной арифметике в
конечном итоге выполняются те же действия –
сложение и сдвиг.
Cложение двоичных чисел
Выполним сложение двух двоичных чисел 110012 и 100012
|
+ |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
||
|
1 |
0 |
1 |
0 |
1 |
0 |
Задание:
Самостоятельно выполните сложение двоичных
чисел:
111002 и 100111112
Вычитание двоичных чисел
Вычитание – обратная операция
сложению так же может быть представлена в виде
сложения, но только с отрицательным числом.
Выполним вычитание двух двоичных чисел 110012
и 100012
|
— |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
|
|
1 |
0 |
0 |
0 |
Задание:
выполните вычитание двух чисел 1011102
и 10012
Умножение и деление двоичных чисел
Умножение и деление производится
поразрядно и сводятся к двум операциям: сложению
и сдвигу.
Выполним умножение двоичных чисел 110012 и 10012
|
|
* |
1 |
1 |
0 |
0 |
1 |
|||
|
1 |
0 |
0 |
1 |
||||||
|
1 |
1 |
0 |
0 |
1 |
|||||
|
0 |
0 |
0 |
0 |
0 |
|||||
|
0 |
0 |
0 |
0 |
0 |
|||||
|
1 |
1 |
0 |
0 |
1 |
|||||
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
Задание:
самостоятельно перемножьте числа 11102
и 100012
Деление так же можно представить
как выполнение операций сложения и сдвига.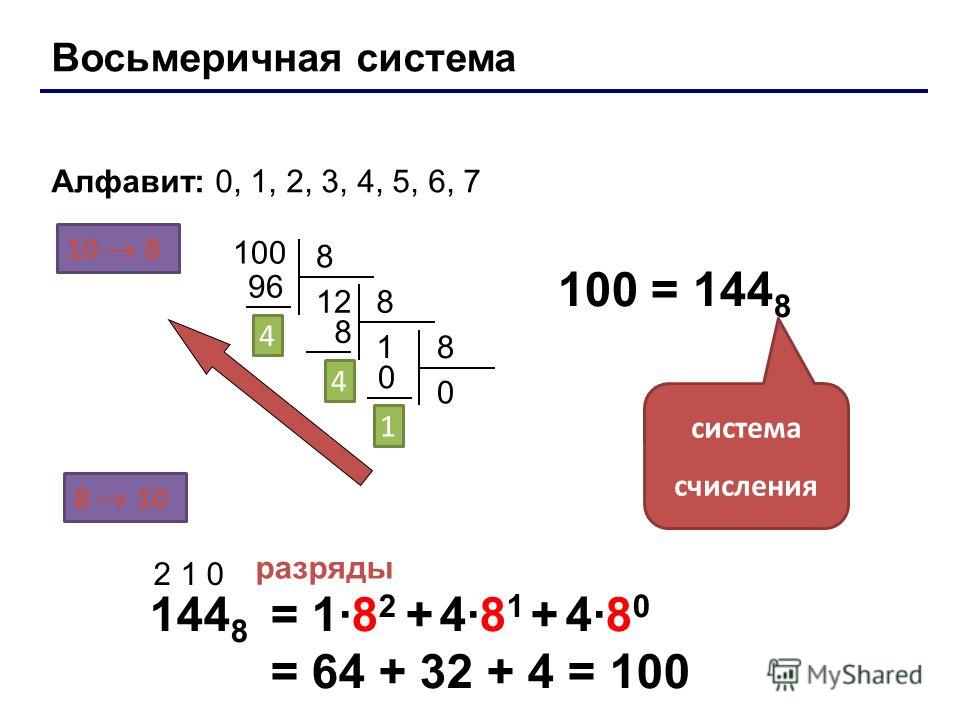
Задание:
выполните самостоятельно деление двоичного числа
1100110 на двоичное число 110
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ В ВОСЬМЕТИЧНОЙ И ШЕСТНАДЦАТИРИЧНОЙ СИСТЕМЕ
Сложение и вычитание в 8-ной и 16-ной системах счисления
При выполнении действий сложения
и вычитания в 8-ной системе счисления необходимо
помнить:
в записи результатов сложения и вычитания могут
быть использованы только цифры восьмеричного
алфавита;
основание восьмеричной системы счисления равен
8, т.е. переполнение наступает, когда результат
сложения больше или равен 8. В этом случае для
записи результата надо вычесть 8, записать
остаток, а к старшему разряду прибавить единицу
переполнения;
если при вычитании приходится занимать единицу в
старшем разряде, эта единица переносится в
младший разряд в виде 8 единиц.
Примеры.
Сложить восьмеричные числа 7708 и 2368
.
|
|
1 |
1 |
|
|
|
+ |
7 |
7 |
0 |
|
|
2 |
3 |
6 |
||
|
1 |
2 |
2 |
6 |
Примеры на закрепление: выполнить
действия в восьмеричной системе счисления.
7158 + 3738
5248 + 578
Выполнить вычитание восьмеричных чисел 7508 и 2368.
|
|
|
4 |
8 |
|
|
_ |
7 |
5 |
0 |
|
|
2 |
3 |
6 |
||
|
|
5 |
1 |
2 |
Примеры на закрепление: выполнить
действия в восьмеричной системе счисления.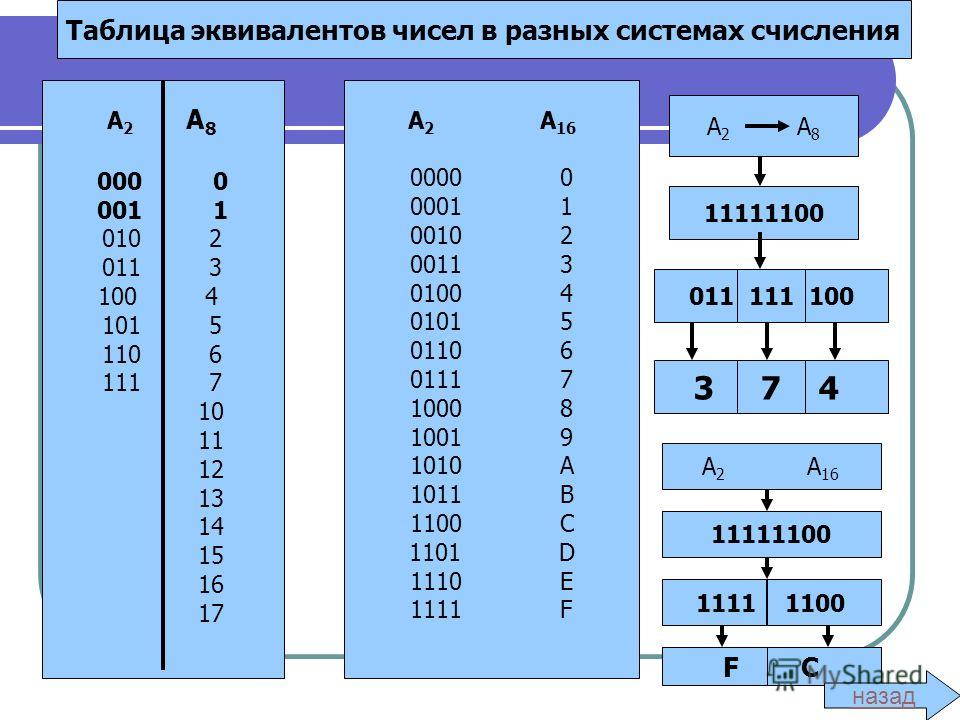
1378 — 72,38
4368 — 2578
При выполнении действий сложения
и вычитания в 16-ной системе счисления
необходимо помнить:
в записи результатов сложения и вычитания могут
быть использованы только цифры
шестнадцатеричного алфавита (0-9, A-F)
Основание шестнадцатеричной системы счисления
равно 16, т.е. переполнение наступает, когда
результат сложения больше или равен 16. В этом
случае для записи результата надо вычесть 16,
записать остаток, а к старшему разряду прибавить
единицу переполнения;
если при вычитании приходится занимать единицу в
старшем разряде, эта единица переносится в
младший разряд в виде 16 единиц.
Примеры.
Сложить шестнадцатеричные числа B0916
и EFA16
|
|
1 |
1 |
|
|
|
+ |
B |
0 |
9 |
|
|
E |
F |
A |
||
|
1 |
A |
0 |
3 |
Примеры на закрепление: выполнить
действия в шестнадцатеричной системе счисления.
A1316 + 1CF16
F0B,816 + 1DA,C116
Выполнить вычитание шестнадцатеричных чисел B0916 и 7FA16.
|
|
10 |
15 |
16 |
|
|
_ |
B |
0 |
9 |
|
|
7 |
F |
A |
||
|
|
3 |
0 |
F |
Примеры на закрепление: выполнить
действия в шестнадцатеричной системе счисления.
A1316 — 1CF16
DFA,B816 — 1AE,9416
9.2. Умножение и деление.
Пример 8. Выполнить операции умножения и деления в:
а) Двоичной системе счисления: 101112 * 10112
101112 Проверим делением. 111111012 101112
10112 10111 10112
10111 _ 1000101
10111 10111__
10111 10111
111111012 10111
0
b) Восьмеричной системе счисления: 4578 * 568
4578 Проверим делением. 331628 4578
331628 4578
5682753 568
3432 3432
2753 3432
331628 0
с) Шестнадцатеричной системе счисления:
1) 420316 * 4416 = 1188CC16 2) 22216 : 2716 = E16
420316
4416
1080C
1080C
1188CC16
10.
 Арифметические операции с числами в различных системах счисления.
Арифметические операции с числами в различных системах счисления.Для того чтобы выполнить арифметические операции с числами в различных системах счисления необходимо перевести данные числа в ту систему счисления, в которой ожидается ответ.
Пример 9. Выполнить арифметические операции с числами в различных системах
счисления: 1011102 + 12638 → х10
а) 1011102 = 1*25 + 0*24 + 1*23 + 1*22 + 1*21 +0*20 = 32 + 0 + 8 + 4 + 2 + 0 = 4610
b) 12638 = 1*83 + 2*82 + 6*81 +3*80 = 512 +128+ 48 + 3 = 69110
c) 4610 + 69110 = 73710
Аналогично вычитание, умножение и деление.
Задания
Упражнение I. Перевод чисел из десятичной системы
счисления в двоичную, восьмеричную и
шестнадцатеричную
системы. Применение
Применение
правил выполнения арифметических операций
с числами в различных системах счисления.
Цель: первичное закрепление пройденной темы, получение навыков перевода чисел
из одной системы счисления в другую систему.
Перевести число из одной системы счисления в другую:
2542010 → x8
11102 → x10
256710 → x16
50078 → x2 → x16
12810 = x2 = x8
13410 = x2 = x16
14010 = x16 = x2
12610 = x8 = x16
2СE16 = x2 = x8
AB, CDE16 = x8 = x2
1ABC, 9D16 = x10
Выполнить арифметические действия в различных системах счисления:
110112 + 1112
11112 + 10102
1000012 + 110012
1603468 + 568
2434458 + 2018
7618 + 2658
10000002 – 1001002
110110112 – 110112
4038 – 648
1102 * 1012
10112 * 1002
228 * 728
368 * 248
1011110112 + 11011102
110111012 +110101112
1011102 + 1100112
10011102 – 1100112
Упражнение II.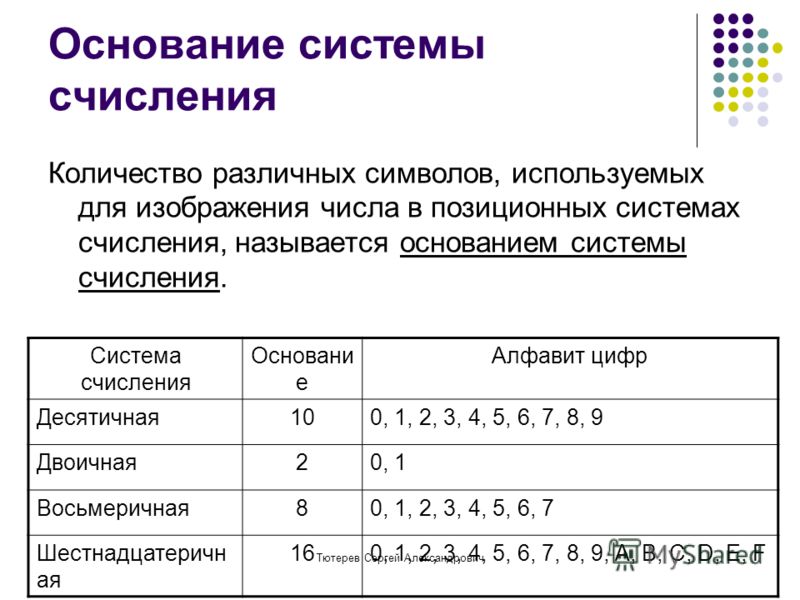 Арифметические
операции в различных
Арифметические
операции в различных
системах счисления.
Цель: закрепление полученных навыков работы с числами в различных системах
счисления.
Исследовательская работа по информатике на тему Деление в восьмеричной, шестнадцатеричной СС
Вот с таким интересным стихотворением мы познакомились на уроке при изучении темы «Системы счисления».
Эта тема является очень важной, так её можно назвать фундаментом информатики, без которого невозможно правильное её понимание. Можно изучить несколько программ и даже научиться программировать на каком-то одном языке, но это не вся информатика, не самая её главная и интересная часть.
Понимание
теоретических основ информатики является необходимым условием для того, чтобы
стать специалистом в этой науке. И потому изучение систем счислений, которые
используются в компьютерах, нужно для понимания того, каким образом
производится обработка числовых данных в компьютере.
В результате мы узнали, что существуют другие системы счисления, в которых есть свой алфавит, своя таблица умножения, сложения и решали задачи, выполняя арифметические действия над числами в двоичной, восьмеричной, шестнадцатеричной системе счисления. Но когда дело дошло до практики, многие столкнулись с проблемой счёта. И тогда я задала сама себе вопрос, а есть ли в этих системах счисления свои признаки делимости, как и в десятичной системе счисления. Ведь все знают, что признак делимости помогает быстро определить, кратно ли число предварительно выбранному числу.
Гипотеза: Мы предполагаем, что в восьмеричной и шестнадцатеричной системе счисления есть свои признаки делимости.
Цели: Изучить теорию о различных системах счисления, найти и доказать существование признаков делимости в различных системах счисления.
Объект исследования: Системы счисления.
Предмет исследования: Признаки делимости.
Задачи:
1. Изучить
теорию, отобрать информацию.
Изучить
теорию, отобрать информацию.
2. Научиться выполнять умножение и деление в двоичной, восьмеричной и шестнадцатеричной системах счисления.
3. Найти признаки делимости в восьмеричной, шестнадцатеричной системе счисления.
Методы исследования:
1. Изучение и анализ источников информации по данной теме.
2. Проведение доказательств.
3. Обобщение.
Глава 1. Система счисления
Нами был изучен и системно обработан информационный материал по данной теме.
За основу мы брали следующие источники: Интернет ресурсы, специальную литературу. Это нам позволило сделать следующие выводы:
1) существуют позиционные и непозиционные системы счисления;
2) в школьном курсе изучаются такие как двоичная, восьмеричная, шестнадцатеричная системы счисления, и правила перевода из одной системы в другую
Виды позиционных систем счисления.
Название | Основание | Алфавит | |
Двоичная СС | 2 | 0, 1 | |
Восьмеричная СС | 8 | 0, 1, 2, 3, 4, 5, 6 и 7 | |
Шестнадцатеричная СС
| 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F | |
Алгоритмы перевода из одной системы счисления в другую.
Так
как мы знаем признаки деления в 10-ой системе счисления, поэтому и
воспользуемся правилом перевода чисел в десятичную систему счисления.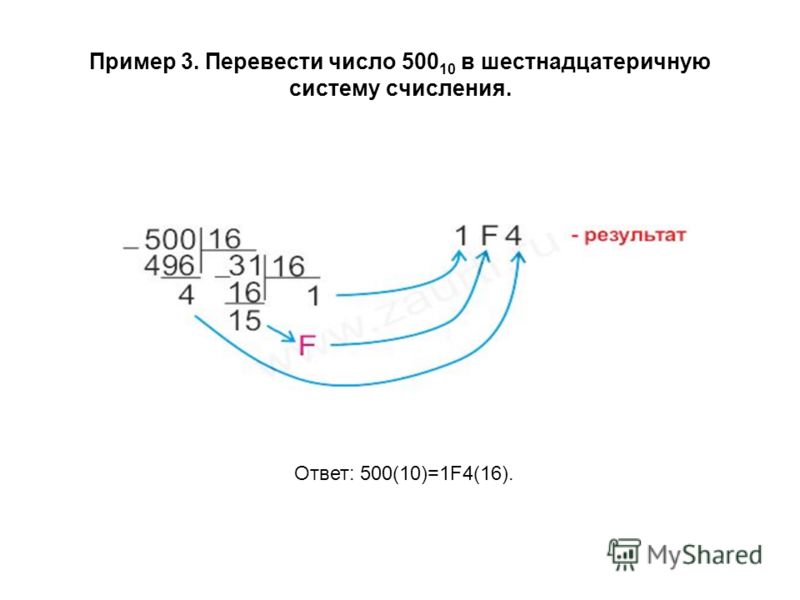
Рис. 1 Правило перевода в десятичную систему счисления
Рис. 2 Правило перевода из десятичной системы счисления
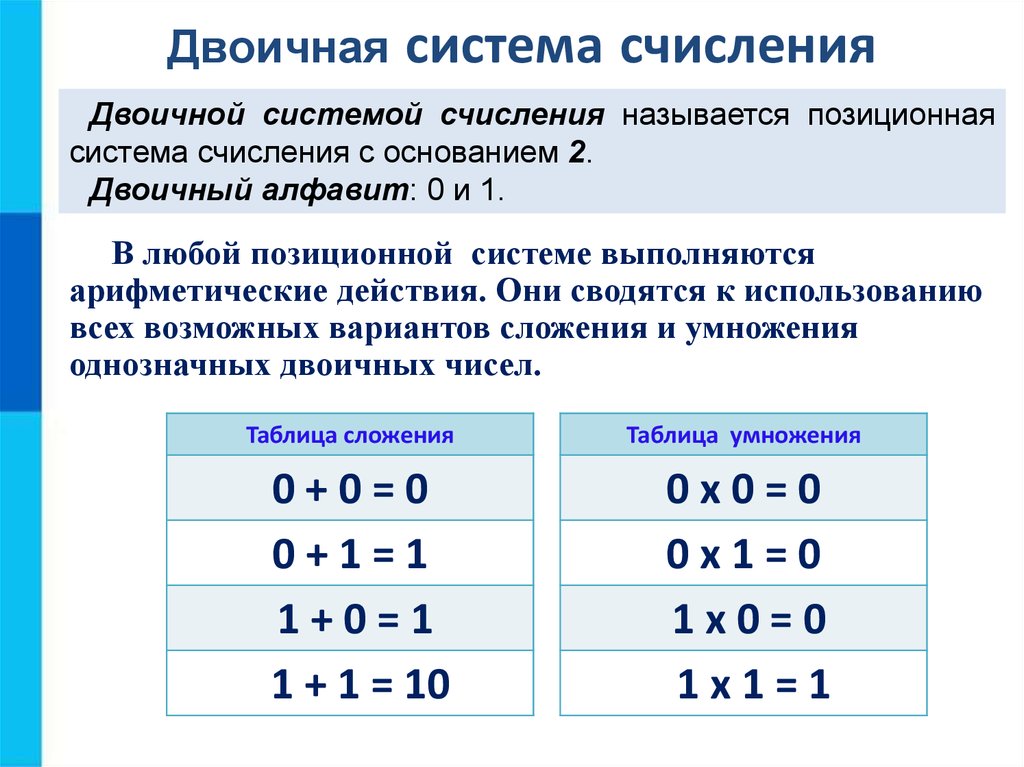
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые соответствуют данному основанию системы счисления.
Восьмеричная система счисления
× | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
2 | 0 | 2 | 4 | 6 | 10 | 12 | 14 | 16 |
3 | 0 | 3 | 6 | 11 | 14 | 17 | 22 | 25 |
4 | 0 | 4 | 10 | 14 | 20 | 24 | 30 | 34 |
5 | 0 | 5 | 12 | 17 | 24 | 31 | 36 | 43 |
6 | 0 | 6 | 14 | 22 | 30 | 36 | 34 | 52 |
7 | 0 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
+ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 |
2 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
3 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 |
4 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 |
5 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 |
6 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 |
7 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
* | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
2 | 0 | 2 | 4 | 6 | 8 | A | C | E | 10 | 12 | 14 | 16 | 18 | 1A | 1C | 1E |
3 | 0 | 3 | 6 | 9 | C | F | 12 | 15 | 18 | 1B | 1E | 21 | 24 | 27 | 2A | 2D |
4 | 0 | 4 | 8 | C | 10 | 14 | 18 | 1C | 20 | 24 | 28 | 2C | 30 | 34 | 38 | 3C |
5 | 0 | 5 | A | F | 14 | 19 | 1E | 23 | 28 | 2D | 32 | 37 | 3C | 41 | 46 | 4B |
6 | 0 | 6 | C | 12 | 18 | 1E | 24 | 2A | 30 | 36 | 3C | 42 | 48 | 4E | 54 | 5A |
7 | 0 | 7 | E | 15 | 1C | 23 | 2A | 31 | 38 | 3F | 46 | 4D | 54 | 5B | 62 | 69 |
8 | 0 | 8 | 10 | 18 | 20 | 28 | 30 | 38 | 40 | 48 | 50 | 52 | 60 | 68 | 70 | 78 |
9 | 0 | 9 | 12 | 1B | 24 | 2D | 36 | 3F | 48 | 51 | 5A | 63 | 6C | 75 | 7E | 87 |
A | 0 | A | 14 | 1E | 28 | 32 | 3C | 46 | 50 | 5A | 64 | 6E | 78 | 82 | 8C | 96 |
B | 0 | B | 16 | 21 | 2C | 37 | 42 | 4D | 52 | 63 | 6E | 79 | 84 | 8F | 9A | A5 |
C | 0 | C | 18 | 24 | 30 | 3C | 48 | 54 | 60 | 6C | 78 | 84 | 90 | 9C | A8 | B4 |
D | 0 | D | 1A | 27 | 34 | 41 | 4E | 5B | 68 | 75 | 82 | 8F | 9C | A9 | B6 | C3 |
E | 0 | E | 1C | 2A | 38 | 46 | 54 | 62 | 70 | 7E | 8C | 9A | A8 | B6 | C4 | D2 |
F | 0 | F | 1E | 2D | 3C | 4B | 5A | 69 | 78 | 87 | 96 | A5 | B4 | C3 | D2 | E1 |
Шестнадцатеричная система счисления
+ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 |
3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 |
4 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 |
5 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 |
6 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 |
7 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
8 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
9 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
A | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
B | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A |
C | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B |
D | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C |
E | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D |
F | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D | 1E |
Глава 2. Признаки делимости
Признаки делимости
2. 1 Признаки делимости в восьмеричной системе счисления.
Признак делимости на 2
Пусть дано двузначное число аb8. Выясним, когда оно будет делиться на 2.
аb8=8а+b
8а делится на 2,так как 8:2=4
Если b делится на 2, то число ab8 будет делиться на 2.
Пусть дано трёхзначное число abc
8. . Выясним, когда оно будет делиться на 2.abc8 = 82a+8b+c=64a+8b+c
64а делится на 2, так как 64:2=32
8b делится на 2, так как 8:2=4
Если с числа abc8 будет делиться на 2, то и число abc8 будет делиться на 2.
Пусть дано abcd
8. Выясним, когда оно будет делиться на 2.abcd8=83a+82b+8c+d=512a+64b+8c+d.
512a делится на 2, так как 512:2=256;
64b делится на 2, так как 64:2=32;
8с
делится на 2, так как 8:2=4.
Если последняя цифра d числа abcd8 будет делиться на 2, то и число abcd8 будет делиться на 2.
Вывод: если последняя цифра числа делится на 2, то число делится на 2.
Пример: 564 : 2 = 172, 754 : 2 = 366
Признак делимости на 3
Пусть дано двухзначное число ab8. Выясним, когда оно будет делиться на 3.
ab8=8а+b=6а+(2а+в)
6а делится на 3,т.к. 6:3=2.
Если сумма (2а+в) будет делиться на 3, то и число ab8 будет делиться на 3.
Пусть дано трёхзначное число аbc8.Выясним, когда оно будет делиться на 3.
аbc8= 82а+8b+с=64а+ 8b+с=63а+6в+(а+2в+с).
63а делится на 3, т.к. 63:3=21
6bделится на 3, т.к. 6:3=2
Если сумма (а+2в+с) будет делиться на 3, то и число abc8 будет делиться на 3.
Пусть дано
четырёхзначное число abc8. Выясним, когда оно будет делиться на 3.
Выясним, когда оно будет делиться на 3.
аbcd8=8а3+8b2+8с+d=510а+63в+6с+(2а+в+2с+d).
510а делится на 3,т.к. 510:3=170
63b делится на 3, т.к. 63:3=21
6с делится на 3,т.к. 6:3=2
Если сумма (2а+в+2с+d) будет делиться на 3, то и число аbcd8 будет делиться на 3.
Вывод: если сумма цифр, занимающих нечётные места и сумма удвоенных цифр, занимающих чётные места, делятся на 3, то и само число делится на 3.
Например, 3234 : 3 = 1064
Признак делимости на 4
Пусть дано двузначное число ab
8. Выясним, когда оно будет делиться на 4.ab8=8a+b
8a делится на 4, т.к. 8:4=2
Если b делится на 4, то ab8 будет делиться на 4.
Пусть дано трёхзначное число abc
8. . Выясним, когда оно будет делиться на 4.abc8 = 82a+8b+c=64a+8b+c.
64a делится на 4, так как 64:4=16.
8b делится на 4,так как 8:4=2.
Если с делится на 4, то число abc8 будет делиться на 4.
Пусть дано abcd
8. Выясним, когда оно будет делиться на 4.abcd8=83a+82b+8c+d=512a+64b+8c+d.
512a делится на 4, так как 512:4=128;
64b делится на 4, так как 64:4=16;
8с делится на 4, так как 8:4=2.
Если d делится на 4, то число abcd8 будет делиться на 4.
Вывод: если последняя цифра числа делится на 4, то число делится на 4.
Например, 374 : 4 =77, 5124 : 4 = 1225
Признак делимости на 7
Пусть дано двухзначное число аd8. Выясним, когда оно будет делиться на 7.
аb8=8а+b=7а+(b+a)
7а делится на 7, т.к. 7:7=1
Если сумма цифр (b+а) числа ab8 делится на 7, то число делится на 7.
Пусть дано трёхзначное число аbc8. Выясним, когда оно будет делиться на 7.
аbc8=82+8b+с=64а+8b+с=b3а+7b+(а+b+с)
63а делится на 7, т.к. 63:7=9
7b делится на 7,т.к. 7:7=1
Если сумма цифр (а+b+c) числа abc8 делится на 7, то число делится на 7.
Пусть дано четырёхзначное число abcd8. Выясним, когда оно будет делиться на 7.
аbcd8=83а+82b+8с+d=512а+64b+8с+d=511а+63b+7с+(а+b+d+c)
511а делится на 7, т.к. 511:7=73
63b делится на 7, т.к. 63:7=9
7с делится на 7, т.к. 7:7=1
Если сумма цифр (а+b+c+d) числа abcd8 делится на 7, то число делится на 7.
Вывод: если сумма цифр числа делится на 7, то число делится на 7.
Например, 464 : 7 = 54, 7275 : 7 = 1033
2. 2 Признаки делимости в шестнадцатеричной системе счисления.
Признак делимости на 2.
Пусть дано abc
16. Выясним, когда оно будет делиться на 2.abc16=162a+16b+c =256a+16b+c.
256a делится на 2, так как 256:2=128;
16b делится на 2, так как 16:2=8;
Если последняя цифра c числа abc16 будет делиться на 2, то и число abc16 будет делиться на 2. Аналогично можно провести доказательство для любого многозначного числа.
Вывод: Шестнадцатеричные числа делятся на 2, если последняя цифра является четной (кроме четных десятичных цифр четными здесь также являются цифры А, С и Е).
Например, 358 : 2 = 1AC, 52 : 2 = 29, 74356 : 2 = 3A1AB
Признак делимости на 3.
Пусть дано abc16. Выясним, когда оно будет делиться на 3.
abc16=162a+16b+c =256a+16b+c= 255a+15b+(a+b+c)
255a делится на 3, так как 255:3=85;
15b делится на 3, так как 15:3=5;
Если
сумма цифр a,b и c числа abc16 будут
делиться на 3, то и число abc16 будет делиться на 3.
Пусть дано abcd16. Выясним, когда оно будет делиться на 3.
abcd16=163a+162b+16c+d =4096a+256b+16c+d= 4095a+255b+15c+(a+b+c+d)
4095a делится на 3, так как 4095:3=1365;
255a делится на 3, так как 255:3=85;
15b делится на 3, так как 15:3=5;
Если сумма цифр a,b,c и d числа abcd16 будут делиться на 3, то и число abcd16 будет делиться на 3.
Вывод: Шестнадцатеричные числа делятся на 3, если сумма цифр делится на 3.
Например, 375 : 3 = 127, 63 : 3 =21, 8346 : 3 = 2BC2
Признак делимости на 4.
Пусть дано abc16. Выясним, когда оно будет делиться на 4.
abc16=162a+16b+c =256a+16b+c
256a делится на 4, так как 256:4=64;
15b делится на 4, так как 16:4=4;
Если
последняя цифра c числа abc16 будут делиться на 4, то и число abc16 будет делиться на 4.
Пусть дано abcd16. Выясним, когда оно будет делиться на 4.
abcd16=163a+162b+16c+d =4096a+256b+16c+d
4096a делится на 4, так как 4096:4=1024;
256a делится на 4, так как 256:4=64;
16b делится на 4, так как 16:4=4;
Если последняя цифра c числа abc16 будут делиться на 4, то и число abc16 будет делиться на 4.
Вывод: Шестнадцатеричные числа делится на 4, если последняя цифра делится на 4.
Например, 354 : 4 = D5
Признак делимости на 5.
Пусть дано abc16. Выясним, когда оно будет делиться на 5.
abc16=162a+16b+c =256a+16b+c= 255a+15b+(a+b+c)
255a делится на 5, так как 255:5=51;
15b делится на 5, так как 15:5=3;
Если
сумма цифр a,b и c числа abc16 будут
делиться на 5, то и число abc16 будет делиться на 5.
Пусть дано abcd16. Выясним, когда оно будет делиться на 5.
abcd16=163a+162b+16c+d =4096a+256b+16c+d= 4095a+255b+15c+(a+b+c+d)
4095a делится на 5, так как 4095:5=819;
255a делится на 5, так как 255:5=51;
15b делится на 5, так как 15:5=3;
Если сумма цифр a,b,c и d числа abcd16 будут делиться на 5, то и число abcd16 будет делиться на 5.
Вывод: Шестнадцатеричные числа делятся на 5, если сумма цифр делится на 5.
Например, 815 : 5 = 19D
Признак делимости на 8
Пусть дано abc16. Выясним, когда оно будет делиться на 8.
abc16=162a+16b+c =256a+16b+c
256a делится на 8, так как 256:8=32;
16b делится на 8, так как 16:8=2;
Если
последняя цифра c числа abc16 будут делиться на 8, то и число abc16 будет делиться на 8.
Пусть дано abcd16. Выясним, когда оно будет делиться на 8.
abc16=163a+162b+16c+d =4096a+256b+16c+d
4096a делится на 8, так как 4096:8=512;
256a делится на 8, так как 256:8=32;
16b делится на 8, так как 16:8=2;
Если последняя цифра c числа abc16 будут делиться на 8, то и число abc16 будет делиться на 8.
Вывод: Шестнадцатеричные числа делятся на 8, если последняя цифра делится на 8. Но если последняя цифра числа будет 0, то число тоже будет делиться на 8, потому что 8+8=10.
Например, 6570 : 8 =CAE, FC8 : 8 = 1F9
2.3 Применение признаков делимости на практике
Задачи, связанные с
делимостью, представляют собой великолепный материал для воспитания
математической культуры учащихся. С их помощью можно показать, что и в
информатике можно решать арифметические задачи, повышая интерес к предмету.
Задача № 1. Можно ли, используя только цифры 3 и 4, записать:
1. число в 8-ой (16 – ой) СС, которое делиться на 6;
2. четное число;
3. число, кратное 5;
Задача № 2
Напишите какое-нибудь девятизначное число в 8-ой СС, в котором нет повторяющихся цифр (все цифры разные) и которое делится без остатка на 4.
1. Напишите наибольшее из таких чисел.
2. Напишите наименьшее из таких чисел.
Ответ: 777777774; 100000004
Задача № 3
Найдите наибольшее четырехзначное шестнадцатеричное число, все цифры которого различны и которое делится на 2, 3, 5. Приведите примеры таких чисел
Ответ: например D31E
Задача № 4
Оля задумала простое восьмеричное трехзначное число,
кратное 3, все цифры которого различны. На какую цифру оно может заканчиваться,
если его последняя цифра равна сумме первых двух. Приведите примеры таких
чисел.
Ответ: 347.
Заключение
В результате выполнения данной работы мы нашли и вывели признаки делимости для восьмеричной и шестнадцатеричной системы счисления. Данное исследование, я думаю, будет полезно, как для учеников, так и для учителей. Ученики могут расширить свой кругозор в области информатики, а учителя при изучении темы «Системы счисления», составлять задачи для развития логического мышления учащихся и повышения интереса к предмету.
В перспективе мы намерены продолжить нашу работу, и рассмотреть признаки делимости на другие числа в восьмеричной и в шестнадцатеричной системе счисления.
Литература
1.
Гашков, С. Б. Системы счисления и их применения
[Текст]/ С.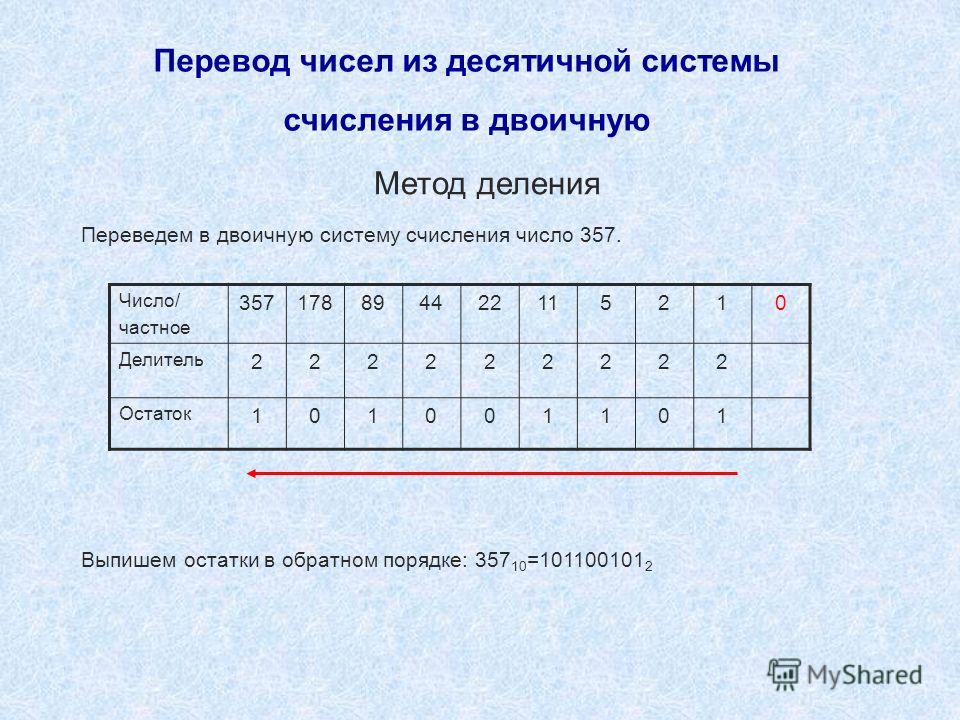 Б. Гашков .- Москва.- «Математическое просвещение», 1999.- 54с.
Б. Гашков .- Москва.- «Математическое просвещение», 1999.- 54с.
2. Гейн А. Г., «Информатика» [Текст ] / А.Г.Гейн, А. И. Сенокосов.- Москва.: Просвещение.- 2002.-116с.
3. Депман, И. Я. За страницами учебника математики [Текст]/ И. Я . Депман, Н. Я. Виленкин .- Москва.: «Просвещение», 1989.- 215с.
4. Кутугин Е. С. Арифметические и логические основы построения компьютера[Текст]/ Е.С. Кутугин – Томск: Школьный ун-т, 2007.-315с.
5. Никольская И.Л. Факультативный курс по математике 7-9[Текст]/ /И. Л. Никольская.- Москва.: Просвещение.- 1991 .- 211с.
Интернет ресурсы
Система счисления [Электронный ресурс] / Режим доступа: http://gurulev.telebit.ru/sistschislenia.htm.- Загл. с экрана
Задачи: системы счисления [Электронный ресурс] / Режим доступа: http://www.tspu.tula.ru/ivt/old_site/umr/timoi/solovieva/Zadaneya/zadachi_ss.htm.- Загл. с экрана
Позиционные системы счисления. Перевод чисел из одной
позиционной системы счисления в другую. Арифметические операции с числами в
позиционных системах счисления [Электронный ресурс] / Режим доступа: www.bymath.net/studyguide/ari/ari5.html.-
Загл. с экрана
Перевод чисел из одной
позиционной системы счисления в другую. Арифметические операции с числами в
позиционных системах счисления [Электронный ресурс] / Режим доступа: www.bymath.net/studyguide/ari/ari5.html.-
Загл. с экрана
Системы счисления, применяемые в ЭВМ счисления [Электронный ресурс] / Режим доступа: http://www.kolomna-school7-ict.narod.ru/st20101.htm.- Загл. с экрана
Информатика. Лекция №3. Системы счисления (продолжение).
Информатика. Лекция №3. Системы счисления (продолжение).Информатика. Лекция №3. Системы счисления (продолжение).
Правила выполнения простейших арифметических действий.
Пример 3.
 16. Сложить двоичные числа 11012 и 110112.
16. Сложить двоичные числа 11012 и 110112.Запишем слагаемые в столбик и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов:
5 4 3 2 1
+ 1 1 0 1
1 1 0 1 1
Процесс образования результата по разрядам описан ниже:
- разряд 1 формируется следующим образом: 1 + 1 = 10; 0 остается в разряде 1, 1 переносится во второй разряд;
- разряд 2 формируется следующим образом: 0 + 1 + 1 = 10, где вторая 1 — единица переноса; 0 остается в разряде 2, 1 переносится в третий разряд;
- третий разряд формируется следующим образом: 1 + 0 + 1 = 10, где вторая 1 — единица переноса; 0 остается в разряде 3, 1 переносится в разряд 4;
- четвертый разряд формируется следующим образом: 1 + 1 + 1 = 11, где третья 1 — единица переноса; 1 остается в разряде 4, 1 переносится в пятый разряд;
- пятый разряд формируется следующим образом: 1 + 1 = 10; где вторая 1 — единица переноса; 0 остается в разряде 5, 1 переносится в шестой разряд.

Таким образом:
1 1 0 1
+ 1 1 0 1 1
1 0 1 0 0 0
Проверим результат. Для этого определим полные значения слагаемых и результата:
11012 = 1*23 +1*22 + 0*21 + 1*20 = 8 + 4 + 1 = 13;
110112 = 1*24 + 1*23 + 0*22 + 1*21 + 1*20 = 16 + 8 + 2 + 1 = 27;
1010002 = 1*25 + 0*24 + 1*23 + 0*22 + 0*21 + 0*21 = 32 + 8 = 40.
Поскольку 13 + 27 = 40, двоичное сложение выполнено верно.
Пример 3.17. Сложить шестнадцатеричные числа 1С16 и 7В16.
Запишем слагаемые в столбик и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов:
+ 1 С
7 В
Процесс образования результата по разрядам описан ниже (он включает преобразование в процессе сложения каждой шестнадцатеричной цифры в десятичное число и обратные действия):
- разряд 1 формируется следующим образом: С16 + В16 = 12 + 11 = 23 = 1716; 7 остается в разряде 1; 1 переносится в разряд 2;
- разряд 2 формируется следующим образом: 116 + 716 + 116 = 916, где вторая 116 — единица переноса.

Таким образом:
1 С
+ 7 В
9 7
Проверим результат. Для этого определим полные значения слагаемых и результата:
1С16 = 1*161 + 12*160 = 16 + 12 = 28;
7В16 = 7*161 + 11*160 = 112 + 11 = 123;
9716 = 9*161 + 7*160 = 144 + 7 = 151.
Поскольку 28 + 123 = 151, сложение выполнено верно.
Правила вычитания
Пример 3.18. Вычесть из двоичного числа 1012 двоичное число 112.
Запишем алгебраические слагаемые в столбик в порядке «уменьшаемое — вычитаемое» и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов:
- 1 0 1
1 1
Процесс образования результата по разрядам описан ниже:
- разряд 1 формируется следующим образом: 1 — 1 = 0;
- разряд 2 формируется следующим образом: поскольку 0 меньше 1 и непосредственное вычитание невозможно, занимаем для уменьшаемого единицу в старшем разряде 3.
 Тогда разряд 2 рассчитывается как 10 — 1 = 1;
Тогда разряд 2 рассчитывается как 10 — 1 = 1;
- третий разряд формируется следующим образом: поскольку единица была занята в предыдущем шаге, в разряде остался 0.
Таким образом:
1 0 1
- 1 1
1 0
Проверим результат. Для этого определим полные значения слагаемых и результата. По таблице имеем::
1012 = 5;
112 = 3;
102 = 2.
Поскольку 5 — 3 = 2, вычитание выполнено верно.
Пример 3.19. Вычесть из шестнадцатеричного числа 9716 шестнадцатеричное число 7В16.
Запишем алгебраические слагаемые в столбик в порядке «уменьшаемое — вычитаемое» и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов:
- 9 7
7 В
Процесс образования результата по разрядам описан ниже:
- разряд 1 формируется следующим образом: поскольку 7 меньше В и непосредственное вычитание невозможно, занимаем для уменьшаемого единицу в старшем разряде 2.
 Тогда 1716 — В16 = 23 — 11 = 12 = С16;
Тогда 1716 — В16 = 23 — 11 = 12 = С16; - разряд 2 формируется следующим образом: поскольку единица была занята в предыдущем шаге, разряд 2 уменьшаемого стал равным 816. Тогда разряд 2 рассчитывается как 8166 — 716 = 116.
Таким образом:
9 7
- 7 В
1 С
Для проверки результата используем данные из примера 3.17.
Таким образом, вычитание выполнено верно.
Правила умножения
Пример 3.20. Умножить двоичное число 1012 на двоичное число 112.
Запишем множители в столбик и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов:
* 1 0 1
1 1
Процесс образования результата по шагам умножения множимого на каждый разряд множителя с последующим сложением показан ниже:
- умножение множимого на разряд 1 множителя дает результат: 1012 * 12 = 1012;
- умножение множимого на разряд 2 множителя дает результат: 1012 * 102 = 10102.
 Здесь значение разряда 2 множителя сформировано по принципам формирования значения числа в позиционных системах счисления;
Здесь значение разряда 2 множителя сформировано по принципам формирования значения числа в позиционных системах счисления;
- для получения окончательного результата складываем результаты предыдущих шагов: 1012 + 10102 = 11112.
Для проверки результата найдем полное значение сомножителей и произведения (см. таблицу):
1012 = 5;
112 = 3;
11112 = 15.
Поскольку 5 * 3 = 15, умножение выполнено верно: 1012 * 112 = 11112.
Пример 3.21. Умножить шестнадцатеричное число 1С16 на шестнадцатеричное число 7В16.
Запишем множители в столбик и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов:
* 1 С
7 В
Процесс образования результата по шагам умножения множимого на каждый разряд множителя с
последующим сложением показан ниже (в процессе умножения выполняем перевод шестнадцатеричных
чисел в десятичные и обратно):
- умножение множимого на разряд 1 множителя дает результат: 1С16 * В16 = 28 * 11 = 308 = 13416;
- умножение множимого на разряд 2 множителя дает результат: 1С16 * 716 = 28 * 112 = 3136 = С4016.
 Здесь значение разряда 2 множителя сформировано по принципам формирования значения числа в позиционных системах счисления;
Здесь значение разряда 2 множителя сформировано по принципам формирования значения числа в позиционных системах счисления;
- для получения окончательного результата складываем результаты предыдущих шагов: 13416 + С4016 = D7416.
Для проверки результата найдем полное значение сомножителей и произведения, воспользовавшись результатами примера 3.17 и правилами формирования полного значения числа:
1С16 = 28;
7В16 = 123;
D7416 = 13*162 + 7*161 + 4*160 = 3444.
Поскольку 28 * 123 = 3444, умножение выполнено верно: 1С16 * 7В16 = D7416.
Правила деления
Рассмотрим правила деления только для двоичных чисел, поскольку деление шестнадцатеричных чисел проще выполнять, переведя их предварительно в десятичную систему счисления.
Пример 3.22. Разделить двоичное число 11112 на двоичное число 112.

Решение задачи представим схемой:
Примеры шестнадцатеричных делений
Комплекты схем с защелкой | Изучайте электронику и электричество безопасно
Snap Circuits упростили разработку электроники. Вы ловко проектируете, строите, анализируете и рисуете схемы, как профессионал! Это игривый инструмент, который в равной степени увлечет детей, любителей, молодых людей и новичков в области электроники и электричества. Они заложат прочную основу для проектирования схем. Это не наборы, а небольшая научная лаборатория в коробке. Прежде всего, они безопасны, не причиняют вреда детям, если они рядом. Доступно множество комплектов схем быстрого доступа, но я стараюсь выбирать только те комплекты, которые стоят менее 75 долларов. Практический комплект для пайки Elenco: в комплект входят учебные доски и материалы для пайки. Это безотказный набор для пайки. Электротехники, студенты и любители должны научиться паять. Это обеспечивает лучшую отработку материала с помощью простых проектов. С помощью этого комплекта вы получите знания по следующим темам. Пайка. Как паять мультивибратор Опыт с печатными платами Двухцветная европейская сирена Сна
Это безотказный набор для пайки. Электротехники, студенты и любители должны научиться паять. Это обеспечивает лучшую отработку материала с помощью простых проектов. С помощью этого комплекта вы получите знания по следующим темам. Пайка. Как паять мультивибратор Опыт с печатными платами Двухцветная европейская сирена Сна
Примеры шестнадцатеричных делений
Примеры шестнадцатеричных деленийЭто моя четвертая и последняя статья о шестнадцатеричной арифметике. В этом посте я решу несколько примеров по делению шестнадцатеричных чисел. Прежде чем приступить к этой теме, вы должны знать, как умножать шестнадцатеричные числа. Вот моя статья об умножении шестнадцатеричных чисел.
Ключевые вопросы:
Как выполнить шестнадцатеричное деление?
Как выполнить деление дробных шестнадцатеричных чисел?
Деление шестнадцатеричных чисел такое же, как и в других системах счисления. Все правила и принципы одинаковы. Вы можете проверить свои результаты с помощью этого онлайн-калькулятора.
Все правила и принципы одинаковы. Вы можете проверить свои результаты с помощью этого онлайн-калькулятора.
5÷6 в этом 5 делимое и 6 делитель
Я рассмотрю три случая с помощью трех примеров. В первом случае делимое и делитель являются целыми числами. Во втором случае делимое имеет дробную часть, а делитель — целое число. В третьем случае и делимое, и делитель имеют дробные части.
Example#01:AE887)16÷3A)16
Сначала составьте таблицу умножения для числа 3A и его кратных чисел
00 3A*1 | 3А |
3А*2 | 74 |
3А*3 | АЕ |
3А*4 | Е8 |
3А*5 | 122 |
3А*6 | 15С |
3А*7 | 196 |
3А*8 | 1D0 |
3А*9 | 20А |
3А*А | 244 |
3А*В | 27Е |
3025. A3
A3
3A⟌AE887
AE
X88
74
147
122
250
244
B0
AE
2
Ответ: 3025.A3) 16
Пример № 02: ECE.46) 16 ÷ 12) 16
САМНЕЙ СОЕДИНЕНИЕ СОЕДИНЕНИЯ СЛЕДУЮЩАЯ САМЕТ для 12
12*1 | |
12*1 | |
12*1 | 12 |
12*2 | 24 |
12*3 | 36 |
12*4 | 48 |
12*5 | 5А |
12*6 | 6С |
12*7 | 7Е |
12*8 | 90 |
12*9 | А2 |
12*А | В4 |
12*В | С6 |
12*С | Д8 |
12*D | ЕА |
D2. 92
92
12⟌ ECE.46
EA
2E
24
A4
A2
26
0005
24
2
Ответ: D2.92) 16
Пример № 03: 257,8A) 16 ÷ 5,1) 16
Сдвигая шестнадцатеричная точка облегчает проблему. Согласно математическому правилу, если вы сдвинете шестнадцатеричную точку делимого на одно место, то вы должны сдвинуть шестнадцатеричную точку делителя.
После переключения
2578.A÷51
51*1 | 51 |
51*2 | А2 |
51*3 | F3 |
51*4 | 144 |
51*5 | 195 |
51*6 | 1Е6 |
51*7 | 237 |
51*8 | 288 |
51*9 | 2D9 |
51*А | 32А |
51*В | 37Б |
51*С | 3CC |
51*D | 41Д |
76. 6D
6D
51⟌2578.A
237
208
1E6
22A
1E6
440
41D
33
Answer: 76.6D)16
популярные посты
Примеры решения восьмеричного сложения
Примеры сложения восьмеричных чисел Это моя первая статья о восьмеричной арифметике. В этом посте я собираюсь объяснить два разных метода сложения восьмеричных чисел. Ключевые вопросы: Как выполнить восьмеричное сложение? Как выполнить сложение дробных восьмеричных чисел? Нарисуйте таблицу восьмеричного сложения. Обсудите два метода восьмеричного сложения. Техника сложения восьмеричных чисел. Существует два метода сложения восьмеричных чисел. Я буду решать каждый пример, используя методы для лучшего понимания. Вы можете проверить свои результаты, используя этот онлайн-калькулятор восьмеричного сложения. Метод № 1: В этом методе вы должны помнить следующие моменты: Думайте о каждом числе как о десятичном числе и добавляйте их как десятичные числа. После добавления каждого столбца, если сумма столбца превышает 7, разделите результат на 8, чтобы оценить эквивалентное восьмеричное значение. Остаток будет частью ответа (подсумма), а частное станет переносом. Пример № 01: 167) 8 +765) 8
Обсудите два метода восьмеричного сложения. Техника сложения восьмеричных чисел. Существует два метода сложения восьмеричных чисел. Я буду решать каждый пример, используя методы для лучшего понимания. Вы можете проверить свои результаты, используя этот онлайн-калькулятор восьмеричного сложения. Метод № 1: В этом методе вы должны помнить следующие моменты: Думайте о каждом числе как о десятичном числе и добавляйте их как десятичные числа. После добавления каждого столбца, если сумма столбца превышает 7, разделите результат на 8, чтобы оценить эквивалентное восьмеричное значение. Остаток будет частью ответа (подсумма), а частное станет переносом. Пример № 01: 167) 8 +765) 8
Читать далее
Решенные примеры вычитания восьмеричных чисел
Примеры восьмеричного вычитания Это моя вторая статья о восьмеричной арифметике. В этом посте я объясню вычитание восьмеричных чисел. Вы можете проверить мою статью о восьмеричном сложении. Ключевые вопросы Как выполнить восьмеричное вычитание? Как выполнить дробное восьмеричное вычитание? Как выполнить восьмеричное вычитание, используя дополнение до 8? Примеры восьмеричного вычитания: Метод №1: Уменьшаемое>Вычитаемое Это метод, который мы использовали в элементарной математике. Все правила, которым мы следуем, остаются такими же, как и в других системах счисления. Заем равен основанию системы счисления. Если вы работаете с основанием 2, вы заимствуете 2. Если вы работаете с основанием 8, вы заимствуете 8. Вы можете проверить свои результаты с помощью этого онлайн-калькулятора. Пример#01: 345) 8 -146) 8 8 2 3 8 3 4 5 -1 4 6 1 7 7 1-й столбец (столбец единиц) вычитания. 5-6 Это невозможно. Вы должны заимствовать из столбца десятков. Число
Все правила, которым мы следуем, остаются такими же, как и в других системах счисления. Заем равен основанию системы счисления. Если вы работаете с основанием 2, вы заимствуете 2. Если вы работаете с основанием 8, вы заимствуете 8. Вы можете проверить свои результаты с помощью этого онлайн-калькулятора. Пример#01: 345) 8 -146) 8 8 2 3 8 3 4 5 -1 4 6 1 7 7 1-й столбец (столбец единиц) вычитания. 5-6 Это невозможно. Вы должны заимствовать из столбца десятков. Число
Читать далее
Примеры шестнадцатеричных умножений
Шестнадцатеричное умножение Это моя третья статья о шестнадцатеричной арифметике. В этом посте я объясню, как умножить два шестнадцатеричных числа. Это так же, как мы умножаем числа в других системах счисления. Прежде чем начать шестнадцатеричное умножение, вы должны знать шестнадцатеричное сложение. Вот мои статьи о шестнадцатеричном сложении и шестнадцатеричном вычитании. Ключевые вопросы: Как выполнить шестнадцатеричное умножение? Как выполнить дробное умножение шестнадцатеричных чисел? Шестнадцатеричная таблица умножения: X 0 1 2 3 4 5 6 7 8 9A B C D E F 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 2 3 4 5 6 7 8 9 A B C D E F 2 0 2 4 6 8 A C E 10 12 14 16 18 1A 1C 1E 3 0 3 6 9 C F 12 15 18 1B 1F 21 24 27 2A 2D 4 0 4 8 C 10 14 18 1C 20 24 28 2C 30 34 38 3C 5
Читать далее
Примеры решения восьмеричного деления
Примеры решения восьмеричного деления Это моя четвертая статья о восьмеричной арифметике. В этой статье я собираюсь решить несколько примеров на восьмеричное деление. Это очень простая задача, а принципы и правила деления остаются прежними. Вот статьи о сложении восьмеричных чисел, вычитании восьмеричных чисел и умножении восьмеричных чисел. Ключевые вопросы: Как выполнить деление восьмеричных чисел? Как выполнить дробное деление восьмеричных чисел Примеры восьмеричного деления: Чтобы решить примеры деления, вы должны знать, как выполнять умножение восьмеричных чисел. Буду решать примеры по каждому случаю. Первый случай, когда делимое и делитель являются целыми числами. Второй случай, когда у делимого есть восьмеричная точка, а делитель — целое число. Третий случай, когда и делимое, и делитель имеют числа с плавающей запятой. Вы можете проверить свои результаты с помощью этого онлайн-конвертера. Example#01:6573) 8 ÷16) 8 Сначала мы делаем таблицу для 16 и их кратных чисел. Десятичный восьмеричный
В этой статье я собираюсь решить несколько примеров на восьмеричное деление. Это очень простая задача, а принципы и правила деления остаются прежними. Вот статьи о сложении восьмеричных чисел, вычитании восьмеричных чисел и умножении восьмеричных чисел. Ключевые вопросы: Как выполнить деление восьмеричных чисел? Как выполнить дробное деление восьмеричных чисел Примеры восьмеричного деления: Чтобы решить примеры деления, вы должны знать, как выполнять умножение восьмеричных чисел. Буду решать примеры по каждому случаю. Первый случай, когда делимое и делитель являются целыми числами. Второй случай, когда у делимого есть восьмеричная точка, а делитель — целое число. Третий случай, когда и делимое, и делитель имеют числа с плавающей запятой. Вы можете проверить свои результаты с помощью этого онлайн-конвертера. Example#01:6573) 8 ÷16) 8 Сначала мы делаем таблицу для 16 и их кратных чисел. Десятичный восьмеричный
Читать далее
Шестнадцатеричный калькулятор
Шестнадцатеричный калькулятор выполняет алгебраические операции над шестнадцатеричными числами.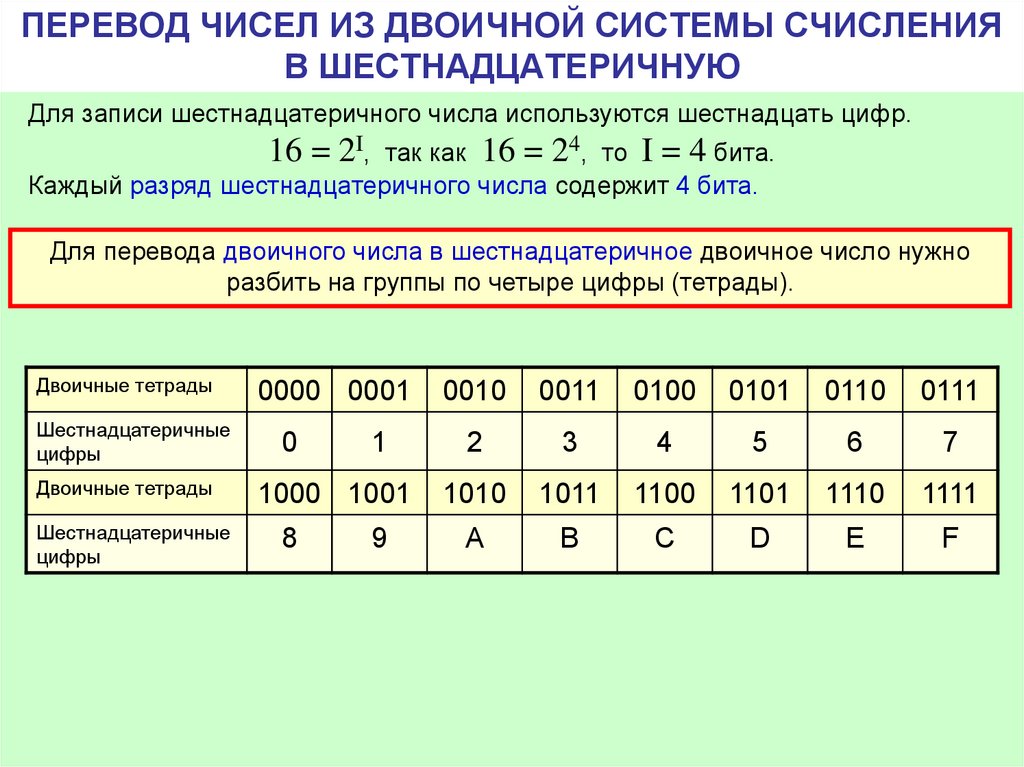 Он может выполнять основные 4 операции, включая сложение, вычитание, умножение и деление.
Он может выполнять основные 4 операции, включая сложение, вычитание, умножение и деление.
Выдаст ответ в шестнадцатеричной системе счисления. Вы найдете все математические операции, выполняемые над десятичной формой введенных шестнадцатеричных чисел.
Что такое шестнадцатеричные числа?
Шестнадцатеричная система счисления аналогична десятичной, двоичной и восьмеричной системам счисления. Он использует основание шестнадцать (16). Шестнадцать шестнадцатеричных цифр включают цифры от 0 до 9.и алфавиты от A до F.
Буква A означает 10, B – 11, C – 12 и т. д. Эта система счисления используется в различных областях компьютера. Основная цель этой системы заключается в том, что она сжимает двоичные числа, чтобы сэкономить место для лучшей работы.
Алгебраические операции над шестнадцатеричными числами
Операции выполняются как в десятичной системе счисления. Разница возникает там, где задействованы преобразования.
В статье ниже мы рассмотрим каждую операцию одну за другой. Но прежде чем перейти к операциям, давайте кратко рассмотрим преобразование десятичного числа в шестнадцатеричное и шестнадцатеричного в десятичное.
Но прежде чем перейти к операциям, давайте кратко рассмотрим преобразование десятичного числа в шестнадцатеричное и шестнадцатеричного в десятичное.
Разделите число на 16 и запишите частное и остаток. Отметьте этот остаток как единицу и найдите его шестнадцатеричный эквивалент. Теперь возьмите предыдущее частное и повторите. Отметьте этот остаток как два.
Продолжайте этот процесс, пока само частное не станет меньше 16. Давайте посмотрим на пример.
Пример:
Преобразование 1256 10 в шестнадцатеричную систему.
Solution:
Division | Quotient | Remainder in base ten | Remainder in base sixteen | Digit number |
1256/16 | 78 | 8 | 8 | 0 |
4 | 14 | E | 1 | |
4/16 | none | 4 | 4 | 2 |
Запишите цифры снизу вверх как 4E8 16 . Вместо этого используйте десятичный преобразователь в шестнадцатеричный.
Вместо этого используйте десятичный преобразователь в шестнадцатеричный.
Примечание: Цифры начинаются с 0, потому что для обратного преобразования нужно возводить эти числа в степень. Степени в таких преобразованиях начинаются с 0. См. следующий заголовок.
Преобразование шестнадцатеричных чисел в десятичныеШестнадцатеричные числа преобразуются в десятичные таким же образом, как двоичные преобразуются в десятичные. Найдите разрядное значение каждого шестнадцатеричного числа. Возведите 16 в эту степень (разрядное значение) и умножьте на цифру. Добавьте все числа.
Пример:
Найдите десятичное значение DEF .
Решение:
Шаг 1: Найдите разрядные значения.
- F на месте 0
- E на месте 1
- D на месте 2
Шаг 2: Возведите эти значения в степень и умножьте на цифры.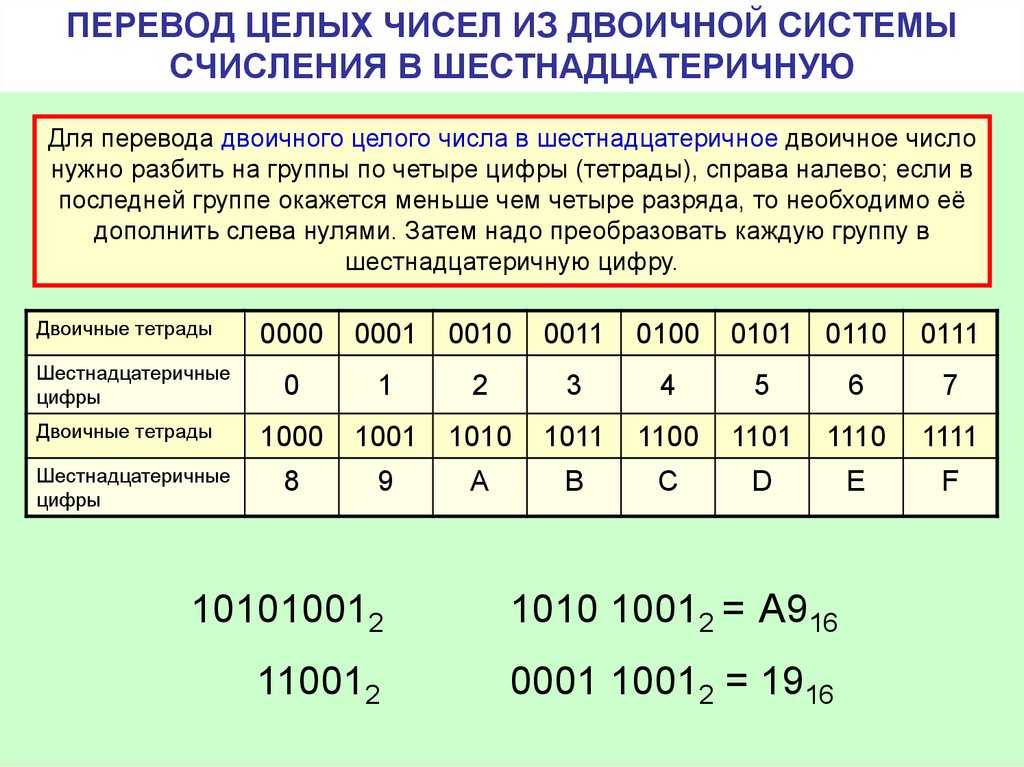
- Как F = 15 10 , 15 10 x 16 0 = 15 10
- E = 14 10 , 14 10 x 16 1 = 224 10
- D = 13 10 , 13 10 x 16 2 = 3328 10
Step 3: Add these numbers .
= 3328 10 + 224 10 + 15 10
= 3567 10
Теперь это время. Попробуйте преобразовать шестнадцатеричное число в десятичное.
Как добавить шестнадцатеричные числа?Измените алфавиты на их десятичные эквиваленты и добавьте шестнадцатеричные числа. Но прежде чем их писать, вы должны изменить их на шестнадцатеричные, так как сложение было в десятичных числах.
Пример шестнадцатеричного добавления:
Добавьте 1E4 и 33D .
Решение:
В этом вычислении мы сначала добавили 4 и D. Поскольку D = 13, тогда 4+13 = 17 10 , что равно 11 16 . Возьмем 1 как перенос в E. Тогда E = 14, поэтому 14+1+3 =18 10 = 12 16 . Наконец, 1+1+3 = 5 10 , что то же самое в шестнадцатеричной системе.
Как вычитать шестнадцатеричные числа?Также похоже на шестнадцатеричное сложение. Но вы должны быть осторожны в заимствовании чисел. При шестнадцатеричном вычитании, когда вы заимствуете 1 из предыдущего числа, вы добавляете 16 к текущему числу. Потому что 16 шестнадцатеричных равно 10 десятичных.
Пример шестнадцатеричного вычитания:Вычесть
5AF из F89.Решение:
В первом столбце число 9 меньше, чем F, которое на самом деле равно 15. Заимствуя 1 из предыдущей цифры 8, вы получаете следующие вычисления: 9 + 16 — 15 = 10 10 = А 16 . Во втором ряду снова требуется заимствование. 8 стало 7. Таким образом, при заимствовании 16 + 7 — A = 16 + 7 — 10 = 14 10 = D 16 . В последней строке есть E в первой строке, потому что она была уменьшена во время предыдущего заимствования. Итак, Е — 5 = 14 — 5 = 9 10 . То же самое и в шестнадцатеричном формате.
Заимствуя 1 из предыдущей цифры 8, вы получаете следующие вычисления: 9 + 16 — 15 = 10 10 = А 16 . Во втором ряду снова требуется заимствование. 8 стало 7. Таким образом, при заимствовании 16 + 7 — A = 16 + 7 — 10 = 14 10 = D 16 . В последней строке есть E в первой строке, потому что она была уменьшена во время предыдущего заимствования. Итак, Е — 5 = 14 — 5 = 9 10 . То же самое и в шестнадцатеричном формате.
Умножать шестнадцатеричные числа довольно сложно. Каждый раз, когда строка умножается на цифру, преобразования будут выполняться так же, как и в последний раз при сложении.
Пример шестнадцатеричного умножения:Умножить
44A на FA .Решение:
Для первого ряда (44A x A):
A, умноженное на A, на самом деле равно 10, умноженному на 10. Ответ 100 10 преобразуется в шестнадцатеричное число 64 16 . 4 остается внизу, а 6 идет в качестве переноса. Далее A x 4 = 40 10 . Теперь добавьте 6 переносов к этому 40 10 , ответ будет 46 10 = 2E 16 . E находится внизу, а 2 снова идет как перенос. Как A x 4 = 40 10 + 2 10 = 42 10 = 2A 16 . Ответ 2AE4.
Ответ 100 10 преобразуется в шестнадцатеричное число 64 16 . 4 остается внизу, а 6 идет в качестве переноса. Далее A x 4 = 40 10 . Теперь добавьте 6 переносов к этому 40 10 , ответ будет 46 10 = 2E 16 . E находится внизу, а 2 снова идет как перенос. Как A x 4 = 40 10 + 2 10 = 42 10 = 2A 16 . Ответ 2AE4.
Для второго ряда (44A x F):
A x F = 10 10 x 15 10 = 150 10 = 96 16 . Оставьте 6 внизу и поставьте 9 в качестве переноски. F x 4 = 15 10 x 4 10 = 60 10 . Добавьте 9 10 , получится 69 10 , что равно 45 16 . Наконец, используйте те же знания, чтобы снова умножить 4 x F и добавить перенос. Окончательный ответ в этой строке: 4456.
Добавьте 2AD4 и 4456 , используя метод сложения.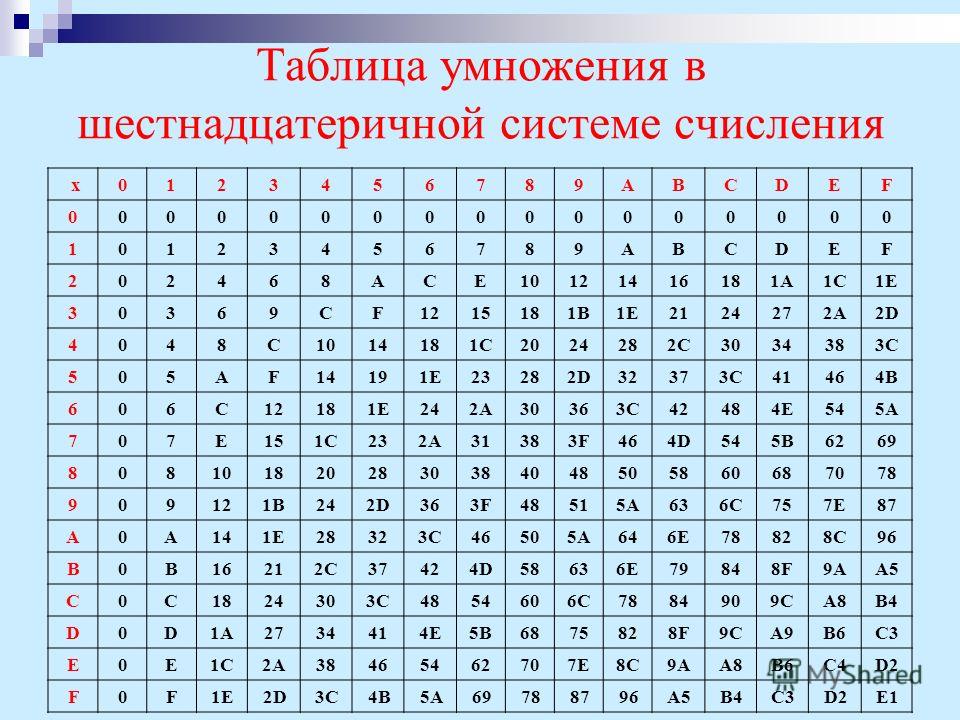
Лучший способ деления шестнадцатеричных чисел — преобразовать шестнадцатеричные числа в десятичные, выполнить деление в длинное число и затем преобразовать обратно. Или другой способ — разделить, используя сами шестнадцатеричные числа.
Для шестнадцатеричных чисел лучше составить таблицу умножения делителей и затем использовать эти значения для выполнения длинного деления.
В приведенном ниже примере представлены шестнадцатеричные числа.
Пример шестнадцатеричного деления:Разделить
DACE на E .Решение:
Шаг 1: Составьте таблицу умножения.
Multiple | Hex multiple | Decimal value |
E x 1 | E | 14 |
E x 2 | 1С | 28 |
E x 3 | 28 | 42 |
E x 4 | 38 | 56 |
E x 5 | 46 | 70 |
E X 6 | 54 | 84 0060 |
E x 7 | 62 | 98 |
E x 8 | 70 | 112 |
E x 9 | 7E | 126 |
E X 10 / E X A | 8C | 140 |
0004 Шаг 2: Выполнить деление в большую сторону.
= DACE / E
Так как D < E, то составьте пару DA. DA 16 = 218 10 . У нас нет такой большой суммы. Это означает умножение E на числа больше A.
Если мы умножим E на F, мы получим D2. На десятичном языке это 14 x 15 = 210.
Так что поместите это под DA. Если вычесть D2 из DA, ответ будет равен 8. Теперь уменьшите C. Чтобы разделить 8С на Е, умножаем Е на А. (см. таблицу).
В конце концов, остается только E. В соответствии с таблицей умножения, которую мы сделали, используйте E.
Шестнадцатеричное сложение, вычитание, умножение и деление
Здесь выполняются основные арифметические операции, такие как сложение, вычитание, умножение и деление для шестнадцатеричных чисел. В шестнадцатеричной системе счисления 16 цифр, начиная с 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Здесь выполняется сложение шестнадцатеричных чисел первый.
Содержание
- 1 шестнадцатеричное добавление
- 1.
 1 Гексадецимальная вычитание
1 Гексадецимальная вычитание- 1,1,1 Альтернативный метод добавления и вычитания шестнадцатеричных чисел
- 1,2 Умножение и разделение Гексадецимальных номеров
- 110
- 1,2 Умножение и подразделение Hexadecimal Numbers 111110 9009 9009 1,2. двумя указанными ниже шагами.
- Добавьте самые правые цифры каждого шестнадцатеричного числа.
- Найти модуль суммы цифр означает разделить сумму на 16, а остаток, полученный таким образом, является шестнадцатеричным эквивалентом суммы, а частное прибавляется к следующей сумме цифр справа. Выполняйте второй шаг, пока мы не добавим последние левые цифры. Давайте решим несколько примеров, чтобы понять процессы.
- Сначала найдите 15-е дополнение или 16-е вычитаемое.
- Сложите уменьшаемое и 15-е дополнение или 16-е вычитаемое, используя описанные выше шаги сложения шестнадцатеричных чисел.
- Отбросьте крайний левый перенос и добавьте 1 к самой правой цифре (только в случае дополнения до 15), и это будет окончательным решением.
- Преобразуйте каждое шестнадцатеричное число в десятичное число.
- Сложите или вычтите десятичные числа, полученные на первом шаге.
- Преобразование десятичного числа, полученного на втором шаге, в шестнадцатеричное число.
- Шестнадцатеричное число, полученное на третьем шаге, является окончательным ответом.
= 100760+40759 0
- Преобразование шестнадцатеричных чисел в десятичные.
- Умножение или деление шестнадцатеричных чисел.
- Десятичное число, полученное на втором шаге, должно быть преобразовано в шестнадцатеричное число, и это окончательное значение.
- Первичная вторичная и уловная память
- Дополнение, вычитание, умножение и деление бинарных чисел
- Дополнение, субтрокция, умножение и разделение из октября
9009
- 111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111110 гг. Шестнадцатеричный формат — определение, преобразование, примеры
9 3 770 EДесятичный в шестнадцатеричный — это система преобразования, которая часто используется в компьютерах и цифровых системах. Десятичная система счисления имеет основание 10. В ней всего 10 обозначений, то есть 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. В то время как шестнадцатеричная система работает с основанием 16, потому что в ней всего 16 обозначений: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и A, B, C, D, E , F.
 Для обозначения двузначных цифр 10, 11, 12, 13, 14, 15 в шестнадцатеричной системе счисления используются символы A, B, C, D, E, F соответственно. Давайте узнаем больше о методах преобразования десятичного числа в шестнадцатеричное и связанных с ним шагах преобразования.
Для обозначения двузначных цифр 10, 11, 12, 13, 14, 15 в шестнадцатеричной системе счисления используются символы A, B, C, D, E, F соответственно. Давайте узнаем больше о методах преобразования десятичного числа в шестнадцатеричное и связанных с ним шагах преобразования.1. Что такое преобразование десятичных чисел в шестнадцатеричные? 2. Как преобразовать десятичное число в шестнадцатеричное? 3. Преобразование десятичного числа в шестнадцатеричное с десятичной точкой 4. Часто задаваемые вопросы о преобразовании десятичных и шестнадцатеричных чисел Что такое преобразование десятичных чисел в шестнадцатеричные?
Преобразование десятичного числа в шестнадцатеричное — это процесс преобразования десятичного числа с основанием 10 в шестнадцатеричное число с основанием 16.
 При преобразовании числа из десятичной системы счисления в шестнадцатеричную систему счисления необходимо тщательно соблюдать основание числа. Число нужно делить на 16, пока частное не станет равным нулю. Обратите внимание на следующую таблицу, в которой показано представление десятичных и шестнадцатеричных чисел.
При преобразовании числа из десятичной системы счисления в шестнадцатеричную систему счисления необходимо тщательно соблюдать основание числа. Число нужно делить на 16, пока частное не станет равным нулю. Обратите внимание на следующую таблицу, в которой показано представление десятичных и шестнадцатеричных чисел.Как преобразовать десятичное число в шестнадцатеричное?
Чтобы преобразовать десятичное число в шестнадцатеричное, нам необходимо выполнить некоторые основные математические вычисления, используя следующие шаги.
- Шаг 1: Разделите заданное значение в десятичной системе счисления на 16 и запишите остаток.
- Шаг 2: Разделите частное на 16. Повторяйте это, пока не получите частное, равное нулю.
- Шаг 3: Используйте символы A, B, C, D, E, F вместо 10, 11, 12, 13, 14, 15 в остатках соответственно, где это необходимо.
- Шаг 4: Следуйте шаблону в обратном порядке, чтобы расположить все значения остатка.

- Шаг 5: Полученное число является требуемым шестнадцатеричным числом.
Формула преобразования десятичных чисел в шестнадцатеричные заданных чисел может быть выражена следующим образом:
P 10 = Q 16
, где P — десятичное число, а Q — шестнадцатеричное число.
Давайте разберемся, как преобразовать десятичное число в шестнадцатеричное с помощью следующего примера.
Пример: Преобразование 5386 в шестнадцатеричное число.
Решение: Мы будем использовать следующие шаги для преобразования 5386 в шестнадцатеричное.
- Шаг 1: Разделите 5386 на 16, чтобы получить 336 в качестве частного, и запишите остаток 10.
- Шаг 2: Разделите частное 336, полученное на предыдущем шаге, на 16, чтобы получить 21 в качестве следующего частного, и запишите остаток 0.
- Шаг 3: Разделите частное 21 на 16, чтобы получить 1 в качестве нового частного, и запишите остаток 5.

- Шаг 4: Разделите частное 1 на 16, чтобы получить 0 в качестве нового частного, и запишите остаток 1. Поскольку мы получили 0 в качестве частного, мы останавливаемся здесь.
- Шаг 5: Теперь поменяйте местами остатки и запишите объединенное число, которое они образуют. Мы должны помнить, что 10 записывается как А в шестнадцатеричной системе счисления.
- Шаг 6: Записав остатки в обратном порядке, получим 150А. Поэтому 5386 выражается как 150А в шестнадцатеричной системе счисления. Это можно записать как \((5386)_{10}\) равно \((150A)_{16}\).
Преобразование десятичного числа в шестнадцатеричное с десятичной точкой
Чтобы преобразовать любое дробное число в шестнадцатеричное, мы преобразуем целую часть обычным способом, как показано выше, и умножаем дробную часть (десятичную часть) на 16. Поскольку основание шестнадцатеричного числа равно 16, мы умножаем дробную часть на 16, пока она не станет 0. Нам нужно записывать целую часть этих произведений после каждого шага.
 Полученный результат представляет собой шестнадцатеричное число заданного дробного числа. Давайте разберемся в этом с помощью примера.
Полученный результат представляет собой шестнадцатеричное число заданного дробного числа. Давайте разберемся в этом с помощью примера.Пример: Преобразование дробного десятичного числа 18,765625 в шестнадцатеричное число.
Решение: Мы будем решать целую и дробную части по отдельности.
- Шаг 1: Сначала поработаем над целой частью. После того, как мы разделим 18 на 16, мы получим частное как 18 ÷ 16 = 1 и остаток как 2.
- Шаг 2: Теперь, когда мы делим 1 на 16, мы получаем частное как 16 ÷ 1 = 0, а остаток как 1.
- Шаг 3: Теперь давайте заметим объединенную форму остатков, перевернув их, что дает 12. Это будет записано как целая часть шестнадцатеричного значения.
- Шаг 4: После этого шага мы будем работать с дробной частью, которая равна 0,765625 .
- Шаг 5: Нам нужно умножить 0,765625 на 16, что даст 0,765625 × 16 = 12,25, в котором мы отметим целую часть 12. Это 12 выражается как C в шестнадцатеричной системе счисления.

- Шаг 6: Теперь мы снова умножим дробную часть этого произведения на 16. После умножения дробной части 0,25 на 16 получаем 0,25 × 16 = 4·9.0010
- Шаг 7: Теперь, после объединения целой части и дробной части шестнадцатеричной формы, мы получаем 12.C4. Поэтому 18.765625 равно 12.C4 в шестнадцатеричной системе счисления. Это означает, что \((18.765625)_{10}\) равно \((12.C4)_{16}\).
☛Связанные темы
- Преобразование шестнадцатеричной системы счисления в двоичную
- Десятичный в восьмеричный
- Восьмеричный в десятичный
- Двоичный код в шестнадцатеричный
- Десятичный в двоичный
- Двоичный код в десятичный
Часто задаваемые вопросы о преобразовании десятичных чисел в шестнадцатеричные
Что такое преобразование десятичных чисел в шестнадцатеричные?
Преобразование десятичного числа в шестнадцатеричное — это процесс преобразования десятичного числа с основанием 10 в шестнадцатеричное число с основанием 16.

Какое базовое значение в десятичной и шестнадцатеричной системе счисления?
Базовое значение десятичного числа представлено 10, а шестнадцатеричное базовое значение представлено 16. Например, \((592)_{10}\) = \((250)_{16}\).
Как преобразовать десятичное число в шестнадцатеричное?
Чтобы преобразовать десятичное число в шестнадцатеричное, мы делим десятичное число на 16, поскольку 16 является базовым значением шестнадцатеричных чисел. Продолжаем делить, пока частное не станет равным нулю. Остатки записывают и записывают в обратном порядке в объединенной форме. Следует отметить, что значения 10, 11, 12, 13, 14, 15 выражаются как A, B, C, D, E и F в шестнадцатеричной форме.
Как преобразовать десятичное число 63 в шестнадцатеричное?
Чтобы преобразовать десятичное число 63 в шестнадцатеричное, мы воспользуемся методом деления. После деления десятичного числа 63 на 16 мы получим остаток как 15 и частное как 3. Здесь мы запишем остаток 15 как F.
 На следующем шаге мы разделим 3/16, где частное равно 0, а остаток равен 3. При объединении цифр в обратном порядке шестнадцатеричное значение 63 равно 3F. Следовательно, \((63)_{10}\) равно \((3F)_{16}\).
На следующем шаге мы разделим 3/16, где частное равно 0, а остаток равен 3. При объединении цифр в обратном порядке шестнадцатеричное значение 63 равно 3F. Следовательно, \((63)_{10}\) равно \((3F)_{16}\).Какое значение имеет число 50 в шестнадцатеричной системе счисления?
Чтобы преобразовать 50 из десятичного числа в шестнадцатеричное, мы будем делить 50 на 16, пока не получим 0 в частном. При делении десятичного числа 50 на 16 мы получим остаток как 2 и частное как 3. На следующем шаге мы разделим 3/16, где полученное частное равно 0, а остаток равен 3. Комбинируя цифры в обратном порядке, мы получаем шестнадцатеричное значение 50 как 32. Следовательно, \((50)_{10}\) равно \( (32)_{16}\).
Преобразование числа 315 из десятичного в шестнадцатеричное.
Чтобы преобразовать 315 из десятичного в шестнадцатеричное, мы начнем делить 315 на 16, пока не получим частное 0. После деления десятичного числа 315 на 16 мы получим остаток 11 и частное 19. На следующем шаге мы разделим 19/16, где полученное частное равно 1, а остаток равен 3.
 Теперь, после деления 1 на 16, мы получим 0 в частном и 1 в остатке. При объединении цифр в обратном порядке шестнадцатеричное значение 315 получается 13B. Следует отметить, что когда мы записываем объединенные остатки в обратном порядке, мы записываем шестнадцатеричное значение для 11, которое равно B. Следовательно, \((315)_{10}\) равно \((13B)_{ 16}\).
Теперь, после деления 1 на 16, мы получим 0 в частном и 1 в остатке. При объединении цифр в обратном порядке шестнадцатеричное значение 315 получается 13B. Следует отметить, что когда мы записываем объединенные остатки в обратном порядке, мы записываем шестнадцатеричное значение для 11, которое равно B. Следовательно, \((315)_{10}\) равно \((13B)_{ 16}\).Системы счисления
Системы счисленияСистемы счисления
Десятичная система счисления (основание 10)
- Использует 10 цифр: 0 9
- 125 = 1*10 2 + 2*10 1 + 5*10 0
Двоичная система счисления (основание 2)
- Использует 2 цифры: 0 и 1
- 110101 = 1*2 5 + 1*2 4 + 0*2 3 + 1*2 2 + 0*2 1 + 1*2 0 0010
Шестнадцатеричная система счисления (основание 16)
- Использует 16 символов: 0 9, A, B, C, D, E, F
- 19F = 1*16 2 + 9*16 1 + 15*16 0
Десятичный
Двоичный
Шестнадцатеричный
0
0000
0
1
0001
1
2
0010
2
3
0011
3
4
0100
4
5
0101
5
6
0110
6
7
0111
7
8
1000
8
9
1001
9
10
1010
А
11
1011
Б
12
1100
С
13
1101
Д
14
1110
Е
15
1111
Ф
Преобразование двоичного => шестнадцатеричное
Начиная справа, разделите 0 и 1 на группы по 4.
 Дополните слева нулями, если необходимо, чтобы сформировать группу из 4. Найдите
соответствующее шестнадцатеричное значение из таблицы.
Дополните слева нулями, если необходимо, чтобы сформировать группу из 4. Найдите
соответствующее шестнадцатеричное значение из таблицы.11011011100011 = 0011 0110 1110 0011 = 3 6 E
9 3 7770 E 3 7770 E
9 3 770 E 9 3 70 . - 111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111110 гг. Шестнадцатеричный формат — определение, преобразование, примеры
Умножить каждый символ на базовое значение, возведенное в позиционную степень а затем добавить каждый продукт.
11011 = 1*2 4 + 1*2 3 + 0*2 2 + 1*2 1 + 1*2 0 = 27
5
5
2AF = 2*16 2 + 10*16 1 + 15*16 0 = 687
Разделите на базовое значение, пока частное не станет равным 0.
 При преобразовании в шестнадцатеричный формат
преобразовать остатки в шестнадцатеричный.
При преобразовании в шестнадцатеричный формат
преобразовать остатки в шестнадцатеричный.415 (в десятичном формате) = 19F (в шестнадцатеричном формате)
Если первая цифра 0 7, положительное шестнадцатеричное число.
Если первая цифра 8 F, отрицательное шестнадцатеричное число.
- Переключить все 0 на 1 и 1 на 0 (нахождение дополнения до 1)
- Добавить 1
- Вычесть число из FFFFFFFF
- Добавить 1
- Преобразование цифры 1 st каждого числа в двоичное число
- Сложить двоичные значения вместе
- Если последние два бита переноса совпадают, переполнения нет.
- Если они разные, переполнение.
- Сгруппируйте цифры двоичного числа в наборы из 4 цифр (или битов). При необходимости добавьте ведущие нули в последнюю группу из 4 слева.
- Преобразуйте двоичные числа в каждом наборе из 4 в эквивалентные шестнадцатеричные цифры.
- Запишите каждую шестнадцатеричную цифру как 4-битное двоичное число
- Помните, что 0 в шестнадцатеричном формате равно 0000 в двоичном!
Вопрос 1: Найдите сумму шестнадцатеричных чисел A23 16 и 1B1 16 ?
Решение: Добавление A23 16 и 1B1 16 показано ниже.
цифра (с самого справа) Остаток Коэффициент 3 + 1 = 4 4 % 16 = 4 4 /16 = 0 9 4 /16 = 0 (QUITIIVE В + 0 = 13 13 % 16 = 13 (Г) 13/16 = 0 (Добавлено коэффициент) A + 1+ 0 = 11 11 % 16 = 11 (B) 11 /1 6 = 0 Таким образом, добавление A23 A23 16 + 1B1 16 = BD4 16 .

Вопрос 2: Найдите сумму шестнадцатеричных чисел 2AC 16 и FAB 16 ?
Решение: Решение вышеуказанной проблемы показано ниже:
Цифра (начиная справа) Остаток Коэффициент C + B = 23 23 % 16 = 7 23/16 = 1 (Конечное добавлено) A + A + 1 = 21 21 % 16 = 16 = 16 = 16 = 16 = 16 = 16 = 16 = 16 = 16. 5 21/16 = 1 (Добавлено коэффициент) 2 + F + 1 = 18 18 % 16 = 2 18 /16 = 1 (коэффициент добавлен) 0 + 0 + 1 = 1 1 % 16 = 1 1 / 16 = 0 Таким образом, сумма шестнадцатеричных чисел 2AC 16 и FAB 16 это 1257 16 .
Вопрос 3: Найдите сложение A2B.D4 16 и 247,65 16 ?
Solution: The solution of the above problem is performed as:
Digit (Starting from Right) Remainder Quotient 4 + 5 = 9 9 % 16 = 9 9 / 16 = 0 (прибавленное частное) D + 6 + 0 = 19 19 % 16 = 3 19 /16 = 1 (коэффициент добавлен) B + 7 + 1 = 19 19 % 16 = 3 19 /16 = 1 (коэффициент добавил.  ) 2 + 4 + 1 = 7
) 2 + 4 + 1 = 77 % 16 = 7 7 / 16 = 0 (добавленное частное) A + 2 + 0 = 12 12 % 16 = 100 7 9 0 / 16 = 0 Таким образом, сумма равна C73,39 16 .
Шестнадцатеричное вычитание
Вычитание шестнадцатеричных чисел выполняется с помощью следующих шагов.
Вопрос 4: Вычтите шестнадцатеричные числа ABC 16 и A3B 16 ?
Решение: здесь мы найдем вычитание двух заданных чисел с использованием дополнения до 15. Таким образом, решение для 15-кратного дополнения A3B 16 выглядит следующим образом:
15 – A = 5
15 – 3 = C (в шестнадцатеричной системе счисления 12 = C)
15 – B = 4
Таким образом, дополнение A3B до 15 равно 5C 906 16 16 .

Теперь добавьте ABC 16 и 5C4 16 .
цифр (начиная с справа) Остаток Коэффициент C + 4 = 16 16 % 16 = 0 16/16 = 1 9 16 /16 = 1 9009 99916 /16 = 1 (добавленное частное) B + C + 1 = 24 24 % 16 = 8 24 / 16 = 1 (добавленное частное) A + 5 + 1 = 16 16 0 % 16/16 = 1 (коэффициент добавлено) 0 + 0 + 1 = 1 1 % 16 = 1 1 /16 = 0 Остальные — 1080 16 . Теперь нам нужно отбросить крайний левый перенос 1, а затем добавить 1 к самой правой цифре.
Так 1080 16 становится 80 16 + 1 = 81 16
Следовательно, ABC 16 – A3B 16 = 81 16 .
Мы можем решить ту же задачу, используя 16-е дополнение вычитаемого.
 Итак, давайте решим задачу этим методом.
Итак, давайте решим задачу этим методом.The 16’s complement of A3B 16
= 15’s complement of A3B 16 + 1
= 5C4 16 + 1
= 5C5 16
Now add ABC 16 and 5C5 16 .
цифра (с самого справа) Остаток Коэффициент C+5 = 16 17%16 = 1 16/16 = 1 (QUITIIVE C+1=24 24%16=8 24/16=1 (прибавленное частное) A+5+1=16 16%16=0 16/16=1 (Добавленное частное) 0+0+1=1 1%16=1 1/16=0 Таким образом, остаток равен 1081 16 . Теперь мы должны отбросить крайний левый перенос 1, тогда полученное число будет окончательным значением.
Следовательно, ABC 16 – A3B 16 =81 16 .
Вопрос 5: Вычтите шестнадцатеричные числа 67A 16 и 549 16 ?
Решение: Решение этой задачи выглядит следующим образом:
Используя дополнение до 15 вычитаемого:
Дополнение до 15 числа 549 16 находится как:
15-5=10 (в шестнадцатеричной системе счисления 10=A)
15-4=11 (в шестнадцатеричной системе счисления 11=B)
15-9=6
Итак, дополнение до 15 AB6 16 .

Теперь добавьте 67A 16 и AB6 16 .
цифра (с справа) Остаток Коэффициент A+6 = 16 16%16 = 0 16/16 = 1 (QUOTIENT) 70057 (QUITIENT) 70057 (QUITIIVE Б+1=19 19%16 = 3 19/16 = 1 (коэффициент добавлен) 6+a+1 = 17 17%16 = 1 17/16 = 1 (коэффициент добавил. ) 0+0+1=1 1%16=1 1/16=0 Таким образом, остаток равен 1130 16 . Теперь отбросьте левый крайний перенос 1 и добавьте 1 к самой правой цифре.
Следовательно, 1130 16 становятся 130 16 и после добавления 1 мы получаем 131 16 .
Со 67А 16 – 549 16 = 131 16 .
By using 16’s complement of subtrahend:
16’s complement of 549 16
= 15’s complement of 549 16 + 1
= AB6 16 +1
= AB7 16
Now add 67A 16 и AB7 16 .

Цифра (начиная справа) Остаток Частное A+7=17 17%16 = 1 17/16 = 1 (коэффициент добавлен) 7+B+1 = 19 19%16 = 3 19/16 = 1 (коэффициент добавил. ) 6+A+1=17 17%16=1 17/16=1 (прибавленное частное) 0+0+1=1 1%16=1 1/16= 0 Таким образом, расставив остаток, мы получим 1131 16 . Теперь отбросьте крайний левый перенос, и мы получим окончательное решение.
Следовательно, после отбрасывания переноса конца 1131 16 .
Получаем 131 16 .
Вопрос 6: Решите ABC 16 +FAB 16 -2AC 16 ?
Решение: сначала складываем ABC 16 и FAB 16 , затем вычитаем 2AC 16 из суммы ABC 16 и FAB 16 .

Цифра (начиная справа) Остаток Частное C+B=23 23%16=7 23/16=1 (Добавлено частное) B+A+1=22 22%16=22 22%16=22 1(добавленное частное) A+F+1=26 26%16=10(A) 26/16=1 (добавленное частное) 0+0+1=07 9006=1 9006 1%16=1 1/16=0 Таким образом, сумма ABC 16 и FAB 16 равна 1A67 16 .
Теперь вычтите 1A67 16 и 2AC 16 .
Дополнение до 15 для 2AC получается как:
15-2=13 (в шестнадцатеричной системе счисления 13=D)
15-A=5
15-C=3
Таким образом, дополнение до 15 для 2AC 606 90 это D53 16 .
Теперь добавьте 1A67 16 и D53 16 .
Цифра (начиная справа) Остаток Частное 7+3=10 10%16=10(A) 10/16=0 (добавленное частное) 6+5+0=11 11%16=11(B) 11/16=0 (добавленное частное) +0=23 23%16=7 23/16=1 (Добавленное частное) 1+0+1=2 2%16=2 2/16=0 Получаем 27BA 16 .
 После отбрасывания 1 из крайней левой цифры 27BA 16 и добавления 1.
После отбрасывания 1 из крайней левой цифры 27BA 16 и добавления 1.Следовательно, 27BA 16 становится 17BA 16 и 17BA 16 +1=17BB 16 .
ABC 16 +FAB 16 -2AC 16 = 17BB 16 .
Альтернативный метод сложения и вычитания шестнадцатеричных чисел
Существует также альтернативный метод сложения и вычитания шестнадцатеричных чисел. Шаги следующие:
Вопрос 7: Добавьте шестнадцатеричные числа A21 16 и 2B1 16 ?
Решение: Чтобы сложить два вышеуказанных шестнадцатеричных числа, мы должны выполнить описанные выше шаги:
Преобразовать A21 16 и 2B1 16 в десятичные числа:
A21 16
= AX16 2 +2 × 16 1 +1 × 16 0
= 10 × 256+2 × 1693 9065
= 2560+32+1
= 2593 9065
= 2560+32+1
= 2593 9065
= 2560+32+1
= 2593 9065
= 2560+32+1
9000 493 90652B1 16
= 2 × 16 2 +BX16 1 +1 × 16 0
= 2 × 256+11 × 16+1 × 10005
= 516+516+= 512+176+
= 512+
9000 4061+= 516+= 512+
= 512+
= 512+
= 512+
= 512+
= 512+
.

= 689 10
ADD 2593 10 и 689 10 :
2593 10 + 689 10 = 3282 10 9 999 10 = 3282 10 9 999 10 = 3282 9 999 10 = 3282 9 .0609
Конвертировать 3282 10 в шестнадцатеричный номер:
16 | 3282 Остаток
16 | 205 2
16 | 12 13 (D)
16 | 0 12 (C)
Таким образом 16 .
Вопрос 8: Вычтите шестнадцатеричные числа ABC 16 и A8C 16 ?
Решение: преобразовать шестнадцатеричные числа ABC 16 и A8C 16 в десятичные цифры:
ABC 16
= AX16 2 +BX16 1 +CX16 0
= 1066 +256 +256 +256 +256 +256 +256 +256 +256 +
+256 +. +176+12 = 2748 10
A8C 16
= AX16 2 +8 × 16 1 +CX16 0 9000
= 100760+CX16 0
= 100760+40759 0
= 100760+80759 0
= 100760.

= 2560+128+12
= 2700 10
Вычесть 2749 10 и 2668 10 :
2748 10 – 2700 10 = 48 10
Convert 48 10 into hexadecimal number:
16|81 Remainder
16|3 0
16|0 3
Итак, ответ 30 16 .
Умножение и деление шестнадцатеричных чисел
Альтернативный метод нахождения умножения или деления шестнадцатеричных чисел показан ниже:
Вопрос 9: Найдите произведение шестнадцатеричных чисел 11A 16 и 5A3 16 ?
Решение: Решение находится вышеуказанным методом как:
Преобразование шестнадцатеричных чисел в десятичные числа:
11A 16
= 1 × 16 2 +1 × 16 1 +AX16 0
= 1 × 256+1 × 16+10 × 1
= 256+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16+16.

= 282 10
5A3 16
= 5 × 16 2 +AX16 1 +3 × 16 0
= 5 × 256 +10 . 1280+160+3
= 1443 10
Теперь умножьте 282 10 и 1443 10 :
282 09 10x 1443 10 = 406926 10
Change 406926 10 into hexadecimal number:
16|406926 Remainder
16|25432 14(E)
16|1589 8
16|99 5
16|6 3
|0 6
Итак, произведение 11A 16 и 5A3 16 — это 6358E 16 .
Вопрос 10: Найдите деление ABC 16 на A1 16 ?
Solution: The solution is as follows:
Change the hexadecimal numbers into decimal numbers:
ABC 16
= Ax16 2 +Bx16 1 +Cx16 0
= 10×256 +11×16+13×1
= 2560+176+12
= 2748 10
A1 16
= AX16 1 +1 × 16 0
= 10 × 16+1 × 1
= 160+1
= 161 10
Дип.

2748 10 /161 10 = 17 10 (около)
Теперь измените 17 10 в гексадецимальный номер:
16 | 17 Остальная ответ 11 16 .
См. Также:
Преобразование шестнадцатеричной => двоичной
Преобразование двоичного/шестнадцатеричного => десятичного
Преобразование десятичного числа => двоичное/шестнадцатеричное
0 16 Ö 1 R1 => 1 16 Ö 25 R9 => 9 16 Ö415 R15 => FАрифметика
Двоичное сложение
1 11 0 0 1 1 1 + 0 + 1 + 0 + 1 + 1 0 1 1 10 11 111111 11010110 + 1101101 101000011Двоичное вычитание
02 0 1 1 10 - 0 - 0 - 1 - 1 0 1 0 1 1 02202 02 1100101110 - 11010001 1001011101Шестнадцатеричное сложение
А27КБ4 39КДФ106 + 6E3095 + A6F278C 110АД49 443Д1892
Шестнадцатеричное вычитание
A52CF3 3B0029 - 2Б7169 - 1765А4 79ББ8А 239А85
Хранение
Основное хранилище памяти компьютера состоит из битов (также называемых двоичными цифрами).

1 бит => двоичный 0 или 1
1 байт => 8 бит => 2 шестнадцатеричных цифры
1 полуслово => 2 байта => 16 бит => 4 шестнадцатеричных цифры
1 полное слово => 4 байта => 32 бита => 8 шестнадцатеричных цифр => 2 полуслова
1 двойное слово => 8 байтов => 64 бита => 16 шестнадцатеричных цифр => 2 полных слова
Наибольшее положительное шестнадцатеричное значение, которое можно сохранить: 7 FFFFFFF
Наибольшее положительное двоичное значение: 0 111111111111111111111111111111
Отрицательные числа сохраняются путем добавления до двух абсолютного числа. значение числа.
Чтобы найти двоичное дополнение до 2:
100111100 => 011000011 + 1 011000100Чтобы найти шестнадцатеричное дополнение до 2:
FFFFFFFF FFFFFFFF FFFFFFFF - 002BCF06 - 00000001 - FFD430FA FFD430F9 FFFFFFFE 002BCF05 + 1 + 1 + 1 FFD430FA FFFFFFFF 002BCF06
Арифметика с использованием дополнения до двух:
Переполнение:
Происходит, когда число становится слишком большим для его схемы представления.

Для проверки на переполнение:
00 <= НЕТ переполнения 729B6320 7 => 0111 + 8A5C973C 8 => 1000 FCF7FA5C 1111 10 <= переполнение 92B176C0 9 => 1001 + 859237A4 8 => 1000 1843AE64 0001 01111 <= переполнение 328AC105 328AC105 3 => 0011 - 807B96AF => 7F846951 => + 7F846951 7 => + 0111 Б20Ф2А56 1011Шестнадцатеричные числа и учебник по шестнадцатеричной системе счисления
Понимание двоичных чисел важно не меньше, чем понимание шестнадцатеричных или шестнадцатеричных чисел. Прежде чем мы углубимся в подробности о шестнадцатеричных числах, я настоятельно рекомендую вам прочитать статью о двоичных числах.

Из него вы узнаете, почему двоичные числа используются в цифровых системах. Это поможет вам понять, почему шестнадцатеричные числа также часто появляются в цифровых системах. Вы также получите краткий обзор десятичной системы (и систем счисления в целом). Наконец, вы научитесь читать двоичные данные, что поможет вам понять, как преобразовывать двоичные данные в шестнадцатеричные.
Как я уже говорил, если вы новичок в цифровой электронике, вам обязательно нужно ее прочитать.
И если вы не новичок, то хороший обзор.
Давайте сломаем шестнадцатеричный код и узнаем о шестнадцатеричных числах!
После двоичных чисел наиболее важными в цифровых приложениях являются шестнадцатеричные числа или числа с основанием 16.
Слово шестнадцатеричное происходит от греческого корня hex — шесть, и латинского корня deci — десять. Следовательно, слово шестнадцатеричный относится к шестнадцати.
Шестнадцатеричные числа используют систему с основанием 16, что означает, что позиционные множители в шестнадцатеричной системе являются степенями 16: 16 0 = 1, 16 1 = 16, 16 2 = 256 и так далее.
 Это похоже на десятичную систему, с которой все были знакомы, только вместо степеней 10 мы имеем дело со степенями 16.
Это похоже на десятичную систему, с которой все были знакомы, только вместо степеней 10 мы имеем дело со степенями 16.Таблица ниже пригодится для определения различных степеней 16. Боже, как быстро они растут !
Обратите внимание, что MSD означает старшую значащую цифру, а LSD — младшую значащую цифру. Извините за разочарование, ЛСД не наркотик — по крайней мере, не в этом посте. 9Рисунок 1: Различные степени числа 16 Однако следующие 6 представлены первыми буквами алфавита: A, B, C, D, E и F.
Первые 16 цифр шестнадцатеричной системы даны в таблице ниже вместе с их десятичной и бинарные эквиваленты.
Рисунок 2: шестнадцатеричные числа и их десятичные и двоичные эквиваленты.
Если вы не слишком хорошо знакомы с шестнадцатеричной системой счисления, использование букв для представления чисел может сначала показаться странным. Имейте в виду, однако, что любая система счисления — это всего лишь набор последовательных символов.
 Форма символов не имеет значения, если вы понимаете, что они означают.
Форма символов не имеет значения, если вы понимаете, что они означают.Помните также, что независимо от системы счисления каждая цифра должна быть представлена одним символом.
Станьте Создателем, которым вы были рождены. Попробуйте Академию Arduino БЕСПЛАТНО!
Если бы мы использовали символы, которые делают десятичное число десять (а не A) при записи чисел в шестнадцатеричном формате, было бы трудно сказать, имели ли мы в виду 10 в десятичном виде или 10 в шестнадцатеричном, что равно 16 в десятичной системе.
Возможно, для этого есть еще более важная причина, о которой мы расскажем в следующем разделе.
Прямо сейчас может быть легко подумать что-то вроде , зачем возиться с шестнадцатеричными числами? База 16 странная и кажется сложной…
Или, может быть, вы уже поняли преимущества использования шестнадцатеричных чисел. Если нет, вы сделаете это через минуту.
Перевод шестнадцатеричных чисел в двоичные на рисунке 2 указывает на очень важную причину популярности шестнадцатеричных чисел.

Шестнадцатеричные числа way более компактны, чем двоичные, и более компактны, чем десятичные числа. Шестнадцатеричные числа упаковывают больше информации в меньшее количество цифр.
Кроме того, двоичные числа трудно читать и записывать, потому что их легко отбросить или немного переставить.
Из-за этого шестнадцатеричный формат широко используется в компьютерных и микропроцессорных приложениях.
Вы наверняка сталкивались с синим экраном на своем компьютере после сбоя. Кроме того, вы часто будете видеть загадочное сообщение вместе с некоторыми шестнадцатеричными числами, такими как 0xa56b170f.
Шестнадцатеричные числа относятся к ячейкам памяти и данным. Если бы ПК выдал это в двоичном виде, весь экран был бы заполнен 1 и 0.
Префикс 0x говорит нам, что это шестнадцатеричное число. Языки программирования C и Java используют эту запись, но вы также можете увидеть шестнадцатеричное число с префиксом 0h.
Почти все размеры компьютерных данных кратны 4.
Преобразование двоичных чисел в шестнадцатеричные Поскольку основание 16 является степенью числа 2 (например, 4), преобразование из двоичного в шестнадцатеричное и наоборот, как мы вскоре увидим, тривиально.
Поскольку основание 16 является степенью числа 2 (например, 4), преобразование из двоичного в шестнадцатеричное и наоборот, как мы вскоре увидим, тривиально.Как обычно, проще всего преобразовать двоичное число в шестнадцатеричное или наоборот с помощью калькулятора. Однако после прочтения этого раздела вы сможете сделать это почти так же быстро.
Вы должны знать все шестнадцатеричные числа от 0 до F (от 0 до 15).
Рисунок 2 показывает нам, что для каждого возможного 4-битного двоичного числа существует шестнадцатеричный эквивалент.
Чтобы преобразовать двоичное число в шестнадцатеричное, просто разбейте двоичное число на 4-битные группы, начиная с младшего бита (крайний правый бит). Затем замените каждую 4-битную группу ее шестнадцатеричным эквивалентом.
Двигаясь влево, вы можете заметить, что в последней группе осталось менее 4 двоичных цифр.
Без пота. Просто дополните последнюю группу достаточным количеством начальных нулей, чтобы получить 4 бита, а затем преобразуйте в шестнадцатеричный формат.

Давайте сделаем пару примеров, чтобы проиллюстрировать это.
Пример 1
Преобразование 1100101001010111 в шестнадцатеричное число.
Решение:
Сначала мы разбиваем двоичное число на группы по 4 бита:
1100 1010 0101 0111
Затем мы просто находим шестнадцатеричные эквиваленты каждой из групп из 4 двоичных цифр, начиная с слева:
1100 1010 0101 0111
| | | |
C A 5 7
1100 = 12 в десятичном виде, то есть C в шестнадцатеричном формате. Следуя аналогичному подходу, мы получаем A для следующей группы, 5 для следующей и, наконец, 7 для последней группы.
Теперь мы пишем CA57 или 0xCA57, чтобы знать, что это шестнадцатеричное число. Бам, бам, спасибо, мэм.
Пример. 2
Преобразовать 11100010100110 в шестнадцатеричный формат.
Решение:
Начиная справа (младший бит), мы разбиваем двоичное число на группы по 4 бита:
11 1000 1010 0110
Поскольку крайняя левая группа состоит только из 2 цифр, мы дополняем ее двумя нулями:
0011 1000 1010 0110
Теперь возьмем шестнадцатеричный эквивалент каждой из 05 групп: 9005:
0011 1000 1010 0110
| | | |
3 8 A 6
Теперь запишем 0x38A6.

Обратите внимание: хотя очевидно, что если строка цифр содержит любую из букв от A до F, строка является шестнадцатеричным числом, не все шестнадцатеричные числа будут содержать буквы. Поэтому, чтобы избежать путаницы, особенно в этом случае, рекомендуется использовать префикс 0x при написании или вводе шестнадцатеричных чисел.
Общий алгоритм преобразования двоичного числа в шестнадцатеричное выглядит следующим образом:
Приведенные выше примеры показывают, что это также просто и тривиально.
Просто повторив алгоритм в обратном порядке, мы можем преобразовать шестнадцатеричное число в двоичное.
Давайте сделаем быстрый пример.

Пример. 3
Преобразование 0xFF09 в двоичный формат.
Решение:
Начиная с крайнего левого, мы запишем каждую шестнадцатеричную цифру в эквивалентном ей двоичном формате: получить: 1111111100001001 или 1111 1111 0000 1001, если мы разобьем для облегчения чтения.
Общий алгоритм преобразования двоичного числа в шестнадцатеричное выглядит следующим образом:
Переход от десятичного числа к шестнадцатеричному немного сложнее, чем от двоичного к шестнадцатеричному, но, как мы увидим, это похоже на преобразование десятичного числа в двоичное, и это не так сложно сделать.
Существует два способа преобразования десятичных чисел в шестнадцатеричные: сумма степеней 16 и повторное деление на 16. Поговорим об обоих.
Сумма степеней 16
Также называемый методом суммы взвешенных шестнадцатеричных цифр, этот метод хорош для более простых преобразований (примерно до 3 шестнадцатеричных цифр).

Например, давайте преобразуем 35 в шестнадцатеричное с помощью этого метода.
При осмотре заметим, что 35 = 32 + 3
Заметим также, что (2 х 16) = 32 и что (3 х 1) = 3.
в первой степени) и 3 единицы (или 3 шестнадцати в нулевой степени).
Следовательно, 32 в десятичном виде = 0x23.
Помните, что любое число, возведенное в нулевую степень, равно единице.
Повторное деление на 16
Приведенный выше метод может стать громоздким для больших чисел.
Разделите десятичное число на 16 и запишите остаток. Обязательно запишите остаток в виде шестнадцатеричной цифры.
Повторяйте этот процесс до тех пор, пока частное не станет равным 0. Последний остаток — это старшая цифра шестнадцатеричного числа.
Пример. 4
Предположим, мы хотим преобразовать 31 581 в шестнадцатеричное число.
31 581 / 16 = 1973, остаток 13 (младшая значащая цифра, или LSD).

1,973 / 16 = 123, остаток 5
123 / 16 = 7, остаток 11
7 / 16 = 0, остаток 7 (старшая значащая цифра или MSD)
Теперь запишем все остатки в виде шестнадцатеричных цифр: 13 = 0xD, 5 = 0x5, 11 = 0xB, 7 = 0x7
Если перечислить их в правильном порядке (MSD крайний слева, LSD крайний справа), мы получим:
31,581 = 0x7B5D
Один из способов сделать это — сначала преобразовать шестнадцатеричное число в двоичное, а затем преобразовать в десятичное.
Другой способ сделать это преобразование состоит в том, чтобы умножить каждую цифру на ее степень 16 позиционного множителя и сложить произведения вместе.
Приведенный ниже пример помогает это проиллюстрировать.
Пример. 5
Преобразование 0x7C6 в десятичное число.
Решение:
Сначала отметим позиционный вес каждой шестнадцатеричной цифры, начиная с LSD: 6 имеет вес 16 0 , C имеет вес 16 1 , а 7 имеет вес 16 2 .

Теперь умножаем каждую цифру на ее позиционный вес. Начнем с MSD:
7 x 16 2 = 7 x 256 = 1792
C x 16 1 = 12 x 16 = 192
6 x 16 = 6 x 7 0 1 = 9
Далее мы суммируем наши результаты: 1792 + 192+ 6 = 1990
Извлекаем «Hex» из шестнадцатеричных чиселИтак, теперь мы знаем, как шестнадцатеричные числа связаны с цифровыми схемами и как конвертировать шестнадцатеричные числа в бинарный и наоборот. Мы также знаем, как преобразовывать шестнадцатеричные числа в десятичные числа и наоборот.
Поскольку шестнадцатеричные числа довольно распространены в мире компьютеров и электроники, я уверен, что они появятся снова.
Только теперь вы узнаете, как с ними бороться. И в качестве бонуса, в следующий раз, когда вы столкнетесь с синим экраном смерти, вы сможете перевести эти шестнадцатеричные цифры в адрес (а) памяти, где произошла ошибка (ы).
Прокомментируйте и расскажите, с чем вы предпочитаете работать: с шестнадцатеричным или двоичным кодом?
Или вы можете прокомментировать и сообщить мне, о каких других темах вы хотели бы услышать.

- 1.


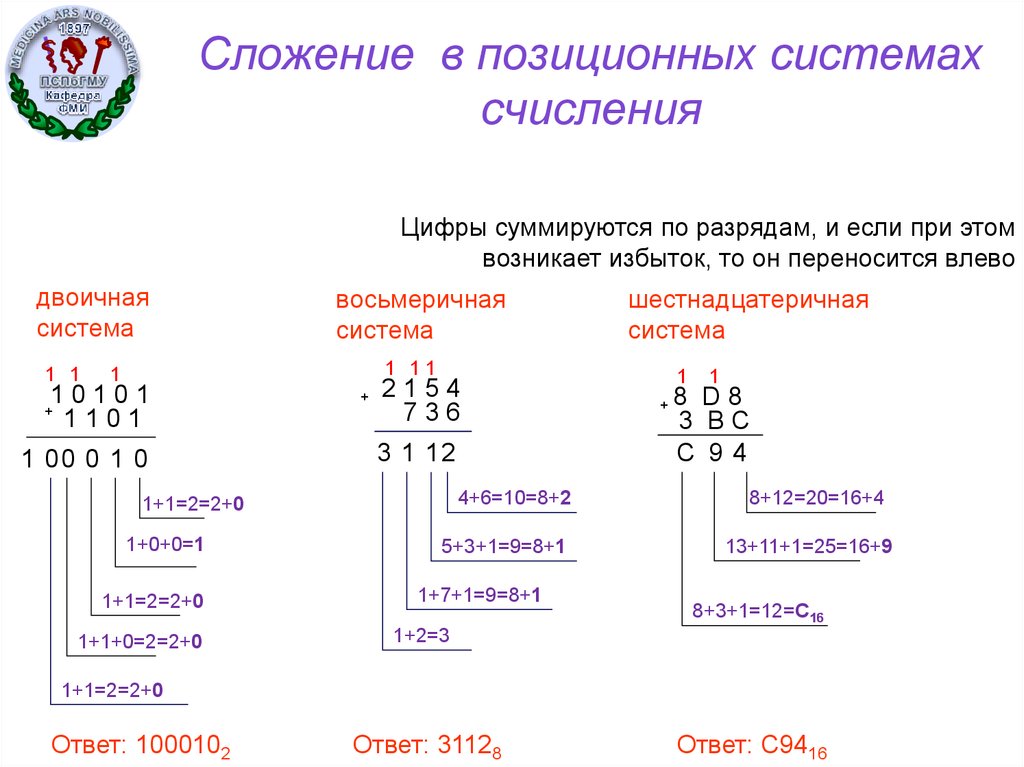 Из этого можно сформулировать правило:
Из этого можно сформулировать правило: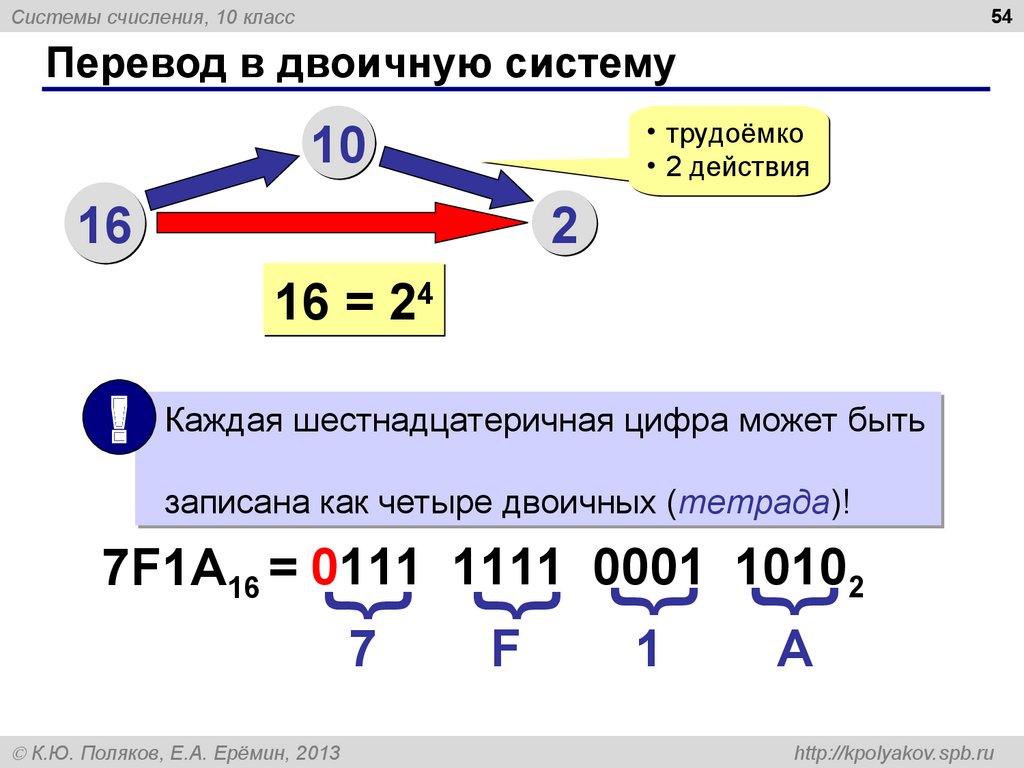


 д.
д.

 д.
д.

 Тогда разряд 2 рассчитывается как 10 — 1 = 1;
Тогда разряд 2 рассчитывается как 10 — 1 = 1;
 Тогда 1716 — В16 = 23 — 11 = 12 = С16;
Тогда 1716 — В16 = 23 — 11 = 12 = С16; Здесь значение разряда 2 множителя сформировано по принципам формирования значения числа в позиционных системах счисления;
Здесь значение разряда 2 множителя сформировано по принципам формирования значения числа в позиционных системах счисления;
 Здесь значение разряда 2 множителя сформировано по принципам формирования значения числа в позиционных системах счисления;
Здесь значение разряда 2 множителя сформировано по принципам формирования значения числа в позиционных системах счисления;
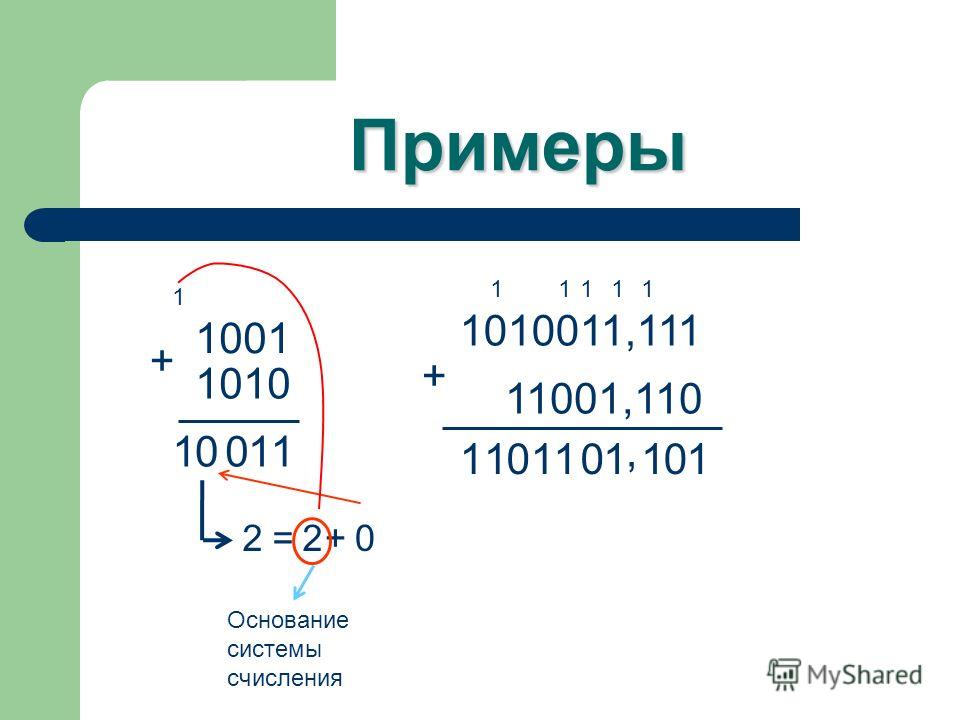 1 Гексадецимальная вычитание
1 Гексадецимальная вычитание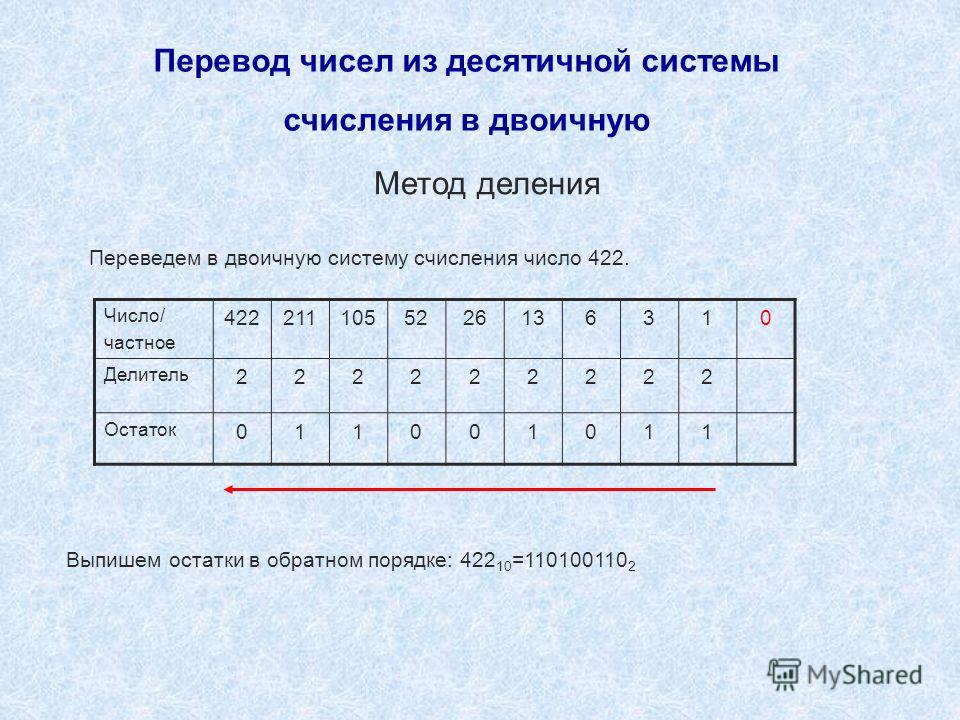
 ) 2 + 4 + 1 = 7
) 2 + 4 + 1 = 7
 Итак, давайте решим задачу этим методом.
Итак, давайте решим задачу этим методом.


 После отбрасывания 1 из крайней левой цифры 27BA 16 и добавления 1.
После отбрасывания 1 из крайней левой цифры 27BA 16 и добавления 1.

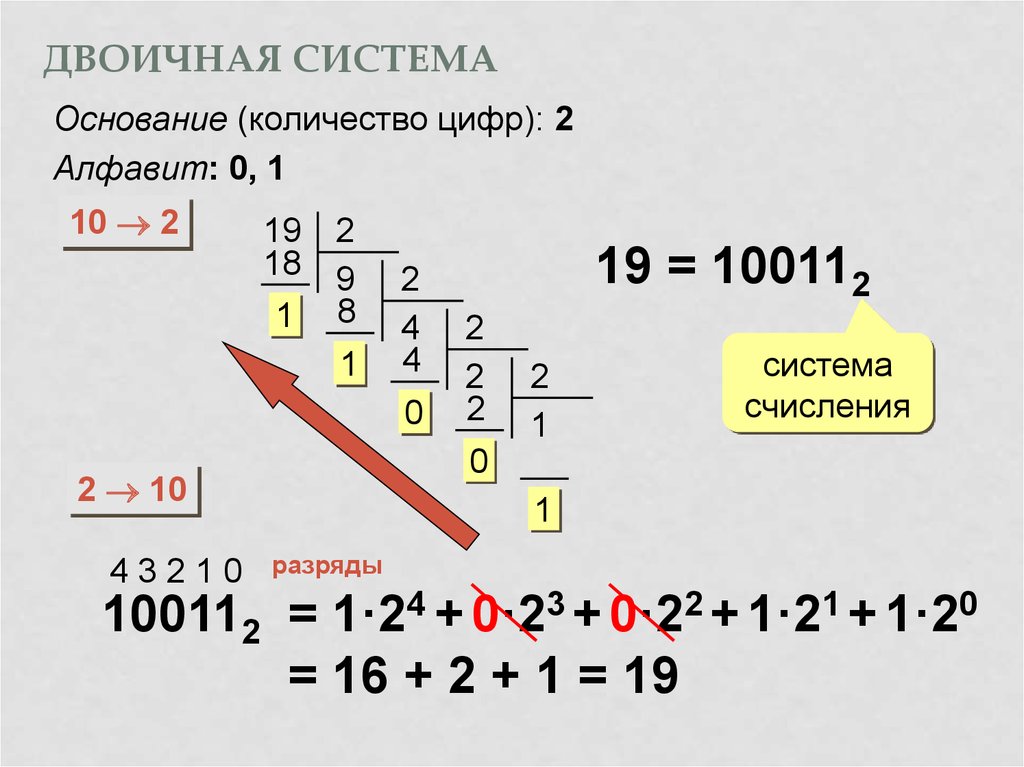

 Для обозначения двузначных цифр 10, 11, 12, 13, 14, 15 в шестнадцатеричной системе счисления используются символы A, B, C, D, E, F соответственно. Давайте узнаем больше о методах преобразования десятичного числа в шестнадцатеричное и связанных с ним шагах преобразования.
Для обозначения двузначных цифр 10, 11, 12, 13, 14, 15 в шестнадцатеричной системе счисления используются символы A, B, C, D, E, F соответственно. Давайте узнаем больше о методах преобразования десятичного числа в шестнадцатеричное и связанных с ним шагах преобразования. При преобразовании числа из десятичной системы счисления в шестнадцатеричную систему счисления необходимо тщательно соблюдать основание числа. Число нужно делить на 16, пока частное не станет равным нулю. Обратите внимание на следующую таблицу, в которой показано представление десятичных и шестнадцатеричных чисел.
При преобразовании числа из десятичной системы счисления в шестнадцатеричную систему счисления необходимо тщательно соблюдать основание числа. Число нужно делить на 16, пока частное не станет равным нулю. Обратите внимание на следующую таблицу, в которой показано представление десятичных и шестнадцатеричных чисел.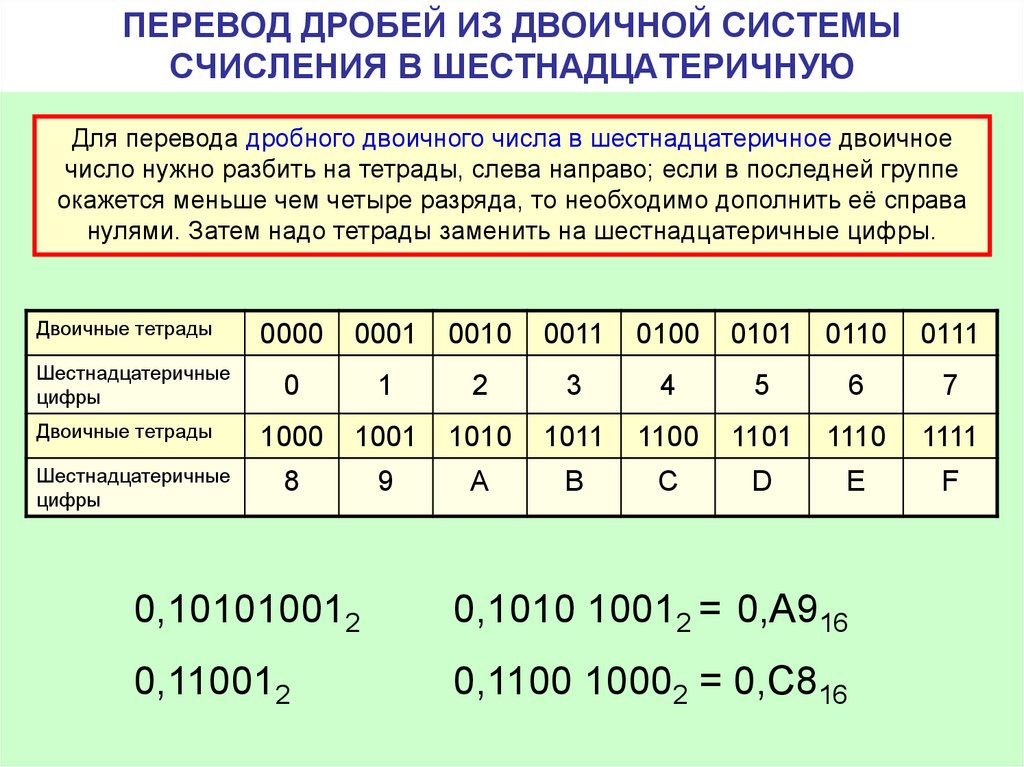

 Полученный результат представляет собой шестнадцатеричное число заданного дробного числа. Давайте разберемся в этом с помощью примера.
Полученный результат представляет собой шестнадцатеричное число заданного дробного числа. Давайте разберемся в этом с помощью примера.

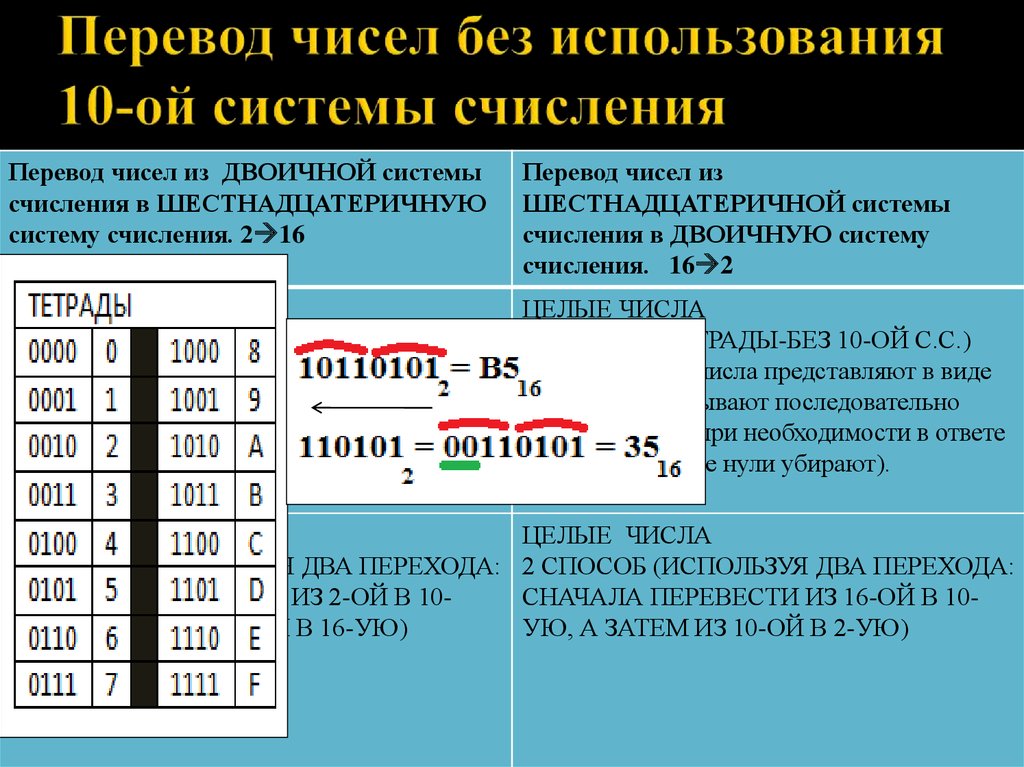 На следующем шаге мы разделим 3/16, где частное равно 0, а остаток равен 3. При объединении цифр в обратном порядке шестнадцатеричное значение 63 равно 3F. Следовательно, \((63)_{10}\) равно \((3F)_{16}\).
На следующем шаге мы разделим 3/16, где частное равно 0, а остаток равен 3. При объединении цифр в обратном порядке шестнадцатеричное значение 63 равно 3F. Следовательно, \((63)_{10}\) равно \((3F)_{16}\). Теперь, после деления 1 на 16, мы получим 0 в частном и 1 в остатке. При объединении цифр в обратном порядке шестнадцатеричное значение 315 получается 13B. Следует отметить, что когда мы записываем объединенные остатки в обратном порядке, мы записываем шестнадцатеричное значение для 11, которое равно B. Следовательно, \((315)_{10}\) равно \((13B)_{ 16}\).
Теперь, после деления 1 на 16, мы получим 0 в частном и 1 в остатке. При объединении цифр в обратном порядке шестнадцатеричное значение 315 получается 13B. Следует отметить, что когда мы записываем объединенные остатки в обратном порядке, мы записываем шестнадцатеричное значение для 11, которое равно B. Следовательно, \((315)_{10}\) равно \((13B)_{ 16}\).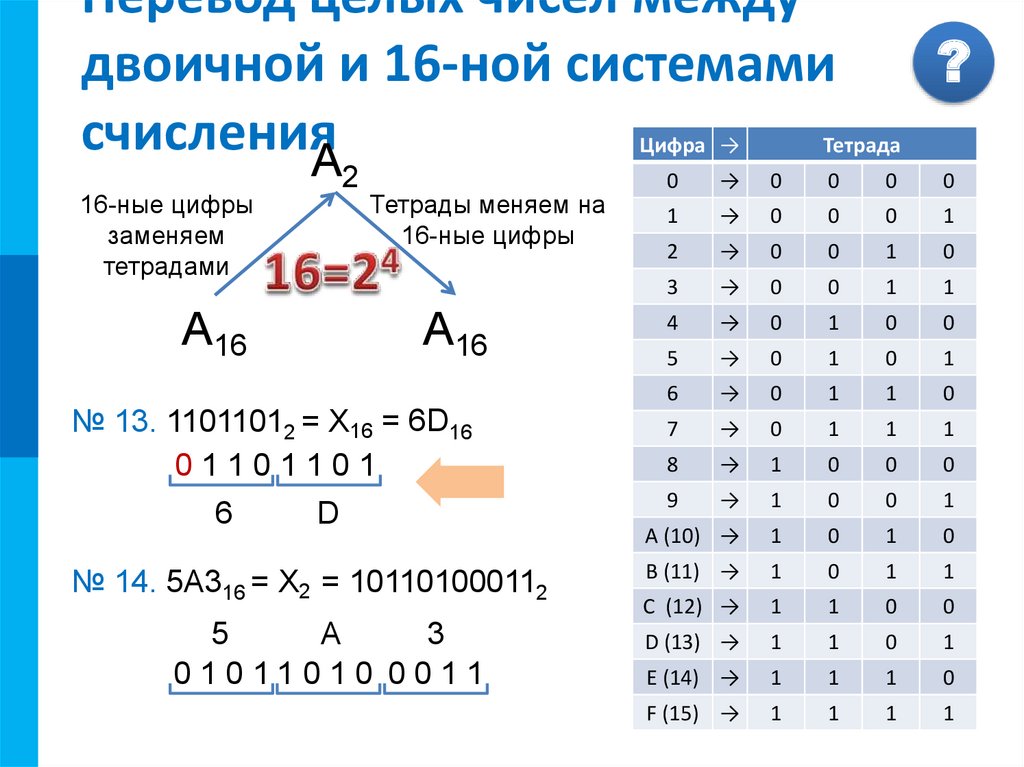 Дополните слева нулями, если необходимо, чтобы сформировать группу из 4. Найдите
соответствующее шестнадцатеричное значение из таблицы.
Дополните слева нулями, если необходимо, чтобы сформировать группу из 4. Найдите
соответствующее шестнадцатеричное значение из таблицы. При преобразовании в шестнадцатеричный формат
преобразовать остатки в шестнадцатеричный.
При преобразовании в шестнадцатеричный формат
преобразовать остатки в шестнадцатеричный.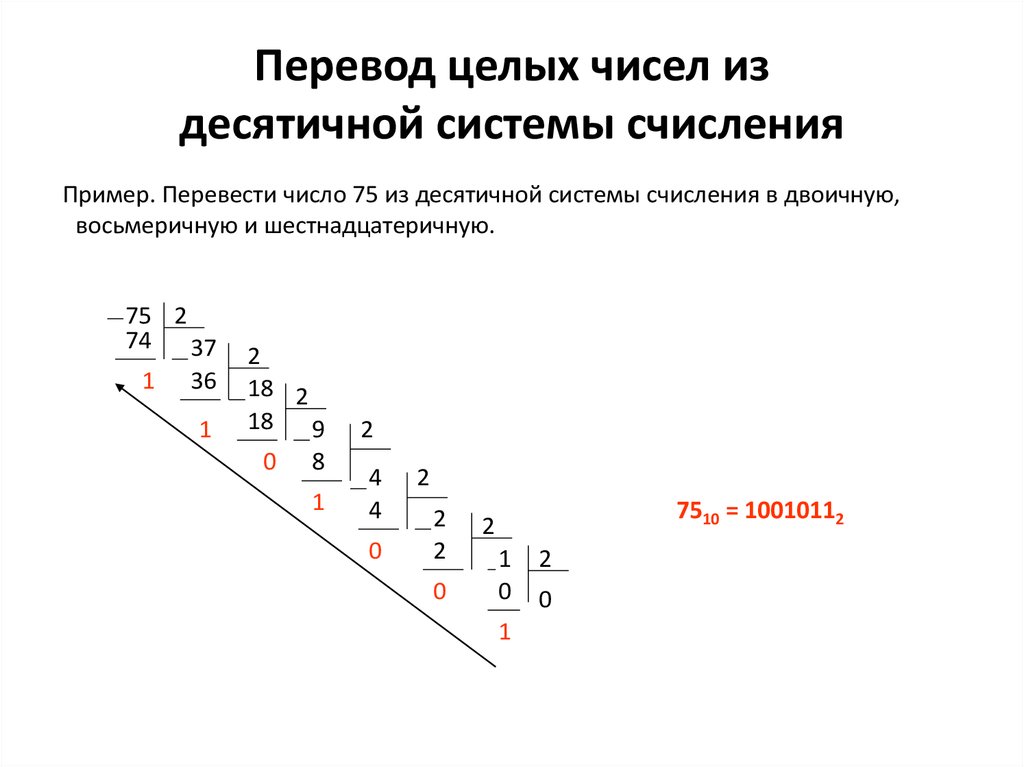
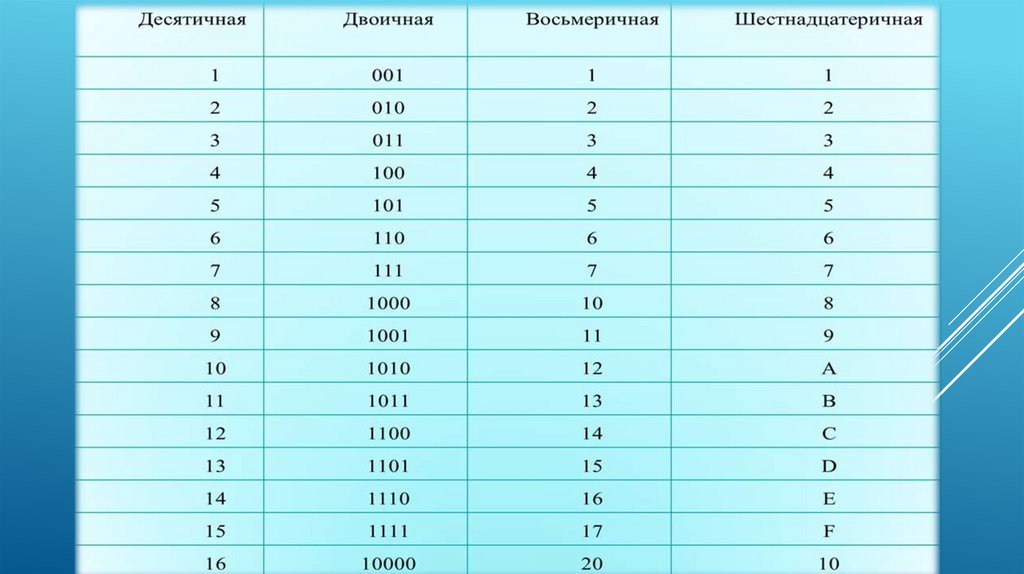

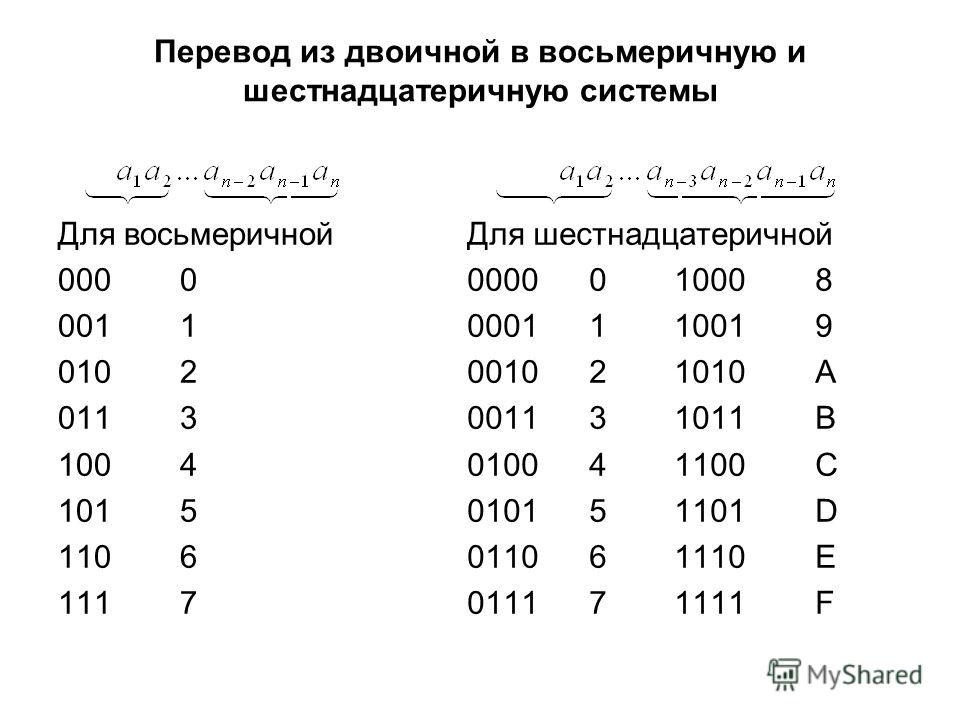 Это похоже на десятичную систему, с которой все были знакомы, только вместо степеней 10 мы имеем дело со степенями 16.
Это похоже на десятичную систему, с которой все были знакомы, только вместо степеней 10 мы имеем дело со степенями 16. Форма символов не имеет значения, если вы понимаете, что они означают.
Форма символов не имеет значения, если вы понимаете, что они означают.
 Поскольку основание 16 является степенью числа 2 (например, 4), преобразование из двоичного в шестнадцатеричное и наоборот, как мы вскоре увидим, тривиально.
Поскольку основание 16 является степенью числа 2 (например, 4), преобразование из двоичного в шестнадцатеричное и наоборот, как мы вскоре увидим, тривиально.