Урок физики «Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца»
Использование на уроке наглядности в виде мультимедийной презентации облегчает усвоение учащимися излагаемого материала. Презентация дает возможность компактно излагать учебный материал, что позволяет больше времени уделить закреплению пройденного материала. Применение анимации позволяет показать движение заряда в магнитном поле в динамике. Изучаемый материал связывает полученные теоретические знания с практикой. Разработку и презентацию можно использовать не только в универсальных, но и в профильных классах, так как они содержат материал повышенного уровня сложности.
Цели: изучить новое физическое явление – действие магнитного поля на
движущийся заряд, вывести формулу и ввести мнемоническое правило для определения
модуля и направления силы Лоренца, показать возможность применения знаний для
расчёта периода обращения частицы в магнитном поле, познакомить учащихся с
практическим применением действия силы Лоренца в ускорителях.
Оборудование: электронный осциллограф, дугообразный магнит, презентация “Сила Лоренца”, мультимедийный проектор.
Тип урока: формирование новых знаний
Ход урока
Актуализация знаний:
Слайд 1.
- Какими свойствами обладает магнитное поле?
- Что такое сила Ампера?
- Как рассчитать силу Ампера?
- Что такое электрический ток?
Слайд 2.
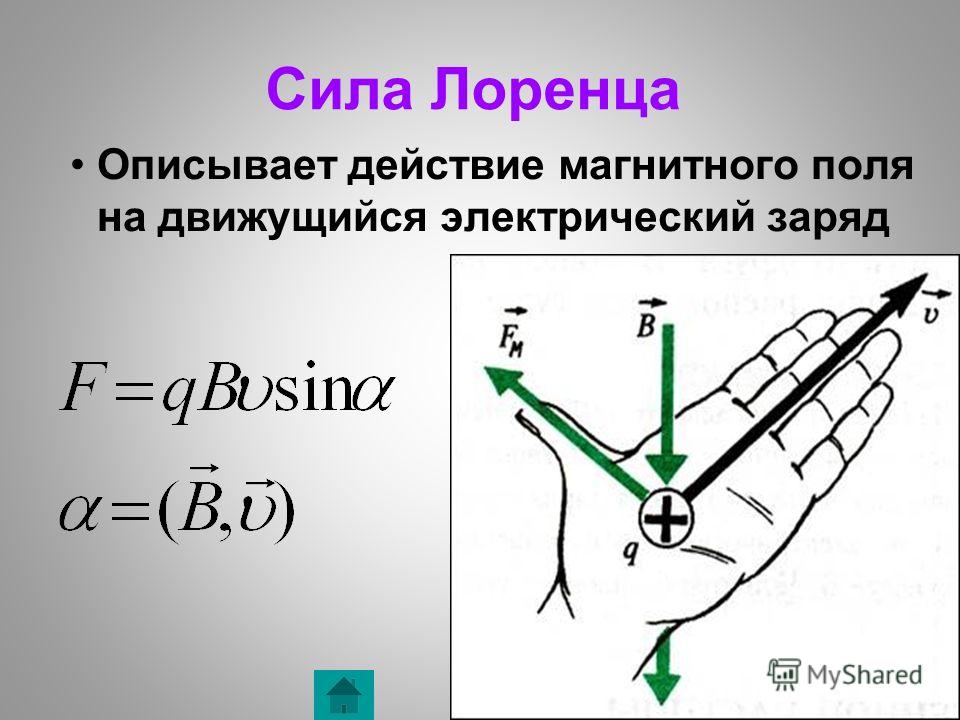
Учитель: Т.к. магнитное поле действует на ток – движущиеся заряженные частицы, то оно действует и на каждую частицу в отдельности. Действие магнитного поля на движущуюся заряженную частицу характеризует сила Лоренца.
Хендрик Антон Лоренц (1853–1928) выдающийся голландский физик и
математик , развил электромагнитную теорию света и электронную теорию материи, а
также сформулировал теорию электричества, магнетизма и света, внёс большой вклад
в развитие теории относительности, лауреат Нобелевской премии 1902г.
Слайд 3.
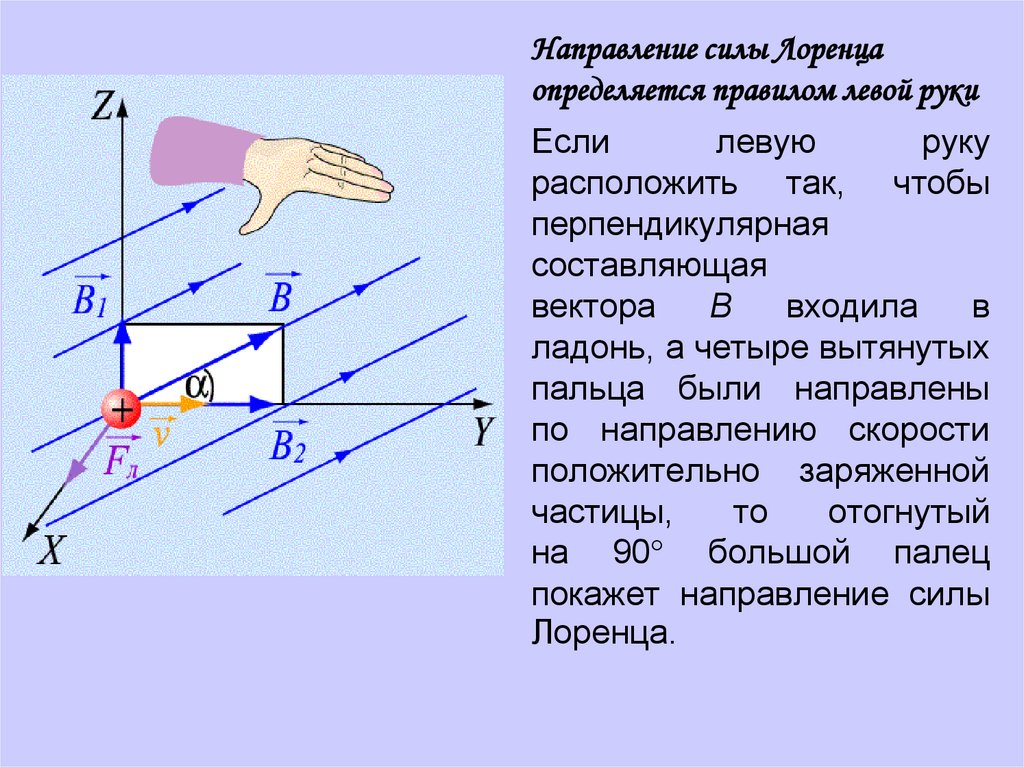
, так как является её долей, значит, для определения её направления можно применить то же мнемоническое правило, что и для определения направления сил Ампера – правило левой руки, с оговоркой, что заряд должен быть положительным, т.к. за направление тока мы принимаем направление движения положительных зарядов. Если же заряд отрицательный, то направление силы меняется на противоположное.
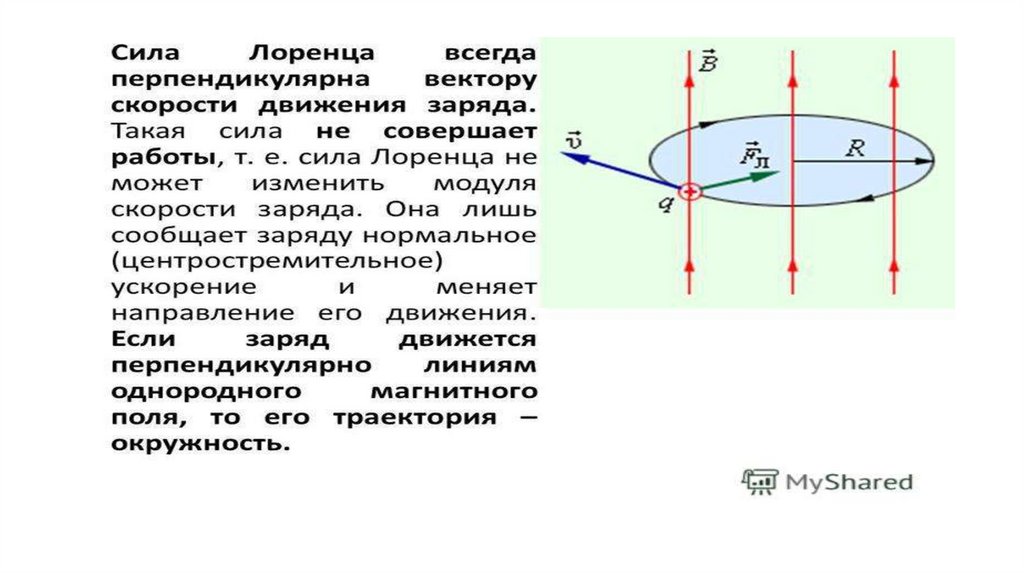
Так как сила, действующая на заряд, оказалась перпендикулярной скорости его движения, то модуль скорости изменяться не будет, а будет меняться направление, т.о. частица будет равномерно двигаться по окружности.
Демонстрационный эксперимент: С помощью прибора для демонстрации движения заряженных частиц под действием силы Лоренца или с помощью электронного осциллографа демонстрируется отклонение электронных пучков магнитным полем.
Слайд 4.
Выведем формулу для расчёта модуля силы Лоренца.
Т.к. она является частью силы, действующей на весь отрезок проводника, находящийся в магнитном поле, то её модуль в N раз меньше силы Ампера. Доведите рассуждение до логического завершения: свяжите силу с параметрами заряженной частицы (зарядом и скоростью)
(Ученики завершают вывод формулы в тетрадях, проверяют с помощью анимированного слайда 4.)
Слайд 5.
Движение заряженной частицы под действием силы Лоренца, если α = 90°
Сила, перпендикулярная скорости, вызывает изменение направления движения, т.е. центростремительное ускорение. Зная формулы расчёта центростремительного ускорения и модуля силы Лоренца, которая его вызывает, и, используя второй закон Ньютона, выведите формулу для расчёта радиуса окружности, по которой будет двигаться частица.
(Ученики завершают вывод формулы в тетрадях, проверяют с помощью анимированного слайда 5.)
Слайд 6.
Теперь не сложно узнать и период обращения частицы, т. к.
, где r
нами только что найдено. Сделайте вывод: чем определяется период обращения
частицы?
к.
, где r
нами только что найдено. Сделайте вывод: чем определяется период обращения
частицы?
(Предполагаемый ответ: магнитной индукцией поля и удельным зарядом частицы, т.е. не зависит от радиуса окружности, по которой частица движется.)
Эти особенности движения зарядов в магнитном поле нашли практическое применение.
Слайд 7.
- Осциллограф
- Кинескоп
- Масс – спектрограф
- Ускорители элементарных частиц (циклотрон, бетатрон, синхрофазотрон)
Слайд 8.
Движение заряженной частицы под действием силы Лоренца, если α ≠ 90°
(С помощью анимации на слайде учитель объясняет, как движется заряженная частица, если её скорость не перпендикулярна силовым линиям магнитного поля и совместно с учащимися находит шаг винтовой линии.)
Слайд 10.
Самостоятельная работа для учащихся с целью закрепления полученных знаний, в ходе которой они могут пользоваться своими записями, текстом учебника, консультацией учителя
Слайд 11.
Домашнее задание §6, самостоятельная работа № 31 (“Физика. Самостоятельные и контрольные работы” Л.А.Кирик), достаточный уровень № 1–3, 10
Подведение итогов урока.
Литература и использованные материалы:
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н.Сотский
- Л.А. Кирик “Физика. Самостоятельные и контрольные работы. 10”, Илекса, 2005.
- Википедия.
Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1.
 «Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца»Сила Лоренца
«Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца»Сила ЛоренцаСилу, действующую на движущуюся заряженную
частицу со стороны магнитного поля, называют
силой Лоренца
Хеендрик Антоен Лоеренц (1853 — 1928)
выдающийся голландский физик и математик ,
развил электромагнитную теорию света и
электронную теорию материи, а также
сформулировал теорию электричества,
магнетизма и света, внёс большой вклад в
развитие теории относительности,
лауреат Нобелевской премии 1902г.
F
FЛ
N
I qn S
F I B l sin
N nS l
F q n SB l sin q NB sin
4. Движущиеся заряженные частицы в магнитном поле
Радиационные пояса Земли. Быстрые заряженные частицыот Солнца (в основном электроны и протоны) попадают в
магнитные ловушки радиационных поясов. Частицы могут
покидать пояса в полярных областях и вторгаться в верхние
слои атмосферы, вызывая полярные сияния.
Магнитная «бутылка». Заряженные частицы не выходят
за пределы «бутылки».
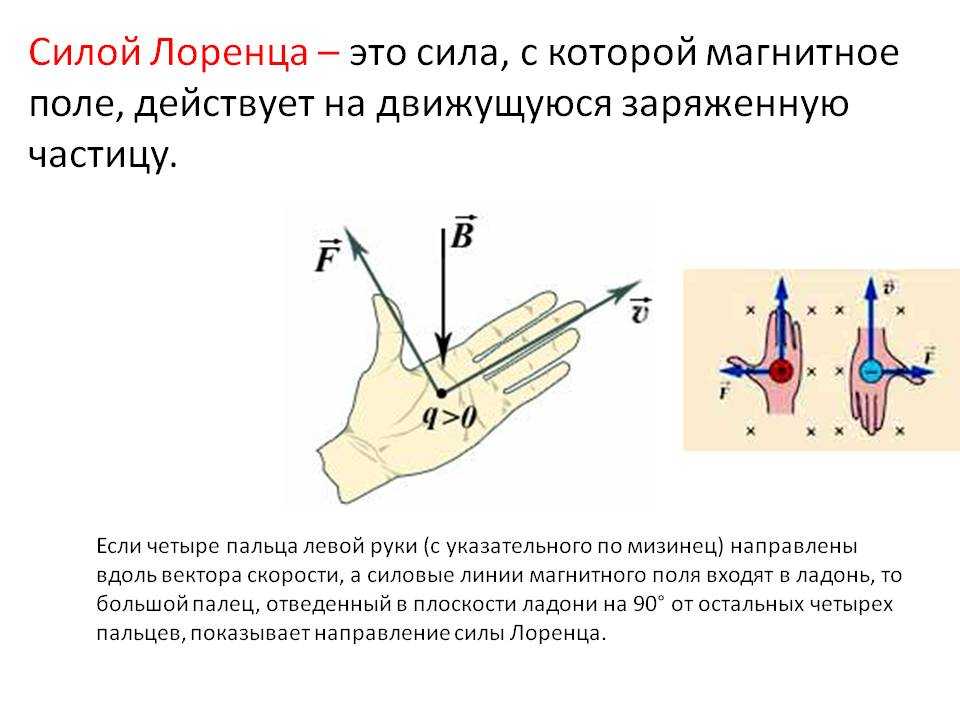 Магнитное поле «бутылки»
Магнитное поле «бутылки»может быть создано с помощью двух круглых катушек с
током.
Движение заряженной частицы по спирали в
однородном магнитном поле.
Селектор скоростей и массспектрометр
Угловая скорость движения заряженной частицы по круговой
траектории называется циклотронной частотой. Циклотронная частота не
зависит от скорости (следовательно, и от кинетической энергии) частицы. Это
обстоятельство используется в циклотронах
10. Использование действия магнитного поля на движущийся заряд
Использование действия магнитного
поля на движущийся заряд
Телевизионные
трубки: летящие к экрану
электроны отклоняются с помощью
магнитного поля
Ускорители
заряженных частиц для
получения частиц с большими энергиями
(циклотрон)
Масс-спектрограф-прибор,
позволяющий
разделять заряженные частицы по их
удельным зарядам, т.
 е. по отношению
е. по отношениюзаряда частицы к ее массе
Радиус
кривизны траектории является
величиной постоянной
Данная
траектория является окружностью
2 r 2 m
T
qB
12. Движение заряженных частиц в магнитном поле
F qBa
m
m
2
a
r
qB 2
m
r
m
r
qB
13. Направление
14. Модуль силы Лоренца
ВСила, действующая на движущуюся
заряженную частицу со стороны
магнитного поля, называется силой
Лоренца
V
FЛ
Fл ↑↑
FA
16. Модуль силы Лоренца
FАI
= ВIl sinα
V
Fл =
I=
V=
А
Л
ВIlFsinα
А
В
N
q
t
l
t
F
Fл =
Вql sinα
tN
; q0 =
Fл = Bq0V sinα
q
N
Движение заряженной частицы под действием силы Лоренца, если α = 90°
F ┴ V
В
V
Сила, перпендикулярная скорости,
вызывает изменение направления
движения.
Центростремительное ускорение:
a=
v
2
По II закону Ньютона F = m a
r
FЛ
ВqV = mV
r=
r
mV
Bq
2
Движение заряженной частицы под действием силы Лоренца, если α = 90°
Т.
 к движение равномерное, то
к движение равномерное, тоT=
В
т.к.
T=
2πr
V
r=
2πmV
BqV
mV
Bq
=
2πm
Bq
19. Применение силы Лоренца
ОсциллографКинескоп
Масс – спектрограф
Ускорители элементарных частиц (циклотрон, бетатрон,
синхрофазотрон)
B
20. Движение заряженной частицы под действием силы Лоренца, если α ≠ 90°
v =vh=v T
cosα
v ┴= v
2πm
T = sinα
║
В
║
h
↔
Bq
V║
V
┴
V
2πm
h = v cosα
Bq
English Русский Правила
SCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и биологические науки.
- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.

- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org org | |
| 1655362766 | |
| Публикация бумаги WeChat |
| Недавно опубликованные статьи |
| Недавно опубликованные статьи |
Новое предложение для черных дыр()
Джон Р.
 Клаудер
КлаудерЖурнал физики высоких энергий, гравитации и космологии Том 9 №1, 10 января 2023 г.
DOI: 10.4236/jhepgc.2023.91006 16 загрузок 94 просмотров
Квантование кинетической энергии детерминированного хаоса()
Виктор Александрович Мирошников
Американский журнал вычислительной математики Том 13 № 1, 10 января 2023 г.
DOI: 10.4236/ajcm.2023.131001 7 загрузок 40 просмотров
Анализ профилей выбросов двигателей для гидроразрыва пласта()
Уильям Ньювенбург, Эндрю С.
 Никс, Дэн Фу, Тони Йенг, Уоррен Землак, Ник Уэллс
Никс, Дэн Фу, Тони Йенг, Уоррен Землак, Ник УэллсЭнергетика и энергетика Том 15 №1, 10 января 2023 г.
DOI: 10.4236/epe.2023.151001 6 загрузок 49 просмотров
Включение 8-го выпуска -го издания AJCC/TNM для определения стадии карциномы аппендикса в шкалу тяжести заболевания перитонеальной поверхности Esquivel (E-PSDSS) у 229 пациентов с муцинозными аппендикулярными новообразованиями ()
Габриэлла Эскивель, Цзин Цю, Джеймс Спеллман, Хесус Эскивель
Открытый журнал гастроэнтерологии Том 13 № 1, 10 января 2023 г.
DOI: 10.4236/ojgas.2023.131001 12 загрузок 69 просмотров
Желтопятнистый рисунок саламандры ( Salamandra infraimmaculata ) в различных местообитаниях на южной границе ее распространения в Израиле()
Гад Дегани, Гад Иш Ам, Амит Биран Иш Ам, Нерия Ятом, Амир Маршанский, Сиван Маргалит, Эйтан Ниссим, Хава Гольдштейн, Нива Шакед
Открытый журнал зоотехники Том 13 № 1, 10 января 2023 г.

DOI: 10.4236/ojas.2023.131008 2 загрузки 26 просмотров
Знания, отношение и практика использования противомикробных препаратов и резистентности среди сельских ветеринарных работников и продавцов ветеринарных препаратов в Камбодже()
Бунна Чеа, Соком Конг, Соха Тим, Найхик Бан, Рити Чран, Вутей Венн, Черри Фернандес-Колорадо, Кроесна Канг
Открытый журнал зоотехники Том 13 № 1, 10 января 2023 г.
DOI: 10.4236/ojas.2023.131007 10 загрузок 85 просмотров
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
Бесплатные информационные бюллетени SCIRP
Copyright © 2006-2023 Scientific Research Publishing Inc. Все права защищены.
ВерхняяВоздействие магнитного поля на вестибулярную систему: расчет давления на купулу за счет силы Лоренца, индуцированной ионным током
. 2012 21 июля; 57 (14): 4477-87.
дои: 10.1088/0031-9155/57/14/4477.
Epub 2012 22 июня.
Антунес 1 , П. М. Гловер, И. Ли, О. С. Миан, Б. Л. День
Принадлежности
принадлежность
- 1 Центр магнитного резонанса сэра Питера Мэнсфилда, Ноттингемский университет, Ноттингем, Великобритания.
- PMID: 22722424
- DOI: 10.1088/0031-9155/57/14/4477
Бесплатная статья
Антунес и др. физ.-мед. биол. .
Бесплатная статья
. 2012 21 июля; 57 (14): 4477-87.
2012 21 июля; 57 (14): 4477-87.
дои: 10.1088/0031-9155/57/14/4477. Epub 2012 22 июня.
Авторы
Антунес 1 , П. М. Гловер, И. Ли, О. С. Миан, Б. Л. Дэй
принадлежность
- 1 Центр магнитного резонанса сэра Питера Мэнсфилда, Ноттингемский университет, Ноттингем, Великобритания.
- PMID: 22722424
- DOI: 10.1088/0031-9155/57/14/4477
Абстрактный
Большие статические магнитные поля могут использоваться в магнитно-резонансной томографии (МРТ).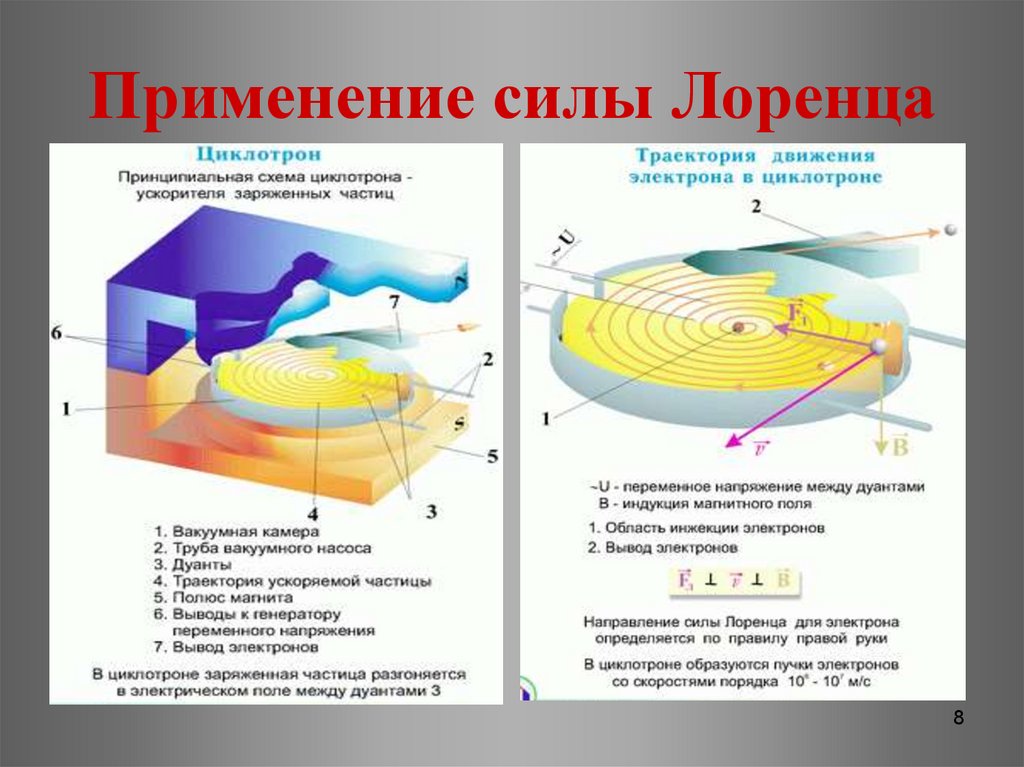 При высокой напряженности магнитного поля (обычно примерно от 3 Тл и выше) люди могут ощущать ряд эффектов. Одним из таких эффектов является легкое головокружение. Недавно Робертс и др. (2011 Current Biology 21 1635-40) предложили механизм силы Лоренца, возникающий в результате ионных токов, возникающих естественным образом в эндолимфе вестибулярной системы. В настоящей работе проведен более детальный расчет сил и результирующих давлений в вестибулярной системе с использованием численной модели. Во-первых, были построены реалистичные трехмерные конечно-элементные карты проводимости и жидкости маточки и одного полукружного канала, содержащие источники тока (темные клетки) и стоки (волосяные клетки) маточки и ампулы. Во-вторых, рассчитываются плотности электрического тока в жидкости. В-третьих, развиваемая сила Лоренца используется непосредственно в уравнении Навье-Стокса и вычисляется транскупулярное давление. Поскольку поле движущей силы относительно велико по сравнению с адвективным ускорением, мы показываем, что можно выполнить аппроксимацию в уравнениях Навье-Стокса, которая сводит задачу к решению более простого уравнения Пуассона.
При высокой напряженности магнитного поля (обычно примерно от 3 Тл и выше) люди могут ощущать ряд эффектов. Одним из таких эффектов является легкое головокружение. Недавно Робертс и др. (2011 Current Biology 21 1635-40) предложили механизм силы Лоренца, возникающий в результате ионных токов, возникающих естественным образом в эндолимфе вестибулярной системы. В настоящей работе проведен более детальный расчет сил и результирующих давлений в вестибулярной системе с использованием численной модели. Во-первых, были построены реалистичные трехмерные конечно-элементные карты проводимости и жидкости маточки и одного полукружного канала, содержащие источники тока (темные клетки) и стоки (волосяные клетки) маточки и ампулы. Во-вторых, рассчитываются плотности электрического тока в жидкости. В-третьих, развиваемая сила Лоренца используется непосредственно в уравнении Навье-Стокса и вычисляется транскупулярное давление. Поскольку поле движущей силы относительно велико по сравнению с адвективным ускорением, мы показываем, что можно выполнить аппроксимацию в уравнениях Навье-Стокса, которая сводит задачу к решению более простого уравнения Пуассона. Это упрощение позволяет быстро и легко рассчитать множество различных направлений приложенного магнитного поля. При 7 Т максимальная разность давлений купулы 1,6 мПа была рассчитана для комбинированных ампулярного (0,7 мкА) и утрикулярного (3,31 мкА) распределенных источников тока, предполагая, что ток покоя волосковых клеток составляет 100 пА на единицу. Эти значения давления на порядок ниже, чем те, которые были предложены Робертсом и др. с использованием упрощенной модели и расчета, и хорошо согласуются с расчетными значениями давления для скоростей нистагма в калорических экспериментах. Эта работа по моделированию подтверждает гипотезу о том, что механизм силы Лоренца вносит значительный вклад в восприятие головокружения, вызванного магнитным полем.
Это упрощение позволяет быстро и легко рассчитать множество различных направлений приложенного магнитного поля. При 7 Т максимальная разность давлений купулы 1,6 мПа была рассчитана для комбинированных ампулярного (0,7 мкА) и утрикулярного (3,31 мкА) распределенных источников тока, предполагая, что ток покоя волосковых клеток составляет 100 пА на единицу. Эти значения давления на порядок ниже, чем те, которые были предложены Робертсом и др. с использованием упрощенной модели и расчета, и хорошо согласуются с расчетными значениями давления для скоростей нистагма в калорических экспериментах. Эта работа по моделированию подтверждает гипотезу о том, что механизм силы Лоренца вносит значительный вклад в восприятие головокружения, вызванного магнитным полем.
Похожие статьи
Вестибулярная стимуляция магнитными полями.
Уорд Б.К., Робертс Д.С., Делла Сантина К.
 С., Кэри Д.П., Зи Д.С.
Уорд Б.К. и соавт.
Энн Н.Ю. Академия наук. 2015 Апрель; 1343 (1): 69-79. doi: 10.1111/nyas.12702. Epub 2015 3 марта.
Энн Н.Ю. Академия наук. 2015.
PMID: 25735662
Бесплатная статья ЧВК.
Обзор.
С., Кэри Д.П., Зи Д.С.
Уорд Б.К. и соавт.
Энн Н.Ю. Академия наук. 2015 Апрель; 1343 (1): 69-79. doi: 10.1111/nyas.12702. Epub 2015 3 марта.
Энн Н.Ю. Академия наук. 2015.
PMID: 25735662
Бесплатная статья ЧВК.
Обзор.Магнитное поле МРТ стимулирует вращательные датчики головного мозга.
Робертс Д.С., Марселли В., Гиллен Д.С., Кэри Д.П., Делла Сантина К.С., Зи Д.С. Робертс, округ Колумбия, и др. Карр Биол. 2011 11 октября; 21 (19): 1635-40. doi: 10.1016/j.cub.2011.08.029. Epub 2011 22 сентября. Карр Биол. 2011. PMID: 21945276 Бесплатная статья ЧВК.
Влияние наклона головы и ориентации крена на магнитно-индуцированное головокружение.
Mian OS, Li Y, Antunes A, Glover PM, Day BL. Миан ОС и др.
 Дж. Физиол. 2016 15 февраля; 594 (4): 1051-67. дои: 10.1113/JP271513. Epub 2015 30 декабря.
Дж. Физиол. 2016.
PMID: 26614577
Бесплатная статья ЧВК.
Дж. Физиол. 2016 15 февраля; 594 (4): 1051-67. дои: 10.1113/JP271513. Epub 2015 30 декабря.
Дж. Физиол. 2016.
PMID: 26614577
Бесплатная статья ЧВК.Десятилетие магнитной вестибулярной стимуляции: от интуиции до физики и клиники.
Уорд Б.К., Робертс Д.С., Отеро-Миллан Дж., Зи Д.С. Уорд Б.К. и соавт. J Нейрофизиол. 20191 июня 121(6):2013-2019. doi: 10.1152/jn.00873.2018. Epub 2019 10 апр. J Нейрофизиол. 2019. PMID: 30969883 Обзор.
Динамическая модель реакции глазного нистагма на сильные магнитные поля.
Гловер PM, Li Y, Antunes A, Mian OS, Day BL. Гловер П.М. и др. физ.-мед. биол. 2014 7 февраля; 59 (3): 631-45. дои: 10.1088/0031-9155/59/3/631. Epub 2014 17 января. физ.-мед.
 биол. 2014.
PMID: 24434733
биол. 2014.
PMID: 24434733
Посмотреть все похожие статьи
Цитируется
Взаимодействие сознания и внутреннего электромагнитного поля.
МакИвер МБ. Макивер МБ. Передний шум нейронов. 2022 17 ноя; 16:1032339. doi: 10.3389/fnhum.2022.1032339. Электронная коллекция 2022. Передний шум нейронов. 2022. PMID: 36466618 Бесплатная статья ЧВК.
Долгосрочные поведенческие эффекты, наблюдаемые у мышей, хронически подвергающихся воздействию статических сверхвысоких магнитных полей.
Ткач И., Бенниворт М.А., Николс-Мид Т., Штойер Э.Л., Ларсон С.Н., Мецгер Г.Дж., Угурбил К. Ткач I и др. Магн Резон Мед. 2021 сен; 86 (3): 1544-1559. doi: 10.1002/mrm.28799. Epub 2021 6 апр.
 Магн Резон Мед. 2021.
PMID: 33821502
Бесплатная статья ЧВК.
Магн Резон Мед. 2021.
PMID: 33821502
Бесплатная статья ЧВК.Модулирующие эффекты магнитной вестибулярной стимуляции на сети в состоянии покоя можно объяснить субъект-специфической ориентацией анатомии внутреннего уха в статическом магнитном поле МР.
Богле Р., Кирш В., Герб Дж., Дитрих М. Богле Р. и др. Дж Нейрол. 2020 декабрь; 267 (Приложение 1): 91-103. doi: 10.1007/s00415-020-09957-3. Epub 2020 11 июня. Дж Нейрол. 2020. PMID: 32529576 Бесплатная статья ЧВК.
Безопасность воздействия сильных статических магнитных полей (2 Тл-12 Тл): исследование на мышах.
Ван С., Луо Дж., Лв Х., Чжан З., Ян Дж., Дун Д., Фан И., Ху Л., Лю М., Ляо З., Ли Дж., Фанг З., Вэй И., Хань В., Шейх А.Б., Инь Д., Шанг П.




 Клаудер
Клаудер Никс, Дэн Фу, Тони Йенг, Уоррен Землак, Ник Уэллс
Никс, Дэн Фу, Тони Йенг, Уоррен Землак, Ник Уэллс
 С., Кэри Д.П., Зи Д.С.
Уорд Б.К. и соавт.
Энн Н.Ю. Академия наук. 2015 Апрель; 1343 (1): 69-79. doi: 10.1111/nyas.12702. Epub 2015 3 марта.
Энн Н.Ю. Академия наук. 2015.
PMID: 25735662
Бесплатная статья ЧВК.
Обзор.
С., Кэри Д.П., Зи Д.С.
Уорд Б.К. и соавт.
Энн Н.Ю. Академия наук. 2015 Апрель; 1343 (1): 69-79. doi: 10.1111/nyas.12702. Epub 2015 3 марта.
Энн Н.Ю. Академия наук. 2015.
PMID: 25735662
Бесплатная статья ЧВК.
Обзор. Дж. Физиол. 2016 15 февраля; 594 (4): 1051-67. дои: 10.1113/JP271513. Epub 2015 30 декабря.
Дж. Физиол. 2016.
PMID: 26614577
Бесплатная статья ЧВК.
Дж. Физиол. 2016 15 февраля; 594 (4): 1051-67. дои: 10.1113/JP271513. Epub 2015 30 декабря.
Дж. Физиол. 2016.
PMID: 26614577
Бесплатная статья ЧВК.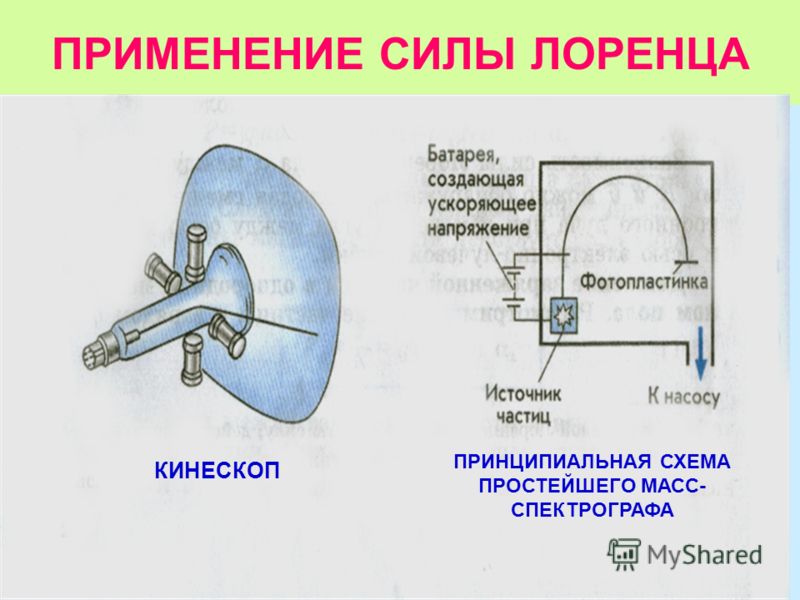 биол. 2014.
PMID: 24434733
биол. 2014.
PMID: 24434733 Магн Резон Мед. 2021.
PMID: 33821502
Бесплатная статья ЧВК.
Магн Резон Мед. 2021.
PMID: 33821502
Бесплатная статья ЧВК.