Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
375519 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.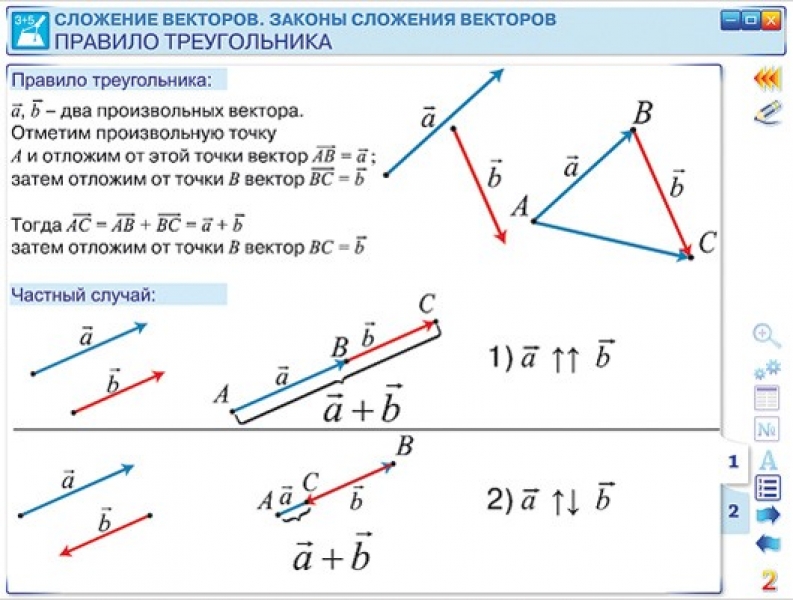
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
Скалярные и векторные величины и действия над ними в физике с примерами
Содержание:
Скалярные и векторные величины:
В 7-м и 8-м классах мы рассматривали различные физические величины. Для одних величин достаточно знать их числовое значение и единицу измерения. Например, масса
На рисунках 14, а и 14, б девочка действует на санки силой, имеющей одно и то же числовое значение. Но в первом случае санки лишь немного погрузились в снег, а во втором — пришли в движение. Значит, сила определяется не только числовым значением, но и направлением. Сила — величина векторная.
Векторной величиной является и скорость движения тел (рис. 15), и многие другие физические величины.
Что нужно знать о векторных величинах (векторах)
Векторы характеризуются модулем и направлением в пространствеМодулем вектора называется его числовое значение.
Вектор изображают в виде направленного отрезка (стрелки). Стрелка указывает, куда направлен вектор (рис. 14, 15). Длина стрелки характеризует модуль вектора (рис. 16). Над буквенным обозначением вектора ставят стрелку, например:
Модуль вектора обозначают той же буквой, но без стрелки над ней или символом Например, модуль вектора на рисунке 16 равен
Модуль любого (не равного нулю) вектора — число положительное.
Векторы равны между собой, если равны их модули и одинаковы направленияРавные векторы лежат на одной и той же прямой или на параллельных прямых и направлены в одну и ту же сторону. На рисунке 17 Однако, несмотря на равенство модулей, так как у векторов различные направления.
Угол между векторамиЧтобы найти угол между векторами (рис. 18, а), нужно совместить их начала (рис. 18, б). Если направления векторов одинаковы, то (рис. 18, в), если противоположны, то (рис. 18, г).
Умножение вектора на число
Произведение вектора на число есть вектор Чему в равен его модуль? Куда направлен вектор
Модуль вектора равен
Если то вектор направлен так же, как вектор а если то противоположно ему.
На рисунке 19 показаны результаты умножения вектора на 2, на 0,5, на (-3) и на (-1) соответственно.
Противоположные векторыВектор называется противоположным вектору если У векторов одинаковые модули, но противоположные направления (рис. 19, а, г).
Сложение векторовВ 7-м классе вы складывали силы, направленные или одинаково, или в противоположные стороны. Результатом сложения в первом случае была сила, модуль которой равен а во втором
То же самое получается и при сложении векторов (рис. 20). Если они направлены одинаково (рис. 20, а), то их сумма имеет модуль Если же направления векторов противоположны (рис. 20, б), то модуль их суммы Обратите внимание: в последнем случае вектор направлен так, как вектор с большим модулем (т. е. как вектор ).
е. как вектор ).
А как сложить векторы, направленные под любым углом друг к другу? Для этого можно использовать любое из двух следующих далее правил.
Правило параллелограммаСовместим начала векторов (рис. 21, а), сохраняя их направления (рис. 21, б). Построим параллелограмм ABCD, принимая векторы за его стороны. Сумма векторов есть вектор совпадающий с диагональю АС параллелограмма: (см. рис. 21, б).
Правило треугольникаСовместим конец вектора с началом вектора сохраняя их направления (рис. 21, в). Вектор проведенный из начала вектора в конец вектора равен сумме (см. рис. 21, в).
Из рисунков 21, б и 21, в ясно, что правило треугольника и правило параллелограмма дают одинаковые результаты. А как найти разность векторов?
Вычитание векторовПусть начала векторов совмещены (рис. 22). Проведем вектор из конца вычитаемого вектора в конец уменьшаемого вектора Вектор есть искомая разность: Докажите с помощью построения, что Такой способ вычитания векторов очень удобен.
Правило многоугольника
Чтобы найти сумму нескольких векторов (например, ), каждый следующий вектор нужно проводить из конца предыдущего (рис. 23). Замыкающий вектор проведенный из начала первого вектора в конец последнего есть сумма данных векторов:
Правило многоугольника следует из правила треугольника.
Модуль суммы векторовНе путайте модуль суммы векторов, т. е. и сумму их модулей Равенство выполняется только для одинаково направленных векторов (см. рис. 20, а на с. 13). Во всех остальных случаях т. е. модуль суммы векторов меньше суммы их модулей. Так получается потому, что в любом треугольнике (см. рис. 21, в) длина одной стороны меньше суммы длин двух других сторон. Проверьте это на примерах.
Нуль-векторПусть вектор равен вектору Тогда их разность т. е. нуль-вектору.
Главные выводы:
- Векторные величины характеризуются модулем и направлением, скалярные — только числовым значением.

- Сумму двух векторов находят по правилу параллелограмма или треугольника.
- Разность двух векторов находят, проводя вектор из конца вычитаемого вектора в конец уменьшаемого (при совмещенных началах векторов).
- Разность векторов можно найти как сумму
- Произведение вектора на число есть вектор При направления векторов совпадают, а при — противоположны. Модуль вектора равен
Скалярные и векторные величины
К пониманию того, что для описания природы нужно использовать язык математики, ученые пришли давно. Собственно, некоторые разделы математики и были созданы для того, чтобы описывать природу кратким и доступным языком. Так, для определения мгновенной скорости, работы переменной силы, объема тел неправильной формы и т. д. были созданы дифференциальное и интегральное исчисления. Для более наглядного описания физических процессов научились строить графики функций, а для быстрой обработки результатов эксперимента придумали методы приближенных вычислений.
Физические величины, используемые в физике для количественной характеристики физических явлений и объектов, делятся на два больших класса:
К скалярным величинам, или скалярам (от лат. scalaris — ступенчатый), относятся величины, которые определяются только значением. Например, масса тела — скалярная величина, и если мы говорим, что масса тела равна двум килограммам (m=2 кг), то полностью определяем эту величину. Сложить две скалярные физические величины означает сложить их значения, представленные в одинаковых единицах. Понятно, что складывать можно только однородные скаляры (например, нельзя складывать массу и время, плотность и работу и т. д.).
Для определения векторных величин важно знать не только их значения, но и направления. Вектор (от лат. vector — носитель) — это направленный отрезок, то есть отрезок, имеющий и длину, и направление.
Правила сложения (вычитания) векторов отличаются от правил сложения (вычитания) скалярных величин.
Сумму двух векторов находят по правилу параллелограмма или по правилу треугольника (рис. 3.1, 3.2). Как найти сумму нескольких векторов, показано на рис. 3.3, как найти разность двух векторов, показано на рис. 3.4.
В результате умножения векторной величины на скалярную величину k получается вектор (рис. 3.5).
Обратите внимание! Единица произведения векторной и скалярной величин определяется как произведение единицы одной величины на единицу другой. Например, нужно найти перемещение самолета, который в течение 0,5 ч летит на север со скоростью 500 км/ч. Вектор перемещения: . Поскольку t > 0, то вектор перемещения будет направлен в ту же сторону, что и вектор скорости , а модуль вектора перемещения будет равен: s v = =t 500 км /ч⋅ = 0 5, ч к 250 м.
Вектор перемещения: . Поскольку t > 0, то вектор перемещения будет направлен в ту же сторону, что и вектор скорости , а модуль вектора перемещения будет равен: s v = =t 500 км /ч⋅ = 0 5, ч к 250 м.
- Заказать решение задач по физике
Как найти проекции вектора на оси координат
Осуществлять математические операции с векторами гораздо сложнее, чем со скалярами, поэтому, решая задачи, от векторных физических величин переходят к их проекциям на оси координат.
Пусть вектор лежит в плоскости XОY (рис. 3.6). Опустим из точки А (начало вектора ) и точки В (конец вектора ) перпендикуляры на ось ОX. Основания этих перпендикуляров — точки — проекции точек А и В на ось ОX, а отрезок — проекция вектора на ось ОX. Проекцию вектора обозначают той же буквой, что и вектор, с указанием оси в нижнем индексе, например: . Если из начала и конца вектора провести перпендикуляры к оси ОY, получим отрезок — проекцию вектора на ось ОY ( ). Знак проекции вектора зависит от направлений вектора и оси координат. Если от проекции начала вектора до проекции его конца нужно двигаться в направлении оси координат, то проекция вектора на эту ось считается положительной, а если наоборот, то проекция вектора считается отрицательной (см. рис. 3.6).
Если от проекции начала вектора до проекции его конца нужно двигаться в направлении оси координат, то проекция вектора на эту ось считается положительной, а если наоборот, то проекция вектора считается отрицательной (см. рис. 3.6).
В общем случае проекцию вектора находят обычными геометрическими методами (рис. 3.7, а). На практике часто приходится иметь дело со случаями, когда вектор параллелен или перпендикулярен оси координат.
Если вектор параллелен оси координат, а его направление совпадает с направлением оси, то его проекция на эту ось положительна и равна модулю вектора (рис. 3.7, б). Если направление вектора противоположно направлению оси координат, то его проекция на эту ось равна модулю вектора, взятому с противоположным знаком (рис. 3.7, в). Если же вектор перпендикулярен оси координат, то его проекция на эту ось равна нулю (рис. 3.7, г). Очень важным свойством проекций является то, что проекция суммы двух векторов (рис. 3.8) или нескольких векторов на координатную ось равна алгебраической сумме проекций этих векторов на данную ось.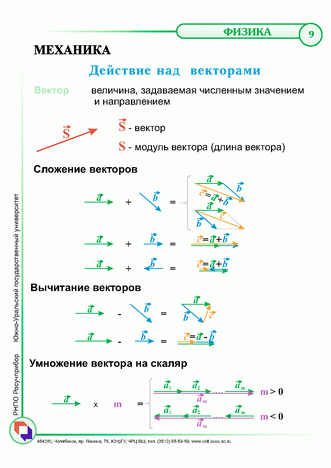
Именно это свойств позволяет заменять в уравнении векторные величины их проекциями — скалярными величинами и далее решать полученное уравнение обычными алгебраическими методами.
Урок-презентация «Вектор. Действия над векторами»
Урок-презентация «Вектор. Действия над векторами»- Родионова Юлия Александровна, учитель физики
Разделы: Математика, Физика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (4 МБ)
Многие физические величины, например, скорость,
ускорение, сила, характеризуются не только
численным значением, но и направлением, то есть
являются векторными величинами. Данный урок –
презентация посвящен изучению понятия вектора и
действия над векторами с примерами решения
физических задач.
Цели урока:
- Образовательные: введение понятия вектор, рассмотрение правил сложения векторов, нахождение проекций вектора на оси координат.
- Развивающие: развитие аналитического мышления, развитие графических навыков у учащихся.
- Воспитательные: воспитание навыков обще ученической деятельности.
Задачи урока:
Тип урока: урок изучения нового материала
Оборудование: мультимедийный проектор.
Описание презентации см. в приложении.
Конспект урока
| Этап урока | Время | Учитель | Ученики |
| Организационный момент | 1 мин. | Приветствие друг друга. | Готовятся к уроку. |
| Актуализация знаний | 5 мин. | Из курса физики вам известно, что все
физические величины имеют численное значение, но
есть физические величины, например, такие как
скорость и силы (слайд 1), которые имеют не
только численные значения, но и направление. То
есть все физические величины можно разделить на
те, которые имеют только численное значение. Их
называют скалярными. И физические величины,
которые характеризуются численным значение и
направлением. Такие физические величины
называют векторными (слайд 2). Их
называют скалярными. И физические величины,
которые характеризуются численным значение и
направлением. Такие физические величины
называют векторными (слайд 2). | Слушают учителя и делают записи в тетрадях. Отвечают на вопросы |
| Сейчас перед вами будут появляться
физические величины. Ваша задача распределить их
на группы (слайд 3). Давай проверим
правильность вашего ответа. Бывает так, что на тело действует несколько сил и необходимо знать куда будет двигаться тело, а для этого надо знать, как можно обращаться с векторными величинами. Сегодня мы с вами и будем говорить о векторах и действиях над ними. | Учащиеся делают свои предположения | ||
| Изучение нового материала | 38 мин. | Тема урока “Векторные величины.
Действия над векторами”. (слайд 4). Учитель
дает определение вектора (слайд 5). Рассмотрим правила действия над векторами. Вектора можно складывать. Сложение векторов возможно по правилу параллелограмма и треугольника. Рассмотрим их последовательно. Учитель объясняет правила сложения векторов (слайд 6). Правило треугольника позволяет нам складывать несколько векторов. Учитель объясняет, как складывать несколько векторов (слайд 7). Вектора не только можно складывать их так же можно и вычитать. Учитель объясняет правила вычитания векторов (слайд 8). | Слушают учителя и делают записи и чертежи в тетрадях |
| Рассмотрим пример физической задачи на
сложение векторов (слайд 9). “Крокодил
переплывает реку перпендикулярно берегу.
Скорость, с которой он гребет равна v1.
Скорость течения реки равна v2. Чему будет
равна скорость крокодила относительно берега
реки?” В курсе физики 7 класса вы находили
равнодействующую сил, действующих на тело. Приведу пример из сказки про репку. (слайд 11) | учащиеся решают задачу | ||
| Теперь перейдем к нахождению проекций вектора на оси координат. Учитель дает определение проекции и объясняет, как найти проекцию вектора на оси координат и модуль вектора (слайд 12, 13). | Учащиеся смотрят на экран. Учащиеся слушают и делают записи в тетрадь | ||
| Решим задачу (слайд 14). “Найдем проекции силы тяжести, которая действует на тело массой 1 кг, на оси координат.” После того как учащиеся получили ответ, учитель показывает правильное решение данной задачи. | Учащиеся решают задачу | ||
| Домашнее задание | 1 мин. | Учащимся задается домашнее задание.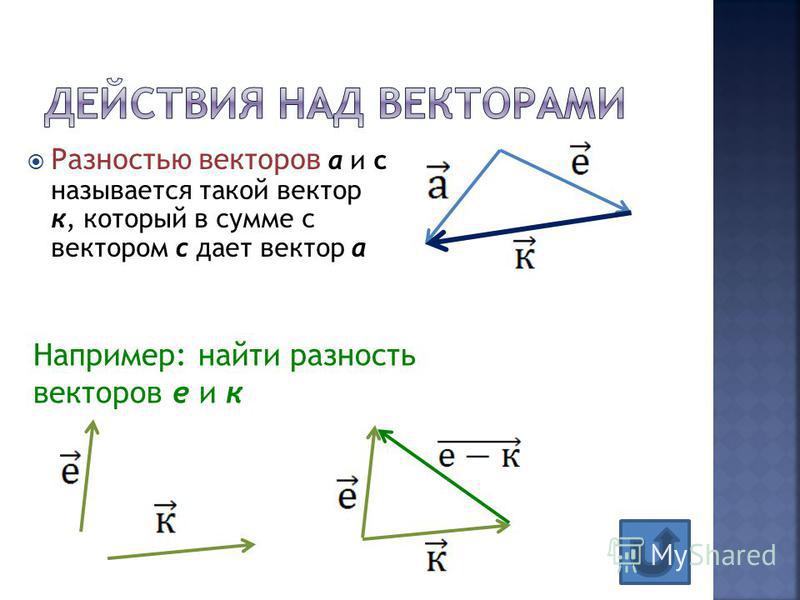 | Записывают д.з. |
Векторы. Действия над векторами
Характеристика урока:
Данный урок является вторым в разделе «Векторы».
Теме «Векторы в пространстве» в примерной программе ФИРО отводится 12 часов.
Темы разбиты следующим образом:
Понятие вектора. Действия над векторами
1.Скалярные и векторные величины. Угол между векторами. Сумма векторов
2.Противоположные векторы. Разность векторов. Умножение вектора на число
3.Коллинеарные векторы. Разложение вектора
Прямоугольная декартова система координат
4.Прямоугольная декартова система координат. Координаты вектора. Длина вектора
5.Скалярное произведение векторов. Свойства скалярного произведения
6.Угол между векторами
Для гуманитарного и естественно-научного профилей профессионального образования более характерным является усиление общекультурной составляющей учебной дисциплины с ориентацией на визуально-образный и логический стили учебной работы.
Урок проводится в нестандартной форме с целью поддержания интереса к предмету. Учащиеся на подобных уроках получают хороший эмоциональный заряд, так как урок проходит в непринужденной доброжелательной обстановке. Важным положительным эффектом применения компьютерной техники на уроке является повышение мотивации учения. При изучении темы “Векторы в пространстве” необходимо актуализировать довольно большой объем знаний, полученных в 9 классе. С использованием компьютера этот процесс идет значительно быстрее, а за счет экономии времени удается рассмотреть большее количество задач, сократить время на повторение пройденного материала и усвоение нового материала за счет большей наглядности и активизации зрительной памяти. Чертеж, выполненный на доске, проигрывает виртуальному уже хотя бы потому, что виртуальный можно воспроизводить в неизменном виде (что актуально для зрительной памяти) любое количество раз; при необходимости можно возвращаться к предыдущим этапам построения.
Использование компьютерных технологий в образовательном процессе вообще и на уроках математики в частности, позволяет придти к следующим выводам:
Мультимедийная система обеспечивает:
Наглядность материала, в том числе, за счет звука, цвета, движения;
Ускорение темпа урока;
Свободу постоянного экспериментирования с целью улучшения методики преподавания;
Последовательный характер обучения за счет планомерного накапливания наглядных электронных пособий, позволяющих с легкостью в любой момент вернуться к уже знакомым, эмоционально окрашенным образам пройденного материала, которые могут быть гораздо экспрессивнее всем известных опорных сигналов.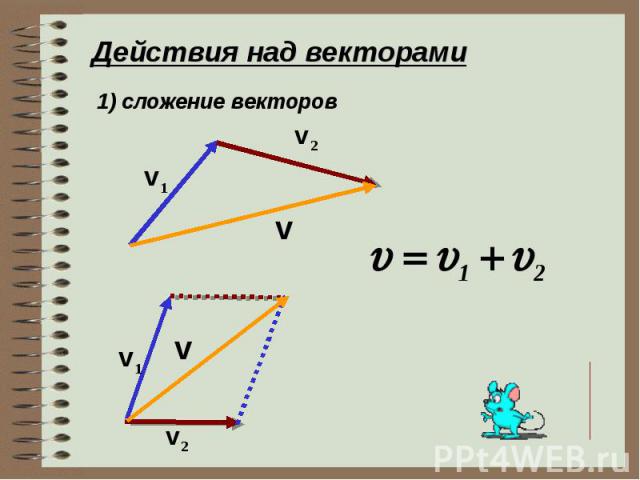
Компьютер на уроке — это педагогическая реальность, которая твердо вошла в нашу жизнь; при этом компьютер можно рассматривать как еще одно дополнение к процессу обучения, а не заменяющее учителя и учебник средство обучения.
В этой теме основной акцент делается на формирование наглядных представлений. Для каждого из рассматриваемых случаев даются определения и некоторые признаки. При изучении определений и свойств векторов основное внимание необходимо уделить усвоению формулировок и умению применять их к решению задач.
Основное внимание направлено на задачи вычисления суммы и разности векторов, нахождения координат вектора, через начало и конец вектора , умножения вектора на число, а также признака коллинеарности векторов. При повторении определений равных и сонаправленых, противоположных и противоположнонаправленных векторов особое внимание следует уделить “реальному” изображению этих векторов. С этой целью различные векторы иллюстрирую на отдельных слайдах и на прямоугольном параллелепипеде.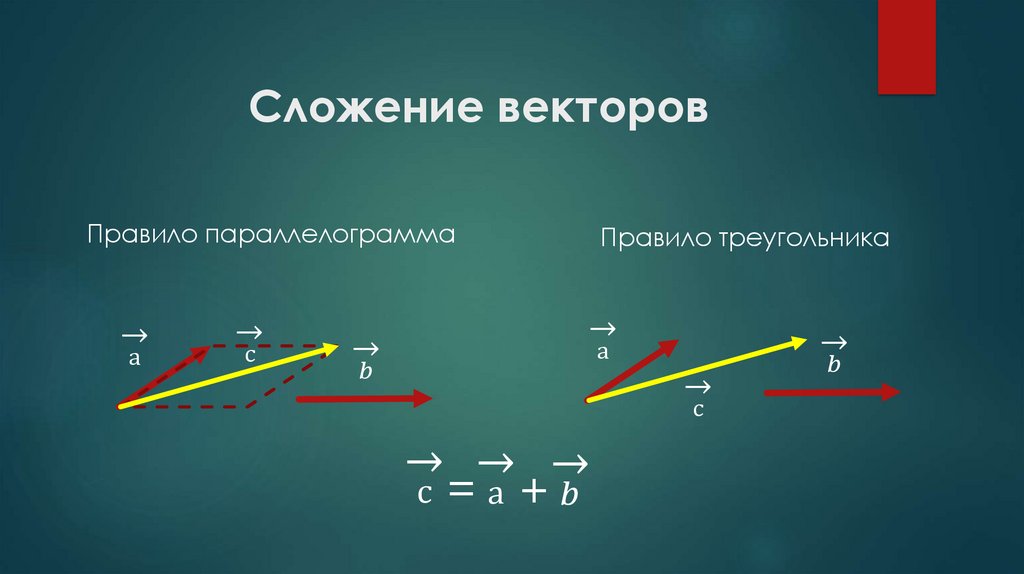
Работая на уроке, учащиеся овладевают:
1. Учебно-интеллектуальными умениями и навыками:
— по формулам вычисляют координаты вектора, длину вектора, сумму и разность векторов, умножают вектор на число.
2. Учебно-исследовательским:
— анализируют учебный материал 9 класса , сравнивают коллинеарные векторы, равные, сонаправленные, противоположные и противоположнонаправленные векторы по их координатам и представляя их графически.
3. Учебно-организационными:
— планируют работу, осуществляют самоконтроль.
Чтобы урок для учащихся был активным и максимально индивидуализированным, чтобы реализовались особенности каждого учащегося, применяю технологию интерактивного обучения с опорными конспектами.
Тема урока: Векторы в пространстве. Действия с векторами
Цели урока:
образовательные:
Ввести понятие вектора в пространстве, его длины, понятие коллинеарных и равных векторов; действия над векторами в пространстве.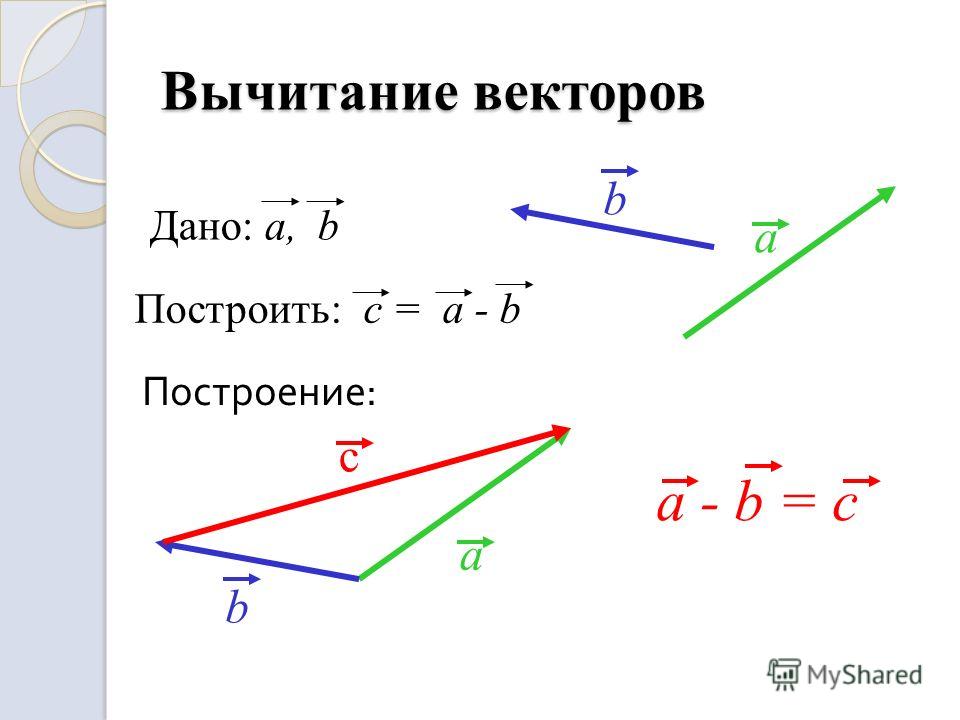
развивающие:
Развитие пространственного воображения учащихся.
Развивать умения строить логическую цепочку рассуждений, анализировать, выделять главное, сравнивать, строить аналогии, обобщать и систематизировать, делать выводы.
Развивать умение работать в должном темпе.
воспитательные:
Воспитание умения слушать, умения работать в малых группах.
методические:
Активизация мыслительно-познавательной деятельности учащихся.
Создание условий для формирования знаний, умений и навыков
Тип урока: урок изучения нового материала.
Вид урока: урок с компьютерным сопровождением.
Интерактивная технология: работа с опорным конспектом, во время компьютерного сопровождения
Учебный предмет: геометрия
Уровень образования школьников: урок проводился с учащимися 1 курса колледжа «Подмосковье».
Метод обучения: наглядный; демонстрация мультимедийной презентации.
Дидактическое обеспечение:
Материально-техническое обеспечение:
Компьютер.
Экран.
Мультимедийный проектор.
Мультимедийная презентация.
Межпредметные связи:
Алгебра: «Действия над действительными числами»
Физика: «Сила», «Скорость», «Движение», «Давление»
А так же биология, химия, экономика, психология, литература
Структура урока:
Организационный момент.
Мотивация учебной деятельности.
Изучение нового материала и применение знаний при решении типовых задач.
Самостоятельное применение знаний, умений и навыков.
Задание на дом.
Рефлексия.
Итог урока.
Ход урока:
Организационный момент.
Преподаватель приветствует учащихся и отмечает в журнале отсутствующих.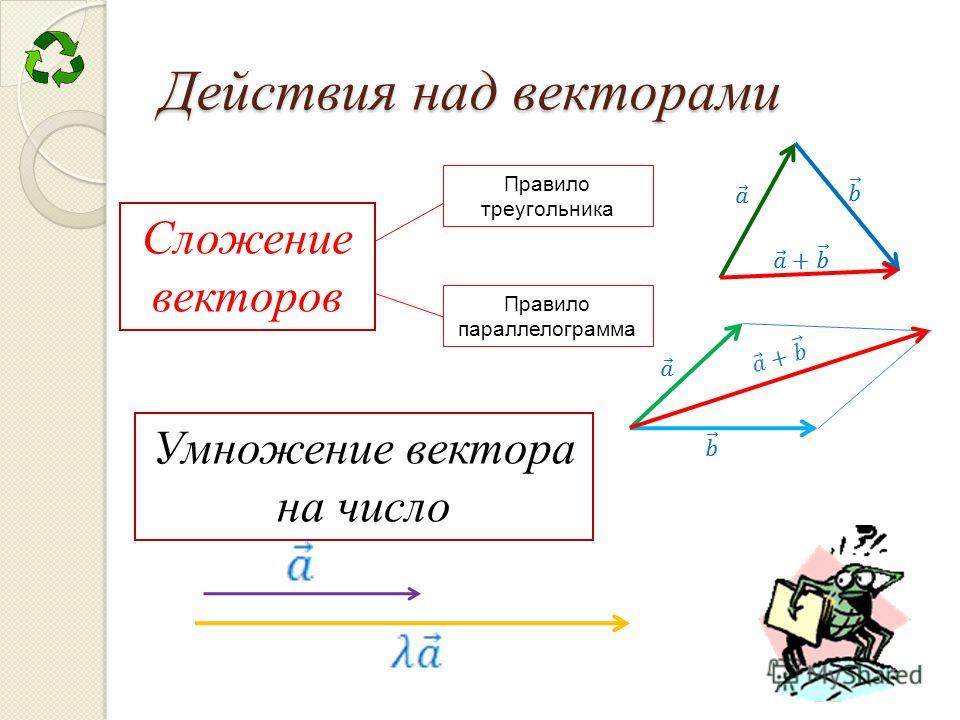
II. Мотивация учебной деятельности.
Вступительное слово преподавателя:
(слайд 1)
Эпиграфом к нашему уроку я взяла высказывание американского физика Юджина Пола Вигнера: “Математика — это наука о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями“. Сегодня как раз мы и будем заниматься такими хитроумными операциями над специально разработанными понятиями.
(слайд 2) Шарада:
Мой первый слог — почтенный срок,
Коль прожит он недаром;
Модель второго на столе,
Румяна, с пылу с жару.
Меня вы встретите везде –
Такой я вездесущий.
А имя громкое мое –
Латинское «несущий».
(Век-тор)
Слайд(3-4)
Преподаватель сообщает тему урока и ставит задачу совместного сотрудничества с учащимися на период урока,
Слайд(5-8)
В наши дни понятие «вектор» постоянно встречается в газетных и журнальных публикациях, в выступлениях политиков, ученых, педагогов.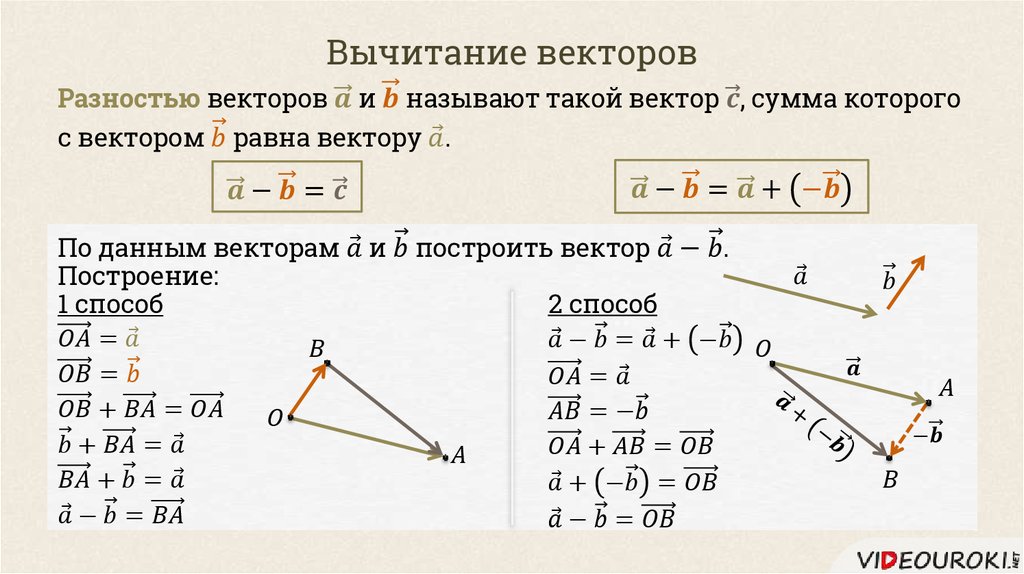 Обсуждая важнейшие процессы в жизни общества, говорят о векторе реформ и его социальной составляющей, о векторе экономических преобразований и его изменении, о направлении вектора развития системы образования.
Обсуждая важнейшие процессы в жизни общества, говорят о векторе реформ и его социальной составляющей, о векторе экономических преобразований и его изменении, о направлении вектора развития системы образования.
С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор.
Понятие о векторе как направленном отрезке вошло в сознание и речь современного образованного человека.
Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел (Гаусс, 1831).
А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839 – 1903), который в 1901 году опубликовал обширный учебник по векторному анализу
Гибсс — американский физик, физикохимик, математик и механик, один из создателей векторного анализа, статистической физики, математической теории термодинамики, что во многом предопределило развитие современных точных наук и естествознания в целом.
Образ Гиббса запечатлён в «Галерее славы великих американцев». Его имя присвоено многим величинам и понятиям химической термодинамики: энергия Гиббса, парадокс Гиббса, правило фаз Гиббса, уравнения Гиббса — Гельмгольца, уравнения Гиббса — Дюгема, лемма Гиббса, треугольник Гиббса — Розебома и др.
(Слайд 6)
Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа.
Слайд(7)
Почти одновременно с ним исследованиями в том же направлении занимался
английский математик — Уильям Кингдон Клиффорд (1845–1879)
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
( Слайд 8) Коши
Слайд(9)
Векторы всюду.
Предлагается учащимся сделать небольшие выступления по заданной теме
1-ый учащийся
Вектор используются везде, даже там, где мы их не замечаем, например в литературе:
Маргарита Алигер, биография которой вызывает искренний интерес у поклонников ее творчества, – знаменитая советская поэтесса, удостоившаяся Сталинской премии второй степени за поэму «Зоя» о бесстрашном подвиге советской девушки Зои Космодемьянской. После семилетки училась в химическом техникуме. С детства писала стихи.
Векторы в физике.
О, физика, наука из наук!
Все впереди!
Как мало за плечами!
Пусть химия нам будет вместо рук,
Пусть станет математика очами.
Не разлучайте этих трех сестер,
Познания всего в подлунном мире.
Тогда лишь будет ум и глаз остер,
И знанье человеческое шире.
Вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись».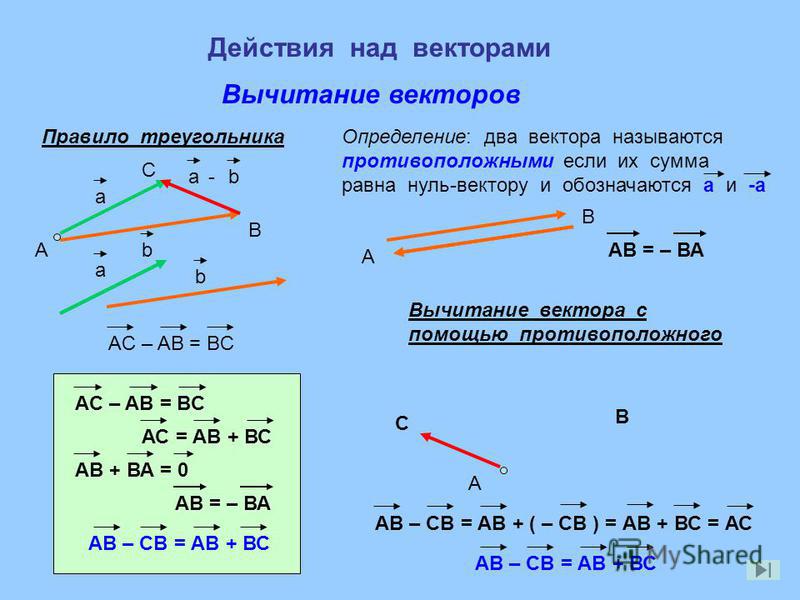 Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу равна нулю. А сила, как известно, векторная величина.
Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу равна нулю. А сила, как известно, векторная величина.
2 –ой учащийся
В химии. Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца. Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее, основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».
3 –ий учащийся
Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы. Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.
Например, вши переносят возбудителей сыпного тифа, крысы – чумы. Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.
4-ый учащийся
Векторы в экономике
Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора. Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.
5-ый учащийся
Векторы в психологии
На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов. Системно-векторная психология позиционируется не как отрасль классической психологии или определенное течение, а как отдельная наука изучения типологии личности.
Вектор – это симбиоз физиологических и психологических качеств человека. Это — характер, темперамент, здоровье, привычки индивида.
Векторы в повседневной жизни
Мы обратили внимание, что векторы, помимо точных наук, встречаются нам каждый день, т.е. повседневно. Векторы – указатели, которые помогают нам быстро найти тот или иной объект, отдел и сэкономить время, или стрелки дорожных знаков.
Слайд(10)
В курсе 9 класса вы изучали векторы на плоскости
Перед нами стоит задача – дать определение вектора в пространстве, научиться находить его длину по координатам начала и конца вектора и рассмотреть основные действия над векторами: сложение, вычитание, умножение на число, а также рассмотреть коллинеарные и компланарные векторы.
Поставленную перед нами задачу мы будем решать на основе сравнительного анализа и установления закономерностей: как давались определения вектора и операций над векторами на плоскости и как они формулируются для векторов в пространстве. На каждой парте лежат опорные конспекты, правую часть которых необходимо заполнить учащимся, пользуясь материалом учебника.
III. Изучение нового материала и применение знаний при решении типовых задач.
На прошлом уроке вы составляли опорные конспекты. где отмечали основные определения и действия с векторами на плоскости. Теперь я предлагаю вам в этих же конспектах заполнить вторую часть их
На плоскости | В пространстве |
Определение. Вектором называется направленный отрезок Длина этого отрезка называется длиной (модулем, абсолютной величиной) вектора. = | | = АВ | Определение. |
Координаты вектора. (х2 – х1; у2 – у1) | Координаты вектора. А1(х1; у1; z1) А2 (х2; у2; z2) (________;_________;__________) |
Длина вектора. (х; у) = + у2 | Длина вектора. (х; у; z) = √ |
Коллинеарные векторы Векторы .лежащие на одной прямой или на парраллельных прямых | Коллинеарные векторы |
Сонаправленные векторы |
. |
Противоположнонаправленные векторы | |
Признак коллинеарности векторов (х1; у1) (x2; y2) = | Признак коллинеарности векторов (х1; у1; z1) (x2; y2; z2) |
Равные векторы. (х1; у1) х1 = х2 (х2; у2) у1 = у2 Векторы равны, если: Равны длины векторов Векторы сонаправлены | Равные векторы. (х1; у1; z1) (х2; у2; z2) Векторы равны, если: 1. 2. |
Противоположные векторы. (х1; у1) x1 = — x2 (x2; y2) y1 = — y2 | Противоположные векторы. (х1; у1; z1) (x2; y2; z2) |
Сумма векторов (х1; у1) и (x2; y2) + = (x1 + y1; x2 + y2) | Сумма векторов (х1; у1; z1) и (x2; y2; z2) + = (______; ______;_______) |
Р азность векторов (х1; у1) и (x2; y2) — = (x1 — y1; x2 — y2) | Разность векторов (х1; у1; z1) и (x2; y2; z2) — = (______; _______;________) |
Умножение вектора на число λ (х; у) = (λх; λу) | Умножение вектора на число λ (х; у; z) = (λх; λу; λz) |
Вопросы:
(слайд12)
Дайте определение вектора в пространстве и запишите его в таблицу.
(слайд 13)
Как найти координаты вектора, зная координаты точек начала и конца вектора., запишите в таблицу
(слайд 14)
Задача Найдите координаты вектора , если М(10; -4; 2) и К(16; 2 -5).
Ответ: (6; 6; -7)
(слайд 15)
Как вычислить длину вектора, зная его координаты, запишите в таблицу
(слайд 16)
Задача 2. Найдите модуль вектора ( — 5; 1; 2).
Ответ:
(слайд 17)
Любая точка пространства является нулевым вектором. Длина нулевого вектора равна 0.
(слайды 18 -20 )
Коллинеарные вектора, сонаправленные, противоположнонаправленные, признак коллинеарности , записать в таблицу
(слайд21)
(слайд 22)
Устно решить задачу. Какие векторы на рисунке сонаправлены, противоположнонаправлены. Найти длины векторов
Найти длины векторов
(слайд23,24)
Равенство векторов, противоположные векторы, записать в таблицу
(слайд25)
Могут быть ли равными векторы?
( слайд26)
Сколько равных векторов изображено на рисунках?
(слайд 27)
При каком значении n векторы (4; 2n — 1; -1) и (4; 9 – 3n; -1) равны?
Ответ: при n = 2
(слайд 28)
Лови ошибку.
(слайд 29)
Назовите векторы.
( слайды30-36)
Дайте определение суммы векторов. А если сложить несколько векторов в пространстве, какая фигура получится?
Заметили ли вы, что многоугольник, который получается при построении суммы нескольких векторов, может оказаться пространственным, т. е. не все его вершины лежат в одной плоскости?
(слайд 37)
Задача 5. Найдите сумму векторов и , если А(2; 3; -1), С(3; -2; 0), а В – произвольная точка пространства
Найдите сумму векторов и , если А(2; 3; -1), С(3; -2; 0), а В – произвольная точка пространства
Ответ: (1; -5; 1)
(слайды 38-39)
Дайте определение разности векторов.,запишите в таблицу
(слайд 40)
Задача 6. Найдите разность векторов и , если В(3; 7; 10), С(1; 9; -6), а А – произвольная точка пространства.
Ответ: (2; -2; 16)
(слайды 41-43)
Как умножается вектор на число?,запишите в таблицу
(слайд 44)
Задача 7. Найдите координаты вектора с = 2а -3b, если а(7; -3; 0) и b(4; 1; -2)
Ответ: (2; -9; 6)
(слайд 45)
Задача 8. Найдите абсолютную величину вектора 3 , если (4; -4; 2) Рассмотреть 2 способа решения.
Ответ: = 18
Самостоятельное применение знаний, умений и навыков.
(слайд 50)
Устный тест:
1. Что называется вектором?
Что называется вектором?
а)любой отрезок
б)отрезок, обозначенный двумя заглавными латинскими буквами
в) отрезок с выбранным направлением
2. Какой вектор является нулевым?
а)длина вектора равна 0
б)вектор лежит на прямой
в)вектор обозначен одной буквой
3. Векторы коллинеарны, если…
а)лежат на прямых
б)лежат на параллельных прямых
в)один из векторов нулевой
5. Векторы называются равными, если …
а)их длины равны
б)их модули равны и векторы направлены в одну сторону
в)они отложены от одной точки
(слайд 52)
Даны векторы (-3; 0; 4) и (2; 4; -4)
Запишите:
Длину вектора .
При каких значениях k и m вектор (k; -3; m) коллинеарен вектору ?
Из векторов (1; 1; -2), (-1; -2; 2), (2; -4; 4), (-4; -4; 2) укажите векторы противоположнонаправленные с вектором .
(Слайд53)
Дано:
Решение
Находим координаты вектора
;
Затем находим координаты вектора
Теперь находим аналогично координаты вектора
Теперь находим сумму данных векторов, складывая соответствующие координаты:
Ответ:
С учетом познавательных и когнитивных способностей необходимо учащимся раздать разноуровневые задания на применение навыков и умений действий над векторами (работа в тетрадях).
Вариант А
Найдите координаты вектора , если
Даны векторы и Найдите координаты и длину вектора .
Вариант В
Даны векторы и Найдите координаты и длину вектора .
Даны векторы Найдите координаты вектора
Найдите длину вектора , если
Вариант С
Даны векторы Найдите координаты вектора
Найдите длину вектора , если
Из точки построен вектор . Найдите координаты точки , если:
Даны векторы и Найдите координаты и длину вектора .
Данный вид работы учащиеся выполняют в тетрадях, после чего учитель собирает тетради для проверки.
V. Задание на дом. (слайд 54)
VI. Рефлексия. (слад 55)
Закончи предложение: Я умею …, я могу …, я знаю ….
VII. Итог урока. Оценивание учащихся.
Скалярные и векторные величины в физике и математике » Kupuk.
 net
netВеличиной в физике и математике называют свойства физических тел, измеряемых при помощи выполнения математических операций. Они имеют единицы измерения и зависят от физических законов и аксиом. Выделяют скалярные и векторные величины, обладающие различными характеристиками и параметрами.
Особенности скалярных величин
Скалярные величины характеризуются только одним параметром — числовым значением. Они разделяются на 2 вида:
- Чистые скаляры. Характеризуются числовым значением, не находящимся в зависимости от осей отсчета — линий пересечения плоских поверхностей в единой системе координат.
- Псевдоскаляры. Находятся при помощи расчета числа, знак которого зависит от положительного направления осей в системе координат.
В физике в список скалярных величин входят:
- Масса — определяет величину материи и ее гравитационные свойства. Измеряется в килограммах и обозначается буквой латинского алфавита m.

- Температура — средняя кинетическая энергия физического тела. Выражается в кельвинах или градусах Цельсия.
- Работа — мера действия силы на физическое тело или систему тел. Измеряется в Джоулях и обозначается латинской буквой A.
- Длина — величина, определяющая дистанцию между 2 концами тела в продольном направлении. Исчисляется в метрах. Особым видом длины является путь — скаляр, выражающий расстояние между начальным и конечным положением объекта, осуществляющего перемещение по заданной траектории.
- Время — продолжительность действия или события. Рассчитывается в секундах.
- Период — время совершения 1 полного колебания. Обозначается символом T и измеряется в секундах.
- Частота — величина, обратная периоду. Определяет количество полных колебаний в единицу времени. Рассчитывается в Герцах.
- Объем — скаляр, обозначающий размер пространства, ограниченного поверхностями со всех сторон. Измеряется в м3.
- Напряжение — измеряет изменение потенциальной энергии тела, приходящейся на единицу заряда.
 Обозначается буквой U и рассчитывается в Вольтах.
Обозначается буквой U и рассчитывается в Вольтах. - Сила тока — скаляр, показывающий число электрических зарядов, проходящих через сечение проводника в единицу времени. Обозначается символом I и рассчитывается в Амперах.
- Энергия — обозначает способность тела осуществлять работу.
Если скаляры выражают одно единственное свойство физического тела, то они называются однородными. Величины, описывающие несколько свойств объекта, именуются разнородными. Однородные скаляры сравнимы: они либо равны, либо одна из них больше или меньше другой. Но скалярные величины разного рода не могут сравниваться друг с другом.
Определение положительного скаляра и его измерения
Понятие положительной скалярной величины и ее измерения позволяет сравнивать между собой однородные скаляры. Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.
Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.
Чтобы получить скалярную величину, достаточно умножить ее числовое значение на ее единицу измерения. Для структуризации и стандартизации вычислений физических параметров тела была разработана Международная система СИ. Она устанавливает единицы измерения для каждой величины. Во время проведения расчетов скалярных величин применяют алгебраические действия — сложение, вычитание, деление и умножение (отдельный подвид — возведение в степень).
Особенности векторных величин
Их определение: «В физике векторными величинами называются свойства материи, характеризующиеся несколькими параметрами: модулем и направлением». Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.
Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.
В физике и математике примерами векторных величин являются:
- Сила — мера взаимодействия физических веществ. Обозначается латинской буквой F и измеряется в Ньютонах. Три закона Исаака Ньютона составляют основу классической механики. С их помощью можно определить массу тела и его ускорение.
- Скорость — расстояние, пройденное материей за определенный временной промежуток. Маркируется символом V и рассчитывается в м/с. Скорость используется для определения пути и времени движения предмета при помощи формулы: S = V * t. Скорость, с которой тело движется по окружности, называется линейной.
- Ускорение — величина, показывающая изменение показателей скорости физического тела. Ускорение свободного падения действует на все тела, придавая им силу тяжести. Оно направлено к ядру Земли и равняется 9,8 м/с2
- Импульс — характеризует величину движения тела.
 Маркируется буквой латинского алфавита p и рассчитывается в кг*м/с. С помощью этой величины человек может определить массу физического тела и скорость ее передвижения.
Маркируется буквой латинского алфавита p и рассчитывается в кг*м/с. С помощью этой величины человек может определить массу физического тела и скорость ее передвижения.
На графиках функции векторные величины изображаются в виде прямой линии, имеющей направление и свои собственные координаты в заданном масштабе.
Свойства векторов
Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка. Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:
- Произведение вектора на косинус между осью и направленным отрезком равен проекции вектора.

- Проекция на ось принимает значения меньше 0, если отрезок с осью образует тупой угол.
- Проекция на ось принимает значение больше 0, если отрезок с осью образует острый угол.
Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.
Построение отрезков с направлением на плоскости осуществляется при помощи его координат для осей абсцисса и ордината. Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.
С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.
Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.
Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.
Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.
С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.
Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.
Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.
Действия над векторами презентация, доклад, проект
§2. Действия над векторами
Векторы можно:
Складывать;
Вычитать;
Умножать на ненулевое число;
Умножать вектор на вектор (скалярно, векторно, смешанно)
П.1. Сложение векторов
Пусть даны векторы и
Тогда суммой данных векторов будет вектор
, координаты которого найдем так:
Сложение векторов можно произвести по правилу треугольника или по правилу параллелограмма.
Правило треугольника сложения векторов
Правило параллелограмма сложения векторов
Свойства сложения векторов
П.2. Вычитание векторов
Пусть даны векторы и
Тогда разностью данных векторов будет вектор
координаты которого найдем так:
П.3. Умножение вектора на ненулевое число
Пусть дан вектор . Тогда произведением данного вектора на число называют вектор
,для которого выполнено:
Векторы и коллинеарные;
;
Векторы , если k>0
векторы , если k
Свойства умножения вектора на число
П. 4. Умножение векторов
4. Умножение векторов
А) Скалярное произведение двух векторов
Скалярным произведением двух векторов называют число равное произведению длин этих векторов на косинус угла между ними.
Пусть даны векторы и
Тогда их скалярное произведение равно:
Свойства скалярного произведения
Теорема
Пусть в ортонормированном базисе даны векторы и . Тогда их скалярное произведение найдем по формуле:
Доказательство: разложим данные векторы по базису .Тогда получим:
Тогда
Ч.т.д.
Следствие 1.
Угол между векторами можно найти так:
Следствие 2
Векторы и перпендикулярны тогда и только тогда, когда .
Следствие 3
Ненулевые векторы и параллельны тогда и только тогда, когда
В) Векторное произведение векторов
Тройка векторов называется упорядоченной, если известно какой из них является первым, вторым и третьим.
Упорядоченная тройка векторов является правой, если после приведения их к общему началу кратчайший поворот от первого ко второму вектору из конца третьего вектора виден против часовой стрелки. Иначе, тройка векторов – левая.
1
2
3
Векторным произведением векторов
называют вектор , для которого выполнено:
Свойства векторного произведения
5. Площадь параллелограмма, построенного на векторах и равна длине вектора
Теорема
Пусть в ортонормированном базисе даны векторы и . Тогда их векторное произведение найдем по формуле:
Тогда их векторное произведение найдем по формуле:
Доказательство:
Разложим данные векторы по базисным векторам, тогда получим
Найдем векторное произведение данных векторов.
Так как
Аналогично по свойствам имеем
Тогда с учетом данных равенств имеем:
Ч.т.д.
С) Смешанное произведение трех векторов
Смешанным произведением векторов
называют число , равное скалярному произведению вектора на вектор , т.е.
Свойства смешанного произведения
Векторы компланарны тогда и только тогда, когда .
На некомпланарных векторах можно построить параллелепипед, объем которого равен .
.
Объем пирамиды равен
Теорема
Пусть даны векторы
,
тогда их смешанное произведение вычисляется по формуле
Доказательство:
Так как по определению смешанное произведение есть число равное
, то найдем сначала координаты вектора, полученного в результате векторного произведения векторов и :
В результате вычисления данного определителя, находим координаты вектора
Найдем скалярное произведение векторов и .
Ч.т.д.
Линейная комбинация векторов
Векторы называются линейно зависимыми, если найдутся такие действительные числа , из которых хотя бы одно не равно нулю, а линейная комбинация данных векторов равна нулю.
Векторы называются линейно независимыми, если равенство нулю их линейной комбинации возможно лишь в случае, когда все действительные числа равны нулю.
Замечание 1
Если хотя бы один из векторов является нулевым, то эти векторы линейно зависимы.
Замечание 2
Если среди n векторов любые (n-1) векторов линейно зависимы, то и все n векторов линейно зависимы.
Теорема 1
Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.
Следствие 1.
Если два вектора неколлинеарны, то они линейно независимы.
Следствие 2.
Среди двух неколлинеарных векторов не может быть нулевого вектора.
Теорема 2
Необходимым и достаточным условием линейной зависимости трех векторов является их компланарность.
Следствие 3
Каковы бы не были неколлинеарные векторы и любой вектор , лежащий с ними в одной плоскости, найдутся такие действительные числа m и n, что
Теорема 3
Любые четыре вектора линейно зависимы.
Утверждение 1
Любая пара неколлинеарных векторов на плоскости образует на этой плоскости базис.
Утверждение 2
Любая тройка некомпланарных векторов образует базис в пространстве.
Скачать презентацию
ньютоновская механика — Каково значение скольжения вектора силы?
$\begingroup$
Сценарий 1:
Здесь $AB$ — линия действия силы $\underline{u}$, причем $AB$ проходит через центр масс бесконечно длинного жесткого и однородного стержня. Здесь $\vec{CD}=\underline{u}$. Теперь, если $\vec{CD}$ сдвигается и $\vec{CD}$ становится $\vec{EF}=\underline{u}$, физический эффект останется прежним. Другими словами, не имеет значения, действует ли вектор $\underline{u}$ в точке $C$ или в точке $E$, воздействие на стержень останется тем же. Таким образом, в этом сценарии есть польза от существования линии действия $AB$.
Другими словами, не имеет значения, действует ли вектор $\underline{u}$ в точке $C$ или в точке $E$, воздействие на стержень останется тем же. Таким образом, в этом сценарии есть польза от существования линии действия $AB$.
Сценарий 2:
Здесь $BA$ — линия действия силы $\underline{u}$, причем $BA$ проходит через центр масс жесткого и однородного стержня. Пусть теперь в точке $O$ стержня действует сила $\vec{OA}=\underline{u}$. Теперь, поскольку сила является скользящим вектором, мы можем скользить $\vec{OA}$, и $\vec{OA}$ становится $\vec{BC}$. Однако у меня есть проблема. У вектора $\vec{BC}$ нет физического смысла/значимости, как у $\vec{OA}$, в отличие от сценария 1. Согласно этому ответу, $\vec{OA}$ можно скользить по его линии действия, а $\vec{OA}$ и $\vec{BC}$ действуют на планку одинаково. Однако, повторяю, я считаю, что $\vec{BC}$ не имеет физического смысла, поскольку ни $B$, ни $C$ не являются точками на стержне. $\vec{OA}$ действует на стержне и имеет физический смысл, поскольку $O$ — точка на стержне. Однако $\vec{BC}$ не действует буквально ни на что, в отличие от $\vec{OA}$, так каков же физический смысл смещения вектора $\vec{OA}$ в этом случае?
Однако $\vec{BC}$ не действует буквально ни на что, в отличие от $\vec{OA}$, так каков же физический смысл смещения вектора $\vec{OA}$ в этом случае?
Мой вопрос:
- В чем смысл смещения $\vec{OA}$ в сценарии 2?
Это может помочь вам ответить на мой вопрос.
- ньютоновская механика
- силы
- векторы
- обозначения
- статика
$\endgroup$
7
$\begingroup$
Слишком длинный комментарий.
Сценарий 2:
Теперь, поскольку сила является скользящим вектором,
Пожалуйста, внимательно прочитайте мой ответ на ваш предыдущий вопрос, в частности
- $\;\ldots$ Здесь,
ясно, что $\vec F$ и $\vec{OA}$ — это « свободных векторов».

и
Мораль такова: после того, как физический сценарий был математически смоделирован (абстрагирован), система классификации < свободный вектор против скользящего вектора против связанного вектора > не нужен; вместо этого тщательно соблюдая формулировку и условия определений и теорем гарантирует, что выполняемые шаги действительны.
- $\;\ldots$ Здесь,
ясно, что $\vec F$ и $\vec{OA}$ — это « свободных векторов».
Сценарий 1:
Здесь $AB$ — линия действия силы $\underline{u}$, а $AB$ проходит через центр масс бесконечно длинного твердого тела. и равномерный бар. Здесь $\vec{CD}=\underline{u}$. Теперь, если $\vec{CD}$ сдвигается, и $\vec{CD}$ становится $\vec{EF}=\underline{u}$, физический эффект останется прежним. Другими словами, это не независимо от того, действует ли вектор $\underline{u}$ в точке $C$ или точка $E$,
В этом (математическом) сценарии, как описано,
- $\vec{CD}$ и $\vec{EF}$ на самом деле являются одним и тем же объектом;
- $\vec{CD}$ не «действует» ни в одной конкретной точке (его название не означает, что он действует в точке $C$)
- о физическом эффекте речи не идет (не указано).

$\endgroup$
10
$\begingroup$
Вы понимаете, что теория твердых тел — это идеализация а не реальность. Реальная сила имеет не только линию действия, но и точку (точки) приложения, а тела упругие, а не жесткие.
Только в контексте этой идеализации можно по-настоящему применить правило скользящих векторов. Вы можете думать о математических силах против реальных сил. Математическая сила имеет величину, направление и линию действия, потому что она также сообщает момент силы (крутящий момент) относительно некоторой точки отсчета.
Именно эта комбинация силы и крутящего момента полностью описывает нагрузку на систему. Любая система сил, производящая одинаковую силу и крутящий момент, неотличима друг от друга (математически). Уравнения движения те же.
Математические силы не имеют точки начала координат, это векторы, принадлежащие где-то вдоль линии действия, где угодно.
На самом деле разумно предположить, что контактная сила действует где-то на поверхности тела (там, где линия действия пересекает тело). Но на другие точки могут действовать и другие силы.
Гравитация действует на все частицы тела и, таким образом, можно считать, что она сосредоточена в центре масс без ограничения общности (для твердых тел).
Плавучесть, аэродинамические силы, магнетизм могут иметь разные точки, в которых они действуют вдали от центра масс.
Но опять же, когда речь идет о ньютоновской механике, точка, на которую действуют силы, не имеет значения, но имеет значение результирующий крутящий момент относительно точки отсчета. Для динамических задач точкой отсчета должен быть центр масс, но для нединамических (статических) задач он может быть где угодно.
$\endgroup$
0
$\begingroup$
Во-первых, Крутящий момент сильно отличается от силы. Крутящий момент является величиной, зависящей от источника, что означает, что он зависит от точки, в которой вы его перемещаете. Если кто-то спросит вас «рассчитать крутящий момент?» Первый вопрос, о какой точке?
Крутящий момент является величиной, зависящей от источника, что означает, что он зависит от точки, в которой вы его перемещаете. Если кто-то спросит вас «рассчитать крутящий момент?» Первый вопрос, о какой точке?
Сравните это с силой: Для силы вы можете вычислить результирующую силу, действующую на тело относительно любой точки пространства, и все точки совпадут. Смотрите ответ Джона здесь.
Однако существует один особый случай, когда Крутящий момент становится своего рода независимой от источника величиной: когда результирующая сила равна нулю. Доказательство
Итак, в принципе, если у вас есть тело, движущееся по Земле, вы можете установить начало системы координат в какой-то точке на Марсе и спросить: «Сколько это тело вращается вокруг этой точки на Марсе?».
Когда все это убрано, что значит, что мы можем перемещать вектор силы по всем этим точкам, и крутящий момент сохраняется? В основном это косвенное следствие того факта, что при расчете крутящего момента по определению $\vec{\tau} = \sum \vec{r_i} \times \vec{F_i}$, то, как масса распределена в пространстве, не имеет значения для расчета.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
электромагнетизм — Что такое вектор?
Спросил
Изменено 1 год, 5 месяцев назад
Просмотрено 342 раза
$\begingroup$
«Введение в электродинамику» Гриффитса имеет следующие строки:
Вектор — это любой набор из трех компонентов, который трансформируется так же, как смещение, при изменении координат.
Как мне интерпретировать эти строки?
Редактировать: Он добавил к этому еще несколько строк.
- электромагнетизм
- векторы
- определение
- геометрия
$\endgroup$
7
$\begingroup$
Существует три основных способа понимания векторов:
- Алгебраический
- Геометрический
- Трансформация
Алгебраическое определение распространено в математике, где векторы определяются как объекты, удовлетворяющие короткому списку аксиом. Это определение без координат.
Это определение без координат.
Геометрическое определение распространено в физике и, в частности, в механике, где вектор определяется как направленная величина. Это также определение без координат.
Трансформационное определение распространено в общей теории относительности, где оно помогает ввести касательные векторы. Оно тесно связано с множеством всех базисов векторного пространства.
В отличие от первых двух определений, оно не является свободным от координат. На самом деле, это настолько далеко от первых определений, насколько это возможно, поскольку нам нужно рассматривать множество всех компонент по всем основаниям!
Мы говорим, что это операционное определение, поскольку, когда мы фактически измеряем вектор, мы на самом деле не измеряем сам вектор напрямую. Вместо этого мы сначала устанавливаем базис и измеряем компоненты вектора относительно этого базиса.
Теперь, если нам представят список из 3 чисел, как мы узнаем, что они исходят из вектора в трехмерном пространстве? Итак, мы просим наблюдателя измерить компоненты объекта относительно множества всех оснований, и мы должны найти определенную связь между ними. То есть, если мы преобразуем основу из одной в другую, то компоненты будут преобразовываться контравариантно. На самом деле существует еще один тип трансформационного вектора, который преобразуется ковариантно. Вот почему принято делить трансформационные векторы на контравариантные и ковариантные векторы.
То есть, если мы преобразуем основу из одной в другую, то компоненты будут преобразовываться контравариантно. На самом деле существует еще один тип трансформационного вектора, который преобразуется ковариантно. Вот почему принято делить трансформационные векторы на контравариантные и ковариантные векторы.
Формализовать определение трансформационного вектора на самом деле непросто. Кажется, что может быть задействован какой-то функтор, включающий категорию всех базисов пространства. Это можно сделать с помощью категории элементов и построения Гротендика.
Учитывая сложность трансформационного определения, мы должны спросить, зачем его использовать? Это связано с тем, что не все векторные пространства представляются нам так же, как пространство вокруг нас, трехмерное пространственное векторное пространство. Например, возьмем, к примеру, цвет или изоспиновое пространство. Здесь мы не можем напрямую видеть вектор цвета или изоспина так же, как мы можем видеть пространственный вектор. Мы можем только ставить базы и брать компоненты. Поэтому трансформационное определение здесь наиболее естественно.
Мы можем только ставить базы и брать компоненты. Поэтому трансформационное определение здесь наиболее естественно.
$\endgroup$
$\begingroup$
Вы можете понять это на нескольких примерах.
В трехмерном пространстве можно задать вектор смещения с компонентами $(\delta x,\delta y,\delta z)$. Вы можете иметь другие векторы, такие как скорость, импульс, сила, ускорение. Чтобы понять разницу между вектором и не-вектором, полезно иметь несколько примеров не-векторов.
Масса $m$, заряд $q$ и температура $T$ не являются векторами, и это очевидно. А как насчет количества $(m, q, T)$? Он состоит из трех компонентов. Это вектор? Ответ — нет, потому что вектор не имеет направления и размера. Можно построить трехмерный график с массой, зарядом и температурой вдоль осей, но нет никакого способа определить своего рода «вращение», которое могло бы преобразовать массу в комбинацию заряда и температуры.
При поиске более вероятных кандидатов на вектор вы можете попробовать такие вещи, как $(yz,zx,xy)$. Сейчас не так просто понять, вектор это или нет.
Таким образом, формализуя это математически, можно сказать, что величина правильно называется «вектором», когда происходит следующее: если мы запишем ее в терминах компонентов, а затем повернем систему координат, то если компоненты изменятся на того же математического правила, что и компоненты $(\delta x, \delta y, \delta z)$ смещения в пространстве, то мы имеем вектор.
Изменение компонент вектора смещения $(\delta x, \delta y, \delta z)$ при повороте осей координат можно получить с помощью матрицы поворота $R$. Если новый набор компонентов какой-то другой величины правильно получен с помощью той же матрицы вращения $R$, то другая величина является вектором.
$\endgroup$
6
$\begingroup$
Здесь мы будем использовать правило суммирования Эйнштейна 9{\mu}$$
Что представляет собой то же соотношение между смещением в A и B
Таким образом, мы показали, что при преобразовании координат компоненты вектора должны преобразовываться так же, как смещение
$\endgroup$
0
$\begingroup$
То, что Гриффитс называет вектором, является, строго говоря, евклидовым вектором в трехмерном пространстве или четырехвектором в четырехмерном пространстве-времени.
Компоненты евклидова вектора (или четырехвектора) представляют собой способ его представления путем задания его проекций вдоль трех (или четырех) координатных осей или углов между вектором и определенными осями. Определение гласит, что если вектор не зависит от используемой нами системы координат (что важно, если он представляет собой физически значимую величину), то его компоненты должны измениться определенным образом, если мы изменим систему координат. Это позволяет нам определить, действительно ли два разных представления (например, одно в декартовых координатах, а другое в сферических координатах) относятся к одному и тому же базовому вектору.
Евклидовы векторы и четырехвекторы являются частными случаями более общего математического понятия вектора в линейной алгебре.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
геометрия — Какая связь между векторами в физике и алгебре?
Спросил
Изменено 9 лет, 4 месяца назад
Просмотрено 3к раз
$\begingroup$
Векторная математика мне очень интересна. Однако нам никогда не говорили о связи между векторами в физике (обычно представляемыми в виде стрелок, например вектором силы) и в алгебре (например, представляемыми в виде матрицы-столбца). Это действительно никогда не объяснялось хорошо в классах.
Однако нам никогда не говорили о связи между векторами в физике (обычно представляемыми в виде стрелок, например вектором силы) и в алгебре (например, представляемыми в виде матрицы-столбца). Это действительно никогда не объяснялось хорошо в классах.
Вот что у меня в голове не укладывается:
- Как можно представить вектор (начиная с алгебраического определения) в виде стрелки? Верно ли предположить, что вектор (в двумерном пространстве) $v = [1,1]$ может быть представлен в виде стрелки из начала координат $[0,0]$ в точку $[1,1] $?
- Если приведенное выше предположение верно, что означает нормализация вектора в физическом представлении?
- Если у меня есть вектор $[1,1]$, будет ли вектор $[-1,1]$ ортогонален этому первому вектору? (Потому что, если вы рисуете стрелки, они перпендикулярны).
- Как можно сдвинуть объект по вектору? Это просто скалярное сложение?
Возможно, эти вопросы звучат очень странно, но они возникают из-за отсутствия подходящего объяснения как в физике, так и в алгебре.
- линейная алгебра
- геометрия
- физика
- интуиция
$\endgroup$
1
$\begingroup$
Физики склонны подчеркивать геометрическую интерпретацию векторов, чего математикам делать не нужно. Это связано с тем, что одно из основных применений векторов в физике — говорить о геометрии некоторой системы, в то время как векторы вообще могут использоваться в более абстрактных смыслах (и, возможно, вообще без геометрической интерпретации).
Что касается вашего первого пункта, то ваша интерпретация верна: это модель векторного пространства как алгебры направлений. Каждая стрелка имеет начальную и конечную точки, которые определяют как длину, так и ориентацию. Это свойства «направления».
Нормализация векторов — это способ потерять информацию о длине при сохранении направленности; это делает векторы единичной длины.
Да, вы правы, говоря, что эти векторы ортогональны. Это часть геометрической интерпретации.
Я не уверен, что вы имеете в виду под «перемещением объекта относительно вектора». Это может быть определение местоположения объекта и простое перемещение каждой точки в направлении вектора. Это лучше описывается сложением векторов.
$\endgroup$
2
$\begingroup$
Вы можете представить вектор как стрелку в декартовых координатах, нарисовав стрелку от (0,0) к вектору (вектору-строке), например <3,2>, взятому как точка на плоскости (3,4). Другими словами, ваш первый пункт верен.
Нормализация вектора — это процесс, посредством которого берется произвольный вектор (a, b) и преобразуется в новый вектор (a’, b’), где длина (a’, b’) равна 1.
Например, нормализовать (3, 4) = (3/5, 4/5). И мы можем проверить, что |(3/5, 4/5)| = sqrt(9/25 + 16/25) = sqrt(25/25) = 1.
Верно. Но имейте в виду, что для любого вектора (x, y) вектор (-x, y) будет перпендикулярен (x, y) только в том случае, если x = y.
$\endgroup$
3
$\begingroup$
Вообще-то, я думаю, у тебя очень хорошая интуиция. «Стрелка» имеет два бита информации: ее длину и направление. Когда у вас есть вектор $v = [a, b]$, он описывает стрелку, которая перемещает $a$ в горизонтальном направлении и $b$ в вертикальном направлении. Поскольку это определяет прямоугольный треугольник, его можно преобразовать в информацию о длине и направлении.
Нормализация вектора просто означает корректировку длины вектора до $1$ без изменения его направления.
Чтобы ответить на ваш вопрос об ортогональности, да, как вы упомянули, $[-1, 1]$ и $[1,1]$ действительно ортогональны из-за геометрического рассуждения, которое вы правильно описали. Однако они ортогональны только стандартному внутреннему произведению . Это подразумевает скалярное произведение, которое имеет множество геометрических связей. Однако в математике мы можем определить многие другие типы внутренних продуктов, которые не имеют таких хороших геометрических связей.
Однако они ортогональны только стандартному внутреннему произведению . Это подразумевает скалярное произведение, которое имеет множество геометрических связей. Однако в математике мы можем определить многие другие типы внутренних продуктов, которые не имеют таких хороших геометрических связей.
$\endgroup$
3
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Понимание скалярных и векторных величин
Все ресурсы по физике для старших классов
6 Диагностические тесты 233 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
Справка по физике для старших классов » Вводные принципы » Понимание скалярных и векторных величин
Что из следующего может быть результатом произведения векторной величины на скалярную величину?
Возможные ответы:
Работа
Вес
Все это происходит из -за продукта вектора и скалярного
Velocity
Напряжение
Правильный ответ:
Объяснение:
Скалярные величины определяются величиной без применимого направления. Напротив, векторные величины должны иметь как величину, так и направление действия.
Напротив, векторные величины должны иметь как величину, так и направление действия.
Произведение векторной величины на скалярную величину всегда будет векторной величиной. Сила является результатом произведения массы (скаляр) и ускорения (вектор). Вес — это тип силы, создаваемой ускорением свободного падения.
Напряжение является скалярной величиной и может быть рассчитано как произведение тока (скалярное) на сопротивление (скалярное).
Работа является векторной величиной и может быть рассчитана как произведение силы (вектор) и перемещения (вектор).
Скорость является вектором и может быть рассчитана как частное смещения (вектор) в единицу времени (скаляр).
Сообщить об ошибке
Скорость является скалярной величиной. Какая векторная величина представляет скорость в приложенном направлении?
Возможные ответы:
Расстояние
Смещение
Скорость
Вес
Ускорение
Правильный ответ:
. Скорость
Скорость
Объяснение:
Скалярные величины определяются величиной без применимого направления. Напротив, векторные величины должны иметь как величину, так и направление действия.
Скорость определяется изменением расстояния в единицу времени. Поскольку расстояние и время являются скалярными величинами, результирующая скорость также является скалярной. Напротив, скорость определяется изменением смещения в единицу времени. Поскольку смещение является вектором, результирующая скорость также является вектором. Величина заданной скорости и заданной скорости могут быть равны, но член скорости будет представлять скорость, приложенную в определенном направлении.
Ускорение — векторная величина, определяемая изменением скорости в единицу времени. Вес создается силой тяжести на объекте; все силы являются векторами.
Сообщить об ошибке
Что из следующего является скалярной величиной?
Возможные ответы:
Ускорение
Сила
Расстояние
Смещение
Скорость
Правильный ответ:
Расстояние
Объяснение:
Скалярные величины определяются величиной без применимого направления. Напротив, векторные величины должны иметь как величину, так и направление действия.
Напротив, векторные величины должны иметь как величину, так и направление действия.
Некоторыми распространенными скалярными величинами являются расстояние, скорость, масса и время. Некоторыми распространенными векторными величинами являются сила, скорость, смещение и ускорение.
Сообщить об ошибке
Какой из них является вектором?
Возможные ответы:
Сила
Расстояние
Время
Емкость
Скорость
Правильный ответ:
Сила
Объяснение:
Вектор имеет как величину, так и направление, тогда как скаляр имеет только величину. Спрашивая, является ли что-то вектором или скаляром, спросите, имеет ли смысл направление — в этом случае единственным вектором является сила. Хотя направление помогло бы со скоростью и расстоянием, они оба являются скалярами; векторная версия скорости — это скорость, а векторная версия расстояния — это перемещение.
Сообщить об ошибке
Какая из этих величин является скалярной?
Возможные ответы:
Velocity
Force
Momentum
Смещение
MASS
Правильный ответ:
MASS
Объяснение:
Скалярная величина может быть определена только величиной, тогда как векторная величина должна определяться как величиной, так и направлением действия.
Из предложенных вариантов ответа масса — единственная скалярная величина. Масса имеет величину, как правило, в килограммах, но не может действовать в направлении. «7kg west», например, бессмысленно.
Напротив, перемещение, скорость, сила и импульс должны быть приложены в заданном направлении. Перемещение — это векторный эквивалент скалярной величины расстояния, а скорость — векторный эквивалент скалярной величины скорости. Силы должны всегда действовать в заданном направлении и не иметь скалярного эквивалента. Точно так же импульс всегда должен быть направленным.
Силы должны всегда действовать в заданном направлении и не иметь скалярного эквивалента. Точно так же импульс всегда должен быть направленным.
Сообщить об ошибке
Ребенок катится по краю катка и финиширует ровно там, где начал. Если каток имеет радиус , каково полное перемещение фигуриста?
Возможные ответы:
Правильный ответ:
Объяснение:
Между измерением смещения и измерением расстояния есть четкое и важное различие. Расстояние является скалярной величиной, что означает, что оно зависит от пройденного пути и не зависит от пройденного направления. Расстояние измеряет общую пройденную длину без какой-либо привязки к начальной точке.
Смещение, напротив, является векторной величиной. Это означает, что при расчете необходимо учитывать как величину длины, так и ее направление. Смещение — это, по сути, чистое расстояние, пройденное относительно начальной точки, независимо от пройденного пути.
В этом вопросе фигуристка финиширует точно в том же месте, где и стартовала. Без какой-либо другой информации мы можем сделать вывод, что ее водоизмещение равно нулю. Неважно, какой путь она выбрала, чтобы вернуться к исходной точке; она могла сделать шаг вперед и шаг назад, проехать весь каток семнадцать раз или просто прыгнуть и приземлиться. Все эти возможности привели бы к нулевому смещению.
Сообщить об ошибке
Какая из следующих величин не является векторной?
Возможные ответы:
Смещение
Ускорение
Вязкость
скорость
Сила
Правильный ответ:
Пояснение:
Вязкость – это мера «густоты» жидкости. Патока, например, является более вязкой жидкостью, чем вода.
Векторные измерения определяются величиной и направлением. Для жидкости иметь измеримую «толщину» логично, но жидкость не может иметь вязкость в направлении. Говорить о том, что жидкость имеет вязкость Восточная, не имеет смысла. Вязкость является скалярной величиной.
Говорить о том, что жидкость имеет вязкость Восточная, не имеет смысла. Вязкость является скалярной величиной.
Перемещение, сила, скорость и ускорение имеют связанные направления и классифицируются как векторные величины.
Сообщить об ошибке
Какая из следующих величин является векторной?
Возможные ответы:
Расстояние
Масса
Яркость
Время
Сила
Правильный ответ:
Объяснение:
Векторные величины определяются как величиной параметра, так и направлением действия. В контракте скалярные величины не зависят от направления и зависят только от величины параметра.
Масса, расстояние, время и яркость — скалярные величины. Это означает, что ни один из этих терминов не может быть применен в данном направлении. Было бы нелогично иметь «три грамма на запад» или «восемнадцать секунд налево». Расстояние является скалярным эквивалентом вектора смещения.
Расстояние является скалярным эквивалентом вектора смещения.
Сила всегда векторная величина, так как направление силы имеет значение при определении параметра. «Четыре ньютона вправо» количественно отличается от «четыре ньютона вниз» или «четыре ньютона влево».
Сообщить об ошибке
Каковы модуль и угол для следующего вектора, измеренного против часовой стрелки от оси x?
Возможные ответы:
Правильный ответ:
Объяснение:
Величина вектора находится по формуле расстояния:
Чтобы вычислить угол, мы должны сначала найти арктангенс:
Это значение угла является главным арктангенсом, но оно находится в четвертом квадранте, а наш вектор — во втором. Мы должны добавить угол 180° к этому значению, чтобы получить окончательный ответ.
Сообщить об ошибке
Вектор имеет величину 3,61 и направление 124° против часовой стрелки от оси x. Выразите в форме единичного вектора.
Возможные ответы:
Правильный ответ:
Объяснение:
Для вектора величина удваивается, но направление остается прежним.
Для наших расчетов мы используем величину:
Координата x — это величина, умноженная на косинус угла, а координата y — это величина, умноженная на синус угла.
Результирующий вектор: .
Сообщить об ошибке
← Предыдущая 1 2 3 4 Следующая →
Уведомление об авторских правах
Все ресурсы по физике для старших классов
6 Диагностические тесты 233 практических теста Вопрос дня Карточки Learn by Concept
Вводные принципы — физика для старших классов
Все ресурсы по физике для старших классов
6 диагностических тестов 233 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущий 1 2 3 4 5 6 7 8 9 Далее →
Справка по физике для старших классов » Вводные принципы
Что из перечисленного не является векторной величиной?
Возможные ответы:
FIRCH
MASS
Угловой момента
Крутящий момент
Смещение
Правильный ответ:
Mass
Объяснение:
Скалярная величина может быть определена только величиной, а векторная величина имеет и величину, и направление действия. Масса является скалярной величиной, потому что она не действует ни в каком конкретном направлении. Фраза «пять килограммов на восток» — чепуха, указывающая на то, что масса не может быть вектором.
Масса является скалярной величиной, потому что она не действует ни в каком конкретном направлении. Фраза «пять килограммов на восток» — чепуха, указывающая на то, что масса не может быть вектором.
Угловой момент, сила, смещение и крутящий момент являются векторными величинами и описывают значение, приложенное в определенном направлении.
Сообщить об ошибке
Каждый из двух векторов имеет величину . Рассмотрим диапазон возможных длин векторной суммы ( результирующего вектора ) двух векторов в зависимости от их направлений. Какова разница в величине между наибольшей возможной длиной и наименьшей возможной длиной результирующего вектора?
Возможные ответы:
Правильный ответ:
Объяснение:
Наибольшая возможная длина векторной суммы двух векторов получается, когда векторы ориентированы в одном направлении. В этом сценарии результирующий вектор будет иметь длину, равную сумме величин двух векторов.
В этом сценарии результирующий вектор будет иметь длину, равную сумме величин двух векторов.
Наименьшая возможная длина векторной суммы получается, когда векторы ориентированы в противоположных направлениях. В этом сценарии результирующий вектор будет иметь длину, равную разнице по величине между двумя векторами.
Наибольшее значение результирующего вектора равно , а наименьшее . Теперь нам нужно найти разницу между этими величинами.
Сообщить об ошибке
Какая из следующих величин является векторной?
Возможные ответы:
Расстояние
Вес
Масса
Плотность
Объем
Правильный ответ: 33
4
4
Объяснение:
Скалярные величины определяются величиной без применимого направления. Напротив, векторные величины должны иметь как величину, так и направление действия.
Масса, расстояние, плотность и объем — все это скалярные величины, просто определяемые величиной. Невозможно иметь направленную массу или плотность, например, «5 килограммов на восток» или «0,6 грамма на литр по часовой стрелке». Расстояние — это скалярная форма смещения. Смещение учитывает направление измерения длины, тогда как расстояние измеряет только величину длины.
Вес определяется как сила тяжести, действующая на объект. Все силы являются векторными величинами.
Сообщить об ошибке
Расстояние — это скалярная величина. Какая векторная величина представляет собой расстояние в приложенном направлении?
Возможные ответы:
Смещение
Вес
MASS
Скорость
Ускорение
Правильный ответ:
Объяснение:
Скалярные величины определяются величиной без применимого направления. Напротив, векторные величины должны иметь как величину, так и направление действия.
Напротив, векторные величины должны иметь как величину, так и направление действия.
Расстояние — это мера длины, учитывающая все длины пути от начальной точки. Перемещение — это векторный эквивалент расстояния. Смещение измеряет длину в заданном направлении от начальной точки без учета пройденного пути. Автомобиль может проехать расстояние 400 метров, но если он в конце концов вернется в исходное положение, его перемещение будет равно нулю.
Скорость — это вектор, измеряющий изменение смещения в единицу времени. Вектор силы, такой как вес, возникает, когда вектор ускорения (например, сила тяжести) применяется к массе. Масса сама по себе является скалярной величиной.
Сообщить об ошибке
Что из следующего может быть результатом произведения векторной величины на скалярную?
Возможные ответы:
Работа
Вес
Все это результат произведения вектора и скаляра
Скорость
Напряжение
Правильный ответ:
Вес
Объяснение:
Скалярные величины определяются величиной без применимого направления. Напротив, векторные величины должны иметь как величину, так и направление действия.
Напротив, векторные величины должны иметь как величину, так и направление действия.
Произведение векторной величины на скалярную величину всегда будет векторной величиной. Сила является результатом произведения массы (скаляр) и ускорения (вектор). Вес — это тип силы, создаваемой ускорением свободного падения.
Напряжение является скалярной величиной и может быть рассчитано как произведение тока (скалярное) на сопротивление (скалярное).
Работа является векторной величиной и может быть рассчитана как произведение силы (вектор) и перемещения (вектор).
Скорость является вектором и может быть рассчитана как частное смещения (вектор) в единицу времени (скаляр).
Сообщить об ошибке
Скорость является скалярной величиной. Какая векторная величина представляет скорость в приложенном направлении?
Возможные ответы:
Расстояние
Смещение
Скорость
Вес
Ускорение
Правильный ответ:
. Скорость
Скорость
Объяснение:
Скалярные величины определяются величиной без применимого направления. Напротив, векторные величины должны иметь как величину, так и направление действия.
Скорость определяется изменением расстояния в единицу времени. Поскольку расстояние и время являются скалярными величинами, результирующая скорость также является скалярной. Напротив, скорость определяется изменением смещения в единицу времени. Поскольку смещение является вектором, результирующая скорость также является вектором. Величина заданной скорости и заданной скорости могут быть равны, но член скорости будет представлять скорость, приложенную в определенном направлении.
Ускорение — векторная величина, определяемая изменением скорости в единицу времени. Вес создается силой тяжести на объекте; все силы являются векторами.
Сообщить об ошибке
Что из следующего является скалярной величиной?
Возможные ответы:
Ускорение
Сила
Расстояние
Смещение
Скорость
Правильный ответ:
Расстояние
Объяснение:
Скалярные величины определяются величиной без применимого направления. Напротив, векторные величины должны иметь как величину, так и направление действия.
Напротив, векторные величины должны иметь как величину, так и направление действия.
Некоторыми распространенными скалярными величинами являются расстояние, скорость, масса и время. Некоторыми распространенными векторными величинами являются сила, скорость, смещение и ускорение.
Сообщить об ошибке
Какой из них является вектором?
Возможные ответы:
Сила
Расстояние
Время
Емкость
Скорость
Правильный ответ:
Сила
Объяснение:
Вектор имеет как величину, так и направление, тогда как скаляр имеет только величину. Спрашивая, является ли что-то вектором или скаляром, спросите, имеет ли смысл направление — в этом случае единственным вектором является сила. Хотя направление помогло бы со скоростью и расстоянием, они оба являются скалярами; векторная версия скорости — это скорость, а векторная версия расстояния — это перемещение.
Сообщить об ошибке
Какая из этих величин является скалярной?
Возможные ответы:
Velocity
Force
Momentum
Смещение
MASS
Правильный ответ:
MASS
Объяснение:
Скалярная величина может быть определена только величиной, тогда как векторная величина должна определяться как величиной, так и направлением действия.
Из предложенных вариантов ответа масса — единственная скалярная величина. Масса имеет величину, как правило, в килограммах, но не может действовать в направлении. «7kg west», например, бессмысленно.
Напротив, перемещение, скорость, сила и импульс должны быть приложены в заданном направлении. Перемещение — это векторный эквивалент скалярной величины расстояния, а скорость — векторный эквивалент скалярной величины скорости. Силы должны всегда действовать в заданном направлении и не иметь скалярного эквивалента. Точно так же импульс всегда должен быть направленным.
Силы должны всегда действовать в заданном направлении и не иметь скалярного эквивалента. Точно так же импульс всегда должен быть направленным.
Сообщить об ошибке
Ребенок катится по краю катка и финиширует ровно там, где начал. Если каток имеет радиус , каково полное перемещение фигуриста?
Возможные ответы:
Правильный ответ:
Объяснение:
Между измерением смещения и измерением расстояния есть четкое и важное различие. Расстояние является скалярной величиной, что означает, что оно зависит от пройденного пути и не зависит от пройденного направления. Расстояние измеряет общую пройденную длину без какой-либо привязки к начальной точке.
Смещение, напротив, является векторной величиной. Это означает, что при расчете необходимо учитывать как величину длины, так и ее направление. Смещение — это, по сути, чистое расстояние, пройденное относительно начальной точки, независимо от пройденного пути.
В этом вопросе фигуристка финиширует точно в том же месте, где и стартовала. Без какой-либо другой информации мы можем сделать вывод, что ее водоизмещение равно нулю. Неважно, какой путь она выбрала, чтобы вернуться к исходной точке; она могла сделать шаг вперед и шаг назад, проехать весь каток семнадцать раз или просто прыгнуть и приземлиться. Все эти возможности привели бы к нулевому смещению.
Сообщить об ошибке
← Предыдущий 1 2 3 4 5 6 7 8 9 Далее →
Уведомление об авторских правах
Все ресурсы по физике для средней школы
6 Диагностические тесты 233 практических теста Вопрос дня Карточки Learn by Concept
21A: Векторы — перекрестное произведение и крутящий момент
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3380
- Джеффри В.
 Шник
Шник - Колледж Святого Ансельма
Не используйте левую руку, применяя правило правой руки для векторного произведения двух векторов (обсуждаемое в этой главе) или правило правой руки для «что-то завитое, что-то прямое», обсуждавшееся в предыдущей главе.
Существует оператор отношения для векторов, который позволяет нам обойти вычисление плеча момента. Оператор отношения называется векторным произведением. Он представлен символом «×», который читается как «крест». Крутящий момент \(\vec{\tau}\) может быть выражен как векторное произведение вектора положения \(\vec{r}\) точки приложения силы и вектора силы \(\vec{ F}\) сам:
\[\vec{\tau}=\vec{r} \times \vec{F} \label{21-1}\]
Прежде чем мы начнем наше математическое обсуждение того, что мы подразумеваем под перекрестным произведением, необходимо сказать несколько слов о векторе \(\vec{r}\). Для вас важно уметь различать вектор положения \(\vec{r}\) для силы и плечо момента, поэтому мы представляем их ниже на одной и той же диаграмме. Мы используем тот же пример, что и раньше:
Мы используем тот же пример, что и раньше:
, в котором мы смотрим прямо вдоль оси вращения (поэтому она выглядит как точка), а сила лежит в плоскости, перпендикулярной этой оси вращения. Мы используем диаграммное соглашение, согласно которому точка, в которой сила приложена к твердому телу, — это точка, в которой один конец стрелки на диаграмме касается твердого тела. Теперь добавим на диаграмму линию действия силы и плечо момента \(r_{\bot}\), а также вектор положения \(\vec{r}\) точки приложения силы .
Плечо момента фактически может быть определено через вектор положения точки приложения силы. Рассмотрим наклонную систему координат \(x\)-\(y\), имеющую начало на оси вращения, с одной осью, параллельной линии действия силы, и одной осью, перпендикулярной линии действия силы. . Мы обозначаем ось \(x\) \(\bot\) как «перпендикулярную», а ось \(y\) \(\|\) как «параллельную».
Теперь мы разобьем вектор положения \(\vec{r}\) на составляющие его векторы вдоль осей \(\bot\) и \(\|\).
Из диаграммы видно, что плечо момента \(r_{\bot}\) есть просто величина вектора составляющих в направлении, перпендикулярном силе, вектора положения точки приложения силы сила.
Теперь давайте обсудим векторное произведение в общих чертах. Рассмотрим два вектора, \(\vec{A}\) и (\vec{B}\), которые не параллельны и не антипараллельны друг другу. Два таких вектора определяют плоскость. Пусть эта плоскость будет плоскостью страницы и определите \(\theta\) как меньший из двух углов между двумя векторами, когда векторы рисуются хвост к хвосту.
Величина вектора векторного произведения \(\vec{A}\times \vec{B}\) определяется выражением\[|\vec{A}\times\vec{B}|=AB sin\theta \label{21-2}\]
Удерживая пальцы на одном уровне с предплечьем, укажите пальцами в направлении первого вектора (тот, который стоит перед «\(\times\)» в математическом выражении векторного произведения; например, \(\vec{ A}\) в \(vec{A}\times\vec{B}\) ).
Теперь поверните вашу руку, как необходимо, вокруг воображаемой оси, проходящей вдоль вашего предплечья и вдоль вашего среднего пальца, пока ваша рука не будет ориентирована так, что, если бы вы сомкнули пальцы, они указывали бы в направлении второго вектора.
Теперь большой палец указывает в направлении вектора векторного произведения. \(\vec{C}=\vec{A}\times\vec{B} \). Вектор векторного произведения \(\vec{C}\) всегда перпендикулярен обоим векторам, которые находятся в векторном произведении (\(\vec{A}\) и \(\vec{B}\) в рассматриваемый случай). Следовательно, если вы нарисуете их так, чтобы оба вектора векторного произведения находились в плоскости страницы, вектор векторного произведения всегда будет перпендикулярен странице, либо прямо на странице, либо прямо вне страницы. . В данном случае это прямо со страницы.
Когда мы используем перекрестное произведение для расчета крутящего момента силы \(\vec{F}\), точка приложения которой имеет вектор положения \(\vec{r}\) относительно точки, относительно которой мы вычисляя крутящий момент, мы получаем осевой вектор крутящего момента \(\vec{\tau}\). Чтобы определить направление вращения, которому будет соответствовать такой вектор крутящего момента, относительно оси, определяемой самим вектором крутящего момента, мы используем Правило правой руки для чего-то вьющегося чего-то прямого. Обратите внимание, что мы рассчитываем крутящий момент относительно точки, а не оси — ось, вокруг которой действует крутящий момент, выходит в ответе.
Обратите внимание, что мы рассчитываем крутящий момент относительно точки, а не оси — ось, вокруг которой действует крутящий момент, выходит в ответе.
Вычисление векторного произведения векторов, заданных в нотациях \(\hat{i}\), \(\hat{j}\), \(\hat{k}\)
Единичные векторы позволяют выполнять простые вычисления перекрестного произведения двух векторов даже при самых общих обстоятельствах, например. обстоятельства, при которых каждый из векторов указывает в произвольном направлении в трехмерном пространстве. Чтобы воспользоваться этим методом, нам нужно знать векторное произведение единичных векторов декартовой оси координат \(\hat{i}\), \(\hat{j}\) и \(\hat{k}\) друг с другом. 9{\circ}=0\), имеем \(|\vec{A}\times\vec{B}|=0\). Что касается единичных векторов, это означает, что:
\[\hat{i}\times\hat{i}=0\]
\[\hat{j}\times\hat{j}=0\]
\[\hat{k}\times\hat{k}=0\]
Далее мы отметим, что величина векторного произведения двух векторов, перпендикулярных друг другу, есть просто обычное произведение величин векторы. Это также видно из уравнения \(\ref{21-2}\):
Это также видно из уравнения \(\ref{21-2}\):
\[|\vec{A}\times\vec{B}|=AB \sin\theta\] 9{\circ}=1\) поэтому
\[|\vec{A}\times\vec{B}|=AB\]
Теперь, если \(\vec{A}\) и \(\vec{ B}\) являются единичными векторами, тогда обе их величины равны 1, поэтому произведение их величин также равно 1. Кроме того, единичные векторы \(\hat{i}\), \(\hat{j}\) и \(\hat{k}\) перпендикулярны друг другу, поэтому величина перекрестного произведения любой из них с любой другой из них является произведением двух величин, то есть 1.
Теперь как насчет направления? Давайте воспользуемся правилом правой руки, чтобы получить направление \(\hat{i} \times \hat{j}\):
С пальцами правой руки, направленными прямо от правого локтя и в том же направлении, что и \(шляпа{i}\), (первый вектор в ‘\(\шляпа{i}\times\ hat{j}\)’ ), чтобы, если сомкнуть пальцы, они указывали в том же направлении, что и \(\hat{j}\), ладонь должна быть обращена в направлении +y. В таком случае вытянутый большой палец должен указывать в направлении +z. Объединяя информацию о величине (величина каждого единичного вектора равна 1) и информации о направлении (+z), мы видим, что \(\hat{i}\times\hat{j}=\hat{k}\). Аналогично: \(\шляпа{j}\times\шляпа{k}=\шляпа{i}\), \(\шляпа{k}\times\шляпа{i}=\шляпа{j}\), \( \шляпа{j}\times\шляпа{i}=-\шляпа{k}\), \(\шляпа{k}\times\шляпа{j}=-\шляпа{i}\) и \(\ шляпа {i} \ раз \ шляпа {k} = — \ шляпа {j} \). Один из способов запомнить это — написать \(\hat{i}\), \(\hat{j}\), \(\hat{k}\) два раза подряд:
Объединяя информацию о величине (величина каждого единичного вектора равна 1) и информации о направлении (+z), мы видим, что \(\hat{i}\times\hat{j}=\hat{k}\). Аналогично: \(\шляпа{j}\times\шляпа{k}=\шляпа{i}\), \(\шляпа{k}\times\шляпа{i}=\шляпа{j}\), \( \шляпа{j}\times\шляпа{i}=-\шляпа{k}\), \(\шляпа{k}\times\шляпа{j}=-\шляпа{i}\) и \(\ шляпа {i} \ раз \ шляпа {k} = — \ шляпа {j} \). Один из способов запомнить это — написать \(\hat{i}\), \(\hat{j}\), \(\hat{k}\) два раза подряд:
\[\шляпа{i},\шляпа{j},\шляпа{k},\шляпа{i},\шляпа{j},\шляпа{k}\]
Затем, пересекая любую из первые три вектора в вектор справа от него дают следующий вектор справа. Но пересечение любого из трех последних векторов с вектором непосредственно слева от него дает отрицательное значение следующего вектора слева (слева направо «+», но справа налево «-»).
Теперь мы готовы рассмотреть общий случай. Любой вектор \(\vec{A}\) может быть выражен через единичные векторы:
\[\vec{A}=A_x \hat{i}+A_y \hat{j}+ A_z \hat{k}\]
Делаем то же самое для вектора \(\vec{B}\), затем позволяет нам записать перекрестный продукт как:
\[\vec{A}\times\vec{B}=(A_x \hat{i}+A_y \hat{j} +A_z \hat{k}) \times (B_x \шляпа{i}+B_y \шляпа{j} +B_z \шляпа{k}) \]
Используя распределительное правило для умножения, мы можем записать это как:
\[\vec{A}\times\ vec{B}=A_x \hat{i} \times (B_x \hat{i}+B_y \hat{j} +B_z \hat{k}) + A_y \hat{j} \times (B_x \hat{i }+B_y \шляпа{j} +B_z \шляпа{k}) + A_z \шляпа{k}\times (B_x \шляпа{i}+B_y \шляпа{j} +B_z \шляпа{k})\]
\[\vec{A}\times\vec{B}=A_x \hat{i} \times B_x \hat{i}+A_x \hat{i} \times B_y \hat{j} +A_x \hat {i} \times B_z \hat{k} + A_y \hat{j} \times B_x \hat{i}+A_y \hat{j} \times B_y \hat{j} +A_y \hat{j} \times B_z \hat{k} + A_z \hat{k} \times B_x \hat{i}+A_z \hat{k} \times B_y \hat{j} +A_z \hat{k} \times B_z \hat{k } \]
Используя в каждом члене коммутативное правило и ассоциативное правило умножения, мы можем записать это как:
\[\vec{A}\times\vec{B}=A_x B_x (\hat{i } \times \hat{i})+A_x B_y (\hat{i} \times \hat{j}) +A_x B_z (\hat{i} \times \hat{k}) + A_y B_x (\hat{ j} \times \hat{i})+A_y B_y (\hat{j} \times \hat{j}) +A_y B_z (\hat{j} \times \hat{k}) + A_z B_x (\hat {k} \times \hat{i})+A_z B_y (\hat{k} \times \hat{j}) +A_z B_z (\hat{k} \times \hat{k})\]
Теперь мы оцениваем перекрестное произведение, которое появляется в каждом терме:
\[\vec{A}\times\vec{B}=A_x B_x (0)+A_x B_y (\hat{k}) +A_x B_z ( -\hat{j}) + A_y B_x (-\hat{k})+A_y B_y (0) +A_y B_z (\hat{i}) + A_z B_x (\hat{j})+A_z B_y (-\ hat{i}) +A_z B_z (0)\]
Удаление нулевых членов и группировка членов с \(\hat{i}\) вместе, членов с \(\hat{j}\) вместе и члены с \(\hat{k}\) вместе дают:
\[\vec{A}\times\vec{B}=A_y B_z(\hat{i})+A_z B_y (-\hat{i })+ A_z B_x (\шляпа{j}) + A_x B_z (-\шляпа{j})+ A_x B_y (\шляпа{k}) + A_y B_x (-\шляпа{k})\]
Факторизация единичных векторов дает:
\[\vec{A}\times\vec{B}=(A_y B_z- A_z B_y)\hat{i}+(A_z B_x — A_x B_z) \hat{j }+ (A_x B_y- A_y B_x) \hat{k}\]
, что можно записать в одну строку как:
\[\vec{A}\times\vec{B}=(A_y B_z- A_z B_y )\hat{i}+(A_z B_x — A_x B_z) \hat{j}+(A_x B_y- A_y B_x) \hat{k} \label{21-3} \]
Это наш конечный результат. Мы можем прийти к этому результату гораздо быстрее, если позаимствуем инструмент из раздела математики, известного как линейная алгебра (математика матриц).
Мы можем прийти к этому результату гораздо быстрее, если позаимствуем инструмент из раздела математики, известного как линейная алгебра (математика матриц).
Формируем матрицу \(3\times 3\)
\[ \begin{bmatrix} \hat{i}&\hat{j}&\hat{k} \\ A_x & A_y & A_z \\ B_x&B_y&B_z \end{bmatrix} \]
, написав \hat{i}, \hat{j}, \hat{k} в качестве первой строки, а затем компоненты первого вектора, который появляется в векторном произведении, как вторую строку и, наконец, компоненты второго вектора, который появляется в перекрестном произведении как последняя строка. Оказывается, перекрестное произведение равно определителю этой матрицы. Мы используем знаки абсолютного значения на всей матрице, чтобы обозначить «детерминант матрицы». Итак, имеем:
\[ \vec{A} \times \vec{B}=\begin{vmatrix} \hat{i}&\hat{j}&\hat{k} \\ A_x & A_y & A_z \\ B_x&B_y&B_z \ end{vmatrix} \label{21-4} \]
Чтобы найти определитель матрицы \(3\times 3\), нужно пройти через верхнюю строку. Для каждого элемента в этой строке вы берете произведение элементов по диагонали, идущей вниз и вправо, минус произведение элементов вниз и влево; и вы складываете три результата (по одному результату для каждого элемента в верхней строке) вместе. Если внизу и на соответствующей стороне нет элементов, вы переходите на другую сторону матрицы (см. ниже), чтобы завершить диагональ.
Если внизу и на соответствующей стороне нет элементов, вы переходите на другую сторону матрицы (см. ниже), чтобы завершить диагональ.
Для первого элемента первой строки, \(\шляпа{i}\), перенесите произведение вниз и вправо,
( это дает \(\шляпа{i} A_yB_z\))
минус произведение вниз и влево
( произведение вниз и влево равно \(\hat{i} A_zB_y\)) )
Для первого элемента в первой строке мы таким образом, есть: \( \hat{i} A_yB_z-\hat{i} A_zB_y \), что может быть записано как: \( (A_yB_z-A_zB_y) \hat{i} \). Повторяя процесс для второго и третьего элементов в первой строке (\(\hat{j}\) и \(\hat{k}\)) мы получаем \( (A_zB_x — A_xB_z) \hat{j} \) и \( (A_xB_y — A_yB_x) \hat{k}\) соответственно. Сложение трех результатов для формирования определителя матрицы приводит к:
\[\vec{A}\times\vec{B}=(A_y B_z- A_z B_y)\hat{i}+(A_z B_x — A_x B_z) \hat{j}+(A_x B_y- A_y B_x) \hat{k} \]
, как мы обнаружили ранее, «трудным путем».


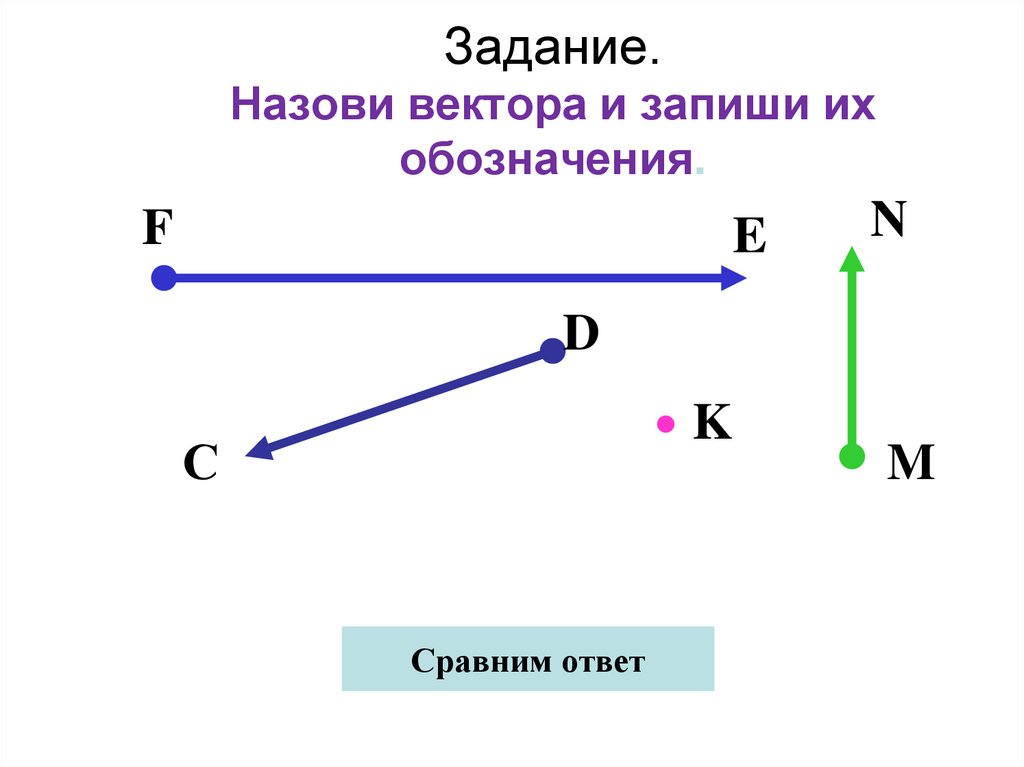 RU
RU


 Давайте вспомним как складывать и вычитать
вектора, направленные вдоль одной прямой (слайд
10).
Давайте вспомним как складывать и вычитать
вектора, направленные вдоль одной прямой (слайд
10).