| САЙТ ПРАКТИКУЮЩЕГО ФИЗИКА | |||||||||||||||||
|
|
Магнитный поток 9 класс онлайн-подготовка на Ростелеком Лицей
Вступление
Вспомним, что при изменении параметров магнитного поля вблизи замкнутого проводника в нем возникает ток.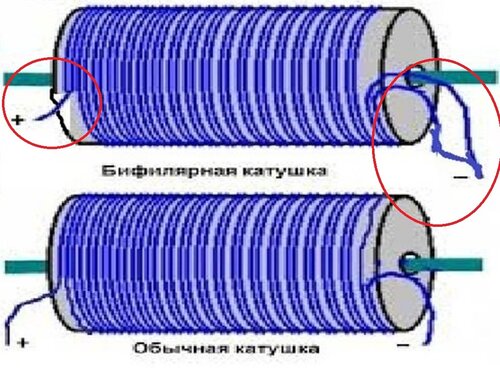 Данный ток получил название тока индукции, а явление – явление электромагнитной индукции.
Данный ток получил название тока индукции, а явление – явление электромагнитной индукции.
Однако остается вопрос, какие конкретно параметры магнитного поля нам необходимо меня для получения данного эффекта. Для начала проведем эксперимент:
Опыт Фарадея
Для его проведения нам необходимо: катушка с большим количеством витков и подключенный к ней амперметр. В ходе проведения опыта обратите внимание на поведение стрелки амперметра (рис. 1).
Рис. 1. Опыты Фарадея
Как мы видим, при опускании и вынимании полосового магнита из катушки в ней образуется индукционный ток.
Проанализируем, изменение какого именно параметра привело к наблюдаемому эффекту. При приближении и отдалении магнита от катушки в ней меняется сила магнитного поля.
Таким образом, величиной, которая влияет на образование тока индукции в катушке, является сила магнитного поля.
Вспомним, что она описывается такой величиной, как магнитная индукция.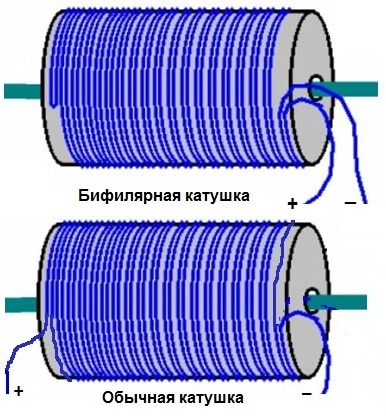 Она является вектором и обозначается и измеряется в Тл.
Она является вектором и обозначается и измеряется в Тл.
Второй опыт
Помещенное перпендикулярно магнитному полю замкнутое проволочное кольцо сжимаем с нескольких сторон, чтобы оно изменило свою форму (рис. 2).
| Рис. 2. Иллюстрация к опыту | |
При этом на протяжении процесса деформации в кольце возникает ток индукции. Что же мы изменяли в этот раз?
Теперь изменению подверглась площадь кольца. Конечно же, вместо кольца можно экспериментировать с любым замкнутым проводником.
Контур – замкнутый проводник (рис. 3).
Рис. 3. Контур
Принцип работы электрогенератора
Рис. 4. Генератор
Его основными элементами являются (рис. 4):
- катушка, которая может вращаться вокруг своей оси;
- установленный вокруг катушки постоянный магнит.

При вращении катушки в магнитном поле можно увидеть, что лампочка загорается (т. е. в цепи возникает ток индукции).
Из этого опыта можно сделать вывод о том, что явление электромагнитной индукции проявляет себя и при повороте катушки или проводящей рамки в магнитном поле (рис. 5), т. е. при изменении угла между магнитными линиями и плоскостью проводника.
Рис. 5. Иллюстрация к опыту
Все три параметра, изменения которых влияют на величину тока индукции, объединяет физическая величина под названием магнитный поток.
Магнитный поток
В – модуль магнитной индукции поля
S – площадь контура
– характеризует расположение плоскости контура относительно магнитной линии.
Магнитный поток измеряют в Веберах (Вб) и обозначают буквой Ф.
Таким образом, магнитный поток пропорционален модулю магнитной индукции поля, площади контура и зависит от расположения плоскости контура относительно магнитной линии.
Задача на анализ параметров магнитного потока
Для того чтобы научиться делать выводы об изменении магнитного потока в элементах различных электрических цепей, что может привести к наличию нежелательных индукционных токов, рассмотрим задачу.
Проволочная катушка со стальным сердечником включена в цепь постоянного тока последовательно с реостатом и ключом (рис. 6).
Рис. 6. Иллюстрация к задаче
Электрический ток, протекающий по веткам катушки, создает в пространстве вокруг нее магнитное поле (рис. 7). В поле катушки и находится такая же катушка .
Рис. 7. Иллюстрация к задаче
Каким образом можно поменять магнитный поток пронизывающий катушку ? Рассмотрите все возможные варианты.
Вспомним, изменение каких параметров приводит к изменению магнитного потока.
Начнем с изменения индукции магнитного поля катушки .Этого возможно добиться, если изменять силу тока, которая порождает ее магнитное поле. Изменять ток в изображенной цепи можно 2-мя способами:
Изменять ток в изображенной цепи можно 2-мя способами:
- Передвижение ползунка реостата
- Включение/выключение ключа
Стоит отметить, что изменение значения тока будет наибольшим от максимального до нуля, что приведет к наибольшему изменению магнитного потока в катушке .
Следующим параметром, изменение которого повлияет на значение магнитного потока, является площадь контура. В нашем случае катушки Но изменить площадь сечения катушки мы не можем. Следовательно, вариант отпадает.
Последним вариантом изменения магнитного потока является поворот катушки относительно магнитных линий катушки . Для достижения максимального результата изменения повернуть катушку необходимо на 90(рис. 8).
Рис. 8. Иллюстрация к задаче
Что же описывается магнитным потоком?
Как мы уже отметили, он зависит:
- От силы магнитного поля
- От площади контура, через который эти магнитные линии проходят
- От угла расположения между контуром и магнитными линиями
Таким образом, магнитный поток характеризует количество магнитных линий, пронизывающих ограниченный контур.
Это легко проверить.
1. Сравним количество линий, которые пронизывают одинаковый контур, но в различных по силе магнитных полях (рис. 9).
В более сильном поле контур пронизывает больше линий.
Рис. 9. Иллюстрация к задаче
2. Если сравнить количество линий, которые в одном и том же однородном магнитном поле пронизывают различные по площади контуры, то их очевидно больше через больший контур (рис. 10).
Рис. 10. Иллюстрация к задаче
3. Если сравнивать поворот контура в магнитном поле на угол к магнитным линиям и его расположение вдоль линий, то в первом случае их количество через плоскость контура будет максимально. А во втором магнитные линии будут скользить вдоль контура и не пронизывать его вовсе (рис. 11).
Рис. 11. Иллюстрация к задаче
В указанных примерах большему числу линий через контур соответствовал больший магнитный поток.
В результате отметим, что поскольку величина тока индукции зависит от изменения магнитной индукции, площади контура и от ее ориентации в пространстве, то принято говорить, что она зависит от изменения магнитного потока.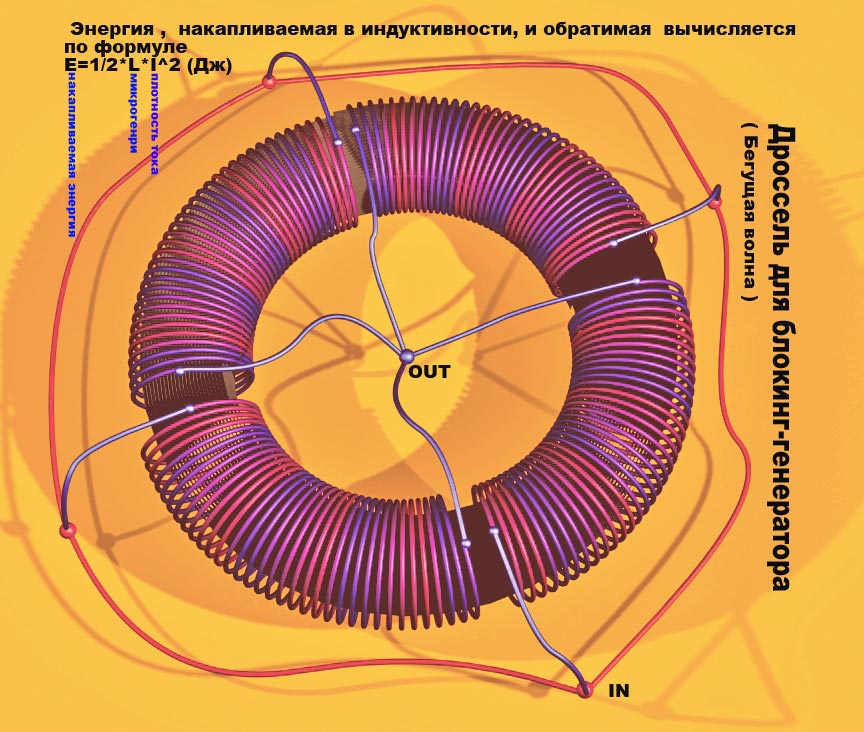
Кроме того, опыты Фарадея показали, что важна скорость изменения магнитного потока. Чем быстрее изменять указанные величины, тем величина индукционного тока будет больше.
Таким образом, можно утверждать, что явление электромагнитной индукции характеризуется скоростью изменения магнитного потока.
Задача на определение условий возникновения индукционного тока
Для того чтобы разобраться со взаимосвязью магнитного потока через контур и явлением электромагнитной индукции в нем, рассмотрим задачу:
Небольшую катушку поступательно перемещают в однородном магнитном поле. Возникает ли в катушке индукционный ток? Ответ обоснуйте.
Рис. 12. Иллюстрация к задаче
Может показаться, что из-за движения катушки могут быть изменения, следствием которых будет являться возникновение тока индукции в ее витках (рис. 12).
Вспомним, что обязательным условием возникновения тока индукции является изменение магнитного потока через витки катушки. Для этого необходимо изменение магнитной индукции через контур катушки. Чего не наблюдается, т. к. по условию поле однородно.
Для этого необходимо изменение магнитной индукции через контур катушки. Чего не наблюдается, т. к. по условию поле однородно.
Кроме этого возможно изменение площади сечения катушки, чего также не наблюдается.
Последний возможный вариант – это изменение угла поворота плоскости катушки к магнитным линиям поля, чего, очевидно, также не происходит, поскольку движение поступательное, а значит, никаких поворотов катушки не наблюдается.
Следовательно, делаем вывод – магнитный поток изменяться не будет, соответственно, никакого тока индукции образовываться в витках катушки тоже не будет.
Сравнение магнитного потока с потоком воды
Название изученной нами новой физической величины магнитного потока не случайно. Дело в том, что магнитный поток через контур можно сравнить с потоком воды через кольцо, которое помещено в трубу (рис. 13). (1)
Чем скорость воды больше, тем больше ее проходит через кольцо в единицу времени. (2)
Чем больше площадь кольца, тем, опять-таки, через него протечет больше воды за наблюдаемое время. (3)
(3)
Если поворачивать кольцо при его поперечном расположении к потоку воды, через плоскость кольца протечет максимальное количество воды. (4)
Если начать его поворачивать под острым углом к потоку, то воды будет протекать все меньше. (5)
Рис. 13. Сравнение магнитного потока с потоком воды
А при повороте вдоль оттока вода вообще не будет проходить сквозь кольцо, а будет скользить вдоль него. (6)
Аналогичные свойства мы с вами рассмотрели для магнитного потока.
Заключение
На уроке мы объяснили, какие параметры магнитного поля и контура необходимо менять для наблюдения явления электромагнитной индукции. Мы объединили это в понятие «магнитный поток».
Список литературы
- Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования.
- Яворский Б. М., Пинский А. А., Основы физики, т.
 2., – М., Физматлит., 2003.
2., – М., Физматлит., 2003. - Элементарный учебник физики. Под ред. Г. С. Ландсберга, Т. 3. – М., 1974.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «festival.1september.ru» (Источник)
- Интернет-портал «nvtc.ee» (Источник)
- Интернет-портал «class-fizika.narod.ru» (Источник)
Домашнее задание
- От чего зависит магнитный поток, пронизывающий площадь плоского контура, помещенного в однородное магнитное поле?
- Как меняется магнитный поток при увеличении в n раз магнитной индукции, если ни площадь, ни ориентация контура не меняются?
- Меняется ли магнитный поток при таком вращении контура, когда линии магнитной индукции то пронизывают его. то скользят по его плоскости?
| ||||||||||||||||||||||||
| Специальный поиск | ||||||||||||||||||||||||
|
Физика Теория вероятностей и мат. Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
|||||||||||||||||||||||
индукция однородного магнитного поля которое Задача 70188 В однородном магнитном поле, индукция которого равна 0,1 Тл, вращается катушка, состоящая из 200 витков. Ось вращения катушки перпендикулярна оси симметрии катушки и направлению магнитного поля. Максимальная ЭДС индукции в катушке равна 0,3 В. Найти период обращения катушки, если площадь поперечного сечения катушки 4 см2.
Задача 70319 Плоский замкнутый металлический контур площадью S1 = 10 см2 деформируется в однородном магнитном поле, индукция которого B = 1·10–2 Тл.
Задача 15434 Круговой проволочный виток площадью S = 0,01 м2 находится в однородном магнитном поле, индукция которого B = 1 Тл. Плоскость витка перпендикулярна к направлению магнитного поля. Найти среднюю ЭДС индукции <εi>, возникающую в витке при выключении поля в течение времени t = 10 мс.
Задача 15435 В однородном магнитном поле, индукция которого равна B = 0,1 Тл, равномерно вращается катушка, состоящая из N = 100 витков проволоки. Частота вращения катушки ν = 5 с–1; площадь поперечного сечения катушки S = 0,01 м2.
Задача 15436 В однородном магнитном поле, индукция которого В = 0,8 Тл, равномерно вращается рамка с угловой скоростью ω = 15 рад/с. Площадь рамки S = 150 см2. Ось вращения находится в плоскости рамки и составляет угол α = 30° с направлением магнитного поля. Найти максимальную э. д. с. индукции εmax во вращающейся рамке.
Задача 15442 В однородном магнитном поле, индукция которого B = 0,1 Тл, вращается катушка, состоящая из N = 200 витков. Ось вращения катушки перпендикулярна к ее оси и к направлению магнитного поля. Период обращения катушки T = 0,2 с; площадь поперечного сечения S = 4 см2. Найти максимальную э. д. с. индукции во вращающейся катушке.
Задача 15456 Круговой контур радиусом r = 2 см помещен в однородное магнитное поле, индукция которого В = 0,2 Тл. Плоскость контура перпендикулярна к направлению магнитного поля. Сопротивление контура R = 1 Ом. Какое количество электричества q пройдет через катушку при повороте ее на угол α = 90°?
Задача 11188 В однородном магнитном поле, индукция которого 0,8 Тл, равномерно с частотой 200 мин–1 вращается катушка, содержащая 250 витков, плотно прилегающих друг к другу. Площадь поперечного сечения катушки 80 см2. Ось вращения перпендикулярно оси катушки и направлению ЭДС, индуцируемую в катушке.
Задача 11493 Проводящий круговой виток радиусом a = 10 см вращается в однородном магнитном поле, индукция которого В = 0,01 Тл, так, что угол между нормалью к его плоскости и вектором В изменяется по закону α = πt (t — время в секундах).
Задача 12642 Плоский контур с током, представляющий собой прямоугольник со сторонами 10 и 20 см помещен в однородное магнитное поле, индукция которого 7·10–3 Тл. По контуру течет ток 5 А. Найти момент сил, действующий на контур с током, если его плоскость составляет угол 100° с линиями поля. К задаче представить рисунок.
Задача 12643 Используя условие предыдущей задачи, определить, какую работу нужно совершить, чтобы угол между плоскостью контура и линиями поля составил 120°?
Задача 12645 В однородном магнитном поле, индукция которого 0,15 Тл, вращается прямоугольная рамка размерами 200 мм × 400 мм. Рамка содержит 850 витков. Найти зависимость ЭДС индукции от времени, если период вращения рамки составляет 0,02 с. Чему равно максимальное значение ЭДС индукции.
Задача 70225 В однородном магнитном поле индукция которого равна 0,5 Тл проводник переместился перпендикулярно линиям магнитного поля на 50 см. При этом была совершена работа равная 55мДж. Чему равна сила тока в проводнике, если его длина равна 45 см?
Задача 13744 В однородном магнитное поле, индукция которого 0,1 Тл, равномерно с частотой 4 Гц вращается рамка площадью 100 кв.
Задача 19379 Однородное магнитное поле, индукция которого В = 0,01 Тл, направлено перпендикулярно однородному электрическому полю напряженностью E = 17 кВ/м. Ион, пройдя ускоряющую разность потенциалов U = 15 кВ и влетев в область, занятую полями, движется равномерно и прямолинейно. Определить отношение заряда к массе иона.
Задача 19645 Катушка в виде соленоида помещена в однородное магнитное поле, индукция которого изменяется со временем так, как показано на графике. Линии индукции параллельны оси катушки. Во сколько раз ЭДС индукции, возникающая на интервале времени от 0 до 2 с больше ЭДС индукции, возникающей на интервале времени от 2 с до 6 с?
Задача 21167 В однородном магнитном поле, индукция которого равна 0,1 Тл, вращается катушка, состоящая из 200 витков.
Задача 21272 В однородном магнитном поле, индукция которого В = 0,75 Тл, равномерно с частотой ν = 11 Гц вращается рамка, содержащая N витков, плотно прилегающих друг к другу. Площадь рамки равна S = 30 см2, ось вращения перпендикулярна к линиям индукции. Мгновенное значение ЭДС индукции в момент времени t = 2,02 с равно εi = 130,63 В. Найти N.
Задача 21849 В однородном магнитном поле, индукция которого равна 0,05 Тл, движется равномерно проводник длиной 15 см. По проводнику течет ток 3 А. Скорость движения проводника равна 20 м/с и перпендикулярна к направлению индукции магнитного поля. Найти работу перемещения проводника за 20 с движения.
Задача 21933 Круговой контур радиусом r = 2 см помещен в однородное магнитное поле, индукция которого В = 0,2 Тл.
Задача 22219 В однородном магнитном поле, индукция которого 0,5 Тл, равномерно с частотой 300 мин–1 вращается катушка, содержащая 200 витков, плотно прилегающих друг к другу. Площадь поперечного сечения катушки 100 см2. Ось вращения перпендикулярна оси катушки и направлению магнитного поля. Определите максимальное значение ЭДС в катушке.
Задача 22675 Альфа-частица движется по окружности радиуса r = 8,3 мм в однородном магнитном поле, индукция В которого 24 мТл. Найти длину волны де Бройля λ такой частицы. Заряд альфа-частицы q численно равен 2е.
Задача 22854 В однородном магнитном поле, индукция которого равна 0,08 Тл, вращается катушка, содержащая 400 витков.
| ||||||||||||||||||||||||
Физика пружин | Как производители понимают дизайн пружин
Физика пружин: как производители проектируют пружины, которые работают
Поместите пружину сжатия рядом с листовой пружиной , и вы увидите два очень разных объекта, между которыми мало общего. поверхность. Пружины бывают самых разных форм и размеров, но независимо от того, как они выглядят, все они работают одинаково. Каждая пружина представляет собой эластичный объект , что означает, что она накапливает и высвобождает энергию. Конструкция пружин и их изготовление зависят от глубокого понимания физики пружин.
Процесс производства пружин и оборудование для изготовления пружин немного сложнее, но сами пружины представляют собой простые механизмы, которые ведут себя очень предсказуемо, если вы знаете, чего ожидать. Понимая физику пружин, производители могут точно предсказать, как пружина будет вести себя в реальном мире, прежде чем они включат намоточный станок.
Загрузите нашу бесплатную электронную книгу: Все о пружинах
Закон Гука: Физика пружин
Помимо хранения и высвобождения энергии, еще одним важным аспектом физики пружин является Закон Гука. Закон Гука гласит, что чем больше вы деформируете пружину, тем больше силы потребуется для ее дальнейшей деформации. Используя пример обычной пружины сжатия, чем больше вы сжимаете пружину, тем больше силы потребуется для ее дальнейшего сжатия.
Британский физик Роберт Гук (на фото справа) впервые опубликовал закон в 1678 году, хотя утверждал, что знал о нем почти два десятилетия. Закон был просто сформулирован на латыни, uttensio, sic vis, , что примерно переводится как «как расширение, так и сила».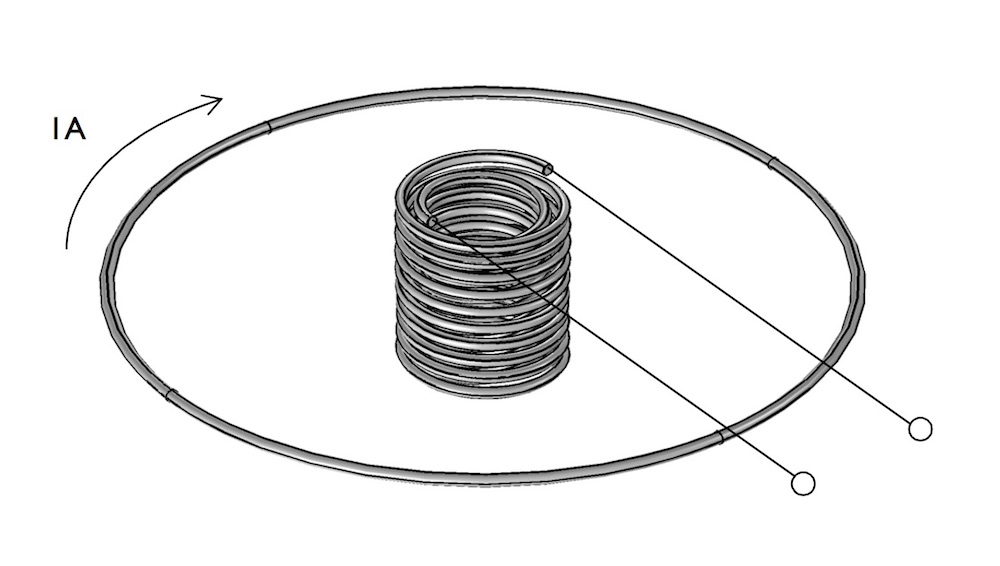 Более современное алгебраическое представление закона: F=kX , где F — сила, k — жесткость пружины , а X — длина деформации.
Более современное алгебраическое представление закона: F=kX , где F — сила, k — жесткость пружины , а X — длина деформации.
Если вы посмотрите на график уравнения, вы увидите прямую линию или линейную скорость изменения силы. Из-за этой особенности пружины, подчиняющиеся закону Гука, попадают в категорию пружин с «линейной силой».
Константа пружины
Константа пружины точно определяет, какая сила потребуется для деформации пружины. Стандартной международной (СИ) единицей измерения жесткости пружины является ньютон/метр, но в Северной Америке они часто измеряются в фунтах/дюйм. Более высокая жесткость пружины означает более жесткую пружину, и наоборот.
Жесткость пружины можно определить по четырем параметрам:
- Диаметр проволоки : диаметр проволоки, входящей в состав пружины
- Диаметр рулона : диаметр каждого рулона, измерение натяжения рулона
- Длина в свободном состоянии : длина пружины в состоянии покоя
- Количество активных витков : количество витков, которые могут свободно расширяться и сжиматься
Материал , из которого изготовлена пружина, также играет роль в определении жесткости пружины наряду с другими физическими свойствами пружины.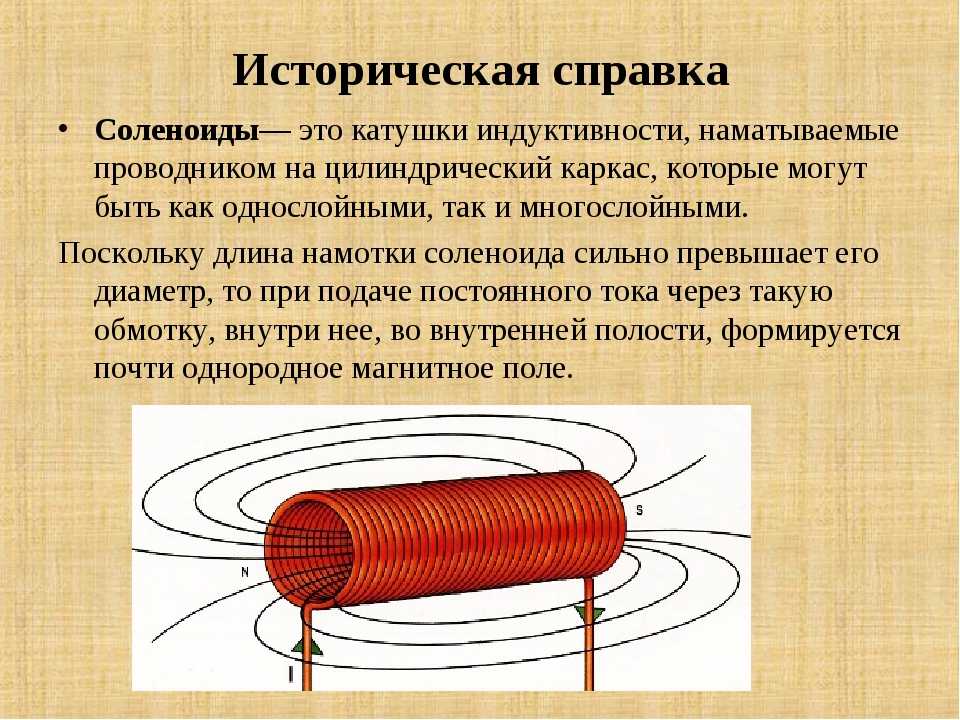
Исключения из закона Гука
В мире пружин существует несколько исключений из закона Гука. Например, слишком растянутая пружина растяжения перестанет соответствовать закону. Длина, на которой пружина останавливается по закону Гука, называется пределом упругости .
Пружины переменного диаметра , такие как конические, выпуклые или вогнутые пружины, могут быть свернуты с различными параметрами силы. Если пружина шаг (расстояние между витками) постоянно, сила конической пружины будет изменяться нелинейно, а это означает, что она не подчиняется закону Гука. Однако шаг пружины также можно варьировать для получения конических пружин, которые действительно подчиняются закону.
Пружины с переменным шагом являются третьим примером пружины, которая не подчиняется закону Гука. Пружины с переменным шагом часто представляют собой пружины сжатия с постоянным диаметром витка, но с переменным шагом.
Пружины постоянной силы, по отношению к закону Гука, часто являются ложными исключениями . Судя по названию и описанию, пружины постоянной силы , а не , подчиняются закону Гука. В конце концов, если сила, которую они прикладывают, постоянна, как сила может меняться в зависимости от длины пружины? Как упоминалось в нашей публикации о пружинах постоянной силы , материал, из которого изготовлены эти пружины, на самом деле соответствует закону Гука. Отличие состоит в том, что упругая часть пружины с постоянной силой — это только та часть, которая меняется со спиральной на прямую. При вдавливании или вытягивании пружины и изменении диаметра витка действующая сила также изменяется. Это изменение, однако, часто незаметно, потому что изменения диаметра катушки очень малы.
Судя по названию и описанию, пружины постоянной силы , а не , подчиняются закону Гука. В конце концов, если сила, которую они прикладывают, постоянна, как сила может меняться в зависимости от длины пружины? Как упоминалось в нашей публикации о пружинах постоянной силы , материал, из которого изготовлены эти пружины, на самом деле соответствует закону Гука. Отличие состоит в том, что упругая часть пружины с постоянной силой — это только та часть, которая меняется со спиральной на прямую. При вдавливании или вытягивании пружины и изменении диаметра витка действующая сила также изменяется. Это изменение, однако, часто незаметно, потому что изменения диаметра катушки очень малы.
Используя передовое оборудование для навивки пружин с ЧПУ AIM , пружины с постоянным усилием можно сконструировать таким образом, чтобы усилие пружины можно было поддерживать постоянным или даже иметь отрицательный градиент при растяжении пружины. Достигнуты отрицательные градиенты порядка 35%.
Почему физика пружин имеет значение при проектировании и производстве пружин
Когда производители производят пружины, они должны знать, как они себя поведут. Очевидно, что та же самая пружина, которая используется для подвески грузовика, не будет работать в шариковой ручке, но во многих механических приложениях мельчайшие различия в поведении пружины будут определять, будет ли система работать или нет.
Например, пружины используются для расширения кровеносных сосудов в медицинских целях. Если жесткость пружины слишком высока или проволока слишком тонкая, пружина может привести к опасному для жизни разрыву. В более широком масштабе системы автомобильной подвески полагаются на чрезвычайно точные пружины, обеспечивающие амортизацию без дестабилизации автомобиля на высоких скоростях.
Все конструктивные характеристики пружины играют роль в определении полезного применения той или иной пружины. Когда производитель настраивает параметры своих станков для намотки пружин, он не просто гадает. Понимая физику пружин, производители могут гарантировать, что они наматывают правильную пружину для работы.
Понимая физику пружин, производители могут гарантировать, что они наматывают правильную пружину для работы.
Для подробного ознакомления с типами пружин и их производством загрузите нашу бесплатную электронную книгу
Все о пружинах7.7: Springs — Engineering LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 21415
- Распространение информационных технологий для продвижения материаловедения (DoITPoMS)
- Кембриджский университет
Набор пружин в ассортименте
Интересным примером кручения является деформация, происходящая при нагружении пружин (витков кручения). Конечно, они имеют широкий спектр инженерных приложений. Обычно они изготавливаются из металлов (с высоким пределом текучести). (Керамика слишком хрупкая, а полимеры недостаточно жесткие: волокнистые композиты также не подходят — см. ниже.) Когда пружина нагружена (сжата или растянута), деформация, испытываемая проволокой, представляет собой деформацию чистого кручения. Это показано на диаграмме ниже.
Конечно, они имеют широкий спектр инженерных приложений. Обычно они изготавливаются из металлов (с высоким пределом текучести). (Керамика слишком хрупкая, а полимеры недостаточно жесткие: волокнистые композиты также не подходят — см. ниже.) Когда пружина нагружена (сжата или растянута), деформация, испытываемая проволокой, представляет собой деформацию чистого кручения. Это показано на диаграмме ниже.
Иллюстрация того, как приложение осевой нагрузки F к пружине вызывает деформацию кручения проволоки и, следовательно, осевое удлинение пружины.
Крутящий момент, действующий на провод, определяется как
.\[T=F\влево(\frac{D}{2}\вправо)\]
, где F — осевая сила, а D — диаметр катушки. В приведенном ниже примере можно показать, что касательное напряжение в проволоке (на расстоянии r от сердечника) равно 9{2}}\]
Измерение растяжения (на оборот) пружины в зависимости от приложенной силы (впервые систематически проведенное Робертом Гуком в его новаторской работе о природе упругости) является очень удобным методом получения упругие константы. Отношение τ к γ , полученное из приведенных выше уравнений, дает модуль сдвига G . Геометрия нагрузки такова, что создается большое осевое растяжение (за оборот), в то время как деформации внутри материала остаются низкими, особенно для пружин с большим передаточным отношением D — w . Конечно, именно поэтому пружины имеют практическое применение — они компенсируют большие прогибы или смещения без деформации материала за пределами его предела упругости (который мал для всех материалов, кроме резины).
Отношение τ к γ , полученное из приведенных выше уравнений, дает модуль сдвига G . Геометрия нагрузки такова, что создается большое осевое растяжение (за оборот), в то время как деформации внутри материала остаются низкими, особенно для пружин с большим передаточным отношением D — w . Конечно, именно поэтому пружины имеют практическое применение — они компенсируют большие прогибы или смещения без деформации материала за пределами его предела упругости (который мал для всех материалов, кроме резины).
Интересно отметить, почему пружины обычно не изготавливаются из волокнистых композитов. Естественная ориентация волокон была бы по длине стержня (проволоки), которая должна быть свернута в катушку. Однако эти волокна очень мало влияют на модуль сдвига в поперечном сечении стержня, который является свойством, определяющим упругие растяжения пружины. С тем же успехом она могла быть сделана исключительно из полимерной матрицы (хотя такие пружины имеют очень низкую жесткость). Только за счет намотки волокон в кольцевом направлении стержня можно повысить сдвиговую жесткость поперечных сечений. Однако это непрактично, по крайней мере, для чего-либо, кроме пружин очень большого размера, поскольку это потребует от волокон большей кривизны, чем это обычно возможно.
Только за счет намотки волокон в кольцевом направлении стержня можно повысить сдвиговую жесткость поперечных сечений. Однако это непрактично, по крайней мере, для чего-либо, кроме пружин очень большого размера, поскольку это потребует от волокон большей кривизны, чем это обычно возможно.
Пример \(\PageIndex{1}\)
Рассмотрим небольшую элементарную длину провода, показанного на рисунке, образующего угол d β на оси катушки. Напряжение сдвига в проволоке, τ , можно найти, заметив, что оно изменяется линейно с расстоянием от центра проволоки ( τ = κ r , где κ — неизвестная константа, а r — расстояние элемента от центра провода) . Теперь крутящий момент можно выразить через внутренние силы в проводе. Сила в отдельном элементе проволоки определяется напряжением сдвига при кручении, τ , умноженным на площадь элемента, 2 π r d r . Таким образом, крутящий момент элемента представляет собой просто эту силу, умноженную на расстояние элемента от нейтральной оси провода, r .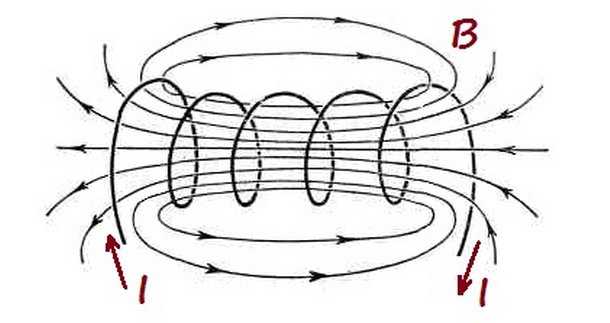 {4}\] 9{4}}{64}\]
{4}\] 9{4}}{64}\]
Местная деформация сдвига в материале определяется как
\[\gamma=r \frac{\mathrm{d} \theta}{\mathrm{d} L}=\ frac{r \mathrm{d} \theta}{(D / 2) \mathrm{d} \beta}\]
, где dθ /d L — скорость скручивания по длине проволоки. Таким образом, инкрементный угол закручивания проволоки связан с соответствующим инкрементным углом поворота катушки как
\[\mathrm{d} \theta=\gamma \frac{(D / 2)}{r} \mathrm{ d} \beta\]
Таким образом, осевое смещение катушки из-за скручивания элементарной секции может быть записано как 9{2}}\]
Эта страница под названием 7.7: Springs распространяется по лицензии CC BY-NC-SA и была создана, изменена и/или курирована организацией «Распространение ИТ для продвижения материаловедения» (DoITPoMS).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ДОИТПОМС
- Лицензия
- CC BY-NC-SA
- Показать оглавление
- нет
- Метки

Курс: Моделирование электромагнитных катушек в COMSOL®
Ищете быстрое руководство по моделированию электромагнитных катушек с помощью программного обеспечения COMSOL Multiphysics® и модуля AC/DC? Мы подготовили курс видеолекций, которые проведут вас по моделированию электромагнитных катушек, призванных показать ключевые аспекты построения таких моделей. Давайте быстро рассмотрим, что в этих видео и как использовать курс с максимальной пользой!
Начало работы с моделированием электромагнитных катушек
Простейшая электромагнитная катушка представляет собой один виток провода с током, как вы увидите практически в любом введении в тему. Часто разумным инженерным упрощением является предположение, что катушку можно рассматривать как замкнутый контур, что означает, что она осесимметрична или неизменна относительно центральной линии.
Простая одновитковая катушка также может быть смоделирована с использованием двумерного осесимметричного предположения.
Именно с этого предположения начинается наш курс моделирования катушек. Первые пять частей мы будем работать в двумерном осесимметричном пространстве.
Части 1–5
В первых пяти частях курса мы даем базовые знания о моделировании катушек и представляем информацию, которая будет построена на оставшихся занятиях. Начнем с построения модели одновитковой катушки в условиях постоянного тока от начала до конца. Воздушная область ограничена бесконечной областью элементов. Мы считаем, что через катушку проходит ток силой 1 ампер, и моделируем ее в двумерной осесимметричной плоскости. Мы также предоставляем некоторые дополнительные сведения о том, почему и как мы можем использовать предположение об осесимметричности 2D.
После расчета модели мы также оцениваем проводимость и сопротивление катушки. Затем мы переходим к перемещению катушки в частотную область. Мы моделируем катушку, возбуждаемую током 1 А, и предполагаем, что изменение тока возбуждения является синусоидальным и происходит с известной частотой.
После построения и проверки модели катушки для постоянного и переменного тока мы обсудим потенциальные проблемы моделирования, о которых вам следует знать при построении этих типов моделей.
После этого мы продолжаем расширять модель катушки, имитируя ее подключение к электрической цепи. Мы делаем это, вводя магнитный сердечник, а также вторичную катушку, через которую снимается часть тока, протекающего через первичную первую катушку. Затем мы покажем, как выполнить некоторую постобработку, чтобы визуализировать величину и направление тока между катушками.
Отсюда мы переходим к моделированию катушек, содержащих несколько витков и различные схемы намотки. Кроме того, мы моделируем катушки вплоть до первой резонансной частоты и вокруг нее, а также плоские катушки. Затем мы заканчиваем всесторонним обзором 9Физический интерфейс 0081 Magnetic Fields и различные функции, содержащиеся в нем, которые вы можете использовать при создании моделей катушек.
После просмотра видеороликов в этой вводной части курса вы познакомитесь с основами методов двухмерного осесимметричного моделирования катушек.
Электромагнитный нагрев в змеевиках
Одно из распространенных применений COMSOL Multiphysics с модулем AC/DC и модулем теплопередачи — моделирование индукционного нагрева — процесса, при котором змеевик используется для нагрева заготовки с течением времени. В следующих пяти частях курса мы подробно рассмотрим эту тему.
Заготовка, подвергающаяся индукционному нагреву с течением времени, с нелинейными свойствами материала.
Части 6–10
В частях с 6 по 10 курса мы демонстрируем полное пошаговое руководство по настройке и решению задач моделирования индукционного нагревательного змеевика. Начнем с создания двумерной осесимметричной модели трехвитковой катушки в свободном пространстве и зададим 1 килоампер тока, протекающего через каждый виток катушки. Также включаем в центр заготовку из титанового сплава. Задача моделируется в частотной области на постоянной частоте 10 кГц. После расчета моделирования мы выполняем некоторую постобработку, чтобы посмотреть на потери в детали заготовки.
Отсюда мы расширяем нашу первоначальную проблему электромагнетизма до проблемы электромагнитного нагрева. Чтобы выяснить, как электромагнитные потери вызывают повышение температуры и в какой степени, мы добавляем в модель катушки вторую физику — теплопередачу. После этого мы покажем вам, как вы можете изменить свойства материала от использования скалярных постоянных значений до функции входных данных модели (в данном случае температуры). Затем мы продолжаем расширять модель, показывая, как изменять профиль нагрева заготовки с течением времени, а также решать задачи с несколькими частотами.
После этого мы углубимся в обсуждение различных тем, касающихся решателей. Мы также обращаемся к соображениям теплового моделирования, которые ранее не рассматривались, включая конвекцию и излучение в тепловую модель. Мы также демонстрируем, как моделировать нагрев движущихся частей.
После завершения этого раздела курса вы должны быть уверены в решении большинства проблем с нагревом змеевика.
Моделирование сил, движения, нелинейностей и др.
Следующие пять частей курса посвящены другому виду мультифизики: связи электромагнитных сил с деформацией и движением деталей, например, в соленоидах.
Смещение электромагнитного привода с течением времени.
Детали 11–15
В частях с 11 по 15 курса мы строим и работаем с несколькими моделями катушек различной геометрии для проведения различных анализов. Это отход от предыдущих частей, где мы обычно работали с одной геометрией и настройкой модели, но внесли в нее изменения, чтобы постепенно усложнять наши модели и расширять анализ.
Мы начнем с демонстрации того, как моделировать электромагнитные силы и делать это точно, что достигается добавлением Расчет силы для нашей модели, а затем использование Глобальной оценки для определения общей силы, наблюдаемой на катушках в модели. Затем мы изучаем, как определить точность оцененных величин силы, что делается быстро и легко посредством адаптации сетки. Создавая впоследствии график, отображающий значения силовых величин в зависимости от измельчения сетки, мы наблюдаем, начинают ли силовые величины сходиться к некоторому значению.
Создавая впоследствии график, отображающий значения силовых величин в зависимости от измельчения сетки, мы наблюдаем, начинают ли силовые величины сходиться к некоторому значению.
Мы переходим к моделированию магнита, движущегося и индуцирующего токи внутри катушки. Магнит определяется с помощью функции области закона Ампера, а движение определяется с помощью нескольких функций Moving Mesh в программном обеспечении. При решении этой модели мы сталкиваемся с некоторыми проблемами, связанными с настройками решателя, в результате несоответствия между исходным термином и начальными значениями модели, которые мы подробно показываем, как решить.
Отсюда мы переходим к моделированию обратной версии предыдущей задачи — соленоидного привода. На этот раз у нас есть катушка, и мы применяем к ней переменный во времени ток, чтобы вызвать движение в соседней части. После этого мы покажем, как моделировать индуктор с нелинейным материалом сердечника. При этом мы затрагиваем темы, обсуждавшиеся ранее с предыдущими моделями, такие как точность решения и сходимость. Мы также покажем вам, как визуализировать усредненные за цикл потери в области сердечника, интегрируя наше уравнение для тока катушки, вводя другое уравнение в нашу модель через 9Интерфейс 0081 Global Evaluation и выполнение глобальной оценки с использованием оператора at.
Мы также покажем вам, как визуализировать усредненные за цикл потери в области сердечника, интегрируя наше уравнение для тока катушки, вводя другое уравнение в нашу модель через 9Интерфейс 0081 Global Evaluation и выполнение глобальной оценки с использованием оператора at.
Наш сеанс завершается другой моделью, в которой мы берем катушку и оптимизируем ее так, чтобы B-поле было максимально однородным по центральной линии геометрии. Мы демонстрируем определение целевой функции и улучшение функции путем изменения тока через витки катушки и положения катушки.
После завершения этого раздела курса вы должны обладать знаниями в области моделирования, расчета и оценки сил, движений и нелинейностей для большинства моделей катушек.
Моделирование трехмерных катушек
В последних пяти частях курса моделирования катушек рассматриваются вопросы, связанные с моделированием трехмерных катушек. Хотя большинство концепций моделирования катушек можно изучить исключительно на 2D-осесимметричной модели, есть некоторые уникальные проблемы, которые необходимо решать в 3D.
Трехмерная модель катушки, показывающая величину тока на катушке и окружающее магнитное поле.
Части 16–20
В частях 16–20 курса мы создадим нашу первую 3D-модель катушки, которую будем решать в стационарном режиме постоянного тока. При построении геометрии нашей катушки в 3D мы используем шаблон спирали, а на концах изгибов катушки выдавливаем катушку в вертикальные прямые трубки. При этом мы покажем вам несколько различных подходов, которые вы можете использовать, чтобы гарантировать, что геометрия катушки является единым доменом. Это можно сделать с помощью Удаление объектов , Объединение или Создание составных доменов , однако это не требуется и в конечном итоге является вопросом предпочтения и учета. Добавление объекта домена Coil в нашу модель, в отличие от ранее для наших 2D осесимметричных моделей катушек, включает подэлемент Geometry Analysis , в котором нам нужно указать, где мы хотим, чтобы ток протекал как в катушку, так и из нее.
При вычислении модели мы получаем сообщение об ошибке, а затем объясняем, почему и как это происходит и как с этим бороться. Новый этап обучения, Анализ геометрии катушки включен в наше исследование, чтобы сначала вычислить текущее направление в структуре. После успешного решения модели с использованием интерфейса Magnetic Fields мы затем решаем ту же задачу, используя интерфейс Magnetic and Electric Fields .
После завершения этих моделей однопроводниковой катушки мы переходим к демонстрации специализированных функций для моделирования различных типов катушек. Мы обсудим и покажем, как вместо явного моделирования витков многовитковой катушки мы можем смоделировать гомогенизированную многовитковую катушку, используя приблизительно эквивалентную геометрию и отрегулировав Настройки функции домена Coil . Другие типы катушек включают тонкие лентовидные катушки; плотно упакованные катушки без зазора между витками; и используя кромку, геометрию катушки проволоки.


 Как взаимодействуют два воздушных провода
троллейбусной линии: ппритягиваются или отталкиваются?
Как взаимодействуют два воздушных провода
троллейбусной линии: ппритягиваются или отталкиваются? Сквозь горизонтальное проводящее кольцо падают
с одинаковой высоты алюминиевый брусок и магнит.
Какой предмет упадет первым?
Сквозь горизонтальное проводящее кольцо падают
с одинаковой высоты алюминиевый брусок и магнит.
Какой предмет упадет первым? Почему в жидкой или газообразной средах не
возникают поперечные волны?
Почему в жидкой или газообразной средах не
возникают поперечные волны?
 Что может произойти, если случайно подключить
трансформатор к источнику постоянного тока?
Что может произойти, если случайно подключить
трансформатор к источнику постоянного тока? Почему на экране телевизора при появлении
летящего вблизи самолёта возникает двойное изображение?
Почему на экране телевизора при появлении
летящего вблизи самолёта возникает двойное изображение?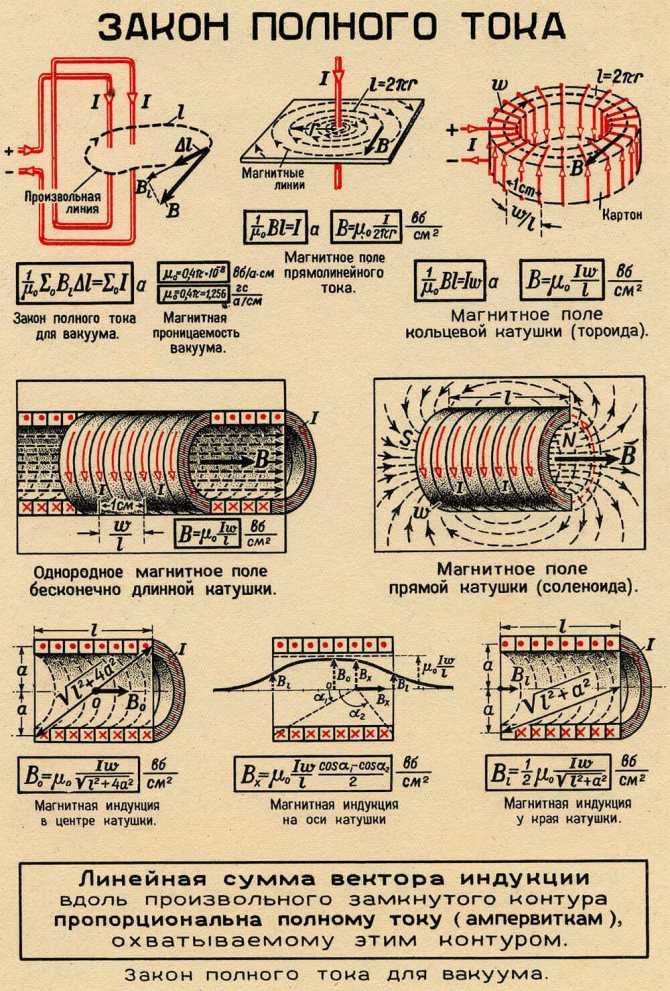 Почему в темной комнате видны только те предметы,
на которые в данный момент направлен луч фонарика?
Почему в темной комнате видны только те предметы,
на которые в данный момент направлен луч фонарика? Объясните это
явление.
Объясните это
явление. В каком случае поверхность рассеивает падающий
на неё свет? Почему?
В каком случае поверхность рассеивает падающий
на неё свет? Почему? Почему?
Почему? Пузырьки воздуха, расположенные на стеблях
и листьях подводных растений кажутся серебристо-зеркальными.
Почему?
Пузырьки воздуха, расположенные на стеблях
и листьях подводных растений кажутся серебристо-зеркальными.
Почему? Какого цвета должно быть стёклышко, сквозь
которое можно увидеть зеленую надпись на белой
бумаге?
Какого цвета должно быть стёклышко, сквозь
которое можно увидеть зеленую надпись на белой
бумаге? Какие изменения при этом наблюдали на экране?
Какие изменения при этом наблюдали на экране? Длина волны красного света в воде равна длине
волны зеленого света в воздухе. Какой цвет увидит
человек под водой, если вода освещена красным
светом?
Длина волны красного света в воде равна длине
волны зеленого света в воздухе. Какой цвет увидит
человек под водой, если вода освещена красным
светом? Почему?
Почему? Чем
это объясняется?
Чем
это объясняется? Что
можно сказать о толщине такой пленки?
Что
можно сказать о толщине такой пленки? Поясните причину
увеличения её кинетической энергии и сравните
энергию падающих и отраженных фотонов.
Поясните причину
увеличения её кинетической энергии и сравните
энергию падающих и отраженных фотонов.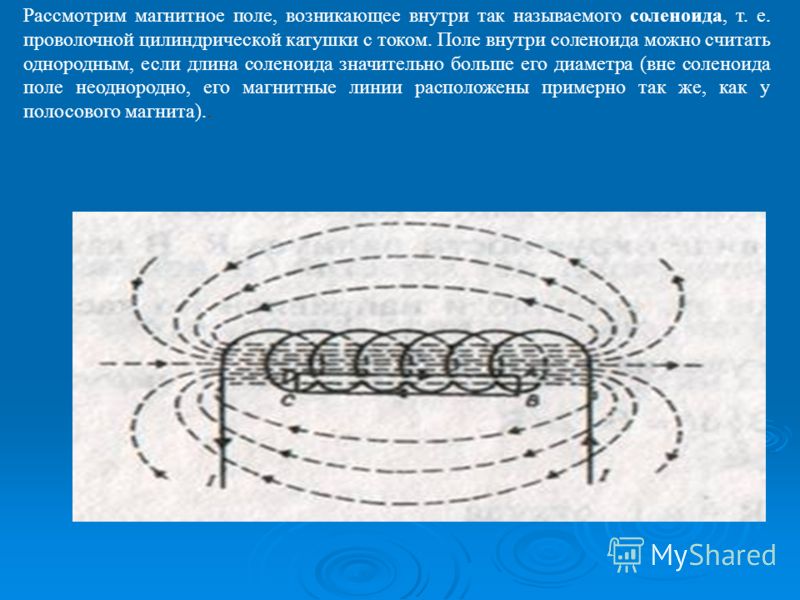 Как изменилась энергия атома водорода, если
электрон в атоме перешел с первой орбиты на третью,
а потом обратно?
Как изменилась энергия атома водорода, если
электрон в атоме перешел с первой орбиты на третью,
а потом обратно? Произошел самопроизвольный распад ядра. Выделилась
или поглотилась энергия во время этого распада?
Ответ обоснуйте.
Произошел самопроизвольный распад ядра. Выделилась
или поглотилась энергия во время этого распада?
Ответ обоснуйте.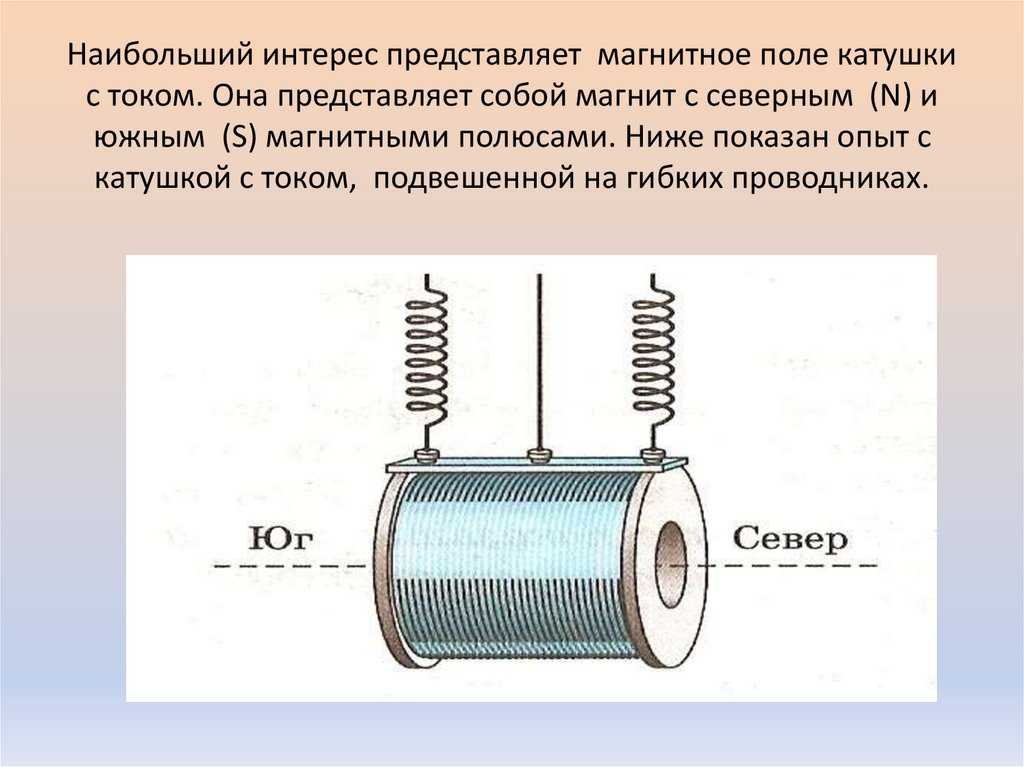 Допустим, что значительный по массе комок земного
вещества, отправленный в глубины космоса, встретился
с куском антивещества. Чем должна закончиться
такая встреча?
Допустим, что значительный по массе комок земного
вещества, отправленный в глубины космоса, встретился
с куском антивещества. Чем должна закончиться
такая встреча?
 статистика
статистика Площадь контура за время τ = 2 с равномерно уменьшается (плоскость контура при этом остается перпендикулярной силовым линиям поля) до величины S2 = 2 см2. Определить силу тока, проходящего по контуру в течение времени τ, если сопротивление контура R = 1 Ом.
Площадь контура за время τ = 2 с равномерно уменьшается (плоскость контура при этом остается перпендикулярной силовым линиям поля) до величины S2 = 2 см2. Определить силу тока, проходящего по контуру в течение времени τ, если сопротивление контура R = 1 Ом.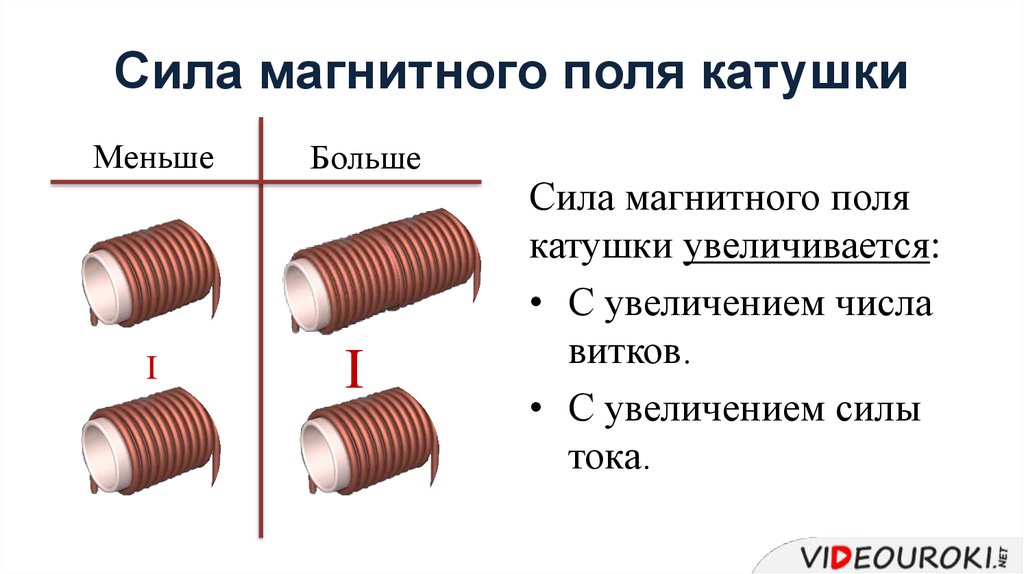 Ось вращения перпендикулярна к оси катушки и направлению магнитного поля. Найти максимальную ЭДС индукции εmaх во вращающейся катушке.
Ось вращения перпендикулярна к оси катушки и направлению магнитного поля. Найти максимальную ЭДС индукции εmaх во вращающейся катушке.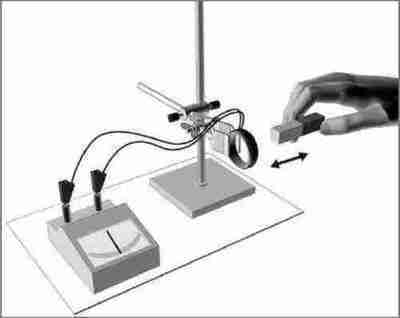
 Какое количество теплоты выделяется в витке за промежуток времени Δt = 0 … 0,5 с, если его сопротивление R = 5 Ом.
Какое количество теплоты выделяется в витке за промежуток времени Δt = 0 … 0,5 с, если его сопротивление R = 5 Ом. см. Сопротивление рамки 16 Ом, число витков рамки 100. Определить максимальное значение мощности, которую необходимо приложить к рамке для осуществления такого вращения.
см. Сопротивление рамки 16 Ом, число витков рамки 100. Определить максимальное значение мощности, которую необходимо приложить к рамке для осуществления такого вращения. Период обращения катушки равен 0,2 с, площадь поперечного сечения катушки 4 см2. Найти максимальную ЭДС индукции во вращающейся катушке.
Период обращения катушки равен 0,2 с, площадь поперечного сечения катушки 4 см2. Найти максимальную ЭДС индукции во вращающейся катушке. Плоскость контура перпендикулярна к направлению магнитного поля. Сопротивление контура R = 1 Ом. Какой заряд q пройдет по катушке при исчезновении магнитного поля?
Плоскость контура перпендикулярна к направлению магнитного поля. Сопротивление контура R = 1 Ом. Какой заряд q пройдет по катушке при исчезновении магнитного поля? Период обращения катушки равен 3,00 с, площадь ее поперечного сечения составляет 6,00 см2. Определить максимальное значение ЭДС индукции во вращающейся катушке и ЭДС индукции через 0,25 с после начала вращения. Первоначально плоскость витков катушки была перпендикулярна магнитному полю.
Период обращения катушки равен 3,00 с, площадь ее поперечного сечения составляет 6,00 см2. Определить максимальное значение ЭДС индукции во вращающейся катушке и ЭДС индукции через 0,25 с после начала вращения. Первоначально плоскость витков катушки была перпендикулярна магнитному полю.