Закон Ома для участка цепи. Последовательное и параллельное соединение проводников. 10 класс. Физика. — Объяснение нового материала.
Комментарии преподавателяЗакон Ома для участка цепиСила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению участка.
Закон Ома оказался справедливым не только для металлов, но и для растворов электролитов. Сформулированный закон имеет место для так называемого однородного участка цепи – участка, не содержащего источников тока.
Математическая запись закона Ома проста, как и его формулировка, но экспериментально подтвердить эту зависимость очень трудно. Сила тока, протекающая по участку цепи, мала. Поэтому используют достаточно чувствительные приборы. Г. Ом изготовил чувствительный прибор для измерения силы тока, а в качестве источника тока использовал термопару. Действие амперметра и вольтметра основано на применение закона Ома для участка цепи. Угол поворота стрелки прибора пропорционален силе тока.
Угол поворота стрелки прибора пропорционален силе тока.
Из математической записи закона Ома:
можно выразить напряжение :
и сопротивление проводника:
.
Таким образом, закон Ома связывает три параметра, характеризующих постоянный электрический ток, проходящий по проводнику, и позволяет находить любой из них, если известны два других.
Закон Ома имеет границы применимости и выполняется только в том случае, когда при прохождении тока температура заметно не меняется. На вольт–амперной характеристике лампы накаливания видно, что график сильно искривляется при напряжении выше 10В, значит, закон Ома выше этого напряжения применять нельзя.
Также нельзя говорить, что сопротивление проводника зависит от напряжения и силы тока в цепи. Сопротивление участка цепи зависит от свойств проводника: длины, площади поперечного сечения и материала, из которого состоит проводник.
где l-длина проводника, s-его площадь поперечного сечения.
ρ –удельное сопротивление проводника – это физическая величина, характеризующая зависимость сопротивления проводника от материала, из которого он изготовлен.
Удельное сопротивление показывает, каким сопротивлением обладает сделанный из этого вещества проводник длиной 1м и площадью поперечного сечения 1м2 .
Из формулы видно, что единицей измерения в системе СИ является Ом·м. Но так как площадь поперечного сечения проводника достаточно мала, используют единицы измерения
при вычислении площадь поперечного сечения проводника следует выражать в мм2.
В заключении хочется заметить, что Ом начал свои опыты, когда был учителем физики в гимназии. В своих экспериментах Ом брал куски проволоки одинакового диаметра, но разного материала и изменял их длину таким образом, чтобы в цепи сила тока имела одинаковое значение. Находящаяся рядом магнитная стрелка отклонялась при прохождении тока в цепи. Установив связь между напряжением и силой тока, Г.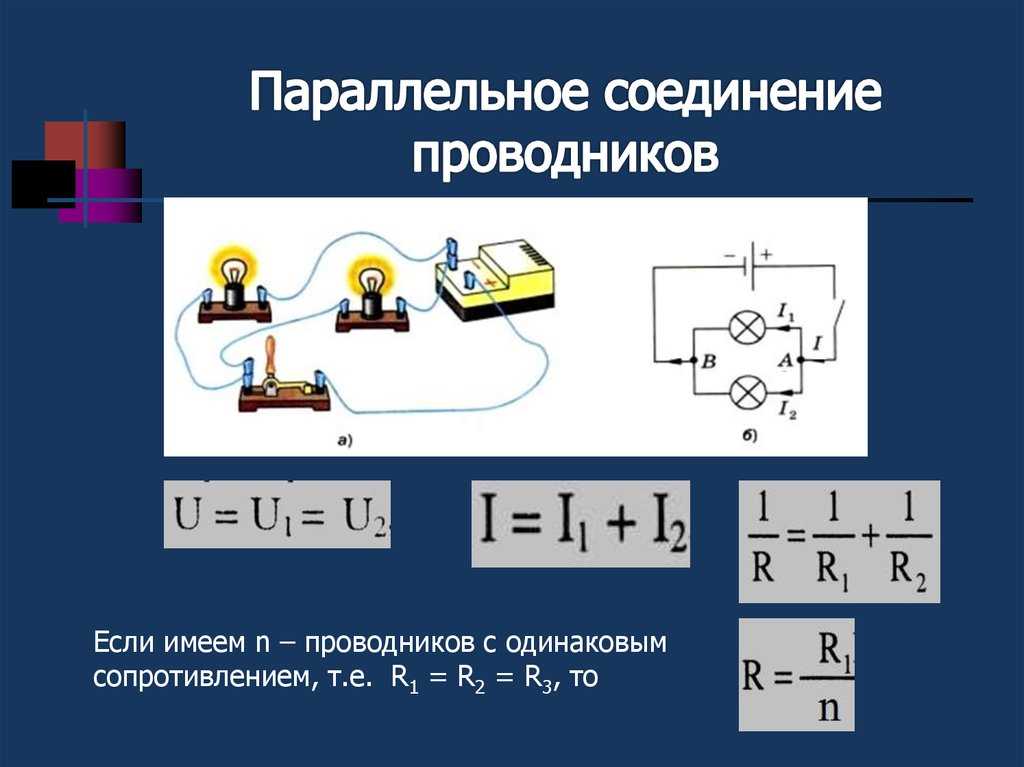 Ом вывел один из основных законов постоянного тока.
Ом вывел один из основных законов постоянного тока.
Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.
На рисунке а изображена цепь последовательного соединения двух электрических ламп, а на рисунке б — схема такого соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.
Рис. Последовательное включение лампочек и источников питания
Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же, т. е.
I = I1 = I2
А чему равно сопротивление последовательно соединённых проводников?
Соединяя проводники последовательно, мы как бы увеличиваем длину проводника.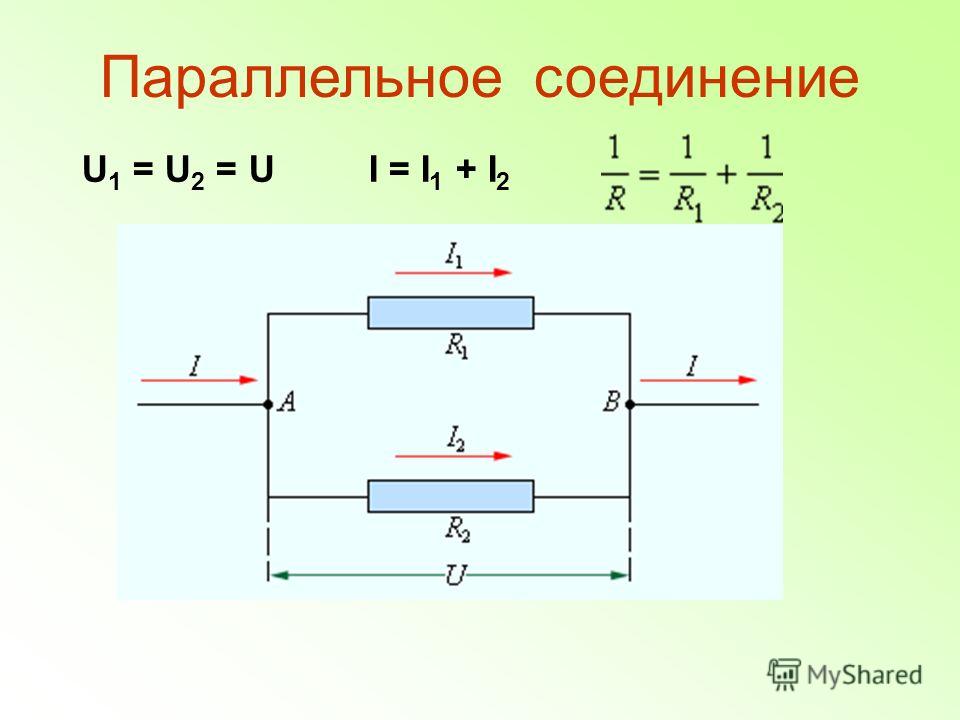 Поэтому сопротивление цепи становится больше сопротивления одного проводника.
Поэтому сопротивление цепи становится больше сопротивления одного проводника.
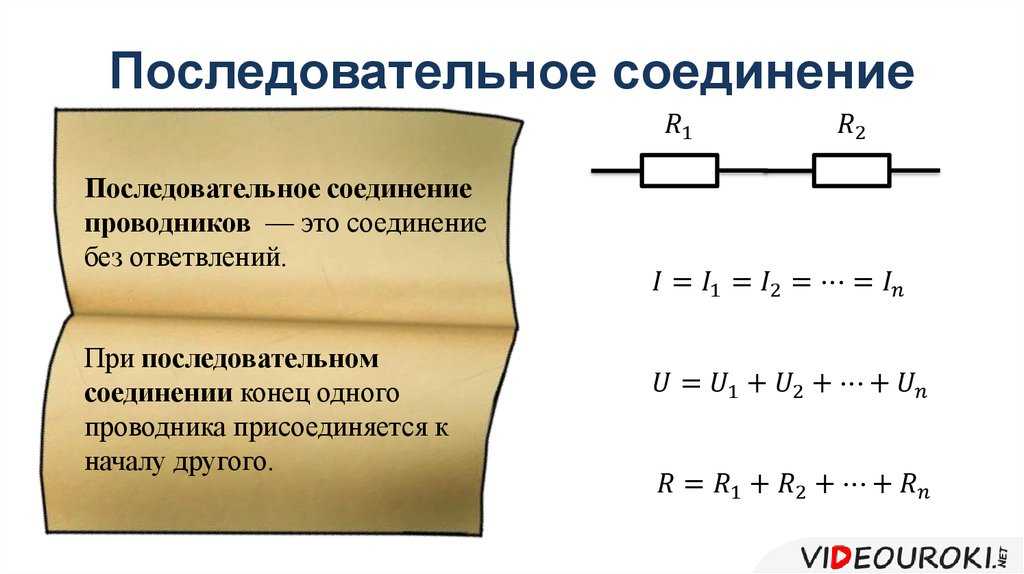
Последовательное соединение проводников
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):
R = R1 + R2
Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:
U1 = IR1, U2 = IR2.
Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
U = U1 + U2.
Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.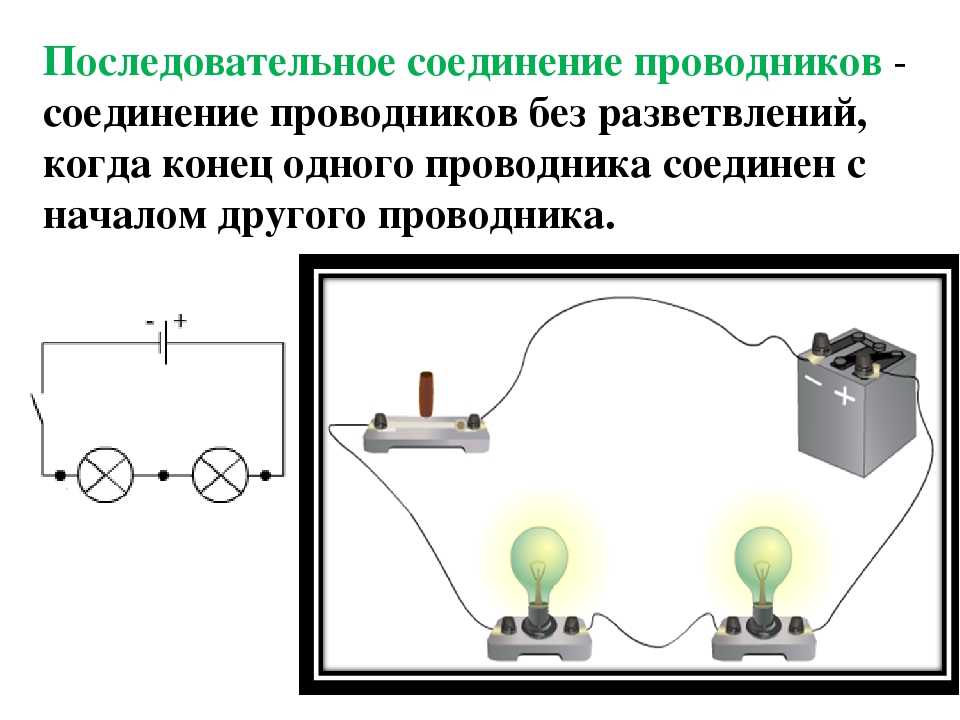
Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.
Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.
Запишем условие задачи и решим её.
Расчет параметров электрической цепи
при параллельном соединении сопротивлений:
1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках
2. напряжение на всех параллельно соединенных участках цепи одинаково
3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :
( R — сопротивление проводника,
1/R — электрическая проводимость проводника)
Если в цепь включены параллельно только два сопротивления, то:
( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )
4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,
работа электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме работ на отдельных участках:
5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:
P=P1+P2
Для двух сопротивлений:
т.е. чем больше сопротивление, тем меньше в нём сила тока.
Домашняя работа.Задание 1. Ответить на вопросы.
- Какое соединение проводников называют последовательным? Изобразите его на схеме.
- Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
- Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
- Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?
- Какое соединение проводников называют параллельным? Изобразите его на схеме.

- Какая из электрических величин одинакова для всех проводников, соединённых параллельно?
- Как выражается сила тока в цепи до её разветвления через силы токов в отдельных ветвях разветвления?
- Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
- Какое соединение проводников применяется в жилых помещениях? Какие напряжения используются для бытовых нужд?
Задание 2.Решите задачи.
1. Две лампочки соединены последовательно. Сила тока на первой лампочке 2А. Найдите общее напряжение и напряжение на каждой из ламп, если сопротивление на первой лампе 3Ом, а на второй 4Ом.
2. Две лампочки соединены параллельно. Напряжение на второй лампочке10В. Найдите силу тока в цепи и на каждой из ламп, если сопротивление на первой лампе 1Ом, а на второй 2Ом.
К занятию прикреплен файл «Это интересно». Вы можете скачать файл в любое удобное для вас время.
Использованные источники:
- http://www.tepka.ru/
- http://class-fizika.narod.ru
- http://www.youtube.com/watch?v=cVKE9NItreo
- http://znaika.ru/catalog/10-klass/physics/
- http://www.youtube.com/watch?v=NB7hOVYe7h0
- https://www.youtube.com/watch?v=cVKE9NItreo
- https://www.youtube.com/watch?v=0hFWeR8ybxs
- http://www.youtube.com/watch?v=EDI8DzWSSWY
- http://www.youtube.com/watch?v=bH_-qGnjJqc
формулы как найти силу тока, общее сопротивление, напряжение
Содержание
- Виды соединений электрических проводников
- Последовательное
- Параллельное
- Смешанное
- Как вычисляются напряжение, сила тока и электрическая мощность в зависимости от подключения
- При параллельном соединении
- При последовательном соединении
- Примеры расчетов
- Для резисторов
- Для лампочек
- Для светодиодов
При разработке электрических цепей применяется последовательное и параллельное соединение проводников.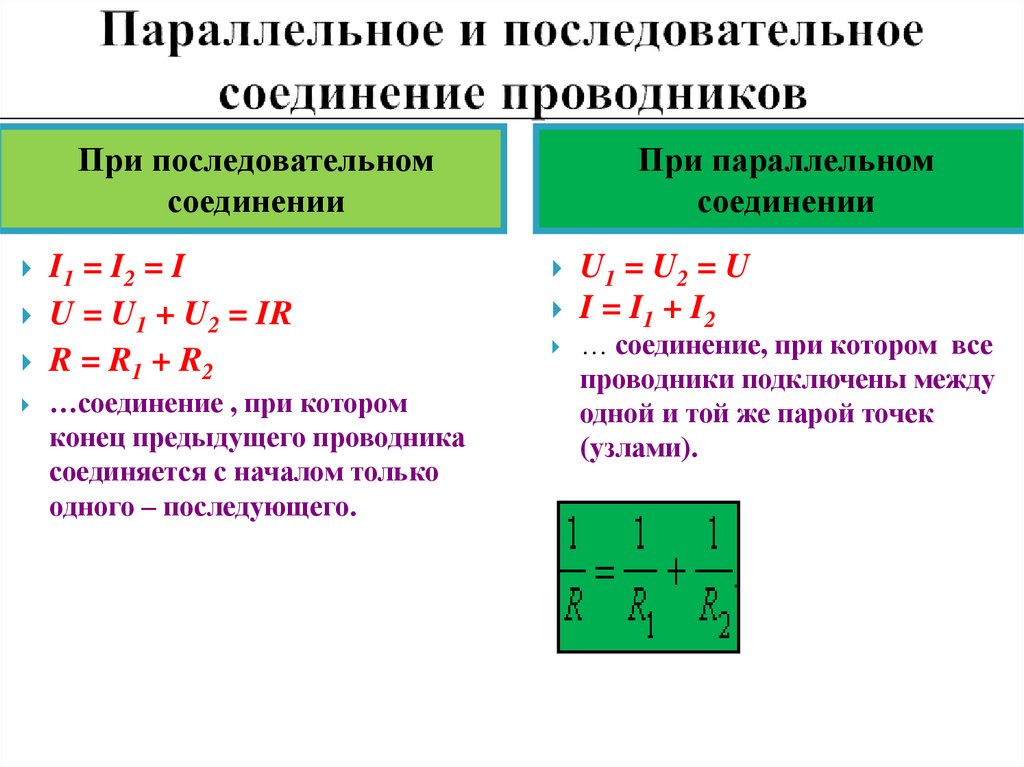 Умение анализировать (как количественно, так и качественно) и рассчитывать такие схемы является базовым принципом знаний электротехники.
Умение анализировать (как количественно, так и качественно) и рассчитывать такие схемы является базовым принципом знаний электротехники.
Виды соединений электрических проводников
Основными схемами подключения являются параллельное и последовательное соединение. Также существуют комбинации из этих двух включений.
Последовательное
При последовательном (в зарубежной терминологии serial) соединении выводы элементов соединяются так, чтобы получилась цепочка. Один вывод устройства подключается к одному соседнему звену, а второй – к другому, с противоположной стороны.
Последовательное соединение и практический пример применения.
Параллельное
При параллельном (parallel) включении одноименные выводы элементов цепи соединяются между собой. Практический пример – лампы в многорожковой люстре или повторители светового сигнала поворота в автомобиле.
Параллельное подключение и практический пример.Смешанное
В одной цепи схема подключения может быть комбинированной – serial+parallel. Часть элементов подключена в параллель, образуя звенья. Эти звенья могут быть включены в последовательную цепочку. Или наоборот – последовательные цепи включаются параллельно.
Часть элементов подключена в параллель, образуя звенья. Эти звенья могут быть включены в последовательную цепочку. Или наоборот – последовательные цепи включаются параллельно.
Комбинированное соединение проводников.
Как вычисляются напряжение, сила тока и электрическая мощность в зависимости от подключения
Параметры электрической цепи рассчитываются по-разному в зависимости от типа подключения. Чтобы разобраться, какова будет сила тока, проходящего через каждое сопротивление, можно воспользоваться первым законом Кирхгофа. Одна из его формулировок гласит, что алгебраическая сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла. Остальные зависимости будут вытекать из данного рассуждения.
При параллельном соединении
Если рассмотреть параллельное соединение, например, трех резисторов, то можно отметить, что втекающий ток I в узле 1 распадается на три ветви I1, I2, I3, причем Кирхгоф утверждает, что их сумма I1+ I2+ I3 = I. В узле 2 все токи стекаются в один ток, и снова I= I1+ I2+ I3.
В узле 2 все токи стекаются в один ток, и снова I= I1+ I2+ I3.
Очевидно, что напряжение на каждом резисторе одинаково и равно U, следовательно, по закону Ома:
- I1=U/R1;
- I2=U/R2;
- I3=U/R3;
- I=U/Rобщ.
Отсюда U/Rобщ= U/R1+ U/R2+ U/R3, после сокращения обеих частей на U получается формула для нахождения общего сопротивления при параллельном соединении резисторов:
1/Rобщ= 1/R1+ 1/R2+ 1/R3.
Параллельная цепь из n элементов.
Отсюда следует, что при параллельном соединении общее сопротивление будет меньше наименьшего сопротивления в наборе. При соединении двух резисторов формула принимает вид Rобщ=R1* R2/(R1+ R2).
Также из равенства I=U/R1+U/R2+U/R3 следует, что токи через параллельно включенные резисторы распределяются обратно пропорционально значениям их сопротивлений – чем выше сопротивление, тем ниже ток, и наоборот.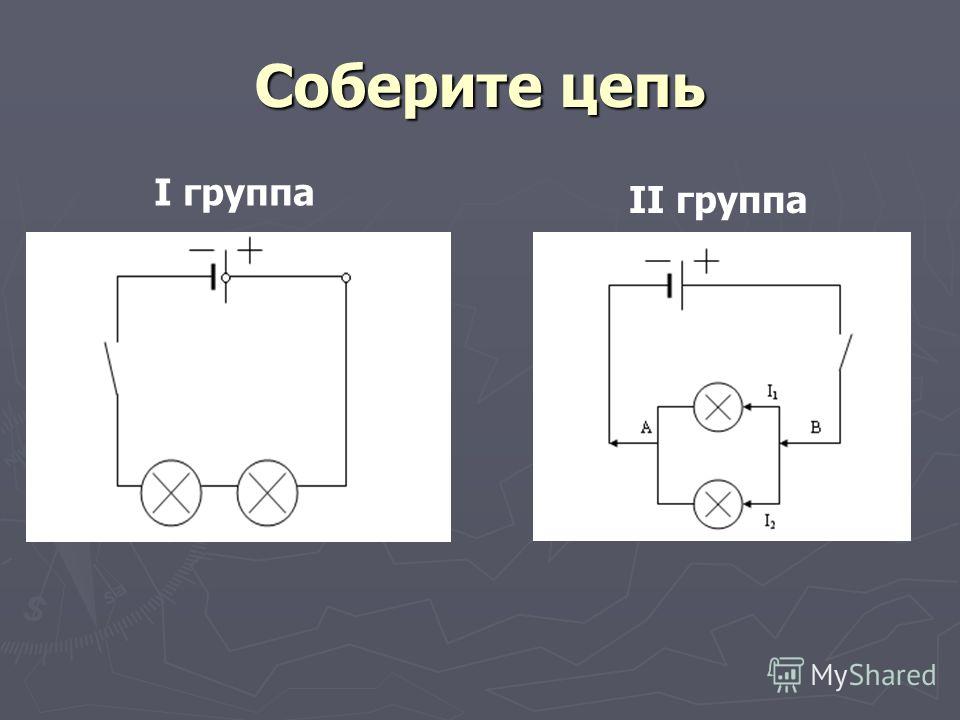 Если все резисторы имеют одинаковый номинал, то ток, текущий через каждый из них, находится делением общего тока на количество сопротивлений. Если элементов в сборке три, то через каждый течет треть общего тока, а если параллельно включены n одинаковых резисторов, то через каждый протекает I/n.
Если все резисторы имеют одинаковый номинал, то ток, текущий через каждый из них, находится делением общего тока на количество сопротивлений. Если элементов в сборке три, то через каждый течет треть общего тока, а если параллельно включены n одинаковых резисторов, то через каждый протекает I/n.
Так как электрическая мощность равна P=U*I, а напряжение на каждом резисторе равно, то мощность, выделяемая на каждом элементе, распределяется пропорционально току и обратно пропорционально сопротивлению резистора. Если все элементы одинаковы, то и мощность на них будет рассеиваться одинаковая.
Для наглядности видео.
При последовательном соединении
Если рассматривать последовательную цепь из трех элементов, можно заметить, что ток, втекающий в узел 1 будет равен вытекающему.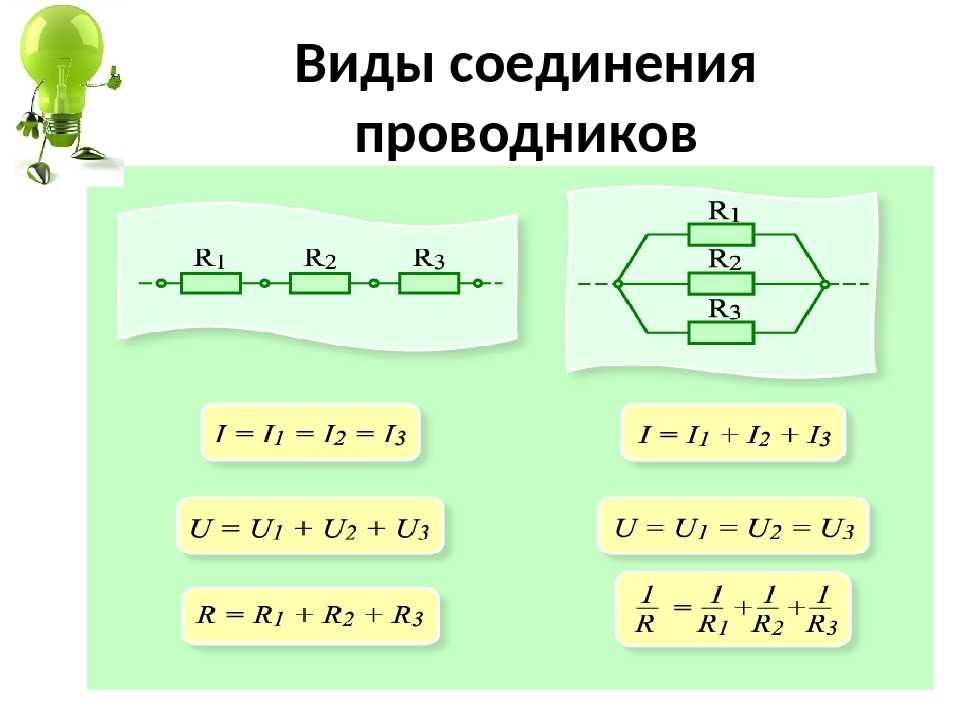 В узле 2 выполняется то же самое соотношение и так до бесконечности.
В узле 2 выполняется то же самое соотношение и так до бесконечности.
Отсюда сила тока в последовательном соединении будет одинакова для любого элемента и равна I. Напряжение, приложенное к цепи и равное I*R, распределится между резисторами:
U=U1+U2+U3=I*R1+I*R2+I*R3 = I* Rобщ
После сокращения на I можно найти общее сопротивление цепи. Оно равно сумме составляющих, и общее значение сопротивления будет выше сопротивления любого элемента:
Rобщ=R1+R2+R3
Очевидно, что падение напряжения в последовательной цепи прямо пропорционально сопротивлению каждого элемента – чем выше сопротивление, тем выше на нем напряжение. Точно так же, эти соотношения выполняются для цепи из n элементов.
Примеры расчетов
В качестве практических примеров можно рассмотреть несколько вариантов расчетов параметров цепи в разных схемах соединения.
Для резисторов
Самым простым примером расчета будет цепь из двух сопротивлений – 10 Ом и 100 Ом, соединенных в цепочку. К цепи приложено 12 вольт.
Последовательная цепь из двух резисторов.Сначала надо найти Rобщ, оно равно сумме R1 и R2. Rобщ=100+10=110 Ом. Отсюда ток в цепи I=U/R=12/110=0,109 ампер. Падение на каждом элементе можно вычислить исходя из равенств U1=I*R1 и U2=I*R2. Отсюда U1=1,1 В, а U2=10,9 В. Очевидно, что U1/U2=R1/R2. На первом элементе будет рассеиваться мощность P1=U1*I=1,1*0,109=0,12 ватт (для практики подойдет стандартный компонент на 0,125 ватт), а на втором – P2=U2*I=10,9*0,109=1,19 ватт (для практической реализации понадобится двухваттник).
Если соединить эти же два резистора параллельно и подать то же самое напряжение, то параметры распределятся по-другому.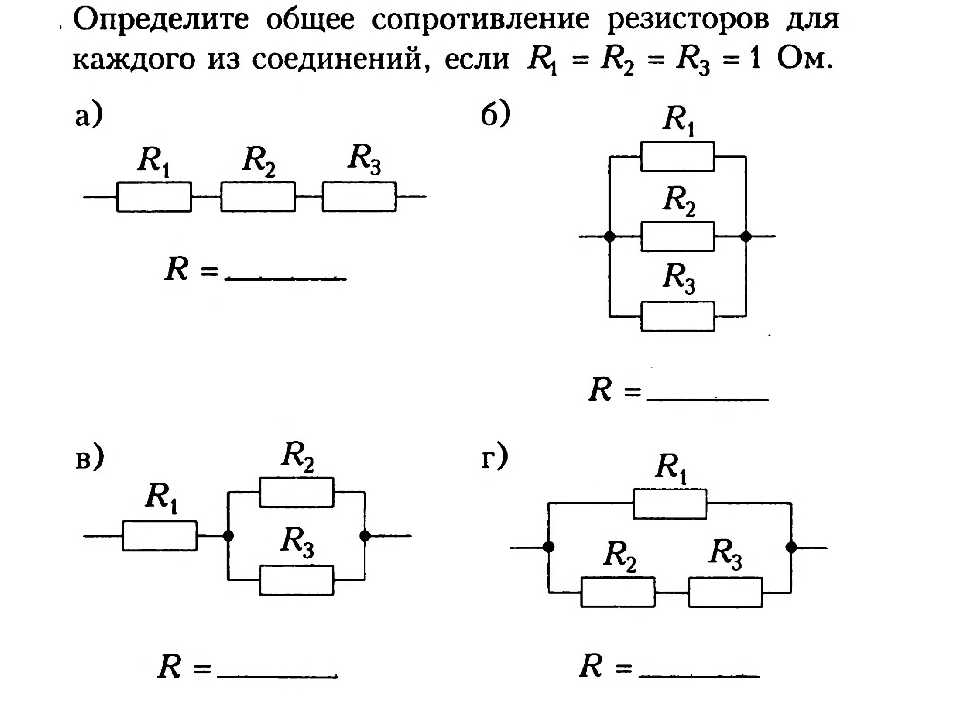
Сначала надо определить Rобщ=R1*R2/(R1+R2)=110*10/(110+10)=1100/120=9,17 Ом (меньше наименьшего значения в 10 Ом). Общий ток составит I=U/Rобщ=12/9,17=1,31 ампер. Через первый элемент потечет I1=U/R1=12/10=1,2 ампер, через второй I2=U/R2=12/100=0,12. Очевидно, что I1+I2=I (с учетом погрешностей округления). Мощности потребуются такие:
- P1=I1*U=1,2*12=14,2 ватт;
- P2=I2*U=0,12*12=1,42 ватт.
Если имеется смешанное соединение элементов, надо сначала преобразовать схему к однотипному виду – параллельному или последовательному. Пусть имеется схема следующего вида.
Преобразование смешанной схемы.В данном случае удобно заменить параллельную сборку R1 и R2 на резистор с эквивалентным сопротивлением R12, а R3 и R4 – на R34.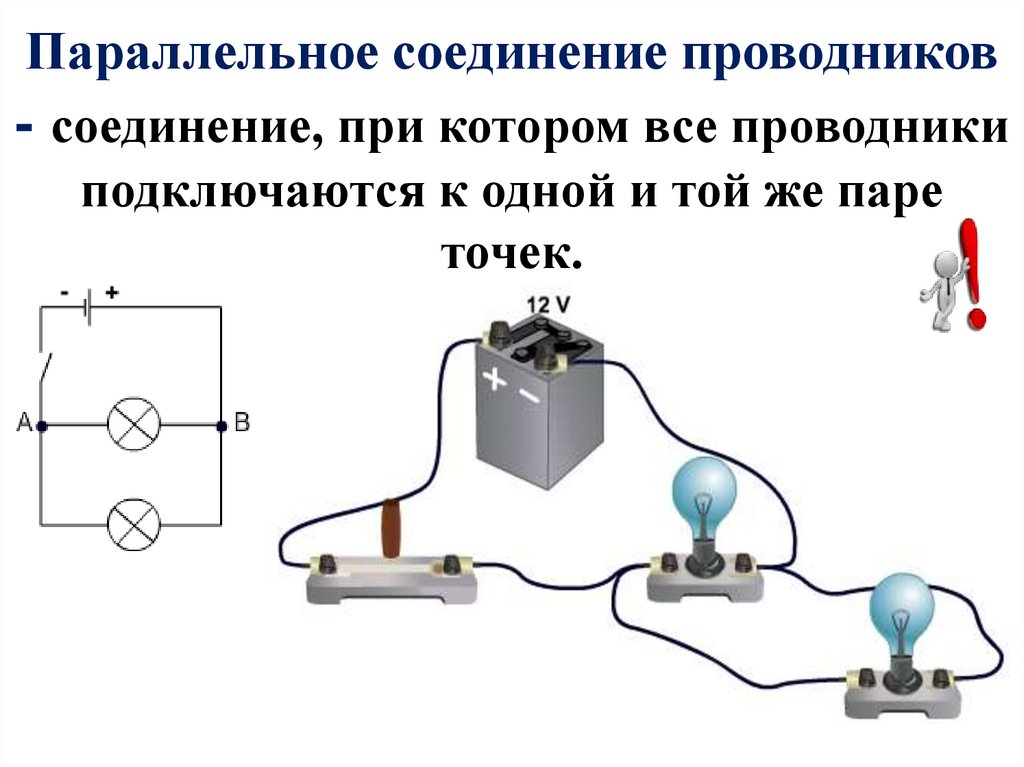 Сначала находится R12=R1*R2/(R1+R2)=9,17 Ом. Тем же способом рассчитывается R34=150*5/(150+5)=4,8 Ом. Тогда общее сопротивление эквивалентной цепи будет равно R12+R34=9,17+4,8=13,97 Ом.
Сначала находится R12=R1*R2/(R1+R2)=9,17 Ом. Тем же способом рассчитывается R34=150*5/(150+5)=4,8 Ом. Тогда общее сопротивление эквивалентной цепи будет равно R12+R34=9,17+4,8=13,97 Ом.
Отсюда I=U/R=12/13,97=0,86 ампер. На “гирлянде» R1R2 падает U12=I*R12=0,86*9,17=7,87 вольт, а на R3R4 падение составит U34= I*R34=0,86*4,8=4,13 вольт. Дальше надо вернуться к исходной схеме и рассмотреть отдельно участок схемы R1R2 с найденными параметрами.
Участок цепи, содержащий R1 и R2.Отсюда I1=U/R1=7,87/10=0,787 ампер, I2=U/R2=7,87/100=0,0787 ампер. По мощностям – P1=U*I1=7,87*0,787=6,2 ватт, P2= U*I2=7,87*0,0787=0,62 ватт.
Аналогично рассчитывается и участок, содержащий элементы R3R4.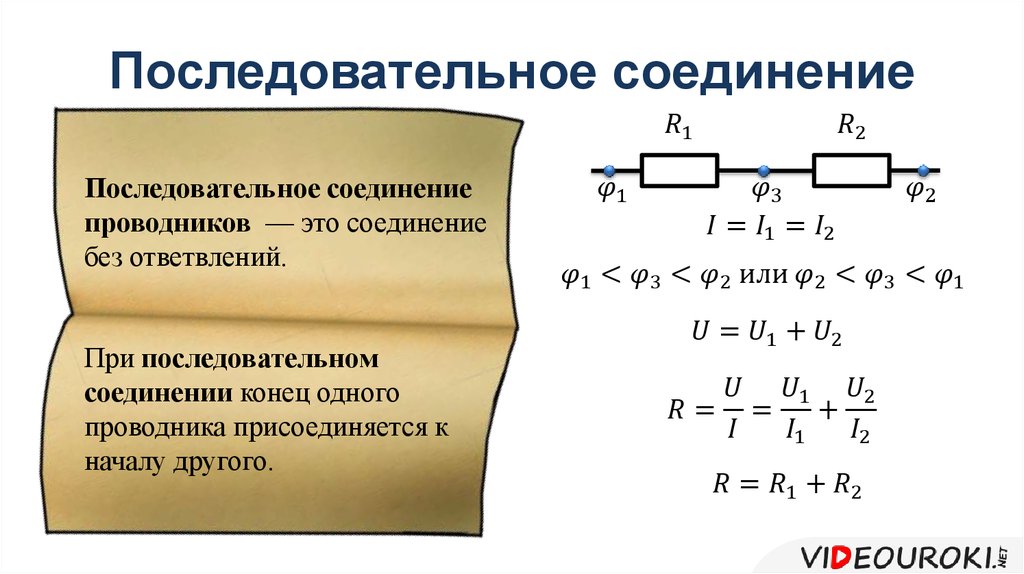
Читайте также
Последовательное и параллельное подключение аккумуляторных батарей
Для лампочек
Точно такими же способами можно рассчитать параметры цепи, состоящей из двух или более лампочек накаливания – на практике с такой ситуацией можно столкнуться чаще. Но есть две проблемы. Первая из них – на лампочках и в технических данных на них не указывается сопротивление нити. Его придется пересчитывать исходя из номинального напряжения и мощности. Так как P=U*I, а I=U*R, то P=U2/R, а R=U2/P. Так, для 10-ваттной лампочки на 12 вольт сопротивление нити будет равно 122/10=144/10=14,4 Ом. Можно рассчитать характеристики цепи для двух последовательно и параллельно соединенных лампочек.
Соединение ламп в цепочку.В первом случае ток, текущий через каждую лампу будет общим, и равным I=U/Rобщ=12/(14,4+14,4)=12/28,8=0,42 А. На каждой лампе упадет U/2=6 вольт. А электрическая мощность каждого элемента составит 0,42*6=2,5 Вт, что составляет ¼ от номинала лампочки. Такое уменьшение произошло из-за двукратного снижения тока и двукратного снижения напряжения. Естественно, лампочки будут светиться далеко не в полный накал. Чтобы довести яркость свечения до нормальной, придется вдвое увеличивать напряжение, что одновременно вдвое увеличит ток.
Такое уменьшение произошло из-за двукратного снижения тока и двукратного снижения напряжения. Естественно, лампочки будут светиться далеко не в полный накал. Чтобы довести яркость свечения до нормальной, придется вдвое увеличивать напряжение, что одновременно вдвое увеличит ток.
Если лампочки соединить в параллель, то на каждой из них упадет номинальный уровень в 12 вольт. Через каждый элемент потечет I=U/R= 12/14,4=0,83 А, а мощность на каждой лампочке будет равна P=U*I=12*0,83=10 ватт, то есть, номинал. И каждая нить будет светить в полный накал. Но вся цепь будет потреблять 20 ватт и через нее потечет 0,83*2=1,66 А, что вдвое больше значения для одной лампы.
Есть и вторая проблема. В общем случае сопротивление зависит от тока и приложенного напряжения, но у ламп накаливания эта зависимость выражена ярко. Нить в холодном состоянии имеет низкое сопротивление, а номинального значения достигает при прогреве в номинальном режиме. Поэтому данные выше расчеты верны лишь для штатного напряжения 12 вольт. В других условиях характеристики лампы будут другими, и, по большому счету, расчет для параллельного случая неточен – сопротивление нити будет меньше 14,4 Ом. Зато это свойство позволяет применять лампу в качестве стабилизатора тока – при увеличении его значения нить нагреется, сопротивление вырастет, ток упадет примерно до прежнего уровня. При его уменьшении произойдет обратный процесс со снижением уровня накала нити лампочки.
В других условиях характеристики лампы будут другими, и, по большому счету, расчет для параллельного случая неточен – сопротивление нити будет меньше 14,4 Ом. Зато это свойство позволяет применять лампу в качестве стабилизатора тока – при увеличении его значения нить нагреется, сопротивление вырастет, ток упадет примерно до прежнего уровня. При его уменьшении произойдет обратный процесс со снижением уровня накала нити лампочки.
Рекомендуем посмотреть видео урок «Просто физика»
Для светодиодов
Еще сложнее ситуация со светодиодами. В отличие от лампочек они стабилизируют напряжение, причем не всегда, а только после открывания. Иными словами, сначала при росте напряжения на последовательной цепочке (LED+резистор), она ведет себя согласно закону Ома. После того, как светодиод открылся (и начал светиться), увеличение падения на нем прекратилось, и рост напряжения на цепочке ведет к росту тока и увеличению U на резисторе. На полупроводниковом приборе напряжение остается стабильным (в зависимости от технологии изготовления – от 1,2 до 3 вольт или выше), хотя ток через него также растет.
После того, как светодиод открылся (и начал светиться), увеличение падения на нем прекратилось, и рост напряжения на цепочке ведет к росту тока и увеличению U на резисторе. На полупроводниковом приборе напряжение остается стабильным (в зависимости от технологии изготовления – от 1,2 до 3 вольт или выше), хотя ток через него также растет.
По мере освоения приемов расчета можно научиться анализировать все более сложные схемы, содержащие как параллельное, так и последовательное подключение элементов. Потом можно переходить к следующему этапу – анализ и расчет устройств, содержащих реактивные (а впоследствии – и нелинейные) компоненты.
Последовательное и параллельное соединение | Частная школа. 8 класс
Конспект по физике для 8 класса «Последовательное и параллельное соединение проводников». Основные способы соединения проводников в электрической цепи. Как определяется сила тока и напряжение в цепи, состоящей из последовательно соединённых проводников.
Конспекты по физике Учебник физики Тесты по физике
До сих пор мы рассматривали простейшие электрические цепи, состоящие из источника тока, одного потребителя (сопротивления) и измерительных приборов — амперметра и вольтметра. Однако на практике использование таких простых цепей довольно ограниченно. Обычно несколько различных потребителей энергии, соединённых между собой, подключаются к одному источнику тока.
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ
При последовательном соединении проводники включаются в цепь поочерёдно друг за другом без разветвлений проводов между ними. В таких цепях электрические заряды последовательно проходят через все элементы цепи.
Соберём цепь, состоящую из двух потребителей, например лампочек, источника тока, ключа и амперметров.
Независимо от положения в цепи амперметры показывают одинаковое значение силы тока.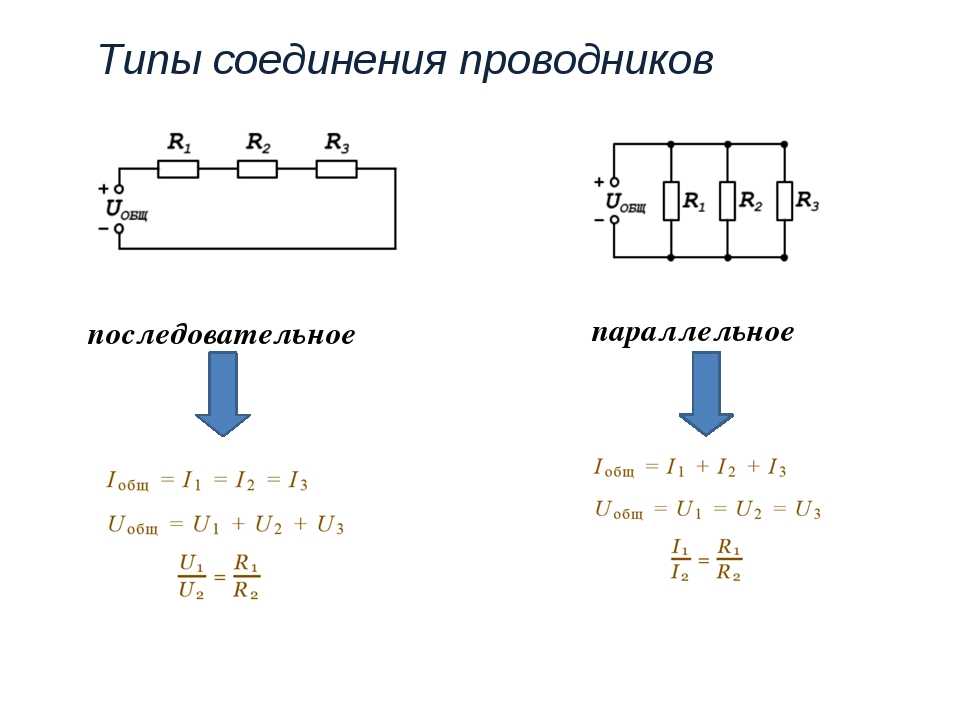 Следовательно, при последовательном соединении сила тока в любых участках цепи одна и та же, т.е. I = I1 = I2.
Следовательно, при последовательном соединении сила тока в любых участках цепи одна и та же, т.е. I = I1 = I2.
При последовательном соединении один проводник следует за другим, и все заряды, проходящие через первый из них, непременно проходят и через второй (в месте соединения проводников накапливания зарядов не происходит). По закону сохранения заряда сила тока в каждом проводнике одинакова и равна полному току I на данном участке цепи.
Сравним напряжения на каждом из проводников U1 и U2 и общее напряжение цепи U. Для этого подключим к каждой из лампочек по отдельному вольтметру, а также подсоединим к ним один общий. Показания вольтметров на каждом из проводников различны. Однако если сложить напряжения U1 и U2, получим, что их сумма равна напряжению во всей цепи U.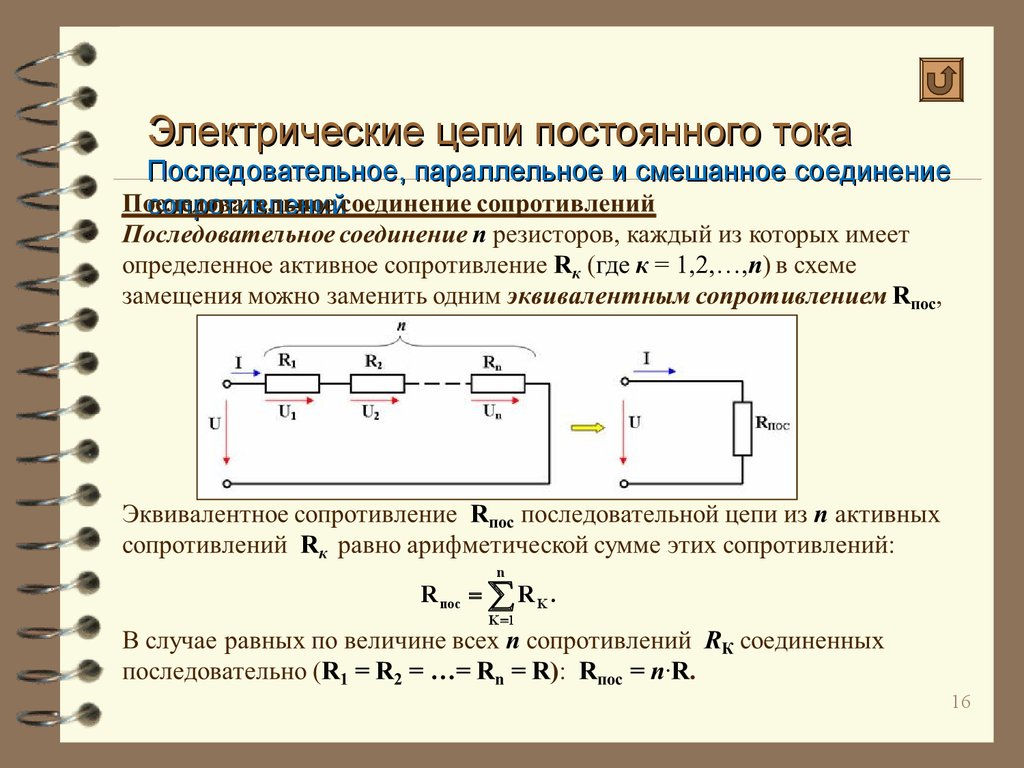
Таким образом, при последовательном соединении полное напряжение в цепи равно сумме напряжений на отдельных участках цепи, т. е. U = U1 + U2
Это равенство следует из закона сохранения энергии. Вспомним, что напряжение показывает, какую работу совершает электрическое поле при перемещении электрического заряда в 1 Кл. Эта работа совершается за счёт энергии движущихся зарядов. Поэтому энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих этот участок.
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ
На практике, помимо последовательного соединения, часто используется другой тип соединения проводников — параллельное.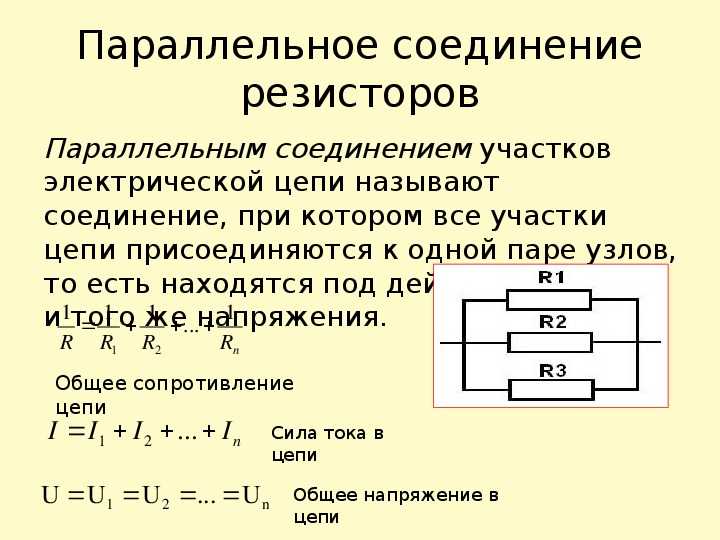
При параллельном соединении все проводники, входящие в него, имеют общее начало и общий конец. Точку А можно считать началом этого соединения, а точку В — концом.
Сравним ток в общей части цепи с токами в каждом из параллельно соединённых участков цепи (ветвей).
Соединим две лампочки параллельно и подключим их к источнику тока. Для определения силы тока в каждой из ветвей соединения каждую лампочку последовательно соединим с амперметром. Третий амперметр измеряет силу тока в неразветвлённой части цепи.
При параллельном соединении ток I, текущий по цепи, в точке В разветвляется на два тока: I1 и I2. Часть тока идёт через одну лампу, часть — через другую. В точке А токи снова соединяются.
Опыт показывает, что сила тока в неразветвлённой части цепи равна сумме сил токов в отдельных проводниках, т. е. I = I1 + I2
При параллельном соединении все проводники подключаются к одному и тому же источнику тока.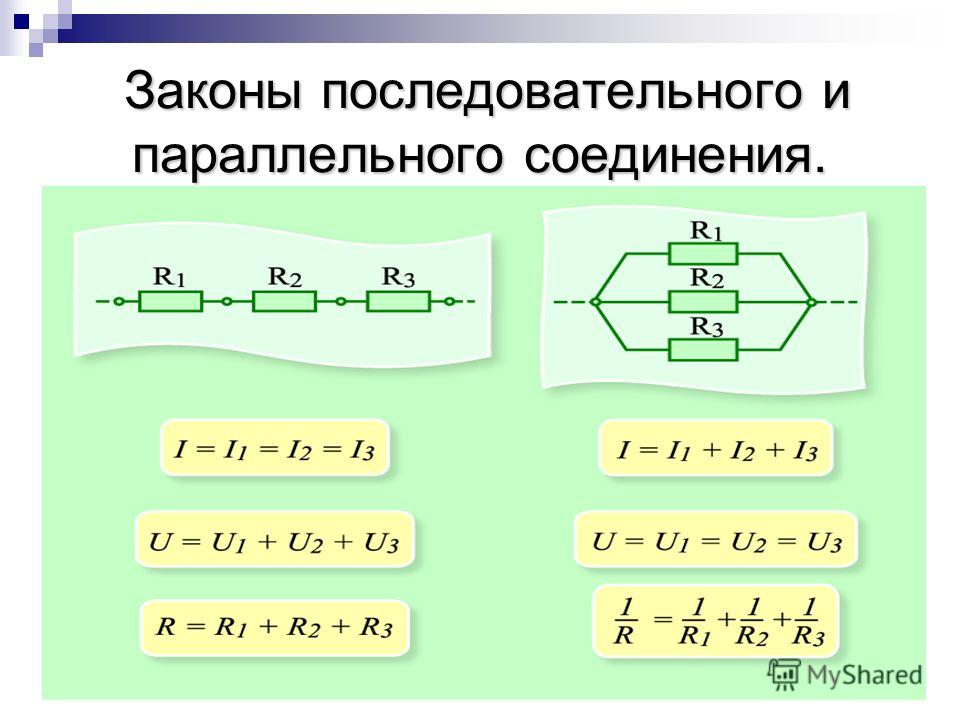
На практике параллельное соединение проводников используется чаще, чем последовательное. Это связано с тем, что все потребители энергии при параллельном соединении работают даже в том случае, если один из них отключается.
Например, если лампочки люстры соединены параллельно, то перегоревшая лампочка не разрывает сеть и оставшиеся лампочки продолжают гореть.
Вы смотрели Конспект по физике для 8 класса «Последовательное и параллельное соединение проводников»
Вернуться к Списку конспектов по физике (Оглавление).
Просмотров: 4 159
Параллельное и последовательное соединение проводников
- Хулхачиева Галина Ходжигоровна
Разделы: Физика
Основная цель: совместное изучение параллельного и последовательного соединения проводников, систематизация знаний учащихся по теме.
Оборудование: компьютер, проектор, оборудование для демонстраций (цепь с последовательно (параллельно) соединенными лампочками)
I. Актуализация знаний учащихся
а) Каково назначение источника тока в электрической цепи?
б) Из каких частей состоит электрическая цепь?
в) Какую электрическую цепь называют замкнутой (разомкнутой)?
г) Сформулируйте и запишите закон Ома для участка цепи.
д) Заполняют матрицы на доске (с составлением обратных задач).
| Сила тока,
|
Напряжение,
В |
Сопротивление,
Ом |
| 220 | 50 | |
| 4,4 | 50 | |
| 4,4 | 220 |
| R,Ом | L,м | S,мм2 | Ом*мм2/м |
| 0,85 | 1 | 0,017 | |
| 100 | 1 | 0,017 | |
| 0,85 | 100 | 1 |
II.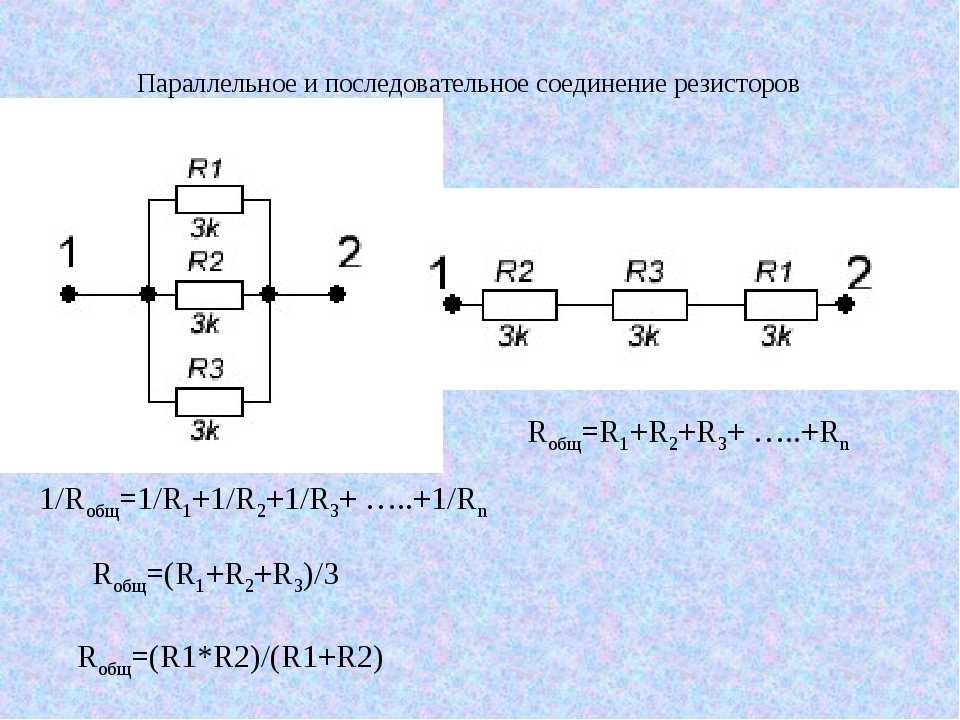 Новая тема.
Новая тема.
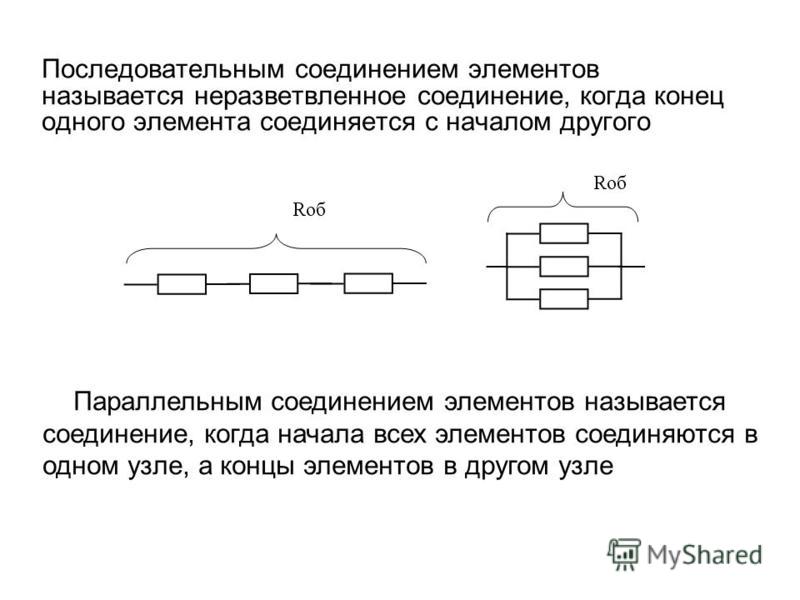
Кратко опишу парные демонстрации, на основе которых удается совместно излагать обе темы. При таком укрупненном изложении появляется возможность использовать совмещенные формулировки правил, запись аналогичных формул в параллельных колонках. Сравним следующие суждения:
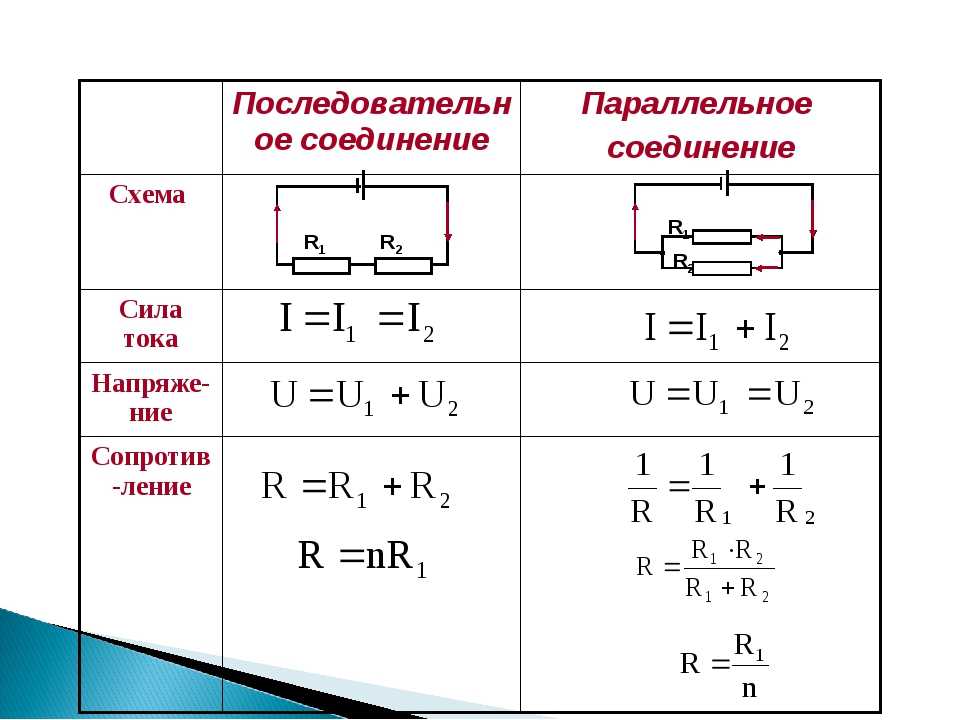
Параллельное соединение проводников. Последовательное соединение проводников
| I = I1 + I2 U =U1 = U2 R = |
I = I1 = I2 U = U1 + U2 R = R1 +R2 |
Сравнивая формулы, записанные, в первых двух строках, формулируем следующие совмещенные правила:
В цепи при соединении проводников складываются.
Методика укрупнения, использованная при объяснении теоретического материала,
создает возможность решение учащимися комплекса родственных качественных
упражнений.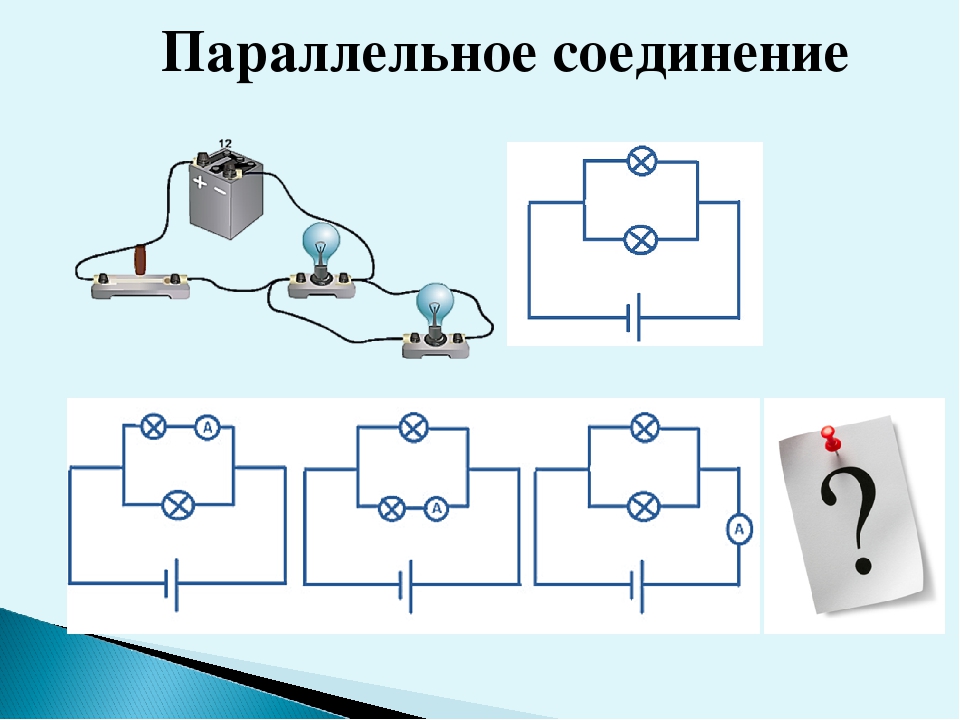
Речь идет о стандартных батареях и лампочках, карманного фонаря (напряжения и сопротивления одинаковы).
Простейшая электрическая цепь: батарея сопротивлением из одной батареи и одной лампочки.
Предлагаю учащимся проанализировать мысленно матрицу следующих комбинаций последовательного и параллельного соединений, как источников тока (батарей) так и потребителей тока (лампочек). Решая качественно данные укрупненные задания, пренебрегаем внутренним сопротивлением батарей и сопротивлением соединительных проводников.
III Решение задач.
Проверить выполнение творческого домашнего задания (составление задач по теме). Наиболее интересное задание решить в классе.
Задача 1. Электрическая цепь состоит из источника тока – батареи
аккумуляторов, создающей в цепи напряжение 6 В, лампочки от карманного фонаря
сопротивлением 13,5 Ом, двух спиралей сопротивлением 3 и 2 Ом, ключа и
соединительных проводов. Все детали цепи соединены последовательно. Начертите
схему цепи. Определите силу тока в цепи, напряжение на концах каждого из
потребителей тока.
Все детали цепи соединены последовательно. Начертите
схему цепи. Определите силу тока в цепи, напряжение на концах каждого из
потребителей тока.
Задача 2. Два проводника сопротивлением10 и 15 Ом соединены параллельно и подключены к напряжению 12 В. Определите силу тока в каждом проводнике и силу тока до разветвления.
Задача 3. Два проводника имеют сопротивления – один 5 Ом, другой 500 Ом. Почему при последовательном соединении этих проводников их общее сопротивление будет больше 500 Ом, а при параллельном соединении меньше 5 Ом?
3. Использование матричных заданий.
По трем данным вычислите неизвестные значения величин.
| Параллельное соединение | Последовательное соединение | ||||||
| U, В | R1, Ом | R2, Ом | I,А | U,В | R1,Ом | R2,Ом | I,А |
| 200 | 300 | 0,6 | 10 | 15 | 6 | ||
| 120 | 100 | 200 | 42 | 5 | 10 | ||
IV. Рефлексия.
Рефлексия.
Суммарное сопротивление при последовательном соединении. Последовательное и параллельное соединение сопротивлений
Содержание:
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для — последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр.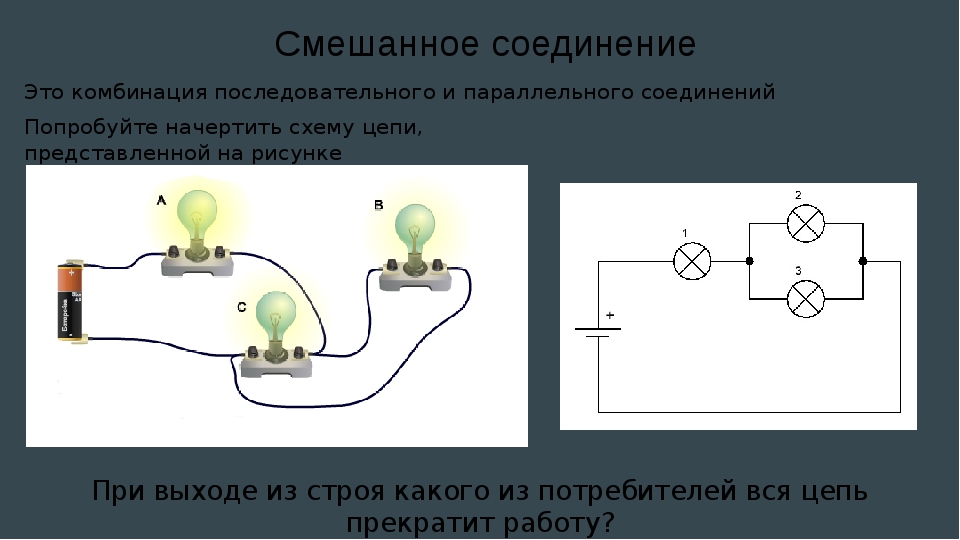 Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав , нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав , нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: + 20, + 10, + 5, + 2, + 1% и так далее до величины + 0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента.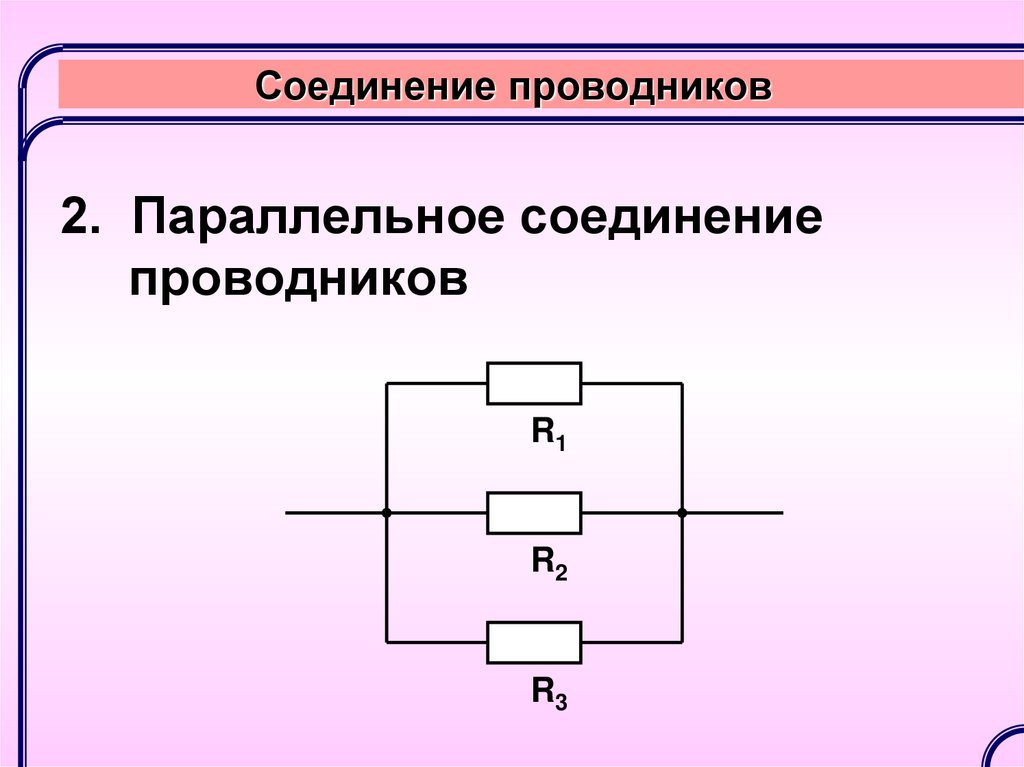 Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, сила тока будет составлять I = U/R = 100/390 = 0,256 A.На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
- P 1 = I 2 x R 1 = 0,256 2 x 200 = 13,11 Вт;
- P 2 = I 2 x R 2 = 0,256 2 x 100 = 6,55 Вт;
- P 3 = I 2 x R 3 = 0,256 2 x 51 = 3,34 Вт;
- P 4 = I 2 x R 4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы — с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R 1 +1/R 2 +1/R 3 +1/R 4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.

- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I 1 = U/R 1 = 100/200 = 0,5A; I 2 = U/R 2 = 100/100 = 1A; I 3 = U/R 3 = 100/51 = 1,96A; I 4 = U/R 4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P 1 = U 2 /R 1 = 100 2 /200 = 50 Вт; P 2 = U 2 /R 2 = 100 2 /100 = 100 Вт; P 3 = U 2 /R 3 = 100 2 /51 = 195,9 Вт; P 4 = U 2 /R 4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р 1 +Р 2 +Р 3 +Р 4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.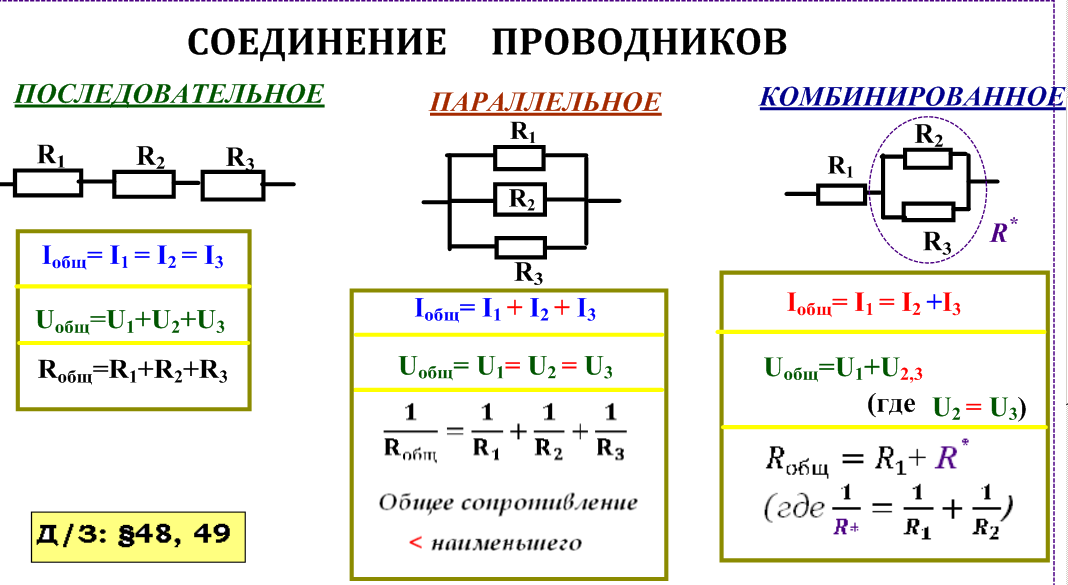
Содержание:
Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей.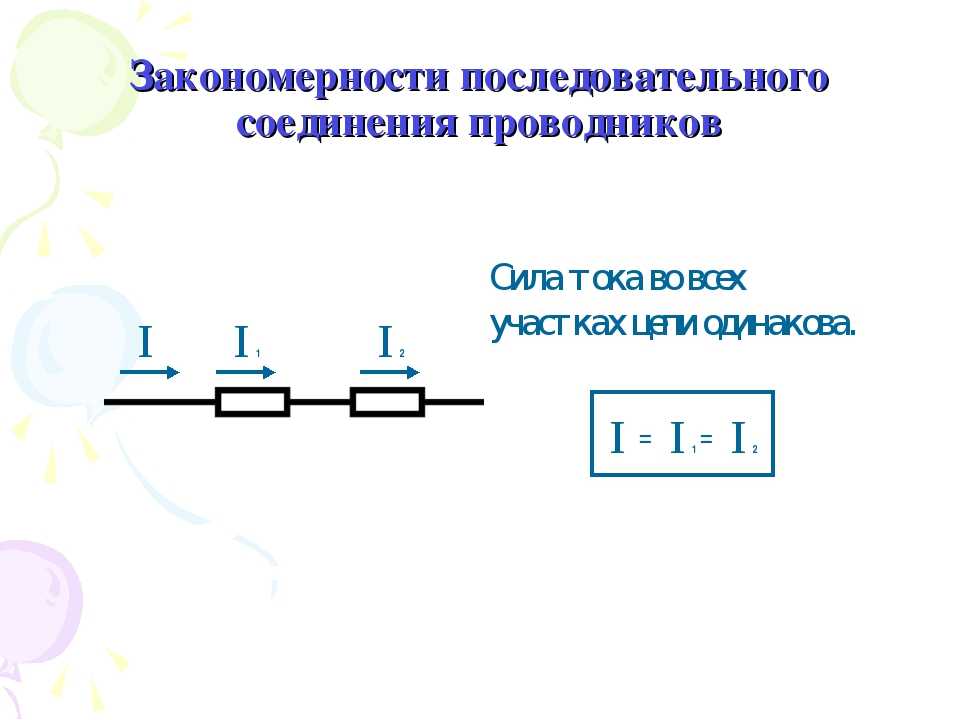 В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.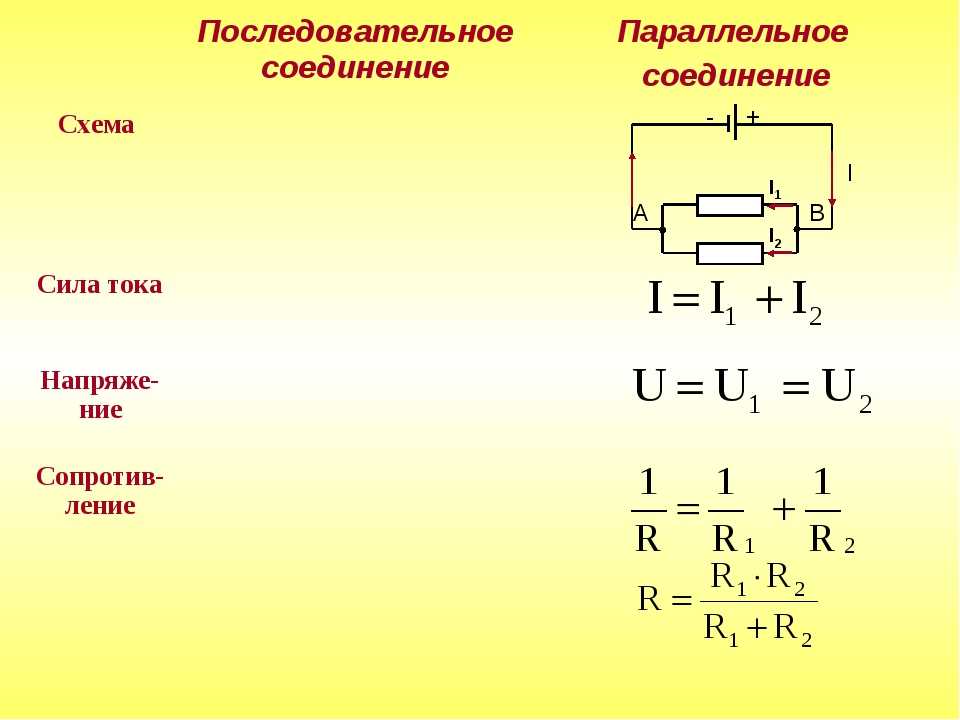
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи.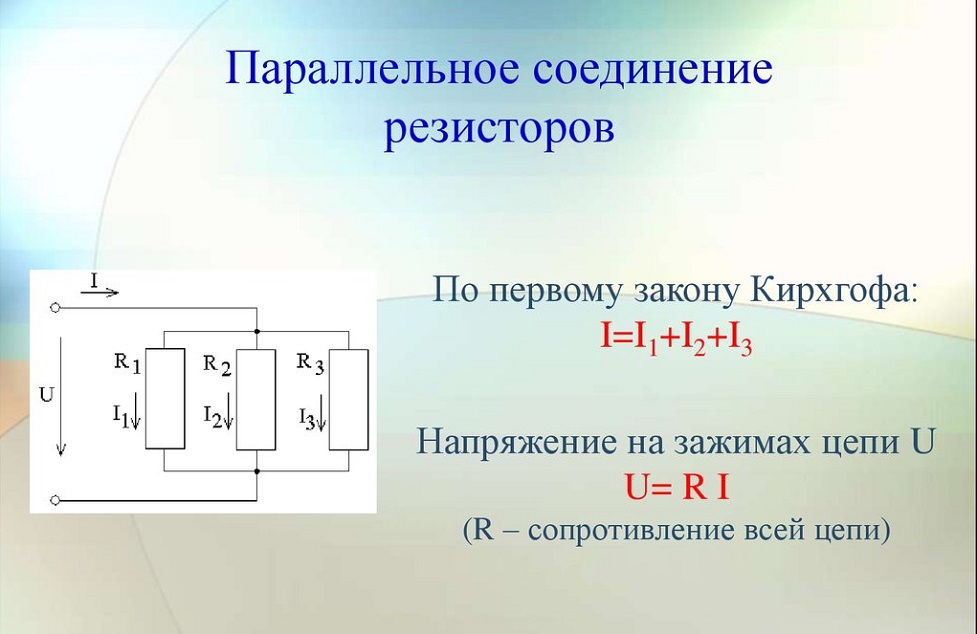 При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.

- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей.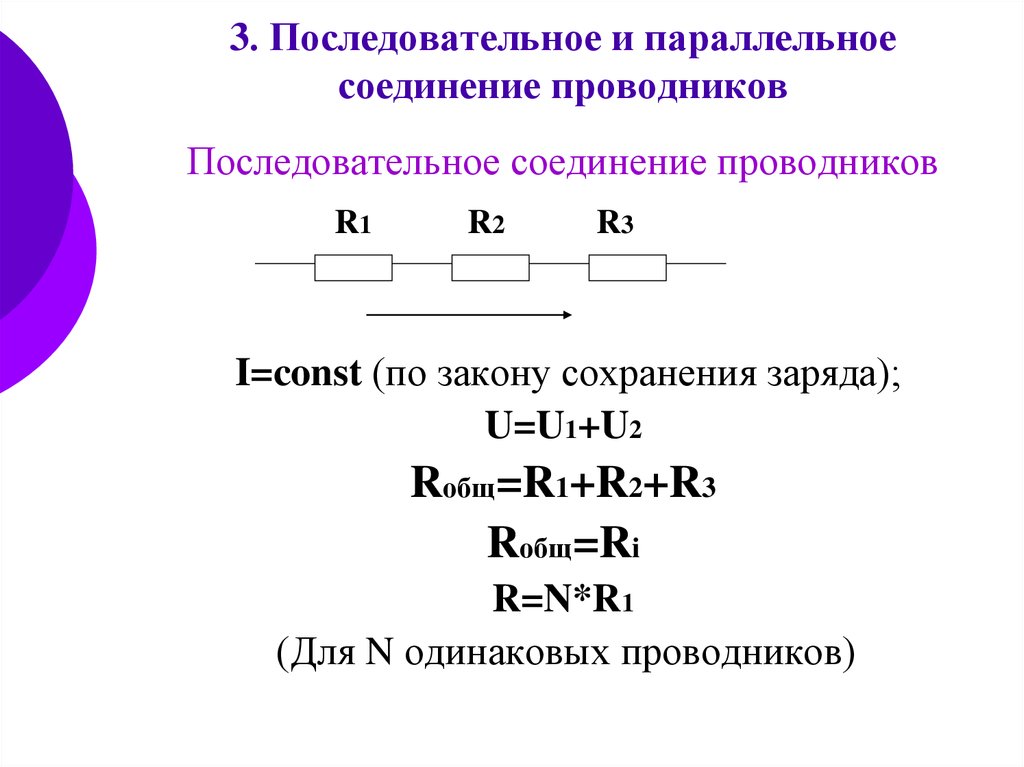 Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.
С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Виды соединений
Резистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:
- Постоянные.
- Переменные.
Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:
- Последовательное.

- Параллельное.
- Смешанное.
Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.
Последовательное соединение проводников
В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.
Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную.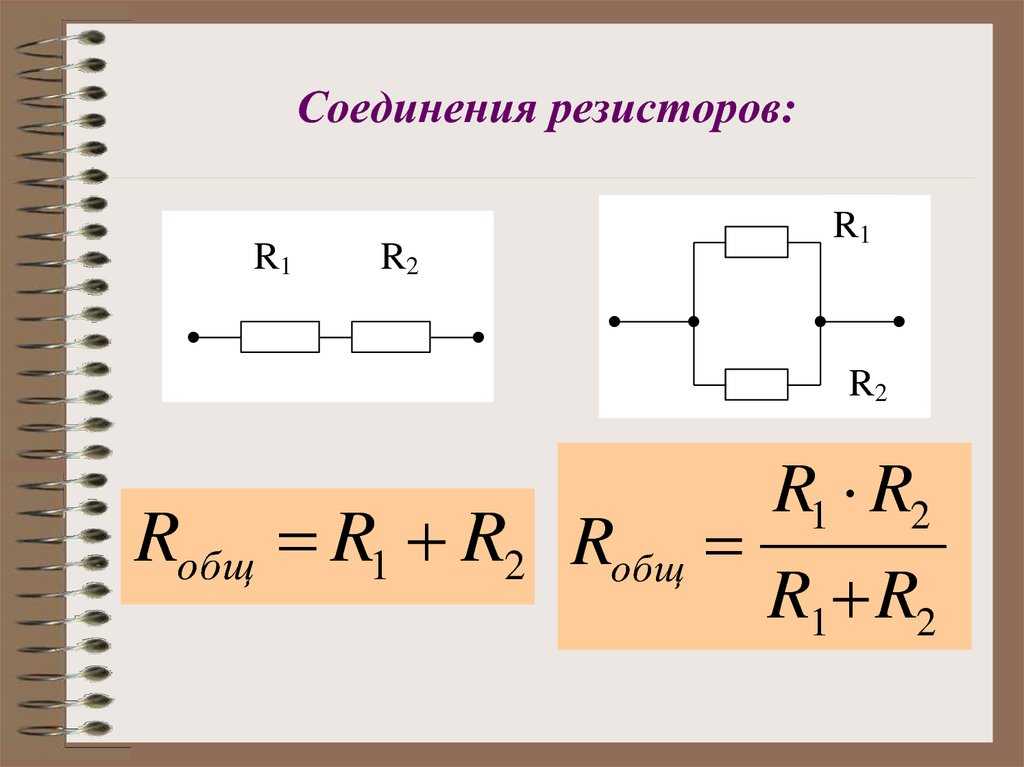 Но если резисторов очень много, то проще воспользоваться специальным калькулятором.
Но если резисторов очень много, то проще воспользоваться специальным калькулятором.
Примером последовательного соединения проводников в быту является ёлочная гирлянда.
Параллельное соединение резисторов
При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.
Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.
В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.
Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.
равно отношению напряжения источника к сопротивлению этого проводника.
Примеры параллельного соединения проводников:
- Освещение.
- Розетки в квартире.
- Производственное оборудование.
Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.
Смешанное соединение проводников
Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.
Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.
В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.
Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.
Шаги
Последовательное соединение
Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений.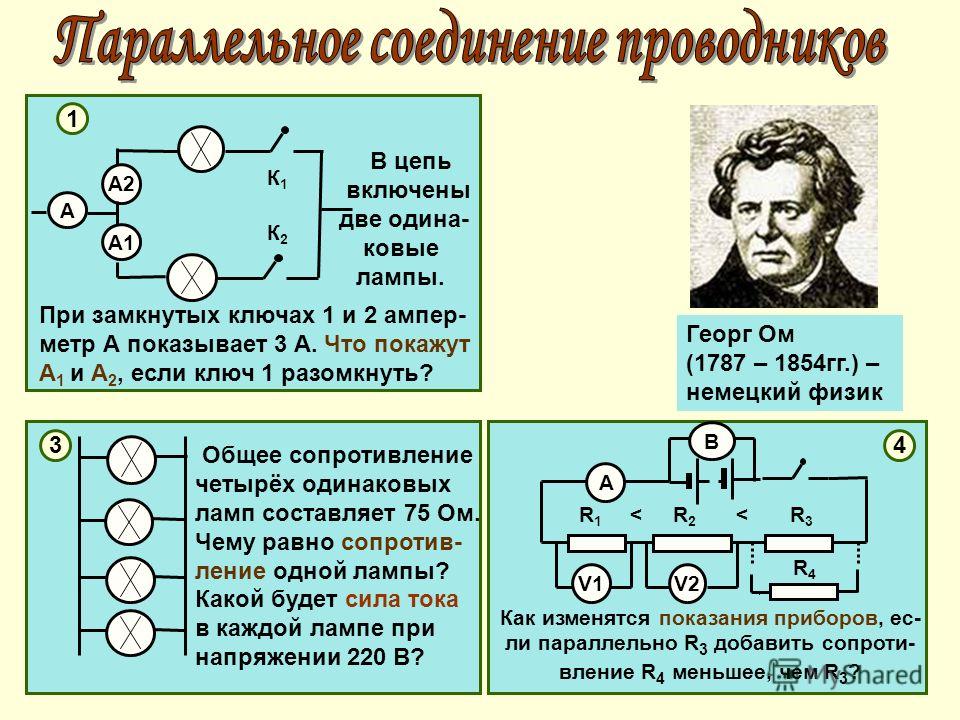 Резисторы или другие элементы расположены друг за другом.
Резисторы или другие элементы расположены друг за другом.
Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь. Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.
- Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.
Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.
Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.
- Например, напряжение источника тока равно 12 В, а сила тока равна 8 А.
 Общее сопротивление последовательной цепи: R O = 12 В / 8 А = 1,5 Ом.
Общее сопротивление последовательной цепи: R O = 12 В / 8 А = 1,5 Ом.
Параллельное соединение
Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.
Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления: , где R 1 – сопротивление первой ветви, R 2 – сопротивление второй ветви и так далее до последней ветви R n .
Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.
Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.

- Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: R O = 9 В / 3 А = 3 Ом.
Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.
Комбинированное соединение
Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.
- Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом.
 Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи: 1 R O = 1 R 1 + 1 R 2 + 1 R 3 + . . . 1 R n {\displaystyle {\frac {1}{R_{O}}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+{\frac {1}{R_{3}}}+…{\frac {1}{R_{n}}}} .
Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.
- В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.
Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.
Последовательное соединение потребителей(элементов) в цепи синусоидального тока:.
 ..
..Привет, мой друг, тебе интересно узнать все про последовательное соединение, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое последовательное соединение, цепь rlc, режимы работы rlc-цепи , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства.
цепь rlc — это электрическая цепь , состоящая из резистора (R), катушки индуктивности (L) и конденсатор (C), подключенный последовательно или параллельно. Название схемы образовано из букв, которые используются для обозначения составляющих компонентов этой схемы, причем последовательность компонентов может отличаться от RLC.
Схема формирует гармонический осциллятор для тока, а резонирует аналогично схеме LC . Добавление резистора увеличивает затухание этих колебаний, которое также известно как затухание . Резистор также снижает пиковую резонансную частоту. В обычных условиях некоторое сопротивление неизбежно, даже если резистор специально не включен в качестве компонента; идеальная, чистая LC-цепь существует только в области сверхпроводимости , физический эффект демонстрируется до сих пор только при температурах намного ниже температуры окружающей среды, наблюдаемой где-либо на поверхности Земли.
Цепи RLC имеют множество применений как схемы генератора . Радиоприемники и телевизоры используют их для настройки для выбора узкого диапазона частот от окружающих радиоволн. В этой роли схему часто называют настроенной схемой. Схема RLC может использоваться как полосовой фильтр , полосовой фильтр , фильтр нижних частот или фильтр верхних частот <358.>. Приложение настройки, например, является примером полосовой фильтрации. Фильтр RLC описывается как схема второго порядка, что означает, что любое напряжение или ток в цепи может быть описано с помощью дифференциального уравнения второго порядка в анализе схемы.
Три элемента схемы, R, L и C, могут быть объединены в несколько различных топологий . Все три последовательных элемента или все три параллельных элемента являются наиболее простыми по концепции и наиболее простыми для анализа. Однако есть и другие устройства, некоторые из которых имеют практическое значение в реальных схемах. Одна из часто встречающихся проблем — это необходимость учитывать сопротивление индуктора.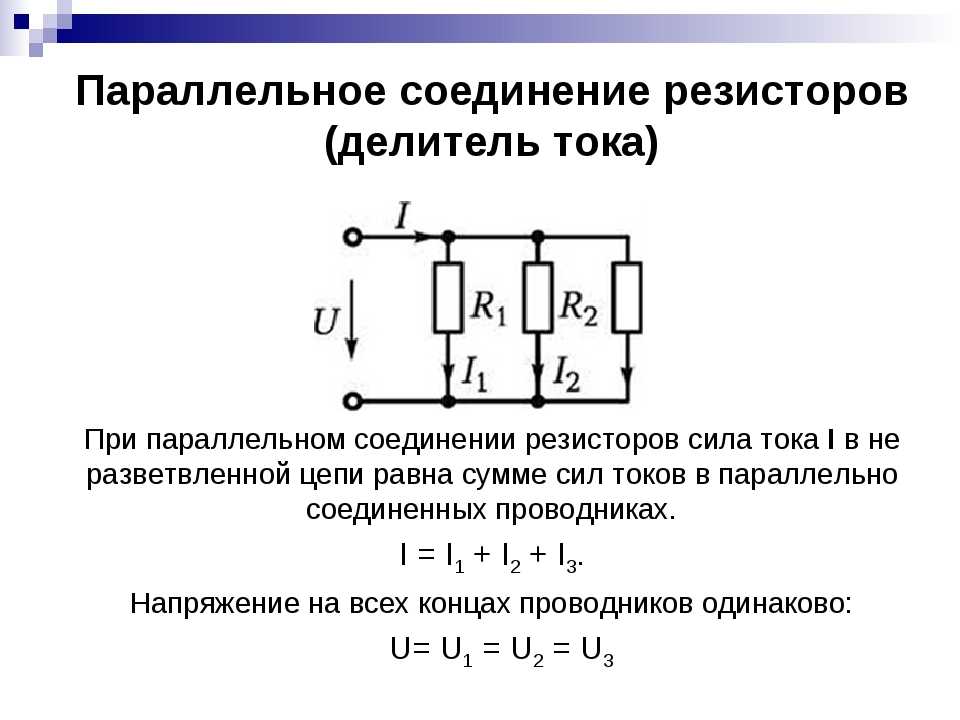 Катушки индуктивности обычно состоят из катушек с проволокой, сопротивление которой обычно нежелательно, но часто оказывает значительное влияние на цепь.Википедия site:livepcwiki.ru
Катушки индуктивности обычно состоят из катушек с проволокой, сопротивление которой обычно нежелательно, но часто оказывает значительное влияние на цепь.Википедия site:livepcwiki.ru
Последовательным соединением участков электрической цепи называют соединение, при котором через все участки проходит один ток (рис.3.5).
Напряжение на каждом последовательно включенном участке пропорционально величине сопротивления этого участка.
При последовательном соединении потребителей с сопротивлениями R1, R2 и R3 (рис. 3.5) напряжение на их зажимах равно
Воспользовавшись вторым законом Кирхгофа для рассматриваемой цепи (рис. 3.5), можно записать
Таким образом, общее (эквивалентное) сопротивление R последовательно включенных сопротивлений (потребителей) равно сумме этих сопротивлений.
Ток в цепи последовательно включенных потребителей (рис. 3.5) определяется выражением
Нетрудно понять, что при изменении сопротивления хотя бы одного потребителя изменяется ток цепи, а следовательно, и режим работы (напряжение) всех последовательно включенных потребителей.
Поэтому последовательное соединение сопротивлений не нашло широкого практического применения.
Следует заметить, что при последовательном соединении резисторов на большем сопротивлении тратится большая мощность
Zэкв – модуль эквивалентного сопротивления (полное сопротивление определяет связь между U и I)
— аргумент, связь между начальными фазами
При протекании токов по элементам электрической цепи, элементы которой соединены последовательно, параллельно или имеют смешанное соединение, могут получаться различные режимы работы этой цепи.
В этом параграфе будут рассмотрены следующие режимы работы электрических цепей.
Резонанс в цепи с последовательным соединением элементов. (Резонанс напряжений). (Рис. 63).
Рис. 63.
Режим работы RLC цепи или LC—цепи, при условии равенства реактивных сопротивлений XC= XL, когда общее напряжение цепи совпадает по фазе с ее током , называется резонансом напряжения.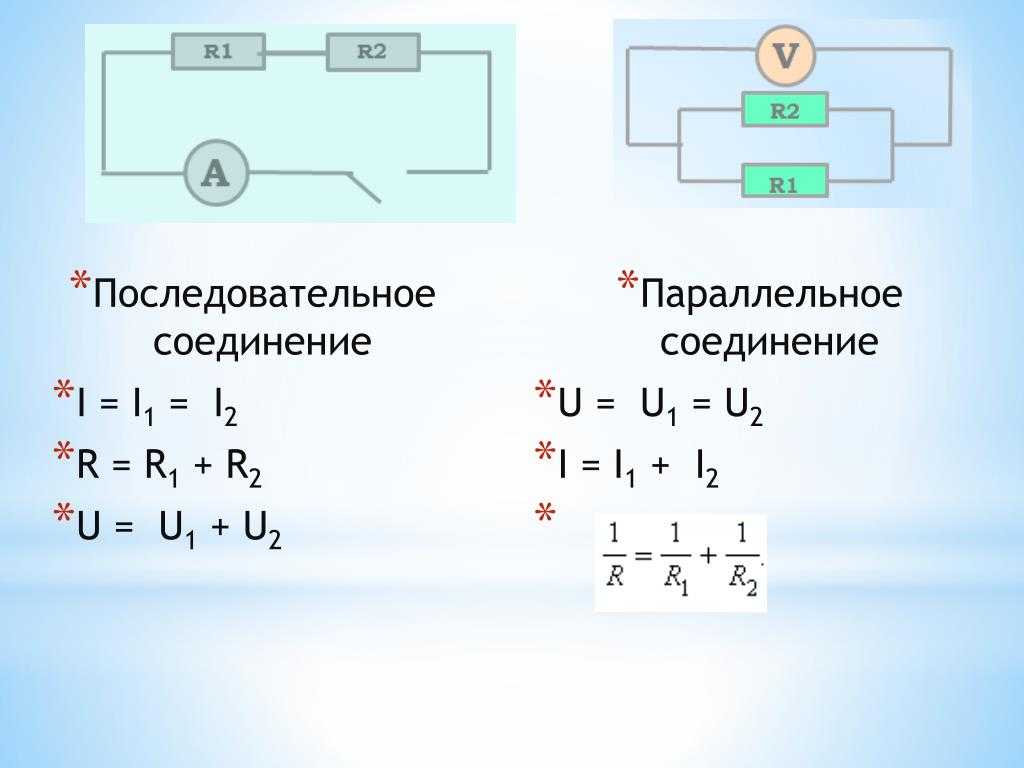
1. Напряжение на входе совпадает по фазе с током, т.е. сдвиг фаз между I и U φ = 0, cos φ = 1
2. Ток в цепи будет наибольшим и как следствие Pmax= I2maxR тоже максимальна, а реактивная мощность равна нулю.
Резонанс в цепи с параллельным соединением элементов. (Резонанс токов). (Рис. 64).
Рис. 64.
Резонанс в цепи с параллельным соединением реальных элементов, т.е. резонанс с учетом потерь в активных сопротивлениях катушки и соединительных проводов. (Рис. 65).
Рис. 65.
Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.
Случай 2. Два резонанса в цепи, при определенном соотношении сопротивлений элементов
С уменьшением коэффициента мощности стоимость потребляемой электроэнергии возрастает .
Критический режим в последовательной RLC-цепи (критический случай апериодического режима) наблюдается, когда корни характеристического полинома последовательной RLC-цепи являются кратными
При этом (согласно уравнению состояния последовательной RLC-цепи, подключенной к источнику напряжения u0 = const) решение
действительно не содержит колебательной составляющей (как и при рассмотрении апериодического режима).
График критического процесса приведен на рис. 23 (где линейная функция и экспонента намечены штриховыми линиями; периодическая составляющая в графике отсутствует, а максимум соответствует постоянной времени τ = 1/α).
Основные понятия
Резонанс
Важным свойством этой схемы является ее способность резонировать на определенной частоте, резонансной частоте . y , f 0 . Частоты измеряются в единицах герц . В этой статье используется угловая частота , ω 0 , поскольку это более удобно с математической точки зрения.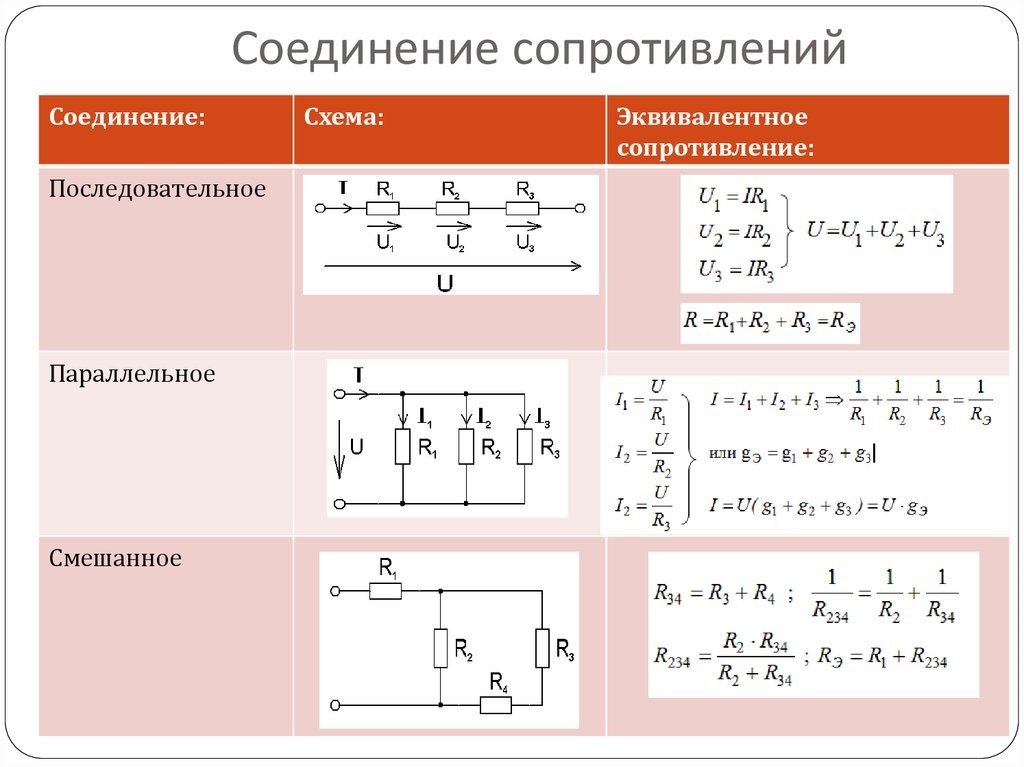 Измеряется в радианах в секунду. Они связаны друг с другом простой пропорцией,
Измеряется в радианах в секунду. Они связаны друг с другом простой пропорцией,
Резонанс возникает, потому что энергия для этой ситуации сохраняется двумя разными способами: в электрическом поле, когда конденсатор заряжается и в магнитном поле, когда ток течет через индуктор. Энергия может передаваться от одного к другому в цепи, и это может быть колебательным. Механическая аналогия — это груз, подвешенный на пружине, которая при отпускании будет колебаться вверх и вниз. Это не мимолетная метафора; Вес на пружине описывается точно таким же дифференциальным уравнением второго порядка, что и цепь RLC, и для всех свойств одной системы будет обнаружено аналогичное свойство другой . Об этом говорит сайт https://intellect.icu . Механическое свойство, отвечающее резистору в цепи, — это трение в системе пружина-груз. Трение будет медленно останавливать любое колебание, если его не движет внешняя сила. Точно так же сопротивление в цепи RLC будет «гасить» колебания, уменьшая их со временем, если в цепи нет источника питания переменного тока.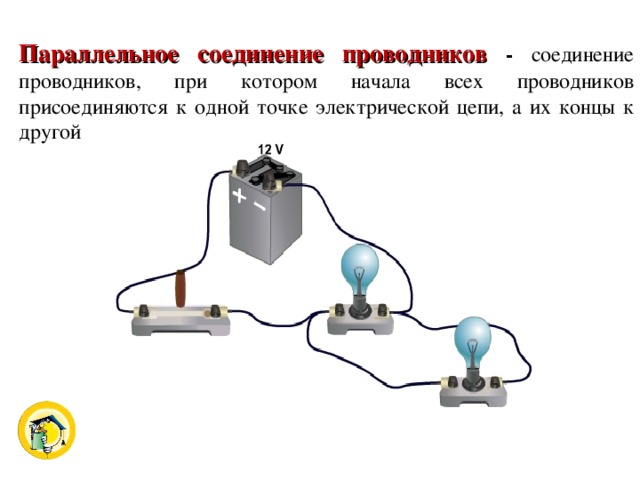
Резонансная частота определяется как частота, на которой импеданс контура минимален. Эквивалентно, его можно определить как частоту, на которой импеданс является чисто реальным (то есть чисто резистивным). Это происходит потому, что импедансы катушки индуктивности и конденсатора в резонансе равны, но имеют противоположный знак и компенсируются. Цепи, в которых L и C подключены параллельно, а не последовательно, на самом деле имеют максимальный импеданс, а не минимальный. По этой причине их часто называют антирезонаторами , однако по-прежнему принято называть частоту, на которой это происходит, резонансной частотой.
Собственная частота
Резонансная частота определяется в терминах импеданса, подаваемого на источник возбуждения. Схема все еще может продолжать колебаться (в течение некоторого времени) после того, как источник возбуждения был удален или она подвергается скачку напряжения (включая скачок до нуля). Это похоже на то, как камертон продолжает звонить после удара, и этот эффект часто называют звоном.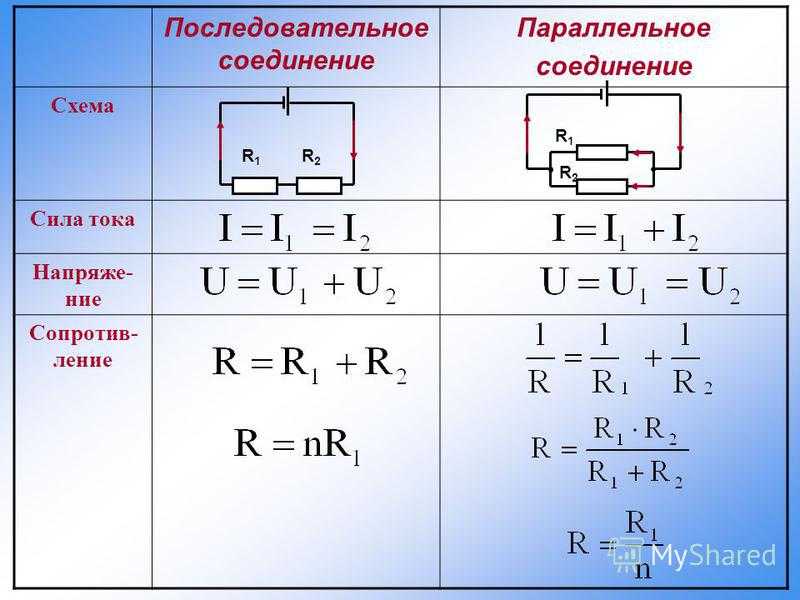 Этот эффект представляет собой пиковую собственную резонансную частоту контура и, как правило, не совсем то же самое, что и частота возбуждаемого резонанса, хотя они обычно довольно близки друг к другу. Разные авторы используют разные термины, чтобы различать эти два явления, но без определения резонансной частоты обычно означает возбуждаемую резонансную частоту. Возбужденная частота может называться незатухающей резонансной частотой или незатухающей собственной частотой, а пиковая частота может называться затухающей резонансной частотой или затухающей собственной частотой. Причина этой терминологии заключается в том, что возбуждаемая резонансная частота в последовательном или параллельном резонансном контуре имеет значение
Этот эффект представляет собой пиковую собственную резонансную частоту контура и, как правило, не совсем то же самое, что и частота возбуждаемого резонанса, хотя они обычно довольно близки друг к другу. Разные авторы используют разные термины, чтобы различать эти два явления, но без определения резонансной частоты обычно означает возбуждаемую резонансную частоту. Возбужденная частота может называться незатухающей резонансной частотой или незатухающей собственной частотой, а пиковая частота может называться затухающей резонансной частотой или затухающей собственной частотой. Причина этой терминологии заключается в том, что возбуждаемая резонансная частота в последовательном или параллельном резонансном контуре имеет значение
Это в точности то же самое, что резонансная частота LC-контура, то есть без резистора. Резонансная частота для контура RLC такая же, как и для контура, в котором нет демпфирования, следовательно, резонансная частота незатухает. Пиковая резонансная частота, с другой стороны, зависит от номинала резистора и описывается как затухающая резонансная частота.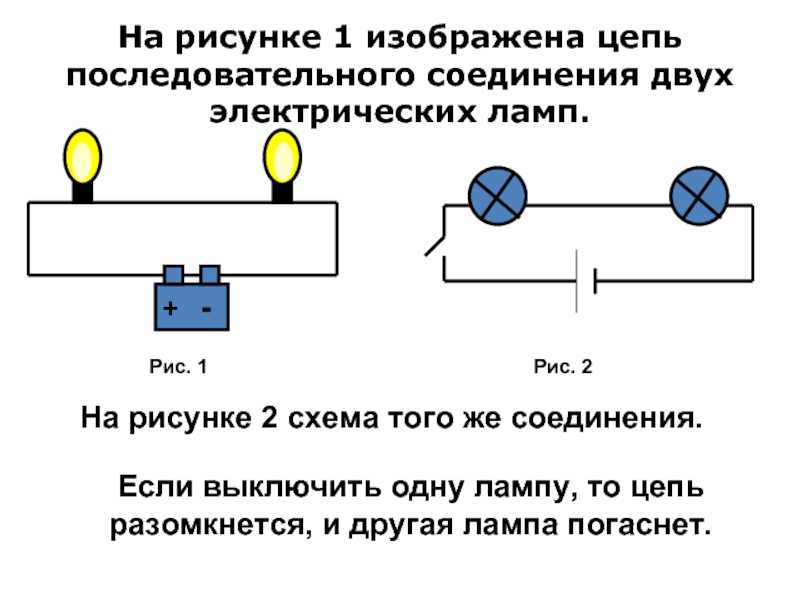 Цепь с сильным демпфированием вообще не будет резонировать, если ее не использовать. Цепь со значением резистора, которое приводит к тому, что она находится на границе звона, называется с критическим демпфированием . Любая сторона критически затухающего сигнала описывается как недостаточное демпфирование (происходит звон) и сверхдемпфирование (звон подавляется).
Цепь с сильным демпфированием вообще не будет резонировать, если ее не использовать. Цепь со значением резистора, которое приводит к тому, что она находится на границе звона, называется с критическим демпфированием . Любая сторона критически затухающего сигнала описывается как недостаточное демпфирование (происходит звон) и сверхдемпфирование (звон подавляется).
Цепи с топологией более сложной, чем прямая последовательная или параллельная (некоторые примеры описаны далее в статье), имеют возбуждаемую резонансную частоту, которая отклоняется от , и для них незатухающая резонансная частота, затухающая резонансная частота и возбуждаемая резонансная частота могут быть разными.
Демпфирование
Демпфирование вызвано сопротивлением в цепи. Он определяет, будет ли цепь резонировать естественным образом (то есть без источника возбуждения). Цепи, которые будут резонировать таким образом, описываются как недемпфированные, а те, которые не будут, — как чрезмерно демпфированные. Затухание демпфирования (символ α) измеряется в неперс в секунду.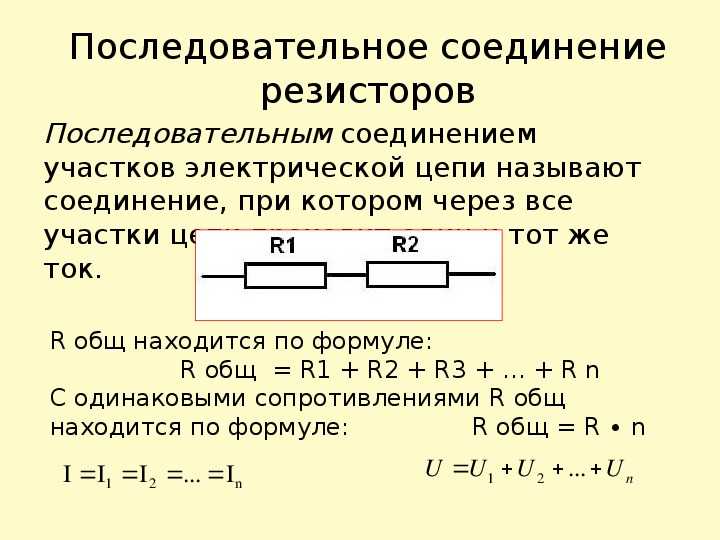 Однако безразмерный коэффициент затухания (символ ζ, дзета) часто является более полезной мерой, которая связана с α соотношением
Однако безразмерный коэффициент затухания (символ ζ, дзета) часто является более полезной мерой, которая связана с α соотношением
Частный случай ζ = 1 называется критическим демпфированием и представляет случай схемы, которая просто на границе колебания. Это минимальное демпфирование, которое можно применить, не вызывая колебаний.
Ширина полосы
Эффект резонанса можно использовать для фильтрации, быстрое изменение импеданса вблизи резонанса может использоваться для пропускания или блокировки сигналов, близких к резонансной частоте. Могут быть сконструированы как полосовые, так и полосовые фильтры, некоторые схемы фильтров показаны ниже в статье. Ключевым параметром в конструкции фильтра является полоса пропускания . Полоса пропускания измеряется между частотами среза , наиболее часто определяемыми как частоты, на которых мощность, передаваемая через цепь, упала до половины значения, передаваемого при резонансе. Есть две из этих частот половинной мощности: одна выше и одна ниже резонансной частоты
где Δω — ширина полосы частот, ω 1 — нижняя частота половинной мощности, а ω 2 — верхняя частота половинной мощности.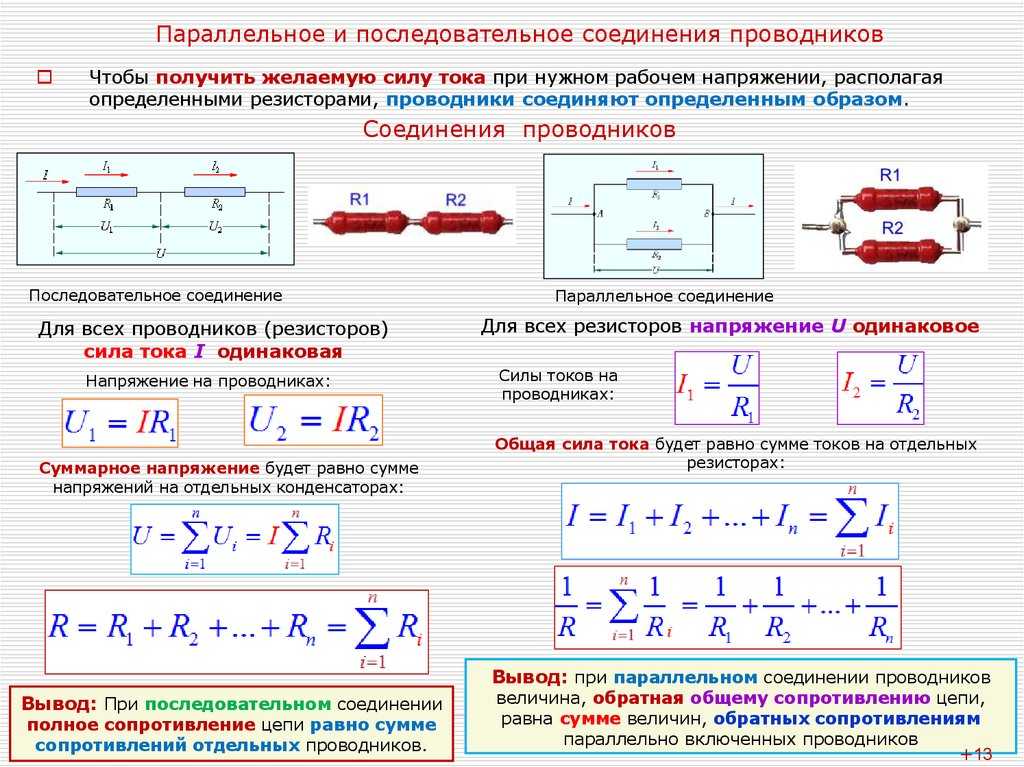 Полоса пропускания связана с ослаблением на
Полоса пропускания связана с ослаблением на
, где единицы измерения — радианы в секунду и неперс на второй соответственно. Для других единиц может потребоваться коэффициент пересчета. Более общая мера ширины полосы — это относительная ширина полосы, которая выражает ширину полосы как долю резонансной частоты и выражается как
Дробная пропускная способность также часто указывается в процентах. Демпфирование цепей фильтров регулируется для достижения требуемой полосы пропускания. Узкополосный фильтр, такой как режекторный фильтр , требует низкого демпфирования. Широкополосный фильтр требует сильного демпфирования.
Добротность
Добротность — широко распространенная мера, используемая для характеристики резонаторов. Он определяется как пиковая энергия, запасенная в цепи, деленная на среднюю энергию, рассеиваемую в ней на радиан при резонансе. Следовательно, схемы с низкой добротностью демпфируются, а схемы с потерями и высокой добротности — недостаточно.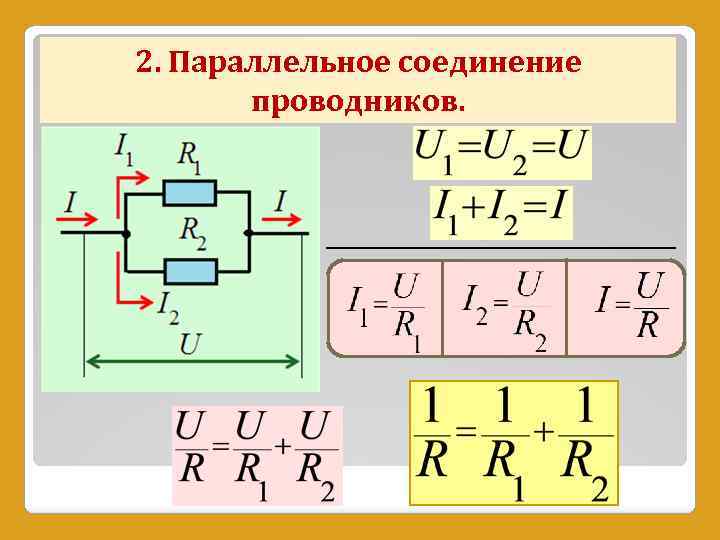 Q относится к пропускной способности; Цепи с низкой добротностью являются широкополосными, а схемы с высокой добротностью — узкополосными. Фактически бывает, что Q является обратной величиной дробной ширины полосы
Q относится к пропускной способности; Цепи с низкой добротностью являются широкополосными, а схемы с высокой добротностью — узкополосными. Фактически бывает, что Q является обратной величиной дробной ширины полосы
Q-фактор прямо пропорциональна избирательности , так как добротность обратно пропорциональна ширине полосы.
Для последовательного резонансного контура добротность можно вычислить следующим образом:
Масштабированные параметры
Параметры ζ, F b и Q масштабируются до ω 0 . Это означает, что схемы со схожими параметрами имеют одинаковые характеристики независимо от того, работают они в одной полосе частот или нет.
В следующей статье дается подробный анализ последовательной цепи RLC. Остальные конфигурации так подробно не описаны, но указаны основные отличия от серийного корпуса. Общая форма дифференциальных уравнений, приведенная в разделе последовательной схемы, применима ко всем схемам второго порядка и может использоваться для описания напряжения или тока в любом элементе каждой цепи.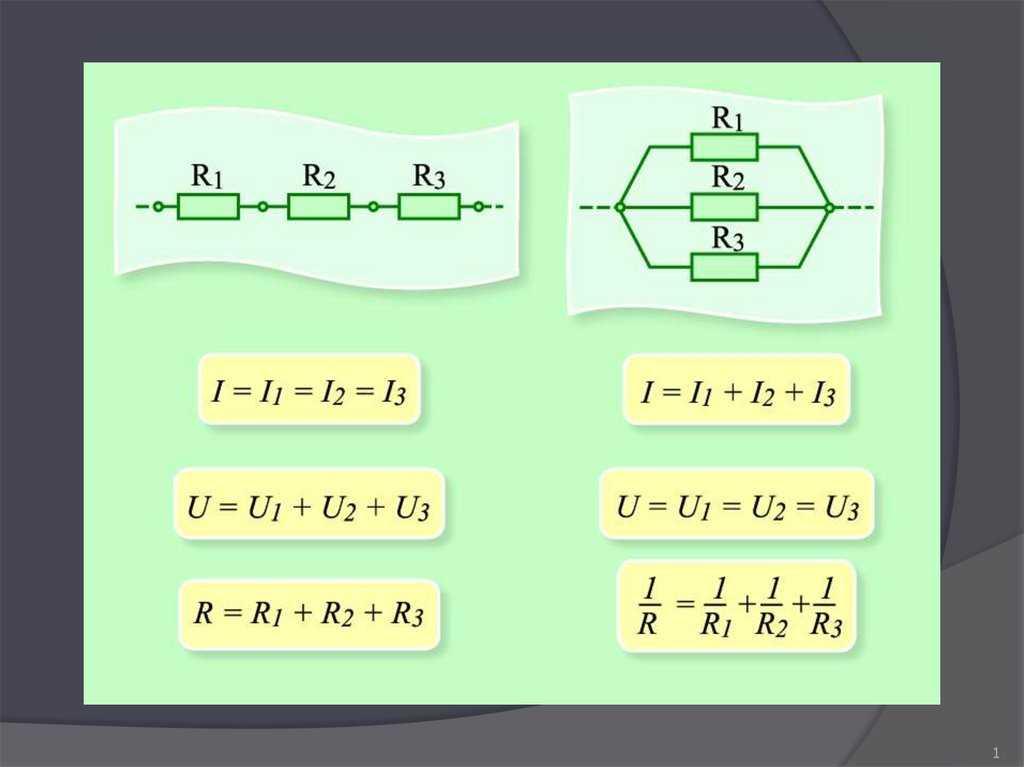
Последовательная цепь
Рисунок 1: Последовательная цепь RLC
- В, источник напряжения, питающий цепь
- I, ток, пропускаемый через цепь
- R, эффективное сопротивление комбинированной нагрузки, источника и компонентов
- L, индуктивность индукторакомпонента
- C, емкость конденсатор компонент
В этой схеме все три компонента включены последовательно с источником напряжения . Основное дифференциальное уравнение можно найти, подставив в закон напряжения Кирхгофа (KVL) определяющее уравнение для каждого из трех элементов. Из KVL
где V R , V L и V C — это напряжения на R, L и C соответственно, а V (t) — изменяющееся во времени напряжение от источника.
Подстановка , и в уравнение выше дает:
Для случая, когда источником является неизменное напряжение, взятие производной по времени и деление на L приводит к следующему дифференциальному уравнению второго порядка:
Полезно выразить это в более общей форме:
α и ω 0 оба выражены в единицах угловой частоты .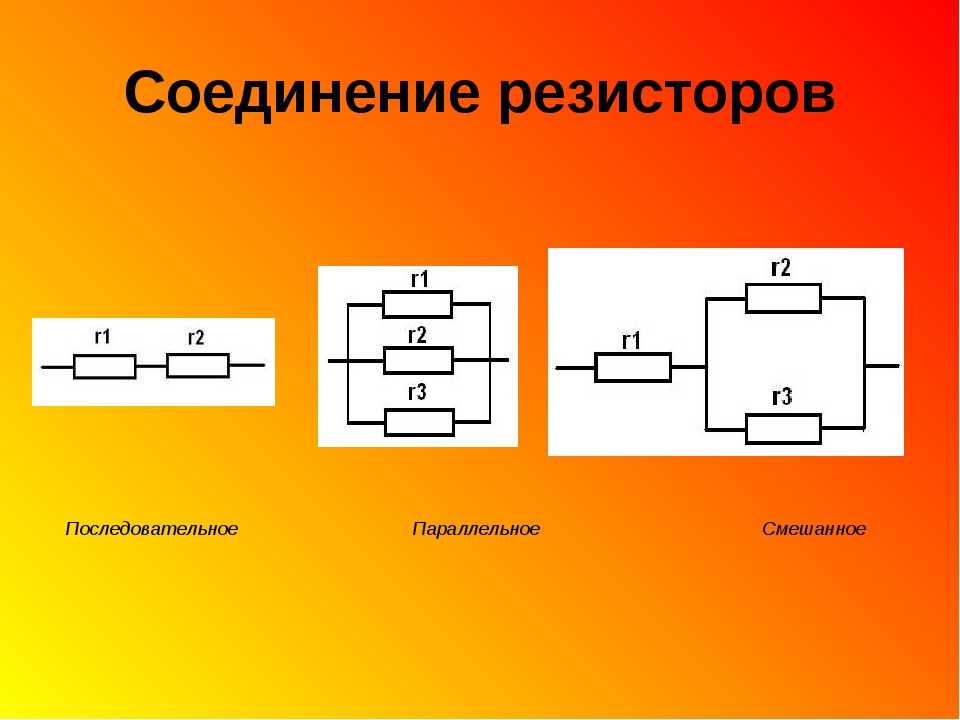 α называется непер частотой или затуханием и является мерой того, насколько быстро переходная характеристика схемы затухнет после устранения стимула. Непер встречается в названии, потому что единицы измерения можно также рассматривать как непер в секунду, где непер — это единица затухания. ω 0 — частота углового резонанса.
α называется непер частотой или затуханием и является мерой того, насколько быстро переходная характеристика схемы затухнет после устранения стимула. Непер встречается в названии, потому что единицы измерения можно также рассматривать как непер в секунду, где непер — это единица затухания. ω 0 — частота углового резонанса.
Для случая последовательной цепи RLC эти два параметра задаются следующим образом:
Полезный параметр — коэффициент затухания ζ, который определяется как отношение этих двух; хотя иногда α упоминается как коэффициент затухания, а ζ не используется.
В случае последовательной цепи RLC коэффициент демпфирования определяется как
Значение коэффициента демпфирования определяет тип переходного процесса,
Переходная характеристика
График, показывающий отклики с пониженным и избыточным демпфированием последовательной цепи RLC. График критического демпфирования — жирная красная кривая.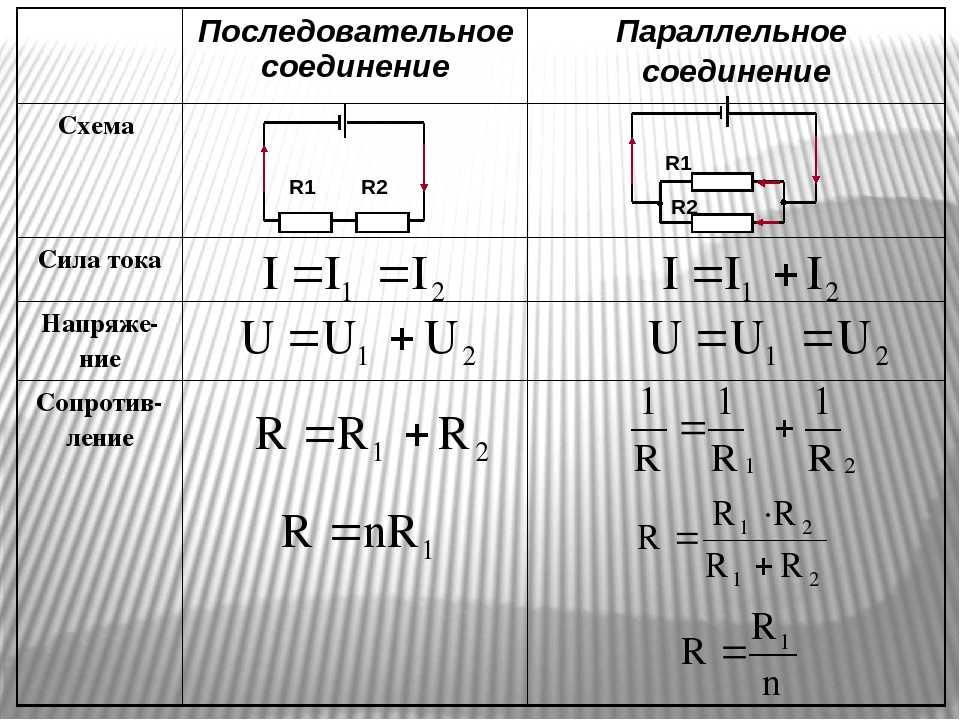 Графики нормализованы для L = 1, C = 1 и ω 0 = 1.
Графики нормализованы для L = 1, C = 1 и ω 0 = 1.
Дифференциальное уравнение имеет характеристическое уравнение ,
Корни уравнения в s-области:
Общее решение дифференциального уравнения представляет собой экспоненту в корне или линейную суперпозицию обоих,
Коэффициенты A 1 и A 2 определяются граничными условиями конкретной анализируемой задачи. То есть они устанавливаются значениями токов и напряжений в цепи в начале переходного процесса и предполагаемым значением, на котором они установятся через бесконечное время. Дифференциальное уравнение для схемы решается тремя разными способами в зависимости от значения ζ. Это избыточное демпфирование (ζ>1), недостаточное демпфирование (ζ < 1), and critically damped (ζ = 1).
сверхдемпфирование
сверхдемпфирование (ζ>1):
Отклик с избыточным демпфированием — это затухание переходного тока без колебаний.
Отклик с недостаточным демпфированием
Отклик с недостаточным демпфированием (ζ < 1) is
Применяя стандартные тригонометрические тождества , две тригонометрические функции могут быть выражены как одна синусоида со сдвигом фазы,
Отклик с недостаточным демпфированием представляет собой затухающее колебание на частоте ω d .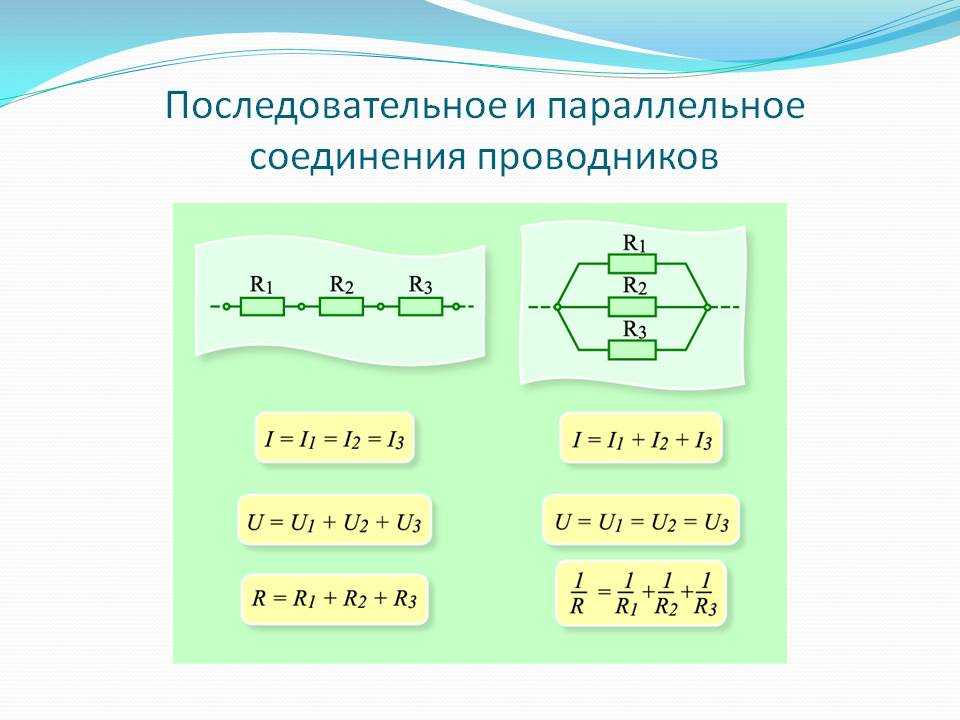 Колебание затухает со скоростью, определяемой затуханием α. Экспонента в α описывает огибающую колебания. B 1 и B 2 (или B 3 и фазовый сдвиг φ во второй форме) являются произвольными константами, определяемыми граничными условиями. Частота ω d определяется как
Колебание затухает со скоростью, определяемой затуханием α. Экспонента в α описывает огибающую колебания. B 1 и B 2 (или B 3 и фазовый сдвиг φ во второй форме) являются произвольными константами, определяемыми граничными условиями. Частота ω d определяется как
Это называется затухающей резонансной частотой или затухающей собственной частотой. Это частота, на которой цепь будет естественным образом колебаться, если не будет управляться внешним источником. Резонансная частота ω 0 , которая представляет собой частоту, на которой цепь будет резонировать под воздействием внешнего колебания, часто может называться незатухающей резонансной частотой, чтобы отличить ее.
Критически затухающий отклик
Критически затухающий отклик (ζ = 1) равен
Критически затухающий отклик представляет отклик схемы, которая затухает в кратчайшие сроки, не допуская колебаний. Это соображение важно в системах управления, где требуется как можно быстрее достичь желаемого состояния без перескока.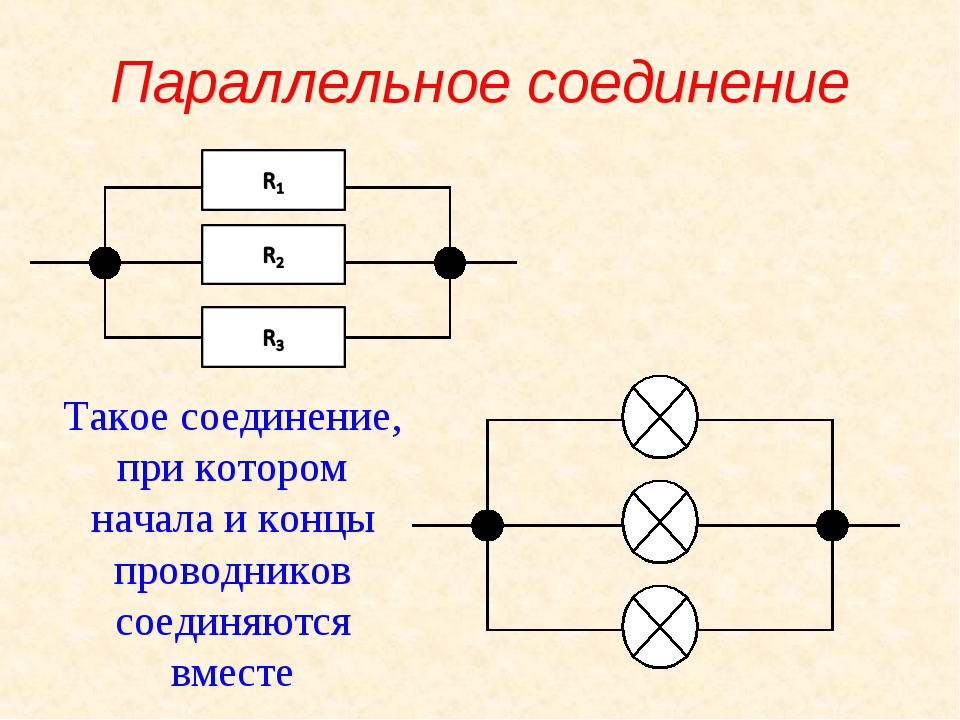 D 1 и D 2 — произвольные константы, определяемые граничными условиями.
D 1 и D 2 — произвольные константы, определяемые граничными условиями.
Область Лапласа
Последовательный RLC может быть проанализирован как для переходных, так и для установившихся Поведение состояния переменного тока с использованием преобразования Лапласа . Если вышеупомянутый источник напряжения формирует сигнал с преобразованным по Лапласу V (s) (где s — комплексная частота s = σ + jω), KVL может применяться в Лапласе. домен:
где I (s) — ток, преобразованный по Лапласу во всех компонентах. Решение относительно I (s):
И переставляя, мы получаем
адмиттанс Лапласа
Решение для лапласовской проводимости Y (s):
Упрощая с использованием параметров α и ω 0 , определенных в предыдущем разделе, мы имеем
Полюсы и нули
нули Y (s) — это такие значения s, что Y (s ) = 0:
полюса Y (s) — это значения s, такие что Y (s) → ∞. По квадратичной формуле находим
Полюса Y (s) идентичны корни s 1 и s 2 характеристического полинома дифференциального уравнения в разделе выше.
Общее решение
Для произвольного V (t) решение, полученное обратным преобразованием I (s), будет:
- В случае недостаточного демпфирования ω 0 >α:
- В случае критического затухания, ω 0 = α:
- В случае сверхдемпфирования ω 0< α:
где ω r = √α — ω 0 , а ch и sinh — обычные гиперболические функции .
Синусоидальное установившееся состояние
График амплитуды Боде для напряжений через элементы последовательной цепи RLC. Собственная частота ω 0 = 1 рад / с, коэффициент демпфирования ζ = 0,4.
Синусоидальное установившееся состояние представлено положением s = jω, где j — мнимая единица . Принимая величину вышеуказанного уравнения с этой заменой:
, а ток как функцию от ω можно найти в
Имеется пиковое значение | I (jω) |.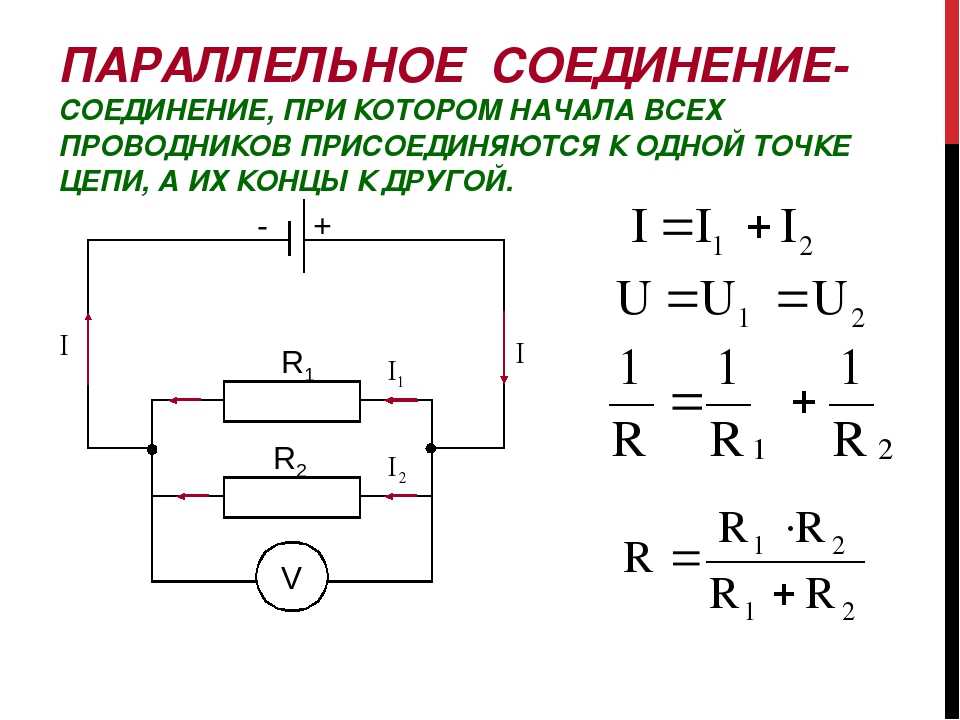 Величина ω на этом пике в данном конкретном случае равна незатухающей собственной резонансной частоте:
Величина ω на этом пике в данном конкретном случае равна незатухающей собственной резонансной частоте:
Из частотной характеристики тока, частотной характеристики напряжений на различных элементах схемы также можно определить.
Параллельная цепь
Рисунок 2. Параллельная цепь RLC
V — источник напряжения, питающий цепь
I — ток, пропускаемый через цепь
R — эквивалентное сопротивление объединенного источник, нагрузка и компоненты
L — индуктивность компонента индуктивности
C — емкость конденсаторного компонента
Свойства параллельной цепи RLC могут быть получены из отношения двойственности электрических цепей и учитывая, что параллельный RLC является двойным импедансом последовательного RLC. Принимая во внимание это, становится ясно, что дифференциальные уравнения, описывающие эту схему, идентичны общему виду уравнений, описывающих последовательный RLC.
Для параллельной схемы затухание α определяется как
и, следовательно, коэффициент демпфирования
Аналогично, другие масштабированные параметры, относительная полоса пропускания и Q также являются обратными друг другу.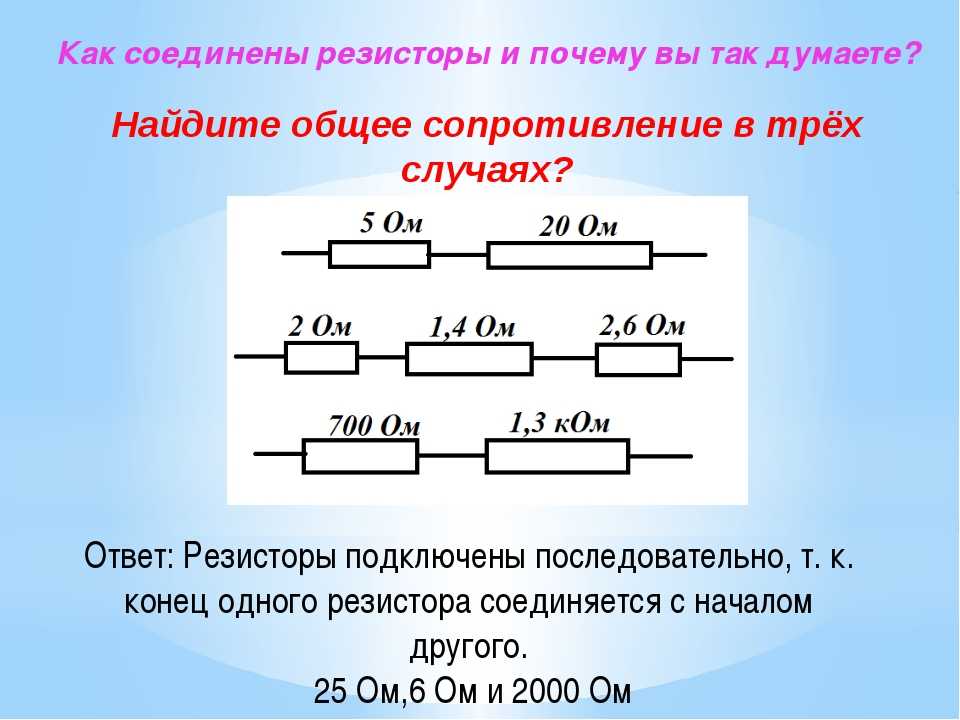 Это означает, что широкополосная схема с низкой добротностью в одной топологии станет узкополосной схемой с высокой добротностью в другой топологии, если будет построена из компонентов с одинаковыми значениями. Дробная полоса пропускания и Q параллельной схемы задаются как
Это означает, что широкополосная схема с низкой добротностью в одной топологии станет узкополосной схемой с высокой добротностью в другой топологии, если будет построена из компонентов с одинаковыми значениями. Дробная полоса пропускания и Q параллельной схемы задаются как
Обратите внимание, что приведенные здесь формулы являются обратными значениям формул для ряда схема, приведенная выше.
Частотная область
Рисунок 3. Синусоидальный анализ установившегося состояния. Нормировано на R = 1 Ω , C = 1 F , L = 1 H и V = 1 V.
Дается комплексная проводимость этой цепи путем сложения проводимости компонентов:
Результатом перехода от последовательного расположения к параллельному расположению в цепи, имеющей пик импеданса при резонансе, а не минимум, поэтому цепь является антирезонатором.
График напротив показывает, что существует минимум частотной характеристики тока на резонансной частоте , когда цепь приводится в действие постоянным напряжением.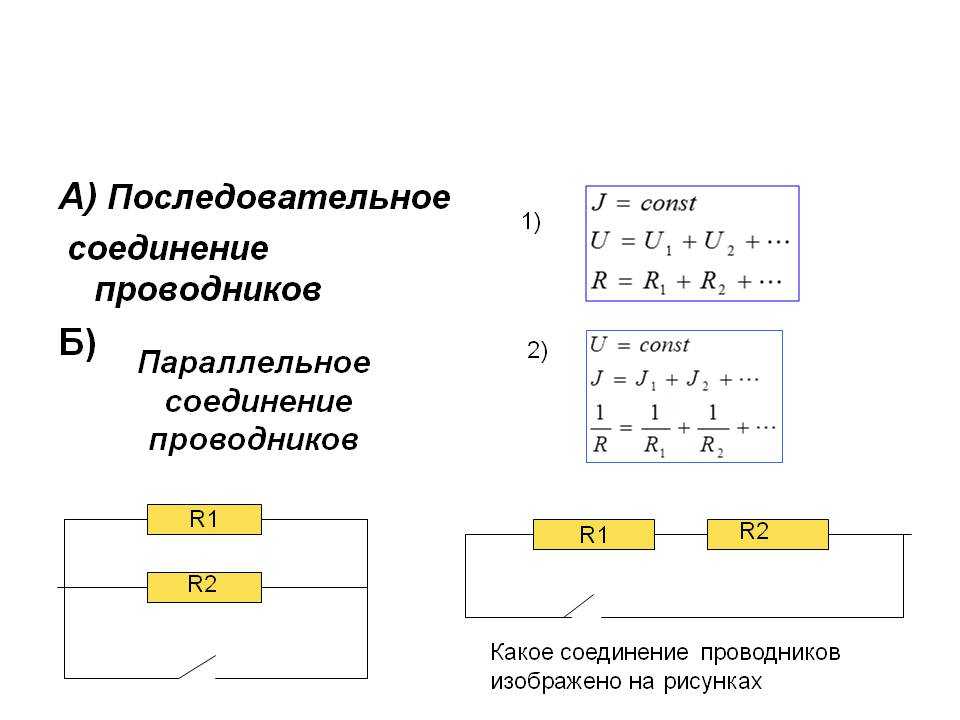 С другой стороны, при управлении постоянным током будет максимум напряжения, который будет следовать той же кривой, что и ток в последовательной цепи.
С другой стороны, при управлении постоянным током будет максимум напряжения, который будет следовать той же кривой, что и ток в последовательной цепи.
Другие конфигурации
Рисунок 4. Параллельная цепь RLC с сопротивлением последовательно с катушкой индуктивности
Последовательный резистор с катушкой индуктивности в параллельной LC-цепи, как показано на рисунке 4, представляет собой топологию, которая обычно встречается необходимо учитывать сопротивление обмотки катушки. Параллельные LC-цепи часто используются для полосовой фильтрации , и добротность в значительной степени определяется этим сопротивлением. Резонансная частота этого контура
Это резонансная частота цепи, определяемая как частота, на которой полная проводимость имеет нулевую мнимую часть. Частота, которая появляется в обобщенной форме характеристического уравнения (которое для этой схемы такое же, как и ранее)
— это не та же частота.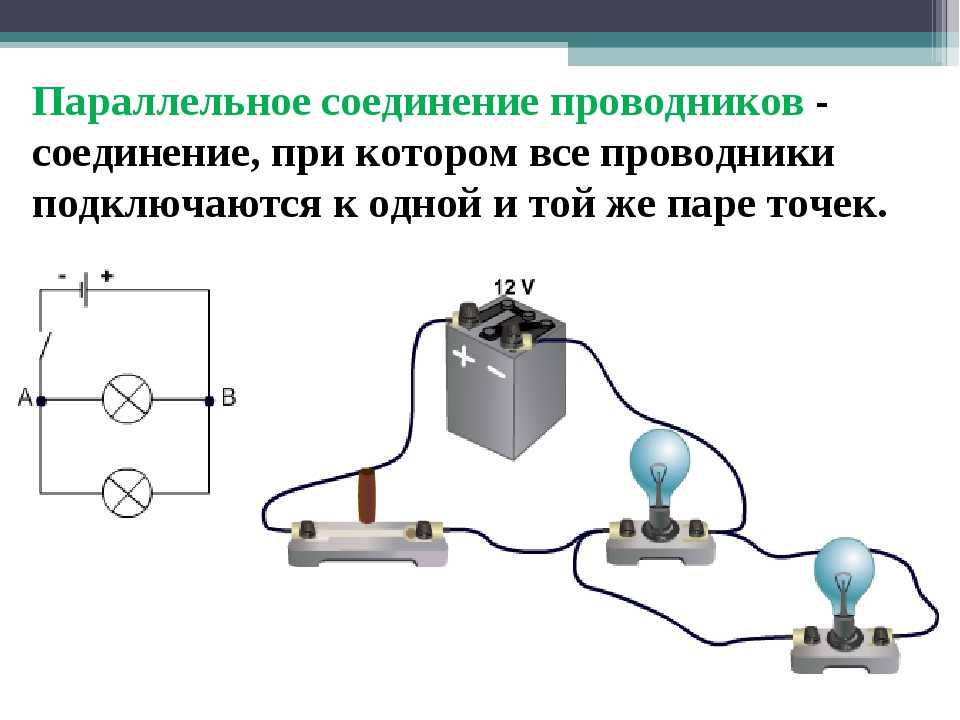 В данном случае это естественная незатухающая резонансная частота:
В данном случае это естественная незатухающая резонансная частота:
Частота ω m , при которой величина импеданса максимальна, равна задается
где Q L = ω ‘0 L / R — коэффициент качества катушки. Это может быть хорошо аппроксимировано выражением
Кроме того, точное значение максимального импеданса определяется как
Для значений Q L больше единицы это может быть хорошо аппроксимировано выражением
Рис. 5. Последовательная цепь RLC с сопротивлением, параллельным конденсатору
В том же ключе, резистор, включенный параллельно конденсатору в последовательной LC-цепи, можно использовать для обозначения конденсатора с диэлектриком с потерями. Эта конфигурация показана на рисунке 5. Резонансная частота (частота, при которой импеданс имеет нулевую мнимую часть) в этом случае определяется выражением
, а частота ω m , при котором величина импеданса минимальна, определяется как
где Q C = ω ′ 0 RC.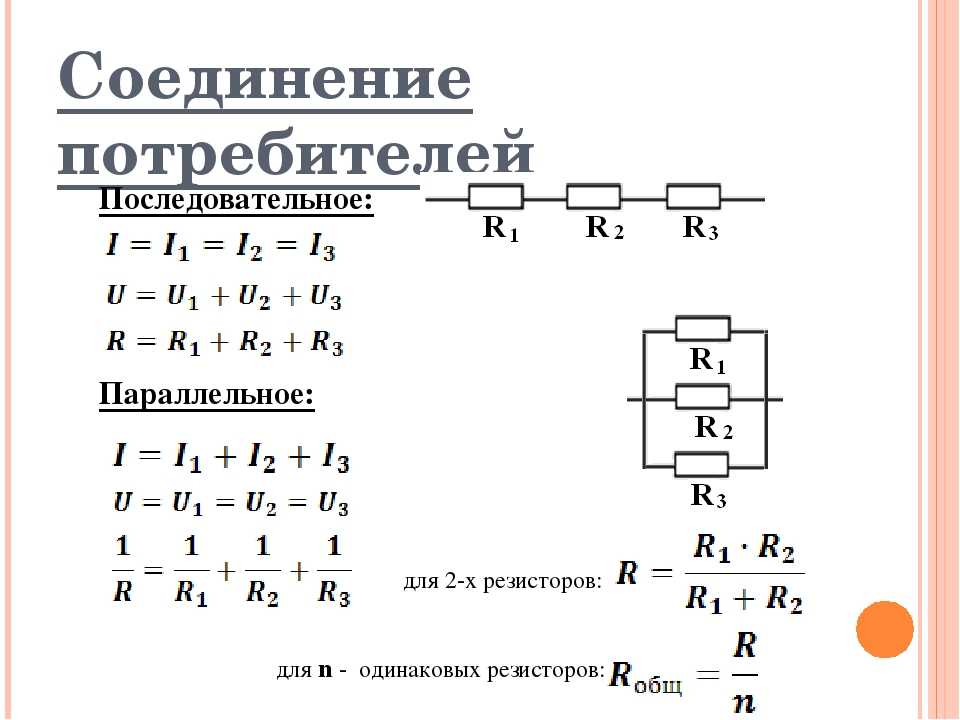
История
Первое свидетельство того, что конденсатор может производить электрические колебания, было обнаружено в 1826 году французским ученым Феликсом Савари . Он обнаружил, что когда лейденская банка разряжалась через проволоку, намотанную вокруг железной иглы, иногда игла оставалась намагниченной в одном направлении, а иногда в противоположном. Он правильно предположил, что это было вызвано затухающим колеблющимся током разряда в проводе, который менял намагниченность иглы назад и вперед до тех пор, пока она не становилась слишком маленькой, чтобы оказывать влияние, оставляя иглу намагниченной в случайном направлении.
Американский физик Джозеф Генри повторил эксперимент Савари в 1842 году и пришел к такому же выводу, очевидно независимо. Британский ученый Уильям Томсон (лорд Кельвин) в 1853 году математически показал, что разряд лейденской банки через индуктивность должен быть колебательным, и вывел его резонансную частоту.
Британский радиоисследователь Оливер Лодж , разрядив большую батарею лейденских банок через длинный провод, создал настроенный контур с его резонансной частотой в звуковом диапазоне, который создавал музыкальный тон из искры при ее разряде.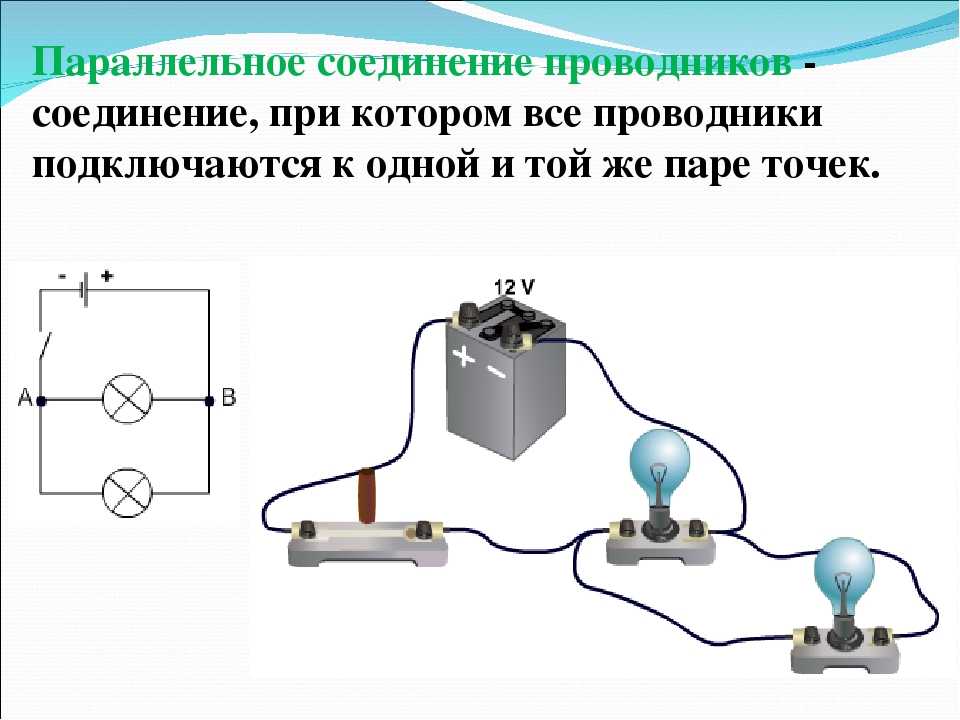 В 1857 году немецкий физик Беренд Вильгельм Феддерсен сфотографировал искру, вызванную резонансным контуром лейденской банки во вращающемся зеркале, предоставив видимые свидетельства колебаний. В 1868 году шотландский физик Джеймс Клерк Максвелл вычислил эффект приложения переменного тока к цепи с индуктивностью и емкостью, показав, что отклик максимален на резонансной частоте.
В 1857 году немецкий физик Беренд Вильгельм Феддерсен сфотографировал искру, вызванную резонансным контуром лейденской банки во вращающемся зеркале, предоставив видимые свидетельства колебаний. В 1868 году шотландский физик Джеймс Клерк Максвелл вычислил эффект приложения переменного тока к цепи с индуктивностью и емкостью, показав, что отклик максимален на резонансной частоте.
Первый пример электрической резонансной кривой был опубликован в 1887 году немецким физиком Генрихом Герцем в его новаторской статье об открытии радиоволн, показывающей длину искры, получаемой от его искрового разрядника LC-резонатора детекторы как функция частоты.
Одной из первых демонстраций резонанса между настроенными схемами был эксперимент Лоджа с «синтонными сосудами» около 1889 года. Он поместил два резонансных контура рядом друг с другом, каждый из которых состоял из лейденского сосуда, подключенного к регулируемая одновитковая катушка с искровым разрядником. Когда высокое напряжение от индукционной катушки прикладывалось к одному настроенному контуру, создавая искры и, следовательно, колеблющиеся токи, искры возбуждались в другом настроенном контуре только тогда, когда индукторы были настроены на резонанс.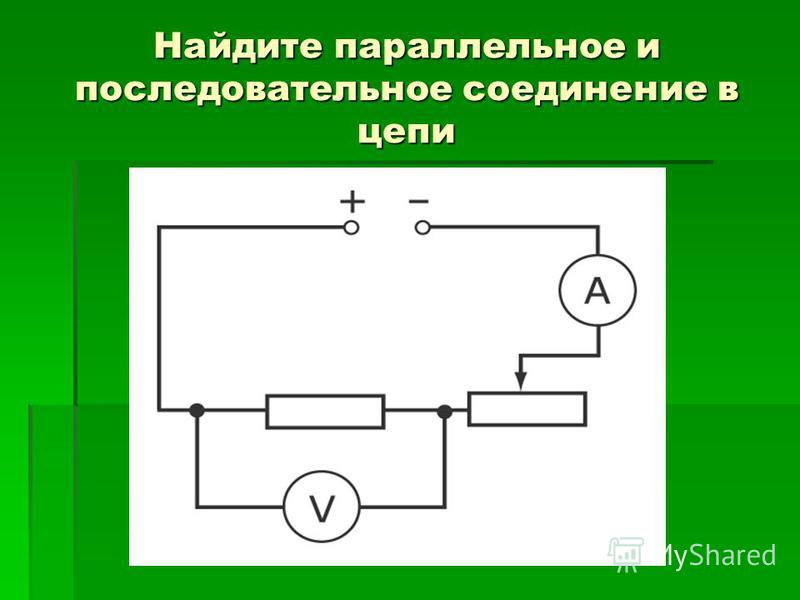 Лодж и некоторые английские ученые предпочли термин «синтония» для этого эффекта, но термин «резонанс» в конце концов прижился.
Лодж и некоторые английские ученые предпочли термин «синтония» для этого эффекта, но термин «резонанс» в конце концов прижился.
Первое практическое использование RLC-схем было в 1890-х годах в радиопередатчиках с искровым разрядником. для настройки приемника на передатчик. Первый патент на радиосистему, позволяющую настройку, был подан Лоджем в 1897 году, хотя первые практические системы были изобретены в 1900 году англо-итальянским пионером радио Гульельмо Маркони .
Приложения
Переменные настраиваемые схемы
Эти схемы очень часто используются в схемах настройки аналоговых радиоприемников. Регулируемая настройка обычно достигается с помощью параллельного пластинчатого переменного конденсатора , который позволяет изменять значение C и настраиваться на станции на разных частотах. Для каскада ПЧ в радиостанции, где настройка предустановлена на заводе, более обычным решением является регулируемый сердечник в катушке индуктивности для регулировки L. В этой конструкции сердечник (сделанный из высокого проницаемость материал, который имеет эффект увеличения индуктивности) имеет резьбу, так что его можно ввинтить или вывинтить из обмотки индуктора, если это необходимо.
Фильтры
|
Рисунок 6. Схема RLC как фильтр нижних частот |
Рисунок 7. Схема RLC как фильтр верхних частот |
|
Рисунок 8. Схема RLC как последовательный полосовой фильтр, включенный последовательно с линией |
Рисунок 9. Схема RLC как параллельный полосовой фильтр в шунте через линию |
|
Рисунок 10. Схема RLC как последовательный полосовой фильтр в шунте через линию |
Рисунок 11. Схема RLC как параллельный полосовой фильтр, включенный последовательно с линией |
В приложении фильтрации резистор становится нагрузкой, которую фильтр работая в.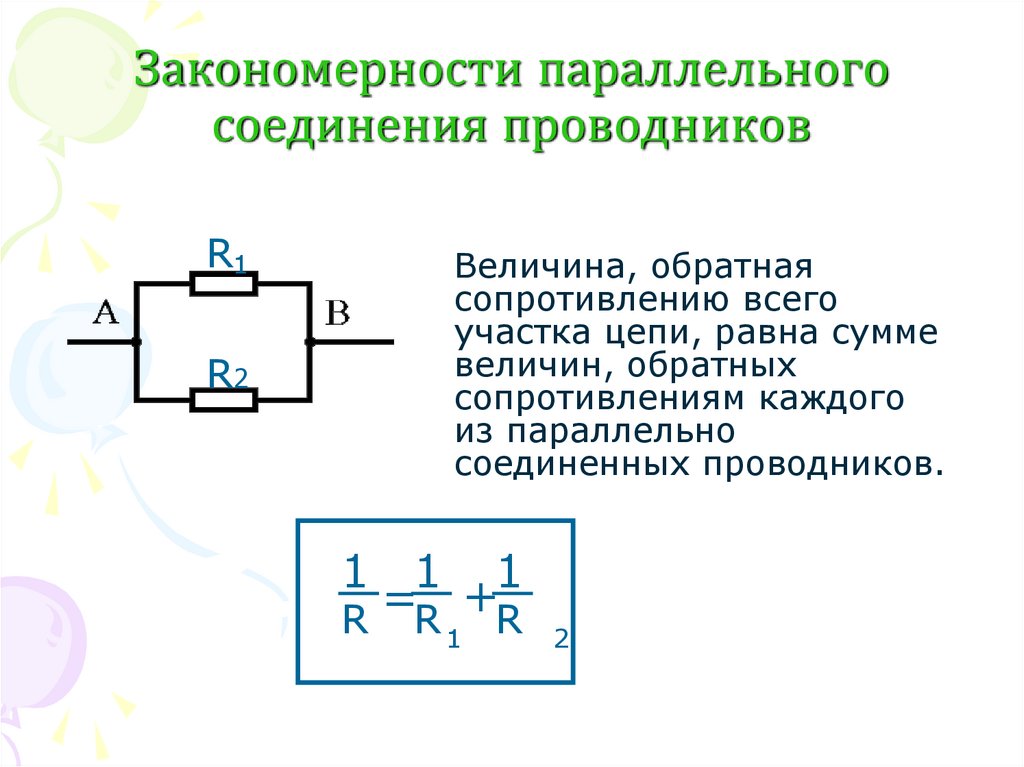 Значение коэффициента демпфирования выбирается исходя из желаемой полосы пропускания фильтра. Для более широкой полосы пропускания требуется большее значение коэффициента демпфирования (и наоборот). Эти три компонента дают дизайнеру три степени свободы. Два из них необходимы для установки полосы пропускания и резонансной частоты. У дизайнера остается один, который можно использовать для масштабирования R, L и C до удобных практических значений. В качестве альтернативы R может быть задано внешней схемой, которая будет использовать последнюю степень свободы.
Значение коэффициента демпфирования выбирается исходя из желаемой полосы пропускания фильтра. Для более широкой полосы пропускания требуется большее значение коэффициента демпфирования (и наоборот). Эти три компонента дают дизайнеру три степени свободы. Два из них необходимы для установки полосы пропускания и резонансной частоты. У дизайнера остается один, который можно использовать для масштабирования R, L и C до удобных практических значений. В качестве альтернативы R может быть задано внешней схемой, которая будет использовать последнюю степень свободы.
Фильтр нижних частот
Схема RLC может использоваться как фильтр нижних частот. Конфигурация схемы показана на рисунке 6. Частота излома, то есть частота точки 3 дБ, задается как
Это также полоса пропускания фильтра. Коэффициент демпфирования определяется как
Фильтр высоких частот
Фильтр верхних частот показан на рисунке 7. Частота излома такая же, как у фильтра нижних частот:
Фильтр имеет полосу заграждения этой ширины.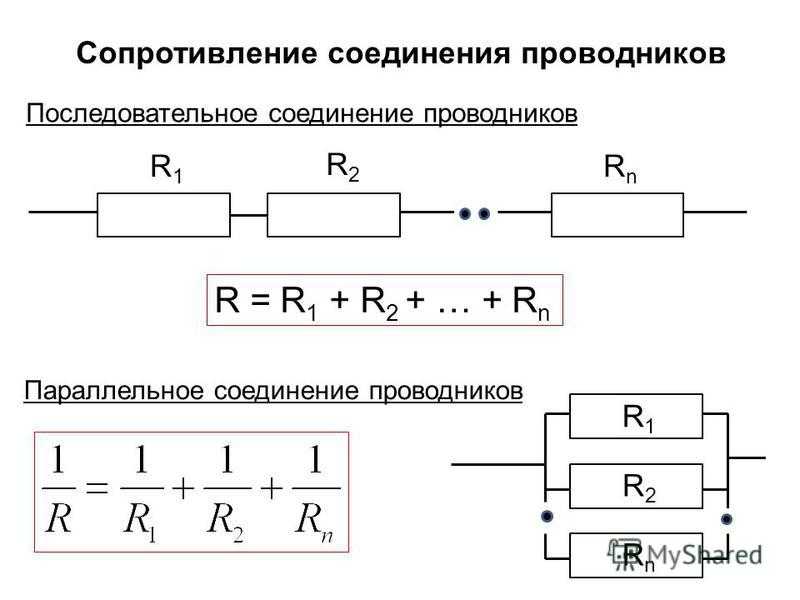
Полосовой фильтр
Полосовой фильтр может быть сформирован со схемой RLC путем размещения последовательной LC-цепи последовательно с нагрузочным резистором или путем размещения параллельной LC-цепи параллельно нагрузке. резистор. Эти устройства показаны на рисунках 8 и 9 соответственно. Центральная частота задается следующим образом:
и ширина полосы для последовательной цепи составляет
Шунтовая версия схемы предназначена для работы от источника с высоким импедансом, то есть постоянного Источник тока. В этих условиях ширина полосы составляет
Полосовой фильтр
На рисунке 10 показан полосовой фильтр, образованный серией LC-цепь шунтируется через нагрузку. На рисунке 11 показан полосовой фильтр, образованный параллельной LC-цепью, включенной последовательно с нагрузкой. Первый случай требует высокого Источник импеданса, так что ток отводится в резонатор, когда он становится низким в резонансе. Во втором случае требуется источник с низким импедансом, чтобы напряжение на антирезонаторе падало, когда он становится высоким при резонансе.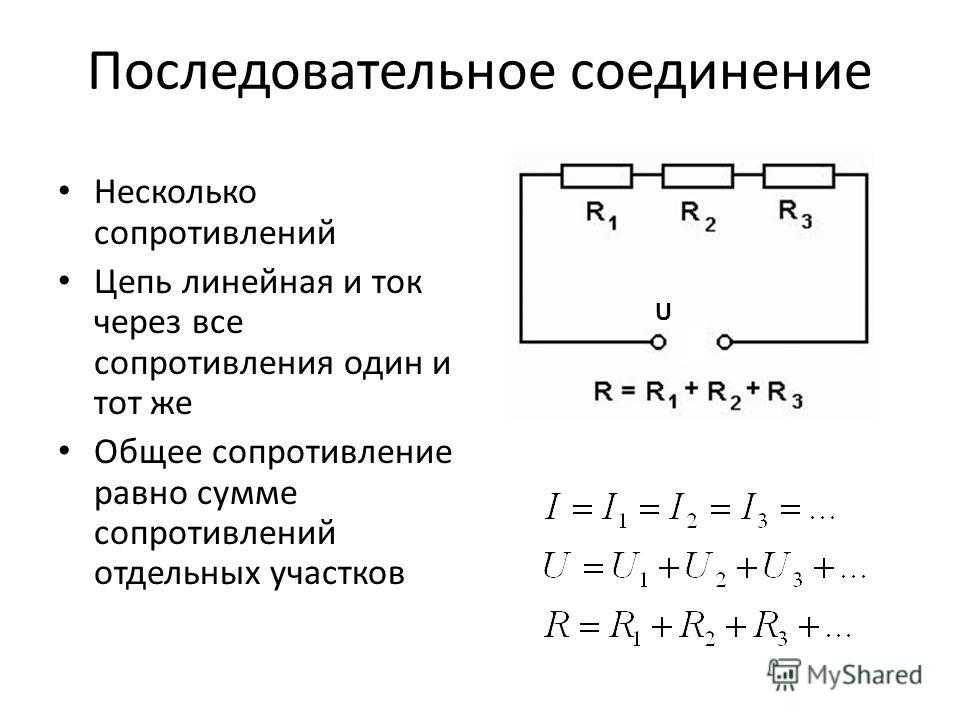
Генераторы
Для применений в схемах генераторов обычно желательно сделать затухание (или, что то же самое, коэффициент затухания) как можно меньше. На практике для достижения этой цели необходимо сделать сопротивление цепи R как можно меньшим физически для последовательной цепи или, в качестве альтернативы, увеличить R до максимально возможного значения для параллельной цепи. В любом случае RLC-схема становится хорошим приближением к идеальной LC-схеме . Однако для схем с очень низким затуханием (высокая добротность) могут стать важными такие вопросы, как диэлектрические потери катушек и конденсаторов.
В схеме генератора
или эквивалентно
В результате
Умножитель напряжения
В последовательной цепи RLC при резонансе ток ограничивается только сопротивление цепи
Если R мало, например, состоящее только из сопротивления обмотки индуктора, тогда этот ток будет большим. Это снизит напряжение на катушке индуктивности
Напряжение равной величины также будет наблюдаться на конденсаторе, но в противофазе к катушке индуктивности. Если R можно сделать достаточно малым, эти напряжения могут в несколько раз превышать входное напряжение. Фактически, коэффициент напряжения — это добротность схемы,
Если R можно сделать достаточно малым, эти напряжения могут в несколько раз превышать входное напряжение. Фактически, коэффициент напряжения — это добротность схемы,
Аналогичный эффект наблюдается с токами в параллельной цепи. Несмотря на то, что внешнему источнику кажется, что цепь имеет высокий импеданс, во внутреннем контуре параллельной катушки индуктивности и конденсатора циркулирует большой ток.
Цепь импульсного разряда
В качестве цепи импульсного разряда может использоваться последовательная RLC-цепь с избыточным демпфированием. Часто бывает полезно знать значения компонентов, которые можно использовать для создания сигнала. Это описывается формой
Такой Схема может состоять из конденсатора накопления энергии, нагрузки в виде сопротивления, некоторой индуктивности цепи и переключателя — и все это последовательно. Начальные условия заключаются в том, что конденсатор находится под напряжением V 0 и в катушке индуктивности нет тока.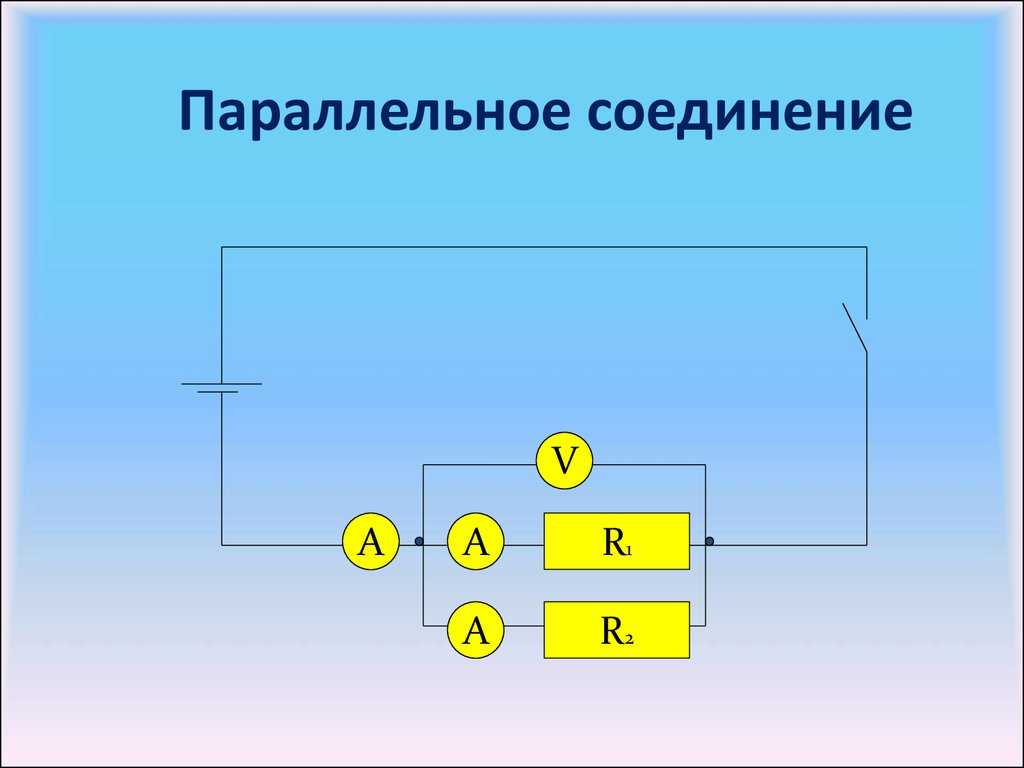 Если индуктивность L известна, то остальные параметры задаются следующим образом — емкость:
Если индуктивность L известна, то остальные параметры задаются следующим образом — емкость:
сопротивление (сумма цепи и нагрузки):
начальное напряжение на клеммах конденсатора:
Перестановка для случая, когда R известно — емкость:
индуктивность (сумма цепи и нагрузки):
начальное напряжение на клеммах конденсатора:
См. также
- RC-цепь
- RL-цепь
- Линейная схема
Тебе нравиться последовательное соединение? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое последовательное соединение, цепь rlc, режимы работы rlc-цепи и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Электротехника, Схемотехника, Аналоговые устройства
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.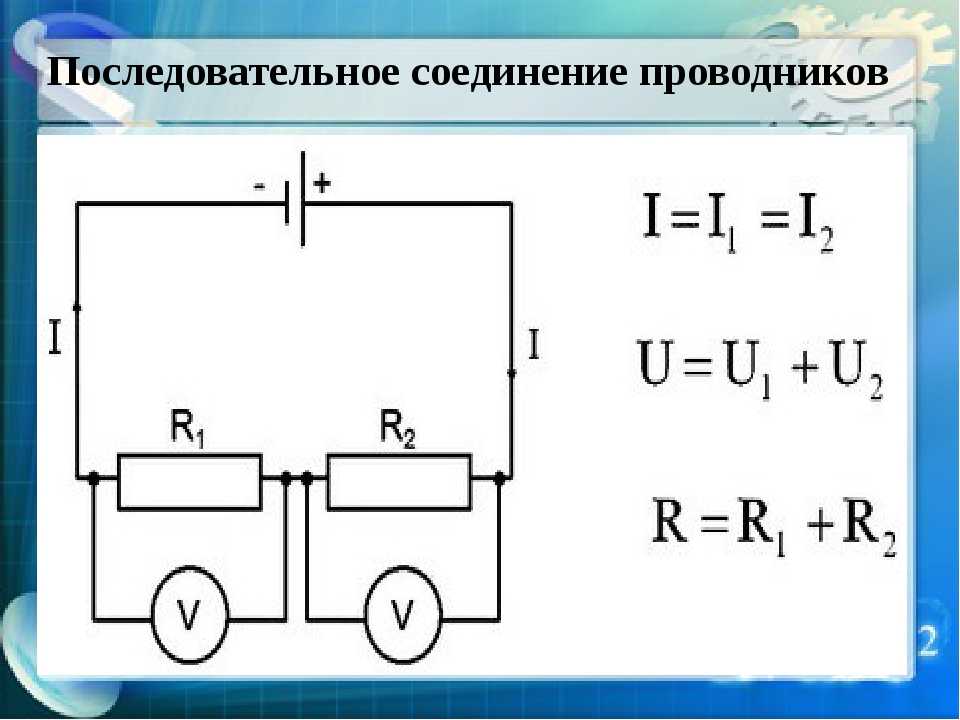
и параллельные цепи: примеры и правила
Мы используем электрические устройства каждый день и постоянно слышим об электрических цепях. Но знаете ли вы, что на самом деле существует два основных типа схем, и что у них обоих разные правила и приложения? Это объяснение погрузится прямо в эти два типа схем, известные как последовательные и параллельные схемы, и чем именно они отличаются, и где мы применяем каждый тип!
Определение параллельной и последовательной цепи
Если мы хотим соединить два компонента схемы вместе в цепи, то у нас есть два способа сделать это последовательно и параллельно.
Цепь серии состоит из компонентов, которые соединены последовательно , т. е. они соединены один за другим в своего рода «цепочку» компонентов.
Параллельная цепь состоит из компонентов, соединенных параллельно . Для этого мы разделяем схему на две части и размещаем компоненты рядом на нескольких разных ветвях, после чего снова объединяем ветви.
Так в чем именно разница между этими двумя типами схем и как мы видим ее на принципиальных схемах?
Разница между последовательными и параллельными цепями
На изображении ниже мы можем очень четко увидеть разницу между электрическими компонентами, которые соединены последовательно или параллельно.
Три лампы соединены слева параллельно, а справа последовательно, Wikimedia Commons CC BY-SA 4.0.
Разница между последовательной и параллельной схемой заключается в том, в какой конфигурации компоненты соединены друг с другом.
Формулы и правила для последовательных и параллельных цепей
Тремя основными величинами, соответствующими цепям, являются напряжение, ток и сопротивление. В общем, напряжение можно рассматривать как «силу», толкающую заряженные частицы через цепь, ток можно рассматривать как количество заряженных частиц, которые могут пройти через цепь, а сопротивление можно рассматривать как сужение дороги или маленькая дверь: чем больше сопротивление, тем меньше дверь, через которую должны пройти заряженные частицы.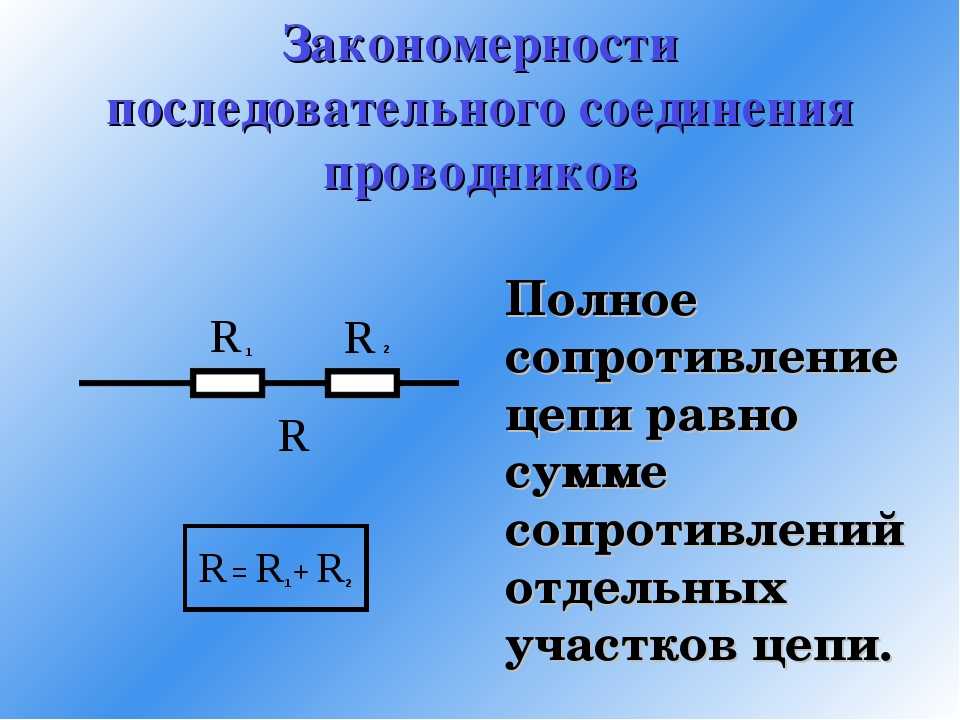
С помощью этих сравнений мы можем понять закон Ома, если сформулируем его следующим образом:
Если мы увеличим толчок (увеличим напряжение) или сделаем дорогу шире (уменьшим сопротивление), больше частиц сможет пройти (ток увеличится).
Правила последовательной цепи
Для последовательной цепи мы находимся в ситуации, показанной на рисунке ниже, в которой два (или более) резистора с сопротивлением и соединены последовательно по напряжению.
Серийная схема A, Wikimedia Commons CC BY-SA 4.0.
Правила для последовательных цепей:
- Общее сопротивление всех резисторов равно сумме сопротивлений отдельных резисторов. Таким образом, полное сопротивление в цепи выше равно.
- Ток через все резисторы одинаков. Зная это, мы можем теперь рассчитать этот ток, используя закон Ома, чтобы быть.
- В результате предыдущего пункта мы можем рассчитать напряжение на отдельных резисторах (и) до 9 и .
 Таким образом, напряжение на резисторах пропорционально их сопротивлениям, а сумма отдельных напряжений равна общему напряжению.
Таким образом, напряжение на резисторах пропорционально их сопротивлениям, а сумма отдельных напряжений равна общему напряжению.
Запомните эти правила, разбираясь в них! Вот способ взглянуть на правила и формулы для последовательных цепей.
- Если вы заряженная частица, вы должны пройти через оба барьера. Общий барьер, с которым вы сталкиваетесь, представляет собой сумму двух отдельных барьеров, потому что вы дважды замедляетесь на своем пути.
- Если ток не везде одинаков, то где-то будет нарастание или потеря заряда, что невозможно в идеальной цепи. Одна партия заряженных частиц не может обогнать другую, потому что ветвь только одна. Добавление большего количества резисторов увеличит общий барьер, поэтому ток будет меньше.
- Это правило следует закону Ома.
Предположим, что два резистора на самом деле являются двумя лампами. Мощность компонента в электрической цепи можно рассчитать по формуле, поэтому мощность лампы 1 равна:
и мы можем сделать аналогичный расчет для лампы 2.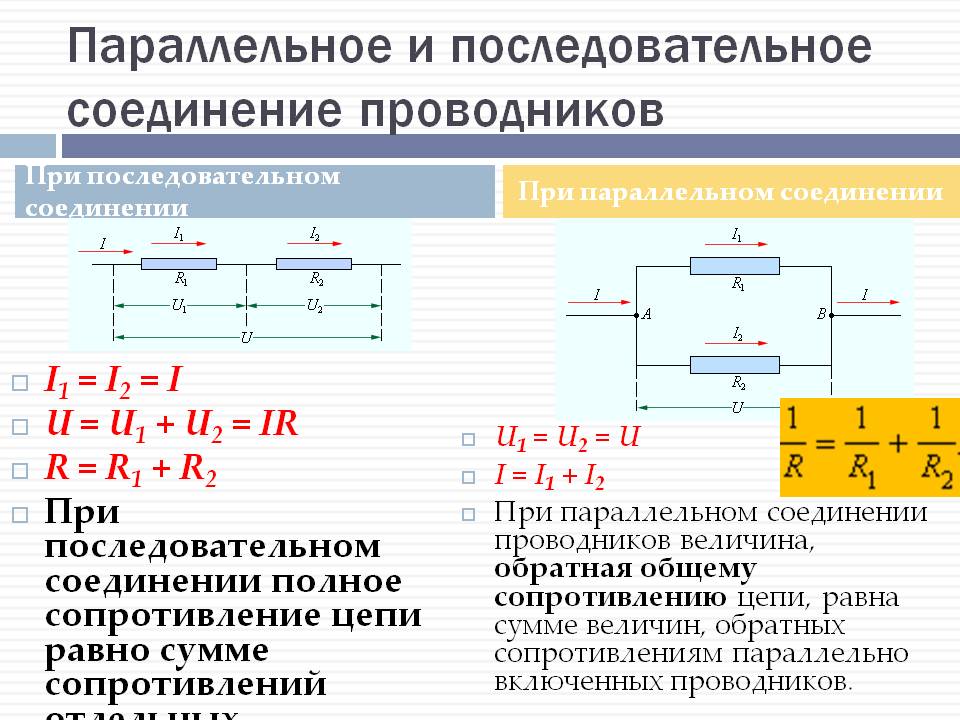 Мы видим, что лампа с большим сопротивлением потребляет больше энергии от последовательной цепи.
Мы видим, что лампа с большим сопротивлением потребляет больше энергии от последовательной цепи.
Правила параллельной цепи
Для параллельной цепи мы находимся в ситуации, показанной на рисунке ниже, в которой два (или более) резистора с сопротивлением и соединены параллельно по напряжению.
Параллельная цепь, Wikimedia Commons CC BY-SA 4.0.
Правила параллельных цепей:
- Напряжение на всех ветвях одинаковое, а именно полное напряжение, а ток через отдельные резисторы можно рассчитать по закону Ома.
- Общий ток представляет собой сумму токов отдельных резисторов. Следовательно, общее сопротивление меньше, чем сопротивление отдельных резисторов.
Вот способ разобраться в этих правилах и формулах для параллельных цепей.
- Оба резистора напрямую подключены к электрической ячейке с обоих концов, поэтому напряжение на них должно быть напряжением ячейки.
- Теперь у заряженных частиц есть несколько способов добраться до другого конца клетки: есть две двери из стороны в сторону, и частицы могут выбирать, к какой из них они хотят встать в очередь.
 Таким образом, через двери можно пропустить больше заряженных частиц.
Таким образом, через двери можно пропустить больше заряженных частиц. - Ток — это количество заряженных частиц, проходящих контрольную точку в секунду. Эта величина везде одинакова, поэтому сумма отдельных токов должна составлять общий ток. Как будто два потока бегунов сливаются воедино на одной большой улице.
Предположим, что два резистора на самом деле являются двумя лампами. Тогда мощность над лампой равна , и мы можем сделать аналогичный расчет для лампы. Мы видим, что лампа с меньшим сопротивлением получает большую мощность от параллельной цепи.
Мы можем рассчитать общее сопротивление параллельной цепи. Рассчитываем:
.
Проще говоря, мы можем сказать, что общее сопротивление параллельной цепи равно обратной сумме обратных величин отдельных сопротивлений. Мы видим, что действительно общее сопротивление меньше, чем сопротивление отдельных резисторов. Это приводит к большему общему току, чем если бы была только одна ветвь. Это означает, что создание параллельных ветвей в цепи уменьшит сопротивление и увеличит ток в цепи. Это имеет смысл в рамках нашей аналогии с дверьми.
Это имеет смысл в рамках нашей аналогии с дверьми.
Пример последовательной и параллельной схемы и расчеты
Давайте рассмотрим сложный пример, сочетающий последовательную и параллельную схемы. См. рисунок ниже для установки. В большинстве практических ситуаций вы можете определить напряжение В 1 самостоятельно и выбрать резисторы, которые вы используете, и ваша задача — найти другие величины. Это то, что мы будем делать.
Цепь, содержащая последовательные и параллельные соединения, с сопротивлениями R и , амперметры A и и вольтметры V и , Wikimedia Commons CC BY-SA 4.0.
Обратите внимание, как напряжения на сопротивлениях измеряются прибором, подключенным параллельно сопротивлениям. Это связано с тем, что напряжение на параллельной цепи одинаково на всех ветвях, поэтому напряжение, которое измеряет вольтметр, совпадает с напряжением на сопротивлении, к которому он подключен параллельно!
Предположим, мы подключили вольтметр последовательно к сопротивлению, на котором мы хотим измерить напряжение. Тогда напряжение будет разделено между вольтметром и сопротивлением, и вольтметр будет измерять только напряжение на себе, что будет близко к общему напряжению, выдаваемому батареей, потому что вольтметры имеют чрезвычайно высокое сопротивление.
Тогда напряжение будет разделено между вольтметром и сопротивлением, и вольтметр будет измерять только напряжение на себе, что будет близко к общему напряжению, выдаваемому батареей, потому что вольтметры имеют чрезвычайно высокое сопротивление.
Обратите также внимание на то, как ток в цепи измеряется прибором, подключенным последовательно к сопротивлениям, через которые мы хотим измерить ток. Это связано с тем, что ток через последовательную цепь везде одинаков, поэтому ток, который измеряет амперметр, такой же, как ток через сопротивления, к которым он подключен последовательно!
Предположим, мы подключили амперметр параллельно сопротивлению, через которое мы хотим измерить ток. Тогда ток будет разделен между амперметром и сопротивлением, и амперметр будет измерять ток только через свою собственную ветвь, а не через ветвь интересующего сопротивления вообще! Этот ток будет очень высоким, потому что амперметры имеют чрезвычайно низкое сопротивление.
Вопрос дает значения , и.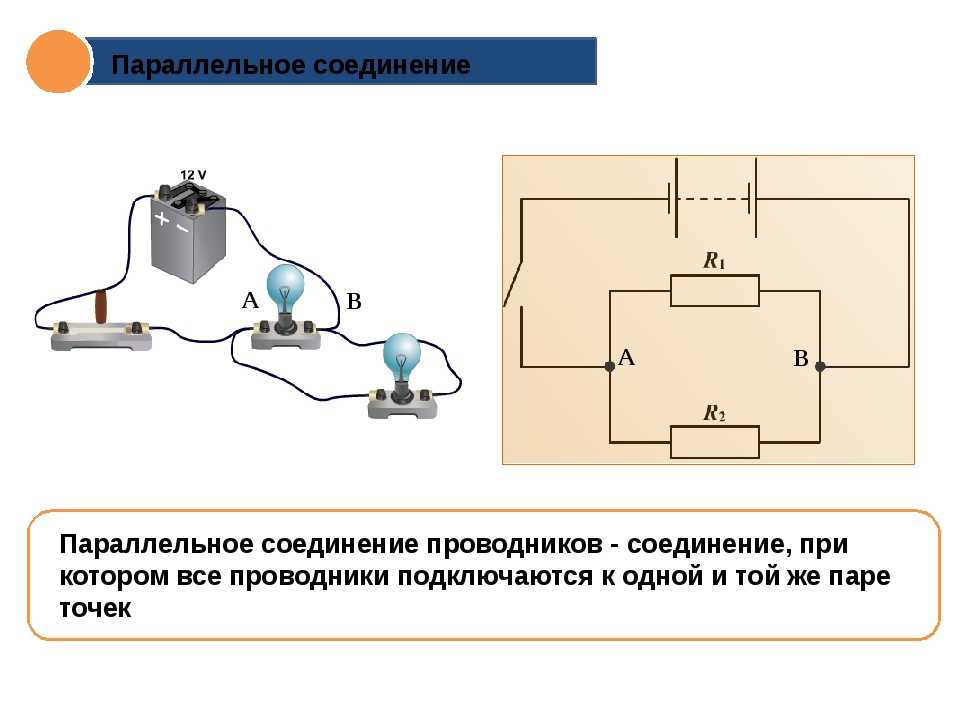
Видим, что у нас параллельная цепь, но одна из ветвей параллельной цепи содержит два резистора, которые соединены последовательно. Приведем общее сопротивление резисторов и название, а общее напряжение над названием.
Из правил параллельных цепей мы знаем, что и. Мы также знаем, что сумма отдельных токов есть общий ток, т.е.
По правилам последовательного соединения мы знаем то и это. Все идет нормально.
Теперь мы можем использовать закон Ома, чтобы сделать вывод, что
И
Тогда общий ток равен
Мы снова используем закон Ома, чтобы узнать, каковы напряжения В 3 и В
И
Теперь мы успешно выразили неизвестные величины через известные величины, так что мы закончили! В процессе мы использовали правила как для последовательных, так и для параллельных схем, потому что эта схема представляет собой комбинацию этих двух.
Идентификация последовательных и параллельных цепей
Определить последовательную цепь довольно легко, потому что последовательные цепи имеют только один провод, по которому может проходить ток: в последовательных цепях нет дополнительных ответвлений.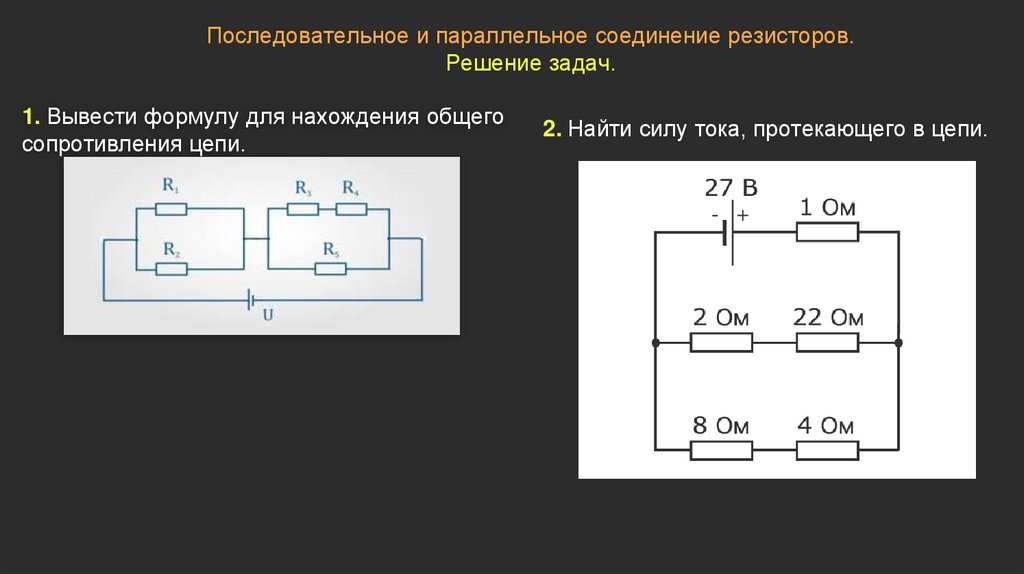 С другой стороны, параллельная цепь — это цепь, в которой все компоненты напрямую подключены к обеим сторонам источника напряжения. Трудности возникают, когда нам нужно идентифицировать компоненты в комбинированной схеме. Короче говоря, компоненты, соединенные последовательно, расположены встречно, а компоненты, соединенные параллельно, расположены бок о бок.
С другой стороны, параллельная цепь — это цепь, в которой все компоненты напрямую подключены к обеим сторонам источника напряжения. Трудности возникают, когда нам нужно идентифицировать компоненты в комбинированной схеме. Короче говоря, компоненты, соединенные последовательно, расположены встречно, а компоненты, соединенные параллельно, расположены бок о бок.
Мы можем рассматривать непрерывный кусок провода как узел : разные узлы разделены компонентами внутри цепи. Два компонента соединены параллельно, если (и только если) они имеют два общих узла, т. е. они соединены с одними и теми же двумя узлами.
Два компонента соединены последовательно, если (и только если) они имеют ровно один общий узел, который не разветвляется между двумя компонентами. Это хорошее упражнение — попытаться идентифицировать узлы на всех рисунках в этой статье. Вы можете сделать это, дав им имена или цвета. Тогда посмотрите, пришли ли вы к правильным выводам о том, как все компоненты связаны на основе этого метода! См.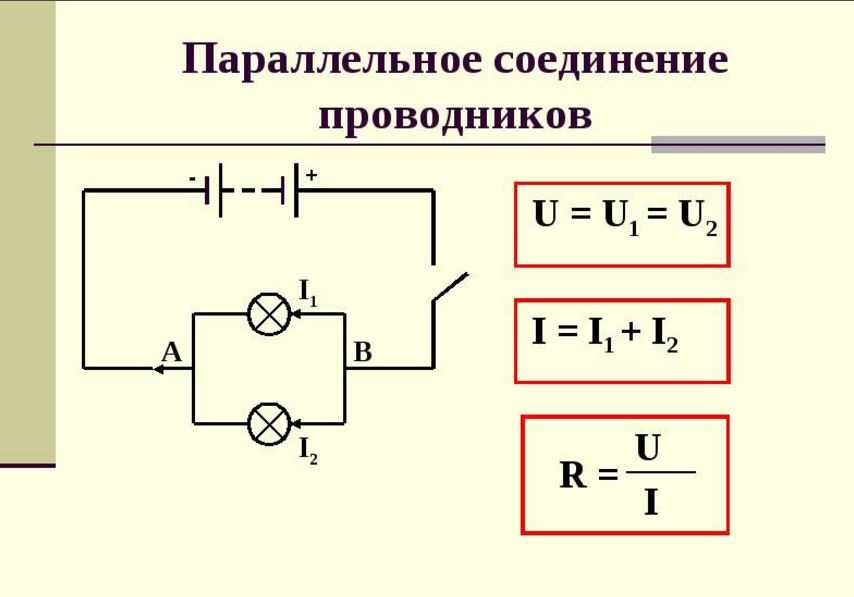 приведенный ниже пример реализации этого метода.
приведенный ниже пример реализации этого метода.
Оба резистора имеют общий синий и красный узел, поэтому они соединены параллельно, адаптировано из Paulgwilliamson, Wikimedia Commons CC BY-SA 4.0.
Использование последовательных и параллельных цепей
В общем, выбор между последовательными и параллельными цепями прост. Мы подключаем выключатель последовательно с лампой так, чтобы отключение тока в выключателе путем его щелчка также отключало ток через лампу. Мы также подключаем резистор последовательно с диодами, чтобы ток через диоды не был слишком большим, предотвращая перегрев диодов.
С другой стороны, мы подключаем фары в автомобилях параллельно, так что, если одна из ветвей цепи выходит из строя, другая ветвь все еще проводит ток. Таким образом, у вас все еще будет одна рабочая фара, если другая выйдет из строя: параллельное подключение добавляет фактор безопасности. Бытовые приборы тоже подключаем параллельно, чтобы они все были под одним напряжением.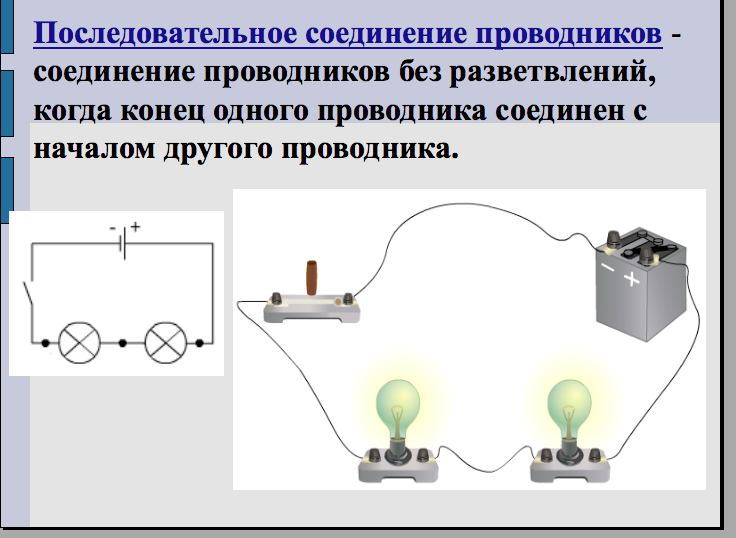 Имея выключатели, соединенные последовательно с отдельными приборами, мы можем управлять током через отдельные приборы. Если бы все приборы были соединены последовательно, нам пришлось бы выбирать между всем включенным и всем выключенным!
Имея выключатели, соединенные последовательно с отдельными приборами, мы можем управлять током через отдельные приборы. Если бы все приборы были соединены последовательно, нам пришлось бы выбирать между всем включенным и всем выключенным!
Последовательные и параллельные цепи — основные выводы
- Последовательное соединение состоит из компонентов, расположенных один за другим.
- Параллельное соединение имеет компоненты, параллельные друг другу.
- Правила последовательного соединения:
- Общее сопротивление всех резисторов равно сумме сопротивлений отдельных резисторов.
- Ток одинаков через все резисторы.
- Напряжение на резисторах пропорционально их сопротивлениям, а сумма отдельных напряжений составляет общее напряжение.
- Правила параллельного соединения:
- Общее сопротивление всех резисторов меньше, чем сопротивление отдельных резисторов, и определяется по формуле.
- Общий ток представляет собой сумму токов отдельных резисторов.

- Напряжение на всех резисторах одинаковое, а именно общее напряжение.
- Для выявления последовательных и параллельных соединений можно использовать метод узлов.
- Всякий раз, когда ситуация требует фактора безопасности, вы обычно видите параллельные соединения, как в бытовых приборах. Последовательные соединения используются для переключения и предотвращения перегрева компонентов.
Параллельные цепи постоянного тока — цепи постоянного тока
Цепи постоянного тока
Параллельная цепь определяется как цепь, имеющая более одного тока. путь, подключенный к общему источнику напряжения. Таким образом, параллельные цепи должны содержать два или более сопротивлений, не соединенных последовательно. Пример базовой параллельной схемы показан на рисунке ниже.
Пример базовой параллельной схемы.
Пуск от источника напряжения ( В с ) и обведите по часовой стрелке
схема. Можно выделить два полных и отдельных пути, в которых
ток может течь.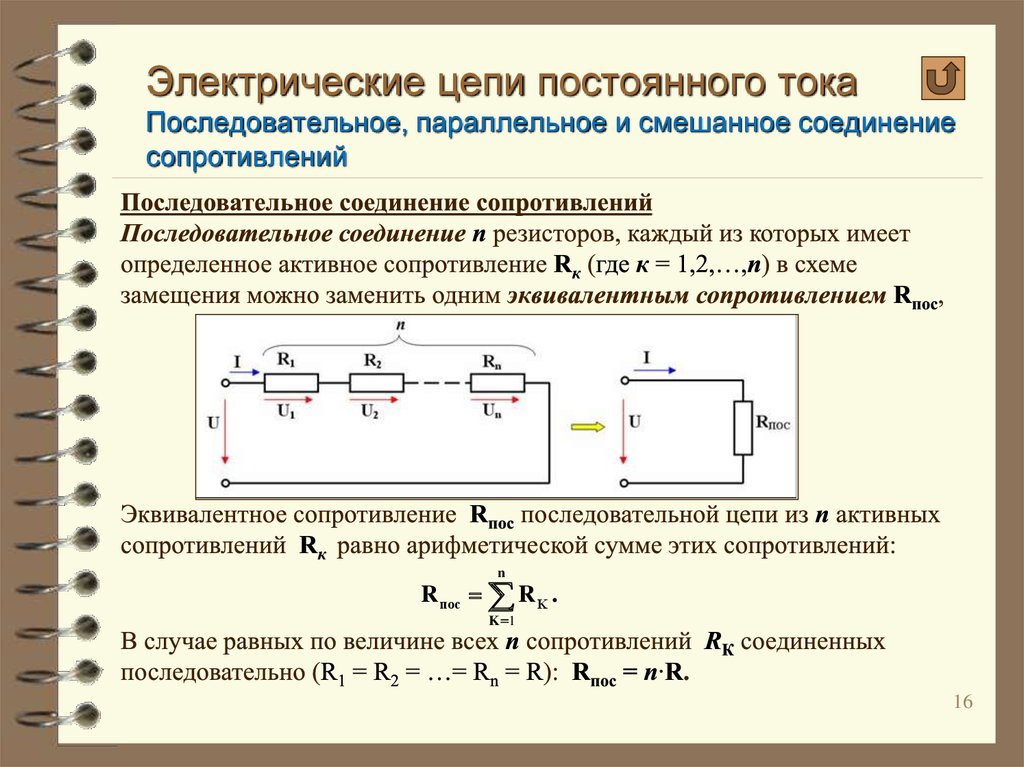 Прослеживается один путь от источника через сопротивление R 1 и обратно к первоисточнику. Другой путь – от
исток, через сопротивление R 2 , и обратно к истоку.
Прослеживается один путь от источника через сопротивление R 1 и обратно к первоисточнику. Другой путь – от
исток, через сопротивление R 2 , и обратно к истоку.
Напряжение в параллельной цепи
Вы видели, что напряжение источника в последовательной цепи делится на пропорционально каждому резистору в цепи. В параллельной цепи, одинаковое напряжение присутствует в каждой ветви. (Ветвь – это часть цепь, которая имеет полный путь для тока.) На рисунке выше это напряжение равно приложенному напряжению ( В с ). Это может быть выражено в виде уравнения:
Измерения напряжения на резисторах параллельной цепи, как показано на рисунке ниже, проверьте это уравнение. Каждый метр показывает одинаковая величина напряжения. Обратите внимание, что напряжение на каждом резистор соответствует приложенному напряжению.
Сравнение напряжения в параллельной цепи.
Пример: Предположим, что ток через резистор параллельной
цепи, как известно, составляет 4,5 мА, а значение резистора составляет 30 кОм. Определить напряжение источника. Схема показана на рисунке ниже.
Определить напряжение источника. Схема показана на рисунке ниже.
Пример проблемы с параллельным подключением.
Дано: R 2 = 30 кОм, I R2 = 4,5 мА
Найти: В R2 = ?, В с = ?
Решение: Выберите правильное уравнение:
Замените известные значения:
Так как напряжение источника равно напряжению ответвления:
Ток в параллельной цепи
Закон Ома гласит, что сила тока в цепи обратно пропорциональна сопротивление цепи. Этот факт справедлив как для последовательных, так и для параллельных цепей.
В последовательной цепи ток проходит по одному пути. Сумма текущих определяется полным сопротивлением цепи и приложенным напряжением. В параллельной цепи ток источника делится между доступные пути .
Поведение тока в параллельных цепях будет показано серией
иллюстрации на примерах цепей с разными значениями сопротивления
при заданном значении приложенного напряжения.
Анализ тока в параллельной цепи.
В части (A) рисунка выше показана базовая последовательная схема. Здесь общий ток должен проходить через единственный резистор. Величину тока можно определить.
Данный:
В с = 50 В, R 1 = 10 Ом
Решение:
Часть (B) рисунка выше показывает тот же резистор ( R 1 ) с второй резистор ( R 2 ) равного номинала, соединенный параллельно через источник напряжения. При применении закона Ома ток через каждый резистор оказывается таким же, как ток через одиночный резистор в части (A).
Данный:
В с = 50 В, R 1 = 10 Ом, R 2 = 10 Ом
Решение:
Очевидно, что если через каждую из двух цепей протекает ток силой 5 ампер. резисторов, должен быть общий ток 10 ампер, взятый из источник.
Общий ток 10 А, как показано на рисунке выше (часть B), оставляет
положительный полюс аккумулятора и течет к точке б .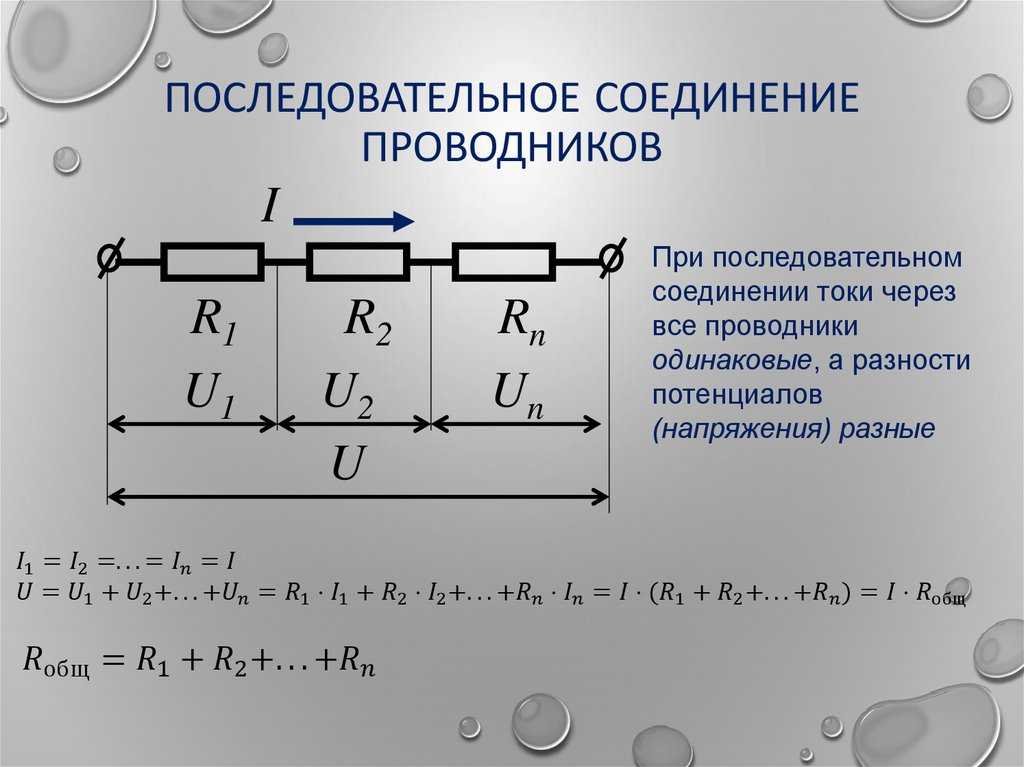 С точки b — это точка соединения двух резисторов, она называется развязка . На переходе b общий ток делится на два
токи по 5 ампер каждый. Эти два тока протекают через свои соответствующие
резисторы и соединиться на стыке и . Тогда полный ток течет от
соединение и обратно к отрицательной клемме источника. Источник
обеспечивает общий ток 10 А, и каждый из двух одинаковых резисторов несет
половина полного тока.
С точки b — это точка соединения двух резисторов, она называется развязка . На переходе b общий ток делится на два
токи по 5 ампер каждый. Эти два тока протекают через свои соответствующие
резисторы и соединиться на стыке и . Тогда полный ток течет от
соединение и обратно к отрицательной клемме источника. Источник
обеспечивает общий ток 10 А, и каждый из двух одинаковых резисторов несет
половина полного тока.
Каждый отдельный путь тока в цепи на рисунке выше (часть B) называется ветвью . Каждая ветвь несет ток, равный часть общего тока. Две или более ветвей образуют сеть .
Из предыдущего объяснения характеристики тока в параллельном цепь можно выразить с помощью следующего общего уравнения:
Сравните часть (A) рисунка ниже с частью (B) схемы на рисунке.
выше. Обратите внимание, что удвоение значения резистора второй ветви
( R 2 ) не влияет на ток в первом
ветвь ( I 1 ), но уменьшает ток второй ветви
( I 2 ) до половины первоначальной стоимости.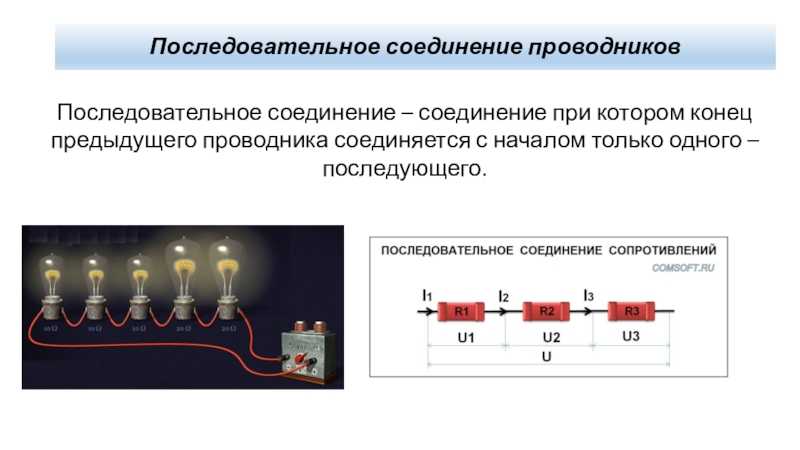 Общая схема
ток падает до значения, равного сумме токов ветвей. Эти
факты проверяются следующими уравнениями.
Общая схема
ток падает до значения, равного сумме токов ветвей. Эти
факты проверяются следующими уравнениями.
Поведение тока в параллельных цепях.
Данный:
В с = 50 В, Р 1 = 10 Ом, R 2 = 20 Ом
Решение:
Величина протекающего тока в ответвленных цепях и общий ток в схема, показанная на рисунке выше (часть B), определяются следующие вычисления.
Данный:
В с = 50 В, R 1 = 10 Ом, R 2 = 10 Ом, R 3 10111 Ом
Решение:
Обратите внимание, что сумма омических значений в каждой цепи, показанной на рисунке
выше равно (30 Ом), и что приложенное напряжение такое же (50 В).
Однако общий ток в части (B) (15 А) в два раза больше, чем в части (A).
(7,5 А). Таким образом, очевидно, что способ, которым резисторы
включенных в цепь, а также их действительные омические значения влияют на общее
Текущий.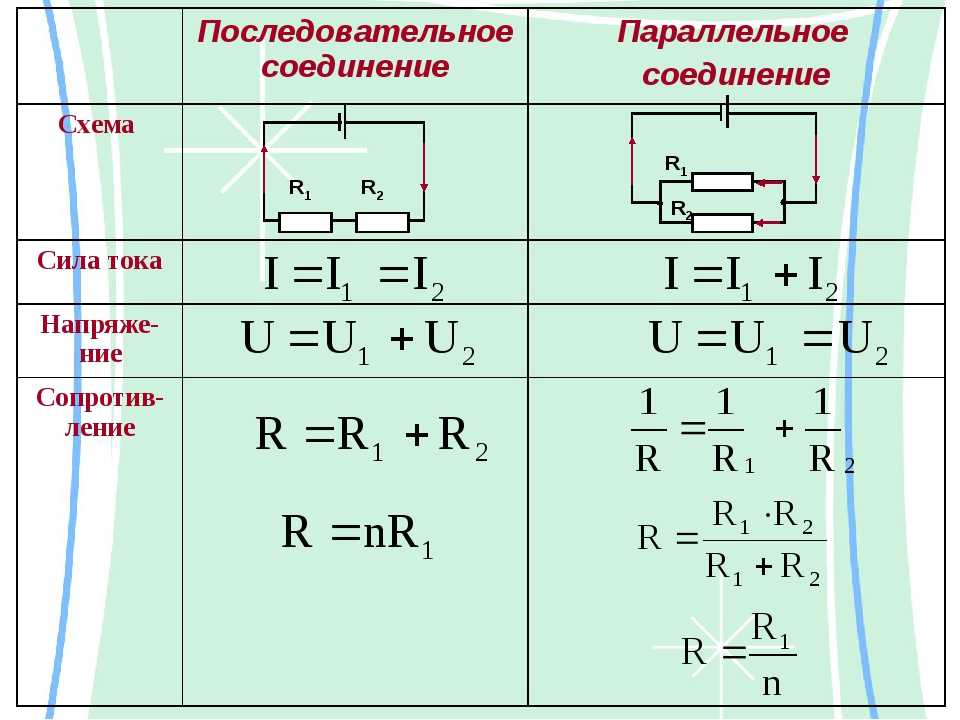
Разделение тока в параллельной сети происходит по определенной схеме. Эта закономерность описывается Действующий закон Кирхгофа.
Примеры параллельных цепей серии— Простой анализ — Wira Electrical
После изучения последовательной и параллельной цепей мы узнаем о примерах последовательно-параллельной цепи, цепи с комбинацией последовательной и параллельной цепей.
В реальных приложениях мы чаще всего находим последовательно-параллельную цепь вместо последовательной или параллельной цепи. Мы можем найти чисто последовательную или параллельную схему, но в нашей жизни в основном это будет комбинация последовательной и параллельной цепи, или мы называем их последовательно-параллельными цепями.
Не волнуйтесь, это не сильно отличается от последовательной или параллельной цепи. Нам нужно только использовать другой подход, чтобы решить эту схему.
Мы должны решить схему для каждой группы параллельных резисторов, чтобы сделать полностью последовательную цепь, а затем решить ее.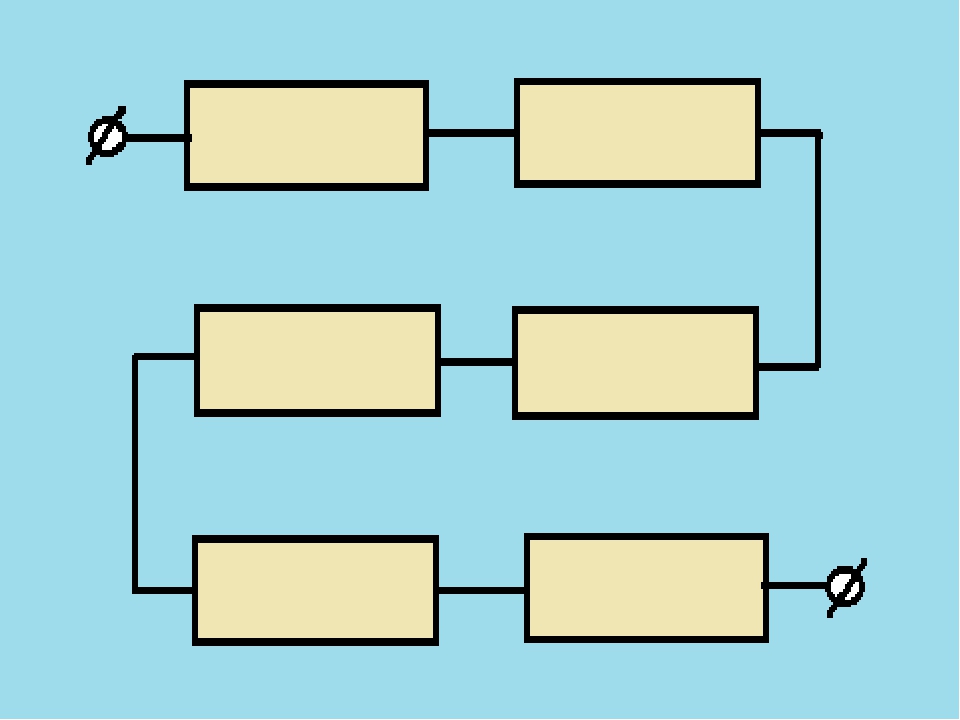 Просто так.
Просто так.
Или мы можем сделать это быстрее, если разложим все последовательные резисторы на эквивалентные последовательные сопротивления. Затем разложите все параллельные резисторы на эквивалентные параллельные сопротивления. Последним шагом является преобразование этих эквивалентных сопротивлений в эквивалентное общее сопротивление.
Со следующего пункта и до самого конца мы узнаем все о том, как работает последовательно-параллельная схема.
Анализ последовательно-параллельной цепиРассмотрим простую последовательно-параллельную цепь ниже.
В приведенной выше схеме мы видим, что у нас есть источник напряжения с 4 резисторами R 1 , R 2 , R 3 и R 4 в последовательно-параллельной комбинации. Резисторы R 1 и R 4 соединены последовательно, а резисторы R 2 и R 3 соединены параллельно.
Перед вычислением общего тока, протекающего в цепи, мы должны найти эквивалентное сопротивление этих четырех резисторов.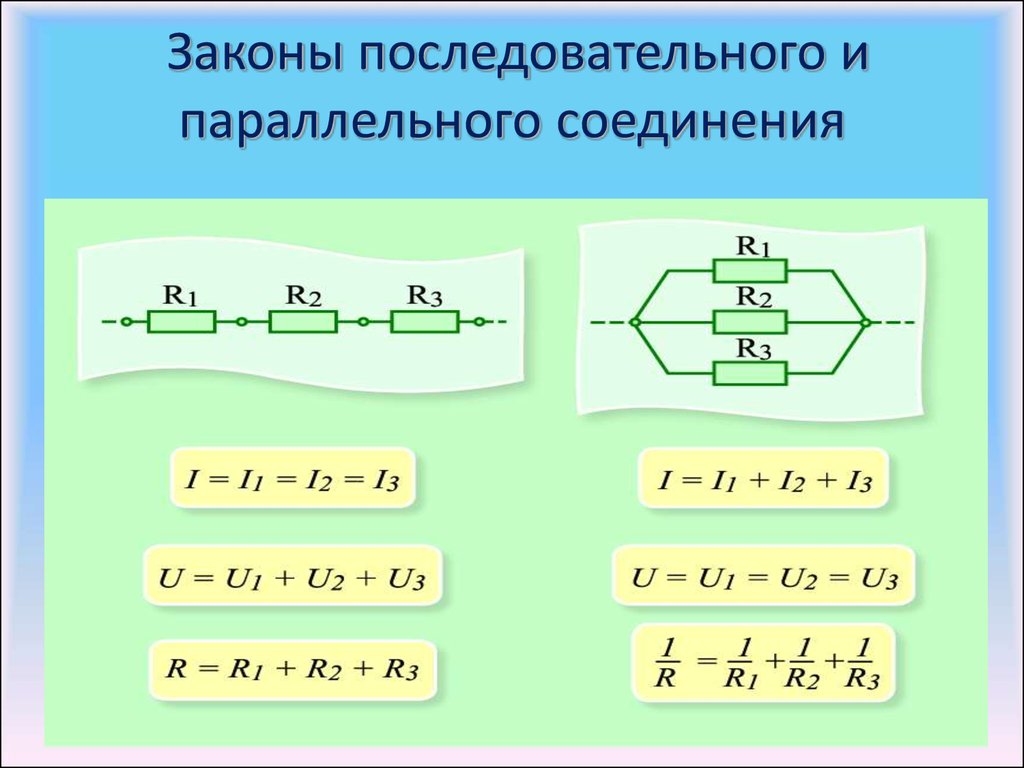
Мы будем использовать эту схему для решения одного из комбинированных примеров последовательной и параллельной цепей. Мы можем использовать два разных подхода, чтобы найти общее сопротивление в этой цепи.
Первый метод , мы решим последовательные резисторы, чтобы получить эквивалентный последовательный резистор (R S ) и параллельные резисторы, чтобы получить эквивалентный параллельный резистор (R P ) отдельно. После этого мы решим эквивалентный резистор (R eq ) для R S и R P , соединенных последовательно.
Найдите эквивалентный серийный резистор, R S :
Найдите эквивалентный параллельный резистор, R P :
Найти эквивалент
, если шаги выше, все еще длинные. мы можем использовать другой подход.
Второй метод , мы составляем одно уравнение, состоящее из всех резисторов сразу. Мы пишем их в порядке от положительной полярности к отрицательной полярности. Таким образом, мы решим схему за один раз.
Таким образом, мы решим схему за один раз.
Наконец, мы можем записать формулу последовательно-параллельной цепи из приведенной выше схемы.
Как анализировать последовательно-параллельную цепьТеперь приступим к анализу последовательно-параллельной цепи. Это будет отличаться от простого примера выше, потому что мы будем анализировать цепь на ее эквивалентное сопротивление, падение напряжения, протекающий ток и многое другое.
Обратите внимание на схему ниже.
Здесь у нас есть один резистор последовательно с источником напряжения и пара параллельных резисторов.
Серийное параллельное эквивалентное сопротивлениеПрежде всего, мы должны найти эквивалентное сопротивление цепи. Мы будем использовать второй метод, одно уравнение, состоящее из последовательно включенных резисторов.
Таким образом, общий ток, протекающий в цепи, равен
Падение напряжения в последовательной параллельной цепи
Теперь приступим к расчету падения напряжения для каждого резистора.
Имейте в виду, что:
- Падение напряжения при последовательном соединении имеет разные значения на каждом резисторе.
- Падение напряжения при параллельном соединении имеет одинаковые значения на каждом резисторе.
Падение напряжения на R 1 (V R1 )
Падение напряжения на R 2 и R 3 эквивалентны падению напряжения на эквивалентном параллельном резисторе (R P ) R 2 и R 3 .
Таким образом, мы также доказываем закон Кирхгофа о напряжении, согласно которому алгебраическая сумма падения напряжения в замкнутой цепи равна нулю.
Тогда падение напряжения на R 2 и R 3 равно 4 В.0010
Далее мы рассчитаем ток, протекающий в цепи.
Имейте в виду, что:
- Ток при последовательном соединении будет иметь постоянное значение через каждый элемент.

- Ток при параллельном соединении будет иметь разные значения в зависимости от сопротивления в каждой ветви.
Поскольку R 1 включен последовательно с источником напряжения, ток (I 1 ) через него равен полному току,
Теперь нам нужно выполнить некоторые математические действия, чтобы определить ток через R 2 и R 3 . Из приведенного выше результата падение напряжения на параллельном резисторе составляет 4 В, поэтому мы будем использовать его вместе с законом Ома для определения его тока.
для I 2 ,
для I 3 ,
Общий ток, поступающий в ветви R 2 , а R 3 — I = 2a, и он разделен на 4// 3 А через левую ветвь и 2/3А через правую ветвь.
Ток, выходящий из ветви, равен
Это доказывает закон Кирхгофа о токах, который гласит, что ток, входящий в узел, равен току, выходящему из узла. Или, другими словами, алгебраическая сумма токов, входящих и исходящих из узла, равна нулю.
Или, другими словами, алгебраическая сумма токов, входящих и исходящих из узла, равна нулю.
Теперь попробуем сделать разомкнутое соединение в последовательно-параллельном соединении. Мы будем использовать ту же схему, что и выше, но мы дадим разомкнутую клемму последовательно с R 9.0117 1 .
Открытый вывод имеет бесконечное сопротивление. Поскольку он соединен последовательно, то эквивалентное полное сопротивление в цепи бесконечно. Таким образом, общий ток (I) равен нулю, и мы не получим никакого падения напряжения, поскольку в остальной части цепи ток не течет.
Затем мы подключаем открытый терминал параллельно с R 2 и R 3 , как показано ниже.
Поскольку через него не будет протекать ток, его можно игнорировать. Для него падение напряжения будет равно падению напряжения на R 2 и R 3 , так как они параллельны.
В отличие от разомкнутой цепи, в большинстве случаев короткое замыкание может повредить цепь и все, что к ней подключено. Сначала делаем короткое замыкание параллельно R1.
Возможно, вы знаете, что электрический ток, скорее всего, выберет путь с наименьшим сопротивлением или импедансом. Таким образом, чем меньше сопротивление, тем больше ток проходит через него. В идеальном состоянии короткое замыкание имеет нулевое сопротивление, поэтому ток, протекающий в ответвлении с нулевым сопротивлением, максимален (бесконечен).
Расчет эквивалентного сопротивления (Rs) для R1 и короткого замыкания параллельно,
Мы можем перерисовать схему в
Поскольку Rs имеет нулевое сопротивление, мы можем заменить его одножильным проводом. Расчет перерисованной схемы такой же простой, как и раньше.
А что если подключить КЗ параллельно R2 и R3?
Эквивалентное сопротивление параллельных резисторов (Rp) равно нулю.
Короткая история, мы можем перерисовать схему ниже.
Примеры расчетов последовательной параллельной цепиДавайте выполним несколько упражнений, чтобы лучше понять.
1. Изучите приведенную ниже схему и найдите эквивалентные сопротивления, падения напряжения и токи.
Мы можем рассчитать эквивалентное сопротивление в одном уравнении, но мы будем рассчитывать каждое параллельное соединение отдельно, потому что нам нужны их соответствующие значения для расчета падения напряжения и тока.
Эквивалентное сопротивление для первых параллельных резисторов:
Эквивалентное сопротивление для второго параллельных резисторов:
Общее эквивалентное сопротивление составляет
Общее ток в цепи:
9000
We можно перерисовать схему на
Падение напряжения на R P1 равно
Падение напряжения на R P2 это
Это доказывает, что
Далее мы рассчитаем токи через каждый резистор.
For I 1 ,
For I 2 ,
For I 3 ,
For I 4 ,
This proves that
2. Изучите приведенную ниже схему и определите эквивалентное сопротивление, падение напряжения и ток.
Эквивалентное сопротивление для параллельных резисторов составляет
Общее эквивалентное сопротивление в цепи составляет
Общее ток в цепи
V RP ) равно
Падение напряжения на R 3 равно
Ток, протекающий через R 1 IS
Ток, протекающий через R 2 ,
Провод, проходящий через R 3 —
серии «Примеры параллельной серии» в реальной жизни, если вы удивляетесь серии «Синг.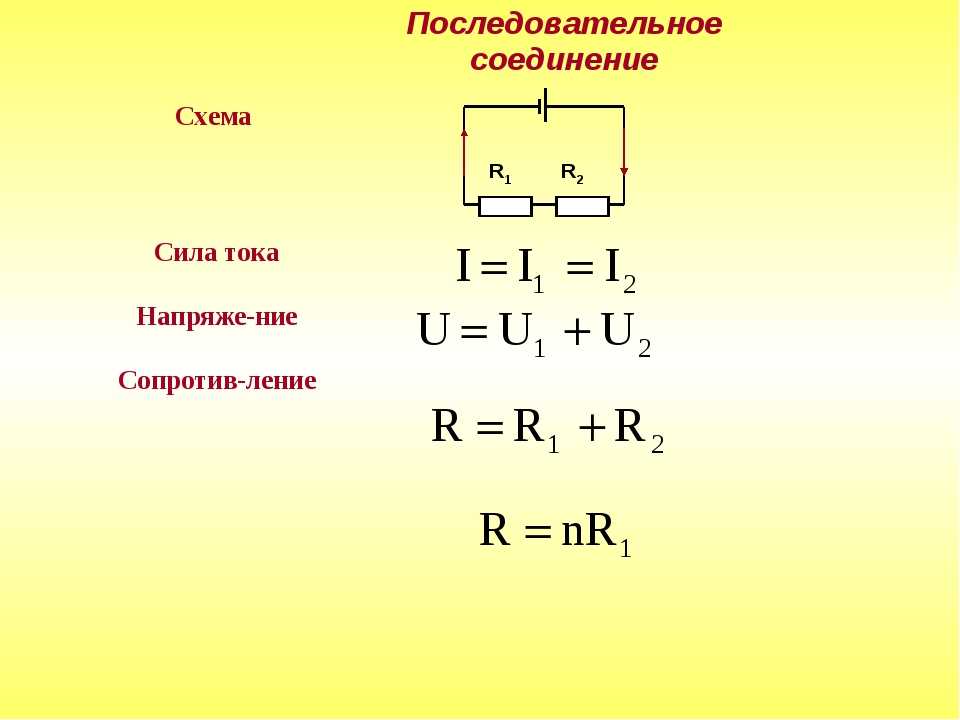 где мы найдем пример последовательно-параллельных цепей в нашей жизни», они уже близки вам. Самый распространенный ответ, который вы найдете, это электрические розетки в вашем доме.
где мы найдем пример последовательно-параллельных цепей в нашей жизни», они уже близки вам. Самый распространенный ответ, который вы найдете, это электрические розетки в вашем доме.
Когда вы выключаете лампу, отсоединяете электронное устройство от розетки или ваша розетка ни к чему не подключена, они не будут мешать другим розеткам. Ваше электронное устройство по-прежнему будет работать нормально и безопасно.
Для последовательной цепи одним из примеров из реальной жизни является гирлянда на рождественской елке. Этот набор световых последовательностей соединен последовательно. Другая последовательная цепь — это соединение между источником питания, выключателем и лампочкой. Они соединены последовательно, чтобы вы могли включать или выключать их с помощью переключателя.
В чем разница между последовательными и параллельными цепями?
Топология цепей — увлекательное и удивительно доступное семейство концепций. Сегодня мы собираемся изучить разницу между последовательными и параллельными схемами.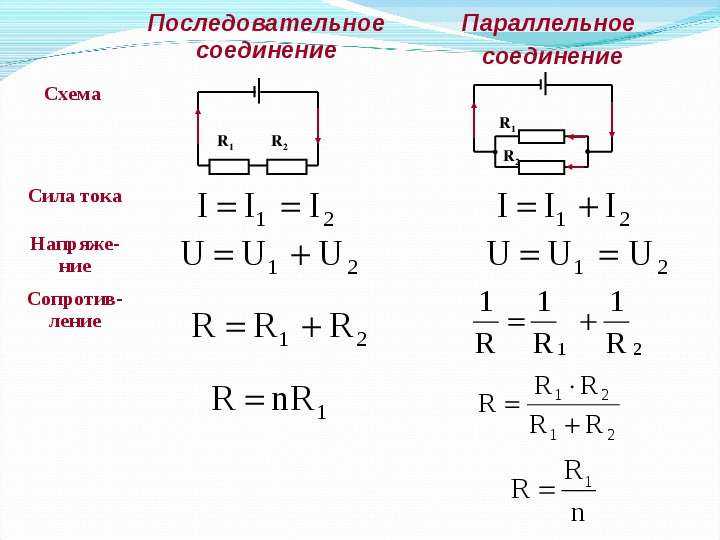
Что такое последовательная цепь? Кроме того, что такое параллельная схема? Даже если вы понятия не имеете, мы уже можем сказать вам, что вы, вероятно, используете оба типа схем каждый день своей жизни.
Понимание разницы между последовательной и параллельной схемой: определение и основные понятия
Проще говоря: последовательная цепь предлагает ток электричества один идеальный путь через лабиринт. Параллельные цепи , с другой стороны, сконфигурированы таким образом, что имеется два или более путей через цепь для прохождения тока. Эти типы цепей считаются «параллельными», потому что путь разветвления тока проходит параллельно самому себе, поскольку он проходит через обе петли одновременно.
Поведение тока в параллельной цепи, когда он проходит через цепь, во многом определяется тем фактом, что электрический ток будет искать области с самым низким напряжением в данной системе, занимая эти области любым возможным способом.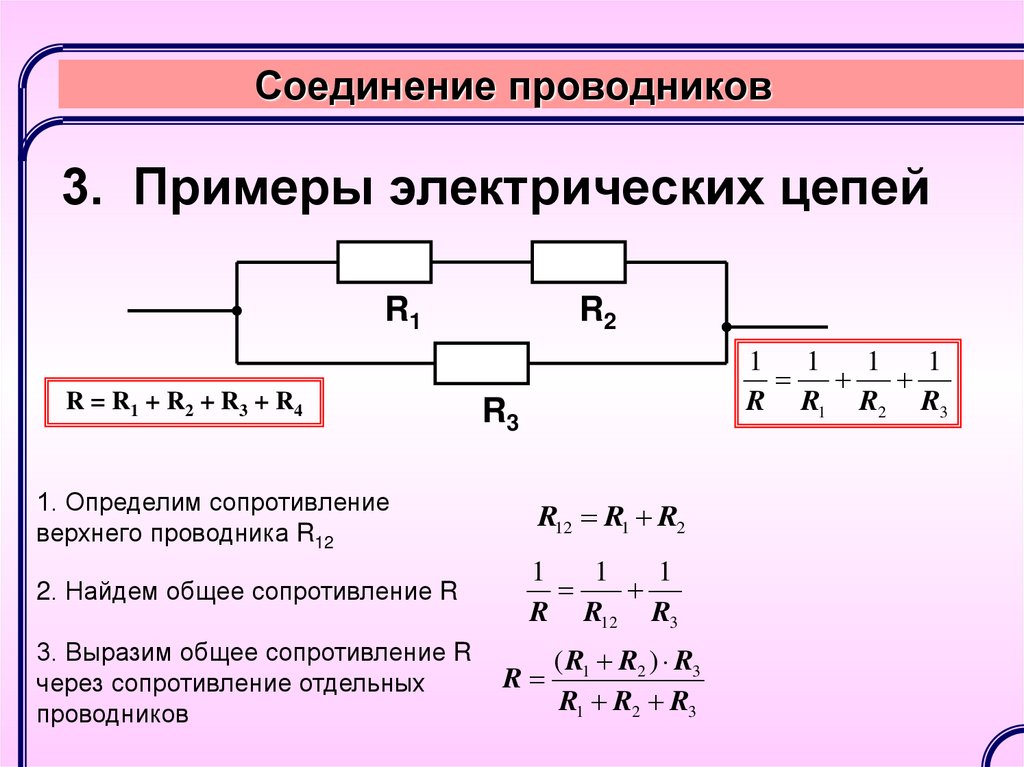
Это не совсем так просто, но вы будете рады узнать, что здесь задействовано всего несколько других правил. Что именно определяет путь наименьшего сопротивления тока?
Связанный: Как проверить напряжение с помощью мультиметра
Серияпротив параллельных цепей: что здесь происходит в Толедо?
Чтобы визуализировать это явление, мы собираемся назвать несколько ключевых словарных слов, о которых следует помнить:
- Ток : Электроэнергия, полученная от источника и переданная по трубопроводу.
- Источник : Откуда поступает электричество? Батарея? Вспышка молнии?
- Трубопровод : Все, что обладает достаточной проводимостью для подачи электричества от источника. Медный провод внутри зарядного кабеля вашего смартфона является одним из примеров электрического канала, который ведет ток от вашего компьютера или зарядного устройства к аккумулятору, нуждающемуся в зарядке.
- Замкнутая цепь : Замкнутая электрическая сеть, в которой ток имеет прямой путь обратно к источнику, образуя полный, непрерывный и неразрывный контур.

- Напряжение : Мера потенциальной энергии на единицу при сравнении любых двух точек в цепи. Это механизм, с помощью которого ток проходит через цепь; избыточное напряжение в одной части системы перетекает в точки с более низким напряжением, постоянно стремясь к равновесию.
- Сопротивление : Любой фактор, препятствующий компенсации напряжения и потоку. Силикон является одним из примеров высокопрочного изоляционного материала, который обычно используется в электронике. Стойкий материал используется для направления потока электричества по всей цепи и предотвращения его выхода из канала.
При визуализации электрического тока мы имеем дело с переносом электронов от атома к атому по проводнику. Объект становится положительно или отрицательно заряженным, когда вокруг него висит больше электронов, чем протонов, которые не покидают атом по своей воле.
Электроны — валюта электричества. Этот перенос электронов является неотъемлемой частью того, как ток передается каждым атомом канала.
Как электроны проходят через последовательные и параллельные цепи?
Думайте обо всех этих электронах, едущих по рельсам трубопровода, как будто они крошечные автомобили, едущие по миниатюрной супермагистрали.
В замкнутой замкнутой цепи электричество следует по своему каналу туда, где оно в конечном итоге «утонет», то есть в точке наименьшего напряжения, доступного для тока, месте, куда оно физически чувствует себя наиболее вынужденным идти. Электричество проходит через замкнутую систему аккуратно и непрерывно, его общее сохраняющееся напряжение естественным образом распределяется по системе, принимая определенное квантовое состояние.
В параллельном контуре, вместо того, чтобы снова и снова путешествовать по этому единственному, петлевому пути, есть «въезды» и «выезды», точки доступа, предлагающие текущему альтернативный живописный маршрут через два или более параллельные ветви. Простое закольцованное состояние теперь по-разному распределяется по цепи.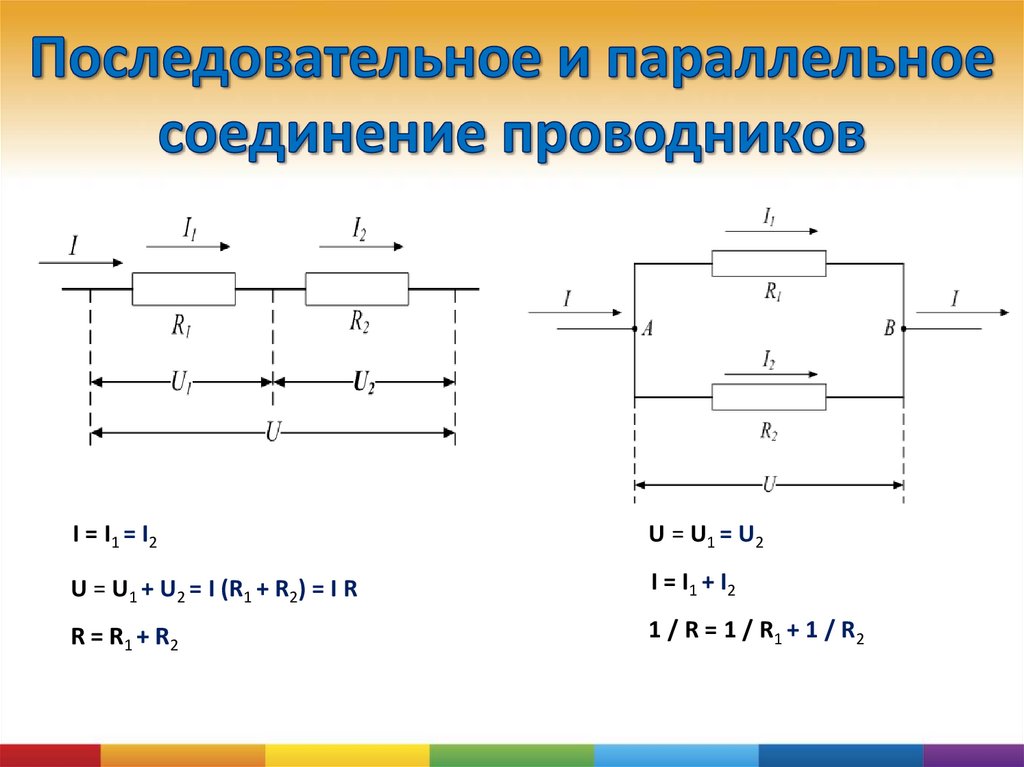
Связанный: Идеи проекта DIY Electronics для студентов инженерных специальностей
Параллельное напряжение: законы Кирхгофа
Мы видели параллельные контуры, которые до некоторой степени напоминают разветвляющиеся кровеносные сосуды. Вся сеть поддерживает кровоток через каждую вену и капилляр, достигая каждого уголка тела, к которому подключена система.
Немецкий физик Густав Кирхгоф был одним из первых, кто математически формализовал анализ цепей. Он смог упростить поведение электричества в цепи, используя два физических закона, которые идут рука об руку.
Ток, протекающий по любой цепи, физически подчиняется этим законам, несмотря ни на что:
- Энергия, втекающая в узел или пересечение ответвляющейся цепи, во многом равна энергии, вытекающей из нее, что позволяет сохранить общий заряд системы.
- Общая сумма результирующих электрических разностей потенциалов по всей системе должна равняться нулю. Компоненты питания, такие как аккумуляторные батареи, вносят свой вклад в эту сумму, питая компоненты, потребляющие энергию, такие как резисторы или приборы, такие как лампочки.

Оба они проясняют, что именно управляет поведением тока в той или иной цепи. Однако этот второй пункт особенно интересен.
По сути, этот второй закон утверждает, что каждый электрон, проходящий через цепь, должен получить ровно столько энергии, сколько он теряет по пути. Если какое-либо требование не выполняется, рассматриваемый путь не является жизнеспособным путем для естественного протекания тока.
Связанный: Малобюджетные проекты электроники DIY для начинающих
Примеры последовательных и параллельных цепей
Наиболее распространенный пример параллельного и последовательного напряжения: рождественские гирлянды. В частности, современные струны против винтажных ламп.
Первоначально рождественские огни были соединены последовательно, односторонней гирляндой из лампочек; при выходе из строя одной лампочки гаснет все, и до перегоревшей лампочки, и после. Цепь теперь разомкнута и фактически разорвана.
Это прискорбное положение дел, но не позволяйте этому первому примеру испортить вам последовательные цепи.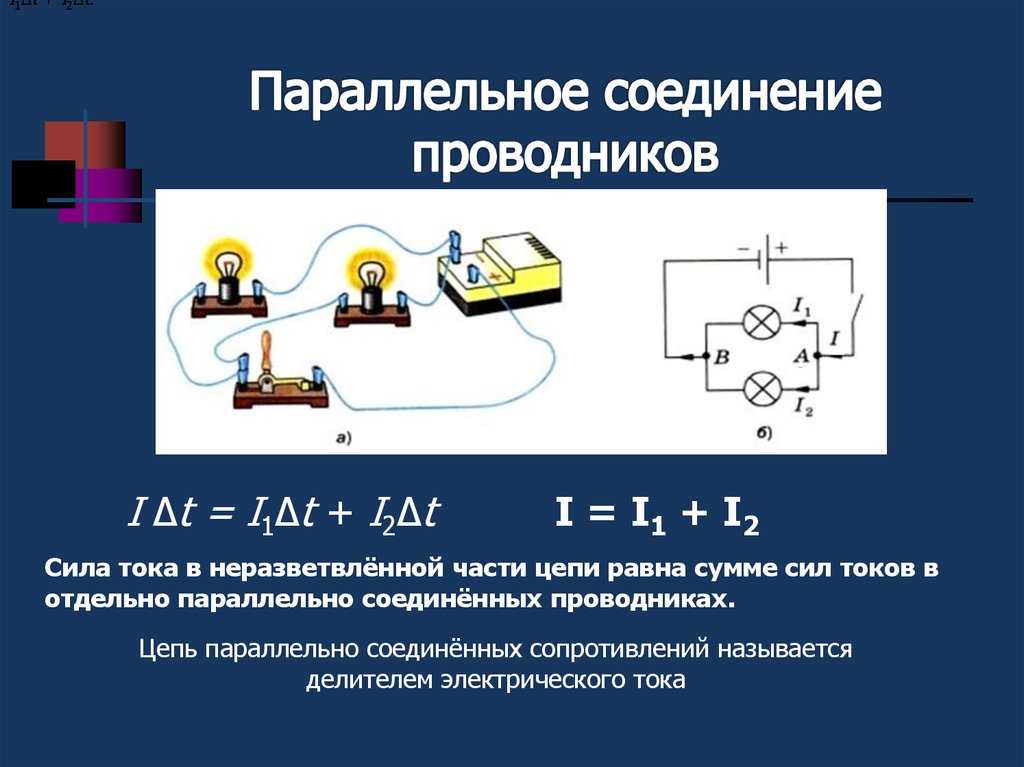 Есть еще много обстоятельств, когда последовательные цепи действительно являются подходящим типом цепи для выбора:
Есть еще много обстоятельств, когда последовательные цепи действительно являются подходящим типом цепи для выбора:
- Простые приспособления, управляющие только одним прибором — например, маленькие светодиоды в некоторых игрушках
- Фонарик или любое другое простое устройство, приводимое в действие нажатием выключателя
- Предохранитель, защищающий большой прибор, такой как стиральная машина, от перегрузки по току; они соединены в последовательную цепь, поэтому после срабатывания предохранителя цепь прерывается
Напротив, параллельные цепи рассчитаны на то, чтобы оставаться в работе при любых условиях. Современные рождественские огни используют параллельную цепь, чтобы предотвратить, например, вышеупомянутую досадную праздничную катастрофу. Даже если останется только одна лампочка, она все равно сможет светить.
Другие распространенные примеры параллельных цепей включают следующее:
- Автомобильные фары подключены параллельно, так что одна сторона остается работоспособной, даже если другая сторона выйдет из строя
- Коммерческие акустические системы используют параллельные цепи по той же причине
- Уличные фонари используют параллельное напряжение, чтобы обеспечить освещение большей части улицы
Ни параллельные, ни последовательные схемы не следует рассматривать как «лучше» или «хуже» друг друга — обе невероятно полезны по-своему в разных обстоятельствах. Если вы знаете, что вам нужно сделать с проектируемой схемой, сторона забора, к которой вы принадлежите, должна быть совершенно очевидной.
Если вы знаете, что вам нужно сделать с проектируемой схемой, сторона забора, к которой вы принадлежите, должна быть совершенно очевидной.
Связанный: что такое мультиметр и где его можно использовать?
Основы цепей: параллельные и последовательные схемы и почему важны обе схемы
Электричество опасно. Понимание того, как работают схемы, — это один из способов обезопасить себя, независимо от того, во что вы ввязываетесь.
Хорошие новости: если вы сможете понять эти и другие концепции в этой области, вы будете вооружены и готовы ко всему, что вам нужно знать, чтобы ваш проект не поджарил ваше тело заживо. как куриный наггетс. Возьмите это у того, кто был там.
Серияпротив параллельного | Сравнение последовательных и параллельных цепей
Существует три основных типа электрических цепей: последовательные, параллельные и комбинированные. Понимание этих схемных конфигураций поможет вам в анализе цепей, и с помощью нескольких основных правил вы сможете легко рассчитать ток и напряжение каждого компонента.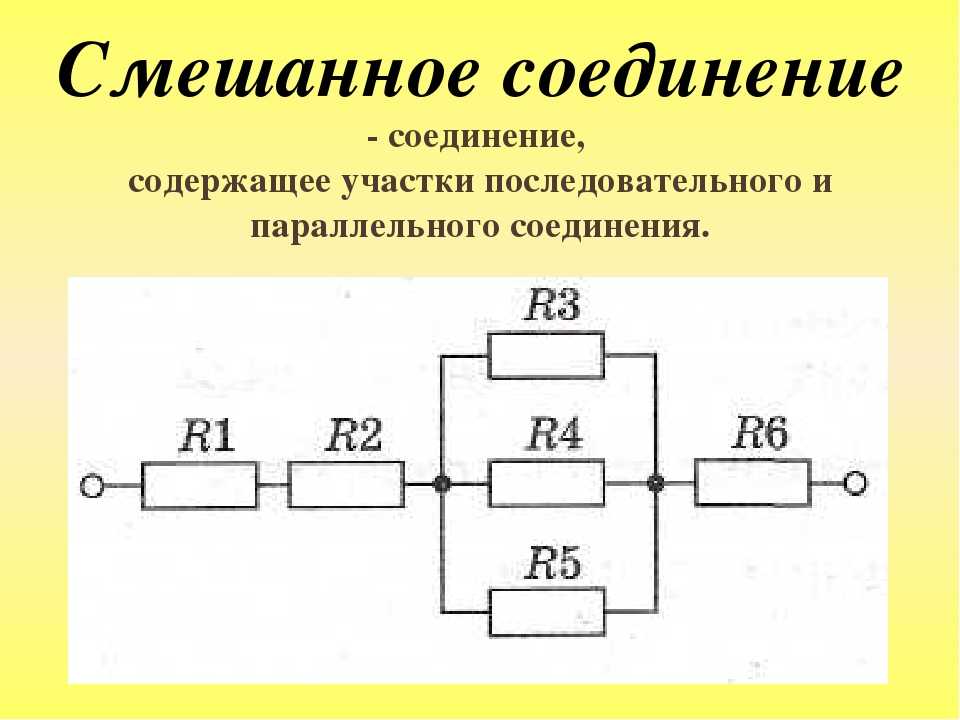 Итак, в этом руководстве давайте более подробно рассмотрим основы последовательной и параллельной цепей, сравним серию с параллельной, а также перечислим некоторые области применения последовательной и параллельной цепей.
Итак, в этом руководстве давайте более подробно рассмотрим основы последовательной и параллельной цепей, сравним серию с параллельной, а также перечислим некоторые области применения последовательной и параллельной цепей.
Краткое описание
Что такое последовательная цепь?
Простая цепь постоянного тока состоит из замкнутого пути, по которому течет постоянный ток. Простейшим источником постоянного тока является батарея, и если мы подключим небольшую лампу к клеммам батареи, то получится простая цепь постоянного тока.
Но практические схемы состоят из большего количества компонентов, чем одна лампа. Если цепь состоит из более чем одного компонента и если все они соединены встык, так что через них протекает один и тот же ток, то такая цепь называется последовательной цепью.
Если мы возьмем в качестве примера простейший электрический компонент, т. е. резистор, то следующая схема показывает три резистора, соединенных последовательно с источником напряжения. В последовательной цепи ток может течь только одним путем.
В последовательной цепи ток может течь только одним путем.
Изображение
Поскольку ток во всех резисторах одинаков, мы можем легко рассчитать напряжение на отдельных резисторах, используя закон Ома.
Если V — напряжение питания, I — ток в цепи, R 1 , R 2 , R 3 — сопротивления, а V R1 , V R2 и V R3 — напряжения на соответствующих резисторах, тогда применяя закон Ома, получаем.
V R1 = I x R 1 , V R2 = I x R 2 and V R3 = I x R 3
V = V R1 + V R2 + V R3 = IR 1 + IR 2 + IR 3
Если R — полное сопротивление цепи, то V = IR и, следовательно,
IR = IR 1 + IR 2 + IR 3
R = R 1 + R 2 + R 3
. СОСТОЯНИЕ к сумме индивидуальных сопротивлений.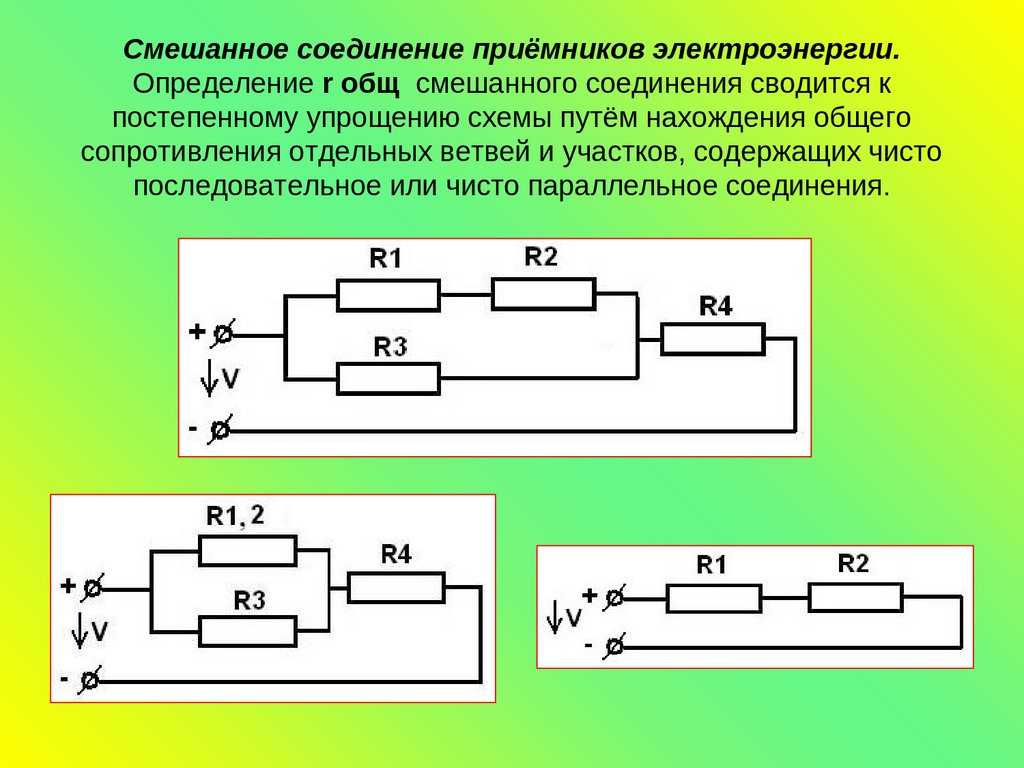
Делитель напряжения
Из приведенного выше объяснения последовательной схемы вы могли заметить интересный момент, касающийся напряжений на отдельных резисторах. Давайте упростим это обсуждение, рассмотрев всего два последовательно соединенных резистора.
Image
Здесь V — напряжение питания, R 1 и R 2 — резисторы, а V R1 и V R2 — напряжения на R 1 и R 2 соответственно.
из закона о Ом
V = IR = V R1 + V R2 = IR 1 + IR 2
, если мы рассчитываем напряжение через R 2 , мы получим
vrestage через R 2 ,
VS. R2 = V * R 2 / (R 1 + R 2 )
Напряжение на R 2 является частью входного напряжения. Это известно как схема делителя напряжения или схема делителя потенциала.
Закон Кирхгофа Закон о напряжении (KVL)
Из предыдущей серии Цепь, состоящая из трех резисторов, мы установили, что напряжение источника равно сумме напряжений на отдельных резисторах.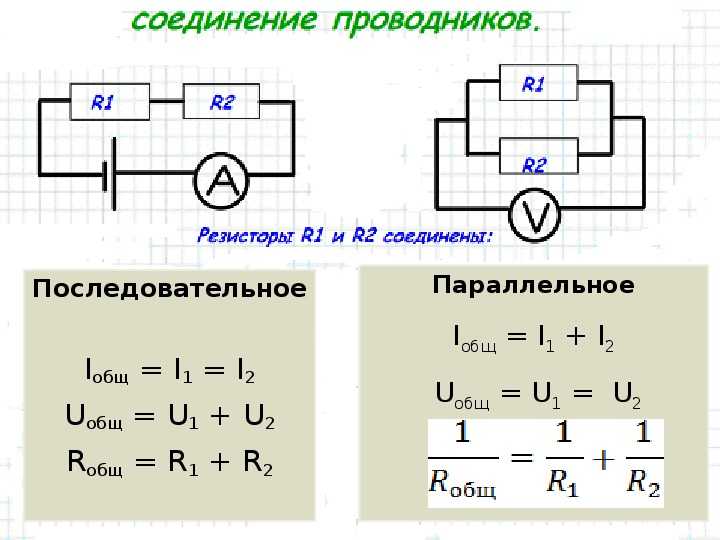
В = В R1 + В R2 + V R3
Преобразовывая это уравнение, мы получаем закон Кирхгофа для напряжения.
В – В R1 – В R2 – В R3 = 0
Согласно Закону Кирхгофа о напряжениях (KVL), алгебраическая сумма напряжений в замкнутом контуре равна нулю.
Применение последовательной схемы
Одним из самых известных применений последовательной схемы являются наши праздничные огни серии. Во время Рождества и праздников мы украшаем наши дома разноцветными огнями, состоящими из нескольких последовательно соединенных ламп.
Image
Основная проблема праздничных светильников этой серии заключается в том, что даже если одна лампочка перегорает, это прерывает подачу тока, и вся серия не загорается.
Что такое параллельная цепь?
В последовательной цепи есть только один путь прохождения тока. При переходе к параллельной цепи будет более одного пути для протекания тока.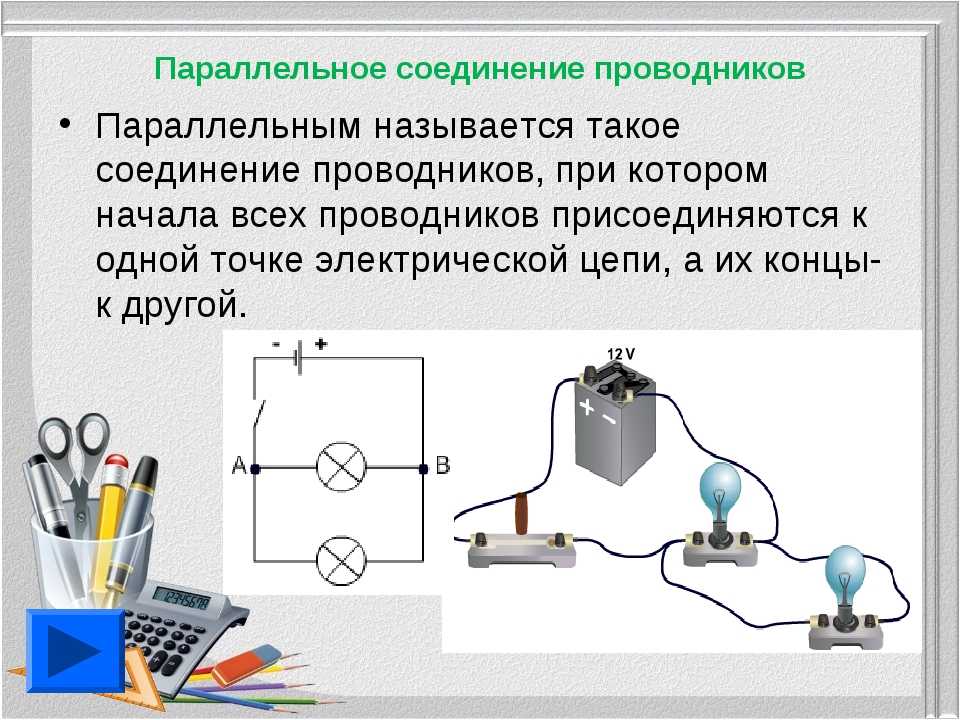 Если еще раз взять три резистора, то на следующих изображениях показаны разные конфигурации трех элементов схемы, соединенных параллельно.
Если еще раз взять три резистора, то на следующих изображениях показаны разные конфигурации трех элементов схемы, соединенных параллельно.
Изображение
Схемы на изображении выше могут выглядеть по-разному, но на самом деле они одинаковы. Если присмотреться, то один конец всех элементов схемы (в данном случае резисторов) общий, а другой конец тоже. Итак, параллельная цепь из двух элементов состоит из двух общих точек.
Чтобы больше узнать о параллельных цепях, рассмотрим следующую схему, в которой у нас есть три резистора, подключенных параллельно к источнику напряжения. Поскольку все три резистора подключены к источнику напряжения, напряжение на всех резисторах одинаково.
Изображение
Но то же самое нельзя сказать о токе, поскольку он имеет несколько путей для протекания. Если I — общий ток, а I R1 , I R2 и I R3 — токи, протекающие через соответствующие резисторы, то общий ток равен сумме отдельных токов.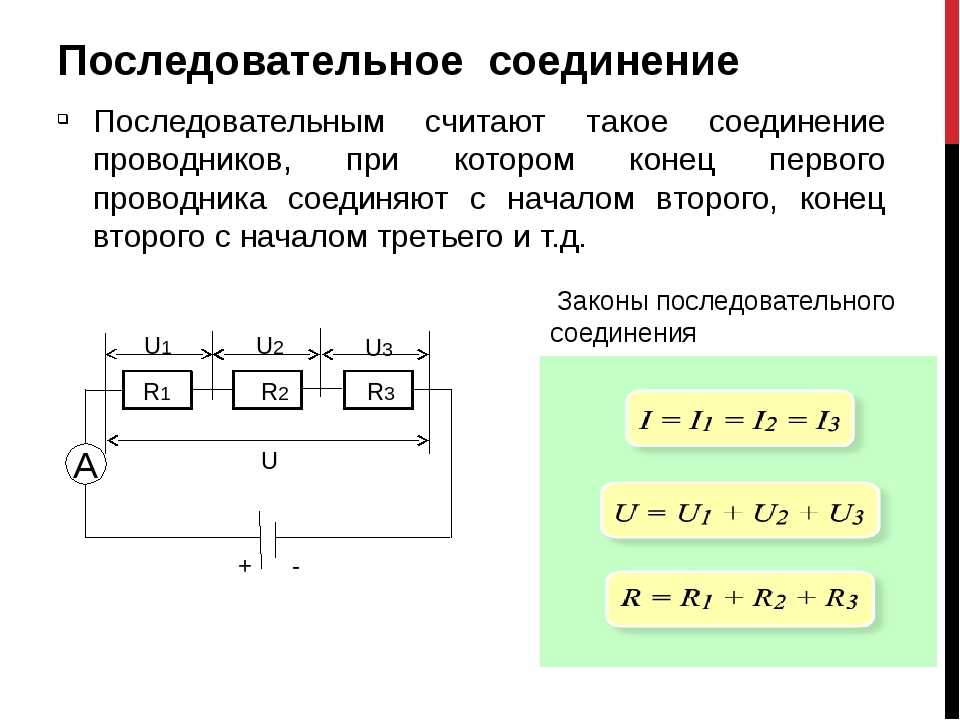
I = I R1 + I R2 + I R3
Применяя закон Ома , получаем I R1 = I / R
8 1 9011 = V / R 2 и I R3 = V / R 3Если R — общее сопротивление цепи, I = V / R. Используя все это в приведенном выше уравнении, мы получаем
V / R = V / R 1 + V / R 2 + V / R 3
Итак, 1/R = 1/R 1 + 1/R 2 + 1/R 3
Для параллельно соединенных резисторов обратная величина общего сопротивления равна сумме обратных величин отдельных сопротивлений.
Кирхгоф Текущий закон (KCL)
Из приведенного выше обсуждения мы получаем общий ток в цепи как сумму отдельных токов в соответствующих резисторах.
I = I R1 + I R2 + I R3
Мы можем изменить приведенное выше уравнение и получить закон тока Кирхгофа.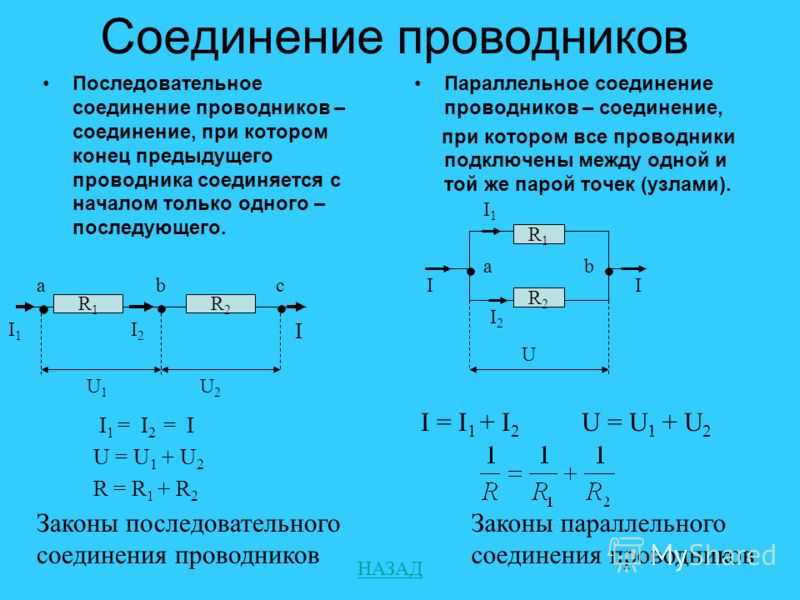
I – I R1 – I R2 – I R3 = 0.
Согласно закону токов Кирхгофа (KCL) алгебраическая сумма токов, входящих в узел и выходящих из узла, равна нулю.
Цепь делителя тока
Точно так же, как последовательная цепь резисторов может быть сконфигурирована как цепь делителя напряжения, параллельная цепь резисторов может привести к цепи делителя тока.
Хотя делитель напряжения довольно популярен, использование делителя тока зависит от приложения.
Применение параллельной схемы
Важным применением параллельной схемы является наша домашняя электропроводка. Базовая проводка во всех домах на самом деле является параллельной конфигурацией. Таким образом, все параллельные ветви получают полные 120 В (или 240 В), а ток зависит от нагрузки.
Изображение
Даже если возникает проблема/неисправность в одной параллельной ветви или цепи, затрагиваются только приборы или устройства, подключенные к этой цепи, в то время как остальные ветви работают нормально.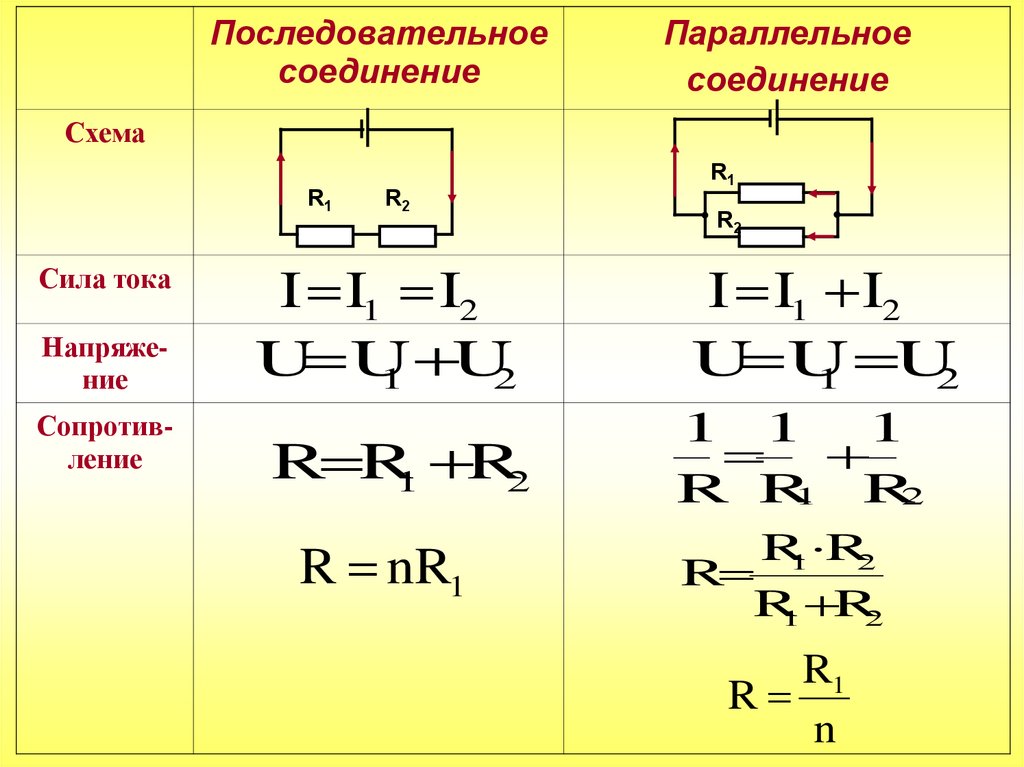
Последовательные и параллельные цепи: сравнение
В следующей таблице показано простое сравнение последовательных и параллельных цепей.
| Серийная цепь | Параллельная цепь |
| В последовательной цепи через все компоненты протекает одинаковый ток. | В параллельной цепи ток может иметь более одного пути. |
| Все компоненты соединены встык с одной общей точкой между компонентами. | Один конец всех компонентов в параллели соединен с общей точкой, а другой конец с другой общей точкой. Итак, параллельная цепь имеет две общие точки. |
| Напряжение на компонентах неодинаково и зависит от индивидуального сопротивления. | Напряжение на всех компонентах в параллельной цепи одинаковое и равно напряжению питания. |
Если в последовательной цепи выходит из строя один компонент, вся цепь перестает функционировать, так как существует только один путь тока.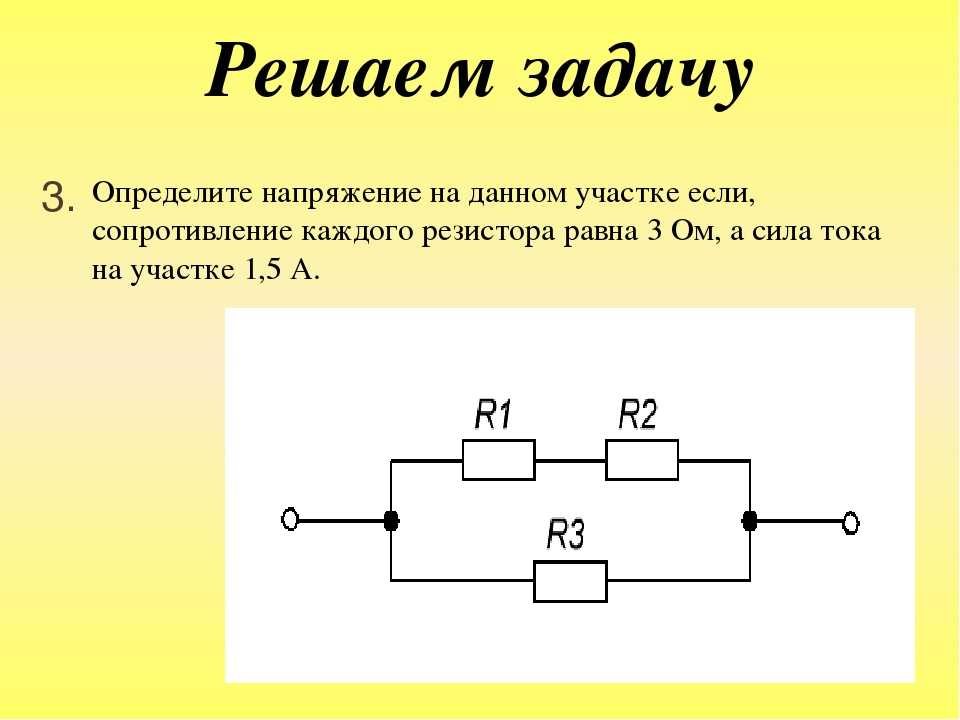 | Даже если одна из параллельных ветвей выходит из строя, остальные ветки продолжают нормально работать. |
| Ток одинаков во всех компонентах, а сумма отдельных напряжений равна напряжению питания. | Напряжение одинаково для всех компонентов, включенных параллельно, а сумма отдельных токов равна общему току в цепи. |
| Если у нас есть три резистора, соединенных последовательно, то эквивалентное сопротивление представляет собой сумму отдельных сопротивлений (R = R 1 + R 2 + R 3 ). | Если мы соединили три резистора параллельно, то обратная величина эквивалентного сопротивления равна сумме обратных величин отдельных сопротивлений (1/R = 1/R 1 + 1/р 2 + 1/р 3 ) |
| Праздничные серийные светильники являются примером последовательной цепи. | Жилая электропроводка имплантирована как параллельная конфигурация. |
Заключение
Последовательные и параллельные цепи — две основные формы электрических цепей. Четкое понимание этих двух схем поможет вам легко проанализировать любую сложную схему. Мы изучили основы последовательной цепи, параллельной цепи, сравнили серию и параллельную цепь, а также некоторые приложения.
Четкое понимание этих двух схем поможет вам легко проанализировать любую сложную схему. Мы изучили основы последовательной цепи, параллельной цепи, сравнили серию и параллельную цепь, а также некоторые приложения.
Объяснение серий и параллельных цепей
Надеемся, что те, кто ищет практическую информацию об электрических цепях и подключении светодиодных компонентов, первыми нашли это руководство. Однако вполне вероятно, что вы уже читали страницу Википедии о последовательных и параллельных схемах здесь, возможно, несколько других результатов поиска Google по этому вопросу, и все еще неясны или хотите получить более конкретную информацию, касающуюся светодиодов. В течение многих лет предоставления обучения, обучения и объяснения концепции электронных схем клиентам мы собрали и подготовили всю важную информацию, необходимую, чтобы помочь вам понять концепцию электрических схем и их связь со светодиодами.
Во-первых, не позволяйте электрическим цепям и проводке светодиодных компонентов звучать пугающе или запутанно — правильное подключение светодиодов может быть простым и понятным, если вы будете следовать этому сообщению.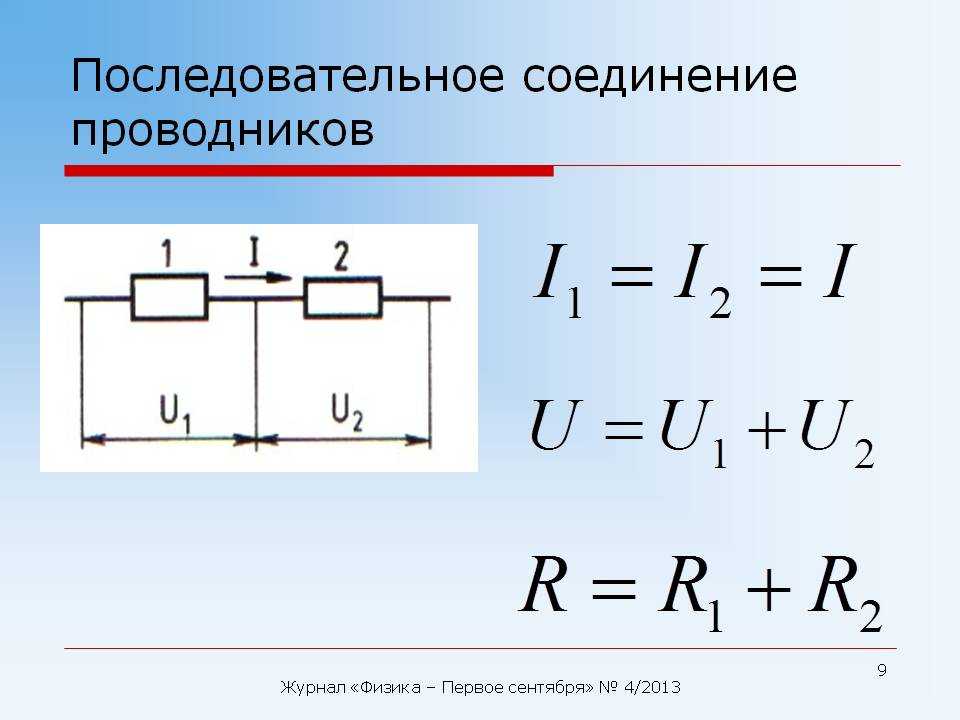 Давайте начнем с самого основного вопроса…
Давайте начнем с самого основного вопроса…
Какой тип схемы мне следует использовать?
Одно лучше другого…Последовательное, параллельное или последовательное/параллельное?
Требования к осветительным приборам часто диктуют, какой тип схемы можно использовать, но, если есть выбор, наиболее эффективным способом работы светодиодов высокой мощности является использование последовательной схемы с драйвером светодиода постоянного тока. Запуск последовательной цепи помогает обеспечить одинаковое количество тока для каждого светодиода. Это означает, что каждый светодиод в цепи будет иметь одинаковую яркость и не позволит одному светодиоду потреблять больше тока, чем другому. Когда каждый светодиод получает одинаковый ток, это помогает устранить такие проблемы, как тепловой разгон.
Не волнуйтесь, параллельная схема по-прежнему является приемлемым вариантом и часто используется; позже мы опишем этот тип схемы.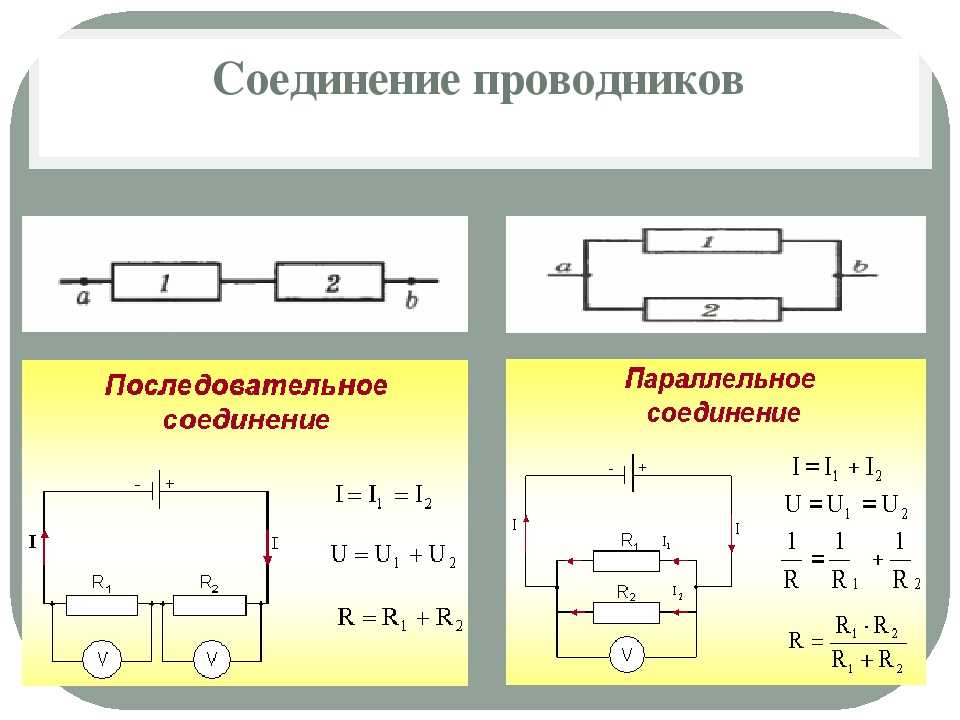
Однако сначала давайте рассмотрим последовательную цепь :
Часто называемую «гирляндной цепью» или «петлей», ток в последовательной цепи следует по одному пути от начала до конца с анодом (положительным ) второго светодиода, подключенного к катоду (минусу) первого. На изображении справа показан пример: чтобы подключить последовательную цепь, как показано, положительный выход драйвера подключается к положительному выводу первого светодиода, а от этого светодиода выполняется соединение от отрицательного к положительному второй светодиод и так далее, до последнего светодиода в цепи. Наконец, последнее соединение светодиода идет от отрицательного контакта светодиода к отрицательному выходу драйвера постоянного тока, создавая непрерывную петлю или гирляндную цепь.
Вот несколько пунктов для справки о последовательной цепи:
- Один и тот же ток протекает через каждый светодиод
- Общее напряжение цепи равно сумме напряжений на каждом светодиоде
- Если один светодиод выйдет из строя, вся схема не будет работать Цепи серии
- проще подключать и устранять неполадки
- Изменение напряжения на каждом светодиоде допустимо
Подача питания на последовательную цепь:
Концепция петли уже не проблема, и вы определенно можете понять, как ее подключить, но как насчет ПИТАНИЕ последовательная цепь.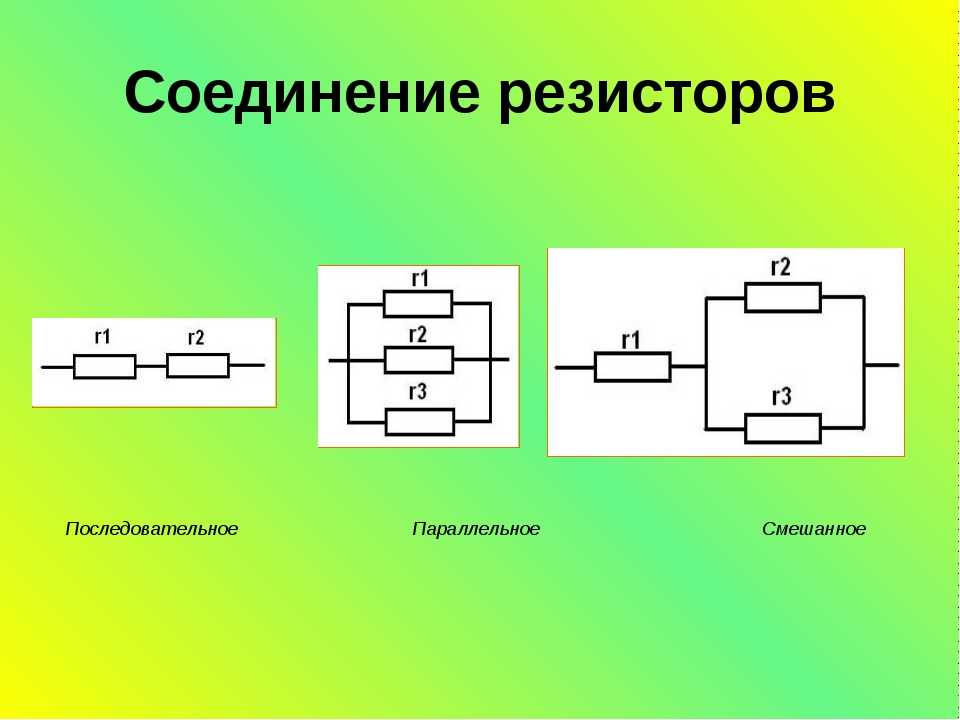
Второй пункт списка выше гласит: «Общее напряжение цепи равно сумме напряжений на каждом светодиоде» . Это означает, что вы должны обеспечить, как минимум, сумму прямых напряжений каждого светодиода. Давайте посмотрим на это, снова используя приведенную выше схему в качестве примера, и предположим, что светодиод представляет собой Cree XP-L с током 1050 мА и прямым напряжением 2,95 В. Сумма трех из этих прямых напряжений светодиода равна 8,85 В ДК . Таким образом, теоретически минимальное входное напряжение, необходимое для работы этой схемы, составляет 8,85 В.
В начале мы упомянули об использовании драйвера светодиодов постоянного тока, потому что эти модули питания могут изменять свое выходное напряжение в соответствии с последовательной схемой. Поскольку светодиоды нагреваются, их прямое напряжение изменяется, поэтому важно использовать драйвер, который может изменять свое выходное напряжение, но поддерживать одинаковый выходной ток. Для более глубокого понимания драйверов светодиодов загляните сюда.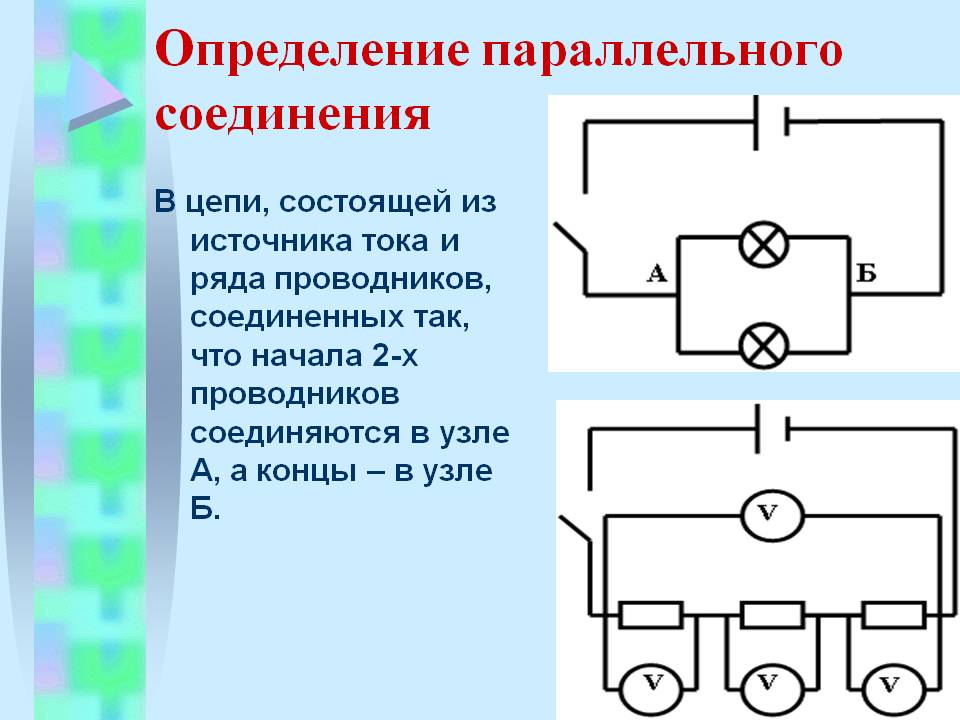 Но в целом важно убедиться, что входное напряжение драйвера может обеспечить выходное напряжение, равное или превышающее 8,85 В, которые мы вычислили выше. Некоторым драйверам требуется вводить немного больше, чтобы учесть питание внутренней схемы драйвера (драйвер BuckBlock требует дополнительных 2 В), в то время как другие имеют функции повышения (FlexBlock), которые позволяют вам вводить меньше.
Но в целом важно убедиться, что входное напряжение драйвера может обеспечить выходное напряжение, равное или превышающее 8,85 В, которые мы вычислили выше. Некоторым драйверам требуется вводить немного больше, чтобы учесть питание внутренней схемы драйвера (драйвер BuckBlock требует дополнительных 2 В), в то время как другие имеют функции повышения (FlexBlock), которые позволяют вам вводить меньше.
Надеюсь, вы сможете найти драйвер, который сможет реализовать вашу светодиодную схему с последовательными диодами, однако есть обстоятельства, которые могут сделать это невозможным. Иногда входного напряжения может быть недостаточно для последовательного питания нескольких светодиодов, или может быть слишком много светодиодов для последовательного включения, или вы просто хотите ограничить стоимость драйверов светодиодов. Какой бы ни была причина, вот как понять и настроить параллельную схему светодиодов.
Параллельная цепь:
Если последовательная цепь получает одинаковый ток для каждого светодиода, параллельная цепь получает одинаковое напряжение для каждого светодиода, а общий ток для каждого светодиода равен общему выходному току драйвера, деленному на количество параллельных светодиоды.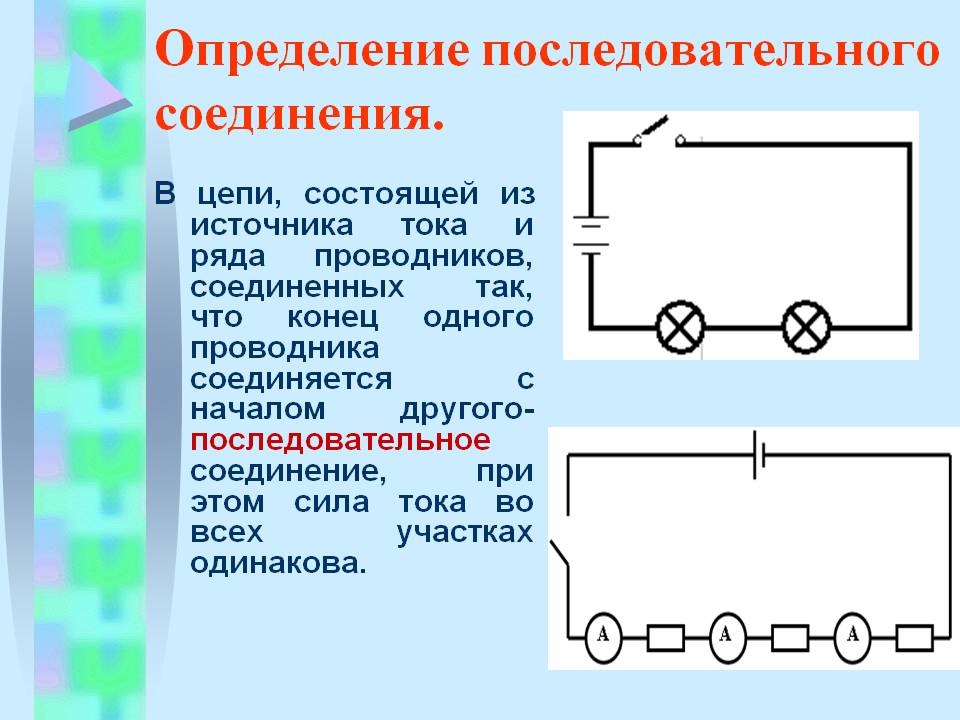
Опять же, не волнуйтесь, здесь мы увидим, как подключить параллельную схему светодиодов, и это должно помочь связать идеи воедино.
В параллельной схеме все положительные соединения соединяются вместе и возвращаются к положительному выходу драйвера светодиодов, а все отрицательные соединения соединяются вместе и возвращаются к отрицательному выходу драйвера. Давайте посмотрим на это на изображении справа.
В примере, показанном с выходным драйвером 1000 мА, каждый светодиод получит 333 мА; общий выход драйвера (1000 мА), разделенный на количество параллельных цепочек (3).
Вот несколько пунктов для справки о параллельной схеме:
- Напряжение на каждом светодиоде одинаковое
- Общий ток равен сумме токов через каждый светодиод
- Общий выходной ток распределяется по каждой параллельной цепи
- В каждой параллельной цепочке требуются точные значения напряжения, чтобы избежать перегрузки по току
Теперь давайте немного повеселимся, объединим их вместе и наметим Series/Parallel Circuit :
Как следует из названия, последовательно-параллельная цепь объединяет элементы каждой цепи.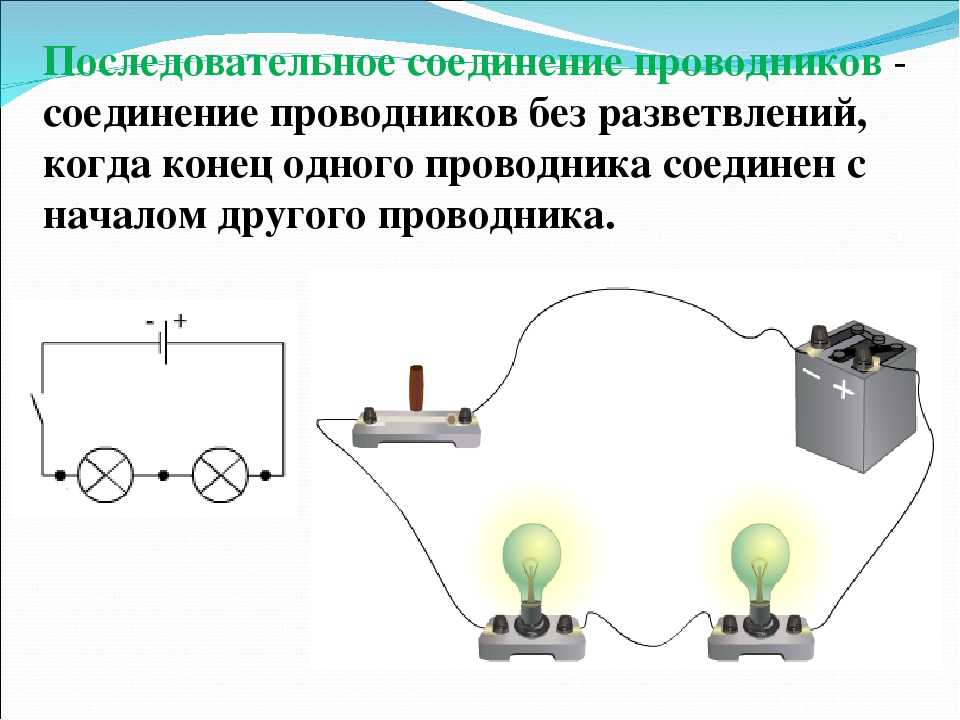 Начнем с последовательной части схемы. Допустим, мы хотим запустить в общей сложности 9 светодиодов Cree XP-L по 700 мА каждый с напряжением 12 В постоянного тока ; прямое напряжение каждого светодиода при 700 мА составляет 2,98 В постоянного тока . Правило номер 2 из пунктов списка последовательной схемы доказывает, что 12 В постоянного тока недостаточно для работы всех 9 светодиодов последовательно (9 x 2,98 = 26,82 В постоянного тока ). Однако 12В постоянного тока достаточно для запуска трех последовательных (3 x 2,98 = 8,94 В постоянного тока ). И из правила параллельной схемы номер 3 мы знаем, что общий выходной ток делится на количество параллельных цепочек. Таким образом, если бы мы использовали BuckBlock на 2100 мА и имели три параллельные цепочки из 3 светодиодов последовательно, то 2100 мА были бы разделены на три, и каждая серия получила бы 700 мА. Пример изображения показывает эту настройку.
Начнем с последовательной части схемы. Допустим, мы хотим запустить в общей сложности 9 светодиодов Cree XP-L по 700 мА каждый с напряжением 12 В постоянного тока ; прямое напряжение каждого светодиода при 700 мА составляет 2,98 В постоянного тока . Правило номер 2 из пунктов списка последовательной схемы доказывает, что 12 В постоянного тока недостаточно для работы всех 9 светодиодов последовательно (9 x 2,98 = 26,82 В постоянного тока ). Однако 12В постоянного тока достаточно для запуска трех последовательных (3 x 2,98 = 8,94 В постоянного тока ). И из правила параллельной схемы номер 3 мы знаем, что общий выходной ток делится на количество параллельных цепочек. Таким образом, если бы мы использовали BuckBlock на 2100 мА и имели три параллельные цепочки из 3 светодиодов последовательно, то 2100 мА были бы разделены на три, и каждая серия получила бы 700 мА. Пример изображения показывает эту настройку.
Если вы пытаетесь собрать светодиодную матрицу, этот инструмент планирования светодиодных цепей поможет вам решить, какую схему использовать.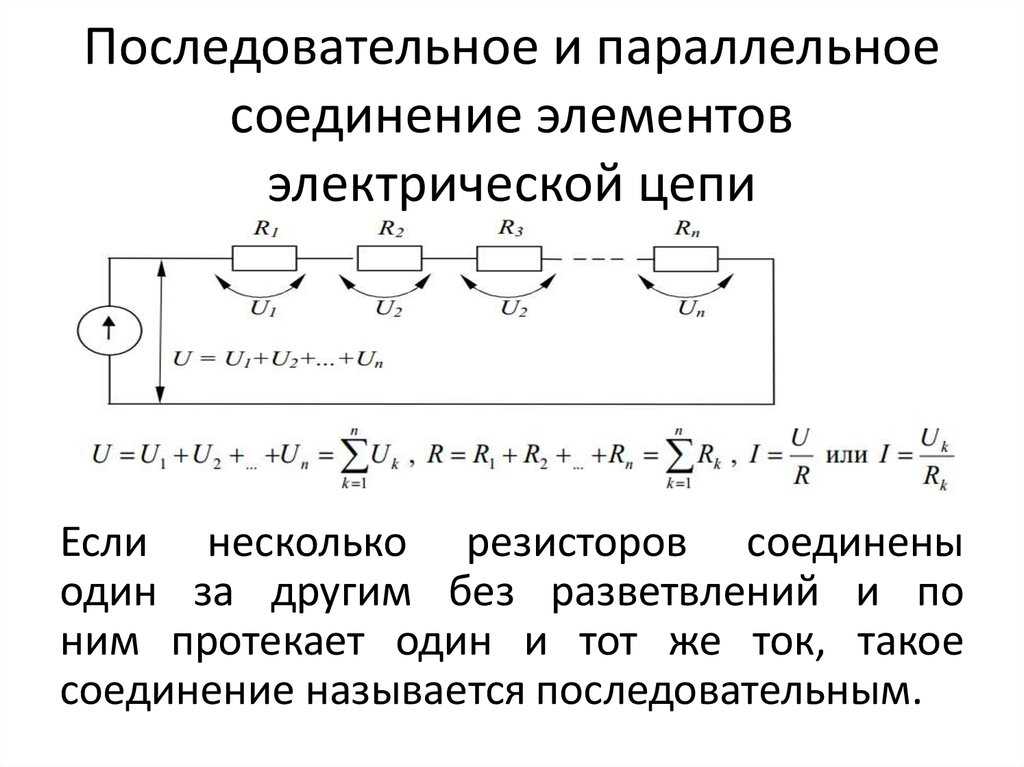 На самом деле это дает вам несколько различных вариантов различных последовательных и последовательно-параллельных цепей, которые будут работать. Все, что вам нужно знать, это ваше входное напряжение, прямое напряжение светодиода и количество светодиодов, которые вы хотите использовать.
На самом деле это дает вам несколько различных вариантов различных последовательных и последовательно-параллельных цепей, которые будут работать. Все, что вам нужно знать, это ваше входное напряжение, прямое напряжение светодиода и количество светодиодов, которые вы хотите использовать.
Неисправность нескольких цепочек светодиодов:
При работе с параллельными и последовательно-параллельными цепями следует помнить, что если цепочка или светодиод перегорают, светодиод/цепочка затем отключается от цепи, поэтому лишние текущая нагрузка, которая шла на этот светодиод, затем будет распределена на остальные. Это не является серьезной проблемой для массивов большего размера, поскольку ток будет рассеиваться в меньших количествах, но как насчет схемы, состоящей всего из 2 светодиодов/цепочек? Тогда ток будет удвоен для оставшегося светодиода/цепочки, что может быть более высокой нагрузкой, чем может выдержать светодиод, что приведет к перегоранию и разрушению вашего светодиода! Убедитесь, что вы всегда помните об этом, и старайтесь иметь настройку, которая не испортит все ваши светодиоды, если один из них перегорит.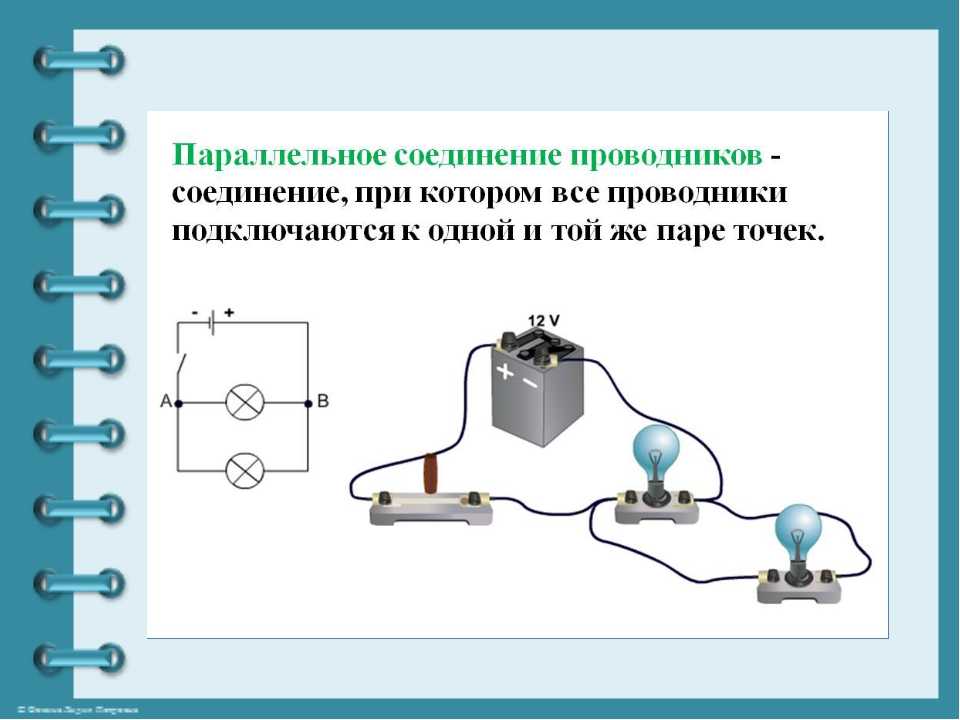


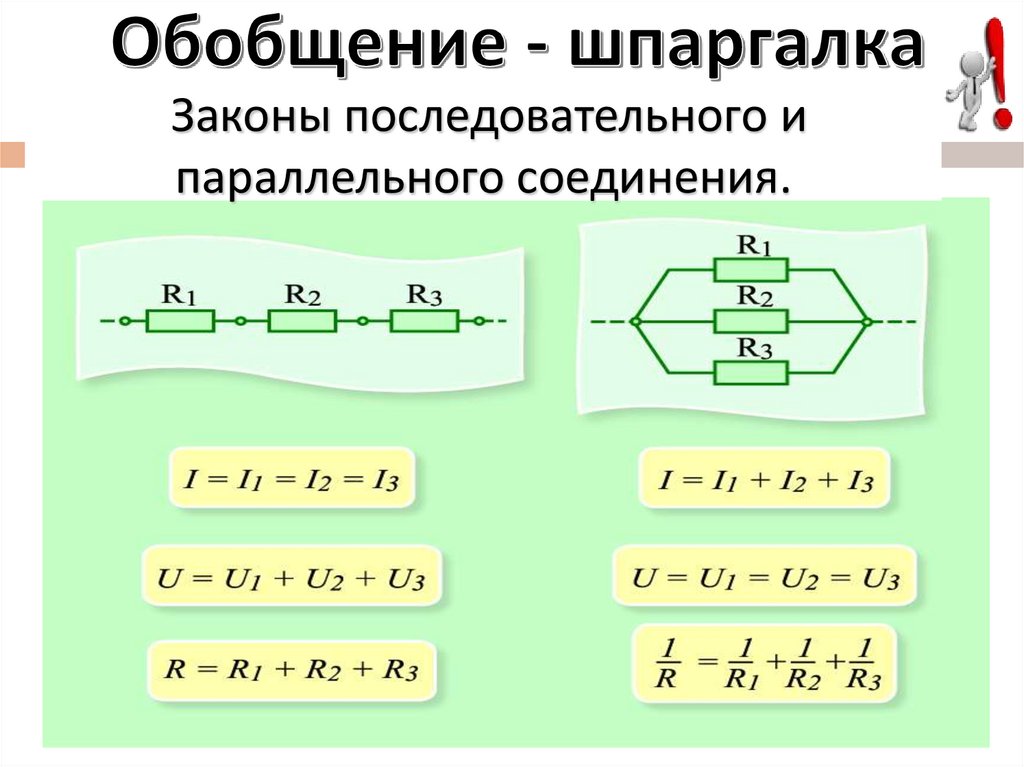
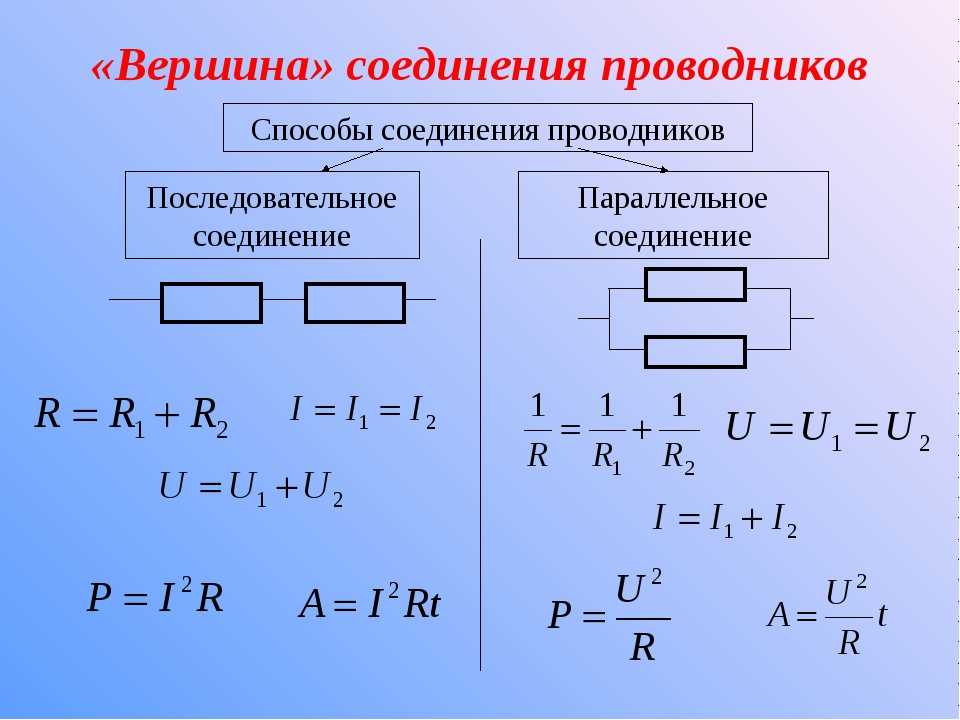
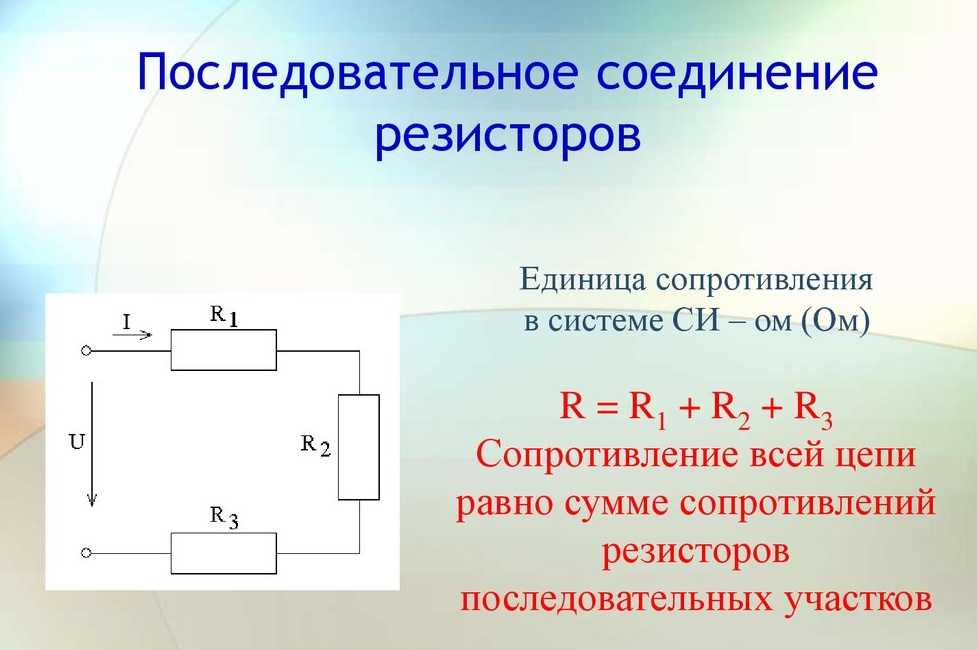
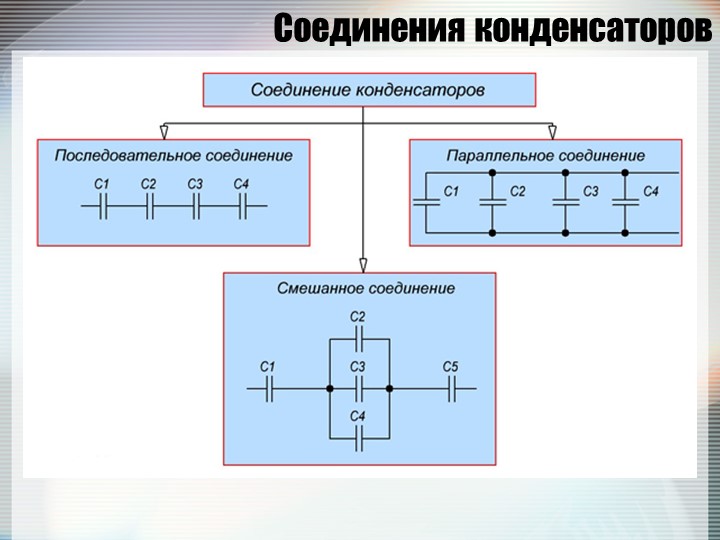

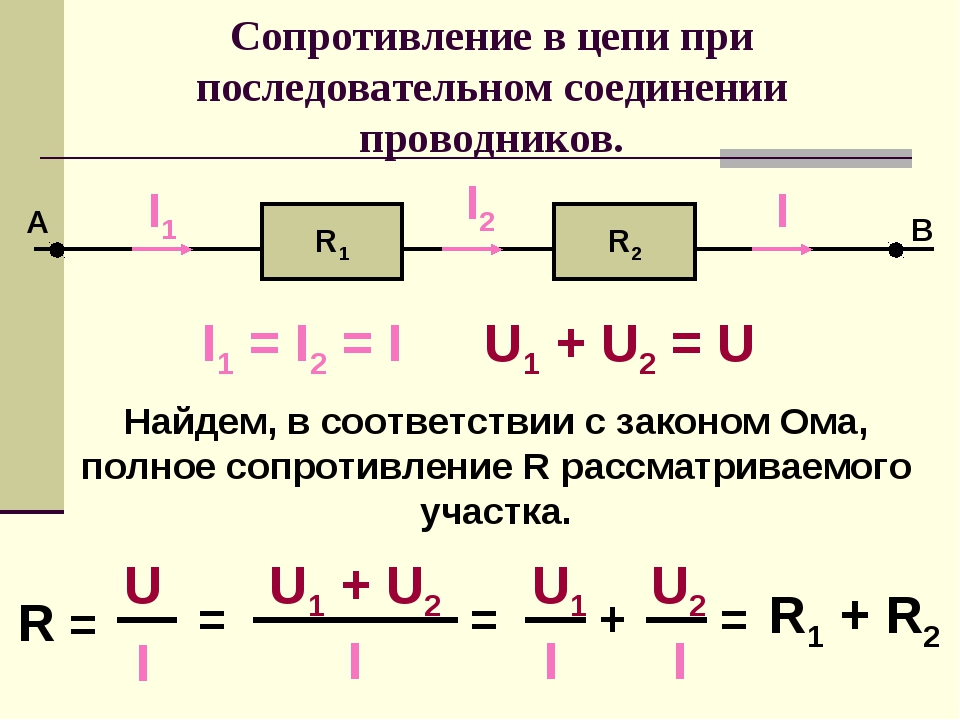 Общее сопротивление последовательной цепи: R O = 12 В / 8 А = 1,5 Ом.
Общее сопротивление последовательной цепи: R O = 12 В / 8 А = 1,5 Ом.
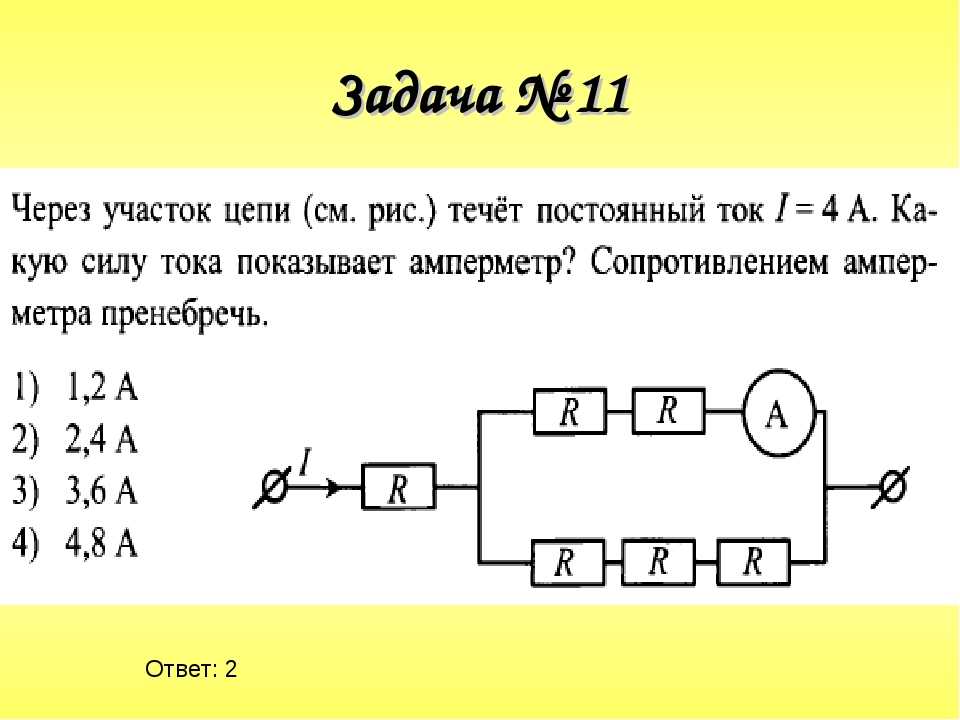 Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
Обведите две параллельные ветви, чтобы выделить их на схеме цепи.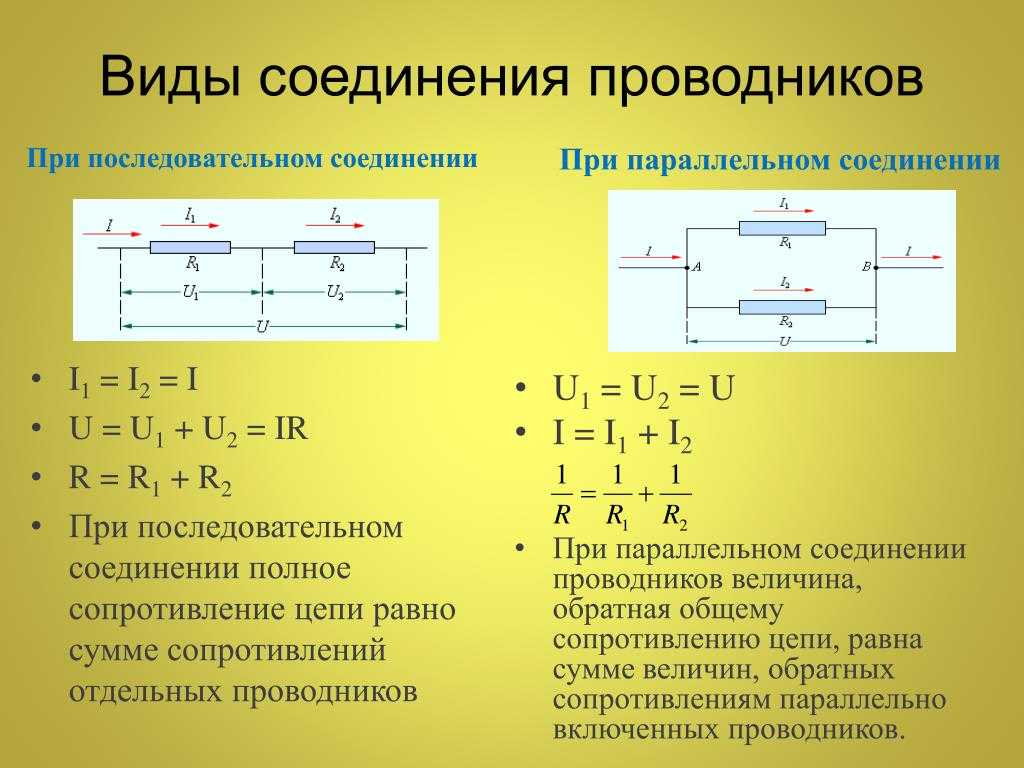 Таким образом, напряжение на резисторах пропорционально их сопротивлениям, а сумма отдельных напряжений равна общему напряжению.
Таким образом, напряжение на резисторах пропорционально их сопротивлениям, а сумма отдельных напряжений равна общему напряжению.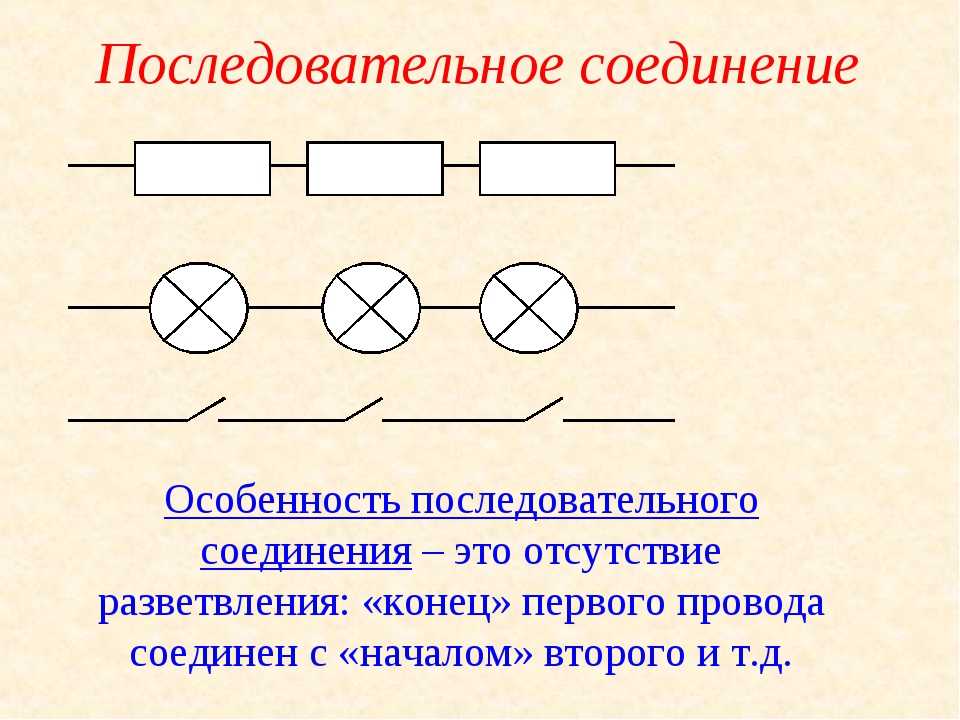 Таким образом, через двери можно пропустить больше заряженных частиц.
Таким образом, через двери можно пропустить больше заряженных частиц.