1
теоретической механики базируются общеинженерные дисциплины: сопротивление материалов, детали машин, теория механизмов и машин и другие. Основной задачей теоретической механики является изучение движения материальных тел под действием сил. Важной частной задачей представляется изучение равновесия тел под действием сил. . Составители: доц. Тавбаев Ж.С., Сапаров Б.Ж. Рецензент: проф. Сафаров И.И Методической пособие обсуждено и одобрено на заседании кафедры «Машины протокол № от « » 2017 г. 
Заведующий кафедрой доц. Т.Т.Сафаров Данное методической пособие обсуждено и одобрено научно- методическим советом факультета «Технология пищевых продуктов» ТКТИ. Протокол № от « » 2017 г. Председатель научно- методического совета доц. О.Қ.Юнусов. 2
положения тела используют системы отсчета. Система отсчета представляет собой некоторое тело и связанную с ним систему координат. В теоретической механике рассматривают тела, движущиеся со скоростями, значительно меньшими скорости света, и имеющие размеры, превосходящие во много раз межмолекулярные расстояния. Рассматриваемые тела считают идеализированными (материальные точки, абсолютно твердые тела и пр.), что позволяет абстрагироваться от второстепенных факторов и выявлять наиболее общие законы механического движения. Механика – одна из древнейших наук, возникшая в связи с потребностями практики. Зарождение механики связано с именами Аристотеля (384– 322 гг. до н.э.) и Архимеда (287–212 гг. до н.э.). Однако наукой в современном смысле слова механика стала лишь с выходом в свет в 1687 году знаменитой работы И.  Ньютона «Математические начала натуральной
философии». Теоретическая механика традиционно делится на три раздела: статику, кинематику и динамику. 3 жүктеу/скачать 4.32 Mb. Достарыңызбен бөлісу: |
Инертность — тело — Большая Энциклопедия Нефти и Газа, статья, страница 2
Cтраница 2
Масса является мерой инертности тел и их гравитационных свойств, которые проявляются в притяжении тел друг к другу. Чем больше масса тел, тем большее притяжение они испытывают друг к другу. [16]
В качестве меры инертности тела в поступательном движении вводят положительную скалярную величину т, называемую массой тела. [17]
Масса — мера инертности тела
Это свойство проявляется в том, что тело под воздействием определенной силы приобретает вполне определенное ускорение.
[18]В качестве меры инертности тела в механике вводится положительная скалярная величина m — масса тела. [19]
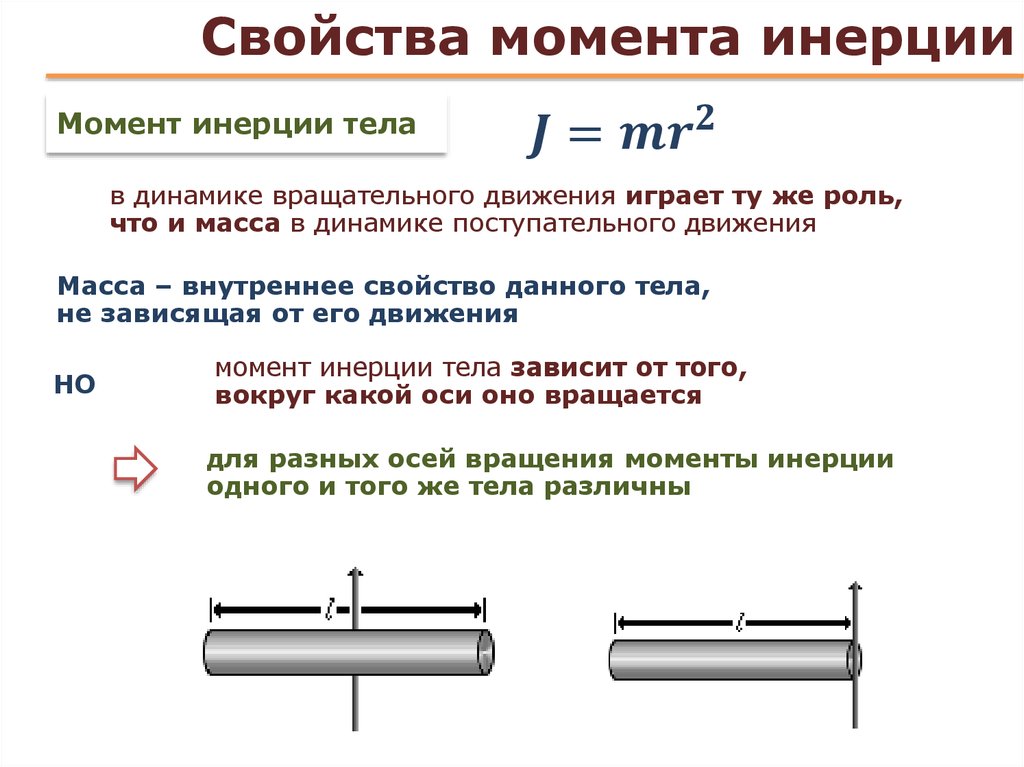
Величина, которая определяет инертность тела по отношению к вращательному движению, называется моментом инерции тела. [20]
Момент инерции является мерой инертности тела, поэтому двигатели с малым моментом инерции разгоняются с большими ускорениями и быстро достигают установившейся частоты вращения. Для эксплуатации в режимах с частыми пусками стремятся выполнить двигатели с малыми моментами инерции, для чего уменьшают диаметры роторов при соответствующем увеличении длин их сердечников. [21]
Величина, являющаяся мерой инертности тела и определяющая количество вещества, содержащееся в теле, называется инертной массой тела. [22]
Момент инерции является мерой инертности тела при вращательном движении.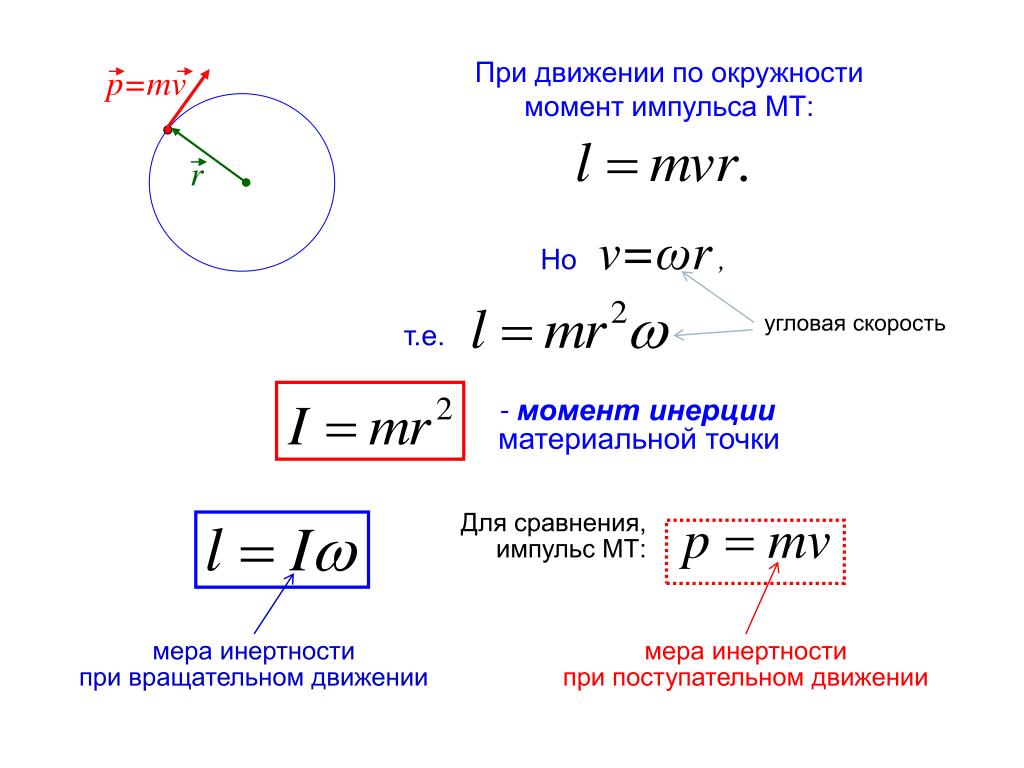
Он играет такую же роль, что и масса при описании поступательного движения тела. Но если масса данного тела в задачах ньютоновской механики считается величиной постоянной, то момент инерции данного тела зависит от положения оси вращения.
[23]
Момент инерции является мерой инертности тела при вращательном движении. Он играет такую же роль, что и масса при описании поступательного движения тела. [24]
Момент инерции является мерой инертности тела, поэтому двигатели с малым моментом инерции разгоняются с большими ускорениями и быстро достигают установившейся частоты вращения. Для эксплуатации в режимах с частыми пусками стремятся выполнить двигатели с малыми моментами инерции, для чего уменьшают диаметры роторов при соответствующем увеличении длин их сердечников. [25]
Величина, являющаяся мерой инертности тела и определяющая количество вещества, содержащееся в теле, называется инертной массой тела. [26]
Момент инерции является мерой инертности тела при вращательном движении.
Он играет такую же роль, что и масса при описании поступательного движения тела. Но если масса данного тела в задачах ньютоновской механики считается величиной постоянной, то момент инерции данного тела зависит от положения оси вращения.
[27]
Момент инерции является мерой инертности тела, поэтому двигатели с малым моментом инерции разгоняются с большими ускорениями и быстро достигают установившейся частоты вращения. [28]
Теперь массой называют меру инертности тела, характеризующую быстроту изменения его скорости под действием данной силы, что ближе, как мы видели, к определению величины тела у Торричелли и Декарта. [29]
Коэффициент пропорциональности / т характеризует инертность тела. [30]
Страницы: 1 2 3 4
Вращательная инерция | Университетская физика
Имя: _________________________________________
Дата: ____________________________
Партнеры:____________________________________________________________
Оборудование 0
- Интерфейс LabPro
- Вращение файл программного обеспечения
- Энкодер
- Аксессуары инерции вращения
- Шкив
- Подвесные грузы
Введение
Инерция вращения является мерой сопротивления объекта изменениям его угловой скорости.
Представьте себе приложение известного крутящего момента к объекту. Прикладывая крутящий момент, измерьте угловое ускорение. Чем меньше результирующее угловое ускорение, тем больше инерция вращения объекта. Таким образом, измеряя приложенный крутящий момент и результирующее угловое ускорение, можно определить инерцию вращения объекта.
В этом упражнении вы повесите известную массу на энкодер с помощью веревки, обернутой вокруг энкодера и над шкивом. Кодер будет ориентирован лицевой стороной вверх, чтобы вы могли устанавливать на него различные объекты и, следовательно, определять инерцию вращения системы. Когда вы отпустите массу, струна передаст крутящий момент энкодеру, что приведет к угловому ускорению. Измерив это угловое ускорение, вы сможете определить инерцию вращения энкодера и его нагрузку.
I. Определение инерции вращения исходной системы
Откройте файл Вращение.
Расположите энкодер и вторичный шкив, как показано на рисунке выше.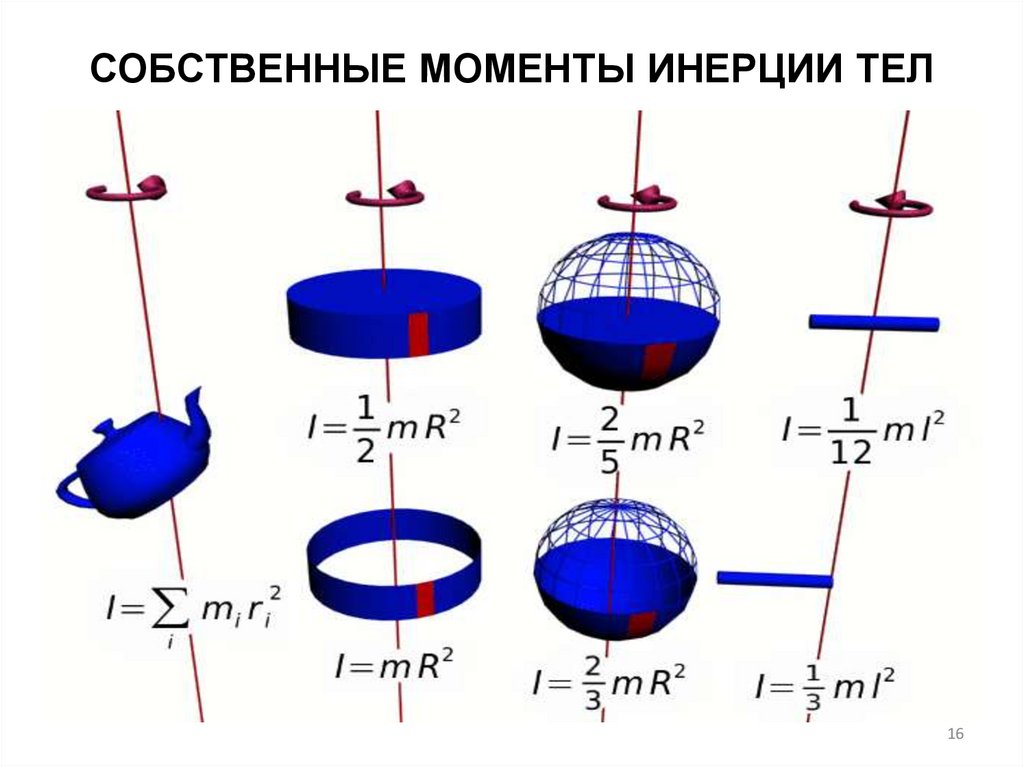
Снимите трехступенчатый шкив и переверните его так, чтобы шкив с наибольшим радиусом оказался сверху. Пока не прикрепляйте длинную штангу с регулируемыми грузами.
Вращайте энкодер, чтобы определить положительное направление. Используя маленькие отверстия в шкиве, чтобы надежно закрепить струну, оберните струну вокруг шкива среднего радиуса, чтобы обеспечить положительное угловое ускорение. Отрегулируйте вторичный шкив так, чтобы струна располагалась горизонтально между шкивами и плавно проходила над вторичным шкивом.
Прикрепите груз массой 5 г к концу нити.
Настройте график для отображения зависимости углового ускорения от времени, нажмите Собрать, и отпустите массу.
Вопрос: Является ли угловое ускорение энкодера приблизительно постоянным при падении массы? Оно должно быть постоянным? Объяснять.
Используйте Анализ/Статистика для определения среднего углового ускорения при падении массы и запишите его ниже. Варьируйте подвесную массу, чтобы завершить таблицу.
Подвесная масса (кг) | Угловое ускорение (рад/с 2 ) |
0,005 | ± |
0,010 | ± |
0,015 | ± |
0,020 | ± |
Приведенные выше данные можно использовать для расчета инерции вращения системы энкодера. Для этого необходимо применить второй закон Ньютона как к энкодеру, так и к падающей массе и объединить результаты. Вы будете руководствоваться этим процессом шаг за шагом.
Вопрос: Нарисуйте диаграмму свободного тела для висящей массы и примените второй закон Ньютона. Пусть направление движения массы положительно.
Вопрос: Нарисуйте диаграмму свободного тела в виде сверху для энкодера и примените вращательную форму второго закона Ньютона. Пусть направление движения энкодера положительное.
Вопрос: Поскольку линейное ускорение массы неизвестно, перепишите уравнение висячей массы, заменив линейное ускорением на угловое.
Вопрос: Поскольку сила, действующая на струну, неизвестна, объедините два уравнения, чтобы исключить этот член.
Вопрос: Решите полученное уравнение для инерции вращения энкодера.
Обратите внимание, что каждая переменная в приведенном выше выражении была измерена и записана в приведенной выше таблице, за исключением радиуса энкодера. Измерьте радиус энкодера и запишите его ниже:
радиус энкодера, R = ____________ м
Используя приведенные выше результаты, рассчитайте инерцию вращения энкодера для каждой попытки и запишите ее ниже.
Подвесная масса (кг) | Угловое ускорение (рад/с 2 ) | Инерция вращения (кг·м 2 ) |
0,005 | ± | ± |
0,010 | ± | ± |
0,015 | ± | ± |
0,020 | ± | ± |
Вопрос: Одинакова ли инерция энкодера в каждом испытании? Должно ли это быть? Объяснять.
Вопрос: Каково среднее значение инерции вращения энкодера с учетом неопределенности.
II. Зависимость инерции вращения от положения
В этом упражнении вы обнаружите, как постоянная масса, расположенная в переменном месте на объекте, влияет на инерцию вращения объекта. Вы начнете с размещения массы далеко от оси вращения объекта, а затем переместите массу к оси вращения.
Вопрос: Считаете ли вы, что инерция вращения будет увеличиваться, уменьшаться или оставаться неизменной при перемещении массы к оси вращения? Объяснять.
Прикрепите длинный металлический стержень к верхней части энкодера. Отцентрируйте стержень между пластиковыми штифтами на трехступенчатом шкиве для устойчивости. Прикрепите к стержню два регулируемых груза, каждый из которых расположен на расстоянии 16 см от центра стержня.
Прикрепите 100 г к концу веревки, нажмите Соберите и отпустите висящий груз. Запишите результат ниже. Прежде чем заполнить следующую таблицу, рассмотрите вопрос, заданный ниже.
Подвесная масса (кг) | Положение массы (м) | Угловое ускорение (рад/с 2 ) | Инерция вращения (кг·м 2 ) |
0,100 | 0,16 | ± | ± |
0,100 | 0,12 | ± | ± |
0,100 | 0,08 | ± | ± |
0,100 | 0,04 | ± | ± |
Вопрос: Вы можете обнаружить, что угловое ускорение становится «менее постоянным» по мере приближения масс к оси вращения.
Объясните, почему это так, и объясните, какую часть данных углового ускорения следует проанализировать, чтобы компенсировать этот эффект.
Создайте график зависимости инерции вращения от положения массы. На основе ваших данных выберите наиболее подходящую функцию и отобразите ее на графике. (Помните, что ваша наилучшая функция должна соответствовать данным и соответствуют известной физической взаимосвязи между инерцией вращения и положением.) Распечатайте и прикрепите свой график в конце этого упражнения.
Вопрос: Запишите числовые константы в вашей функции наилучшего соответствия ниже. Каждое числовое значение должно иметь как неопределенность, так и единицы измерения.
Вопрос: Рассмотрим член пересечения в вашей функции наилучшего соответствия. Какой физический параметр системы представляет этот член? Понятно объяснить.
Вопрос: Рассмотрим другой термин(ы) в вашей функции наилучшего соответствия. Какой физический параметр системы представляет каждый член? Если вы можете легко определить фактическое значение этого параметра, сделайте это и сравните его с наиболее подходящим значением.
III. Измерение инерции вращения металлического диска
В этом последнем упражнении вы измерите инерцию вращения металлического диска.
Снимите металлический стержень с энкодера, переверните 3-ступенчатый шкив и прикрепите металлический диск к 3-ступенчатому шкиву.
Прикрепите 20 г к концу веревки, нажмите Соберите и отпустите висящий груз. Запишите результат ниже.
Заполните таблицу.
Подвесная масса (кг) | Угловое ускорение (рад/с 2 ) | Инерция вращения (кг·м 2 ) |
0,020 | ± | ± |
0,030 | ± | ± |
0,040 | ± | ± |
0,050 | ± | ± |
Вопрос: Каково среднее значение с неопределенностью для инерции вращения металлического диска? (Подсказка: это не просто среднее значение столбца инерции вращения выше.
)
Вопрос: Измерьте радиус металлического диска. Используя этот результат и полученный выше результат, определите массу металлического диска с единицами и неопределенностями.
Вопрос: Определите фактическую массу металлического диска и сравните ее со значением, которое вы определили выше. Прокомментируйте соответствие между этими значениями.
вращательное движение
вращательное движение| Вращательное движение | последнее обновление 5 марта 2003 г. |
дом
|
меню заметок
O цели
Цель этого лаборатория должна
- исследовать движение жесткое вращающееся тело
- определить момент инерции тела вращения
№ примечания к главе 8
стр.73 — 91 вашего лабораторного журнала
Поскольку мы редко имеем дело с «точечных» частиц в реальной жизни, мы должны стремиться понять вращательные движение. В отличие от точечных частиц, реальные объекты (двух- или трехмерные объекты) будут вращаться или поворачиваться, когда на них воздействует нецентральная сила. Такой «нецентральная сила» называется крутящим моментом . Это крутящий момент, который мы применяем гаечный ключ, чтобы повернуть гайку, и крутящий момент, который мы применяем, чтобы крутить педали нашего велосипеда.
Следующее, что вы должны понять, чтобы узнать о вращении движение есть то, что называется моментом инерции.
- Момент инерции тела есть сопротивление тела изменению его вращательного движения. движение.
Аналогичен обычному инерция (масса), которая представляет собой величину сопротивления изменению линейного движения (ускорение).
Участие в классе: Что, по вашему мнению, лучше момент инерции, линейка вращается вокруг оси, идущей по своей длине или линейка, вращающаяся вокруг оси, проходящей перпендикулярно лицо?Как только вы освоите эти концепции, изучение остальной части вращательной кинематики легко. Каждое уравнение во вращательной кинематике есть линейный аналог, который вы уже знаете, и легко перейти от одного к другому. (Вы можете сохранить эту таблицу для вашего курса лекций! Примечание: 170 студентов, пожалуйста, замените дельту на бесконечно малую. изменение d такое, что v = dx/dt)
Уравнение вращения
или концепция
Линейный аналоговый
Преобразование из
от линейного до вращательногомомент инерции (I)
масса (м)
крутящий момент ( )
= Iсилы (Ф)
Ф = ма= г х F
(где r — расстояние от центра масс до места действия силы применяется)угловой смещение ( )
линейный водоизмещение (с)
(где s = дуговое расстояние)угловая скорость ( )
линейный скорость (v)
угловой ускорение ( )
линейный ускорение (а)
угловой импульс (L)
L = Iлинейный импульс (p)
p = mvвращательный кинетическая энергия (К вращение )
К = 1/2 I 2линейный кинетическая энергия (К)
К = 1/2 мВ 2
Теперь к ситуации в нашей лаборатории.Крутящий момент, который мы будем применять (
применяется ) будет вызвано подвешиванием массы (m) на цилиндре. Другой крутящий момент вызванное трением ( трение ).чистый крутящий момент = применено — фрикционная = I
Обратите внимание, что это уравнение является линейным уравнением. Если вы нанесете на график по сравнению с . затем наклон этого графика — момент инерции (I), а точка пересечения y — это момент трения крутящий момент ( трение ).
73 — 91 вашего лабораторного журнала
У нас есть три металлических цилиндра разных
радиусы, соединенные друг с другом. Это объект, который мы будем вращать.
Мы приложим крутящий момент к этому объекту, чтобы заставить его вращаться.Что мы необходимо найти приложенный крутящий момент и угловое ускорение.
мг — Т = ма
Чтобы решить это уравнение, нам нужно знать ускорение масса. Для этого мы можем измерить количество времени, которое требуется для массы опуститься на пол. Используя ваше уравнение движения, вы знаете, что:a = 2y/t 2
где y — высота, масса падает, а t — время, за которое масса падает до пол.
Измерение а также даст нам угловое ускорение, так как
= и /р
где r — радиус цилиндра, к которому прикреплена масса.
Применяется
крутящий момент = r x F применяется , как показано в таблице выше. Это означает
что больший крутящий момент будет приложен, когда радиус цилиндра
больше. В нашей лаборатории мы будем применять четыре различных крутящих момента, изменяя
радиуса и изменением приложенной силы. Мы можем легко найти приложенную силу.
Приложенная сила представляет собой натяжение (T) струны. Напряжение дается
по (см. схему свободного тела на стр. 75):Р Процедура:
- Измерение радиусов малой оси, большей оси и колеса, как показано на схеме Направо. (Вы можете использовать штангенциркуль, чтобы измерить диаметр и разделить на два, чтобы получить радиус.)
- Измерить толщину цилиндров. В вашей таблице данных это называется «длиной оси». Журнал все это в таблицах данных на страницах 83 и 85.
- Масса всего аппарат (состоящий из колеса, малой оси и большей оси) выбит на колесе. Обязательно отметьте эту массу на стр. 85.
- Связать массу 50 г к малой оси. Намотайте лишнюю струну на маленькую ось.
- Измерить высоту от низа массы до пола (как показано на схеме).
- Измерить количество времени, за которое масса упадет на пол.
- Повторить шаг 6 четыре раза больше раз, чтобы вы могли найти SD и SDM для измерения времени.
