определение, сложение, умножение, скалярное и векторное произведение
В статье узнаете что такое вектор, векторные компоненты, единичный вектор, как складывать вектора, умножать вектора на скаляр, скалярное, векторное и смешанное произведение двух векторов.
Сохранение физической величины с вектором обычно означает совершенно иную ситуацию, чем просто сохранение ее скалярной длины. Постоянное значение импульса p (скаляр) может означать совершенно иную ситуацию, чем постоянный вектор p.

Вектор должен иметь три необходимые характеристики: значение (длина), направление, начало и конец.
Любое изменение любого из этих признаков — длины, направления или начало с концом — означает, что создан другой вектор. Два вектора равны тогда и только тогда, когда они имеют равную длину, направление и начало с концом.
Векторные компоненты
Компонентами вектора являются его проекции на оси системы координат.

Также в трехмерном пространстве векторы A называются векторами, которые являются проекциями этого вектора A на оси системы координат.
Имея вектор A, мы погружаем его в систему координат x, y, z. Векторы, являющиеся проекциями вектора A на оси системы, называются векторными компонентами вектора A. Вектор A является векторной суммой составляющих векторов Ax, Ay и Az .

Единичный вектор
Единичный вектор, имеющий то же направление, что и вектор, на который он ссылается, важен, но его длина всегда равна 1.

Единичные векторы осей координат. Мы также присваиваем единичные векторы оси системы отсчета. а) относится к правовращающей системе и б) к левосторонней системе.

Сложение векторов
Сумма вектора обычно не совпадает с суммой скалярных величин:

Добавление двух или более векторов друг к другу сводится к добавлению их компонентов, то есть проекций на опорные оси. Результирующий вектор называется случайным вектором. Для двух векторов результирующий вектор является диагональю параллелограмма, построенного на этих векторах. Метод параллелограмма.

В случае большего числа векторов результирующий вектор получается путем рисования одного из этих векторов, затем в конце первого вектора мы начинаем второй, в конце второго мы даем начало третьего и так далее. Полученный вектор является вектором, начало которого находится в начале первого из добавленных векторов. и его конец в конце последнего. При изменении порядка сложения результирующий вектор (красный) не меняет длину, направление:


Это правило добавления векторов также действует в трехмерном пространстве:

Умножение вектора на скаляр

Самым простым умножением, выполняемым на векторах, является умножение вектора на скаляр (число). Такое умножение не меняет направление вектора, но, как правило, меняет его длину и может изменить его конец (когда скаляр является отрицательным числом). Когда вектор A умножается на α-скаляр, мы получаем новый вектор B:

Скалярное произведение и векторное произведение двух векторов являются очень важными направления в физике и геометрии. Существует также смешанное произведение трех векторов.
Скалярное произведение двух векторов
Формально скалярное произведение векторов представляет собой точку, и ее значение определяется зависимостью

Скалярное произведение описывает способ, которым оба вектора видят друг друга, то есть как долго тень (проекция) отбрасывает каждый из векторов в своего партнера, когда угол между ними равен φ

B cos φ — длина тени, которую вектор B выбрасывает в вектор A. Аналогично, A cos φ — длина тени, которую вектор A выбрасывает в вектор B.
Когда длина проекции (тени) одного из векторов равна нулю, тогда длина проекции второго вектора равна нулю, то есть A • B = 0. Это означает, что эти векторы не работают в одном и том же направлении вообще. Работа, которую мы выполняем при движении автомобиля, зависит не только от приложенной силы F, но и от угла, который создает направление силы и направление пути.
Так как единичные векторы оси системы отсчета х, у и z, которые обозначают векторы ех, еY и еz, перпендикулярны друг к другу, то в виду того, что А • В = АВcosφ и что cos 0 = 1 и cos 90o = 0, мы получаем произведение значений этих единичных векторов:

Выполнение аналогичного умножения на векторы A и B

мы получили новое выражение для скалярного произведения двух векторов A и B

Значение скалярного произведения двух векторов A и B можно записать в виде двух эквивалентных выражений:

Сравнивая оба выражения, мы находим выражение для угла между векторами A и B:

Векторное произведение двух векторов
Многие важные величины в науке и технике определяются вектором, который является произведением двух других векторов. В таких случаях произведение этих векторов, называемое векторным произведением , приводит к третьему вектору.
В этом случае задача состоит в том, чтобы определить все три особенности вектора C, являющегося произведением векторного произведения векторов A и B:
- длина
- направление
- начало и конец
Произведение векторов A и B , приводящее к третьему вектору C, отмечено диагональным крестом

Направление
Вектор С такой, что вектор перпендикулярен к плоскости, образованной векторами A и B, которая перпендикулярна как к вектору A и B.

Длина
вектор С равен значению параллелограмма, построенного на векторах А и В. Числовой C = ABsin φ.

Начало и конец
Вектор С определяет правое направление движения шнека во время нанесения первого вектора, а именно А или B.
Изменение порядка применения векторов означает изменение знака векторного произведения.

Таким образом, действительное свойство векторного произведения выглядит следующим образом A*B= -B*A
В отличие от скалярного произведения, векторное произведение некоммутативно.

Мы встретимся с векторным произведением на протяжении всего курса физики. Это также часто встречается в механике, а также в науке об электричестве и магнетизме.
В повседневной жизни векторное произведение находится в виде момента силы во вращательном движении. Мы воздействуем на вращательное движение тем эффективнее, чем больше применяем момент силы.
При откручивании гайки гаечным ключом речь идет не только о силе F, но и о способе ее применения (длина рычага R и угол, который создает рычаг с направлением силы).

Все эти зависимости элегантно включены в одно выражение в виде векторного произведения:

Хотя составляющие вектора C, который является произведением векторного произведения векторов A и B, уже включены в его длину и направление, но имея данные составляющих векторов A и B, мы можем использовать их для определения компонентов вектора C в форме матрицы:

Удобнее всего рассчитать этот определитель, расширив относительно первой строки.
Смешанное произведение трех векторов
Смешанное произведение трех векторов является скалярным значением, равным значению детерминанта

Геометрическая интерпретация: смешанное произведение численно равно объему V параллелепипеда, растянутому по векторам A, B и C:

Циклическая корректировка векторов в смешанном произведении не меняет значение этого произведения, то есть:

Скалярное произведение двух векторов и его свойства
Определение. Скалярным произведением двух векторов  и
и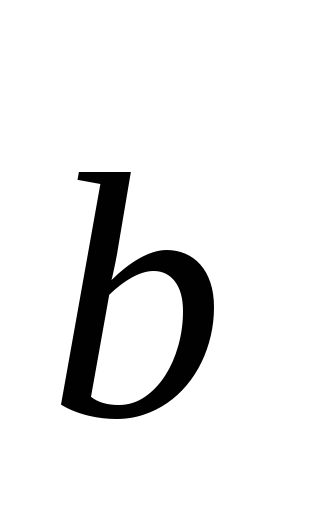 называется
число, равное произведению модулей
векторов
называется
число, равное произведению модулей
векторов и
и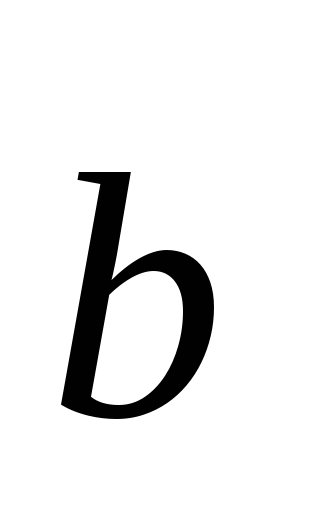 на
косинус угла между ними.
на
косинус угла между ними.
Скалярное
произведение векторов  и
и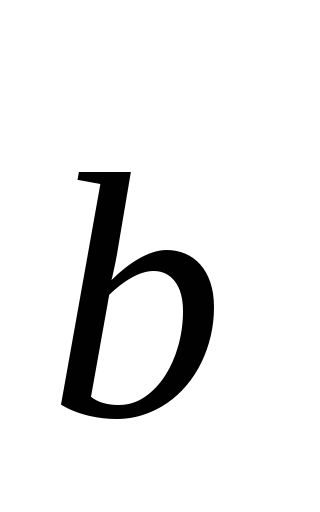 обозначают
обозначают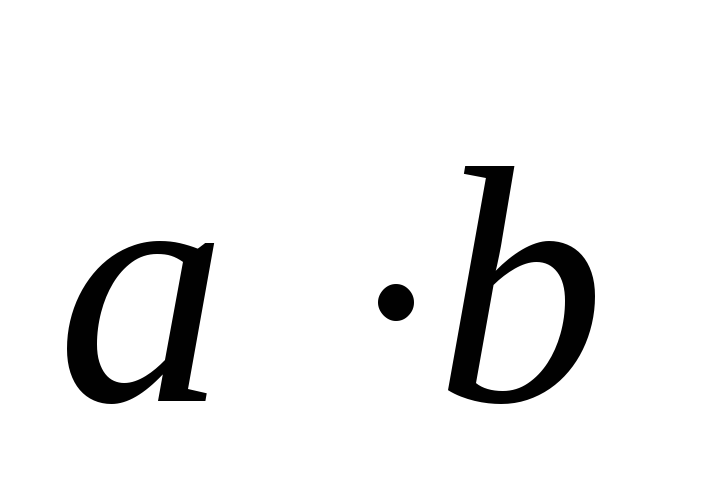 ,
или
,
или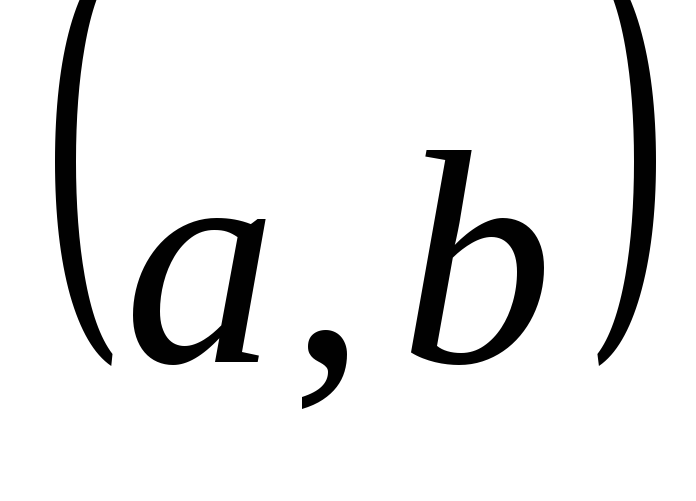
Итак, по определению
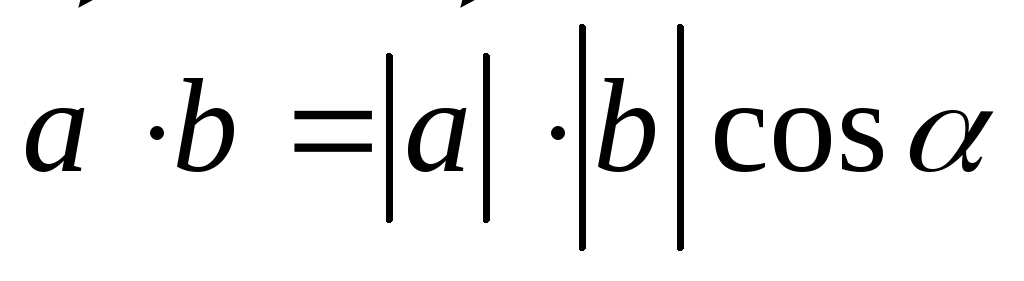 ,
,
где  —
угол между векторами
—
угол между векторами та
та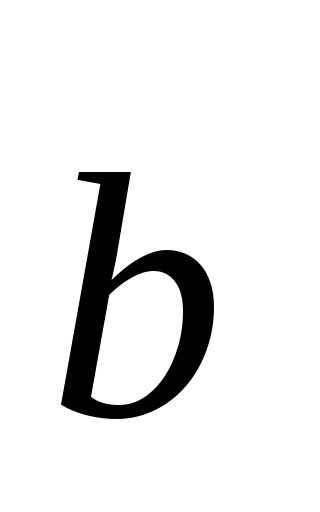 .
.
Если хотя бы один из векторов нулевой, то угол не определен и скалярное произведение по определению считают равным нулю.
Поскольку по формуле
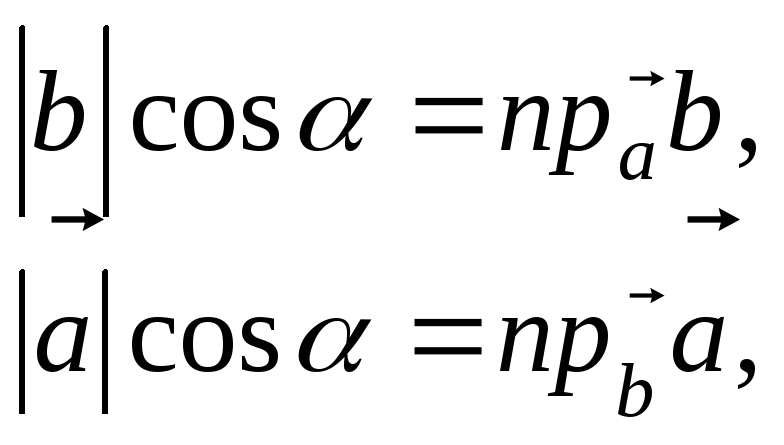
то формулу скалярного произведения можно записать еще и таким образом:
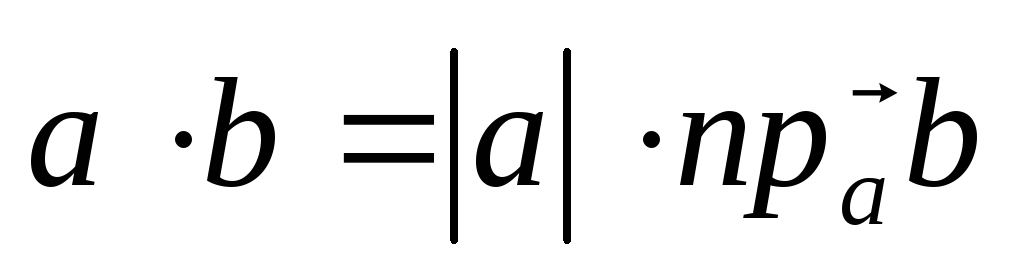
или
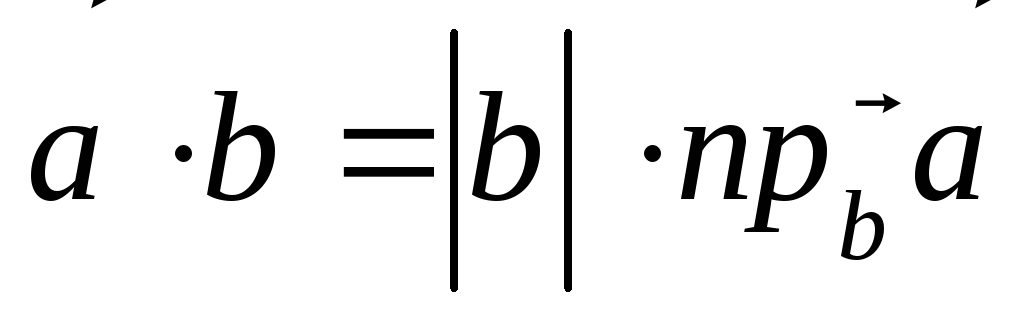 .
.
Таким образом, скалярное произведение двух векторов равно произведению модуля одного из векторов на проекцию второго вектора на направление первого.
Скалярное произведение имеет следующие свойства
1.Скалярное
произведение коммутативно, то есть для
любых векторов 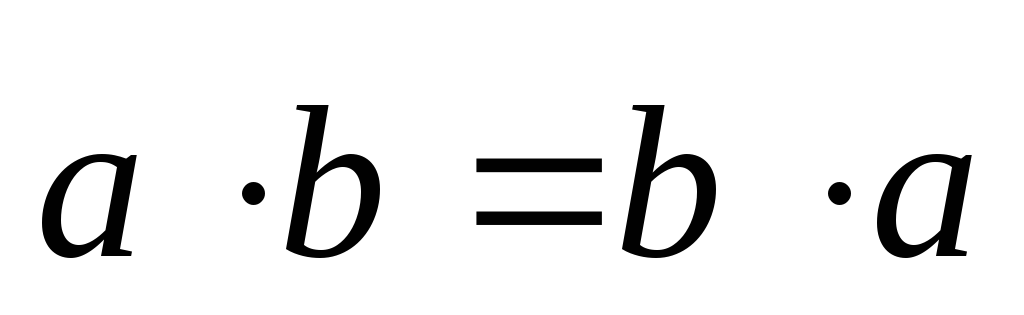 . (2.14)
. (2.14)
2. 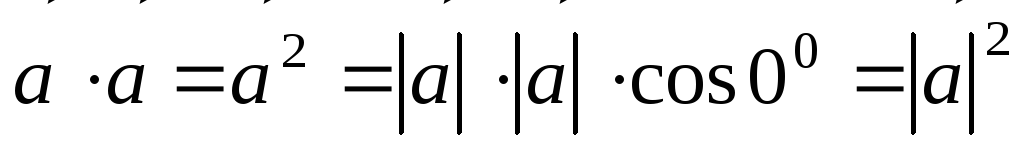 ,
т.е. для произвольного вектора его
скалярный квадрат равняется квадрату
модуля этого вектора. Отсюда
,
т.е. для произвольного вектора его
скалярный квадрат равняется квадрату
модуля этого вектора. Отсюда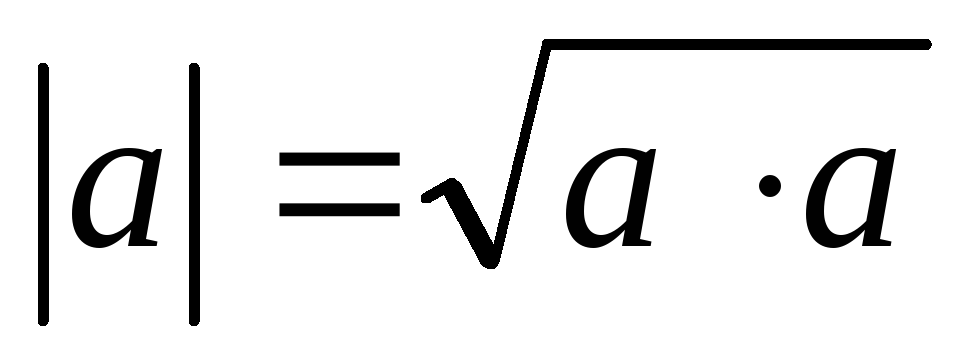 . (2.15)
. (2.15)
3. Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них равен нулю.
4.
Скалярное произведение ассоциативно
относительно скалярного множителя, то
есть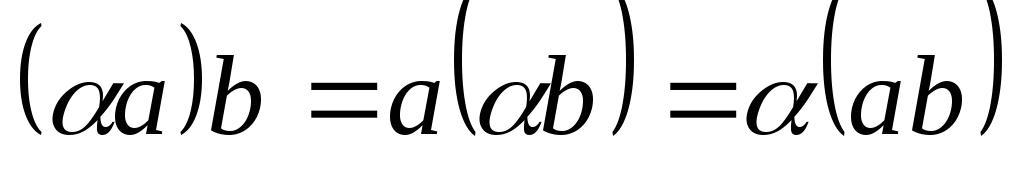
5.
Скалярное произведение дистрибутивный
относительно сложения, то есть для
произвольных трех векторов 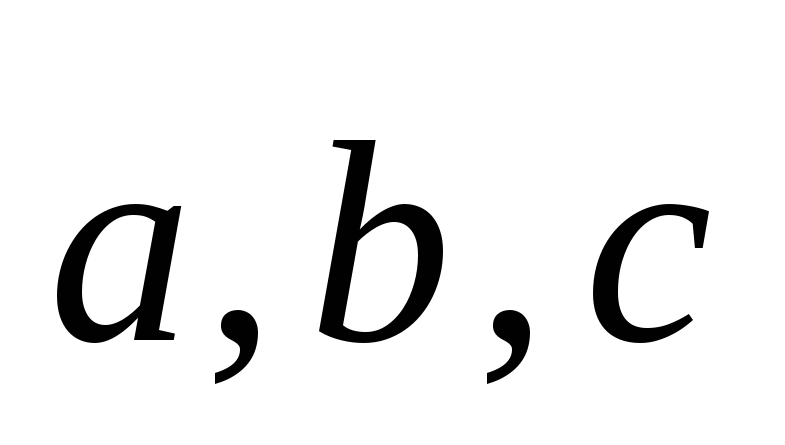 имеет место равенство
имеет место равенство
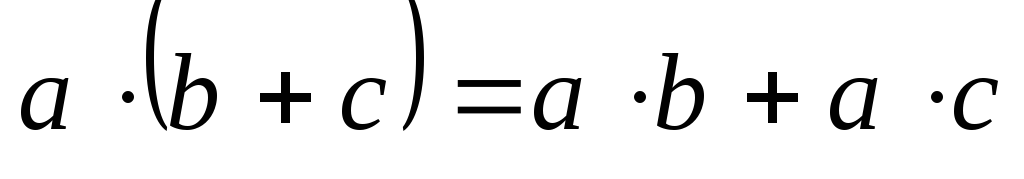 .
.
6. Векторы ортонормального базиса удовлетворяют соотношениям:
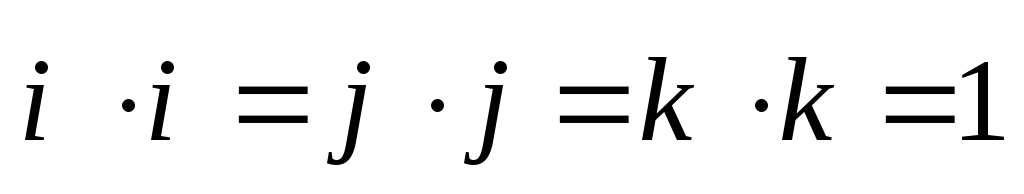 ,
,
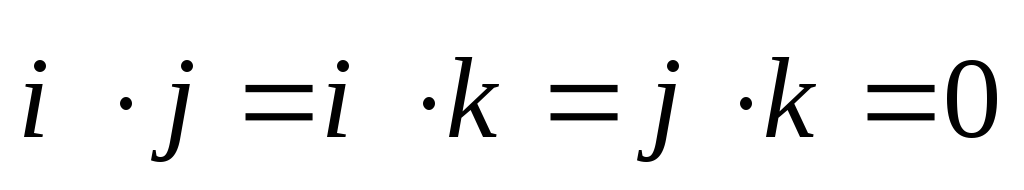 .
.
Рассмотрим
теперь два вектора  и
и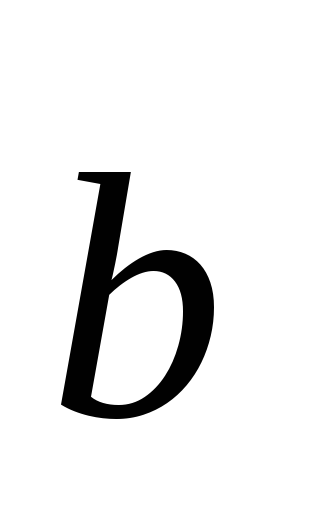 ,
которые заданы координатами в
прямоугольной системе координат:
,
которые заданы координатами в
прямоугольной системе координат: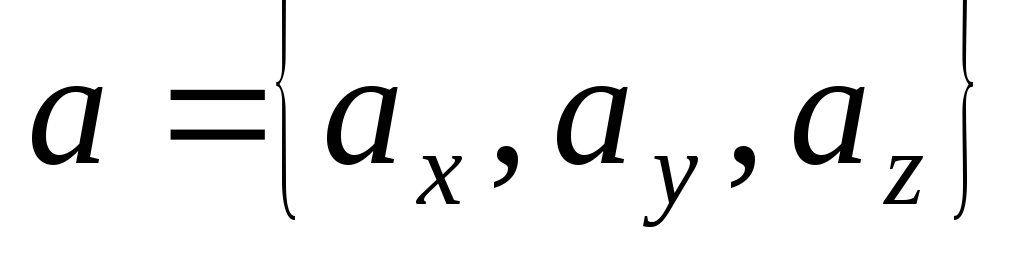 ;
;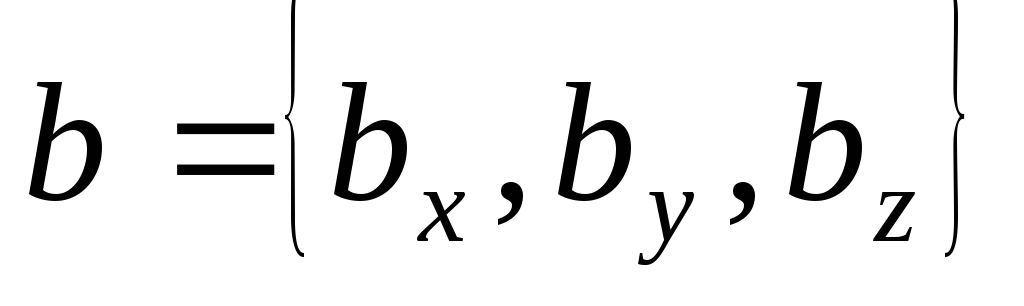 ,
,
Т.е.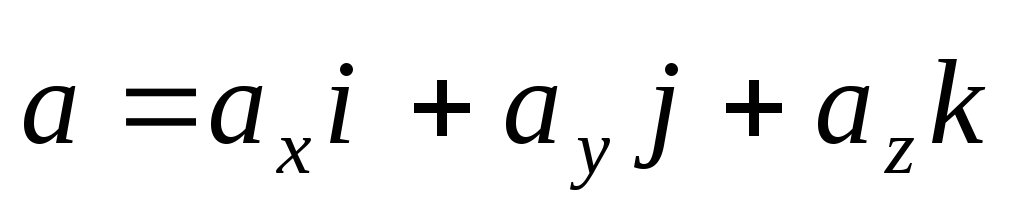 ,
,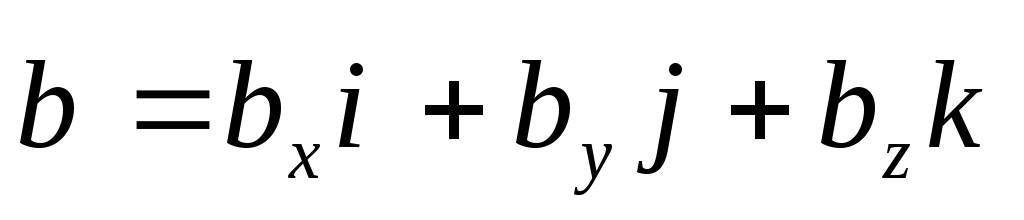
Тогда, пользуясь перечисленными свойствами скалярного произведения, получим,
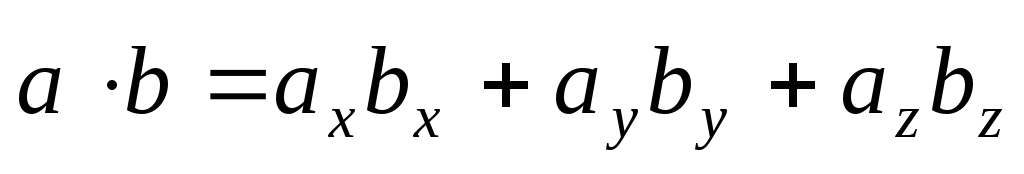 ,
скалярное произведение двух векторов
в ортонормальном базисе равно сумме
произведений их соответствующих
координат.
,
скалярное произведение двух векторов
в ортонормальном базисе равно сумме
произведений их соответствующих
координат.
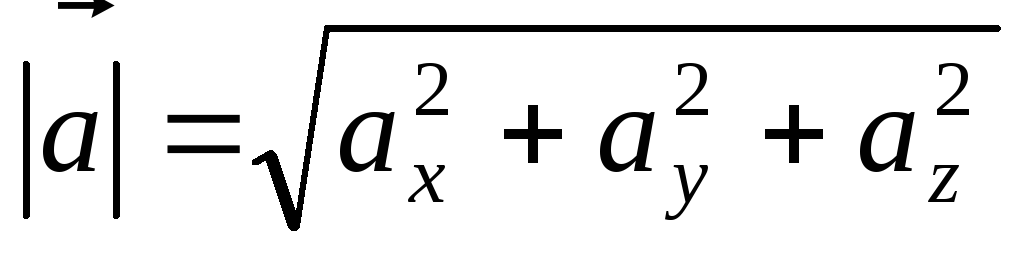 ,
модуль вектора равен корню квадратному
из суммы квадратов его координат.
,
модуль вектора равен корню квадратному
из суммы квадратов его координат.
Косинус
угла между двумя векторами 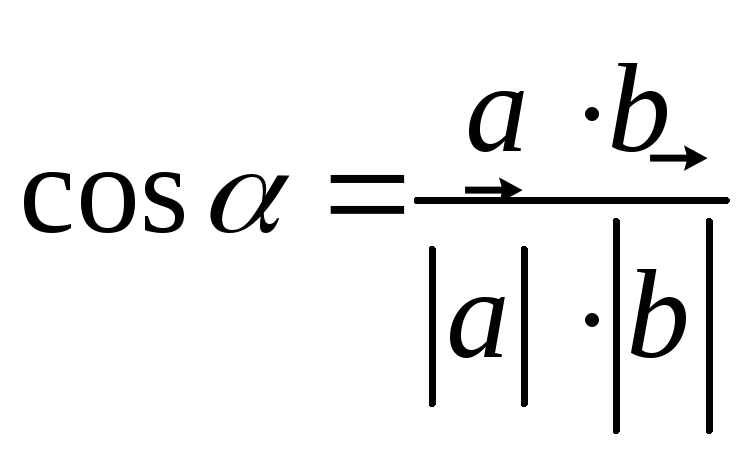 .
.
Для ортонормального базиса получим:
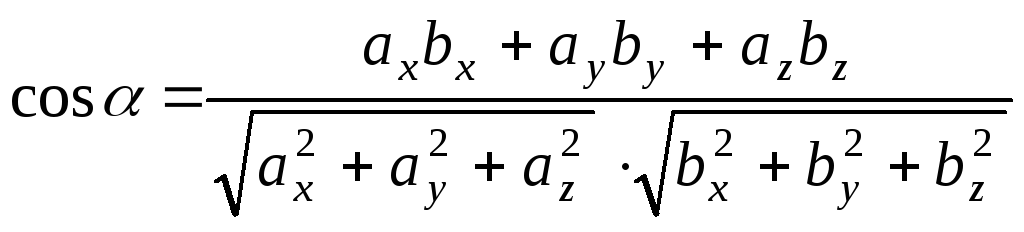
и
условие ортогональности двух векторов
приобретает вид: 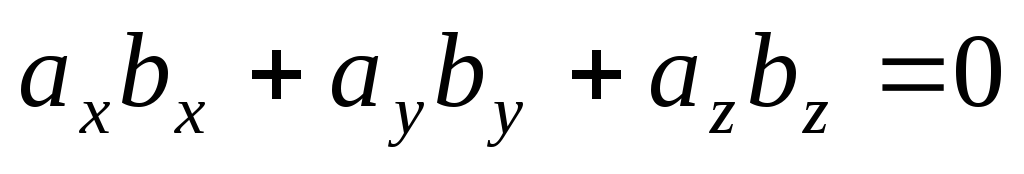 .
.
Если 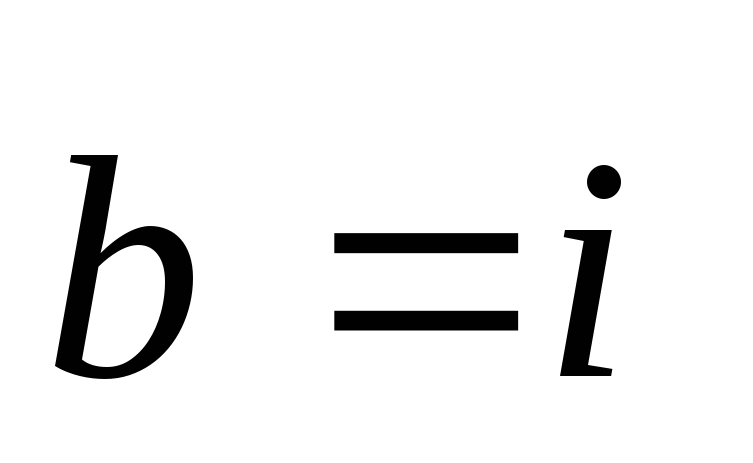 ,
,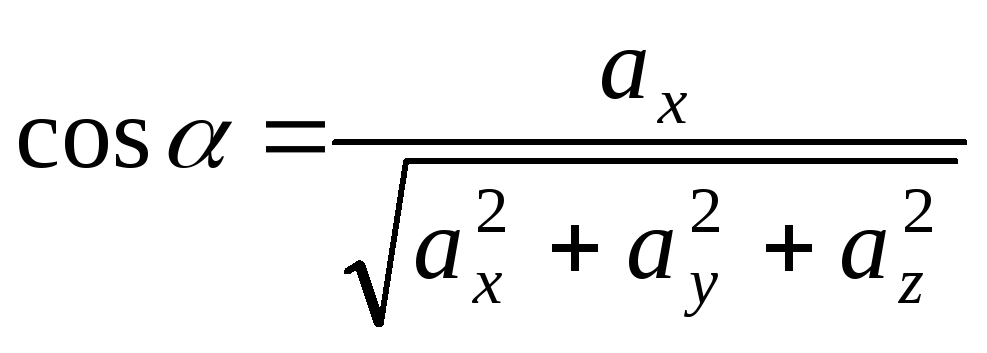 ,
,
при 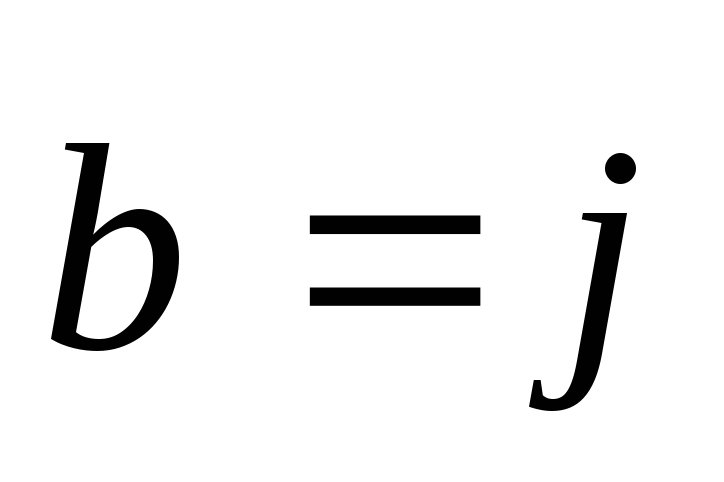
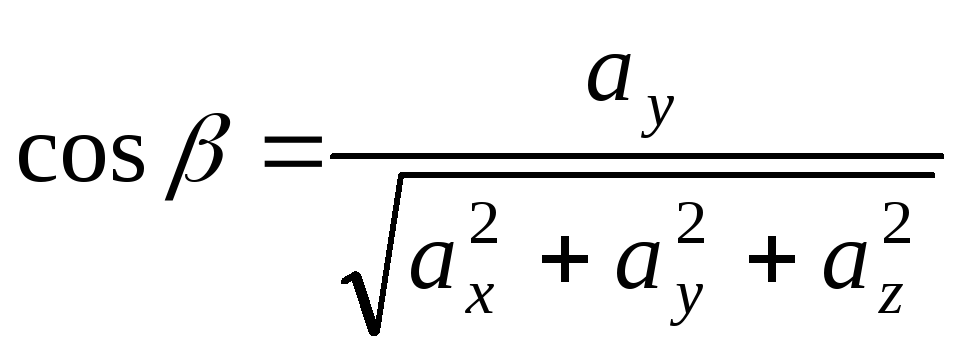 ,
,
при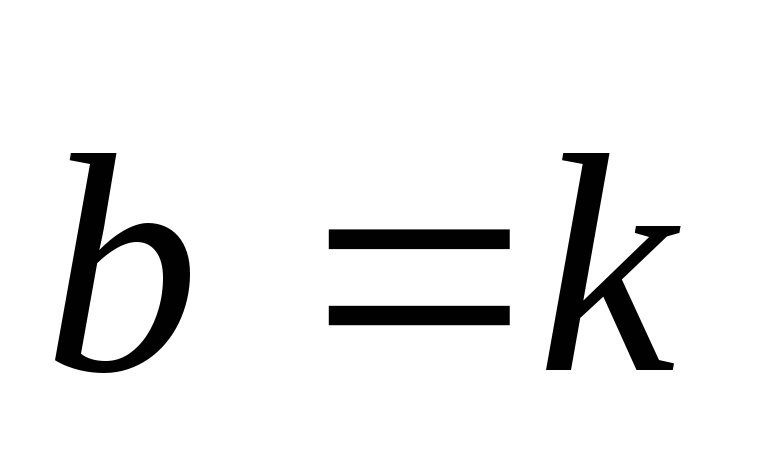
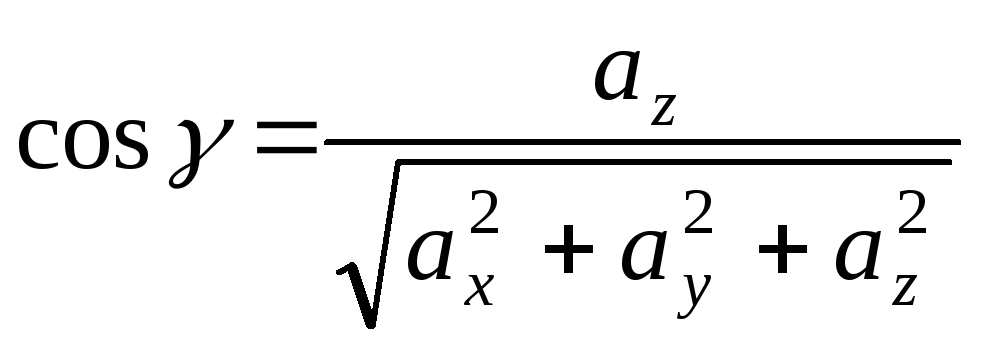 .
.Векторное произведение двух векторов, его свойства
Определение
2.21. Векторным произведением вектора  на вектор
на вектор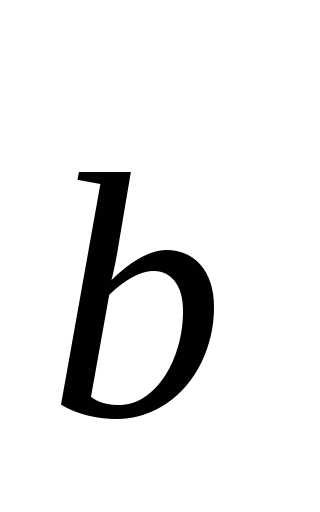 называется вектор
называется вектор (рис. 2.15), у которого: 1) длина численно
равняется площади параллелограмма,
построенного на этих векторах.
(рис. 2.15), у которого: 1) длина численно
равняется площади параллелограмма,
построенного на этих векторах.
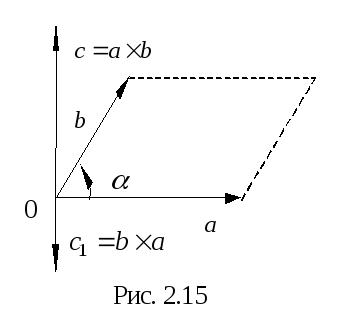
 перпендикулярен к плоскости, в которой
лежат векторы
перпендикулярен к плоскости, в которой
лежат векторы и
и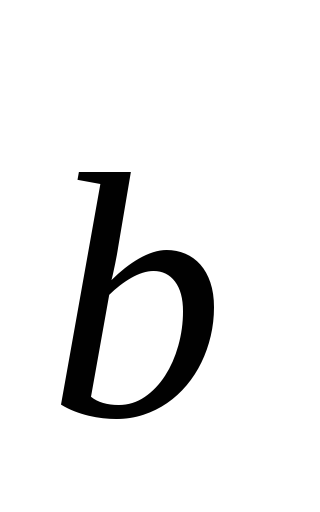 ,
т.е.
,
т.е.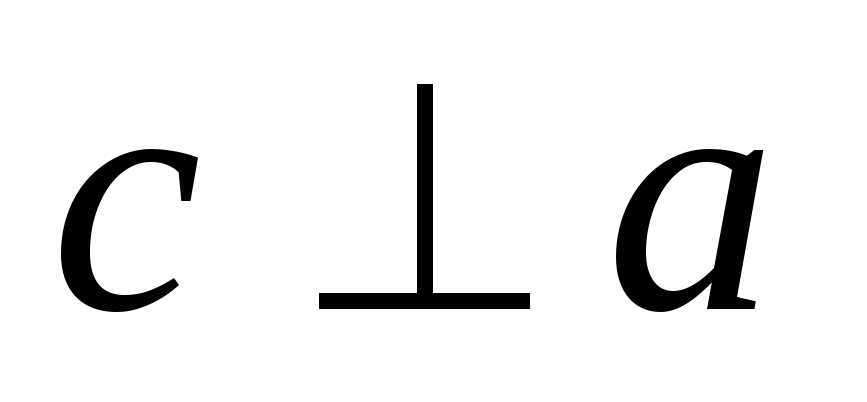 и
и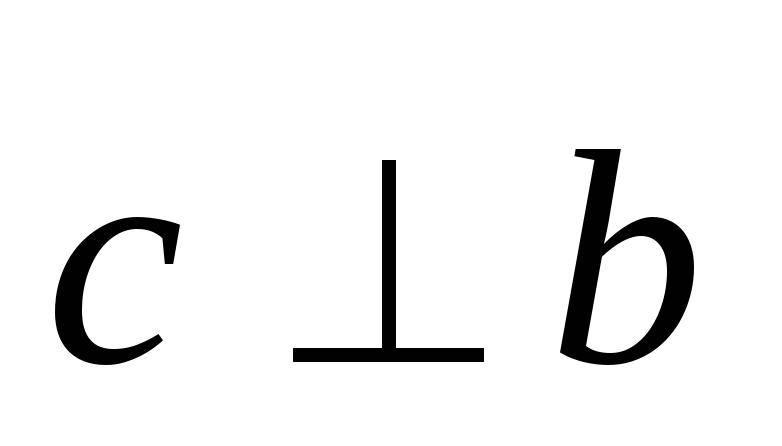 ;
;3)
вектор  направлен
таким образом, чтобы кратчайший поворот
от вектора
направлен
таким образом, чтобы кратчайший поворот
от вектора
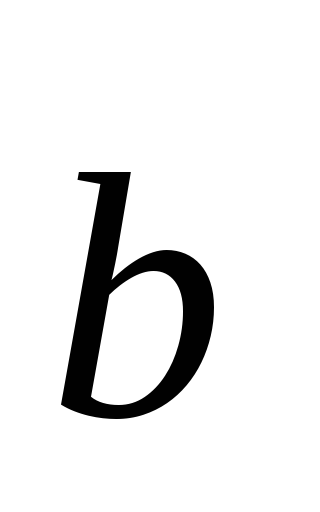 осуществлялся против часовой стрелки,
если смотреть на него из конца вектора
осуществлялся против часовой стрелки,
если смотреть на него из конца вектора .
. Векторное
произведение векторов  и
и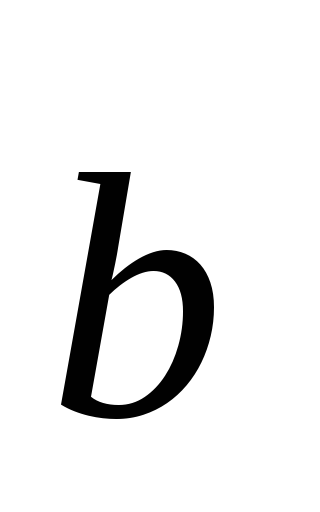 обозначается символом
обозначается символом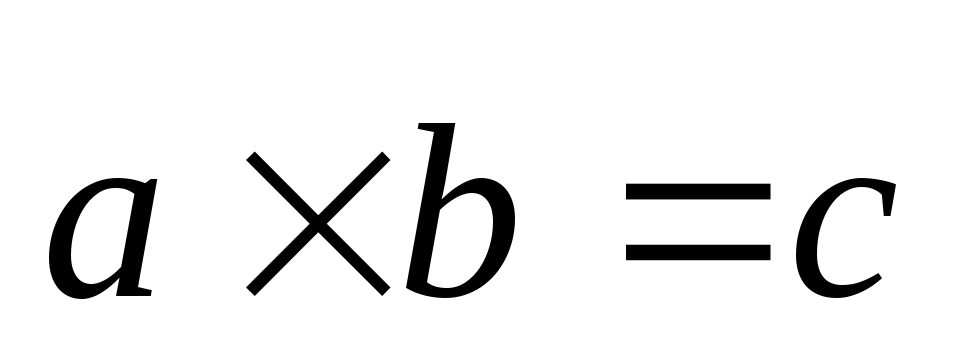 или
или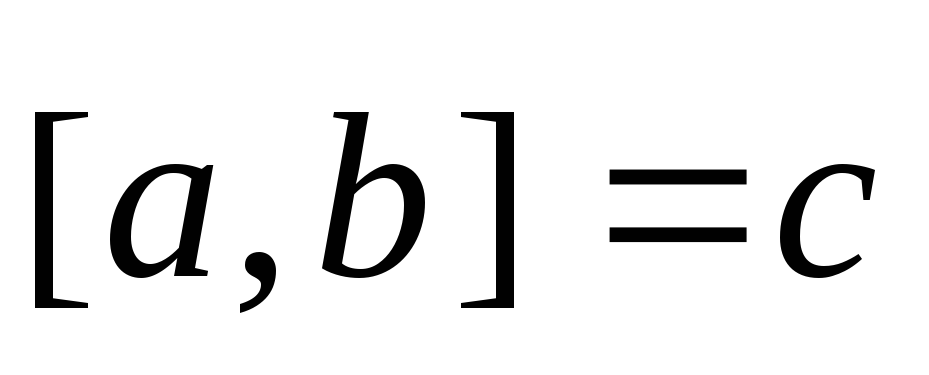
Из
определения вытекает, что 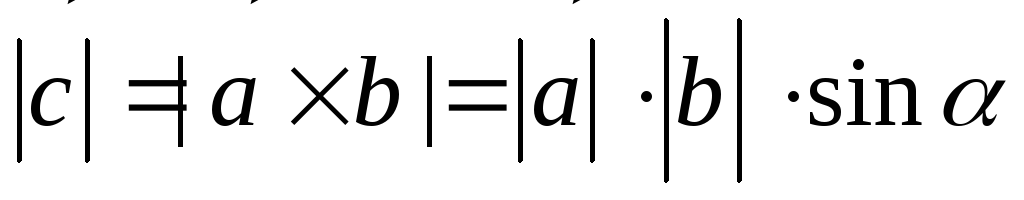 .Свойства:
.Свойства:
1) 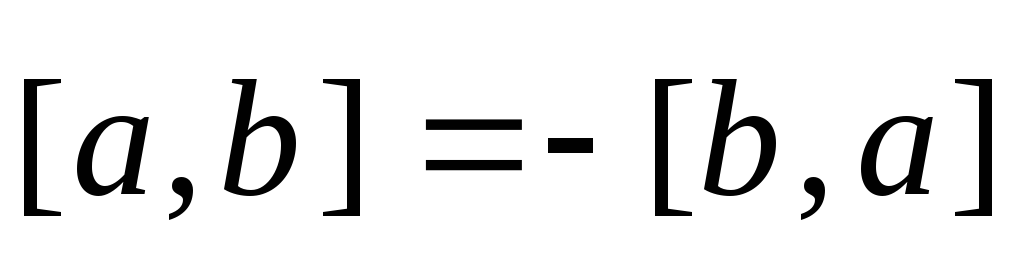 — антикоммутативность;
— антикоммутативность;
2) 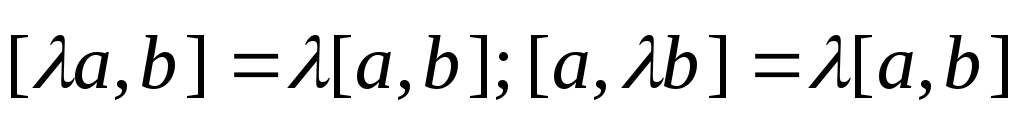 — ассоциативность относительно скалярного
множителя;
— ассоциативность относительно скалярного
множителя;
3) 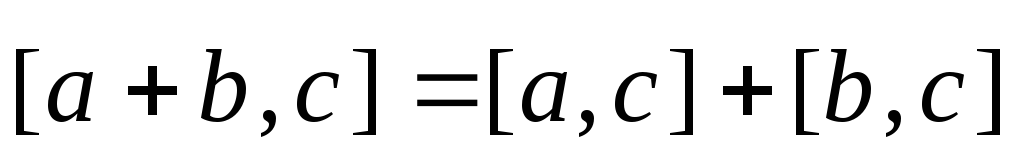 — дистрибутивность относительно сложения;
— дистрибутивность относительно сложения;
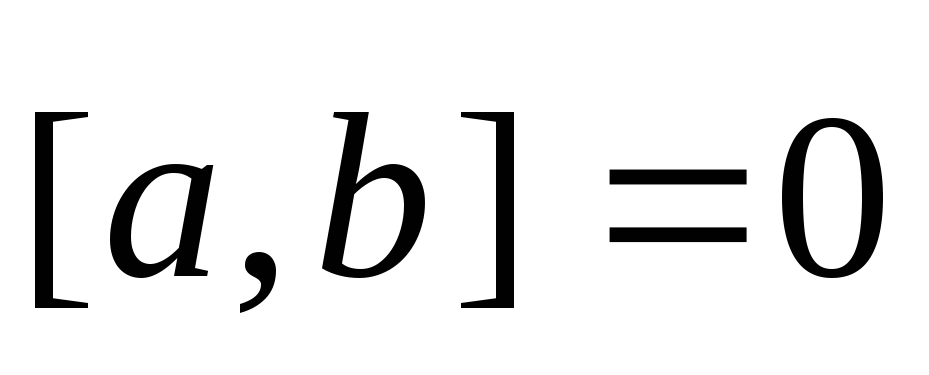 означает коллинеарность векторов
означает коллинеарность векторов и
и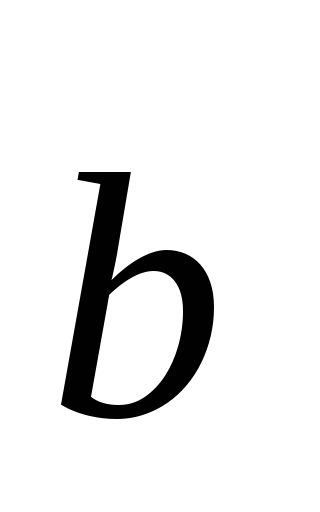 .
. Для
векторного произведения основных ортов 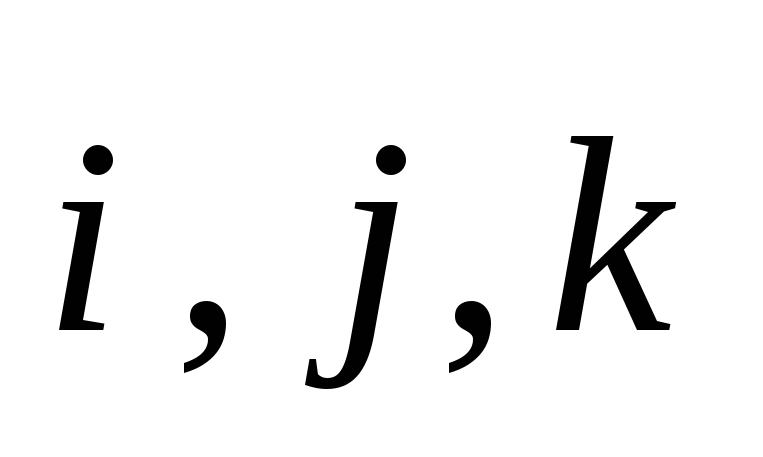 справедлива такая таблица (табл.2.1).
справедлива такая таблица (табл.2.1).
Таблица 2.1
С
использованием этой таблицы можно
доказать, что если векторы  и
и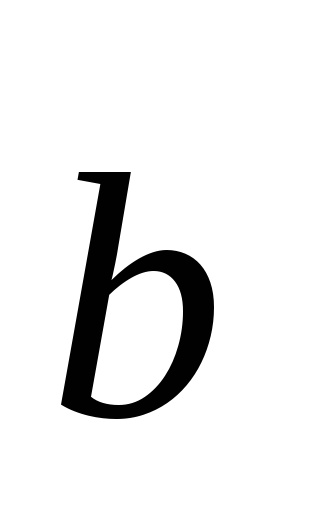
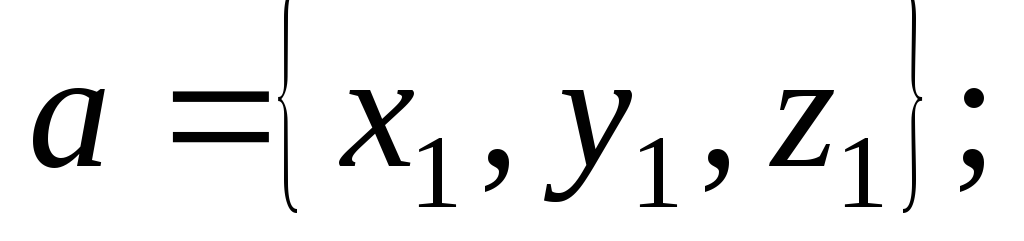
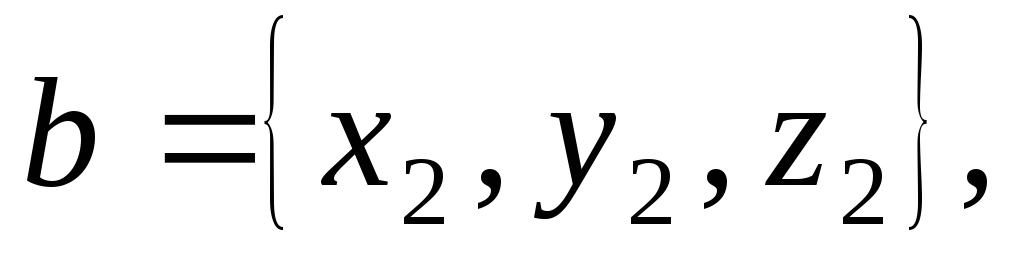 т.е.
т.е.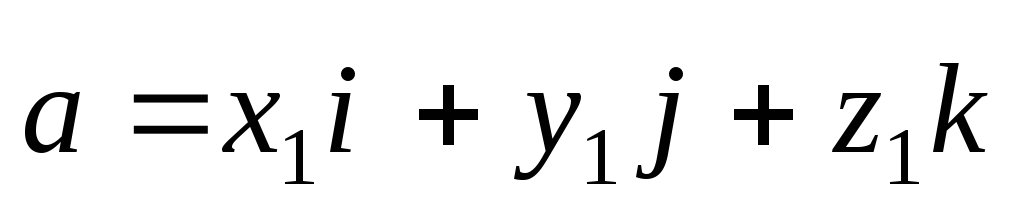 ;
; 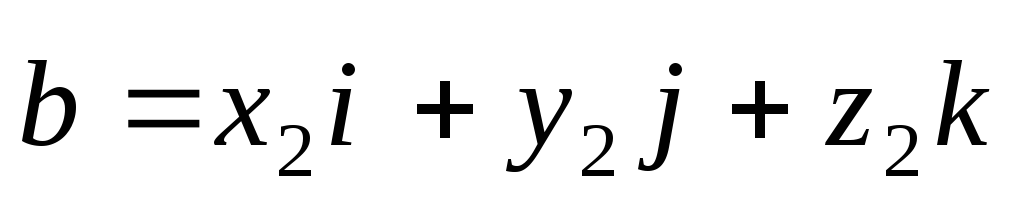 ,
,
то
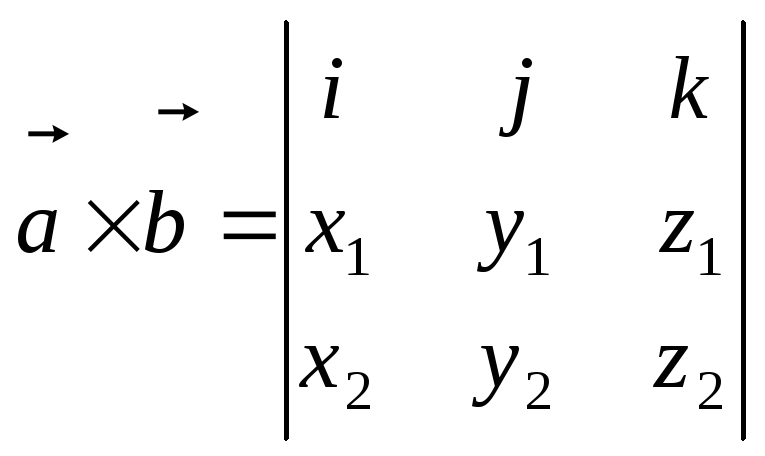 .
.
Если  и
и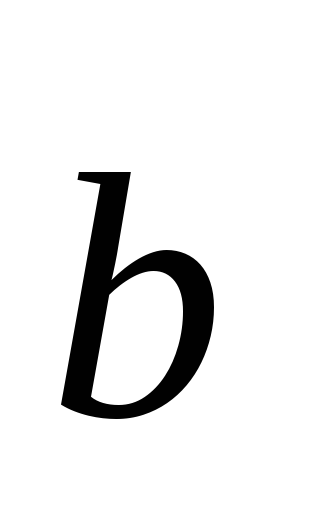 коллинеарны,
то
коллинеарны,
то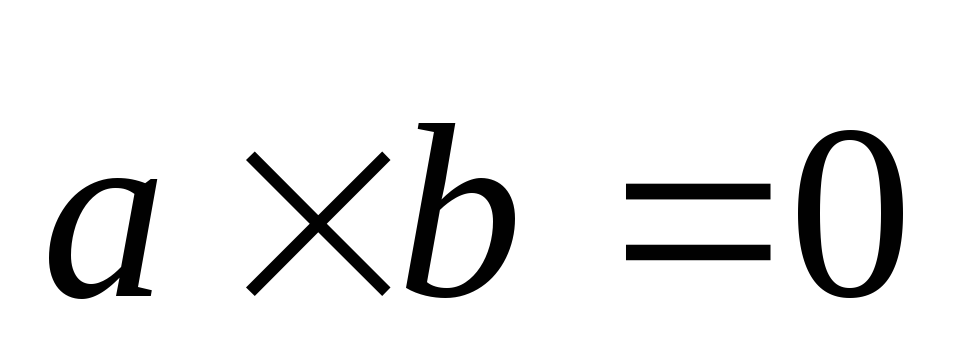 и из (2.31) получим, что
и из (2.31) получим, что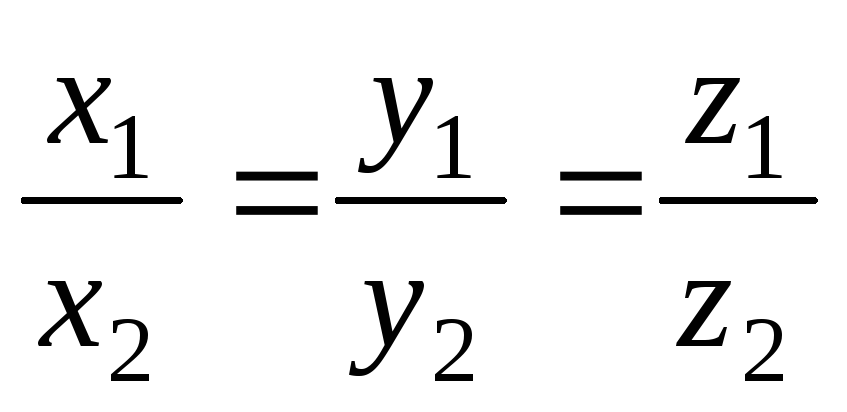 ,
—
условие коллинеарности векторов.
,
—
условие коллинеарности векторов.
Векторное
произведение может использоваться для
вычисления площади параллелограмма, а
значит, треугольника и любого плоского
многоугольника, а также для вычисления
момента силы. В случае, когда тело
неподвижно закреплено в т. ,
а в т.
,
а в т. этого тела приложена сила
этого тела приложена сила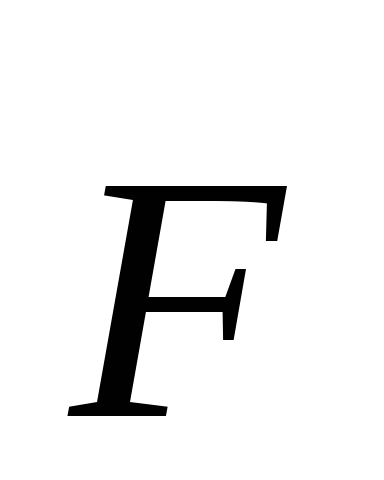 ,
тогда момент силы
,
тогда момент силы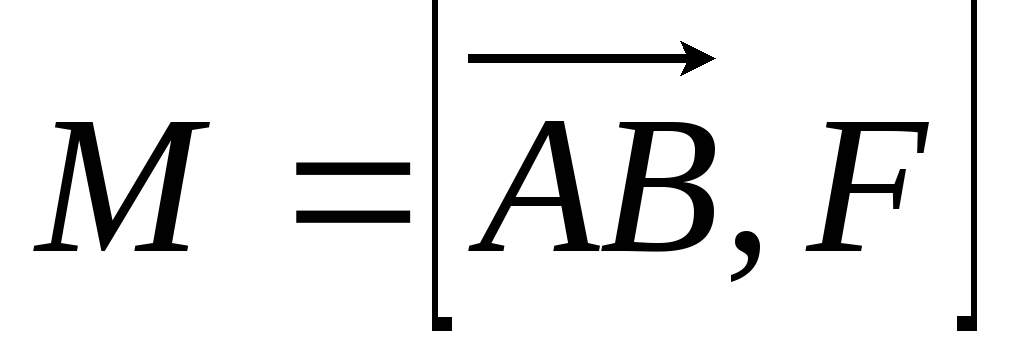 ,
а величина момента равна
,
а величина момента равна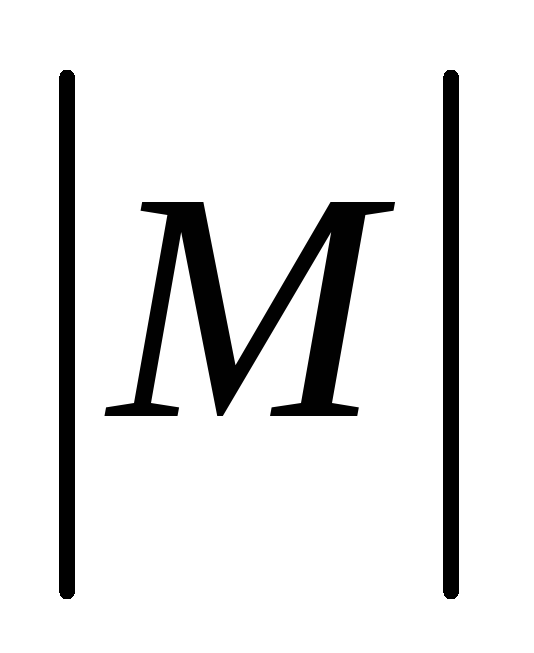 .
.
Пример Сила 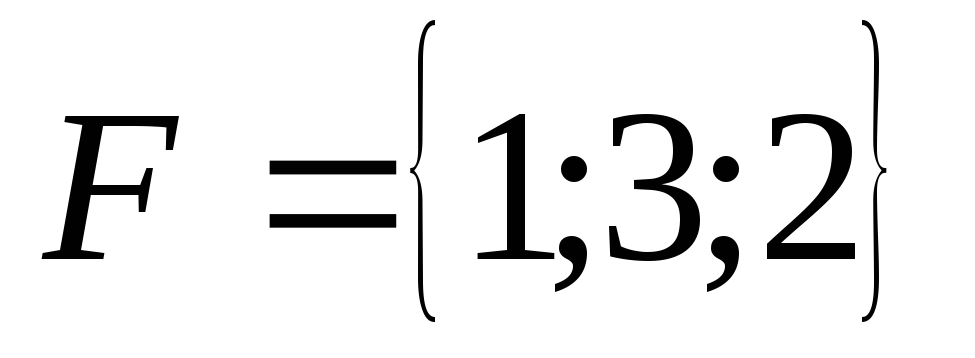 приложена к точке
приложена к точке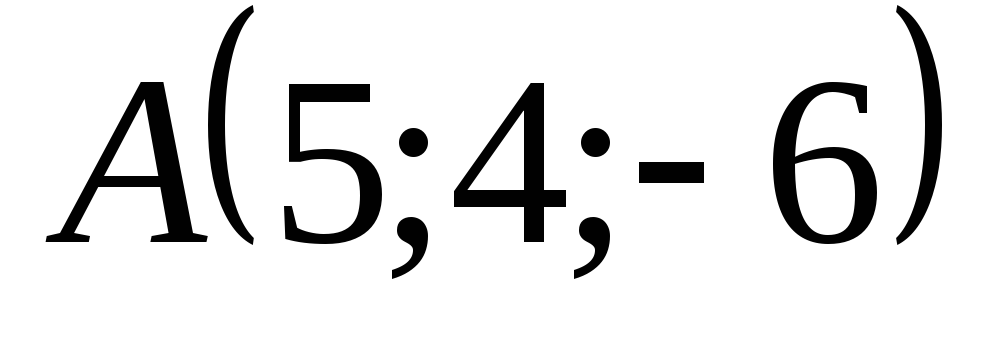 .
Определить момент этой силы относительно
начала координат.
.
Определить момент этой силы относительно
начала координат.
Скалярное произведение векторов Википедия
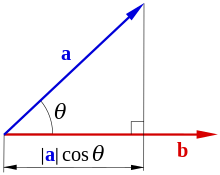 Скалярное произведение векторов (a,b){\displaystyle (\mathbf {a} ,\mathbf {b} )} равно произведению |a||b|cos(θ){\displaystyle |\mathbf {a} ||\mathbf {b} |\cos(\theta )}
Скалярное произведение векторов (a,b){\displaystyle (\mathbf {a} ,\mathbf {b} )} равно произведению |a||b|cos(θ){\displaystyle |\mathbf {a} ||\mathbf {b} |\cos(\theta )}Скаля́рное произведе́ние (иногда называемое внутренним произведением) — операция над двумя векторами, результатом которой является скаляр, то есть число, не зависящее от выбора системы координат.
Обычно для скалярного произведения векторов a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } используется одно из следующих обозначений.
- (a,b){\displaystyle (\mathbf {a} ,\mathbf {b} )}
- a⋅b, a→⋅b→{\displaystyle \mathbf {a} \cdot \mathbf {b} ,\ {\vec {a}}\cdot {\vec {b}}} или просто ab{\displaystyle \mathbf {a} \mathbf {b} }
- ⟨a,b⟩{\displaystyle \langle \mathbf {a} ,\mathbf {b} \rangle } или (обозначение Дирака, применяемое в квантовой механике для векторов состояния[1]): ⟨a|b⟩{\displaystyle \langle a|b\rangle }
В простейшем случае обычного пространства скалярное произведение ненулевых векторов a{\displaystyle \mathbf {a} } и b
12. Скалярное произведение векторов, свойства, приложения.
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
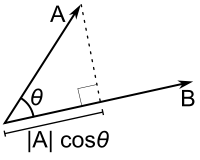
Скалярное
произведение векторов 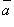 и
и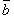 :
: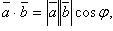 где
где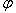 —
угол между векторами
—
угол между векторами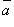 и
и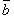 ;
если
;
если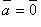 либо
либо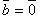 ,
то
,
то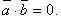 Из определения скалярного произведения
следует, что
Из определения скалярного произведения
следует, что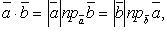 где,
например,
где,
например,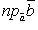 есть
величина проекции вектора
есть
величина проекции вектора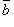 на
направление вектора
на
направление вектора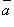 .
.
Скалярный
квадрат вектора: 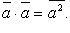
Свойства скалярного произведения:
теорема косинусов легко выводится с использованием скалярного произведения:
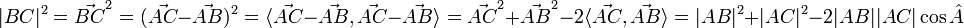
Угол между
векторами: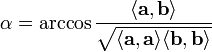
Оценка угла
между векторами: в формуле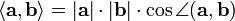 знак определяется только косинусом
угла (нормы векторов всегда положительны).
Поэтому скалярное произведение > 0,
если угол между векторами острый, и <
0, если угол между векторами тупой.
знак определяется только косинусом
угла (нормы векторов всегда положительны).
Поэтому скалярное произведение > 0,
если угол между векторами острый, и <
0, если угол между векторами тупой.
Проекция
вектора 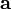 на направление, определяемое
единичным вектором
на направление, определяемое
единичным вектором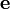 :
: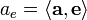 ,
,
условие
ортогональности[2] (перпендикулярности)
векторов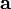 и
и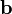 :
: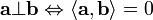
Площадь
параллелограмма, натянутого на два
вектора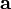 и
и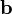 ,
равна
,
равна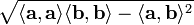
Скалярное произведение в координатах
Если 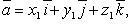
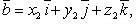 то
то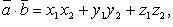
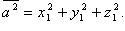
Угол между векторами
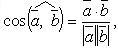
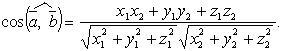
13. Векторное произведение векторов
Векторное произведение векторов.
Векторным
произведением вектора 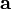 на вектор
на вектор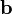 в пространстве
в пространстве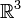 называется вектор
называется вектор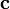 ,
удовлетворяющий следующим требованиям:
,
удовлетворяющий следующим требованиям:
длина вектора 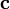 равна произведению длин векторов
равна произведению длин векторов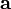 и
и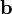 на синус угла
на синус угла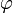 между ними:
между ними: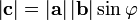 ;
;
вектор 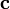 ортогонален каждому из векторов
ортогонален каждому из векторов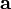 и
и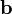 ;
;
вектор 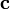 направлен так, что тройка векторов
направлен так, что тройка векторов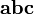 является правой.
является правой.
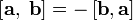
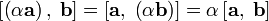
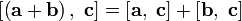
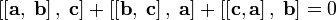
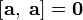
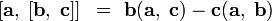
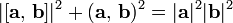
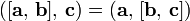
14.Смешанное произведение векторов
Сме́шанное
произведе́ние 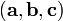 векторов
векторов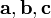 — скалярное произведение вектора
— скалярное произведение вектора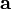 на векторное произведение векторов
на векторное произведение векторов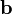 и
и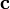 :
:
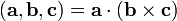 .
.
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрический
смысл: Модуль смешанного произведения
численно равен объёму параллелепипеда,
образованного векторами 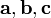 .
.
Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
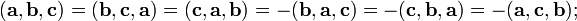

т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
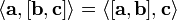
Смешанное
произведение 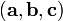 в правой декартовой системе координат
(в ортонормированном базисе) равно
определителю матрицы, составленной из
векторов
в правой декартовой системе координат
(в ортонормированном базисе) равно
определителю матрицы, составленной из
векторов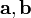 и
и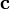 :
:
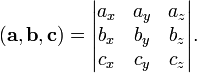
Смешанное
произведение 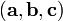 в левой декартовой системе координат
(в ортонормированном базисе) равно
определителю матрицы, составленной из
векторов
в левой декартовой системе координат
(в ортонормированном базисе) равно
определителю матрицы, составленной из
векторов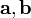 и
и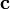 ,
взятому со знаком «минус»:
,
взятому со знаком «минус»:
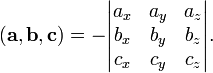
В частности,
Если любые два вектора параллельны, то с любым третьим вектором они образуют смешанное произведение равное нулю.
Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.
Геометрический
смысл — Смешанное произведение 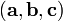 по абсолютному значению равно объёму
параллелепипеда образованного векторами
по абсолютному значению равно объёму
параллелепипеда образованного векторами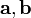 и
и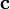 ;
знак зависит от того, является ли эта
тройка векторов правой или левой.
;
знак зависит от того, является ли эта
тройка векторов правой или левой.
15.Прямая линия на плоскости, её общее уравнение и его исследование.
Пусть на плоскости введена прямоугольная декартова система координат Оxy.
Теорема.
Всякое уравнение
первой степени вида 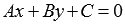 ,
где А, В и С – некоторые действительные
числа, причем А и В одновременно не равны
нулю, задает прямую линию в прямоугольной
системе координат Oxy на плоскости, и
любая прямая в прямоугольной системе
координат Oxy на плоскости задается
уравнением вида
,
где А, В и С – некоторые действительные
числа, причем А и В одновременно не равны
нулю, задает прямую линию в прямоугольной
системе координат Oxy на плоскости, и
любая прямая в прямоугольной системе
координат Oxy на плоскости задается
уравнением вида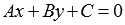 при
некотором наборе значений A, B и C.
при
некотором наборе значений A, B и C.
Докажемсначала, что уравнение вида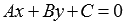 задает
прямую на плоскости.
задает
прямую на плоскости.
Пусть координаты
точки 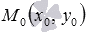 удовлетворяют
уравнению
удовлетворяют
уравнению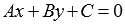 ,
то есть,
,
то есть,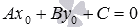 .
Вычтем из левой и правой частей уравнения
.
Вычтем из левой и правой частей уравнения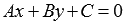 соответственно
левую и правую части равенства
соответственно
левую и правую части равенства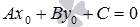 ,
при этом получаем уравнение вида
,
при этом получаем уравнение вида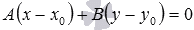 ,
которое эквивалентно
,
которое эквивалентно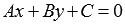 .
.
Уравнение 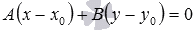 представляет
собой необходимое и достаточное условие
перпендикулярности двух векторов
представляет
собой необходимое и достаточное условие
перпендикулярности двух векторов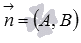 и
и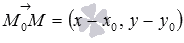 .
То есть, множество всех точек
.
То есть, множество всех точек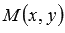 определяет
в прямоугольной системе координат Oxy
прямую линию, перпендикулярную направлению
вектора
определяет
в прямоугольной системе координат Oxy
прямую линию, перпендикулярную направлению
вектора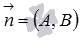 .
Если бы это было не так, то векторы
.
Если бы это было не так, то векторы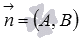 и
и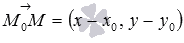 не
были бы перпендикулярными и равенство
не
были бы перпендикулярными и равенство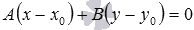 не
выполнялось бы.
не
выполнялось бы.
Таким образом,
уравнение 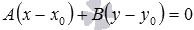 задает
прямую линию в прямоугольной декартовой
системе координат Oxy на плоскости,
следовательно, эквивалентное ему
уравнение вида
задает
прямую линию в прямоугольной декартовой
системе координат Oxy на плоскости,
следовательно, эквивалентное ему
уравнение вида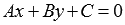 задает
эту же прямую. На этом первая часть
теоремы доказана.
задает
эту же прямую. На этом первая часть
теоремы доказана.
Теперь докажем,
что всякая прямая в прямоугольной
системе координат Oxy на плоскости
определяется уравнением первой степени
вида 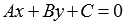 .
.
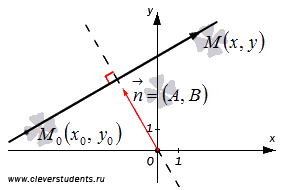
Пусть в
прямоугольной системе координат Oxy на
плоскости задана прямая a,
проходящая через точку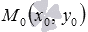 ,
,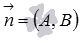 —
нормальный вектор прямойa, и пусть
—
нормальный вектор прямойa, и пусть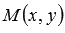 —
плавающая точка этой прямой. Тогда
векторы
—
плавающая точка этой прямой. Тогда
векторы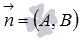 и
и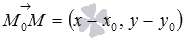 перпендикулярны,
следовательно, их скалярное произведение
равно нулю, то есть,
перпендикулярны,
следовательно, их скалярное произведение
равно нулю, то есть, .
Полученное равенство можно переписать
в виде
.
Полученное равенство можно переписать
в виде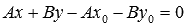 .
Если принять
.
Если принять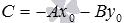 ,
то получим уравнение
,
то получим уравнение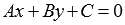 ,
которое соответствует прямойa.
,
которое соответствует прямойa.
На этом доказательство теоремы завершено.
Скалярное произведение векторов — Викиверситет
Пусть a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } — два ненулевых вектора. Если отложить их от одной точки O{\displaystyle O}, получится угол между этими векторами (точнее между несущими их полупрямыми, исходящими из точки O{\displaystyle O}). Этот угол обозначают a,b^{\displaystyle {\widehat {\mathbf {a} ,\mathbf {b} }}}.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
a⋅b=(a,b)=|a||b|cos(a,b^){\displaystyle \mathbf {a} \cdot \mathbf {b} =(\mathbf {a} ,\mathbf {b} )=|\mathbf {a} ||\mathbf {b} |\cos({\widehat {\mathbf {a} ,\mathbf {b} }})}
Если один из векторов нулевой, то угол не определен, и произведение считают равным нулю.
Свойства скалярного произведения:
- Коммутативность: a⋅b=b⋅a{\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} }
- Линейность по первому аргументу: (a1+a2)⋅b=a1⋅b+a2⋅b{\displaystyle (\mathbf {a} _{1}+\mathbf {a} _{2})\cdot \mathbf {b} =\mathbf {a} _{1}\cdot \mathbf {b} +\mathbf {a} _{2}\cdot \mathbf {b} } и (αa)⋅b=α(a⋅b){\displaystyle (\alpha \mathbf {a} )\cdot \mathbf {b} =\alpha (\mathbf {a} \cdot \mathbf {b} )}
- Положительная определенность: a⋅a=|a|2≥0{\displaystyle \mathbf {a} \cdot \mathbf {a} =|\mathbf {a} |^{2}\geq 0}, причем a⋅a=0{\displaystyle \mathbf {a} \cdot \mathbf {a} =0} тогда и только тогда, когда a=0{\displaystyle \mathbf {a} =\mathbf {0} }
Геометрический смысл скалярного произведения[править]
Связь с проекциями[править]
Алгебраическое значение проекции вектора a{\displaystyle \mathbf {a} } на вектор b{\displaystyle \mathbf {b} } вдоль прямой, перпендикулярной b{\displaystyle \mathbf {b} }, очевидно, равно
| |prba|=|a|cos(a,b^){\displaystyle |\mathrm {pr} _{\mathbf {b} }\mathbf {a} |=|\mathbf {a} |\cos({\widehat {\mathbf {a} ,\mathbf {b} }})} |
Аналогично
| |prab|=|b|cos(a,b^){\displaystyle |\mathrm {pr} _{\mathbf {a} }\mathbf {b} |=|\mathbf {b} |\cos({\widehat {\mathbf {a} ,\mathbf {b} }})} |
Таким образом, скалярное произведение
| a⋅b=|a||prab|=|b||prba|{\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathrm {pr} _{\mathbf {a} }\mathbf {b} |=|\mathbf {b} ||\mathrm {pr} _{\mathbf {b} }\mathbf {a} |} |
Связь с длинами[править]
Рассмотрим скалярное произведение вектора на самого себя.
| a⋅a=|a||a|cos(a,a^)=|a|2{\displaystyle \mathbf {a} \cdot \mathbf {a} =|\mathbf {a} ||\mathbf {a} |\cos({\widehat {\mathbf {a} ,\mathbf {a} }})=|\mathbf {a} |^{2}} |
Связь с углами[править]
Рассмотрим скалярное произведение единичных векторов. Поскольку их длины равны 1, то
| a⋅b=|a||b|cos(a,b^)=cos(a,b^){\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos({\widehat {\mathbf {a} ,\mathbf {b} }})=\cos({\widehat {\mathbf {a} ,\mathbf {b} }})} |
Скалярное произведение в ортонормированной системе координат[править]
Пусть заданы координаты двух векторов a={a1,a2,a3}{\displaystyle \mathbf {a} =\{a_{1},a_{2},a_{3}\}} и b={b1,b2,b3}{\displaystyle \mathbf {b} =\{b_{1},b_{2},b_{3}\}} в ортонормированной системе координат.
| a⋅b=(a1e1+a2e2+a3e3)⋅(b1e1+b2e2+b3e3)==a1b1e1⋅e1+a2b2e2⋅e2+a3b3e3⋅e3+(a1b2+a2b1)e1⋅e2+(a1b3+a3b1)e1⋅e3+(a2b3+a3b2)e2⋅e3{\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=(a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\mathbf {e} _{3})\cdot (b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2}+b_{3}\mathbf {e} _{3})=\\&=a_{1}b_{1}\mathbf {e} _{1}\cdot \mathbf {e} _{1}+a_{2}b_{2}\mathbf {e} _{2}\cdot \mathbf {e} _{2}+a_{3}b_{3}\mathbf {e} _{3}\cdot \mathbf {e} _{3}+(a_{1}b_{2}+a_{2}b_{1})\mathbf {e} _{1}\cdot \mathbf {e} _{2}+(a_{1}b_{3}+a_{3}b_{1})\mathbf {e} _{1}\cdot \mathbf {e} _{3}+(a_{2}b_{3}+a_{3}b_{2})\mathbf {e} _{2}\cdot \mathbf {e} _{3}\end{aligned}}} |
В ортонормированной системе координат e1⋅e1=e2⋅e2=e3⋅e3=1{\displaystyle \mathbf {e} _{1}\cdot \mathbf {e} _{1}=\mathbf {e} _{2}\cdot \mathbf {e} _{2}=\mathbf {e} _{3}\cdot \mathbf {e} _{3}=1} и e1⋅e2=e1⋅e3=e2⋅e3=0{\displaystyle \mathbf {e} _{1}\cdot \mathbf {e} _{2}=\mathbf {e} _{1}\cdot \mathbf {e} _{3}=\mathbf {e} _{2}\cdot \mathbf {e} _{3}=0}, так как cos0=1,cosπ2=0{\displaystyle \cos 0=1,\;\cos {\tfrac {\pi }{2}}=0}. Поэтому
| a⋅b=a1b1+a2b2+a3b3{\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}} |
Аксиоматический подход[править]
При аксиоматическом подходе скалярное произведение определяется как некоторая функция, аргументы которой — два вектора, результат — число, не зависящее от системы координат, обладающее свойствами:
- Коммутативность
- Линейность по первому аргументу
- Положительная определенность
Тогда производными понятиями становятся
- Длина вектора — число, вычисляемое по правилу |a|=a⋅a{\displaystyle |\mathbf {a} |={\sqrt {\mathbf {a} \cdot \mathbf {a} }}}
- Угол между ненулевыми векторами — число, косинус которого cos(a,b^)=a⋅b|a||b|{\displaystyle \cos({\widehat {\mathbf {a} ,\mathbf {b} }})={\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} ||\mathbf {b} |}}}
- Ортогональные (перпендикулярные) векторы — векторы, скалярное произведение которых равно 0.
Задачи
Скалярное, векторное и смешанное произведение
векторы. ДЕЙСТВИЯ НАД векторами. Скалярное,
ВЕКТОРНОЕ, СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
1. Векторы, Действия над векторами.
Основные определения.
Определение 1. Величина, полностью характеризуемая своим числовым значением в выбранной системе единиц, называется скалярной или скаляром.
(Масса тела, объем, время и т.д.)
Определение 2. Величина, характеризуемая числовым значением и направлением, называется векторной или вектором.
(Перемещение, сила, скорость и т.д.)
Обозначения: 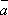 ,
, 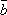 или
или 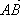 ,
, 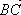 .
.
Геометрический вектор – это направленный отрезок.
Для
вектора 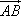 –
точка А – начало, точка В – конец вектора.
–
точка А – начало, точка В – конец вектора.
Определение 3. Модуль вектора – это длина отрезка AB.
Определение
4. Вектор,
модуль которого равен нулю, называется нулевым, обозначается  .
.
Определение 5. Векторы, расположенные на параллельных прямых или на одной прямой называются коллинеарными. Если два коллинеарных вектора имеют одинаковое направление, то они называются сонаправленными.
Определение 6. Два вектора считаются равными, если они сонаправлены и равны по модулю.
Действия над векторами.
1) Сложение векторов.
Опр.
6. Суммой двух векторов 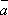 и
и 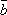 является
диагональ параллелограмма, построенного
на этих векторах, исходящая из общей
точки их приложения (правило
параллелограмма).
является
диагональ параллелограмма, построенного
на этих векторах, исходящая из общей
точки их приложения (правило
параллелограмма).
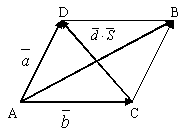
Рис.1.
Опр.
7. Суммой трех
векторов 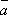 ,
, 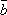 ,
,  называется
диагональ параллелепипеда, построенного
на этих векторах (правило
параллелепипеда).
называется
диагональ параллелепипеда, построенного
на этих векторах (правило
параллелепипеда).
Опр. 8. Если А, В, С –
произвольные точки, то 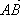 +
+ 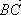 =
= 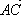 (правило
треугольника).
(правило
треугольника).
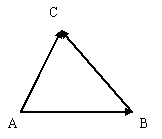
рис.2
Свойства сложения.
1о. 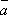 +
+ 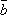 =
= 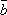 +
+ 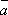 (переместительный
закон).
(переместительный
закон).
2о. 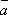 +
(
+
(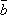 +
+  )
= (
)
= (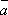 +
+ 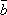 )
+
)
+  =
(
=
(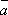 +
+  )
+
)
+ 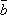 (сочетательный
закон).
(сочетательный
закон).
3о. 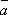 +
(–
+
(–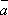 )
+
)
+  .
.
2) Вычитание векторов.
Опр.
9. Под разностью векторов 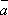 и
и 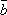 понимают
вектор
понимают
вектор 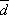 =
= 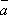 –
– 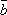 такой,
что
такой,
что 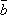 +
+ 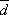 =
= 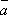 .
.
В параллелограмме – это другая диагональ СД (см.рис.1).
3) Умножение вектора на число.
Опр.
10. Произведением вектора 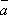 на скаляр k называется вектор
на скаляр k называется вектор
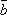 = k
= k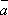 =
= 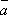 k,
k,
имеющий длину ka, и направление, которого:
1.
совпадает
с направлением вектора 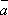 ,
если k > 0;
,
если k > 0;
2.
противоположно
направлению вектора 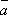 ,
если k < 0;
,
если k < 0;
3. произвольно, если k = 0.
Свойства умножения вектора на число.
1о. (k
+ l)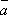 = k
= k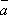 +
l
+
l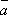 .
.
k(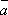 +
+ 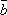 )
= k
)
= k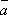 + k
+ k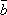 .
.
2o. k(l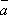 )
= (kl)
)
= (kl)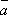 .
.
3o. 1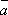 =
= 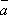 , (–1)
, (–1) 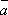 = –
= – 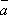 , 0
, 0 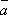 =
=  .
.
Свойства векторов.
Опр.
11. Два
вектора 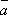 и
и 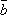 называются коллинеарными,
если они расположены на параллельных
прямых или на одной
прямой.
называются коллинеарными,
если они расположены на параллельных
прямых или на одной
прямой.
Нулевой
вектор  коллинеарен
любому вектору.
коллинеарен
любому вектору.
Теорема
1. Два ненулевых вектора 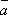 и
и 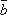 коллинеарны,
когда они пропорциональны т.е.
коллинеарны,
когда они пропорциональны т.е.
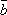 = k
= k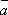 , k – скаляр.
, k – скаляр.
Опр.
12. Три вектора 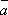 ,
, 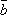 ,
,  называются компланарными,
если они параллельны некоторой плоскости
или лежат в ней.
называются компланарными,
если они параллельны некоторой плоскости
или лежат в ней.
Теорема
2. Три ненулевых вектора 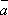 ,
, 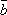 ,
,  компланарны,
когда один из них является линейной
комбинацией двух других, т.е.
компланарны,
когда один из них является линейной
комбинацией двух других, т.е.
 = k
= k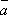 + l
+ l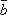 , k ,l –
скаляры.
, k ,l –
скаляры.
Проекция вектора на ось.
Теорема
3. Проекция
вектора 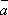 на
ось (направленная прямая) l равна произведению длины вектора
на
ось (направленная прямая) l равна произведению длины вектора 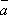 на
косинус угла между направлением вектора
и направлением оси, т.е.
на
косинус угла между направлением вектора
и направлением оси, т.е. 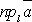 = a cos , =
(
= a cos , =
(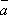 , l).
, l).
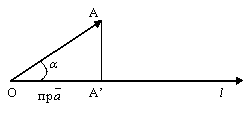
рис.3.
2. Координаты вектора
Опр.
13. Проекции вектора 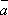 на
координатные оси Ох, Оу, Оz называются координатами
вектора. Обозначение:
на
координатные оси Ох, Оу, Оz называются координатами
вектора. Обозначение: 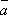 ax, ay, az.
ax, ay, az.
Длина
вектора: 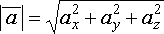

Пример: Вычислить
длину вектора 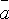
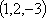 .
.
Решение: 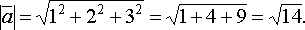
Расстояние
между точками 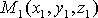 и
и 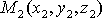 вычисляется
по формуле:
вычисляется
по формуле:
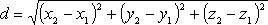 .
.
Пример: Найти расстояние между точками М (2,3,-1) и К (4,5,2).

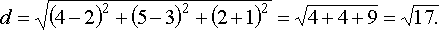
Действия над векторами в координатной форме.
Даны
векторы 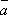 =ax, ay, az
и
=ax, ay, az
и 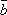 =bx, by, bz.
=bx, by, bz.
1. (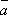
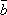 )=ax bx, ay by, az bz.
)=ax bx, ay by, az bz.
2. 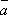 =ax, ay, az,
где – скаляр.
=ax, ay, az,
где – скаляр.
Скалярное произведение векторов.
Определение: Под
скалярным произведением двух векторов 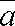 и
и 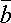
понимается
число, равное произведению длин этих
векторов на косинус угла между ними,
т.е. 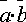 =
=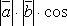
 ,
,  —
угол между векторами
—
угол между векторами 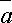 и
и 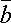 .
.
Свойства скалярного произведения:
1. 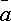
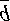 =
=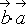

2. ( +
+ 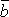 )
)  =
=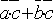
3. 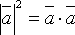
4. 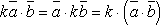
5. 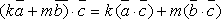 ,
где
,
где 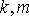 –
скаляры.
–
скаляры.
6.
два
вектора перпендикулярны (ортогональны),
если 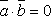 .
.
7. 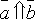 тогда
и только тогда, когда
тогда
и только тогда, когда 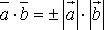 .
.
Скалярное
произведение в координатной форме имеет
вид: 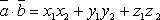 , где
, где 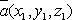 и
и 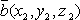 .
.
Пример: Найти
скалярное произведение векторов 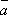
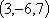 и
и 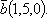
Решение: 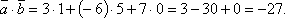
Векторное проведение векторов.
Определение:
Под векторным произведением двух
векторов 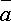 и
и 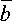 понимается
вектор,
понимается
вектор, 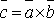 для
которого:
для
которого:
-модуль
равен площади параллелограмма,
построенного на данных векторах, т.е. 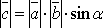 ,
где
,
где 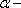 угол
между векторами
угол
между векторами  и
и 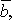
-этот
вектор перпендикулярен перемножаемым
векторам, т.е. 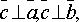
-если
векторы 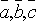 неколлинеарны,
то они образуют правую тройку векторов.
неколлинеарны,
то они образуют правую тройку векторов.
Свойства векторного произведения:
1.При
изменении порядка сомножителей векторное
произведение меняет свой знак на
обратный, сохраняя модуль, т.е. 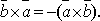
2.Векторный
квадрат равен нуль-вектору, т.е. 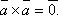
3.Скалярный
множитель можно выносить за знак
векторного произведения, т.е. 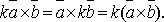
4.Для
любых трех векторов 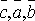 справедливо
равенство
справедливо
равенство 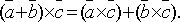
5.Необходимое
и достаточное условие коллинеарности
двух векторов 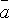 и
и 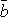 :
:
Векторное произведение в координатной форме.
Если
известны координаты векторов 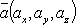 и
и 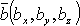 , то
их векторное произведение находится
по формуле:
, то
их векторное произведение находится
по формуле:
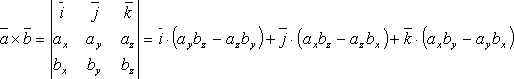 .
.
Тогда
из определения векторного произведения
следует, что площадь параллелограмма,
построенного на векторах 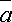 и
и 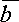 ,
вычисляется по формуле:
,
вычисляется по формуле:
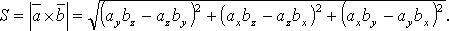
Пример: Вычислить
площадь треугольника с вершинами 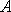 (1;-1;2),
(1;-1;2), 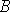 (5;-6;2),
(5;-6;2), 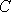 (1;3;-1).
(1;3;-1).
Решение: 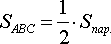 .
.
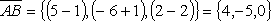 ,
, 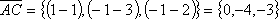 ,
тогда площадь треугольника АВС будет
вычисляться следующим образом:
,
тогда площадь треугольника АВС будет
вычисляться следующим образом:
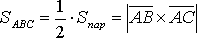 ,
,

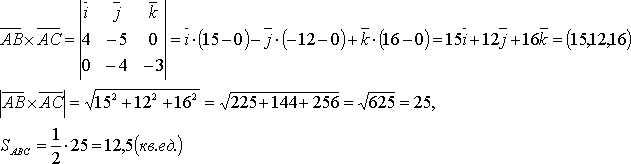
Смешанное произведение векторов.
Определение: Смешанным
(векторно-скалярным) произведением
векторов 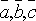 называется
число, определяемое по формуле:
называется
число, определяемое по формуле: 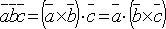 .
.
Свойства смешанного произведения:
1.Смешанное
произведение не меняется при циклической
перестановке его сомножителей, т.е.  .
.
2.При
перестановке двух соседних сомножителей
смешанное произведение меняет свой
знак на противоположный, т.е. 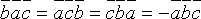 .
.
3.Необходимое
и достаточное условие компланарности
трех векторов 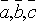 :
: 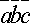 =0.
=0.
4.Смешанное
произведение трех векторов равно объему
параллелепипеда, построенного на этих
векторах, взятому со знаком плюс, если
эти векторы образуют правую тройку, и
со знаком минус, если они образуют левую
тройку, т.е. 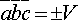 .
.
Если
известны координаты векторов 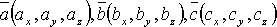 , то
смешанное произведение находится по
формуле:
, то
смешанное произведение находится по
формуле: 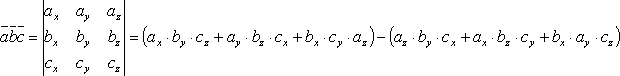
Пример: Вычислить
смешанное произведение векторов 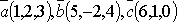 .
.
Решение: 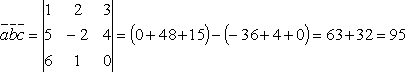
3. Базис системы векторов.
Определение. Под системой векторов понимают несколько векторов, принадлежащих одному и тому же пространству R.
Замечание. Если система состоит из конечного числа векторов, то их обозначают одной и той же буквой с разными индексами.
Пример. 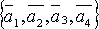
Определение. Любой
вектор вида 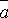 =
=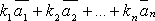 называется
линейной комбинацией векторов
называется
линейной комбинацией векторов 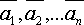 .
Числа
.
Числа 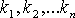 — коэффициентами
линейной комбинации.
— коэффициентами
линейной комбинации.
Пример. 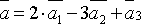 .
.
Определение.
Если вектор 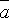 является
линейной комбинацией векторов
является
линейной комбинацией векторов 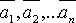 , то говорят, что вектор
, то говорят, что вектор 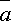 линейно
выражается через векторы
линейно
выражается через векторы 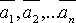 .
.
Определение. Система векторов называется линейно-независимой, если ни один вектор системы не может быть как линейная комбинация остальных векторов. В противном случае систему называют линейно-зависимой.
Пример.
Система векторов 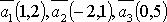 линейно-зависима,
т. к. вектор
линейно-зависима,
т. к. вектор 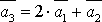 .
.
Определение базиса. Система векторов образует базис, если:
1) она линейно-независима,
2) любой вектор пространства через нее линейно выражается.
Пример
1. Базис
пространства 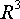 :
: 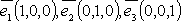 .
.
2. В системе векторов 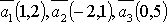 базисом являются векторы:
базисом являются векторы: 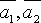 ,
т.к.
,
т.к. 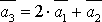 линейно
выражается через векторы
линейно
выражается через векторы 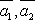 .
.
Замечание. Чтобы найти базис данной системы векторов необходимо:
1) записать координаты векторов в матрицу,
2) с помощью элементарных преобразований привести матрицу к треугольному виду,
3) ненулевые строки матрицы будут являться базисом системы,
4) количество векторов в базисе равно рангу матрицы.
Скалярное произведение двух векторов и физический смысл
Обозначение скалярного произведения: a·b или ab или (a, b), на письме пишется со стрелочкой, т.е. $\vec a\vec b$
Скалярное произведение вектора а на вектор b называется произведение их модулей (длин) на косинус угла между ними, т.е.
a·b =|a|·|b|·cos(a,^b)
или
a·b =|a|·|b|·cos(φ)
a·b>0 — угол острый между векторами;
a·b<0 — угол тупой между векторами;
a·b=0 — угол прямой между векторами.
Примечание
Скалярное умножение не распространяется на случай трёх сомножителей.
Физический смысл скалярного произведения заключается в том, что работа А равна произведению производимой постоянной силой F при перемещении тела на вектор a и составляющий с направлением силы F угол φ. Эта связь выражается формулой:
A = |F|·|a|=|F|·|a|·cosφ
A — работа, скалярная величина;
a — вектор перемещения (смещения) материальной точки;
F — вектор силы действующий на эту точку;
φ — угол силы F действующий к смещению a

Пример 1
Длины векторов a и b соответственно равны 3 м и 2 м, а угол между ними 1200.
Найти скалярное произведение a·b.
Решение
a·b=|a|·|b|·cos(a,^b)=3·2·cos(1200)=−3 м2
Пример 2
Длины вектор силы F имеет модуль 4 кг, длина вектора смещения а равна 2 м. Пусть сила F действует под углом φ=600 к смещению a.
Найти работу силы.
Решение
F·a=|F|·|a|·cosφ=4·2·cos(600)=4·2·0.5=4 м2

