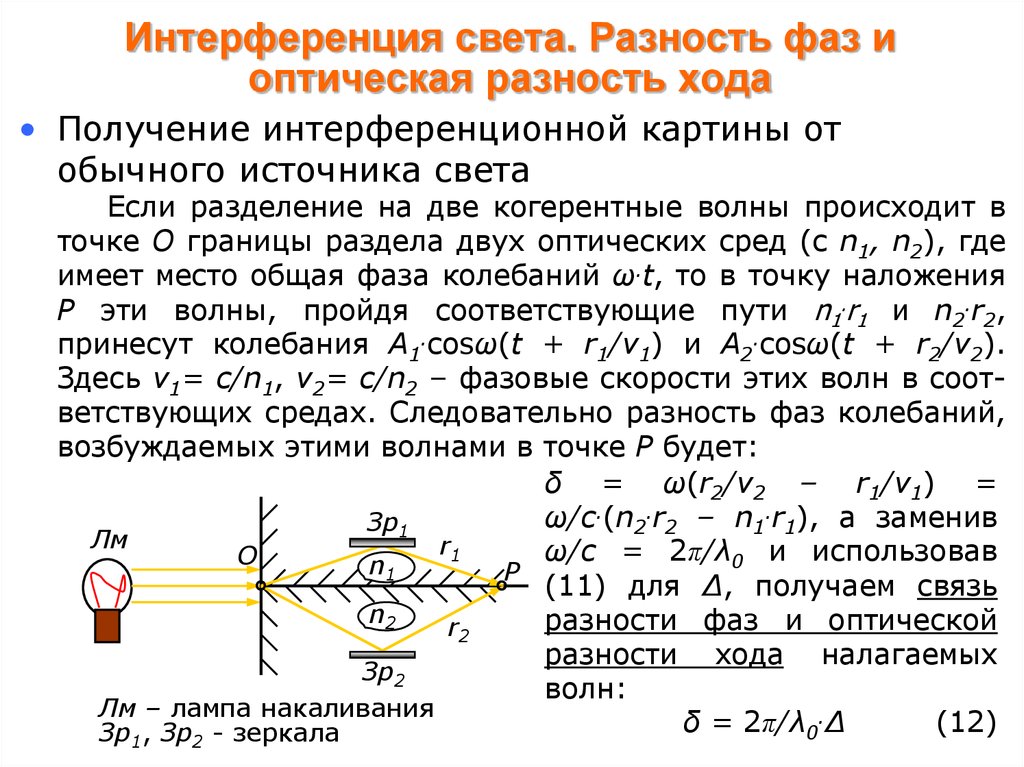
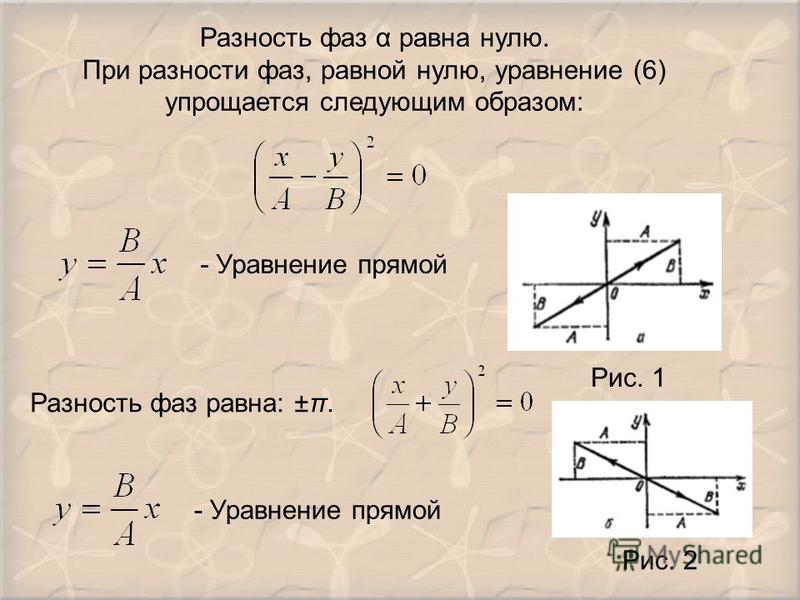
5. Измерения разности фаз
Фаза является физической величиной, характеризующей аргумент синусоидальной функции времени, описывающей колебательный процесс. Фазой напряжения , является величина. Очевидно, мгновенная фаза линейно зависит от времени. Поэтому для двух гармонических колебаний с разными частотами
, (5.1)
разность фаз также является линейной функцией времени.
В практике радиоизмерений наиболее важной измерительной задачей является измерение разности фаз двух гармонических колебаний с равными частотами. При этом разность фаз равна разности начальных фаз
. (5.2)
Модуль этой величины называют фазовым сдвигом. Для двух негармонических колебаний понятие разности фаз можно ввести как разность моментов времени (t2 – t1), в которые эти колебания имеют одинаковые фазы. Например, если в моменты перехода колебаний через нуль их напряжения будут иметь одинаковые направления изменений, можно выразить разность фаз через разность моментов времени, приравнивая мгновенные фазы
,
откуда
, (5. 3)
3)
где T — это период. В этом случае измеряют время задержки τ, которое определяется формулой
. (5.4)
В качестве xд, то есть меры разности фаз, могут быть применены либо фазовый сдвиг, создаваемый мерой фазового сдвига, либо известный интервал времени, в качестве которого используется период колебаний со стабильной и хорошо известной частотой. Рассмотрим меры фазового сдвига, устройства и методы измерения разности фаз.
Фазовращателем называется устройство, с помощью которого вводится в электрическую цепь известный и регулируемый фазовый сдвиг. Если фазовращатель используется в качестве меры фазового сдвига, то к нему придается шкала, градуировочный график или таблица, позволяющие производить отсчет вносимого фазового сдвига. Конструкция и принцип действия фазовращателя зависят от диапазона частот, для которого он предназначен.
Н
изкочастотные фазовращатели
создают на основе неуравновешенного
четырехплечного моста (рис.
На плечи R1 и R2 равных сопротивлений подают входное напряжение uвх. Плечи R и C являются фазосдвигающими: напряжения uR и uC сдвинуты относительно друг друга на 90˚. Сумма этих напряжений всегда равна входному напряжению. Сопротивление R можно изменять от до нуля до бесконечности; емкость C постоянна. При изменении сопротивления значения амплитуд UR и UC изменяются. На векторной диаграмме (рис. 5.2) показано взаимное расположение векторов напряжений (
 Практически между нагрузкой и выходом
фазовращателя включают усилитель или
повторитель с конечнымZвх,
так что пределы изменения фазового
сдвига составляют приблизительно от
10 до 160˚.
Практически между нагрузкой и выходом
фазовращателя включают усилитель или
повторитель с конечнымZвх,
так что пределы изменения фазового
сдвига составляют приблизительно от
10 до 160˚.Т
акой фазовращатель предназначен для работы на одной частоте. При переходе на другую частоту необходимо использовать другой градуировочный график или подключать другой конденсатор.
С
хема рис. 5.3. обеспечивает фазовый сдвиг от 0 до 360˚. Изменение фазы на выходе фазовращателя при данной частоте ω и постоянной емкости конденсаторов осуществляется одновременным и одинаковым изменением сопротивлений сдвоенных резисторов R2 и R3. Емкостные фазовращатели применяются при низких частотах сигналов. В конечном счете в фазовращателе производится преобразование сопротивления в фазовый сдвиг
 Сам фазовращатель является перестраиваемой
многозначной мерой фазового сдвига.
Сам фазовращатель является перестраиваемой
многозначной мерой фазового сдвига.Для сверхвысоких частот применяют фазовращатели, принцип действия которых основан на изменении электрической длины тракта. К таким фазовращателям относятся фазовращатели тромбонные и диэлектрические. Волноводный фазовращатель (рис. 5.4) включает фазовый сдвиг, пропорциональный удвоенному перемещению U-образной подвижной части
,
где λв — длина волн в волноводе. Таким образом, отсчитывая перемещение подвижной части, определяют изменение сдвига фазы.
Д
иэлектрический волноводный
фазовращатель (рис. 5.5) состоит из отрезков
волновода, внутри которого параллельно
векторуЕ электромагнитного поля помещена тонкая
пластина из высококачественного
диэлектрика. Форма пластины подбирается
такой, чтобы отражения от нее были
минимальными. При ее перемещении от
узкой стенки к оси волновода изменяется
длина волны в частично заполненном
диэлектриком волноводе и, следовательно,
изменяется электрическая длина при
фиксированной геометрической длине.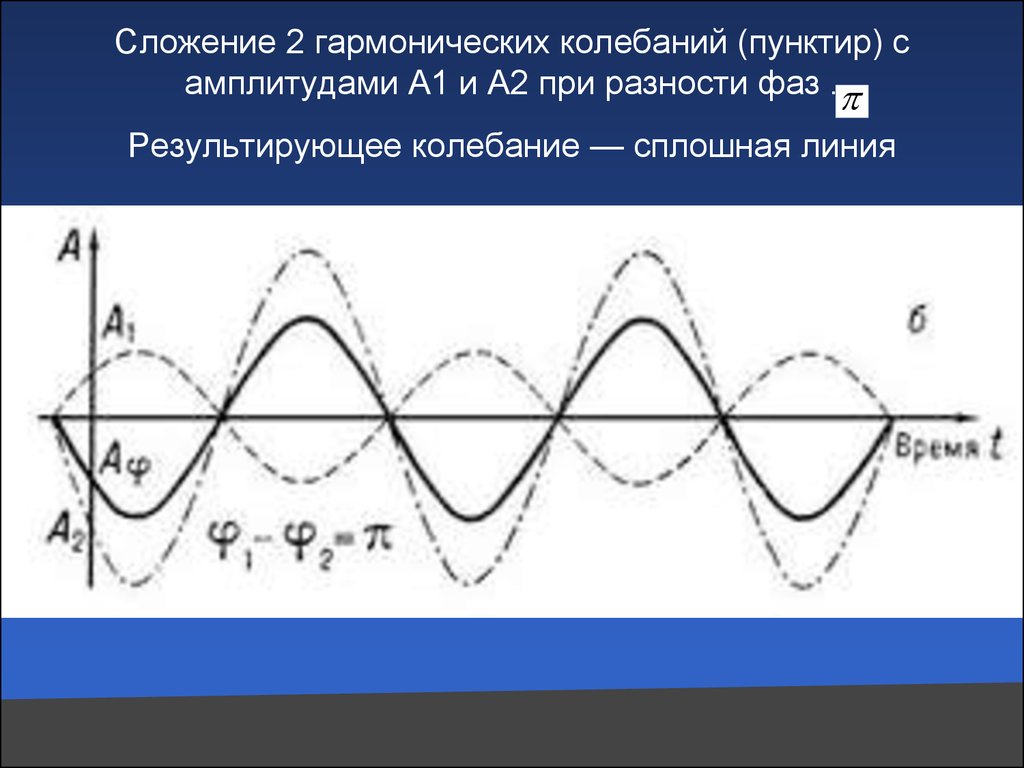
Фазовращатель с любым отсчетным устройством может быть применен в качестве меры фазового сдвига, если его предварительно отградуируют.
| ||||||||||||||
| Специальный поиск | ||||||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Помощь Контакты Билеты |
|||||||||||||
разность фаз колебаний Задача 11496 Определить скорость распространения волн в упругой среде, если разность фаз колебаний двух точек, отстоящих друг от друга на Δx = 15 см, равна π/2. Частота колебаний 25 Гц.
Задача 12184 С какой скоростью распространяются волны вдоль прямой, если разность фаз колебаний двух точек, отстающих друг от друга на 10 см, равно π/2. а частота колебаний 3 Гц.
Задача 12188 Какова разность фаз колебаний двух точек, находящихся на расстоянии соответственно 10 и 16 м от источника.
Задача 12192 Определить, на каком расстоянии находятся две точки среды, расположенные на одном луче и совершающие колебания с разностью фаз 0,12π, если длина волны 12,6 м.
Задача 13937 Колебательный процесс распространяется вдоль прямой со скоростью 40 м/с. Частота колебаний 5 Гц. Определить в радианах разность фаз колебаний между источником и точкой, находящейся на расстоянии 3 м от источника.
Задача 14561 Разность фаз колебаний источника волн в упругой среде равна Δφ = 0,5π рад, и точки этой среды находятся на расстоянии l = 2 м от источника. Частота колебаний составляет ν = 5 Гц. Рассчитайте величину фазовой скорости волны.
Задача 16988 Определить разность фаз колебаний источника волн и точки среды, отстоящей на 2 м от источника.
Задача 18133 Определить скорость распространения волн в упругой среде, если разность фаз колебания двух точек, отстоящих друг от друга на 10 см, равна 30°. Частота колебаний 50 Гц.
Задача 19330 В схеме Юнга на экране наблюдается картина интерференции (λ = 450 нм). Геометрические длины путей до (·) А на экране от верхнего источника = 700,003 мм; от нижнего = 700,006 мм. Определить разность фаз колебаний в (·) А и порядок интерференции k. Система находится в бензоле (n = 1,5).
Задача 19820 На рисунке представлена схема разбиения волновой поверхности Ф на зоны Френеля. Разность хода между лучами N1P и N2P и разность фаз колебаний вторичных источников в точках N1 и N2 равна .
Задача 21006 Определить скорость распространения волн в упругой среде, если разность фаз колебаний двух точек M и P, отстоящих от источника на расстояниях 20 м и 10 м, равна π/2 рад. Фаза колебаний точки M в момент времени 0,1 с равна π рад. Начальная фаза колебаний источника равна нулю (колебания источника происходят по закону синуса).
Задача 21025 Разность фаз колебаний двух точек М и Р равна 60°. Длина волны соответствующих колебаний равна 15 м. Найти наименьшее расстояние, на котором находятся эти точки. Как изменится это расстояние, если разность фаз и длину волны увеличить в 2 раза?
Задача 22389 Плоская гармоническая волна с амплитудой А = 4 см распространяется в однородной и изотропной среде.
Задача 23418 Определить разность фаз Δφ колебаний двух точек, лежащих на луче плоской волны на расстоянии Δl = 1 м друг от друга, если длина волны λ = 0,5 м.
| ||||||||||||||
Разность ходаи разность фаз. — Мегаобучалка
Интерференция двух лучей. Принцип получения интерференционной картины. условия максимумов и минимумов. Разность фаз и разность хода. Примеры: а) Интерференция в тонкой пленке; б) кольца Ньютона. Применение интерференции света.
1. Получение интерференционной картины
В 1803г. английский физик Т.Юнг с помощью двух щелей получил на экране интерференционную картину. Его опыт заключался в следующем: источником света служила ярко освещенная щельS, от которой световая волна падала на две узкие равноудаленные щели S1 и S2, параллельные S (рис. 2.2). Щели S1 и S2 можно считать когерентными источниками света, а все три упомянутые щели можно рассматривать как точечные источники, свет от которых распространяется во всех направлениях. Волны, идущие от S1 и S2, накладываясь друг на друга, интерферируют. Интерференционная картина наблюдается на экране Э (рис. 2.2).
английский физик Т.Юнг с помощью двух щелей получил на экране интерференционную картину. Его опыт заключался в следующем: источником света служила ярко освещенная щельS, от которой световая волна падала на две узкие равноудаленные щели S1 и S2, параллельные S (рис. 2.2). Щели S1 и S2 можно считать когерентными источниками света, а все три упомянутые щели можно рассматривать как точечные источники, свет от которых распространяется во всех направлениях. Волны, идущие от S1 и S2, накладываясь друг на друга, интерферируют. Интерференционная картина наблюдается на экране Э (рис. 2.2).
Обозначим расстояние между щелями S1 и S2 равным d, а между щелями и экраном — l, причем l » d (рис. 2.3 а). Точка О – центр экрана, она расположена симметрично относительно щелей S1 и S2. Результат интерференции волн в произвольной точке экрана М, находящейся на расстоянии х от его центра О, должен определяться разностью хода Δ = l2— l1. Математический расчет дает для разности хода Δ = хd/l. В тех местах экрана, которые удовлетворяют условию , образуется интерференционный максимум. Отсюда
Математический расчет дает для разности хода Δ = хd/l. В тех местах экрана, которые удовлетворяют условию , образуется интерференционный максимум. Отсюда
.
В тех местах экрана, где , волны “гасят” друг друга и образуется интерференционный минимум. Отсюда
.
Шириной интерференционной полосы Δх называется расстояние между соседними максимумами или минимумами
.
Величина Δх постоянна при заданных d, l и λ и не зависит от порядка интерференции m. Таким образом, при освещении щелей монохроматическим светом на экране наблюдается чередование светлых и темных полос одинаковой ширины (рис. 2.3 б). Чтобы полосы были хорошо различимы, Δхдолжна быть порядка 5 мм, тогда при λ = 500 нм отношение l/d равно 10000, т.е. выполняется условие l » d.
При освещении щелей белым светом интерференционные максимумы становятся радужными. Это происходит из-за того, что положение интерференционного максимума зависит от длины волны падающего света, а белый свет содержит в себе все цвета спектра. Максимумы коротких длин волн (фиолетовых) будут располагаться ближе к центру экрана, за ними следуют максимумы синих длин волн и т.д. до самых длинных красных (рис. 2.3 в). В середине экрана при m = 0 максимумы всех волн совпадут из-за отсутствия разности хода и получится белая полоса.
Максимумы коротких длин волн (фиолетовых) будут располагаться ближе к центру экрана, за ними следуют максимумы синих длин волн и т.д. до самых длинных красных (рис. 2.3 в). В середине экрана при m = 0 максимумы всех волн совпадут из-за отсутствия разности хода и получится белая полоса.
2.Условия максимума и минимума интерференции
При сложении двух колебаний амплитуда результирующего колебания зависит от разности фаз складываемых колебаний:
, (1)
так как . Здесь – волновое число; длина волны зависит от показателя преломления среды, в которой распространяется волна; величина в раз меньше, чем длина волны в вакууме:
. (2)
С учетом этого соотношения разность фаз колебаний светового вектора двух волн в точке наблюдения , согласно формуле (1):
(3)
Здесь – оптическая разность хода волн; – оптическая длина пути; это произведение геометрического пути волны (от источника света до точки наблюдения) на показатель преломления среды, в которой это расстояние пройдено.
Условие максимумов интенсивности света в точке наблюдения :
(4)
т. е. колебания световых векторов двух волн в точке происходят в одинаковой фазе, при этом в любой момент времени .
Условие минимумов интенсивности света в точке :
; … (5)
т. е. колебания складываемых световых векторов в точке происходят в противофазе, при этом в любой момент времени .
Отметим, что при сложении двух колебаний на векторной диаграмме (где колебание изображают вращающимся вектором амплитуды ) разность фаз колебаний – это угол между векторами , а амплитуда результирующего колебания (равна сумме векторов амплитуд). Условию максимумов интенсивности (4) соответствует рис. 6 а, а условию минимумов (5)
Разность ходаи разность фаз.
Разность хода
Изменению разности фаз на соответствует изменение разности хода на .
В вакууме оптическая разность хода в отличие от разности фаз имеет наглядную интерпретацию. Если две интерферирующие волны испускаются одним источником света, то разность хода — это геометрическая разность длин путей, по которым два интерферирующих луча от одной точки источника достигли одной точки экрана.
Если две интерферирующие волны испускаются одним источником света, то разность хода — это геометрическая разность длин путей, по которым два интерферирующих луча от одной точки источника достигли одной точки экрана.
Например, в оптической схеме опыта Юнга, изображенной на рис. 18, разность хода для точки P на экране находится по формуле:
.
В изотропной среде скорость света в раз меньше, чем в вакууме, здесь — показатель преломления среды. Частота света в среде и в вакууме одинакова, поэтому длина волны в среде в раз меньше. В соответствии с соотношением вместо реального уменьшения длины волны можно рассматривать неизменную и соответствующее увеличение длины пути луча. С этой целью вводится понятие оптической длины пути, которая в раз больше геометрической длины. Далее, употребляя термин «разность хода», всегда будем иметь в виду оптическую разность хода.
Заменяя разность фаз интерферирующих волн оптической разностью хода, получаем следующее выражение для интенсивности интерференционной картины:
.
Приемники света в оптическом диапазоне реагируют на интенсивность света, а не на напряженность электрического или магнитного полей. Поэтому измеряемые в опыте величины, ширина полос и видность, также могут быть выражены через интенсивность, а значит и через оптическую разность хода. Следовательно, понятие оптической разности хода позволяет свести оптическую задачу по интерференции к геометрической задаче отыскания разности хода.
Отметим, что разность хода лучей можно отсчитывать не только как разность длин путей от источника до точки наблюдения, но и как разность длин путей от двух точек любой поверхности равной фазы волны до точки наблюдения. При этом, конечно, две точки на поверхности равной фазы — не произвольные точки, а должны быть точками, через которые реально проходят лучи, попадающие в точку наблюдения. Так на рис. 18 , поэтому две щели находятся на поверхности равной фазы, и, следовательно, разность хода можно найти по упрощенной формуле . Этот прием часто используется при решении задач.
Разность фаз
Графики двух периодических функций (колебаний) одинаковой частоты задержаны (сдвинуты) один относительно другого. Задержка во времени эквивалентна соответствующей разности фаз.
А).Интерференция в тонких пленках
Луч света длиной волны λ падает на пленку толщиной dпод углом падения i(рис. 4.6) и делится на два: луч 1 отражается от верхней грани, а луч 2 преломляется, проходит в пленка расстояние АВ, затем отражается от нижней грани, проходит расстояние ВС и затем преломляется. Два луча собираются линзой в одной точка, расположенной в фокальной плоскости линзы. Для расчета картины интерференции на экране найдем оптическую разность хода лучей 1 и 2.
Разность хода лучей 1 и 2 в точке Аравна нулю, так как они двигались вместе, составляя луч падающего на пластинку света. После линии ОС (она перпендикулярна лучам 1 и 2) их разность хода не изменяется, так как линза не дает дополнительной разности хода для этих лучей. Поэтому оптическая разность хода возникает при переходе лучей от точки А к линии ОС:
Поэтому оптическая разность хода возникает при переходе лучей от точки А к линии ОС:
|
∆ = (АВ + ВС)n – ОА + λ0/2. (4.3)
Оптическим ходом луча называют произведение
геометрического хода (АВ +ВС) на показатель
преломления среды, в которой распространяется луч. На участке АО луч 1 распространяется в воздухе, для которого nВ = 1. В формулу для оптической разности хода введено слагаемое λ0/2, так как вектор напряженности луча 1 при отражении от оптически более плотной среды изменяет свою фазу на π или луч 1 теряет полволны. λ0 – длина волны в вакууме. Подставляя параметры пленки и угол падения в формулу (4.3), для оптической разности хода можно окончательно записать:
.(4.4)
Для данного примера условия наблюдения максимумов и минимумов будут выглядеть таким образом:
максимумы:
минимумы:
Отметим, что для наблюдения интерференционной картины нужно брать тонкую пленку, чтобы для естественного света лучи 1 и 2 после линии ОСбыликогерентными: ОС ≤ rк (из за пространственной когерентности) и ∆ ≤ lк (из за временной когерентности).
Как видно из формулы (4.4), оптическую разность хода лучей ∆ можно изменять либо изменением угла падения i, либо изменяя толщину пленки d. Рассмотрим полученные интерференционные картины.
Если на пленку одинаковой толщины d падает монохроматический свет под одним и тем же углом i и выполняется условие максимума, то пленка в отраженных лучах будет светлой (имеющий цвет падающей длины волны). При выполнении условия минимума отраженных лучей не будет. Свет не отражаясь, проходит через пленку.
|
Если на пленку с линейно изменяющейся толщиной d (клин) (рис. 4.7) падает монохроматический свет под одним и тем же углом i, то в отраженных лучах будут наблюдаться полосы равной толщины. Если на этот клин направить белый свет, то максимумы превратятся в спектры.
В пределах каждого максимума цвет будет плавно меняться от красного к фиолетовому.
Б). Кольца Ньютона.
Кольца Ньютона, являющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис.32.9). Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падении света имеющие вид концентрических окружностей.
Рис.32.9. Схема наблюдения колец Ньютона.
В отраженном свете оптическая разность хода (с учетом потери полуволны при отражении), согласно (32.9), при условии, что показатель преломления воздуха n = 1, а i = 0,где d — ширина зазора. Из рис. 32.9 следует, чтоR2 = (R – d)2 + r2, где R — радиус кривизны линзы, r — радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая, что d мало, получим Следовательно, (32.12)Приравняв (32.12) к условиям максимума (32.3) и минимума (32.4), получим выражения для радиусов m-го светлого кольца и m-го темного кольца соответственно (m = 0,1,2,…), — светлое кольцо,
Учитывая, что d мало, получим Следовательно, (32.12)Приравняв (32.12) к условиям максимума (32.3) и минимума (32.4), получим выражения для радиусов m-го светлого кольца и m-го темного кольца соответственно (m = 0,1,2,…), — светлое кольцо,
(m = 0,1,2,…) – темное кольцо.
Разность фаз и фазовый сдвиг
Положение волновой частицы периодической формы волны известно как «Фаза» волны. Полная фаза полного цикла сигнала равна 360 0 .
[адсенс1]
Когда две или более волны одной частоты интерферируют в среде или движутся по одному и тому же пути, «фаза» волн играет важную роль для получения желаемого результата без возникновения шума.
Фазу также можно определить как «относительное смещение двух волн относительно друг друга».
Фаза также может быть выражена в радианах и градусах. Один радиан = 57,3 градуса.
Схема
Разность фаз
Разность фаз синусоидальной волны можно определить как «интервал времени, на который волна опережает другую волну или отстает от нее», и разность фаз не является свойством только одной волны, это относительное свойство двух или более волн. Это также называется «фазовым углом» или «фазовым смещением».
Это также называется «фазовым углом» или «фазовым смещением».
Разность фаз, представленная греческой буквой фи (Φ). Полная фаза сигнала может быть определена как 2π радиан или 360 градусов.
Опережающая фаза означает, что волна опережает другую волну с той же частотой, а Отстающая фаза означает, что волна отстает от другой волны с той же частотой.
Фазовая квадратура: когда разность фаз между двумя волнами составляет 90 0 (это может быть = + 90 0 или – 90 0 ), говорят, что волны находятся в «фазовой квадратуре».
Противофаза: когда разность фаз между двумя волнами составляет 180 0 (может быть = + 180 0 или – 180 0 ), то говорят, что волны находятся в «фазовой оппозиции».
Чтобы лучше понять эту концепцию, обратите внимание на рисунок ниже.
Временной интервал и фаза сигнала обратно пропорциональны друг другу. Это означает, что
t град = 1 / (360 f ) (градусы)
t рад = 1 / (6,28 f ) (радиан)
Где f — частота сигнала, а t — период времени.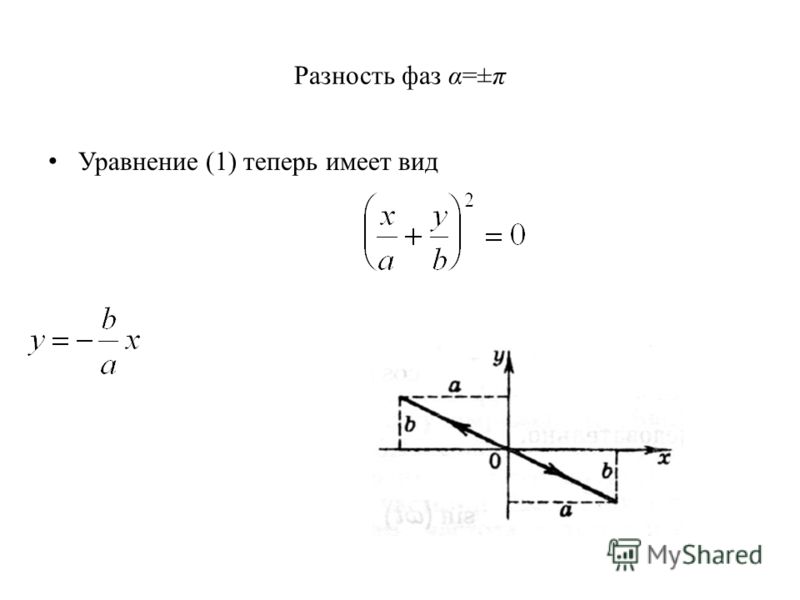
Например, если две синусоидальные волны имеют одинаковую частоту и фазовый сдвиг π/2 радиан, то фазы волн можно определить как (nπ + 1) и nπ радиан.
Фазовый сдвиг сигналов также может быть представлен в виде периода времени (T). Например, + 6 мс и – 7 мс и т. д.
Вернуться к началу
[adsense2]
Уравнение разности фаз
Разность фаз синусоидальных сигналов может быть выражена приведенным ниже уравнением, используя максимальное напряжение или амплитуду сигналов: )
Где
Amax – амплитуда синусоиды измерения
ωt — угловая скорость (радиан/сек)
Φ — фазовый угол. (Радианы или градусы)
Если Φ < 0, то говорят, что фазовый угол волны находится в отрицательной фазе. Точно так же, если Φ > 0, то говорят, что фазовый угол волны находится в положительной фазе.
Соотношение фаз синусоидального сигнала
Каждый сигнал переменного тока будет иметь свой ток, напряжение и частоту. Если напряжение и угловые скорости двух сигналов одинаковы, то их фаза также одинакова в любой момент времени.
Если напряжение и угловые скорости двух сигналов одинаковы, то их фаза также одинакова в любой момент времени.
На приведенном выше рисунке мы видим три волны, которые начинаются в начале координат, опережают в начале координат и отстают в начале координат соответственно.
Вернуться к началу
Разность фаз сигналов
Не в фазе
Когда чередующиеся сигналы имеют одинаковую частоту, но разные фазы, говорят, что они «не в фазе». Разность фаз не равна нулю для расфазированных волн. Обратите внимание на приведенный ниже рисунок, который описывает несовпадающую по фазе концепцию двух синусоидальных волн. Для синфазных сигналов запаздывание составляет доли длины волны, такие как 1/2, 2/3, 3/5… и т. д.
На приведенном выше рисунке волна «B» опережает на 90 0 (Φ = 90 0 ) волну «A». Таким образом, мы можем сказать, что две волны не совпадают по фазе.
Для волн, не совпадающих по фазе, есть два условия. Это
Это
1. Фаза опережения
2. Фаза отставания
Фаза опережения
Когда два сигнала одной и той же частоты движутся вдоль одной и той же оси, и один сигнал опережает другой, тогда это называется «волна опережающей фазы». .
Уравнения тока и напряжения для опережающих фазированных сигналов:
Напряжение (Vt) = Vm sin ωt
Ток (it) = Im sin (ωt – Φ)
Где Φ — опережающий фазовый угол.
Отставание по фазе
Когда два сигнала одной частоты движутся вдоль одной и той же оси, и один сигнал отстает от другого, это называется «Отставание по фазе».
Уравнения напряжения и тока для опережающих фазированных сигналов:
Напряжение (Vt) = Vm sin ωt
Ток (it) = Im sin (ωt + Φ)
Где Φ — фазовый угол отставания.
Синфазные синусоидальные волны
Когда разница между фазами двух чередующихся волн равна нулю, волны называются синфазными. Это может произойти, когда два сигнала имеют одинаковую частоту и одинаковую фазу. Для синфазных сигналов запаздывание представляет собой целое число длин волн, например 0, 1, 2, 3… Синфазные сигналы показаны на рисунке ниже.
Для синфазных сигналов запаздывание представляет собой целое число длин волн, например 0, 1, 2, 3… Синфазные сигналы показаны на рисунке ниже.
Сигналы на приведенном выше рисунке имеют разную амплитуду (максимальное напряжение), но имеют одинаковую частоту.
Пример: Если две синусоидальные волны A и B не совпадают по фазе, а разность фаз составляет 25 0 , то мы можем объяснить соотношение между волнами как
Волна «A» опережает волну «B» на 25 0 или волна ‘B’ отстает от волны ‘A’ на 25 0 . Таким образом, ток и напряжение этих сигналов также изменяются в зависимости от фазового сдвига нефазированных сигналов.
Вернуться к началу
Соотношение фаз напряжения и тока к R, L, C
Цепь RLC также называется «резонансной схемой». Ниже поясняется поведение напряжения и тока резистора, конденсатора и катушек индуктивности по отношению к фазе.
- Резистор: В резисторе ток и напряжение находятся в одной фазе.
 Таким образом, разность фаз между ними измеряется как 0, .
Таким образом, разность фаз между ними измеряется как 0, . - Конденсатор: в конденсаторе ток и напряжение не совпадают по фазе, и ток опережает напряжение на 90 0 . Таким образом, разность фаз между током и напряжением в конденсаторе измеряется как 90 0 .
- Катушка индуктивности: в катушке индуктивности ток и напряжение не совпадают по фазе. Напряжение опережает ток на 90 0 . Таким образом, разность фаз между напряжением и током в конденсаторе измеряется как 90 0 . Это прямо противоположно природе конденсатора.
ПРИМЕЧАНИЕ:
Существует простой способ запомнить соотношение между напряжением и током без какой-либо путаницы. Этот метод C I V I L
Первые 3 буквы C I V означают, что в конденсаторе I (ток) опережает V (напряжение).
Наверх
Резюме
- Мы можем обобщить эту общую концепцию как
- Фаза: Положение движущейся частицы формы волны называется «Фазой» и измеряется в «Радианах или градусах».

- Разность фаз: Интервал времени, на который волна опережает другую волну или отстает от нее, называется «Разностью фаз» или «Угол фаз». Он определяется буквой «Ф».
- Фазовый угол измеряется в «радианах/с» или «градусах/с», а фаза полного цикла указывается как «360 0 ».
- Не в фазе: когда чередующиеся сигналы имеют одинаковую частоту, но разные фазы, говорят, что они «вне фазы».
- В фазе: Когда разница между фазами двух чередующихся волн равна нулю, говорят, что они находятся в фазе.
- Опережающая фаза: сигнал опережает другой сигнал с той же частотой.
- Отставание фазы: сигнал отстает от другого сигнала с той же частотой.
- В цепях LRC соотношение фаз между напряжением и током будет
- В резисторах: фазы напряжения и тока совпадают. Таким образом, разность фаз равна 0, .
- В конденсаторах: Ток опережает напряжение на 90 градусов. Таким образом, разность фаз равна 90 0 .
- В индукторах: напряжение опережает ток на 90 градусов.
 Таким образом, разность фаз равна 90 0 .
Таким образом, разность фаз равна 90 0 .
Вернуться к началу
Что такое разность фаз в цепях переменного тока? Понятие фазы и разности фаз
Разность фаз определяется как задержка между двумя или более переменными величинами при достижении максимумов или переходов через ноль, что приводит к разнице их фаз. Эта разница между двумя волнами измеряется в градусах или радианах и также известна как 9.0235 фазовый сдвиг .
Иногда определяется как разница между двумя или более синусоидальными сигналами относительно опорной оси. Он обозначается φ и соответствует смещению формы сигнала по горизонтальной оси от общей точки отсчета.
Мы подробно обсудим разность фаз цепей переменного тока позже, сначала давайте разберемся-
Что такое фаза?
Фаза переменных величин определяется в терминах смещения и периода времени. С точки зрения смещения фаза представляет собой угол от контрольной точки, на который вектор, представляющий переменную величину, перемещается до рассматриваемой точки.
Чтобы понять это, взгляните на рисунок, приведенный ниже:
На приведенном выше рисунке ось x является базовой осью, и в момент времени A фаза φ переменной величины равна 0⁰ при смещении, фаза той же величины в момент времени B представляет собой угол (в градусах или радианах), через который прошел вектор, учитывая ту же опорную ось, то есть ось x. Как правило, фаза переменной величины варьируется от 0 от до 2π дюймов рад или 0⁰ до 360⁰ .
Кроме того, с точки зрения периода времени фаза в любой конкретный момент определяется как доля периода времени, на который она опережает относительно контрольного момента. Рассмотрим представление сигнала, приведенное ниже:
Здесь 0 считается эталонным моментом, таким образом, фаза переменной величины в точке A равна T/4, а в точке B равна 3T/4.
Предположим, что сравнение между двумя переменными величинами выполняется в соответствии с перекрытием их пиков и пересечением нуля.
Таким образом, когда пересечения пика и нуля переменных величин с одинаковой частотой совпадают, говорят, что такие величины равны в фазе . Проще говоря, мы можем сказать, что когда две переменные величины одной и той же частоты достигают своих максимальных положительных, отрицательных и нулевых значений в один и тот же момент времени в течение одного полного цикла независимо от их амплитуды, то говорят, что такие величины имеют одинаковую фазу. . Это объяснение ясно показано на рисунке, приведенном ниже:
И наоборот, когда пик и пересечение нуля переменных величин с одной и той же частотой не совпадают, то говорят, что эти величины не совпадают по фазе по отношению друг к другу, и между двумя существует определенная разница в фазе. . Вкратце можно сказать, что когда две переменные величины одной и той же частоты достигают своих положительных и отрицательных пиков и нулевых значений в разные моменты времени в одном полном цикле, рассматривая одну и ту же ось отсчета, то между ними существует разность фаз.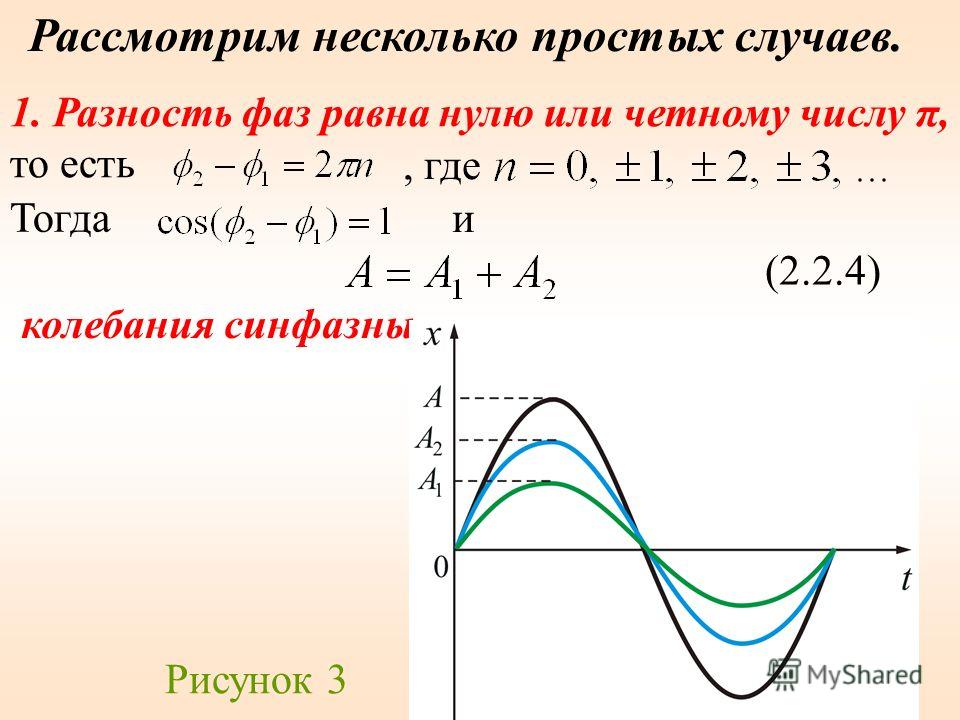 Несовпадение по фазе между двумя переменными величинами ясно показано на рисунке ниже:
Несовпадение по фазе между двумя переменными величинами ясно показано на рисунке ниже:
Уравнение для разности фаз
Общее уравнение переменных величин задается следующим образом:
: φ представляет фазу переменной величины,
A м 5 , 90 амплитуда сигнала ωt представляет собой угловую частоту сигнала.
Здесь φ может быть как положительным, так и отрицательным .
Теперь возникает вопрос, когда φ положительна, а когда отрицательна?
Прежде чем разбираться в положительных и отрицательных фазовых сдвигах, уясните условие нулевой разности фаз.
Таким образом, когда фаза переменной величины равна 0, тогда мгновенное значение синусоидальной величины находится при t = 0, что считается опорным. Цифра, приведенная ниже, указывает φ = 0⁰.
Положительный фазовый сдвиг : Когда переменная величина начинается до t=0, что считается эталоном, положительный наклон переменной величины смещается влево, пересекая горизонтальную ось перед эталоном. Таким образом, в таком случае φ>0 и угол будет иметь положительный характер. Это приводит к ведущему фазовому углу.
Таким образом, в таком случае φ>0 и угол будет иметь положительный характер. Это приводит к ведущему фазовому углу.
Обратно можно сказать, что в случае положительной фазы переменная величина имеет некоторое положительное мгновенное значение при t = 0. Это ясно показано ниже:
На приведенном ниже рисунке форма волны напряжения, которая начинается до опорной точки, а другая — это форма волны тока, которая точно начинается в момент t=0, т. е. опорная. Обычно в чисто индуктивной цепи напряжение опережает ток .
Здесь ток отстает от напряжения на угол φ.
Отрицательный фазовый сдвиг : Когда переменная величина начинается после t=0, т. е. контрольной точки, тогда ее положительный наклон смещается вправо и, таким образом, пересекает горизонтальную ось после контрольной точки. Поэтому здесь φ<0, и угол будет иметь отрицательный характер. Когда фазовый угол отрицателен, он представляет собой запаздывающий фазовый угол.
Для отрицательной фазы переменная величина имеет некоторое отрицательное мгновенное значение при t = 0, как показано здесь:
На приведенном ниже рисунке представлены кривые тока и напряжения, и ясно видно, что кривая напряжения начинается после опорного значения, а кривая тока начинается точно с опорного значения. Как правило, в чисто емкостных цепях ток опережает напряжение .
Здесь напряжение отстает от тока на угол φ.
Соотношение между синусоидальными сигналами напряжения и тока очень важно при работе с цепями переменного тока, поскольку они составляют основу анализа цепей переменного тока.
Разность фаз: определение, формула и уравнение
Фаза волны — это значение, представляющее долю цикла волны . В волне полный цикл от гребня до гребня или впадины до впадины равен 2π [рад]. Таким образом, каждая часть этой длины меньше 2π [рад]. Половина цикла равна π [рад], а четверть цикла равна π/2 [рад]. Фаза измеряется в радианах, которые являются безразмерными единицами.
Фаза измеряется в радианах, которые являются безразмерными единицами.
Рисунок 1. Волновые циклы делятся на радианы, причем каждый цикл охватывает расстояние в 2π [рад]. Циклы повторяются через 2π [рад] (красные значения). Каждое значение больше 2π [рад] является повторением значений от 0π [рад] до 2π [рад]. Источник: Мануэль Р. Камачо, StudySmarter.
Формула фазы волны
Чтобы рассчитать фазу волны в произвольной позиции, вам необходимо определить, насколько далеко эта позиция находится от начала вашего цикла волны. В простейшем случае, если ваша волна может быть аппроксимирована функцией синуса или косинуса, ваше волновое уравнение можно упростить следующим образом:
Здесь A — максимальная амплитуда волны, x — значение на горизонтальной оси, который повторяется от 0 до 2π для функций синуса/косинуса, а y — высота волны в точке x. Фаза любой точки x может быть определена с помощью приведенного ниже уравнения:
Уравнение дает вам значение x в радианах, которое вам нужно преобразовать в градусы, чтобы получить фазу. Это делается путем умножения x на 180 градусов и последующего деления на π.
Это делается путем умножения x на 180 градусов и последующего деления на π.
Иногда волна может быть представлена выражением, например. В этих случаях волна не совпадает по фазе на радианы.
Разность фаз волн
Разность фаз волн возникает, когда две волны движутся и их циклы не совпадают. Разность фаз известна как разница циклов между двумя волнами в одной и той же точке.
Перекрывающиеся волны с одинаковым циклом называются волнами в фазе, а волны с разностью фаз, которые не перекрываются, называются волнами вне фазы. Волны, которые не совпадают по фазе, могут компенсировать друг друга из , в то время как волны в фазе могут усиливать друг друга .
Формула разности фаз
Если две волны имеют одинаковую частоту/период, мы можем вычислить их разность фаз. Нам нужно будет вычислить разницу в радианах между двумя гребнями, которые находятся рядом друг с другом, как показано на следующем рисунке.
Рис. 2. Разница фаз между двумя волнами i(t) и u(t), меняющимися в зависимости от времени t, вызывает пространственную разницу в их распространении. Источник: Мануэль Р. Камачо, StudySmarter.
Эта разность является разностью фаз:
Вот пример расчета фазы волны и разности фаз волны.
Волна с максимальной амплитудой A 2 метра представлена синусоидальной функцией. Рассчитайте фазу волны, когда волна имеет амплитуду y = 1,9.0005
Используя соотношение y = A • Sin (x) и найдя x, мы получаем следующее уравнение: скажем, другая волна с той же частотой и амплитудой находится в противофазе с первой волной, причем ее фаза в той же точке х равна 15 градусам. Какова разница фаз между ними?
Сначала нам нужно рассчитать фазу в радианах для 15 градусов.
Вычитая обе фазы, получаем разность фаз:
В этом случае мы видим, что волны сдвинуты по фазе на π/12, что составляет 15 градусов.
Волны в фазе
Когда волны в фазе, их гребни и впадины совпадают друг с другом, как показано на рисунке 3. Волны в фазе испытывают конструктивную интерференцию. Если они изменяются во времени (i(t) и u(t)), они объединяют свою интенсивность (справа: фиолетовый).
Волны в фазе испытывают конструктивную интерференцию. Если они изменяются во времени (i(t) и u(t)), они объединяют свою интенсивность (справа: фиолетовый).
Рис. 3. Конструктивное вмешательство. Источник: Мануэль Р. Камачо, StudySmarter.
Несовпадающие по фазе волны
Несовпадающие по фазе волны производят нерегулярные колебания, поскольку гребни и впадины не перекрываются. В крайних случаях, когда фазы сдвинуты на π [рад] или на 180 градусов, волны компенсируют друг друга, если они имеют одинаковую амплитуду (см. рисунок ниже). В этом случае говорят, что волны находятся в противофазе, и эффект этого известен как деструктивная интерференция.
Рис. 4. Противофазные волны испытывают деструктивную интерференцию. В этом случае волны i(t) и u(t) имеют разность фаз на 180 градусов, в результате чего они компенсируют друг друга. Источник: Мануэль Р. Камачо, StudySmarter.
Разность фаз в различных волновых явлениях
Разность фаз вызывает различные эффекты в зависимости от волновых явлений, которые можно использовать для многих практических приложений.
- Сейсмические волны : системы пружин, масс и резонаторов используют циклическое движение для противодействия вибрациям, создаваемым сейсмическими волнами. Системы, установленные во многих зданиях, уменьшают амплитуду колебаний, тем самым снижая структурные напряжения.
- Технологии шумоподавления : Многие технологии шумоподавления используют систему датчиков для измерения входящих частот и создания звукового сигнала, который подавляет эти входящие звуковые волны. Таким образом, входящие звуковые волны уменьшают свою амплитуду, что в звуке напрямую связано с интенсивностью шума.
- Энергетические системы: , где используется переменный ток, напряжение и ток могут иметь разность фаз. Это используется для идентификации цепи, поскольку его значение будет отрицательным в емкостных цепях и положительным в индуктивных цепях.
Сейсмическая технология опирается на системы пружинных масс для противодействия движению сейсмических волн, как, например, в башне Taipei 101. Маятник представляет собой шар весом 660 метрических тонн. Когда сильный ветер или сейсмические волны обрушиваются на здание, маятник качается взад и вперед, качаясь в направлении, противоположном направлению движения здания.
Маятник представляет собой шар весом 660 метрических тонн. Когда сильный ветер или сейсмические волны обрушиваются на здание, маятник качается взад и вперед, качаясь в направлении, противоположном направлению движения здания.
Рисунок 5. Движение маятника на башне Taipei 101 не совпадает по фазе с движением здания на 180 градусов. Силам, действующим на здание (Fb), противодействует сила маятника (Fp) (маятник показан серым цветом). Источник: Мануэль Р. Камачо, Study Smarter.
Маятник уменьшает колебания здания, а также рассеивает энергию, действуя как демпфер настроенной массы. Пример маятника в действии наблюдался в 2015 году, когда из-за тайфуна шарик маятника качнулся более чем на метр.
Разность фаз — основные выводы
- Разность фаз — это значение, представляющее часть цикла волны.
- В фазе волны перекрываются и создают конструктивную интерференцию, увеличивающую их максимумы и минимумы.
- Противофазные волны создают деструктивную интерференцию, которая создает нерегулярные узоры.



 механика
механика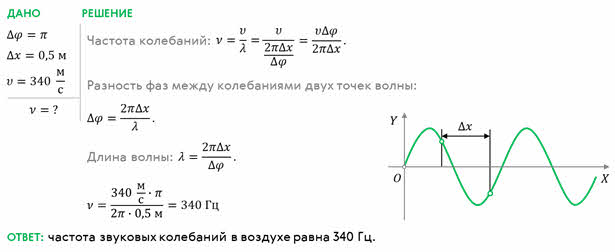

 ..
.. Скорость распространения волны υ = 20 м/с. Разность фаз колебаний двух точек среды, находящихся на расстоянии х1 = 3 м и х2 = 5 м от источника колебаний в направлении распространения волны, равна Δφ = 0,4π. Определить длину волны λ и записать уравнение волны.
Скорость распространения волны υ = 20 м/с. Разность фаз колебаний двух точек среды, находящихся на расстоянии х1 = 3 м и х2 = 5 м от источника колебаний в направлении распространения волны, равна Δφ = 0,4π. Определить длину волны λ и записать уравнение волны. Таким образом, разность фаз между ними измеряется как 0,
Таким образом, разность фаз между ними измеряется как 0,
 Таким образом, разность фаз равна 90 0 .
Таким образом, разность фаз равна 90 0 .