НОУ ИНТУИТ | Лекция | Основы информатики
< Лекция 11 || Лекция 1: 12345678910
Аннотация: В этой лекции раскрывается базовая терминология информатики. Рассматриваются технические средства хранения информации, ее кодирование, системы счисления. Показывается история развития ЭВМ, говорится о принципах построения и управления компьютером, компьютерных вирусах. Значительное внимание уделено правовой охране программ и лицензии GPL.
Ключевые слова: свойства информации, группа, Теория информации, формальный язык, анализ, информатика, разделы, архитектура, операции, ПО, умозаключение, информация, определение, плоскость, достоверность, ясность, понятность, поиск, тип носителя, дерево, запись, floppy disk, ZIP, hard, диск, кодирование, компьютер, печать, вывод, знание, количество информации, бит, единица измерения, BIT, ложь, byte, байт, KOI8-R, пробел, килобайт, мегабайт, гигабайт, файл, хранилище данных, базы данных, поток, OS/2, произвольное, тип данных, standard, information, interchangeable, alt, кодировка, кодирование символов, диапазон, текстовые файлы, непозиционная система счисления, место, основание, сложение, вычитание, умножение, двоичная система счисления, binary digit, делимое, octal, hexadecimal, composability, максимальная степень, типы информации, обратный код, двоичное представление, мантисса, символ алфавита, таблица кодировки, векторная графика, picture element, растровая графика, электрический сигнал, память компьютера, ЦАП, MIDI, поколение ЭВМ, arithmetic, печатающее устройство, transistor, алгоритмический язык, algorithmic language, машинный язык, транслятор, многоязычность, artificial intelligence, expert system, типы задач, суперкомпьютер, вычислительная задача, файловый сервер, подкласс, архитектура компьютера, процесс обработки данных, внешнее запоминающее устройство, винчестер, запрос прерывания, CPU, storage device, input device, output device, communications device, процессор, память, арифметико-логическое устройство, мышь, controller, контроллер, производительность, RAM, random access, memory, ROM, read, разрядность, быстродействие, материнская плата, SIMM, DIMM, disc drive, последовательным доступом, keyboard, microphonics, scanner, лист, диаметр, знакоместо, шрифт, printer, множества, печатающая головка, Интернет, modem, скорость передачи, модем, сетевая карта, длина цепочки, компьютерные вирусы
intuit.ru/2010/edi»>Термином информатика обозначают совокупность дисциплин, изучающих свойства информации, а также способы представления, накопления, обработки и передачи информации с помощью технических средств. В англоязычных странах применяют термин computer science — компьютерная наука.Теоретическую основу информатики образует группа фундаментальных наук, которую в равной степени можно отнести как к математике, так и к кибернетике: теория информации, теория алгоритмов, математическая логика, теория формальных языков и грамматик, комбинаторный анализ и т. д. Кроме них информатика включает такие разделы, как архитектура ЭВМ, операционные системы, теория баз данных, технология программирования и многие другие.
Информационная технология есть совокупность конкретных технических и программных средств, с помощью которых мы выполняем разнообразные операции по обработке информации во всех сферах нашей жизни и деятельности.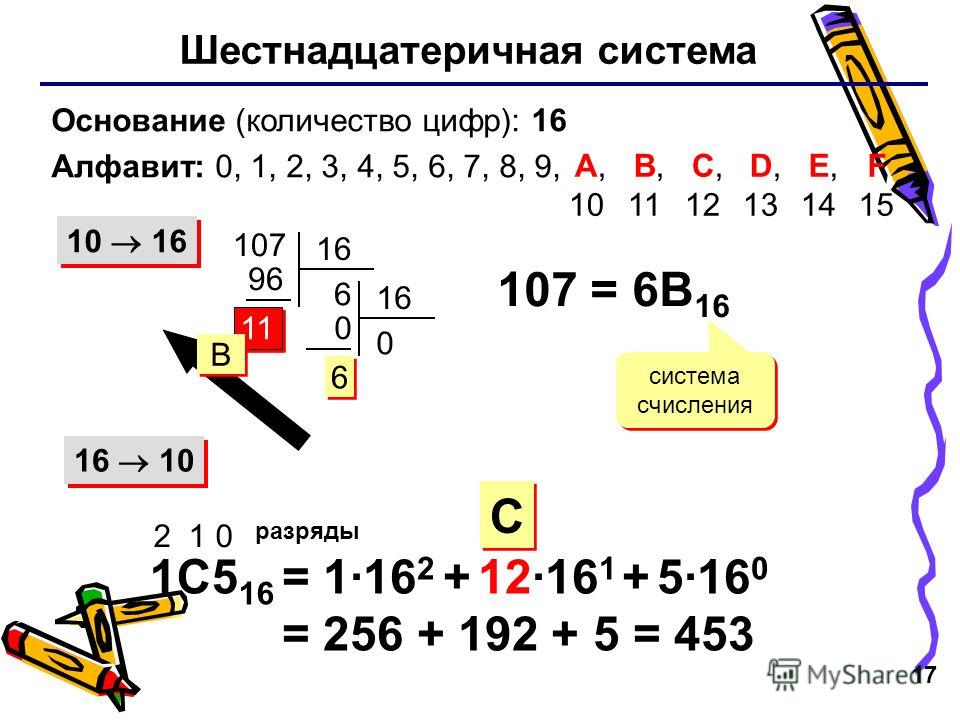 Иногда информационную технологию называют компьютерной технологией или прикладной информатикой.
Иногда информационную технологию называют компьютерной технологией или прикладной информатикой.
Информационные процессы
Термин информация ведет свое происхождение от латинского слова informatio, означающего разъяснение, изложение, осведомленность. Информацию мы передаем друг другу в устной и письменной форме, а также в форме жестов и знаков. Любую нужную информацию мы осмысливаем, передаем другим и делаем определенные умозаключения на ее основе.
Информацию мы извлекаем из учебников и книг, газет и журналов, телепередач и кинофильмов. Записываем ее в тетрадях и конспектах. В производственной деятельности информация передается в виде текстов и чертежей, справок и отчетов, таблиц и других документов. Такого рода информация может предоставляться и с помощью ЭВМ.
В любом виде информация для нас выражает сведения о ком-то или о чем-то. Она отражает происходящее или происшедшее в нашем мире, например, что мы делали вчера или будем делать завтра, как провели летний отпуск или каков будет характер будущей работы. При этом информация обязательно должна получить некоторую форму — форму рассказа, рисунка, статьи и т. д. Чертежи и музыкальные произведения, книги и картины, спектакли и кинофильмы — все это формы представления информации.
Она отражает происходящее или происшедшее в нашем мире, например, что мы делали вчера или будем делать завтра, как провели летний отпуск или каков будет характер будущей работы. При этом информация обязательно должна получить некоторую форму — форму рассказа, рисунка, статьи и т. д. Чертежи и музыкальные произведения, книги и картины, спектакли и кинофильмы — все это формы представления информации.
Информация, в какой бы форме она ни предоставлялась, является некоторым отражением реального или вымышленного мира. Поэтому информация — это отражение предметного мира с помощью знаков и сигналов.
Стоит отметить, что абсолютно точное определение информации дать невозможно, это такое же первичное понятие, как точка или плоскость в геометрии.
Получение информации — это получение фактов, сведений и данных о свойствах, структуре или взаимодействии объектов и явлений окружающего нас мира. Предметное содержание информации позволяет уяснить ее основные свойства — достоверность, полноту, ценность, актуальность, ясность и понятность.
Предметное содержание информации позволяет уяснить ее основные свойства — достоверность, полноту, ценность, актуальность, ясность и понятность.
- Информация достоверна, если она не искажает истинное положение дел. Недостоверная информация может привести к неправильному пониманию или принятию неправильных решений.
- Информация полна, если ее достаточно для понимания и принятия решений. Неполнота информации сдерживает принятие решений или может повлечь ошибки.
- Ценность информации зависит от того, какие задачи мы можем решить с ее помощью.
- При работе в постоянно изменяющихся условиях важно иметь актуальную, т. е. соответствующую действительности, информацию.
- Информация становится понятной, если она выражена языком, доступным людям, для которых она предназначена.

Информационная деятельность человека
Накопление человечеством опыта и знаний при освоении природы смешалось с освоением информации. Именно этот процесс и привел к образованию инфосферы. Такое понятие, как обработка информации, появилось совсем недавно, но обрабатывать информацию люди начали еще в древние времена.
Сначала из поколения в поколение информация передавалась устно. Это были сведения о профессиональных навыках, например, о приемах охоты, обработки охотничьих трофеев, способах земледелия и др. Но затем информацию стали фиксировать в виде графических образов окружающего мира. Первые наскальные рисунки, изображающие животных, растения и людей, появились примерно 20-30 тысяч лет назад.
Начатый поиск более современных способов фиксирования информации привел к появлению письменности. На чем только люди не писали! В Индии — на пальмовых листьях, в Вавилоне — на глиняных плитках, на Руси пользовались берестой. Как видим, письменность — новый шаг человечества в области хранения и передачи информации. Однако первым революционным явлением в этой сфере стало изобретение печатного станка, благодаря которому появилась книга и, таким образом, стало возможно массовое тиражирование профессиональных знаний, зафиксированных на материальном носителе.
Как видим, письменность — новый шаг человечества в области хранения и передачи информации. Однако первым революционным явлением в этой сфере стало изобретение печатного станка, благодаря которому появилась книга и, таким образом, стало возможно массовое тиражирование профессиональных знаний, зафиксированных на материальном носителе.
Сегодня потоки книг, сливаясь с потоками технической документации и многотомной справочной литературой, образуют океаны информации. Эту информацию необходимо хранить и передавать потребителю, для чего нужен мобильный и емкий носитель.
Но книга является неудобным, сложным, дорогим, а главное «медленным» носителем информации. Вся многогранность содержания раскрывается человеку при перелистывании, чтении и рассматривании книги. Она не может непосредственно влиять на производственный процесс. Сначала человеку необходимо найти нужную ему книгу, освоить накопленные в ней знания, которые позже смогут дать толчок дальнейшему развитию производства. Книга, как носитель информации, сегодня уже отстает от стремительного продвижения человечества по пути освоения природы.
Книга, как носитель информации, сегодня уже отстает от стремительного продвижения человечества по пути освоения природы.
Был и другой вид информационной деятельности. Отдельные государства, стремясь к расширению своих территорий, проводили агрессивную политику по отношению к своим соседям. Подготовка и ведение боевых действий требовали информации о военном потенциале противника. Ее добывали, например, через разведчиков. Тогда остро встал вопрос о защите информации от утечки в посторонние руки. Стали развиваться методы кодирования, разрабатываться способы быстрой и безопасной пересылки информации.
Шли годы, рос объем информации, которой обменивалось общество. Для сбора, переработки и распространения информации создавались издательства и типографии — родилась информационная промышленность. Газеты, журналы и другие издания, выпускаемые большими тиражами, зачастую кроме полезной информации обрушивали на человека огромное количество и ненужных, бесполезных сведений.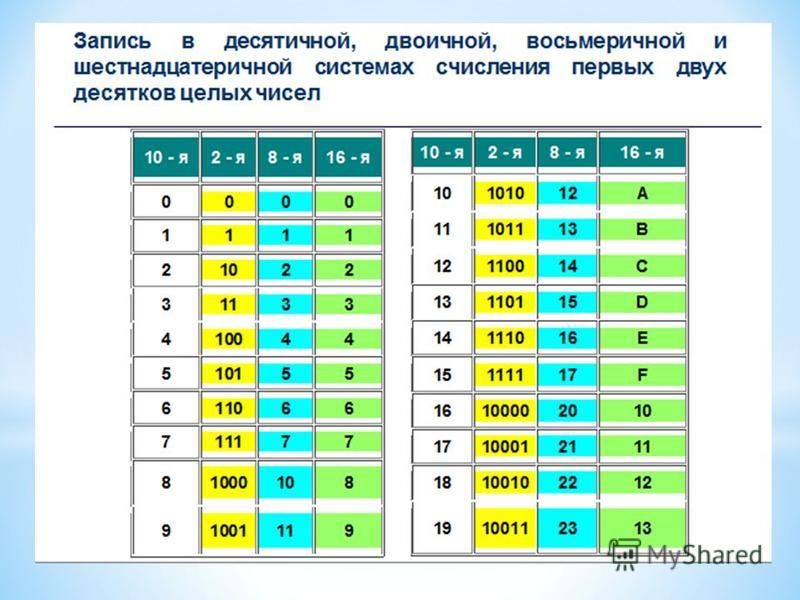 Для обозначения таких лишних сведений придумали специальный термин — информационный шум. Помимо печати появились и другие средства массовой информации — радио и телевидение. И общество привыкло к тому, что когда говорят об информации, то речь идет о сведениях, полученных через радио, газеты и т. д.
Для обозначения таких лишних сведений придумали специальный термин — информационный шум. Помимо печати появились и другие средства массовой информации — радио и телевидение. И общество привыкло к тому, что когда говорят об информации, то речь идет о сведениях, полученных через радио, газеты и т. д.
Революционным изобретением XX века явилась электронная вычислительная машина (ЭВМ). Она является как носителем информации, так и средством доставки ее потребителю. В совокупности с линиями связи, такими, как проводная, радио, космическая и оптическая, ЭВМ делает доступной любую часть гигантского океана информации, которая без непосредственного воздействия на человека может влиять на работу производственного оборудования, например, на станки с программным управлением.
Дальше >>
< Лекция 11 || Лекция 1: 12345678910
Системы счисления — презентация онлайн
Похожие презентации:
Системы счисления. (9 класс)
(9 класс)
Системы счисления
Системы счисления
Системы счисления
Системы счисления (Лекция 02)
Системы счисления
Системы счисления
Системы счисления
Системы счисления
Теоретические основы информатики. Системы счисления
Тема
«Системы счисления»
2. Введение
Современный человек в повседневной жизнипостоянно сталкивается с числами и цифрами — они
с нами везде. Различные системы счисления
используются всегда, когда появляется потребность
в числовых расчётах, начиная с вычислений
учениками младших классов, выполняемых
карандашом на бумаге, заканчивая вычислениями,
выполняемыми на суперкомпьютерах.
3. История систем счисления
Система счисления – это определённый способпредставления чисел и соответствующие ему правила
действия над ними.
Системы счисления
Позиционные
Непозиционные
Цель создания системы счисления- выработка
наиболее удобного способа записи количественной
информации.

4. Древние системы счисления:
5. Позиционные и непозиционные системы счисления
Непозиционныесистемы
Позиционные
системы
От положения цифры в
записи числа не зависит
величина, которую она
обозначает.
Величина, обозначаемая
цифрой в записи числа,
зависит от ее позиции.
Основание – количество
используемых цифр.
Позиция – место каждой
цифры.
6. Запись числа в позиционной системе счисления
Любое целое число в позиционной системе можнозаписать в форме многочлена:
где — основание системы счисления, – цифры числа,
записанного в данной системе счисления, — количество
разрядов числа.
Так, например число 629310запишется в форме
многочлена следующим образом:
629310=6·103 + 2·102 + 9·101 + 3·100
7. Примеры позиционных систем счисления:
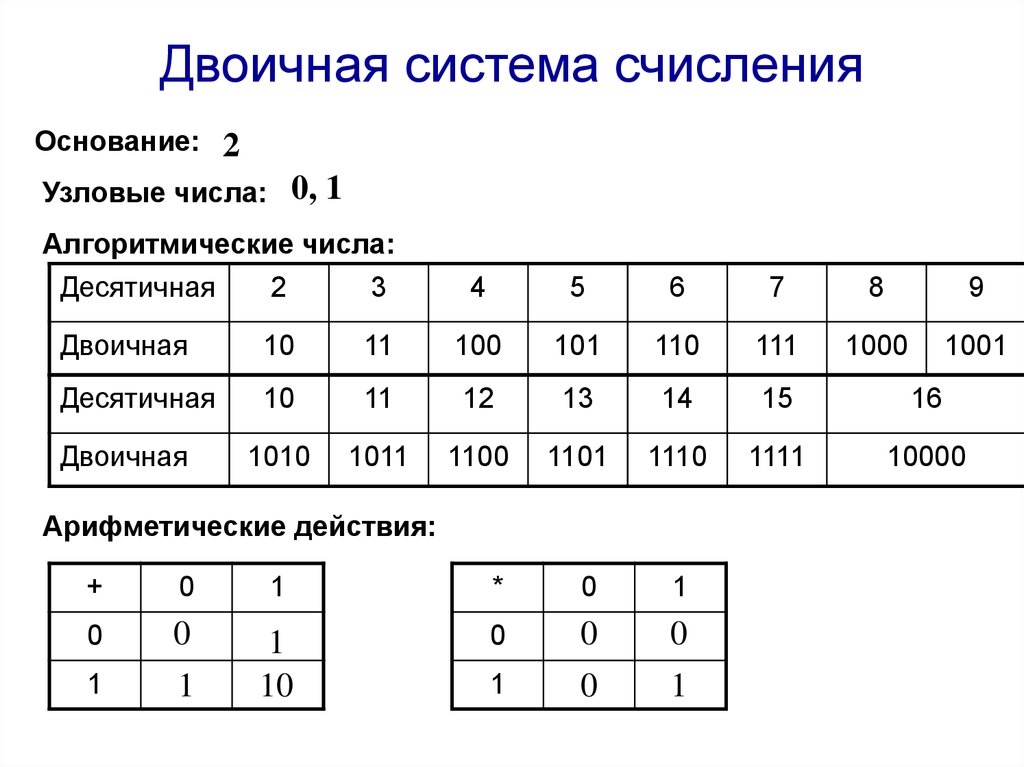
ДвоичнаяСистема счисления с основанием 2,
используются два символа — 0 и 1.
Восьмеричная
Система счисления с основанием 8,
используются цифры от 0 до 7.

Десятичная
Система с основанием 10, наиболее
распространённая система счисления в мире.
Двенадцатеричная
Система с основанием 12. Используются цифры
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B.
Шестнадцатеричная С основанием 16, используются цифры от 0 до 9
и латинские буквы от A до F для обозначения
цифр от 10 до 15.
Шестидесятеричная
Система с основанием 60, используется в
измерении углов и, в частности, долготы и
широты.
8. История двоичной системы счисления
Двоичная система счисления была придуманаматематиками и философами ещё до появления компьютеров
(XVII — XIX вв.).
Пропагандистом двоичной системы был знаменитый Г.В.
Лейбниц. Он отмечал особую простоту алгоритмов
арифметических действий в двоичной арифметике в
сравнении с другими системами и придавал ей
определенный философский смысл.
В 1936 — 1938 годах американский инженер и математик
Клод Шеннон нашёл замечательные применения двоичной
системы при конструировании электронных схем.
9. Двоичная система счисления
(бинарнаясистема счисления, binary) — позиционная
система счисления с основанием 2.
Неудобством этой системы счисления является
необходимость перевода исходных данных из десятичной
системы в двоичную при вводе их в машину и обратного
перевода из двоичной в десятичную при выводе
результатов вычислений.
Главное достоинство двоичной системы — простота
алгоритмов сложения, вычитания, умножения и деления.
10. Сложение, вычитание, умножение и деление в двоичной системе счисления
Сложение Вычитание Умножение Деление0 + 0 = 0;
0 + 1 = 1;
1 + 0 = 1;
1 + 1 = 10.
0 — 0 = 0;
1 — 0 = 1;
1 — 1 = 0;
10 — 1 = 1.
0 · 1 = 0;
1 · 1 = 1.
0 / 1 = 0;
1 / 1 = 1.
11. Двоичное кодирование в компьютере
В конце ХХ века, века компьютеризации,человечество пользуется двоичной системой
ежедневно, так как вся информация, обрабатываемая современными ЭВМ, хранится в них в
двоичном виде.
В современные компьютеры мы можем вводить
текстовую информацию, числовые значения, а также
графическую и звуковую информацию. Количество
информации, хранящейся в ЭВМ, измеряется ее
«длиной» (или «объемом»), которая выражается в битах
(от английского binary digit – двоичная цифра).
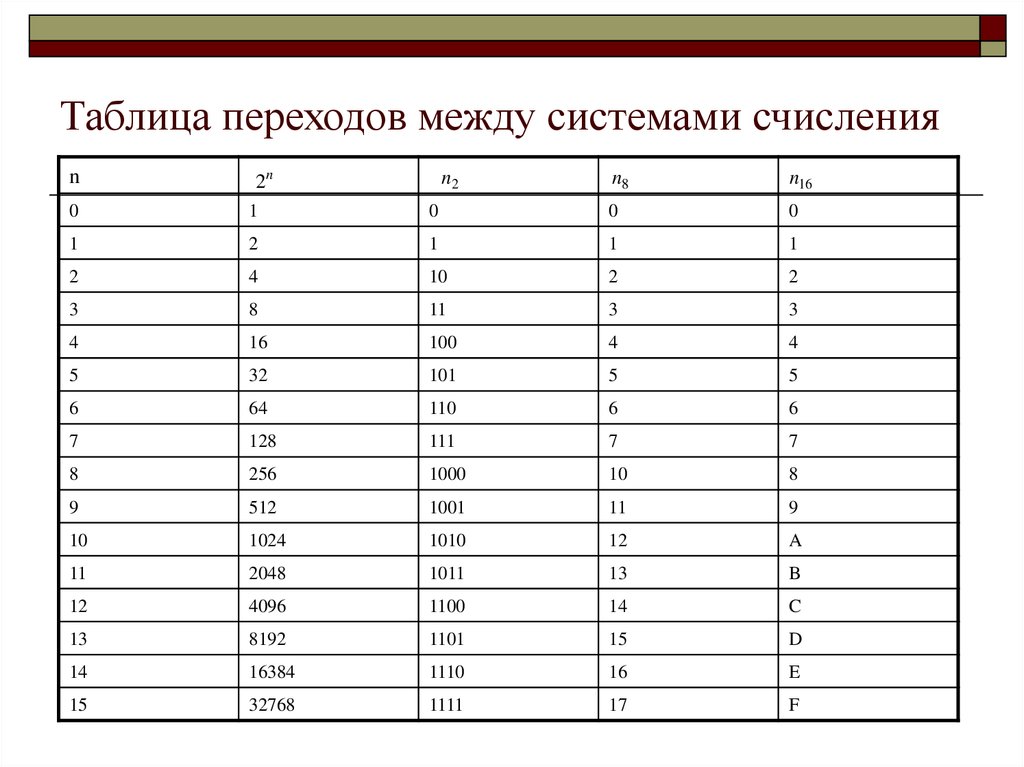
12. Перевод чисел из одной системы счисления в другую
13. Заключение
Высшим достижением древней арифметикиявляется открытие позиционного принципа
представления чисел.
Нужно признать важность не только самой
распространенной системы, которой мы пользуемся
ежедневно. Но и каждой по отдельности. Ведь в
разных областях используются разные системы
счисления, со своими особенностями и
характерными свойствами.
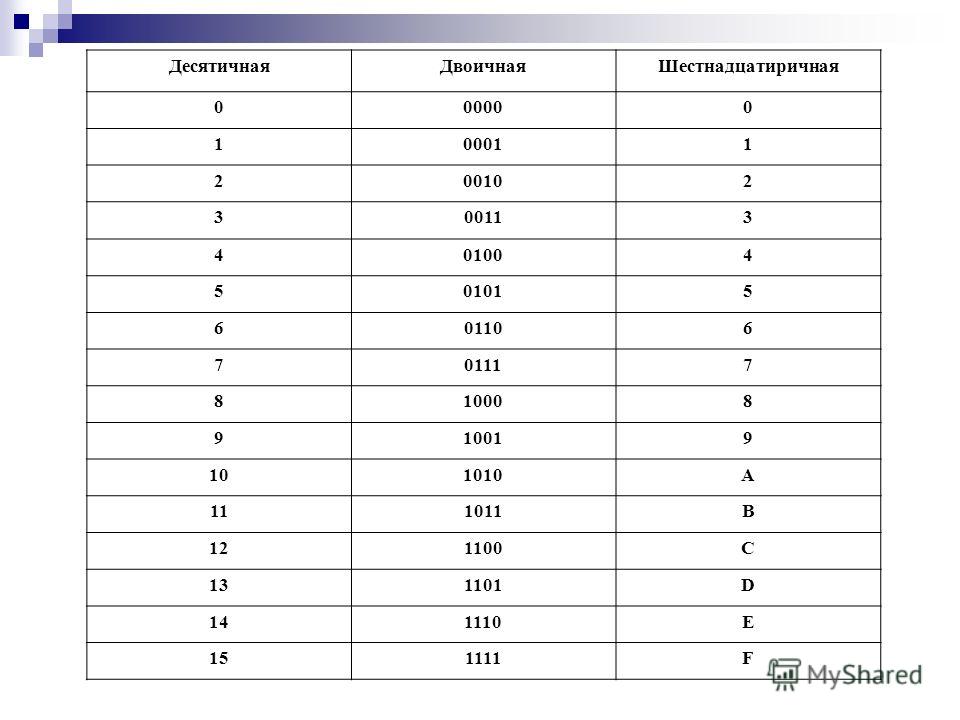
Десятичная
Двоичная
Восьмеричная
Шестнадцатеричная
1
001
1
1
2
010
2
2
3
011
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10
15.
 Перевод двоичного числа в десятичноеПеревод чисел
Перевод двоичного числа в десятичноеПеревод чиселДля перевода двоичного числа в десятичное
необходимо его записать в виде многочлена,
состоящего из произведений цифр числа и
соответствующей степени числа 2, и вычислить по
правилам десятичной арифметики:
16. Перевод восьмеричного числа в десятичное
Перевод чиселДля перевода восьмеричного числа в
десятичное необходимо его записать в виде
многочлена, состоящего из произведений цифр
числа и соответствующей степени числа 8, и
вычислить по правилам десятичной
арифметики:
17. Перевод шестнадцатеричного числа в десятичное
Перевод чиселДля перевода шестнадцатеричного числа в
десятичное необходимо его записать в виде
многочлена, состоящего из произведений цифр
числа и соответствующей степени числа 16, и
вычислить по правилам десятичной
арифметики:
18. Перевод десятичного числа в двоичную систему
Перевод чиселДля перевода десятичного числа в двоичную
систему его необходимо последовательно делить на 2 до
тех пор, пока не останется остаток, меньший или равный
1.
 Число в двоичной системе записывается как
Число в двоичной системе записывается какпоследовательность последнего результата деления и
остатков от деления в обратном порядке.
Пример: Число
перевести в двоичную систему
счисления:
19. Перевод десятичного числа в восьмеричную систему
Перевод чиселДля перевода десятичного числа в восьмеричную
систему его необходимо последовательно делить на 8 до тех
пор, пока не останется остаток, меньший или равный 7.
Число в восьмеричной системе записывается как
последовательность цифр последнего результата деления и
остатков от деления в обратном порядке.
Пример: Число
перевести в восьмеричную систему
счисления:
20. Перевод десятичного числа в шестнадцатеричную систему
Перевод чиселДля перевода десятичного числа в шестнадцатеричную
систему его необходимо последовательно делить на 16 до тех
пор, пока не останется остаток, меньший или равный 15. Число
в шестнадцатеричной системе записывается как
последовательность цифр последнего результата деления и
остатков от деления в обратном порядке.

Пример: Число
перевести в шестнадцатеричную
систему счисления:
21. Перевод чисел из двоичной системы в восьмеричную
Перевод чиселЧтобы перевести число из двоичной системы в
восьмеричную, его нужно разбить на триады (тройки цифр),
начиная с младшего разряда, в случае необходимости
дополнив старшую триаду нулями, и каждую триаду заменить
соответствующей восьмеричной цифрой. При переводе
необходимо пользоваться двоично-восьмеричной таблицей:
2-ная
000
001
010
011
100
101
110
111
8-ная
0
1
2
3
4
5
6
7
Пример: Число
систему счисления:
перевести в восьмеричную
22. Перевод из двоичной системы в шестнадцатеричную
Перевод чиселЧтобы перевести число из двоичной системы в
шестнадцатеричную, его нужно разбить на тетрады
(четверки цифр).
Двоично-шестнадцатеричная таблица:
2-ная
0000
0001
0010
0011
0100
0101
0110
0111
16-ная
0
1
2
3
4
5
6
7
2-ная
1000
1001
1010
1011
1100
1101
1110
1111
16-ная
8
9
A
B
C
D
E
F
Пример: Число
перевести в
шестнадцатеричную систему счисления:
23.
 Перевод восьмеричного числа в двоичноеПеревод чисел
Перевод восьмеричного числа в двоичноеПеревод чиселДля перевода восьмеричного числа в двоичное
необходимо каждую цифру заменить эквивалентной
ей двоичной триадой.
2-ная
000
001
010
011
100
101
110
111
8-ная
0
1
2
3
4
5
6
7
Пример: Число
счисления:
перевести в двоичную систему
24. Перевод шестнадцатеричного числа в двоичное
Перевод чиселДля перевода шестнадцатеричного числа в двоичное
необходимо каждую цифру заменить эквивалентной ей
двоичной тетрадой.
2-ная
0000
0001
0010
0011
0100
0101
0110
0111
16-ная 0
1
2
3
4
5
6
7
2-ная
1001
1010
1011
1100
1101
1110
1111
9
A
B
C
D
E
F
1000
16-ная 8
Пример: Число
счисления:
перевести в двоичную систему
25. Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно
Перевод чиселПри переходе из восьмеричной системы счисления
в шестнадцатеричную и обратно, необходим
промежуточный перевод чисел в двоичную систему.

Пример 1: Число
перевести в восьмеричную
систему счисления:
Пример 2: Число
перевести в
шестнадцатеричную систему счисления:
26. Единичная система
Древние системы счисленияВ древние времена, когда появилась потребность в записи
чисел, количество предметов, изображалось нанесением
Археологами найдены такие «записи» при раскопках
культурных слоев, относящихся к периоду палеолита (10–11
тысяч лет до н.э.).
В такой системе применялся только один вид знаков –
палочка. Каждое число обозначалось с помощью строки,
составленной из палочек, количество которых равнялось
обозначаемому числу.
English Русский Правила
Презентация — Системы счисления
Поделиться
17,100
просмотров
Презентации / Алгебра / Системы счисления
Скачать презентацию Понравилось | 10
Текст этой презентации
Слайд 1
Тема «Системы счисления»
Слайд 2
Введение
Современный человек в повседневной жизни постоянно сталкивается с числами и цифрами — они с нами везде. Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений учениками младших классов, выполняемых карандашом на бумаге, заканчивая вычислениями, выполняемыми на суперкомпьютерах.
Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений учениками младших классов, выполняемых карандашом на бумаге, заканчивая вычислениями, выполняемыми на суперкомпьютерах.
Слайд 3
Система счисления – это определённый способ представления чисел и соответствующие ему правила действия над ними. Цель создания системы счисления- выработка наиболее удобного способа записи количественной информации.
История систем счисления
Системы счисления
Позиционные
Непозиционные
Слайд 4
Древние системы счисления:
Единичная система
Древнегреческая нумерация
Славянская нумерация
Римская нумерация
Слайд 5
Позиционные и непозиционные системы счисления
Непозиционные системы Позиционные системы
От положения цифры в записи числа не зависит величина, которую она обозначает. Величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Основание – количество используемых цифр. Позиция – место каждой цифры.
Позиция – место каждой цифры.
Слайд 6
Запись числа в позиционной системе счисления
Любое целое число в позиционной системе можно записать в форме многочлена: Хs=An · Sn-1 + An-1 · Sn-2 + An-2 · Sn-3 +…+ A2 · S1 + A1 · S0
где S — основание системы счисления, А – цифры числа, записанного в данной системе счисления, n — количество разрядов числа.
Так, например число 629310запишется в форме многочлена следующим образом:
629310=6·103 + 2·102 + 9·101 + 3·100
Слайд 7
Примеры позиционных систем счисления:
Двоичная Система счисления с основанием 2, используются два символа — 0 и 1.
Восьмеричная Система счисления с основанием 8, используются цифры от 0 до 7.
Десятичная Система с основанием 10, наиболее распространённая система счисления в мире.
Двенадцатеричная Система с основанием 12. Используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B.
Шестнадцатеричная С основанием 16, используются цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Шестидесятеричная Система с основанием 60, используется в измерении углов и, в частности, долготы и широты.
Слайд 8
История двоичной системы счисления
Двоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.). Пропагандистом двоичной системы был знаменитый Г.В. Лейбниц. Он отмечал особую простоту алгоритмов арифметических действий в двоичной арифметике в сравнении с другими системами и придавал ей определенный философский смысл.
В 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем.
Слайд 9
Двоичная система счисления
Двоичная система счисления (бинарная система счисления, binary) — позиционная система счисления с основанием 2. Неудобством этой системы счисления является необходимость перевода исходных данных из десятичной системы в двоичную при вводе их в машину и обратного перевода из двоичной в десятичную при выводе результатов вычислений. Главное достоинство двоичной системы — простота алгоритмов сложения, вычитания, умножения и деления.
Главное достоинство двоичной системы — простота алгоритмов сложения, вычитания, умножения и деления.
Слайд 10
Сложение, вычитание, умножение и деление в двоичной системе счисления
Сложение Вычитание Умножение Деление
0 + 0 = 0;
0 + 1 = 1;
1 + 0 = 1;
1 + 1 = 10. 0 — 0 = 0;
1 — 0 = 1;
1 — 1 = 0;
10 — 1 = 1. 0 · 1 = 0; 1 · 1 = 1. 0 / 1 = 0; 1 / 1 = 1.
Слайд 11
Двоичное кодирование в компьютере
В конце ХХ века, века компьютеризации, человечество пользуется двоичной системой ежедневно, так как вся информация, обраба- тываемая современными ЭВМ, хранится в них в двоичном виде.
В современные компьютеры мы можем вводить текстовую информацию, числовые значения, а также графическую и звуковую информацию. Количество информации, хранящейся в ЭВМ, измеряется ее «длиной» (или «объемом»), которая выражается в битах (от английского binary digit – двоичная цифра).
Слайд 12
Перевод чисел из одной системы счисления в другую
8
16
Слайд 13
Заключение
Высшим достижением древней арифметики является открытие позиционного принципа представления чисел.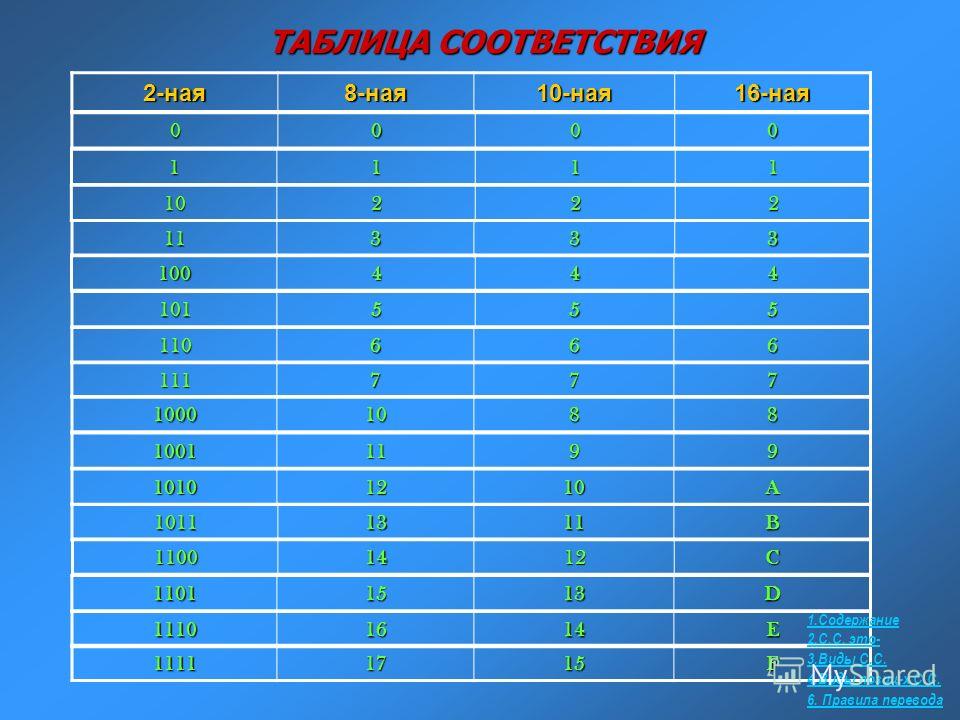 Нужно признать важность не только самой распространенной системы, которой мы пользуемся ежедневно. Но и каждой по отдельности. Ведь в разных областях используются разные системы счисления, со своими особенностями и характерными свойствами.
Нужно признать важность не только самой распространенной системы, которой мы пользуемся ежедневно. Но и каждой по отдельности. Ведь в разных областях используются разные системы счисления, со своими особенностями и характерными свойствами.
Слайд 14
Десятичная Двоичная Восьмеричная Шестнадцатеричная
1 001 1 1
2 010 2 2
3 011 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F
16 10000 20 10
Слайд 15
Перевод двоичного числа в десятичное
Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики: Х10= Аn·2n-1 + Аn-1·2n-2 + Аn-2·2n-3 +…+А2·21 + А1·20
Перевод чисел
Слайд 16
Перевод восьмеричного числа в десятичное
Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
Х10= Аn·8n-1 + Аn-1·8n-2 + Аn-2·8n-3 +…+А2·81 + А1·80
Перевод чисел
Слайд 17
Перевод шестнадцатеричного числа в десятичное
Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
Х10= Аn·16n-1 + Аn-1·16n-2 + Аn-2·16n-3 +…+А2·161 + А1·160
Перевод чисел
Слайд 18
Перевод десятичного числа в двоичную систему
Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример: Число 2210 перевести в двоичную систему счисления: 2210=101102
Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример: Число 2210 перевести в двоичную систему счисления: 2210=101102
Перевод чисел
Слайд 19
Перевод десятичного числа в восьмеричную систему
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример: Число 57110 перевести в восьмеричную систему счисления: 57110=10738
Перевод чисел
Слайд 20
Перевод десятичного числа в шестнадцатеричную систему
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.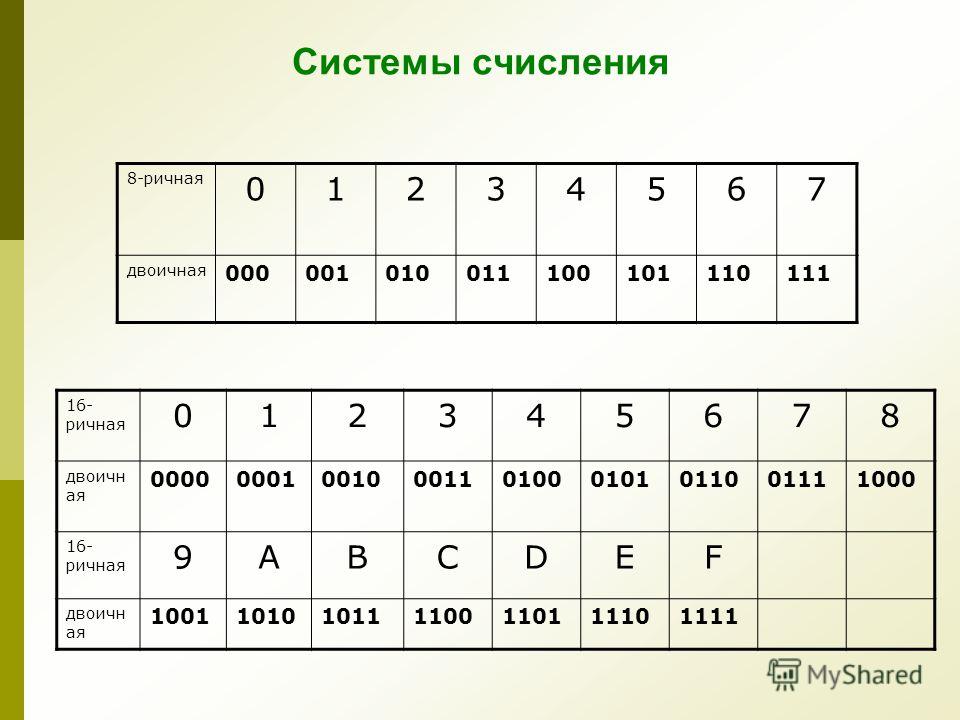 Пример: Число 746710 перевести в шестнадцатеричную систему счисления: 746710=1D2B16
Пример: Число 746710 перевести в шестнадцатеричную систему счисления: 746710=1D2B16
Перевод чисел
Слайд 21
Перевод чисел из двоичной системы в восьмеричную
Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой. При переводе необходимо пользоваться двоично-восьмеричной таблицей: Пример: Число 10010112 перевести в восьмеричную систему счисления: 001 001 0112=1138
2-ная 000 001 010 011 100 101 110 111
8-ная 0 1 2 3 4 5 6 7
Перевод чисел
Слайд 22
Перевод из двоичной системы в шестнадцатеричную
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр).
Двоично-шестнадцатеричная таблица: Пример: Число 10111000112 перевести в шестнадцатеричную систему счисления:
0010 1110 00112=2E316
2-ная 0000 0001 0010 0011 0100 0101 0110 0111
16-ная 0 1 2 3 4 5 6 7
2-ная 1000 1001 1010 1011 1100 1101 1110 1111
16-ная 8 9 A B C D E F
Перевод чисел
Слайд 23
Перевод восьмеричного числа в двоичное
Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой. Пример: Число 5318 перевести в двоичную систему счисления:
5318=101 011 0012
Пример: Число 5318 перевести в двоичную систему счисления:
5318=101 011 0012
2-ная 000 001 010 011 100 101 110 111
8-ная 0 1 2 3 4 5 6 7
Перевод чисел
Слайд 24
Перевод шестнадцатеричного числа в двоичное
Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой. Пример: Число ЕЕ816 перевести в двоичную систему счисления:
ЕЕ816=1110111010002
2-ная 0000 0001 0010 0011 0100 0101 0110 0111
16-ная 0 1 2 3 4 5 6 7
2-ная 1000 1001 1010 1011 1100 1101 1110 1111
16-ная 8 9 A B C D E F
Перевод чисел
Слайд 25
Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1: Число FEA16 перевести в восьмеричную систему счисления:
FEA16=1111111010102=111 111 101 0102=77528
Пример 2: Число 66358 перевести в шестнадцатеричную систему счисления: 66358=1101100111012=1101 1001 11012=D9D16
Перевод чисел
Слайд 26
Единичная система
В древние времена, когда появилась потребность в записи чисел, количество предметов, изображалось нанесением черточек или засечек на какой-либо твердой поверхности.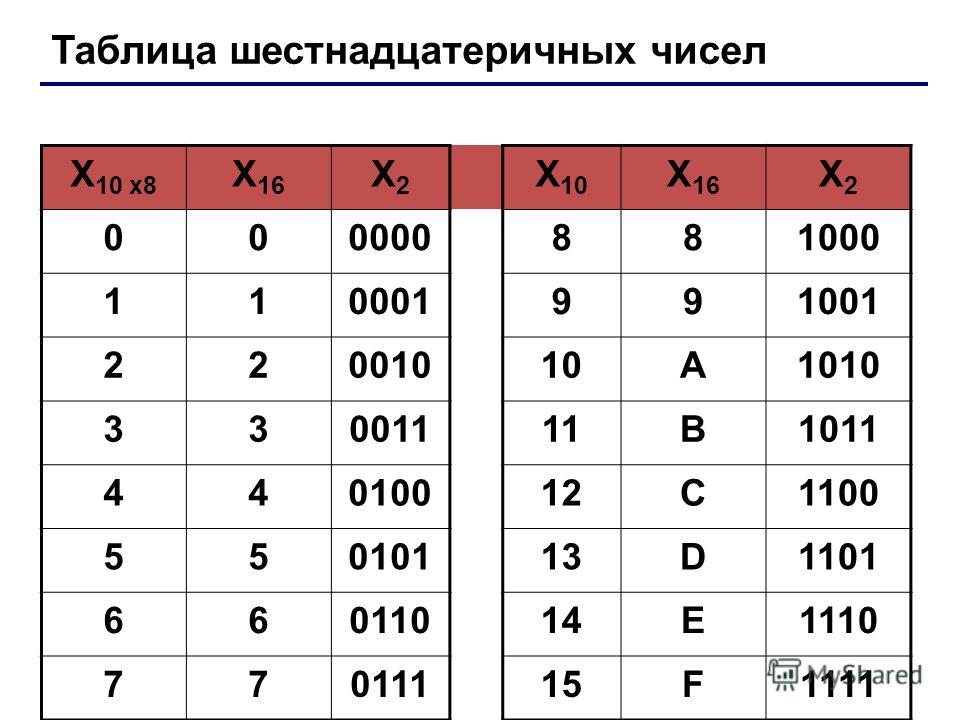 Археологами найдены такие «записи» при раскопках культурных слоев, относящихся к периоду палеолита (10–11 тысяч лет до н.э.).
В такой системе применялся только один вид знаков – палочка. Каждое число обозначалось с помощью строки, составленной из палочек, количество которых равнялось обозначаемому числу.
Археологами найдены такие «записи» при раскопках культурных слоев, относящихся к периоду палеолита (10–11 тысяч лет до н.э.).
В такой системе применялся только один вид знаков – палочка. Каждое число обозначалось с помощью строки, составленной из палочек, количество которых равнялось обозначаемому числу.
Древние системы счисления
Слайд 27
Древнегреческая нумерация
Аттическая нумерация
Ионийская система
В третьем веке до н.э. аттическая нумерация была вытеснена ионийской системой.
В древнейшее время в Греции была распространена аттическая нумерация.
Древние системы счисления
Слайд 28
Славянская нумерация
В России славянская нумерация сохранилась до конца XVII века. Южные и восточные славянские народы для записи чисел пользовались алфавитной нумерацией. Славянская нумерация сохранялась только в богослужебных книгах. Над буквой, обозначавшей цифру, ставился специальный значок: («титло»). Для обозначения тысяч перед числом (слева внизу) ставился особый знак .
Z
Древние системы счисления
Слайд 29
Римская нумерация
Древние римляне пользовались нумерацией, которая сохраняется до настоящего времени под именем «римской нумерации». Мы пользуемся ей для обозначения веков, юбилейных дат, наименования съездов и конференций, для нумерации глав книги или строф стихотворения.
I — 1 V — 5 X — 10 L — 50 C — 100 D — 500 М — 1000
Запись цифр в римской нумерации:
Древние системы счисления
Слайд 30
Ионийская система
Обозначение чисел в ионийской системе нумерации
Слайд 31
Обозначение чисел в древнеславянской системе нумерации
Славянская нумерация
Похожие презентации
Тест «Системы линейных уравнений и их применение» Обобщение «Интеграл Стилтьеса» Помощь учащимся в подготовке к экземанам егэ по теме «Задачи с параметрами» Обобщающий урок по теме «Уравнения и неравенства с двумя переменными» Геометрическая прогрессия вокруг нас
Система счисления
Введение в систему счисления
В годы развития технологий мир стал свидетелем бури перемен. Различные понятия предметов и механизмов образуют технику. А математика играет важную роль в развитии технологий и науки. Термин «Математика» очерчен как методологическая реализация материи. Различные разделы математики помогают нам систематизировать нашу жизнь. Математика важна не только в области науки, но и в области компьютерных наук.
Различные понятия предметов и механизмов образуют технику. А математика играет важную роль в развитии технологий и науки. Термин «Математика» очерчен как методологическая реализация материи. Различные разделы математики помогают нам систематизировать нашу жизнь. Математика важна не только в области науки, но и в области компьютерных наук.
Согласно индийской системе счисления, система счисления, одна из важнейших частей информатики, в основном связана с математикой. Существует много типов систем счисления, которые имеют дело с различными числовыми значениями. Система счисления представляет порядок определенного ряда чисел. Проще говоря, систему счисления можно назвать математическим представлением данного числа. Некоторые из основных типов систем счисления: двоичная, десятичная, шестнадцатеричная, восьмеричная и т. д.
Великий Арьябхата в древности открыл технику чисел в индийско-арабской системе счисления. Поэтому он широко известен как отец системы счисления. В этой статье мы рассмотрим возможности системы счисления и попытаемся развить глубокое понимание темы.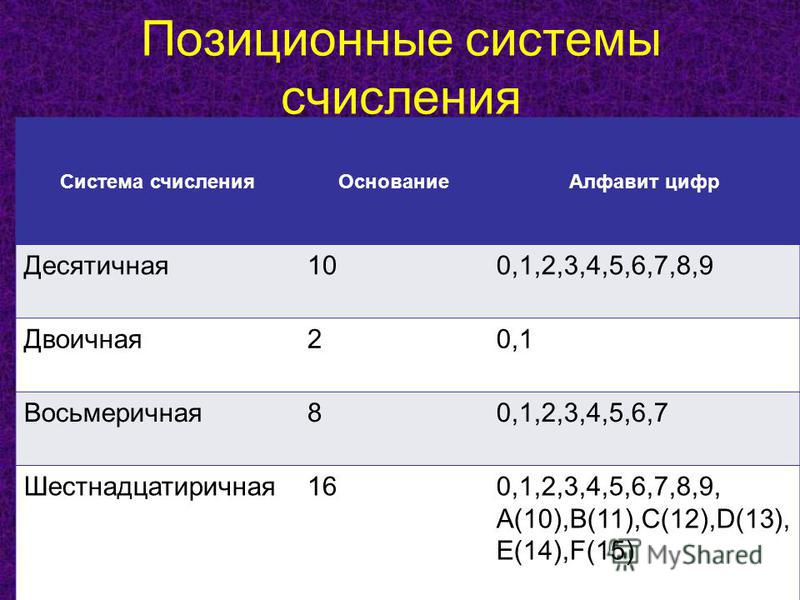
Определение системы счисления в математике
Система счисления может быть выделена как система письма или математическая запись для выражения некоторых чисел данного набора в соответствии с индийской системой счисления. В разных системах счисления одна и та же система счисления может определять другие числа. Например, 11 в десятичной системе представляет собой число, тогда как в двоичной системе оно представляет число три, а в унарной системе счисления оно представляет число два.
Свойства системы счисления –
- Система счисления используется для отображения полезного набора чисел.
- Обеспечивает стандартное представление каждого числа, присутствующего в системе счисления.
- Отображает арифметическую и алгебраическую структуру чисел.
Система счисления в настоящее время основана на позиционных системах, т. е. зависит от позиционных характеристик. Поэтому значение чисел изображается их положением чисел в соответствующем представлении. Давайте проясним это на примере; 4 в 40 и 4 в 400 представляют 4 десятка и четыре сотни соответственно. Эта система появляется в отличие от древней системы счисления в египетской цивилизации, греческой или еврейской системы счисления, которые не были основаны на положении, что делало их более дипломатичными для понимания.
Давайте проясним это на примере; 4 в 40 и 4 в 400 представляют 4 десятка и четыре сотни соответственно. Эта система появляется в отличие от древней системы счисления в египетской цивилизации, греческой или еврейской системы счисления, которые не были основаны на положении, что делало их более дипломатичными для понимания.
Область компьютеров и информатики реализует два основных ряда систем. В частности, двоичная система счисления, которая представляет числа в форме 0 и 1, и шестнадцатеричная система счисления, которая включает использование 16 символов — 0,1,2,3,4,5,6,7,8. ,9, A, B, C, D, E, F. Римские числа от одного до ста и так далее также являются частью систем счисления. Поэтому в системе счисления мы можем использовать от 1 до 100 римских цифр и более.
Вы также можете скачать всю систему счисления в системе счисления хинди Maths в Интернете бесплатно.
Типы системы счисления
Система счисления – это особый метод представления нескольких чисел из заданного набора с помощью их позиционных значений. Система счисления делится в основном на четыре типа —
Система счисления делится в основном на четыре типа —
Десятичная система счисления (основание 10) — также известная как десятичная или деканарная система счисления. Это один из стандартных способов представления целых и нецелых чисел в определенной последовательности. В десятичной системе счисления обозначение чисел также называется десятичной записью.
Двоичная система счисления (основание 2) — также известная как система счисления с основанием 2. Эта система счисления обычно использует два типа символов для обозначения конкретных чисел, то есть 0 и 1. Двоичная система счисления относится к позиционному понятию с основанием 2. Каждая цифра в этой системе выделена как бит.
Восьмеричная система счисления (основание 8) — также известная как система счисления с основанием 8. Он реализует числа от 0 до 7. Мы можем быстро сформировать восьмеричные числа, сгруппировав двоичные числа в три (начиная справа).
Шестнадцатеричная система счисления (основание 16) — также известная как система счисления с основанием 16.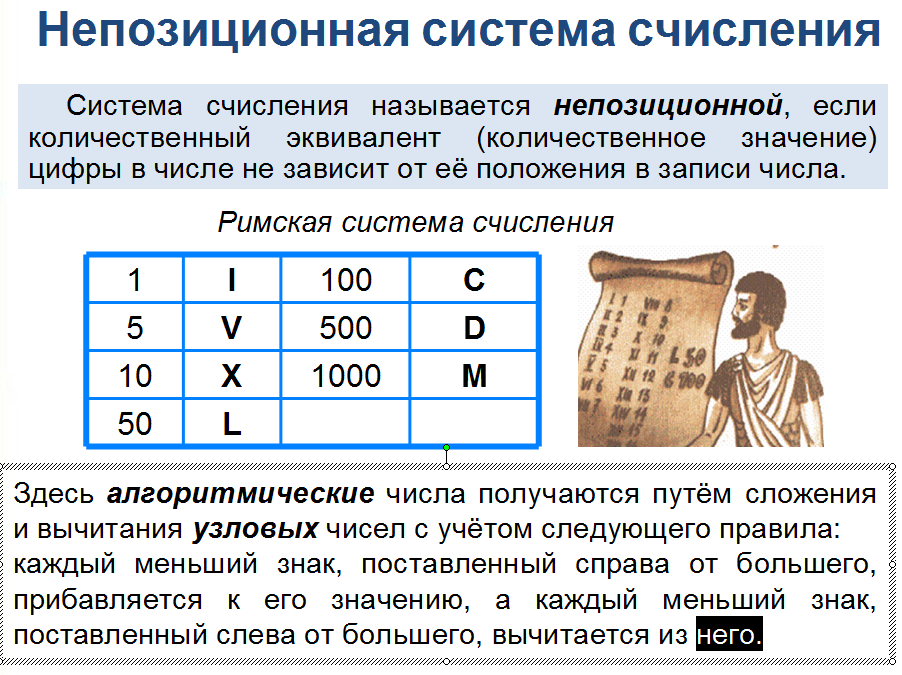 Это позиционная система счисления, в которой числа располагаются по основанию или основанию 16. Шестнадцатеричная система счисления обычно использует 16 цифр для представления чисел от 0 до 9 и от A до F.
Это позиционная система счисления, в которой числа располагаются по основанию или основанию 16. Шестнадцатеричная система счисления обычно использует 16 цифр для представления чисел от 0 до 9 и от A до F.
Десятичная система счисления
Десятичная система счисления Система счисления также цитируется как десятичная система счисления. Это один из стандартных механизмов представления целых и нецелых чисел. Это индийско-арабская система счисления, в которой способ выражения чисел широко известен как десятичная система счисления. Обычно его выделяют как обозначение чисел в десятичной системе счисления.
Десятичная система счисления включает в себя основание 10, так как она реализует десять цифр от 0 до 9. В десятичной системе счисления число, указанное слева от десятичной точки, представляет единицы, десятки, сотни, тысячи и т. д. .
Каждая позиция чисел представляет определенную степень по основанию 10. Например, десятичное число 5687 включает семь в разряде единиц, восемь в разряде десятков, шесть в разряде сотен и пять в разряде тысяч. Значение целого числа следующее:
Значение целого числа следующее:
(5 x 10³) + (6 x 10²) + (8 x 10¹) + (7 x 1)
= (5 x 1000) + (6 x 100) + (8 x 10) + (7 x 1) )
= 5000 + 600 + 80 + 7
= 5687
В систему счисления вводится также понятие бесконечной десятичной дроби, которое определяет десятичное значение, повторяющееся бесконечное число раз.
Двоичная система счисления
Механизм современной двоичной системы счисления был разработан в 16-м и 17-м веках опытными учеными. Однако идея была вдохновлена системой двоичных чисел, выделенной ранее в древнюю эпоху Египта, Индии и Китая. В математике и электронике двоичное число может быть представлено как число, представленное в системе счисления с основанием 2.
Следовательно, его также можно определить как позиционную запись с использованием системы счисления 2. Каждая цифра чисел в двоичной системе называется битом. Двоичная система счисления представляет собой простой и удобный механизм для пользователей. Поэтому на сегодняшний день он реализован практически всеми современными компьютерными устройствами. Двоичная система счисления обычно использует две двоичные цифры для обозначения расположения чисел, то есть 0 и 1. Например, 110101 — это двоичное число.
Поэтому на сегодняшний день он реализован практически всеми современными компьютерными устройствами. Двоичная система счисления обычно использует две двоичные цифры для обозначения расположения чисел, то есть 0 и 1. Например, 110101 — это двоичное число.
Число в двоичной системе счисления может быть преобразовано в любую другую систему счисления в соответствии с требованиями пользователя. Двоичная система счисления сегодня является одной из наиболее интенсивно используемых систем счисления на различных компьютерных устройствах.
Восьмеричная система счисления
Восьмеричная система счисления использует цифры от 0 до 7, поэтому она является системой счисления с основанием 8. Мы можем создавать восьмеричные числа из двоичных, располагая последовательные двоичные цифры в группу из трех цифр. Например, мы можем представить десятичное число 74 в двоичном формате как 1001010.
Восьмеричные числа имеют огромное значение в компьютерных приложениях. Восьмеричное число является одной из наиболее часто используемых систем счисления в современном мире технологий и компьютеров. Мы можем легко преобразовать восьмеричное число в десятичное число.
Восьмеричное число является одной из наиболее часто используемых систем счисления в современном мире технологий и компьютеров. Мы можем легко преобразовать восьмеричное число в десятичное число.
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления или шестнадцатеричная система счисления — это позиционное число с основанием 16. Это одна из наиболее часто используемых систем счисления для длинных двоичных значений. Он представляет собой удобный компактный и легко понятный формат по сравнению с длинными двоичными строками с 0 и 1.
Шестнадцатеричная система счисления использует шестнадцать различных цифр для размещения чисел в различных комбинациях. Итак, возможных цифр шестнадцатеричной системы счисления шестнадцать. В шестнадцатеричной системе счисления числа изображаются цифрами от 0 до 9.и алфавиты от A до F.
Хотя двоичные строки могут быть дипломатическими и длинными, мы можем упростить их, разбив эти длинные двоичные числа на более мелкие группы, чтобы их было удобно понимать и использовать. Например, группа двоичных цифр 1101, 0101, 1100 и 11112 более удобна для понимания по сравнению с 11010101110011112, когда они все сгруппированы.
Например, группа двоичных цифр 1101, 0101, 1100 и 11112 более удобна для понимания по сравнению с 11010101110011112, когда они все сгруппированы.
Шестнадцатеричная система счисления является одной из самых фантастических сторон сложности при работе с компьютерами и адресами памяти по сравнению с двоичной или десятичной системами счисления.
Числа от 0 до 10 — обитатели исходной десятичной системы. Но нам нужна шестнадцатеричная система счисления для представления числа от 10 до 15 с использованием заглавных букв от A до F. различные системы счисления –
Десятичная система счисления (основание 10) – также известная как десятичная или деканарная система счисления. Он представляет целые и нецелые числа в определенной последовательности. В десятичной системе счисления числа обозначаются с использованием базового значения 10.
Двоичная система счисления (основание 2) — также упоминается как система счисления с основанием 2. Эта система счисления обычно использует два типа символов для обозначения конкретных чисел, то есть 0 и 1. Двоичная система счисления выделяет позиционное понятие с основанием или основанием 2.
Двоичная система счисления выделяет позиционное понятие с основанием или основанием 2.
Он использует числа от 0 до 7. Восьмеричная система счисления определяет позиционное обозначение числа, реализующее основание или основание 8.
Шестнадцатеричная система счисления (Основание 16) – также называется системой счисления с основанием 16. Это позиционная запись чисел с использованием основания или системы счисления 16. Шестнадцатеричная система обычно реализует 16 цифр, представляющих числа, в диапазоне от 0 до 9.и от A до F.
Таким образом, таблица систем счисления играет важную роль в изображении базы всех действительных систем счисления.
Преобразование системы счисления
Системы счисления включают различные методы, позволяющие преобразовывать одну систему счисления в другую.
Двоичная система счисления в десятичную
Процесс преобразования двоичной системы счисления в десятичную заключается в простом умножении битов двоичного числа на соответствующие веса позиций. И затем мы должны добавить все эти продукты. Поэтому теперь мы получаем результат после преобразования двоичного числа в десятичное.
И затем мы должны добавить все эти продукты. Поэтому теперь мы получаем результат после преобразования двоичного числа в десятичное.
Двоичное число в восьмеричное
Преобразование двоичного числа в восьмеричное включает два этапа:
Во-первых, мы должны создать пару, включающую три бита по обе стороны от двоичных точек. Если мы обнаружим, что в трехбитной паре остался один или два бита, то к крайним углам можно добавить необходимое количество нулей.
Далее мы должны собрать и записать все восьмеричные цифры.
Двоичный код в шестнадцатеричный
Преобразование двоичного кода в шестнадцатеричный состоит из двух шагов, а именно:
- Сначала мы должны создать пары из четырех битов по обе стороны от двоичной точки. Если мы обнаружим, что один, два или три бита остались в паре четырехбитных пар, нули могут быть добавлены по мере необходимости на крайних концах.
- Теперь мы должны записать шестнадцатеричные цифры соответственно каждой паре.

Преобразование десятичного числа в двоичное
Мы можем преобразовать десятичное число в двоичное, выполнив два шага: ).
Преобразование десятичного числа в восьмеричное
Процедура преобразования восьмеричного числа в десятичное в основном такая же, как и двоичное преобразование в десятичное. Единственное отличие состоит в том, что вы должны выполнять операции деления и умножения с частным с основанием 8.
Преобразование десятичного числа в шестнадцатеричное
Процедура преобразования восьмеричного числа в десятичное в основном такая же, как и двоичное преобразование в десятичное. Единственное отличие состоит в том, что вы должны выполнять операции деления и умножения с частным с основанием 16.
Вы можете использовать обратный метод для преобразования восьмеричной системы счисления в другие системы счисления или преобразования шестнадцатеричной системы счисления в другие системы счисления.
Вы также можете преобразовать восьмеричное число в шестнадцатеричное следующими способами:
- Чтобы преобразовать восьмеричное число в шестнадцатеричное, сначала мы должны преобразовать восьмеричное число в двоичный эквивалент.
- Затем, чтобы получить окончательный восьмеричный результат в десятичный, мы должны преобразовать двоичное число в шестнадцатеричное число.
Система счисления в компьютере
Система счисления не только царица математики, но и играет решающую роль в области компьютеров. Компьютер, хотя и является блестящей машиной, не может понять человеческий язык. Поэтому всякий раз, когда мы что-то вводим в компьютер, он сначала переводит это в число для понимания. Компьютер знаком только с позиционной системой счисления, включающей лишь несколько символов, обозначаемых цифрами. Эти символы отображают различные значения в зависимости от позиций, которые они занимают в памяти компьютера. Таким образом, мы можем определить значение или положение каждой цифры в числе следующими способами:
- Сбор информации о цифре
- Поиск позиции цифры в данном числе
- Знание системы счисления (здесь нижняя часть системы счисления напоминает количество цифр, с которыми работает соответствующая система)
Широко используются четыре различных системы счисления: десятичная система счисления, двоичная система счисления, восьмеричная система счисления и шестнадцатеричная система счисления. Поэтому первичный механизм представления и работы с числами можно назвать системой счисления. Двоичная система счисления является одной из наиболее широко используемых систем счисления после десятичной системы счисления в технике и компьютерах.
Поэтому первичный механизм представления и работы с числами можно назвать системой счисления. Двоичная система счисления является одной из наиболее широко используемых систем счисления после десятичной системы счисления в технике и компьютерах.
Часто задаваемые вопросы
Q1: Определение систем счисления. И упомянуть его типы?
Ответ — Систему счисления можно описать как механизм письма или математическую нотацию для отображения некоторых чисел данного набора в действенной форме. В различных системах счисления одна и та же система счисления может определять разные числа. Например, 11 в десятичной системе представляет собой число, тогда как в двоичной системе оно представляет число три, а в унарной системе счисления оно представляет число два.
Существует четыре типа систем счисления: десятичная система счисления (с базовым значением 10, двоичная система счисления (с базовым значением 2), восьмеричная система счисления (с базовым значением 8), шестнадцатеричная система счисления (с базовым значением 16).
Q2: Почему важна система счисления?
Ответ – Система счисления является одним из жизненно важных методов для обозначения чисел. использоваться для представления количества учащихся в школе или числа учащихся, стоящих на конвейере.Основа или базовое число отображает количество цифр, используемых в системе счисления.
Базовое число или основание могут различаться в зависимости от четырех типов систем счисления: Десятичная система счисления (с базовым значением 10, Двоичная система счисления (с базовым значением 2), Восьмеричная система счисления (с базовым значением 8), Шестнадцатеричная система счисления Система счисления (с базовым значением 16)
Q3: Что такое базовое число и что такое базовое число 1, система счисления называется?
Например, двоичная система счисления имеет основание или основание 2, десятичная имеет основание 10, восьмеричное десятичное имеет основание 8, а шестнадцатеричное имеет основание 16.
Систему счисления с основанием 1 можно назвать унарной системой, самой простой и наиболее удобной системой счисления для обозначения натуральных чисел. В унарной системе счисления мы обозначаем ноль пустой строкой с отсутствием символа. Например, числа 2, 4, 5 будут представлены в унарной системе счисления как 11,1111,11111.
Q4: Что такое двоичная система счисления? Почему это важно?
Ответ – Двоичное число может быть определено как число, представленное в системе счисления с основанием 2. Следовательно, это также может быть обозначено как позиционная запись с использованием системы счисления 2. Каждая цифра чисел в двоичной системе известна немного. Двоичная система счисления представляет собой простой и удобный механизм для пользователей. Поэтому на сегодняшний день он реализован практически всеми современными компьютерными устройствами. Двоичная система счисления обычно использует две двоичные цифры для обозначения расположения чисел, то есть 0 и 1. Например, 101110 — это двоичное число. Важность двоичного числа достигла новых высот в современном мире технологий.
Например, 101110 — это двоичное число. Важность двоичного числа достигла новых высот в современном мире технологий.
Q5: Как преобразовать восьмеричную систему счисления в двоичную систему счисления?
Ans – Восьмеричные числа представляют собой числа с основанием 8. Напротив, двоичные числа – это числа с основанием 2.
Преобразование восьмеричного числа в десятичное представляет собой двухэтапную процедуру. Во-первых, нам нужно перевести восьмеричную систему счисления в десятичную. Затем нам нужно преобразовать десятичную систему счисления в двоичную.
Преобразовать восьмеричное число в десятичное –
- Шаг 1. Определите количество цифр в заданном числе. Предположим, что количество цифр равно «n».
- Шаг 2. Затем мы должны умножить каждую цифру числа на 8n-1, когда цифра занимает n-ю позицию от правого угла числа. И если число содержит десятичную часть, нам нужно умножить каждую цифру в десятичной части на «8-m», так как цифра занимает m-е место от десятичной точки.

- Теперь мы должны сложить все члены, полученные после умножения.
Теперь преобразуйте десятичное число в двоичное, чтобы получить результаты.
Q6: Что такое международная система нумерации?
Ответ. В международной системе счисления мы предоставляем эффективный механизм для удобного понимания больших чисел. Например, давайте познакомимся с Международной системой счисления с числами – единицы (1), десятки (10), сотни (100) и так далее.
Q7: Как преобразовать шестнадцатеричное число в десятичное?
Ответ – Чтобы преобразовать шестнадцатеричную систему счисления в десятичную, нам нужно начать с умножения шестнадцатеричного числа на 16. Затем вы должны возвести в него степень нуля, а затем вы должны каждый раз увеличивать емкость на единицу. .
Q8: Как эффективно решить проблемы системы счисления?
Ответ – 98 Эффективно решать задачи системы счисления; вы должны развить глубокое понимание темы. Вы должны потратить время на изучение концепций и различных методов. Вы также можете обратиться к решениям NCERT по математике класса 9, чтобы получить последние вопросы и попрактиковаться в них. Решения NCERT для бумаги по математике класса 9 и система счисления на хинди по математике находятся в свободном доступе в Интернете.
Вы должны потратить время на изучение концепций и различных методов. Вы также можете обратиться к решениям NCERT по математике класса 9, чтобы получить последние вопросы и попрактиковаться в них. Решения NCERT для бумаги по математике класса 9 и система счисления на хинди по математике находятся в свободном доступе в Интернете.
Система нумерации дней года
Система нумерации дней годаAZMET используется система нумерации дней года (DOY). Это распространенный формат, используемый в исследовательских данных и в вооруженных силах. Система Day-of-Year игнорирует существование месяцев и чисел. каждый день года подряд.
В обычные годы мы нумеруем каждый день года от 1 до 365. В високосный год мы вставляем «високосный день» (29 февраля), в день 60-го года, таким образом, остаток года сдвигается «вниз» на один день. Система Day-of-Year используется как в дневных, так и в почасовых файлах данных.
Есть и другие агентства по сбору данных о погоде, которые используют разные календарные форматы для своих данных.
 Они установили длину всех лет в 366
дней. Их «високосный день» (29 февраля; DOY 60) оставлен пустым (нули или нулевые значения данных).
для невисокосных лет. В високосные годы позиция високосного дня содержит данные.
AZMET не использует этот метод. Наши годы различаются по продолжительности.
Они установили длину всех лет в 366
дней. Их «високосный день» (29 февраля; DOY 60) оставлен пустым (нули или нулевые значения данных).
для невисокосных лет. В високосные годы позиция високосного дня содержит данные.
AZMET не использует этот метод. Наши годы различаются по продолжительности. AZMET использует 24-часовой формат времени.
Мы нумеруем каждый час дня от 1 до 24.
[Мы не используем «цифровые часы» с двоеточием (т.е. от 1:00 до 24:00).
Мы также не используем формат от 100 до 2400.]
Все данные AZMET собираются, хранятся и представляются в
местное время Аризоны, которое находится в часовом поясе Горного стандарта.
Аризона не участвует в переходе на летнее время.
Таким образом, время, указанное в файлах данных AZMET,
всегда на семь часов «отстаёт» от универсального скоординированного времени (UTC)
(также известное как среднее время по Гринвичу; зулусское время).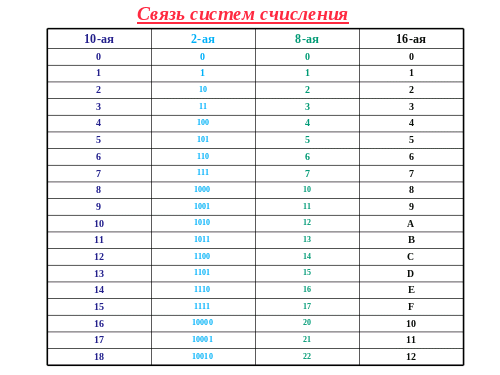
- Дополнительная информация о «Универсальном времени»
Преобразование «всеобщего времени» в часовые пояса США
Ниже приведены несколько таблиц и списков, чтобы помочь вам визуализировать систему «День года»: В этой первой таблице числа дней года сгруппированы по месяцам: День года по месяцам ======================================== Обычный год Високосный год -------------- --------------- 1–31 января 1–31 января 32 - 59 фев.32 - 60 фев. 60–90 марта 61–91 марта 91–120 апр. 92–121 апр. 121–151 мая 122–152 мая 152–181 июня 153–182 июня Июль 182–212 Июль 183–213 213–243 авг. 214–244 авг. 244–273 сент. 245–274 сент. 274–304 окт. 275–305 окт. 305–334 ноября 306–335 ноября дек. 335–365 дек. 336–366
Во второй календарной таблице Верхнее число в каждом поле представляет собой обычный календарный день месяца.
Нижнее число в каждом поле представляет день года (DOY).
январь +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| | | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| | +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ февраль +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| | 32| 33| 34| 35| 36| 37| 38| 39| 40| 41| 42| 43| 44| 45| 46| 47| 48| 49| 50| +---+---+---+---+---+---+---+---+---+******-+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28*29* ПРИМЕЧАНИЕ. В високосные годы прибавляйте 1 | | 51| 52| 53| 54| 55| 56| 57| 58| 59 * 60 * для каждого дня года после 29 февраля | +---+---+---+---+---+---+---+---+---+******-+---+- --+---+---+---+---+---+---+ Маршировать +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| | 60| 61| 62| 63| 64| 65| 66| 67| 68| 69| 70| 71| 72| 73| 74| 75| 76| 77| 78| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ | | 79| 80| 81| 82| 83| 84| 85| 86| 87| 88| 89| 90| в високосные годы.| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ апреля +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| | 91| 92| 93| 94| 95| 96| 97| 98| 99|100|101|102|103|104|105|106|107|108|109| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| Добавить 1 к ДОЙ | |110|111|112|113|114|115|116|117|118|119|120| в високосные годы. | +---+---+---+---+---+---+---+---+---+---+---+----- --------------------------+ Май +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| |121|122|123|124|125|126|127|128|129|130|131|132|133|134|135|136|137|138|139| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ | |140|141|142|143|144|145|146|147|148|149|150|151| в високосные годы. | +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ Июнь +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| |152|153|154|155|156|157|158|159|160|161|162|163|164|165|166|167|168|169|170| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| Добавить 1 к ДОЙ | |171|172|173|174|175|176|177|178|179|180|181| в високосные годы. | +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ Июль +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| |182|183|184|185|186|187|188|189|190|191|192|193|194|195|196|197|198|199|200| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ | |201|202|203|204|205|206|207|208|209|210|211|212| в високосные годы.
| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ Август +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| |213|214|215|216|217|218|219|220|221|222|223|224|225|226|227|228|229|230|231| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ | |232|233|234|235|236|237|238|239|240|241|242|243| в високосные годы. | +---+---+---+---+---+---+---+---+---+---+---+---+- --------------------------+ Сентябрь +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| |244|245|246|247|248|249|250|251|252|253|254|255|256|257|258|259|260|261|262| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| Добавить 1 к ДОЙ | |263|264|265|266|267|268|269|270|271|272|273| в високосные годы.
| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ Октябрь +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| |274|275|276|277|278|279|280|281|282|283|284|285|286|287|288|289|290|291|292| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ | |293|294|295|296|297|298|299|300|301|302|303|304| в високосные годы. | +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ ноябрь +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| |305|306|307|308|309|310|311|312|313|314|315|316|317|318|319|320|321|322|323| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| Добавить 1 к ДОЙ | |324|325|326|327|328|329|330|331|332|333|334| в високосные годы.
| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ Декабрь +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| |335|336|337|338|339|340|341|342|343|344|345|346|347|348|349|350|351|352|353| +---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+ | 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ | |354|355|356|357|358|359|360|361|362|363|364|365| в високосные годы. | +---+---+---+---+---+---+---+---+---+---+---+---+- --------------------------+ Джулианский нормальный прыжок День Год Год ----- ------ ------ 1 = 1 января 1 января 2 = 2 января 2 января 3 = 3 января 3 января 4 = 4 января 4 января 5 = 5 января 5 января 6 = 6 января 6 января 7 = 7 января 7 января 8 = 8 января 8 января 9= 9 января 9 января 10 = 10 января 10 января 11 = 11 января 11 января 12 = 12 января 12 января 13 = 13 января 13 января 14 = 14 января 14 января 15 = 15 января 15 января 16 = 16 января 16 января 17 = 17 января 17 января 18 = 18 января 18 января 19 = 19 января 19 января 20 = 20 января 20 января 21 = 21 января 21 января 22 = 22 января 22 января 23 = 23 января 23 января 24 = 24 января 24 января 25 = 25 января 25 января 26 = 26 января 26 января 27 = 27 января 27 января 28 = 28 января 28 января 29= 29 января 29 января 30 = 30 января 30 января 31 = 31 января 31 января 32 = 1 февраля 1 февраля 33 = 2 февраля 2 февраля 34 = 3 февраля 3 февраля 35 = 4 февраля 4 февраля 36 = 5 февраля 5 февраля 37 = 6 февраля 6 февраля 38 = 7 февраля 7 февраля 39 = 8 февраля 8 февраля 40 = 9 февраля 9 февраля 41 = 10 февраля 10 февраля 42 = 11 февраля 11 февраля 43 = 12 февраля 12 февраля 44 = 13 февраля 13 февраля 45 = 14 февраля 14 февраля 46 = 15 февраля 15 февраля 47 = 16 февраля 16 февраля 48 = 17 февраля 17 февраля 49= 18 февраля 18 февраля 50 = 19 февраля 19 февраля 51 = 20 февраля 20 февраля 52 = 21 февраля 21 февраля 53 = 22 февраля 22 февраля 54 = 23 февраля 23 февраля 55 = 24 февраля 24 февраля 56 = 25 февраля 25 февраля 57 = 26 февраля 26 февраля 58 = 27 февраля 27 февраля 59 = 28 февраля 28 февраля 60 = 1 марта 29 февраля 61 = 2 марта 1 марта 62 = 3 марта 2 марта 63 = 4 марта 3 марта 64 = 5 марта 4 марта 65 = 6 марта 5 марта 66 = 7 марта 6 марта 67 = 8 марта 7 марта 68 = 9 марта8 марта 69 = 10 марта 9 марта 70 = 11 марта 10 марта 71 = 12 марта 11 марта 72 = 13 марта 12 марта 73 = 14 марта 13 марта 74 = 15 марта 14 марта 75 = 16 марта 15 марта 76 = 17 марта 16 марта 77 = 18 марта 17 марта 78 = 19 марта 18 марта 79 = 20 марта 19 марта 80 = 21 марта 20 марта 81 = 22 марта 21 марта 82 = 23 марта 22 марта 83 = 24 марта 23 марта 84 = 25 марта 24 марта 85 = 26 марта 25 марта 86 = 27 марта 26 марта 87 = 28 марта 27 марта 88 = 29 марта28 марта 89 = 30 марта 29 марта 90 = 31 марта 30 марта 91 = 1 апреля 31 марта 92 = 2 апреля 1 апреля 93 = 3 апр 2 апр 94 = 4 апреля 3 апреля 95 = 5 апреля 4 апреля 96 = 6 апреля 5 апреля 97 = 7 апреля 6 апреля 98 = 8 апреля 7 апреля 99 = 9 апреля 8 апреля 100 = 10 апреля 9 апреля 101 = 11 апреля 10 апреля 102 = 12 апр 11 апр 103 = 13 апр 12 апр 104 = 14 апр 13 апр 105 = 15 апреля 14 апреля 106 = 16 апр 15 апр 107 = 17 апр 16 апр 108 = 18 апр 17 апр 109= 19 апр 18 апр 110 = 20 апреля 19 апреля 111 = 21 апреля 20 апреля 112 = 22 апреля 21 апреля 113 = 23 апреля 22 апреля 114 = 24 апреля 23 апреля 115 = 25 апреля 24 апреля 116 = 26 апреля 25 апреля 117 = 27 апреля 26 апреля 118 = 28 апреля 27 апреля 119 = 29 апреля 28 апреля 120 = 30 апреля 29 апреля 121 = 1 мая 30 апреля 122 = 2 мая 1 мая 123 = 3 мая 2 мая 124 = 4 мая 3 мая 125 = 5 мая 4 мая 126 = 6 мая 5 мая 127 = 7 мая 6 мая 128 = 8 мая 7 мая 129= 9 мая 8 мая 130 = 10 мая 9 мая 131 = 11 мая 10 мая 132 = 12 мая 11 мая 133 = 13 мая 12 мая 134 = 14 мая 13 мая 135 = 15 мая 14 мая 136 = 16 мая 15 мая 137 = 17 мая 16 мая 138 = 18 мая 17 мая 139 = 19 мая 18 мая 140 = 20 мая 19 мая 141 = 21 мая 20 мая 142 = 22 мая 21 мая 143 = 23 мая 22 мая 144 = 24 мая 23 мая 145 = 25 мая 24 мая 146 = 26 мая 25 мая 147 = 27 мая 26 мая 148 = 28 мая 27 мая 149= 29 мая 28 мая 150 = 30 мая 29 мая 151 = 31 мая 30 мая 152 = 1 июня 31 мая 153 = 2 июня 1 июня 154 = 3 июня 2 июня 155 = 4 июня 3 июня 156 = 5 июня 4 июня 157 = 6 июня 5 июня 158 = 7 июня 6 июня 159 = 8 июня 7 июня 160 = 9 июня 8 июня 161 = 10 июня 9 июня 162 = 11 июня 10 июня 163 = 12 июня 11 июня 164 = 13 июня 12 июня 165 = 14 июня 13 июня 166 = 15 июня 14 июня 167 = 16 июня 15 июня 168 = 17 июня 16 июня 169= 18 июня 17 июня 170 = 19 июня 18 июня 171 = 20 июня 19 июня 172 = 21 июня 20 июня 173 = 22 июня — 21 июня 174 = 23 июня 22 июня 175 = 24 июня 23 июня 176 = 25 июня 24 июня 177 = 26 июня 25 июня 178 = 27 июня 26 июня 179 = 28 июня 27 июня 180 = 29 июня 28 июня 181 = 30 июня 29 июня 182 = 1 июля 30 июня 183 = 2 июля 1 июля 184 = 3 июля 2 июля 185 = 4 июля 3 июля 186 = 5 июля 4 июля 187 = 6 июля 5 июля 188 = 7 июля 6 июля 189= 8 июля 7 июля 190 = 9 июля 8 июля 191 = 10 июля 9 июля 192 = 11 июля 10 июля 193 = 12 июля 11 июля 194 = 13 июля 12 июля 195 = 14 июля 13 июля 196 = 15 июля 14 июля 197 = 16 июля 15 июля 198 = 17 июля 16 июля 199 = 18 июля 17 июля 200 = 19 июля 18 июля 201 = 20 июля 19 июля 202 = 21 июля 20 июля 203 = 22 июля 21 июля 204 = 23 июля 22 июля 205 = 24 июля 23 июля 206 = 25 июля 24 июля 207 = 26 июля 25 июля 208 = 27 июля 26 июля 209= 28 июля 27 июля 210 = 29 июля 28 июля 211 = 30 июля 29 июля 212 = 31 июля 30 июля 213 = 1 августа 31 июля 214 = 2 августа 1 августа 215 = 3 августа 2 августа 216 = 4 августа 3 августа 217 = 5 августа 4 августа 218 = 6 августа 5 августа 219 = 7 августа 6 августа 220 = 8 августа 7 августа 221 = 9 августа 8 августа 222 = 10 августа — 9 августа 223 = 11 августа 10 августа 224 = 12 августа 11 августа 225 = 13 августа 12 августа 226 = 14 августа 13 августа 227 = 15 августа 14 августа 228 = 16 августа 15 августа 229= 17 августа 16 августа 230 = 18 августа 17 августа 231 = 19 августа 18 августа 232 = 20 августа 19 августа 233 = 21 августа 20 августа 234 = 22 августа 21 августа 235 = 23 августа 22 августа 236 = 24 августа 23 августа 237 = 25 августа 24 августа 238 = 26 августа 25 августа 239 = 27 августа 26 августа 240 = 28 августа 27 августа 241 = 29 августа 28 августа 242 = 30 августа 29 августа 243 = 31 августа 30 августа 244 = 1 сентября 31 августа 245 = 2 сентября 1 сентября 246 = 3 сентября 2 сентября 247 = 4 сентября 3 сентября 248 = 5 сентября 4 сентября 249= 6 сентября 5 сентября 250 = 7 сентября 6 сентября 251 = 8 сентября 7 сентября 252 = 9 сентября 8 сентября 253 = 10 сентября 9 сентября 254 = 11 сентября 10 сентября 255 = 12 сентября 11 сентября 256 = 13 сентября 12 сентября 257 = 14 сентября 13 сентября 258 = 15 сентября 14 сентября 259 = 16 сентября 15 сентября 260 = 17 сентября 16 сентября 261 = 18 сентября 17 сентября 262 = 19 сентября 18 сентября 263 = 20 сентября 19 сентября 264 = 21 сентября 20 сентября 265 = 22 сентября 21 сентября 266 = 23 сентября 22 сентября 267 = 24 сентября 23 сентября 268 = 25 сентября 24 сентября 269= 26 сентября 25 сентября 270 = 27 сентября 26 сентября 271 = 28 сентября 27 сентября 272 = 29 сентября 28 сентября 273 = 30 сентября 29 сентября 274 = 1 октября 30 сентября 275 = 2 октября 1 октября 276 = 3 октября 2 октября 277 = 4 октября 3 октября 278 = 5 октября 4 октября 279 = 6 октября 5 октября 280 = 7 октября 6 октября 281 = 8 октября 7 октября 282 = 9 октября 8 октября 283 = 10 октября 9 октября 284 = 11 октября 10 октября 285 = 12 октября 11 октября 286 = 13 октября 12 октября 287 = 14 октября 13 октября 288 = 15 октября 14 октября 289= 16 октября 15 октября 290 = 17 октября 16 октября 291 = 18 октября 17 октября 292 = 19 октября 18 октября 293 = 20 октября 19 октября 294 = 21 октября 20 октября 295 = 22 октября 21 октября 296 = 23 октября 22 октября 297 = 24 октября 23 октября 298 = 25 октября 24 октября 299 = 26 октября 25 октября 300 = 27 октября 26 октября 301 = 28 октября 27 октября 302 = 29 октября 28 октября 303 = 30 октября 29 октября 304 = 31 октября 30 октября 305 = 1 ноября 31 октября 306 = 2 ноября 1 ноября 307 = 3 ноября 2 ноября 308 = 4 ноября 3 ноября 309= 5 ноября 4 ноября 310 = 6 ноября 5 ноября 311 = 7 ноября 6 ноября 312 = 8 ноября 7 ноября 313 = 9 ноября 8 ноября 314 = 10 ноября 9 ноября 315 = 11 ноября 10 ноября 316 = 12 ноября 11 ноября 317 = 13 ноября 12 ноября 318 = 14 ноября 13 ноября 319 = 15 ноября 14 ноября 320 = 16 ноября 15 ноября 321 = 17 ноября 16 ноября 322 = 18 ноября 17 ноября 323 = 19 ноября 18 ноября 324 = 20 ноября 19 ноября 325 = 21 ноября 20 ноября 326 = 22 ноября 21 ноября 327 = 23 ноября 22 ноября 328 = 24 ноября 23 ноября 329= 25 ноября 24 ноября 330 = 26 ноября 25 ноября 331 = 27 ноября 26 ноября 332 = 28 ноября 27 ноября 333 = 29 ноября 28 ноября 334 = 30 ноября 29 ноября 335 = 1 декабря 30 ноября 336 = 2 декабря 1 декабря 337 = 3 декабря 2 декабря 338 = 4 декабря 3 декабря 339 = 5 декабря 4 декабря 340 = 6 декабря 5 декабря 341 = 7 декабря 6 декабря 342 = 8 декабря 7 декабря 343 = 9 декабря 8 декабря 344 = 10 декабря 9 декабря 345 = 11 декабря 10 декабря 346 = 12 декабря 11 декабря 347 = 13 декабря 12 декабря 348 = 14 декабря 13 декабря 349= 15 декабря 14 декабря 350 = 16 декабря 15 декабря 351 = 17 декабря 16 декабря 352 = 18 декабря 17 декабря 353 = 19 декабря 18 декабря 354 = 20 декабря 19 декабря 355 = 21 декабря 20 декабря 356 = 22 декабря 21 декабря 357 = 23 декабря 22 декабря 358 = 24 декабря 23 декабря 359 = 25 декабря 24 декабря 360 = 26 декабря 25 декабря 361 = 27 декабря 26 декабря 362 = 28 декабря 27 декабря 363 = 29 декабря 28 декабря 364 = 30 декабря 29 декабря 365 = 31 декабря 30 декабря 366 = 31 декабря Юлианские дни по месяцам ======================================== Обычный год Високосный год -------------- --------------- 1–31 января 1–31 января 32 - 59 фев.
32 - 60 фев. 60–90 марта 61–91 марта 91–120 апр. 92–121 апр. 121–151 мая 122–152 мая 152–181 июня 153–182 июня Июль 182–212 Июль 183–213 213–243 авг. 214–244 авг. 244–273 сент. 245–274 сент. 274–304 окт. 275–305 окт. 305–334 ноября 306–335 ноября дек. 335–365 дек. 336–366 Последние високосные годы: прошлые и будущие високосные годы =================================================== ============ * 1984 - Високосный год 1896 1936 1972 2008 1985 1904 1940 1976 2012 1986 1908 1944 1980 2016 1987 1912 1948 1984 2020 * 1988 - Високосный год 1916 1952 1988 2024 1989 1920 1956 1992 2028 1990 1924 1960 1996 2032 1991 1928 1964 2000 2036 * 1992 - Високосный год 1932 1968 2004 2040 1993 г. 1994 г. 1995 г. * 1996 - Високосный год (Правило большого пальца: високосные годы = годы президентских выборов в США) Официальные правила високосного года: Если год делится без остатка на 4, то он високосный.
Примеры: 1996/4 = 499, следовательно, это високосный год. 1997 / 4 = 499,25, следовательно, это не високосный год. Первое исключение: Из тех лет, которые без остатка делятся на 4, если год тоже без остатка делится на 100, это НЕ високосный год. Пример: 1900 / 4 = 475 1900/100 = 19, следовательно, это НЕ високосный год. Второе исключение: Из тех лет, которые без остатка делятся на 4 и 100, если год тоже без остатка делится на 400, это високосный год. Пример: 2000 / 4 = 500 2000 / 100 = 20 2000/400 = 5, следовательно, это високосный год. 1900/400 = 4,75, следовательно, это НЕ високосный год. Юлианский календарь был разработан Юлием Цезарем и египтянами. астроном Сосиген в 46 году до н. Они стремились создать 12 месячный календарь, основанный на солнечном году; время, необходимое для Земля совершает один полный оборот вокруг Солнца, что составляет 365,2422 дня.
(До этого римляне и большинство других цивилизаций использовали лунную или лунно-солнечный гибридный календарь; только в Египте был строго солнечный календарь.) Они установили нормальный год равным 365 дням, затем обозначили каждый четвертый год (високосный год) будет состоять из 366 дней. Это должно было исправить частичное .2422 день, который отсутствует в текущем году и в каждом из предыдущие три года. Для этого они включили «равномерно делится на 4 'правило в их календаре. Юлианский календарь был принят Никейским собором в 325 году нашей эры. Однако к 1582 году нашей эры количество прошлых високосных лет было чрезмерно исправлено. (0,2422 умножить на 4 года = 0,9688 дней, а не 1 день) и юлианский календарь выиграл 10 дней на реальной орбите Земли. положение вокруг солнца. Если не остановить, Пасха в конце концов происходят летом. Чтобы исправить это, Папа Григорий XIII пропустил 10 дней. с 1582 г. и ввел в действие первое и второе исключения («равно делимое на 100 и на 400'), как описано выше.
Первое исключение исключает високосный год каждые 100 лет. Используя только первое исключение, календарь через несколько столетий был бы немного недокорректирован. То есть он отстал бы от истинного орбитального положения Земли. Понимая это, математики Папы Римского добавили второе исключение который включает високосный год каждые 400 лет (1600, 2000, 2400 и т. д.). Эти правила не полностью корректируют календарь до идеальных 365,2422 дней. в год; к 5000 году нашей эры он выиграет 1 день и еще регулировка будет необходима. Раздел «календарь» любого хорошего альманаха проверит эти данные. правила относительно високосных лет ----- ВРЕМЯ: Все данные AZMET собираются, хранятся и представляются в местное время Аризоны, которое находится в часовом поясе Горного стандарта. Аризона не участвует в переходе на летнее время. Поэтому время, указанное в файлах данных AZMET, всегда на семь часов отстает от универсального скоординированного времени (UTC) (иначе: Среднее время по Гринвичу; Зулусское время).

- Дополнительная информация о «Универсальном времени»
UTC Аризона Аризона 12 часов
------ ------- -------------
8:00 1:00 1:00
9:00 2:00 2:00
10:00 3:00 3:00
11:00 4:00 4:00
12:00 5:00 5:00
13:00 6:00 6:00
14:00 7:00 7:00
15:00 8:00 8:00
16:00 9:00 9:00
17:00 10:00 10:00
18:00 11:00 11:00
19:00 12:00 00:00
20:00 13:00 13:00
21:00 14:00 14:00
22:00 15:00 15:00
23:00 16:00 16:00
24:00 17:00 17:00
13:00 18:00 18:00
14:00 19:00 19:00
15:00 20:00 20:00
16:00 21:00 21:00
17:00 22:00 22:00
18:00 23:00 23:00
7:00 24:00 12:00
Чикагский стиль (16-е издание) Раздаточный материал | Центр писательского мастерства Хоу
Chicago Style имеет две системы цитирования: (1) Notes and Bibliography или (2) Author-Date. В этом буклете описывается система Notes and Bibliography , которая обычно используется в истории и гуманитарных науках.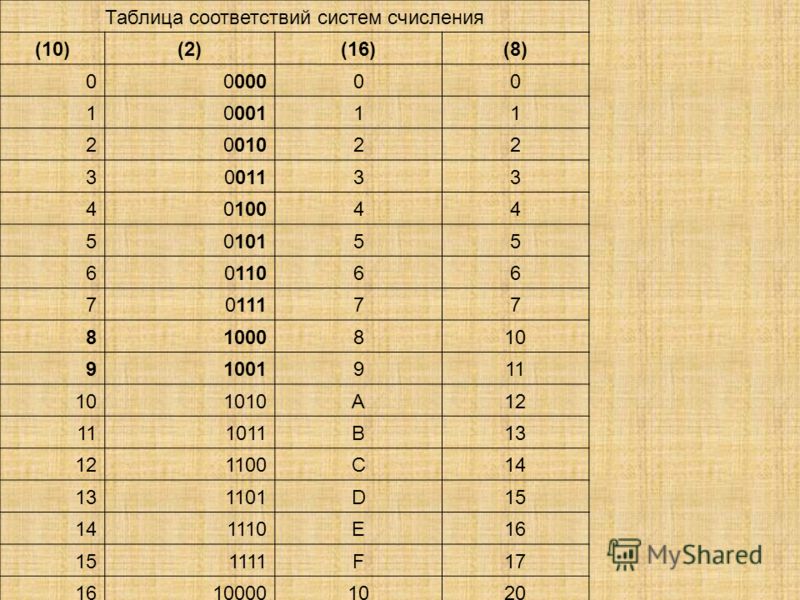
При использовании Чикагской системы примечаний и библиографии (NB) вы будете использовать надстрочные индексы в тексте для ссылки на цитаты в сносках или концевых сносках. Вы также будете цитировать все источники из текста в библиографии в конце документа.
Надстрочные индексы
Чикаго использует надстрочные индексы ( 1, 2, 3 ) в тексте, чтобы направлять читателей к цитате в сноске или концевой сноске. Вы будете использовать каждый номер надстрочного индекса только один раз.
В тексте размещайте надстрочные цифры в конце предложения или предложения и после всех знаков препинания, включая запятые, точки и кавычки.
Титаник затонул во время своего первого рейса после столкновения с айсбергом 14 апреля 1912 года. 1
Сноски и концевые сноски
В сносках внизу страницы приводится список ссылок на информацию, цитируемую на этой странице. В примечаниях перечислены все цитаты в конце документа. Общий формат цитаты одинаков как для сносок, так и для концевых сносок, в зависимости от того, что вы выберете.
Общий формат цитаты одинаков как для сносок, так и для концевых сносок, в зависимости от того, что вы выберете.
- Начинайте цитату с соответствующего номера, напечатанного обычным шрифтом или надстрочным индексом, после чего следует точка.
- 1. Джеймс Смит…
- 1 . Джеймс Смит…
- Отступ первой строки каждой цитаты на полдюйма. Следующие строки для одной и той же цитаты будут выравниваться по левому краю.
- Начинайте цитирование с автора(ов). Напишите все имена авторов в обычном порядке (имя фамилия).
- Для 2–3 авторов укажите имена всех авторов и объедините их с помощью «и».
- Для 4 или более авторов укажите только первого автора, а затем «et al.» (что означает «и все остальные»). Поставьте точку после «al». и не используйте запятую между именем автора и «и др.». (Джеймс Смит и др.)
- Укажите номер страницы только для конкретной цитаты или факта, который вы цитируете в этом конкретном предложении.
 Диапазон страниц для полных статей появится в библиографии.
Диапазон страниц для полных статей появится в библиографии. - При первом цитировании источника укажите всю необходимую информацию. При дополнительном цитировании одного и того же источника указывайте только фамилию автора, сокращенное название работы и номера страниц для этой цитаты или факта.
- 2. Фамилия автора, Сокращенное название книги , #.
- 2. AuthorLastName, «Сокращенное название статьи или веб-страницы», #.
- При последовательном цитировании одного и того же источника используйте слово «там же». (что означает «там же») вместо повторения имени автора или названия работы. Включите номер страницы, если он отличается от предыдущей цитаты.
- 3. Там же, #.
Информация, представленная в каждой цитате, будет отличаться для каждого типа источника. Вы можете проверить этот формат на Purdue OWL. Вот несколько примеров сносок/концевых сносок для распространенных типов источников:
Общий формат
#. AuthorFirstName LastName, Название книги Курсивом (Город издания: Издательство, год издания),
AuthorFirstName LastName, Название книги Курсивом (Город издания: Издательство, год издания),
Номер страницы для цитаты/факта.
Пример, цитируется впервые
1. Уолтер Лорд, Ночь продолжается: невыразимые истории и секреты гибели «Непотопляемого»
Корабль — Титаник (Нью-Йорк: Open Road Integrated Media, 2012), 7.
Пример, дополнительное время цитирования
13. Лорд, Night Lives On , 20.
Общий формат
#. AuthorFirstName LastName, «Название статьи в кавычках», в Название книги курсивом , изд. EditorFirstName
LastName (Город публикации: Издательство, год публикации), номер страницы для цитаты/факта.
Пример, цитируется впервые
2. Лоуренс Бисли, «Потеря корабля «Титаник», его история и уроки», в История «Титаника»: как рассказывалось
по выжившим , изд. Джек Винокур (Нью-Йорк: Dover Publications, 1960), 46.
Пример, дополнительное время цитирования
15. Лоуренс, Потеря СС Титаник , 40.
Общий формат
#. AuthorFirstName LastName, «Название статьи в кавычках», Название журнала курсивом том №, №. выпуск №
(год издания): номер страницы для цитаты/факта.
Пример, цитируется впервые
3. Бруно С. Фрей, Дэвид А. Сэвидж и Бенно Торглер, «Взаимодействие естественных инстинктов выживания и усвоенных
социальных норм. Исследование Титаник и Лузитания Бедствия», Труды Национальной академии наук 107, вып. 11
(2010): 4862.
Пример, дополнительное время цитирования
17. Фрей, Сэвидж и Торглер, «Взаимодействие», 4863.
Общий формат
#. AuthorFirstName LastName, «Название статьи в кавычках», Название газеты курсивом , день месяца, год
публикации, http://www.fullURL.com/ (для интернет-газет).
Пример, цитируется впервые.
 2012 г., http://www.nytimes.com/2012/04/10/science/a-new-look-at-natures-role-in-the-
2012 г., http://www.nytimes.com/2012/04/10/science/a-new-look-at-natures-role-in-the-titanics-sinking.html?_r=0.
Пример, дополнительное время цитирования
19. Броуд, «Новый взгляд».
Общий формат
#. AuthorFirstName LastName, «Название веб-страницы в кавычках», Название веб-сайта, выделенное курсивом , День месяца,
год публикации, http://www.fullURL.com/.
Пример, цитируется впервые
5. Канал National Geographic, «Титаник: факты о строителях, жертвах и выживших»,
Канал National Geographic , 12 декабря 2012 г., http: //channel.nationalgeographic.com/titanic-100-years/articles/titanic-the-
последнее слово-с-Джеймсом-Кэмероном-факты/.
Пример, дополнительное время цитирования
21. Канал National Geographic, «Titanic Facts».
Библиография
Библиография содержит полные ссылки на каждый источник, использованный в вашей статье, а также может включать дополнительную литературу, которая показалась вам полезной.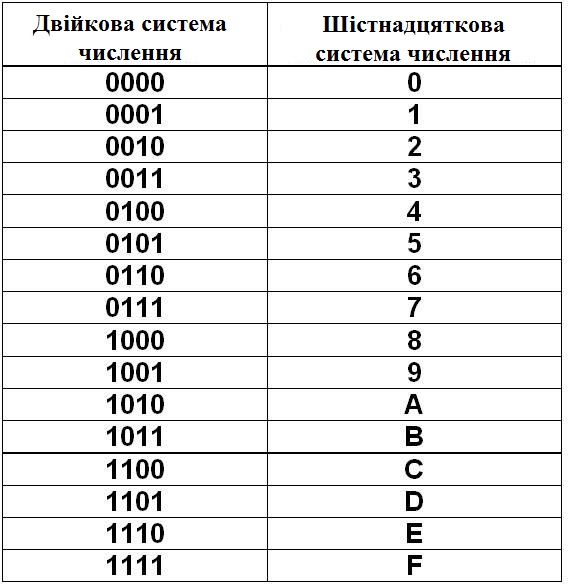 Следуйте этим общим примечаниям к формату Чикаго:
Следуйте этим общим примечаниям к формату Чикаго:
- Начните библиографию с новой страницы. Напишите «Библиография» в верхней части страницы и отцентрируйте ее, не выделяя жирным шрифтом или курсивом.
- Создать висячий отступ для всех цитат, чтобы каждая строка после первой была с отступом в полдюйма. Выполните следующие действия в Microsoft Word:
- Выделите все цитаты в библиографии.
- Щелкните правой кнопкой мыши и выберите «Абзац».
- В разделе «Отступ» перейдите к «Специальный» и выберите «Висячие» в раскрывающемся меню.
- Алфавит источников по фамилии автора. Если автора нет, расположите в алфавитном порядке по первому основному слову в названии.
- Начинайте цитирование с автора(ов). Напишите имя первого автора в обратном порядке (Фамилия, Имя), а имя каждого последующего автора напишите в обычном порядке (Имя Фамилия).
- Для 4-7 авторов включите все имена в библиографию.
- Для 8 или более авторов укажите первые 7 имен, а затем «и др.
 ». (Эллисон, Лоррейн, Молли Браун, Ноэль Ротс, Глэдис Черри, Джейкоб Астор, Эмили Пейдж, Люсиль Гордон и др.)
». (Эллисон, Лоррейн, Молли Браун, Ноэль Ротс, Глэдис Черри, Джейкоб Астор, Эмили Пейдж, Люсиль Гордон и др.)
- Выделяйте книги и журналы курсивом и заключайте в кавычки заголовки статей и веб-страниц. Полностью заглавные буквы (кроме артиклей и предлогов).
- «Заголовок статьи будет выглядеть так.»
- Название книги будет выглядеть так .
- Когда вас попросят указать месяц публикации, сократите месяц в соответствии со следующими стандартами:
- Январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь
Информация, представленная в каждой цитате, будет отличаться для каждого типа источника. Вы можете проверить этот формат на Purdue OWL. Вот несколько примеров библиографических ссылок на распространенные типы источников:
Общий формат
Фамилия автора, Имя. Название книги курсивом . Город издания: Издательство, год издания.
Пример
Лорд, Уолтер. Ночь продолжается: нерассказанные истории и секреты гибели «Непотопляемого»
Корабль — Титаник. Нью-Йорк: Open Road Integrated Media, 2012.
Общий формат
Фамилия автора, имя. «Название статьи в кавычках». В Название книги курсивом , отредактировано EditorFirstName
Фамилия, диапазон страниц для статьи. Город издания: Издательство, год издания.
Пример
Бисли, Лоуренс. «Потеря СС Титаник, его история и уроки». В История Титаника: как рассказали
его выжившие , под редакцией Джека Винокура, 1-110. Нью-Йорк: Dover Publications, 1960.
Общий формат
Фамилия автора, имя. «Название статьи в кавычках». Название журнала, выделенное курсивом том №, вып. issue#
(год издания): диапазон страниц для статьи.
Пример
Фрей, Бруно С., Дэвид А. Сэвидж и Бенно Торглер. «Взаимодействие естественных инстинктов выживания и интернализованных социальных норм
, изучение катастроф Титаника и Лузитании ». Труды Национальной академии наук 107, вып. 11
Труды Национальной академии наук 107, вып. 11
(2010): 4862-4865.
Общий формат
Фамилия автора, Имя. «Название статьи в кавычках». Название газеты курсивом , Месяц День, Год
издания. http://www.fullURL.com/ (для интернет-газет).
Пример
Броуд, Уильям Дж. «Новый взгляд на роль природы в гибели Титаника : айсберг был лишь частью этого».
The New York Times , 9 апреля 2012 г. http://www.nytimes.com/2012/04/10/science/a-new-look-at-natures-
-titanics-sinking.html?_r=0.Общий формат
Фамилия автора, Имя. «Название веб-страницы в кавычках». Название веб-сайта Курсив . Месяц День, Год
публикации. http://www.fullURL.com/.
Пример
Канал National Geographic. «Факты о Титанике: несколько быстрых фактов о ее строителях, ее жертвах и выживших».
Канал National Geographic . 12 декабря 2012 г. http://channel.nationalgeographic.com/titanic-100-years/articles/
http://channel.nationalgeographic.com/titanic-100-years/articles/
titanic-the-final-word-with-james-cameron-facts/.
Стиль и формат
В Чикаго цитаты, которые занимают 5 или более строк, должны быть отформатированы как блочные цитаты. Это означает, что в цитате не будет кавычек, она будет разделена одинарным интервалом и будет иметь отступ в полдюйма от остальной части абзаца. Например:
Многие ученые по-прежнему предпочитают людей компьютерам:
Человеческий мозг с его гибкостью и способностью к воображению по-прежнему во многих отношениях превосходит электронную модель. Компьютер никогда не бывает утомленным, озабоченным или небрежным, поэтому он прекрасно запоминает и соблюдает правила. Но у него нет воображения даже у очень молодого человеческого мозга, который не только может забыть правила, но и может найти в них лазейки и варианты. Электронный интеллект может обрабатывать информацию, как горящий дом, но при этом не может думать. 22
Заголовки разделов Формат для каждого уровня заголовка в Чикаго можно увидеть ниже. Все заголовки должны быть выполнены шрифтом одного размера и типа.
Все заголовки должны быть выполнены шрифтом одного размера и типа.
Заголовок уровня 1: Выровнен по центру, выделен полужирным шрифтом или курсивом и полностью заглавными буквами
Заголовок уровня 2: Выровнен по центру, выделен полностью заглавными буквами, без выделения жирным шрифтом/курсивом
Текст абзаца для раздела уровня 2 начинается со следующей строки.
Заголовок уровня 3: с выравниванием по левому краю, полужирным или курсивом и с заглавными буквами
Текст абзаца для раздела уровня 3 будет начинаться со следующей строки.
Заголовок уровня 4: выравнивание по левому краю и строчные буквы, без полужирного/курсивного начертания
Текст абзаца для раздела уровня 4 будет начинаться со следующей строки.
Заголовок уровня 5: выравнивание по левому краю, строчные буквы, полужирный или курсив, за которым следует точка. Текст абзаца для раздела уровня 5 будет начинаться со следующей строки.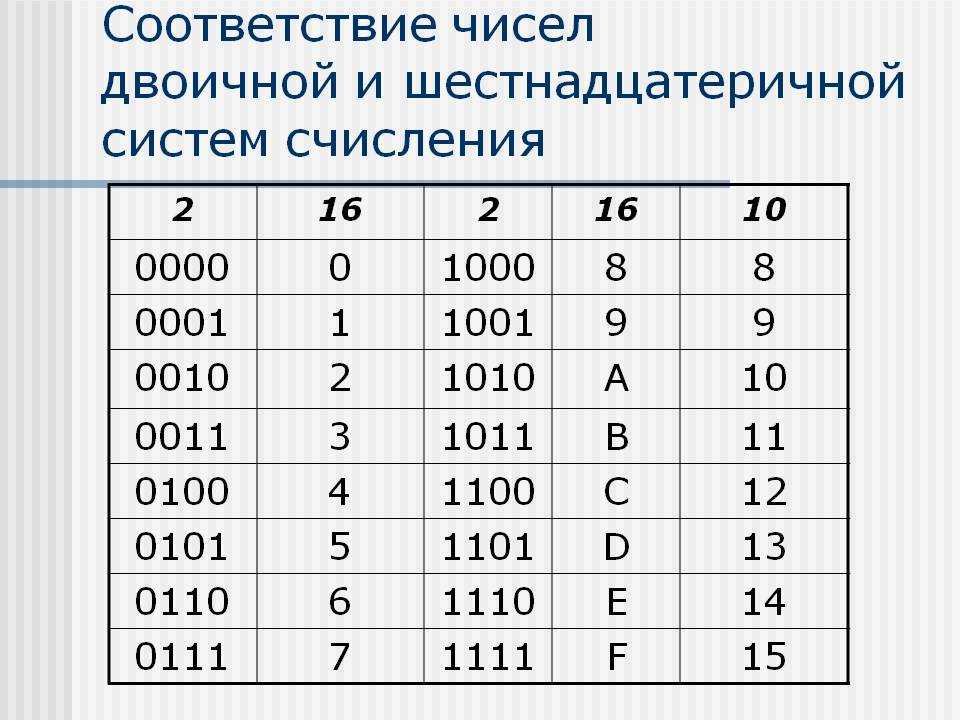




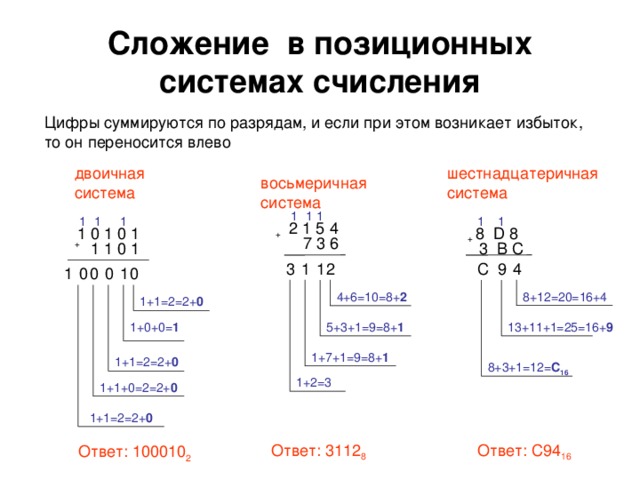
 Нижнее число в каждом поле представляет день года (DOY).
Нижнее число в каждом поле представляет день года (DOY).
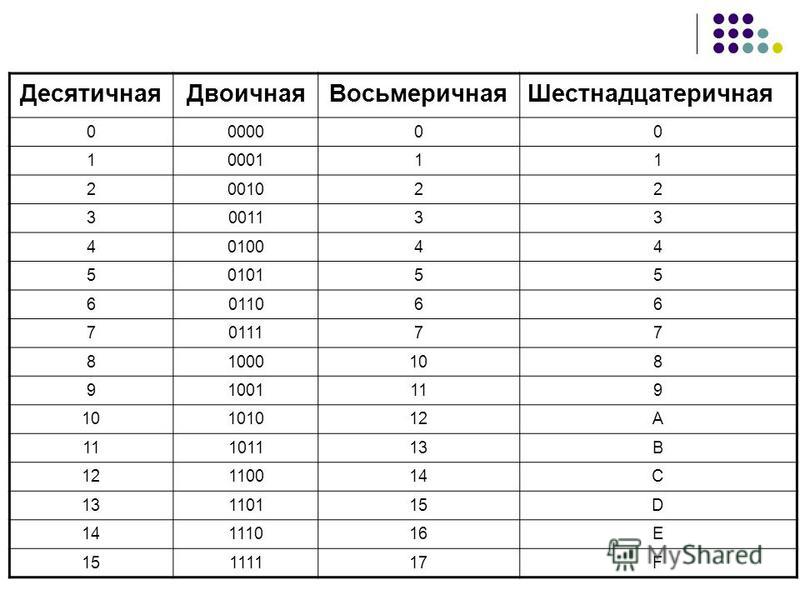 |
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
Июнь
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|152|153|154|155|156|157|158|159|160|161|162|163|164|165|166|167|168|169|170|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| Добавить 1 к ДОЙ |
|171|172|173|174|175|176|177|178|179|180|181| в високосные годы. |
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
Июль
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|182|183|184|185|186|187|188|189|190|191|192|193|194|195|196|197|198|199|200|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ |
|201|202|203|204|205|206|207|208|209|210|211|212| в високосные годы.
|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
Июнь
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|152|153|154|155|156|157|158|159|160|161|162|163|164|165|166|167|168|169|170|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| Добавить 1 к ДОЙ |
|171|172|173|174|175|176|177|178|179|180|181| в високосные годы. |
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
Июль
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|182|183|184|185|186|187|188|189|190|191|192|193|194|195|196|197|198|199|200|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ |
|201|202|203|204|205|206|207|208|209|210|211|212| в високосные годы. |
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
Август
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|213|214|215|216|217|218|219|220|221|222|223|224|225|226|227|228|229|230|231|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ |
|232|233|234|235|236|237|238|239|240|241|242|243| в високосные годы. |
+---+---+---+---+---+---+---+---+---+---+---+---+- --------------------------+
Сентябрь
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|244|245|246|247|248|249|250|251|252|253|254|255|256|257|258|259|260|261|262|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| Добавить 1 к ДОЙ |
|263|264|265|266|267|268|269|270|271|272|273| в високосные годы.
|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
Август
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|213|214|215|216|217|218|219|220|221|222|223|224|225|226|227|228|229|230|231|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ |
|232|233|234|235|236|237|238|239|240|241|242|243| в високосные годы. |
+---+---+---+---+---+---+---+---+---+---+---+---+- --------------------------+
Сентябрь
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|244|245|246|247|248|249|250|251|252|253|254|255|256|257|258|259|260|261|262|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| Добавить 1 к ДОЙ |
|263|264|265|266|267|268|269|270|271|272|273| в високосные годы. |
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
Октябрь
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|274|275|276|277|278|279|280|281|282|283|284|285|286|287|288|289|290|291|292|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ |
|293|294|295|296|297|298|299|300|301|302|303|304| в високосные годы. |
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
ноябрь
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|305|306|307|308|309|310|311|312|313|314|315|316|317|318|319|320|321|322|323|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| Добавить 1 к ДОЙ |
|324|325|326|327|328|329|330|331|332|333|334| в високосные годы.
|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
Октябрь
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|274|275|276|277|278|279|280|281|282|283|284|285|286|287|288|289|290|291|292|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ |
|293|294|295|296|297|298|299|300|301|302|303|304| в високосные годы. |
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
ноябрь
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|305|306|307|308|309|310|311|312|313|314|315|316|317|318|319|320|321|322|323|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| Добавить 1 к ДОЙ |
|324|325|326|327|328|329|330|331|332|333|334| в високосные годы. |
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
Декабрь
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|335|336|337|338|339|340|341|342|343|344|345|346|347|348|349|350|351|352|353|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ |
|354|355|356|357|358|359|360|361|362|363|364|365| в високосные годы. |
+---+---+---+---+---+---+---+---+---+---+---+---+- --------------------------+
Джулианский нормальный прыжок
День Год Год
----- ------ ------
1 = 1 января 1 января
2 = 2 января 2 января
3 = 3 января 3 января
4 = 4 января 4 января
5 = 5 января 5 января
6 = 6 января 6 января
7 = 7 января 7 января
8 = 8 января 8 января
9= 9 января 9 января
10 = 10 января 10 января
11 = 11 января 11 января
12 = 12 января 12 января
13 = 13 января 13 января
14 = 14 января 14 января
15 = 15 января 15 января
16 = 16 января 16 января
17 = 17 января 17 января
18 = 18 января 18 января
19 = 19 января 19 января
20 = 20 января 20 января
21 = 21 января 21 января
22 = 22 января 22 января
23 = 23 января 23 января
24 = 24 января 24 января
25 = 25 января 25 января
26 = 26 января 26 января
27 = 27 января 27 января
28 = 28 января 28 января
29= 29 января 29 января
30 = 30 января 30 января
31 = 31 января 31 января
32 = 1 февраля 1 февраля
33 = 2 февраля 2 февраля
34 = 3 февраля 3 февраля
35 = 4 февраля 4 февраля
36 = 5 февраля 5 февраля
37 = 6 февраля 6 февраля
38 = 7 февраля 7 февраля
39 = 8 февраля 8 февраля
40 = 9 февраля 9 февраля
41 = 10 февраля 10 февраля
42 = 11 февраля 11 февраля
43 = 12 февраля 12 февраля
44 = 13 февраля 13 февраля
45 = 14 февраля 14 февраля
46 = 15 февраля 15 февраля
47 = 16 февраля 16 февраля
48 = 17 февраля 17 февраля
49= 18 февраля 18 февраля
50 = 19 февраля 19 февраля
51 = 20 февраля 20 февраля
52 = 21 февраля 21 февраля
53 = 22 февраля 22 февраля
54 = 23 февраля 23 февраля
55 = 24 февраля 24 февраля
56 = 25 февраля 25 февраля
57 = 26 февраля 26 февраля
58 = 27 февраля 27 февраля
59 = 28 февраля 28 февраля
60 = 1 марта 29 февраля
61 = 2 марта 1 марта
62 = 3 марта 2 марта
63 = 4 марта 3 марта
64 = 5 марта 4 марта
65 = 6 марта 5 марта
66 = 7 марта 6 марта
67 = 8 марта 7 марта
68 = 9 марта8 марта
69 = 10 марта 9 марта
70 = 11 марта 10 марта
71 = 12 марта 11 марта
72 = 13 марта 12 марта
73 = 14 марта 13 марта
74 = 15 марта 14 марта
75 = 16 марта 15 марта
76 = 17 марта 16 марта
77 = 18 марта 17 марта
78 = 19 марта 18 марта
79 = 20 марта 19 марта
80 = 21 марта 20 марта
81 = 22 марта 21 марта
82 = 23 марта 22 марта
83 = 24 марта 23 марта
84 = 25 марта 24 марта
85 = 26 марта 25 марта
86 = 27 марта 26 марта
87 = 28 марта 27 марта
88 = 29 марта28 марта
89 = 30 марта 29 марта
90 = 31 марта 30 марта
91 = 1 апреля 31 марта
92 = 2 апреля 1 апреля
93 = 3 апр 2 апр
94 = 4 апреля 3 апреля
95 = 5 апреля 4 апреля
96 = 6 апреля 5 апреля
97 = 7 апреля 6 апреля
98 = 8 апреля 7 апреля
99 = 9 апреля 8 апреля
100 = 10 апреля 9 апреля
101 = 11 апреля 10 апреля
102 = 12 апр 11 апр
103 = 13 апр 12 апр
104 = 14 апр 13 апр
105 = 15 апреля 14 апреля
106 = 16 апр 15 апр
107 = 17 апр 16 апр
108 = 18 апр 17 апр
109= 19 апр 18 апр
110 = 20 апреля 19 апреля
111 = 21 апреля 20 апреля
112 = 22 апреля 21 апреля
113 = 23 апреля 22 апреля
114 = 24 апреля 23 апреля
115 = 25 апреля 24 апреля
116 = 26 апреля 25 апреля
117 = 27 апреля 26 апреля
118 = 28 апреля 27 апреля
119 = 29 апреля 28 апреля
120 = 30 апреля 29 апреля
121 = 1 мая 30 апреля
122 = 2 мая 1 мая
123 = 3 мая 2 мая
124 = 4 мая 3 мая
125 = 5 мая 4 мая
126 = 6 мая 5 мая
127 = 7 мая 6 мая
128 = 8 мая 7 мая
129= 9 мая 8 мая
130 = 10 мая 9 мая
131 = 11 мая 10 мая
132 = 12 мая 11 мая
133 = 13 мая 12 мая
134 = 14 мая 13 мая
135 = 15 мая 14 мая
136 = 16 мая 15 мая
137 = 17 мая 16 мая
138 = 18 мая 17 мая
139 = 19 мая 18 мая
140 = 20 мая 19 мая
141 = 21 мая 20 мая
142 = 22 мая 21 мая
143 = 23 мая 22 мая
144 = 24 мая 23 мая
145 = 25 мая 24 мая
146 = 26 мая 25 мая
147 = 27 мая 26 мая
148 = 28 мая 27 мая
149= 29 мая 28 мая
150 = 30 мая 29 мая
151 = 31 мая 30 мая
152 = 1 июня 31 мая
153 = 2 июня 1 июня
154 = 3 июня 2 июня
155 = 4 июня 3 июня
156 = 5 июня 4 июня
157 = 6 июня 5 июня
158 = 7 июня 6 июня
159 = 8 июня 7 июня
160 = 9 июня 8 июня
161 = 10 июня 9 июня
162 = 11 июня 10 июня
163 = 12 июня 11 июня
164 = 13 июня 12 июня
165 = 14 июня 13 июня
166 = 15 июня 14 июня
167 = 16 июня 15 июня
168 = 17 июня 16 июня
169= 18 июня 17 июня
170 = 19 июня 18 июня
171 = 20 июня 19 июня
172 = 21 июня 20 июня
173 = 22 июня — 21 июня
174 = 23 июня 22 июня
175 = 24 июня 23 июня
176 = 25 июня 24 июня
177 = 26 июня 25 июня
178 = 27 июня 26 июня
179 = 28 июня 27 июня
180 = 29 июня 28 июня
181 = 30 июня 29 июня
182 = 1 июля 30 июня
183 = 2 июля 1 июля
184 = 3 июля 2 июля
185 = 4 июля 3 июля
186 = 5 июля 4 июля
187 = 6 июля 5 июля
188 = 7 июля 6 июля
189= 8 июля 7 июля
190 = 9 июля 8 июля
191 = 10 июля 9 июля
192 = 11 июля 10 июля
193 = 12 июля 11 июля
194 = 13 июля 12 июля
195 = 14 июля 13 июля
196 = 15 июля 14 июля
197 = 16 июля 15 июля
198 = 17 июля 16 июля
199 = 18 июля 17 июля
200 = 19 июля 18 июля
201 = 20 июля 19 июля
202 = 21 июля 20 июля
203 = 22 июля 21 июля
204 = 23 июля 22 июля
205 = 24 июля 23 июля
206 = 25 июля 24 июля
207 = 26 июля 25 июля
208 = 27 июля 26 июля
209= 28 июля 27 июля
210 = 29 июля 28 июля
211 = 30 июля 29 июля
212 = 31 июля 30 июля
213 = 1 августа 31 июля
214 = 2 августа 1 августа
215 = 3 августа 2 августа
216 = 4 августа 3 августа
217 = 5 августа 4 августа
218 = 6 августа 5 августа
219 = 7 августа 6 августа
220 = 8 августа 7 августа
221 = 9 августа 8 августа
222 = 10 августа — 9 августа
223 = 11 августа 10 августа
224 = 12 августа 11 августа
225 = 13 августа 12 августа
226 = 14 августа 13 августа
227 = 15 августа 14 августа
228 = 16 августа 15 августа
229= 17 августа 16 августа
230 = 18 августа 17 августа
231 = 19 августа 18 августа
232 = 20 августа 19 августа
233 = 21 августа 20 августа
234 = 22 августа 21 августа
235 = 23 августа 22 августа
236 = 24 августа 23 августа
237 = 25 августа 24 августа
238 = 26 августа 25 августа
239 = 27 августа 26 августа
240 = 28 августа 27 августа
241 = 29 августа 28 августа
242 = 30 августа 29 августа
243 = 31 августа 30 августа
244 = 1 сентября 31 августа
245 = 2 сентября 1 сентября
246 = 3 сентября 2 сентября
247 = 4 сентября 3 сентября
248 = 5 сентября 4 сентября
249= 6 сентября 5 сентября
250 = 7 сентября 6 сентября
251 = 8 сентября 7 сентября
252 = 9 сентября 8 сентября
253 = 10 сентября 9 сентября
254 = 11 сентября 10 сентября
255 = 12 сентября 11 сентября
256 = 13 сентября 12 сентября
257 = 14 сентября 13 сентября
258 = 15 сентября 14 сентября
259 = 16 сентября 15 сентября
260 = 17 сентября 16 сентября
261 = 18 сентября 17 сентября
262 = 19 сентября 18 сентября
263 = 20 сентября 19 сентября
264 = 21 сентября 20 сентября
265 = 22 сентября 21 сентября
266 = 23 сентября 22 сентября
267 = 24 сентября 23 сентября
268 = 25 сентября 24 сентября
269= 26 сентября 25 сентября
270 = 27 сентября 26 сентября
271 = 28 сентября 27 сентября
272 = 29 сентября 28 сентября
273 = 30 сентября 29 сентября
274 = 1 октября 30 сентября
275 = 2 октября 1 октября
276 = 3 октября 2 октября
277 = 4 октября 3 октября
278 = 5 октября 4 октября
279 = 6 октября 5 октября
280 = 7 октября 6 октября
281 = 8 октября 7 октября
282 = 9 октября 8 октября
283 = 10 октября 9 октября
284 = 11 октября 10 октября
285 = 12 октября 11 октября
286 = 13 октября 12 октября
287 = 14 октября 13 октября
288 = 15 октября 14 октября
289= 16 октября 15 октября
290 = 17 октября 16 октября
291 = 18 октября 17 октября
292 = 19 октября 18 октября
293 = 20 октября 19 октября
294 = 21 октября 20 октября
295 = 22 октября 21 октября
296 = 23 октября 22 октября
297 = 24 октября 23 октября
298 = 25 октября 24 октября
299 = 26 октября 25 октября
300 = 27 октября 26 октября
301 = 28 октября 27 октября
302 = 29 октября 28 октября
303 = 30 октября 29 октября
304 = 31 октября 30 октября
305 = 1 ноября 31 октября
306 = 2 ноября 1 ноября
307 = 3 ноября 2 ноября
308 = 4 ноября 3 ноября
309= 5 ноября 4 ноября
310 = 6 ноября 5 ноября
311 = 7 ноября 6 ноября
312 = 8 ноября 7 ноября
313 = 9 ноября 8 ноября
314 = 10 ноября 9 ноября
315 = 11 ноября 10 ноября
316 = 12 ноября 11 ноября
317 = 13 ноября 12 ноября
318 = 14 ноября 13 ноября
319 = 15 ноября 14 ноября
320 = 16 ноября 15 ноября
321 = 17 ноября 16 ноября
322 = 18 ноября 17 ноября
323 = 19 ноября 18 ноября
324 = 20 ноября 19 ноября
325 = 21 ноября 20 ноября
326 = 22 ноября 21 ноября
327 = 23 ноября 22 ноября
328 = 24 ноября 23 ноября
329= 25 ноября 24 ноября
330 = 26 ноября 25 ноября
331 = 27 ноября 26 ноября
332 = 28 ноября 27 ноября
333 = 29 ноября 28 ноября
334 = 30 ноября 29 ноября
335 = 1 декабря 30 ноября
336 = 2 декабря 1 декабря
337 = 3 декабря 2 декабря
338 = 4 декабря 3 декабря
339 = 5 декабря 4 декабря
340 = 6 декабря 5 декабря
341 = 7 декабря 6 декабря
342 = 8 декабря 7 декабря
343 = 9 декабря 8 декабря
344 = 10 декабря 9 декабря
345 = 11 декабря 10 декабря
346 = 12 декабря 11 декабря
347 = 13 декабря 12 декабря
348 = 14 декабря 13 декабря
349= 15 декабря 14 декабря
350 = 16 декабря 15 декабря
351 = 17 декабря 16 декабря
352 = 18 декабря 17 декабря
353 = 19 декабря 18 декабря
354 = 20 декабря 19 декабря
355 = 21 декабря 20 декабря
356 = 22 декабря 21 декабря
357 = 23 декабря 22 декабря
358 = 24 декабря 23 декабря
359 = 25 декабря 24 декабря
360 = 26 декабря 25 декабря
361 = 27 декабря 26 декабря
362 = 28 декабря 27 декабря
363 = 29 декабря 28 декабря
364 = 30 декабря 29 декабря
365 = 31 декабря 30 декабря
366 = 31 декабря
Юлианские дни по месяцам
========================================
Обычный год Високосный год
-------------- ---------------
1–31 января 1–31 января
32 - 59 фев.
|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
Декабрь
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19|
|335|336|337|338|339|340|341|342|343|344|345|346|347|348|349|350|351|352|353|
+---+---+---+---+---+---+---+---+---+---+---+---+- --+---+---+---+---+---+---+
| 20| 21| 22| 23| 24| 25| 26| 27| 28| 29| 30| 31| Добавить 1 к ДОЙ |
|354|355|356|357|358|359|360|361|362|363|364|365| в високосные годы. |
+---+---+---+---+---+---+---+---+---+---+---+---+- --------------------------+
Джулианский нормальный прыжок
День Год Год
----- ------ ------
1 = 1 января 1 января
2 = 2 января 2 января
3 = 3 января 3 января
4 = 4 января 4 января
5 = 5 января 5 января
6 = 6 января 6 января
7 = 7 января 7 января
8 = 8 января 8 января
9= 9 января 9 января
10 = 10 января 10 января
11 = 11 января 11 января
12 = 12 января 12 января
13 = 13 января 13 января
14 = 14 января 14 января
15 = 15 января 15 января
16 = 16 января 16 января
17 = 17 января 17 января
18 = 18 января 18 января
19 = 19 января 19 января
20 = 20 января 20 января
21 = 21 января 21 января
22 = 22 января 22 января
23 = 23 января 23 января
24 = 24 января 24 января
25 = 25 января 25 января
26 = 26 января 26 января
27 = 27 января 27 января
28 = 28 января 28 января
29= 29 января 29 января
30 = 30 января 30 января
31 = 31 января 31 января
32 = 1 февраля 1 февраля
33 = 2 февраля 2 февраля
34 = 3 февраля 3 февраля
35 = 4 февраля 4 февраля
36 = 5 февраля 5 февраля
37 = 6 февраля 6 февраля
38 = 7 февраля 7 февраля
39 = 8 февраля 8 февраля
40 = 9 февраля 9 февраля
41 = 10 февраля 10 февраля
42 = 11 февраля 11 февраля
43 = 12 февраля 12 февраля
44 = 13 февраля 13 февраля
45 = 14 февраля 14 февраля
46 = 15 февраля 15 февраля
47 = 16 февраля 16 февраля
48 = 17 февраля 17 февраля
49= 18 февраля 18 февраля
50 = 19 февраля 19 февраля
51 = 20 февраля 20 февраля
52 = 21 февраля 21 февраля
53 = 22 февраля 22 февраля
54 = 23 февраля 23 февраля
55 = 24 февраля 24 февраля
56 = 25 февраля 25 февраля
57 = 26 февраля 26 февраля
58 = 27 февраля 27 февраля
59 = 28 февраля 28 февраля
60 = 1 марта 29 февраля
61 = 2 марта 1 марта
62 = 3 марта 2 марта
63 = 4 марта 3 марта
64 = 5 марта 4 марта
65 = 6 марта 5 марта
66 = 7 марта 6 марта
67 = 8 марта 7 марта
68 = 9 марта8 марта
69 = 10 марта 9 марта
70 = 11 марта 10 марта
71 = 12 марта 11 марта
72 = 13 марта 12 марта
73 = 14 марта 13 марта
74 = 15 марта 14 марта
75 = 16 марта 15 марта
76 = 17 марта 16 марта
77 = 18 марта 17 марта
78 = 19 марта 18 марта
79 = 20 марта 19 марта
80 = 21 марта 20 марта
81 = 22 марта 21 марта
82 = 23 марта 22 марта
83 = 24 марта 23 марта
84 = 25 марта 24 марта
85 = 26 марта 25 марта
86 = 27 марта 26 марта
87 = 28 марта 27 марта
88 = 29 марта28 марта
89 = 30 марта 29 марта
90 = 31 марта 30 марта
91 = 1 апреля 31 марта
92 = 2 апреля 1 апреля
93 = 3 апр 2 апр
94 = 4 апреля 3 апреля
95 = 5 апреля 4 апреля
96 = 6 апреля 5 апреля
97 = 7 апреля 6 апреля
98 = 8 апреля 7 апреля
99 = 9 апреля 8 апреля
100 = 10 апреля 9 апреля
101 = 11 апреля 10 апреля
102 = 12 апр 11 апр
103 = 13 апр 12 апр
104 = 14 апр 13 апр
105 = 15 апреля 14 апреля
106 = 16 апр 15 апр
107 = 17 апр 16 апр
108 = 18 апр 17 апр
109= 19 апр 18 апр
110 = 20 апреля 19 апреля
111 = 21 апреля 20 апреля
112 = 22 апреля 21 апреля
113 = 23 апреля 22 апреля
114 = 24 апреля 23 апреля
115 = 25 апреля 24 апреля
116 = 26 апреля 25 апреля
117 = 27 апреля 26 апреля
118 = 28 апреля 27 апреля
119 = 29 апреля 28 апреля
120 = 30 апреля 29 апреля
121 = 1 мая 30 апреля
122 = 2 мая 1 мая
123 = 3 мая 2 мая
124 = 4 мая 3 мая
125 = 5 мая 4 мая
126 = 6 мая 5 мая
127 = 7 мая 6 мая
128 = 8 мая 7 мая
129= 9 мая 8 мая
130 = 10 мая 9 мая
131 = 11 мая 10 мая
132 = 12 мая 11 мая
133 = 13 мая 12 мая
134 = 14 мая 13 мая
135 = 15 мая 14 мая
136 = 16 мая 15 мая
137 = 17 мая 16 мая
138 = 18 мая 17 мая
139 = 19 мая 18 мая
140 = 20 мая 19 мая
141 = 21 мая 20 мая
142 = 22 мая 21 мая
143 = 23 мая 22 мая
144 = 24 мая 23 мая
145 = 25 мая 24 мая
146 = 26 мая 25 мая
147 = 27 мая 26 мая
148 = 28 мая 27 мая
149= 29 мая 28 мая
150 = 30 мая 29 мая
151 = 31 мая 30 мая
152 = 1 июня 31 мая
153 = 2 июня 1 июня
154 = 3 июня 2 июня
155 = 4 июня 3 июня
156 = 5 июня 4 июня
157 = 6 июня 5 июня
158 = 7 июня 6 июня
159 = 8 июня 7 июня
160 = 9 июня 8 июня
161 = 10 июня 9 июня
162 = 11 июня 10 июня
163 = 12 июня 11 июня
164 = 13 июня 12 июня
165 = 14 июня 13 июня
166 = 15 июня 14 июня
167 = 16 июня 15 июня
168 = 17 июня 16 июня
169= 18 июня 17 июня
170 = 19 июня 18 июня
171 = 20 июня 19 июня
172 = 21 июня 20 июня
173 = 22 июня — 21 июня
174 = 23 июня 22 июня
175 = 24 июня 23 июня
176 = 25 июня 24 июня
177 = 26 июня 25 июня
178 = 27 июня 26 июня
179 = 28 июня 27 июня
180 = 29 июня 28 июня
181 = 30 июня 29 июня
182 = 1 июля 30 июня
183 = 2 июля 1 июля
184 = 3 июля 2 июля
185 = 4 июля 3 июля
186 = 5 июля 4 июля
187 = 6 июля 5 июля
188 = 7 июля 6 июля
189= 8 июля 7 июля
190 = 9 июля 8 июля
191 = 10 июля 9 июля
192 = 11 июля 10 июля
193 = 12 июля 11 июля
194 = 13 июля 12 июля
195 = 14 июля 13 июля
196 = 15 июля 14 июля
197 = 16 июля 15 июля
198 = 17 июля 16 июля
199 = 18 июля 17 июля
200 = 19 июля 18 июля
201 = 20 июля 19 июля
202 = 21 июля 20 июля
203 = 22 июля 21 июля
204 = 23 июля 22 июля
205 = 24 июля 23 июля
206 = 25 июля 24 июля
207 = 26 июля 25 июля
208 = 27 июля 26 июля
209= 28 июля 27 июля
210 = 29 июля 28 июля
211 = 30 июля 29 июля
212 = 31 июля 30 июля
213 = 1 августа 31 июля
214 = 2 августа 1 августа
215 = 3 августа 2 августа
216 = 4 августа 3 августа
217 = 5 августа 4 августа
218 = 6 августа 5 августа
219 = 7 августа 6 августа
220 = 8 августа 7 августа
221 = 9 августа 8 августа
222 = 10 августа — 9 августа
223 = 11 августа 10 августа
224 = 12 августа 11 августа
225 = 13 августа 12 августа
226 = 14 августа 13 августа
227 = 15 августа 14 августа
228 = 16 августа 15 августа
229= 17 августа 16 августа
230 = 18 августа 17 августа
231 = 19 августа 18 августа
232 = 20 августа 19 августа
233 = 21 августа 20 августа
234 = 22 августа 21 августа
235 = 23 августа 22 августа
236 = 24 августа 23 августа
237 = 25 августа 24 августа
238 = 26 августа 25 августа
239 = 27 августа 26 августа
240 = 28 августа 27 августа
241 = 29 августа 28 августа
242 = 30 августа 29 августа
243 = 31 августа 30 августа
244 = 1 сентября 31 августа
245 = 2 сентября 1 сентября
246 = 3 сентября 2 сентября
247 = 4 сентября 3 сентября
248 = 5 сентября 4 сентября
249= 6 сентября 5 сентября
250 = 7 сентября 6 сентября
251 = 8 сентября 7 сентября
252 = 9 сентября 8 сентября
253 = 10 сентября 9 сентября
254 = 11 сентября 10 сентября
255 = 12 сентября 11 сентября
256 = 13 сентября 12 сентября
257 = 14 сентября 13 сентября
258 = 15 сентября 14 сентября
259 = 16 сентября 15 сентября
260 = 17 сентября 16 сентября
261 = 18 сентября 17 сентября
262 = 19 сентября 18 сентября
263 = 20 сентября 19 сентября
264 = 21 сентября 20 сентября
265 = 22 сентября 21 сентября
266 = 23 сентября 22 сентября
267 = 24 сентября 23 сентября
268 = 25 сентября 24 сентября
269= 26 сентября 25 сентября
270 = 27 сентября 26 сентября
271 = 28 сентября 27 сентября
272 = 29 сентября 28 сентября
273 = 30 сентября 29 сентября
274 = 1 октября 30 сентября
275 = 2 октября 1 октября
276 = 3 октября 2 октября
277 = 4 октября 3 октября
278 = 5 октября 4 октября
279 = 6 октября 5 октября
280 = 7 октября 6 октября
281 = 8 октября 7 октября
282 = 9 октября 8 октября
283 = 10 октября 9 октября
284 = 11 октября 10 октября
285 = 12 октября 11 октября
286 = 13 октября 12 октября
287 = 14 октября 13 октября
288 = 15 октября 14 октября
289= 16 октября 15 октября
290 = 17 октября 16 октября
291 = 18 октября 17 октября
292 = 19 октября 18 октября
293 = 20 октября 19 октября
294 = 21 октября 20 октября
295 = 22 октября 21 октября
296 = 23 октября 22 октября
297 = 24 октября 23 октября
298 = 25 октября 24 октября
299 = 26 октября 25 октября
300 = 27 октября 26 октября
301 = 28 октября 27 октября
302 = 29 октября 28 октября
303 = 30 октября 29 октября
304 = 31 октября 30 октября
305 = 1 ноября 31 октября
306 = 2 ноября 1 ноября
307 = 3 ноября 2 ноября
308 = 4 ноября 3 ноября
309= 5 ноября 4 ноября
310 = 6 ноября 5 ноября
311 = 7 ноября 6 ноября
312 = 8 ноября 7 ноября
313 = 9 ноября 8 ноября
314 = 10 ноября 9 ноября
315 = 11 ноября 10 ноября
316 = 12 ноября 11 ноября
317 = 13 ноября 12 ноября
318 = 14 ноября 13 ноября
319 = 15 ноября 14 ноября
320 = 16 ноября 15 ноября
321 = 17 ноября 16 ноября
322 = 18 ноября 17 ноября
323 = 19 ноября 18 ноября
324 = 20 ноября 19 ноября
325 = 21 ноября 20 ноября
326 = 22 ноября 21 ноября
327 = 23 ноября 22 ноября
328 = 24 ноября 23 ноября
329= 25 ноября 24 ноября
330 = 26 ноября 25 ноября
331 = 27 ноября 26 ноября
332 = 28 ноября 27 ноября
333 = 29 ноября 28 ноября
334 = 30 ноября 29 ноября
335 = 1 декабря 30 ноября
336 = 2 декабря 1 декабря
337 = 3 декабря 2 декабря
338 = 4 декабря 3 декабря
339 = 5 декабря 4 декабря
340 = 6 декабря 5 декабря
341 = 7 декабря 6 декабря
342 = 8 декабря 7 декабря
343 = 9 декабря 8 декабря
344 = 10 декабря 9 декабря
345 = 11 декабря 10 декабря
346 = 12 декабря 11 декабря
347 = 13 декабря 12 декабря
348 = 14 декабря 13 декабря
349= 15 декабря 14 декабря
350 = 16 декабря 15 декабря
351 = 17 декабря 16 декабря
352 = 18 декабря 17 декабря
353 = 19 декабря 18 декабря
354 = 20 декабря 19 декабря
355 = 21 декабря 20 декабря
356 = 22 декабря 21 декабря
357 = 23 декабря 22 декабря
358 = 24 декабря 23 декабря
359 = 25 декабря 24 декабря
360 = 26 декабря 25 декабря
361 = 27 декабря 26 декабря
362 = 28 декабря 27 декабря
363 = 29 декабря 28 декабря
364 = 30 декабря 29 декабря
365 = 31 декабря 30 декабря
366 = 31 декабря
Юлианские дни по месяцам
========================================
Обычный год Високосный год
-------------- ---------------
1–31 января 1–31 января
32 - 59 фев. 32 - 60 фев.
60–90 марта 61–91 марта
91–120 апр. 92–121 апр.
121–151 мая 122–152 мая
152–181 июня 153–182 июня
Июль 182–212 Июль 183–213
213–243 авг. 214–244 авг.
244–273 сент. 245–274 сент.
274–304 окт. 275–305 окт.
305–334 ноября 306–335 ноября
дек. 335–365 дек. 336–366
Последние високосные годы: прошлые и будущие високосные годы
=================================================== ============
* 1984 - Високосный год 1896 1936 1972 2008
1985 1904 1940 1976 2012
1986 1908 1944 1980 2016
1987 1912 1948 1984 2020
* 1988 - Високосный год 1916 1952 1988 2024
1989 1920 1956 1992 2028
1990 1924 1960 1996 2032
1991 1928 1964 2000 2036
* 1992 - Високосный год 1932 1968 2004 2040
1993 г.
1994 г.
1995 г.
* 1996 - Високосный год
(Правило большого пальца: високосные годы = годы президентских выборов в США)
Официальные правила високосного года:
Если год делится без остатка на 4, то он високосный.
32 - 60 фев.
60–90 марта 61–91 марта
91–120 апр. 92–121 апр.
121–151 мая 122–152 мая
152–181 июня 153–182 июня
Июль 182–212 Июль 183–213
213–243 авг. 214–244 авг.
244–273 сент. 245–274 сент.
274–304 окт. 275–305 окт.
305–334 ноября 306–335 ноября
дек. 335–365 дек. 336–366
Последние високосные годы: прошлые и будущие високосные годы
=================================================== ============
* 1984 - Високосный год 1896 1936 1972 2008
1985 1904 1940 1976 2012
1986 1908 1944 1980 2016
1987 1912 1948 1984 2020
* 1988 - Високосный год 1916 1952 1988 2024
1989 1920 1956 1992 2028
1990 1924 1960 1996 2032
1991 1928 1964 2000 2036
* 1992 - Високосный год 1932 1968 2004 2040
1993 г.
1994 г.
1995 г.
* 1996 - Високосный год
(Правило большого пальца: високосные годы = годы президентских выборов в США)
Официальные правила високосного года:
Если год делится без остатка на 4, то он високосный. Примеры: 1996/4 = 499, следовательно, это високосный год.
1997 / 4 = 499,25, следовательно, это не високосный год.
Первое исключение:
Из тех лет, которые без остатка делятся на 4,
если год тоже без остатка делится на 100,
это НЕ високосный год.
Пример: 1900 / 4 = 475
1900/100 = 19, следовательно, это НЕ високосный год.
Второе исключение:
Из тех лет, которые без остатка делятся на 4 и 100,
если год тоже без остатка делится на 400,
это високосный год.
Пример: 2000 / 4 = 500
2000 / 100 = 20
2000/400 = 5, следовательно, это високосный год.
1900/400 = 4,75, следовательно, это НЕ високосный год.
Юлианский календарь был разработан Юлием Цезарем и египтянами.
астроном Сосиген в 46 году до н. Они стремились создать 12
месячный календарь, основанный на солнечном году; время, необходимое для
Земля совершает один полный оборот вокруг Солнца, что составляет 365,2422 дня.
Примеры: 1996/4 = 499, следовательно, это високосный год.
1997 / 4 = 499,25, следовательно, это не високосный год.
Первое исключение:
Из тех лет, которые без остатка делятся на 4,
если год тоже без остатка делится на 100,
это НЕ високосный год.
Пример: 1900 / 4 = 475
1900/100 = 19, следовательно, это НЕ високосный год.
Второе исключение:
Из тех лет, которые без остатка делятся на 4 и 100,
если год тоже без остатка делится на 400,
это високосный год.
Пример: 2000 / 4 = 500
2000 / 100 = 20
2000/400 = 5, следовательно, это високосный год.
1900/400 = 4,75, следовательно, это НЕ високосный год.
Юлианский календарь был разработан Юлием Цезарем и египтянами.
астроном Сосиген в 46 году до н. Они стремились создать 12
месячный календарь, основанный на солнечном году; время, необходимое для
Земля совершает один полный оборот вокруг Солнца, что составляет 365,2422 дня. (До этого римляне и большинство других цивилизаций использовали лунную или
лунно-солнечный гибридный календарь; только в Египте был строго солнечный календарь.)
Они установили нормальный год равным 365 дням, затем обозначили каждый четвертый
год (високосный год) будет состоять из 366 дней. Это должно было исправить частичное
.2422 день, который отсутствует в текущем году и в каждом из
предыдущие три года. Для этого они включили «равномерно
делится на 4 'правило в их календаре.
Юлианский календарь был принят Никейским собором в 325 году нашей эры.
Однако к 1582 году нашей эры количество прошлых високосных лет было чрезмерно исправлено.
(0,2422 умножить на 4 года = 0,9688 дней, а не 1 день)
и юлианский календарь выиграл 10 дней на реальной орбите Земли.
положение вокруг солнца. Если не остановить, Пасха в конце концов
происходят летом. Чтобы исправить это, Папа Григорий XIII пропустил 10 дней.
с 1582 г. и ввел в действие первое и второе исключения («равно делимое
на 100 и на 400'), как описано выше.
(До этого римляне и большинство других цивилизаций использовали лунную или
лунно-солнечный гибридный календарь; только в Египте был строго солнечный календарь.)
Они установили нормальный год равным 365 дням, затем обозначили каждый четвертый
год (високосный год) будет состоять из 366 дней. Это должно было исправить частичное
.2422 день, который отсутствует в текущем году и в каждом из
предыдущие три года. Для этого они включили «равномерно
делится на 4 'правило в их календаре.
Юлианский календарь был принят Никейским собором в 325 году нашей эры.
Однако к 1582 году нашей эры количество прошлых високосных лет было чрезмерно исправлено.
(0,2422 умножить на 4 года = 0,9688 дней, а не 1 день)
и юлианский календарь выиграл 10 дней на реальной орбите Земли.
положение вокруг солнца. Если не остановить, Пасха в конце концов
происходят летом. Чтобы исправить это, Папа Григорий XIII пропустил 10 дней.
с 1582 г. и ввел в действие первое и второе исключения («равно делимое
на 100 и на 400'), как описано выше. Первое исключение исключает
високосный год каждые 100 лет. Используя только первое исключение,
календарь через несколько столетий был бы немного недокорректирован.
То есть он отстал бы от истинного орбитального положения Земли.
Понимая это, математики Папы Римского добавили второе исключение
который включает високосный год каждые 400 лет (1600, 2000, 2400 и т. д.).
Эти правила не полностью корректируют календарь до идеальных 365,2422 дней.
в год; к 5000 году нашей эры он выиграет 1 день и еще
регулировка будет необходима.
Раздел «календарь» любого хорошего альманаха проверит эти данные.
правила относительно високосных лет
-----
ВРЕМЯ:
Все данные AZMET собираются, хранятся и представляются в
местное время Аризоны, которое находится в часовом поясе Горного стандарта.
Аризона не участвует в переходе на летнее время.
Поэтому время, указанное в файлах данных AZMET,
всегда на семь часов отстает от универсального скоординированного времени (UTC)
(иначе: Среднее время по Гринвичу; Зулусское время).
Первое исключение исключает
високосный год каждые 100 лет. Используя только первое исключение,
календарь через несколько столетий был бы немного недокорректирован.
То есть он отстал бы от истинного орбитального положения Земли.
Понимая это, математики Папы Римского добавили второе исключение
который включает високосный год каждые 400 лет (1600, 2000, 2400 и т. д.).
Эти правила не полностью корректируют календарь до идеальных 365,2422 дней.
в год; к 5000 году нашей эры он выиграет 1 день и еще
регулировка будет необходима.
Раздел «календарь» любого хорошего альманаха проверит эти данные.
правила относительно високосных лет
-----
ВРЕМЯ:
Все данные AZMET собираются, хранятся и представляются в
местное время Аризоны, которое находится в часовом поясе Горного стандарта.
Аризона не участвует в переходе на летнее время.
Поэтому время, указанное в файлах данных AZMET,
всегда на семь часов отстает от универсального скоординированного времени (UTC)
(иначе: Среднее время по Гринвичу; Зулусское время).
 Диапазон страниц для полных статей появится в библиографии.
Диапазон страниц для полных статей появится в библиографии. ». (Эллисон, Лоррейн, Молли Браун, Ноэль Ротс, Глэдис Черри, Джейкоб Астор, Эмили Пейдж, Люсиль Гордон и др.)
». (Эллисон, Лоррейн, Молли Браун, Ноэль Ротс, Глэдис Черри, Джейкоб Астор, Эмили Пейдж, Люсиль Гордон и др.)