Фигуры Лиссажу — Википедия

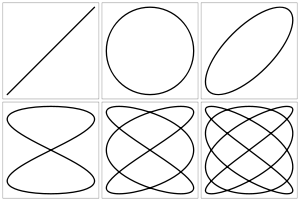
Фигу́ры Лиссажу́ — траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях.

Впервые изучены французским учёным Жюлем Антуаном Лиссажу.

Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или π{\displaystyle \pi } вырождаются в отрезки прямых, а при разности фаз π2{\displaystyle {\frac {\pi }{2}}} и равенстве амплитуд превращаются в окружность.

Если периоды обоих колебаний близки, то разность фаз линейно изменяется, вследствие чего наблюдаемый эллипс всё время деформируется. Это явление используется в электронике для сравнения частот и подстройки одной частоты под вторую — опорную частоту.

При многократно отличающихся по величине периодах колебаний фигуры Лиссажу представляют собой запутанную картину и не наблюдаются, например, на экране осциллографа, — в этом случае наблюдается светящийся прямоугольник.

Если отношение периодов представляет собой рациональное число, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в исходное положение, причем с совпадающим с исходным вектором скорости точки, в результате получаются замкнутые траектории. Если отношение периодов иррациональное число, то порождаются незамкнутые траектории.

Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.

Математическое выражение для кривой Лиссажу[править | править код]

{x(t)=Asin⁡(at+δ)y(t)=Bsin⁡(bt){\displaystyle \left\{{\begin{aligned}&x(t)=A\sin(at+\delta )\\&y(t)=B\sin(bt)\\\end{aligned}}\right.}

где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз

Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности (A = B, δ = π/2 радиан) и отрезка прямой (δ = 0). Ещё один пример фигуры Лиссажу — парабола (b/a = 2, δ = π/4). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии

a/b — рациональное число.

Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и

δ=N−1Nπ2 {\displaystyle \delta ={\frac {N-1}{N}}{\frac {\pi }{2}}\ }

являются полиномами Чебышёва первого рода степени N.

Анимация внизу показывает изменение кривых при постоянно возрастающем соотношении ab{\displaystyle {\frac {a}{b}}} от 0 до 1 с шагом 0.01. (δ=0)

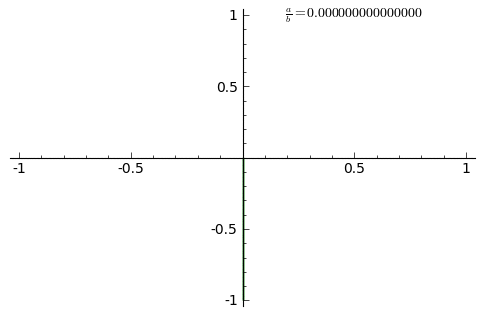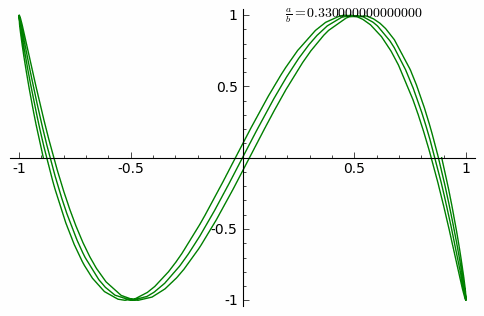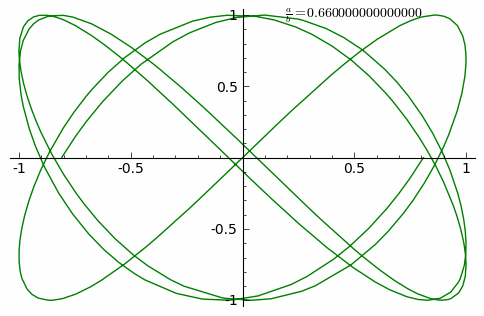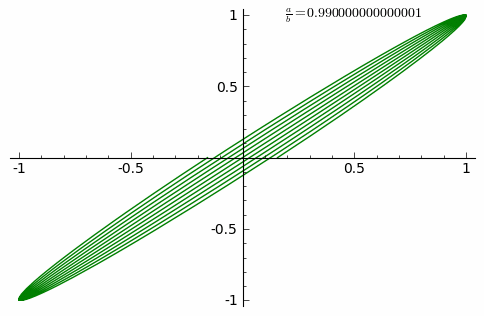
Примеры фигур Лиссажу ниже с

δ = π/2, нечётным натуральным числом a, и также натуральным числом b, и |a − b| = 1.

Применение в технике — сравнение частот[править | править код]

Фигура Лиссажу на экране осциллографа

Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причем период цикла вращения является величиной, обратной разности частот, например, период оборота равен 2 с — разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счет кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.

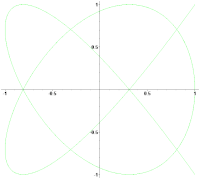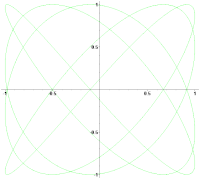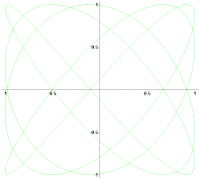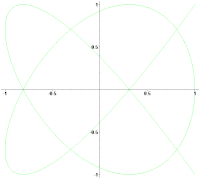Вращение фигуры Лиссажу при незначительной расстройке частот

• Справочник по радиоэлектронным устройствам. В 2 томах / Под ред. Д. П. Линде. — М.: Энергия, 1978.
• Яворский Б. М., Детлаф А. А. Справочник по физике. — М.: Наука, 1981.

Фигуры Лиссажу | Практическая электроника

Что такое фигуры Лиссажу?

Фигуры Лиссажу представляют из себя различные геометрически-красивые рисунки, которые вычерчиваются точкой, колеблющейся в двух взаимно-перпендикулярных направлениях на одной плоскости.

Чтобы было более понятно, давайте представим девочку на качели из покрышки:

И вот представьте, что сзади ее раскачивает папа, а сбоку – мама. То есть наша девочка будет одновременно летать вперед-назад, а также влево-вправо. Долго ли она продержится – это уже другой вопрос). Если в солнечный денек посмотреть на землю, то мы увидим, что тень девочки вырисовывает различную траекторию полета.

Почему бы нам не поиграться пучком электронов, отклоняя его одновременно и по вертикали и по горизонтали? Вспоминаем, как выглядит электронно-лучевая трубка осциллографа:

где

1 – это горизонтальные пластины

2 – вертикальные пластины

ну и остальные детали – это составляющие электронной пушки.

Подаем на вертикальные пластины один синусоидальный сигнал, а на горизонтальные – другой синусоидальный сигнал. В результате точка на осциллографе будет вырисовывать различные линии и кривые, в зависимости от частоты сигналов. Хотя, цифровой осциллограф и аналоговый почти не похожи по внутренней начинке, но принцип действия у них все равно схож.

Требуемые приборы для получения и наблюдения фигур Лиссажу

Итак, для того, чтобы вырисовывать фигуры Лиссажу, нам потребуются два генератора частоты.

Генератор №1

 

Генератор №2

и осциллограф с функцией XY-режима. В моем случае это цифровой осциллограф OWON

Думаю, почти во всех современных осциллографах есть режим XY, будь это аналоговый или цифровой осциллограф.

 

Режим XY-осциллографа

Как вы помните, при простом использовании осциллографа у нас по оси X было время, а по оси Y – напряжение. Поэтому, по умолчанию,  мы  на осциллографе смотрим изменение напряжения во времени. Но если с помощью нехитрой кнопки переключить в режим XY, то у нас по Y будет напряжение и по X…. тоже напряжение, но уже с другого генератора частоты. Если включить в таком режиме только один генератор, то мы увидим только одну прямую линию либо по вертикали, либо по горизонтали. Это аналогично тому, если бы нашу девочку раскачивал только папа или только мама. Наша девочка летела бы только по одной прямой траектории.

А что будет, если сбоку нашу девочку будет раскачивать мама, а сзади – папа?  Тут уже траектория девочки будет хаотичной. Но во всяком хаосе рождается порядок. И первым его заметил французский математик Жюль Антуан Лиссажу.

Получаем фигуры Лиссажу на практике

Цепляем на один канал один генератор частоты, а на другой канал – другой генератор частоты:

На осциллографе мы должны увидеть два сигнала с разных генераторов частоты, благо у меня осциллограф двухканальный:

Теперь переводим осциллограф в режим XY. На моем осциллографе это делается с помощью кнопки Display

Ну а потом с помощью дисплейных клавиш выбираем режим XY

И получается примерно вот такая хаотическая картинка:

Ну еще бы, один генератор дергает точку по X, другой по Y и у каждого генератора разная частота.

А давайте возьмем один генератор и с него подадим сигнал на два канала сразу. Частота и фаза совпадают и на первом и втором канале, так как мы берем сигнал с одного и то же генератора. В результате у нас будет вот такая картинка:

Если взять 100 Герц  на первом генераторе и на втором генераторе, то получим что-то типа этого:

В реальности же получается круг, который все время крутится и превращается то в эллипс, то в прямую, так как  очень ровно подобрать частоту на первом и втором генераторе очень сложно. Хотя на практике можно подавать сигнал на один канал напрямую, а на другой – через фазовращатель.

Если увеличить частоту на одном из генераторов вдвое, то можно наблюдать уже другие фигуры:

Эта фигура тоже все время крутится на осциллографе.

Увеличиваем на одном генераторе частоту в кратное число раз, то есть было 100, потом 200, 300 и тд и получаем абсолютно новые 3D фигуры 😉

Различное отношение частот одного генератора к другому дает различные фигуры Лиссажу:

Вот такие фигуры вы будете видеть на экране своего осциллографа:

А вот такие фигуры Лиссажу получаются, если использовать пилообразный сигнал с обоих генераторов сразу при разных отношениях коэффициентов

А вот такие фигуры получаются, если на одном оставить синус, а на втором поставить пилу:

Заключение

В основном фигуры Лиссажу в электронике можно использовать тогда, когда надо узнать частоту неизвестного генератора через образцовый генератор, частоту которого мы знаем, а также узнать сдвиг фаз между двумя одинаковыми сигналами. Ну и второе применение  – это чисто визуальный кайф при вращении этих фигур на экранчике вашего осциллографа 😉

Фигуры Лиссажу — это… Что такое Фигуры Лиссажу?

Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или вырождаются в отрезки прямых, а при разности фаз и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.

Математическое выражение для кривой Лиссажу

где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз

Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид прямой (A = B, δ = π/2 радиан) и отрезка прямой (δ = 0). Ещё один пример фигуры Лиссажу — парабола (a/b = 2, δ = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a/b — рациональное число.

Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и

являются полиномами Чебышева первого рода степени N.

Примеры

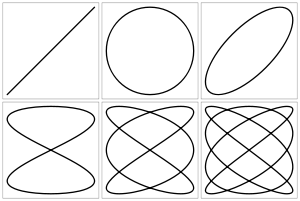
Анимация внизу показывает изменение кривых при постоянно возрастающем соотношении от 0 до 1 с шагом 0.01. (δ=0)

Примеры фигур Лиссажу ниже с δ = π/2, нечётным натуральным числом a, и также натуральным числом b, и |a − b| = 1.

Применение в технике — сравнение частот

Фигура Лиссажу на экране осциллографа

Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причем период цикла вращения является величиной, обратной разности частот, например, период оборота равен 2 с — разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счет кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.

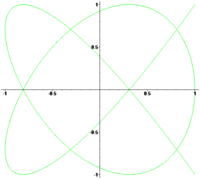Вращение фигуры Лиссажу при незначительной расстройке частот

Литература

• Справочник по радиоэлектронным устройствам. В 2-х томах; Под ред. Д. П. Линде — М.: Энергия, 1978
• Справочник по физике. Яворский Б. М., Детлаф А. А. — М.: Наука, 1981

См. также

Ссылки

15)Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу

Допустим, что материальная точка (тело) может совершать колебания как вдоль оси x, так и вдоль перпендикулярной оси Y. Если возбудить оба колебания, материальная точка будет двигаться по некоторой криволинейной траектории, форма которой зависит от разности фаз колебаний. Выберем начало отсчета времени так, чтобы начальная фаза одного колебания была равна нулю. Тогда уравнения запишутся следующим образом:

x=A·cos(ωt)  y=B·cos(ωt+α) (22)

где α — разность фаз складываемых колебаний, A и B — амплитуды колебаний.

Выражения (22) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (22) параметр . Из первого уравнения следует, что:

cos(ωt)=x/A (23)

следовательно,

sin(ωt)=±√(1-x²/A²) (24)

Теперь развернем косинус во втором уравнении из (22) по формуле для косинуса суммы (y/B=cos(ωt)·cosα-sin(ωt)·sinα) и подставим в него вместо cos(ωt) и sin(ωt) их значения (23) и (24). В результате получим:

y/B=(x/A)·cosα∓sinα√(1-x²/A²)

Перенесем все члены без корня в левую часть уравнения и возведем его в квадрат. После несложных преобразований получим уравнение эллипса, оси которого повернуты относительно координатных осей:

(x²/A²)+(y²/B²)-(2·xy·cosα/AB)=sin²α (25)

Ориентация эллипса и величина полуосей зависят довольно сложным образом от амплитуд A и B и разности фаз α.

Рассмотрим некоторые частные случаи:

1. Разность фаз α=0.

В этом случае уравнение (25) примет вид [(x/A)-(y/B)]²=0, откуда получается уравнение прямой:

y=Bx/A (26).

Результирующее движение является гармоническим с частотой ω и амплитудой √(A²+B²) (р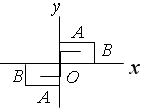ис 8).

  Рис. 8

2. Разность фаз α=±π. В этом случае уравнение (25) примет вид [(x/A)+(y/B)]²=0, откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой (рис.9):

y=-Bx/A (27)

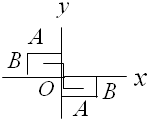  Рис. 9

3. Разность фаз α=±π/2.

Уравнение (25) переходит в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний (рис.10):

[(x/A)+(y/B)]²=1 (28)

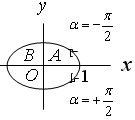  Рис. 10

При равенстве амплитуд A и B эллипс вырождается в окружность. Случаи α=+π/2 и α=-π/2 отличаются направлением движения по эллипсу или по окружности.  Если α=+π/2, уравнения (22) можно записать следующим образом: x=A·cosωt; y=-B·sinωt.

В момент t=0 тело находится в точке 1 (рис 10). В последующие моменты времени, координата x уменьшается, а координата y становится отрицательной. Следовательно, движение совершается по часовой стрелке.

Если α=-π/2, уравнения колебаний имеют вид: x=A·cosωt; y=B·sinωt. Отсюда можно заключить, что движение происходит против часовой стрелки.

Из сказанного следует, что равномерное движение по окружности радиусом R с угловой скоростью ω может быть представлено как сумма двух взаимно перпендикулярных колебаний:

x=R·cosωt  y=±R·sinωt (29)

(знак «+» в выражении для y соответствует движению против часовой стрелки, знак «-» – по часовой стрелке).

В случае, когда частоты взаимно перпендикулярных колебаний отличаются на очень малую величину Δω, их можно рассматривать как колебания одинаковой частоты, но с медленно изменяющейся разностью фаз. В самом деле, уравнения колебаний можно представить следующим образом:

x=A·cosωt  y=B·cos[ωt+(Δω+α)],

где выражение (Δω+α) рассматривается как разность фаз, медленно изменяющуюся со временем по линейному закону.

Результирующее движение в этом случае происходит по медленно видоизменяющейся кривой, которая будет последовательно принимать форму, отвечающую всем значениям разности фаз от -π до π.

Если частоты взаимно перпендикулярных колебаний неодинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу.

На рис.11 показана одна из простейших траекторий, получающаяся при отношении частот 1:2 и разности фаз π/2. Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу.

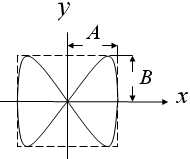  Рис. 11

Фигуры Лиссажу позволяют найти частоту одного из колебаний, если известна частота другого. Это обусловлено тем, что кратность частот легко находится с помощью секущих, параллельных координатным осям.

Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами иамплитудами обоих колебаний. 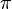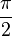В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или вырождаются в отрезки прямых, а при разности фаз и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.

Математическое выражение для кривой Лиссажу

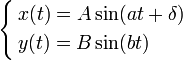
где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз

Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности (A = B, δ = π/2 радиан) и отрезка прямой (δ = 0). Ещё один пример фигуры Лиссажу — парабола (a/b = 2, δ = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a/b — рациональное число.

Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и

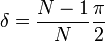
являются полиномами Чебышева первого рода степени N.

Фигуры Лиссажу

      Рассмотрим некоторые частные случаи решений уравнения (2.3.2).

      1. Начальные фазы колебаний одинаковы:

 т.е.

      Тогда уравнение (2.3.2) примет вид:

    или      ;

      отсюда получим уравнение результирующего колебания:

(2.4.1)

      Это   уравнение   прямой,    проходящей    через   начало   координат   (рис. 2.7, а). Следовательно, в результате сложения двух взаимно перпендикулярных колебаний с одинаковыми начальными фазами будут происходить колебания вдоль прямой, проходящей через начало координат.

а	б	в
Рис. 2.7

      Такие колебания называются линейно поляризованными.

      2. Начальная разность фаз равна π. Тогда , следовательно

;

.

      Уравнение колебания в этом случае

(2.4.2)

      То есть точка тоже будет колебаться вдоль прямой, проходящей через начало координат, но прямая лежит в других четвертях по сравнению с первым случаем (рис. 2.7, б).

      Амплитуда результирующего колебания в обоих случаях равна:

.

(2.4.3)

      3. Начальная разность фаз равна π/2. Проанализируем уравнение (2.3.2), учитывая, что       .

.

(2.4.4)

      Это уравнение эллипса с полуосями А₁ и А₂  (рис. 2.7, в). Случай эллиптически поляризованных колебаний.

      При  получим уравнение окружности (циркулярно-поляризованные колебания).

      4. Все остальные разности фаз дают эллипсы с различным углом наклона относительно осей координат.

      Необходимо отметить, что все рассматриваемые случаи, все        кривые – это эллипсы (даже прямая – частный случай эллипса).

      Фигуры, получаемые при сложении взаимно перпендикулярных колебаний разных частот, называются фигурами Лиссажу (Ж. Лиссажу (1822–1880) – французский физик). В простейших случаях можно сравнить частоты по виду фигур.

      В приведенных выше примерах рассматривались простейшие случаи, когда  Если , то в результате будут получаться уже не эллипсы, а более сложные фигуры Лиссажу. В табл. 1 приведены несколько фигур Лиссажу для разных соотношений частот колебаний и заданной разности фаз .

Таблица 1

---

Фигура Лиссажу — это… Что такое Фигура Лиссажу?



Фигура Лиссажу

Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822—80). Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или π вырождаются в отрезки прямых, а при разности фаз π/2 и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.

Применение в технике — сравнение частот

Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причем период цикла вращения является величиной, обратной разности частот, например, период оборота равен 2 с — разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счет кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.

Литература

• Справочник по радиоэлектронным устройствам. В 2-х томах; Под ред. Д. П. Линде — М.: Энергия, 1978
• Справочник по физике. Яворский Б. М., Детлаф А. А. — М.: Наука, 1981

Ссылки

См. также

Wikimedia Foundation. 2010.

• Фигура (форма предмета)
• Фигура (археология)

Смотреть что такое «Фигура Лиссажу» в других словарях:

• фигура Лиссажу — Lissajous o figūra statusas T sritis automatika atitikmenys: angl. Lissajous figure vok. Lissajous Figur, f rus. фигура Лиссажу, f pranc. figure de Lissajous, f ryšiai: sinonimas – Lisažu figūra …   Automatikos terminų žodynas

• фигура Лиссажу — Lisažu figūra statusas T sritis fizika atitikmenys: angl. Lissajous figure vok. Lissajous Figur, f rus. фигура Лиссажу, f pranc. figure de Lissajous, f …   Fizikos terminų žodynas

• Лиссажу фигуры — Фигуры Лиссажу замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822 80). Вид фигур… …   Википедия

• Фигуры Лиссажу — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между… …   Википедия

• Осциллограф — (лат. oscillo  качаюсь + греч …   Википедия

• Осциллятор Чуа — Рисунок 1  Схема Чуа. L,G,C1,C2 пассивные элементы, g диод Чуа. В классическом варианте предлагаются следующие значения элементов: L=1/7Гн;G=0.7См;C1=1/9Ф;C2=1Ф Простейшая электрическая цепь, демонстрирующая режимы хаотических колебаний.… …   Википедия

• Осцилограф — Цифровой осциллограф Цифровой осциллограф Agilent InfiniiVision 7000 Series Осциллограф Осциллограф ( …   Википедия

• Цепь Чуа — Рисунок 1  Цепь Чуа. L,G,C1,C2 пассивные элементы, g диод Чуа. В классическом варианте предлагаются следующие значения элементов: L=1/7Гн;G=0.7См;C1=1/9Ф;C2=1Ф Цепь Чуа, схема Чуа  простейшая электрическая цепь, демонстрирующая режимы… …   Википедия

• Lissajous figure — Lissajous o figūra statusas T sritis automatika atitikmenys: angl. Lissajous figure vok. Lissajous Figur, f rus. фигура Лиссажу, f pranc. figure de Lissajous, f ryšiai: sinonimas – Lisažu figūra …   Automatikos terminų žodynas

• Lissajous’o figūra — statusas T sritis automatika atitikmenys: angl. Lissajous figure vok. Lissajous Figur, f rus. фигура Лиссажу, f pranc. figure de Lissajous, f ryšiai: sinonimas – Lisažu figūra …   Automatikos terminų žodynas

Лиссажу фигуры — это… Что такое Лиссажу фигуры?



Лиссажу фигуры

Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822—80). Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или π вырождаются в отрезки прямых, а при разности фаз π/2 и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.

Применение в технике — сравнение частот

Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причем период цикла вращения является величиной, обратной разности частот, например, период оборота равен 2 с — разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счет кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.

Литература

• Справочник по радиоэлектронным устройствам. В 2-х томах; Под ред. Д. П. Линде — М.: Энергия, 1978
• Справочник по физике. Яворский Б. М., Детлаф А. А. — М.: Наука, 1981

Ссылки

См. также

Wikimedia Foundation. 2010.

• Лиссабонское соглашение
• Лиссенцефалия

Смотреть что такое «Лиссажу фигуры» в других словарях:

• ЛИССАЖУ ФИГУРЫ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонич. колебания в двух взаимно перпендикулярных направлениях. Впервые изучены франц. учёным Ж. Лиссажу (J. Lissajous). Вид Л. ф. зависит от соотношения между периодами… …   Физическая энциклопедия

• ЛИССАЖУ ФИГУРЫ — замкнутые траектории, описываемые точкой, совершающей одновременно два гармонических колебательных движения в двух взаимно перпендикулярных направлениях. Вид этих фигур зависит от соотношения между периодами (частотами), фазами и амплитудами… …   Большая политехническая энциклопедия

• ЛИССАЖУ ФИГУРЫ — [по имени франц. физика Ж. Лиссажу (J. Lissajous; 1822 80)] замкнутые траектории точки, совершающей одновременно 2 гармонич. колебат. движения в двух взаимно перпендикулярных направлениях. Вид Л. ф. зависит от соотношений между периодами… …   Большой энциклопедический политехнический словарь

• ЛИССАЖУ ФИГУРЫ — замкнутые траектории точки, совершающей одновременно два гармонич. колебат. движения в двух взаимно перпендикулярных направлениях. Вид Л.ф. зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний и позволяет… …   Естествознание. Энциклопедический словарь

• Лиссажу фигуры —         замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822 80). Вид Л. ф. зависит от… …   Большая советская энциклопедия

• Фигуры Лиссажу — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между… …   Википедия

• фигуры Лиссажу — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN Lissajous figures …   Справочник технического переводчика

• Лиссажу, Жюль Антуан — Жюль Антуан Лиссажу (фр. Jules Antoine Lissajous; 4 марта 1822, Версаль, Франция …   Википедия

• Фигуры Хладни — Примеры фигур Хладни из книги Э.Хладни «Акустика» Фигуры Хладни  фигуры, о …   Википедия

• Фигура Лиссажу — Фигуры Лиссажу замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822 80). Вид фигур… …   Википедия