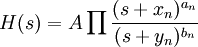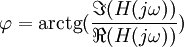Фазово-частотная характеристика (ФЧХ) фильтров и звук
Цепи аналогового сигнала просто невозможно представить без различных фильтров. Фильтры существуют разные и для разных целей. Не будем влезать в дебри схемотехники, а рассмотрим как фильтры Чебышева, Баттерворта и Бесселя влияют на фазовую характеристику(ФЧХ) переменного сигнала. И кто из них лучше для звука и почему.
Чтобы не возникало разногласий, будем придерживаться общепринятой терминологии. Поэтому перед тем как начать, предлагаю для начала взглянуть на следующую картинку:
А затем прочитать отрывочек из Википедии:
Фазочастотная характеристика (ФЧХ) — это зависимость разности фаз между выходным и входным сигналами от частоты сигнала, функция, выражающая (описывающая) эту зависимость, также — график этой функции.
Для однозначности так же будем считать, что у нас Фильтр Низких Частот (ФНЧ). Все то же самое относится и к фильтру высоких частот.
Порядок фильтра
Обычно, когда встает вопрос о создании фильтра, первым делом необходимо определиться с тем, какая нужна крутизна спада. Она напрямую определяет порядок фильтра. Чем выше порядок ФНЧ, тем круче будет спад частотной характеристики выше частоты среза.
Для удобства, на этом и последующих графиках приводится нормированная частота. Т.е. как если бы все частоты были поделены на частоту среза фильтра.
Но чем выше порядок фильтра — тем сложнее он будет в реализации и капризнее в настройке. При этом, чем выше порядок, тем худшее воздействие он будет оказывать на частотные и/или фазовые характеристики сигнала.
Обычно, когда нужен фильтр высокого порядка, для упрощения схемотехники и расчетов, прибегают к последовательному включению двух, трех и более фильтров второго порядка. Это конечно облегчает задачу, но при таком включении требуется либо разные коэффициенты усиления каждого фильтра, либо разные частоты среза. Но это уже выходит за рамки данной статьи.
Влияние фильтра на ФЧХ
Влияние фильтра на фазовую характеристику сигнала не менее значимо, чем его влияние на АЧХ. Для звуковых сигналов влияние ФЧХ фильтра на сигнал может оказаться решающим при выборе типа фильтра.
Не считая активного элемента (транзистора или микросхемы), активные фильтры, обычно, строятся на RC цепях. Каждая RC цепь — это полюс фильтра, перегибающий АЧХ в нужном нам направлении. Но одновременно с этим, каждая RC — цепь вносить конечную временную задержку в сигнал.
Такая задержка приводит к тому, что сигнал после фильтра будет сдвинут по фазе относительно исходного сигнала. Вся проблема заключается в том, что эта задержка может быть различна для разных частот.
Это касается любого фильтра. Но разница между типами фильтров в том, что они имеют разную фазово-частотную характеристику и разную крутизну среза.
Фильтра Чебышева и звук?
Начнем с фильтра Чебышева. Он имеет самый резкий спад частотной характеристики. Но вносимый им фазовый сдвиг сильно меняется во всей полосе пропускания. По этой причине фильтр Чебышева не применяется в высококачественных звуковых цепях.
Но это не единственный минус. Фильтра Чебышева так же имеет и большую неравномерность АЧХ в полосе пропускания. При этом сумма максимумов и минимумов равна порядку фильтра
На следующем графике приведены амплитудно-частотные (левая шкала) и фазово-частотные (правая шкала) характеристики для фильтра Чебышева 8-го порядка. Все тоже самое свойственно и фильтрам Чебышева более низких порядков.
Минимальное влияние на ФЧХ
Амплитудно частотная характеристика (АЧХ) фильтра Бесселя (он же Томпсона) линейна во всей полосе пропускания. Но его главным достоинством, является отсутствие вносимых фазовых искажений. Т.е. для всех частот в полосе пропускания задержка одинакова.
В плане ФЧХ он идеален для применения в звуковых цепях. Но его ложкой дегтя является самый пологий спад среди всех фильтров. Более пологий спад имеет только обычная RC-цепь.
На следующем рисунке приводится сравнение крутизны срезов фильтров разного типа: 1- Бесселя, 2 — Баттерворта, 3-Чебышева (неравномерность 0.5 дБ).
Фильтр Баттерворта имеет близкие характеристики к фильтру Бесселя, но у него более крутой спад АЧХ. За это приходится расплачиваться неодинаковостью запаздывания для разных частот..
Зависимость времени запаздывания сигнала от частот для фильтров Бесселя(1) и Баттерворда(2) второго порядка, нормированных по частоте, показаны на следующем рисунке:
Обратите внимание что на графике показана циклическая частота (омега). Для перевода в герцы необходимо умножить ее на 2π. Помимо этог
Логарифмическая фазовая частотная характеристика — это… Что такое Логарифмическая фазовая частотная характеристика?

Логарифмическая амплитудно-фазовая частотная характеристика (ЛАФЧХ) — представление частотного отклика линейной стационарной системы в логарифмическом масштабе.
ЛАФЧХ строится в виде двух графиков: логарифмической амплитудно-частотной характеристики и фазо-частотной характеристики, которые обычно располагаются друг под другом.
Анализ систем с помощью ЛАФЧХ весьма прост и удобен, поэтому находит широкое применение в различных отраслях техники, таких как цифровая обработка сигналов, электротехника и теория управления.
Названия
В западной литературе используется название диаграмма Боде или график Боде, по имени выдающегося инженера Хенрика Боде (англ. Hendrik Wade Bode).
В инженерных кругах название обычно сокращается до ЛАХ.
В пакете прикладных программ для инженерных вычислений bode.
Использование
Свойства и особенности
Если передаточная функция системы является рациональной, тогда ЛАФЧХ может быть аппроксимирована прямыми линиями. Это удобно при рисовании ЛАФЧХ вручную, а также при составлении ЛАФЧХ простых систем.
С помощью ЛАФЧХ удобно проводить синтез систем систем управления, а также цифровых и аналоговых фильтров: в соответствии с определёнными критериями качества строится желаемая ЛАФЧХ, аппроксимированная с помощью прямых линий, которая затем разбивается на ЛАФЧХ отдельных элементарных звеньев, из которых восстанавливается передаточная функция системы (регулятора) или фильтра.
ЛАЧХ
На графике ЛАЧХ абсциссой является частота в логарифмическом масштабе, по оси ординат отложена амплитуда передаточной функции в децибелах.
Представление АЧХ в логарифмическом масштабе упрощает построение характеристик сложных систем, так как позволяет заменить операцию перемножения АЧХ звеньев сложением, что вытекает из свойства логарифма: 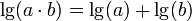 .
.
ФЧХ
На графике фазо-частотной характеристики абсциссой является частота в логарифмическом масштабе, по оси ординат отложен фазовый сдвиг выходного сигнала системы относительно входного (обычно в градусах).
Также возможен вариант, когда по оси ординат откладывается фазовый сдвиг в логарифмическом масштабе, в этом случае характеристика будет называться ЛФЧХ.
Случай минимально-фазовых систем
Амлитуда и фаза системы редко меняются независимо друг от друга — при изменении амплитуды меняется и фаза и наоборот. Для минимально-фазовых систем ЛФЧХ и ЛАЧХ могут быть однозначно определены друг из друга с помощью преобразования Гильберта.
Построение ЛАФЧХ
Основная идея основывается на следующем математическом правиле сложения логарифмов. Если передаточную функцию можно представить в виде дробно-рациональной функции
 ,
,
то:
После разбиения передаточной функции на элементарные звенья можно построить ЛАФЧХ каждого отдельного звена, а результирующую ЛАФЧХ получить простым сложением.
Аппроксимация ЛАЧХ прямыми линиями
При построении ЛАЧХ для оси ординат обычно используется масштаб 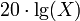 , то есть значение АЧХ, равное 100 превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:
, то есть значение АЧХ, равное 100 превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:
- где
 — комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:
— комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:  ,
,  и
и  — константы, а
— константы, а  — передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:
— передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:
- в каждом
 , где
, где  (нуль), наклон линии увеличивается на
(нуль), наклон линии увеличивается на  дБ на декаду.
дБ на декаду.
- в каждом
- в каждом
 , где
, где  (полюс), наклон линии уменьшается на
(полюс), наклон линии уменьшается на  дБ на декаду.
дБ на декаду.
- в каждом
- Начальное значение графика можно найти простой подстановкой значения круговой частоты
 в передаточную функцию.
в передаточную функцию.
- Начальное значение графика можно найти простой подстановкой значения круговой частоты
- Начальный наклон графика зависит от числа и порядка нулей и полюсов, которые меньше начального значения частоты. Он может быть найден с помощью первых двух правил.
- В случае наличия комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка,
 , наклон менятся в точке
, наклон менятся в точке  сразу на
сразу на  дБ на декаду.
дБ на декаду.
- В случае наличия комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка,
Корректировка аппроксимированной ЛАЧХ
Для корректировки ЛАЧХ, аппроксимированную прямыми линиями надо:
- в каждом нуле поставить точку на
 дБ выше линии (
дБ выше линии ( дБ для двух комплексно-сопряжённых нулей)
дБ для двух комплексно-сопряжённых нулей)
- в каждом нуле поставить точку на
- в каждом полюсе поставить точку на
 дБ ниже линии (
дБ ниже линии ( дБ для двух комплексно-сопряжённых полюсов)
дБ для двух комплексно-сопряжённых полюсов)
- в каждом полюсе поставить точку на
- плавно соединить точки, используя прямые линии в качестве асимптот
Аппроксимация ФЧХ
Для построения аппроксимированной ФЧХ используют запись передаточной функции в том же виде, что и для ЛАЧХ:
Основной принцип построения ФЧХ — начертить отдельные графики для каждого полюса или нуля, затем сложив их. Точная кривая фазо-частотной характеристики задаётся уравнением:
Для того, чтобы нарисовать ФЧХ для каждого полюса или нуля, используют следующие правила:
Анализ устойчивости по ЛАФЧХ
ЛАФЧХ некоторых элементарных звеньев
Ниже представлена таблица, в которую помещены передаточные функции и ЛАФЧХ некоторых типовых элементарных звеньев. Большая часть линейных стационарных систем может быть представлена в виде соединения таких звеньев. В таблице  — комплексная переменная.
— комплексная переменная.
Примечания
См. также
Wikimedia Foundation. 2010.
ЛФЧХ — это… Что такое ЛФЧХ?

Логарифмическая амплитудно-фазовая частотная характеристика (ЛАФЧХ) — представление частотного отклика линейной стационарной системы в логарифмическом масштабе.
ЛАФЧХ строится в виде двух графиков: логарифмической амплитудно-частотной характеристики и фазо-частотной характеристики, которые обычно располагаются друг под другом.
Анализ систем с помощью ЛАФЧХ весьма прост и удобен, поэтому находит широкое применение в различных отраслях техники, таких как цифровая обработка сигналов, электротехника и теория управления.
Названия
В западной литературе используется название диаграмма Боде или график Боде, по имени выдающегося инженера Хенрика Боде (англ. Hendrik Wade Bode).
В инженерных кругах название обычно сокращается до ЛАХ.
В пакете прикладных программ для инженерных вычислений bode.
Использование
Свойства и особенности
Если передаточная функция системы является рациональной, тогда ЛАФЧХ может быть аппроксимирована прямыми линиями. Это удобно при рисовании ЛАФЧХ вручную, а также при составлении ЛАФЧХ простых систем.
С помощью ЛАФЧХ удобно проводить синтез систем систем управления, а также цифровых и аналоговых фильтров: в соответствии с определёнными критериями качества строится желаемая ЛАФЧХ, аппроксимированная с помощью прямых линий, которая затем разбивается на ЛАФЧХ отдельных элементарных звеньев, из которых восстанавливается передаточная функция системы (регулятора) или фильтра.
ЛАЧХ
На графике ЛАЧХ абсциссой является частота в логарифмическом масштабе, по оси ординат отложена амплитуда передаточной функции в децибелах.
Представление АЧХ в логарифмическом масштабе упрощает построение характеристик сложных систем, так как позволяет заменить операцию перемножения АЧХ звеньев сложением, что вытекает из свойства логарифма: 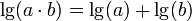 .
.
ФЧХ
На графике фазо-частотной характеристики абсциссой является частота в логарифмическом масштабе, по оси ординат отложен фазовый сдвиг выходного сигнала системы относительно входного (обычно в градусах).
Также возможен вариант, когда по оси ординат откладывается фазовый сдвиг в логарифмическом масштабе, в этом случае характеристика будет называться ЛФЧХ.
Случай минимально-фазовых систем
Амлитуда и фаза системы редко меняются независимо друг от друга — при изменении амплитуды меняется и фаза и наоборот. Для минимально-фазовых систем ЛФЧХ и ЛАЧХ могут быть однозначно определены друг из друга с помощью преобразования Гильберта.
Построение ЛАФЧХ
Основная идея основывается на следующем математическом правиле сложения логарифмов. Если передаточную функцию можно представить в виде дробно-рациональной функции
 ,
,
то:
После разбиения передаточной функции на элементарные звенья можно построить ЛАФЧХ каждого отдельного звена, а результирующую ЛАФЧХ получить простым сложением.
Аппроксимация ЛАЧХ прямыми линиями
При построении ЛАЧХ для оси ординат обычно используется масштаб 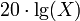 , то есть значение АЧХ, равное 100 превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:
, то есть значение АЧХ, равное 100 превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:
- где
 — комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:
— комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:  ,
,  и
и  — константы, а
— константы, а  — передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:
— передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:
- в каждом
 , где
, где  (нуль), наклон линии увеличивается на
(нуль), наклон линии увеличивается на  дБ на декаду.
дБ на декаду.
- в каждом
- в каждом
 , где
, где  (полюс), наклон линии уменьшается на
(полюс), наклон линии уменьшается на  дБ на декаду.
дБ на декаду.
- в каждом
- Начальное значение графика можно найти простой подстановкой значения круговой частоты
 в передаточную функцию.
в передаточную функцию.
- Начальное значение графика можно найти простой подстановкой значения круговой частоты
- Начальный наклон графика зависит от числа и порядка нулей и полюсов, которые меньше начального значения частоты. Он может быть найден с помощью первых двух правил.
- В случае наличия комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка,
 , наклон менятся в точке
, наклон менятся в точке  сразу на
сразу на  дБ на декаду.
дБ на декаду.
- В случае наличия комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка,
Корректировка аппроксимированной ЛАЧХ
Для корректировки ЛАЧХ, аппроксимированную прямыми линиями надо:
- в каждом нуле поставить точку на
 дБ выше линии (
дБ выше линии ( дБ для двух комплексно-сопряжённых нулей)
дБ для двух комплексно-сопряжённых нулей)
- в каждом нуле поставить точку на
- в каждом полюсе поставить точку на
 дБ ниже линии (
дБ ниже линии ( дБ для двух комплексно-сопряжённых полюсов)
дБ для двух комплексно-сопряжённых полюсов)
- в каждом полюсе поставить точку на
- плавно соединить точки, используя прямые линии в качестве асимптот
Аппроксимация ФЧХ
Для построения аппроксимированной ФЧХ используют запись передаточной функции в том же виде, что и для ЛАЧХ:
Основной принцип построения ФЧХ — начертить отдельные графики для каждого полюса или нуля, затем сложив их. Точная кривая фазо-частотной характеристики задаётся уравнением:
Для того, чтобы нарисовать ФЧХ для каждого полюса или нуля, используют следующие правила:
Анализ устойчивости по ЛАФЧХ
ЛАФЧХ некоторых элементарных звеньев
Ниже представлена таблица, в которую помещены передаточные функции и ЛАФЧХ некоторых типовых элементарных звеньев. Большая часть линейных стационарных систем может быть представлена в виде соединения таких звеньев. В таблице  — комплексная переменная.
— комплексная переменная.
Примечания
См. также
Wikimedia Foundation. 2010.
Понятие амплитудночастотной и фазочастотной характеристик системы. Методы экспериментального снятия АЧХ и ФЧХ.
Амплиту́дно-часто́тная характери́стика (АЧХ) — зависимость амплитуды выходного сигнала некоторой системы от частоты её входного гармонического сигнала. Иногда эту характеристику называют «частотным откликом системы».
АЧХ в теории автоматического управления
АЧХ в математической теории линейных стационарных систем описывает зависимость модуля комплексной передаточной функции линейной системы от частоты. Значение АЧХ при некоторой частоте указывает, во сколько раз амплитуда сигнала на выходе системы отличается от амплитуды входного сигнала на этой же частоте.
На графике АЧХ в декартовых координатах по оси абсцисс откладывается частота, а по оси ординат — отношение амплитуд выходного и входного сигналов системы.
Обычно для оси частоты используется логарифмический масштаб, так как отображаемый диапазон частот может изменяться в достаточно широких пределах (от единиц до миллионов герц или рад/с). В случае, когда логарифмический масштаб используется и на оси ординат, АЧХ принято называть логарифмической амплитудно-частотной характеристикой.
ЛАЧХ широкое применяется в теории автоматического управления в связи с простотой построения и наглядностью при исследовании поведения систем автоматического регулирования.
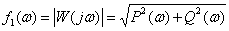
Фа́зочасто́тная характеристика (ФЧХ) — зависимость разности фаз между выходным и входным сигналами от частоты сигнала, функция, выражающая (описывающая) эту зависимость, также — график этой функции.
Для линейной электрической цепи, зависимость сдвига по фазе между гармоническими колебаниями на выходе и входе этой цепи от частоты гармонических колебаний на входе.
Часто ФЧХ используют для оценки фазовых искажений формы сложного сигнала, вызываемых неодинаковой задержкой во времени его отдельных гармонических составляющих при их прохождении по цепи.
Определение ФЧХ
В теории управления ФЧХ звена определяется тангенсом отношения мнимой части передаточной функции к действительной.
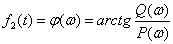
Для выяснения физического смысла частотной характеристики рассмотрим динамическое звено с передаточной функцией 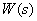 и импульсной характеристикой
и импульсной характеристикой 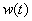 , на вход которого подаем гармонический сигнал
, на вход которого подаем гармонический сигнал 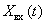 .
.
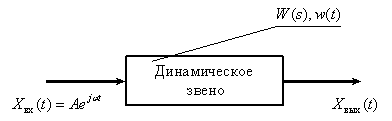
Рис. 3
Вспомним, что решение линейного дифференциального уравнения динамического звена, в рамках классического метода, состоит из двух составляющих – свободной и установившейся.
Установившаяся составляющая в случае гармонической функции времени, стоящей в правой части уравнения, так же является гармонической функцией времени. Поэтом установившийся сигнал на выходе динамического звена можно описать следующим выражением
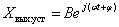 .
.
Сигнал на выходе звена определим с помощью теоремы об умножении изображений

В результате получаем
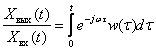 .
.
Для перехода к установившемуся режиму полагаем 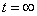 , тогда получаем
, тогда получаем
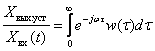
Но, с другой стороны, имеем по определению прямого преобразования Фурье
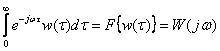 .
.
Поэтому
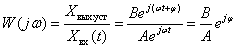 .
.
Отсюда следует простой алгоритм экспериментального определения частотной характеристики линейного динамического звена, объекта или системы управления для конкретной частоты 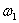 :
:
1. Подать на вход объекта синусоидальный сигнал частоты 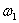
2. Дождаться затухания свободной составляющей переходного процесса.
3. Измерить амплитуду выходного сигнала и сдвиг его по фазе относительно входного сигнала.
4. Отношение амплитуды выходного установившегося сигнала к амплитуде входного сигнала определит модуль частотной характеристики при частоте 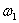 .
.
5. Сдвиг фазы выходного сигнала относительно входного сигнала определит угол (аргумент) частотной характеристики при частоте 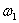 .
.
Применяя данный алгоритм для частот от нуля до бесконечности, можно экспериментальным путем определить частотную характеристику конкретного устройства. Функциональная схема экспериментальной установки для снятия частотных характеристик имеет вид
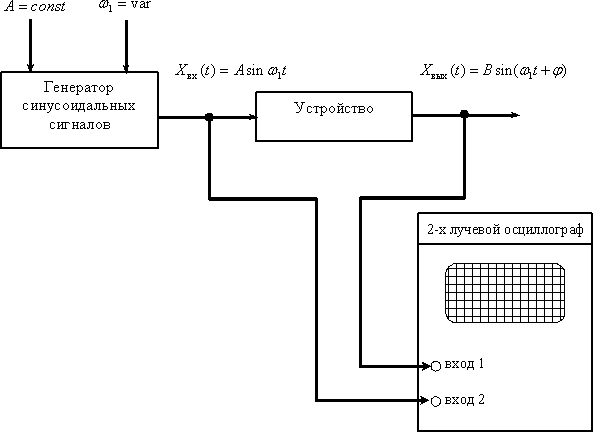
Рис. 4
При частоте 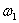 на экране осциллографа получаем после затухания свободной составляющей следующую картину –
на экране осциллографа получаем после затухания свободной составляющей следующую картину –
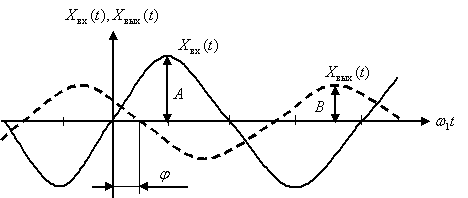
Рис. 5
На основании рис. 5 можно построить на комплексной плоскости точку, принадлежащую частотной характеристике устройства, а совокупность точек при изменении частоты от нуля до величины, когда амплитуда выходного установившегося сигнала станет пренебрежимо мала, будет представлять собой амплитудно-фазовую частотную характеристику (АФЧХ). Как видно из рисунка, по этим данным может быть построена любая необходимая частотная характеристика устройства.

Рис. 6
Для экспериментального получения частотных характеристик различных объектов в инженерной практике используют специализированные приборы, а в последнее время широко используют для таких целей персональные компьютеры, оснащенные специализированными платами ввода-вывода и пакетами прикладных программ.
Учитывая все вышеизложенное, становится ясным и физический смысл частотной характеристики.
Она показывает, во сколько раз изменяет динамическое звено (устройство), работающее в установившемся режиме, амплитуду входной синусоиды частоты 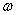 , и на какой угол сдвигает входную синусоиду по фазе.
, и на какой угол сдвигает входную синусоиду по фазе.
31. Понятие амплитудночастотной и фазочастотной характеристик системы, методы расчета собственной и резонансной частоты системы.
Амплиту́дно-часто́тная характери́стика (АЧХ) — зависимость амплитуды выходного сигнала некоторой системы от частоты её входного гармонического сигнала. Иногда эту характеристику называют «частотным откликом системы».
АЧХ в теории автоматического управления
АЧХ в математической теории линейных стационарных систем описывает зависимость модуля комплексной передаточной функции линейной системы от частоты. Значение АЧХ при некоторой частоте указывает, во сколько раз амплитуда сигнала на выходе системы отличается от амплитуды входного сигнала на этой же частоте.
На графике АЧХ в декартовых координатах по оси абсцисс откладывается частота, а по оси ординат — отношение амплитуд выходного и входного сигналов системы.
Обычно для оси частоты используется логарифмический масштаб, так как отображаемый диапазон частот может изменяться в достаточно широких пределах (от единиц до миллионов герц или рад/с). В случае, когда логарифмический масштаб используется и на оси ординат, АЧХ принято называть логарифмической амплитудно-частотной характеристикой.
ЛАЧХ широкое применяется в теории автоматического управления в связи с простотой построения и наглядностью при исследовании поведения систем автоматического регулирования.
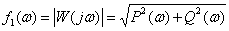
Фа́зочасто́тная характеристика (ФЧХ) — зависимость разности фаз между выходным и входным сигналами от частоты сигнала, функция, выражающая (описывающая) эту зависимость, также — график этой функции.
Для линейной электрической цепи, зависимость сдвига по фазе между гармоническими колебаниями на выходе и входе этой цепи от частоты гармонических колебаний на входе.
Часто ФЧХ используют для оценки фазовых искажений формы сложного сигнала, вызываемых неодинаковой задержкой во времени его отдельных гармонических составляющих при их прохождении по цепи.
Определение ФЧХ
В теории управления ФЧХ звена определяется тангенсом отношения мнимой части передаточной функции к действительной.
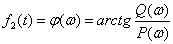
32. Переходная характеристика системы. Методы экспериментального снятия переходных характеристик. Виды переходных характеристик.
Переходная характеристика системы– это реакция на единичное ступенчатое воздействие при нулевых начальных условиях объекта управления и характеризует его динамические свойства. Получение переходной характеристики экспериментальным путем с последующим получением параметров ОУ – первый шаг на пути к определению настроек ПИД-регулятора, ПИ-регулятора, П-регулятора.
Зачастую на практике речь идет о разгонной характеристике.
Разгонная переходная характеристика объекта будет получена в том случае, если на вход подать ступенчатое воздействие, отличное от единицы. Зачастую на реальном объекте подают входное воздействие в несколько процентов хода исполнительного механизма, а потом делят выходное воздействие на входное.
В устойчивых АСР возможны виды переходных процессов:
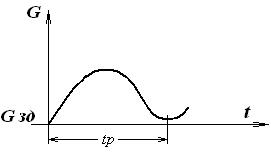
(а)- апериодический сходящийся процесс, имеет одну амплитуду колебания
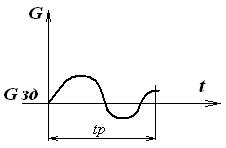
(б)- затухающий колебательный процесс
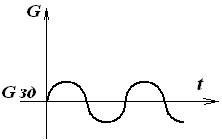
(в)- колебательный процесс с постоянной амплитудой колебания.
АСР находится на грани устойчивости.
Логарифмическая амплитудно-фазовая частотная характеристика — это… Что такое Логарифмическая амплитудно-фазовая частотная характеристика?

Логарифмическая амплитудно-фазовая частотная характеристика (ЛАФЧХ) — представление частотного отклика линейной стационарной системы в логарифмическом масштабе.
ЛАФЧХ строится в виде двух графиков: логарифмической амплитудно-частотной характеристики и фазо-частотной характеристики, которые обычно располагаются друг под другом.
Анализ систем с помощью ЛАФЧХ весьма прост и удобен, поэтому находит широкое применение в различных отраслях техники, таких как цифровая обработка сигналов, электротехника и теория управления.
Названия
В западной литературе используется название диаграмма Боде или график Боде, по имени выдающегося инженера Хенрика Боде (англ. Hendrik Wade Bode).
В инженерных кругах название обычно сокращается до ЛАХ.
В пакете прикладных программ для инженерных вычислений bode.
Использование
Свойства и особенности
Если передаточная функция системы является рациональной, тогда ЛАФЧХ может быть аппроксимирована прямыми линиями. Это удобно при рисовании ЛАФЧХ вручную, а также при составлении ЛАФЧХ простых систем.
С помощью ЛАФЧХ удобно проводить синтез систем систем управления, а также цифровых и аналоговых фильтров: в соответствии с определёнными критериями качества строится желаемая ЛАФЧХ, аппроксимированная с помощью прямых линий, которая затем разбивается на ЛАФЧХ отдельных элементарных звеньев, из которых восстанавливается передаточная функция системы (регулятора) или фильтра.
ЛАЧХ
На графике ЛАЧХ абсциссой является частота в логарифмическом масштабе, по оси ординат отложена амплитуда передаточной функции в децибелах.
Представление АЧХ в логарифмическом масштабе упрощает построение характеристик сложных систем, так как позволяет заменить операцию перемножения АЧХ звеньев сложением, что вытекает из свойства логарифма: 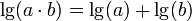 .
.
ФЧХ
На графике фазо-частотной характеристики абсциссой является частота в логарифмическом масштабе, по оси ординат отложен фазовый сдвиг выходного сигнала системы относительно входного (обычно в градусах).
Также возможен вариант, когда по оси ординат откладывается фазовый сдвиг в логарифмическом масштабе, в этом случае характеристика будет называться ЛФЧХ.
Случай минимально-фазовых систем
Амлитуда и фаза системы редко меняются независимо друг от друга — при изменении амплитуды меняется и фаза и наоборот. Для минимально-фазовых систем ЛФЧХ и ЛАЧХ могут быть однозначно определены друг из друга с помощью преобразования Гильберта.
Построение ЛАФЧХ
Основная идея основывается на следующем математическом правиле сложения логарифмов. Если передаточную функцию можно представить в виде дробно-рациональной функции
 ,
,
то:
После разбиения передаточной функции на элементарные звенья можно построить ЛАФЧХ каждого отдельного звена, а результирующую ЛАФЧХ получить простым сложением.
Аппроксимация ЛАЧХ прямыми линиями
При построении ЛАЧХ для оси ординат обычно используется масштаб 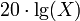 , то есть значение АЧХ, равное 100 превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:
, то есть значение АЧХ, равное 100 превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:
- где
 — комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:
— комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:  ,
,  и
и  — константы, а
— константы, а  — передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:
— передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:
- в каждом
 , где
, где  (нуль), наклон линии увеличивается на
(нуль), наклон линии увеличивается на  дБ на декаду.
дБ на декаду.
- в каждом
- в каждом
 , где
, где  (полюс), наклон линии уменьшается на
(полюс), наклон линии уменьшается на  дБ на декаду.
дБ на декаду.
- в каждом
- Начальное значение графика можно найти простой подстановкой значения круговой частоты
 в передаточную функцию.
в передаточную функцию.
- Начальное значение графика можно найти простой подстановкой значения круговой частоты
- Начальный наклон графика зависит от числа и порядка нулей и полюсов, которые меньше начального значения частоты. Он может быть найден с помощью первых двух правил.
- В случае наличия комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка,
 , наклон менятся в точке
, наклон менятся в точке  сразу на
сразу на  дБ на декаду.
дБ на декаду.
- В случае наличия комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка,
Корректировка аппроксимированной ЛАЧХ
Для корректировки ЛАЧХ, аппроксимированную прямыми линиями надо:
- в каждом нуле поставить точку на
 дБ выше линии (
дБ выше линии ( дБ для двух комплексно-сопряжённых нулей)
дБ для двух комплексно-сопряжённых нулей)
- в каждом нуле поставить точку на
- в каждом полюсе поставить точку на
 дБ ниже линии (
дБ ниже линии ( дБ для двух комплексно-сопряжённых полюсов)
дБ для двух комплексно-сопряжённых полюсов)
- в каждом полюсе поставить точку на
- плавно соединить точки, используя прямые линии в качестве асимптот
Аппроксимация ФЧХ
Для построения аппроксимированной ФЧХ используют запись передаточной функции в том же виде, что и для ЛАЧХ:
Основной принцип построения ФЧХ — начертить отдельные графики для каждого полюса или нуля, затем сложив их. Точная кривая фазо-частотной характеристики задаётся уравнением:
Для того, чтобы нарисовать ФЧХ для каждого полюса или нуля, используют следующие правила:
Анализ устойчивости по ЛАФЧХ
ЛАФЧХ некоторых элементарных звеньев
Ниже представлена таблица, в которую помещены передаточные функции и ЛАФЧХ некоторых типовых элементарных звеньев. Большая часть линейных стационарных систем может быть представлена в виде соединения таких звеньев. В таблице  — комплексная переменная.
— комплексная переменная.
Примечания
См. также
Wikimedia Foundation. 2010.
1.4 Амплитудно-частотная и фазочастотная характеристики
Амплитудно-частотная и фазочастотная характеристики определяют возможности по усилению гармонических колебаний различных частот. Из-за наличия в усилителе реактивных элементов (в том числе и паразитных), сопротивление которых зависит от частоты, коэффициент передачи такого усилителя зависит от частоты.
Коэффициент передачи усилителя гармонических сигналов в общем случае является комплексной величиной
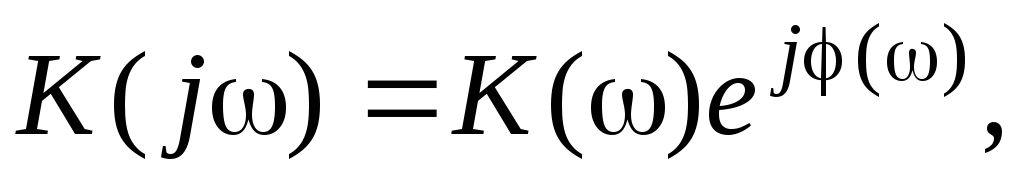 (1.1)
(1.1)
где 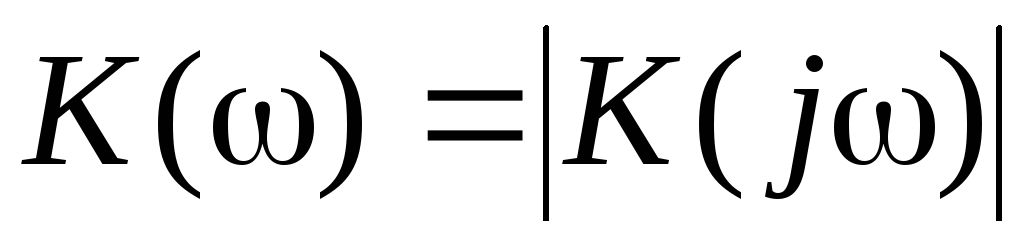 – модуль коэффициента передачи;
– модуль коэффициента передачи;
 –аргумент
коэффициента передачи.
–аргумент
коэффициента передачи.
Зависимость модуля коэффициента передачи усилителя от частоты входного гармонического сигнала называют амплитудно-частотной характеристикой усилителя (АЧХ). Фазочастотной характеристикой усилителя (ФЧХ) называют зависимость фазового сдвига выходного гармонического колебания относительно входного при изменении частоты.
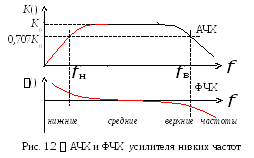
Примерный
вид АЧХ и ФЧХ для усилителя низкой
частоты (УНЧ) показан на рис. 1.2. За
границами рабочего диапазона частот,
характеризуемого коэффициентом усиления 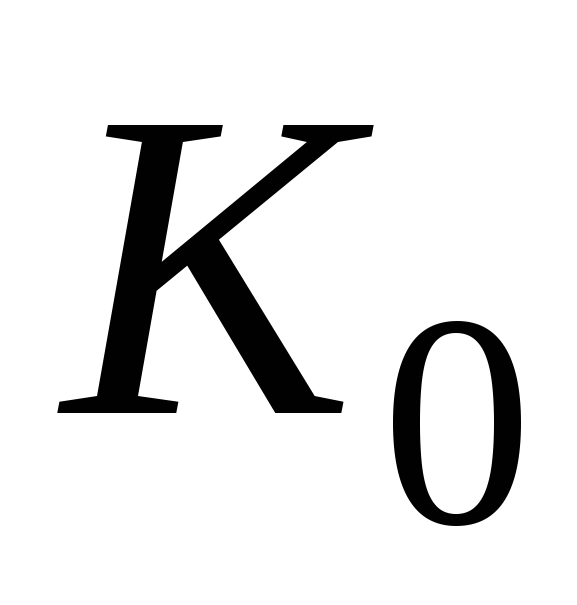 и близким к нулю фазовым сдвигом,
появляются частотные и фазовые искажения.
Частоты
и близким к нулю фазовым сдвигом,
появляются частотные и фазовые искажения.
Частоты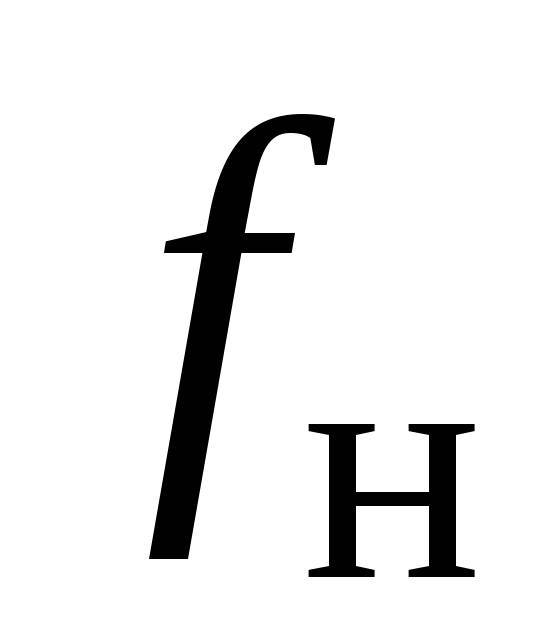 и
и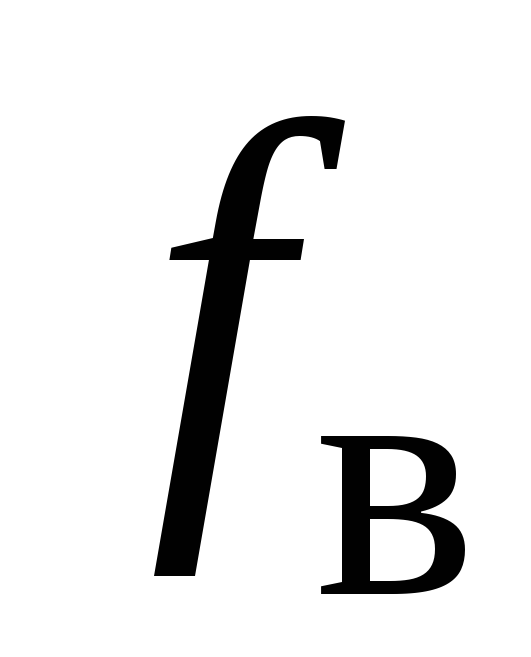 ,
на которых коэффициент передачи падает
до уровня 0,707
,
на которых коэффициент передачи падает
до уровня 0,707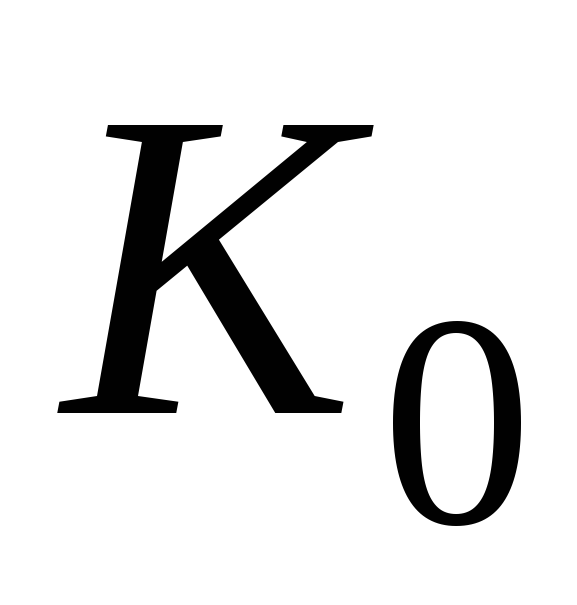 =
=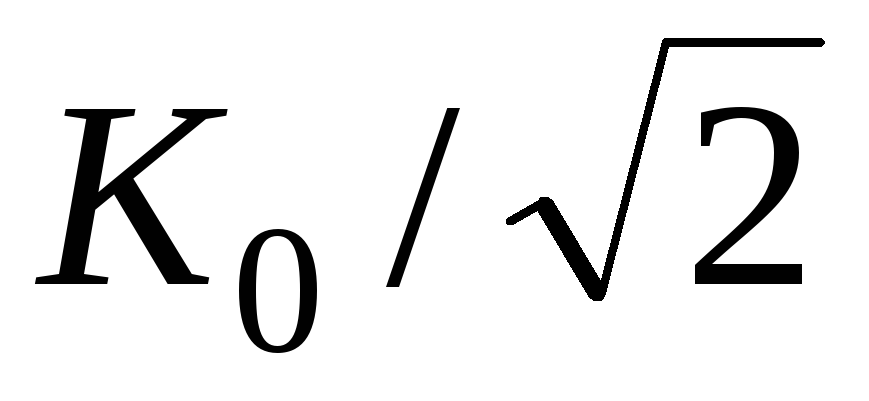 ,
называются нижней и верхней граничными
частотами, а разность между ними
,
называются нижней и верхней граничными
частотами, а разность между ними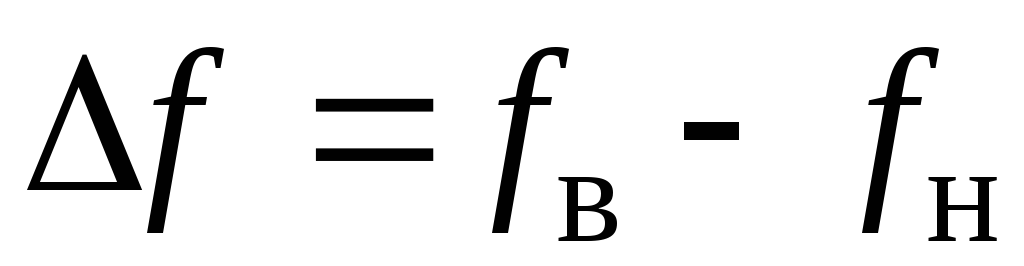 называют полосой пропускания усилителя.
Для неискаженного усиления сигналов
звукового диапазона требуются усилители
с полосой пропускания от 20 Гц до 20 кГц.
называют полосой пропускания усилителя.
Для неискаженного усиления сигналов
звукового диапазона требуются усилители
с полосой пропускания от 20 Гц до 20 кГц.
1.5 Переходная характеристика
Об
искажениях усиливаемого импульсного
сигнала (например, в видеоусилителях)
можно судить по переходной характеристике
усилителя. Переходной характеристикой 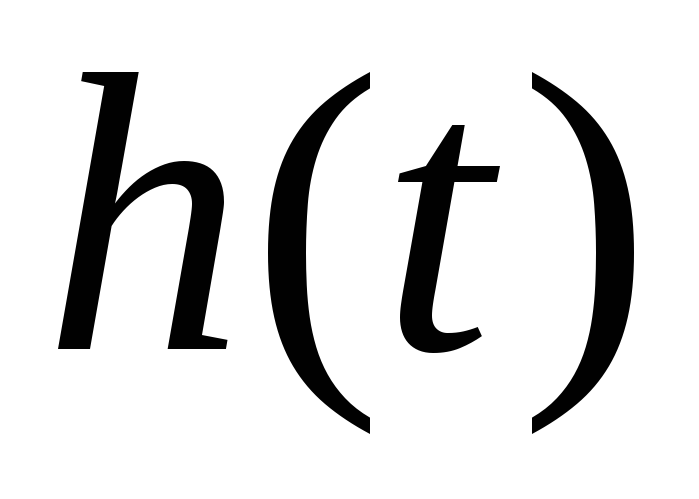 усилителя называют реакцию усилителя
на входное воздействие в виде единичного
скачка (ступеньки) тока или напряжения:
усилителя называют реакцию усилителя
на входное воздействие в виде единичного
скачка (ступеньки) тока или напряжения:
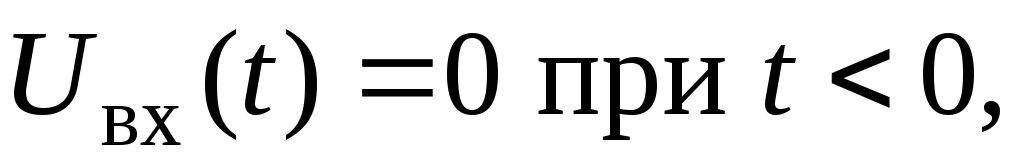
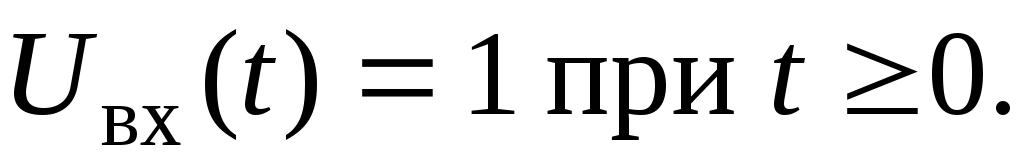
А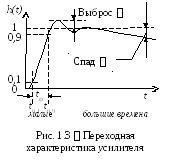 налитически
переходную характеристику
налитически
переходную характеристику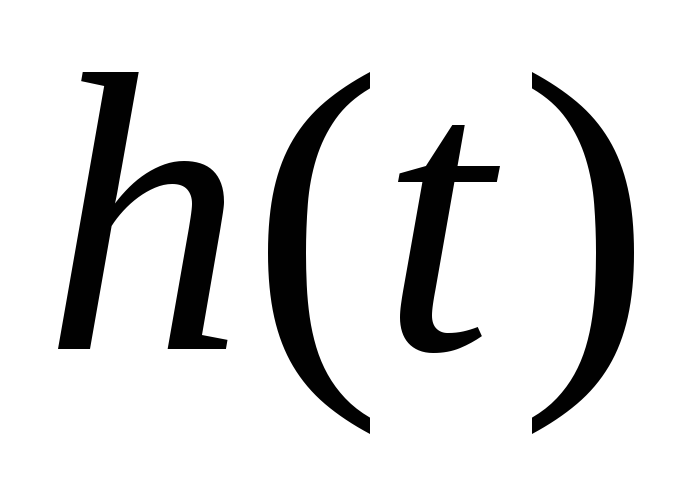 можно определить как оригинал операторного
выражения
можно определить как оригинал операторного
выражения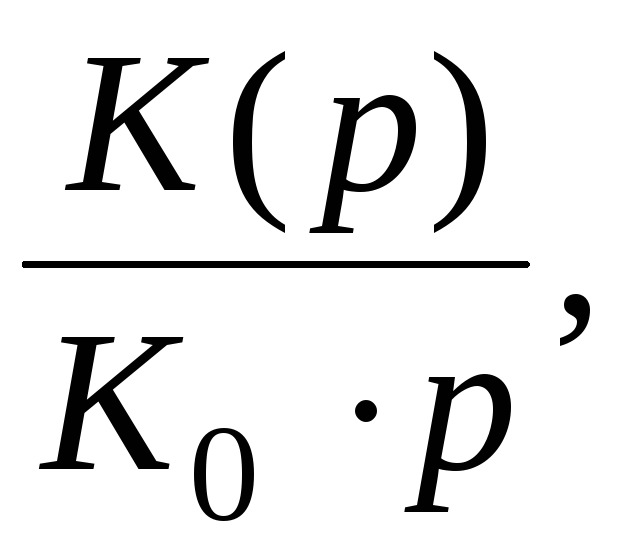 где
где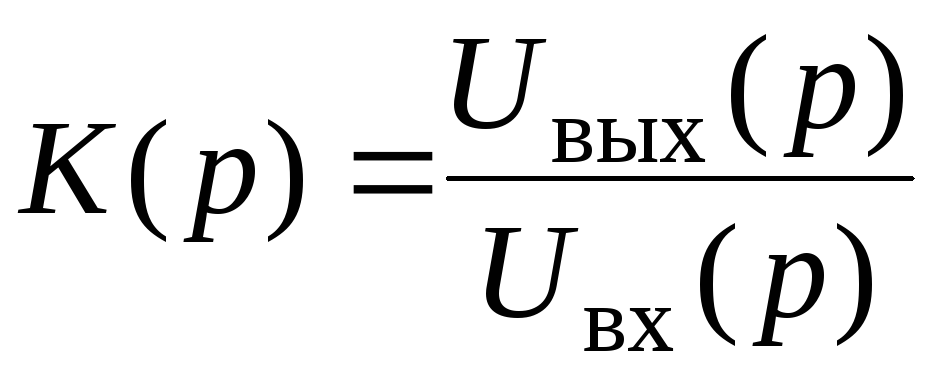 – операторный коэффициент передачи
(передаточная функция усилителя).
Возможный вид переходнойхарактеристики
усилителя приведен
на рис. 1.3.
– операторный коэффициент передачи
(передаточная функция усилителя).
Возможный вид переходнойхарактеристики
усилителя приведен
на рис. 1.3.
Представляют интерес сле-дующие параметры переходной характеристики:
1)
время нарастания фронта 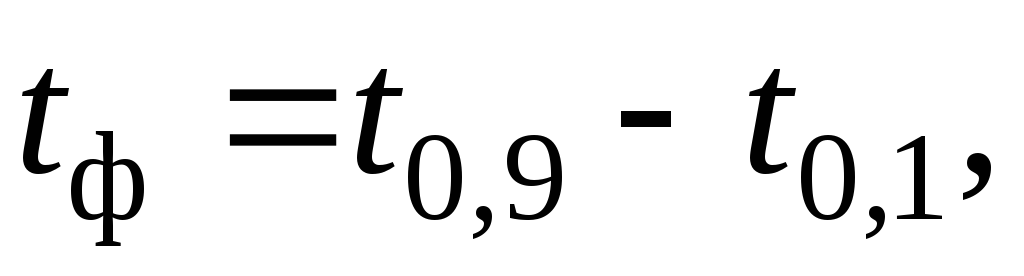 определяемое как время, в течение
которого выходной импульс нарастает
от уровня 0,1 до уровня 0,9 от установившегося
значения
определяемое как время, в течение
которого выходной импульс нарастает
от уровня 0,1 до уровня 0,9 от установившегося
значения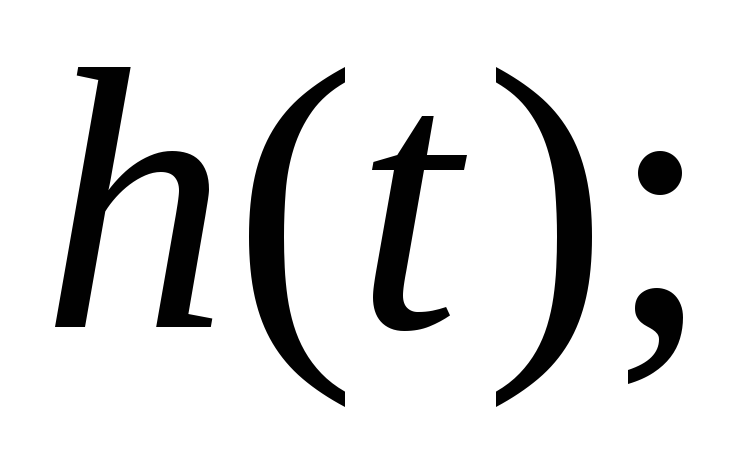
2)
относительный выброс фронта импульса 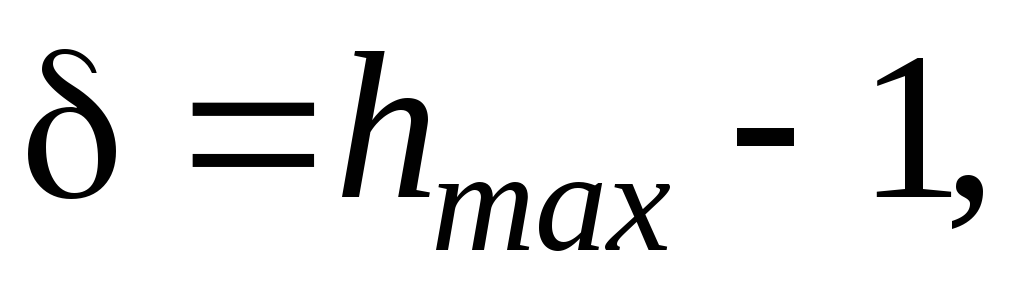 представляющий собой превышение
выходного сигнала над его установившимся
значением;
представляющий собой превышение
выходного сигнала над его установившимся
значением;
3)
относительный спад плоской вершины
выходного импульса 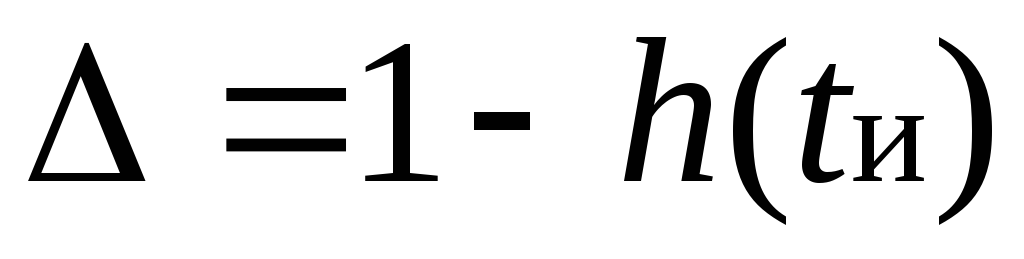 за время действия входного импульса
прямоугольной формы длительностью
за время действия входного импульса
прямоугольной формы длительностью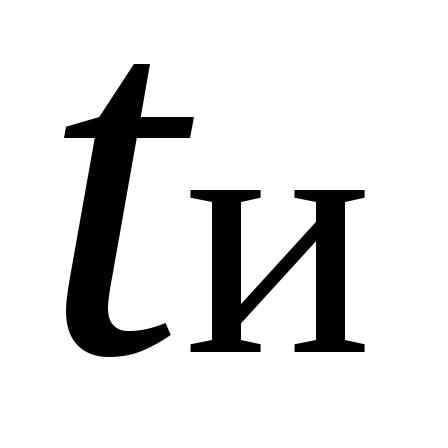 .
.
1.6 Линейные и нелинейные искажения
Хотя усилители должны усиливать сигналы без искажений, в действительности формы входного и выходного колебаний в точности не совпадают. Уровень искажений формы сигналов оценивается коэффициентами искажений. Искажения сигнала разделяют на линейные и нелинейные.
Линейные искажения, вносимые усилителем, обусловлены непостоянством его АЧХ и нелинейностью ФЧХ. Если усилитель не имеет нелинейных искажений и на его вход подан гармонический сигнал, то его выходной сигнал будет чисто гармоническим. Меняются лишь амплитуда и фаза и, следовательно, никаких искажений формы сигнала в таком усилителе не будет. Человеческое ухо нечувствительно к фазовым искажениям, поэтому линейные искажения усилителей звуковых сигналов оцениваются только по АЧХ. Степень неравномерности АЧХ оценивают коэффициентом частотных искажений
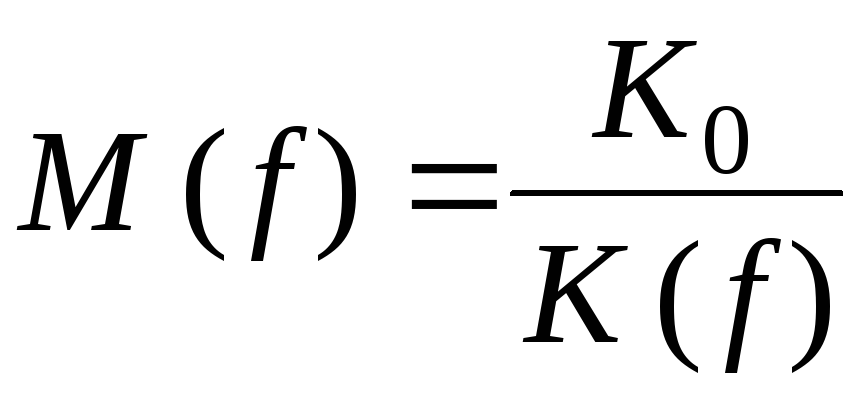 или
или 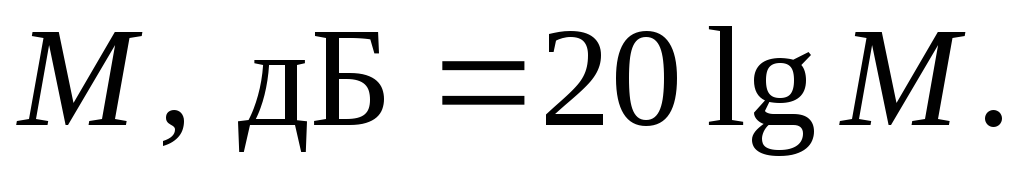
На
граничных частотах полосы пропускания
(упомянутый ранее уровень 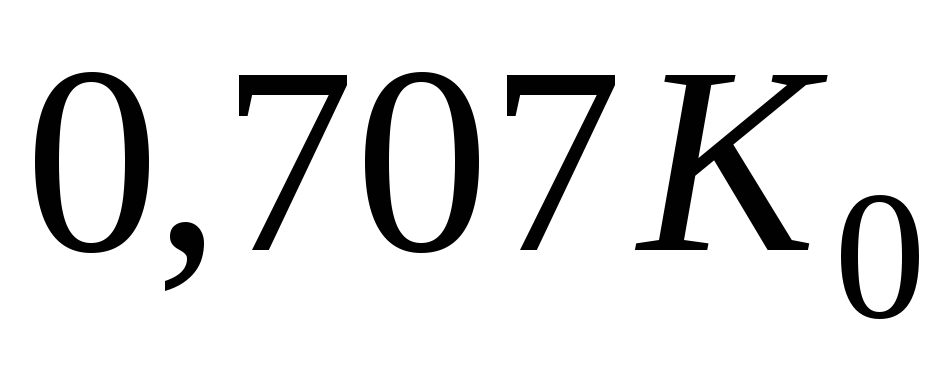 )
коэффициент частотных искажений равен
)
коэффициент частотных искажений равен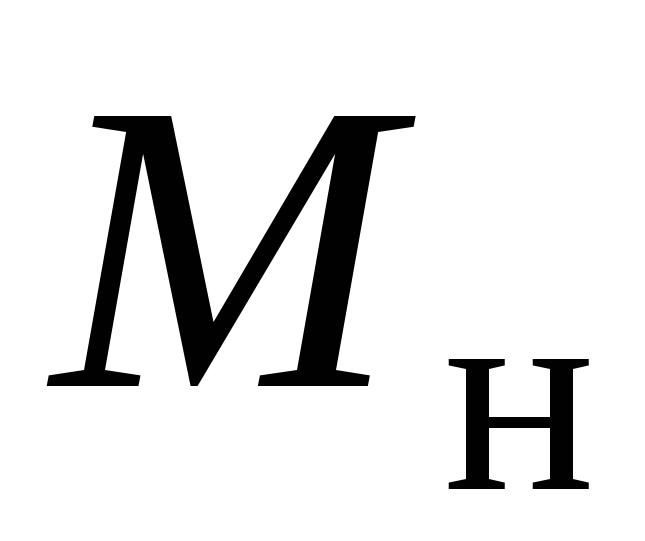
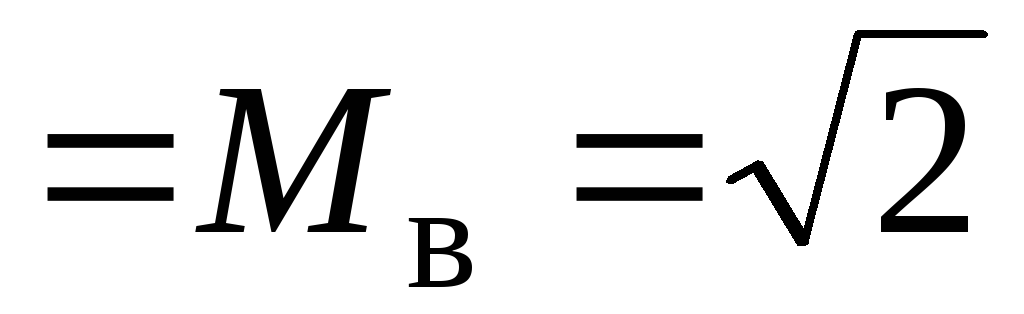 или
или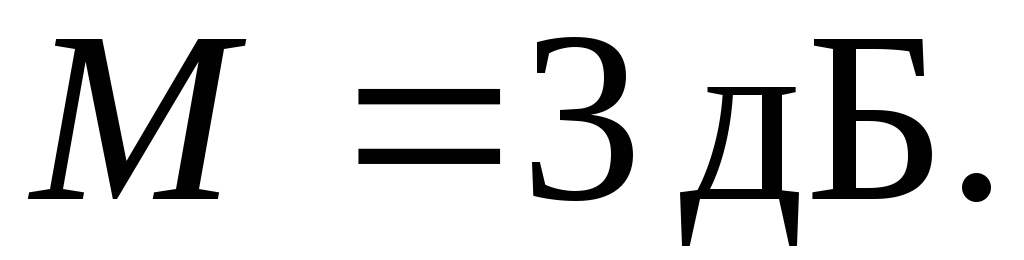
Входной
сигнал сложной формы можно разложить
на гармонические составляющие (с помощью
ряда или интеграла Фурье), определить
сдвиг фазы и изменение амплитуды на
выходе усилителя отдельно каждой
составляющей, а затем сложить их.
Очевидно, что если фазовый сдвиг 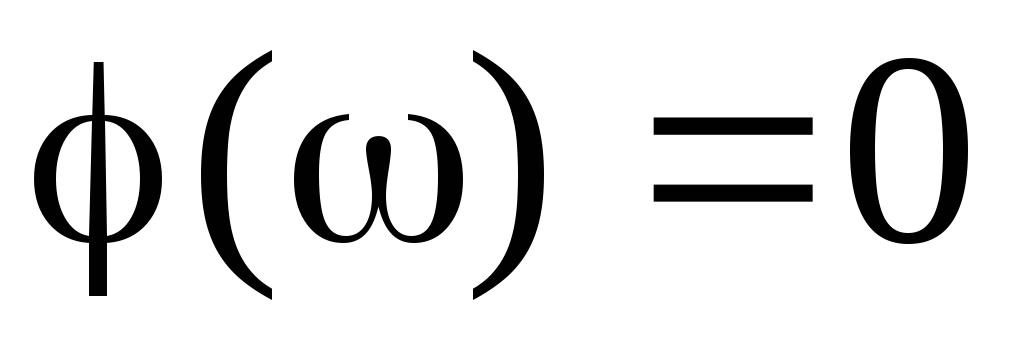 или
или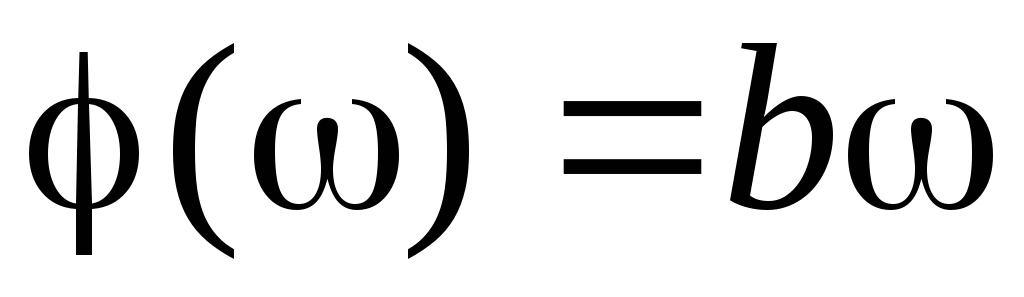 (гдеb=const)
и
(гдеb=const)
и 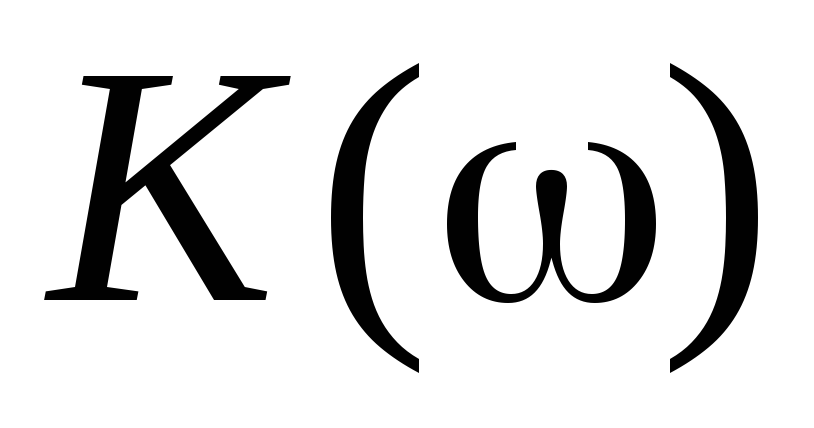 =const,
то форма сложного сигнала останется
неизменной; произойдет лишь его сдвиг
во времени относительно входного сигнала
(еслиb ≠
0). В реальных усилителях
=const,
то форма сложного сигнала останется
неизменной; произойдет лишь его сдвиг
во времени относительно входного сигнала
(еслиb ≠
0). В реальных усилителях 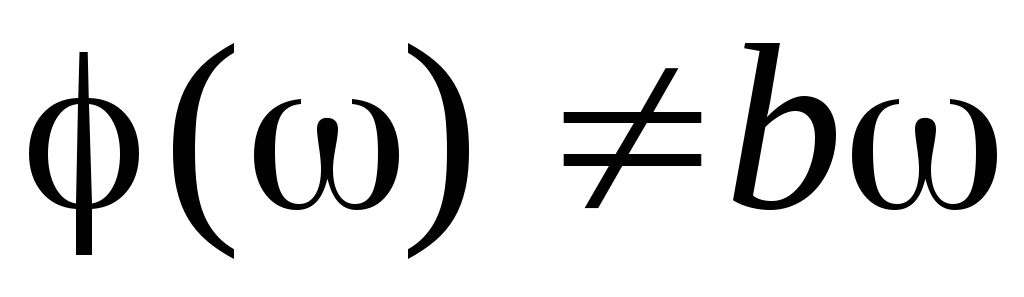 и
и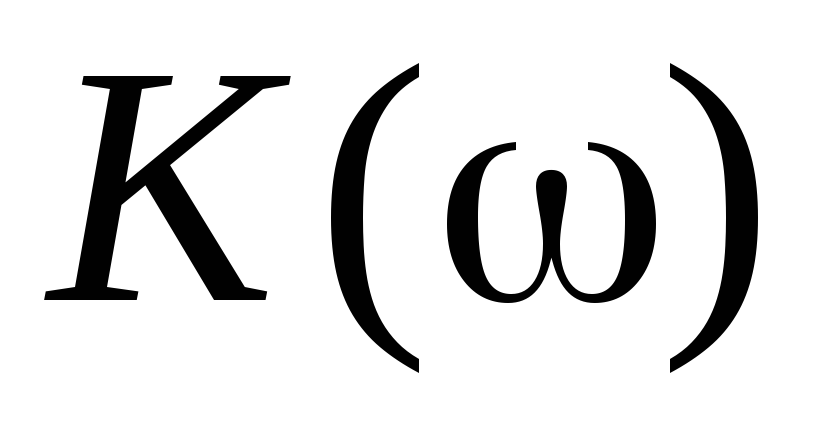 ≠
const, поэтому вследствие сдвига фазы и
изменения амплитуды гармонических
составляющих искажается и форма сложного
сигнала.
≠
const, поэтому вследствие сдвига фазы и
изменения амплитуды гармонических
составляющих искажается и форма сложного
сигнала.
Линейные
искажения, возникающие при усилении
прямоугольных импульсов, оценивают по
переходной характеристике с помощью 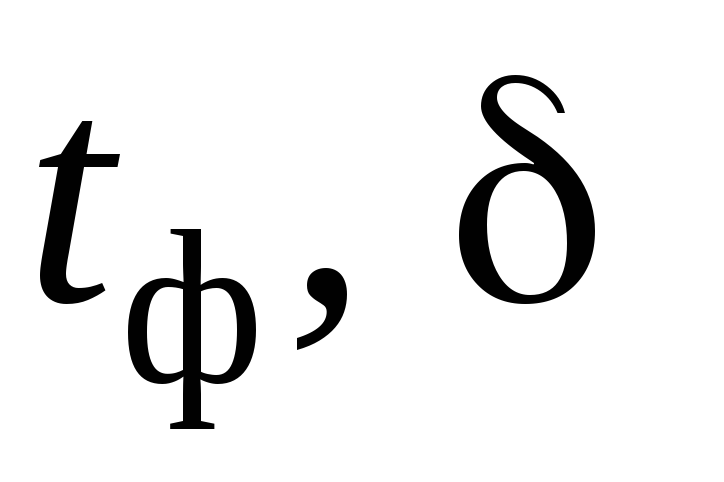 и
и .
.
АЧХ, ФЧХ и переходная характеристика усилителя однозначно связаны друг с другом. Области верхних частот соответствует переходная характеристика в области малых времен. Время нарастания фронта импульса обратно пропорционально верхней граничной частоте и может быть оценено по формуле
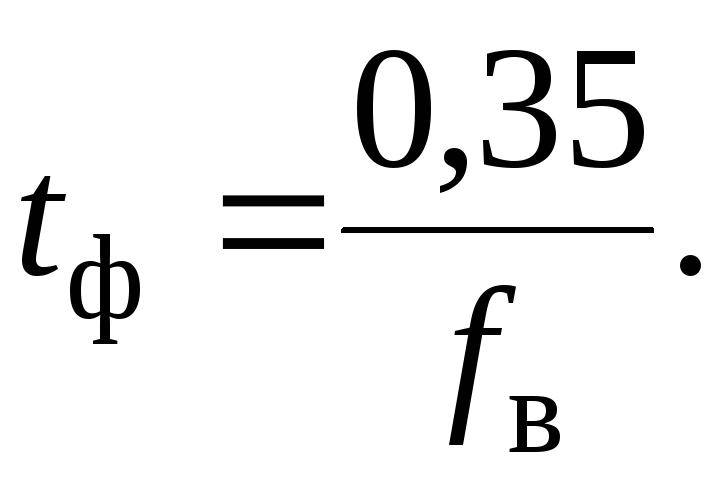
Области
нижних частот соответствует переходная
характеристика в области больших времен.
Спад импульса пропорционален нижней
граничной частоте 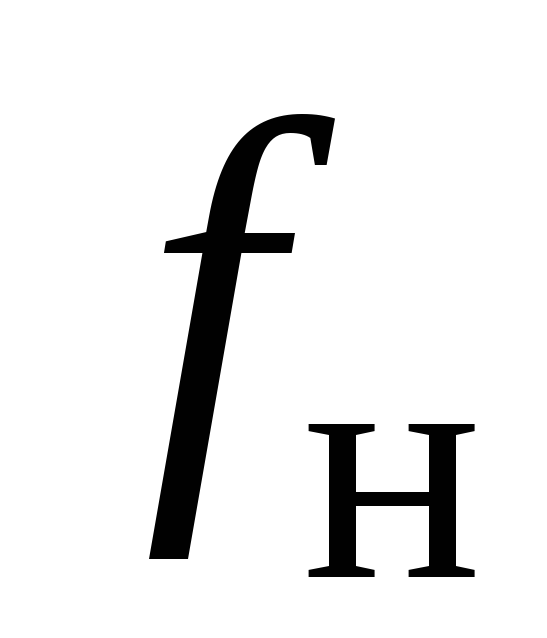 и длительности импульса.
и длительности импульса.
Для
неискаженного усиления импульсных
сигналов усилитель должен обеспечить
равномерное усиление широкого спектра
частот. Чем круче фронт входного сигнала,
тем шире его спектр в области верхних
частот. В этом случае стремятся расширить
полосу пропускания в области верхних
частот, т.е. обеспечить возможно меньшие
искажения в области малых времен. Если
же усиливаемый импульс содержит медленно
изменяющиеся участки, то для более
точного его воспроизведения требуется
расширить полосу пропускания в области
нижних частот (в идеале
иметь 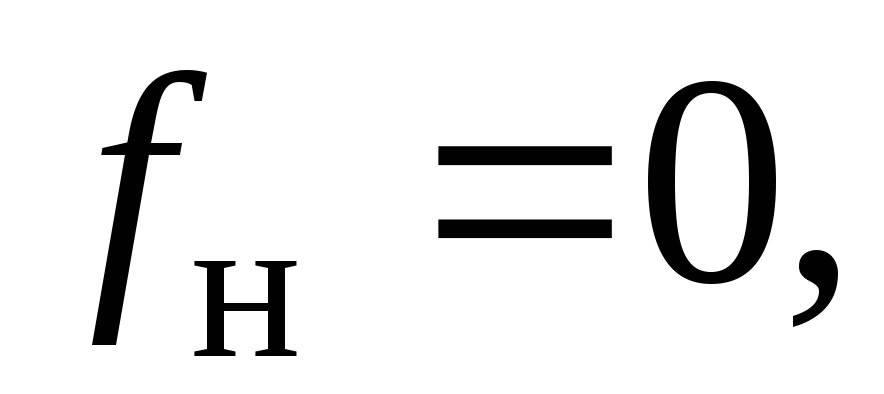 как в УПТ), т.е. уменьшить искажения в
области больших времен. Частотные,
фазовые и переходные искажения относятся
к числу линейных искажений.
как в УПТ), т.е. уменьшить искажения в
области больших времен. Частотные,
фазовые и переходные искажения относятся
к числу линейных искажений.
Если при гармоническом входном сигнале выходной сигнал усилителя по форме отличается от гармонического, то в усилителе имеются нелинейные искажения. Нелинейные искажения обусловлены нелинейностью вольт-амперной характеристики (ВАХ) активных элементов, используемых в усилителе. Нелинейные искажения со спектральной точки зрения – это появление в выходном сигнале усилителя не только усиленного входного сигнала, но и его высших гармоник.
При усилении гармонического сигнала степень нелинейности принято оценивать коэффициентом нелинейных искажений (коэффициентом гармоник)
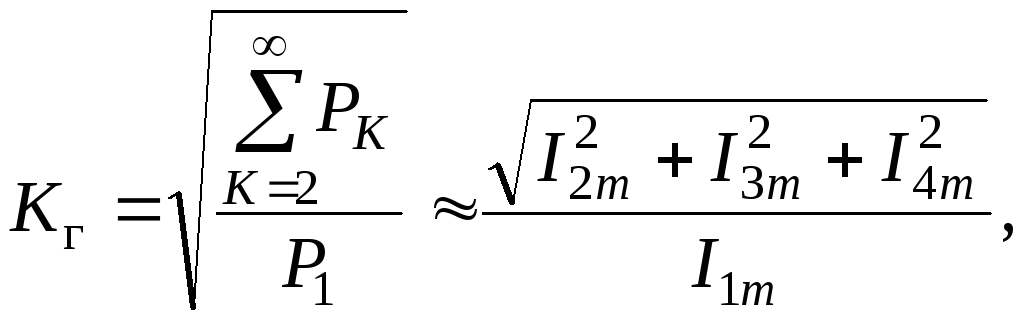 (1.2)
(1.2)
где 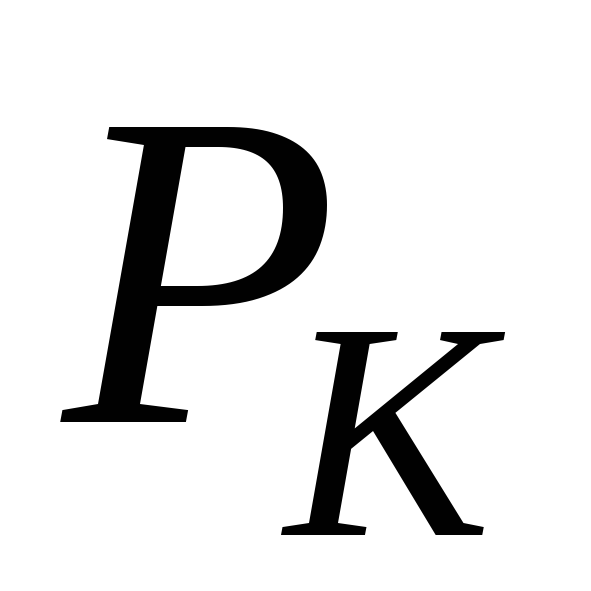
мощность K-й
гармоники выходного сигнала;
мощность K-й
гармоники выходного сигнала;
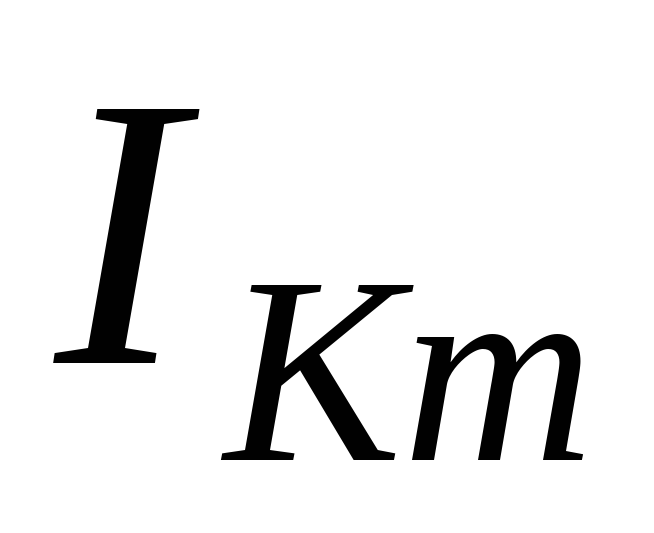
амплитудное
значение K-й
гармоники выходного тока;
амплитудное
значение K-й
гармоники выходного тока;
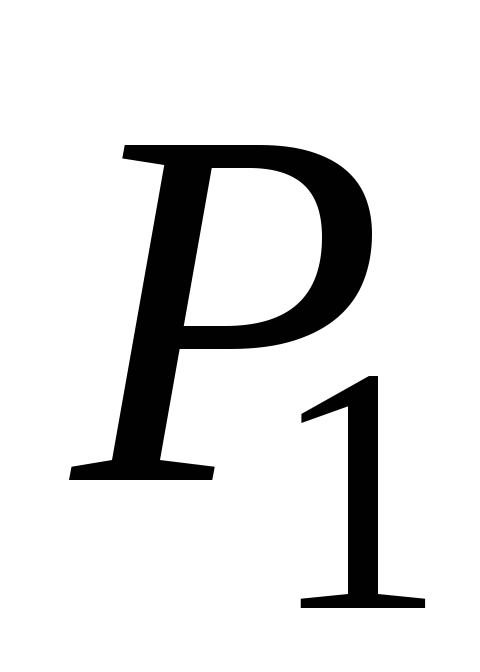 мощность первой
гармоники выходного сигнала;
мощность первой
гармоники выходного сигнала;
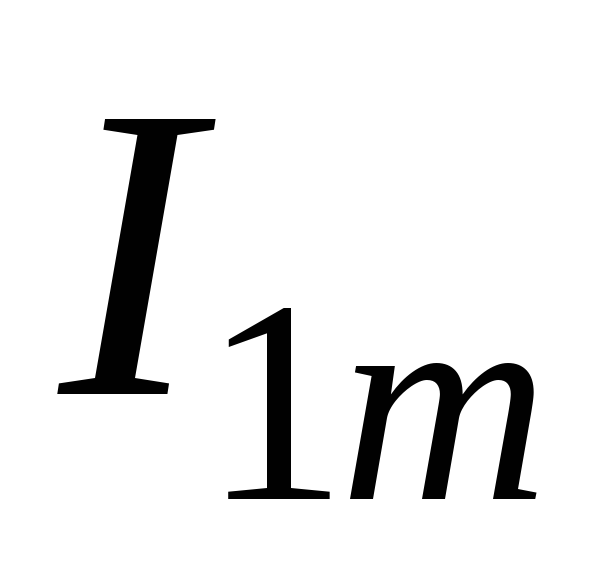 амплитудное
значение первой гармоники выходного
тока.
амплитудное
значение первой гармоники выходного
тока.
Логарифмическая амплитудная частотная характеристика — это… Что такое Логарифмическая амплитудная частотная характеристика?

Логарифмическая амплитудно-фазовая частотная характеристика (ЛАФЧХ) — представление частотного отклика линейной стационарной системы в логарифмическом масштабе.
ЛАФЧХ строится в виде двух графиков: логарифмической амплитудно-частотной характеристики и фазо-частотной характеристики, которые обычно располагаются друг под другом.
Анализ систем с помощью ЛАФЧХ весьма прост и удобен, поэтому находит широкое применение в различных отраслях техники, таких как цифровая обработка сигналов, электротехника и теория управления.
Названия
В западной литературе используется название диаграмма Боде или график Боде, по имени выдающегося инженера Хенрика Боде (англ. Hendrik Wade Bode).
В инженерных кругах название обычно сокращается до ЛАХ.
В пакете прикладных программ для инженерных вычислений bode.
Использование
Свойства и особенности
Если передаточная функция системы является рациональной, тогда ЛАФЧХ может быть аппроксимирована прямыми линиями. Это удобно при рисовании ЛАФЧХ вручную, а также при составлении ЛАФЧХ простых систем.
С помощью ЛАФЧХ удобно проводить синтез систем систем управления, а также цифровых и аналоговых фильтров: в соответствии с определёнными критериями качества строится желаемая ЛАФЧХ, аппроксимированная с помощью прямых линий, которая затем разбивается на ЛАФЧХ отдельных элементарных звеньев, из которых восстанавливается передаточная функция системы (регулятора) или фильтра.
ЛАЧХ
На графике ЛАЧХ абсциссой является частота в логарифмическом масштабе, по оси ординат отложена амплитуда передаточной функции в децибелах.
Представление АЧХ в логарифмическом масштабе упрощает построение характеристик сложных систем, так как позволяет заменить операцию перемножения АЧХ звеньев сложением, что вытекает из свойства логарифма: 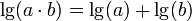 .
.
ФЧХ
На графике фазо-частотной характеристики абсциссой является частота в логарифмическом масштабе, по оси ординат отложен фазовый сдвиг выходного сигнала системы относительно входного (обычно в градусах).
Также возможен вариант, когда по оси ординат откладывается фазовый сдвиг в логарифмическом масштабе, в этом случае характеристика будет называться ЛФЧХ.
Случай минимально-фазовых систем
Амлитуда и фаза системы редко меняются независимо друг от друга — при изменении амплитуды меняется и фаза и наоборот. Для минимально-фазовых систем ЛФЧХ и ЛАЧХ могут быть однозначно определены друг из друга с помощью преобразования Гильберта.
Построение ЛАФЧХ
Основная идея основывается на следующем математическом правиле сложения логарифмов. Если передаточную функцию можно представить в виде дробно-рациональной функции
 ,
,
то:
После разбиения передаточной функции на элементарные звенья можно построить ЛАФЧХ каждого отдельного звена, а результирующую ЛАФЧХ получить простым сложением.
Аппроксимация ЛАЧХ прямыми линиями
При построении ЛАЧХ для оси ординат обычно используется масштаб 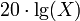 , то есть значение АЧХ, равное 100 превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:
, то есть значение АЧХ, равное 100 превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:
- где
 — комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:
— комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:  ,
,  и
и  — константы, а
— константы, а  — передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:
— передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:
- в каждом
 , где
, где  (нуль), наклон линии увеличивается на
(нуль), наклон линии увеличивается на  дБ на декаду.
дБ на декаду.
- в каждом
- в каждом
 , где
, где  (полюс), наклон линии уменьшается на
(полюс), наклон линии уменьшается на  дБ на декаду.
дБ на декаду.
- в каждом
- Начальное значение графика можно найти простой подстановкой значения круговой частоты
 в передаточную функцию.
в передаточную функцию.
- Начальное значение графика можно найти простой подстановкой значения круговой частоты
- Начальный наклон графика зависит от числа и порядка нулей и полюсов, которые меньше начального значения частоты. Он может быть найден с помощью первых двух правил.
- В случае наличия комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка,
 , наклон менятся в точке
, наклон менятся в точке  сразу на
сразу на  дБ на декаду.
дБ на декаду.
- В случае наличия комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка,
Корректировка аппроксимированной ЛАЧХ
Для корректировки ЛАЧХ, аппроксимированную прямыми линиями надо:
- в каждом нуле поставить точку на
 дБ выше линии (
дБ выше линии ( дБ для двух комплексно-сопряжённых нулей)
дБ для двух комплексно-сопряжённых нулей)
- в каждом нуле поставить точку на
- в каждом полюсе поставить точку на
 дБ ниже линии (
дБ ниже линии ( дБ для двух комплексно-сопряжённых полюсов)
дБ для двух комплексно-сопряжённых полюсов)
- в каждом полюсе поставить точку на
- плавно соединить точки, используя прямые линии в качестве асимптот
Аппроксимация ФЧХ
Для построения аппроксимированной ФЧХ используют запись передаточной функции в том же виде, что и для ЛАЧХ:
Основной принцип построения ФЧХ — начертить отдельные графики для каждого полюса или нуля, затем сложив их. Точная кривая фазо-частотной характеристики задаётся уравнением:
Для того, чтобы нарисовать ФЧХ для каждого полюса или нуля, используют следующие правила:
Анализ устойчивости по ЛАФЧХ
ЛАФЧХ некоторых элементарных звеньев
Ниже представлена таблица, в которую помещены передаточные функции и ЛАФЧХ некоторых типовых элементарных звеньев. Большая часть линейных стационарных систем может быть представлена в виде соединения таких звеньев. В таблице  — комплексная переменная.
— комплексная переменная.
Примечания
См. также
Wikimedia Foundation. 2010.


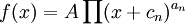 ,
,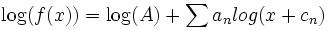
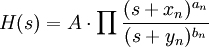
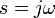 ,
, 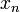 и
и 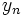 — константы, а
— константы, а 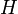 — передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:
— передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила: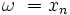 (нуль), наклон линии увеличивается на
(нуль), наклон линии увеличивается на 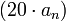 дБ на декаду.
дБ на декаду.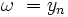 (полюс), наклон линии уменьшается на
(полюс), наклон линии уменьшается на 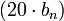 дБ на декаду.
дБ на декаду.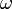 в передаточную функцию.
в передаточную функцию.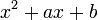 , наклон менятся в точке
, наклон менятся в точке 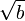 сразу на
сразу на 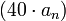 дБ на декаду.
дБ на декаду.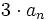 дБ выше линии (
дБ выше линии (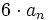 дБ для двух комплексно-сопряжённых нулей)
дБ для двух комплексно-сопряжённых нулей)