Элемент (электрического) тока — определение термина

векторная величина, равная произведению электрического тока проводимости вдоль линейного проводника и бесконечно малого отрезка этого проводника.

Научные статьи на тему «Элемент (электрического) тока»

Электрическая цепь: понятие и основные элементы Электрическая цепь – это совокупность различных объектов…
Вспомогательные элементы электрической цепи….
Все элементы электрической цепи охватываются одним электромагнитным процессом….
значения тока и электродвижущей силы, то такие элементы называют линейными….
новые элементы: конденсаторы, трансформаторы, индуктивные катушки; тем, что переменный ток и напряжение

Статья от экспертов

Процессы, происходящие в ХИТ, подчиняются и описываются законами химии и электрохимии, внешнее поведение ХИТ как элемента электрической цепи описывается и подчиняется законам физики и электротехники.

Процессы, происходящие внутри ХИТ, имеют нелинейный характер (поляризация, скачки потенциалов на границе сред и др.), а процессы, происходящие вне ХИТ, – линейный характер, и подчиняются известным законам Ома, Джоуля–Ленца и другим. Это является основной причиной отсутствия общего математического описания ХИТ как электротехнического устройства. Подавляющее большинство научных работ о ХИТ посвящено исследованию процессов на поверхности и внутри электродов, в электролите, сепараторах и других частях ХИТ и истолкованию его внешнего поведения, т. е. измерению и расчету напряжения и электрического тока. Описание системами уравнений внешнего поведения ХИТ как элемента электрической цепи и классификация ХИТ по четырем группам по виду общего уравнения разряда и другие положения оказались плодот…

Creative Commons

Научный журнал

элементов и устройств, которые предназначены для протекания электрического тока. …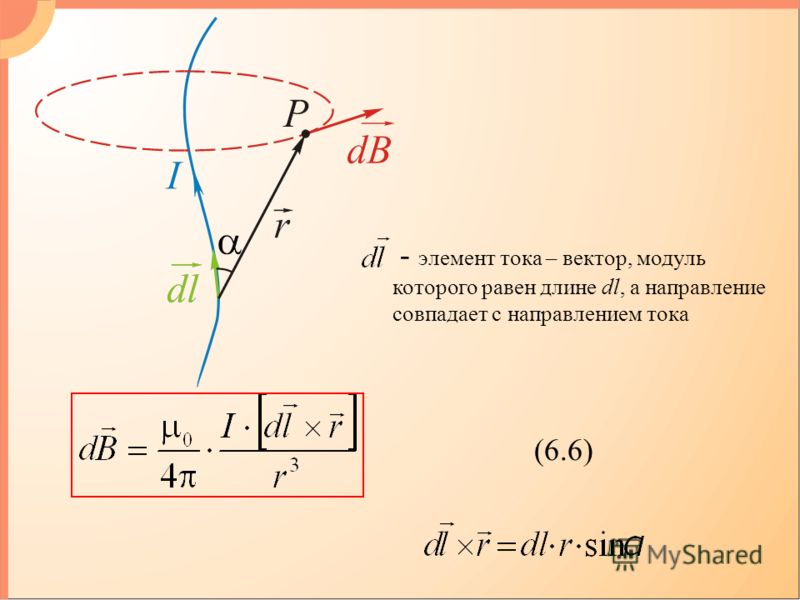
К линейным электрическим цепям относятся такие цепи, которые содержать линейные элементы, то есть

элементы…
Род электрического тока….
Согласно данному признаку электрические цепи делятся на цепи переменного и постоянного тока….
ток.

Статья от экспертов

Предлагается способ выявления элемента с пониженным сопротивлением изоляции в разветвленной сети постоянного оперативного тока электростанций и подстанций, основанный на изменении фазы тока в поврежденном присоединении за счет появления активной составляющей проводимости при появлении тока утечки. Для этого предлагается применить одновременное наложение на сеть синусоидального контрольного тока и импульсов тока высокой частоты, синхронизированных с моментом перехода через ноль напряжения синусоидального сигнала на полюсах сети.

Creative Commons

Научный журнал

Повышай знания с онлайн-тренажером от Автор24!

1. Напиши термин
2. Выбери определение из предложенных или загрузи свое
3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных карточек

Закон Био–Савара • Джеймс Трефил, энциклопедия «Двести законов мироздания»

200 законов мироздания > Физика

Магнитное поле в точке пространства, создаваемое малым отрезком проводника, по которому течет электрический ток, пропорционально силе тока, обратно пропорционально квадрату расстояния от этой точки до проводника и направлено перпендикулярно по отношению и к току, и к направлению на проводник.

Одним из величайших прорывов в естествознании XIX века стала серия открытий, позволивших установить неразрывную связь между двумя, казалось бы, не связанными между собой природными феноменами — электричеством и магнетизмом, — которые на поверку оказались просто двумя сторонами одной медали. Одним из первых фрагментов пазла, который предстояло собрать ученым, стало осознание того, что движущиеся электрические заряды (то есть электрический ток) могут порождать магнитное поле. Это открытие сделал датский ученый Ханс Кристиан Эрстед (

см. открытие Эрстеда), а представил его в количественной форме французский ученый Андре-Мари Ампер (см. Закон Ампера). Обобщением этой работы стал закон Био—Савара (его еще называют «закон Био—Савара—Лапласа». — Прим. переводчика), содержащий окончательную формулировку соотношения между электрическими токами и магнитными полями, которые они производят.

Жан Батист Био, яркий и смелый ученый, был профессором физики в Сорбонне и действительным членом французской Академии наук.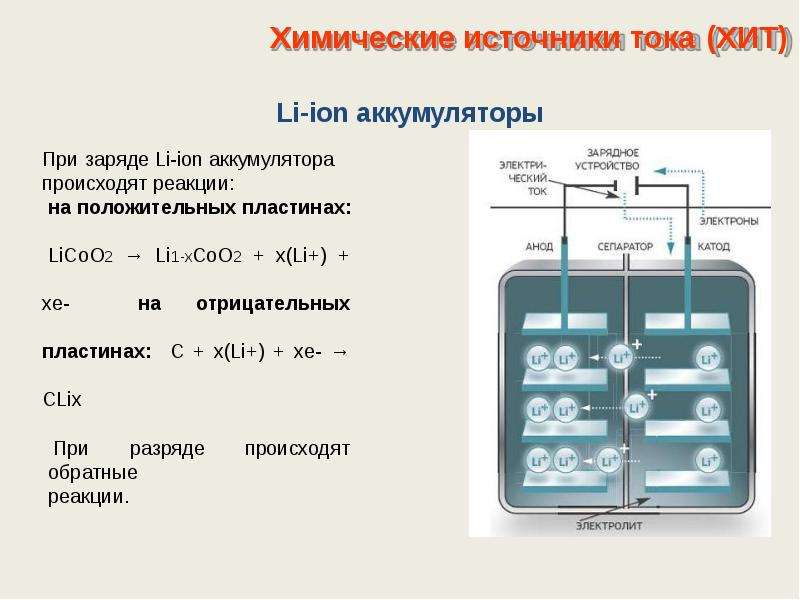

Сразу после открытия Эрстеда вместе со своим коллегой Феликсом Саваром он принялся за изучение взаимосвязи между электрическим током и магнитными полями.

В отличие от Ампера, изучавшего магнитные поля опосредованно, путем измерения силы взаимодействия между парами проводников с током, Био и Савар предприняли прямые измерения магнитных полей, используя для этого множество легких магнитных стрелок компасов. Смысл их закона проще всего понять, если представить себе, что проводник с током разбит на крошечные отрезки — т. н. элементы тока

(такой подход предложил ученым их старший коллега Пьер Симон Лаплас (Pierre-Simon Laplace, 1749–1827), стоявший у истоков дифференциального и интегрального исчисления, который затем и обобщил полученные результаты. — Прим. переводчика). На каждом из этих крошечных отрезков кривизной проводника можно пренебречь — их можно рассматривать как отрезки прямой. Так вот, согласно закону Био—Савара, магнитное поле В на расстоянии r от такого элемента тока пропорционально

IL/r²

где I — сила тока, а L — длина элемента тока.

Я уже упоминал, что закон Био—Савара является наиболее полным формальным обобщением взаимосвязи между электрическим током и магнитным полем. Это значит, что можно взять проводник с током сколь угодно сложной и асимметричной конфигурации и разбить его на элементы тока. Каждый элемент вносит свой вклад в магнитное поле в рассчитываемой точке. Сделав эти расчеты, мы можем затем просуммировать вклад от каждого элемента проводника и найти общее магнитное поле (этот процесс суммирования относится к области высшей математики и выглядит он достаточно сложно). Таким образом, закон Ампера является частным случаем закона Био—Савара для случая линейного проводника.

Я еще не сказал, что закон Био—Савара предсказывает также направление получающегося магнитного поля. Это направление можно определить с помощью так называемого

правила правой руки, ставшего настоящим бичом целых поколений студентов физических и технических вузов. Правило гласит: если вытянутый указательный палец правой руки показывает направление электрического тока в элементе тока, а средний палец направлен на точку, в которой вы вычисляете магнитное поле, то выставленный под прямым углом к двум другим пальцам большой палец укажет направление магнитного поля.

Как я уже говорил, полное математическое выражение закона Био—Савара требует довольно сложных вычислений, поскольку оно представляет собой интегральное уравнение. Оно является, по сути, общим решением четвертого

уравнения Максвелла.

См. также:

1864	Уравнения Максвелла
1879	Эффект Холла

Феликс САВАР
Félix Savart, 1791–1841

Французский врач и физик. Родился в Мезьере. Получив медицинское образование, Савар, тем не менее, поступил на работу в Коллеж де Франс в качестве профессора акустики. Там он изучал принцип работы музыкальных инструментов, прежде всего скрипки, на примере колебаний песчаных волн в слое песка на плоской поверхности, отражающих акустические колебания. Кроме того, он изобрел

колесо Савара для точного измерения высоты музыкальных тонов и кварцевую пластину Савара для изучения поляризации света. Однако самая известная работа ученого — его сотрудничество с Био, вылившееся в закон Био—Савара.

---

Жан Батист БИО
Jean-Baptiste Biot, 1774–1862

Французский физик. Родился в Париже, вырос в годы Великой французской революции и до начала занятий физикой успел отслужить в армии. Затем стал одним из первых студентов только что открытой Парижской политехнической школы, по окончании которой продолжал заниматься академической наукой, со временем заняв должность профессора физики в Коллеж де Франс в Париже. В 1803 году был командирован Министерством внутренних дел для расследования обстоятельств метеоритного дождя в городок Эгль. Ему впервые удалось доказать, что метеориты имеют внеземное происхождение и в буквальном смысле падают к нам с неба (в то время в это практически не верили). На следующий год Био вместе с Жозефом Луи Гей-Люссаком (Joseph-Louis Gay-Lussac, 1778–1850) впервые в истории поднялся в воздух на воздушном шаре в научно-исследовательских целях — для изучения характеристик магнитного поля Земли на больших высотах.

2/R

Ответить

Написать комментарий

---

1785	Закон Кулона
1820	Открытие Эрстеда
1820	Закон Ампера
1820	Закон Био—Савара
1831	Законы электромагнитной индукции Фарадея
1833	Правило Ленца

---

1662

Закон Бойля—Мариотта

III в. до н. э.

Закон Архимеда

Новостная рассылка  

«Элементы» в соцсетях: 

электромагнетизм — Каково точное определение *направления* тока и элемента тока для проводника?

спросил 1 год, 2 месяца назад

Изменено 1 год, 2 месяца назад

Просмотрено 165 раз

$\begingroup$

Закон Био–Савара гласит, что магнитное поле, создаваемое элементарной цилиндрической системой, через которую проходит постоянный ток $I$ в точке на расстоянии $r$, определяется выражением $$d\vec{B}=\frac{ \mu_o}{4\pi}\frac{Id\vec{s}\times \vec{r}}{r^2}. $$ $\mu_o$ — константа, а произведение $Id\vec{s}$ называется текущим элементом, но что такое $d\vec{s}$? Это вектор, величина которого равна длине элемента в направлении тока, протекающего через него. Направление тока определяется как направление движения положительных зарядов. Но факт, что в проводнике заряды сталкиваются друг с другом и атомными решетками. Поэтому нелепо слишком серьезно относиться к определению направления тока 9 .0013 минимум для жил . Следовательно, когда мы говорим, что направление тока в проводнике является таким, мы имеем в виду, что положительные заряды имеют тенденцию двигаться в этом направлении. Таким образом, направление тока, как определено, слишком расплывчато, по крайней мере, для проводников , чтобы его можно было использовать для определения вектора, подобного $d\vec{s}$. Но ни в одной книге или статье этот вопрос не поднимается и не обсуждается, поэтому я спрашиваю его здесь.

• электромагнетизм
• электростатика
• магнитные поля
• электрические поля
• электрические токи

$\endgroup$

3

$\begingroup$

Переменные, такие как магнитное поле $\vec B$, ток $I$ и связанное с ним направление $\vec{ds}$ являются макроскопическими величинами . Это означает, что они усредняются по объему, который намного больше, чем элементы, составляющие систему. См. понятие термодинамического предела для строгого определения между макроскопическими и микроскопическими величинами.

В вашем конкретном вопросе ток $I$ в законе Био-Савара усредняется как по времени, так и по пространству, что устраняет необходимость учитывать тонкое движение отдельных протонов или электронов. Цитата Джексона:

До сих пор мы рассматривали электромагнитные поля и источники в вакууме. Уравнения Максвелла (I.1b) для электрического и магнитного полей E и B могут быть рассматривать как уравнения, описывающие поля повсюду в пространстве, при условии, что все указаны источники p и J. Для небольшого числа определенных источников, определяющих нация полей — разрешимая проблема; но для макроскопических агрегатов вещества, решение уравнений практически невозможно. Есть два аспекта здесь. Во-первых, количество отдельных источников, заряженных частиц в каждом атома и ядра непомерно велик. Другой аспект заключается в том, что для макроскопических наблюдения подробное поведение полей, с их резкими изменениями в пространство над атомными расстояниями не имеет значения. Что имеет значение, так это среднее значение поле или источник над объемом большим по сравнению с объемом, занимаемым отдельного атома или молекулы. Мы называем такие усредненные величины макроскопическими полями и макроскопические источники. В разделе 6.6 подробно показано, что макроскопическая Уравнения Максвелла имеют вид (I.1а), где Е и В — усредненные значения Е и В микроскопический или вакуумный Maxwell

— Классическая электродинамика , JD Jackson 1999, pg 13.

Бывают ситуации, когда вы не можете игнорировать эти микроскопические колебания. Например, в очень чувствительных электрических цепях. См. пример теплового шума в электрических цепях.

$\endgroup$

$\begingroup$

Нормальный проводник является (близким приближением) омическим, т. е. подчиняется закону Ома. плотность тока направлена ​​и пропорциональна электрическое поле. Решение для внутреннего поля фасонный проводник (например, изогнутая проволока или отрезок листового металл) менее знакомая проблема, чем внешнее поле в статическом электричестве, но это можно сделать.

Хаотическая природа столкновений электронов проводимости при комнатной температуре вносит большой вклад в закон Ома, и определяет проводимость. Однако при большом количестве полезных носителей тока нет необходимости рассматривать отдельные электроны или столкновения. Средние движения жидкости подвижных электронов равны все, что мы считаем.

$\endgroup$

5

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Закон Био-Савара — заявление, формула, примеры, приложения, важность, видео, решенные проблемы и часто задаваемые вопросы

Мы знаем, что электромагнетизм — важная область физики, которая имеет дело с электромагнитной силой. Обычно он имеет дело с магнитной силой и электрическим током. Расскажите о законе, связывающем магнитные поля с электрическим током – законе Био-Савара.

Содержание Что такое Закон Био-Савара? Что представляет собой формула закона Био-Савара? Применение закона Био-Савара Важность закона Био-Савара Решенные задачи по закону Био-Савара Часто задаваемые вопросы – Часто задаваемые вопросы

Что такое закон Био-Савара?

Закон Био-Савара представляет собой уравнение, определяющее магнитное поле, создаваемое сегментом с током. Этот сегмент принимается за векторную величину, известную как текущий элемент.

Что такое формула закона Био-Савара?

Рассмотрим проводник с током «i» в определенном направлении, как показано на рисунке выше. Возьмите небольшой отрезок проволоки длиной ds. Направление этого элемента совпадает с направлением тока, так что он образует вектор ids.

Чтобы узнать магнитное поле, создаваемое в точке благодаря этому маленькому элементу, можно применить закон Био-Савара. Пусть вектор положения рассматриваемой точки, взятый из текущего элемента, равен 92})\конец{массив} \)

Где μ ₀ — проницаемость свободного пространства, равная 4π × 10 ^-7 TmA ^-1 .

Направление магнитного поля всегда находится в плоскости, перпендикулярной линии элемента и вектора положения. Это дается правилом большого пальца правой руки, где большой палец указывает направление обычного тока, а остальные пальцы показывают направление магнитного поля.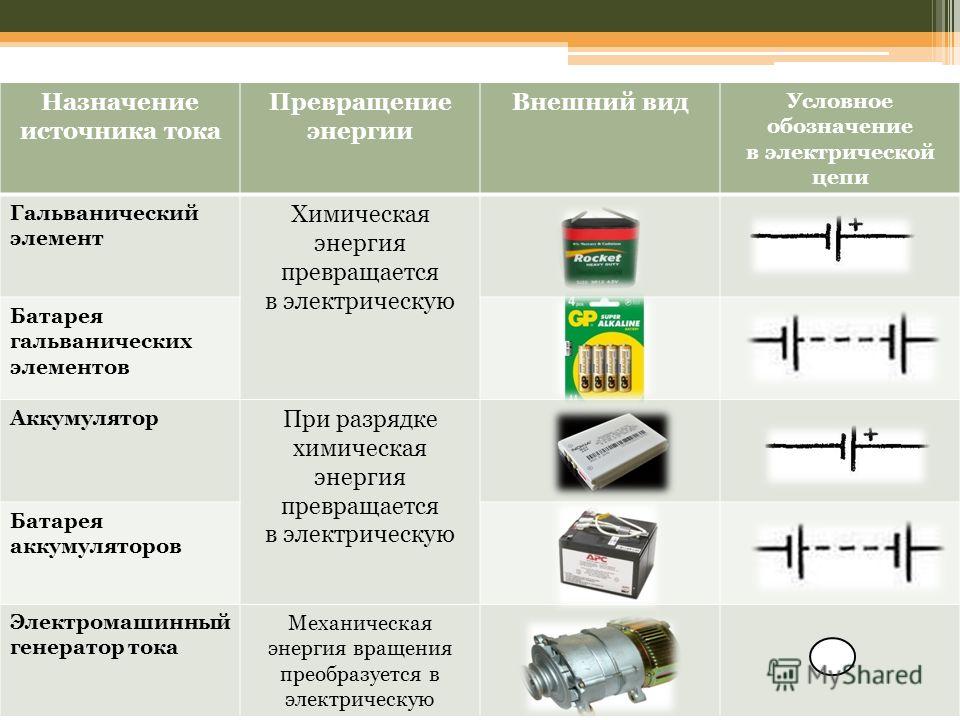

На рисунке выше направление магнитного поля указывает на страницу.

Применение закона Био-Савара

Ниже приведены некоторые приложения закона Био-Савара.

• Мы можем использовать закон Био-Савара для расчета магнитных откликов даже на атомном или молекулярном уровне.
• Он также используется в аэродинамической теории для расчета скорости, создаваемой вихревыми линиями.

Важность закона Био-Савара

Ниже приведены значения закона Био-Савара:

• Закон Био-Савара подобен закону Кулона в электростатике.
• Закон применим и к очень маленьким проводникам, по которым течет ток.
• Закон применим для симметричного распределения тока.

Ускорьте подготовку к основному и расширенному экзамену JEE с помощью

Просмотрите это видео о магнетизме и силе, действующей на диэлектрик в заряженном конденсаторе

Решенные задачи по закону Био-Савара

Q1. Определить величину магнитного поля проволочной петли в центре окружности радиусом Р  и текущий  I.

Ответ: Величина магнитного поля проволочной петли определяется как:

\(\begin{array}{l}\frac{\mu _{0}I}{2R}\end{array} \)

Q2. По круглой катушке радиусом 5 × 10 90 150 -2 90 151 м и 40 виткам течет ток силой 0,25 А. Определить магнитное поле круглой катушки в центре.

Ответ:  Радиус круглой катушки = 5 × 10 9{-2}м}\конец{массив} \)

= 1,2 × 10 ^-4 Т

Q3. Определить магнитное поле в центре полукруглого отрезка проволоки радиусом 0,20 м. Ток, переносимый полукруглым отрезком провода, составляет 150 А.

Ответ: Радиус полукруглого отрезка проволоки = 0,20 м

Ток, переносимый полукруглым отрезком провода = 150 А

Магнитное поле задается как: 

\(\begin{array}{l}B=\frac{\mu _{0}NI}{2a}\end{array} \) 9{2}}\end{array} \)

, что соответствует закону Кулона.

Назовите одно свойство, которое нельзя рассчитать по закону Био-Савара.

Напряженность электрического поля нельзя рассчитать по закону Био-Савара. Он используется для расчета напряженности магнитного поля. Далее это используется для расчета плотности потока и проницаемости по формуле

\(\begin{array}{l}B=\mu H\end{array} \)

.

Рассмотрим круглый проводник радиусом 2 м, по которому течет ток 8 А. Определить напряженность магнитного поля в центре круглого проводника. 9{-7}T\конец{массив} \)

.

Чему равно магнитное поле в центре проводника, когда в проводнике протекает ток силой 9 А и с бесконечным радиусом?

Для расчета магнитного поля используется следующая формула:

\(\begin{array}{l}\frac{\mu _{0}I}{2R}\end{array} \)

Поскольку R бесконечно , магнитное поле будет равно 0.