Измерение действующих значений | Видео

Cмотри подробную информацию (описание, характеристики, cхемы и др.):

• НПСИ-ДНТВ нормирующий измерительный преобразователь действующих значений напряжения (до 500 В) и тока с сигнализацией
• НПСИ-ДНТН нормирующий измерительный преобразователь действующих значений напряжения (до 50 В) и тока с сигнализацией
• НПСИ-200-ДН, НПСИ-200-ДТ нормирующие преобразователи действующих значений напряжения и тока
• НПСИ-МС1 преобразователь мощности, действующих значений напряжения и тока, коэффициента мощности нагрузки пром. сети
• НПСИ-500-МС1 измерительный преобразователь параметров однофазной сети с интерфейсами RS-485 и USB
• НПСИ-500-МС3 измерительный преобразователь параметров трёхфазной сети с интерфейсами RS-485 и USB

Добрый день, уважаемые коллеги!

Задача измерения действующих значений  тока и напряжения в электрической сети очень распространена. Научно-производственная фирма “КонтрАвт” предлагает целый ряд измерительных преобразователей, которые позволяют производить эти измерения и преобразовывать измеренные значения в унифицированные сигналы. 

В конце видео мы приведем  перечень таких преобразователей. А сейчас мы сосредоточимся на обсуждении  ряда вопросов,  связанных с измерением этих величин.

Несмотря на распространенность и “привычность” этих параметров,  результат измерения сильно зависит от применяемого метода измерения,  а главное, от того, насколько этот метод соответствует  особенностям  измеряемых сигналов. 

Попробуем  в этом разобраться. 

Мы начнем с определения.

Определение действующих значений. 

Обсудим простейшие методы измерения действующих значений гармонических сигналов.

Основное внимание уделим методам измерения негармонических сигналов, которые реализованы в преобразователях НПФ “КонтрАвт” и укажем те факторы, которые влияют на точность измерения.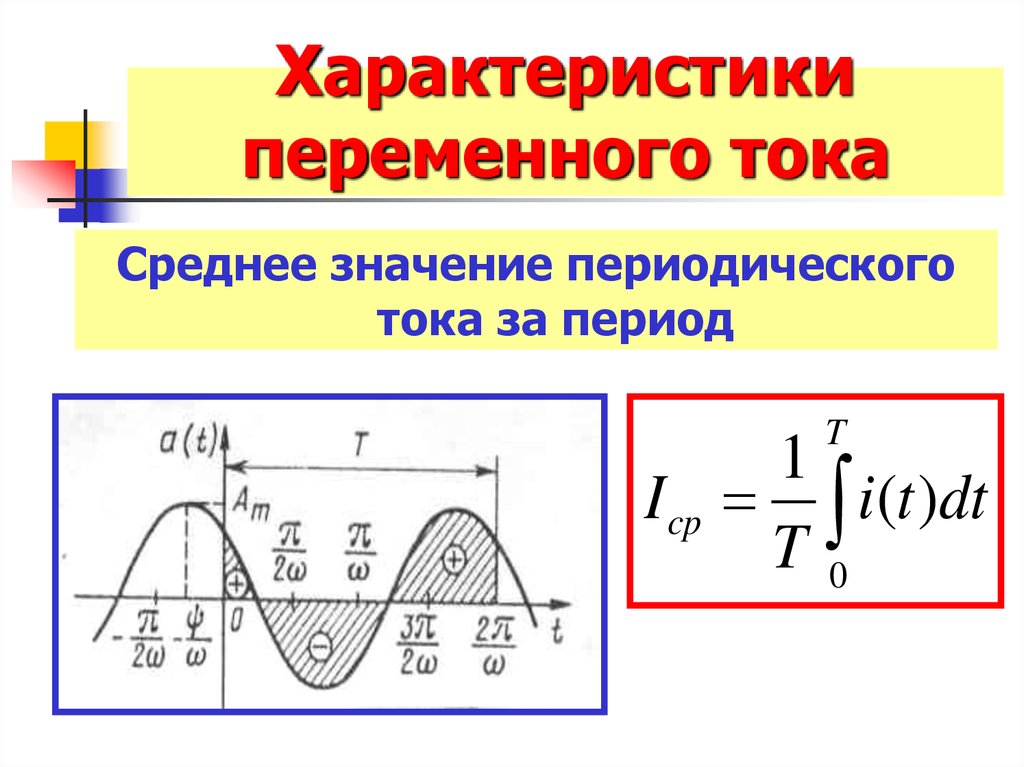

“Гармонические сигналы”

Когда говорят о сигнале в сети переменного тока 50 Гц, то обычно имеют в виду гармонический (синусоидальный) сигнал. (график гармонического сигнала) Это идеальный случай.

 

 

Само значение переменного сигнала редко представляет самостоятельный интерес на практике. Более интересным оказывается измерение некоторых определенных характеристик переменных сигналов, дающих представление о сигнале в целом. 

“Действующее значение”

Одним из таких обобщенных параметров, описывающим энергетические свойства переменного сигнала, его способность совершать работу, является “действующее значение сигнала” или по другому ”среднеквадратичное значение”.

 

Графики наглядно показывают, что измерительные преобразователи измеряют  и преобразуют не сам сигнал, а  характеризующий его параметр — действующее значение.

 

Дадим  математическое  определение.

Действующее значение есть квадратный корень  из среднего значения квадрата сигнала. Усреднение проводится по времени за период переменного сигнала Т:

 

       

где — мгновенные значения напряжения и тока. 

Физический смысл действующего значения напряжения заключается в том, что оно соответствует такому постоянному напряжению, которое выделяет на активной нагрузке такое же тепло. Поэтому применяется еще термин «эффективное» значение. Таким образом, действующее значение позволяет сравнивать с энергетической точки зрения переменный сигнал с постоянным. 

 “Для гармонических сигналов“

 

Мы дали математическое определение  и выяснили физический смысл действующего значения.  

Рассмотрим теперь  метод его измерения  в частном случае гармонического (синусоидального ) сигнала. 

Действующие значения напряжения Uд и тока Iд для гармонического (синусоидального) сигнала можно математически рассчитать и установить связь  с амплитудами Um и  Im:

.

Отсюда сразу следует метод измерения действующего значение путем измерения амплитуды. 

Второй метод — измерение через средневыпрямленное значение. 

Средневыпрямленное значение — это среднее значение модуля сигнала:

     

Средневыпрямленные значения для гармонического сигнала выражаются через  их амплитуды следующими соотношениями:

Как видим, среднеквадратичные и средневыпрямленные значения линейно связаны между собой: 

Метод измерения действующего значения на основе средневыпрямленного весьма распространен, прежде всего, потому, что его реализация аналоговыми схемотехническими решениями достаточна проста.

“Несинусоидальные сигналы”

Недостаток этих двух методов измерения заключается в том, что они применимы  только для синусоидального  сигнала. На практике сигналы тока и  напряжения могут сильно  отличаться от  правильной синусоидальной формы.

Поэтому попытка измерения среднеквадратичного  значения негармонических сигналов с  помощью выпрямительных приборов приводит к большим погрешностям измерения. 

Почему форма  напряжения и тока в сети может отличаться от синусоидальной? 

Основная причина — применение нелинейных устройств в качестве нагрузки или управляющих элементов. На  графиках приведены эпюры напряжения для тиристорного регулятора, однополупериодного и двухполупериодного выпрямителей.

Это значит, что для измерения действующих значений  сигналов несинусоидальной формы необходимо применять методы измерений, позволяющие вычислять значения непосредственно по  формулам.

       

Про такие методы измерения говорят TRUE RMS.

Большую помощь в этом оказывают цифровые методы измерения  и обработки сигналов. Они позволяют проводить измерение действующих значений с высокой точностью и для сигналов несинусоидальной формы. 

Однако, и в этом случае есть некоторые особенности измерения, которые надо учитывать.   

Проблемы две и обе они вытекают из формулы для действующих значений:

1. Первая — это погрешности, связанные с численным интегрированием с конечным шагом дискретизации сигнала, особенно при наличии высших гармоник.
2. Вторая — частота в сети на практике может не совпадать с периодом усреднения

Рассмотрим как эти две проблемы решаются в измерительных преобразователях действующих значений напряжения и тока серии НПСИ, выпускаемых НПФ “КонтрАвт”

 “Особенности измерения ”

Итак первая проблема: Влияние  частоты дискретизации на точность вычисления интеграла.

Как мы говорили ранее, практический интерес представляет ситуация, когда измеряется действующее значение  напряжения (тока) сети  частотой 50 Гц, но форма сигнала не является чисто гармонической (синусоидальной).  Это означает в спектре сетевого напряжения будут присутствовать высшие гармоники, кратные 50 Гц.  

При цифровом интегрировании непрерывный интеграл заменяется суммой дискретных отсчетов, при этом точность интегрирования напрямую зависит от периода дискретизации Δt.

 

В преобразователях НПСИ частота дискретизации составляет 10 кГц, а усреднение   производится на 4 периодах сетевого напряжения, то есть на интервале 80 мс.

При частоте дискретизации 10 кГц,  максимально допустимая  гармоника в спектре сетевого напряжения будет 20-ая, с частотой 1000 Гц. Для более высоких не хватает частоты дискретизации. 

При измерении действующих значений синусоидальных сигналов погрешность вычислений пропорциональна квадрату отношения интервала дискретизации к периоду гармоники (Δt/Тгарм)2. 

Для основной гармоники сетевого напряжения 50 Гц погрешность вычислений составляет всего 0,0025 % и ее можно не принимать в расчет. 

На частоте 500 Гц эта вычислительная погрешность составляет уже 0,25%, а на частоте максимально допустимой гармоники 1000 Гц (20 -ая гармоника) — погрешность 1 %. 

Для преобразователя НПСИ заявленная основная погрешность составляет 0.5%.  Поэтому, если в сети  присутствуют  только первые 7-8 гармоник, то преобразователи НПСИ будет измерять действующие значения без дополнительной погрешности,  При наличии более высоких гармоник  необходимо учитывать учитывать дополнительную погрешность.

Вторая особенность заключается в том, что частота в сети может отличаться от 50 Гц и на периоде усреднения укладывается не  целое число периодов. В результате  переменная составляющая не будет полностью обнуляться и измеренные  значения будут колебаться. Эти колебания могут рассматриваться как дополнительная погрешность измерения. 

Российскими стандартами установлено, что нормально допустимые и предельно допустимые отклонения частоты сети не должны превышать соответственно ± 0,2 Гц и ± 0,4 Гц. 

При отклонении частоты на 0,2 Гц от частоты 50 Гц возникают колебания результата  измерения порядка 0,4%. 

В связи с этим  одно важное замечание. 

Преобразователи НПСИ позволяют измерять  гармоники, кратные 50 Гц, вплоть до частоты 1000 Гц, но их нельзя применять для частот не кратных 50 Гц (например, 64 Гц). 

Аналогичная ситуация будет, если сигнал не является периодическим.

 

“Борьба с погрешностью”

Есть три основные причины, из-за которых возникают  флуктуации измеренных действующих значений. О первых двух мы только что рассказали: 

1. Погрешность измерения высших гармоник
2. Отклонение частоты от 50 Гц.
3. Наличие шумоподобных и импульсных помех.

Все три приводят к погрешности измерения.

Для борьбы с этими явлениями в преобразователях НПСИ можно  включить усреднение измеренных значений. Это простой и эффективный метод позволяет практически полностью исключить эти колебания, но его применение приводит к повышению инерционности измерения. Первичное усреднение происходит на интервале 80 мс при  измерении самого действующего значения. Кроме того, в преобразователях НПСИ предусмотрена дополнительная возможность усреднения с временами усреднения от 1 с до 50 с, но дополнительное усреднение может быть и отключено. 

Пользователю следует выбрать оптимальное соотношение погрешности и быстродействия.

 “Приборы НПСИ”

Вначале уже говорили, что НПФ “КонтрАвт” выпускает целый ряд измерительных преобразователей измерения и преобразования в  унифицированные сигналы тока и напряжения

Вот их перечень:

• НПСИ-ДНТВ (до 500 В), НПСИ-ДНТН (до 50 В), программируемые тип и диапазон измерения
• НПСИ-200-ДН (напряжение) и НПСИ-200-ДТ (ток) — фиксированные диапазоны  
• НПСИ-МС1 — ток, напряжение, мощность, 1 фаза,  программируемые
• НПCИ-500-МС1 ( 1 фаза) и НПСИ-500-МС3 (3 фаза) — ток, напряжения мощности, программируемые, RS-485

В этой линейке приборов есть преобразователи с программируемым  типом  и диапазоном измерения, есть с фиксированным преобразованием. Есть преобразователи, которые  измеряют всю совокупность параметров в одно- и трехфазной сети (действующие значения тока и напряжения, все виды мощности, частоту сети и ряд других параметры),  а также преобразуют их в токовые сигналы и передают  по интерфейсу RS-485.

Во всех реализован описанный метод измерения, позволяющий измерять периодические несинусоидальные сигналы с основной частотой 50 Гц с гармониками вплоть до 20 (частота 1000 Гц), а также  сигналы с постоянной составляющей (постоянные сигналы).  Дополнительное усреднение измеренных значений эффективно повышает точность  и стабильность измерения.  

“Завершение”

На этом мы заканчиваем обсуждение методов измерения действующих значений напряжения и тока.

 

 

Общая электротехника с основами электроники

Общая электротехника с основами электроники

Попов В. С., Николаев С. А. Общая электротехника с основами электроники, М., «Энергия», 1972, — 504 c. В книге рассмотрены электрические цепи, электрические машины и трансформаторы, электротехнические намерения и приборы, электропривод и аппаратура управления, передача и распределение электрической энергии, электронные лампы, газоразрядные приборы, полупроводниковые приборы, фотоэлектрические приборы, усилители и генераторы, Книга предназначена для учащихся техникумов неэлектротехнических специальностей. Оглавление Предисловие Введение Часть первая. Общая электротехника 1-1. Основные понятия 1-2. Электрическое напряжение. Потенциал 1-3. Электропроводность 1-4. Электрическая емкость. Конденсаторы 1-5. Соединение конденсаторов 1-6. Энергия электрического поля 1-8. Электроизоляционные материалы Глава вторая. Электрические цепи постоянного тока 2-1. Электрический ток 2-2. Электрическая цепь и ее элементы 2-3. Закон Ома 2-4. Электрические сопротивление и проводимость 2-5. Зависимость сопротивления от температуры 2-6. Проводниковые материалы 2-7. Работа и мощность 2-8. Преобразование электрической энергии в тепловую 2-9. Электрическая нагрузка проводов и защита их от перегрузки 2-10. Потеря напряжения в проводах 2-11. Первый закон Кирхгофа 2-12. Последовательное соединение сопротивлений — приемников энергии 2-13. Параллельное соединение сопротивлений — приемников энергии 2-14. Смешенное соединение сопротивлений 2-15. Два режима работы источника питания 2-16. Второй закон Кирхгофа 2-17. Расчет сложных цепей 2-18. Химические источники питания 2-19. Соединение химических источников питания 2-20. Нелинейные электрические цепи 2-21. Лабораторная работа. Потеря напряжения в линии Глава третья. Электромагнетизм 3-1. Магнитное поле тока. Магнитная индукция. Магнитный поток 3-2. Электромагнитная сила 3-3. Взаимодействие параллельных проводов с токами 3-4. Магнитная проницаемость 3-5. Напряженность магнитного поля. Магнитное напряжение 3-6. Закон полного тока 3-7. Магнитное поле катушки с током 3-8. Ферромагнетики, их намагничивание и перемагничивание 3-9. Ферромагнитные материалы 3-10. Магнитная цепь и ее расчет 3-11. Электромагниты 3-12. Электромагнитная индукция 3-13. Принцип работы электрического генератора 3-14. Принцип работы электродвигателя 3-15. Вихревые токи 3-16. Индуктивность. Электродвижущая сила самоиндукции 3-17. Энергия магнитного поля 3-18. Взаимная индуктивность Глава четвертая. Электрические машины постоянного тока 4-1. Назначение машин постоянного тока 4-2. Устройство машины постоянного тока 4-3. Принцип работы машины постоянного тока 4-4. Устройство обмотки якоря 4-5. Электродвижущая сила обмотки якоря 4-6. Электромагнитный момент на валу машины 4-7. 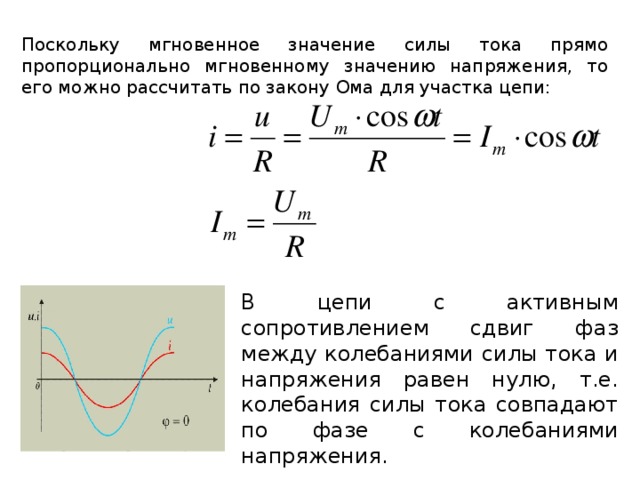Механическая мощность машины постоянного тока 4-8. Реакция якоря машины постоянного тока 4-9. Коммутация тока 4-10. Понятие о номинальных данных и характеристиках электрических машин 4-11. Генератор с независимым возбуждением 4-12. Генератор с параллельным возбуждением 4-13. Генератор со смешанным возбуждением 4-14. Электродвигатели постоянного тока 4-15. Электродвигатель с параллельным возбуждением 4-16. Электродвигатель с независимым возбуждением 4-17. Электродвигатели с. последовательным и со смешанным возбуждением 4-18. Потери и коэффициент полезного действия 4-19. Лабораторная работа. Электродвигатель с параллельным возбуждением 4-20. Лабораторная работа. Генератор с параллельным возбуждением Главе пятая. Основные понятия, относящиеся к переменным токам 5-1. Переменный ток 5-2. Получение синусоидальной э. д. с. 5-3. Сдвиг фаз 5-4. Действующие значения тока и напряжения 5-5. Векторная диаграмма Глава шестая. Цепи переменного тока 6-1. Особенности цепей переменного тока 6-2. Цепь с сопротивлением 6-3. Цепь с индуктивностью 6-4. Цепь с активным сопротивлением и индуктивностью 6-5. Неразветвленная цепь с активными сопротивлениями и индуктивностями 6-6. Разветвленная цепь с активными сопротивлениями и индуктивностями 6-7. Цепь с емкостью 6-8. Колебательный контур 6-9. Резонанс напряжений 6-10. Резонанс токов 6-11. Коэффициент мощности 6-12. Активная и реактивная энергия 6-13. Лабораторная работа. Цепь переменного тока с активным сопротивлением, индуктивностью и емкостью 6-14. Лабораторная работа. Параллельное соединение катушки и конденсатора Глава седьмая. Трехфазные цепи 7-1. Трехфазные системы 7-2. Соединение обмоток генератора звездой 7-3. Соединение обмоток генератора треугольником 7-4. Соединение приемников энергии звездой 7-5. Соединение приемников энергии треугольником 7-6. Лабораторная работа. Трехфазные цепи Глава восьмая. Электротехнические измерения и приборы 8-1. Основные понятия 8-2. Классификация электроизмерительных приборов 8-3. Измерительные механизмы приборов 8-4. Измерение тока и напряжения 8-5. Измерение мощности 8-6. Измерение электрической энергии 8-7. Измерение сопротивлений 8-8. Измерение неэлектрических величин электрическими методами 8-9. Лабораторная работа. Измерение сопротивлений 8-10. Лабораторная работа. Поверка индукционного счетчика 8-11. Лабораторная работа. Измерение мощности в трехфазной цепи Глава девятая. Трансформаторы 9-1. Назначение трансформаторов 9-2. Принцип действия и устройство однофазного трансформатора 9-3. Холостой ход однофазного трансформатора 9-4. Работа нагруженного трансформатора и диаграмма магнитодвижущих сил (м. д. с.) 9-5. Изменение напряжения трансформатора при нагрузке 9-6. Мощность потерь в обмотках нагруженного трансформатора 9-7. Трехфазный трансформатор 9-8. Регулирование напряжения трансформаторов 9-9. Автотрансформаторы 9-10. Трансформаторы для дуговой электросварки 9-11. Измерительные трансформаторы 9-12. Коэффициент полезного действия трансформатора 9-13. Нагрев и охлаждение трансформаторов 9-14. Лабораторная работа. Однофазный трансформатор Глава десятая. Электрические машины переменного тока 10-1. Назначение машин переменного тока. Асинхронные электродвигатели 10-2. Получение вращающегося магнитного поля 10-3. Обмотка статора асинхронного электродвигателя 10-4. Обмотка ротора асинхронного двигателя 10-5. Принцип действия асинхронного двигателя 10-6. Электродвижущие силы в обмотках статора и ротора 10-7. Сопротивления обмотки ротора 10-8. Токи в обмотке ротора 10-9. Вращающий момент двигателя 10-10. Пуск в ход асинхронных двигателей 10-11. Регулирование частоты вращения асинхронного двигателя 10-12. Однофазный асинхронный двигатель 10-13. Потери и к. п. д. асинхронного двигателя 10-14. Синхронные машины 10-15. Универсальный коллекторный двигатель 10-16. Лабораторная работа. Трехфазный асинхронный электродвигатель Глава одиннадцатая. Электропривод и аппаратура управления 11-1. Система электропривода 11-2. Нагрев и охлаждение электрических машин 11-3. Выбор мощности двигателя при продолжительном режиме 11-4. Выбор мощности двигателя при кратковременном режиме 11-5. Выбор мощности двигателя при повторно-кратковременном режиме 11-6. Рубильники 11-7. Пакетные выключатели 11-8. Реостаты для пуска и регулирования электродвигателей 11-9. Контроллеры 11-10. Плавкие предохранители 11-11. Автоматические воздушные выключатели 11-12. Контакторы 11-13. Реле 11-14. Схема управления асинхронным двигателем с помощью реверсивного магнитного пускателя 11-15. Схема включения двухскоростного асинхронного двигателя 11-16. Автоматический пуск асинхронного двигателя с кольцами 11-17. Автоматический пуск двигателя постоянного тока с параллельным возбуждением 11-18. Лабораторная работа. Сборка и проверка работы схемы релейноконтакторного управления трехфазным асинхронным двигателем с короткозамкнутым ротором Глава двенадцатая. Передача и распределение электрической энергии 12-1. Схемы электроснабжения промышленных предприятий. 12-2. Трансформаторные подстанции и распределительные устройства промышленных предприятий 12-3. Электрические сети промышленных предприятий 12-4. Защитное заземление Часть вторая. Основы промышленной электроники 13-1. Классификация и применение электронных приборов 13-2. Движение электронов в электрическом поле 13-3. Движение электронов в магнитном поле 13-4. Электронная эмиссия 13-5. Катоды электровакуумных приборов 13-6. Двухэлектродные электронные лампы — диоды 13-7. Применение двухэлектродных ламп Глава четырнадцатая. Трехэлектродные лампы. Четырех- и пятиэлектродные лампы. Усилители 14-1. Устройство и принцип работы триода 14-2. Статические характеристики триода 14-3. Параметры триода 14-4. Простейший каскад усиления 14-5. Характеристики и параметры простейшего каскада усиления 14-6. Типы триодов 14-7. Четырехэлектродные лампы — тетроды 14-8. Пятиэлектродные лампы — пентоды 14-9. Комбинированные и многосеточные лампы. Типы ламп 14-10. Общие понятия, относящиеся к усилителям 14-11. Режимы работы усилителей 14-12. Многокаскадные ламповые усилители 14-13. Обратная связь в усилителях 14-14. Лабораторная работа. Снятие анодных и анодно-сеточных характеристик триода и определение по ним статических параметров 14-15. Лабораторная работа. Снятие частотных характеристик усилителя напряжения низкой частоты Глава пятнадцатая. Газоразрядные приборы и их применение 15-1. Виды газового разряда и его вольт-амперная характеристика 15-2. Ионные приборы с несамостоятельным дуговым разрядом 15-3. Приборы с тлеющим разрядом 15-4. Ионные приборы с самостоятельным дуговым разрядом 15-5. Обозначения газоразрядных приборов 15-6. Лабораторная работа. Снятие анодносеточных и пусковых характеристик тиратрона Глава шестнадцатая. Электронные генераторы. Осциллографы 16-1. Генераторы синусоидальных напряжений 16-2. Зарядка и разряд конденсатора 16-3. Релаксационные генераторы (генераторы пилообразного напряжения) 16-4. Мультивибраторы 16-5. Электроннолучевые трубки 16-6. Электроннолучевой осциллограф 16-7. Обозначения электроннолучевых трубок 16-8. Лабораторная работа. Экспериментальное, определение кривых напряжений в схемах выпрямителей Глава семнадцатая. Полупроводниковые приборы и их применение 17-1. Собственная электропроводность полупроводников 17-2. Примесная электропроводность полупроводников 17-3. Полупроводниковый вентиль 17-4. Германиевые и кремниевые диоды 17-5. Меднозакисные и селеновые диоды 17-6. Применение полупроводниковых вентилей и схемы выпрямителей 17-7. Обозначения полупроводниковых диодов 17-8. Кремниевые стабилитроны (опорные диоды) 17-9. Транзисторы 17-10. Применение транзисторов для усиления колебаний 17-11. Схемы включения и характеристики транзисторов 17-12. Обозначения полупроводниковых триодов 17-13. Лабораторная работа. Снятие характеристик транзистора Глава восемнадцатая. Фотоэлектронные приборы и электронные реле 18-1. Фотоэлементы с внешним фотоэффектом 18-2. Фоторезисторы 18-3. Полупроводниковые фотоэлементы 18-4. Электронные и ионные реле 18-5. Лабораторная работа. Электронное реле — триггер

Анализ генерации переменного тока: эффективные значения, фазовый угол и частота

Анализ процесса производства электроэнергии переменного тока и переменного тока, который мы используем почти во всех аспектах нашей жизни, необходим для лучшего понимания того, как мощность переменного тока используется в современных технологиях.

Действующие значения

Выходное напряжение генератора переменного тока можно выразить двумя способами. Один из них — графически с использованием синусоиды (рис. 3). Второй способ — алгебраически по уравнению e = E _max sin ωt, которые будут рассмотрены далее в тексте.

Рисунок 3: Синусоида напряжения

Когда напряжение создается генератором переменного тока, результирующий ток изменяется пропорционально напряжению. Когда катушка генератора вращается на 360°, выходное напряжение проходит один полный цикл. За один цикл напряжение увеличивается от нуля до E в одном направлении, уменьшается до нуля, увеличивается до E _max в обратном направлении (отрицательное E _max ), а затем снова уменьшается до нуля. Значение Е _max возникает при 90° и называется пиковым напряжением. Время, за которое генератор совершает один цикл, называется периодом, а количество циклов в секунду называется частотой (измеряется в герцах).

Одним из способов обозначения напряжения или тока переменного тока является пиковое напряжение (E _p ) или пиковый ток (I _p ). Это максимальное напряжение или ток для синусоидальной волны переменного тока.

Другое значение, значение размаха (E _p-p или I _p ), представляет собой величину напряжения или диапазона тока, охватываемого синусоидой. Однако значение, наиболее часто используемое для переменного тока, является эффективным значением. Эффективное значение переменного тока — это количество переменного тока, которое производит такой же эффект нагрева, как и равное количество постоянного тока.

Проще говоря, эффективное значение одного ампера переменного тока будет выделять в проводнике такое же количество тепла в заданное время, как один ампер постоянного тока. Нагревательный эффект данного переменного тока пропорционален квадрату тока. Эффективное значение переменного тока можно рассчитать, возведя в квадрат все амплитуды синусоиды за один период, взяв среднее значение этих значений, а затем извлекая квадратный корень. Эффективное значение, являющееся корнем среднего (среднего) квадрата токов, известно как среднеквадратичное или среднеквадратичное значение. Чтобы понять значение эффективного тока, приложенного к синусоиде, обратитесь к рисунку 4.9.0003

Значения I нанесены на верхнюю кривую, а соответствующие значения I ² нанесены на нижнюю кривую. Кривая I ²  имеет вдвое большую частоту, чем I, и изменяется выше и ниже новой оси. Новая ось представляет собой среднее значение значений I ² , а квадратный корень из этого значения представляет собой среднеквадратичное значение или эффективное значение тока. Среднее значение равно ½ I _max ² . Тогда среднеквадратичное значение равно

. Существует шесть основных уравнений, которые используются для преобразования значения переменного напряжения или тока в другое значение, как указано ниже.

• Среднее значение = пиковое значение x 0,637
• Эффективное значение (RMS) = пиковое значение x 0,707
• Пиковое значение = среднее значение x 1,57
• Эффективное значение (RMS) = среднее значение x 1,11
• Пиковое значение = эффективное значение (RMS) x 1,414
• Среднее значение = эффективное (RMS) x 0,9

Обычно встречающиеся значения тока (I) и напряжения (E) считаются среднеквадратичными; поэтому индекс не используется.

Рисунок 4: Действующее значение тока

Другим полезным значением является среднее значение амплитуды в течение положительной половины цикла.

Уравнение ниже представляет собой математическое соотношение между I _av  , I _max и I. av , E _max и E.

E _av = 0,637 E _max   = 0,9 E

Пример 1:

Пиковое значение напряжения в цепи переменного тока составляет 200 В. Каково среднеквадратичное значение напряжения?

E   =  0,707E _max

E = 0,707 x 200 = 141,4 В Чему равно среднее значение силы тока в цепи?

I _ср = 0,637 I _макс

I _ср = 0,637 x 10 = 6,37 ампер

Фазовый угол

Фазовый угол — это доля цикла в градусах, которая прошла с момента прохождения напряжения или тока через заданное значение. Заданное значение обычно равно нулю. Возвращаясь к рисунку 3, примем точку 1 за начальную точку или нулевую фазу. Фаза в точке 2 составляет 30°, в точке 3 — 60°, в точке 4 — 90° и так далее до точки 13, где фаза равна 360° или нулю. Чаще используется термин «разность фаз».

Рис. 5: Соотношение фаз

Разность фаз можно использовать для описания двух различных напряжений с одинаковой частотой, которые проходят через нулевые значения в одном и том же направлении в разное время. На рис. 5 углы по оси обозначают фазы напряжений e ₁ и e ₂ в любой момент времени.

При 120° e ₁ проходит через нулевое значение, которое на 60° опережает e ₂   ( e ₂  равно нулю при 180°). Говорят, что напряжение e ₁ ведет e ₂ на 60 электрических градусов, или можно сказать, что e ₂ отстает от e ₁ на 60 электрических градусов.

Разность фаз также используется для сравнения двух разных токов или тока и напряжения. Если разность фаз между двумя токами, двумя напряжениями или напряжением и током составляет ноль градусов, говорят, что они «синфазны». Если разность фаз отличается от нуля, говорят, что они «не совпадают по фазе».

Расчет напряжения

Приведенное ниже уравнение представляет собой математическое представление напряжения, связанного с любой конкретной ориентацией катушки (индуктора).

E = E _MAX SINθ

, где

E = индуцированная EMF
E _MAX = максимальный индуцированный EMF
θ = Угол из ссылки (градуал или радианы)

Пример 1:

ЭДС индукции в катушке создает максимальную ЭДС 120 В, когда угол от точки отсчета составляет 45 °?

e = E _max sinθ

e = 120 В Sin (45)

e = 84,84 В

Максимальное индуцированное напряжение также можно назвать пиковым напряжением E _p . Если (t) — время, за которое катушка поворачивается на угол (θ), то угловая скорость (ω) катушки равна θ/t и выражается в радианах/сек.

Приведенное ниже уравнение является математическим представлением угловой скорости.

θ = ωt

где

ω = угловая скорость (радиан/сек)
t = время поворота на угол от точки отсчета (сек)
θ = угол от точки отсчета (радианы)

Используя законы подстановки, соотношение между индуцированным напряжением и максимальным индуцированным напряжением , а угловая скорость может быть выражена.

Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между индуцируемым напряжением, максимальным напряжением и угловой скоростью и равно выходной мощности генератора переменного тока.

e = E _max sin(ωt)

где
e = ЭДС индукции (вольт)
E _max = максимальная ЭДС индукции (вольт)
ω = угловая скорость (радиан/с) t 9017 время поворота на угол от точки отсчета (сек)

Расчет тока

Максимальный индуцированный ток рассчитывается аналогичным образом. Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между максимальным индуцированным током и угловой скоростью.

i = I _max sin(ωt)

где

i = индукционный ток (ампер) = время поворота на угол от точки отсчета (сек)

Расчет частоты

Частота переменного напряжения или тока может быть напрямую связана с угловой скоростью вращающейся катушки. Единицы угловой скорости — радианы в секунду, а 2π радиан — это полный оборот.

Радиан — это угол, опирающийся на дугу, равную радиусу окружности. Один радиан равен 57,3 градуса. Один цикл синусоидальной волны генерируется, когда катушка вращается на 2π радиан.

Приведенное ниже уравнение представляет собой математическое соотношение между частотой (f) и угловой скоростью (ω) в цепи переменного тока.

ω = 2πf

где

ω = угловая скорость (радиан/с)
f = частота (Гц)

Найдите: 1. Угловую скорость 2. Угол отсчета в 1 мс 3. ЭДС индукции в этой точке

Решение:

1. ω = 2πf

ω = 2 (3,14) (60 Гц) = 376,8 Радианы/Сек

2. θ = Ω

θ = (376.8 Радиан/секунду) (секунду) .001 с) = 0,3768 Радианы

3. E = E _MAX SINθ

E = (120 В) (SIN 0,3768 Radians)
E = (120 В) (0,3679)
E = 44,15 V

Будьте первым, кто получит эксклюзивный контент прямо на вашу электронную почту.

Обещаем не спамить. Вы можете отписаться в любое время.

Неверный адрес электронной почты

Среднеквадратичное значение напряжения переменного тока

Переменный сигнал или сигнал переменного тока, который связан с переменным током, представляет собой периодический сигнал, который чередует положительные и отрицательные значения. Синусоидальная или синусоидальная волна является наиболее распространенной изменяющейся во времени волной, которая используется для представления формы волны переменного тока.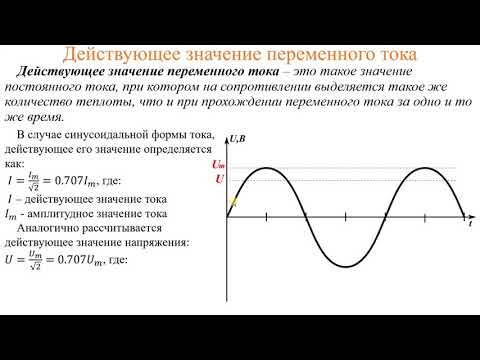

[adsense1]

В случае постоянного тока значения напряжения и тока обычно стабильны во времени. Легко выразить величину напряжения или тока, т. е. сколько напряжения или тока присутствует в любой части цепи.

В случае переменного тока, в отличие от постоянного, они не могут быть охарактеризованы одной величиной, так как амплитуда сигнала переменного тока непрерывно изменяется во времени.

Существует множество способов представления амплитуды сигнала переменного тока. Некоторые из них

• Мгновенное значение
• Пиковое значение
• Значение размаха
• Среднее значение
• Среднеквадратичное значение

В предыдущих разделах мы рассмотрели среднее значение напряжения и мгновенные значения сигнала переменного тока. Здесь описана еще одна важная тема о форме волны переменного тока, среднеквадратичное напряжение формы волны переменного тока.

[adsense2]

Outline

Среднеквадратичное значение напряжения переменного тока

Среднеквадратичное значение означает «среднеквадратичное» значение. Среднеквадратичное значение напряжения определяется как «квадратный корень из средних значений квадратов всех мгновенных напряжений в волне форма». Среднеквадратичное значение можно найти следующим образом: входные данные возводятся в квадрат и вычисляется среднее значение.

Это дает среднюю мощность. Для расчета напряжения берется квадратный корень из ранее полученного среднего значения. Следовательно, это называется среднеквадратичным напряжением.

Среднеквадратичное значение используется для получения постоянного эквивалента переменного тока, который будет рассеивать такое же количество тепла, когда любое значение применяется к резистору. Переменный ток с максимальным значением 1,4 ампера будет выделять такое же тепло через резистор, как и постоянный ток 1 ампер.

Следовательно, среднеквадратичное значение также иногда называют эквивалентным значением или эквивалентным значением постоянного тока. Измерение среднеквадратичного значения напряжения или тока формы волны переменного тока — лучший способ соотнести величины переменного и постоянного тока.

Среднеквадратичное значение также называется «действующим значением», которое является эквивалентом значения постоянного тока, тока или напряжения, при котором переменный сигнал производит такую ​​же мощность, что и постоянный ток.

Как правило, напряжение сети представляет собой среднеквадратичное значение. В Индии, например, напряжение питания находится в пределах 220-240В. На самом деле это среднеквадратичное значение переменного тока, которое эквивалентно производству той же мощности, что и 220–240 В постоянного тока.

Среднеквадратичное значение используется только для обозначения сигналов переменного тока, т. е. изменяющихся во времени синусоидальных сигналов, таких как переменное напряжение, переменный ток или других сложных сигналов, амплитуда которых изменяется со временем. Среднеквадратичное значение не применимо к цепям постоянного тока, где величина постоянна во времени.

Процесс определения среднеквадратичного значения напряжения очень похож на процесс определения среднего значения напряжения. Существует два метода определения среднеквадратичного значения напряжения сигнала. Это: графический метод и аналитический метод.

Графический метод

В этом методе мы найдем среднеквадратичное значение напряжения, используя средние координаты или мгновенные значения напряжения формы волны переменного тока.

Четкий вывод среднеквадратичного значения включает несколько этапов, показанных ниже.

ШАГ 1

В каждой форме волны переменного тока у нас есть много мгновенных напряжений, и количество мгновенных напряжений зависит от длительности синхронизации. Например, если форма волны разделена на n средних ординат, то в момент времени t = 2 мгновенное напряжение формы волны переменного тока равно V2.

Аналогично, в экземпляре t = n мгновенное напряжение равно van и т. д. Итак, сначала мы находим мгновенные значения напряжения каждого экземпляра периодической формы волны, например V1, V2, V3 и Vn.

Чтобы найти среднеквадратичное напряжение формы волны, мы должны найти квадратные значения каждого значения напряжения формы волны переменного тока. Это дает «квадратную» часть среднеквадратичного значения.

V1 ² +V2 ² +V3 ² +V4 ² +—-

ЭТАП 2

Нахождение среднего значения суммы квадратов значений напряжения. Делим сумму квадратов на количество середин ординат. Это дает «среднюю» часть RMS.

Среднее значение всех значений напряжения формы волны переменного тока периодической формы волны даст нам наиболее точное значение среднеквадратичного значения напряжения. Как правило, во всех математических приближениях мы устанавливаем средние значения, чтобы не допустить ошибок и установить наиболее точное значение вычислений.

Если у нас есть Vn значений напряжения в n экземплярах, среднее значение рассчитывается, как показано ниже.

Квадратный корень из этого значения дает среднеквадратичное значение формы волны переменного тока. Формула для расчета среднеквадратичного значения напряжения показана ниже.

Где n — количество экземпляров,

V1, V2, V3, V4 …. — мгновенные значения напряжения сигнала.

Пример

Если у нас есть переменный сигнал с максимальной амплитудой 20 Вольт, давайте найдем его среднеквадратичное значение напряжения.
Мы делим сигнал на 10 средних значений ординаты следующим образом.

Следовательно, среднеквадратичное значение напряжения переменного тока с пиковым напряжением 20 В составляет 14,15 В.

Графический метод является очень эффективным методом определения среднеквадратичных значений всех типов сигналов, включая сигналы сложной формы.

Аналитический метод

Другим методом, используемым для определения среднеквадратичного значения напряжения (или тока) периодической формы волны переменного тока, является аналитический или математический метод. Этот метод подходит для волн синусоидальной формы.

В этом методе среднеквадратичное значение напряжения вычисляется путем анализа площади под кривой сигнала переменного тока. Этот метод проще, чем графический, при работе с чистыми синусоидальными сигналами.

Периодический синусоидальный сигнал с периодом времени Т определяется выражением СКЗ = √[1/T ∫ ₀ ^t В _м ² cos ² (ωt) dt]

Для одного полного цикла или периода формы волны пределы интегрирования составляют от 0 до 360 ⁰ . Таким образом, интегрируя через нижний и верхний пределы, мы получаем

Комплексное уравнение можно еще больше упростить, разделив его на ω = 2π / T. Тогда сокращенное уравнение для среднеквадратичного значения напряжения будет следующим:

В _{Среднеквадратичное значение} = В _м /2 = В _м *0,707

Уравнение среднеквадратичного напряжения

Среднеквадратичное напряжение вычисляется с использованием других значений напряжения формы волны, таких как пиковое напряжение, размах напряжения и среднее напряжение.

В пересчете на значение пикового напряжения

Среднеквадратичное значение напряжения переменного тока составляет 0,707 или 1/√2 пикового значения напряжения. Среднеквадратичное значение можно рассчитать, разделив пиковое напряжение на квадратный корень из 2 (почти 0,707).

В _СКЗ = В _{ПИКОВОЕ} x 1 /√2

В _СКЗ = В _{ПИКОВОЕ} x 0,707

Расчетное значение напряжения от пика до пика5 можно умножить на 900 размах напряжения с 1/22 или 0,35355. Размах напряжения представлен как V

_PP .

V _ОБС = V _P-P-P x 1 / 2√2

V _ОБС = V _P-P-P-P x 0,353

С точки зрения среднего значения напряжения

Напряжение RMS переменного волны составляет 1.1107 раз по сравнению со средним значением напряжения.

V _ОБЗОР = V _AVG x π / 2√2

V _ОБРАТА = V _AVG x 1,1107

выражаются в виде среднеквадратичных значений.

Обычно мы говорим, что напряжение в бытовой сети составляет около 220 Вольт переменного тока. Фактически это означает, что среднеквадратичное напряжение бытовой сети составляет 220 В.

Значение

RMS дает эквивалентные значения постоянного тока формы сигнала переменного тока.

Все измерительное оборудование, такое как амперметры и вольтметры, измеряет только среднеквадратичное значение. В некоторых дорогих вольтметрах сначала вычисляется пиковое напряжение и затем, умножая его на 0,707, получаем среднеквадратичное значение напряжения, наиболее точно.

Среднеквадратичное значение используется для определения коэффициента амплитуды и коэффициента формы сигнала переменного тока, которые являются ключевыми факторами, определяющими производительность системы.

Форм-фактор и пик-фактор

Для сигнала переменного тока, такого как синусоидальный сигнал, среднеквадратичное значение, пиковое значение и среднее значение являются тремя важными величинами, которые описывают амплитуду. Эти три значения зависят друг от друга.

Помимо этих трех величин, существуют некоторые отношения, которые обычно определяются между этими тремя основными измерениями. Это форм-фактор и пиковый (или пиковый) фактор.

Форм-фактор

«Форм-фактор — это отношение среднеквадратичного значения напряжения переменного сигнала к его среднему напряжению».
Форм-фактор представлен K _f .

Форм-фактор = среднеквадратичное напряжение / среднее напряжение

K _f = В _{среднеквадратичное значение} / В _AVG

От отношения между средним значением напряжения и среднеквадратичным значением синусоидальной формы волны переменного тока к пику (или макс. ), мы можем рассчитать форм-фактор как

K _f = 0,707 В _МАКС / 0,637 В _МАКС

= 1,11

Пик-фактор представляет собой отношение пикового напряжения

его среднеквадратичное значение напряжения». Мы также называем это «пиковым фактором» или «амплитудным фактором».

Крест-фактор представлен KP.

Крест-фактор = Пиковое напряжение / Среднеквадратичное значение напряжения

KP = В _{ПИКОВОЕ} (или В _МАКС. ) / В как

KP = V _MAX / 0,707 VMAX

= 1,414

Итог

• Сигналы, которые периодически чередуются относительно оси, называются «переменным сигналом» или «переменным сигналом».
• Среднеквадратичное значение напряжения означает среднеквадратичное значение напряжения. Среднеквадратичное значение определяется как «квадратный корень из средних значений квадратов мгновенных напряжений в форме волны, изменяющейся во времени».
• Представление среднеквадратичного значения является стандартным способом измерения переменного тока и напряжения, поскольку оно дает эквивалентные значения постоянного тока.
• Существует два метода расчета среднеквадратичного значения напряжения сигнала: графический метод и аналитический метод.
• Формула для среднеквадратичного значения напряжения в графическом методе равна 9.0054

• Формула для среднеквадратичного значения напряжения в аналитическом методе:

В _{СКЗ =} √[1/T ∫ ₀ ^t В _м ² cos ² (ωt) dt]

• Уравнения среднеквадратичного значения напряжения в терминах других значений напряжения:

VRMS = Vпик x 1 / √2

VRMS = Vпик-пик x 1 / 2√2

VRMS = Vavg x π / 2√2

• Мы можем измерить коэффициент амплитуды и коэффициент формы переменного сигнала где коэффициент амплитуды представляет собой отношение пикового значения к среднеквадратичному значению, а коэффициент формы представляет собой отношение среднеквадратичного значения к среднему значению.