Момент инерции абсолютно твердого тела. Урок №14

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

Физика. 10 класс. Урок №14.
«Недостаточно только получить знания, надо
найти им применение. Недостаточно только
желать, надо делать.»
Гёте
© Фокина Лидия Петровна
Знаешь ли ты?
Почему вместо обычных колес на
велосипедах гонщиков устанавливают
сплошные диски?
Если ты затрудняешься ответить на данный вопрос
сейчас, то я уверенн, что ты на него сможешь ответить
в конце этого урока.

© Фокина Лидия Петровна
Физика. 10 класс. Урок №14.
Тема урока:
Момент инерции
абсолютно твердого тела
Цели обучения:
10.2.2.5 – использовать теорему Штейнера для
расчета момента инерции материальных тел
© Фокина Лидия Петровна
Давайте вспомним!
1. Что такое инерция?
Инерция – это физическое явление. Оно
состоит в том, что любое тело, на которое не
действуют другие тела (или действие других
тел скомпенсировано), сохраняет состояние
покоя или движется равномерно и
прямолинейно
2. Какое тело в физике называют абсолютно
твердым телом?
Абсолютно твердое тело – это тело,
расстояние между частями которого не
меняется при действии на него любых сил.

© Фокина Лидия Петровна
Рассмотрим вращение материальной точки
массой m вокруг неподвижного центра О.
Докажем, что инерциальные свойства данной
точки зависят не только от массы, но и от
радиуса вращения.
Запишем второй закон
Ньютона для точки массой m,
движущейся по окружности
под действием силы ,
тангенциальное ускорение
будет создавать касательная
к траектории составляющая
© Фокина Лидия Петровна
Тангенциальное ускорение связано с угловым
ускорением формулой
Учитывая это получим:
Умножим обе части данного уравнения на радиус
окружности, по которой двигалась
рассматриваемая точка, получим:
, где
M — момент силы
— момент инерции
© Фокина Лидия Петровна
Величину, равную произведению массы на
квадрат радиуса окружности, по которой
движется тело, называют моментом
инерции.
Момент инерцииобозначают
буквой I.
Единица измерения момента
инерции [I] = 1 кг м2
-второй закон Ньютона для
вращающегося тела
© Фокина Лидия Петровна
Мы нашли момент инерции материальной точки,
вращающейся вокруг неподвижного центра.
А как найти момент инерции абсолютно твердого тела?
Момент инерции твердого тела равен сумме
моментов инерций материальных точек, из
которых состоит это тело:
Инертные свойства вращающихся тел зависят
не только от массы, но и от ее распределения
по объему тела и радиуса вращения.
© Фокина Лидия Петровна
стр 49-50 Таблица 6. Моменты инерции тел
© Фокина Лидия Петровна
Теорема Штейнера
Если для тела известен момент инерции I0
относительно оси, проходящей через центр
масс, то момент инерции относительно любой
оси, параллельной центральной, можно найти
по формуле, полученной швейцарским ученымматематиком Штейнером:
d – расстояние от центра масс до оси вращения
© Фокина Лидия Петровна
Задача №1
Определите момент инерции I тонкого однородного стержня
длиной l=30 см и m=100 г относительно оси, перпендикулярной
стержню и проходящей через: 1) его конец; 2) его середину; 3)
точку отстоящую от конца стержня на 1/3 его длины
Дано: CИ
Решение:
(из таблицы)
l= 30 см 0,3 м
m = 100 г 0,1 кг
I-?
1) расстояние от центра масс до
конца стержня
© Фокина Лидия Петровна
2) ось вращения проходит через центр масс
3) Расстояние от центра масс до оси, отстоящей
от конца стержня на 1/3 его длины
Ответ:
© Фокина Лидия Петровна
Выполни самостоятельно!
1.
Определите момент инерции стержня длиной l,
вращающегося вокруг своего конца. Во сколько раз
увеличился момент инерции в сравнении с моментом
инерции стержня, вращающегося вокруг центра масс?
2.
Определите момент инерции материальной точки, масса
которой 50 г, относительно оси, отстоящей от точки на
расстоянии 20 см.
3.
Найти момент инерции обруча массой и
радиусом относительно оси, проходящей через его край
перпендикулярно обручу.
§9 стр 48-51
© Фокина Лидия Петровна
Итоги урока
Момент инерции – скалярная физическая величина, мера
инертности во вращательном движении вокруг оси,
подобно тому, как масса тела является мерой его
инертности в поступательном движении.
© Фокина Лидия Петровна

Момент инерции материальной точки,
вращающейся по окружности радиуса R,
можно рассчитать по формуле …
I=mR2
Момент инерции тела измеряется в …
кг м2
Момент инерции тела относительно
любой оси, параллельной центральной,
можно вычислить применяя …
теорему
Штейнера
Формула, полученная Штейнером …
I=I0+ md2
© Фокина Лидия Петровна

English     Русский Правила

Определение момента инерции маховика

Лабораторная работа 1-4.

Определение момента инерции маховика

Приборы и принадлежности: маховик, секундомер, штангенциркуль, набор грузов по 200 и 300 г, вертикальный масштаб.

Цель работы:

1. Изучить основной закон динамики вращательного движения твердого тела;
2. Определить момент инерции маховика.

 

Основной закон динамики вращательного движения твердого тела

 

При вращении твердого тела вокруг неподвижной оси все частицы тела совершают плоское движение, причем линейные скорости и ускорения различных частиц различны. Угловая скорость вращения одинакова для всех частей тела. Если угловая скорость изменяется во времени, то это изменение можно характеризовать угловым ускорением.

Для заданного вращающего тела угловое ускорение определяется действием сумм моментов сил. Такая зависимость должна существовать потому, что равновесие тела определяется равенством нулю моментов сил. Как только момент сил относительно оси вращения не будет равен нулю, нарушится равновесие, начнется вращательное движение и возникнет угловое ускорение.

Для отыскания связи между угловым ускорением тела и моментами сил, действующих на него, рассмотрим движение одной какой-то выделенной частицы вращающего тела (рис. 4-1).

Пусть частица массой Δmi находится на расстоянии ri от оси вращения ОО’. На частицу могут действовать как внутренние, так и внешние силы. Внешние силы приложены со стороны других тел, а внутренние – со стороны других частиц того же тела. Обозначим через fi величину проекции суммы внутренних сил, действующих на Δmi на направление, перпендикулярное к ri.

Fi – есть проекция на то же направление суммы внешних сил. К каждой точке вращающегося тела применим второй закон Ньютона:

Fi + fi = Δmi ∙ ai                                          (4-1)

Где ai – линейное ускорение точки, связанное с угловым ускорением вращающегося тела соотношением

ai = ε ∙ ri

Подставляя в (4-1) значение ai, а затем умножая справа и слева уравнение (4-1) на ri, получим:

Fi ∙ ri + fi ∙ ri = Δmi ∙ ri2 ∙ ε                             

              (4-2)

Величина Δmi ∙ ri2, численно равная произведению массы частицы на квадрат расстояния до оси вращения, называется моментом инерции точки относительно оси вращения.

Величины Fi ∙ ri и fi ∙ ri определяют моменты внешних и внутренних сил, действующих на i-ю точку.

Произведение вращающей силы Fi на радиус окружности ri, описываемой точкой приложения силы, называется вращающим моментом (моментом вращающей силы).

Уравнения (4-1) и (4-2) по всем элементам тела, получим:

ΣFi ∙ ri + Σfi ∙ ri = εΣΔmi ∙ ri2                         (4-3)

Рисунок 4.1

 

Угловое ускорение постоянно дл всех элементов системы поэтому его можно вынести за знак суммы.

Величина J = ΣΔmi ∙ ri2, равная сумме моментов инерции отдельных точек, называется моментом инерции тела относительно оси вращения.

Момент инерции тела есть величина, характеризующая инертность тела при вращении.

Величина Σfi ∙ ri равна нулю, т.к. каждая внутренняя сила имеет равную и противоположную ей силу, приложенную к другой частице с тем же самым плечом.

Величина М = ΣFi ∙ ri определяет момент всех внешних сил, приложенных к телу.

Вводя обозначение момента инерции тела J и момента сил М, перепишем уравнение (4-3) в виде:

                                     (4-4)

Это есть основной закон динамики твердого тела, вращающегося вокруг неподвижной оси. Это закон аналогичен основному закону динамики для поступательного движения. Только вместо величины силы в уравнение (4-4) входит момент сил относительно оси, вместо линейного ускорения – угловое ускорение, вместо массы – момент инерции тела относительно оси вращения. Основной закон вращательного движения в форме уравнения (4-4) применим для таких вращающихся систем, у которых момент инерции в процессе вращения остается постоянным.

Если при вращении момент инерции изменяется, то применяется более общая форма основного закона вращения тела – закон изменения момента количества движения:

                                (4-5)

Величина М ∙ Δt – называется импульсом момента сил, а величина – моментом количества движения.

Согласно равенству (4-5) изменение момента количества движения твердого тела численно равно импульсу момента приложенных к нему сил.

При отсутствии момента сил момент количества движения остается постоянным. Это следствие известно под названием закона сохранения момента количества движения.

 

Описание прибора и вывод расчетной формулы

 

Маховик (рис. 4.2) представляет собой массивный диск, плотно сидящий на валу. Вал может вращаться в подшипниках с малым трением около горизонтальной оси ОО’. Ось вращения проходит через центр тяжести маховика. На валу плотно насажен шкив, снабженный болтиком, на который надевается петля нити и нить наматывается в несколько оборотов на шкив.

Рисунок 4.2

На свободный конец нити помещен груз Q, приводящий всю систему в равноускоренное движение.

Под действием груза Q на маховик будет действовать вращающий момент М, равный произведению силы f, приложенной к нити (натяжение нити) на плечо, т. е.

                          (4-6)

где D – диаметр шкива.

Если тело Q действует на нить с силой f, то нить действует на тело Q с силой F (сила F приложена к телу). В соответствии с третьим законом Ньютона эти силы равны по величине, но противоположны по направлению, т.е.

                           (4-7)

Для определения силы F рассмотрим движение тела Q вниз. На тело Q действуют две силы: со стороны земли – Р (сила тяжести), со стороны нити – F. Под действием этих сил груз будет совершать движение с ускорением а, которое определяем из уравнения:

Р – F = m ∙ a,                              (4-8)

где m – масса груза.

Отсюда:

F = m ∙ (g-a),                               (4-9)

где g – ускорение силы тяжести.

Вращающий момент М с учетом (4-9) и (4-7) определяется выражением:

                      (4-10)

Момент инерции маховика на основании уравнения (4-4) равен:

                (4-11)

где ε – угловое ускорение маховика и шкива;

а – линейное ускорение.

Угловое ускорение шкива Е и линейное ускорение а точек его цилиндрической поверхности связаны следующими соотношениями

,                                      (4-12)

где r – радиус шкива.

Измеряя секундомером время опускания груза Q с высоты h, найдем величину линейного ускорения:

                                          (4-13)

С учетом (4-12) и (4-13) получим формулу для определения момента инерции маховика:

                 (4-14)

 

Порядок выполнения работы

 

1. На технических весах определяем массу m1 и m2 грузов Q1 иQ2 с точностью до 0,1 г и измеряем штангенциркулем диаметр шкива D.
2. Нить на которой укреплен груз Q1, закрепляем на болтик шкива. Поднимаем груз Q1 на высоту h, близкую к максимальной. Измеряем масштабной линейкой с точностью до 0,5 см высоту h (от нижнего торца груза до пола).
3. Определяем время опускания груза Q1 с высоты h. Для этого одновременно опускаем маховик и включаем секундомер. В момент удара груза о пол секундомер выключаем. Записываем результаты измерений в таблицу и повторяем опыт пять раз.
4. Повторяем опыт с грузом Q2 (масса m2).

 

№ п.п	1	2	3	4	5	1	2	3	4	5
t, с	9,7	9,8	9,9	9,7	9,8	7,0	7,1	7,2	6,9	7,1
	t’ср = 9,78 c					t’ср = 7,06

 

 

Обработка результатов

1. По формуле (4-14) подсчитываем дважды момент инерции маховика, используя результаты измерений (t для обоих грузов Q).

Для груза массой 200 г:

Для груза массой 300 г:

2. Для одного из измерений, например первого, определяем относительную и абсолютную погрешности измерения, момента инерции.

Относительную погрешность определяем по формуле:

Абсолютную погрешность – по формуле

3. Результаты одного из измерений момента инерции маховика представляем в виде:

J = (JI ± ΔJI) кГм2.

J = 0,19 ± 0,05 кГм2.

 

Контрольные вопросы.

1. Каково основное уравнение динамики вращательного движения твердого тела?

 

 – основной закон динамики твердого тела, вращающегося вокруг неподвижной оси.

 

2. Как определяется момент силы относительно произвольной оси?

 

Моментом силы  относительно произвольной оси z называется векторное произведение радиус-вектора  и составляющей ей перпендикулярно силы, приложенной к точке А.

 

3. Что называют моментом инерции тела?

 

 

 Момент инерции твердого тела сумма моментов инерции составляющих его частиц М = ΣFi ∙ ri.

 

4. Что называют моментом инерции точки?

 

Произведение массы точки на квадрат ее расстояния до оси назовем моментом инерции материальной точки относительно оси.

 

5. Как формулируется закон изменения количества движения?

 

Количеством движения (импульсом) механической системы называют величину, равную сумме количеств движения (импульсов) всех тел, входящих в систему. Импульс внешних сил, действующих на тела системы, — это сумма импульсов всех внешних сил, действующих на тела системы.

Закон об изменении количества движения системы утверждает:

Изменение количества движения системы за некоторый промежуток времени равно импульсу внешних сил, действующих на систему, за тот же промежуток времени.

 

6. Вывод расчетной формулы для момента инерции маховика.

 

Под действием груза Q на маховик будет действовать вращающий момент М, равный произведению силы f, приложенной к нити (натяжение нити) на плечо, т.е.

                          (4-6)

где D – диаметр шкива.

Если тело Q действует на нить с силой f, то нить действует на тело Q с силой F (сила F приложена к телу). В соответствии с третьим законом Ньютона эти силы равны по величине, но противоположны по направлению, т.е.

                           (4-7)

Для определения силы F рассмотрим движение тела Q вниз. На тело Q действуют две силы: со стороны земли – Р (сила тяжести), со стороны нити – F. Под действием этих сил груз будет совершать движение с ускорением а, которое определяем из уравнения:

Р – F = m ∙ a,                              (4-8)

где m – масса груза.

Отсюда:

F = m ∙ (g-a),                               (4-9)

где g – ускорение силы тяжести.

Вращающий момент М с учетом (4-9) и (4-7) определяется выражением:

                      (4-10)

Момент инерции маховика на основании уравнения (4-4) равен:

                (4-11)

где ε – угловое ускорение маховика и шкива;

а – линейное ускорение.

Угловое ускорение шкива Е и линейное ускорение а точек его цилиндрической поверхности связаны следующими соотношениями

,                                      (4-12)

где r – радиус шкива.

Измеряя секундомером время опускания груза Q с высоты h, найдем величину линейного ускорения:

11. ВРАЩЕНИЕ

11. ВРАЩЕНИЕ
• 11. ВРАЩЕНИЕ
  • 11.1. Вращательные переменные
  • 11.2. Постоянное угловое ускорение
  • 11.3. Связь между линейными и угловыми переменными
  • 11.4. Кинетическая энергия вращения
  • 11.5. Расчет инерции вращения
  • 11.6. Крутящий момент
  • 11.7. Работа

---

В этой главе мы будем иметь дело с вращением твердого тела вокруг фиксированная ось. Каждая точка тела движется по окружности, центр которой лежит на ось вращения, и каждая точка испытывает одинаковое угловое смещение в течение определенного интервала времени.

Рисунок 11.1. Связь между s и [тета].

Предположим, что ось z нашей системы координат совпадает с осью вращения твердого тела. Ось x и ось y приняты равными перпендикулярно оси z. Каждая часть твердого тела движется по окружности вокруг оси Z. Предположим, что заданная точка A на теле покрывает линейную расстояние s при вращении (см. рис. 11.1). В течение одного полного точка обращения А проходит расстояние, равное 2[pi]r. В таком случае угол вращения равно 2[pi] радианам. Для ситуации, показанной на рис. 11.1, угол поворота можно легко рассчитать:

При описании вращения твердого тела необходимо выбрать опорная линия, относительно которой измеряется угол поворота. На рисунке 11.1 опорная линия соединяет начало системы координат и точка A. Угол поворота – это угол между опорной линия и ось абсцисс (как показано на рис. 11.1).

Если угол поворота [тета] зависит от времени, имеет смысл ввести понятие угловой скорости и угловое ускорение. угловая скорость [омега] определяется как

Единицей угловой скорости является рад/с. Угловая скорость может быть положительный (вращение против часовой стрелки) или отрицательный (вращение по часовой стрелке). угловое ускорение a определяется как

Единицей углового ускорения является рад/с ² .

Для описания вращения вокруг точки (а не фиксированной ось) концепция 9Введен вектор угловой скорости 0023 . модуль вектора угловой скорости равен модулю угловая скорость вращения вокруг фиксированной оси (как определено выше). направление вектора скорости параллельно оси вращения и нужно использовать правило правой руки, чтобы определить, направлен ли вектор вверх или вниз.

Проблема 7P

Колесо вращается с угловым ускорением a, равным

где t — время, a и b — константы. Если колесо имеет начальная угловая скорость [омега] ₀ , напишите уравнения для (а) угловая скорость и (б) угол поворота как функция времени.

Чтобы решить эту проблему, мы начнем с рассмотрения отношения между угловое ускорение и угловая скорость

Это соотношение можно переписать как

Подставив заданное угловое ускорение, получим для углового скорость

Угол поворота связан с угловой скоростью

Подставив полученное выражение для [omega](t) угол вращение можно рассчитать

и поэтому

Если угловое ускорение a постоянно (не зависит от времени), то следующие уравнения могут быть использованы для расчета [омега] и [тета] в любое время т:

Обратите внимание, что эти уравнения очень похожи на уравнения для линейного движение.

Проблема 19P

Колесо, находящееся в состоянии покоя, вращается с постоянным углом ускорение 2,0 рад/с ² . В течение определенного интервала в 3,0 с оборотов через 90 рад. а) Сколько времени вращалось колесо до старта? интервала 3,0 с? (б). Какова была угловая скорость колеса в момент начало интервала 3,0 с?

Время t = 0 с определяется как момент, когда колесо находится в состоянии покоя. Следовательно, [омега] ₀ = 0 рад/с. Угол поворота в любое более позднее время измеряется относительно положения тела в момент времени t = 0 с: [тета] ₀ = 0 рад. Уравнения вращения теперь задаются как

Угол поворота на интервале 3,0 с будет зависеть от времени:

В нашей задаче вращение [Delta][theta] за период [Delta]t равно данный. Время, в течение которого колесо вращалось до периода времени [Delta]t можно легко рассчитать

Угловая скорость колеса в начале этого периода равна

Пример отношения между угловыми и линейными переменными имеет уже обсуждалось. На рис. 1 показано, как расстояние s, пройденное точка A, связана с радиусом окружности и углом поворота

скорость точки А можно получить, продифференцировав эту уравнение относительно времени

Для вывода этого уравнения мы предположили, что для вращения вокруг фиксированная ось расстояние r от точки A до оси вращения постоянно (независимо от времени), что верно для твердого тела. ускорение точки А можно определить следующим образом

Ускорение a _t равно тангенциальной составляющей линейное ускорение, связанное с изменением величины скорости точки А. Однако мы видели, что объект совершая круговое движение, также испытывает радиальное ускорение . Величина радиальной составляющей, _р ,

Используя полученное ранее выражение для v через [омега] и r, радиальную составляющую ускорения можно переписать следующим образом

На рис. 11.2 показано направление как радиального, так и тангенциального составляющие ускорения точки А. Радиальная составляющая всегда присутствует до тех пор, пока [omega] не равно нулю; тангенциальная составляющая присутствует только в том случае, если угловое ускорение не равно нулю.

Рисунок 11.2. Составляющие ускорения точки А.

Можно сделать вывод, что при вращении твердого тела вокруг неподвижной оси, каждая часть тела имеет одинаковую угловую скорость [омега] и одинаковую угловое ускорение а, но точки, находящиеся на разных расстояниях от оси вращения имеют разные линейные скорости и разные линейные ускорения.

Полную кинетическую энергию вращающегося тела можно найти, просуммировав кинетическая энергия каждой отдельной частицы:

Для вывода этого уравнения мы использовали тот факт, что угловая скорость одинакова для каждой частицы твердого тела. Количество в скобках говорит нам, как масса вращающегося тела распределяется вокруг оси вращение. Эта величина называется момент инерции (или инерция вращения)

Единицей для I является кг м ² . Используя это определение, мы можем запишите кинетическую энергию вращающегося объекта как

Примечание: во многих предыдущих задачах мы предполагали, что имеем дело с безмассовые шкивы. Это предположение гарантирует, что, применяя сохранение механической энергии, мы не должны рассматривать кинетическую энергию, связанную с вращение шкива.

Чтобы вычислить момент инерции твердого тела, мы должны проинтегрировать по все тело

Если момент инерции относительно оси, проходящей через центр массы известен момент инерции относительно любой другой оси, параллельной ей, можно найти, применив теорему о параллельных осях

где я _см это момент инерции относительно оси, проходящей через центр масс, M — полная масса тела, а h — перпендикулярное расстояние между двумя параллельными осями.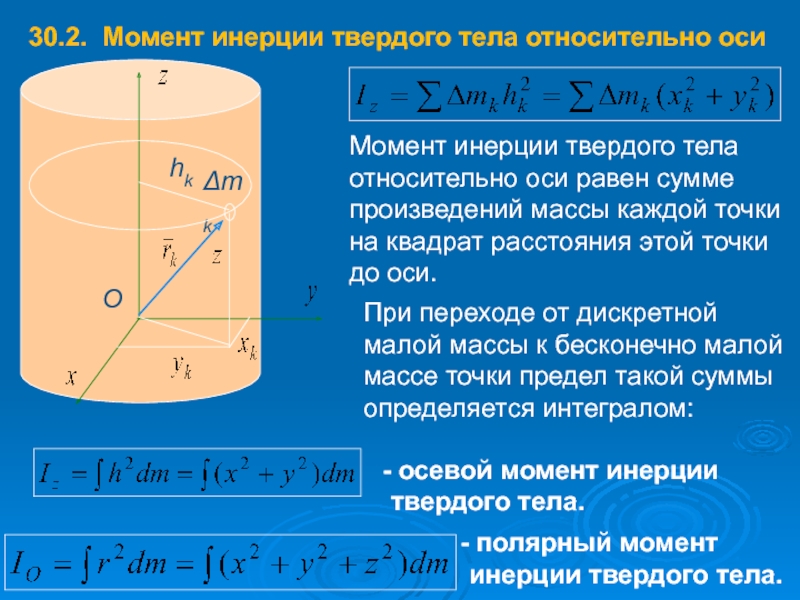

Пример задачи 11-8

Определить момент инерции однородного стержня массы m и длины L о ось под прямым углом к ​​стержню, хотя его центр масс (см. рис. 11.3).

Масса единицы длины стержня равна m/L. Масса dm элемента стержень длиной dx равен

Вклад этой массы в общий момент инерции стержня это

Полный момент инерции стержня можно определить, проинтегрировав по всем частям штанги:

Момент инерции стержня вокруг его конечной точки (см. рис. 11.4) теперь можно рассчитать с помощью теоремы о параллельных осях

Рисунок 11.3. Пример задачи 11-8.

Рисунок 11.4. Пример задачи 11.8.

Пример: Момент инерции диска

Рисунок 11. 5. Момент инерции диска.

Однородный диск имеет радиус R и полную массу M. Плотность диск указан

Чтобы вычислить момент инерции всего диска, сначала посмотрим на небольшой участок диска (см. рис. 5). Площадь кольца, расположенного на расстояние r от центра и ширина dr равна

Масса этого кольца

Вклад этого кольца в общий момент инерции диск указан

Полный момент инерции теперь можно найти, просуммировав все кольца:

Подставляя расчетную плотность, получаем

Предположим, что к точке А приложена сила F (см. рис. 11.6). Точка А часть твердого тела с осью вращения, проходящей через начало координат. Предположим, что угол между силой F и вектором положения r равен [phi]. силу F можно разложить на две составляющие: одну, параллельную положению вектор и один перпендикулярно вектору положения. Очевидно, что компонента, параллельная вектору положения, не может вызвать вращение жесткой тело.

Величина составляющей силы, перпендикулярной вектор положения задается как

Рисунок 11.6. Момент затяжки

Тангенциальная составляющая приложенной силы F создаст вращение объекта; реальная угловая скорость будет зависеть не только от приложенная сила, но и от расстояния между осью вращения и точкой А. Для описания действия силы вводится понятие крутящего момента.

Тангенциальная составляющая F, F _t , создаст тангенциальную ускорение а _т

Крутящий момент [тау] можно переписать как

.

Тангенциальное ускорение a _t связано с угловое ускорение a

Делаем вывод, что

Это всего лишь второй закон Ньютона для вращения.

Пример задачи 11-11

На рис. 11.7 показан однородный диск массой M и радиусом R. Диск устанавливается на неподвижную ось. Брусок массой m висит на шнуре, который оборачивается вокруг обода диска. Найдите ускорение падения блок, угловое ускорение диска и натяжение шнура.

Рисунок 11.7. Пример задачи 11-10.

Силы, действующие на массу и диск, показаны на рис. 11.8. С масса m движется вниз, сила тяжести m ^. г сусла превышает натяжение Т шнура. Линейное ускорение массы m равно определяется как положительный, если он указывает вниз:

Однородный диск вращается за счет наличия массы m. крутящий момент, создаваемый натяжением T шнура на диске, равен

Результирующее угловое ускорение a диска может быть получено из крутящий момент

или

Рисунок 11. 8. Пример задачи 11-10.

Момент инерции диска равен

Угловое ускорение a равно

Однако линейное ускорение шнура равно a, поэтому линейное ускорение обода диска также должно быть а. Линейный ускорение обода и угловое ускорение a связаны следующим образом

Комбинируя это выражение с предыдущим выражением, мы можем сделать вывод что

Если мы объединим это выражение с ранее полученным выражением для

мы можем рассчитать a и T:

Мы видим, что ускорение падающего бруска всегда меньше гравитационное ускорение, но приближается к g, когда масса диска становится много меньше массы m. Угловое ускорение a может быть получено от

Рисунок 11. 9. Работа, совершаемая силой.

Предположим, что к концу стержня (с пренебрежимо малая масса). Под действием силы F система вращается на угол [Delta][theta] (см. рис. 11.9). Работа, совершаемая силой F, равна определяется тангенциальной составляющей F

Здесь r d[theta] — длина дуги, пройденной частицей. Суммарная работа силы за конечное число оборотов (от [тета] _i до [тета] _f ) определяется как

Это уравнение очень похоже на то, что мы получили для линейного движения:

Теперь можно рассчитать общую проделанную работу

или

Это можно переписать как

.

Это соотношение показывает, что работа крутящего момента, действующая на твердую тела равно изменению кинетической энергии вращения этого тела.

---

Присылайте комментарии, вопросы и/или предложения по электронной почте [email protected] и/или посетите домашнюю страницу Frank Wolfs.

Жесткий корпус | bartleby

Что такое твердое тело?

Твердое тело — это объект, который не меняет своей формы и не подвергается какой-либо значительной деформации под действием внешней силы или движения. Математически говоря, расстояние между любыми двумя точками внутри тела не меняется ни при каких обстоятельствах.

Механика твердого тела

Анализируя твердое тело в различных ситуациях, мы используем математическое свойство твердого тела для анализа большинства ситуаций. Три состояния движения твердого тела:

• Равновесие
• Поступательное движение
• Вращательное движение

Равновесие

Когда твердое тело находится в равновесии, его вектор скорости остается неизменным. Он не испытывает никакого линейного или вращательного ускорения. Когда на него действуют несколько сил и он остается в равновесии, тогда векторная сумма всех сил и моментов относительно любой точки всегда равна нулю.

Предположим, что твердое тело «А» остается в равновесии под действием различных сил в разных точках тела. i-я сила обычно отображается в точке P от выбранной оси отсчета.

Сумма всех сил, действующих на тело, определяется выражением

Сумма всех сил =∑iFi

Сумма моментов всех сил относительно точки O определяется выражением

Сумма всех сил моменты = ∑iriFi

Применяя условие равновесия, получаем, ∑iriFi=0 и ∑iFi=0

Поступательное движение

Говорят, что твердое тело находится в поступательном движении, когда все точки движущегося тела движутся равномерно в одном направлении или по одной линии.

В результате движущиеся точки не меняют своей ориентации,

• не вибрируют
• не вращаются

В этом случае все точки внутри тела имеют одинаковую скорость и ускорение.

Например, ракета, запущенная с пусковой установки, имеет все точки, движущиеся с одинаковой скоростью. Скорость и ускорение всех частиц в любой момент времени определяются с помощью законов Ньютона и кинематических уравнений.

Второй закон движения Ньютона гласит, что результирующая внешняя сила связана с ускорением следующим образом:

∑iFi=Ma

Здесь «a» — ускорение тела, а M — его масса. Левая часть представляет собой векторную сумму всех внешних сил, действующих на тело.

В чисто поступательном движении равнодействующая сил может быть ненулевой, но сумма моментов всех сил должна быть равна нулю.

Вращательное движение

Говорят, что тело находится во вращательном движении, когда все частицы движутся по окружности вокруг точки, которая называется точкой вращения. Угол, образуемый линией, соединяющей точку вращения (O) и случайную точку (P) с заданной базовой осью, изменяется со временем. Другими словами, угловое положение точки изменяется со временем, как показано на рисунке ниже. На рисунке θ — начальное угловое положение точки, а P — ее начальное положение для заданных опорных осей. P’ — конечное положение, а θ’ — конечное угловое положение точки.

Изменение угла в течение периода времени определяется выражением,

∆θ=θ’-θ

Скорость изменения углового положения аналогична скорости при поступательном движении и называется угловой скоростью. Точно так же существует угловое ускорение. Вращение твердого тела происходит вокруг воображаемой линии, называемой осью вращения. Ось вращения перпендикулярна плоскости вращения тела. Теперь объект на рисунке вращается в плоскости XY, ось вращения проходит через O и перпендикулярна плоскости XY. Подобно перемещению, мы можем использовать законы Ньютона и кинематические уравнения для определения углового положения, скорости и ускорения в любой момент времени. Вместо силы в поступательном движении здесь мы используем момент или крутящий момент силы относительно оси вращения. Величина, называемая моментом инерции, заменяет массу. Момент инерции твердого тела относительно оси вращения определяется выражением

Момент инерции 

I=∑imiri2

Здесь mi – масса i-го элемента тела, а ri – перпендикулярное расстояние элемента от оси вращения, как показано на рисунке.

Теперь второй закон движения в механике вращения принимает вид:

∑iri→×Fi→=Iα

результирующий момент, действующий на твердое тело. Для одиночной силы F на расстоянии r от данной оси ее крутящий момент относительно оси определяется выражением

Крутящий момент

τ→=r→×F→

Крутящий момент аналогичен силе при вращательном движении.

Твердое тело может совершать комбинацию этих движений. Но условие недеформации выполняется несмотря ни на что. Расстояние между любыми двумя точками остается постоянным. Это также можно сказать другими словами, что относительная скорость вдоль линии, соединяющей любые две точки, равна нулю. Если мы возьмем твердый стержень длины L в движении, Если две точки A и B имеют разные скорости, как показано на рисунке, относительная скорость точки вдоль линии соединения (или длина стержня в этом случае) равна нулю .

На приведенном выше рисунке, если мы вычислим компоненты скоростей точек A и B вдоль стержня и применим условие, мы получим,

vACosα- vBCosβ=0

Контекст и приложения

профессиональные экзамены как для бакалавриата, так и для магистратуры, особенно для

• Бакалавр технологии (машиностроение)
• Магистр технологии (машиностроение)
• Бакалавр наук в области физики

Практические задачи

Q 1 . Когда твердое тело находится в трансляционном движении, все частицы внутри тела имеют

1. такую ​​же скорость
2. То же ускорение
3. Различная скорость
4. Оба (A) и (B)

Ответ : (d)- Оба (a) и (b)

Объяснение — Когда твердое тело находится в поступательном движении, все частицы внутри тела имеют одинаковую скорость и ускорение.

Q 2. Векторное векторное произведение силы на расстояние положения силы дает 006

Ответ : (a) Крутящий момент силы

Объяснение — Векторное векторное произведение силы и расстояния положения силы дает крутящий момент или момент силы.

Q 3. Какой из следующих законов движения Ньютона утверждает, что сила пропорциональна ускорению?

1. Ньютон I закон движения
2. Ньютон II закон движения
3. Фарадей закон движения
4. Ньютон III закон движения

Ответ : (b) Ньютона’ s II закон движения

Объяснение — Ньютона II Закон гласит, что ускорение тела пропорционально силе.

В 4. Какова сумма крутящих моментов при чисто поступательном движении?

1. Ноль
2. Меньше нуля
3. Больше нуля
4. Не могу сказать

Ответ : (a) — Ноль

906 63 Пояснение — В чистом переводе сумма крутящих моментов всегда равна нулю .

Q 5. Что из перечисленного ниже характерно для твердого тела?

1. Поворотный
2. Нерастяжимый и недеформируемый
3. Подвижный
4. Изгибаемый

Ответ : (b)-Нерастяжимый и недеформируемый

Объяснение — Твердое тело нерастяжимо и недеформируемо.

Формулы

Если твердое тело находится в равновесии, то

• Второй закон Ньютона для поступательного движения определяется формулой                                                     ∑iFi=Ma
  • Момент инерции тела определяется выражением,

  I=∑imiri2

  • Второй закон Ньютона во вращательном движении определяется формулой 03 Механика
  • Вращательное движение
  • Кинематика
  • Центр масс
  • Момент инерции
  • Угловое движение

  Мы обеспечим вас пошаговыми решениями миллионов задач из учебников, экспертами в любой области наготове 24 часа в сутки, 7 дней в неделю, когда вы запутались, и многое другое .