Моментом инерции материальной точки относительно оси называют величину — Студопедия
Поделись с друзьями:
ЛАБОРАТОРНАЯ РАБОТА № 4
ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы
Исследование крутильных колебаний и измерение момента инерции тела сложной формы.
Теоретическая часть
Момент инерции. Теорема Штейнера
Моментом инерции материальной точки относительно оси называют величину
,
где mi – масса материальной точки, ri – расстояние от материальной точки до оси.
Моментом инерции тела относительно оси называют сумму моментов инерции материальных точек, составляющих его
.
Представляя тело состоящим из малых частей объемом dV и массы dm, его момент инерции можно рассчитать интегрированием
, (2.
1)
где ρ – плотность.
Рассчитаем, например, момент инерции тонкого однородного стержня массы m и длины l относительно оси перпендикулярной стержню и проходящей через его середину (рис. 2.1).
| ||||
равен . (2.2)
Если известен момент инерции тела относительно оси, проходящей через центр масс, то момент инерции тела относительно любой параллельной оси можно определить, воспользовавшись теоремой Штейнера, согласно которой момент инерции J тела относительно произвольной оси равен сумме момента инерции Jс тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями
.
|
Используя уравнение (2.2), теорему Штейнера и уравнение (2.1) рассчитаем момент инерции параллелепипеда относительно оси симметрии.
Рис. 2.2
.
, (2.4)
где а и b – длины сторон параллелепипеда, расположенные в горизонтальной плоскости, m – масса параллелепипеда.
Момента инерции тела относительно оси является мерой инертности тела при вращательном движении и зависит не только от массы тела, но и от распределения ее в пространстве относительно оси.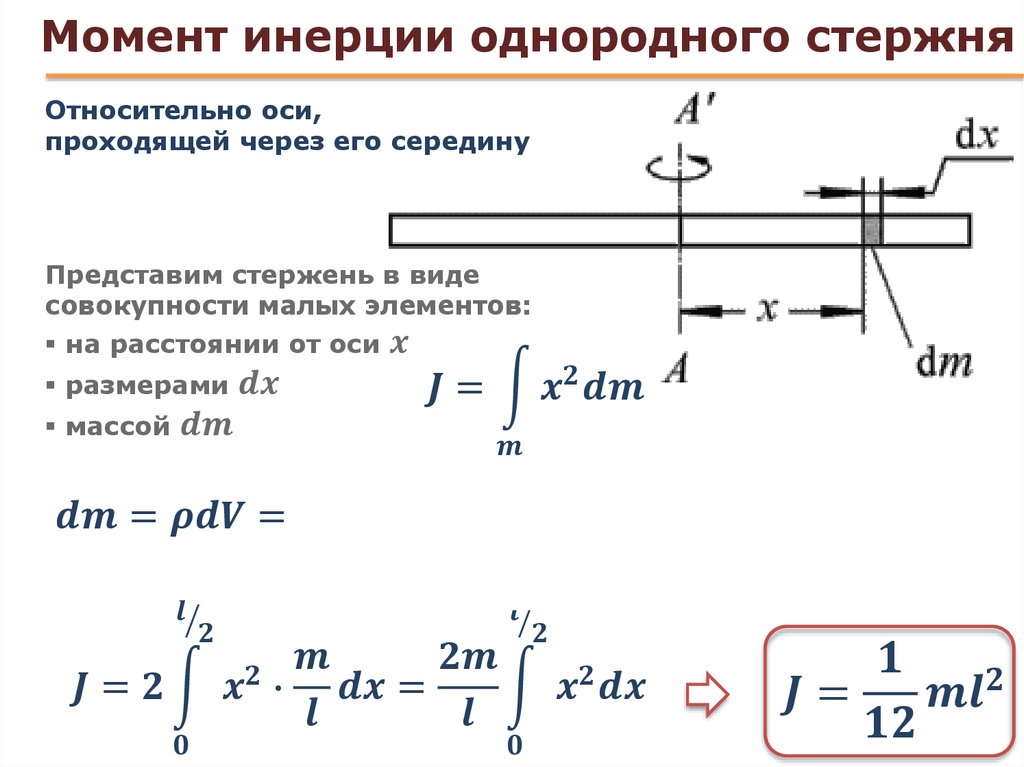
Тело обладает определенным моментом инерции относительно любой оси независимо от того вращается оно или покоится.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Вращение твердого тела
Для кинематического описания вращения твердого тела удобно использовать угловые величины: угловое перемещение Δφ, угловую скорость ω
и угловое ускорение ε
В этих формулах углы выражаются в радианах. При вращении твердого тела относительно неподвижной оси все его точки движутся с одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями. За положительное направление вращения обычно принимают направление против часовой стрелки.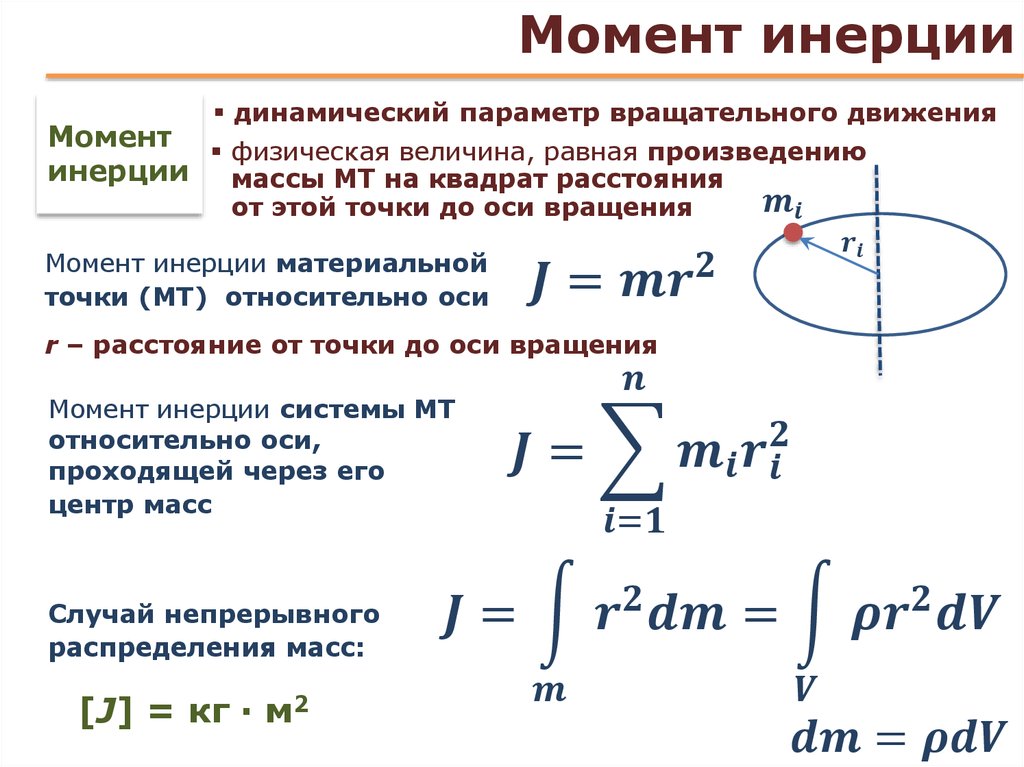
| Рисунок 1.23.1. Вращение диска относительно оси, проходящей через его центр O |
При малых угловых перемещениях Δφ модуль вектора линейного перемещения некоторого элемента массы Δm вращающегося твердого тела выражается соотношением:
| Δs = rΔφ, |
где r – модуль радиус-вектора (рис. 1.23.1). Отсюда следует связь между модулями линейной и угловой скоростей:
| υ = rω, |
и между модулями линейного и углового ускорения:
| a = aτ = rε. |
Векторы и направлены по касательной к окружности радиуса r.
Следует вспомнить, что при движении тела по окружности возникает также нормальное или центростремительное ускорение, модуль которого есть
Разобьем вращающееся тело на малые элементы Δmi. Расстояния до оси вращения обозначим через ri, модули линейных скоростей – через υi. Тогда кинетическую энергию вращающегося тела можно записать в виде:
Физическая величина зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:
В пределе при Δm → 0 эта сумма переходит в интеграл.
Единица измерения момента инерции в СИ – килограмм-метр в квадрате (кг∙м2). Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде
Эта формула очень похожа на выражение для кинетической энергии поступательно движущегося тела только теперь вместо массы m в формулу входит момент инерции I, а вместо линейной скорости υ – угловая скорость ω.
Момент инерции в динамике вращательного движения играет ту же роль, что и масса тела в динамике поступательного движения. Но есть и принципиальная разница. Если масса – внутреннее свойство данного тела, не зависящее от его движения, то момент инерции тела зависит от того, вокруг какой оси оно вращается. Для разных осей вращения моменты инерции одного и того же тела различны.
Во многих задачах рассматривается случай, когда ось вращения твердого тела проходит через его центр массы. Положение xC, yC центра масс для простого случая системы из двух частиц с массами m1 и m2, расположенными в плоскости XY в точках с координатами x1, y1 и x2, y2 (рис. 1.23.2), определяется выражениями:
| Рисунок 1.23.2. Центр масс C системы из двух частиц |
В векторной форме это соотношение принимает вид:
Аналогично, для системы из многих частиц радиус-вектор центра масс определяется выражением
Для сплошного тела суммы в выражении для заменяются интегралами.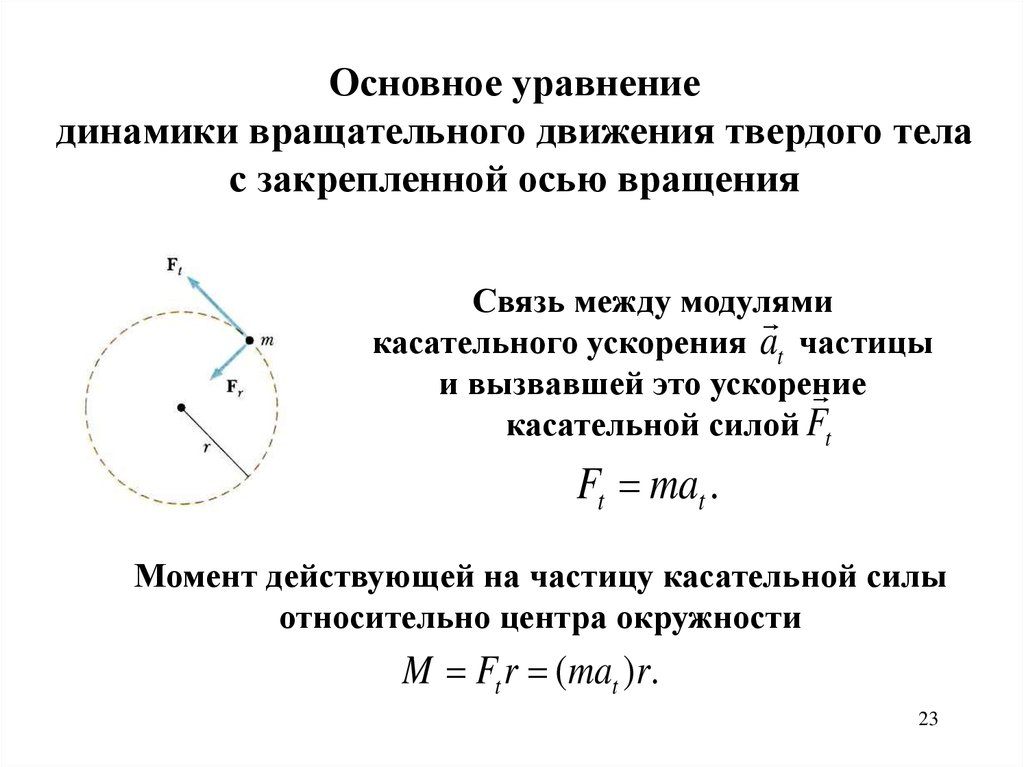
Легко видеть, что в однородном поле тяготения центр масс совпадает с центром тяжести. Если в однородном поле тяготения твердое тело сложной формы подвесить за центр масс, то оно будет находиться в безразличном состоянии равновесия. Поэтому положение центра масс тела сложной формы можно практически определить путем последовательного подвешивания его за несколько точек и отмечая по отвесу вертикальные линии (рис. 1.23.3).
| Рисунок 1.23.3. Определение положения центра масс C тела сложной формы. A1, A2, A3 точки подвеса |
Равнодействующая сил тяжести в однородном поле тяготения приложена к центру масс тела. Если тело подвешено за центр масс, то оно находится в состоянии безразличного равновесия (см. §1.14).
Любое движение твердого тела можно представить как сумму двух движений: поступательного движения со скоростью центра масс тела и вращения относительно оси, проходящей через центр масс.
Примером может служить колесо, которое катится без проскальзывания по горизонтальной поверхности (рис. 1.23.4). При качении колеса все его точки движутся в плоскостях, параллельных плоскости рисунка. Такое движение называется плоским.
При плоском движении кинетическая энергия движущегося твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, проходящей через центр масс тела и перпендикулярной плоскостям, в которых движутся все точки тела:
где m – полная масса тела, IC – момент инерции тела относительно оси, проходящей через центр масс.
| Рисунок 1.23.4. Качение колеса как сумма поступательного движения со скоростью и вращения с угловой скоростью относительно оси O, проходящей через центр масс |
В механике доказывается теорема о движении центра масс: под действием внешних сил центр масс любого тела или системы взаимодействующих тел движется как материальная точка, в которой сосредоточена вся масса системы.
Иллюстрацией этого утверждения может служить рис. 1.23.5, на котором изображено движение тела под действием силы тяжести. Центр масс тела движется по параболической траектории как материальная точка, в то время как все другие точки движутся по более сложным траекториям.
| Рисунок 1.23.5. Движение твердого тела под действием силы тяжести |
Если твердое тело вращается относительно некоторой неподвижной оси, то его момент инерции I можно выразить через момент инерции IC этого тела относительно оси, проходящей через центр масс тела и параллельной первой.
| Рисунок 1.23.6. К доказательству теоремы о параллельном переносе оси вращения |
Рассмотрим сечение твердого тела произвольной формы, изображенное на рис. 1.23.6. Выберем координатную систему XY с началом координат O в центре масс C тела.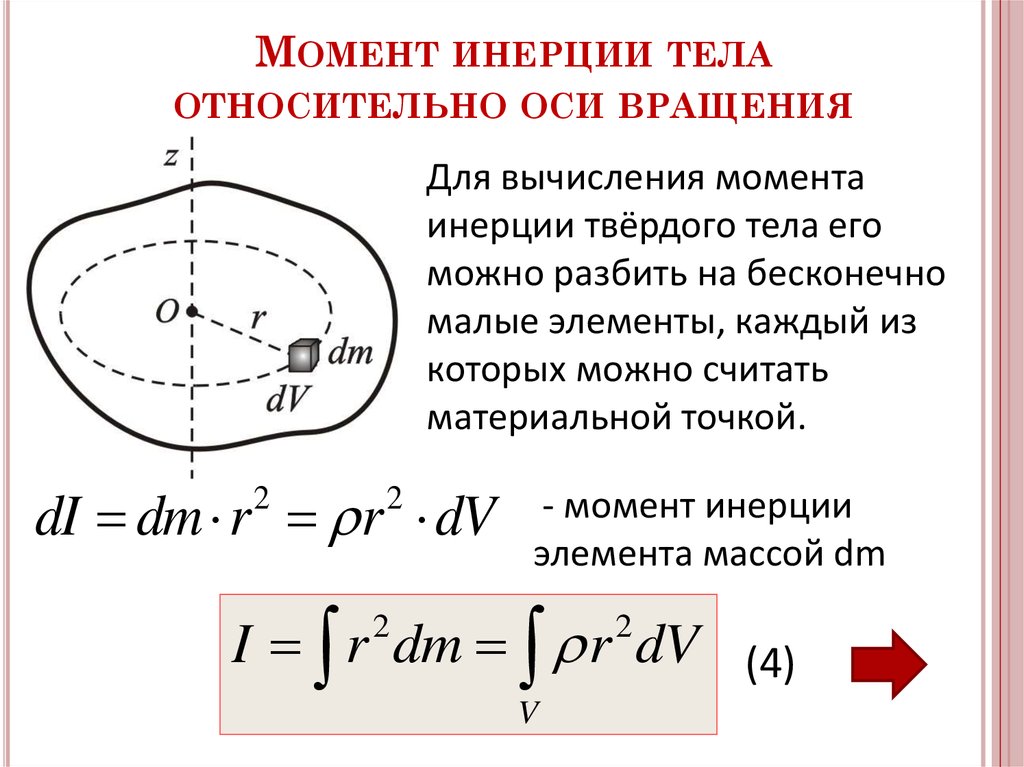
Пусть одна из осей вращения проходит через центр масс C, а другая через произвольную точку P, расположенную на расстоянии d от начала координат. Обе оси перпендикулярны плоскости чертежа. Пусть Δmi – некоторый малый элемент массы твердого тела. По определению момента инерции:
Выражение для IP можно переписать в виде:
Поскольку начало координат совпадает с центром масс C, последние два члена обращаются в нуль. Это следует из определения центра масс. Следовательно,
|
где m – полная масса тела.
Этот результат называют теоремой Штейнера (теоремой о параллельном переносе оси вращения).
Модель. Момент инерции |
На рис. 1.23.7 изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
| Рисунок 1.23.7. Моменты инерции IC некоторых однородных твердых тел |
Второй закон Ньютона может быть обобщен на случай вращения твердого тела относительно неподвижной оси. На рис. 1.23.8 изображено некоторое твердое тело, вращающееся относительно оси, перпендикулярной плоскости рисунка и проходящей через точку O. Выделим произвольный малый элемент массы Δmi. На него действуют внешние и внутренние силы. Равнодействующая всех сил есть Ее можно разложить на две составляющие: касательную составляющую и радиальную Радиальная составляющая создает центростремительное ускорение an.
| Рисунок 1.23.8. Касательная и радиальная составляющие силы действующей на элемент Δmi твердого тела |
Касательная составляющая вызывает тангенциальное ускорение массы Δmi. Второй закон Ньютона, записанный в скалярной форме, дает
| Δmiaiτ = Fiτ = Fi sin θ или Δmiriε = Fi sin θ, |
где – угловое ускорение всех точек твердого тела.
Если обе части написанного выше уравнения умножить на ri, то мы получим:
Здесь – плечо силы – момент силы.
Теперь нужно аналогичные соотношения записать для всех элементов массы Δmi вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:
Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.
Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M. В итоге:
|
Это и есть основное уравнение динамики вращательного движения твердого тела. Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими. Обычно за положительное направление вращения принимают направление против часовой стрелки.
Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины , , определяются как векторы, направленные по оси вращения.
При изучении поступательного движения тел вводится понятие импульса тела (см. §1.16). Аналогично, при изучении вращательного движения вводится понятие момента импульса.
Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L:
|
Поскольку уравнение вращательного движения можно представить в виде:
Окончательно будем иметь:
Это уравнение, полученное здесь для случая, когда I = const, справедливо и в общем случае, когда момент инерции тела изменяется в процессе движения.
Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = Iω относительно данной оси сохраняется:
| ΔL = 0, если M = 0. |
Следовательно,
|
Это и есть закон сохранения момента импульса. Иллюстрацией этого закона может служить неупругое вращательное столкновение двух дисков, насажанных на общую ось (рис. 1.23.9).
| Рисунок 1.23.9. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I1ω1 = (I1 + I2)ω |
Закон сохранения момента импульса справедлив для любой замкнутой системы тел.
Он выполняется, например, при движении планет по эллиптическим орбитам вокруг Солнца (второй закон Кеплера).
Уравнение вращательного движения тела можно записывать не только относительно неподвижной или равномерно движущейся оси, но и относительно оси, движущейся с ускорением.
Основное уравнение динамики вращательного движения не изменяет своего вида и в случае ускоренно движущихся осей при условии, что ось вращения проходит через центр массы тела и что ее направление в пространстве остается неизменным. Примером может служить качение тела (обруч, цилиндр, шар) по наклонной плоскости с трением (рис. 1.23.10).
| Рисунок 1.23.10. Качение симметричного тела по наклонной плоскости |
Ось вращения O проходит через центр масс тела. Моменты силы тяжести и силы реакции относительно оси O равны нулю. Момент M создает только сила трения: M = FтрR.
Уравнение вращательного движения:
где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, IC – момент инерции относительно оси O, проходящей через центр масс.
Второй закон Ньютона для поступательного движения центра масс записывается в виде:
| ma = mg sin α – Fтр. |
Исключая из этих уравнений Fтр, получим окончательно:
Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара а у сплошного однородного цилиндра Следовательно, шар будет скатываться быстрее цилиндра.
Момент инерции | Определение, формула и расчет
У вас возникла проблема и вам нужен наш сервис?
Наши специалисты Baumüller Services занимаются ремонтом , капитальным ремонтом, запасными частями, заменой двигателей и электроники , а также многими другими вопросами послепродажного обслуживания.
Обратитесь в Baumüller Services
Опишите нам свой запрос, и ответственное контактное лицо свяжется с вами в кратчайшие сроки.
Сообщение
Неверный ввод
Компания и контактное лицо
Приветствие
Г-н
Г-жа
Неверный ввод
Имя
Пожалуйста, введите имя 900 07
Фамилия (*)
Пожалуйста, заполните фамилию
Фамилия
Неверный ввод
Компания (*)
Пожалуйста, заполните название компании
Страна (*)
Пожалуйста, выберите—Uni Тед КоролевствоСоединенные ШтатыИрландияИндия—АфганистанАландские островаАлбанияАлжирАмериканское СамоаАндорраАнголаАнгильяАнтарктидаАнтигуа и БарбудаАргентинаАрменияАрубаАвстралияАвстрияАзербайджанБагамыБахрейнБангладешБарбадосБеларусьБельгияБелизБенинБермудыБутанБоливияБонайре, Синт-Эстатиус и СабаБосния и ГерцеговинаБотсванаОстров БувеБразилияБританская территория в Индийском океанеБрунейБолгарияБуркина-ФасоБурундиКамбоджаКамерунКанадаКабо-ВердеКаймановы островаЦентральноафриканская РеспубликаЧадЧилиКитайОстров РождестваКокосовые острова (Килинг)КолумбияКоморские островаКонгоОстрова КукаКоста-РикаКот-д’ИвуарХорваты иаКубаКюрасаоКипрЧехияДемократическая Республика КонгоДанияДжибутиДоминикаДоминиканская РеспубликаЭквадорЕгипетСальвадорЭкваториальная ГвинеяЭритреяЭстонияЭфиопияФолклендские (Мальвинские) островаФарерские островаФиджиФинляндияФранцияФранцузская ГвианаФранцузская ПолинезияФранцузские Южные ТерриторииГабонГамбияГрузияГерманияГанаГибрал деготьГрецияГренландияГренадаГваделупаГуамГватемалаГернсиГвинеяГвинея-БисауГайанаГаитиСлышали Острова и острова МакдональдыГондурасГонконгВенгрияИсландияИндияИндонезияИранИракИрландияОстров МэнИзраильИталияЯмайкаЯпонияДжерсиИорданияКазахстанКенияКирибатиКосовоКувейтКыргызстанЛаосЛатвияЛиванЛесотоЛиберияЛивияЛихтенштейнЛитваЛюксембургМакаоМакедонияМадагаскар МалавиМалайзияМальдивыМалиМальтаМаршалловы островаМартиникаМавританияМаврикийМайоттаМексикаМикронезияМолдаваМонакоМонголияЧерногорияМонтенегроМонтсерратМароккоМозамбикМьянма (Бирма)НамибияНауруНепалНидерландыНовая КаледонияНовая ЗеландияНикарагуаНигерНигерияНиуэ Остров НорфолкСеверная КореяСеверные Марианские острова НорвегияОманПакистанПалауПалестинаПанамаПапуа-Новая ГвинеяПарагвайПеруФилиппиныПиткэрнПольшаПортугалияПуэрто-РикоКатарРеюньонРумынияРоссияРуандаСент-БартельмиСент-ХеленаСент-Китс и НевисСент-ЛюсияСен-МартинСен-Пьер и МикелонСент-Винсент и ГренадиныСамоаСан-МариноСан-Томе и ПринсипиСаудовская Аравия enegalСербияСейшельские островаСьерра-ЛеонеСингапурСинт-МартенСловакияСловенияСоломоновы островаСомалиЮжная АфрикаЮжная Георгия и Южные Сандвичевы островаЮг КореяЮжный СуданИспанияШри-ЛанкаСуданСуринамШпицберген и Ян-МайенСвазилендШвецияШвейцарияСирияТайваньТаджикистанТанзанияТаиландТимор-Лешти (Восточный Тимор)ТогоТокелауТонгаТринидад и ТобагоТунисТурцияТуркменистанОстрова Теркс и КайкосТувалуУгандаУкраинаОбъединенные Арабские ЭмиратыВеликобританияСШАУругвайУз БекистанВануатуВатиканВенесуэлаВьетнамВиргинские острова, Британские Виргинские острова, СШАУоллис и ФутунаЗападная СахараЙеменЗамбияЗимбабве
Пожалуйста, выберите страну
Улица, номер
Пожалуйста, укажите улицу и номер
Почтовый индекс (*)
Пожалуйста, укажите почтовый индекс
Город (*) 900 06
Неверный ввод
Пожалуйста, укажите местонахождение вашей компании, чтобы мы могли найти нужное контактное лицо для вашего региона.
Как бы вы хотели, чтобы с вами связались?
по телефону
по электронной почте
Bitte geben Sie an, wie wir Sie kontaktieren sollen.
Код страны
Неверный ввод
Телефон
Неверный ввод
completePhone
Неверный ввод
Электронная почта (*)
Частные домены электронной почты исключены
Spamschutz (*)
Защита от спама не удалась.
Поля, отмеченные звездочкой (*), обязательны для заполнения.
Хотите связаться с нами напрямую?
Baumüller Nürnberg GmbH Ostendstraße 80-90
90482 Нюрнберг
Германия
+49 911 5432 0
mail@baumueller.
com
Ваш ресурс по физике » Уроки » Момент инерции
Мы обсудили вращательные аналоги всех важных линейных величин, кроме одной: массы. Можно подумать, что массу не нужно описывать по-другому. Я имею в виду, это довольно базовое количество, верно?
Но подумайте об этом. Масса является мерой инерции, тенденции объекта сопротивляться изменениям в его движении. Теперь представьте, что груз раскачивается на веревке по кругу. Сначала вы крутите его по маленькому кругу, а затем по большому кругу с той же скоростью. Изменить его движение (в данном случае остановить) будет сложнее, когда он будет раскачиваться по большому кругу, поэтому этот угловой аналог каким-то образом зависит от радиуса вращения.
Это называется моментом инерции (или угловой инерцией) и обозначается скаляром, если только мы не говорим о тензорном моменте инерции, который мы использовали бы, если бы а) мы не знали ось вращения и б) мы знали, что такое тензоры. Сначала мы определим его для точечной массы, но сначала нам нужно указать ось вращения.
В формуле нашего примера будет использоваться -ось. Хотя это не так важно; одна ось бессмысленна, пока мы не настроим другие. В любом случае, если расстояние частицы от -оси равно , (Естественно, мы можем заменить s на s или s или любую другую произвольную ось.)
Конечно, это не очень полезно, если мы не имеем дело с точечными массами, что обычно и бывает. К счастью, момент инерции является аддитивным, поэтому мы можем (приготовьтесь к этому, это будет звучать знакомо) разбить наши объекты на множество маленьких кусочков массы и сложить их все с нашим любимым знаком интеграла:
В качестве примера найдем выражение для момента инерции твердого шара с одинаковой плотностью, массой и радиусом относительно оси . В сферических координатах (самых удобных, поскольку мы имеем дело со сферой) , поэтому в нашем интеграле . Обратите внимание, что мы используем сферические координаты вида , что важно, поскольку в разных текстах используются разные системы. Далее мы воспользуемся определением объемной плотности и решим для .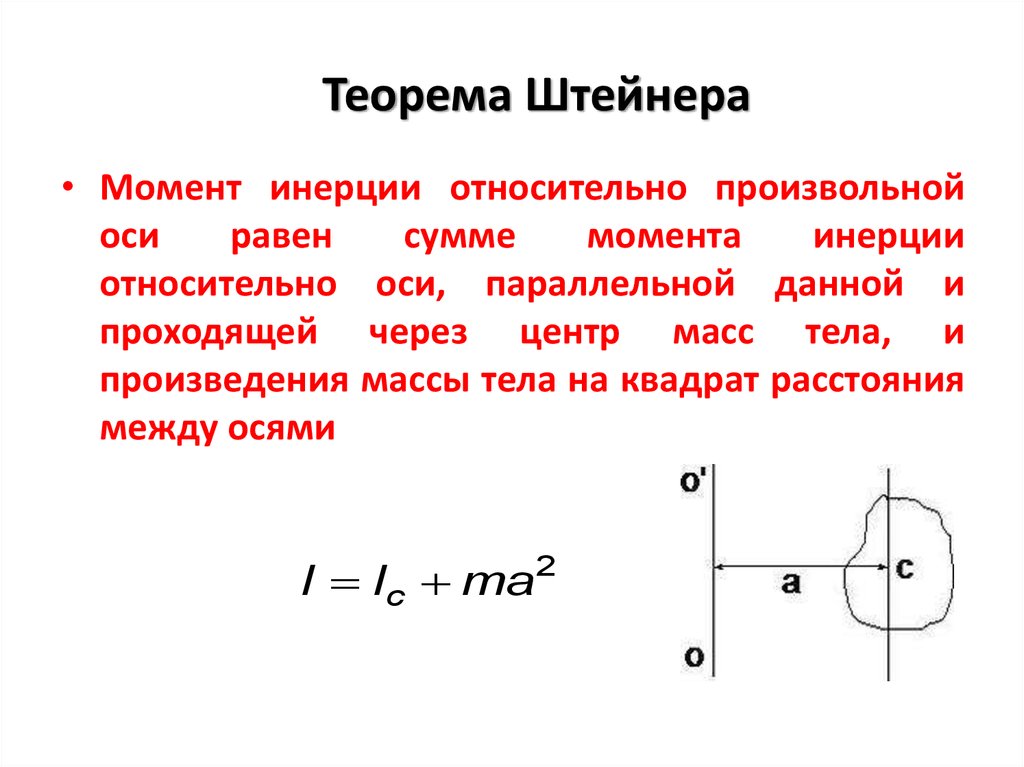
Теперь у вас есть выбор: оценить это или заставить сделать это ваш калькулятор. Я рекомендую последнее, тем более что лично я ненавижу сферические координаты. Если вы попробуете это вручную, вам понадобится идентификатор вместе с некоторой заменой. Во всяком случае, результат что мы можем помочь, отметив, что и мы знаем, что для сферы , поэтому который мы подставляем обратно в уравнение, чтобы получить Вау!
Вот краткий справочник некоторых часто используемых моментов инерции. Предположим, что каждый объект имеет массу. Размеры будут, каждый только там, где это применимо, радиус , высота и длина . (Вы можете вывести их самостоятельно, используя очень похожие и во многих случаях более простые методы, но если вы понимаете, как вы может этого вполне достаточно. Мы также определим оси фигур так, чтобы фигура указывала направление.
