|
Конспект урока
Формула вычисления скалярного произведения векторов по определению: Формула вычисления скалярного произведения векторов через координаты: Основная литература: Гусева В.А., Куланин Е.Д. Геометрия. Профильный уровень. 10 класс — М.: Бином, 2010 — с. 130-148 Погорелов А.В. Геометрия. Учеб. для 7-11 кл. общеобразоват. Учреждение — 13-е изд-е. — М.: Просвещение, 2014. — с. 51-52 Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7-9 кл. 20-е изд-е. — М.: Просвещение, 2010. — с. 259-270. Открытые электронные ресурсы: Решу ЕГЭ образовательный портал для подготовки к экзаменам Теоретический материал для самостоятельного изучения Работа по теме урока. Объяснение новой темы Угол между векторами Если векторы не являются сонаправленными, то лучи ОА и ОB образуют угол АОВ. Определение: Два вектора называются перпендикулярными, если угол между ними равен 90°. Доказательство утверждений:
Угол между векторами.
Сформулируем основные свойства скалярного произведения векторов.
Примеры и разбор решения заданий тренировочного модуля
Дано: прямоугольный параллелепипед, где . Найти и . Решение: ранее в таких случаях мы пытались по рисунку находить величины углов. Но теперь мы владеем формулой косинуса угла между прямыми. Только для этого необходимо знать координаты направляющих векторов прямых. В данном случае, для прямой BD направляющим может является вектор BD , а для прямой
Тогда не трудно определить координаты точек B, D, C и D1. Точка B(0;0;0). Точка D(1;1;0). Точка C(0;1;0) . А точка D (1;1;2). Теперь не трудно найти координаты векторовBD и CD как разности соответствующих координат конца и начала вектора. Получаем, что вектор BD {1-0;1-0;0-0}. А вектор CD{1-0;1-1;2-0}. Теперь можем воспользоваться формулой косинуса угла между прямыми. Подставим координаты направляющих векторов. Рис. 15 Пример 2. Дано: DABC – пирамида; DA ⊥ DB ⊥ DC; DA = DB = DC = а. Найдите: косинус угла между прямыми DC и CM (СМ – высота треугольника АВС), поставьте ему в соответствие верный вариант ответа из предложенных ниже: Решение:
Применив формулу косинуса угла между векторами, получим .
жүктеу/скачать 100,64 Kb. Достарыңызбен бөлісу: |
ПЗ №34 Скалярное произведение векторов и его свойства
Практическое занятие №34 Скалярное произведение векторов и его свойства
Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними. Скалярное произведение векторов и принято обозначать или точкой , или круглыми скобками . Т.е. , где – угол между векторами и .
Свойства скалярного произведения векторов
1. Скалярное произведение обладает переместительным свойством, то есть
.
2. Скалярное произведение обладает распределительным свойством, то есть
.
3. Скалярное произведение обладает сочетательным свойством относительно числового множителя, то есть
.
4. Скалярное произведение вектора самого на себя называется скалярным квадратом вектора. Скалярный квадрат вектора равен квадрату его модуля. То есть
.
Из этого равенства следует, что .
5. Скалярное произведение одноименных ортов равно единице.
.
6. Скалярное произведение разноименных ортов равно нулю.
.
7. Скалярное произведение векторов, заданных своими координатами:
,
если и .
8. Угол между двумя векторами:
.
9. Если , то .
10. Проекция вектора на вектор :
.
Если вектора заданы своими координатами, т.е. , то
.
Пример. Пусть , , .
Решение.
1) Из определения скалярного произведения имеем: .
Следовательно: .
.
.
2) По свойствам скалярного произведения , если .
. Т.о. , следовательно, и не ортогональны.
3) По свойствам скалярного произведения проекцию вектора на вектор можно найти по формуле: .
.
Следовательно, .
№2 Векторы и заданы своими координатами. Требуется:
1) вычислить , ;
2) найти длину вектора ;
3) проверить, верно ли, что , если и ;
4) найти проекцию вектора на вектор ;
5) изобразить векторы и в декартовой системе координат.
Пример. Пусть .
Решение.
1) По свойствам скалярного произведения ,
если и . Таким образом
.
Найдем координаты векторов и .
.
.
Тогда
.
2) По формулам скалярного произведения .
Найдем координаты вектора :
.
Таким образом . Тогда
.
3) тогда и только тогда, когда .
Найдем координаты векторов и . если и .
.
Таким образом .
.
Таким образом .
Найдем скалярное произведение векторов и .
.
Так как , то вектора и не ортогональны.
4) По свойствам скалярного произведения проекцию вектора на вектор можно найти по формуле: .
Скалярное произведение было вычислено ранее, поэтому нам осталось вычислить . Так как , то
.
Таким образом
.
.
Видео-урок: скалярное произведение двух векторов
Стенограмма видео
В этом видео мы говорим о
скалярное произведение двух векторов.
Мы будем изучать технику
для объединения двух векторов таким образом, чтобы результатом была величина, имеющая
величина, но не направление, то есть является скаляром.
Сначала мы можем задаться вопросом, почему
мы когда-нибудь хотели бы сделать это. Почему мы хотим взять два
векторы, мы могли бы назвать их 𝐀 и 𝐁, которые оба имеют величину и направление
связаны с ними и комбинируем их таким образом, что мы теряем информацию? То есть мы теряем направление
Информация. Хотя на самом деле там
физические ситуации, когда это полезно. Рассмотрим этот пример коробки
опираясь на ровную поверхность. Допустим, нажав на
коробка с вектором силы, показанным здесь, наша цель — толкать коробку по поверхности
чтобы он сместился. Теперь, если мы действительно в состоянии сделать
это, если, применяя эту силу 𝐅, мы можем сместить коробку на это смещение
𝐝.
Но сколько работы у нас сделано? Оказывается, этот метод мы учимся брать скалярное произведение двух векторов. Обратите внимание, что в этой ситуации мы имеют два вектора: силу, которую мы прикладываем к ящику, и смещение. И пока мы работаем, мы хотим вычислить зависит от этих векторов, сама работа не является векторной величиной, а скорее является скалярной величиной. Итак, мы хотим объединить векторы силы и смещения таким образом, чтобы получился скаляр. Сделаем это с помощью операции известное как скалярное произведение. Символически эта операция представлены так же, как мы сделали здесь, используя точку между двумя векторами, которые мы комбинируя.
По этой причине скалярное произведение
двух векторов также известен как скалярное произведение.
Таким образом, эти два члена, скалярное произведение
и скалярное произведение означают одно и то же. Сейчас есть парочка
различные способы вычисления скалярного или скалярного произведения. Один из способов сделать это — использовать то, что мы
можно назвать геометрическим подходом. Думая с этой точки зрения,
давайте представим эти два вектора 𝐀 и 𝐁, которые мы назвали здесь. И допустим, что это вектор
𝐀 и что вот это вектор 𝐁. Если бы мы вычислили скаляр
произведения 𝐀 и 𝐁, мы могли бы показать, что это происходит, переместив эти векторы так, чтобы
хвосты каждого из них перекрываются. Мы можем сделать это, скажем, сместив
вектор 𝐀.
Сделав это, мы считаем
более короткий из наших двух векторов, в данном случае это вектор 𝐀. И тогда мы спрашиваем себя, насколько
вектора 𝐀 лежит вдоль или перекрывает вектор 𝐁. Мы можем начать выяснять это с
рисуем линию, которая идет от кончика нашего более короткого вектора, а затем спускается к
более длинный вектор пересекает этот более длинный вектор под углом 90 градусов.
Итак, каково это расстояние, которое
мы выделили? Если мы зададим угол между вектором
𝐀 и вектор 𝐁 имя, скажем, мы называем это 𝜃. Затем это расстояние мы отметили
в оранжевом цвете равна величине 𝐀, умноженной на косинус этого угла. Мы могли бы сказать, что это то, насколько
вектора 𝐀 лежит вдоль вектора 𝐁. И как только мы вычислили это,
мы довольно близки к вычислению скалярного или скалярного произведения наших двух векторов 𝐀
и 𝐁. 𝐀 точка 𝐁 равна этому перекрытию
между векторами 𝐀 и 𝐁 величина более короткого вектора, умноженная на косинус
угол между ними, умноженный на величину более длинного вектора, в данном случае
вектор 𝐁.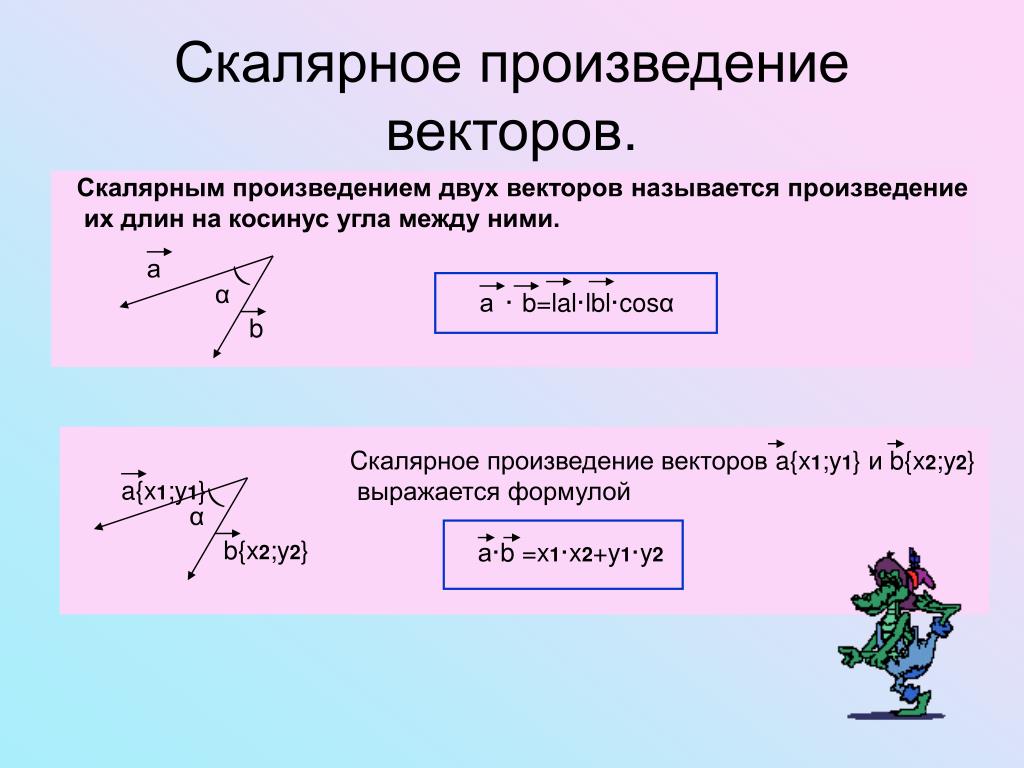
И мы можем изменить это
выражение и запишите его таким образом. Величина одного вектора, умноженная на
величина других, умноженная на cos угла между ними.
Итак, возвращаясь к нашему примеру толкая этот ящик и вычисляя работу, которую мы совершаем над ящиком, мы можем сказать, что если угол между вектором силы, которую мы прикладываем к ящику, и перемещением ящика равен 𝜃. Тогда совершенная нами работа равна величина 𝐅, умноженная на величину 𝐝, умноженная на косинус этого угла 𝜃. Это равно скалярному произведению из 𝐅 и 𝐝. И обратите внимание, что этот продукт действительно скалярная величина. У него нет направления, но он есть. иметь величину.
В этом геометрическом объяснении
скалярное произведение, мы предполагали, что один из двух векторов, которые мы комбинируем,
короче другого. Но на самом деле это не обязательно
случай, чтобы вычислить скалярное произведение двух векторов.
Даже если, например, векторы 𝐀
и векторы 𝐁 были одинаковой величины, мы все еще могли вычислить их перекрытие
путь. И затем при умножении этого
перекрываются на величину другого вектора, в данном случае вектора 𝐁, мы бы
вычислить их скалярное произведение. Поэтому не нужно слишком зацикливаться на
какой вектор короче или длиннее. Это просто способ помочь нам
визуализируйте, что такое скалярное произведение.
Как мы упоминали ранее,
Геометрический подход не единственный для вычисления скалярного произведения. Есть также то, что мы могли бы назвать
алгебраический способ сделать это. Чтобы увидеть, как это работает, давайте
представьте, что у нас есть эти два вектора 𝐀 и 𝐁, не нарисованные графически. Но вместо этого они написаны
их составные части, как это. Итак, вектор 𝐀 определяется своим 𝑥-
и 𝑦-компоненты.
И точно так же вектор 𝐁 имеет некоторые
величина в 𝐢-направлении и некоторая величина в 𝐣. Когда 𝐀 и 𝐁 определены, это
Таким образом, мы можем вычислить их скалярное произведение следующим образом. Умножаем 𝑥-компоненты
каждый вектор, и мы добавляем это произведение к произведению их 𝑦-компонент.
Теперь независимо от того, какой из этих
два подхода, которые мы используем, мы все равно получим один и тот же ответ. Мы по-прежнему будем считать 𝐀 точка
𝐁. И заметьте, кстати, что когда
мы вычисляем скалярное произведение, порядок появления двух векторов, 𝐀 точка 𝐁
или 𝐁 точка 𝐀, не имеет значения для нашего ответа. Например, в нашем верхнем уравнении
если бы мы вычислили 𝐁 dot 𝐀, то изменился бы только порядок, в котором
величины этих двух векторов появляются в этом произведении. И мы знаем, что несмотря ни на что
Заказ, продукт будет таким же.
Аналогично, в нашем нижнем уравнении 𝐁
точка 𝐀 будет просто включать переключение порядка, в котором эти компоненты
умноженный. Но этот переключатель не изменит
окончательный ответ, который мы вычисляем. Это одинаково в любом случае. Таким образом, в обоих случаях мы можем сказать, что
𝐀 точка 𝐁 равна 𝐁 точка 𝐀.
Когда мы идем вычислять скаляр или
скалярного произведения, иногда мы сталкиваемся с особыми случаями того, как два вектора
мы объединяем, направлены. Один из таких случаев, когда два
векторов, которые мы рассматриваем, мы можем назвать их 𝐀 и 𝐁, указывать на одно и то же
направление. В этом случае угол
между ними, мы назвали этот угол 𝜃, равен нулю градусов. Это указывает на то, что два вектора
параллельны друг другу. И мы можем вспомнить, что cos
ноль градусов равен единице. Это максимальное значение, которое
функция косинуса достигает.
Итак, мы можем сказать, что когда наши двое
векторы параллельны и угол между ними равен нулю градусов, то их скаляр
произведение является максимальным положительным значением. И это возвращается к факту
что косинус нуля градусов является максимальным положительным значением косинуса
функция.
Еще один особый случай, когда наш два вектора 𝐀 и 𝐁 расположены под углом 90 градусов друг к другу. Это означает, что 𝜃 равно 90 градусов. И мы можем вспомнить, что cos 90 градусов это ноль. Это говорит нам о том, что для двух векторов перпендикулярны друг другу, их скалярное произведение равно нулю. И это соответствует нашему геометрическое понимание скалярного произведения. Когда два вектора перпендикулярны, они совершенно не пересекаются друг с другом. Это согласуется со скаляром или скалярное произведение нуля.
И последнее особенное
случай для рассмотрения.
Здесь векторы 𝐀 и 𝐁 указывают на
противоположные направления. Дело не в том, что они параллельны, а в том, что
скорее они антипараллельны. В этом случае угол между
они равны 180 градусам, а косис этого угла отрицателен. Это наибольшее отрицательное значение
функция косинуса может достичь. Итак, мы можем сказать, что когда два
векторы антипараллельны, когда угол между ними равен 180 градусов. Тогда их скалярное произведение равно
максимальное отрицательное значение.
Возможно, вас удивит, что
скалярное произведение может быть отрицательным. Ведь мы не рассчитываем
вектор, поэтому не должно ли наше скалярное произведение всегда быть неотрицательным? Разве это не всегда должно быть положительным или
нуль? Но на самом деле можно иметь
отрицательная скалярная величина. И если мы изменим наше нажатие коробки
расположение немного, мы можем увидеть пример этого.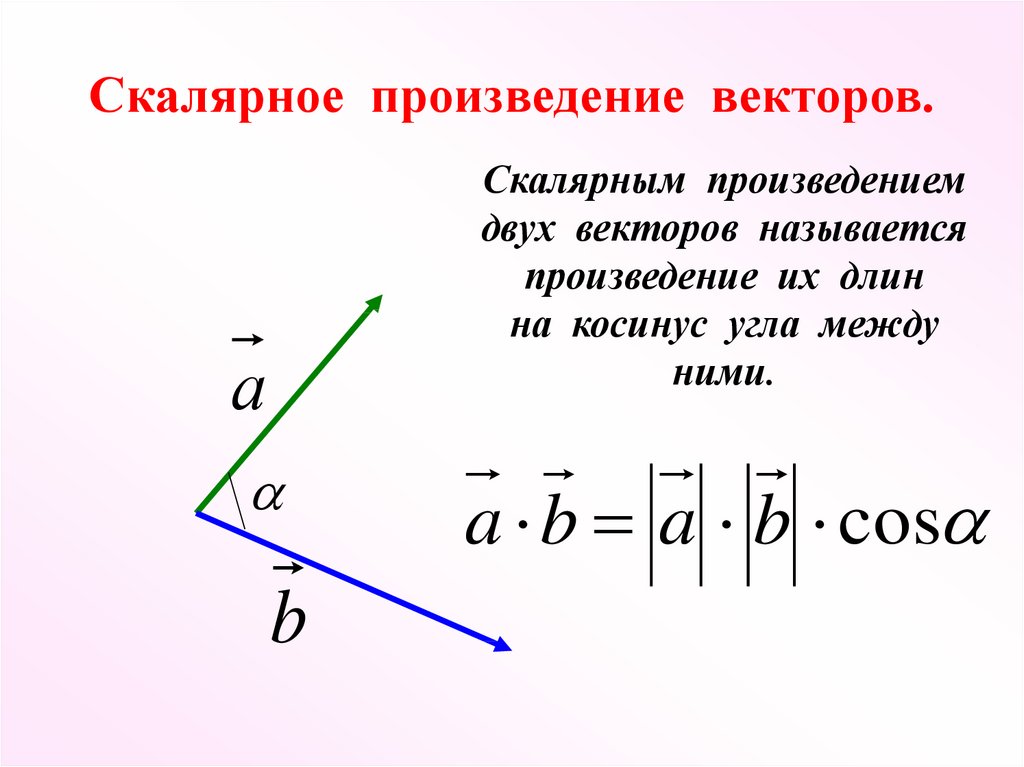
Скажем, вместо того, чтобы нажимать
вперед на ящике, как сейчас, вместо этого мы тянем его. Таким образом, вектор силы указывает на
нас и от вектора смещения. Теперь, если есть какая-то большая сила
воздействуя на коробку и толкая ее вправо, которую мы здесь не нарисовали. Тогда вполне возможно, что
несмотря на то, что мы тянем коробку влево, коробка смещается в
правильно.
И мы видим, что это
пример одного из наших частных случаев углов между нашими двумя векторами. Здесь 𝜃 равно 180 градусам,
что означает, что cos этого угла отрицателен. Итак, когда мы умножаем это
отрицательное число на положительную величину 𝐅 и положительную величину 𝐝,
мы получим общий отрицательный результат для работы, которую мы делаем над коробкой. Таким образом, скалярные величины могут быть
отрицательно, и мы видим, что это происходит здесь. Теперь, когда мы знаем эти
отношения для вычисления скалярного или скалярного произведения двух векторов, давайте получим
немного потренируйтесь, используя их на примере.
Предположим, что два вектора 𝐩 равны два 𝐢 плюс три 𝐣 и 𝐪 равно шести 𝐢 плюс четыре 𝐣. Вычислите 𝐩 точку 𝐪.
Это представление здесь этих два вектора говорят нам, что мы должны вычислить их скалярное или скалярное произведение. И мы видим, что нам дано два векторы 𝐩 и 𝐪 в их компонентной форме. Итак, мы можем начать с того, что вспомним что скалярное произведение двух векторов на их компоненты равно 𝑥-компонента первого вектора, умноженная на 𝑥-компонента второго вектора. Добавлено в 𝑦-компоненту первый вектор, умноженный на 𝑦-компоненту второго. В этом уравнении мы назвали наш векторов 𝐀 и 𝐁, но это всего лишь общие названия для любых векторов, которые лежат в 𝑥𝑦-самолет.
В этом примере то, что мы хотим
рассчитать 𝐩 точка 𝐪. И чтобы сделать это, мы можем следовать этому
рецепт объединения компонентов этих векторов.
Сначала возьмем 𝑥-компоненту
наш первый вектор — это 𝐩, а 𝑥-компонента этого вектора равна двум. И умножаем это на
𝑥-компонента нашего второго вектора. Этот второй вектор равен 𝐪 и что
𝑥-компонента равна шести. Итак, у нас есть дважды шесть. И к этому мы добавляем
𝑦-компонента нашего первого вектора. Этот первый вектор равен 𝐩 и что
𝑦-компонента умножается на 𝑦-компоненту нашего второго вектора втрое. Этот второй вектор равен 𝐪 и что
𝑦-компонента равна четырем.
Итак, у нас есть 𝐩 точка 𝐪 равно дважды шесть плюс трижды четыре. Дважды шесть будет 12 и так будет три раза четыре. Итак, наш окончательный ответ — 24. И обратите внимание, что, действительно, это ответ — скалярная величина. Он имеет величину, но не направление.
Давайте теперь посмотрим на второй пример. упражнение.
На диаграмме показаны два вектора, 𝐀
и 𝐁.
Каждый из квадратов сетки в
на диаграмме длина стороны равна единице. Вычислите 𝐀 точка 𝐁.
Мы видим на нашей диаграмме два наших векторы, 𝐀 и 𝐁, и что они расположены на шагах сетки. Нам говорят, что каждый из этих квадраты сетки имеют длину стороны, равную единице. Нам не говорят единицы этих длины, а просто то, что длины сторон могут быть представлены одной единственной единицей, какая бы ни была наша единица. Зная это, мы хотим вычислить скалярное произведение 𝐀 и 𝐁.
Теперь мы можем вспомнить, что скаляр
произведение предполагает объединение двух векторов. Итак, у нас хорошее начало
потому что 𝐀 и 𝐁 — векторы. И мы можем вспомнить далее, что,
математически скалярное произведение двух общих векторов, 𝐀 и 𝐁, равно
произведение их 𝑥-компонент плюс произведение их 𝑦-компонент. Теперь, для наших двух конкретных векторов,
также называемые 𝐀 и 𝐁, мы пока не знаем их 𝑥- и 𝑦-компоненты, но можем использовать
эта сетка, чтобы узнать.
Мы можем начать с укладки координатные оси на этой сетке. Допустим, что для нашего происхождения мы выберите место, где хвосты векторов 𝐀 и 𝐁 перекрываются. Итак, скажем, что это наша 𝑥-ось, а это наша 𝑦. Относительно этих осей можно определяют 𝑥- и 𝑦-компоненты наших двух векторов. Как примечание, мы могли бы выбрать любая ориентация наших 𝑥- и 𝑦-осей, если они перпендикулярны одной другой и квантифицированные векторы 𝐀 и 𝐁 таким образом. И наш ответ выйдет тем же.
Используя эти специальные 𝑥- и
𝑦-оси, выпишем компоненты вектора 𝐀. Мы можем видеть, что вдоль оси 𝑥,
вектор 𝐀 расширяется на одну, две, три единицы. Итак, это означает, что вектор 𝐀 равен
до трех 𝐢, три единицы в 𝑥-направлении, плюс некоторое количество в
𝑦-направление. Начиная снова с начала, мы
подсчитайте одну, две, три единицы и убедитесь, что это вертикальная протяженность вектора
𝐀.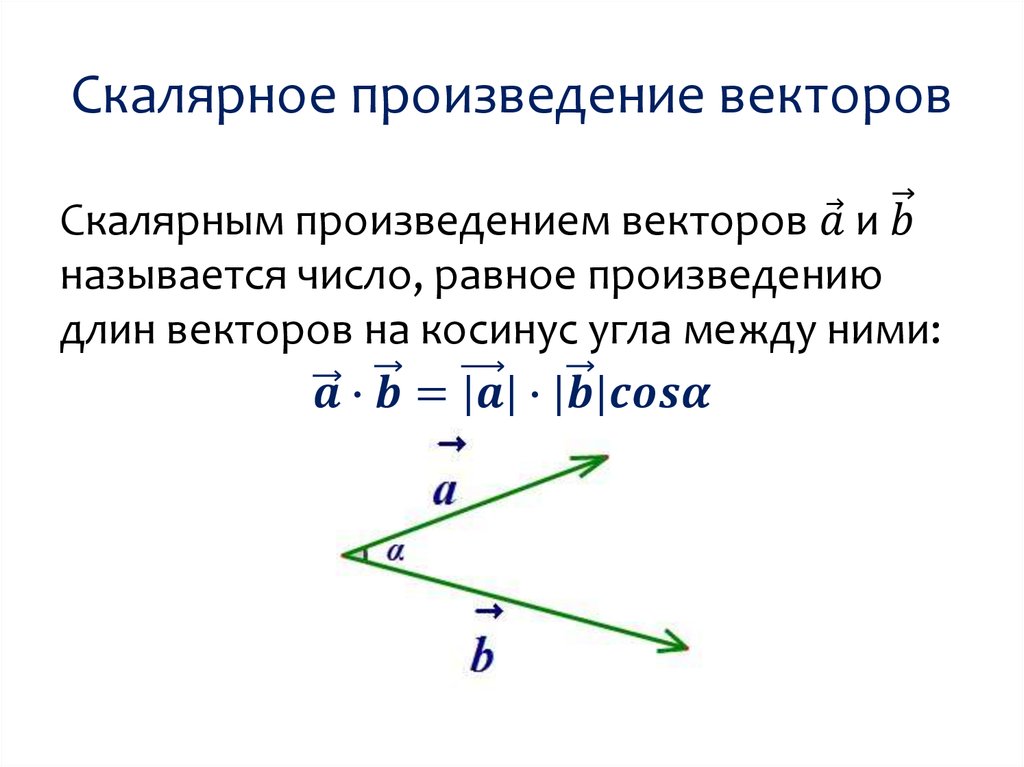
Следовательно, мы можем написать вектор 𝐀
как три 𝐢 плюс три 𝐣. И сейчас мы будем делать то же самое
для вектора 𝐁. 𝑥-компонента вектора 𝐁 равна
равна одной, двум, трем, четырем, пяти, шести единицам, а ее 𝑦-компонента равна единице
Ед. изм. И мы можем записать это как один 𝐣 или
просто 𝐣, так что вектор 𝐁 в целом равен шести 𝐢 плюс 𝐣.
Теперь, когда мы знаем компоненты
наши два вектора, мы можем использовать это соотношение, чтобы найти их скалярное произведение. 𝐀 точка 𝐁 равна
𝑥-компонента вектора 𝐀, мы видим, что 𝑥-компонента равна трем, умноженным на
𝑥-компонента вектора 𝐁. И мы видим, что 𝑥-компонента
шесть. Итак, у нас есть трижды шесть. И к этому мы добавляем
𝑦-компонента вектора 𝐀. Эта 𝑦-компонента равна трем
умножается на 𝑦-компоненту вектора 𝐁. И эта 𝑦-компонента, как мы видели, равна
один.
Итак, 𝐀 точка 𝐁 равна трем
умножить на шесть плюс три раза один, и это равно 18 плюс три или 21. Это 𝐀 точка 𝐁, также называемая
скаляр или скалярное произведение 𝐀 и 𝐁.
Давайте на минутку подведем итог тому, что мы узнали о скалярном произведении двух векторов. На этом уроке мы увидели, что скаляр, также называемый точечным произведением двух векторов, дает скаляр количество. Мы видели, что один из способов вычислить скалярное произведение, символически представленное таким образом, состоит в том, чтобы умножить величины двух вовлеченных векторов, умноженные на косинус угла между векторы. И второе, что мы назвали алгебраический способ вычисления скалярного произведения состоит в объединении векторов по их компонентам части. Произведение 𝑥-компонент плюс произведение 𝑦-компонент.
И, наконец, мы посмотрели, что мы
называется некоторыми частными случаями ориентации между двумя вовлеченными векторами.
Когда 𝐀 параллельно 𝐁, то
угол между ними равен нулю градусов, а их скалярное произведение максимально положительно.
стоимость. Когда 𝐀 перпендикулярно 𝐁
хотя угол между ними составляет 90 градусов, между ними нет перекрытия.
векторов, а их скалярное произведение равно нулю. И, наконец, когда 𝐀
антипараллельны 𝐁, то есть угол между ними равен 180 градусам, то скаляр
или скалярное произведение этих двух векторов имеет максимальное отрицательное значение. Это краткое изложение скаляра
произведение двух векторов.
Скалярное произведение — IB Math Stuff
Новый сайт вопросов и ответов
Есть вопрос?
Спросите его здесь
Physics Site
IB Физика.
+ Исчисление
Прочее
Увиденное на прошлых экзаменах IB
Считаете сайт полезным?
Подарите нам немного социальной любви…
Генерация биткойнов для
Ты и я.
Как это работает.
Скалярное произведение
Три имени Все одинаковые
Векторы можно умножать двумя разными способами, но студенту SL нужно знать только о способе, называемом «скалярным произведением», и результатом умножения всегда является скаляр . Второй тип не входит в программу SL, но полезен во многих приложениях, включая основы физики, такие как крутящий момент.
Математики, похоже, имеют дурную привычку называть одно и то же явление несколькими именами (физики, кажется, лучше избегают этого). В этом случае скалярное произведение, скалярное произведение и скалярное произведение относятся к одной и той же векторной операции. Вам нужно знать все три термина.
Forumlae
Формулу скалярного произведения можно записать двумя способами, оба из которых приведены в брошюре данных IB:
(1)
\begin{align} v \cdot w = |v| |ш| потому что \ тета \ конец {выравнивание}
Где $\theta$ — угол между двумя векторами.
Его также можно записать как:
(2)
\begin{align} v \cdot w = v_1 w_1 + v_2 w_2 + v_3 w_3 \end{align}
Когда векторы определены как:
(3)
\begin{align} v={\begin{pmatrix} v_1\\ v_2\\ v_3 \end{pmatrix}} \: \: \: w=\begin{pmatrix} w_1 \\ w_2 \\ w_3 \end {pmatrix} \end{align}
Перпендикулярно и параллельно
Если два вектора $v$ и $w$ перпендикулярны на , то скалярное произведение будет равно нулю.
(4)
\begin{align} v \cdot w = 0 \end{align}
Если два вектора $v$ и $w$ параллельны , то скалярное произведение их единичных векторов будет равно 1 (т.е. косинус угол между ними будет равен единице).
(5)
\begin{align} \frac{v}{|v|} \cdot \frac{w}{|w|} = cos \theta = 1 \end{align}
Раздел(ы) ниже предназначены для тех, кто хочет немного больше понять, откуда берутся эти формулы.
