Краткий курс теоретической механики
Краткий курс теоретической механики
ОглавлениеПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮВВЕДЕНИЕ Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ § 3. СВЯЗИ И ИХ РЕАКЦИИ Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ) § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ Глава V.  ПЛОСКАЯ СИСТЕМА СИЛ ПЛОСКАЯ СИСТЕМА СИЛ§ 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ § 17. РЕШЕНИЕ ЗАДАЧ § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ) § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ Глава VI. ТРЕНИЕ § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ § 27. ТРЕНИЕ КАЧЕНИЯ Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ Глава VIII. ЦЕНТР ТЯЖЕСТИ § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ  ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА§ 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ § 38. ВЕКТОР СКОРОСТИ ТОЧКИ § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ § 46. РЕШЕНИЕ ЗАДАЧ § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ § 50.  РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ§ 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ § 57. РЕШЕНИЕ ЗАДАЧ § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ § 64.  ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ§ 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА) § 67. РЕШЕНИЕ ЗАДАЧ Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ § 75. СИСТЕМЫ ЕДИНИЦ § 76. ОСНОВНЫЕ ВИДЫ СИЛ Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ) § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ § 80.  § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ) § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ) § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ § 87. РАБОТА СИЛЫ. МОЩНОСТЬ § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ) § 96. 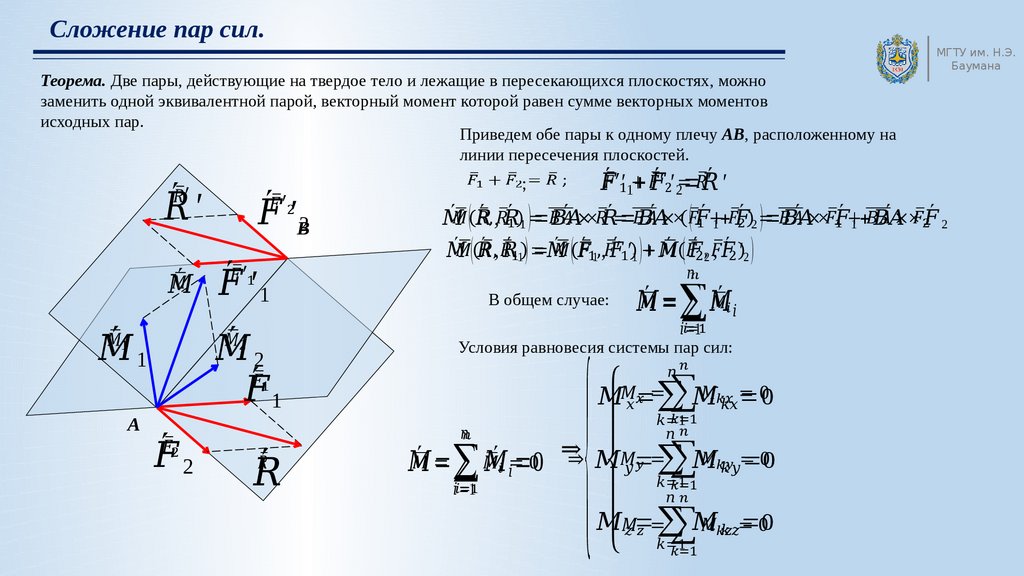 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНСГлава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС § 109. РЕШЕНИЕ ЗАДАЧ Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ  КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ§ 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ) § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ § 118. РЕШЕНИЕ ЗАДАЧ § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 124. РЕШЕНИЕ ЗАДАЧ § 125. СМЕШАННЫЕ ЗАДАЧИ § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ.  ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИГлава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XXVII. ПРИНЦИП ДАЛАМБЕРА § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ § 135. РЕШЕНИЕ ЗАДАЧ § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ § 140. РЕШЕНИЕ ЗАДАЧ § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ Глава XXIX. 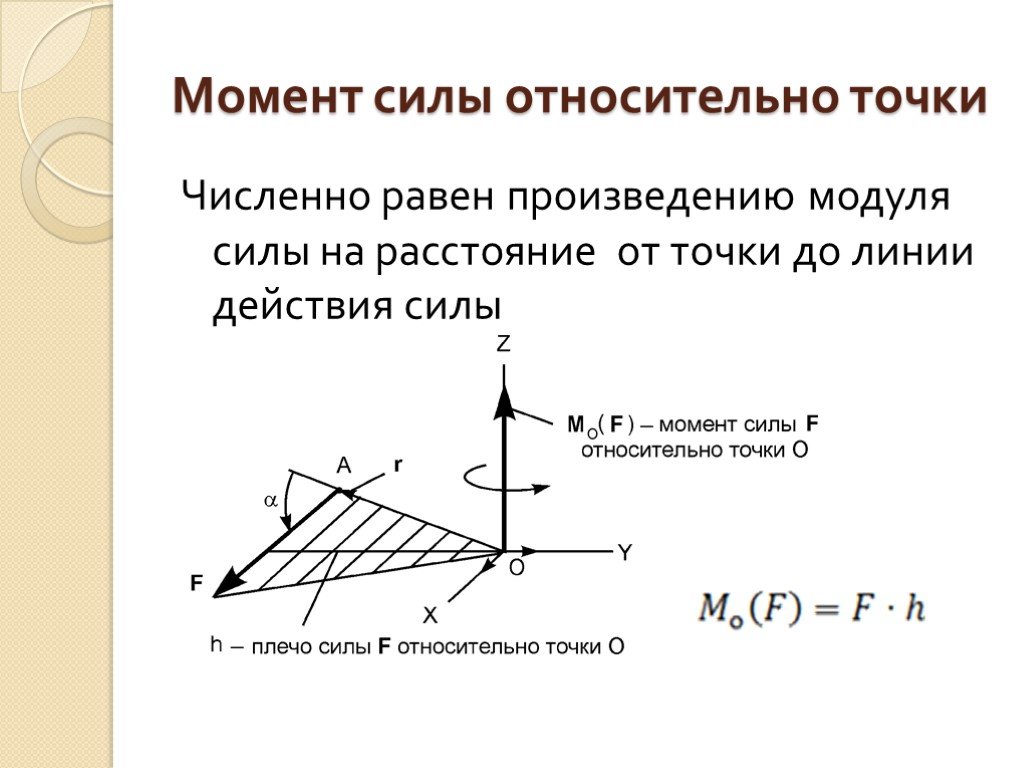 УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ§ 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ § 143. ОБОБЩЕННЫЕ СИЛЫ § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 145. УРАВНЕНИЯ ЛАГРАНЖА § 146. РЕШЕНИЕ ЗАДАЧ Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ) § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. 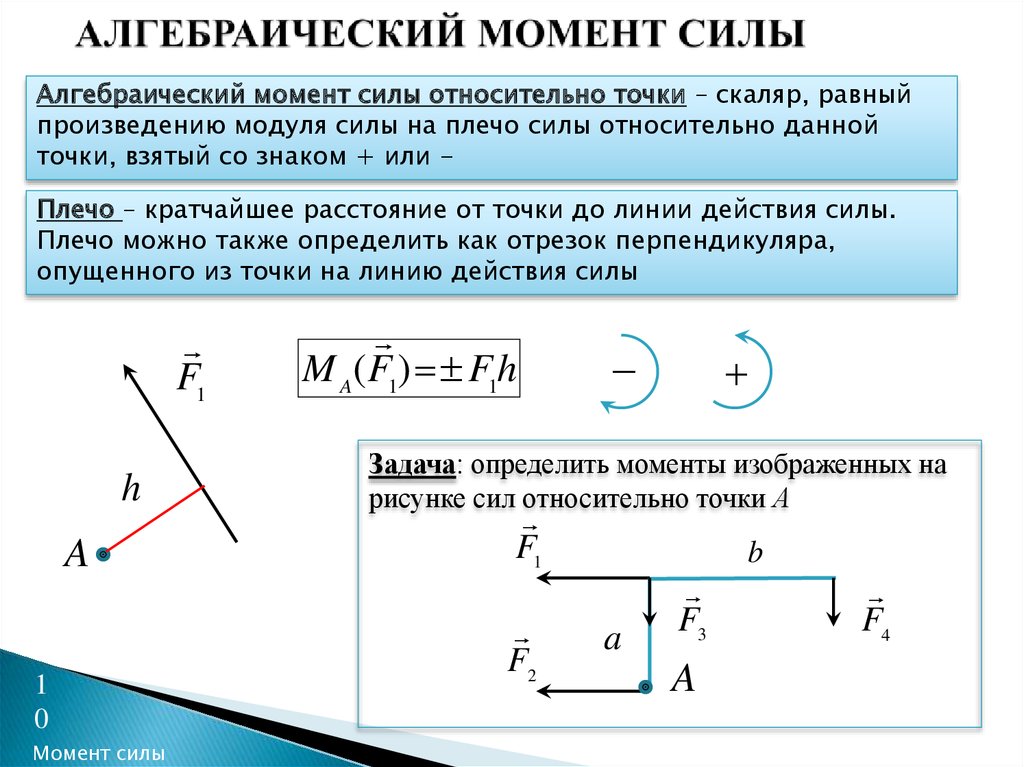 ЦЕНТР УДАРА ЦЕНТР УДАРА |
Момент силы относительно центра (точки)
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА СТАТИКА
Лекция №22. 2.1 Момент силы относительно центра (точки)
3. Момент силы относительно центра
Z
mO r F
B
mO F h
F
mO
h
O
r
A
Моментом силы F относительно центра
(точки) О называется вектор mO F равный векторному произведению радиуса вектора r , проведенного из центра О в точку А приложения силы, и
вектора силы F :
mO F r F
B
Z
F
mO
h
A
r
O
Вектор mO F приложен в точке О и направлен плоскости, проходящей через центр О и силу F , в ту сторону, откуда сила видна стремящейся повернуть
тело вокруг центра О против хода часовой стрелки.

Модуль mO F равен произведению модуля силы F на плечо h:
mO
= F·h,
где плечо h перпендикуляр, опущенный из центра О на линию действия
силы F .
Момент mO F характеризует вращательный эффект силы
но центра (точки) О.
F
относитель-
5. Свойства момента силы:
Момент силы относительно центра не изменяется при переносе силы вдольлинии ее действия в любую точку.
Если линия действия силы проходит через центр О (h = 0), то момент силы
относительно центра О равен нулю.
Для плоской системы сил при вычислении моментов сил относительно точки
(центра), находящейся в той же плоскости, пользуются понятием алгебраического момента силы относительно точки.
Алгебраический момент силы F относительно
точки О равен взятому с соответствующим знаком
произведению модуля силы на ее плечо:
mО( F ) = F h.
Момент считается положительным, если сила
стремится повернуть тело вокруг точки О против хода
часовой стрелки, и отрицательным по ходу часовой
стрелки:
mO ( F1 ) F1 h2 ;
mO ( F2 ) F2 h3 .

F1
h2 О
h3
F2
6. Теорема Вариньона
При определении алгебраического момента силы относительноточки в случае, когда сложно найти плечо h, следует разложить
силу на составляющие, плечи которых найти проще, (часто параллельно осям координат), и применить теорему Вариньона:
если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки О равен
сумме моментов составляющих сил, относительно той же
точки
mO ( R ) mO ( Fk ), где R Fk .
7. 2.2 Теория пар сил, свойства пар сил
Парой сил называется система двух равныхпо модулю, параллельных и направленных в
противоположные стороны сил ( F F ).
Плоскость, в которой лежат силы F и F , называется плоскостью пары, а кратчайшее расстояние d между линиями действия сил плечом пары.
Пара сил не может быть заменена одной эквивалентной ей силой, т.е. не имеет равнодействующей, так как R F F 0.
Пара может быть уравновешена только
другой парой сил.
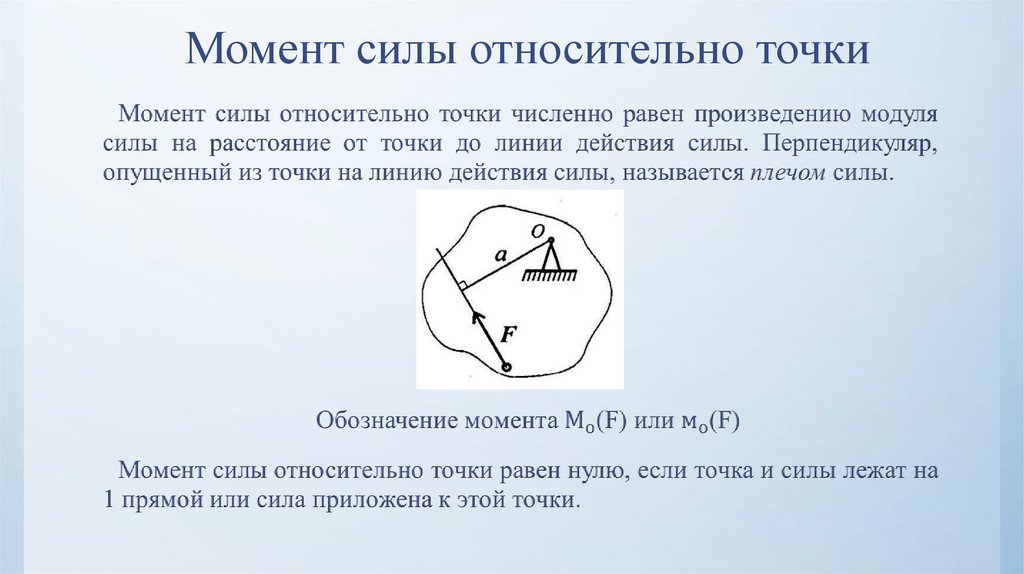
Под действием пары сил тело вращается.
Вращательный эффект пары, характеризуется
моментом пары.
F
B
A
F
d
8. Момент пары сил
Моментом пары называется вектор равный векторному произведениюm r F
,
модуль которого равен произведению модуля одной из сил пары на ее плечо
m F d.
Вектор m направлен перпендикулярно
плоскости пары в ту сторону, откуда пара
видна стремящейся повернуть тело против
хода часовой стрелки. Момент пары m
свободный вектор, т. е. его можно прикладывать в любой точке тела.
m
B
F d
F
r
A
9. Свойства пар сил
1. Момент пары равен сумме моментов сил пары относительно произвольного центра (точки) О:mO mO ( F ) mO ( F ) .
2. Момент пары относительно любого центра
F
mO равен моменту пары m:
mO F h F (h d ) F d m.
mO m
h
d
B
A
F
O
3. Момент пары равен моменту одной из сил пары относительно точки
приложения другой силы пары:
m mB ( F ) mA ( F ).
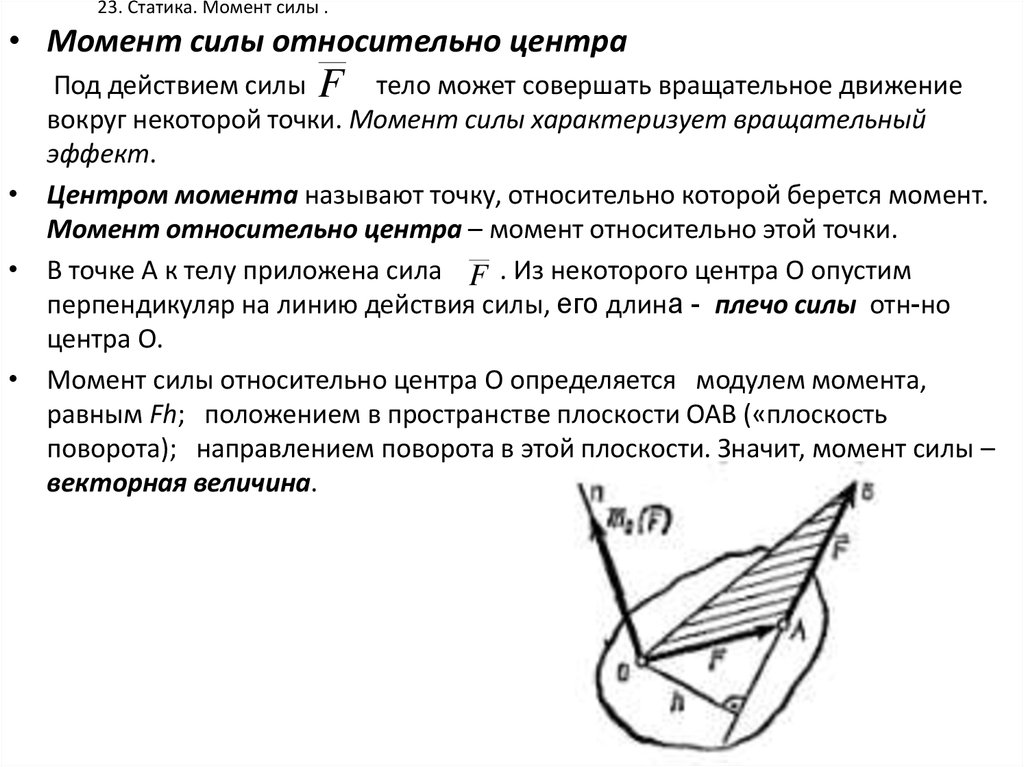
4. Теорема. Пары сил с равными моментами эквивалентны.
Следствия:
Пару сил, приложенную к твердому телу, можно заменить другой
парой в той же плоскости, если при такой замене не изменяется величина момента пары и его направление:
Пару сил можно переносить в плоскость, параллельную плоскости
пары.
5. Теорема. Совокупность нескольких пар с моментами m1 , m2, mn
эквивалентна одной паре, момент
сумме моментов данных пар:
m которой равен геометрической
m m1 m2 mn .
6. Если на тело действует пространственная система пар, то тело находится в равновесии, если векторная сумма моментов пар равна нулю:
m 0.
7. Если пары лежат в одной плоскости, то
момент пары считают величиной алгебраической,
так как в этом случае все вектора моментов пар
параллельны.
Алгебраический момент пары равен взятому
с соответствующим знаком произведению модуля
одной из сил пары на плечо пары:
Z
m1
mn
Y
X
m2
m F d .
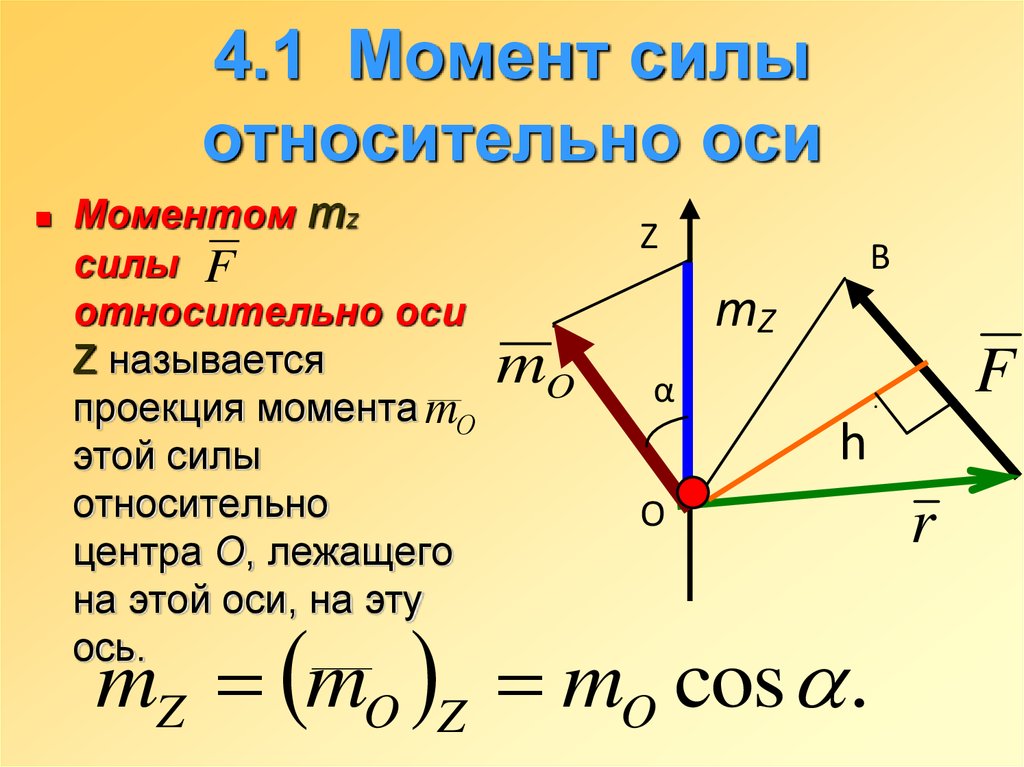
Знак «+» соответствует повороту тела под действием пары против хода часовой
стрелки,
«─» по ходу часовой стрелки.
Пары сил на плоскости часто изображается
Y
дуговой стрелкой, показывающей направление
поворота тела парой.
8. Если на тело действует плоская система пар, то
тело находится в равновесии, если сумма моментов пар
равна нулю:
m
k
0.
m1
O
m2
X
English Русский Правила
Объяснение урока: Момент силы относительно точки в 2D: скаляр
В этом объяснении мы узнаем, как найти сумму моментов группы сил, действующих на тело относительно точки в 2D.
Ненулевая результирующая сила, действующая на твердое тело, создает линейное ускорение тела в направлении, в котором действует результирующая сила, что приводит к смещению центра масс тела в этом направлении.
Сила, действующая на тело, может также приводить к угловому ускорению тела относительно точки, вызывая вращение тела. Величина углового ускорения тела от действия силы пропорциональна моменту силы относительно точки.
На следующем рисунке показан тонкий стержень, подвешенный вертикально в точке 𝑃. На стержень горизонтально действует сила ⃑𝐹. Момент силы действует так, что стержень поворачивается на 𝑃.
На следующем рисунке показано, что стержень вращается по часовой стрелке из-за момента ⃑𝐹 относительно 𝑃.
Предположим, что линия действия ⃑𝐹 меняется так, что линия проходит через 𝑃, как показано на следующем рисунке.
Стержень не вращается вокруг 𝑃 из-за момента ⃑𝐹. Чтобы ⃑𝐹 имел ненулевой момент относительно 𝑃, должно быть ненулевое расстояние между 𝑃 и линией действия ⃑𝐹.
Когда линия, соединяющая точку 𝑃 и точку, в которой действует сила ⃑𝐹, и линия действия силы ⃑𝐹 перпендикулярны, модуль момента силы относительно точки 𝑃 является произведением модуля ⃑𝐹 и расстояние 𝑑 между точкой и линией действия силы. Это можно выразить как 𝑀=𝐹𝑑.
Используя ньютоны в качестве единицы силы и метры в качестве единицы расстояния, единицей момента силы является ньютон-метр (Н⋅м).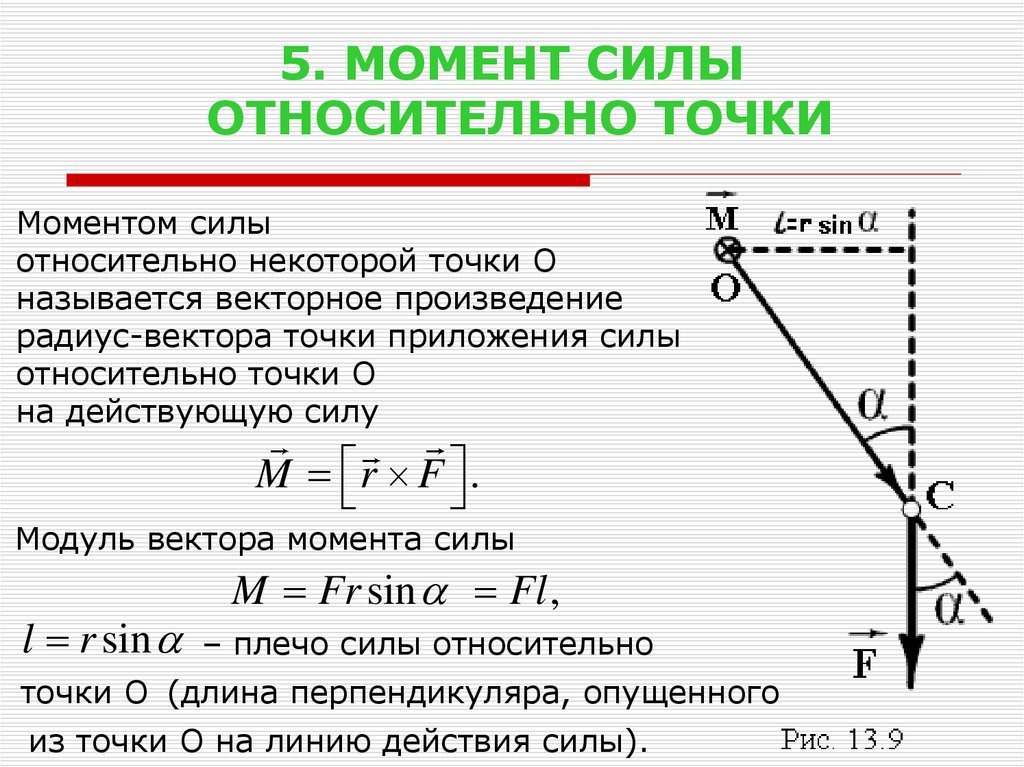
Единица ньютон-метр кажется той же единицей, что и работа, совершаемая силой, но расстояние в метрах имеет совсем другое значение для момента силы, чем для работы, совершаемой силой . Для работы, совершаемой силой, 𝑑 — это расстояние, на которое тело перемещается вдоль линии действия силы, действующей на тело для его перемещения. Для момента силы 𝑑 — это расстояние между линией действия силы и точкой, относительно которой создается момент.
Теперь рассмотрим пример расчета момента относительно точки.
Пример 1: Определение модуля момента силы относительно точки
Если сила величиной 498 Н находится на расстоянии 8 см от точки 𝐴, найдите норму момента силы относительно точки 𝐴, ответив в ньютон-метры.
Ответ
Вопрос говорит нам, что существует сила величины 498 Н, действующая в точке на расстоянии 8 см от точки 𝐴. В вопросе не уточняется, что расстояние 8 см и линия действия силы перпендикулярны, но это можно предположить, если ничто не указывает на обратное. Вопрос задает норму силы, то есть ее величину.
Вопрос задает норму силы, то есть ее величину.
Момент можно рассчитать по формуле 𝑀=𝐹𝑑.
Ответ должен быть дан в ньютон-метрах. Величина силы равна 498 Н.
Значение 𝑑 не равно 8, так как расстояние не 8 м, а 8 см. 8 см необходимо преобразовать в значение в метрах, поэтому 𝑑=0,08 м.
Значения силы теперь используются в формуле для решения: 𝑀=498×0,08=39,84⋅.Нм
Момент силы может вызвать вращение тела по часовой стрелке или против часовой стрелки, как показано на следующем рисунке.
Сила ⃑𝐹 создает момент по часовой стрелке 𝑀 относительно 𝑃, а сила ⃑𝐹 создает момент против часовой стрелки 𝑀 относительно 𝑃. Сумма 𝑀 и 𝑀 равна 𝑀net, где 𝑀=𝑀−𝑀,net, поскольку моменты против часовой стрелки считаются положительными.
Теперь рассмотрим пример расчета момента относительно точки, в которой учитывается направление вращения, обусловленное моментом, и расстояние от точки, в которой момент приближается, до точки, на которую действует сила, равно прямо не дано.
Пример 2: Момент силы относительно точки в двух измерениях
Определите момент силы величины 11 Н относительно точки 𝑂, дав ответ в Н⋅м.
Ответ
Чтобы ответить на этот вопрос, мы должны предположить, что сила 11 Н является единственной силой, действующей на объект. Поскольку никакие другие значения не приводятся, это разумное предположение.
Вопрос кажется довольно сложным, поэтому полезно помнить, что для определения момента силы относительно 𝑂 требуются только два значения. Одним из требуемых значений является величина силы, которая составляет 11 Н. Другое требуемое значение — это расстояние от 𝑂 до линии действия силы. Это расстояние показано на следующем рисунке как 𝑑.
Момент, создаваемый силой, действующей на тело, эквивалентен силе, действующей в точке на расстоянии 𝑑 по горизонтали и на нулевом расстоянии по вертикали от 𝑂. Сила может действовать на тело в любой точке тела вдоль линии действия силы, создавая такой же момент.
Можно определить 𝑑, построив прямоугольный треугольник с вертикальной стороной, соединяющей точку на теле, отстоящую на 36 см по горизонтали от 𝑂, с точкой, расположенной ниже по вертикали, которая пересекает прямую, перпендикулярную линии действия силы, проходит через точку, в которой действует сила, как показано на следующем рисунке.
Сторона треугольника, образованного противоположным углу 𝜃, равна 𝐷, и определение 𝐷 позволяет определить 𝑑 с помощью уравнения 𝑑=0,36−(0,26−𝐷).
Обратите внимание, что расстояния 36 см и 26 см были преобразованы в 0,36 м и 0,26 м соответственно, так что ответ можно дать в ньютон-метрах.
Значение 𝐷 можно найти, если известен угол 𝜃, так как 𝜃 — это угол прямоугольного треугольника напротив 𝐷, где гипотенуза 𝐷 имеет длину 29 см. 29 см также преобразуются в 0,29.м, чтобы ответ можно было дать в ньютон-метрах.
Для определения 𝐷 используется следующее уравнение: sin𝜃=𝐷0,29.
Поскольку угол 60∘, показанный на рисунке, является частью прямого угла, состоящего из угла 60∘ и угла 𝜃, отсюда следует, что 𝜃=(90−60)=30,∘∘∘
As sin(30 )=12∘, 12=𝐷0,29.
Создание 𝐷 субъектом дает 𝐷=0,292=0,145.
Ранее было установлено, что 𝑑=0,36−0,26+𝐷, поэтому 𝑑 находится из 𝑑=0,36−0,26+0,145=0,245 м
Поскольку 𝑀=𝐹𝑑,𝑀=11×0,245=2,695⋅.Нм
Однако это не полное решение, поскольку вращение из-за 𝑀 происходит либо по часовой стрелке, либо против часовой стрелки. На следующем рисунке показано, что сила должна перемещать объект вниз, что приводит к вращению тела по часовой стрелке.
Поскольку моменты по часовой стрелке считаются отрицательными, момент определяется выражением 𝑀=−2,695⋅.Нм
Теперь рассмотрим пример, в котором определяется чистый момент от действия нескольких сил.
Пример 3. Нахождение суммы моментов сил, действующих на стержень
𝐴𝐵 представляет собой стержень длиной 114 см и незначительным весом. На стержень действуют силы величиной 83 Н, 225 Н, 163 Н и 136 Н, как показано на следующем рисунке. 𝐶 и 𝐷 — точки трисекции 𝐴𝐵, а точка 𝑂 — середина стержня. Найдите алгебраическую сумму моментов этих сил относительно точки 𝑂.
Ответ
Длина стержня 114 см, а длины 𝐵𝐷, 𝐷𝐶 и 𝐶𝐴 равны 𝑑=1143=38 см см, что равно длине 𝐴𝑂.
Длина 𝐷𝑂 определяется как 𝐷𝑂=3812=19 см, что равно длине 𝐶𝑂.
Силы, действующие в точках 𝐴 и 𝐷, создают моменты против часовой стрелки относительно 𝑂, а силы, действующие в точках 𝐵 и 𝐶, создают моменты по часовой стрелке около 𝑂. Таким образом, чистый момент относительно 𝑂 определяется выражением 𝑀=(83×57)+(163×19)−(136×57)−(225×19)=−4199⋅.netNcm
Чтобы сила создавала момент, сила должна иметь ненулевую составляющую, действующую перпендикулярно к линии, соединяющей точку, вокруг которой создается момент, и точку, на которую действует сила. Рассмотрим следующий рисунок.
Если 𝜃 равно нулю, то силовая линия ⃑𝐹 должна проходить через
𝑃 и, таким образом, это даст нулевой момент относительно 𝑃. Если
𝜃=90∘,
тогда ⃑𝐹 производит свой максимальный момент около 𝑃. Следовательно, расчет момента силы должен включать угол, под которым действует сила.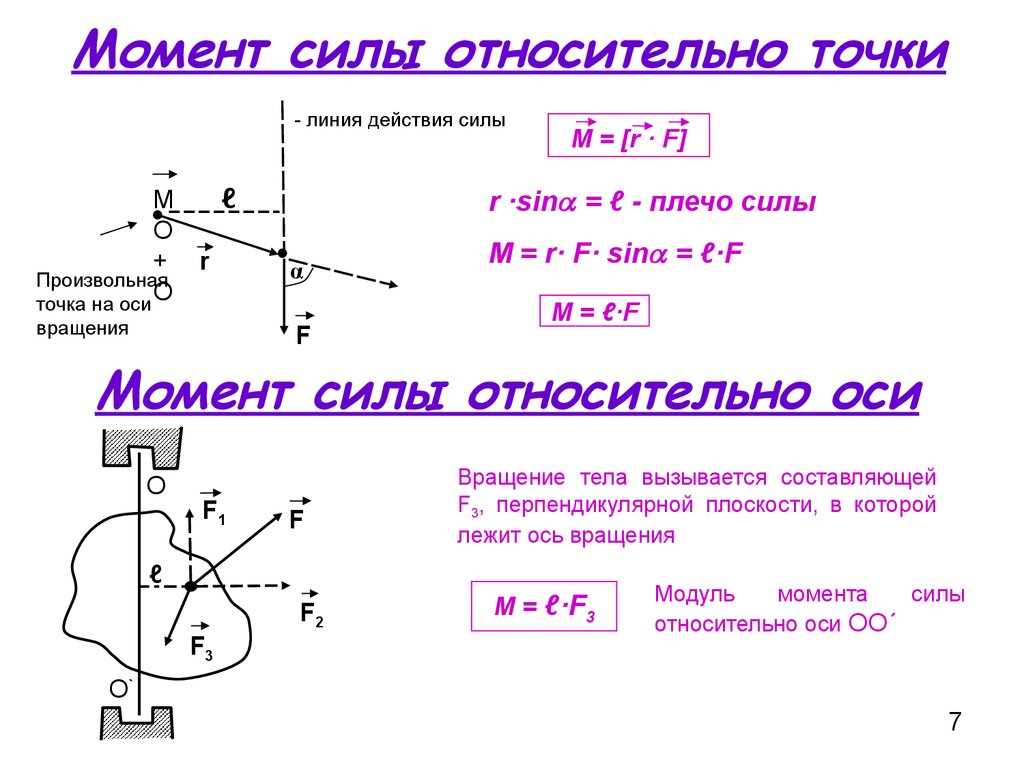
Определение
Момент силы относительно точки 𝑃 представляет собой расстояние 𝑑 от 𝑃 до точки, где действует сила, умноженное на составляющую силы, перпендикулярную направлению линии, пересекающей 𝑃, и точке, где действует сила действует. Это можно записать как 𝑀=𝐹𝑑𝜃,sin, где 𝐹 — величина силы, а 𝜃 — угол между направлением силы и направлением линии, пересекающей 𝑃, и точкой, в которой действует сила.
Теперь давайте теперь рассмотрим пример, где необходимо учитывать углы, под которыми действуют силы.
Пример 4. Нахождение величины суммы моментов трех сил, действующих вдоль равностороннего треугольника
Три силы, измеряемые в ньютонах, действуют вдоль сторон равностороннего треугольника 𝐴𝐵𝐶 как показано на рисунке. Учитывая, что длина стороны треугольника равна 7 см, определите алгебраическую сумму моментов сил относительно середины треугольника 𝐴𝐵, округленную до двух знаков после запятой.
Ответ
Вопрос касается моментов относительно середины 𝐴𝐵, которая показана как точка
𝑃 на следующем рисунке. Длина 𝐴𝐵 7 см. Поскольку 𝑃 находится в середине 𝐴𝐵, длинадлинасм𝐴𝑃=𝐵𝑃=3,5.
Длина 𝐴𝐵 7 см. Поскольку 𝑃 находится в середине 𝐴𝐵, длинадлинасм𝐴𝑃=𝐵𝑃=3,5.
Линия действия силы 300 Н проходит вдоль 𝐴𝐵, поэтому она проходит через 𝑃, создавая нулевой момент относительно 𝑃, и ею можно пренебречь.
Поскольку треугольник 𝐴𝐵𝐶 равносторонний, все его внутренние углы равны 60∘. На следующем рисунке показаны ненулевые моменты относительно 𝑃.
Треугольник 𝑃𝐵𝐶 — прямоугольный треугольник с углом 60∘, для которых длина стороны, прилегающей к углу, равна 3,5 см и длина стороны, противоположной углу, равна 𝑃𝐶. У нас есть, следовательно, tan(60)=𝑃𝐶3,5; ∘ следовательно, 𝑃𝐶=3,5√3.cm
На следующем рисунке показаны величины действующих сил, углы, под которыми они действуют, и их расстояния от 𝑃.
Сила 150 Н и сила 100 Н действуют по часовой стрелке, поэтому обе отрицательны.
Используя формулу 𝑀=𝐹𝑑𝜃, грех в момент около 𝑃 из-за
Сила 150 Н определяется выражением
𝑀=−150×3.5√3(30)⋅𝑀=−525√32⋅. ∘sinNcmNcm
∘sinNcmNcm
Момент около 𝑃 из-за силы 100 Н определяется выражением 𝑀=−100×3.5(60)⋅,𝑀=−175√3⋅.∘sinNcmNcm
Сумма моментов относительно 𝑃 равна 𝑀net, которая является суммой 𝑀 и 𝑀. Вопрос запрашивает это значение до двух знаков после запятой: 𝑀=−525√32+175√3=−875√32=−757,77⋅.netNcm
Давайте теперь рассмотрим другой такой пример.
Пример 5. Нахождение точки на прямоугольнике по сумме моментов сил, действующих вокруг нее действующие вдоль 𝐵𝐴, 𝐵𝐶, 𝐶𝐷 и 𝐶𝐴 соответственно. Если точка 𝐸∈𝐵𝐶, где сумма моментов сил относительно 𝐸 равна 53 Н⋅см в направлении 𝐴𝐵𝐶𝐷, определить длину 𝐵𝐸.
Ответ
Силы, действующие на прямоугольник, и точки, в которых они действуют, показаны на следующем рисунке.
Силу в точке 𝐴, действующую вдоль 𝐶𝐴, можно разложить на перпендикулярные составляющие. Для решения этой силы необходимо знать угол от 𝐴𝐵 к линии действия силы, который показан как 𝜃 на следующем рисунке и равен углу, образуемому линией действия силы с 𝐶𝐷.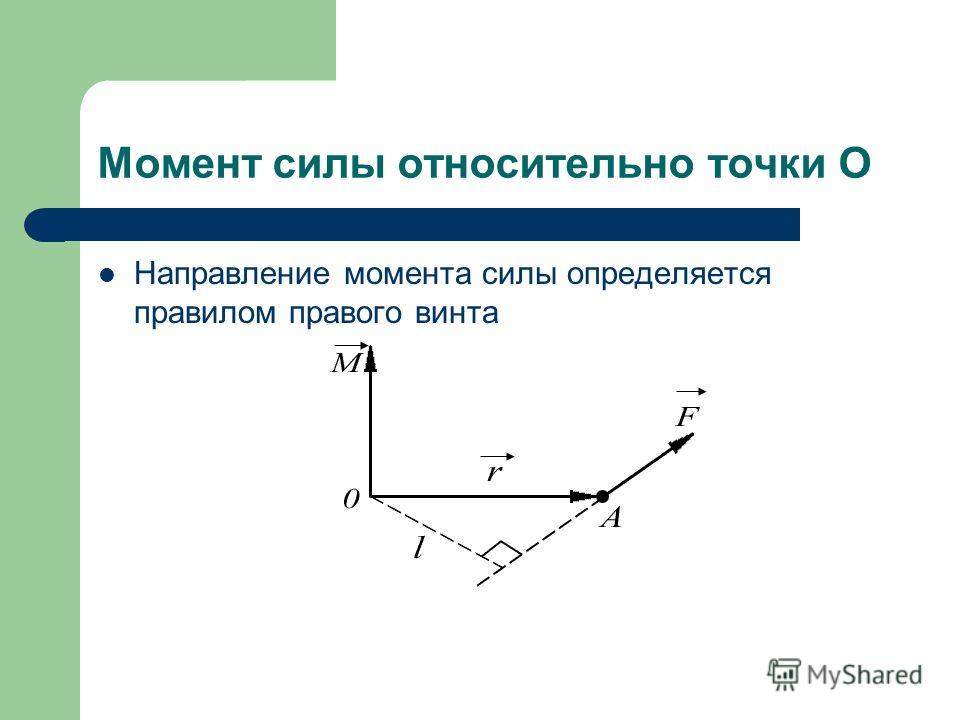
𝐴𝐷𝐶 — прямоугольный треугольник. Длина 𝐴𝐶 определяется как 𝐴𝐶=√8+6=√100=10.см
Таким образом, мы имеем, что sincos𝜃=810=45,𝜃=610=35.
Составляющая силы в 30 ньютонов вдоль 𝐷𝐴 равна 𝐹=3045=24,Н, а составляющая силы в 30 ньютонов вдоль 𝐵𝐴 равна 𝐹=3035=18.N
𝐹 и сила в 24 ньютона, действующая в 𝐴, действуют вдоль одной и той же линии, поэтому результирующая сила, действующая в 𝐴, равна 𝐹=24+18=42.N
На следующем рисунке показаны компоненты сил действующая перпендикулярно и параллельно 𝐵𝐶, которая пересекает точку 𝐸, о которой известен суммарный момент.
Момент около 𝐸, обусловленный каждым компонентом, представляет собой расстояние от линии действия компонента до 𝐸, перпендикулярное направлению компонента.
На следующем рисунке показаны величины и направления моментов относительно 𝐸 от каждой силы, а также суммарный момент относительно 𝐸.
Чистый момент относительно 𝐸 можно приравнять к сумме моментов относительно 𝐸 за счет компонентов: 144+64−8𝑦−42𝑦=53.
Мы можем изменить это выражение, чтобы сделать 𝑦 подлежащим следующим образом: −50𝑦=53−64−144=−155𝑦=−155−50=3,1 см
Подведем итог тому, что мы узнали из этих примеров.
Ключевые точки
- Момент силы ⃑𝐹 относительно точки 𝑃 представляет собой расстояние 𝑑 от 𝑃 до точки, где действует сила, умноженное на составляющую силы, перпендикулярную направлению линии, пересекающей 𝑃 и точку где действует сила. Это можно записать как 𝑀=𝐹𝑑𝜃,sin, где 𝐹 — величина силы, а 𝜃 — угол между направлением силы и направлением линии, пересекающей 𝑃, и точкой, в которой действует сила.
- Чистый момент, обусловленный набором моментов относительно точки, представляет собой сумму моментов относительно точки по часовой стрелке и против часовой стрелки, где моменты против часовой стрелки положительны.
ньютоновская механика — Почему момент зависит от расстояния от точки вращения до силы?
спросил
Изменено 23 дня назад
Просмотрено 5к раз
$\begingroup$
Формула для момента:
$$M = Fd$$
Где F — сила, приложенная к объекту, а d — расстояние по перпендикуляру от точки вращения до линии действия силы.
Почему? Интуитивно понятно, что момент зависит от силы, поскольку сила «увеличивает интенсивность». Но почему расстояние? Почему расстояние от линии действия силы до точки напряженности влияет на момент?
Я НЕ ищу вывод приведенной выше формулы из формулы перекрестного произведения, я ищу интуицию. Я понимаю, как, когда я поворачиваю ключ, если ключ короче, его труднее поворачивать, но я не понимаю, ПОЧЕМУ.
Спасибо.
- ньютоновская механика
- классическая механика
- крутящий момент
- статика
$\endgroup$
$\begingroup$
Почему?
Поскольку момент есть проявление силы на расстоянии, точно так же скорость а есть проявление вращения на расстоянии. Учитывая две точки A и B , вы знаете, что $$ \vec{M}_A = \vec{r}_{AB} \times \vec{F}_B \\ \vec{v}_A = \vec{r}_{AB} \times \vec{\omega}_B $$
Сила в B вызывает крутящий момент в A , подобно тому как вращение в B вызывает скорость в A .
Так почему же?
И силы/моменты, и скорости/вращения являются трехмерными винтами, обладающими следующими свойствами. а) линия направления, б) амплитуда, в) шаг. Забудьте пока о b) и c) и сосредоточьтесь на линии.
Как описать линию в 3D. Линия имеет 4 степени свободы и обычно представляется с помощью 6 компонентов с так называемыми координатами Плюкера. Здесь участвуют два вектора, каждый из которых имеет 3 компонента. Первый вектор, который я называю $\vec{F}$, задает направление прямой линии, но его величина не важна. Таким образом, от вектора используются две степени свободы. Второй вектор, который я называю $\vec{M}$, дает момент линии относительно начала координат и используется для описания ближайшей точки линии к началу координат. Он тоже использует две степени свободы, потому что точка по линии неважно. Он представляет собой либо а) момент силы вдоль линии, либо б) скорость тела, вращающегося вокруг линии. Расположение линии определяется как
$$ \vec{r} = \frac{\vec{F} \times \vec{M}}{\vec{F} \cdot \vec{F}} = — \frac{\vec{M} \times \vec{F}}{\vec{F} \cdot \vec{F}} $$ в зависимости от того, что вам больше нравится.
Аналогично для движений
$$ \vec{r} = \frac{\vec{\omega} \times \vec{v}}{\vec{\omega} \cdot \vec{\omega}} = — \frac{\vec{v} \times \vec{\omega}}{\vec{\omega} \cdot \vec{\omega}} $$.
Итак, момент есть проявление линии на расстоянии.
$\endgroup$
2
$\begingroup$
Я понимаю, как когда я поворачиваю ключ, если ключ короче, его труднее поворачивать, но я не понимаю, ПОЧЕМУ.
Предположим, что болт можно открутить за один оборот, и на этот процесс расходуется $E$ джоулей. Тогда, поскольку $w=F d$, имеем $$E=2\pi rF.$$ Таким образом $$F=\frac{E}{2\pi r}.$$ Вот почему открутить болт с помощью короткого ключа сложнее. Вам нужно нажимать сильнее. Отвечает ли это на ваш вопрос?
$\endgroup$
$\begingroup$
Причина, по которой крутящий момент (сила вращения) зависит от расстояния $d$ от точки вращения (т. е. почему крутящий момент является моментом), заключается в следующем:
е. почему крутящий момент является моментом), заключается в следующем:
Крутящий момент определяется как изменение углового момента; если масса постоянна, это означает изменение угловой скорости.
Чтобы добиться изменения угловой скорости с помощью тангенциальной силы $F$, нам нужно пройти большее расстояние, когда мы находимся дальше от центра. Или другими словами, сила $F$ изменяет только линейную скорость; для достижения изменения угловой скорости требуется тем больше, чем дальше мы находимся.
$\endgroup$
1
$\begingroup$
Лучшим определением крутящего момента (или момента) является работа на единицу угла поворота (в джоулях на радиан), которую может совершить сила, действующая таким образом, что она стремится вызвать вращение. Это означает, что вам нужна составляющая силы, действующей вдоль дуги, умноженная на длину дуги, деленная на угол (в радианах).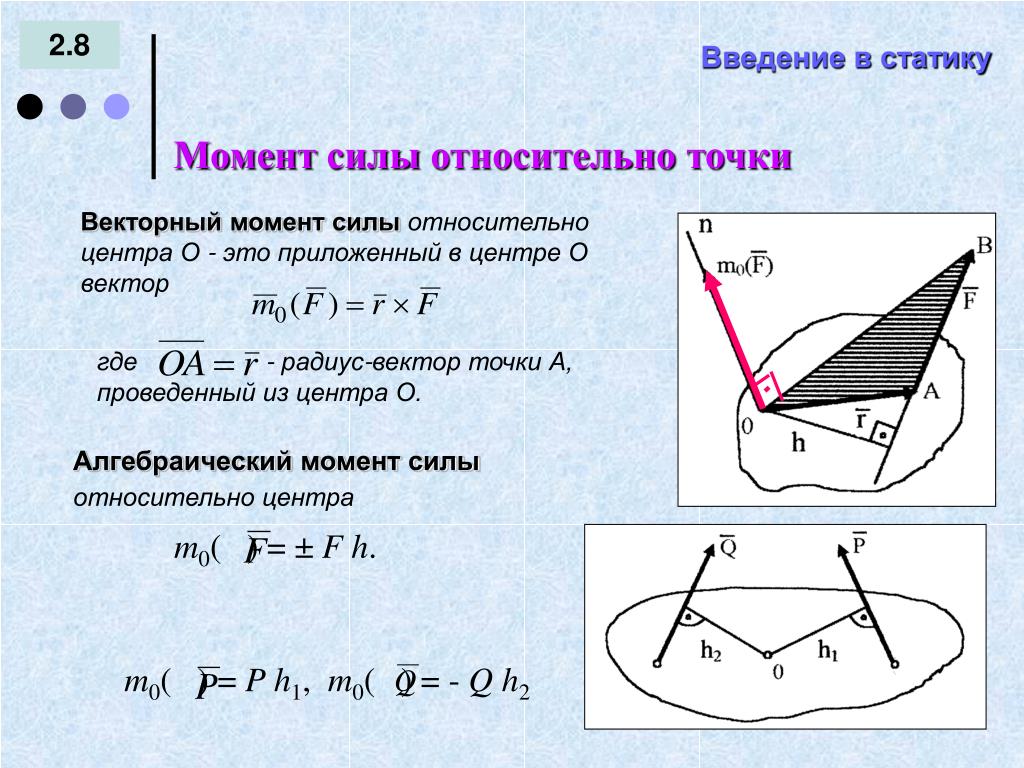 Но длина дуги s = rθ, а s/θ = r. Таким образом, вы в конечном итоге умножаете составляющую силы на радиус.
Но длина дуги s = rθ, а s/θ = r. Таким образом, вы в конечном итоге умножаете составляющую силы на радиус.
$\endgroup$
$\begingroup$
Поймите, что есть компромисс. Вы можете применить меньшее усилие с помощью большего ключа, но вам придется переместить его на большее расстояние (длина дуги), чтобы выполнить тот же объем работы (сила x расстояние).
$\endgroup$
$\begingroup$
Это совершенно не инстинктивно, поскольку вы просите об интуиции. Я не знаю, насколько математически обоснована моя теория, но, пожалуйста, не стесняйтесь сделать ее строгой.
Возможно, когда мы удаляемся от точки приложения силы на большее расстояние, мы можем начертить больший круг и, таким образом, получить большее расстояние для прохождения и приложения силы, по существу, выполняя больше работы. И это каким-то образом соответствует большему крутящему моменту.
$\endgroup$
$\begingroup$
Интуитивно понятно, что крутящий момент — это количество «крутящего момента», которое вы можете придать чему-то. Принцип, который вы упомянули, основан на том, как работает гаечный ключ: он увеличивает $r$ от вашей руки и всего, что вы пытаетесь свернуть, например. болт — и таким образом увеличивает крутящий момент.
Или, наоборот, если бы нам дали набор гаечных ключей и сказали попробовать с их помощью открутить различные болты, мы бы заметили, что длинными гаечными ключами легче крутить болт, чем короткими, а если взять длинный гаечный ключ и использовать его с вашей рукой близко к болту, это было бы не так просто. Таким образом, если бы нам затем поручили разработать меру силы поворота болта, которую можно проявить при использовании данного гаечного ключа, необходимо принять во внимание как прямую силу, приложенную , так и , а также длину гаечного ключа.
Таким образом, математическое выражение уточняет это, описывая точную форму зависимости. (Кроме того, синусоидальная часть, опущенная в выражении, приведенном в OP, фактически просто отражает, что это перпендикулярная часть силы, которая вызывает крутящий момент. Это должно иметь смысл, поскольку скорость вращения всегда перпендикулярна радиальной Следовательно, чтобы изменить скорость вращения, вам нужна сила в этом направлении.)
$\endgroup$
$\begingroup$
Я не профессор физики или что-то в этом роде, и я в основном использую свое воображение и палку, чтобы решить это, но я думаю, что причина в следующем: чем больше расстояние от оси вращения, тем больше радиус окружности, описываемой ручкой гаечного ключа вокруг оси, и, следовательно, тем больше перимитер этой окружности (pi x 2r).
Это означает, что при одном и том же повороте оси рукоятка длинного ключа должна пройти большее расстояние, чем рукоятка короткого ключа. Итак, это также должно работать в обратном направлении, расстояние, пройденное ручкой длинного ключа, заставит стержень вращаться меньше, чем если бы такое же расстояние было пройдено ручкой короткого ключа. (Думайте о расстояниях как о периметрах воображаемых окружностей, по которым рукоятки этих ключей перемещаются вокруг оси или винта при его вращении.)
Итак, это также должно работать в обратном направлении, расстояние, пройденное ручкой длинного ключа, заставит стержень вращаться меньше, чем если бы такое же расстояние было пройдено ручкой короткого ключа. (Думайте о расстояниях как о периметрах воображаемых окружностей, по которым рукоятки этих ключей перемещаются вокруг оси или винта при его вращении.)
Это должно означать, что, используя более длинный ключ, мы можем разделить усилие, необходимое для поворота оси, на более мелкие части: поскольку для меньшего поворота оси (на меньший угол) требуется меньшее усилие, мы можем приложить меньшее усилие к рукоятку гаечного ключа, все еще заставляя его вращаться вокруг оси, тогда как, если бы мы использовали более короткий ключ, заставляя ручку этого ключа перемещаться на такое же расстояние вокруг оси, это заставило бы сам стержень вращаться больше и, следовательно, потребовало бы более высокого усилия. .
Итак, если я прав, это означает, что прикладывая меньшую силу (хотя и в течение более длительного периода времени: поскольку рукоятка гаечного ключа должна перемещаться на большее расстояние) к более длинному гаечному ключу, мы можем повернуть шарнир, который потребовалось гораздо большее усилие, чтобы повернуть с помощью более короткого ключа.
подумайте об этом принципе применительно к автомобилю. машине не нужно использовать всю мощность двигателя, чтобы куда-то ехать. может использовать минимальную мощность двигателя и двигаться очень медленно. в конце концов он достигнет места назначения.
так или иначе, я надеюсь, что я прав, и я надеюсь, что это помогло.
$\endgroup$
1
$\begingroup$
Интуиция, я думаю, может быть, это потому, что, когда вы прикладываете силу на дальнем расстоянии, больше этого объекта следует за движением, которое дает сила. Когда я встряхиваю свой карандаш, зажимая его конец, он движется намного больше, чем когда я держу его ближе к кончику карандаша, потому что больше карандаша повторяет движение, которое я придал карандашу, когда я встряхиваю его, когда он длиннее. . Представьте себе угол в 30 градусов, хоть он и узкий, если линии образующие угол длинные, то он довольно широкий, я думаю поэтому расстояние влияет на момент
Еще одна вещь, хотя и небольшая, может заключаться в том, что если вы сожмете карандаш ближе к кончику, это означает, что часть карандаша окажется за вашими пальцами, и вес этой части карандаша может уменьшить движение, потому что ваши пальцы должны приложите достаточную силу, чтобы сдвинуть весь карандаш, чтобы он качался и двигался, кончик карандаша не сгибался, чтобы он качался.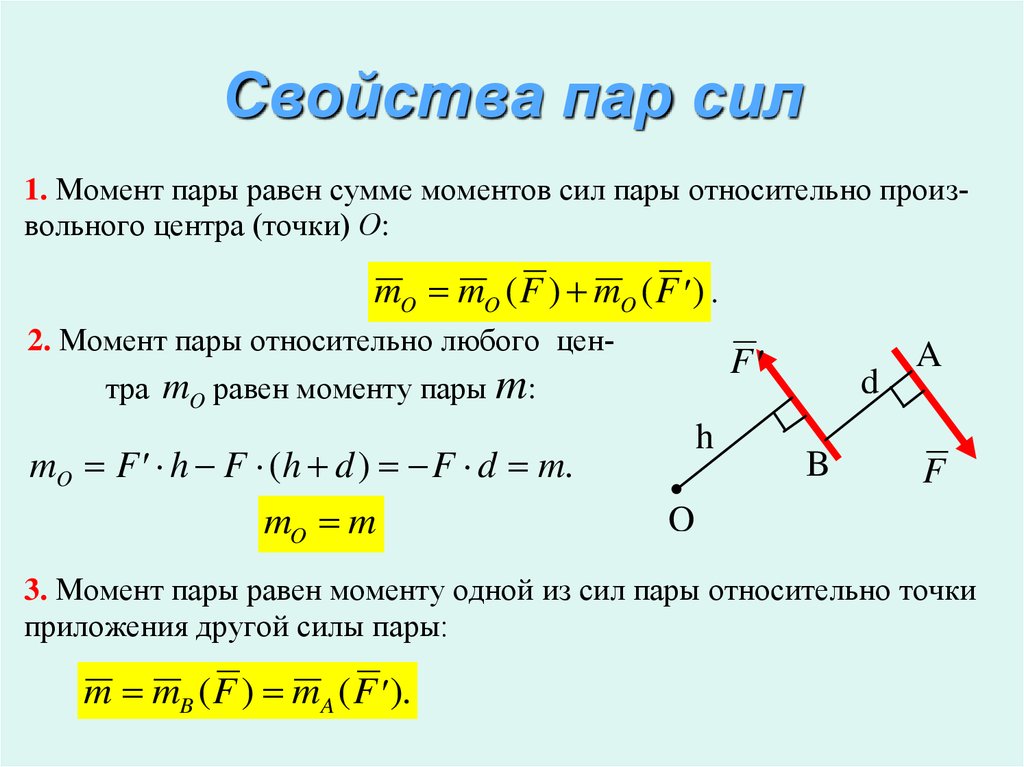
$\endgroup$
$\begingroup$
кажется вы задали любопытный вопрос мне 14 лет и я решаю такие вопросы своим воображением без вывода сложных математических формул и прочего.
так что просто представьте себе отрезок линии и сделайте две точки (поворот) в начале), а на самой внешней стороне теперь подумайте о перемещении этой линии вокруг этого стержня {так вы увидите, что сила в углу перемещает отрезок линии по кругу }
теперь возьмите еще один отрезок линии, сделайте две точки (поворот) в начале), а на самой внешней стороне и 3-ю в центре примените силу к самой внешней точке на линии с центром в центре, и теперь вы можете видеть, что линия движется в круговое направление. теперь приложите силу немного между точкой, в которой вы видите меньше движения, и в центре, где вы не видите никакого движения.
теперь просто снова перейдите к первому шагу и переместите его от самого внешнего конца, вы увидите, что внешняя сторона сегмента линии имеет большую силу, чем внутренняя, и если у нее больше силы, чем она попытается толкнуть опорное слово назад и, следовательно, приведет двигаться вперед.


