Краткий курс теоретической механики

Краткий курс теоретической механики

Тарг С. М. Краткий курс теоретической механики: Учеб. для втузов.— 10-е изд., перераб. и доп. — М.: Высш. шк., 1986.— 416 с. В книге изложены основы механики материальной точки, системы материальных точек и твердого тела в объеме, соответствующем программам технических вузов. Приведено много примеров и задач, решения которых сопровождаются соответствующими методическими указаниями. В 10-м издании (9-е — 1974 г.) значительно изменены и более компактно изложены вопросы статики; в разделе «Динамика» дополнительно рассмотрены приложения общих теорем к изучению движения жидкости, малые колебания системы и некоторые другие вопросы. Для студентов очных и заочных технических вузов. Оглавление ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ ВВЕДЕНИЕ Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ § 3. СВЯЗИ И ИХ РЕАКЦИИ Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ) § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ Глава V. ПЛОСКАЯ СИСТЕМА СИЛ § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ § 17. РЕШЕНИЕ ЗАДАЧ § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ) § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ Глава VI. ТРЕНИЕ § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ § 27. ТРЕНИЕ КАЧЕНИЯ Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ Глава VIII. ЦЕНТР ТЯЖЕСТИ § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ § 38. ВЕКТОР СКОРОСТИ ТОЧКИ § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ § 46. РЕШЕНИЕ ЗАДАЧ § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ § 50. 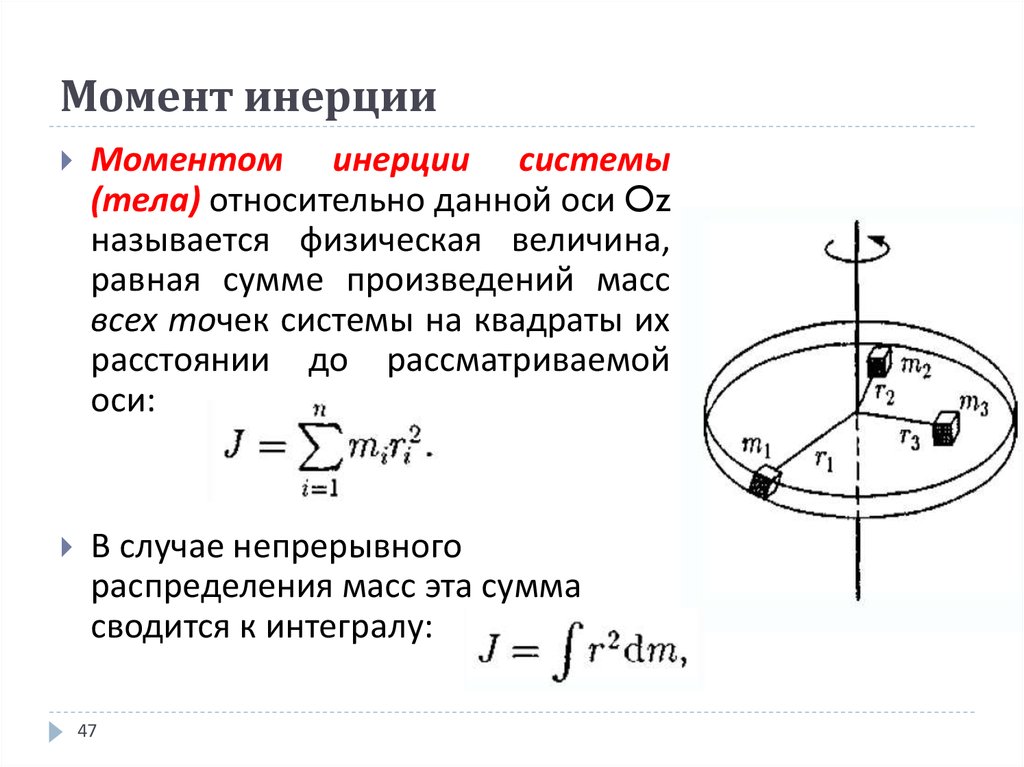РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ § 57. РЕШЕНИЕ ЗАДАЧ § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА) § 67. РЕШЕНИЕ ЗАДАЧ Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ Раздел третий. ДИНАМИКА ТОЧКИ Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ § 75. СИСТЕМЫ ЕДИНИЦ § 76. ОСНОВНЫЕ ВИДЫ СИЛ Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ) § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ) § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ) § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ § 87. РАБОТА СИЛЫ. МОЩНОСТЬ § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ) § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС § 109. РЕШЕНИЕ ЗАДАЧ Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ § 110. 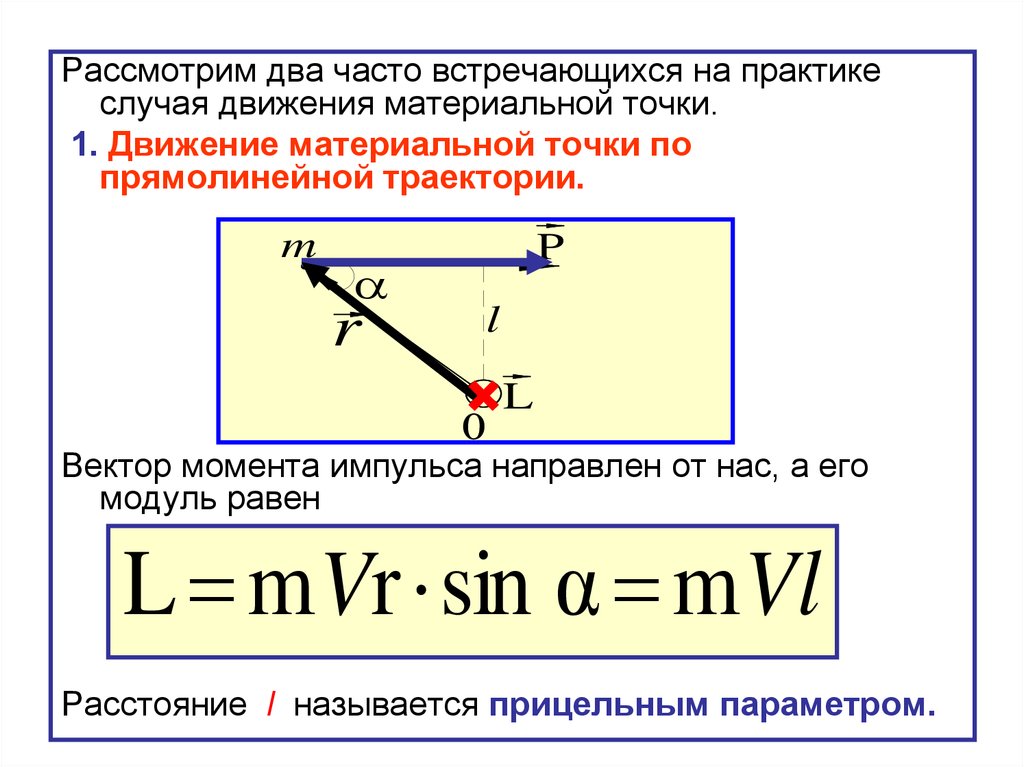КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ) § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ § 118. РЕШЕНИЕ ЗАДАЧ § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 124. РЕШЕНИЕ ЗАДАЧ § 125. СМЕШАННЫЕ ЗАДАЧИ § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XXVII. ПРИНЦИП ДАЛАМБЕРА § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ § 135. РЕШЕНИЕ ЗАДАЧ § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ § 140. РЕШЕНИЕ ЗАДАЧ § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ § 143. ОБОБЩЕННЫЕ СИЛЫ § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 145. УРАВНЕНИЯ ЛАГРАНЖА § 146. РЕШЕНИЕ ЗАДАЧ Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ) § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА

Что такое главный вектор сил инерции?

Прочее › Чем отличается › Чем отличается главный вектор от равнодействующей плоской системы произвольно расположенных сил?

Следовательно, главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.

1. Что такое главный вектор сил и чему он равен?
2. Как определить главный момент сил инерции?
3. Чему равна сила инерции материальной точки?
4. Как вычислить момент инерции тела относительно оси проходящей через центр масс?
5. Что значит вектор силы?
6. В чем заключается разница между главным вектором и равнодействующей силой?
7. Что такое главный момент инерции?
8. Как направлен главный вектор сил инерции?
9. Что такое момент инерции своими словами?
10. Что такое сила инерции?
11. Какие бывают силы инерции?
12. Откуда берется сила инерции?
13. В чем измеряется инерция?
14. Для чего нужен Тензор инерции?
15. Чем больше момент инерции?
16. Чему равны главный вектор и главный момент произвольной системы сил при равновесии тела?
17. Что называется сходящимися силами?
18. Что такое произвольная плоская система сил?
19. В чем заключается принцип Даламбера?
20. Какая формула определяет момент силы?
21. Как связаны момент силы и момент инерции?
22. Какой закон инерции?
23. Что делает тело в состоянии инерции?
24. Как преодолеть инерцию?
25. Что называют моментом инерции тела?
26. Чему равен момент сопротивления?
27. Что такое момент инерции и от чего он зависит?
28. Чему равен главный вектор и главный момент произвольной плоской системы сил?
29. Чему равен главный вектор в системе сходящихся сил?
30. Чему равен главный момент в системе сходящихся сил?

Что такое главный вектор сил и чему он равен?

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил: R = F1 + F2 + + Fn = Fi.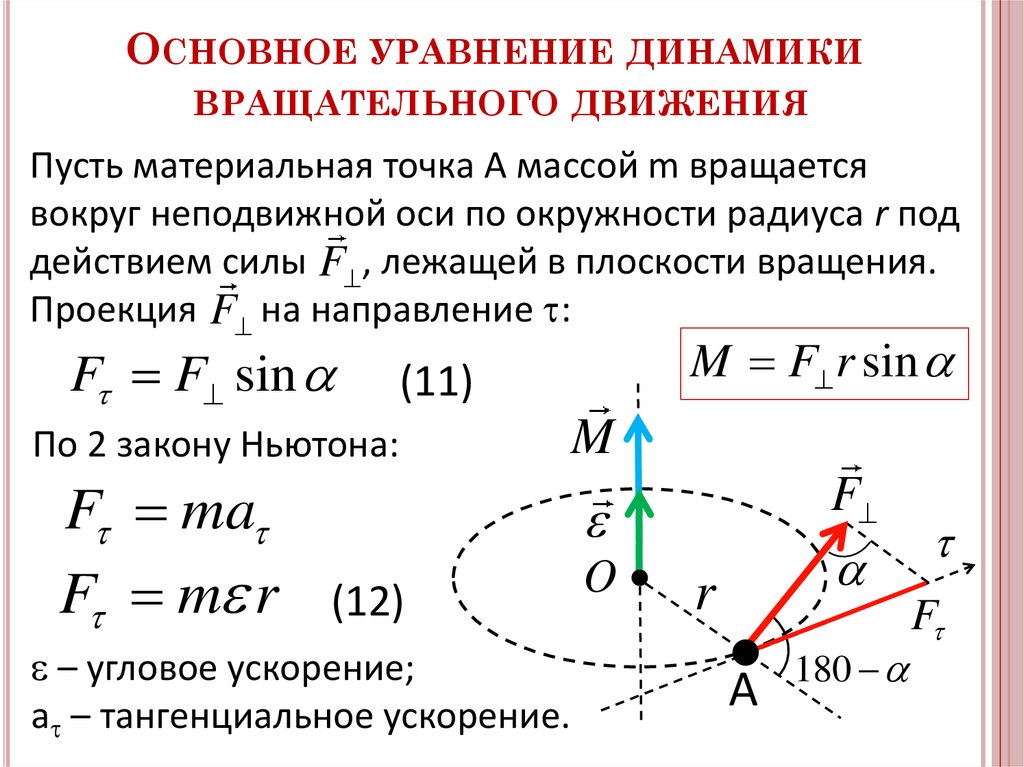

Как определить главный момент сил инерции?

То есть главный момент сил инерции относительно центра О равен взятому с обратным знаком вектору, выражающему производную по времени от кинетического момента системы относительно того же центра.

Чему равна сила инерции материальной точки?

Сила инерции Сила инерции, векторная величина, численно равная произведению массы т материальной точки на ее ускорение w и направленная противоположно ускорению.

Как вычислить момент инерции тела относительно оси проходящей через центр масс?

15. Теорема Гюйгенса-Штейнера: момент инерции тела относительно данной оси A равен моменту инерции тела отно- сительно оси параллельной данной и проходящей через центр масс тела C + произ- ведение массы тела на квадрат расстояния между осями a: IA = IC + ma2.

Что значит вектор силы?

Вектор силы — образное представление, видение того, какие линии сил организуют тело человека. Вектор силы — это то, что создает впечателение о человеке. Вектор силы — это способ самоорганизации своего тела и своего статуса, способ самовнушение телом.

В чем заключается разница между главным вектором и равнодействующей силой?

Главным вектором называют силу, равную векторной сумме всех действующих в системе сил: В отличие от равнодействующей, величину которой находят (когда она существует) по той же формуле, при определении главного вектора не конкретизируется точка приложения этой силы.

Что такое главный момент инерции?

Центробежный момент инерции

Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела.

Как направлен главный вектор сил инерции?

Следовательно, главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.

Что такое момент инерции своими словами?

Свойство любого объекта, который может вращаться. Это скалярная величина, которая показывает, насколько трудно изменить скорость вращения объекта вокруг текущей оси вращения. Иными словами, во вращательном движении тело вращается вокруг фиксированной оси.

Что такое сила инерции?

Силы, действующие на тела в неинерциальных системах отсчета, и не обусловленные взаимодействием этих тел с другими телами, называются силами инерции.

Какие бывают силы инерции?

В классической физике силы инерции встречаются в двух различных ситуациях в зависимости от системы отсчёта, в которой производится наблюдение. Это — сила, приложенная к связи при наблюдении в инерциальной СО, или сила, приложенная к рассматриваемому телу, при наблюдении в неинерциальной системе отсчёта.

Откуда берется сила инерции?

Силы инерции возникают только в системе отсчета, движущейся с ускорением, т. е. это кажущиеся силы. Силы, вызывающие ускорение данного тела, и силы инерции, возникающие вследствие ускорения, всегда равны по величине и противоположно направлены.

В чем измеряется инерция?

Килограмм — метр в квадрате — единица измерения момента инерции в Международной системе единиц. Эта единица является производной в системе СИ. Килограмм — метр в квадрате — это момент инерции материальной точки, имеющей массу один килограмм, движущейся по окружность радиуса 1 метр, вокруг оси вращения.

Для чего нужен Тензор инерции?

Тензор инерции — в механике абсолютно твёрдого тела — тензорная величина, связывающая момент импульса тела и кинетическую энергию его вращения с угловой скоростью: в компонентах это выглядит так: Используя определение момента импульса системы N материальных точек (перенумерованных в формулах ниже индексом k):

Чем больше момент инерции?

Определение момента инерции

То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

Чему равны главный вектор и главный момент произвольной системы сил при равновесии тела?

Для равновесия твердрго тела, находящегося под действием плоской системы сил, необходимо и достаточно, чтобы главный вектор этой системы сил и ее алгебраический главный момент были равны нулю, то есть R = 0, LO = 0, где О — любой центр, расположенный в плоскости действия сил системы.

Что называется сходящимися силами?

Систе́ма сходя́щихся сил — это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке.

Что такое произвольная плоская система сил?

Плоская произвольная система сил — система сил, как угодно расположенных, в одной плоскости.

В чем заключается принцип Даламбера?

ДАламбера принцип Д’Аламбера принцип, один из основных принципов динамики, согласно которому, если к заданным (активным) силам, действующим на точки механической системы, и реакциям наложенных связей присоединить силы инерции, то получится уравновешенная система сил.

Какая формула определяет момент силы?

Модуль вектора MO равен произведению модуля силы на её плечо h (кратчайшее расстояние от точки O до линии действия силы), т. е. MO=Fh. М.

Как связаны момент силы и момент инерции?

Произведение момента инерции твердого тела относительно неподвижной оси вращения на его угловое ускорение равно моменту внешних сил относи- тельно той же оси.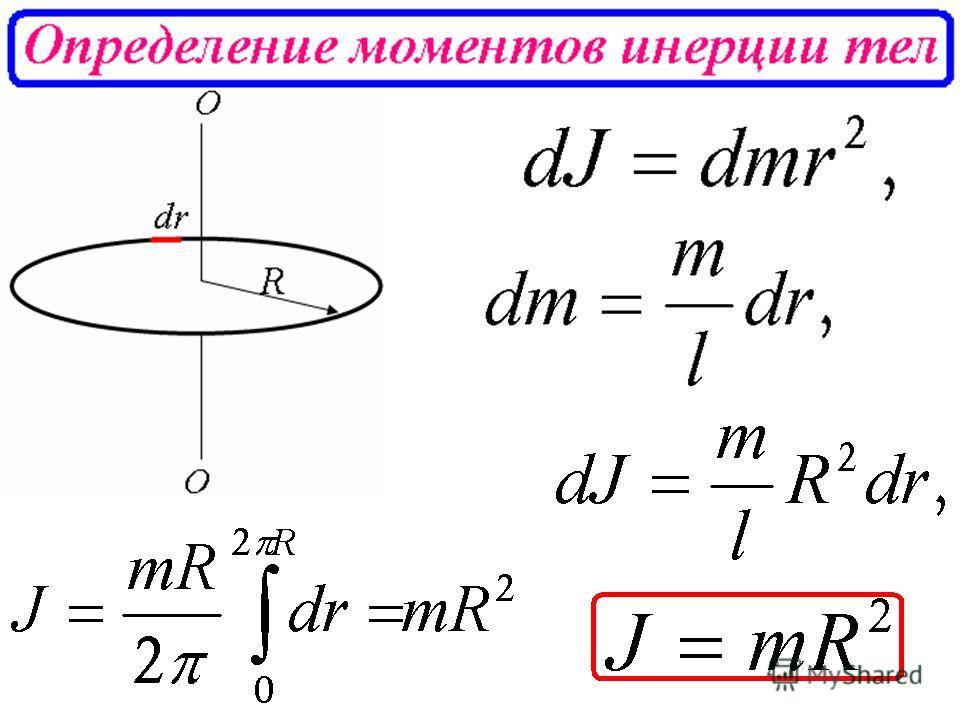 Это уравнение выражает собой основной закон динамики для тела, вращающегося вокруг неподвижной оси.

Какой закон инерции?

Закон инерции называют первым законом Ньютона, или первым законом механики.

Что делает тело в состоянии инерции?

Инерцией называется свойство тел сохранять своё состояние покоя или прямолинейного движения с постоянной скоростью, пока на тело не действуют внешние силы. Чтобы сила разогнала или затормозила движущееся тело, она должна действовать определённое время — скорость тела может измениться только постепенно.

Как преодолеть инерцию?

Закон инерции гласит, что всякое тело пребывает в состоянии покоя или прямолинейного равномерного движения до тех пор, пока действующие на него силы не изменят это состояние.Заполните свой бак:

• Вздремнуть 20 минут.
• Начать пить воду.
• Есть питательные, здоровые закуски.
• Заняться йогой или пилатесом.

Что называют моментом инерции тела?

Момент инерции тела — мера инертности твердых тел при вращательном движении. Его роль такая же, что и массы при поступательном движении. Момент инерции тела зависит от материала, размеров и формы тела, а также от расположения тела относительно оси.

Чему равен момент сопротивления?

Называется отношение полярного момента инерции к расстоянию от полюса, расположенного в центре тяжести поперечного сечения, до наиболее удалённой точки сечения: Wp=Ipρмакс.

Что такое момент инерции и от чего он зависит?

МОМЕ́НТ ИНЕ́РЦИИ тела, скалярная величина, мера инертности тела при его непоступательном (вращательном) движении. Величина М. и. зависит от распределения масс в теле.

Чему равен главный вектор и главный момент произвольной плоской системы сил?

Для равновесия произвольной плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор и главный момент этой системы сил равнялись нулю.

Чему равен главный вектор в системе сходящихся сил?

Сходящейся называется система сил, линии действия которых пересекаются в одной точке. Вектор, равный геометрической сумме сил какой-либо системы называется главным вектором этой системы сил. 1.1.

Чему равен главный момент в системе сходящихся сил?

Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.

Определение, Формула, Единица измерения, Фактор, Расчет

В этой статье вы узнаете полный обзор момента инерции , такой как его определение, формула различных разделов, единицы, зависящие факторы, расчет и многое другое.

В физике и механике момент инерции играет важную роль при анализе вращательного движения тел.

Момент инерции, связанный с динамикой.

Используется для расчета крутящего момента, необходимого для вращения объекта вокруг заданной оси, а также углового ускорения объекта под действием заданного крутящего момента. Он также используется для определения устойчивости объекта при его вращении, а также для прогнозирования движения объектов под действием внешних сил или моментов.

Мы также обсуждали полярный момент инерции, момент инерции площади, первый момент площади в нашей предыдущей статье, здесь мы узнаем только о моменте инерции.

Что такое момент инерции?

Момент инерции, также известный как вращательная инерция, момент инерции массы, угловая масса и секундный момент массы, является мерой сопротивления объекта изменению его вращательного движения.

Определяется как сумма произведений массы каждой частицы в объекте и квадрата ее расстояния от оси вращения объекта.

Чем больше момент инерции, тем сложнее изменить скорость или направление вращения объекта.

Момент инерции объекта зависит от формы, размера и распределения массы объекта.

Например, сплошной цилиндр имеет другой момент инерции, чем полый цилиндр того же размера и массы. Как правило, объекты с большей массой, сосредоточенной в направлении их центра масс, имеют меньший момент инерции, чем объекты с более равномерно распределенной массой.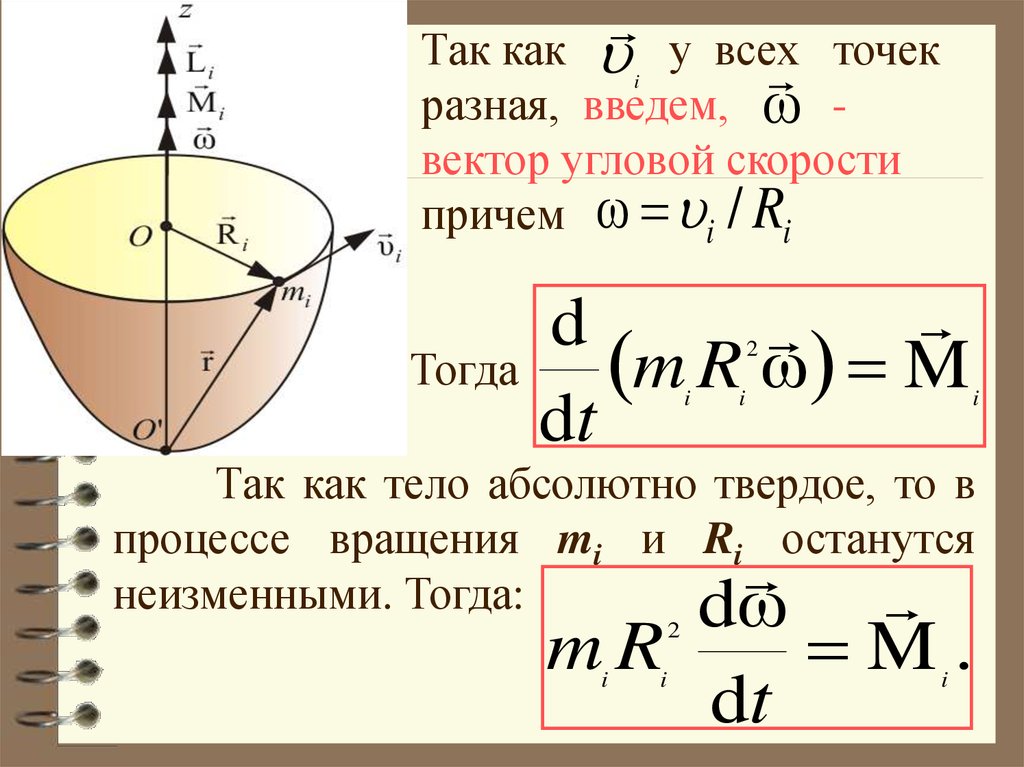

Обычно обозначается символом I.

Формула момента инерции

В выражениях для крутящего момента и углового момента для твердых тел (которые считаются объемными объектами) мы встретили термин Σmr².

Эта величина называется моментом инерции (I) массивного объекта. Для точки массой m на расстоянии r от фиксированной оси момент инерции определяется как mr².

Момент инерции точечной массы,

 I = mr²

Где,

m = масса тела

r = расстояние от оси вращения.

 Итак,

Момент инерции объемных объектов,

 I = Σmr²

При поступательном движении масса является мерой инерции; точно так же для вращательного движения момент инерции является мерой вращательной инерции.

В общем случае масса является неизменной величиной материи (за исключением движения, сравнимого со светом).

Но момент инерции тела не является постоянной величиной.

Зависит не только от массы тела, но и от того, как масса распределена вокруг оси вращения.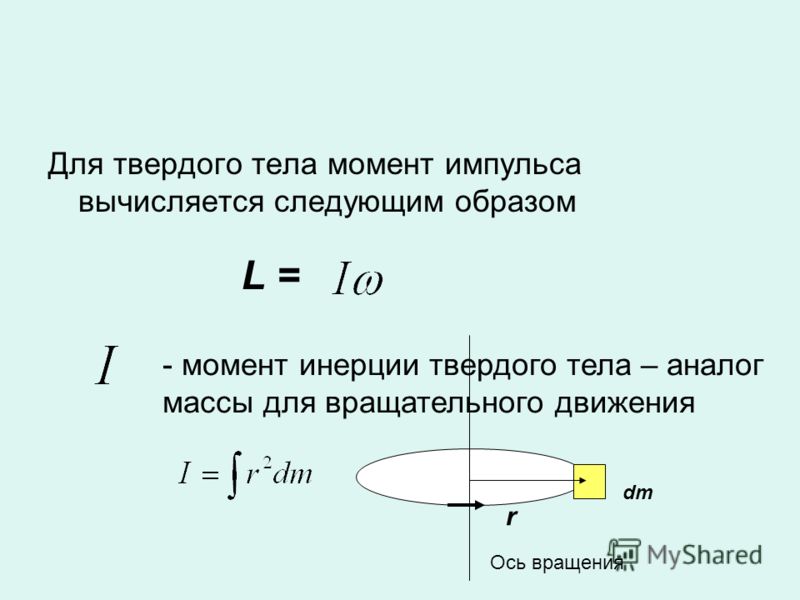

Найти момент инерции равномерно распределенной массы; мы должны рассматривать бесконечно малую массу (dm) как точечную массу и принимать ее положение (r) относительно оси.

Момент инерции этой точечной массы теперь можно записать как

 dI = (dm)r²

Мы получаем момент инерции всего объемного объекта путем интегрирования приведенного выше выражения.

I =  ∫ dI =  ∫(dm)r²

I =  ∫r²dm

Мы можем использовать приведенное выше выражение для определения момента инерции некоторых обычных объемных объектов, представляющих интерес, таких как стержни, кольца, диски,

Единица момента инерции

В системе СИ

Как известно, момент инерции

I = Σmr²

Итак,

I = кг-м²

I = кг-м² или кг-мм²

Аналогично в системе СГС будет

I = кг-см²

инерция, кг-м² или кг-мм² или кг-см² и его размер ML².

Факторы, от которых зависит момент инерции

Момент инерции тела зависит от нескольких факторов, включая:

• Форма тела
• Размер тела
• Распределение массы внутри тела
• Ориентация корпуса
• Ось вращения
• Свойства материала корпуса

Форма корпуса

Момент инерции обычно меньше для тела с более компактной и симметричной формой и больше для тела с более вытянутой или неправильной формы.

Размер тела 

Момент инерции, как правило, больше у более крупного тела, чем у меньшего тела той же формы и распределения массы.

Распределение массы внутри тела

Момент инерции обычно больше у тела с более централизованным распределением массы и меньше у тела с более равномерным распределением массы.

Ориентация тела

Момент инерции тела может изменяться в зависимости от ориентации тела относительно оси вращения.

Ось вращения

Момент инерции тела зависит от расположения оси вращения относительно тела.

Например, момент инерции тела, вращающегося вокруг оси, проходящей через его центр масс, обычно меньше, чем момент инерции относительно оси, не проходящей через центр масс.

Свойства материала тела

На момент инерции тела могут влиять свойства материала тела, такие как плотность и жесткость материала.

Момент инерции для различных форм

Теперь шаг за шагом мы узнаем момент инерции различных сечений.

Момент инерции однородного стержня

Рассмотрим однородный стержень массы M и длины l, как показано на рисунке.

Найдем выражение для момента инерции этого стержня относительно оси, проходящей через центр масс и перпендикулярной стержню.

Сначала необходимо установить начало системы координат так, чтобы оно совпадало с центром масс, который также является геометрическим центром стержня.

Стержень теперь находится вдоль оси x. Возьмем бесконечно малую массу dm на расстоянии x от начала координат.

Момент инерции dl этой массы dm относительно оси равен,

dI = dm.x²

Поскольку масса распределена равномерно, масса на единицу длины стержня составляет, 

λ = M/L

Масса dm бесконечно малой длины M as, 

dm = λ.dx = (M/L).dx

Момент инерции I всего стержня можно найти путем интегрирования dI,

I = ∫ dI =   ∫dm.x² = ∫ {(M/L).dx}.x²

Поскольку масса распределена по обе стороны от начала координат, пределы интегрирования берутся от -L/2 до L/2.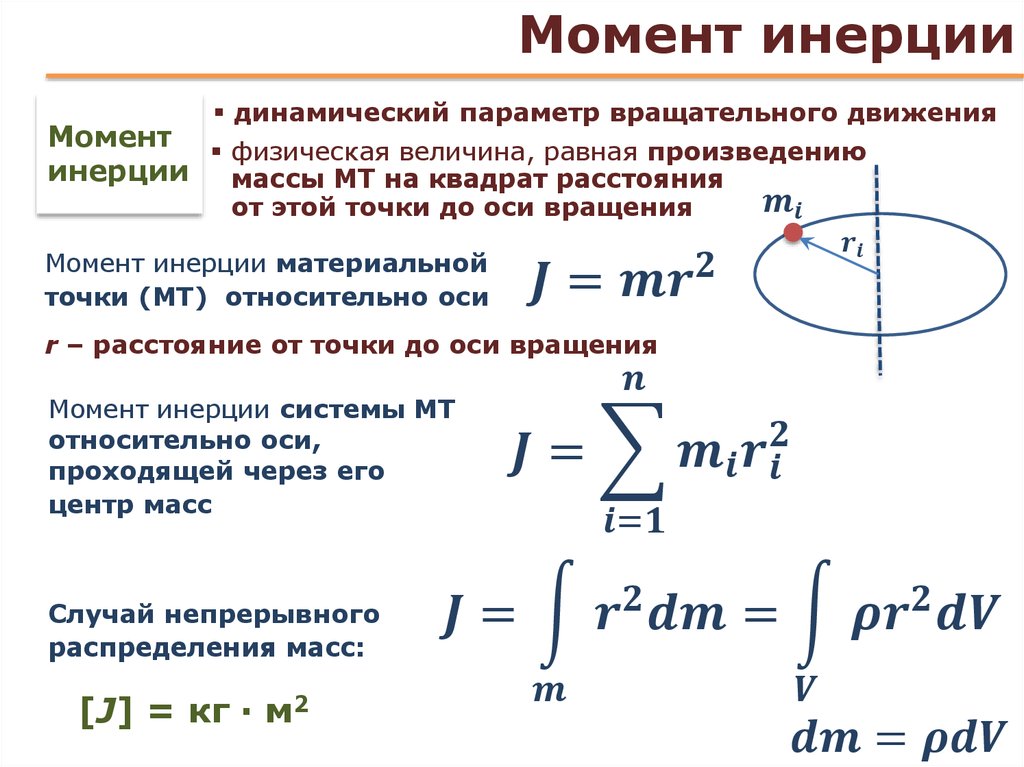

Итак,

I = (M/L) ∫ x².dx      (от -L/2 до L/2)

Однородное кольцо

Рассмотрим однородное кольцо массой М и радиусом R. Чтобы найти момент инерции кольца относительно оси, проходящей через его центр и перпендикулярной плоскости, возьмем бесконечно малую массу (дм) длина (dx) кольца. Это (dm) расположено на расстоянии R, которое является радиусом кольца от оси, как показано на рисунке.

Момент инерции dl этой малой массы dm равен

dl = dm.R²

Длина кольца равна его окружности (2πR).

Поскольку масса распределена равномерно, масса на единицу длины λ равна,

 λ =  масса/длина  = M/2πR

Масса (dm) бесконечно малой длины составляет, 

dm = λ.dx = (M/2πR).dx

Теперь момент инерции всего кольца равен

I = ∫ dI =   ∫dm.R² = ∫ {(M/2πr).dx}.R²

I = (MR/2π) ∫dx

Чтобы охватить всю длину кольца, пределы интегрирования берутся от 0 до 2πR.

I = (MR/2π) ∫dx       (от 0 до 2πR)

После интегрирования

I = M. R²

Момент инерции однородного диска

Рассмотрим диск массой M и радиусом R. Этот диск состоит из множества бесконечно малых колец, как показано на рисунке.

Рассмотрим одно такое кольцо массой dm, толщиной dr и радиусом r.

Момент инерции dl этого маленького кольца,

dI = (dm).r²

Поскольку масса распределена равномерно, масса на единицу площади

σ = масса/площадь = (M/π.R²)

Где,

σ = поверхностная плотность массы

Масса бесконечно малого кольца равна

dm = σ.2πrdr = (M/π.R²).2πrdr

Где член 2πrdr — площадь этого элементарного кольца, 2πr — длина, а dr — толщина .

dm = (2M/R²).rdr

Итак,

dI = (dm).r²

dI = (2M/R²).r³dr

Момент инерции всего диска равен,

I = ∫dI

Чтобы охватить всю длину диска, пределы интегрирования взяты от 0 до R.

I =  ∫(2M/R²) .r³dr       (От 0 до R)

После разрешения

I = 1/2(MR²)

Аналогичным образом можно найти

Момент инерции однородной сплошной сферы

I = (2MR²)/5

Момент инерции однородной полой сферы

I = (2MR²)/3

Момент инерции сплошного цилиндра

I = (1/2).

m.r²

Момент инерции полого цилиндра

I = (1/2).m(R² + r²)

Момент инерции сплошной прямоугольной пластины

I = (1/12).M(h² + w²)

Момент инерции относительно осей x’ и y’

Иногда необходимо вычислить момент инерции тела относительно осей x’ и y’ оси.

Мы можем рассчитать момент инерции для осей x’ и y’, используя две теоремы.

• Теорема о параллельных осях
• Теорема о перпендикулярной оси

Теорема о параллельной оси

Теорема о параллельной оси утверждает, что момент инерции плоского сечения относительно любой оси, параллельной центральной оси, равен моменту инерции сечения относительно центральной оси плюс произведение площади сечения на квадрат расстояния между двумя осями.

Математически можно записать как

Iₓ, = Iₓ + Ad²

Где,

A = площадь тела

Iₓ = момент инерции относительно точки x

d = расстояние по перпендикуляру между двумя линиями x и x’.

Iₓ, = Момент инерции относительно точки x’

Аналогичный метод можно применить для расчета момента инерции относительно оси y’.

Теорема о перпендикулярной оси

Теорема утверждает, что момент инерции плоского ламинарного тела относительно оси, перпендикулярной его плоскости, равен сумме моментов инерции относительно двух перпендикулярных осей, лежащих в плоскости тела, таких, что все три оси взаимно перпендикулярны и имеют общую точку.

Эту теорему также называют теоремой о полярной оси.

Математически,

Iz = Iₓ + Iᵧ

Где,

Iz = Момент инерции относительно оси Z

Iₓ = Момент инерции относительно оси X

5

5

Расчет момента инерции

Вопрос

Сплошной цилиндр имеет радиус 5 см и высоту 10 см. Имеет массу 2 кг. Вычислите момент инерции цилиндра относительно его оси симметрии.

Решение

Дано,

r = 5 см

h = 10 см

m = 2 кг

Как известно,

Момент инерции твердого цилиндра относительно его оси симметрии определяется по формуле :

I = (1/2). m.r²

Где I — момент инерции, m — масса цилиндра, r — радиус цилиндра.

После подстановки вышеуказанных значений получаем:

I = (1/2) × 2 × 5²

= 50 кг-см²

Момент инерции цилиндра равен 50 кг-см².

Итак, здесь вы должны знать все аспекты, связанные с моментом инерции .

Если у вас есть какие-либо сомнения, вы можете задать их мне по почте или на странице контактов.

Спасибо

Жесткий корпус | bartleby

Что такое твердое тело?

Твердое тело — это объект, который не меняет своей формы и не подвергается какой-либо значительной деформации под действием внешней силы или движения. Математически говоря, расстояние между любыми двумя точками внутри тела не меняется ни при каких обстоятельствах.

Механика твердого тела

Анализируя твердое тело в различных ситуациях, мы используем математическое свойство твердого тела для анализа большинства ситуаций. Три состояния движения твердого тела:

• Равновесие
• Поступательное движение
• Вращательное движение

Равновесие

Когда твердое тело находится в равновесии, его вектор скорости остается неизменным. Он не испытывает никакого линейного или вращательного ускорения. Когда на него действуют несколько сил и он остается в равновесии, тогда векторная сумма всех сил и моментов относительно любой точки всегда равна нулю.

Рассмотрим твердое тело «А», которое находится в равновесии под действием различных сил в разных положениях тела. i-я сила обычно отображается в точке P от выбранной оси отсчета.

Сумма всех сил, действующих на тело, определяется выражением

Сумма всех сил =∑iFi

Сумма моментов всех сил относительно точки O определяется выражением

Сумма всех сил моменты = ∑iriFi

Применяя условие равновесия, получаем, ∑iriFi=0 и ∑iFi=0

Поступательное движение

Говорят, что твердое тело находится в поступательном движении, когда все точки движущегося тела движутся равномерно в одном направлении или по одной линии.

В результате движущиеся точки не меняют своей ориентации,

• не вибрируют
• не вращаются

В этом случае все точки внутри тела имеют одинаковую скорость и ускорение.

Например, у ракеты, запущенной с пусковой установки, все точки движутся с одинаковой скоростью. Скорость и ускорение всех частиц в любой момент времени определяются с помощью законов Ньютона и кинематических уравнений.

Второй закон движения Ньютона гласит, что результирующая внешняя сила связана с ускорением следующим образом:

∑iFi=Ma

Здесь «a» — ускорение тела, а M — его масса. Левая часть представляет собой векторную сумму всех внешних сил, действующих на тело.

При чисто поступательном движении равнодействующая сил может быть ненулевой, но сумма моментов всех сил должна быть равна нулю.

Вращательное движение

Говорят, что тело находится во вращательном движении, когда все частицы движутся по окружности вокруг точки, которая называется точкой вращения. Угол, образуемый линией, соединяющей точку вращения (O) и случайную точку (P) с заданной базовой осью, изменяется со временем. Другими словами, угловое положение точки изменяется со временем, как показано на рисунке ниже. На рисунке θ — начальное угловое положение точки, а P — ее начальное положение для заданных опорных осей. P’ — конечное положение, а θ’ — конечное угловое положение точки.

Изменение угла в течение периода времени определяется выражением,

∆θ=θ’-θ

Скорость изменения углового положения аналогична скорости при поступательном движении и называется угловой скоростью. Точно так же существует угловое ускорение. Вращение твердого тела происходит вокруг воображаемой линии, называемой осью вращения. Ось вращения перпендикулярна плоскости вращения тела. Теперь объект на рисунке вращается в плоскости XY, ось вращения проходит через O и перпендикулярна плоскости XY. Подобно перемещению, мы можем использовать законы Ньютона и кинематические уравнения для определения углового положения, скорости и ускорения в любой момент времени. Вместо силы в поступательном движении здесь мы используем момент или крутящий момент силы относительно оси вращения. Величина, называемая моментом инерции, заменяет массу. Момент инерции твердого тела относительно оси вращения определяется выражением

Момент инерции 

I=∑imiri2

Здесь mi – масса i-го элемента тела, а ri – перпендикулярное расстояние элемента от оси вращения, как показано на рисунке.

Теперь второй закон движения в механике вращения принимает вид:

∑iri→×Fi→=Iα

результирующий момент, действующий на твердое тело. Для одиночной силы F на расстоянии r от данной оси ее крутящий момент относительно оси определяется выражением

Крутящий момент

τ→=r→×F→

Крутящий момент аналогичен силе при вращательном движении.

Твердое тело может совершать комбинацию этих движений. Но условие недеформации выполняется несмотря ни на что. Расстояние между любыми двумя точками остается постоянным. Это также можно сказать другими словами, что относительная скорость вдоль линии, соединяющей любые две точки, равна нулю.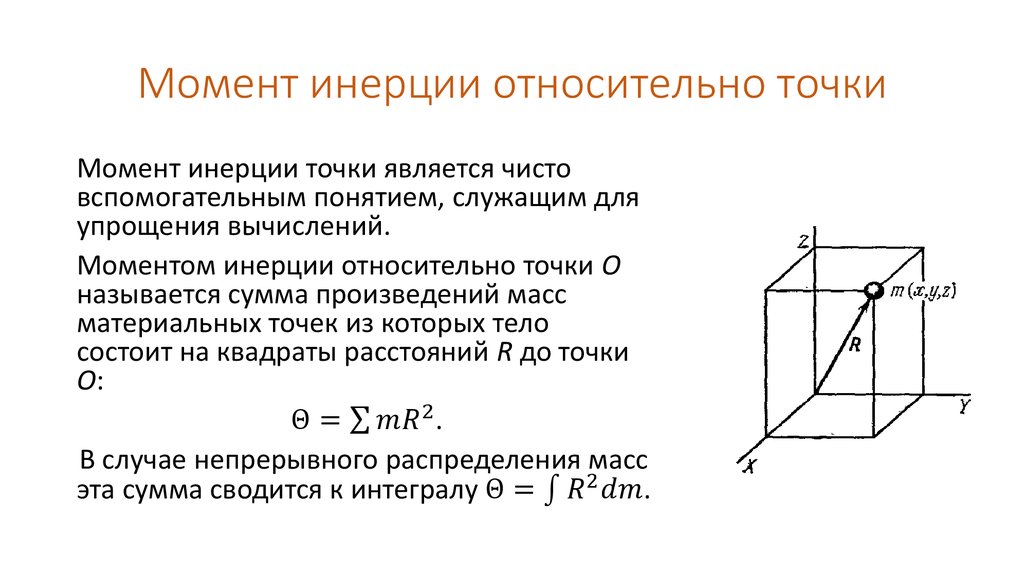 Если мы возьмем твердый стержень длины L в движении, Если две точки A и B имеют разные скорости, как показано на рисунке, относительная скорость точки вдоль линии соединения (или длина стержня в этом случае) равна нулю .

На приведенном выше рисунке, если мы вычислим компоненты скоростей точек A и B вдоль стержня и применим условие, мы получим

vACosα- vBCosβ=0

Контекст и приложения

профессиональные экзамены как для студентов, так и для выпускников, особенно для

• Бакалавриат в области технологии (машиностроение)
• Магистр технологии (машиностроение)
• Бакалавр в области физики

Практические задачи

Q 1 . Когда твердое тело находится в поступательном движении, все частицы внутри тела имеют

1. Одинаковую скорость
2. Одинаковое ускорение
3. Разную скорость
4. Оба (a) и (b)

Ответ : (d)- Оба (a) и (b)

Объяснение — Когда твердое тело находится в поступательном движении, все частицы внутри тела имеют одинаковую скорость и ускорение.

Q 2. Векторное векторное произведение силы на расстояние положения силы дает

Ответ : (a) Крутящий момент силы

Объяснение — Векторное векторное произведение силы и расстояния положения силы дает крутящий момент или момент силы.

Q 3. Какой из следующих законов движения Ньютона утверждает, что сила пропорциональна ускорению?

1. Newton’s Law of Motion
2. Newton’s II Закон о движении
3. Faraday Law of Motion
4. Newton’s III Law Motion

. Закон гласит, что ускорение тела пропорционально силе.

Вопрос 4. Какова сумма крутящих моментов при чисто поступательном движении?

1. Ноль
2. Меньше нуля
3. Больше нуля
4. Не могу сказать

Ответ : (a) — Ноль

.

Q 5. Что из следующего характерно для твердого тела?

1. Поворотный
2. Нерастяжимый и недеформируемый
3. Подвижный
4. Сгибаемый

Ответ : (b)-Нерастяжимый и недеформируемый

Объяснение — Твердое тело нерастяжимо и недеформируемо.

Формулы

Если в равновесии находится твердый корпус, то второй закон Ньютона в трансляционном движении дается,

∑ifi = ma

• Момент инерции тела дается на
• момент инерции тела,
• .0108

I = ∑IMiri2

• Второй закон Ньютона в движении вращения дается,

∑IR → I × F → Iα

• Newton’s Laws
• Mechanics
• Rutation Motion
. Центр масс
• Момент инерции
• Угловое движение

Мы обеспечим вас пошаговыми решениями миллионов задач из учебников, экспертами в любой области наготове 24 часа в сутки, 7 дней в неделю, когда вы запутались, и многое другое .