Конденсатор
Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.
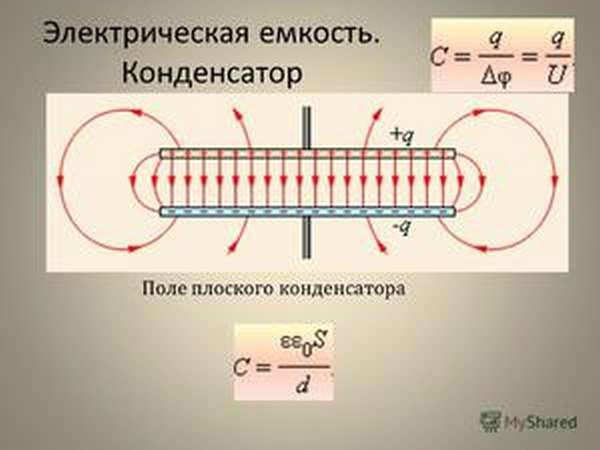
Конденсатор — это устройство для накопления электрического заряда; он состоит из двух проводников (обкладок), расположенных близко друг к другу, но не соприкасающихся. Типичный плоский конденсатор представляет собой пару параллельных пластин площадью А, разделенных небольшим промежутком d (рис. 25.1, а). Часто пластины, разделяют прокладкой из бумаги или другого диэлектрика (изолятора) и сворачивают в рулон (рис. 25.1,6).
Предположим, что конденсатор подключен к источнику напряжения, например к батарее. (Батарея — это устройство, на клеммах которого поддерживается относительно постоянная разность потенциалов). Подсоединенный к батарее конденсатор быстро заряжается: одна его обкладка приобретает положительный заряд, другая-равный по величине отрицательный (рис. 25.2).
Заряд, приобретаемый каждой из обкладок конденсатора, пропорционален разности потенциалов
Q = CVba (25.1)
Коэффициент пропорциональности С называется емкостью конденсатора. Единица емкости, кулон на вольт, называется фарад (Ф). На практике чаще всего применяются конденсаторы емкостью от 1 пФ (пикофарад, 10-12Ф) до 1 мкФ (микрофарад, 10-6 Ф). Формулу (25.1) впервые вывел Вольт в конце XVIII в.
Определение емкости конденсатора
Емкость С служит характеристикой данного конденсатора. Величина емкости С зависит от размеров, формы и взаимного расположения обкладок, а также от вещества, заполняющего промежуток между обкладками. В этом разделе мы будем считать, что между обкладками находится вакуум или воздух.
Емкость конденсатора, согласно (25.1), можно определить экспериментально, непосредственно измерив заряд Q пластины при известной разности потенциалов Vba.
Если геометрическая конфигурация конденсаторов достаточно проста, то можно определить емкость С аналитически. Для иллюстрации рассчитаем емкость С конденсатора с параллельными пластинами площадью А, находящимися на расстоянии d друг от друга (плоский конденсатор) (рис. 25.3). Будем считать, что величина d мала по сравнению с размерами пластин, так что электрическое поле
Поскольку плотность заряда равна σ = Q/A, то
Напряженность электрического поля связана с разностью потенциалов соотношением
Мы можем взять интеграл от одной пластины до другой вдоль траектории, направленной навстречу силовым линиям:
Установив связь между
Справедливость полученного вывода очевидна: чем больше площадь А, тем «свободнее» разместятся на ней заряды, отталкивание между ними будет меньше и каждая пластина сможет удерживать больший заряд. Чем больше расстояние d между пластинами, тем слабее заряды на одной пластине будут притягивать заряды на другой: на пластины от батареи поступает меньше заряда и емкость оказывается меньше.
Обратим также внимание, что формула справедлива при использовании в качестве диэлектрика — вакуума. Для других изоляторов используется коэффициент диэлектрической проницаемости
Тогда, с учётом коэффициента, ёмкость конденсатора будет равна:
С = Кε0 A/d , либо С = ε A/d
Например, для некоторых диэлектриков коэффициент К будет равен:
Вакуум: К = 1.0000
Воздух (1 атм): К = 1.0006
Парафин: К = 2.2
Эбонит: К = 2.8
Пластик (поливинильный): К = 2.8-4.5
Бумага: К = 3-7
Кварц: К = 4.3
Стекло: К = 4-7
Фарфор: К = 6-8
Слюда: К = 7
Более подробно это будет рассмотрено далее в публикации — «Диэлектрики».
Продолжение следует. Коротко о следующей публикации:
Последовательное и параллельное соединения конденсаторов.
Конденсаторы можно соединять различными способами. На практике это используют очень часто, и емкость комбинации конденсаторов зависит от того, как они соединены. Два основных способа соединения — параллельное и последовательное.
Альтернативные статьи:
Дизель-генератор,
Асинхронный генератор.
Замечания и предложения принимаются и приветствуются!
Областей применения этого устройства сейчас много, чем и обусловлен их большой ассортимент. Они различаются по материалам, из которых изготовлены, назначению, диапазону основного параметра. Но главной характеристикой конденсатора является его емкость.
Принцип работы конденсатора
Конструкция
На схемах конденсатор обозначается в виде двух параллельных линий, не связанных между собой:
Это соответствует его простейшей конструкции — двум пластинам (обкладкам), разделенным диэлектриком. Фактическое исполнение этого изделия чаще всего представляет собой завернутые в рулон обкладки с прослойкой диэлектрика или иные причудливые формы, но суть остается той же самой.
Емкость конденсатора
Электрическая ёмкость – способность проводника накапливать электрические заряды. Чем больше заряд вмещает проводник при данной разности потенциалов, тем больше ёмкость. Зависимость между зарядом Q и потенциалом φ выражается формулой:
C=Q/φ
где Q заряд в кулонах (Кл), φ потенциал в вольтах (В).
 Емкость измеряется в фарадах (Ф), что вы помните еще с уроков физики. На практике чаще встречаются более мелкие единицы: миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ).
Емкость измеряется в фарадах (Ф), что вы помните еще с уроков физики. На практике чаще встречаются более мелкие единицы: миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ).
Накопительная способность зависит от геометрических параметров проводника, диэлектрической проницаемости среды, где он находится. Так, для сферы из проводящего материала она будет выражаться формулой:
C=4πεε0R
где ε0—8,854·10^−12 Ф/м, электрическая постоянная, а ε диэлектрическая проницаемость среды (табличная величина для каждого вещества).
В реальной жизни нам чаще приходится иметь дело не с одним проводником, а с системами таковых. Так, в обычном плоском конденсаторе емкость будет прямо пропорциональна площади пластин и обратно — расстоянию между ними:
C=εε0S/d
ε здесь — диэлектрическая проницаемость прокладки между пластинами.
Емкость параллельных и последовательных систем
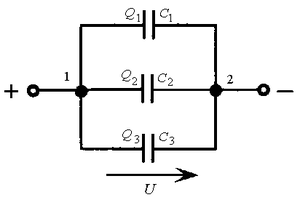
Параллельное соединение емкостей представляет собой один большой конденсатор с тем же слоем диэлектрика и суммарной площадью пластин, поэтому общая емкость системы представляет собой сумму таковых у каждого из элементов. Напряжение при параллельном соединении будет одним и тем же, а заряд распределится между элементами схемы.
C=C1+C2+C3
Последовательное соединение конденсаторов характеризуется общим зарядом и распределенным напряжением между элементами. Поэтому суммируется не емкость, а обратная ей величина:
1/C=1/С1+1/С2+1/С3
Из формулы емкости одиночного конденсатора можно вывести, что при одинаковых элементах, соединенных последовательно, их можно представить в виде одного большого с той же площадью обкладки, но с суммарной толщиной диэлектрика.
Свойства конденсатора
Реактивное сопротивление
Конденсатор не может проводить постоянный ток, что видно из его конструкции. В такой цепи он может только заряжаться. Зато в цепях переменного тока он прекрасно работает, постоянно перезаряжаясь. Если не ограничения, исходящие из свойств диэлектрика (его можно пробить при превышении предела напряжения), этот элемент заряжался бы бесконечно (т. н. идеальный конденсатор, что-то вроде абсолютно черного тела и идеального газа) в цепи постоянного тока, а ток через него проходить не будет. Проще говоря, сопротивление конденсатора в цепи постоянного тока бесконечно.
При переменном токе ситуация иная: чем выше частота в цепи, тем меньше сопротивление элемента. Такое сопротивление называется реактивным, и оно обратно пропорционально частоте и емкости:
Z=1/2πfC
где f частота в герцах.
Накопитель энергии
Энергия, запасенная заряженным конденсатором, может быть выражена формулой:
E=(CU^2)/2=(q^2)/2C
где U напряжение между обкладками, а q накопленный заряд.
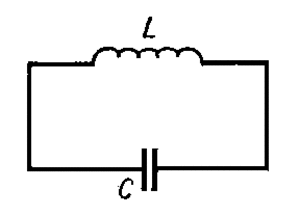
Конденсатор в колебательном контуре
В замкнутом контуре, содержащем катушку и конденсатор, может быть сгенерирован переменный ток.
После зарядки конденсатора он начнет саморазряжаться, давая возрастающий по силе ток. Энергия разряженного конденсатора станет равной нулю, зато магнитная энергия катушки — максимальной. Изменение величины тока вызывает ЭДС самоиндукции катушки, и она по инерции пропустит ток в сторону второй обкладки, пока та полностью не зарядится. В идеальном случае такие колебания бесконечны, а в реальности они быстро затухают. Частота колебаний зависит от параметров как катушки, так и конденсатора:
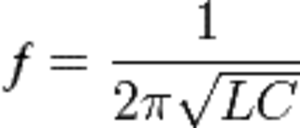
где L индуктивность катушки.
Паразитная индуктивность
Конденсатор может обладать собственной индуктивностью, что можно наблюдать при повышении частоты тока в цепи. В идеальном случае эта величина незначительна, и ей можно пренебречь, но в реальности, когда обкладки представляют собой свернутые пластинки, не считаться с этим параметром нельзя, особенно если речь идет о высоких частотах. В таких случаях конденсатор совмещает в себе две функции, и представляет собой своеобразный колебательный контур с собственной резонансной частотой.
Чтобы добиться корректной работы схемы, рекомендуется применять конденсаторы, у которых резонансная f больше собственной частоты в цепи.
Эксплуатационные характеристики
Помимо указанных выше емкости, собственной индуктивности и энергоемкости, реальные конденсаторы (а не идеальные) обладают еще рядом свойств, которые нужно учитывать при выборе этого элемента для цепи. К ним относятся:
 номинальное напряжение,
номинальное напряжение,- полярность,
- ток утечки,
- сопротивление материала обкладок,
- диэлектрические потери,
- зависимость емкости от температуры.
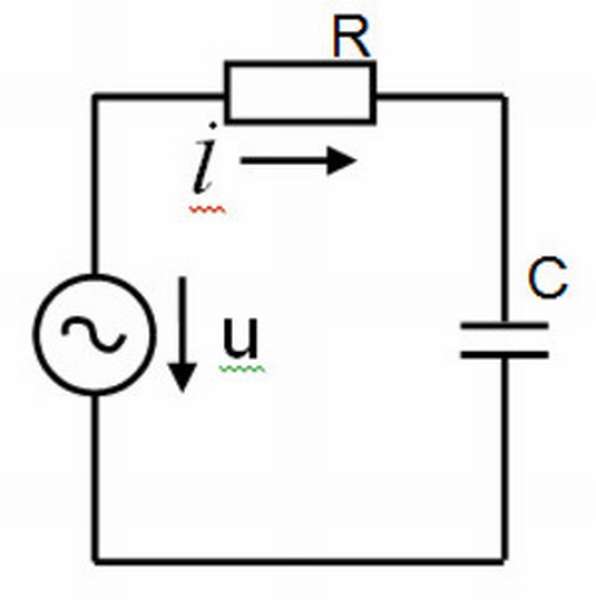
Чтобы понять, откуда берутся потери, необходимо разъяснить, что представляют собой графики синусоидальных тока и напряжения в этом элементе. Когда конденсатор заряжен максимально, ток в его обкладках равен нулю. Соответственно, когда ток максимален, напряжение отсутствует. То есть напряжение и ток сдвинуты по фазе на угол 90 градусов. В идеале конденсатор обладает только реактивной мощностью:
Q=UIsin 90
В реальности же обкладки конденсатора обладают собственным сопротивлением, а часть энергии расходуется на нагрев диэлектрика, что обуславливает ее потери. Чаще всего они незначительны, но иногда ими пренебрегать нельзя. Основной характеристикой этого явления служит тангенс угла диэлектрических потерь, представляющий собой отношение активной мощности (даваемой малыми потерями в диэлектрике) и реактивной. Измерить эту величину можно теоретически, представив реальную емкость в виде эквивалентной схемы замещения — параллельной или последовательной.
Определение тангенса угла диэлектрических потерь

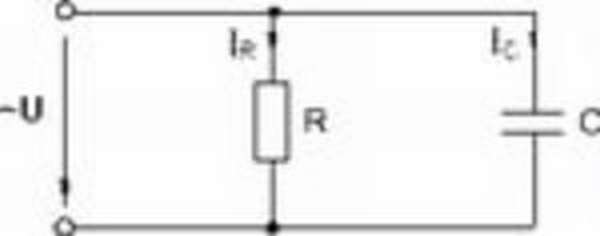
При параллельном соединении величина потерь определяется отношением токов:
tgδ = Ir/Ic = 1/(ωCR)
В случае последовательного соединения угол вычисляется соотношением напряжений:
tgδ = Ur/Uc = ωCR
В реальности для замеров tgδ пользуются прибором, собранным по мостовой схеме. Его применяют для диагностики потерь в изоляции у высоковольтного оборудования. С помощью измерительных мостов можно измерять и другие параметры сетей.
Номинальное напряжение
Этот параметр указывается на маркировке. Он показывает предельную величину напряжения, которое может быть подано на обкладки. Превышение номинала может привести к пробою конденсатора и выходу его из строя. Зависит этот параметр от свойств диэлектрика и его толщины.
Полярность
Некоторые конденсаторы имеют полярность, то есть в схему его необходимо подключать строго определенным образом. Связано это с тем, что в качестве одной из обкладок используется какой-либо электролит, а диэлектриком служит оксидная пленка на другом электроде. При изменении полярности электролит просто разрушает пленку и конденсатор перестает работать.
Температурный коэффициент емкости
Он выражается отношением ΔC/CΔT где ΔT изменение температуры окружающей среды. Чаще всего эта зависимость линейна и незначительна, но для конденсаторов, работающих в агрессивных условиях, ТКЕ указывается в виде графика.
Разрушение конденсатора
 Выход конденсатора из строя обусловлен двумя основными причинами — пробоем и перегревом. И если в случае пробоя некоторые их виды способны к самовосстановлению, то перегрев со временем приводит к разрушению.
Выход конденсатора из строя обусловлен двумя основными причинами — пробоем и перегревом. И если в случае пробоя некоторые их виды способны к самовосстановлению, то перегрев со временем приводит к разрушению.
Перегрев обусловлен как внешними причинами (нагреванием соседних элементов схемы), так и внутренними, в частности, последовательным эквивалентным сопротивлением обкладок. В электролитических конденсаторах он приводит к испарению электролита, а в оксиднополупроводниковых — к пробою и химической реакции между танталом и оксидом марганца.
Опасность разрушения в том, что часто оно происходит с вероятностью взрыва корпуса.
Техническое исполнение конденсаторов
Классифицировать конденсаторы можно по нескольким группам. Так, в зависимости от возможности регулировать емкость их разделяют на постоянные, переменные и подстроечные. По своей форме они могут быть цилиндрическими, сферическими и плоскими. Можно делить их по назначению. Но самой распространенной классификацией является таковая по типу диэлектрика.
Бумажные конденсаторы
В качестве диэлектрика используется бумага, очень часто промасленная. Как правило, такие конденсаторы отличает большой размер, но были варианты и в небольшом исполнении, без промасливания. Используются в качестве стабилизирующих и накопительных устройств, а из бытовой электроники постепенно вытесняются более современными пленочными моделями.
При отсутствии промасливания имеют существенный недостаток — реагируют на влажность воздуха даже при герметичной упаковке. Промокшая бумага увеличивает энергопотери.
Диэлектрик в виде органических пленок
Пленки могут быть выполнены из органических полимеров, таких как:
- полиэтилентерифталат,
- полиамид,
- поликарбонат,
- полисульфон,
- полипропилен,
- полистирол,
- фторопласт (политетрафторэтилен).
По сравнению с предыдущими, такие конденсаторы имеют более компактные размеры, не увеличивают диэлектрические потери при увеличении влажности, но многие из них подвергаются риску выхода из строя при перегреве, а те, что этого недостатка лишены, отличаются более высокой стоимостью.
Твердый неорганический диэлектрик
Это может быть слюда, стекло и керамика.
Преимуществом этих конденсаторов считается их стабильность и линейность зависимости емкости от температуры, приложенного напряжения, а у некоторых — даже от радиации. Но иногда сама такая зависимость становится проблемой, и чем она менее выражена, тем дороже изделие.
Оксидный диэлектрик
С ним выпускаются алюминиевые, твердотельные и танталовые конденсаторы. Они имеют полярность, поэтому выходят из строя при неправильном подключении и превышении номинала напряжения. Но при этом они обладают хорошей емкостью, компактны и стабильны в работе. При правильной эксплуатации могут работать около 50 тыс. часов.
Вакуум
Такие устройства представляют собой стеклянную или керамическую колбу с двумя электродами, откуда выкачан воздух. В них практически отсутствуют потери, но малая емкость и хрупкость ограничивают сферу их применения радиостанциями, где величина емкости не так важна, а вот устойчивость к нагреву имеет принципиальное значение.
Двойной электрический слой
Если посмотреть, для чего нужен конденсатор, то можно понять, что этот тип — не совсем он. Скорее, это дополнительный или резервный источник питания, в качестве чего они и используются. Одни категория таких устройств — ионисторы — содержат в себе активированный уголь и слой электролита, другие работают на ионах лития. Емкость этих приборов может составлять до сотен фарад. К их недостаткам можно отнести высокую стоимость и активное сопротивление с токами утечки.
Маркировка конденсаторов
 Каким бы ни был конденсатор, есть два обязательным параметра, которые должны быть отражены в маркировке — это его емкость и номинальное напряжение.
Каким бы ни был конденсатор, есть два обязательным параметра, которые должны быть отражены в маркировке — это его емкость и номинальное напряжение.
Помимо этого, на большинстве из них существует цифро-буквенное обозначение его характеристик. В соответствии с российскими стандартами конденсаторы маркируются четырьмя знаками.
Первая буква К означает «конденсатор», следующая цифра — вид диэлектрика, далее следует указатель назначения в виде буквы, последний значок может означать как тип конструкции, так и номер разработки, это уже зависит от завода-изготовителя. Третий пункт часто пропускается. Используется такая маркировка на достаточно крупных изделиях, где ее можно разместить. По ГОСТ расшифровка будет выглядеть так:
Первые буквы:
- К — конденсатор постоянной емкости.
- КТ — подстроечник.
- КП — конденсатор переменной емкости.
Вторая группа — тип диэлектрика:
 1, 61 вакуум,
1, 61 вакуум,- 2, 60 воздух,
- 3 газ,
- 4 твердый,
- 10, 15 керамика,
- 20 кварц,
- 21 стекло,
- 22 стеклокерамика,
- 23 стеклоэмаль,
- 31, 32 слюда,
- 40, 41, 42 бумага,
- 50 алюминиевый электролитический,
- 51 танталовый,
- 52 объемно-пористый,
- 53, 54 оксидные,
- 71 полистирол,
- 72 фторопласт,
- 73 ПЭТ,
- 75 комбинированный,
- 76 лак и пленка,
- 77 поликарбонат.
На маленьких конденсаторах всего этого не разместить, поэтому там применяется сокращенная маркировка, которая с непривычки может даже потребовать калькулятора, а иногда — лупу. В этой маркировке зашифрованы емкость, номинал напряжения и отклонения от основного параметра. Остальные параметры наносить нет смысла: это, как правило, керамические конденсаторы.
Маркировка керамических конденсаторов
Например, обозначение 109 расшифровывается как 1 пикофарад, а 100–10 пикофарад, 681–680 пикофарад, или 0,68 нанофарад, а 104- 100 тыс. пФ или 100нФ
Часто можно встретить первую букву единицы измерения в качестве запятой: p50–0,5 пФ, 1n5–1,5 нФ, 15μ – 15 мкФ, 15m – 15 мФ. Иногда вместо p пишется R.
После трех цифр может стоять буква, означающая разброс параметра емкости:
 B +/-0,1 пФ.
B +/-0,1 пФ.- C +/-0,25 пФ.
- D- +/-0,5 пФ.
- F +/-1%.
- G +/-2%.
- J +/-5%.
- K +/-10%.
- M +/-20%.
- Z до 80% отклонение.
Если вы высчитываете характеристику цепи в единицах СИ, то для того, чтобы найти емкость в фарадах, необходимо помнить показатели степеней числа 10:
- -3 миллифарады,
- -6 микрофарады,
- -9 нанофарады,
- -12 пикофарады.
Таким образом, 01 пФ — это 0,1 *10^-12 Ф.
На устройствах SMD емкость в пикофарадах обозначает буква, а цифра после нее — степень 10, на которую надо умножить это значение.
| буква | C | буква | C | буква | C | буква | C |
| A | 1 | J | 2,2 | S | 4,7 | a | 2,5 |
| B | 1,1 | K | 2,4 | T | 5,1 | b | 3,5 |
| C | 1,2 | L | 2,7 | U | 5,6 | d | 4 |
| D | 1,3 | M | 3 | V | 6,2 | e | 4,5 |
| E | 1,5 | N | 3,3 | W | 6,8 | f | 5 |
| F | 1,6 | P | 3,6 | X | 7,5 | m | 6 |
| G | 1,8 | Q | 3,9 | Y | 8,2 | n | 7 |
| Y | 2 | R | 4,3 | Z | 9,1 | t | 8 |
Номинальное рабочее напряжение таким же образом может маркироваться буквой, если полностью его написать проблематично. В России принят следующий стандарт буквенного обозначения номинала:
| буква | V | буква | V |
| I | 1 | K | 63 |
| R | 1,6 | L | 80 |
| M | 2,5 | N | 100 |
| A | 3,2 | P | 125 |
| C | 4 | Q | 160 |
| B | 6,3 | Z | 200 |
| D | 10 | W | 250 |
| E | 16 | X | 315 |
| F | 20 | T | 350 |
| G | 25 | Y | 400 |
| H | 32 | U | 450 |
| S | 40 | V | 500 |
| J | 50 |
Несмотря на списки и таблицы, лучше все-таки изучить кодировку конкретного производителя — в разных странах они могут отличаться.
К некоторым конденсаторам прилагается более развернутое описание их характеристик.
Емкость конденсатора 
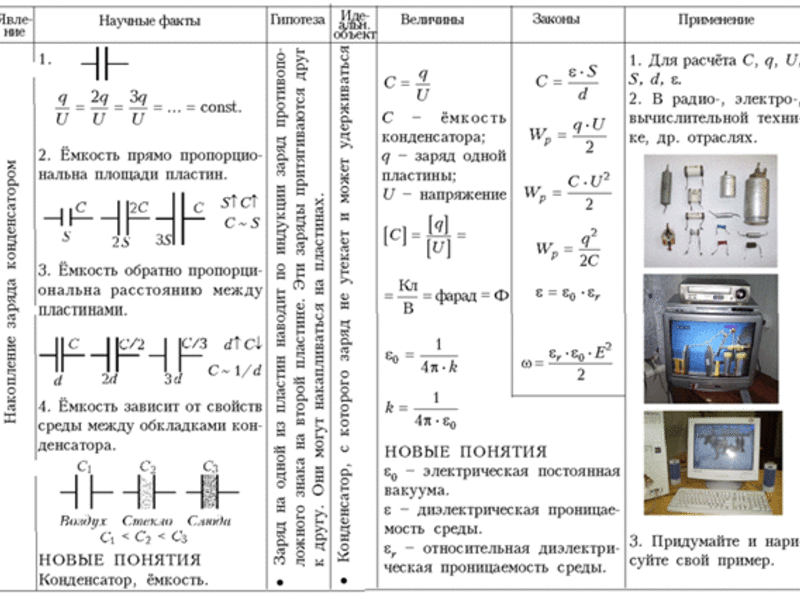



Две металлические пластины (обкладки) или два проводника любой формы, разделенные диэлектриком, называются электрическим конденсатором. Электрическая емкость конденсатора будет зависеть от площади пластины и расстояния между пластинами. Конденсатором, так же, являются два провода электрической сети. Каждый провод, изолированный от земли, можно тоже рассматривать как конденсатор, причем одной из его обкладок будет служить провод, а другой — земля.
Конденсаторы электрическая емкость которых может быть любой, образуются не только в естественных условиях, но и специально изготовляются на электротехнических заводах.
Конденсаторы обладают свойством накапливать и удерживать равные по величине и разные по знаку (разноименные) электрические заряды.
Конденсатор будет заряжен, если на его обкладках накоплены разноименные электрические заряды. В этом случае между обкладками конденсатора, как и вокруг любых заряженных тел, существует электрическое поле и возникает электрическое напряжение между любыми точками поля. В частности, существует напряжение и между обкладками конденсатора U, которое пропорционально величине электрического заряда q на любой из обкладок. Эта зависимость становится понятной, если вспомнить, что электрическое напряжение зависит от напряженности электрического поля, а последняя пропорциональна величине заряда, вокруг которого создается электрическое поле.
Свойство конденсатора накапливать и удерживать электрические заряды характеризуется емкостью конденсатора.
Емкостью конденсатора (обозначение С) называется постоянная величина, равная отношению величины заряда одной из обкладок конденсатора к напряжению между обкладками.
Таким образом, расчетная электрическая емкость конденсатора формула размещена ниже:
Емкость конденсатора измеряется в фарадах (Ф). Емкостью в одну фараду обладает конденсатор, у которого при напряжении в 1 в (1 вольт) заряды на каждой обкладке составляют 1 к (1 кулон), т. е.
Однако фарада является очень крупной единицей, поэтому на практике чаще пользуются более мелкими единицами:
микрофарадой (мкф), составляющей миллионную долю фарады,
1 мкф = 10-6 ф
и пикофарадой (пф), составляющей миллионную долю микрофарады,
1 пф= 10-6 мкф = 10-12 ф.
На чертежах конденсатор условно изображается, как показано на рисунке ниже.
Что такое конденсаторы и электрическая емкость смотрите видео ниже:

Что собой представляет электрическая емкость. Единицы измерения и формулы для расчета данной величины. Электроемкость аккумуляторов и конденсаторов.
В электротехнике часто встречается понятие ёмкости. При этом речь идёт не о ведре или другом сосуде, а об электрической ёмкости проводника, аккумулятора и конденсатора. Путать эти понятия нельзя. В этой статье мы разберемся, что такое электрическая ёмкость, от чего она зависит и в каких единицах измеряется. Содержание:
Определение
Для проводников электрической ёмкостью называется величина, которая характеризует способность тела накапливать электрический заряд. Это и есть её физический смысл. Обозначается латинской буквой C. Она равна отношению заряда к потенциалу, если это записать в виде формулы, то получается следующее:
C=q/Ф
Электроемкость любого предмета зависит от его формы и геометрических размеров. Если рассмотреть проводник в форме шара, в качестве примера, то формула для расчета её величины будет иметь вид:

Эта формула справедлива для уединенного проводника. Если расположить рядом два проводника и разделить их диэлектриком, тогда получится конденсатор. Об этом немного позже, сейчас давайте разберемся, в чем измеряется электроемкость.
Единица измерения электрической ёмкости — фарад. Если разложить её на составляющие согласно формуле то:
1 фарад =1 Кл/1 В
Исторически сложилось так, что размерность этой единицы выбрана не совсем верно. Дело в том, что на практике приходится работать с величинами электроемкости: мили-, микро-, нано- и пикофарад. Что равняется долям фарада, а именно:
1 мФ = 10^(-3) Ф
1 мкФ = 10^(-6) Ф
1 нФ = 10^(-9) Ф
1 пФ = 10^(-12) Ф
Конденсаторы
Конденсатор — это две пластины из проводящего материала, расположенные друг напротив друга, между которым находится слой диэлектрика. В заряженном состоянии обкладки имеют разные потенциалы: одна из них будет положительной, а вторая отрицательной. Электроемкость конденсатора зависит от величины заряда на его обкладках и разности потенциалов, напряжения между ними. Между пластинами возникает электростатическое поле, которое удерживает заряды на обкладках. Формула электрической емкости конденсатора в общем случае:
C=q/U
Если сказать простыми словами, то емкость конденсатора зависит от площади пластин и расстояния между ними, а также относительной диэлектрической проницаемости материала, расположенного между ними. Их различают по используемому диэлектрику:
- керамические;
- плёночные;
- слюдяные;
- металлобумажные;
- электролитические;
- танталовые и пр.
По форме обкладок:
- плоские;
- цилиндрические;
- сферические и пр.
Так как формула площади фигуры зависит от её формы, то и формула ёмкости будет разной для каждого случая.
Для плоского конденсатора:

Для двух концентрических сфер с общим центром:

Для цилиндрического конденсатора:

Как и у других элементов электрической цепи и в этом случае есть два основных способа соединения конденсаторов: параллельное и последовательное.
От этого зависит итоговая электрическая емкость полученной цепи. Расчёты ёмкости нескольких конденсаторов напоминают расчёты сопротивления резисторов в разном включении, только формулы для способов соединения расположены наоборот, то есть:
- При параллельном соединении общая электроемкость цепи является суммой емкостей каждого из элементов. Каждый следующий подключенный увеличивает итоговую емкость
Cобщ=C1+C2+C3
- При последовательном подключении электроемкость цепи снижается, подобно снижение сопротивления в цепи параллельно включённых резисторов. То есть:
Cобщ=(1/С1)+ (1/С2)+ (1/С3)
Важно! В параллельной схеме соединения напряжения на обкладках каждого элемента одинаковы. Это используют для получения больших значений электроемкости. В последовательном включении двух элементов напряжения на обкладках каждого из конденсаторов составляют по половине общего напряжения. Для трёх – трети и так далее.
Аккумуляторы и электроемкость
Основными характеристиками аккумуляторных батарей является:
- Номинальное напряжение.
- Емкость.
- Максимальный ток разряда.
В данном случае для определения количественной характеристики времени работы или, говоря простым языком, чтобы рассчитать, на какое время работы прибора хватит аккумулятора, используют величину ёмкости.
В аккумуляторных батареях для описания электрической ёмкости используют следующие размерности:
- А*ч — ампер-часы для больших аккумуляторов, например автомобильных.
- мА*ч — милиампер-часы, для аккумуляторов для носимых устройств, например смартфонов, квадрокопетров и электронных сигарет.
- Вт*часы — ватт-часы.
Эти характеристики позволяют определить, сколько времени работы выдержит аккумулятор при конкретной нагрузке. Для определения электрическую емкость аккумулятора измеряют в кулонах (Кл). В свою очередь кулон равен количеству электричества, переданному аккумулятору при силе тока 1А за 1с. Тогда если перевести в часы, то при токе в 1А за 1 час передается 3600 Кл.
Одним из способов измерения емкости аккумулятора является его разряд заведомо известным током, при этом вы должны замерить время разряда. Допустим, если аккумулятор разрядился до минимального уровня напряжения за 10 часов током в 5А – значит его емкость 50 А*ч
Электроемкость – это важная величина в электронике и электротехнике. На практике конденсаторы применяются практически в каждой схеме электронного устройства. Например, в блоках питания – для сглаживания пульсаций, уменьшения влияния высоковольтных всплесков на силовые ключи. Во времязадающих цепях различных схем, а также в ШИМ-контроллерах для того, чтобы задать рабочую частоту. Аккумуляторы также применяются повсеместно. Вообще задачи накапливания энергии и сдвига фаз встречаются очень часто.
Более подробно изучить вопрос поможет предоставленное видео:
Кратко объяснение изложено в этом видео уроке:
Теперь вы знаете, что такое электрическая емкость, в каких единицах происходит ее измерение и от чего зависит данная величина. Надеемся, предоставленная информация была для вас полезной и понятной!
Материалы по теме:
- Как определить емкость конденсатора
- Что такое электрический заряд
- Закон Кулона простыми словами
Нравится
 0)Не нравится
0)Не нравится 0)
0)Наряду с резисторами одними из наиболее часто используемых электронных компонентов являются конденсаторы. И в этой статье мы разберемся, из чего они состоят, как работают и для чего применяются! Давайте, в первую очередь, рассмотрим устройство и принцип работы конденсаторов. А затем плавно перейдем к основным свойствам и характеристикам – заряду, энергии и, конечно же, емкости конденсатора. Как видите, нам сегодня предстоит изучить много интересных моментов 🙂
Плоский конденсатор.
Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:
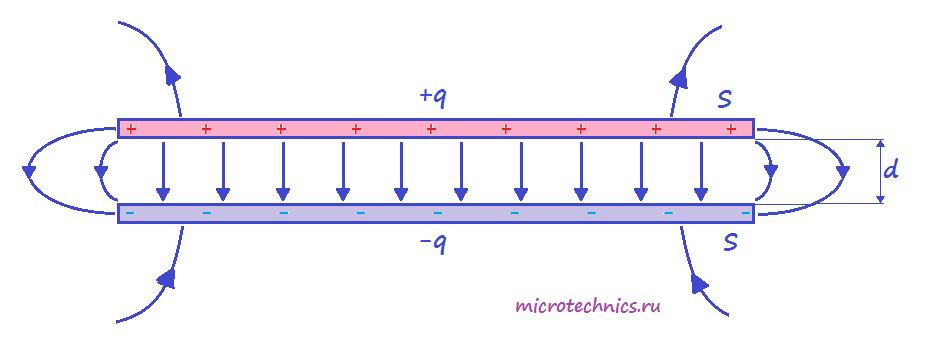
Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).
А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.
Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:
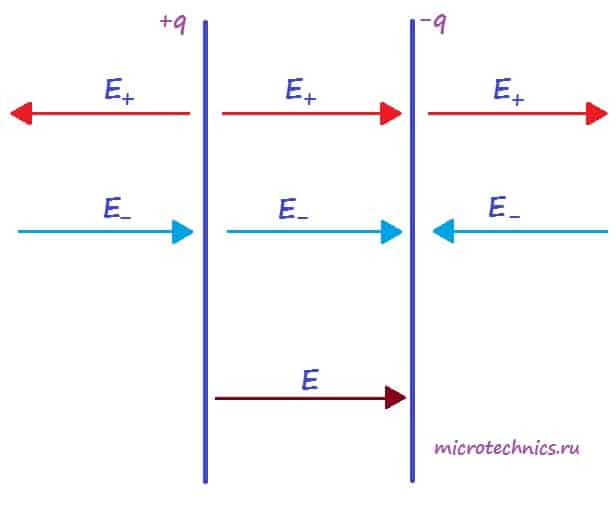
Каждая из обкладок конденсатора в отдельности создает электрическое поле:
- положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
- отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}
Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:
E = \frac{\sigma}{2\varepsilon_0\thinspace\varepsilon}
Здесь \sigma– это поверхностная плотность заряда: \sigma = \frac{q}{S}, а \varepsilon – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:
E_+ = E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S}
Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:
E = E_+ + E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S} + \frac{q}{2\varepsilon_0\thinspace\varepsilon S} = \frac{q}{\varepsilon_0\thinspace\varepsilon S}
А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0 🙂
Процессы зарядки и разрядки конденсаторов.
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:
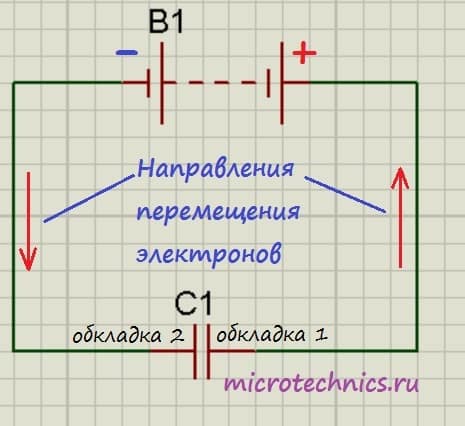
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?
Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.
Как видите, здесь нет ничего сложного 🙂
Емкость и энергия конденсатора.
Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда конденсатора q одного из проводников к разности потенциалов между проводниками:
C = \frac{q}{\Delta\varphi} = \frac{q}{U}
Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:
U = Ed = \frac{qd}{\varepsilon_0\thinspace\varepsilon S}
Здесь у нас d – это расстояние между пластинами конденсатора, а q – заряд конденсатора. Подставим эту формулу в выражение для емкости:
C = \frac{q\varepsilon_0\thinspace\varepsilon S}{qd} = \frac{\varepsilon_0\thinspace\varepsilon S}{d}
Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить \varepsilon = 1.
Для запасенной энергии конденсатора справедливы следующие выражения:
W = \frac{CU^2}{2} = \frac{qU}{2} = \frac{q^2}{2C}
Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.
Итак, мы сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики! Так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку. Не пропустите!
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agaris Agard Agard Agard Agard Agard 2000 12000000- Классы
- Решения RS Aggarwal класса 10
- Решения RS Aggarwal класса 11
- Решения RS Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- 80003 Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Предыдущий год Вопросник
- CBSE Предыдущий год Вопросники Класс 10
- CBSE Предыдущий год Вопросник класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для класса 4 Maths
- Решения NCERT для класса 4 EVS
- Решения NCERT для класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Математика
- Решения NCERT для класса 6 Наука
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки 9 класса Глава 1
- Решения NCERT для науки 9 класса Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для 9 класса Наука Глава 4
- Решения NCERT для 9 класса Наука Глава 5
- Решения NCERT для 9 класса Наука Глава 6
- Решения NCERT для 9 класса Наука Глава 7
- Решения NCERT для 9 класса Научная глава 8
- Решения NCERT для 9 класса Научная глава
- Научные решения NCERT для 9 класса Научная глава 10
- Научные решения NCERT для 9 класса Научная глава 12
- Научные решения NCERT для 9 класса Научная глава 11
- Решения NCERT для 9 класса Научная глава 13
- Решения NCERT для 9 класса Научная глава 14
- Решения NCERT для класса 9 Science Глава 15
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10, глава 12
- Решения NCERT для математики класса 10, глава 13
- соль NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1 Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Класс 11 Бизнес Исследования Syllabus
| Определение, формула, единица измерения и факты
Емкость , свойство электрического проводника или набора проводников, которое измеряется количеством отделенного электрического заряда, который может быть накоплен в нем на единицу изменения электрического потенциала. Емкость также подразумевает соответствующее хранение электрической энергии. Если электрический заряд передается между двумя первоначально незаряженными проводниками, оба становятся одинаково заряженными, один положительно, другой отрицательно, и между ними устанавливается разность потенциалов.Емкость C представляет собой отношение величины заряда q на любом проводнике к разности потенциалов V между проводниками, или просто C = q / V.
Британика Викторина
Гаджеты и технологии: факты или вымысел?
Виртуальная реальность используется только в игрушках.
Как в практической, так и в научной системе «метр-килограмм-секунда» единицей электрического заряда является кулон, а единицей разности потенциалов — вольт, поэтому единица емкости, называемая фарадом (обозначается символом F), равна единице. кулон на вольт. Один фарад — чрезвычайно большая емкость. Удобными частями общего пользования являются одна миллионная часть фарада, называемая микрофарадом ( μ F), и одна миллионная часть микрофарада, называемая пикофарадом (pF; более старый термин, микромикрофарад, μμ F).В электростатической системе единиц емкость имеет размеры расстояния.
Емкость в электрических цепях преднамеренно вводится устройством, называемым конденсатором. Она была открыта прусским ученым Эвальдом Георгом фон Клейстом в 1745 году и независимо голландским физиком Питером ван Мюссенбруком примерно в то же время, когда проводились исследования электростатических явлений. Они обнаружили, что электричество, полученное от электростатической машины, может храниться в течение некоторого времени, а затем высвобождаться.Устройство, которое стало называться лейденской банкой, состояло из стеклянного пузырька или банки с пробкой, заполненных водой, с гвоздем, пробивающим пробку и опускающимся в воду. Держа банку в руке и прикасаясь гвоздем к проводнику электростатического станка, они обнаружили, что удар от гвоздя может быть получен после отсоединения, касаясь его свободной рукой. Эта реакция показала, что часть электричества от машины была сохранена.
Простой, но фундаментальный шаг в эволюции конденсатора был сделан английским астрономом Джоном Бевисом в 1747 году, когда он заменил воду металлической фольгой, образуя подкладку на внутренней поверхности стекла и другую, покрывающую внешнюю поверхность.Конденсатор этой формы с проводником, выступающим из горловины банки и касающимся футеровки, имел в качестве своих основных физических характеристик два проводника расширенной области, почти одинаково разделенных изоляционным или диэлектрическим слоем, выполненным настолько тонким, насколько это практически возможно. Эти особенности были сохранены в каждой современной форме конденсатора.
Получите эксклюзивный доступ к контенту из нашего первого издания 1768 года с вашей подпиской. Подпишитесь сегодняКонденсатор, также называемый конденсатором, таким образом, по существу представляет собой сэндвич из двух пластин проводящего материала, разделенных изолирующим материалом, или диэлектрика.Его основной функцией является хранение электрической энергии. Конденсаторы отличаются размерами и геометрическим расположением пластин, а также типом используемого диэлектрического материала. Следовательно, они имеют такие названия, как слюдяные, бумажные, керамические, воздушные и электролитические конденсаторы. Их емкость может быть фиксированной или регулируемой в диапазоне значений для использования в схемах настройки.
Энергия, накопленная конденсатором, соответствует работе, выполняемой (например, батареей) по созданию противоположных зарядов на двух пластинах при приложенном напряжении.Количество заряда, которое может храниться, зависит от площади пластин, расстояния между ними, диэлектрического материала в пространстве и приложенного напряжения.
Конденсатор, включенный в цепь переменного тока (AC), попеременно заряжается и разряжается каждый полупериод. Время, доступное для зарядки или разрядки, таким образом, зависит от частоты тока, и, если требуемое время больше, чем длина полупериода, поляризация (разделение заряда) не завершена.В таких условиях диэлектрическая проницаемость оказывается меньше, чем наблюдаемая в цепи постоянного тока, и изменяется с частотой, становясь ниже на более высоких частотах. Во время смены полярности пластин заряды должны смещаться через диэлектрик сначала в одном направлении, а затем в другом, и преодоление противоположности, с которой они сталкиваются, приводит к выделению тепла, известного как диэлектрические потери, характеристика, которая должна быть учитывается при применении конденсаторов в электрических цепях, например, в радиоприемниках и телевизионных приемниках.Диэлектрические потери зависят от частоты и диэлектрического материала.
За исключением утечки (обычно небольшой) через диэлектрик, ток не проходит через конденсатор, когда он подвергается постоянному напряжению. Однако переменный ток легко проходит и называется током смещения.
Как работают конденсаторы | HowStuffWorks
В некотором смысле, конденсатор немного похож на батарею. Хотя конденсаторы и батареи работают совершенно по-разному, они накапливают электрическую энергию . Если вы читали, как работают батареи, то вы знаете, что батарея имеет два контакта. Внутри батареи химические реакции производят электроны на одном терминале и поглощают электроны на другом терминале. Конденсатор намного проще, чем батарея, поскольку он не может производить новые электроны — он только хранит их.
В этой статье мы узнаем, что такое конденсатор, что он делает и как он используется в электронике. Мы также посмотрим на историю конденсатора и как несколько человек помогли сформировать его прогресс.
Внутри конденсатора клеммы соединяются с двумя металлическими пластинами , разделенными непроводящим веществом, или диэлектрик . Вы можете легко сделать конденсатор из двух кусков алюминиевой фольги и куска бумаги.Это не будет особенно хорошим конденсатором с точки зрения его емкости хранения, но он будет работать.
Теоретически, диэлектрик может быть любым непроводящим веществом. Однако для практического применения используются специальные материалы, которые наилучшим образом соответствуют функциям конденсатора. Слюда, керамика, целлюлоза, фарфор, майлар, тефлон и даже воздух являются одними из непроводящих материалов. Диэлектрик определяет, какой это конденсатор и для чего он лучше всего подходит. В зависимости от размера и типа диэлектрика, некоторые конденсаторы лучше подходят для высокочастотных применений, а некоторые — для применения под высоким напряжением.Конденсаторы могут быть изготовлены для любых целей, от самого маленького пластикового конденсатора в вашем калькуляторе до ультраконденсатора, который может питать пригородную шину. НАСА использует стеклянные конденсаторы, чтобы помочь разбудить схему космического челнока и развернуть космические зонды. Вот некоторые из различных типов конденсаторов и как они используются.
- Air — Часто используется в схемах радионастройки
- Mylar — Наиболее часто используется для схем таймера, таких как часы, будильники и счетчики
- Стекло — Хорошо для применений с высоким напряжением
- Керамика — Используется для высокочастотных целей, таких как антенны, рентгеновские лучи и MRI машины
- Суперконденсатор — Силовые и гибридные машины
В следующем разделе мы подробнее рассмотрим работу конденсаторов.
,Емкость определяется как способность элемента накапливать электрический заряд. Конденсатор накапливает электрическую энергию в форме электрического поля двумя электродами конденсатора, один из которых положительный, а другой отрицательный.
Другими словами, емкость — это мера заряда на единицу напряжения, которая может храниться в элементе. Он обозначен (C), а его единица равна Фарад (F).
Содержание:
Емкость в основном подразделяется на два типа; это собственная емкость и взаимная емкость. Вещество, обладающее большей собственной емкостью, накапливает больше электрических зарядов, а вещество, имеющее низкую емкость, накапливает меньше электрических зарядов.
Объяснение и получение емкости
Если две параллельные пластины соединены, перекрывают друг друга и подключены к источнику постоянного напряжения, как показано на рисунке.Две пластины разделены изолирующим диэлектриком, так что заряд не пересекает друг друга. Один вывод параллельной пластины подключен к положительному источнику питания, а другой — к отрицательному источнику питания. Когда источник питания включен, конденсатор начинает заряжаться, и он накапливает энергию, даже если источник питания выключен.
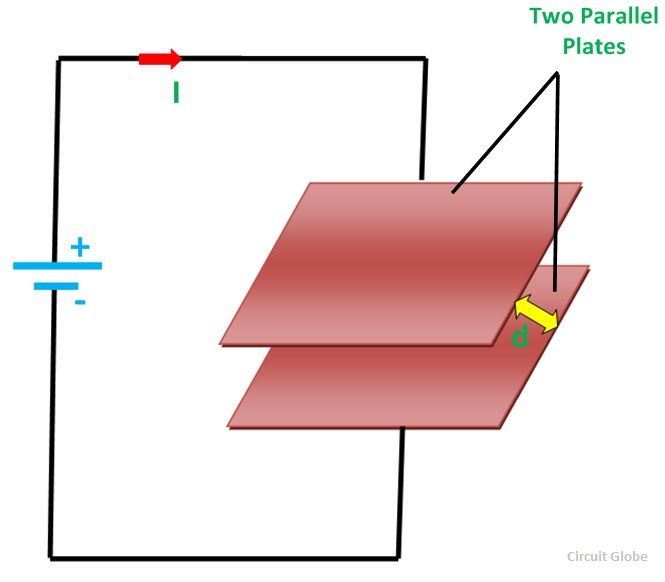 Уравнение емкости определяется как:
Уравнение емкости определяется как:
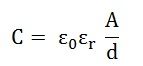
Где,
- C — емкость в Фараде или Микро Фараде
- A — площадь перекрытия двух пластин в квадратном метре
- d — расстояние разделения между двумя плитами в метрах
- ε 0 известен как электрическая постоянная
- ε r — диэлектрическая проницаемость материала между двумя пластинами
Емкость называется одним фарадом, если один кулон заряда сохраняется с одним вольтом на двух электродах элемента.Элемент, который имеет емкость, называется конденсатором.
Заряд конденсатора в любой момент времени составляет
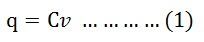
q — это количество заряда, которое может храниться в конденсаторе с емкостью (C) от разности потенциалов (v) вольт.
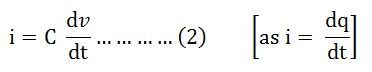
Где i, q и v представляют собой мгновенные значения тока, заряда и напряжения соответственно.
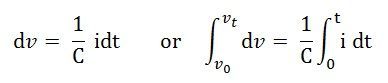
Где
В 0 — начальное напряжение конденсатора
В т является конечным напряжением конденсатора
Сейчас
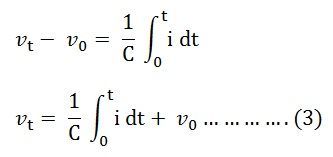
Мощность, потребляемая конденсатором, определяется уравнением, приведенным ниже.
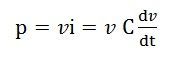
Энергия, накопленная на конденсаторе, равна
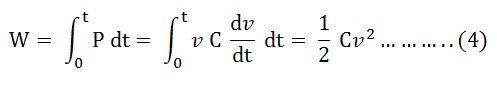
Ток через конденсатор равен нулю, если приложенное напряжение на конденсаторе является постоянным.это означает, что когда на конденсатор подается напряжение постоянного тока без начального заряда, конденсатор сначала действует как короткое замыкание, но как только он полностью заряжается, конденсатор начинает вести себя как разомкнутая цепь.
Конденсатор только накапливает энергию и никогда не рассеивает энергию в любой форме. Он может хранить конечное количество энергии, даже если ток через конденсатор равен нулю.
Типы конденсаторов
Различные типы конденсаторов
.

 номинальное напряжение,
номинальное напряжение, 1, 61 вакуум,
1, 61 вакуум, B +/-0,1 пФ.
B +/-0,1 пФ.