Волновая оптика
Волновая оптика
Световые волны рассматриваются по своей природе как электромагнитные волны, обладающие всеми их свойствами.
Волновая оптика – раздел оптики, объясняющий оптические явления на основе волновой природы света.
Волновая оптика описывает такие оптические явления, как интерференция, дифракция, поляризация, дисперсия.
Интерференция света
Электромагнитные волны, как и механические волны, обладают принципом суперпозиции, то есть, если в среде одновременно распространяются несколько волн, то они распространяются независимо друг от друга. Однако, в тех местах, где одни колебания накладываются на другие колебания, их амплитуды векторно складываются. При этом может наблюдаться как увеличение интенсивности света (когда накладываются волны с одинаковыми фазами), так и ослабление интенсивности (при сложении волн с противоположными фазами). Это явление получило название
Интерференция света – это сложение двух и более волн, вследствие которого наблюдается устойчивая картина усиления и ослабления световых колебаний в разных точках пространства.
Интерферировать могут лишь когерентные волны, т.е. волны имеющие одинаковую частоту и постоянную во времени разность фаз. Когерентные источники в природе отсутствуют, но они могут быть получены разными способами. Один из них показан на рисунке. Здесь показано, как с помощью экрана Э1 с двумя узкими щелями получают из одного источника света S два когерентных. Интерференционную картину в виде чередующихся светлых и темных полос наблюдают на экране Э2
Условие интерференционного максимума:
.
Условие интерференционного минимума:
где Δ – геометрическая разность хода волн,
k – порядок интерференционного max или min.
Интерференционные картины можно наблюдать на тонких масляных пленках на поверхности воды, мыльных пузырях, крыльях стрекоз, цвета побежалости на поверхности металла после нагрева. Явление интерференции в тонких пленках находит применение для определения длин волн излучения источников света, для контроля качества обработки полированной поверхности, определения коэффициента расширения тел при нагревании и т.д. Существуют специальные приборы –
Дифракция света
Дифракция – это способность волн огибать встречающиеся на их пути препятствия, отклоняться от прямолинейного распространения. Чтобы наблюдать дифракцию световых волн, необходимы определённые условия: либо размеры препятствий (или отверстий) должны быть очень малыми, либо расстояние от препятствия до наблюдаемой картины должно быть велико. Возьмем на пути лучей от точечного источника света S поставим преграду с очень маленьким отверстием диаметра d,тогда на экране Э увидим систему чередующихся светлых и тёмных колец (при условии, что d << L, см. рис.)
Чем уже отверстие, тем на больший угол отклоняются лучи за отверстием, тем больше диаметр колец. Если вместо круглого отверстия будет узкая щель, то дифракционная картина будет иметь вид чередующихся светлых и темных полос. При использовании белого света дифракционная картина приобретает радужную окраску.
Дифракционные картины нередко наблюдаются в естественных условиях. Например, цветные кольца, окружающие источник света, наблюдаемый сквозь туман или через запотевшее оконное стекло, или при рассматривании яркого источника через ресницы. Для наблюдения дифракции используются специальные приборы – дифракционные решетки.
Дифракционная решетка (одномерная) представляет собой систему параллельных равноотстоящих друг от друга щелей равной ширины. Простейшая дифракционная решетка может быть изготовлена из стеклянной пластинки, на которой алмазным резцом нанесены параллельные царапины с неповрежденными промежутками между ними (щелями). Расстояние между соседними щелями называется периодом или постоянной решетки d (рис.).
где а – расстояние между соседними щелями,
b – ширина щели.
Разность хода Δ лучей, приходящихся в произвольную точку Р от двух соседних щелей будет:
Очевидно, колебания в точке Р будут усиливать друг друга, если разность фаз лучей будет равна 0 или отличатся на 2π, чему соответствует:
где k = 0, 1, 2, 3…
Тогда условием наблюдения максимумов (усиления колебаний) света будет:
где k = 0, 1, 2, 3…
Вследствие дифракции происходит неравномерное перераспределение световой энергии между максимумами.
Дифракционная решетка является спектральным прибором. С ее помощью можно определять длины волн в спектрах излучения источников (например, звезд):
Поляризация света
Как
было
показано
выше, свет,
излучаемый
большинством
источников,
представляет
собой
наложение
огромного
количества
волн, испущенных
отдельными
атомами. Так
как атомы
излучают
независимо
друг от
друга, то пространственная
ориентация
векторов
Луч, в котором колебания вектора происходят только в одном направлении (имеют полярность), называется плоскополяризованным (или линейнополяризованным) (рис. б).
Плоскость, в которой совершает колебания вектор называется плоскость колебаний. Плоскость, в которой колеблется вектор (или ), назвали плоскостью поляризации. Угол между этими плоскостями 900.
Естественный свет можно превратить в поляризованный с помощью приборов которые называются поляризаторами. При падении естественного света на границу раздела сред, с разными показателями преломления, отраженный и преломленный луч всегда поляризованы.
Дисперсия света.
Дисперсия света – зависимость показателя преломления (скорости света) в среде от длины волны.
Дисперсия – причина разложения в спектр белого света, который состоит из 7 цветов: КОЖЗГСФ.
Свет одного цвета имеет определенную длину волны λ и называется монохроматическим.
ВОЛНОВАЯ ОПТИКА
ЛЕКЦИЯ № 8
Световые волны.
Законы геометрической (лучевой) оптики
Световые волны. Интенсивность света. Световой поток. Законы геометрической оптики. Полное внутреннее отражение
Оптика – это раздел физики, изучающий природу светового излучения, его распространение и взаимодействие с веществом. Раздел оптики, в котором изучается волновая природа света, называется волновой оптикой. Волновая природа света лежит в основе таких явлений, как интерференция, дифракция, поляризация. Раздел оптики, в котором не учитываются волновые свойства света и который основывается на понятии луча, называется геометрической оптикой.
§ 1. СВЕТОВЫЕ ВОЛНЫ
Согласно современным представлениям, свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других – как поток особых частиц (фотонов). Такое свойство называется корпускулярноволновым дуализмом (корпускула – частица, дуализм – двойственность). В этой части курса лекций будем рассматривать волновые явления света.
Световая волна – это электромагнитная волна с длиной волны в вакууме в диапазоне:
l 0 | = (0,4 ¸ 0,76 ) ×10 − 6 м = 0,4 ¸ 0,76 мкм = 400 ¸ 760 нм = | |||||||
= 4 000 ¸ |
|
|
|
|
| |||
7 600 A . |
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
A – |
| ангстрем – единица измерения длины. 1A = 10−10 м. |
| |||||
Волны такого диапазона воспринимаются человеческим глазом. | ||||||||
Излучение с длиной волны меньше 400 нм называют ультрафиолетовым, а | ||||||||
с большей, чем 760 нм, – | инфракрасным. |
|
|
| ||||
Частота n световой волны для видимого света: |
| |||||||
n = |
| с | = (0,39¸0,75) × 1015 Гц, |
|
|
| ||
|
|
|
|
| ||||
|
| l0 |
|
|
|
|
| |
с = 3×108 м/с — скорость света в вакууме. |
|
| ||||||
Скорость | света | совпадает | со | скоростью | распространения | |||
электромагнитной волны. |
|
|
| |||||
Показатель преломления
Скорость распространения света в среде, как и любой электромагнитной волны, равна (см. (7.3)):

v = |
| c |
| . | |
|
|
| |||
εμ | |||||
|
|
|
|
Для характеристики оптических свойств среды вводится показатель преломления. Отношение скорости света в вакууме к скорости света в данной среде называется абсолютным показателем преломления:
n = | c | . |
|
|
| (8.1) | |
|
| ||||||
| v |
| |||||
С учетом (7.3) |
| ||||||
n = |
| ≈ |
| , |
| ||
εμ | ε | (8.2) | |||||
так как для большинства прозрачных веществ μ=1.
Формула (8.2) связывает оптические свойства вещества с его электрическими свойствами. Для любой среды, кроме вакуума, n> 1. Для вакуума n = 1, для газов при нормальных условиях n≈ 1.
Показатель преломления характеризует оптическую плотность среды. Среда с большим показателем преломления называется оптически более плотной. Обозначим абсолютные показатели преломления для двух сред:
n1 = | c |
| и | n 2 = | c | . |
| ||
v1 |
|
| |||||||
|
|
|
| v2 |
| ||||
Тогда относительный показатель преломления равен: | |||||||||
n21 = | n2 | = | v1 | , |
|
| (8.3) | ||
n1 | v2 |
|
| ||||||
|
|
|
|
|
|
| |||
где v1 и v2 – | скорости света в первой и второй среде, соответственно. | ||||||||
Так как | диэлектрическая | проницаемость среды ε зависит от частоты | |||||||
электромагнитной волны, то n = n(ν) или n = n(λ) – показатель преломления будет зависеть от длины волны света (см. лекции № 16, 17).
Зависимость показателя преломления от длины волны (или частоты) называется дисперсией.
В световой волне, как и в любой электромагнитной волне, колеблются векторы E и H. Эти векторы перпендикулярны друг другу и направлению
вектора v . Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие виды воздействий вызываются колебаниями электрического вектора. Поэтому световой вектор – это вектор напряженности электрического поля световой (электромагнитной) волны.
Для монохроматической световой волны изменение во времени и пространстве проекции светового вектора на направление, вдоль которого он
колеблется, будет описываться уравнением: |
|
E = Emсos(ωt − kr + α). | (8.4) |
Сравните (7.4) и (8.4). |
|

Здесь k – волновое число; r – расстояние, отсчитываемое вдоль направления распространения волны; Em – амплитуда световой волны. Для плоской волны E m = const , для сферической убывает как 1/r.
§ 2. ИНТЕНСИВНОСТЬ СВЕТА. СВЕТОВОЙ ПОТОК
Частота световых волн очень велика, поэтому приемник света или глаз фиксирует усредненный по времени поток. Интенсивностью света называется модуль среднего по времени значения плотности энергии в данной точке пространства. Для световой волны, как и для любой электромагнитной волны, интенсивность (см (7.8)) равна:
I = <EH> .
Для световой волны μ≈ 1, поэтому из (7.5) следует:

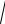 μ0H =
μ0H = 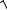
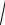 ε0 ε E ,
ε0 ε E ,
откуда с учетом (8.2):
H = |
|
|
| ε0 |
| E ~ nE . | (8.5) | ||
ε | |||||||||
|
|
| |||||||
|
|
|
| μ | 0 |
|
|
| |
|
|
|
|
|
|
|
| ||
Подставим в (7.8) формулы (8.4) и (8.5). После усреднения получим:
I = | 1 | nEm2 |
| ε0 |
| . |
|
| |||||
2 |
|
| μ0 | |||
Значит интенсивность световой волны:
Следовательно, интенсивность света пропорциональна квадрату амплитуды световой волны и показателю преломления. Заметим, что для
вакуума и воздуха n = 1, поэтому I ~ E2m (сравните с (7.9)).
Для характеристики интенсивности света с учетом его способности вызывать зрительное ощущение вводится величина Ф, называемая световым потоком. Действие света на глаз сильно зависит от длины волны. Наиболее
чувствителен глаз к излучению с длиной волны λз = 555 нм (зеленый цвет).
Для других волн чувствительность глаза ниже, а вне интервала (400– 760 нм) чувствительность глаза равна нулю.
Световым потоком называется поток световой энергии, оцениваемый по зрительному ощущению. Единицей светового потока является люмен (лм). Соответственно, интенсивность измеряется либо в энергетических единицах (Вт/м2), либо в световых единицах (лм/м2).
Интенсивность света характеризует численное значение средней энергии, переносимой световой волной в единицу времени через единицу площади площадки, поставленной перпендикулярно направлению распространения волны. Линии, вдоль которых распространяется световая энергия, называют лучами. Раздел оптики, в котором изучаются законы распространения светового

излучения на основе представлений о световых лучах, называется геометрической, или лучевой оптикой.
§ 3. ОСНОВНЫЕ ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
Геометрическая оптика – это приближенное рассмотрение распространения света в предположении, что свет распространяется вдоль некоторых линий – лучей (лучевая оптика). В этом приближении пренебрегают конечностью длин волн света, полагая, что λ→ 0.
Геометрическая оптика позволяет во многих случаях достаточно хорошо рассчитать оптическую систему. Но в ряде случаев реальный расчет оптических систем требует учета волновой природы света.
Первые три закона геометрической оптики известны с древних времен. 1. Закон прямолинейного распространения света.
Закон прямолинейного распространения света утверждает, что в
однороднойсреде свет распространяется прямолинейно.
Если среда неоднородна, т. е. ее показатель преломления изменяется от точки к точке, или n = n( r ) , то свет не будет распространяться по прямой. При
наличии резких неоднородностей, таких, как отверстия в непрозрачных экранах, границы этих экранов, наблюдается отклонение света от прямолинейного распространения.
2. Закон независимости световых лучей утверждает, что лучи при пересечениине возмущают друг друга. При больших интенсивностях этот закон не соблюдается, происходит рассеяние света на свете.
3 и 4. Законы отражения и преломления утверждают, что на границе раздела двух сред происходит отражение и преломление светового луча. Отраженный и преломленный лучи лежат в одной плоскости с падающим
лучом и перпендикуляром, восстановленным к границе раздела в точке падения
(рис. 8.1).
Угол падения равен углу отражения:
Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой:
| sini | = | n2 | = n21 | . | (8.8) |
|
|
| ||||
| sinr n1 |
|
|
| ||
Закон преломления был открыт в XVIIв. В. Снеллиусом и Р. Декартом.
Законы отражения и преломления могут нарушаться в анизотропных средах, т. е. средах, преломления зависит от направления в пространстве.
Рис. 8.1
для которых показатель
Волновая оптика
Оптика — раздел физики, в котором изучаются природа света, его распространение и явления, наблюдаемые при взаимодействии светаcвеществом.
Оптическое излучение представляет собой электромагнитные волны, и поэтому оптика является частью общего учения об электромагнитном поле.
В оптике рассматривается распространение электромагнитных волн, преимущественно видимого и близких к нему широких областей спектра – инфракрасного и ультрафиолетового диапазонов электромагнитного излучения.
В зависимости от круга рассматриваемых явлений оптику делят на геометрическую (лучевую), волновую (физическую), квантовую (корпускулярную). Волновая оптика изучает круг явлений, в основе которых лежит волновая природа света.
В электромагнитной волне колеблются два вектора: вектор напряженности электрического (E)и напряженности магнитного(H)полей (Рис.8). Вектор напряженности электрического поляEназывают световым вектором, так как физиологическое, фотохимическое, фотоэлектрическое и др. действия света вызываются колебаниями электрического вектора.
Уравнение плоской электромагнитной волны, распространяющейся вдоль положительного направления оси X, имеет вид:
E=Emcos(t–kx+)илиH=Hmcos(t–kx+α ), (39)
где
ω- круговая (или циклическая частота), k-волновое число, .
.
В различных средах свет распространяется с различными скоростями:
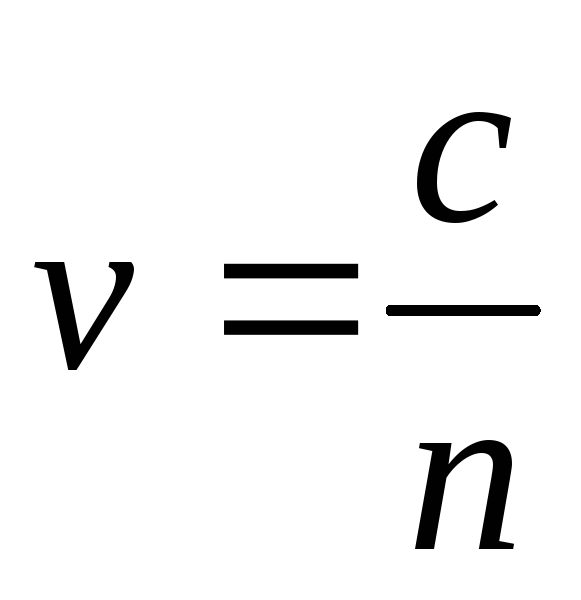 ,
,
где c– скорость света в вакууме,v– скорость света в среде с показателем
преломленияn. Максвелл установил,
что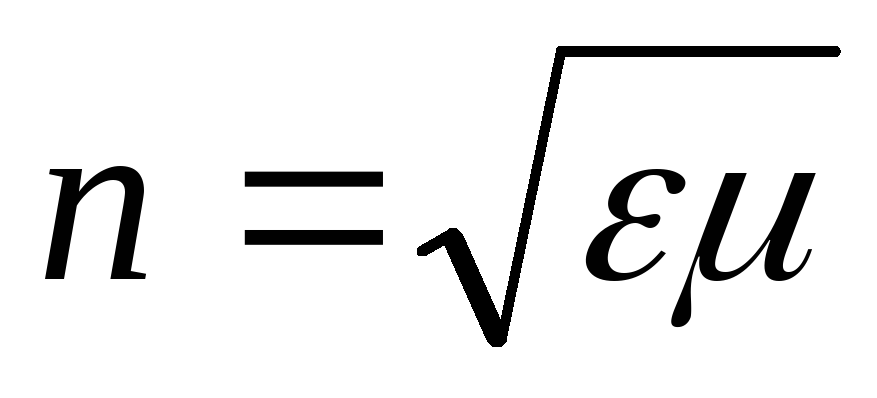 ,
где–диэлектрическая
проницаемость,– магнитная проницаемость среды.
Диэлектрическая проницаемость зависит
от частоты излучения, следовательно, и
показатель преломления зависит от
частоты, т.е. скорость распространения
электромагнитных волн зависит от частотыv=v()или длины волныv=v().
Зависимость показателя преломления
света (скорости света в среде) от длины
волны носит название дисперсии света.
,
где–диэлектрическая
проницаемость,– магнитная проницаемость среды.
Диэлектрическая проницаемость зависит
от частоты излучения, следовательно, и
показатель преломления зависит от
частоты, т.е. скорость распространения
электромагнитных волн зависит от частотыv=v()или длины волныv=v().
Зависимость показателя преломления
света (скорости света в среде) от длины
волны носит название дисперсии света.
«Средний» человеческий глаз воспринимает излучение длиной волны от 0,4 мкм до 0,76мкм (в ангстремах от 4000 Å до 7600 Å). Длина волны в вакууме 0=c/, в среде=v/ =c/ n=0 /n.
Частота видимого света лежит в пределах:
= (0,390,75)1015Гц.
Принятое в настоящее время значение скорости света в вакууме
с=(2,997924580,00000001)108м /с.
Волновая теория света основывается на принципе Гюйгенса: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени.
Основными явлениями, которые рассматриваются в волновой оптике, являются: интерференция, дифракция и поляризация света, а также законы и эффекты, связанные с этими явлениями.
Интерференция света
Интерференция света — сложение в пространстве двух или нескольких когерентных световых волн, при котором в разных точках пространства получается усиление или ослабление амплитуды результирующей волны.
Пусть в данной точке М две монохроматические волны с циклической частотойсо возбуждают два колебания, причем до точкиМ одна волнапрошла в среде с показателем преломления n1путьs1 с фазовой скоростьюvl, а вторая — в средеп2 путьs2 с фазовой скоростьюv2:
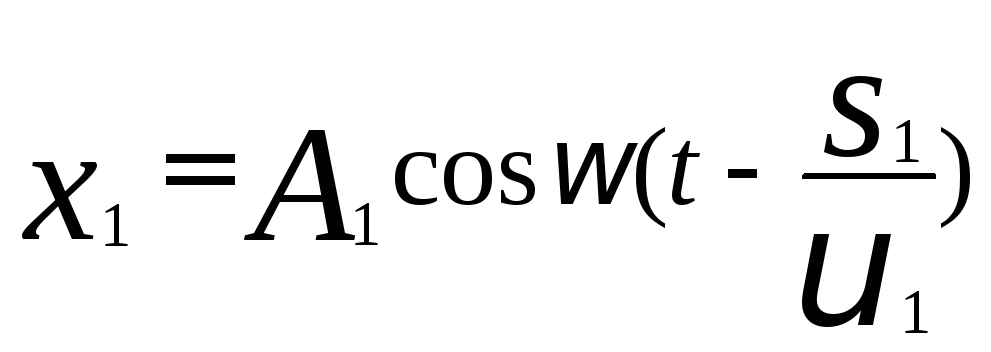 ,
, 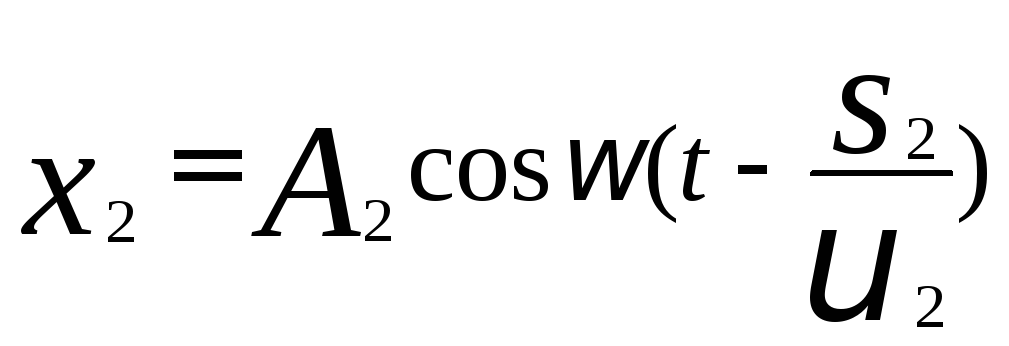 (40)
(40)
Амплитуда результирующего колебания: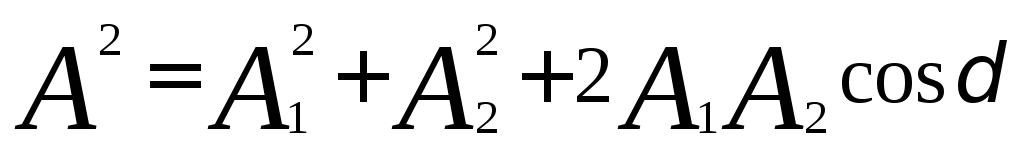 . (41)
. (41)
Интенсивностьрезультирующей волны:
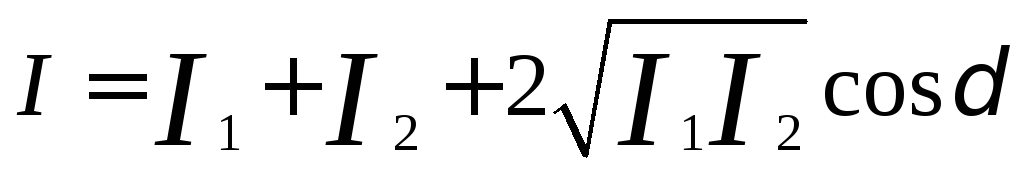 (42)
(42)
Разность
фаз  колебаний,
возбуждаемых в точке М,
равна
колебаний,
возбуждаемых в точке М,
равна
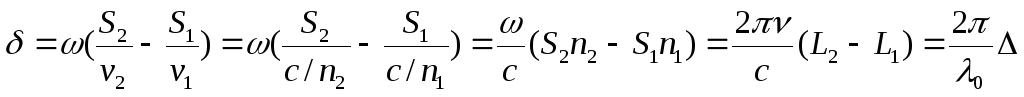 (43)
(43)
(Использовали: v = c/n;  = 2
= 2 v ; c/v =
v ; c/v =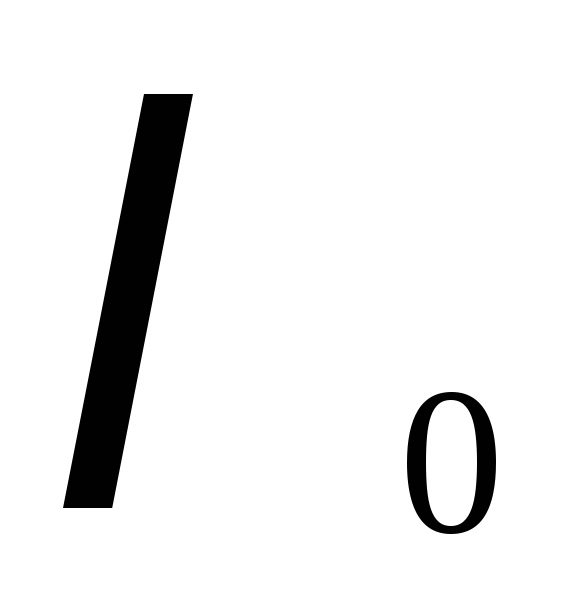 —
длина волны в вакууме).
—
длина волны в вакууме).
Произведение геометрической
длины пути s световой
волны в данной среде
на показатель
преломления этой
среды п называется оптической длиной пути L = s n.
n.
Разность  оптических
длин проходимых волнамипутей
называется оптической
разностью хода.
оптических
длин проходимых волнамипутей
называется оптической
разностью хода.
Условие интерференционного максимума:
Если оптическая разность хода ∆ равна целому числу длин волн в вакууме (четному числу полуволн)
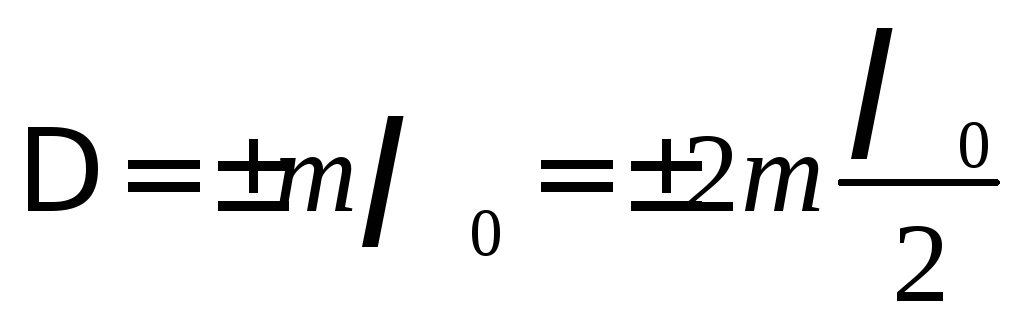 (m = 0,1,2,…), (44)
(m = 0,1,2,…), (44)
то  и
колебания, возбуждаемые в точке М, будут
происходить в одинаковой фазе.
и
колебания, возбуждаемые в точке М, будут
происходить в одинаковой фазе.
Условие интерференционного минимума.
Если оптическая разность хода Δ равна нечетному числу полуволн
 (m = 0,1, 2,…),
(45)
(m = 0,1, 2,…),
(45)
то 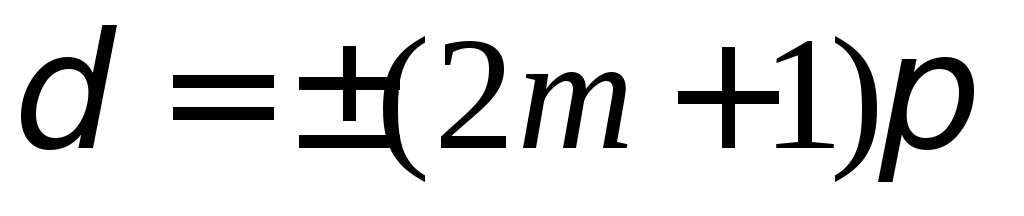 и колебания, возбуждаемые в точкеМ, будутпроисходить в
противофазе. Колебания будут гасить друг друга.
и колебания, возбуждаемые в точкеМ, будутпроисходить в
противофазе. Колебания будут гасить друг друга.
Иногда разность фаз колебаний обозначают как Δφ, тогда связь разности фаз с оптической разностью хода световых волн
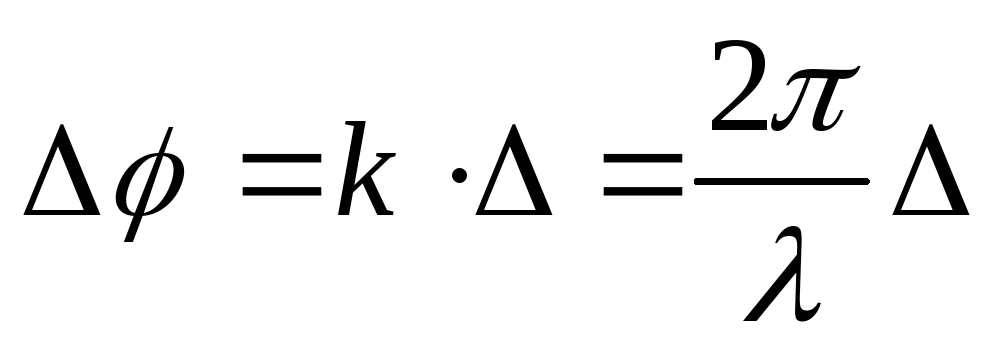 , (46)
, (46)
где k– волновое числоk=2/.
Если разность фаз возбуждаемых волнами колебаний в точке наблюдения остается постоянной во времени, то волны называютсякогерентными. Источники таких волн также называются когерентными.
В случае некогерентных волн разность фаз складываемых колебаний все время меняется и интенсивность, наблюдаемая при наложении таких волн, равна сумме интенсивностей, создаваемых каждой из волн в отдельности:
I=I1+I2
Подчеркнём ещё раз, что в случае когерентных волн происходит перераспределение интенсивности света в пространстве: в одних местах возникают максимумы, а в других – минимумы интенсивности света. В случае равенства интенсивностей волн (I1=I2), в минимумахI=0, в максимумахI=4I1.
Для естественных источников невозможно добиться когерентности. До изобретения лазеров, во всех приборах когерентные световые пучки получали разделением волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладывали друг на друга и наблюдали интерференционную картину. Например, в методе Юнга (рис.8) свет от
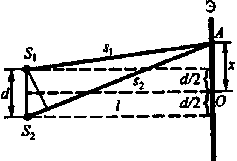
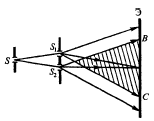
Рис.8. Рис.9.
ярко освещённой щели S падает на две щели S1S2, играющие роль когерентных источников. Интерференционная картинаBC наблюдается на экранеЭ.
Другие методы разделения пучков: зеркала Френеля, бипризма Френеля, зеркало Ллойда.
Расчёт интерференционной
картины от двух щелей позволяет определить
положение максимумов и минимумов. Две
щели S1 иS2 находятся на расстоянииd друг от друга и являются когерентными
источниками (рис.9). ЭкранЭ параллелен
щелям и находится от них на расстоянии .
.
Положение
максимумов: 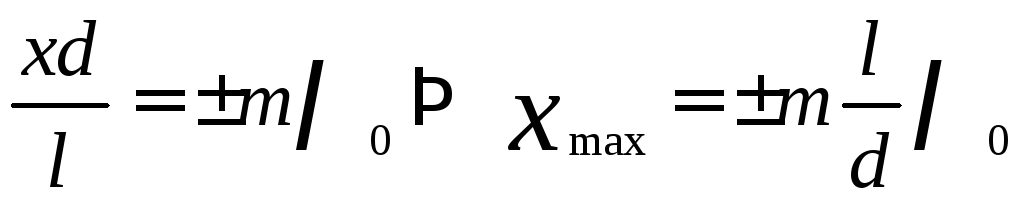 (m=0,1,2,…) (47)
(m=0,1,2,…) (47)
Положение
минимумов: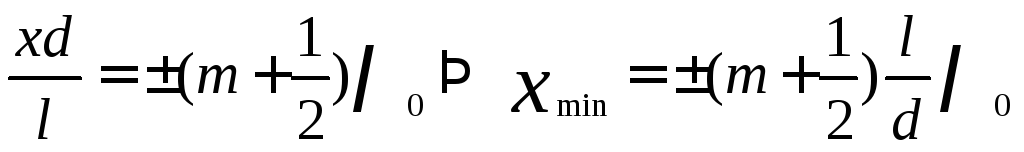 (m=0,1,…) (48)
(m=0,1,…) (48)
Расстояние  между
двумя соседними максимумами (минимумами)
называетсяшириной интерференционной
полосы:
между
двумя соседними максимумами (минимумами)
называетсяшириной интерференционной
полосы:
 (49)
(49)
Интерференционная картина представляет собой чередование на экране светлых и темных полос, параллельных друг другу.
При падении света на тонкие прозрачные пластинки или плёнки, имеющие одинаковую толщину d (Рис.10), оптическая разность хода световых волн, возникающая при отражении монохроматического света от верхней и нижней поверхности тонкой пленки,
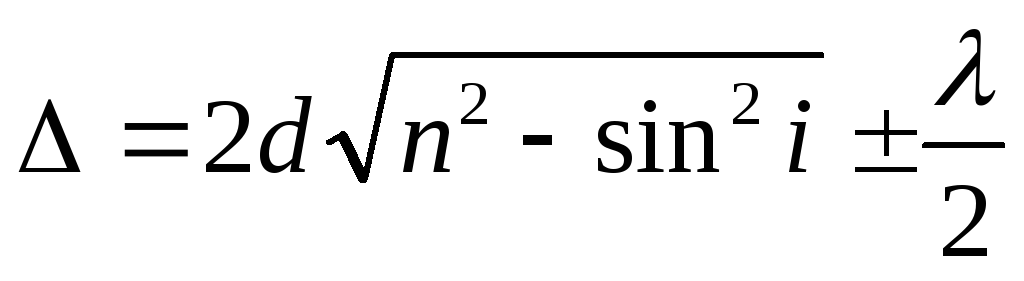 (50)
(50)
или
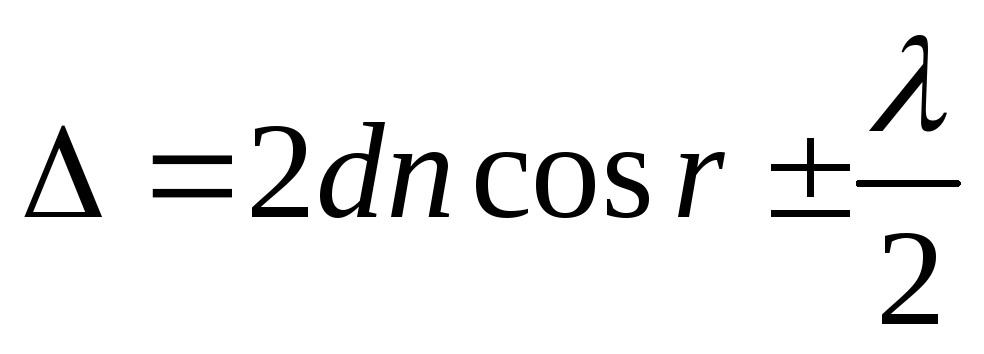 (51)
(51)
где d – толщина пленки,n– показатель преломления пленки,i– угол падения светового луча,r– угол преломления луча света в пленке.
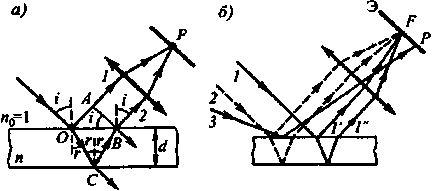
параллельны друг другу, поэтому говорят,
что полосы равного наклона локализованы в Рис.10.
бесконечности. Для их наблюдения используют собирающую линзу и экран. Интерференционная картина на экране будет иметь вид концентрических колец с центром в фокусе линзы.
Рассмотрим случай,
когда прозрачная пластинка имеет
переменную толщину ( клин с малым
углом между боковыми гранями). ( Рис.11)
между боковыми гранями). ( Рис.11)
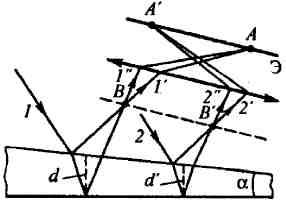
Интенсивность интерференционной картины, формируемой лучами, отраженными от верхней и нижней поверхностей клина, зависит от толщины клина в данной точке (d иd‘ для лучей 1 и 2 соответственно). Когерентные пары лучей (1’ и 1″, 2’ и 2″) пересекаются вблизи поверхности клина (точкиВ иВ’) и собираются линзой на экране (в точкахА иА’). Таким образом, на экране
возникает система интерференционных полос — полос равной Рис.11толщины — каждая из которых возникает при отражении от мест
пластинки, имеющих одинаковую толщину. Полосы равной толщины локализованы вблизи поверхности клина (в плоскости, отмеченной пунктиромВ-В).
Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются приотражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны.
Радиусы светлых и темных колец Ньютона:
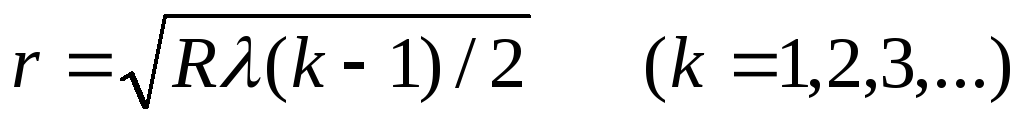 (52)
(52)
где R– радиус кривизны линзы,k– номер кольца. Четнымkсоответствуют радиусы светлых колец, нечетнымk– радиусы темных колец. Значениюk=1 соответствуетr=0, т.е. точка в месте касания пластинки и линзы. Интерференцию можно наблюдать ив проходящем свете, причемв проходящем свете максимумы интерференции соответствуют минимумам интерференции в отраженном свете и наоборот.
Волновая оптика — Традиция

Волновая о́птика или физическая оптика — раздел оптики, который основан на принципе Гюйгенса и моделирует распространение сложных фронтов импульса через оптические системы, включая и амплитуду и фазу волны.
Волновая оптика рассматривает распространение света с учётом его волновой природы. Наиболее широко наблюдаемые явления волновой оптики — интерференция, дифракция, поляризация и т. п.
У истоков развития науки об оптике (сначала геометрической, затем — и волновой) было Зрительное восприятие, зрение и физико-математические модели, гипотезы и теории, объясняющие феноменологию оптических явлений, наблюдаемых глазом. Само название (от др.-греч. ὀπτική — в переводе оптика) определила область физики под названием Оптика.
Линза — не что иное, как упрощённая модель хрусталика человеческого глаза, сетчатка глаза — природный эквивалент светочувствительных фотоматериалов, а глаз в целом — аналог биологического «фотоаппарата».
Оптика, как направление в физике изучает закономерности взаимодействие спектра видимых, а также примыкающих к ним невидимых электромагнитных волн со средой и веществом.
Корпускулярно-волновой дуализм[править]
Оптика оказалась одним из первых разделов физики, где проявилась ограниченность классических представлений о природе. Была установлена двойственная природа света:
- Корпускулярная теория света, берущая начало от Ньютона, рассматривает его как поток частиц — квантов света или фотонов. В соответствие с идеей Планка любое излучение происходит дискретно, причём минимальная порция энергии (энергия фотона) имеет величину \(\varepsilon = h\nu \) , где частота \(\nu\) соответствует частоте излучённого света, а \(~h\) есть постоянная Планка. Использование представлений о свете, как потоке частиц, объясняет явление фотоэффекта и закономерности теории излучения.
- Волновая теория света, берущая начало от Гюйгенса, рассматривает свет как совокупность, поперечных монохроматических электромагнитных волн, а наблюдаемые оптические эффекты как результат сложения (интерференции) этих волн. При этом считается, что в отсутствие перехода энергии излучения в другие виды энергии, эти волны не влияют друг на друга в том смысле, что, вызвавшая в некоторой области пространства интерференционные явления, волна продолжает распространяться дальше без изменения своих характеристик. Волновая теория электромагнитного излучения нашла своё теоретическое описание в работах Максвелла в форме уравнений Максвелла. Использование представления о свете, как волне, позволяет объяснить явления, связанные с интерференцией и дифракцией, в том числе структуру светового поля (построение изображений и голографию).
Основные закономерности[править]
Электромагнитный спектр принято делить на радиоволны, инфракрасное, видимое, ультрафиолетовое, рентгеновское и гамма-излучения. Эти участки спектра различаются не по своей природе, а по способу генерации и приёма излучения. Поэтому между ними нет резких переходов, сами участки перекрываются, а границы между ними условны.
Волновые и квантовые закономерности являются общими для всего спектра электромагнитного излучения. В зависимости от длины волны, на первый план выступают разные явления, разные методы исследования и разные практические применения. Поэтому на оптику нельзя смотреть как на замкнутую дисциплину, изучающую только видимую область спектра, отделенную от других областей чёткими границами. Закономерности и результаты, найденные в этих других областях, могут оказаться применимыми в видимой области спектра и наоборот.
Современная оптика охватывает области оптической науки и разработок, которые стали популярными в 20-ом столетии. Эти области оптической науки в основном касаются электромагнитных или квантовых свойств света, но на самом деле включают другие области.
Физическая (волновая) оптика[править]
 Трёхгранная призма раcщепляет белый свет, лучи с разной длиной волны преломляются по-разному
Трёхгранная призма раcщепляет белый свет, лучи с разной длиной волны преломляются по-разному Единичная параболическая линза преломления Х-лучей
Единичная параболическая линза преломления Х-лучейФизическая оптика или оптика волны основывается на принципе Гюйгенса и моделирует распространение сложных фронтов импульса через оптические системы, включая и амплитуду и фазу волны. Эта техника обычно применяется в цифровой форме на компьютере и может объяснять дифракцию, интерференцию, эффекты поляризации, так же как аберрацию, природу преломления Х-лучей и природу других сложных эффектов. Приближения все еще используются, однако, таким образом это не полная электромагнитная модель теории волны распространения света. Для полной модели (в настоящее время) требуется в вычислительном отношении решить много проблем. Хотя некоторые небольшие проблемы с использованием известных полных моделей волны могут решаться.[1]
Рентгеновская оптика преломления[править]
 Линза из кремния для преломления Х-лучей
Линза из кремния для преломления Х-лучейРентгеновская оптика преломления — оптика, отличаются новыми свойствами и характкристиками, обеспечивающая преломление и фокусировку Х-лучей аналогично тонким линзам на базе преломляющих линз, фокусирующих оптических элементов, на базе киноформных преломляющих профилей и оптических элементов призм, полученных из кремния.
Преломляющие Х-излучения оптические элементы и на их базе оптические устройства (микроскопы, телескопы и др.) отличаются новыми свойствами и характкристиками, которые дают возможность получать более высокое разрешение в микроскопи, телескопии по сравнению с существующими рентгенооптическими системаии. Применение, например, рентгеновских преломляющих составных линз является более перспективным напрвлением в исследованиях атомно-молекулярного и структурного анализа тонких плёнок, изучения скрытых слоёв, синтезированных периодических систем, например, фотонных кристаллов.
Темы, связанные с современной оптикой[править]
- ↑ Б. М. Яворский и А. А. Детлаф Справочник по физике. — М.: Наука, 1971
Физическая оптика — Википедия
Материал из Википедии — свободной энциклопедии
Физическая оптика используется для объяснения таких эффектов, как дифракцияВ физике физическая оптика или волновая оптика — это раздел оптики, в котором изучают интерференцию, дифракцию, поляризацию и другие явления, для которых представление света в виде лучей геометрической оптики недопустимо. Такое использование, однако, не включает такие эффекты, как квантовый шум в оптической связи, что изучается в подразделе теории когерентности .
Физическая оптика также обладает приближениями, обычно используемыми в оптике, электротехнике и прикладной физике. В этом контексте это промежуточное приближение между геометрической оптикой, которая игнорирует волновые эффекты, и электромагнетитной теорией, которая является точной. Слово «физический» означает, что она более физическая, чем геометрическая или лучевая оптика, а не то, что это точная физическая теория.[1]:11–13
Это приближение состоит в использовании лучевой оптики для оценки поля на поверхности и последующим интегрированием этого поля по поверхности для расчёта прошедшего или рассеянного поля. Это напоминает борновское приближение, в котором детали проблемы рассматриваются как возмущение. В оптике это стандартный способ оценки дифракционных эффектов. В радиофизике это приближение используется для оценки аналогичных оптическим эффектов. приближение физической оптики моделирует несколько интерференционных, дифракционных и поляризационных эффектов, но не зависимость дифракции от поляризации. Поскольку это высокочастотное приближение, оно более точно описывает оптику, чем радиофизику.
Задача физической оптики обычно состоит из интегрирования поля, полученного из геометрической оптики, над линзой, зеркалом или апертурой для расчета прошедшего или рассеянного света.
При радиолокационном рассеянии это обычно означает нахождение приближённого тока, который был бы обнаружен на касательной плоскости в геометрически освещенной части поверхности рассеивателя. Ток на затенённых участках принимается за ноль. Рассеянное поле затем получается посредством интегрирования по этим приближенным токам. Это полезно для тел с большими гладкими выпуклыми формами и для поверхностей с потерями (с низким отражением).
Поле геометрической оптики или ток обычно не точны вблизи краёв или теневых границ, если только они не дополнены расчётами дифракции и моделью ползучей волны.
Стандартная теория физической оптики имеет некоторые недостатки в оценке рассеянных полей, что приводит к снижению точности в случае отличия задачи от простого отражения.[2][3] Усовершенствованная теория, введённая в 2004 году, даёт точные решения задач, связанных с дифракцией волн на проводящих рассеивателях.
- Serway, Raymond A. Physics for Scientists and Engineers (6th ed.) (англ.). — Brooks/Cole (англ.)русск.. — ISBN 0-534-40842-7. Serway, Raymond A. Physics for Scientists and Engineers (6th ed.) (англ.). — Brooks/Cole (англ.)русск.. — ISBN 0-534-40842-7. Serway, Raymond A. Physics for Scientists and Engineers (6th ed.) (англ.). — Brooks/Cole (англ.)русск.. — ISBN 0-534-40842-7.
- Akhmanov, A. Physical Optics (англ.). — Oxford University Press. — ISBN 0-19-851795-5. Akhmanov, A. Physical Optics (англ.). — Oxford University Press. — ISBN 0-19-851795-5. Akhmanov, A. Physical Optics (англ.). — Oxford University Press. — ISBN 0-19-851795-5.
- S.G.; Hay. A double-edge-diffraction Gaussian-series method for efficient physical optics analysis of dual-shaped-reflector antennas (англ.) // IEEE Transactions on Antennas and Propagation (англ.)русск. : journal. — 2005. — August (vol. 53). — DOI:10.1109/tap.2005.851855. — Bibcode: 2005ITAP…53.2597H.
- J. S.; Asvestas. The physical optics method in electromagnetic scattering (англ.) // Journal of Mathematical Physics : journal. — 1980. — February (vol. 21, no. 2). — P. 290—299. — DOI:10.1063/1.524413. — Bibcode: 1980JMP….21..290A.
- Д. В. Скобельцын. Физическая оптика. — М.: Наука, 1964. — 321 с. — (Труды Физического Института им. П. Н. Лебедева). (недоступная ссылка)
- Р. В. Дичбурн, Л. А. Вайнштейн, О. А. Шустин, И. А. Яковлев. Физическая оптика. — М.: Наука, 1965. — 631 с. (недоступная ссылка)
ВОЛНОВАЯ ОПТИКА • Большая российская энциклопедия
-

-

-

В книжной версии
Том 5. Москва, 2006, стр. 641
-

Скопировать библиографическую ссылку:
Авторы: А. И. Одинцов
ВОЛНОВА́Я О́ПТИКА, раздел физич. оптики, изучающий явления, связанные с волновой природой света. Волновой характер распространения света был установлен ещё Х. Гюйгенсом во 2-й пол. 17 в. Существенное развитие В. о. получила в исследованиях Т. Юнга, О. Френеля, Д. Араго, когда были проведены опыты, позволившие не только наблюдать, но и объяснить интерференцию, дифракцию и поляризацию света, что не могла объяснить геометрическая оптика. В. о. рассматривает распространение световых волн в разл. средах, отражение и преломление света на границах сред (см. Френеля формулы), дисперсию и рассеяние света в веществе и др. Световые волны, представляющие собой колебания электромагнитного поля, описываются общими уравнениями классич. электродинамики (см. Максвелла уравнения). Эти уравнения дополняются уравнениями квантовой механики, связывающими величины диэлектрич. и магнитной проницаемости с молекулярным строением и свойствами вещества. Такой подход позволяет изучать волновые оптич. явления в разл. средах (см. Кристаллооптика, Магнитооптика, Молекулярная оптика). Особенности распространения световых волн в движущихся средах (см. Электродинамика движущихся сред), а также в сильных гравитационных полях объясняются в специальной и общей относительности теории. В. о., использующая классич. описание светового поля, не в состоянии дать последовательного объяснения процессов испускания и поглощения света, которое требует введения представлений о квантах света – фотонах (см. Квантовая оптика, Корпускулярно-волновой дуализм). Ряд задач В. о. решается и при более простом описании светового поля с помощью волнового уравнения.
В. о. устанавливает границы применимости геометрич. оптики, даёт математич. обоснование используемых в ней соотношений (уравнение эйконала, Ферма принцип и др.). В промежуточной области, когда длина волны света значительно меньше геометрич. размеров оптич. системы, но вместе с тем дифракционные искажения пучков являются существенными, применяются методы квазиоптики.
Волновые явления в нелинейных средах рассматриваются в нелинейной оптике. Распространение световых волн в случайно-неоднородных средах, в т. ч. в атмосфере, исследуется методами статистической оптики. Совр. В. о. изучает формирование когерентных световых пучков в оптич. резонаторах лазеров и преобразование пучков методами голографии, фурье-оптики и адаптивной оптики. Быстро развивающимися направлениями являются также исследования нелинейных оптич. явлений в волоконных световодах (см. Волоконная оптика) и в планарных (плёночных) оптич. системах (см. Интегральная оптика).
Лекция 2 Волновая оптика
Корпускулярная и волновая теории света.
В 17 веке Ньютон развил корпускулярную теорию света. Свет – поток частиц-корпускул (твердых шариков). Красный свет – большие шарики, фиолетовый – малые. Известные тогда явления света: отражение, преломление, дисперсия – этой теорией объяснялись.
В тоже время Гук выдвинул волновую теорию. Свет – волна в среде. Эта теория тоже объясняла известные тогда оптические явления.
Благодаря авторитету Ньютона в 17 веке победила корпускулярная теория.
В 19 веке изучаются явления интерференции, дифракции и поляризации света. Эти явления объясняются только волновой теорией. Поскольку явления отражения, преломления и дисперсии тоже можно объяснить волновой теорией все физики стали ее сторонниками.
Триумфом волновой теории стал 1861 год, когда Максвелл обосновал электромагнитную теорию света. Казалось, что в оптике все сделано, все объяснено. Но в конце 19 и вначале 20 века было открыто явление теплового излучения абсолютно черного тела, эффект Комптона, фотоэффект. Не смотря на все усилия физиков, волновая теория не смогла объяснить эти явления.
В начале 20 века появилась квантовая теория света. Ее создали Планк и Эйнштейн. Согласно этой теории свет имеет двойственную природу. В одних экспериментах он проявляет волновые свойства, в других – корпускулярные.
Волновая оптика изучает оптические
явления, считая свет электромагнитной
волной. Оптика рассматривает часть
излучений воспринимаемых глазом –
видимый свет. Длина волны  меняется от 380нм до 770нм
меняется от 380нм до 770нм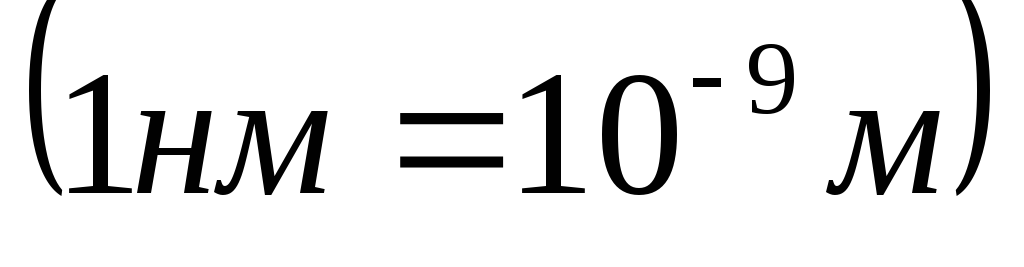 .
Свет с длинами волн
.
Свет с длинами волн нм
называется ультрафиолетовым, с
нм
называется ультрафиолетовым, с нм
– инфракрасным.
нм
– инфракрасным.
В электромагнитной волне колеблются
вектора  и
и .
Опыт показывает, что физиологические,
фотохимические, фотоэлектрические и
другие свойства света вызываются
колебаниями электрического вектора
.
Опыт показывает, что физиологические,
фотохимические, фотоэлектрические и
другие свойства света вызываются
колебаниями электрического вектора .
В дальнейшем име6нно его мы будем называть
световым вектором.
.
В дальнейшем име6нно его мы будем называть
световым вектором.
Характерным свойством излучения является частота, которая не зависит от среды. Длина волны от среды зависит. При переходе из одной среды в другую меняется скорость света и поэтому меняется длина волны.
Скорость света в среде равна: 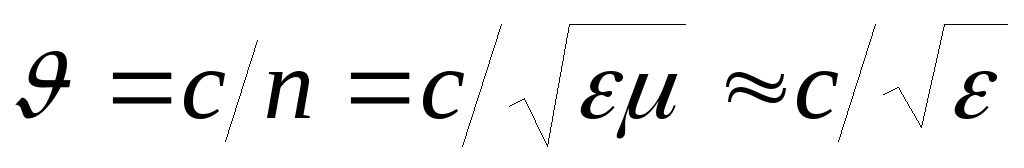 ,
где
,
где — показатель преломления среды,
— показатель преломления среды, — электрическая, а
— электрическая, а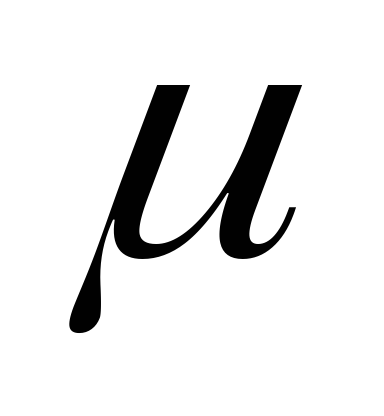 — магнитная проницаемость среды. Для
большинства сред
— магнитная проницаемость среды. Для
большинства сред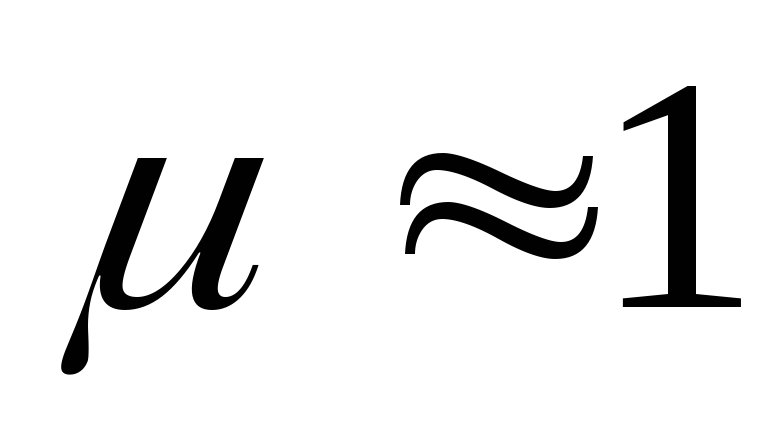 .
.
Длина волны в среде равна: 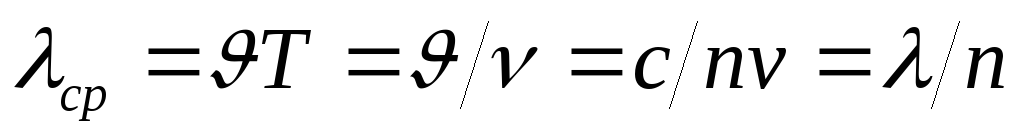 ,
где
,
где — длина волны в вакууме.
— длина волны в вакууме.
Интерференция света.
Интерференцией света называется наложение двух и более когерентных волн, в результате чего происходит перераспределение энергии светового потока в пространстве и наблюдаются интерференционные максимумы и минимумы.
Волны, имеющие одинаковую частоту и постоянную во времени разность фаз называются когерентными. рассмотрим почему волны должны быть когерентны, чтобы получилась интерференционная картина.
Пусть в некоторой точке пространства две волны одинаковой частоты, накладываясь друг на друга, породили колебания одинакового направления:
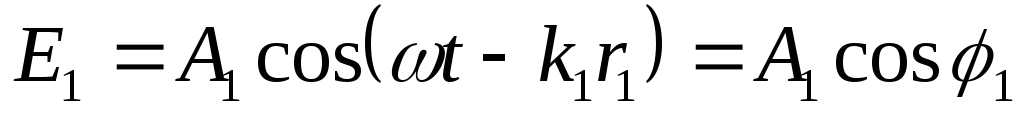 и
и
Амплитуда результирующего колебания вычисляется по теореме косинусов:
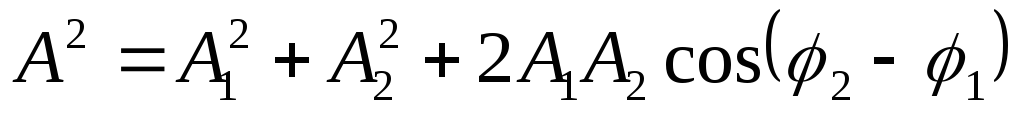 .
.
Интенсивность и энергия результирующего
колебания пропорциональна квадрату
амплитуды (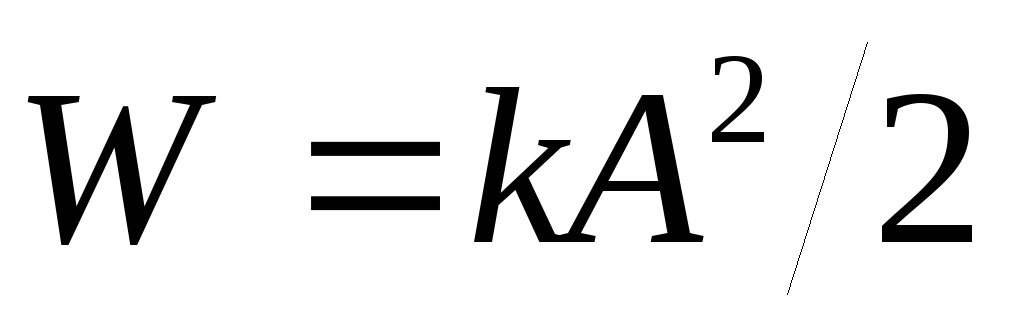 ,
,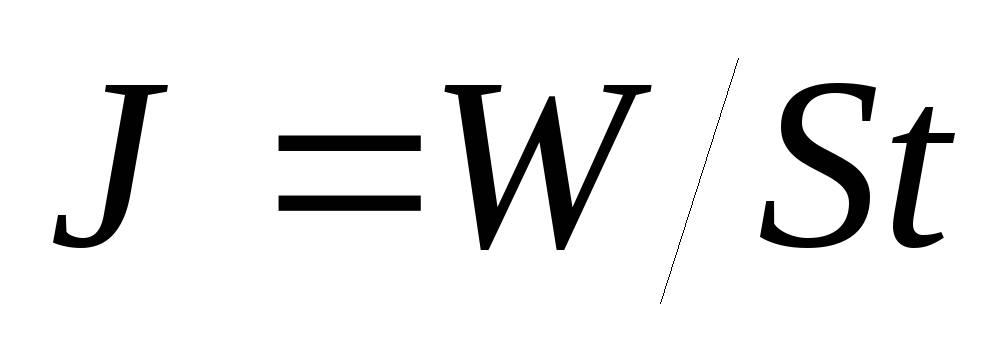 ).
Картина в данной точке пространства
будет устойчивой если
).
Картина в данной точке пространства
будет устойчивой если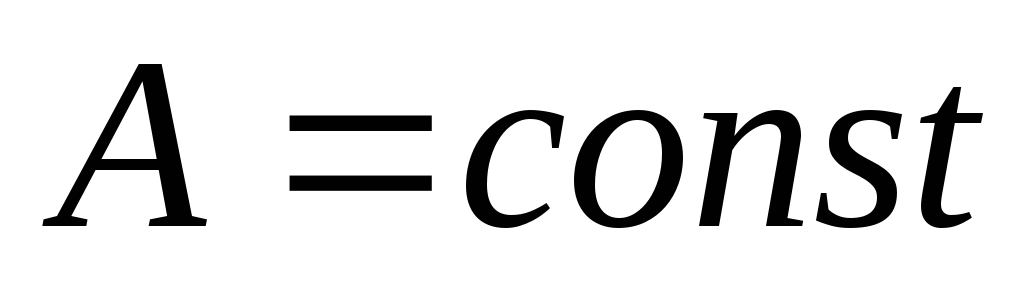 и
и .
Значения косинуса могут меняться от
.
Значения косинуса могут меняться от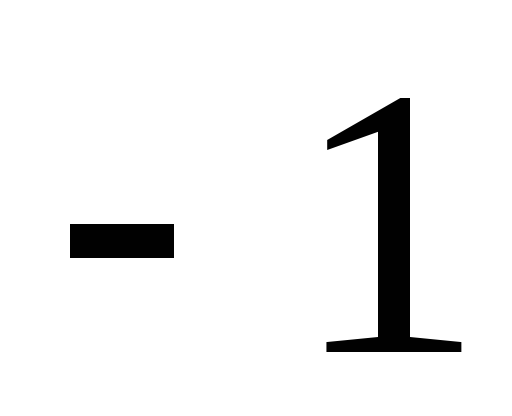 до
до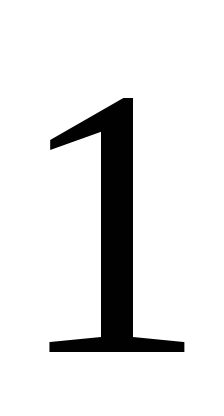 .
В тех точках пространства, где
.
В тех точках пространства, где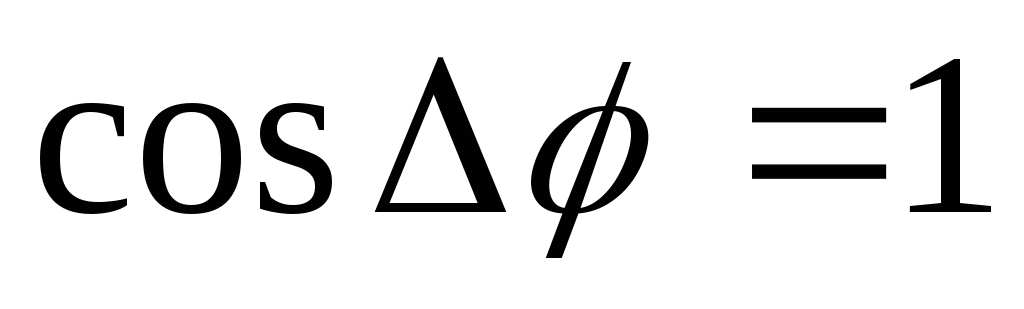 :
:
 ,
,
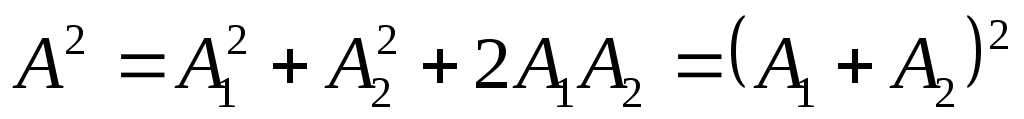 ,
,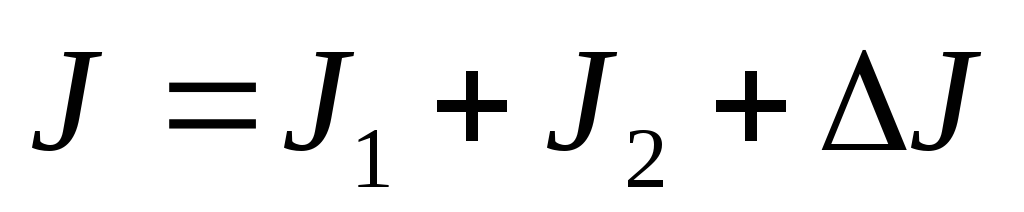 ,
,
происходит усиление интенсивности. Это интерференционные максимумы.
В тех точках пространства, где 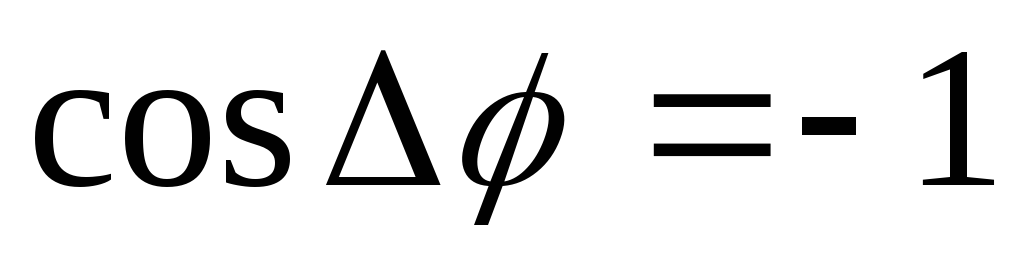 :
:
 ,
,
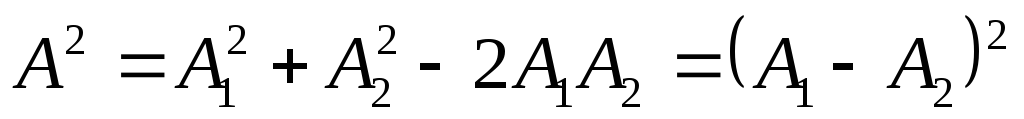 ,
,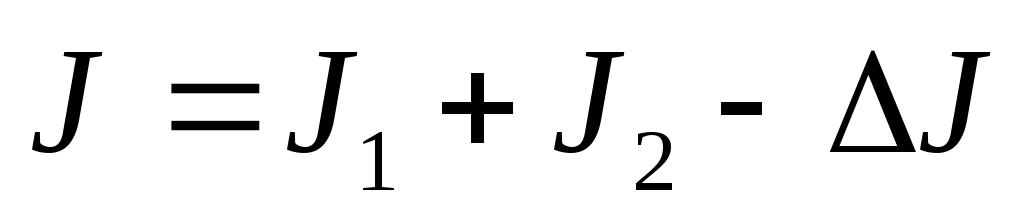 ,
,
наблюдаются интерференционные минимумы. Происходит как бы перетекание энергии из минимума в максимум.
Для не когерентных волн 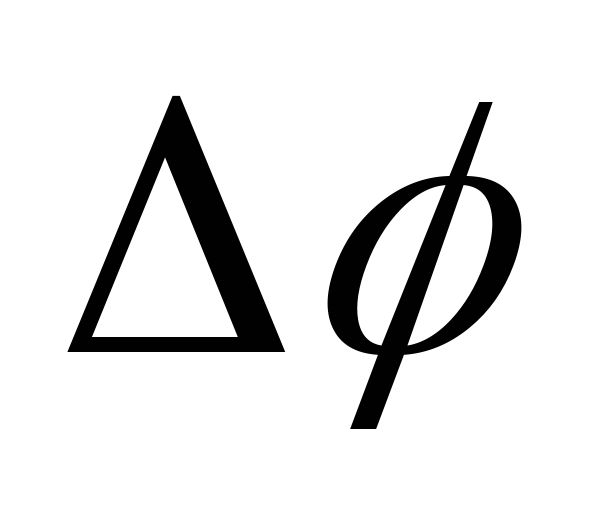 меняется,
меняется, тоже меняется, его среднее значение
равно нулю:
тоже меняется, его среднее значение
равно нулю: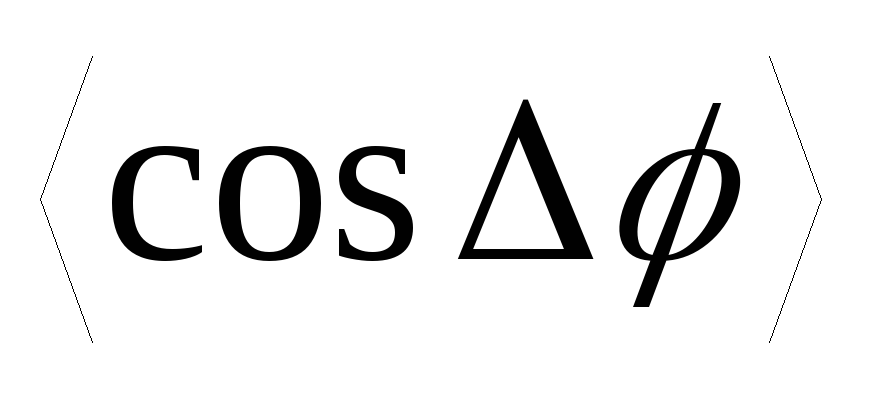 =0
=0
. Тогда  ,
,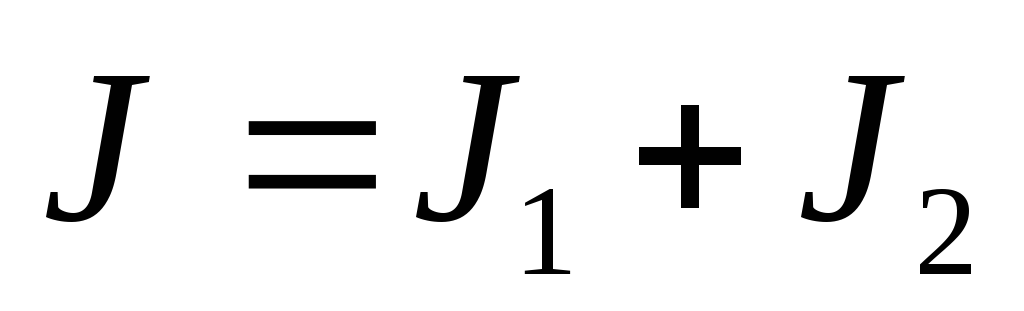 ,
то есть перераспределения энергии не
наблюдается. Происходит просто сложение
интенсивностей, интерференции нет.
,
то есть перераспределения энергии не
наблюдается. Происходит просто сложение
интенсивностей, интерференции нет.

