Динамика твёрдого тела. Лекция 4 презентация, доклад
Динамика твёрдого тела
Составила: ОБОЛОНСКАЯ О.С.
к.ф.-м.н.
Содержание:
1. Введение.
2. Моментом силы.
3. Основной закон динамики вращательного движения.
4. Момент инерции твердого тела.
5. Момент инерции тонкостенного полого цилиндра (кольца).
6. Момент инерции однородного диска ( сплошного цилиндра).
7. Момент инерции шара относительно оси симметрии.
8. Момент инерции тонкого однородного стержня.
9. Теорема Штейнера.
10. Кинетическая энергия вращения.
11. Момент импульса и закон его сохранения.
До сих пор мы рассматривали движение материальной точки. Далее мы будем рассматривать движение абсолютно твёрдого тела.
В механике под абсолютно твёрдым телом понимают такую идеальную систему материальных точек, расстояние между которыми при любых движениях остаются неизменными.
Вращательное движение вокруг оси – это такое движение твёрдого тела, при котором траектория любой его точки является окружностью. Центры всех окружностей лежат на одной прямой, названной осью вращения.
1.Момент силы
Для того чтобы вызвать вращение тела, недостаточно просто приложить силу, необходимо создать так называемый вращательный момент или момент силы.
Различают понятие момента силы относительно центра точки О и силы относительно оси.
Направление определяется правилом правого винта. Модуль момента силы по определению векторного произведения.
Модуль момента силы по определению векторного произведения.
где — плечо силы.
Кратчайшее расстояние (перпендикуляр) от точки вращения до линии действия силы называется плечом силы.
Моментом силы относительно оси называется проекция момента силы относительно точки на эту ось. — величина алгебраическая, берётся со знаком «плюс» если поворот под действием с положительным направлением оси z виден против часовой стрелки.
Основной закон динамики вращательного движения.
Рассмотрим вращательное движение твёрдого тела относительно неподвижной вертикальной оси z.
Пусть — внешняя сила, действующая на i-ю материальную точку mi. Направление в общем случае произвольно. Эту силу можно разложить на 3 компонента.
.
Умножив обе части этого уравнения на :
Аналогичные уравнения можно написать для всех остальных материальных точек, затем просуммируем их, вынося (т.к. оно постоянно для всех материальных точек вращающегося твёрдого тела) за знак суммы, получим:
Величина равная произведению массы материальной точки на квадрат её расстояния до оси вращения, называется моментом инерции точки относительно этой оси.
Величина , равная сумме моментов инерции материальной точки твёрдого тела, называется моментом инерции тела относительно оси z.
по определению момента силы F относительно оси z.
— представляет собой полный момент внешних сил относительно оси вращения z. Он равен алгебраической сумме моментов сил, действующих на материальные точки твердого тела. Тогда используя введенные понятия момента инерции тела и момента силы, уравнение можно переписать в виде:
или в векторном виде:
Это соотношение является основным законом динамики вращения движения или 2-ым законом Ньютона для вращения движения. Он аналогичен — 2-ому закону Ньютона поступательного движения.
— момент силы характеризует вращательный эффект силы.
— роль линейного ускорения играет при вращении твёрдого тела угловое ускорение.
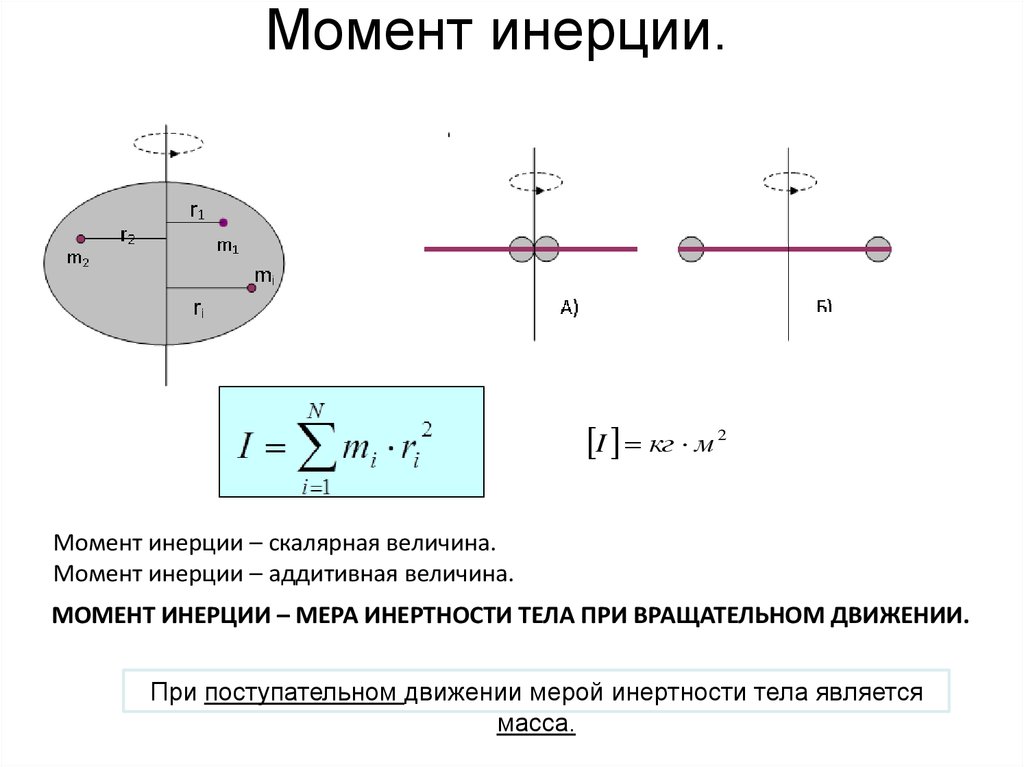
Момент инерции твердого тела
Момент инерции твердого тела:
— есть величина аддитивная. Это значит, что момент инерции тела равен сумме моментов инерции его частей. Судя по определению, момент инерции относительно данной оси зависит не только от массы тела, но и от распределения масс относительно оси.
понятие плотности вещества ,
где — элементарный объём, получим:
это соотношение является приближенным, причём тем больше точным, чем меньше элементарные объёмы . Следовательно, если перейти к пределу →0, получим для момента инерции
Таким образом вычисляется момент инерции однородного твёрдого тела (однородным называется твёрдое тело свойства которого во всех точках одинаковые, то есть для каждой точки твёрдого тела ).
Выведем формулы момента инерции некоторых тел правильной геометрической формы.
Момент инерции тонкостенного полого цилиндра (кольца)
Относительно оси z, перпендикулярной плоскости цилиндра, проходящей через центр. Пусть масса цилиндра m равномерно распределена по ободу, радиус его R. Разобьем цилиндр на элементарные полоски mi. Ввиду малой толщины стенок цилиндра можно считать, что все части такой полоски лежат на одинаковом расстоянии от оси z, равном R. Тогда момент инерции такой полоски Ii=miR2
— масса цилиндра.
Момент инерции однородного диска ( сплошного цилиндра)
Относительно оси z, проходящей через центр и перпендикулярно диску (цилиндру).
Объём такого слоя равен:
Тогда момент инерции всего диска:
Так как масса диска , то
Момент инерции толстостенного диска, радиусами R1 и R2, определяется интегрированием от R1 до R2 только надо учесть, что масса диска равна
Тогда
Тогда — момент инерции толстостенного диска (цилиндра).
Момент инерции шара относительно оси симметрии.
— момент инерции шара.
Момент инерции тонкого однородного стержня
Момент инерции тонкого стержня относительно оси, перпендикулярной стержню и проходящей через его середину:
Пусть масса стержня m и длины его l , площадь поперечного сечения S.
Разобьём стержень на элементарные объёмы , находящегося на расстоянии r от оси ОО´ , тогда
— момент инерции тонкого стержня.
Теорема Штейнера
Если определён момент инерции тела относительно оси, проходящей через центр тяжести тела, то очень просто определить момент инерции этого тела относительно любой параллельной ей оси. Определение момента инерции таким образом производится по теореме Штейнера:
Момент инерции тела I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр инерции тела и произведения массы тела на квадрат расстояния между осями.
Рассмотрим пример.
Момент инерции тонкого стержня относительно оси, перпендикулярна стержню и проходящей через его конец.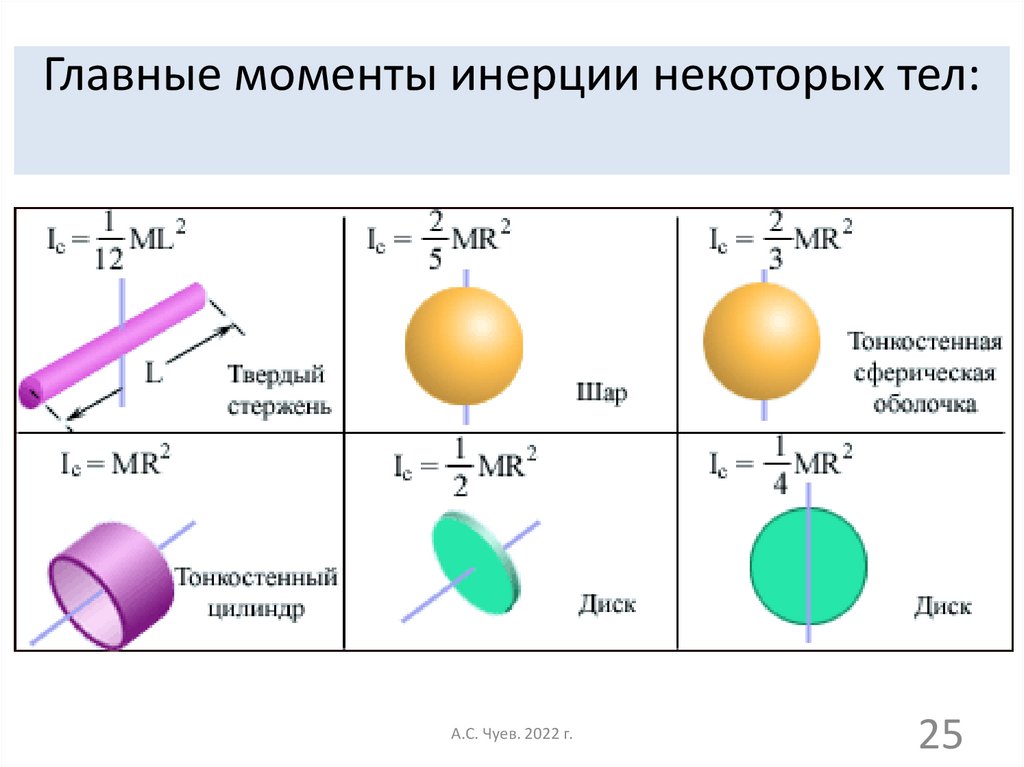
Кинетическая энергия вращения
Рассмотрим абсолютно твердое тело вращающееся около неподвижной оси z, проходящей через него. Мысленно разобьем это тело на маленькие объемы с элементарными массами m1, m2,…, mn, находящиеся на расстоянии r1, r2,…, rn от оси.
При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов ri, и имеют различные линейные скорости . Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
или
где — момент инерции тела относительно оси z.
— элементарные массы, находящиеся на расстоянии от оси,
υi — линейные скорости материальной точки,
ω – угловая скорость вращения.
Таким образом, кинетическая энергия вращающегося тела
Из сравнения формулы (*) с выражением для кинетической энергии тела, движущегося
поступательно, следует, что момент инерции –
мера инертности тела при вращательном движении. Формула (*) справедлива для тела, вращающегося вокруг неподвижной оси.
В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
где m — масса катящегося тела;
υс — скорость центра масс тела;
— момент инерции тела относительно оси, проходящей через его центр масс;
ω — угловая скорость тела.
Момент импульса и закон его сохранения.
Аналогом импульса во вращательном движении «играет» момент импульса тела относительно оси.
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
,
где — радиус-вектор, проведённый из точки О в точку А;
— импульс материальной точки.
— псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .
Модуль вектора момента импульса
где α – угол между векторами и ,
l – плечо вектора относительно точки О.
Моментом импульса относительно неподвижной оси z называется скалярная величина , равная проекции на эту ось вектора момента импульса, определённого относительно произвольной точки О данной оси. Момент импульса не зависит от положения точки О на оси z.
При вращении абсолютно твёрдого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса с некоторой скоростью . Скорость и импульс перпендикулярны этому радиусу, то есть радиус является плечом вектора . Поэтому можем записать, что момент импульса отдельной частицы равен
и направлен по оси в сторону, определяемую правилом правого винта.
Момент импульса твёрдого тела относительно оси есть сумма моментов импульса отдельных частиц:
Используя формулу , получим
, то есть
Таким образом, момент импульса твёрдого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
Продифференцируем уравнение (**) по времени:
,
— уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси.
Производная момента импульса твёрдого тела относительно оси равна моменту силы относительно той же оси.
Имеет место векторное равенство:
В замкнутой системе внешних сил и , откуда — закон сохранения момента импульса.
Момент импульса замкнутой системы сохраняется, то есть не изменяется с течением времени.
Аналогично, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, чтобы уменьшить свой момент инерции и увеличить тем самым угловую скорость вращения.
Спасибо за внимание!!!
Скачать презентацию
|
Random converter |
Конвертер момента инерцииКонвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления. Единицы СИкилограмм кв. метр [кг·м²]? килограмм кв. сантиметр [кг·см²]? килограмм кв. миллиметр [кг·мм²]? грамм кв. сантиметр [г·см²]? грамм кв. миллиметр [г·мм²]? Метрические единицы, не входящие в СИкилограмм-сила метр кв. секунда [кгс·м·с²]? Британские и американские единицыунция кв. унция-сила дюйм кв. секунда ? фунт кв. фут [фунт·фут²]? фунт-сила фут кв. секунда ? фунт кв. дюйм [фунт·дюйм²]? фунт-сила дюйм кв. секунда ? слаг кв. фут [слаг·фут²]? УскорениеЗнаете ли вы, что пилоты истребителей носят противоперегрузочные костюмы, которые давят на живот и ноги и таким образом предотвращают отток крови от мозга при ускорениях? Маховик сделан так, чтобы его высокий момент инерции оказывал сопротивление изменениям в скорости его вращения. Это позволяет хранить в нем энергию, которая накапливается в нем в результате вращения. Общие сведения В спорте Высокой момент инерции Низкий момент инерции Общие сведенияМомент инерции — это свойство тела противостоять изменению скорости вращения. Чем момент инерции выше — тем больше это противостояние. В центробежном регуляторе скорость вращения двигателя контролируется с помощью момента инерции: с достижением определенной скорости количество топлива, подаваемого в двигатель, уменьшается. Двигатель вращает два шара в верней части устройства, и, при увеличении скорости они расходятся, увеличивая момент инерции всего устройства. Когда момент инерции достигает определенной величины, это устройство ограничивает поступление топлива. Определить момент инерции для тел простой геометрической формы и с постоянной плотностью можно, используя общепринятые формулы. Для тел более сложных форм используют математический анализ. В зависимости от того, как вес распределен внутри тел, два тела с одинаковой массой могут иметь разный момент инерции. I = 2mr²/5 Тут m — это масса шара, а r — его радиус. Если взять два шара одинаковой массы, с радиусом первого вдвое больше радиуса второго, то момент инерции большего шара будет в 2²=4 раза больше первого. В этой формуле радиус — это расстояние от центра вращения до наиболее удаленной от этого центра точки на теле, для которого измеряется момент инерции. Если взять цилиндр с массой m, которая равна массе одного из шаров выше, и с расстоянием L от центра вращения до самой удаленной точки, так что эта величина равна радиусу этого шара, то момент инерции цилиндра I будет равен: I = mr²/3 в случае, если цилиндр вращается вокруг его основания. Момент инерции будет равен: I = mr²/12 если цилиндр вращается вокруг оси, проходящей через его центр по длине. При таком вращении цилиндр становится похожим на пропеллер. В спортеЧасто, уменьшив или увеличив момент инерции, можно улучшить показатели в спорте. Высокий момент инерции поддерживает постоянную скорость вращения или помогает сохранить равновесие, даже если скорость равна нулю. Если скорость равна нулю, то человек или предмет просто не вращается. Малый момент инерции, наоборот, позволяет легко изменить скорость вращения. То есть, уменьшение момента инерции уменьшает количество энергии, необходимой для того, чтобы увеличить или уменьшить скорость вращения. Высокой момент инерцииСерфингист вытянул руки, чтобы увеличить момент инерции и тем самым улучшить равновесие на доске. В некоторых случаях, необходимо чтобы вращательное движение продолжалось и не останавливалось, несмотря на то, что силы, действующие на тело, противостоят этому движению. К примеру, гимнастам, танцорам, ныряльщикам или фигуристам, которые крутятся или переворачиваются на льду или в воздухе, необходимо продолжать это движение в течение определенного времени. Для этого они могут увеличить момент инерции, увеличив вес тела. Можно добиться этого, держа во время вращения грузы, которые потом отпускают или отбрасывают, когда такой большой момент инерции уже не нужен. Это не всегда целесообразно и может быть даже опасно, если груз отлетит не в ту сторону и нанесет повреждения или травмы. Два человека могут также взяться за руки во время вращения, соединив свой вес, а потом отпустить друг друга, когда им не нужно больше крутиться. Этот прием нередко используется в фигурном катании. Вместо массы можно также увеличить радиус от центра вращения до точки, наиболее от него удаленной. Спортсмену, например ныряльщику, может понадобиться увеличить момент инерции перед тем, как он входит в воду. Когда он крутится в воздухе и принимает правильное направление, он распрямляется, чтобы остановить вращение, и в то же время увеличить радиус и, соответственно, момент инерции. Таким образом, его нулевую скорость вращения труднее изменить, и спортсмен входит в воду под правильным углом. Такой прием используют также танцоры, гимнасты и фигуристы в время танцев и упражнений, чтобы после вращения в воздухе аккуратно приземлиться. Вес распределен по длинной штанге, чтобы улучшить равновесие и обеспечить безопасность спортсмена. Несмотря на это, лучше всего заниматься тяжелой атлетикой с товарищем, который в случае необходимости может подстраховать. Как мы только что увидели, чем выше момент инерции — тем легче поддерживать постоянную скорость вращения, даже если она равна нулю, то есть тело находится в состоянии покоя. Момент инерции часто используют и в тяжелой атлетике. Вес дисков распределяется по штанге, чтобы обеспечить безопасность во время упражнений по поднятию штанги. Если вместо штанги поднимать предмет меньшего размера, но одинакового со штангой веса, например мешок с песком или гирю, то даже совсем небольшое смещение угла подъема может быть опасным. Если спортсмен толкает гирю вверх, но под углом, то она может начать вращаться вокруг своей оси. Большой вес и маленький радиус гири означает, что, по сравнению со штангой того же веса, ее намного легче начать вращать. Поэтому если она начнет вращаться вокруг своей оси, ее очень трудно остановить. Спортсмену легко потерять контроль над гирей и уронить ее. У гирь очень высокий момент инерции. Упражняться с ними нужно очень осторожно, так как легко потерять над ними контроль. Гири желательно двигать плавно, и держать их как можно дальше от тела, чтобы не получить травму в результате случайного удара гирей. Для обеспечения безопасности во время тренировок с гирями обычно смещают центр вращения как можно дальше от центра гири. Чаще всего новый центр вращения — на теле спортсмена, например в районе плеча. Низкий момент инерцииФигуристка прижимает руки к туловищу, чтобы увеличить момент инерции. При этом ее скорость вращения увеличивается. В спорте нередко бывает нужно увеличить или уменьшить скорость вращения, используя как можно меньше энергии. Для этого спортсмены выбирают снаряды и инвентарь с малым моментом инерции, или уменьшают момент инерции своего тела. В некоторых случаях важен общий момент инерции тела спортсмена. В этой ситуации спортсмены прижимают руки и ноги к туловищу, чтобы уменьшить момент инерции во время вращения. Это позволяет им ускорить движение и вращаться быстрее. Такой прием используют в фигурном катании, нырянии, гимнастике и в танцах. Чтобы испытать на себе этот эффект не обязательно заниматься одним из этих видов спорта, достаточно просто сесть в офисное кресло, раскрутить сидение, выставив руки и ноги, а потом прижать руки и ноги к корпусу. Момент инерции очень важен во время вращения спортивного инвентаря. Чем ниже момент инерции инвентаря, тем быстрее можно его вращать. Это дает спортсменам дополнительное время, чтобы следить за противниками, и часто это помогает сделать более точный размах или удар. В других видах спорта вращается не все тело спортсмена, а только его часть, например рука битой или клюшкой для гольфа. В этом случае вес распределен по бите или клюшке так, чтобы увеличить момент инерции. Это важно также для мечей, как настоящих, так и деревянных мечей для тренировок в восточных единоборствах, да и для любых других снарядов, которые спортсмены крутят или вращают, включая мячи для боулинга. Момент инерции влияет также на то, каким тяжелым кажется инвентарь во время его использования и насколько много затрачивается энергии на изменение его скорости вращения. Чем меньше момент инерции — тем обычно легче кажется инвентарь, и тем быстрее его можно вращать. Это позволяет спортсмену больше времени наблюдать за противником перед тем, как начать движение. Следует помнить, что при одинаковой скорости вращения биты, та, у которой более высокий момент инерции передаст при ударе большую скорость мячу, хоть и вращать эту биту нужно с затратой большего количества энергии. Поэтому снаряд с низким моментом инерции не обязательно лучше — в некоторых случаях спортсмены, наоборот, отдают предпочтение снарядам с высоким моментом инерции. Такие снаряды развивают мышцы, что помогает, в свою очередь, ускорить реакцию. На клюшках для гольфа и теннисных ракетках обычно указана информация об их моменте инерции, а на бейсбольных битах ее чаще всего не пишут. Почему это так — неизвестно, хотя вероятно это связано с маркетингом в спорте. В любом случае, если информации о моменте инерции спортивного снаряда нет, то стоит перед покупкой хорошо испробовать этот снаряд, и сравнить с несколькими другими, чтобы определить, подходит ли он вам для ваших целей. Литература Автор статьи: Kateryna Yuri Вас могут заинтересовать и другие конвертеры из группы «Механика»:Плоский угол Конвертер угловой скорости и частоты вращения Конвертер ускорения Конвертер углового ускорения Конвертер площади Конвертер плотности Конвертер энергии и работы Конвертер силы Конвертер длины и расстояния Конвертер массы Конвертер момента силы Конвертер мощности Конвертер давления, механического напряжения, модуля Юнга Конвертер удельного объема Конвертер вращающего момента Конвертер объема и единиц измерения в кулинарных рецептах Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер линейной скорости Компактный калькулятор Полный калькулятор Определения единиц Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ. |
Определение и значение инерции — Merriam-Webster
инерция i-ˈnər-shə
-shē-ə
1
а
: свойство материи, благодаря которому она остается в покое или в равномерном движении по одной и той же прямой, если на нее не действует какая-либо внешняя сила
б
: аналогичное свойство других физических величин (например, электричества)
2
: нежелание двигаться, прилагать усилия или изменяться : инертность
инерционный
и-нəр-шəл
-shē-əl
имя прилагательное
инерционно
i-ˈnər-sh(ə-)lē
наречие
Знаете ли вы?
Инерция — это неотъемлемое свойство тела, заставляющее его сопротивляться любой силе, вызывающей изменение его движения. Тело в покое и тело в движении противодействуют силам, которые могут вызвать ускорение. Инерция тела может быть измерена его массой, которая определяет его сопротивление действию силы, или его моментом инерции относительно определенной оси, который измеряет его сопротивление действию крутящего момента вокруг той же оси.
Тело в покое и тело в движении противодействуют силам, которые могут вызвать ускорение. Инерция тела может быть измерена его массой, которая определяет его сопротивление действию силы, или его моментом инерции относительно определенной оси, который измеряет его сопротивление действию крутящего момента вокруг той же оси.
Синонимы
- безделье
- праздность
- лень
- бесшумность
- ленивец
Просмотреть все синонимы и антонимы в тезаурусе
Примеры предложений
Он винит правительственную инерцию за ограбление.
После 10 лет на неудовлетворительной работе она преодолела свою инерцию и вернулась в школу.
Недавние примеры в Интернете
Инженеры Burns & McDonnell, каждый по-своему, указывали на борьбу с инерция старого и требования нового.
— Ллевелин Кинг, Forbes , 21 июня 2022 г.
Но после недели отдыха ваша система разум-тело может быть восстановлена, но все еще привязана к инерции ничегонеделания.
— Внешний онлайн , 5 ноября 2020 г.
Как и в случае с другими инициативами, будут возникать перегибы, сбои и разногласия по поводу управления и целей, а также трудности с прохождением обычных 9 этапов.0065 инерция и межведомственная координация осложнений.
— Стив Лопес, Los Angeles Times , 12 ноября 2022 г. Однако, вероятно, наиболее значительным препятствием, препятствующим внедрению органных чипов, является инерция .
— Джим Корбетт, Forbes , 26 мая 2022 г.
Grace Superchips станет частью здания инерции по отношению к хорошо масштабируемому ArmV9.Архитектура в центре обработки данных.
— Дэйв Альтавилла, Forbes , 25 августа 2022 г.
Из-за системной и институциональной инерции в сочетании с корыстными интересами, работающими против перемен.
— Дэвид Марчезефото, иллюстрация Браулио Амадо, New York Times , 22 апреля 2022 г.
Инерция вкладчиков может быть сильной в ущерб им.
— Джо Пинскер, 9 лет.0065 WSJ , 3 октября 2022 г.
Эта инерция наиболее сильна в таких местах, как Виндзор, третье старейшее колониальное поселение Австралии, примерно в часе езды от Сиднея.
Однако, вероятно, наиболее значительным препятствием, препятствующим внедрению органных чипов, является инерция .
— Джим Корбетт, Forbes , 26 мая 2022 г.
Grace Superchips станет частью здания инерции по отношению к хорошо масштабируемому ArmV9.Архитектура в центре обработки данных.
— Дэйв Альтавилла, Forbes , 25 августа 2022 г.
Из-за системной и институциональной инерции в сочетании с корыстными интересами, работающими против перемен.
— Дэвид Марчезефото, иллюстрация Браулио Амадо, New York Times , 22 апреля 2022 г.
Инерция вкладчиков может быть сильной в ущерб им.
— Джо Пинскер, 9 лет.0065 WSJ , 3 октября 2022 г.
Эта инерция наиболее сильна в таких местах, как Виндзор, третье старейшее колониальное поселение Австралии, примерно в часе езды от Сиднея. —Майкл Э. Миллер, Washington Post , 16 сентября 2022 г.
Узнать больше
—Майкл Э. Миллер, Washington Post , 16 сентября 2022 г.
Узнать больше
Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «инерция». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
История слов
Этимология
Новая латынь, от латиницы, неумение, от инерт-, инерс
Первое известное использование
1713, в значении, определенном в пункте 1a
Путешественник во времени
Первое известное использование инерции было в 1713 году
Посмотреть другие слова того же года
Словарные статьи Около
инерцияинертный газ
инерция
инерционная сила
Посмотреть другие записи поблизости
Процитировать эту запись «Инерция».
 Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/inertia. По состоянию на 26 декабря 2022 г.
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/inertia. По состоянию на 26 декабря 2022 г.Ссылка на копию
Детское определение
инерция
существительное
инерция in-ˈər-shə
-shē-ə
1
: свойство материи оставаться в покое или в неизменном движении, если на нее не действует какая-либо внешняя сила инерционный
-шел
имя прилагательное
Медицинское определение
инерция
существительное
инерция ин-ˈər-shə, -shē-ə
1
а
: свойство материи, благодаря которому она остается в покое или в равномерном движении по одной и той же прямой, если на нее не действует какая-либо внешняя сила
б
: аналогичное свойство других физических величин (таких как электричество)
2
: отсутствие активности или движения
— используемые, в частности, при родах матки, когда ее сокращения слабые или нерегулярные
Подробнее от Merriam-Webster на
инерцияNglish: Перевод Инерции для носителей испанского языка
Британская английская: перевод inertia . Последнее обновление: — Обновлены примеры предложений
Последнее обновление: — Обновлены примеры предложений
Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!
Merriam-Webster без сокращений
безмятежный
См. Определения и примеры »
Получайте ежедневно по электронной почте Слово дня!
Сложные слова, которые вы должны знать
- Часто используется для описания «хода времени», что означает неумолимый значит?
- Медленный Непредсказуемый
- Стриж Безжалостный
Проверьте свои знания и, возможно, узнаете что-нибудь по ходу дела.
ПРОЙДИТЕ ТЕСТ
Сможете ли вы составить 12 слов из 7 букв?
ИГРАТЬ
Объяснение полярного момента инерции
Полярный момент инерции объекта — это его способность сопротивляться отклонению из-за приложенного крутящего момента. Он в значительной степени основан на поперечном сечении объекта вдоль оси, к которой приложен крутящий момент.
Содержание
- Как рассчитать полярный момент инерции?
- Полярный момент инерции сплошного круглого сечения
- Полярный момент инерции полого круглого сечения
- Полярный момент инерции квадратного сечения
- Полярный момент инерции прямоугольного сечения
- Разница между моментом инерции и полярным моментом инерции
- Что такое полярный момент инерции и произведение инерции?
Как рассчитать полярный момент инерции?
Скручивание объекта будет происходить вокруг оси, откуда рассчитывается полярный момент инерции. Например, если у вас есть скручиваемая трубка, площадь поперечного сечения, необходимая для расчета, будет равна площади круглого поперечного сечения трубки.
Например, если у вас есть скручиваемая трубка, площадь поперечного сечения, необходимая для расчета, будет равна площади круглого поперечного сечения трубки.
По сути, полярный момент инерции — это сопротивление объекта (будь то в форме балки, трубы или вала) деформации (пластической или нет) из-за приложенного крутящего момента. Обратите внимание, что крутящий момент — это крутящая сила, а кручение — это крутящий момент, возникающий в результате приложенного крутящего момента. Полярный момент инерции полностью зависит от площади поперечного сечения крутящегося объекта, а не от типа материала.
Формула для полярного момента инерции выглядит следующим образом. Это двойной интеграл по площади поперечного сечения:
где:
- Дж = полярный момент инерции (м 4 )
- r = расстояние до элемента dA (м)
- дА = элемент дифференциала площади
Эта общая формула немного сбивает с толку, поскольку включает в себя двойной интеграл и то, что кажется радиусом, несмотря на то, что не каждая площадь поперечного сечения представляет собой круг. К счастью, существуют разные стандартные формулы для расчета полярного момента инерции для цилиндров различного поперечного сечения. Давайте посмотрим на некоторые из наиболее распространенных:
К счастью, существуют разные стандартные формулы для расчета полярного момента инерции для цилиндров различного поперечного сечения. Давайте посмотрим на некоторые из наиболее распространенных:
Твердое круглое поперечное сечение Полярный момент инерции
где:
- D = диаметр окружности
Полярный момент инерции полого круглого сечения
где:
- D = внешний диаметр трубы/окружности (м)
- d = внутренний диаметр трубы/окружности (м)
Квадратное сечение Полярный момент инерции
где:
- a = длина стороны (м)
Прямоугольное поперечное сечение Полярный момент инерции
где:
- б/д = две длины сторон (м)
В этих формулах уже выполнено двойное интегрирование, и они оставлены в упрощенном виде. Существуют также упрощенные формулы для других распространенных площадей поперечного сечения, таких как треугольные, шестиугольные и цилиндры с гнездами переменной формы.
Есть несколько факторов, влияющих на полярный момент инерции. И чем больше полярный момент, тем «жестче» объект, независимо от состава материала или модуля сдвига.
Формулы показывают, что полярный момент инерции можно увеличить, увеличив размер цилиндрического объекта. Этот вывод естественно следует из того факта, что более крупный объект требует большей силы, чтобы осмысленно скрутить его!
Для сравнения, если бы у вас был квадратный цилиндр по сравнению с цилиндрическим цилиндром с одинаковым радиусом, то квадратный цилиндр имел бы более высокий полярный момент инерции. Так почему же мы видим больше примеров круглых цилиндров в реальном мире? Что ж, есть несколько других факторов, которые следует учитывать, когда квадратные сечения могут работать хуже, а круглые цилиндры лучше зацепляются для таких вещей, как гайки, подшипники и шайбы.
Разница между моментом инерции и полярным моментом инерции
Момент инерции, также известный как массовый момент инерции, — это не то же самое, что его полярный аналог. Есть несколько других названий этого качества, также известных как: угловая масса, второй момент массы и инерция вращения.
Есть несколько других названий этого качества, также известных как: угловая масса, второй момент массы и инерция вращения.
Момент инерции массы представляет собой не сопротивление крутящему моменту, а способность объекта сопротивляться вращению или изменению направления вращения. Это зависит от распределения массы тела относительно оси вращения, а не от его формы, хотя форма может влиять на то, как на самом деле распределяется эта масса. Формула для массового момента инерции:
Для точечной массы:
Для обычного тела:
где:
- I = момент инерции массы (кг-м 2 )
- м = масса (кг)
- r = расстояние между осью и вращающейся массой (м)
- k = инерционная постоянная, зависящая от формы тела (безразмерная)
- τ = приложенный крутящий момент (Н-м)
- α = угловое ускорение (рад/сек 2 )
- L = угловой момент (кг-м 2 /с)
- ω = угловая скорость (рад/с)
Здесь очевидно, что момент инерции массы в гораздо большей степени связан с весом тела и энергией вращения, а также с расстоянием от оси вращения, чем с его формой, хотя форма может играть роль. Полярный момент инерции можно рассматривать как распределение площади относительно оси вращения, тогда как момент массы связан с распределением массы вокруг нее.
Полярный момент инерции можно рассматривать как распределение площади относительно оси вращения, тогда как момент массы связан с распределением массы вокруг нее.
Что такое полярный момент инерции и произведение инерции?
Произведение инерции — это еще один способ изучения распределения массы внутри вращающегося объекта, а также того, вращается ли этот объект вокруг оси, которая делает вращение симметричным. Если объект симметричен относительно своей оси вращения, то произведение инерции равно нулю. Если объект не распределен равномерно вокруг своей оси вращения, то у него будет некоторый продукт инерции.
Произведение инерции больше связано с массовым моментом инерции, чем с полярным моментом. Он может быть положительным, отрицательным или нулевым в зависимости от того, где находится объект по отношению к осям координат. Если на самом деле существует ненулевое произведение инерции, можно создать теоретическую ситуацию, в которой вращение симметрично, а произведение равно нулю, сместив оси в точку, где они известны как «главные оси».


 Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыИмпульс (количество движения)Импульс силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыИмпульс (количество движения)Импульс силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева дюйм ?
дюйм ?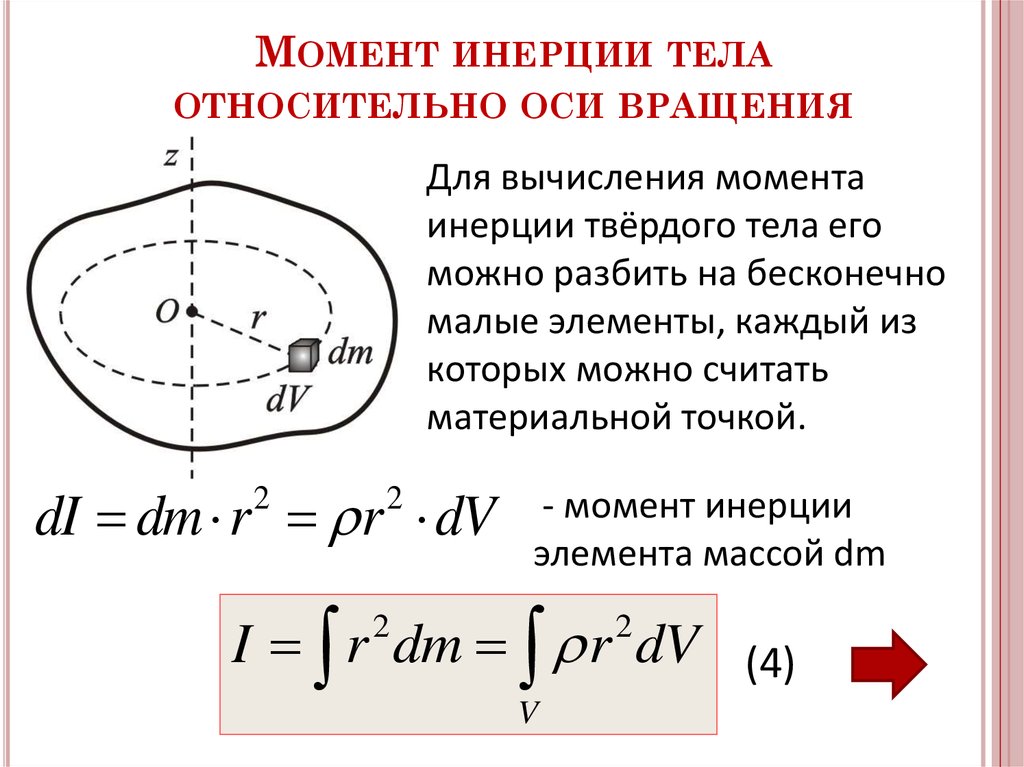 Момент инерции часто сравнивают с понятием массы для прямолинейного движения, так как масса определяет, насколько тело сопротивляется такому движению. Распределение массы по объему тела не влияет на прямолинейное движение, но имеет большое значение при вращении, так как от него зависит момент инерции.
Момент инерции часто сравнивают с понятием массы для прямолинейного движения, так как масса определяет, насколько тело сопротивляется такому движению. Распределение массы по объему тела не влияет на прямолинейное движение, но имеет большое значение при вращении, так как от него зависит момент инерции. Например, момент инерции I для однородного шара, с одинаковой по всему объему плотностью, находят по формуле:
Например, момент инерции I для однородного шара, с одинаковой по всему объему плотностью, находят по формуле: Вторую формулу легко получить из первой: радиус от центра вращения до наиболее удаленной точки равен половине длины цилиндра, но так как этот радиус возведен в квадрат, то 1/2 L (или r) становится 1/4 L² (или r²). В любом случае, глядя на эти формулы, легко заметить, что форма тела и даже просто смещение центра вращения существенно влияют на момент инерции. Момент инерции играет важную роль в спорте и в механике, и его регулируют, изменяя массу или форму предметов и даже тела спортсмена.
Вторую формулу легко получить из первой: радиус от центра вращения до наиболее удаленной точки равен половине длины цилиндра, но так как этот радиус возведен в квадрат, то 1/2 L (или r) становится 1/4 L² (или r²). В любом случае, глядя на эти формулы, легко заметить, что форма тела и даже просто смещение центра вращения существенно влияют на момент инерции. Момент инерции играет важную роль в спорте и в механике, и его регулируют, изменяя массу или форму предметов и даже тела спортсмена. Момент инерции настолько важен в спорте, что некоторые исследователи считают, что для упражнений, в которых используется несколько снарядов или спортивного инвентаря одинакового веса, но разных конфигураций, следует подбирать снаряды и инвентарь с близким моментом инерции. Это практикуется, например, в гольфе: некоторые считают, что если использовать клюшки с одинаковым моментом инерции, то это поможет спортсмену улучшить свинг, то есть основной удар по мячу. В других видах спорта спортсмены иногда, наоборот, выбирают инвентарь с разным моментом инерции, в зависимости от того, какого эффекта они хотят добиться, например как быстро им необходимо ударить мяч клюшкой, или битой. Некоторые используют спортивный инвентарь с высоким моментом инерции, чтобы увеличить силу и выносливость мышц, не добавляя веса к снаряду. Так, например, момент инерции бейсбольной биты влияет на то, какую скорость она придаст мячу.
Момент инерции настолько важен в спорте, что некоторые исследователи считают, что для упражнений, в которых используется несколько снарядов или спортивного инвентаря одинакового веса, но разных конфигураций, следует подбирать снаряды и инвентарь с близким моментом инерции. Это практикуется, например, в гольфе: некоторые считают, что если использовать клюшки с одинаковым моментом инерции, то это поможет спортсмену улучшить свинг, то есть основной удар по мячу. В других видах спорта спортсмены иногда, наоборот, выбирают инвентарь с разным моментом инерции, в зависимости от того, какого эффекта они хотят добиться, например как быстро им необходимо ударить мяч клюшкой, или битой. Некоторые используют спортивный инвентарь с высоким моментом инерции, чтобы увеличить силу и выносливость мышц, не добавляя веса к снаряду. Так, например, момент инерции бейсбольной биты влияет на то, какую скорость она придаст мячу. Оаху, Гавайи.
Оаху, Гавайи. Для этого можно вытянуть руки или ноги в стороны от туловища, или взять в руки длинный шест.
Для этого можно вытянуть руки или ноги в стороны от туловища, или взять в руки длинный шест. Это бывает нужно как для того, чтобы поддержать вращение, как и для поддержания равновесия в отсутствии вращения. Например, чтобы не упасть, акробаты, которые ходят по канату, часто держат в руках длинный шест, увеличивая тем самым радиус от центра вращения до самой отдаленной от него точки.
Это бывает нужно как для того, чтобы поддержать вращение, как и для поддержания равновесия в отсутствии вращения. Например, чтобы не упасть, акробаты, которые ходят по канату, часто держат в руках длинный шест, увеличивая тем самым радиус от центра вращения до самой отдаленной от него точки.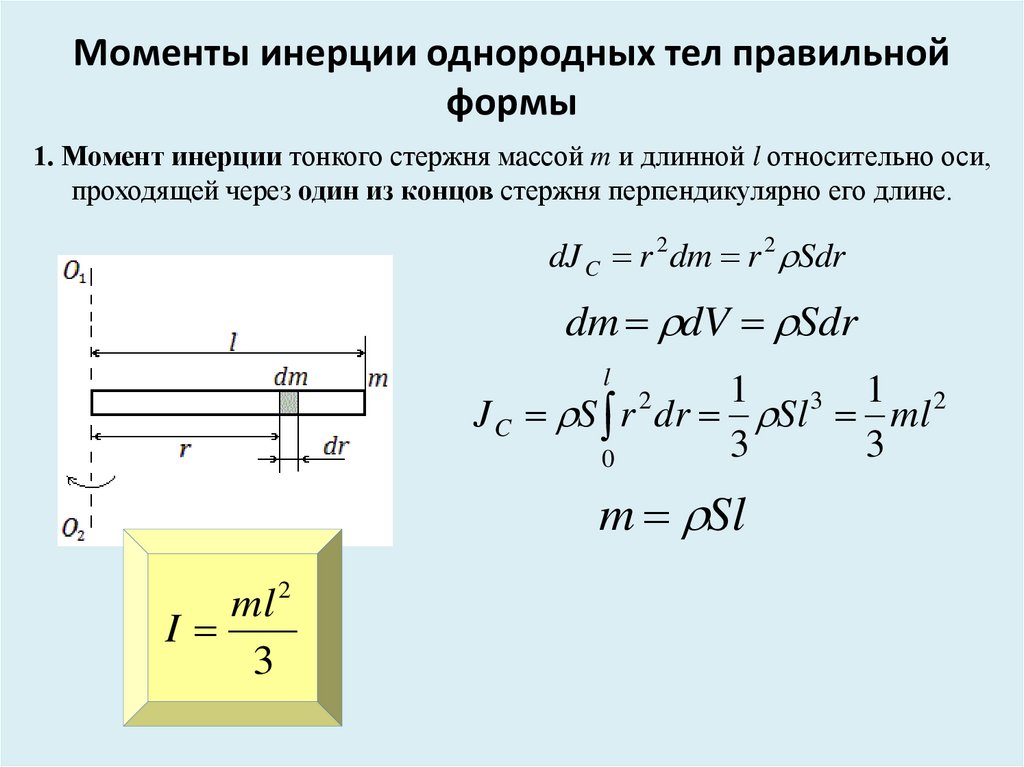 Это особенно опасно, если спортсмен поднимает гирю над головой стоя, или над грудью лежа. Даже если гиря не упадет, спортсмен может повредить кисти рук, пытаясь предотвратить вращение и падение. То же самое может произойти при упражнениях с особо тяжелой штангой, поэтому крепление дисков у штанг, предназначенных для упражнений с очень большим весом — подвижно. Диски прокручиваются вокруг своей оси во время подъема штанги, а сама штанга остается неподвижной. Штанги, предназначенные для Олимпийских игр, которые так и называются, олимпийскими штангами, имеют именно такую конструкцию.
Это особенно опасно, если спортсмен поднимает гирю над головой стоя, или над грудью лежа. Даже если гиря не упадет, спортсмен может повредить кисти рук, пытаясь предотвратить вращение и падение. То же самое может произойти при упражнениях с особо тяжелой штангой, поэтому крепление дисков у штанг, предназначенных для упражнений с очень большим весом — подвижно. Диски прокручиваются вокруг своей оси во время подъема штанги, а сама штанга остается неподвижной. Штанги, предназначенные для Олимпийских игр, которые так и называются, олимпийскими штангами, имеют именно такую конструкцию. То есть, обычно гирю не вращают с помощью кисти руки или вокруг локтевого сустава. Ее, наоборот, качают из стороны в сторону или вверх и вниз вокруг туловища, иначе работа с ней опасна.
То есть, обычно гирю не вращают с помощью кисти руки или вокруг локтевого сустава. Ее, наоборот, качают из стороны в сторону или вверх и вниз вокруг туловища, иначе работа с ней опасна. При этом скорость вращения увеличится.
При этом скорость вращения увеличится. Иногда это дополнительное время дает преимущество в спортивных играх, так как спортсмен может быстрее реагировать на движения противника. За эти дополнительные секунды становится проще предсказать траекторию движения противника, или мяча, например в теннисе и бейсболе, и сделать более точный удар.
Иногда это дополнительное время дает преимущество в спортивных играх, так как спортсмен может быстрее реагировать на движения противника. За эти дополнительные секунды становится проще предсказать траекторию движения противника, или мяча, например в теннисе и бейсболе, и сделать более точный удар.