Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением. Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t \rightarrow 0$ материальная точка проходит путь ds, который называют элементарным. При этом:
$$d s=|d \bar{r}|=v d t$$
где $\bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=v\left(t_{2}-t_{1}\right)(5)$$
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой, чему равно перемещение, если точка двигалась 1-2-3-4.
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 — 2 = 4 (m)$$
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$
Ответ. Путь равен 20 м, перемещение равно 4 м.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. {5}=5(m)$$
{5}=5(m)$$
Ответ. s=5м.
Читать дальше: Формула равноускоренного движения.
Константы и единицы
Константы и единицы| Обозначение | Название | Величина |
|---|---|---|
| e | единица заряда | 1.6·10-19 Кл |
| 1/α = ћс/e2 | постоянная тонкой структуры | 137.0 |
| c | скорость света в вакууме | 2.998·1010 см/с |
| h | постоянная Планка | 6.626·10-27 эрг .с |
| ћ | приведенная постоянная Планка | 6.582·10-22 МэВ·с |
| ћс | константа конверсии | 197.3 Мэв·Фм |
| k | константа Больцмана | 8.617·10-11 МэВ/град |
| re | 2. 818 Фм 818 Фм | |
| ћ/mec | комптоновская длина волны электрона | 386.2 Фм |
| ћ/mpc | комптоновская длина волны протона | 0.210 Фм |
| комптоновская длина волны пиона | 1.414 Фм | |
| атомная единица массы | 931.5 МэВ/c2 | |
| me | масса электрона | 0.511 МэВ/c2 |
| mn | масса нейтрона | 939.6 МэВ/c2 |
| mp | масса протона | 938.3 МэВ/c2 |
| масса π−, π+ | 139.6 МэВ/c2 | |
| масса π0 | 135.0 МэВ/c2 | |
| масса W—,W+-бозонов | 80.2 ГэВ/c2 | |
| масса Z-бозона | 91. 2 ГэВ/c2 2 ГэВ/c2 | |
| NA | число Авогадро | 6.02 |
| μN = ћe/2mpc | ядерный магнетон | 3.152·10-18 МэВ/Г |
| магнитный момент протона | 2.793μN | |
| магнитный момент нейтрона | 1.913μN |
| 1 Фм = 10-13 см | 1 а.е.м. = 1.66 .10-24 г | 1 Гр = 1 Дж/кг = 100 рад |
| 1 барн = 10-24 см2 | 1 эВ = 1.602 .10-19 Дж | 1 P = 2.58 .10-4 Кл/кг |
| 1 эВ/c2 = 1.783 | 1 Ки = 3.7 .1010 Бк | 1 Зв = 100 бэр |
| 1 мэВ = 10-3 эВ, 1 кэВ = 103 эВ, 1 МэВ = 106 эВ, 1 ГэВ = 109 эВ, 1 ТэВ = 1012 эВ, 1 ПэВ = 1015 эВ, | ||
терминология — Термин для: «равно и противоположно» и «сумма до нуля» (физика)
спросил
Изменено 6 лет, 6 месяцев назад
Просмотрено 4к раз
Я ищу слово или термин, который соответствует обоим из следующих условий:
- равные и противоположные
- И
- сумма до нуля
Я специально рассматриваю термин для парных отношений в контексте физики .
Вот несколько примеров:
НОМЕР
- ( +5 ) <> ( -5 )
- равная величина
- противоположный знак
- (+5) ДОБАВИТЬ (-5) суммы до нуля
ВЕКТОР / СИЛА
- (величина 5 угол 0 градусов) <> (величина 5 угол 180 градусов)
- равная величина
- противоположное направление
- (величина 5, угол 0 градусов) ДОБАВИТЬ (величина 5, угол 180 градусов) в сумме дает ноль
ЭЛЕКТРИЧЕСКИЙ ЗАРЯД
- ( 2+ ) <> ( 2- )
- равная величина
- Знак встречного заряда
- ( 2+ ) ДОБАВИТЬ ( 2- ) суммы до нуля
До сих пор я нашел термины:
уравновешивающая : сила, способная уравновесить другую силу и создать равновесие
~ но это только для сил
антипараллельная : пространстве, два направленных отрезка, часто называемых векторами в прикладной математике, являются антипараллельными, если они поддерживаются параллельными прямыми и имеют противоположные направления
~ но это только для векторов и не означает, что строго равны
Что может помочь передать именно то, что я ищу, так это рассмотрение парных отношений с «противоположного конца» — позвольте мне еще раз выразить мои примеры с этой точки зрения:
ЧИСЛО
- мы начать с числа ( 0 )
- разбиваем (0) на
- (+5) <> (-5)
ВЕКТОР/СИЛА
- мы начинаем с вектора/силы (величина 0)
- мы разбиваем (величина 0) на
- (величина 5, угол 0 градусов) <> (величина 5, угол 180 градусов)
ЭЛЕКТРИЧЕСКАЯ ЗАРЯДКА
- начинаем с зарядки ( 0 )
- мы разделяем заряд ( 0 ) на
- ( 2+ ) <> ( 2- )
- терминология
- наука
Аддитивное обратное.
В математике аддитивным обратным числом а является число, которое, при добавлении к a дает ноль. Это число также известно как противоположное (число),[1] изменение знака и отрицание.[2] Для действительного числа оно меняет знак: противоположное положительному числу отрицательное, а противоположное отрицательному числу положительное. Ноль — это аддитивная, обратная самой себе.
Векторы —
Все следующие примеры на самом деле являются абелевыми группами:
Комплексные числа: −(a + bi) = (−a) + (−b)i. На сложной плоскости, эта операция поворачивает комплексное число на 180 градусов вокруг начала координат (см. изображение выше).
Сложение вещественных и комплекснозначных функций: здесь аддитивной обратной > функции f является функция −f, определяемая формулой (−f )(x) = − f (x) для всех x, таких что f + (−f ) = o , нулевая функция ( o(x) = 0 для всех x ).
В более общем смысле то, что предшествует, применяется ко всем функциям со значениями в абелевой группе («ноль» означает затем единичный элемент этой группы):
Последовательности, матрицы и сети также являются особыми видами функций.
В векторном пространстве добавка обратный -v часто называют вектором, противоположным вектору v; у него то же самое величины как первоначального, так и противоположного направления. Аддитивная инверсия соответствует скалярному умножению на −1. Для евклидова пространства это точечное отражение в начале координат. Векторы в прямо противоположных направлениях (умноженные на отрицательные числа) иногда называют антипараллельный.
векторные пространственнозначные функции (не обязательно линейные),
В модульной арифметике модульная аддитивная обратная величина x также определено: это число a такое, что a + x ≡ 0 (mod n). Эта добавка инверсия всегда существует. Например, число, обратное 3 по модулю 11, равно 8. потому что это решение 3 + x ≡ 0 (mod 11).
Из Википедии — Аддитивная обратная
1
Как насчет того, чтобы просто сказать «сбалансированный»? Из Оксфордских словарей:
Состояние, при котором различные элементы равны или находятся в правильных пропорциях.
Если вам нужно что-то, что более прямо передает идею об их эквивалентности, я бы предложил симметричный:
Состоят из одинаковых частей, обращенных друг к другу или вокруг оси; показывая симметрию.
Или, в этом случае, можно даже сказать «антисимметричный»:
Неизменный по величине, но измененный по знаку в результате замены двух переменных или определенной операции симметрии.
4
Это лучшее, что я могу придумать: взаимно уравновешивающие
взаимное : направленное друг к другу
противовес : оказывать противоположное, но равное действие к (чему-то): уравновесить (что-то), находясь напротив
1
Спасибо всем за предложения — вы привели меня к хорошему ответу, поэтому я решил опубликовать его как ответ на мой собственный вопрос.
Я провел поиск по этим двум предложениям:
- @Phil Sweet : inverse
- @Will Kunkel : симметрия
Я нашел это:
- Определение оператора инверсии симметрии заключается в том, что он преобразует вектор в другой вектор той же величины, но антипараллельной ориентации.
(приятно видеть слово антипараллельный омолаживающий)
Итак, возвращаясь к моему первоначальному вопросу и примерам, я продолжу это утверждение:
«Все нижеперечисленное может быть классифицировано как пары инверсионной симметрии »
ЧИСЛО
- (+5) <> (-5)
ВЕКТОР / СИЛА
- (величина 5 угол 0 градусов) <> (величина 5 угол 180 градусов)
ЭЛЕКТРИЧЕСКАЯ ЗАРЯДКА
- ( 2+ ) <> ( 2- )
Я могу немного уточнить термины, но меня это вполне устраивает.
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Поступательное движение — Скорость и скорость
Ниже приведена стенограмма моего обучающего видео MCAT Physics Video 5 — Физическая скорость и скорость в поступательном движении
(Нажмите здесь, чтобы посмотреть на YouTube)
[Начало стенограммы]
Лия здесь с сайта leah5sci.com/MCAT, и в этом видео я расскажу вам о скорости и скорости в том виде, в каком они появляются в поступательном движении MCAT. Вы можете просмотреть всю мою серию о поступательном движении, посетив мой веб-сайт https://leah5sci.com/MCATPHYSICS.
На MCAT скорость и скорость могут использоваться для обозначения одного и того же понятия, но есть разница, и важно, чтобы вы ее понимали. В предыдущем видео показано, как скорость является скалярной, что означает, что она имеет только величину, а скорость является вектором, учитывая, что она имеет величину и направление.
В качестве примера я могу сказать, что я пробежал пять миль в час, это моя скорость, или я пробежал пять миль в час на северо-запад, учитывая, что у меня есть направление, которое определяет скорость. Формулы скорости и скорости очень похожи, но на самом деле они означают совершенно разные вещи. Мы будем использовать S для скорости, а скорость равна расстоянию во времени (S = расстояние/время). Скорость — это вектор, и в физике вас учили, что стрелка над буквой V на MCAT, мы просто предположим, что мы знаем, что это вектор, и формула представляет собой смещение во времени (V = смещение/время), которое мы увидим написанным как дельта x над дельтой t.
Формулы скорости и скорости очень похожи, но на самом деле они означают совершенно разные вещи. Мы будем использовать S для скорости, а скорость равна расстоянию во времени (S = расстояние/время). Скорость — это вектор, и в физике вас учили, что стрелка над буквой V на MCAT, мы просто предположим, что мы знаем, что это вектор, и формула представляет собой смещение во времени (V = смещение/время), которое мы увидим написанным как дельта x над дельтой t.
Каждый раз, когда вы видите этот треугольник в уравнении, треугольник обозначает дельту и означает разницу или просто конечную минус начальную. Дельта x означает, что X окончательное минус X начальное, а дельта t равно T конечное минус T начальное. Другими словами, мы находим полное перемещение или общее изменение расстояния по отношению к общему изменению во времени.
Поскольку скорость является вектором, скорость будет направлена в направлении смещения. В зависимости от того, что вы используете в качестве учебного пособия, вы можете увидеть формулу, написанную совершенно по-разному, но не позволяйте ей сбить вас с толку. Когда вы учитесь, а не просто запоминаете, убедитесь, что вам удобно работать с единицами измерения и манипулировать ими, чтобы вы могли решать уравнения в любом формате.
Когда вы учитесь, а не просто запоминаете, убедитесь, что вам удобно работать с единицами измерения и манипулировать ими, чтобы вы могли решать уравнения в любом формате.
Давайте еще немного поиграем. Мы изменим нашу дельту t так, чтобы она была просто временем, мы хотим сохранить дельту x вместо просто x, потому что вы можете начать с ненулевой начальной точки, поэтому вам придется использовать начальную X и конечную X. У нас есть V вместо дельта V, потому что мы предполагаем, что у нас есть постоянная средняя скорость. Если вам нужно найти среднее значение между A и B, вы просто пишете A плюс B над двумя (A+B/2), и это ваше среднее значение.
Для средней скорости у нас есть V1 плюс V2 больше 2 (V1+V2/2), и это даст нам среднее значение или просто V, как мы используем его в выражении. Но теперь предположим, что вас попросили решить для X. Каждый раз, когда вам говорят только X, предполагайте, что это ваш финальный X. Первое, что мы хотим сделать, это переписать или понять уравнение в формате, который дает нам X. И это даст нам следующее: V равно X final минус X initial над t, и затем мы решим для X final алгебраически.
Первое, что мы хотим сделать, это переписать или понять уравнение в формате, который дает нам X. И это даст нам следующее: V равно X final минус X initial над t, и затем мы решим для X final алгебраически.
Первое, что мы хотим сделать после PEMDAS, помните, что у вас есть скобки степени умножения, деления, сложения и вычитания. Мы делим на t, поэтому мы хотим перенести это на другую сторону, умножив обе части на t. Перепишем его так, чтобы было понятно: Vt равно X final минус X initial (Vt=Xf – Xi). У нас есть минус начальный X, поэтому мы хотим перенести это на другую сторону, пересечь начальный X с обеих сторон, и это дает нам наше окончательное уравнение для конечного X или просто X равно начальному X плюс Vt (X = Xi + Vt).
Это формат, который я выучил по физике и который мне наиболее удобен. Если исходное значение X равно нулю, то ваша формула просто равна X равно Vt, где V — средняя или постоянная скорость.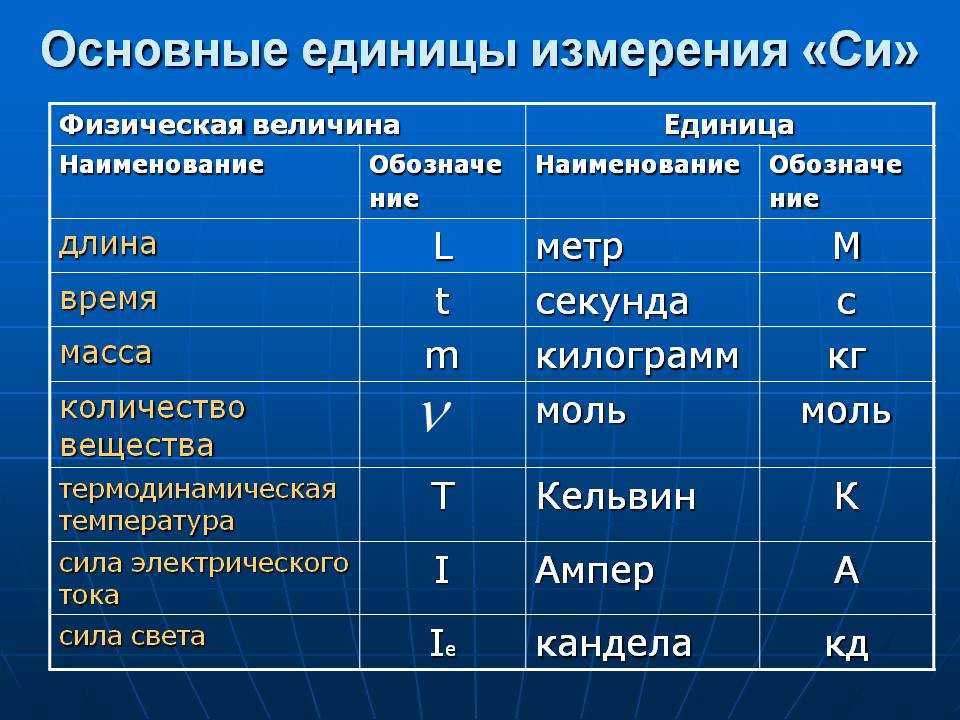
Давайте попробуем еще раз решить на время. Первое, что нам нужно сделать, это вывести время из знаменателя, потому что вам нужно, чтобы ваше неизвестное было отдельной единицей. Итак, мы подводим его к числителю еще раз, умножая обе части на t, но на этот раз мы делим обе части на V, чтобы изолировать t. Это дает нам, что t само по себе равно делению x на V.
Для получения полного списка кинематических уравнений MCAT, включая мое руководство о том, как узнать, какую формулу использовать и когда, посетите мой веб-сайт https://leah5sci.com/MCATPHYSICS, найдите Шпаргалку в разделе «Поступательное движение».
Давайте закончим практическим вопросом:
Найдите скорость и скорость, если девушка пройдет 1,4 мили за 20 минут, чтобы добраться до дома подруги. Дома находятся ровно в 0,7 мили друг от друга.
Причина, по которой указаны два расстояния, заключается в том, что если два дома находятся ровно в 0,7 мили, это не означает, что вы должны пройти всего семь миль, чтобы добраться туда. Скажем, на пути есть улицы, проспекты или общие препятствия, вы можете обнаружить, что идете по пути, который выглядит так, в общей сложности 1,4 мили, хотя на карте указано 0,7 мили.
Скажем, на пути есть улицы, проспекты или общие препятствия, вы можете обнаружить, что идете по пути, который выглядит так, в общей сложности 1,4 мили, хотя на карте указано 0,7 мили.
Здесь вы увидите четкое различие между скоростью и скоростью. Помните, что формула скорости – это фактическое расстояние во времени (S=d/t). Фактическое пройденное расстояние составляет 1,4 мили, а время — 20 минут. Итак, давайте решим в милях в минуту.
У нас одна целая четыре больше двадцати. Если мы попытаемся сделать длинное деление, на MCAT это займет слишком много времени. Вместо этого мы воспользуемся приемом умножения верхнего и нижнего числа на десять, сдвинув десятичную дробь на одну позицию вправо, что даст нам четырнадцать на двести.
Если вам не нравится этот трюк, вернитесь к моей серии по математике на моем веб-сайте https://leah5sci.com/MCATMATH.
Я избавился от десятичной дроби, что немного упростило задачу, но четырнадцать на двести все равно слишком сложно.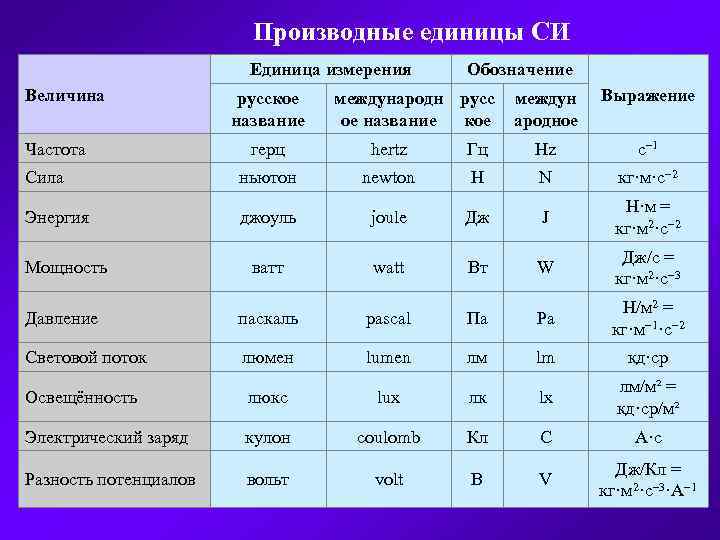 Я ищу число, которое я могу разделить на оба из них, чтобы упростить. Четырнадцать и двести разделить на два. Четырнадцать разделить на два — семь, двести на два — сто. Семь на сто — это число, деленное на десять, что приводит нас к другому моему трюку — перемещению десятичной дроби назад.
Я ищу число, которое я могу разделить на оба из них, чтобы упростить. Четырнадцать и двести разделить на два. Четырнадцать разделить на два — семь, двести на два — сто. Семь на сто — это число, деленное на десять, что приводит нас к другому моему трюку — перемещению десятичной дроби назад.
Если у меня есть два нуля, я делю, перемещая запятую на два знака назад, и это дает мне 0,07 мили в минуту. Это Скорость. Теперь давайте искать скорость. Помните, что скорость равна Delta X по t, где полное перемещение. Несмотря на то, что девушка прошла 1,4 мили, фактическое перемещение по прямой составляет всего 0,7 мили. Итак, это уравнение записывается как 0,7 мили за 20 минут. Теперь дельта x будет равна x final минус x initial. X final равно 0,7, X initial равно 0, поэтому мы использовали только 0,7.
Если бы мы не начали с нуля, у нас было бы другое значение дельты x, так что обязательно имейте это в виду. Еще раз, мы переместим десятичную дробь вправо вверху и внизу, чтобы избавиться от этой десятичной дроби, это дает мне семь больше двухсот. Опять же, что-то, что заняло бы слишком много времени, чтобы вычислить делением в большую сторону, поэтому мы можем попробовать два разных трюка.
Опять же, что-то, что заняло бы слишком много времени, чтобы вычислить делением в большую сторону, поэтому мы можем попробовать два разных трюка.
Первый трюк, который мы должны использовать, — это оценка. Помните на MCAT, достаточно близко достаточно хорошо. Семь на двести довольно близко к семи на двести десять. Семь и два десять делятся на семь. Семь разделить на семь — это один, двадцать один на семь — это три, и теперь у нас есть один больше тридцати. Мы можем оценить это дальше.
Один больше тридцати равен одному больше трех, умноженному на один больше десяти. Вы должны быть знакомы с десятичными значениями обыкновенных дробей. Один больше трех — три целых три десятых (0,33). Ноль целых три три раза один больше десяти или просто разделить на десять, сдвиньте десятичную дробь назад на одну позицию, и это будет равно нулю целых три мили в минуту (0,033 мил/мин).
Этот трюк обычно экономит время, здесь я нашел его слишком длинным, поэтому попробуем другой трюк. Если мы посмотрим на семь на двести, в идеале любое число, деленное на сто, очень легко запомнить, потому что у нас есть единица, за которой следуют нули. Чтобы получить двести в сто, мы должны разделить на два, поэтому мы также делим семь на два. Это не так просто, но если подумать, половина семи — это три целых пять десятых, половина шести — это три, и у нас осталась одна лишняя, половина одного — это половина, и это дает нам три целых пять десятых.
Если мы посмотрим на семь на двести, в идеале любое число, деленное на сто, очень легко запомнить, потому что у нас есть единица, за которой следуют нули. Чтобы получить двести в сто, мы должны разделить на два, поэтому мы также делим семь на два. Это не так просто, но если подумать, половина семи — это три целых пять десятых, половина шести — это три, и у нас осталась одна лишняя, половина одного — это половина, и это дает нам три целых пять десятых.
Три целых пять сотых намного проще работать, мы делим на десять с двумя нулями. Мы перемещаем десятичную дробь на два пробела назад, и это дает нам ноль целых три десятых пять (0,035), что очень близко к 0,33. Используйте любой трюк, который кажется вам более естественным, но что бы вы ни делали, НЕ прибегайте к делению в длину, это займет слишком много времени.
Не забудьте присоединиться ко мне в следующем видео поступательного движения, где я рассказываю об ускорении в связи с кинематикой MCAT.
Вы застряли на определенной теме MCAT? Я предлагаю частное онлайн-обучение, где я фокусируюсь на ваших потребностях, чтобы укрепить ваши индивидуальные слабости. Подробную информацию о репетиторстве можно найти по ссылке ниже или на моем веб-сайте leah5sci.com/MCATTutor.
Вы перегружены огромным объемом информации, необходимой для MCAT? Вы обеспокоены тем, что отсутствие надлежащего учебного плана и низкий балл MCAT помешают вам поступить в медицинскую школу? Моя новая электронная книга «Стратегия экзамена MCAT — это 6-недельное руководство по преодолению MCAT» поможет вам сформулировать конкретный план обучения, помогая вам понять, где вы находитесь сейчас, определить свои цели и выяснить, что нужно для их достижения, и это ваше БЕСПЛАТНО когда вы подписываетесь на мою рассылку по электронной почте на McatExamStrategy.com. Подписавшись на мою рассылку по электронной почте, вы также будете первыми, кто узнает, когда у меня появятся новые видео, шпаргалка по учебному пособию MCAT, советы и многое другое! Снова ссылка McatExamStrategy.



