Скалярное произведение векторов 9 класс онлайн-подготовка на Ростелеком Лицей

 

 

Тема: Соотношения между сторонами и углами треугольника. Раздел 3. Скалярное произведение векторов

 

Урок: Скалярное произведение векторов

 

1. Тема урока, введение

 

 

Тема урока: «Скалярное произведение векторов». На этом уроке мы рассмотрим скалярное произведение векторов и решим задачи на вычисление скалярного произведения.

 

 

2. Напоминание основных сведений о векторах

 

 

Напомним кратко основные сведения, которые мы знаем о векторах.

 

1.  Определение. Вектор – это направленный отрезок, обозначение 

2.  Операции с векторами.

а)   Сложение векторов.

Правило параллелограмма.

Правило треугольника.

б)   Умножение вектора на число.

3. Угол между векторами.

4. Скалярное произведение векторов.

Скалярное произведение векторов – это произведение их длин на косинус угла между ними.

Заметим, что  – это проекция вектора  на направление вектора  . Из определения следует, что скалярное произведение векторов – это число, характеризующее взаимное расположение векторов.

 

 

3. Анализ формулы скалярного произведения векторов

 

 

Рассмотрим некоторые частные случаи взаимного расположения векторов.

 

1.  Перпендикулярные векторы.

Если , то   и  .

Сила в направлении  не совершает никакой работы, скалярное произведение Обратно: если , то   в силу равенства .

Получаем следующий важный вывод: Скалярное произведение векторов равно нулю тогда и только тогда, когда векторы перпендикулярны.

2. Коллинеарные векторы.

Рассмотрим коллинеарные векторы: они могут быть сонаправлены или противоположно направлены.

а) Сонаправленные векторы.

, поэтому Таким образом,

б) Противоположно направленные векторы.

, поэтому  

Таким образом,

3. Равные векторы. Рассмотрим случай, когда

Определение: Скалярное произведение  называется скалярным квадратом вектора и обозначается  ,  . Свойство: Скалярный квадрат вектора равен квадрату его длины,  .

 

4. Решение задач на вычисление скалярного произведения векторов

 

 

Следует научиться вычислять скалярное произведение векторов не только в частных, но и в общих случаях. Рассмотрим следующую задачу.

 

Задача. Вычислить скалярное произведение векторов  и  , если  , угол между ними равен:

а)    

б)   

в)  

 

а) Дано:

Найти: Решение: Ответ:

б)  Дано:

Найти: Решение: или  Ответ: 0.

в) Дано:

Найти:

Решение:Ответ:

 

 

5. Вычисление скалярного произведения векторов в геометрических задачах

 

 

Векторы часто присутствуют и в различных геометрических фигурах. Рассмотрим следующую задачу.

 

Задача. В равностороннем треугольнике ABC со стороной a проведена высота  BD. Вычислить скалярное произведение векторов:

а)                       

б)  

в)  

г)  

Решение:

а)   Ответ:

б) Для определения угла между векторами отложим вектор  от точки

. Ответ: .

в)    Ответ: 0.

г)   Ответ:

 

 

6. Вычисление скалярного произведения векторов в физической задаче

 

 

Задача. К одной и той же точке приложены две силы  и  , действующие под углом  друг к другу, причем . Найти величину равнодействующей силы  .

 

Дано:

Найти: .

Решение:

Ответ:

 

7. Заключение

 

 

Итак, мы рассмотрели разные задачи на вычисление скалярного произведения векторов. На следующем уроке мы рассмотрим скалярное произведение векторов в координатах.

 

 

Список литературы

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А. В. Геометрия. Уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. E-science.ru (Источник).
2. Mathematics.ru (Источник). 

 

Домашнее задание

1. Атанасян Л. С. и др. Геометрия 7–9 классы. №№1041, 1042.

 

 

 

Аналитическая геометрия

Аналитическая геометрия

Привалов И.И. Аналитическая геометрия. М.: Наука, 1966. — 272 с. Учебник для студентов высших технических заведений. Содержит разделы: Аналитическая геометрия на плоскости, Аналитическая геометрия в пространстве. Много решенных примеров и задач. Оглавление ВВЕДЕНИЕ ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций. § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 6. Построение прямой линии по ее уравнению. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости. § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 16. Расстояние от дайной точки до данной прямой. 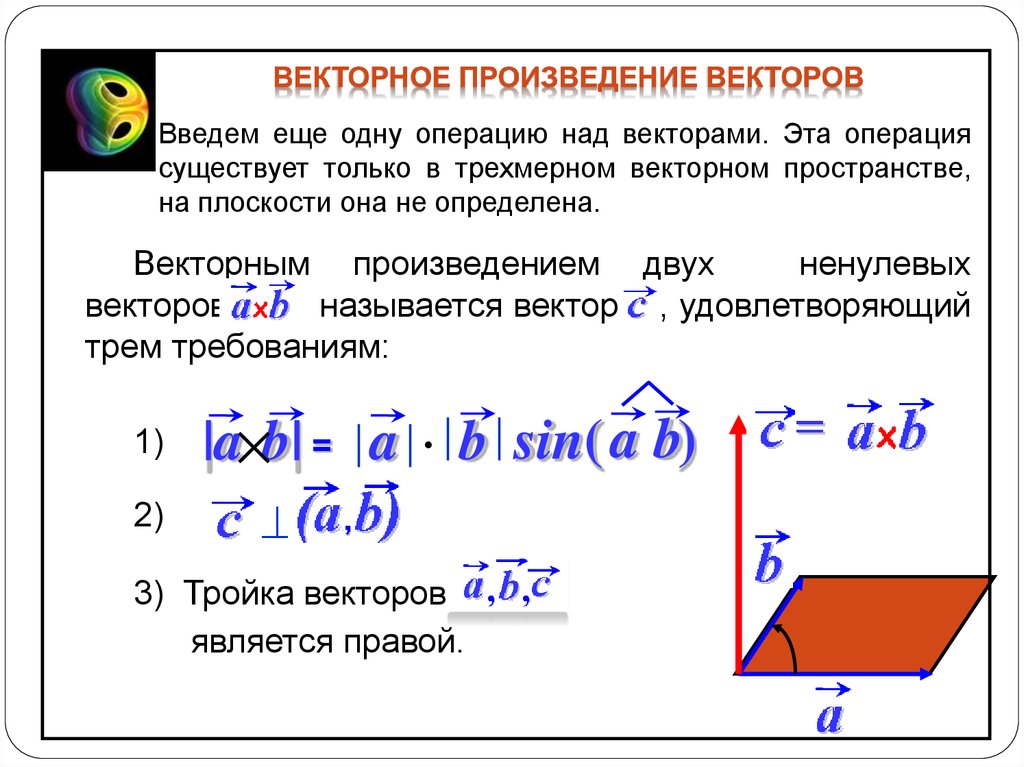§ 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 11. Уравнение конического сечения в полярных координатах. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры. § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 2. Однородная система двух уравнений с тремя неизвестными. § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии. Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. § 4. Вычисление угла между двумя осями в пространстве. Упражнения ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 9. Скалярное произведение векторов, заданных проекциями. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. § 16. Двойное векторное произведение. Упражнения ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ § 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. 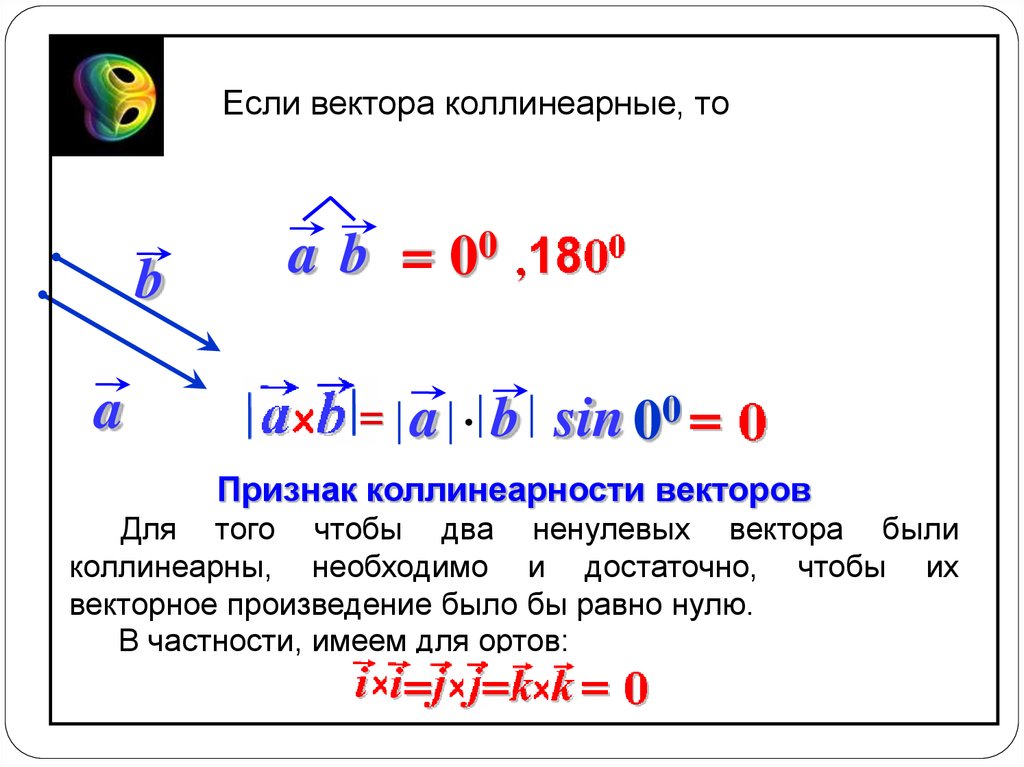§ 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 3. Исследование общего уравнения плоскости. § 4. Уравнение плоскости в отрезках. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой. § 3. Угол между двумя прямыми линиями. § 4. Условия параллельности и перпендикулярности двух прямых. § 5. Уравнения прямой, проходящей через две данные точки. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 9. Пересечение прямой с плоскостью. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова. Упражнения Ответы

Перекрестное произведение | Определение, формула и свойства

перекрестное произведение

Просмотреть все материалы

Связанные темы:

продукт

См.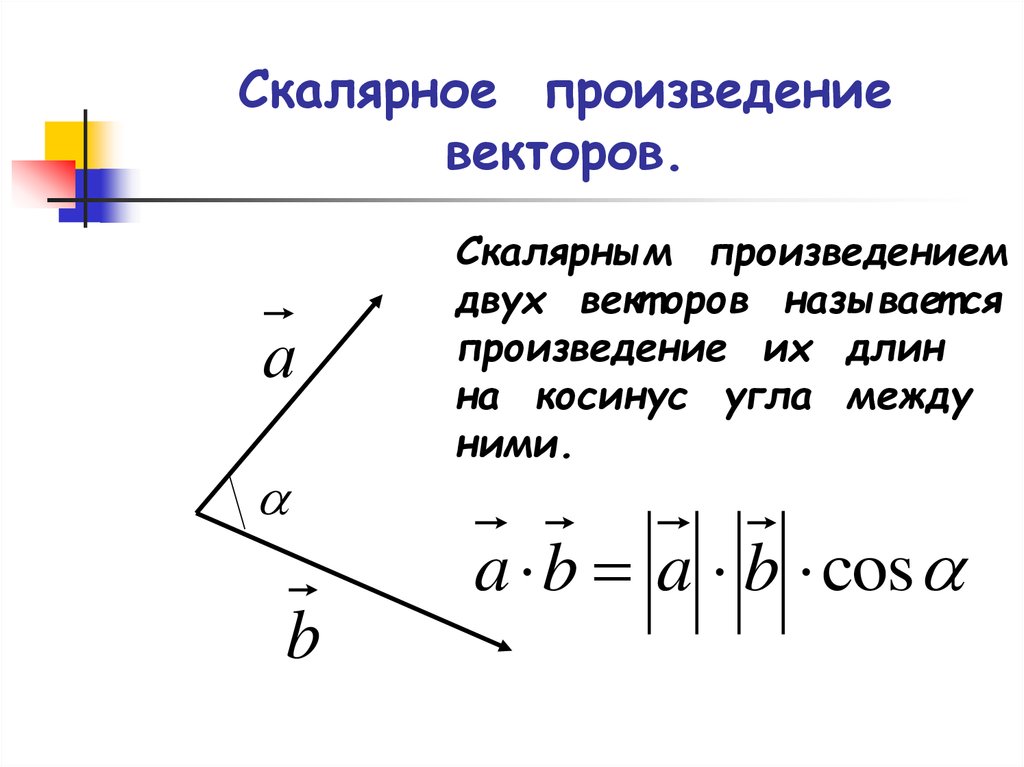 все связанные материалы →

векторное произведение , также называемое векторным произведением , метод умножения двух векторов, который дает вектор, перпендикулярный обоим векторам, участвующим в умножении; то есть a × b = c, где c перпендикулярно и a, и b. Величина c определяется произведением величин a и b и синуса угла

θ между a и b, то есть |a × b| = |с| = |а| |б| sin θ . Таким образом, величина c представляет собой площадь параллелограмма, образованного элементами a и b, причем |a| является базой и |b| sin θ — высота параллелограмма. Перекрестное произведение отличается от скалярного произведения, которое дает скаляр при умножении двух векторов.

Направление c находится по правилу правой руки. Это правило указывает на то, что пятка правой руки помещается в точку, где соединяются два хвоста векторов, а затем пальцы правой руки загибаются в направлении от а к b. Когда это будет сделано, большой палец правой руки будет указывать в направлении векторного произведения c. Ясно, что из этого определения векторное пространство для векторного произведения является трехмерным пространством. Если, например, два заданных вектора в перекрестном произведении оба находятся в x y результирующий вектор перпендикулярен этим двум векторам, а это означает, что вектор параллелен оси z .

для двух векторов a = ( A _x , A _Y , A _Z ) и B = ( B _x , B _Y 202020202020202020192019201919201920 2020202020202019201920192019 . _{. z} ), перекрестное произведение находится путем вычисления определителя матрицы с единичными векторами x, y и z, являющимися первой строкой, и векторами a и b, являющимися двумя последними строками. Определитель создает следующую формулу для векторного произведения: a × b = x ( A _Y B _Z — A _Z B _Y ) + Y ( A _Z ) + Y ( A _Z ) + Y ( A _Z ) + Y ( A _Z ) + Y ( A _Z ) + Y ( A _Z ). _x B _Z ) + Z ( A _x B _y — A _Y B _x 2020202020202020202.202020202.202020202037 . , a × b = 0. Кроме того, поскольку вращение от b к a противоположно вращению от a к b, a × b = −b × a. Это показывает, что перекрестное произведение является не коммутативным, а распределительным законом a × ( b + d) = (a × b) + (a × d). Другие свойства включают свойство Якоби, a × (b × c) + b × (c × a) + c × (a × b) = 0; скалярное кратное свойство при заданной константе k , k (a × b) = k a × b = a × k b; и свойство нулевого вектора, a × b = 0, где либо a, либо b — нулевой вектор, с все элементы равны нулю.

Перекрестное произведение имеет множество применений в науке. Одним из таких примеров является крутящий момент, который позволяет устанавливать винты и позволяет педалям велосипеда перемещать его вперед. Уравнение для крутящего момента: τ = F × r, где τ — крутящий момент, F — приложенная сила, а r — вектор от оси вращения к месту приложения силы.

Другим ярким примером является сила Лоренца, сила, действующая на заряженную частицу q , движущуюся со скоростью v через электрическое поле E и магнитное поле B. Полная электромагнитная сила F, действующая на заряженную частицу, определяется выражением F = q E + q v × B.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Кен Стюарт

Внутреннее (точечное) произведение двух векторов. Приложения в машинном обучении

Highlight : В этом посте мы рассмотрим один из основных операторов в линейной алгебре. Он известен как точечный продукт или внутренний продукт двух векторов. Большинство из вас уже знакомы с этим оператором, и на самом деле это довольно легко объяснить. И все же мы дадим некоторые дополнительные идеи, а также некоторую базовую информацию о том, как использовать его в Python.

Обзор учебника:

1. Скалярный продукт :: Определение и свойства
2. Линейные функции
3. Примеры и реализация

Скалярный продукт :: Определение и свойства

Прежде всего, когда вы применяете скалярное произведение к двум векторам, они должны быть одного размера.

Например, у нас есть два вектора или два упорядоченных списка векторов. Мы применяем скалярное произведение таким образом, что сначала поэлементно умножаем эти два упорядоченных вектора. Давайте посмотрим на пример. Умножаем поэлементно: \(2\cdot 8\), \(7\cdot 2\), \(1\cdot 8\).

Затем мы суммируем эти члены умножения. Интересно, что результатом скалярного произведения является скаляр.

Сначала, как обычно, рассмотрим векторы в 2D-плоскости. Их легко визуализировать, и они дают нам интуитивное представление о том, что такое точечный продукт. Итак, мы будем наблюдать два вектора \(\vec{v} \) и \(\vec{w} \). Скалярное произведение этих двух векторов можно интерпретировать как проекцию вектора \(\vec{w} \) на вектор \(\vec{v} \) . Затем мы умножаем длину спроецированного вектора \(\vec{w} \) на \(\vec{v} \) и длину \(\vec{v} \). 9{\circ} \) (острый угол).

Если векторы перпендикулярны, то внутренний продукт равен нулю. Это важное свойство! О таких векторах говорят, что они ортогональны.

В случае, если векторы образуют тупой угол, внутренний продукт будет отрицательным.

Так сказать, еще один трюк со скалярным произведением. Итак, мы видим, что скалярный продукт — это коммутативная векторная операция. По сути, это означает, что мы можем спроецировать \(\vec{v} \) на \(\vec{w} \), в этом случае у нас будет длина спроецированного \(\vec{v} \), умноженная на длину из \(\vec{w} \), поэтому мы получим тот же результат.

Давайте подробнее рассмотрим свойство коммутативности скалярного произведения.

Если \(\vec{v} \) и \(\vec{w} \) имеют одинаковую длину, мы могли бы использовать симметрию. Итак, мы видим, что длина проекции \(\vec{w} \) на \(\vec{v} \) такая же, как длина \(\vec{v} \), проецируемая на \ (\vec{ш} \). Таким образом, становится ясно, что внутренний продукт одинаков для обоих подходов к расчету.

Кроме того, можно предположить, что один из векторов, скажем, \(\vec{v} \), в три раза длиннее, чем \(\vec{w} \). Теперь мы видим, что у нас не может быть проекций одинаковой длины. Однако мы можем интерпретировать это \(3\vec{v} \) как простое масштабирование вектора \(\vec{v} \).

Напомним, что масштабирование вектора с помощью скаляра на самом деле является масштабированием его длины.

Следовательно, мы можем наблюдать вектор, имеющий тот же размер, что и \(\vec{w} \), масштабированный с помощью скаляра. Теперь у нас есть скаляр, умноженный на вектор \(\vec{v} \), и скалярное произведение с \(\vec{w} \) будет таким же, как умножение \(3 \) на \(\vec{ v} \) и \(\vec{w} \). Это показывает, что внутренний продукт действительно является коммутативной операцией.

Линейные функции

Теперь снова поговорим о линейных функциях. Но теперь мы рассмотрим функции, в которых входные и выходные размерности не совпадают. Например, у нас есть двумерный входной вектор, и с помощью функции \(L \) он даст нам одномерный выходной вектор.

Для линейных преобразований выполняются следующие свойства:

Например, линия с равномерно расположенными на ней точками будет преобразована в 1D-линию. Здесь обратите внимание, что на самом деле мы отображаем точек с координатами ( x , y ) в одну координату (например, на какую-то линию z )! Важно, чтобы расстояние между точками на отображаемой линии было равноудаленным. Это свойство линейного преобразования.

Теперь давайте посмотрим, что произойдет, если мы применим линейное преобразование [1 -2] к вектору \(\vec{w} \). Он отображается так, что его значение равно \(-2 \). Это преобразование отображает 2D-пространство в 1D-пространство, которое представляет собой линию. И это преобразование \(\begin{bmatrix}1 & -2\end{bmatrix} \) показывает, как мы отображаем один базисный вектор. Таким образом, это \(1 \) не изменит наш вектор \(\hat{i} \) (остается прежним), но изменит наш вектор \(\hat{j} \).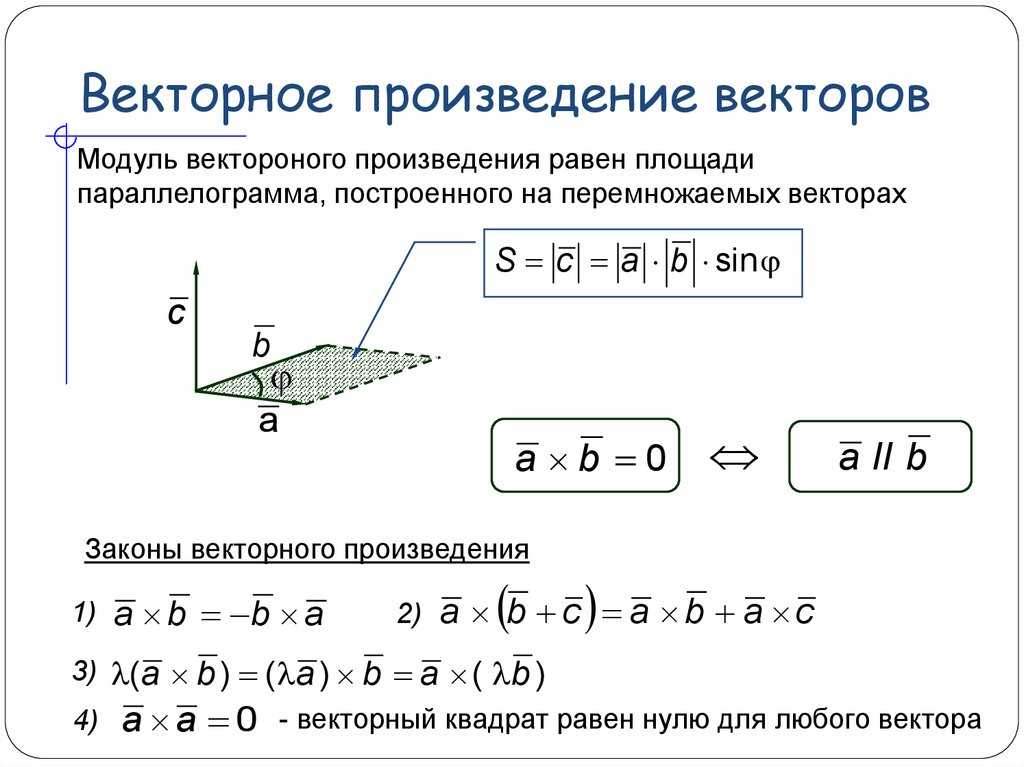 \(\hat{j} \)vector будет сопоставлен с -2. Итак, используя эту идею о том, что любой вектор можно разложить на комбинацию базисных векторов, мы можем получить следующую формулу.

Все это можно пояснить на этом примере. Вы можете подумать об этом: как 2-D точки будут проецироваться на одну линию.

У нас есть вектор, который идет от \(0 \) до \(\hat{u} \). Кроме того, у нас много двумерных точек. Нас интересует, где эти двумерные точки (векторы!) будут проецироваться на одну линию?

Давайте посмотрим, где вектор \(\hat{i} \) приземлится на единичный вектор \(\hat{u} \), определяющий эту линию. Если мы воспользуемся так называемой линией симметрии, то придем к выводу, что \(u_{x} \) будет проекцией \(\hat{i} \). это тоже x – координата вектора \(\hat{u} \).

То же верно и для вектора \(\hat{i} \). Он будет спроецирован в вектор длины \(u_{y} \). Итак, какой будет проекция произвольного вектора, имеющего две ненулевые ( x , y ) координаты.

Мы видим, что \(u_{x} \) и \(u_{y} \) определяют нашу проекционную матрицу. Они сообщат нам, где приземлится наш базисный вектор: \(u_{x} \) и \(u_{y} \)

Другими словами, если мы представим наш вектор с помощью базисных векторов, мы получим координаты ( х , и ). Если мы умножим эти координаты на \(u_{x} \) и \(u_{y} \) соответственно и суммируем эти два произведения, мы получим позицию, в которой наш исходный вектор (x, y) окажется на линия, заданная вектором \(\hat{u} \). Эта позиция будет нашей новой координатой для одномерной системы координат \(\hat{u} \).

Определив это преобразование, мы можем рассматривать каждый вектор как разложение этих двух векторов и, следовательно, можем получить результат. Теперь мы видим, что векторные произведения матриц двойственны интерпретации скалярного произведения.

Примеры и реализация

Умножение строки на столбец является основой для всех матричных умножений. Из двух векторов получается одно число.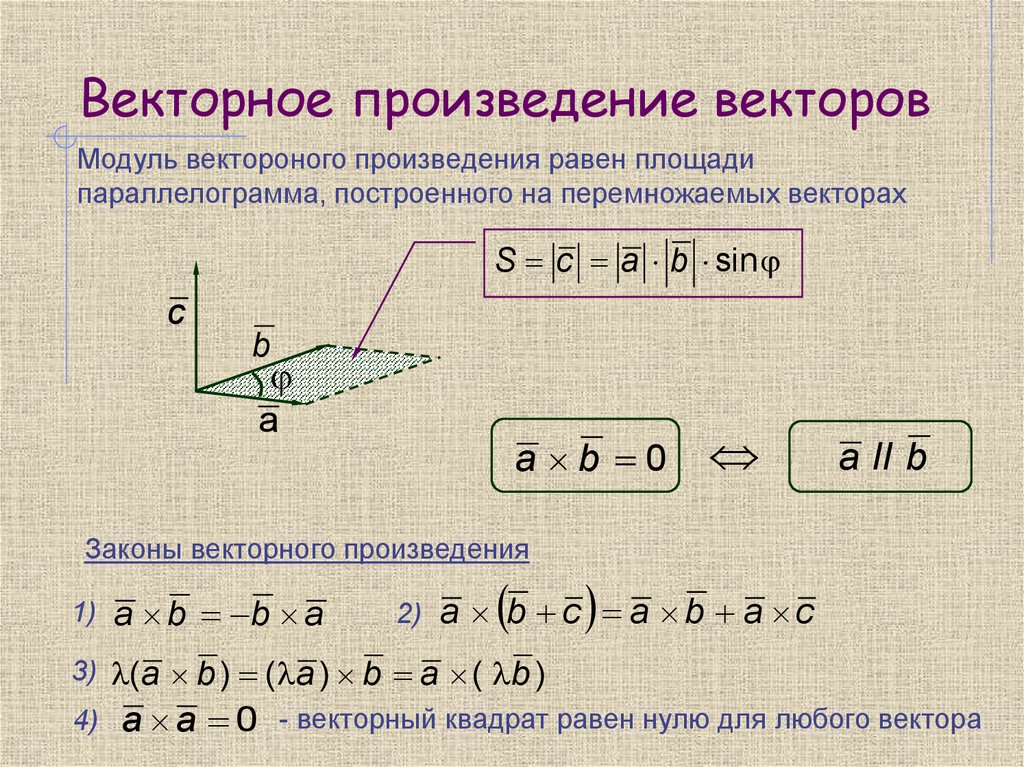 Это число называется внутренним произведением двух векторов. Другими словами, произведение матрицы \(1\) на \(n\) (вектор-строка) и матрицы \(n\times 1\) (вектор-столбец) является скаляром.

Для начала несколько простых примеров:

\(\vec{v}= \begin{bmatrix}1\\2\end{bmatrix} \), \(\vec{w}= \begin{ bmatrix}4\\5\end{bmatrix} \)

Скалярное произведение равно

$$ \vec{v}\cdot\vec{w} = 1\cdot 4+2\cdot 5= 4+10= 14 $$

Другой пример показывает два вектора, внутреннее произведение которых равно \(0\).

\(\vec{v}= \begin{bmatrix}1\\3\\2\end{bmatrix} \), \(\vec{w}= \begin{bmatrix}4\\-4\\ 4\end{bmatrix} \)

$$ \vec{v}\cdot\vec{w} = 0 $$

$$ 1\cdot 4+3\cdot \left (-4 \right)+2 \cdot 4= 0 $$

Теперь наши векторы \(\vec{v} \) и \(\vec{w} \) имеют размер \(3 \).

С другой стороны, мы можем вычислить длину отдельного вектора, используя скалярное произведение, и применить квадратный корень. Это иногда называют «нормой» вектора.

$$ \vec{v}= \begin{bmatrix}1\\3\\2\end{bmatrix} $$

$$ \vec{v}\cdot\vec{v}= 1+9+ 4= 14 $$               

Длина равна \(\left \| \vec{v} \right \|= \sqrt{14} \)     

Это может быть очень полезно, когда нам нужно нормализовать наши векторы. В этом случае мы хотим, чтобы вектор имел длину \(1 \). В принципе, если у нас есть длина нашего вектора, равная \(4\), то понятно, что нам нужно разделить его на \(4\). В этом случае, когда у нас есть \(\sqrt{14} \), и мы просто разделим каждый элемент нашего вектора на \(\sqrt{14} \), и это будет наш результирующий вектор:

$$ \vec{u}= \frac{\vec{v}}{\left \| \vec{v} \right \|}= \frac{1}{\sqrt{14}}\begin{bmatrix}1\\3\\2\end{bmatrix} $$

$$ \left \| \vec{u} \right \|= 1 $$

$$ \frac{1}{14}+\frac{9}{14}+\frac{4}{14} = 1 $$

Мы с помощью этого подхода также можно получить угол между двумя векторами. Возьмем скалярное произведение между векторами \(\vec{v} \) и \(\vec{w} \), и если мы нормализуем это произведение, то получим угол между векторами \(\vec{v} \) и \ (\vec{ш} \).

9{\circ} $$

Это уравнение доказывает, что на самом деле все абсолютные значения косинуса меньше единицы. Итак, у нас есть следующая форма, где абсолютное значение скалярного произведения всегда меньше размера вектора \(\vec{v} \), умноженного на вектор \(\vec{w} \).

$$ \слева | \cos \theta  \right |\leq 1 $$

$$ \left | \vec{v}\cdot \vec{w} \right |\leq \left \| \vec{v} \право \|\лево \| \vec{w} \право \| $$

Один из способов определить скалярное произведение — записать его следующим образом:

$$ \vec{v}\cdot \vec{w}= v_{1}w_{1}+ v_{2}w_{2} $$

Кроме того, определение единичного вектора очень интересно . Например, вектор \(\vec{v} \) с координатами \(\left (1,1 \right ) \) можно нормализовать следующим образом. Мы можем разделить \(\vec{v} \) на длину \(\vec{v} \), и это будет наш единичный вектор, который имеет длину \(\frac{1}{\sqrt{2}} \).

С другой стороны, мы можем видеть, что векторы длины \(1 \), которые начинаются в центре системы координат, определяют единичную окружность. Итак, каждый единичный вектор должен лежать на этой окружности. Кроме того, интересно, что длина — это одно, но другое свойство возникает, если мы возьмем скалярное произведение с нашим базисным вектором \(\hat{i} \) и нашим единичным вектором \(\hat{u} \). Эта проекция является хорошо известным результатом тригонометрии. Получаем \(\cos\theta\) по оси \(x\) и \(\sin\theta\) по оси \(y\). Более того, мы можем получить наши координаты единичного вектора, поставив \(\cos\theta\) для компонента \(x\) и \(\sin\theta\) для компонента \(y\). Таким образом, мы можем определить угол между двумя векторами.

Сводка

Вау! Действительно, мы представили множество идей и концепций, связанных с внутренним или скалярным произведением двух векторов. Мы понимаем, насколько важна линейная алгебра. Также очень часто у нас будут похожие приложения. Например, мы будем использовать нормализацию наших данных, используя идеи скалярного произведения. Это лишь одно из множества приложений с точечными продуктами.