Закон Кулона — PhysBook

Закон Кулона

В 1785 г. французский физик Шарль Кулон экспериментально установил основной закон электростатики – закон взаимодействия двух неподвижных точечных заряженных тел или частиц.

Закон взаимодействия неподвижных электрических зарядов – закон Кулона – основной (фундаментальный) физический закон и может быть установлен только опытным путем. Ни из каких других законов природы он не вытекает.

Если обозначить модули зарядов через |q₁| и |q₂|, то закон Кулона можно записать в следующей форме:

\(~F = k \cdot \dfrac{|q_1| \cdot |q_2|}{r^2}\) , (1)

где k – коэффициент пропорциональности, значение которого зависит от выбора единиц электрического заряда. В системе СИ \(~k = \dfrac{1}{4 \pi \cdot \varepsilon_0} = 9 \cdot 10^9\) Н·м²/Кл², где ε₀ – электрическая постоянная, равная 8,85·10^-12 Кл²/Н·м² .

Формулировка закона:

сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.

Эту силу называют кулоновской.

Закон Кулона в данной формулировке справедлив только для точечных заряженных тел, т.к. только для них понятие расстояния между зарядами имеет определенный смысл. Точечных заряженных тел в природе нет. Но если расстояние между телами во много раз больше их размеров, то ни форма, ни размеры заряженных тел существенно, как показывает опыт, не влияют на взаимодействие между ними. В этом случае тела можно рассматривать как точечные.

Легко обнаружить, что два заряженных шарика, подвешенные на нитях, либо притягиваются друг к другу, либо отталкиваются. Отсюда следует, что силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела. Подобные силы называют

центральными. Если через \(~\vec F_{1,2}\) обозначить силу действующую на первый заряд со стороны второго, а через \(~\vec F_{2,1}\) – силу, действующую на второй заряд со стороны первого (рис. 1), то, согласно третьему закону Ньютона, \(~\vec F_{1,2} = -\vec F_{2,1}\) . Обозначим через \(\vec r_{1,2}\) радиус-вектор, проведенный от второго заряда к первому (рис. 2), тогда

\(~\vec F_{1,2} = k \cdot \dfrac{q_1 \cdot q_2}{r^3_{1,2}} \cdot \vec r_{1,2}\) . (2)

• Рис. 1

• Рис. 2

Если знаки зарядов q₁ и q₂ одинаковы, то направление силы \(~\vec F_{1,2}\) совпадает с направлением вектора \(~\vec r_{1,2}\) ; в противном случае векторы \(~\vec F_{1,2}\) и \(~\vec r_{1,2}\) направлены в противоположные стороны.

Зная закон взаимодействия точечных заряженных тел, можно вычислить силу взаимодействия любых заряженных тел. Для этого тела нужно мысленно разбить на такие малые элементы, чтобы каждый из них можно было считать точечным. Складывая геометрически силы взаимодействия всех этих элементов друг с другом, можно вычислить результирующую силу взаимодействия.

Открытие закона Кулона – первый конкретный шаг в изучении свойств электрического заряда. Наличие электрического заряда у тел или элементарных частиц означает, что они взаимодействуют друг с другом по закону Кулона. Никаких отклонений от строгого выполнения закона Кулона в настоящее время не обнаружено.

Опыт Кулона

Необходимость проведения экспериментов Кулона была вызвана тем, что в середине XVIII в. накопилось много качественных данных об электрических явлениях. Возникла потребность дать им количественную интерпретацию. Поскольку силы электрического взаимодействия были относительно невелики, возникла серьезная проблема в создании метода, который позволил бы произвести замеры и получить необходимый количественный материал.

Французский инженер и ученый Ш. Кулон предложил метод измерения малых сил, который основывался на следующем экспериментальном факте, обнаруженном самим ученым: сила, возникающая при упругой деформации металлической проволоки, прямо пропорциональна углу закручивания, четвертой степени диаметра проволоки и обратно пропорциональна ее длине:

\(~F_{ynp} = k \cdot \dfrac{d^4}{l} \cdot \varphi\) ,

где d – диаметр, l – длина проволоки, φ – угол закручивания. В приведенном математическом выражении коэффициент пропорциональности k находился опытным путем и зависел от природы материала, из которого изготавливалась проволока.

Данная закономерность была использована в так называемых крутильных весах. Созданные весы позволили измерить ничтожно малые силы порядка 5·10^-8 Н.

• а

• б

Рис. 3

Крутильные весы (рис. 3, а) состояли из легкого стеклянного коромысла 9 длиной 10,83 см, подвешенного на серебряной проволоке 5 длиной около 75 см, диаметром 0,22 см. На одном конце коромысла располагался позолоченный бузиновый шарик 8, а на другом – противовес 6 – бумажный кружок, смоченный в скипидаре. Верхний конец проволоки прикреплялся к головке прибора 1. Здесь же имелся указатель 2, с помощью которого отсчитывался угол закручивания нити по круговой шкале 3. Шкала была проградуирована. Вся эта система размещалась в стеклянных цилиндрах 4 и 11. В верхней крышке нижнего цилиндра имелось отверстие, в которое вставлялась стеклянная палочка с шариком 7 на конце. В опытах применялись шарики с диаметрами в пределах 0,45 – 0,68 см.

Перед началом эксперимента указатель головки устанавливался на нулевой отметке. Затем шарик 7 заряжался от предварительно наэлектризованного шарика 12. При соприкосновении шарика 7 с подвижным шариком 8 происходило перераспределение заряда. Однако из-за того, что диаметры шариков были одинаковыми, одинаковыми были и заряды на шариках 7 и 8.

Вследствие электростатического отталкивания шариков (рис. 3, б) коромысло 9 поворачивалось на некоторый угол γ (по шкале 10). С помощью головки 1 это коромысло возвращалось в исходное положение. По шкале 3 указатель

2 позволял определять угол α закручивания нити. Общий угол закручивания нити φ = γ + α. Сила же взаимодействия шариков была пропорциональна φ, т. е. по углу закручивания можно судить о величине этой силы.

При неизменном расстоянии между шариками (оно фиксировалось по шкале 10 в градусной мере) исследовалась зависимость силы электрического взаимодействия точечных тел от величины заряда на них.

Для определения зависимости силы от заряда шариков Кулон нашел простой и остроумный способ изменения заряда одного из шариков. Для этого он соединял заряженный шарик (шарики 7 или 8) с таким же по размерам незаряженным (шарик 12 на изолирующей ручке). Заряд при этом распределялся поровну между шариками, что и уменьшало исследуемый заряд в 2, 4 и т. д. раз. Новое значение силы при новом значении заряда опять определялось экспериментально. При этом выяснилось,

что сила прямо пропорциональна произведению зарядов шариков:

\(~F \sim q_1 \cdot q_2\) .

Зависимость силы электрического взаимодействия от расстояния была обнаружена следующим образом. После сообщения шарикам заряда (он был у них одинаковый) коромысло отклонялось на некоторый угол γ. Затем поворотом головки 1 уменьшался этот угол до γ₁. Общий угол закручивания φ₁ = α₁ + (γ

— γ₁)(α₁ – угол поворота головки). При уменьшении углового расстояния шариков до γ₂ общий угол закручивания φ₂ = α₂ + (γ — γ₂) . Было замечено, что, если γ₁ = 2γ₂, ТО φ₂ = 4φ₁, т. е. при уменьшении расстояния в 2 раза сила взаимодействия возрастала в 4 раза. Во столько же раз увеличился момент силы, так как при деформации кручения момент силы прямо пропорционален углу закручивания, а значит, и сила (плечо силы оставалось неизменным). Отсюда вытекает вывод: сила взаимодействия двух заряженных шариков обратно пропорциональна квадрату расстояния между ними:

\(~F \sim \dfrac{1}{r^2}\) .

Литература

1. Мякишев Г.Я. Физика: Электродинамика. 10-11 кл.: учеб. для углубленного изучения физики / Г.Я. Мякишев, А.З. Синяков, Б.А. Слободсков. – М.: Дрофа, 2005. – 476 с.
2. Вольштейн С. Л. и др. Методы физической науки в школе: Пособие для учителя / С.Л. Вольштейн, С.В. Позойский, В.В. Усанов; Под ред. С.Л. Вольштейна. – Мн.: Нар. асвета, 1988. – 144 с.

Закон Кулона

Компьютерная программа является иллюстрацией по теме «Закон Кулона».

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами.

На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел.

Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).

Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.

Коэффициент k в системе СИ обычно записывают в виде:

где ε₀ – электрическая постоянная.

Модель может быть использована в режиме ручного переключения кадров и в режиме автоматической демонстрации (Фильм).

КУЛОНА ЗАКОН — это… Что такое КУЛОНА ЗАКОН?

— один из осн. законов электростатики, определяющий величину и направление силы взаимодействия между двумя неподвижными точечными зарядами. Экспериментально с достаточной точностью впервые доказан около 1773 Г. Кавендишем (Н. Cavendish), использовавшим метод сферич. конденсатора: отсутствие поля внутри заряж. сферы доказывает, что сила эл.-статич. взаимодействия меняется обратно пропорционально квадрату расстояния; однако результаты Кавендиша не были опубликованы. В 1785 закон был установлен Ш. О. Кулоном (Ch. A. Coulomb) с помощью спец. крутильных весов. Согласно К. з., два точечных заряда взаимодействуют друг с другом в вакууме с силой, пропорциональной произведению величин зарядов e₁ и е₂ и обратно пропорциональной квадрату расстояния г между ними: F=ke₁e₂/r², где k — коэф. пропорциональности, зависящий от выбора единиц измерений. В Гаусса системе единиц k=1, в СИ k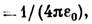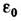— электрическая постоянная. Сила взаимодействия направлена по прямой, соединяющей заряды, причём одноимённые заряды отталкиваются, а разноимённые притягиваются. Силы, определяемые К. з., подчиняются принципу суперпозиции. В однородном диэлектрике сила взаимодействия между точечными зарядами уменьшается в 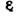раз: где 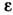— диэлектрич. проницаемость. 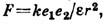К. з. является одним из эксперим. оснований клас-сич. электродинамики. Его обобщение приводит к Гаусса теореме (интегр. форма К. з.) и её дифференц. аналогу — одному из ур-ний Максвелла: 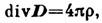где D — вектор электрич. индукции, 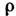— плотность заряда. Для макроскопич. расстояний с помощью экспериментов в земных условиях, проведённых по методу Кавендиша, доказано (1971), что показатель степени для г в К. з. не может отличаться от -2 более чем на 6 *10^-16, Из опытов по рассеянию 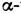частиц следует, что К. з. не нарушается вплоть до расстояний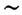

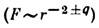
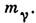10 ^-12 см. Впрочем, для описания взаимодействия заряж. частиц на таких расстояниях понятия, с помощью к-рых формулируется К. з., в частности понятия силы и положения частицы, вообще говоря, неприменимы. В этой области пространственных масштабов действуют законы квантовой физики. К. з. можно считать одним из предельных следствий квантовой электродинамики (КЭД), в рамках к-рой взаимодействие заряж. частиц обусловлено обменом фотонами. Вследствие этого эксперименты по проверке выводов КЭД можно рассматривать как опыты по проверке К. з. Так, опыты по аннигиляции электронов и позитронов показали, что отклонений от законов КЭД не наблюдается вплоть до расстояний ~10^-16 см. С др. стороны, макроскопич. опыты по уточнению К. з. служат для проверки постулатов КЭД: оценка макс. отклонения показателя степени для г в К. з.

от -2 позволяет определить верх. предел возможной массы покоя фотона В частности, поправка 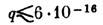соответствует кг.

К. з. наз. также закон, определяющий 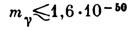силу взаимодействия двух магн. полюсов: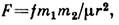

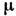где m₁ и m₂ — т. н. магн. заряды, — магн. проницаемость среды, f — коэф. пропорциональности, зависящий от выбора системы единиц и в общем случае не равный k. Установлен Ш. О. Кулоном практически одновременно с законом взаимодействия электрич. зарядов. Этот закон, однако, не имеет столь общего характера, как закон для электрич. сил, вследствие искусственности представления о точечных магн. полюсах.

Лит.: Тамм И. Е., Основы теории электричества, 9 изд., М., 1976, гл. 1; Ландау Л. Д., Лифшиц Е. М., Теория поля, 7 изд., М., 1988, гл. 5; Сивухин Д. В., Общий курс физики, 2 изд., т. 3 — Электричество, М., 1983.

С. Р. Филонович,

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.

Обсуждение:Закон Кулона — Википедия

Материал из Википедии — свободной энциклопедии

Примечательно что закон Кулона Кулон переоткрыл сам того не зная. В 1771 к аналогичному выводу пришел Кавендиш Генри (10.10.1731—24.2.1810). Но Кавендиш не счёл целесообразным это публиковать. И вообще был очень замкнутым человеком.

Сейчас смог найти под рукой только
Храмов Ю. А. Физики: Биографический справочник. — 2-е изд., испр. и дополн. — М.: Наука, Главная редакция физико-математической литературы, 1983.

может Кавендиш тоже переоткрыл :)—Berserkerus 22:50, 18 мая 2007 (UTC)

а вообще-то англичане славились научно-технологическим шпионажем. не удивлюсь что Кавендиш на самом деле был после и просто проверял инфу —Berserkerus 22:52, 18 мая 2007 (UTC)

Вывод закона Кулона в квантовой теории поля. ВП:ОРИС?[править код]

Хотелось бы увидеть ВП:АИ для этого раздела. К квантовой теории поля подобный «квазиквантовый оценочный подход» отношения не имеет. Фразы типа: «Решение данной задачи невозможно без изучения статистической физики и квантовой теории поля. Поэтому просто приведем готовые результаты и выведем закон силы…» делают сомнительным ценность подобного «вывода». Излучение абсолютно чёрного тела к вакууму взаимодействия электронов с виртуальными фотонами имеет крайне отдалённое отношение (достаточно спросить — какова его температура?). Гремучая смесь из классической силы, соотношения неопределённости и фактов теории излучения делает всё это крайне подозрительным. —Source 18:02, 4 мая 2010 (UTC)

Источник, в котором обсуждается квантовый вывод закона Кулона[править код]

См. книгу: Д. Фриш, А. Торндайк, «Элементарные частицы», М., 1966, Атомиздат, пер. с англ. В.В. Емельяновой, под ред. И.И. Тугова, УДК 539.12 (023). Квантовый вывод закона Кулона обсуждается на стр. 98-102 в гл. 8 «Изучение сил между элементарными частицами», параграф «Квантовая теория сил, пропорциональных 1r2{\displaystyle {\frac {1}{r^{2}}}}. Если хотите, могу отсканировать эти страницы и переслать Вам по e-mail.

Если не затруднит. Я с интересом посмотрю. В свободном доступе этой книги я не нашёл. E-mail на моей странице. К слову, иногда заходите и на свою страниц обсуждения (или нажимайте список наблюдения). Удаление произошло после отсутствия Вашего ответа там, и обсуждения этой проблемы с другим участником. —Source 17:05, 5 мая 2010 (UTC)

Ну, и у меня небольшие претензии оформительского характера. Прошу ссылки на литературу оформить как принято в Вики и стиль статьи на более энциклопедический поправить. Сейчас он скорее журнальный. —Dodonov 17:32, 5 мая 2010 (UTC)

Курица или яйцо?[править код]

Касательно всего «вывода», дождусь обещанной Вами книги. Однако, уже вторая фраза: «Строго обоснованные расчеты осуществляются путем построения диаграмм Фейнмана [2] и здесь для простоты опущены.» ставит в тупик. Вы действительно считаете, что для обоснования («вывода») закона Кулона подходит квантовая электродинамика? На самом деле, ситуация в точности обратная. Классический закон Кулона (экспериментальный факт) + СТО = Уравнения Максвелла. Уравнения Максвелла + Квантовая механика = Квантовая электродинамика (КЭД). Это конечно упрощённая схема, но другой нет! Обратное движение от (КЭД) к закону Кулона вполне уместно, но уже как поправки к его классической версии (бегущая константа связи, свойства вакуума и т.п.). Вот это, действительно, стоит отразить в статье.

Вообще, «вывод» закона Кулона тема достаточно скользкая. Есть экспериментальный факт. Это, как говаривал Фандорин — раз. Существуют рассуждения связанные с размерностью пространства (площадь сферы = r^2). Однако, они фактически подменяют закон Кулона эквивалентным законом Гаусса в интегральной форме, поэтому выводом не являются. Это — два. Существуют различные соображения выделенности силы 1/r^2 среди других функций (замкнутость траекторий, дополнительный закон сохранения и т.п.). Но они не являются выводом, а относятся к оборотам «интересно заметить». Наконец существуют различные модельные выводы (типа Теория гравитации Лесажа), но они не выдерживают критики. Недавно видел статьи посвящённые выводу из энтропийных соображений. Но выглядят они тоже не очень убедительно. Поэтому, при всём моём личном желании получить закон Кулона из первых принципов, приходится пока признавать правоту Ньютона, касательно не измышления гипотез.—Source 18:10, 5 мая 2010 (UTC)

Добавил про отклонения от закона Кулона вследствие нелинейных эффектов КЭД, буду благодарен за уточнения Raoul NK 11:55, 6 мая 2010 (UTC)

Очень хорошо написано. Я там формулу, как мне кажется, в более понятном виде привёл и ссылок немного поставил. —Source 12:34, 6 мая 2010 (UTC)

Спасибо за уточнение, сейчас ещё поищу ссылки на потенциал в сильных внешних полях, может, у Вас что-нибудь есть? Raoul NK 14:14, 6 мая 2010 (UTC)

Классическая монография: Гриб А.А., Мамаев С.Г., Мостепаненко В.М. «Вакуумные квантовые эффекты в сильных полях» (есть на homelinux). Но она не числится в списке моих любимых книг 🙂 —Source 14:25, 6 мая 2010 (UTC).

Кулоновского потенциала я там, к сожалению, не нашёл. Нагуглил ссылку на расчёт потенциала во внешнем магнитном поле, а вот во внешнем электрическом — упс 🙁 Raoul NK 15:15, 6 мая 2010 (UTC)

Да, в книге Фриша и Торндайка «Элементарные частицы» закон Кулона в этом месте не упоминается и не обсуждается. Авторы обсуждают не закон Кулона, а точку зрения на закон обратных квадратов для электрических сил с позиций квантовой электродинамики. Извините. Я исправил свою ошибку.

Здраствуйте. После первой формулы: «В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:» идёт пояснение переменных и постоянных используемых в этой формуле. Так, вот цитирую: «(Вектор r12)- радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами -r12)». Возможно правильней будет «расстоянию между зарядами — q1 и q2» ? —spiker01 17:07, 29 мая 2011 (UTC)