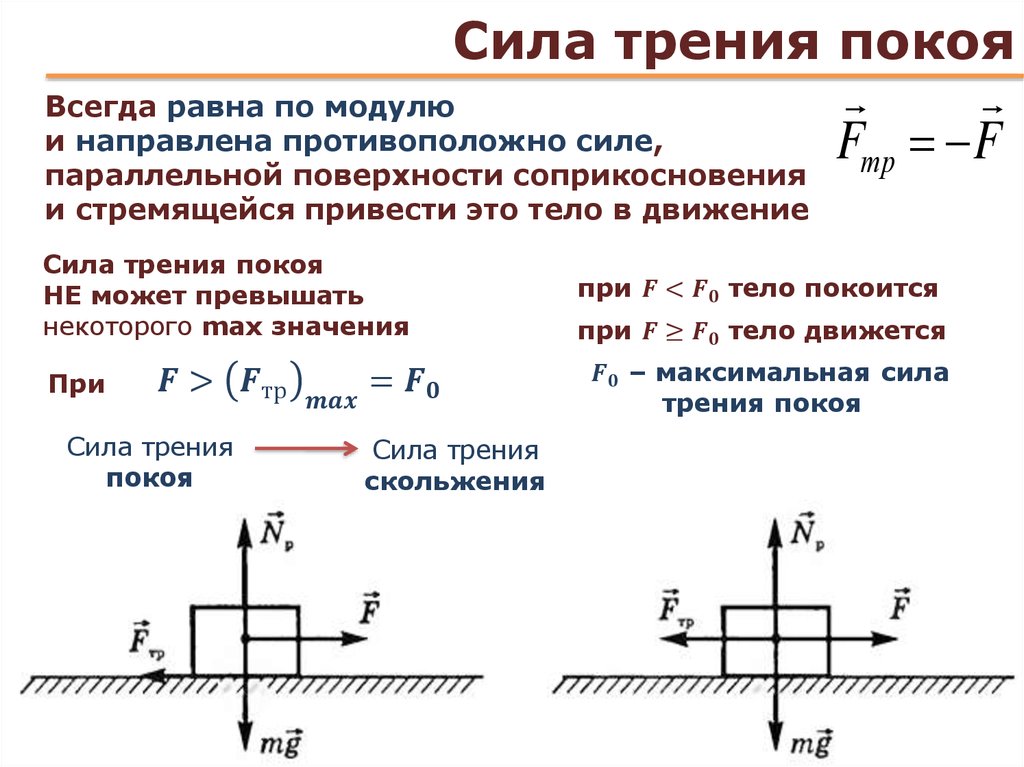
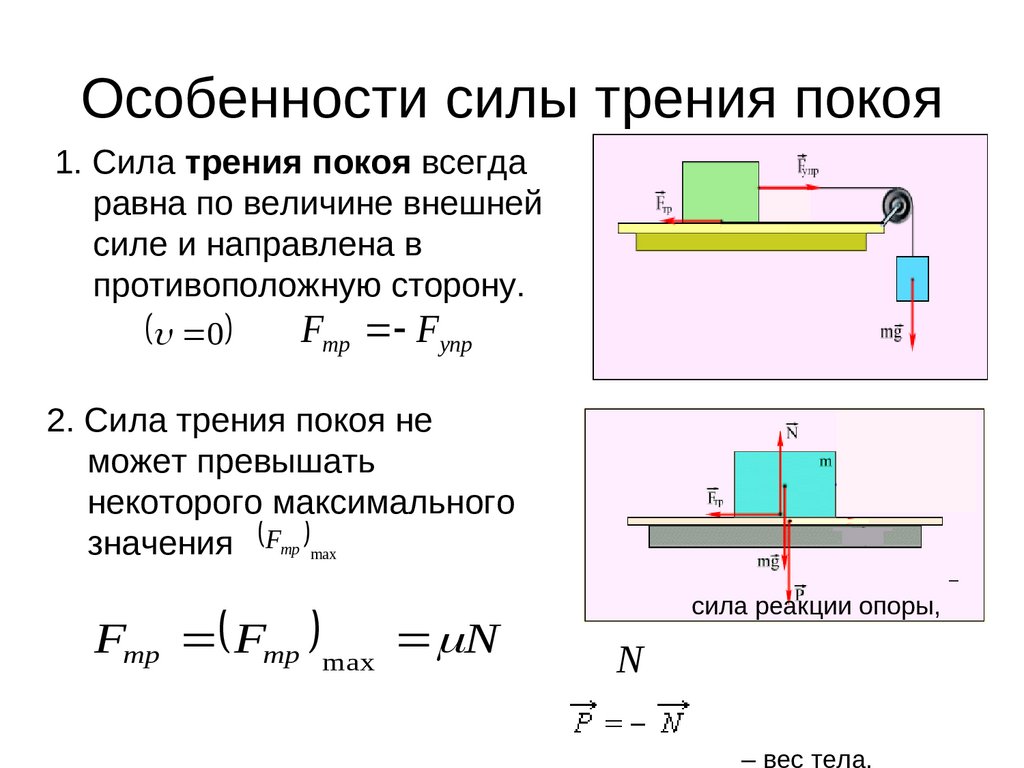
практическая работа сила трения | Методическая разработка по физике (9 класс) на тему:
Практическая работа «Измерение коэффициента трения скольжения»
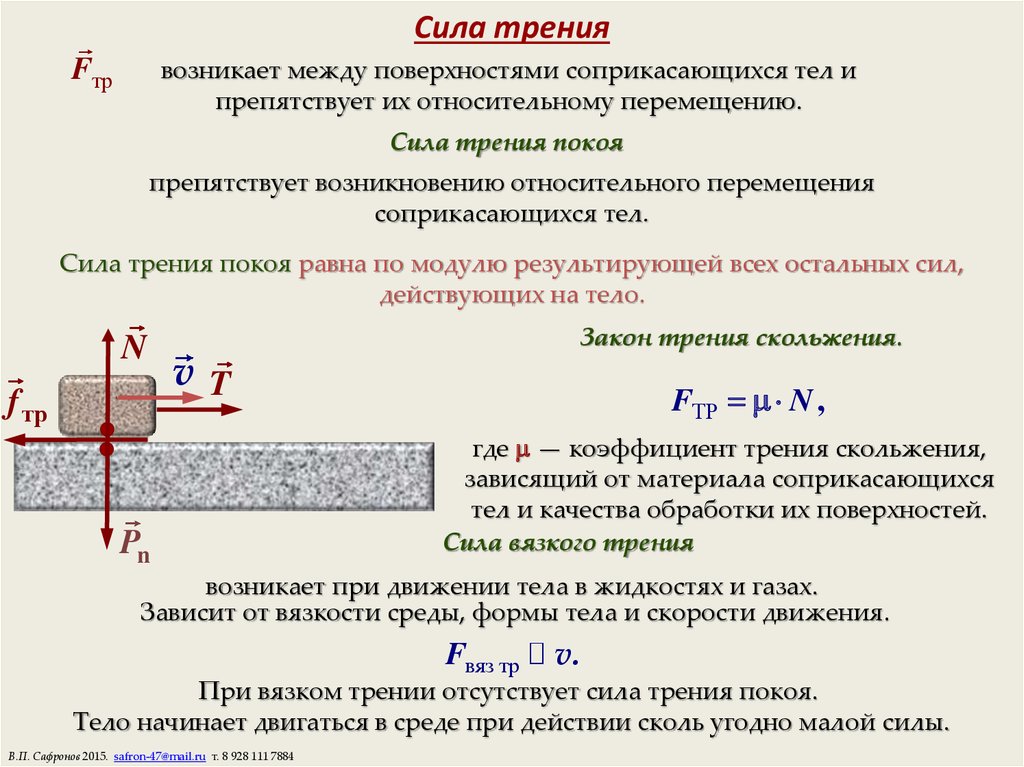
Цель работы: определить коэффициент трения деревянного бруска, скользящего по деревянной линейке, используя формулу Fтр = = μN.
Приборы и материалы: динамометр, деревянный брусок; деревянная линейка; набор грузов.
С помощью динамометра измеряют силу, с которой нужно тянуть брусок с грузами по горизонтальной поверхности так, чтобы он двигался равномерно. Эта сила равна по модулю силе трения Fтp, действующей на брусок. С помощью того же динамометра можно найти вес бруска с грузом. Этот вес по модулю равен силе нормального давления N бруска на поверхность, по которой он скользит. Определив, таким образом, значения силы трения при различных значениях силы нормального давления, необходимо построить график зависимости Fтр от N и найти среднее значение коэффициента трения.
Порядок выполнения работы
1. Положите брусок на горизонтально расположенную деревянную линейку. На брусок поставьте груз.
На брусок поставьте груз.
2. Прикрепив к бруску динамометр, как можно более равномерно тяните его вдоль линейки. Замерьте при этом показание динамометра.
3. Взвесьте брусок и груз.
4. К первому грузу добавьте второй, третий грузы, каждый раз взвешивая брусок и грузы и измеряя силу трения.
По результатам измерений заполните таблицу:
Измеряемая величина | Брусок с одним грузом | Брусок с двумя грузами | Брусок с тремя грузами |
Вес бруска с грузами, Н | |||
Сила трения при скольжении на широкой грани, Н | |||
Коэффициент трения | |||
Сила трения при скольжении на узкой грани, Н | |||
Коэффициент трения |
5.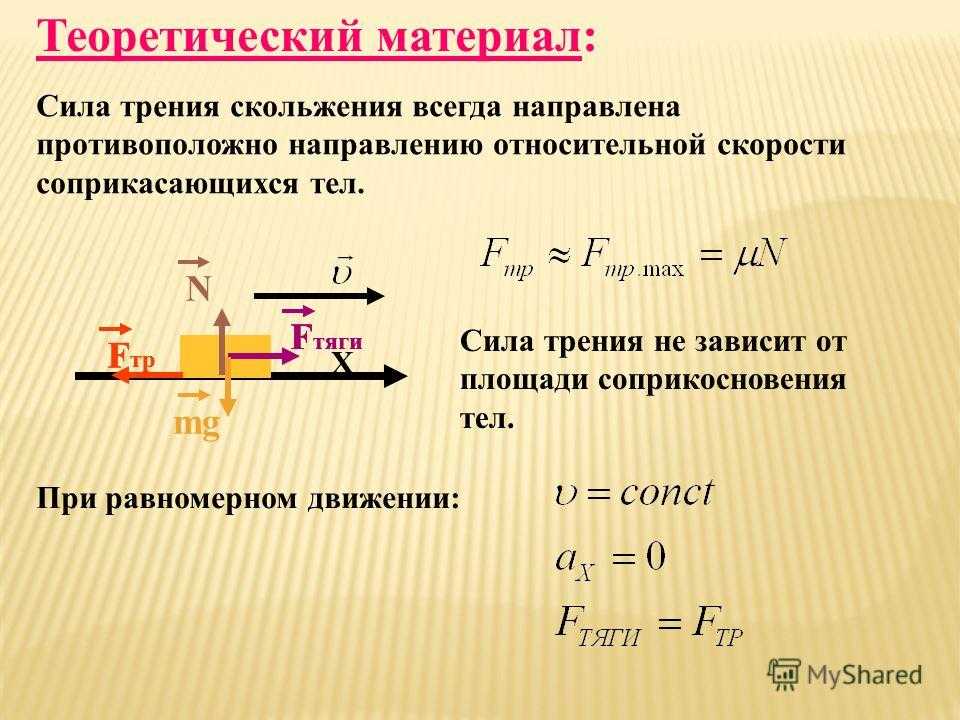 По результатам измерений постройте график зависимости силы трения от силы давления.
По результатам измерений постройте график зависимости силы трения от силы давления.
6. Повторите измерения, перечисленные в п. 4 положив брусок на узкую грань. Результаты измерений занесите в таблицу.
7. По новым данным постройте график зависимости модуля силы трения от модуля силы нормального давления.
Ответьте на вопрос:
1. Зависит ли коэффициент трения скольжения от площади опоры тела?
Практическая работа «Измерение коэффициента трения скольжения»
Цель работы: определить коэффициент трения деревянного бруска, скользящего по деревянной линейке, используя формулу Fтр = = μN.
Приборы и материалы: динамометр, деревянный брусок; деревянная линейка; набор грузов.
С помощью динамометра измеряют силу, с которой нужно тянуть брусок с грузами по горизонтальной поверхности так, чтобы он двигался равномерно. Эта сила равна по модулю силе трения Fтp, действующей на брусок. С помощью того же динамометра можно найти вес бруска с грузом. Этот вес по модулю равен силе нормального давления N бруска на поверхность, по которой он скользит.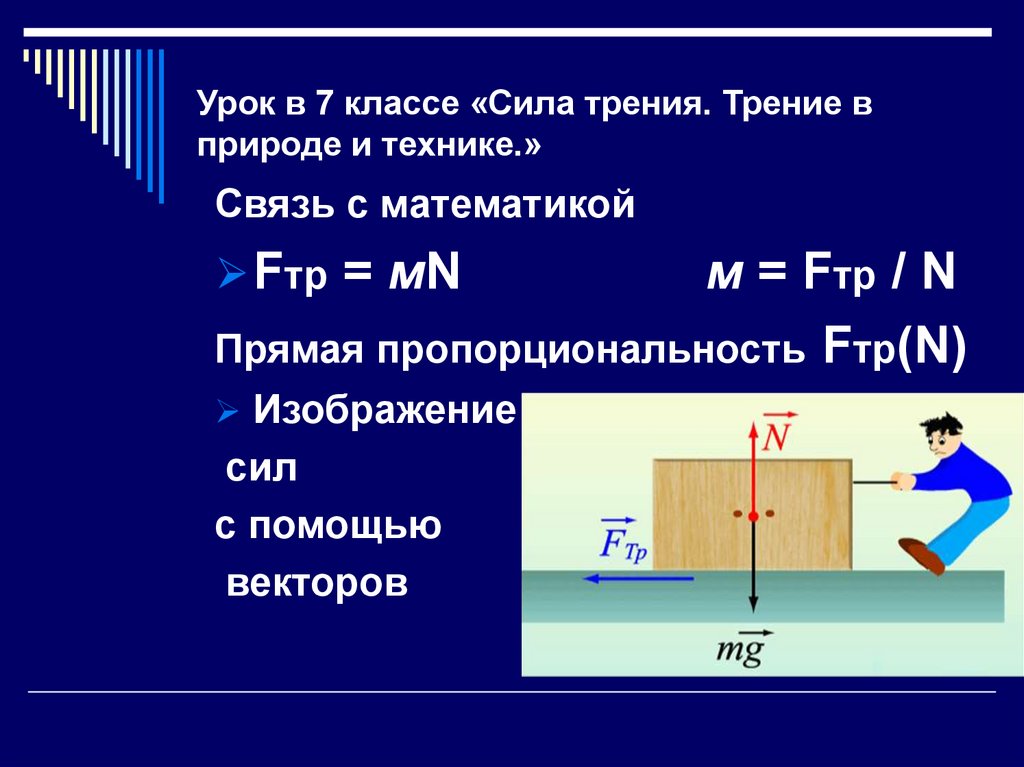 Определив, таким образом, значения силы трения при различных значениях силы нормального давления, необходимо построить график зависимости Fтр от N и найти среднее значение коэффициента трения.
Определив, таким образом, значения силы трения при различных значениях силы нормального давления, необходимо построить график зависимости Fтр от N и найти среднее значение коэффициента трения.
Основным измерительным прибором в этой работе является динамометр. Динамометр имеет погрешность Δд =0,05 Н. Она и равна погрешности измерения, если указатель совпадает со штрихом шкалы. Если же указатель в процессе измерения не совпадает со штрихом шкалы (или колеблется), то погрешность измерения силы равна ΔF = 0,1 Н.
Порядок выполнения работы
1. Положите брусок на горизонтально расположенную деревянную линейку. На брусок поставьте груз.
2. Прикрепив к бруску динамометр, как можно более равномерно тяните его вдоль линейки. Замерьте при этом показание динамометра.
3. Взвесьте брусок и груз.
4. К первому грузу добавьте второй, третий грузы, каждый раз взвешивая брусок и грузы и измеряя силу трения.
По результатам измерений заполните таблицу:
Измеряемая величина | Брусок с одним грузом | Брусок с двумя грузами | Брусок с тремя грузами |
Вес бруска с грузами, Н | |||
Сила трения при скольжении на широкой грани, Н | |||
Коэффициент трения | |||
Сила трения при скольжении на узкой грани, Н | |||
Коэффициент трения |
5. По результатам измерений постройте график зависимости силы трения от силы давления.
По результатам измерений постройте график зависимости силы трения от силы давления.
6. Повторите измерения, перечисленные в п. 4 положив брусок на узкую грань. Результаты измерений занесите в таблицу.
7. По новым данным постройте график зависимости модуля силы трения от модуля силы нормального давления.
Ответьте на вопрос:
1. Зависит ли коэффициент трения скольжения от площади опоры тела?
Как трение связано с обычной силой
: Стивен Хольцнер и
Обновлено: 03-26-2016
Из книги: Физика I для Dummies
Physics I для Dummies
Exploore Book Buy Book Book Book Book Book Book Book Book На Amazon
Согласно законам физики, сила трения F трение , всегда противодействует силе, которую вы прикладываете, когда пытаетесь сдвинуть объект.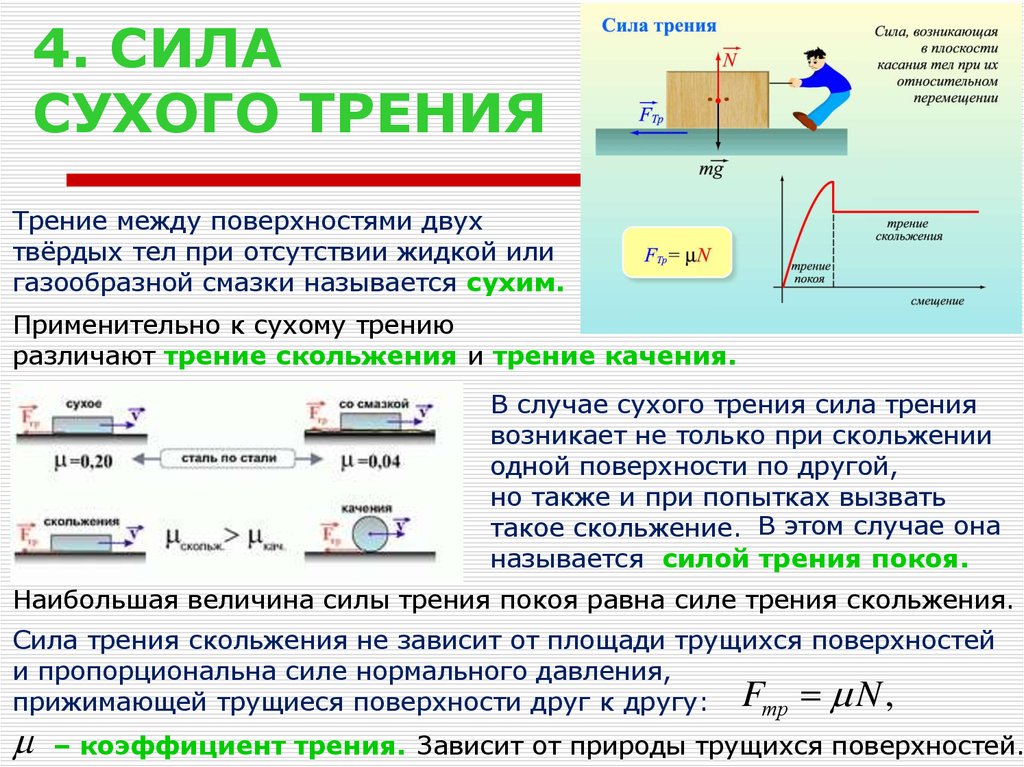 Трение пропорционально силе, с которой объект давит на поверхность, по которой вы пытаетесь его скользить.
Трение пропорционально силе, с которой объект давит на поверхность, по которой вы пытаетесь его скользить.
Силы, действующие на слиток золота.
Как видно из рисунка, сила, с которой золотой слиток давит на землю в этой ситуации, равна как раз его весу, или мг. Земля давит с той же силой в соответствии с третьим законом Ньютона.
Третий закон Ньютона известен, особенно в кругах борцов и водителей, но вы можете не узнать его во всей его физической красе: «Всякий раз, когда одно тело действует на другое тело с силой, второе тело оказывает противоположно направленную силу. одинаковой величины на первом теле». Более популярная версия: «На каждое действие есть равное и противоположное противодействие». Но для физики лучше изначально задуманный вариант выразить в терминах сил, а не действий.
Сила, действующая на слиток перпендикулярно поверхности, называется нормальной силой, и ее символом является Н. Нормальная сила не обязательно равна силе гравитации; это сила, перпендикулярная поверхности, по которой скользит объект.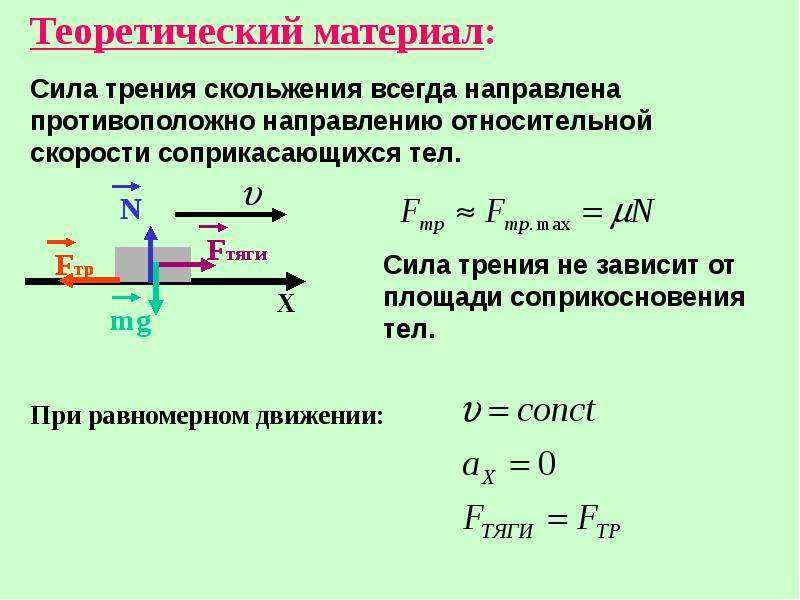 Другими словами, нормальная сила — это сила, прижимающая две поверхности друг к другу, и чем сильнее нормальная сила, тем сильнее сила трения.
Другими словами, нормальная сила — это сила, прижимающая две поверхности друг к другу, и чем сильнее нормальная сила, тем сильнее сила трения.
В случае с фигурой, поскольку слиток скользит по горизонтальной поверхности и притягивается силой, параллельной земле, нормальная сила имеет ту же величину, что и вес слитка, поэтому F нормальный = мг. У вас есть нормальная сила, которая представляет собой силу, прижимающую слиток к земле.
Эта статья из книги:
- Физика I Для чайников,
Об авторе книги:
Доктор Стивен Хольцнер написал более 40 книг по физике и программированию. Он был редактором журнала
 Доктор Хольцнер получил докторскую степень в Корнелле.
Доктор Хольцнер получил докторскую степень в Корнелле.Эту статью можно найти в категории:
- Физика,
5.4 Наклонные плоскости | Техасский шлюз
Цели обученияСтатическое и кинетическое трениеРабота с наклонными плоскостямиПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Различие между статическим трением и кинетическим трением
- Решение задач с наклонными плоскостями
| кинетическое трение | статическое трение |
Статическое трение и кинетическое трение
Вспомним из предыдущей главы, что трение — это сила, противодействующая движению и постоянно присутствующая вокруг нас.
Существуют различные виды трения — кинетическое и статическое. Кинетическое трение действует на движущийся объект, а статическое трение действует на объект или систему в состоянии покоя. Максимальное статическое трение обычно больше, чем кинетическое трение между объектами.
Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу. Вы можете давить на ящик все сильнее и сильнее и вообще не двигать его. Это означает, что статическое трение реагирует на то, что вы делаете — оно увеличивается, чтобы быть равным вашему толчку и в противоположном направлении. Но если вы, наконец, нажмете достаточно сильно, ящик, кажется, внезапно соскользнет и начнет двигаться. Начав движение, его легче поддерживать в движении, чем было запустить, потому что кинетическая сила трения меньше, чем статическая сила трения. Если бы вы добавили массу к ящику (например, поместив на него коробку), вам пришлось бы толкать его еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться.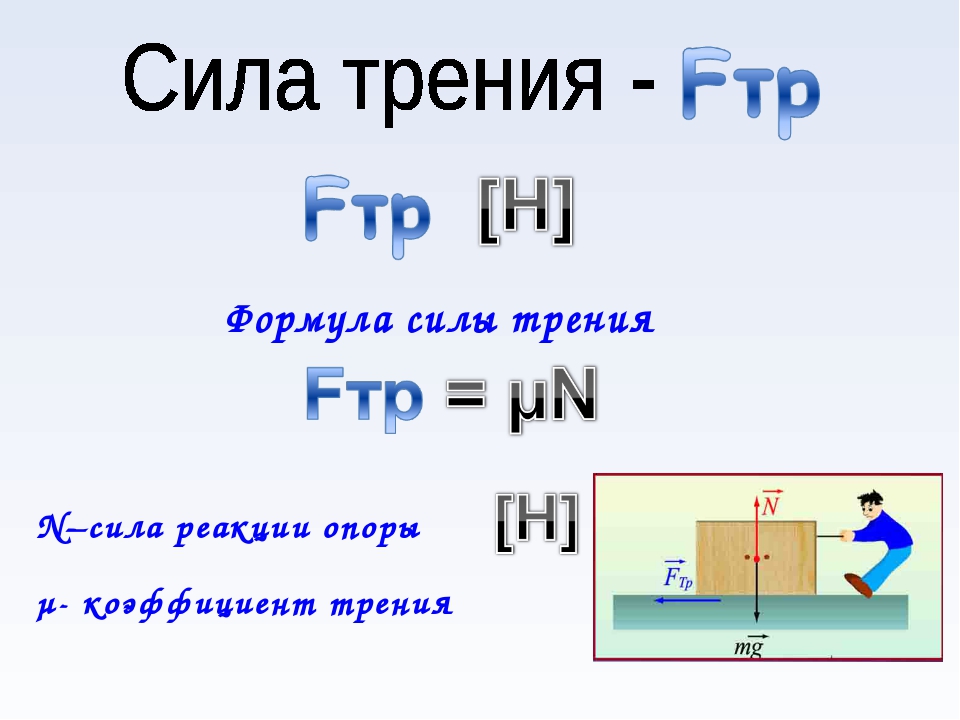
На рис. 5.35 показано, как возникает трение на границе раздела двух объектов. Увеличение этих поверхностей показывает, что они являются шероховатыми на микроскопическом уровне. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударами только кончиками поверхности, отламывать точки или делать и то, и другое. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения.
Рисунок 5.35 Силы трения, такие как
Величина силы трения имеет две формы: одна для статического трения, другая для кинетического трения. Когда между объектами нет движения, величина трения покоя f s равна
Когда между объектами нет движения, величина трения покоя f s равна
fs≤μsNs,fs≤μsNs,
, где μs μs — коэффициент трения покоя, а Н — величина нормальной силы. Напомним, что нормальная сила противодействует силе тяжести и действует перпендикулярно поверхности в этом примере, но не всегда.
Поскольку символ ≤ ≤ означает меньше или равно, это уравнение говорит о том, что трение покоя может иметь максимальное значение мксН. мксН. То есть
fs(max)=µsN.fs(max)=µsN.
Статическое трение представляет собой реактивную силу, которая увеличивается, чтобы быть равной и противоположной любой прилагаемой силе, вплоть до ее максимального предела. Когда приложенная сила превышает f с(макс.), объект будет двигаться. Когда объект движется, величина кинетического трения f k определяется выражением
fk=µkN.fk=µkN.
где μkμk — коэффициент кинетического трения.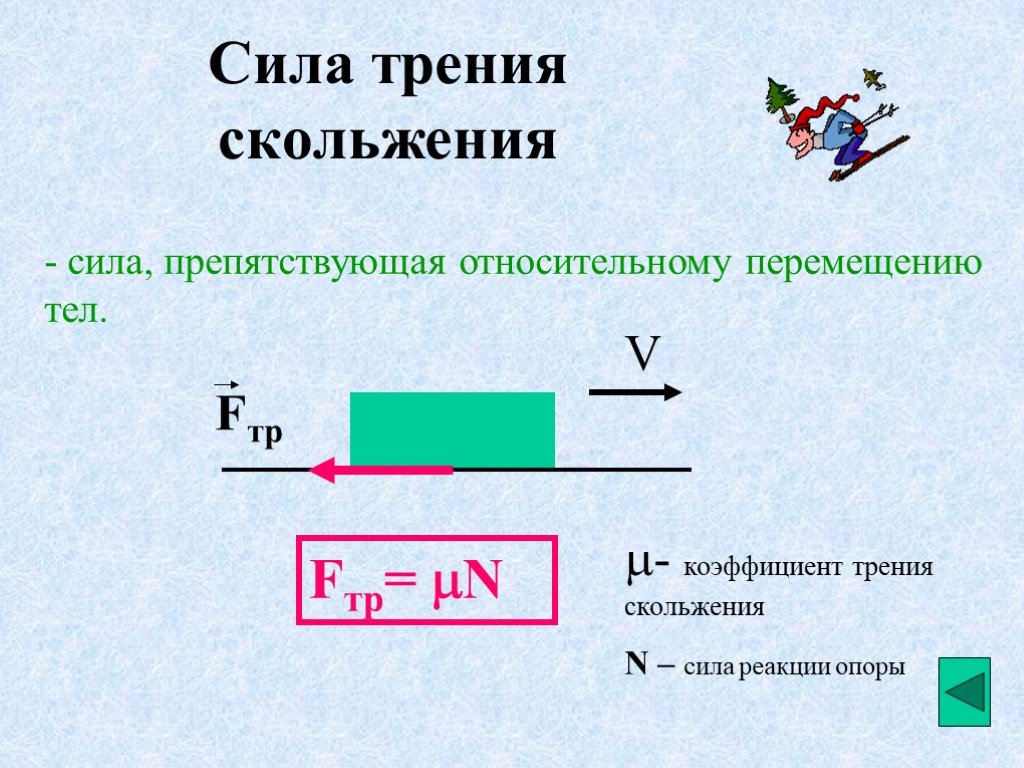
Трение варьируется от поверхности к поверхности, потому что разные вещества более шероховатые, чем другие. В таблице 5.2 сравниваются значения статического и кинетического трения для различных поверхностей. Коэффициент трения зависит от двух соприкасающихся поверхностей.
| Система | Статическое трение мкс мкс | Кинетическое трение мкк мкк |
| Резина на сухом бетоне | 0,7 | |
| Резина на мокром бетоне | 0,7 | 0,5 |
| Дерево на дереве | 0,5 | 0,3 |
| Вощеная древесина на мокром снегу | 0,14 | 0,1 |
| Металл на дереве | 0,5 | 0,3 |
| Сталь по стали (сухая) | 0,6 | 0,3 |
| Сталь по стали (промасленный) | 0,03 | |
| Тефлон на стали | 0,04 | 0,04 |
| Кость, смазанная синовиальной жидкостью | 0,016 | 0,015 |
| Туфли на дереве | 0,9 | 0,7 |
| Обувь на льду | 0,1 | 0,05 |
| Лед на льду | 0,1 | 0,03 |
| Сталь на льду | 0,4 | 0,02 |
Таблица 5. 2 Коэффициенты статического и кинетического трения
2 Коэффициенты статического и кинетического трения
Поскольку направление трения всегда противоположно направлению движения, трение происходит параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с усилием, параллельным полу), имеет массу 100 кг, то нормальная сила будет равна его весу
Вт=мг=(100 кг)(9,80 м/с2)=980 Н, Вт=мг=(100 кг)(9,80 м/с2)=980 Н,
перпендикулярно полу. Если бы коэффициент статического трения был равен 0,45, вам пришлось бы приложить параллельную полу силу, превышающую
.фс(макс)=мксN=(0,45)(980 Н)=440 Нфс(макс)=мксN=(0,45)(980 Н)=440 Н
для перемещения ящика. Когда есть движение, трение меньше, а коэффициент кинетического трения может быть равен 0,30, так что сила всего 290 Н
fk=µkN=(0,30)(980 N)=290 Nfk=µkN=(0,30)(980 N)=290 N
будет поддерживать его движение с постоянной скоростью. Если бы пол был смазан, оба коэффициента были бы намного меньше, чем без смазки. Коэффициент трения не имеет единиц измерения и обычно представляет собой число от 0 до 1,0.
Коэффициент трения не имеет единиц измерения и обычно представляет собой число от 0 до 1,0.
Работа с наклонными плоскостями
Ранее мы обсуждали, что когда объект лежит на горизонтальной поверхности, на него действует нормальная сила, равная по величине его весу. До сих пор мы имели дело только с нормальной силой в одном измерении, с гравитацией и нормальной силой, действующими перпендикулярно поверхности в противоположных направлениях (гравитация направлена вниз, а нормальная сила направлена вверх). Теперь, когда у вас есть навыки работы с силами в двух измерениях, мы можем исследовать, что происходит с весом и нормальной силой на наклонной поверхности, такой как наклонная плоскость. Для задач с наклонной плоскостью легче разбить силы на составляющие, если мы повернем систему координат, как показано на рис. 5.36. Первым шагом при постановке задачи является разложение силы веса на составляющие.
Рис. 5.36 На диаграмме показаны перпендикулярная и горизонтальная составляющие веса на наклонной плоскости.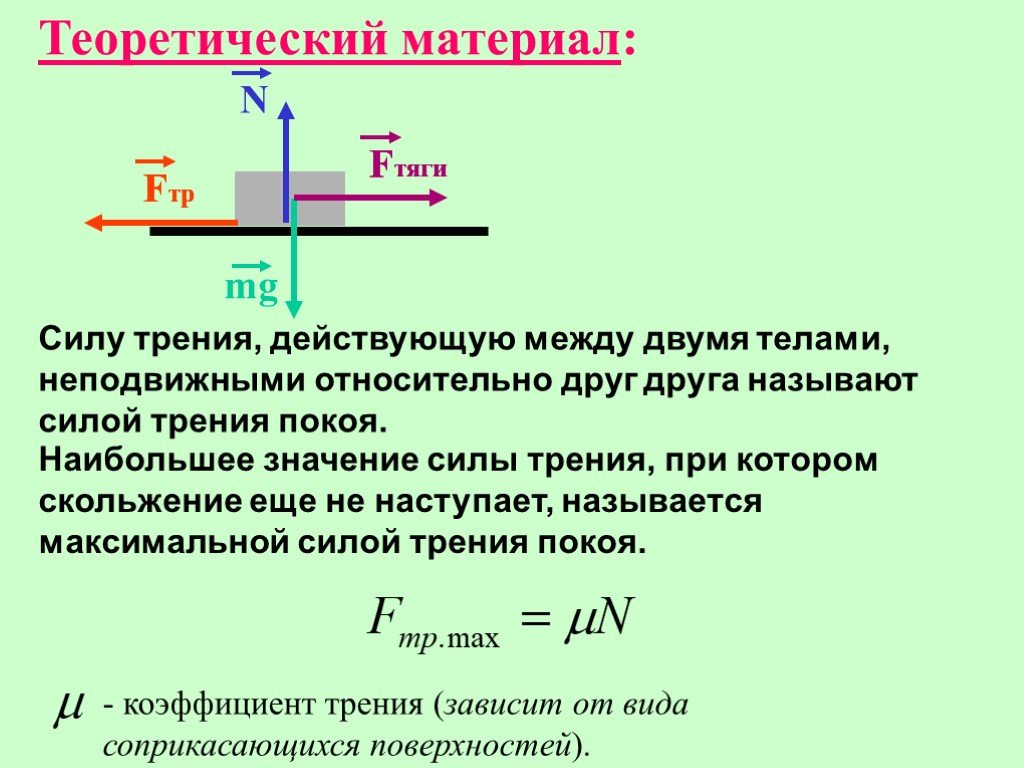
Когда объект покоится на наклонной плоскости, составляющей угол θ θ с горизонталью, сила тяжести, действующая на объект, делится на две составляющие: сила, действующая перпендикулярно плоскости, w⊥ w⊥, и сила, действующая параллельно на плоскость, w|| ш||. Перпендикулярная сила веса, w⊥ w⊥, обычно равна по величине и противоположна по направлению нормальной силе, N. N. Сила, действующая параллельно плоскости, w|| w||, заставляет объект ускоряться вниз по склону. Сила трения f f противодействует движению объекта, поэтому она действует вверх по плоскости.
Важно соблюдать осторожность при разложении веса объекта на составляющие. Если угол наклона находится под углом θ θ к горизонтали, то величины компонентов веса равны
w||=wsin(θ)=mgsin(θ) и w||=wsin(θ)=mgsin(θ) и
w⊥=wcos(θ)=mgcos(θ).w⊥=wcos(θ) = мгкос(θ).
Вместо того, чтобы запоминать эти уравнения, полезно уметь определять их разумом. Для этого нарисуйте прямоугольный треугольник, образованный тремя весовыми векторами. Обратите внимание, что угол наклона такой же, как угол, образованный между w w и w⊥ w⊥. Зная это свойство, можно с помощью тригонометрии определить величину весовых составляющих
Обратите внимание, что угол наклона такой же, как угол, образованный между w w и w⊥ w⊥. Зная это свойство, можно с помощью тригонометрии определить величину весовых составляющих
cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)
sin(θ)=w||ww ||=wsin(θ)=mgsin(θ).sin(θ)=w||ww||=wsin(θ)=mgsin(θ).
Watch Physics
Компоненты силы наклонной плоскости
В этом видео показано, как вес объекта на наклонной плоскости разбивается на составляющие, перпендикулярные и параллельные поверхности плоскости. Он объясняет геометрию для нахождения угла более подробно.
Нажмите, чтобы просмотреть содержание
Проверка захвата
В этом видеоролике показано, как вес объекта на наклонной плоскости разбивается на составляющие, перпендикулярные и параллельные поверхности плоскости. Он объясняет геометрию для нахождения угла более подробно.
Когда поверхность плоская, можно сказать, что одна из составляющих гравитационной силы равна нулю; Который из? Что происходит с величинами перпендикулярной и параллельной составляющих гравитационной силы по мере увеличения угла наклона?
- Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая уменьшается, а перпендикулярная составляющая увеличивается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.
- Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая уменьшается, а перпендикулярная составляющая увеличивается. Это связано с тем, что косинус угла увеличивается, а синус угла уменьшается.
- Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна.
 По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.
По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается. - Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла увеличивается, а синус угла уменьшается.
Советы по достижению успеха
Нормальная сила представлена переменной Н. Н. Не следует путать с символом ньютона, который также обозначается буквой Н. Важно различать эти символы, тем более что единицами нормальной силы (NN) являются ньютоны (N). Например, нормальная сила, Н Н, с которой пол действует на стул, может быть Н=100 Н. Н=100 Н. Одно важное отличие состоит в том, что нормальная сила — это вектор, а ньютон — это просто единица.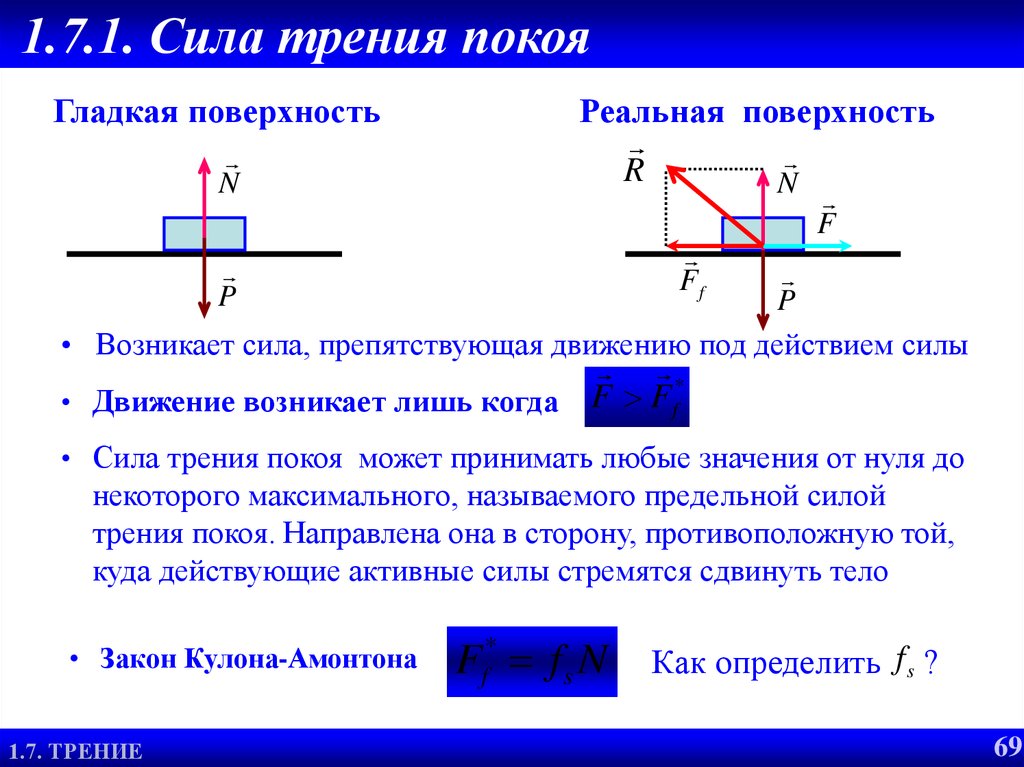 Будьте осторожны, чтобы не перепутать эти буквы в своих вычислениях!
Будьте осторожны, чтобы не перепутать эти буквы в своих вычислениях!
Для обзора, процесс решения задач наклонной плоскости выглядит следующим образом:
- Нарисуйте схему задачи.
- Определите известные и неизвестные количества и определите интересующую систему.
- Нарисуйте диаграмму свободного тела (это эскиз, показывающий все силы, действующие на объект) с системой координат, повернутой под тем же углом, что и наклонная плоскость. Разделите векторы на горизонтальную и вертикальную составляющие и нарисуйте их на диаграмме свободного тела.
- Запишите второй закон Ньютона в горизонтальном и вертикальном направлениях и сложите силы, действующие на объект. Если объект не ускоряется в определенном направлении (например, в направлении x ), то F net x = 0. Если объект ускоряется в этом направлении, F net x = м а .

- Проверьте свой ответ. Разумный ли ответ? Единицы правильные?
Рабочий пример
Определение коэффициента кинетического трения на наклонной плоскости
Лыжник массой 62 кг, изображенный на рис. 5.37(а), скользит по заснеженному склону под углом 25 градусов. Найдите коэффициент кинетического трения лыжника, если известно, что трение равно 45,0 Н.
Рис. 5.37 Используйте диаграмму, чтобы найти коэффициент кинетического трения для лыжника.
Стратегия
Величина кинетического трения равна 45,0 Н. Кинетическое трение связано с нормальной силой N как fk=µkN fk=µkN. Следовательно, мы можем найти коэффициент кинетического трения, сначала найдя нормальную силу лыжника на склоне. Нормальная сила всегда перпендикулярна поверхности, а поскольку движение перпендикулярно поверхности отсутствует, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону.
То есть
N=w⊥=w cos(25∘)=mg cos(25∘).N=w⊥=w cos(25∘)=mg cos(25∘).
Подставляя это в выражение для кинетического трения, получаем
fk=µkmg cos 25∘,fk=µkmg cos 25∘,
, которое теперь можно решить для коэффициента кинетического трения µ k .
Решение
Решение для µk µk дает
µk=fkw cos 25∘=fkmg cos 25∘.µk=fkw cos 25∘=fkmg cos 25∘.
Подставив известные значения в правую часть уравнения,
мкк=45,0 Н(62 кг)(9,80 м/с2)(0,906)=0,082,мкк=45,0 Н(62 кг)(9,80 м/с2 )(0,906)=0,082.
Обсуждение
Этот результат немного меньше, чем коэффициент, указанный в таблице 5.1 для вощеной древесины на снегу, но все же разумен, так как значения коэффициентов трения могут сильно различаться. В подобных ситуациях, когда объект массой м скользит по склону, образующему угол θ с горизонтом, трение определяется формулой fk=μkmg cosθ. fk=мкмг cosθ.
fk=мкмг cosθ.
Рабочий пример
Вес на склоне, двумерная задача
Масса лыжника, включая снаряжение, составляет 60,0 кг. (См. рис. 5.38(b).) (a) Каково ее ускорение, если трением можно пренебречь? б) Чему равно ее ускорение, если сила трения равна 45,0 Н?
Рисунок 5.38 Теперь используйте диаграмму, чтобы найти ускорение лыжника, если трением можно пренебречь и если сила трения равна 45,0 Н.
Стратегия
Наиболее удобной системой координат для движения по склону является та, в которой одна координата параллельна склону, а другая перпендикулярна склону. Помните, что движения вдоль перпендикулярных осей независимы. Мы используем символ ⊥ ⊥ для обозначения перпендикуляра и || || значит параллельно.
Единственными внешними силами, действующими на систему, являются вес лыжника, трение и нормальная сила, действующая на лыжный склон, обозначенные w w, f f и N N на диаграмме свободного тела. N N всегда перпендикулярно склону, а f f параллельно ему. Но w w не направлен ни по одной из осей, поэтому мы должны разбить его на составляющие вдоль выбранных осей. Определим w|| ш|| быть компонентом веса, параллельным наклону, и w⊥ w⊥ компонентом веса, перпендикулярным наклону. Как только это будет сделано, мы можем рассмотреть две отдельные проблемы сил, параллельных склону, и сил, перпендикулярных склону.
Но w w не направлен ни по одной из осей, поэтому мы должны разбить его на составляющие вдоль выбранных осей. Определим w|| ш|| быть компонентом веса, параллельным наклону, и w⊥ w⊥ компонентом веса, перпендикулярным наклону. Как только это будет сделано, мы можем рассмотреть две отдельные проблемы сил, параллельных склону, и сил, перпендикулярных склону.
Решение
Величина составляющей веса, параллельной наклону, равна w||=wsin(25°)=mg sin(25°) w||=wsin(25°)=mg sin(25°) , а величина составляющей веса, перпендикулярной наклону, равна w⊥=wcos(25°)=mg cos(25°). w⊥=wcos(25°)=mg cos(25°).
(a) Пренебрегая трением: поскольку ускорение параллельно наклону, нам нужно учитывать только силы, параллельные наклону. Силы, перпендикулярные склону, складываются в ноль, так как в этом направлении нет ускорения. Силы, параллельные склону, представляют собой вес лыжника, параллельный склону w|| ш|| и трение f f. При отсутствии трения по второму закону Ньютона ускорение, параллельное склону, равно
a||=Fnet ||m,a||=Fnet ||m,
Где результирующая сила, параллельная склону Fnet ||=w||=mgsin(25°) Fnet ||=w|| =mgsin(25°), так что
a||=Fnet ||m=mg sin(25°)m=g sin(25°)=(9,80 м/с2)(0,423)=4,14 м/с2a| |=Fnet ||m=mg sin(25°)m=g sin(25°)=(9,80 м/с2)(0,423)=4,14 м/с2
— ускорение.
(b) Включая трение: Теперь у нас есть заданное значение трения, и мы знаем, что его направление параллельно склону и оно препятствует движению между контактирующими поверхностями. Таким образом, чистая внешняя сила теперь равна 9.0005
Fnet ||=w||−f,Fnet ||=w||–f,
и подставляя это во второй закон Ньютона, a||=Fnet ||m a||=Fnet ||m , дает
a||=Fnet ||m=w||−fm=mg sin(25°)−fm.a||=Fnet ||m=w||−fm=mg sin(25°)−fm.
Подставляем известные значения, чтобы получить
a||=(60,0 кг)(9,80 м/с2)(0,423)−45,0 N60,0 кг,a||=(60,0 кг)(9,80 м/с2)(0,423 )−45,0 N60,0 кг,
или
a||=3,39 м/с2, a||=3,39 м/с2,
, что представляет собой ускорение, параллельное наклону, при наличии противодействующего трения 45 Н.
Обсуждение
Поскольку трение всегда препятствует движению между поверхностями, ускорение при наличии трения меньше, чем при его отсутствии.
Практические задачи
Когда объект находится на наклонной плоскости, составляющей угол θ с горизонтом, как выражается составляющая силы веса объекта, параллельная наклону?
Тело массой 5 кг лежит на плоскости, наклоненной под углом 30∘ к горизонту. Какая составляющая силы веса параллельна наклону?
Какая составляющая силы веса параллельна наклону?
- 4,33 Н
- 5,0 Н
- 24,5Н
- 42.43С
Snap Lab
Трение под углом: скольжение монеты
Объект будет скользить по наклонной плоскости с постоянной скоростью, если результирующая сила, действующая на объект, равна нулю. Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано в первом рабочем примере, кинетическое трение на склоне fk=µkmg cosθ fk=µkmg cosθ, а составляющая веса вниз по склону равна mg sinθ mg sinθ. Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Написание этих
fk=Fgxμkmg cosθ=mg sinθ.fk=Fgxμkmg cosθ=mg sinθ.
Решая для µk µk, поскольку tanθ=sinθ/cosθ tanθ=sinθ/cosθ мы находим, что
Материалы:
- 1 монета
- 1 книга
- 1 транспортир
- Положите монету плоской стороной на книгу и наклоняйте ее, пока монета не будет скользить по книге с постоянной скоростью.
 Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться.
Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться. - Измерьте угол наклона относительно горизонтали и найдите µk µk.
- Положите монету плоской стороной на книгу и наклоняйте ее, пока монета не будет скользить по книге с постоянной скоростью.
Проверка захвата
Верно или неверно — если известны только углы двух векторов, мы можем найти угол их результирующего вектора сложения.
- Правда
- Ложь
Проверьте свое понимание
Упражнение 9
Что такое трение?
- Трение — это внутренняя сила, противодействующая относительному движению объекта.
- Трение — это внутренняя сила, которая ускоряет относительное движение объекта.
- Трение — это внешняя сила, противодействующая относительному движению объекта.
- Трение — это внешняя сила, увеличивающая скорость относительного движения объекта.

Упражнение 10
Какие существуют две разновидности трения? На что действует каждый?
- Кинетическое и статическое трение действуют на движущийся объект.
- Кинетическое трение действует на движущийся объект, а статическое трение действует на покоящийся объект.
- Кинетическое трение действует на неподвижный объект, а статическое трение действует на движущийся объект.
- Кинетическое и статическое трение действуют на покоящийся объект.
Упражнение 11
Какое значение между статическим и кинетическим трением между двумя поверхностями больше? Почему?
- Кинетическое трение имеет большее значение, потому что трение между двумя поверхностями больше, когда две поверхности находятся в относительном движении.



 По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.
По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.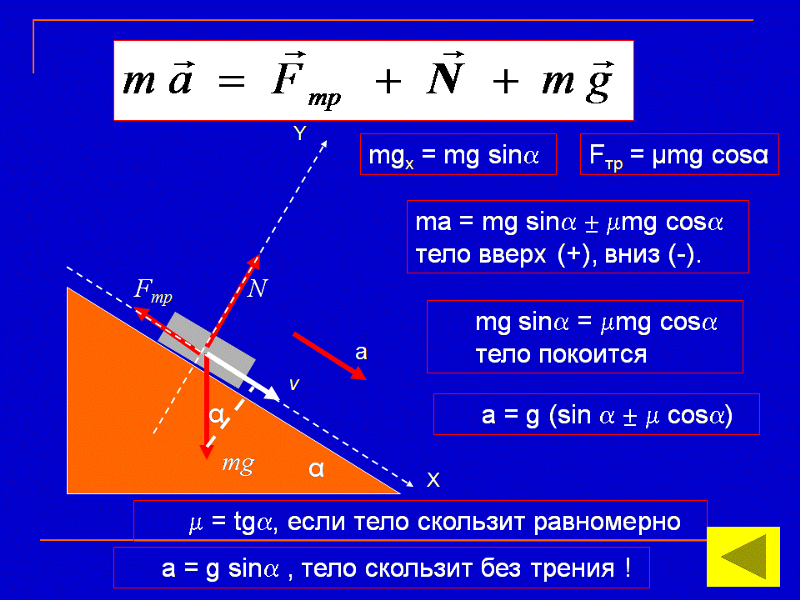
 Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться.
Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться.