Site Loader
Posted on 23.12.2020

Серия cs325 (CITIZEN Electronics Co.,Ltd. )

CITIZEN Electronics Co.,Ltd.

Общие характеристики

РазделКварцевые резонаторы
Стабильность при 25°C
Стабильность в рабочем температурном диапазоне
Монтаж
Нагрузочная ёмкость
Рабочая температура
Размер3.2×2.5×0.6 мм

Документация на серию cs325

  • найти cs325.pdf

    Товары серии cs325

    НаименованиеiУпаковкаЧастота
    CS325-12.000MABJ-UT (CIT)

     
    CS325-13.000MABJ-UT (CIT)

     
    CS325-13. 560MABJ-UT (CIT)

     
    CS325-14.31818MABJ-UT (CIT)

     
    CS325-16.000MABJ-UT (CIT)

     
    CS325-16.384MABJ-UT (CIT)

     
    CS325-18.432MABJ-UT (CIT)

     
    CS325-18.9375MABJ-UT (CIT)

     
    CS325-19.069928MABJ-UT (CIT)

     
    CS325-19.
    200MABJ-UT (CIT)

     
    CS325-20.500MABJ-UT (CIT)

     
    CS325-24.000MABJ-UT (CIT)

     
    CS325-24.500MABJ-UT (CIT)

     
    CS325-24.576MABJ-UT (CIT)

     
    CS325-24.975MABJ-UT (CIT)

     
    CS325-25.000MABJ-UT (CIT)

     
    CS325-26. 000MABJ-UT (CIT)

     
    CS325-26.650MABJ-UT (CIT)

     
    CS325-27.000MABJ-UT (CIT)

     
    CS325-27.120MABJ-UT (CIT)

     
    CS325-28.6363MABJ-UT (CIT)

     
    CS325-29.49120MABJ-UT (CIT)

     
    CS325-30.000MABJ-UT (CIT)

     
    CS325-32. 000MABJ-UT (CIT)

     
    CS325-33.000MABJ-UT (CIT)

     
    CS325-33.3333MABJ-UT (CIT)

     
    CS325-37.050MABJ-UT (CIT)

     
    CS325-40.000MABJ-UT (CIT)

     
    CS325-44.000MABJ-UT (CIT)

     
    CS325-48.000MABJ-UT (CIT)

     
    CS325-52. 000MABJ-UT (CIT)

     
    CS325-53.125MABJ-UT (CIT)

     

    КВАРЦЕВЫЕ РЕЗОНАТОРЫ ИМПОРТНОГО ПРОИЗВОДСТВА

    • Главная
    • База знаний
    • КВАРЦЕВЫЕ РЕЗОНАТОРЫ ИМПОРТНОГО ПРОИЗВОДСТВА

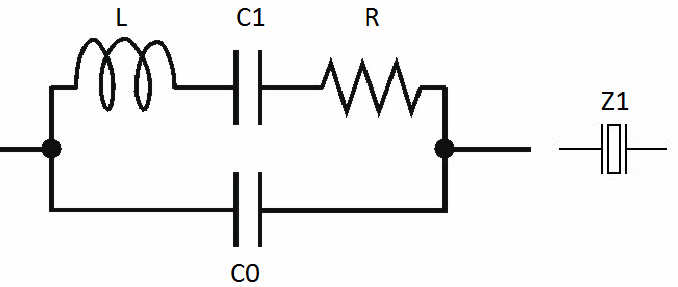
    Кварцевые резонаторы являются пассивными компонентами радиоэлектронной аппаратуры и предназначены для использования в аналогово-цифровых цепях для стабилизации и выделения электрических колебаний определенной частоты или полосы частот. Принцип работы этого элемента следующий — в широкой полосе частот сопротивление прибора имеет емкостной характер и только на некоторых (рабочих) частотах имеет резко выраженный резонанс (уменьшение сопротивления).

    Кварцевый резонатор имеет лучшие характеристики, чем другие приборы для стабилизации частоты (колебательные контуры, пьезокерамические резонаторы): такие как стабильность по частоте (уход частоты) и температуре (изменение частоты резонанса в зависимости от температуры окружающей среды).

    Избирательный, ярко выраженный резонансный характер сопротивления этих компонентов определяет основные области применения кварцевых резонаторов — высокостабильные генераторы тактовых сигналов и опорных частот, цепи частотной селекции, синтезаторы частоты и т.д

    Импортные кварцевые резонаторы

    В настоящее время доступны кварцевые резонаторы в корпусах типа:
    • HC-49/U — ближайший отечественный аналог — корпус МД
    • HC-49/US — отличие от HC-49/U — меньшая высота
    • Кварцевые резонаторы для схем отсчета времени на частоту 32,768 кГц
    Компоненты сертифицированы в соответсвии с международным стандартом ISO 9002

    Отличительные черты:

    • Низкая стоимость
    • Промышленный стандарт
    • Широкий частотный диапазон
    • Низкое изменение рабочей частоты с течением времени
    • Резонаторы AT
    		    

    Внешний вид корпусов типа HC-49

    Основные технические характеристики:

    Параметр Корпус Величина Условия генерации Габаритный чертеж
    Частотный диапазон HC-49/U 1,8 — 30 МГц Основная гармоника
    Корпуc L, мм
    HC-49/U 13,0±0,2
    HC-49/US 3,5
    25 — 75 МГц Третья гармоника
    75 — 100 МГц Пятая гармоника
    HC-49/US 3 — 33,5 МГц Основная гармоника
    26 — 75 МГц Третья гармоника
    Стабильность частоты HC-49/U ±30 x10-6 Tокр. среды=25°C
    HC-49/US
    Температурная стабильность частоты HC-49/U ±50 x10-6 -20…+70°C
    HC-49/US -10…+60°C
    Диапазон рабочих температур HC-49/U -20…+70°C  
    HC-49/US -10…+60°C
    Параллельная ёмкость HC-49/U не более 7 пФ
    HC-49/US
    Нагрузочная ёмкость HC-49/U 20 пФ (8. ..50 пФ)
    HC-49/US
    Старение HC-49/U 5×10-6 за год
    HC-49/US

    Технические параметры кварцевых резонаторов:

    • Тип резонатора АТ — специальный угол среза пластины кристалла кварца, при котором готовый резонатор обладает превосходной стабильностью частоты по температуре окружающей среды.
    • Последовательное эквивалентное сопротивление — импеданс резонатора, находящегося в последовательном резонансе.
    • Стабильность частоты — отклонение частоты от номинальной. Обычно выражается в миллионных долях от номинальной частоты резонатора — Nx10-6. Соответствующая иностранная маркировка — ppm (part per million — часть на миллион).
    • Температурная стабильность частоты — изменение частоты при изменении температуры резонатора.
    • Сопротивление изоляции — сопротивление между выводами резонатора (обычные значения порядка МОм)
    • Нагрузочная емкость — любая внешняя емкость, включенная последовательно с резонатором, становится элементом, изменяющим частоту резонанса. Варьируя нагрузочную емкость, можно, в некоторых пределах, изменять резонансную частоту. Некоторые изготовители иногда заранее рекомендуют использовать стандартные значения нагрузочной емкости для точной настройки резонансной частоты.
    • Диапазон рабочих температур — диапазон температур, в котором резонатор будет работать с отклонением частоты, не превышающим указанного для данного типа.
    • Гармоники — у резонаторов с типом среза АТ, которые сами по себе являются резонаторами толщинно — сдвиговых колебаний, в добавление к основной частоте резонанса возможно также проявление колебаний нечетных гармоник (3xFосн,5xFосн,7xFосн).
    • «Старение» — медленные изменения параметров резонатора по истечении некоторого периода времени.

     

    Номиналы стандартной сетки частот для импортных резонаторов, предлагаемые ЗАО «Промэлектроника»

    Для корпусов типа U

    Резонансная частота, МГц Рекомендуемая
    нагрузочная
    емкость, пФ    		 Rк, (Ом) Резонансная частота, МГц Рекомендуемая
    нагрузочная
    емкость, пФ    		 Rк, (Ом) Резонансная частота, МГц Рекомендуемая
    нагрузочная
    емкость, пФ    		 Rк, (Ом) Резонансная частота, МГц Рекомендуемая
    нагрузочная
    емкость, пФ    		 Rк, (Ом)
    1,8432 16; 30 600 5 16; 20 70 11 16 35 20,945   25
    2 0; 16; 20 450 5,12 16 70 11,0592 0 35 22 16 25
    2,048 16 450 6 16; 20 70 11,15 16 35 22,1184 0 25
    2,4576 0; 16 350 6,144 0; 16 70 11,165 16 35 24 0; 16; 32 25
    2,5 16 350 6,4 20 70 12 16 35 24,576 16 25
    3   150 6,5   70 13,4725 16 35 25 16; 20 25
    3,072 30 150 7 0; 16 50 13,5   35 26,48 16 25
    3,2 16 150 7,158   50 13,6 16 35 26,535   25
    3,2768 16 150 7,2 16 50 13,875 20 35 26,735 16 25
    3,579545 16 90 7,3728 0 50 14   35 26,945 16 25
    3,6 0 90 8 0 50 14,318 0 35 27** 16; 20 25/40
    3,6864 0 90 8,192 0 50 14,7456 16 35 27,2* 16 25
    3,9 16 90 8,867238 16 50 15   35 30 0; 16 40
    4 0 70 9   50 16 16 35 32   40
    4,032 0 70 9,216 16 50 16,384 0 35 32,768 16 40
    4,096 16 70 9,6 16, 30 50 16,588 16 35 33 16 40
    4,25 16 70 9,8304 16 50 16,667 16 35 36,5 16 40
    4,433619 16; 18; 20 70 10 0; 16; 32 35 16,67 0 35 37,768 16 40
    4,5   70 10,235 16 35 18 16 35 40 16 40
    4,608 0; 16 70 10,24 16; 20 35 18,432 0; 16; 32 35 50 16 40
    4,756 16 70 10,245 20 35 19,6608 0 35 70 16 40
    4,8   70 10,5 16 35 20 0; 32 25 100***   60
    4,9152 0 70 10,7 16 35 20,48   25      

    * работают на третьей гармонике.
    ** работают на первой и третьей гармонике.
    *** работают на пятой гармонике.
    Rк — эквивалентное последовательное сопротивление

    Для корпусов типа US


    Резонансная частота, МГц Рекомендуемая
    нагрузочная
    емкость, пФ    		 Rк, (Ом) Резонансная частота, МГц Рекомендуемая
    нагрузочная
    емкость, пФ    		 Rк, (Ом) Резонансная частота, МГц Рекомендуемая
    нагрузочная
    емкость, пФ    		 Rк, (Ом) Резонансная частота, МГц Рекомендуемая
    нагрузочная
    емкость, пФ    		 Rк, (Ом)
    1     9,216 16 50  15,36 20  40 29,4912    50
    3,6864 16, 30  150 12,288 0, 20  40 16,67 0  40 30* 0, 16  100
    5,5   80  12,8 16  40 16,9344 16, 20  40 32*    80
    7,5 16  70 13,56 0, 20  40 17,7344 20  40      

    *работают на третьей гармонике.
    Rк — эквивалентное последовательное сопротивление

    Кварцевые резонаторы для схем отсчета времени на частоту 32,768 кГц поставляются в следующих корпусах:

    • MMTF-32 — цилиндрический, для монтажа в отверстия
    • MTF-38 — цилиндрический, для монтажа в отверстия
    • DT38T — цилиндрический, для монтажа в отверстия
    • MG3A — малогабаритный для поверхностного монтажа
    Корпус типа DT-26
    (MMTF-32)    		 Корпус типа MTF38 Корпус типа DT-38(DT38T) Корпус типа MG3A
    Габаритный чертеж корпусов типа MMTF-32, MTF38, DT38T Габаритный чертеж корпуса типа MG3A
    Тип корпуса Размеры, мм
    D L L1 A
    MMTF32 2. 0±0.2 6.0±0.2 7.5±0.1 0.7±0.2
    MTF38 3,0 max 8.9 max 8.0 min 1.1
    DT38T 3.0 6.2 10 1.1
    		  

    • Наименование

      К продаже

      Цена от

    К продаже:

    7 764 шт.

    Цена от:

    9,74₽

    Резонатор: наука о резонансе, механике, волнах и звуке

    В этом упражнении деревянные штифты разной длины, каждый из которых нагружен одинаковой массой, вибрируют с одинаковой частотой. Когда вибрация соответствует резонансной частоте одного из дюбелей, этот дюбель вибрирует с большой амплитудой.

    Предмет: 

    Науки о Земле

    Геология

    Инженерия и технологии

    Реальные проблемы и решения

    Physics

    Mechanics

    Waves

    Keywords: 

    resonance

    earthquakes

    model

    frequency

    exhibit-based

    NGSS and EP&Cs: 

    ESS

    ESS3

    PS

    PS2

    PS4

    ETS

    ETS1

    CCC

    Закономерности

    Причина и следствие

    Масштаб, доля и количество

    Структура и функция


    Демонстрация видео

    Инструменты и материалы

    • Дрель и сверла 1/4 дюйма и 3/8 дюйма (для метрических размеров замените сверла 6 и 10 мм)
    • Два фута (60 сантиметров) длина дерева два на четыре (в метрических единицах два на четыре составляет 5 x 10 сантиметров)
    • Три деревянных дюбеля диаметром 1/4 дюйма (6 миллиметров) длиной 1 1/2 фута (45 см), длиной 2 фута (60 см) и длиной 2 1/2 фута (75 см).
    • Двухфутовый (60 см) дюбель диаметром 3/8 дюйма (10 мм)
    • Молоток
    • Четыре твердых резиновых мяча диаметром не менее 1 дюйма (2,5 см).
    • Дополнительно: столярный клей и тиски (рекомендуется)

    Сборка

    1. Начиная с трех дюймов (7,5 см) от одного конца, просверлите четыре отверстия на расстоянии примерно 6 дюймов (15 см) друг от друга вдоль центральной линии широкой стороны 2 на 4 (в точках 3, 9).-, 15- и 21-дюймовые марки). Первые три отверстия должны быть 1/4 дюйма (6 мм), а четвертое отверстие должно быть 3/8 дюйма (или 10 мм).
    2. Вставьте дюбели в соответствующие отверстия. Будем надеяться, что дюбели войдут в отверстия и будут надежно удерживаться на месте, но иногда размеры дюбелей неточны. Если посадка слишком тугая, попробуйте осторожно вбить дюбель молотком; если посадка настолько свободна, что дюбель шатается, попробуйте подправить его деревянными зубочистками. Если у вас все еще возникают проблемы, вы можете попробовать такие вещи, как шлифование дюбеля по размеру, повторное сверление отверстия сверлом немного другого размера или вклеивание дюбеля в отверстие.
    3. Просверлите отверстие диаметром 1/4 дюйма (6 мм) в середине трех резиновых шариков и отверстие диаметром 3/8 дюйма (или 10 мм) в середине четвертого шарика. Лучший способ сделать это — поместить шарики в хорошие тиски и медленно просверлить.
    4. Поместите резиновый шарик на конец каждого дюбеля. Это добавляет относительно большую массу к каждому дюбелю. (Обратите внимание, что это будет работать, даже если вы не кладете резиновые шарики на штифты, но шарики снижают резонансные частоты и облегчают просмотр движения. Вы можете заменить куски глины примерно одинакового размера или теннисные мячи, хотя теннисные шарики полые, поэтому они имеют тенденцию шлепаться на концах штифтов.)

    Действия и уведомления

    Возьмите два на четыре за каждый конец и двигайте его вдоль стола вперед и назад. Когда вы меняете скорость встряхивания, разные штифты будут раскачиваться вперед и назад с большей или меньшей амплитудой. Когда вы встряхиваете с нужной частотой, чтобы вызвать сильную вибрацию одного штифта, другой штифт может почти не вибрировать.

    Обратите внимание, какие дюбели сильно вибрируют на более низких частотах, а какие сильно вибрируют на более высоких частотах.

    Что происходит?

    Когда вы толкаете кого-то на качелях, серия небольших толчков заставляет качели двигаться с большой амплитудой. Для этого вы рассчитываете свои толчки так, чтобы они соответствовали естественной частоте качания, скорости, с которой качание имеет тенденцию двигаться вперед и назад.

    Здесь работает тот же принцип. Когда вы встряхиваете сборку два на четыре с нужной частотой, серия небольших встряхиваний в сумме приводит к сильной вибрации определенного штифта. Встряхивающая балка заставляет дюбель вибрировать. Если следующее встряхивание рассчитано как раз для того, чтобы усилить следующую вибрацию дюбеля, вибрация дюбеля нарастает. Этот процесс использования серии небольших входных сигналов для создания большого движения известен как 9.0119 резонанс .

    Чем длиннее дюбель, тем медленнее он вибрирует и тем ниже его собственная частота. Таким образом, длинный штифт будет резонировать на более низких частотах, чем короткий.

    Более жесткие дюбели имеют более высокие резонансные частоты. Штифт размером 3/8 дюйма (9,5 мм) намного жестче, чем штифт размером 1/4 дюйма (6 мм), поэтому он имеет тенденцию резонировать на более высоких частотах, чем более тонкие штифты. Обратите также внимание, что каждый штифт может иметь более одной резонансной частоты.

    Не все объекты резонируют. Любой объект, который рассеивает энергию быстрее, чем добавляется, не будет резонировать. Попробуйте, например, потрясти дюбели под водой. Трение дюбеля, движущегося по воде, рассеивает энергию быстрее, чем вы ее добавляете. Поскольку движение штифта не будет нарастать на какой-либо частоте, резонанса не будет.

    Дальше

    Точно так же, как у каждого дюбеля есть свои собственные частоты вибрации, при которых возникает резонанс, так и большинство объектов имеют тенденцию вибрировать на определенных частотах. Возможно, вы замечали, что части вашего автомобиля гремят на определенной скорости или что определенные объекты вибрируют и жужжат в ответ на определенную ноту из вашей стереосистемы. Это повседневные примеры резонанса.

    Резонанс также был ответственен за впечатляющие разрушения. При землетрясениях здания часто повреждаются, когда частота сотрясения земли очень близка или совпадает с одной из резонансных частот зданий. В 1940 году мост Такома-Нарроуз недалеко от города Такома, штат Вашингтон, разлетелся на куски, когда сильный ветер толкнул его с нужной частотой. В 1960-х годах крыло реактивного самолета Lockheed Electra неоднократно выходило из строя, пока инженеры не обнаружили, что причиной его разрушения была его резонансная частота. В 1981, подвесная дорожка в отеле Канзас-Сити рухнула, когда люди, танцующие на конструкции, вызвали резонансную вибрацию.

    В армии войска всегда маршируют по мосту не в ногу; армейские автомобили проезжают через неравные промежутки времени. Эти методы позволяют избежать вибрации на резонансной частоте моста.


    Похожие закуски

    Резонансные кольца

    Продемонстрируйте, как разные предметы вибрируют на разных частотах.

    Спагетти-резонанс

    Продемонстрируйте резонанс, встряхивая сушеные спагетти.

    Шаткие отложения

    Смоделируйте отказ заземления в явлении, называемом разжижением.



    Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

    Атрибуция: Педагогический институт Exploratorium

    Звук | Свойства, типы и факты

    графическое изображение звуковой волны

    Герман фон Гельмгольц Эрик Цеплер
    Похожие темы:
    прием звука музыкальный звук ультразвук инфразвук громкость

    Просмотреть весь связанный контент →

    Резюме

    Прочтите краткий обзор этой темы

    звук , механическое нарушение состояния равновесия, которое распространяется через упругую материальную среду. Возможно и чисто субъективное определение звука, как воспринимаемого ухом, но такое определение не особенно просветляет и излишне ограничивает, ибо полезно говорить о звуках, не слышимых человеческим ухом, таких как как те, которые производятся собачьими свистками или гидролокационным оборудованием.

    Изучение звука следует начинать со свойств звуковых волн. Есть два основных типа волн, поперечные и продольные, различающиеся по способу распространения волны. В поперечной волне, такой как волна, генерируемая натянутой веревкой, когда один конец качается вперед и назад, движение, составляющее волну, перпендикулярно или поперечно направлению (вдоль веревки), в котором движется волна. Важное семейство поперечных волн генерируется электромагнитными источниками, такими как свет или радио, в которых электрические и магнитные поля, составляющие волну, колеблются перпендикулярно направлению распространения.

    Посмотрите на подвешенную вибрирующую пружину, чтобы узнать о распространении звуковых волн.

    Посмотрите все видео к этой статье. волна. Продольную волну можно создать в спиральной пружине, сжав несколько витков вместе, чтобы сформировать сжатие, а затем расслабив их, позволяя сжатию пройти по всей длине пружины. Воздух можно рассматривать как состоящий из слоев, аналогичных таким катушкам, со звуковой волной, распространяющейся по мере того, как слои воздуха «толкают» и «тянут» друг друга, подобно сжатию, движущемуся вниз по пружине.

    Таким образом, звуковая волна состоит из чередующихся сжатий и разрежений или областей высокого и низкого давления, движущихся с определенной скоростью. Иными словами, оно состоит из периодического (то есть колебательного или вибрационного) изменения давления, происходящего вокруг равновесного давления, преобладающего в определенное время и в определенном месте. Равновесное давление и синусоидальные изменения, вызванные прохождением чистой звуковой волны (то есть волны одной частоты), представлены на рис. 1А и 1В соответственно.

    Викторина «Британника»

    Физика и естественное право

    Обсуждение звуковых волн и их распространения можно начать с рассмотрения плоской волны одной частоты, проходящей через воздух. Плоская волна — это волна, которая распространяется в пространстве как плоскость, а не как сфера с увеличивающимся радиусом. Таким образом, он не совсем точно отражает звук (см. Ниже Круговые и сферические волны). Волна одной частоты будет слышна как чистый звук, подобный звуку, создаваемому легким ударом камертона. Как теоретическая модель, она помогает объяснить многие свойства звуковой волны.

    Рисунок 1C – другое представление звуковой волны, показанной на рисунке 1B. Как показано синусоидальной кривой, изменение давления в звуковой волне повторяется в пространстве на определенном расстоянии. Это расстояние известно как длина волны звука, обычно измеряемая в метрах и обозначаемая λ. Когда волна распространяется по воздуху, одной полной длине волны требуется определенный период времени, чтобы пройти определенную точку в пространстве; этот период, представленный T , обычно измеряется в долях секунды. Кроме того, в течение каждого интервала времени в одну секунду через точку в пространстве проходит определенное количество длин волн. Известное как частота звуковой волны, количество длин волн, проходящих в секунду, традиционно измеряется в герцах или килогерцах и обозначается 9.0119 ф .

    Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас

    Знать о волнах и математической зависимости между частотой и периодом волн

    Посмотреть все видео к этой статье

    Существует обратная зависимость между частотой волны и ее периодом, такая, что

    Распознать разницу между частотой и амплитудой с помощью изучение звуковых волн

    Посмотреть все видео к этой статье

    Это означает, что звуковые волны с высокими частотами имеют короткие периоды, а низкочастотные — с длинными. Например, звуковая волна с частотой 20 герц будет иметь период 0,05 секунды (, то есть 20 длин волн в секунду × 0,05 секунды/длина волны = 1), в то время как звуковая волна в 20 кГц будет иметь период 0,00005 секунды (20 000 длин волн в секунду × 0,00005 секунды/длина волны = 1). Между 20 герцами и 20 килогерцами находится частотный диапазон слуха человека. Физическое свойство частоты физиологически воспринимается как высота тона, так что чем выше частота, тем выше воспринимаемая высота тона. Существует также связь между длиной волны звуковой волны, ее частотой или периодом и скоростью волны ( S ), так что

    Математические значения

    Равновесное значение давления, представленное равномерно расположенными линиями на рис. 1А и осью графика на рис. 1С, равно атмосферному давлению, которое преобладало бы в отсутствие звуковой волны. При прохождении сжатий и разрежений, составляющих звуковую волну, возникнут колебания выше и ниже атмосферного давления. Величина этого отклонения от равновесия известна как амплитуда звуковой волны; измеряется в паскалях или ньютонах на квадратный метр, обозначается буквой 9.0119 А . Смещение или возмущение плоской звуковой волны можно математически описать общим уравнением движения волны, которое в упрощенном виде записывается так:

    Это уравнение описывает синусоидальную волну, которая повторяется после перемещения вправо на расстояние λ x ) со скоростью, определяемой уравнением (2).

    Амплитуда звуковой волны определяет ее интенсивность, которая в свою очередь воспринимается ухом как громкость. Интенсивность звука определяется как средняя скорость передачи энергии на единицу площади, перпендикулярную направлению распространения волны. Его связь с амплитудой можно записать как где ρ — равновесная плотность воздуха (измеряется в килограммах на кубический метр), а S — скорость звука (в метрах в секунду). Интенсивность ( I ) измеряется в ваттах на квадратный метр, причем ватт является стандартной единицей мощности в электрическом или механическом использовании.

    Значение атмосферного давления при «стандартных атмосферных условиях» обычно составляет примерно 10 5 паскалей или 10 5 ньютонов на квадратный метр. Минимальная амплитуда изменения давления, воспринимаемая человеческим ухом, составляет около 10 -5 паскалей, а амплитуда давления на пороге боли составляет около 10 паскалей, поэтому изменение давления в звуковых волнах очень мало по сравнению с давлением атмосферы. В этих условиях звуковая волна распространяется линейно, то есть продолжает распространяться в воздухе с очень небольшими потерями, рассеиванием или изменением формы. Однако, когда амплитуда волны достигает примерно 100 паскалей (примерно одна тысячная атмосферного давления), в распространении волны возникают значительные нелинейности.

    Нелинейность возникает из-за особого воздействия на давление воздуха, вызванного синусоидальным смещением молекул воздуха. Когда колебательное движение, образующее волну, мало, увеличение и уменьшение давления также малы и почти равны. Но когда движение волны велико, каждое сжатие создает избыточное давление большей амплитуды, чем уменьшение давления, вызванное каждым разрежением. Это можно предсказать с помощью закона идеального газа, который гласит, что увеличение объема газа наполовину снижает его давление только на одну треть, а уменьшение его объема наполовину увеличивает давление в два раза. Результатом является чистый избыток давления — явление, значимое только для волн с амплитудой выше примерно 100 паскалей.

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *