Частота колебаний в контуре: Найдите период и частоту колебаний в колебательном контуре , содержащем катушку индуктивностью 70 Гн и… — RC74 — интернет-магазин радиоуправляемых моделей

2={1\over LC}$$

Рис. 2. График электрических колебаний в контуре.

Содержание

Формула Томсона

Из последнего соотношения можно получить значение периода электромагнитных колебаний:

$$T={2\pi\over \omega}={2\pi\sqrt{LC}}$$

Данная формула впервые была получена У. Томсоном и носит его имя.

Рис. 3. У. Томсон (Кельвин).

Из данной формулы можно видеть, что время одного колебания (период) тем дольше, тем больше индуктивность и емкость. Это происходит потому, что большая емкость требует больше времени для полной зарядки. А большая индуктивность при изменении тока порождает большую ЭДС самоиндукции, которая, согласно правилу Ленца, направлена так, чтобы сопротивляться причине, ее порождающей. Таким образом, ток через большую индуктивность меняется медленнее, что также увеличивает период колебаний.

Во многих случаях удобнее использовать формулу частоты электромагнитных колебаний, которая получается из формулы Томсона, если учесть, что период и частота – взаимно обратны:

$$\nu ={1\over 2\pi\sqrt{LC}}$$

Что мы узнали?

Простейшей системой, в которой возможны электромагнитные колебания, является колебательный контур, состоящий из катушки индуктивности и конденсатора. Частота электромагнитных колебаний в контуре может быть получена из значений емкости конденсатора и индуктивности катушки с использованием формулы Томсона.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.4

Средняя оценка: 4.4

Всего получено оценок: 107.

А какая ваша оценка?

Военно-техническая подготовка

1.4. Колебательный контур.

1.4.1. Свободные колебания в контуре.

Свободные (или собственные) колебания — это колебания в системе под действием внутренних сил после того, как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие).

Пусть конденсатор ёмкостью C заряжен до напряжения U0 . Энергия, запасённая в конденсаторе составляет

При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток I , что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.

Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора

EC = 0. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна

где L — индуктивность катушки, I0 — максимальное значение тока.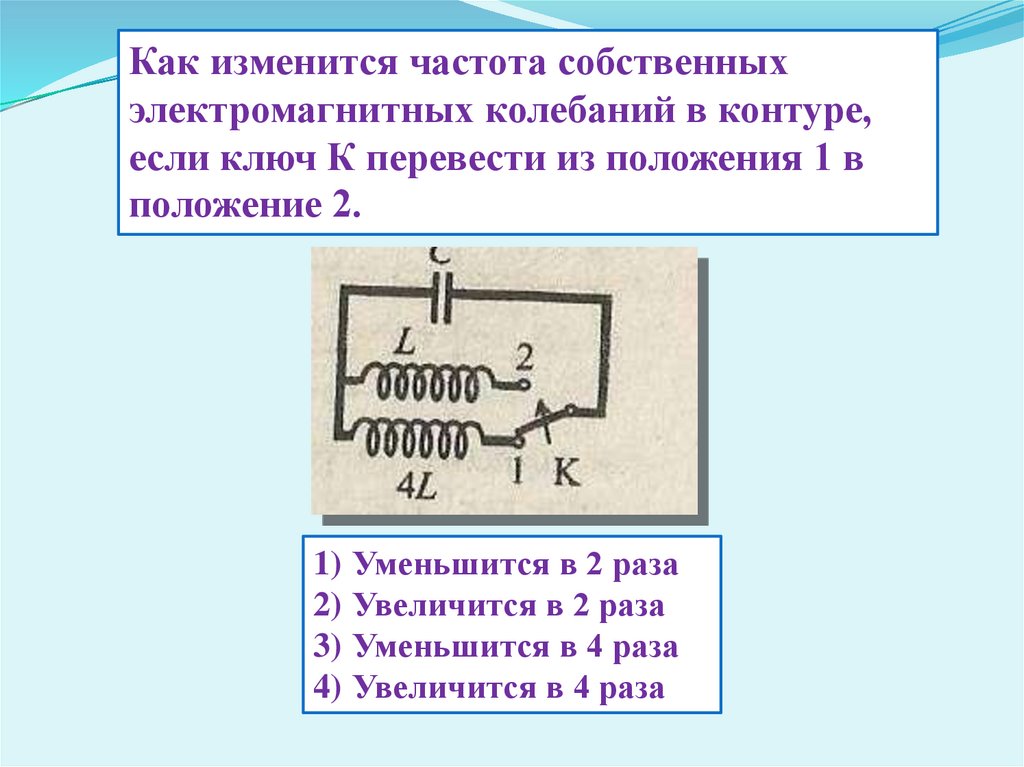

После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения —

U0 .

В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.

Рис 1. Пример: Осциллограмма LC контура во время замыкания заряженного конденсатора на катушку индуктивности.
С = 240нФ(заряженный), L = 360нГн, F0 ≈ 542кГц.

1.4.2. Вынужденные колебания в контуре.

Вынужденные колебания

— колебания, происходящие под воздействием внешних периодических сил.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:

Консервативный гармонический осциллятор

Второй закон Ньютона для такого осциллятора запишется в виде:

Если ввести обозначения:

и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:

Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного.

Общее решение однородного уравнения было уже получено здесь и оно имеет вид:

где A , φ — произвольные постоянные, которые определяются из начальных условий.

Найдём частное решение. Для этого подставим в уравнение решение вида:

и получим значение для константы:

Тогда окончательное решение запишется в виде:

1.4.3. Резонанс в колебательном контуре.

Резонанс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты собственных колебаний с частотой колебаний вынуждающей силы.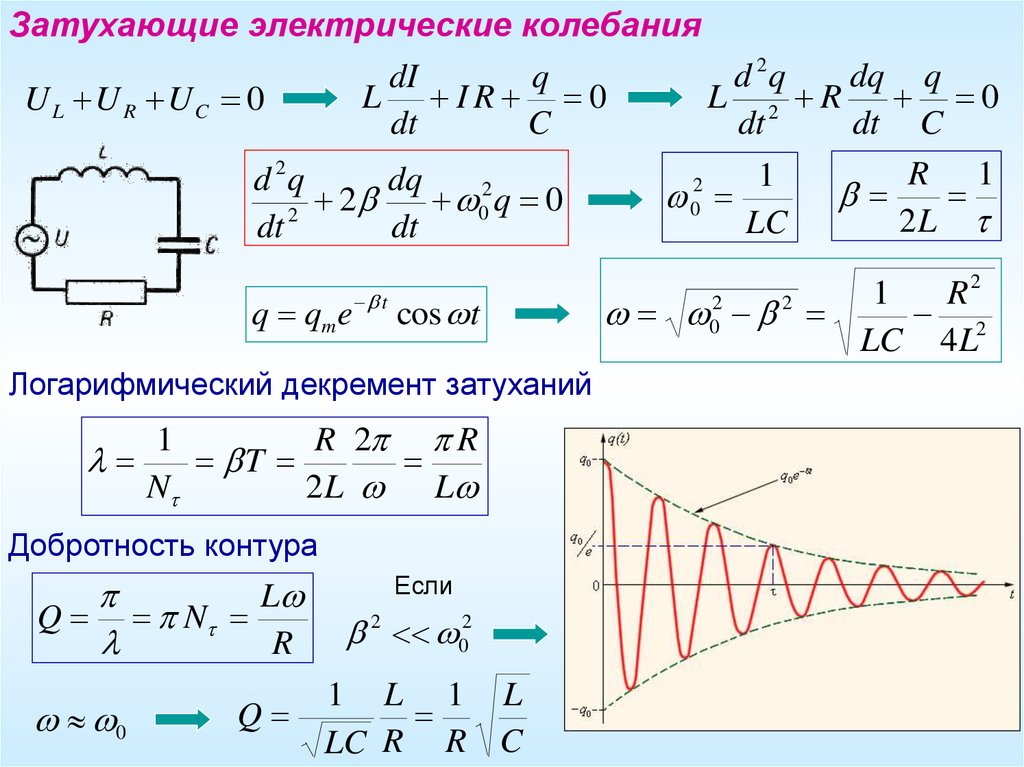

В результате резонанса при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

При достижении резонанса, импеданс (комплексное сопротивление двухполюсника (электрической цепи, содержащей две точки для соединения с другими цепями) для гармонического сигнала) последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

где ω = 2πf ;

f — резонансная частота в герцах;

L — индуктивность в генри;

C — ёмкость в фарадах.

Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы (параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.).

Рис 2. Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания.

1.4.4. Связанные цепи.

Если изменение тока в одном из элементов цепи приводит к появлению э.д.с. в другом элементе, то эти два элемента индуктивно связаны, а возникающая э.д.с. называется э.д.с. взаимной индукции.

Степень индуктивной связи двух элементов цепи характеризуется коэффициентом связи

где М – взаимная индуктивность элементов цепи,

L 1 и L 2 – индуктивности элементов.

При расчете цепей с взаимной индуктивностью следует на схеме отметить стрелками выбираемые положительные направления токов в ветвях (или контурных токов). Кроме того, одинаковыми условными значками (звездочками, точками, буквами и т.п.) обозначить одноименные зажимы каждой пары индуктивно связанных катушек.

Одноименными называются такие зажимы, при одинаковом положительном направлении токов относительно которых, магнитные потоки самоиндукции и взаимной индукции складываются.

1.4.5. Кварцевый резонатор.

Кварцевый резонатор — прибор, в котором пьезоэлектрический эффект и явление механического резонанса используются для построения высокодобротного резонансного элемента электронной схемы.

На пластинку, кольцо или брусок, вырезанные из кристалла кварца определённым образом, нанесены 2 и более электродов — проводящие полоски.

Пластинка закреплена и имеет собственную резонансную частоту механических колебаний.

При подаче напряжения на электроды благодаря пьезоэлектрическому эффекту происходит изгибание, сжатие или сдвиг в зависимости от того, каким образом вырезан кусок кристалла.

Однако колеблющаяся пластинка в результате того же пьезоэлектрического эффекта создаёт во внешней цепи противо-ЭДС, что можно рассматривать как явление, эквивалентное работе катушки индуктивности в колебательном контуре.

Если частота подаваемого напряжения равна или близка к частоте собственных механических колебаний пластинки, затраты энергии на поддержание колебаний пластинки оказываются намного ниже, нежели при большом отличии частоты. Это тоже соответствует поведению колебательного контура.

Рис 3. Эквивалентная схема.

Условное обозначение кварцевого резонатора (сверху) и его эквивалентная схема (снизу)

C0 — собственная ёмкость кристалла, образуемая кристаллодержателем и/или обкладками резонатора.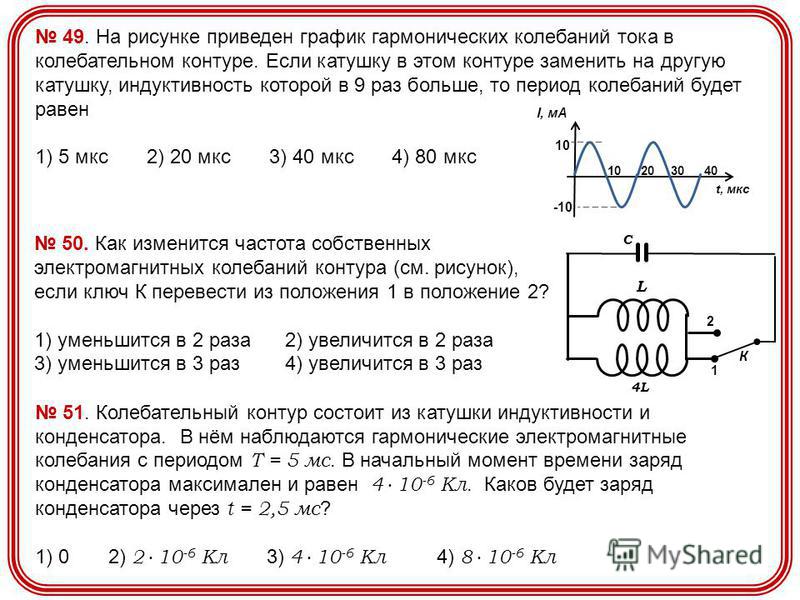

C1, L1 — эквивалентная ёмкость и индуктивность механической колебательной системы резонатора.

R1 — эквивалентное сопротивление потерь механической колебательной системы.

16.2 Период и частота колебаний – College Physics: OpenStax

Глава 16 Колебательное движение и волны

Резюме

Наблюдайте за колебаниями гитарной струны.
Определить частоту колебаний.

Рисунок 1. Струны этой гитары вибрируют через равные промежутки времени. (Фото: JAR)

Когда вы дергаете гитарную струну, в результате получается устойчивый звук, который длится долго. Каждое последующее колебание струны занимает такое же время, как и предыдущее. Мы определяем периодическое движение — движение, которое повторяется через равные промежутки времени, например гитарная струна или объект на пружине, движущийся вверх и вниз. Время совершения одного колебания остается постоянным и называется периодом [латекс]\boldsymbol{T}.[/latex]Его единицей обычно являются секунды, но может быть и любая удобная единица времени. Слово «период» относится ко времени какого-либо события, повторяющегося или нет; но нас прежде всего будет интересовать периодическое движение, которое по определению является повторяющимся. Понятие, тесно связанное с периодом, — это частота события. Например, если вы получаете зарплату два раза в месяц, частота выплат — две в месяц, а период между проверками — полмесяца. Частота [латекс]\boldsymbol{f}[/латекс] определяется как количество событий в единицу времени. Для периодического движения частота – это число колебаний в единицу времени. Соотношение между частотой и периодом составляет

[латекс]\boldsymbol{f\:=}[/латекс][латекс]\boldsymbol{\frac{1}{T}}[/латекс]

Единицей частоты в системе СИ является циклов в секунду , которая определяется как герц (Гц):

[латекс]\boldsymbol{1\textbf{Гц}=1}[/латекс][латекс]\boldsymbol{\frac{\textbf{цикл}}{\textbf{сек}}}[/латекс][латекс] \boldsymbol{\textbf{или}1\textbf{Гц}=}[/latex][латекс]\boldsymbol{\frac{1}{\textbf{s}}}[/latex]

Цикл – это одно полное колебание. Обратите внимание, что вибрация может быть одиночным или множественным событием, тогда как колебания обычно повторяются в течение значительного числа циклов.

Пример 1. Определение частоты двух колебаний: медицинский ультразвук и средний период C

Мы можем использовать формулы, представленные в этом модуле, для определения как частоты на основе известных колебаний, так и колебаний на основе известной частоты. Давайте попробуем по одному примеру каждого. (a) Медицинское устройство визуализации производит ультразвук путем колебаний с периодом 0,400 мкс. Какова частота этих колебаний? (b) Частота среднего C на типичном музыкальном инструменте составляет 264 Гц. За какое время совершается одно полное колебание?

Стратегия

На оба вопроса (a) и (b) можно ответить, используя соотношение между периодом и частотой. В вопросе (a) задан период[latex]\boldsymbol{T}[/latex], и нас просят найти частоту[latex]\boldsymbol{f}.[/latex]В вопросе (b) частота [latex]\boldsymbol{f}[/latex]дан и нас просят найти период[latex]\boldsymbol{T}. [/latex]

Решение a

Замена[latex]\boldsymbol {0.400\:\mu\textbf{s}}[/latex]для[латекса]\boldsymbol{T}[/latex]в[латексе]\boldsymbol{f=\frac{1}{T}}:[/ латекс] 96\textbf{Гц}}.[/латекс]

Обсуждение a

Частота звука, найденная в (а), намного выше, чем самая высокая частота, которую может слышать человек, и поэтому называется ультразвуком. Соответствующие колебания на этой частоте генерируют ультразвук, используемый для неинвазивной медицинской диагностики, например, для наблюдения за плодом в утробе матери.

Решение b

Определите известные значения:
Время одного полного колебания равно периоду[latex]\boldsymbol{T}:[/latex]
[латекс]\boldsymbol{f=}[/латекс][латекс]\boldsymbol{\frac{1}{T}}.[/латекс]
Решите для[латекс]\жирныйсимвол{Т}:[/латекс]
[латекс]\boldsymbol{T\:=}[/латекс][латекс]\boldsymbol{\frac{1}{f}}.[/латекс]
Подставить заданное значение частоты в полученное выражение:
[латекс]\boldsymbol{T\:=}[/латекс][латекс]\boldsymbol{\frac{1}{f}}[/латекс][латекс]\boldsymbol{=}[/латекс][латекс] \boldsymbol{\frac{1}{264\textbf{Гц}}}[/latex][латекс]\boldsymbol{=}[/latex][латекс]\boldsymbol{\frac{1}{264\textbf{циклы /s}}}[/латекс][латекс]\boldsymbol{=3,79{-3}\textbf{s}=3,79\textbf{мс}}. [/latex]

Обсуждение

Период, найденный в (b), представляет собой время за цикл, но это значение часто указывается просто как время в удобных единицах (в данном случае мс или миллисекунды).

период: время, необходимое для совершения одного колебания

периодическое движение: движение, повторяющееся через равные промежутки времени

частота: количество событий в единицу времени

Напишите выражение для частоты колебаний LC-контура.

КУМАР ПРАКАШАН-ПЕРЕМЕННОГО ТОКА-СЕКЦИЯ-D MCQs (КОНКУРСНЫЕ ЭКЗАМЕНЫ)

21 видео

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео ке ки киси ават!

Войти, если уже куплено0005

30559407